Received Probability of Vortex Modes Carried by Localized Wave of Bessel–Gaussian Amplitude Envelope in Turbulent Seawater
Abstract
:1. Introduction
2. Theoretical Model
2.1. Seawater Turbulence and Localized Wave of Bessel–Gaussian Amplitude Envelope
2.2. Spectrum Average Mutual Coherence Function of Localized Wave of Bessel–Gaussian Amplitude Envelope
2.2.1. Spectrum Average Coherence Length of Spherical Wave
2.2.2. Spectrum Average Mutual Coherence Function
2.3. Received Probability of Signal Vortex Modes
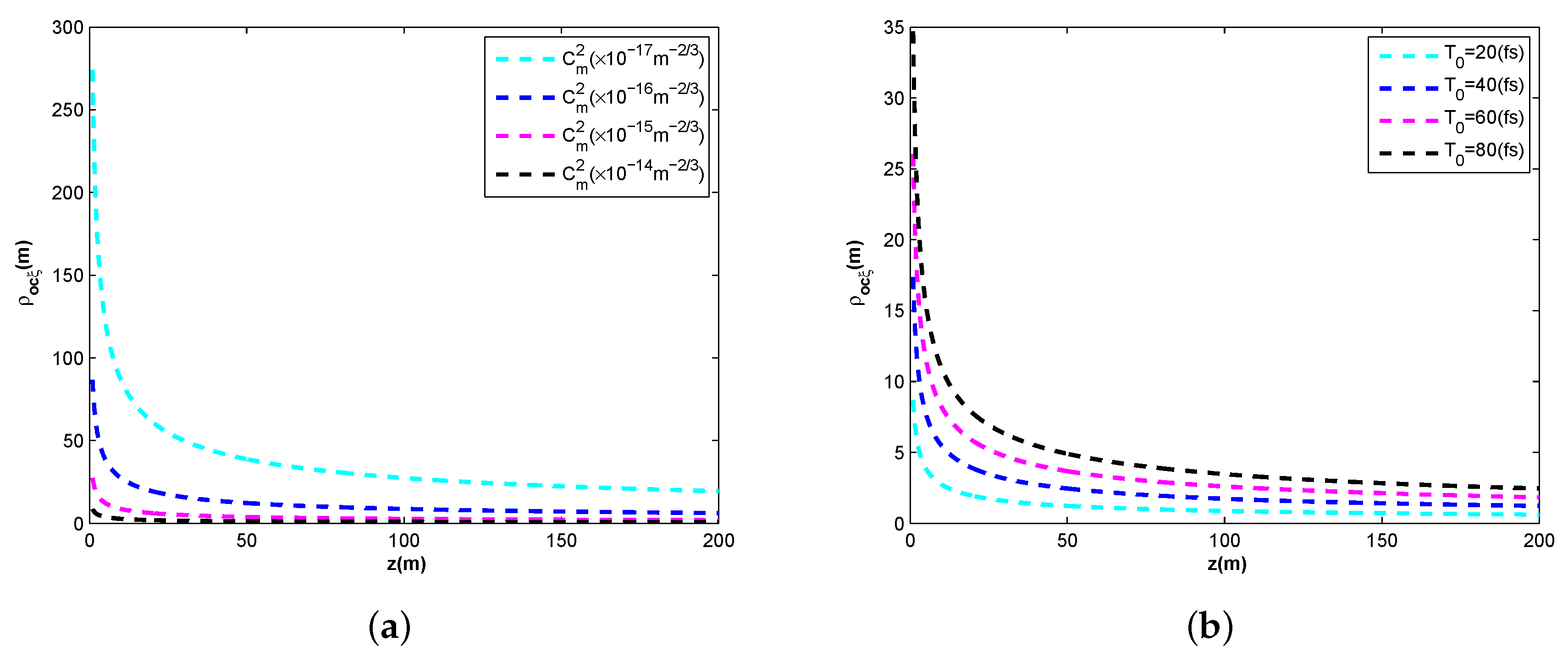
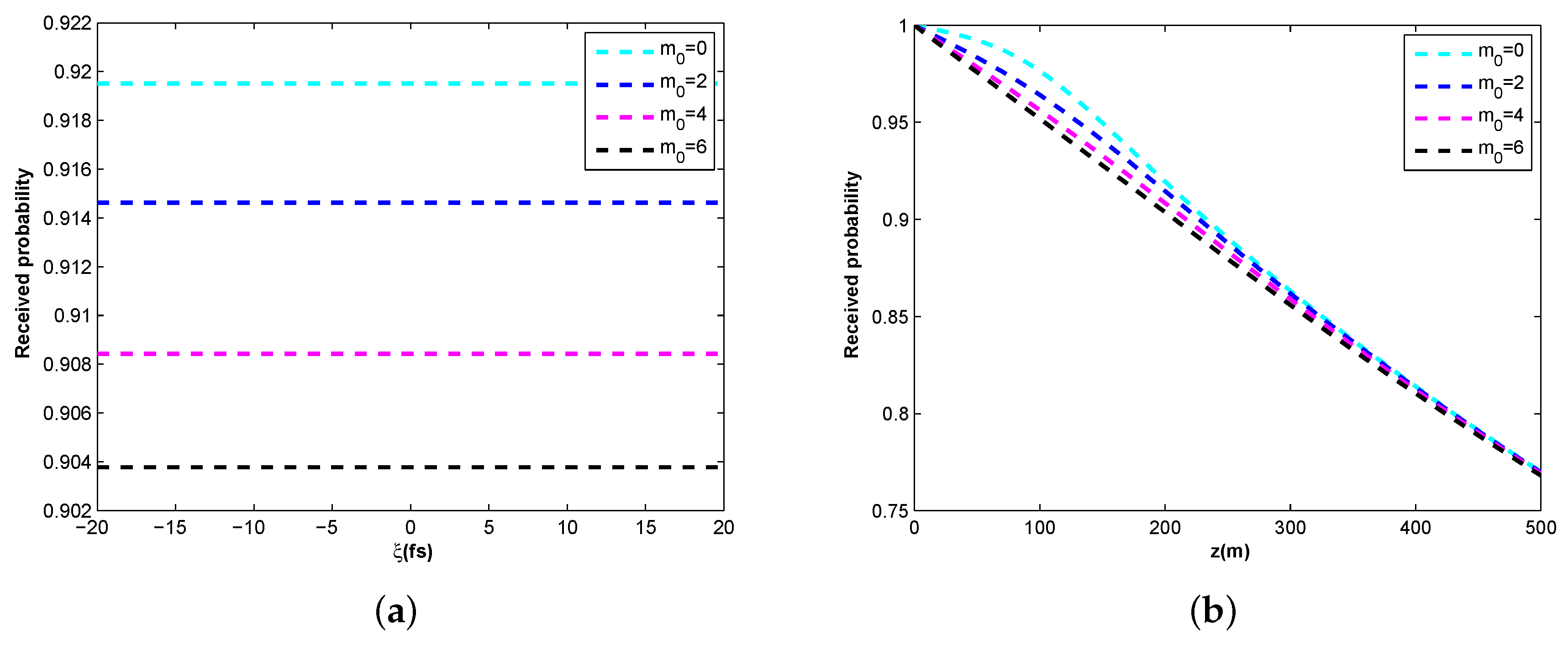
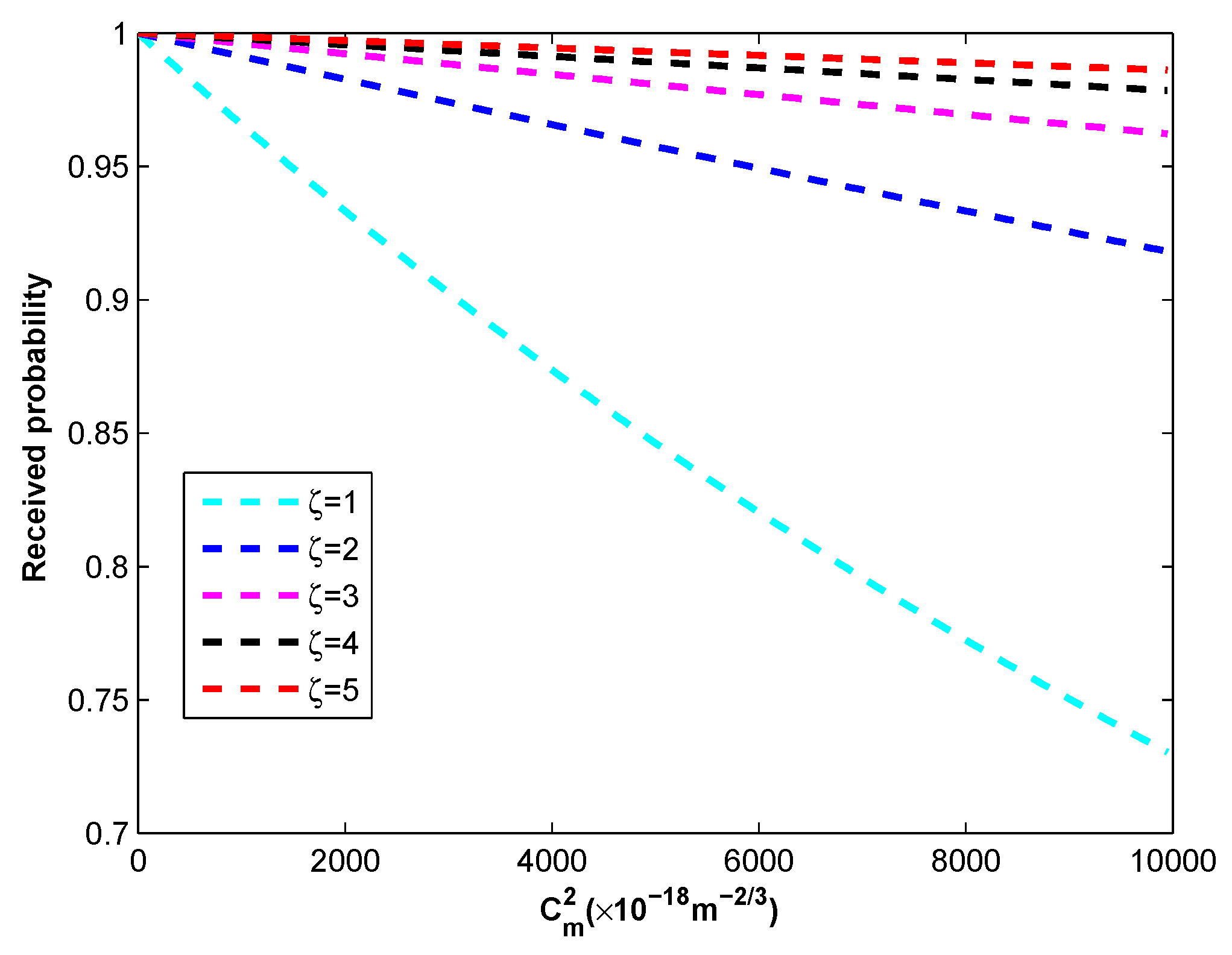
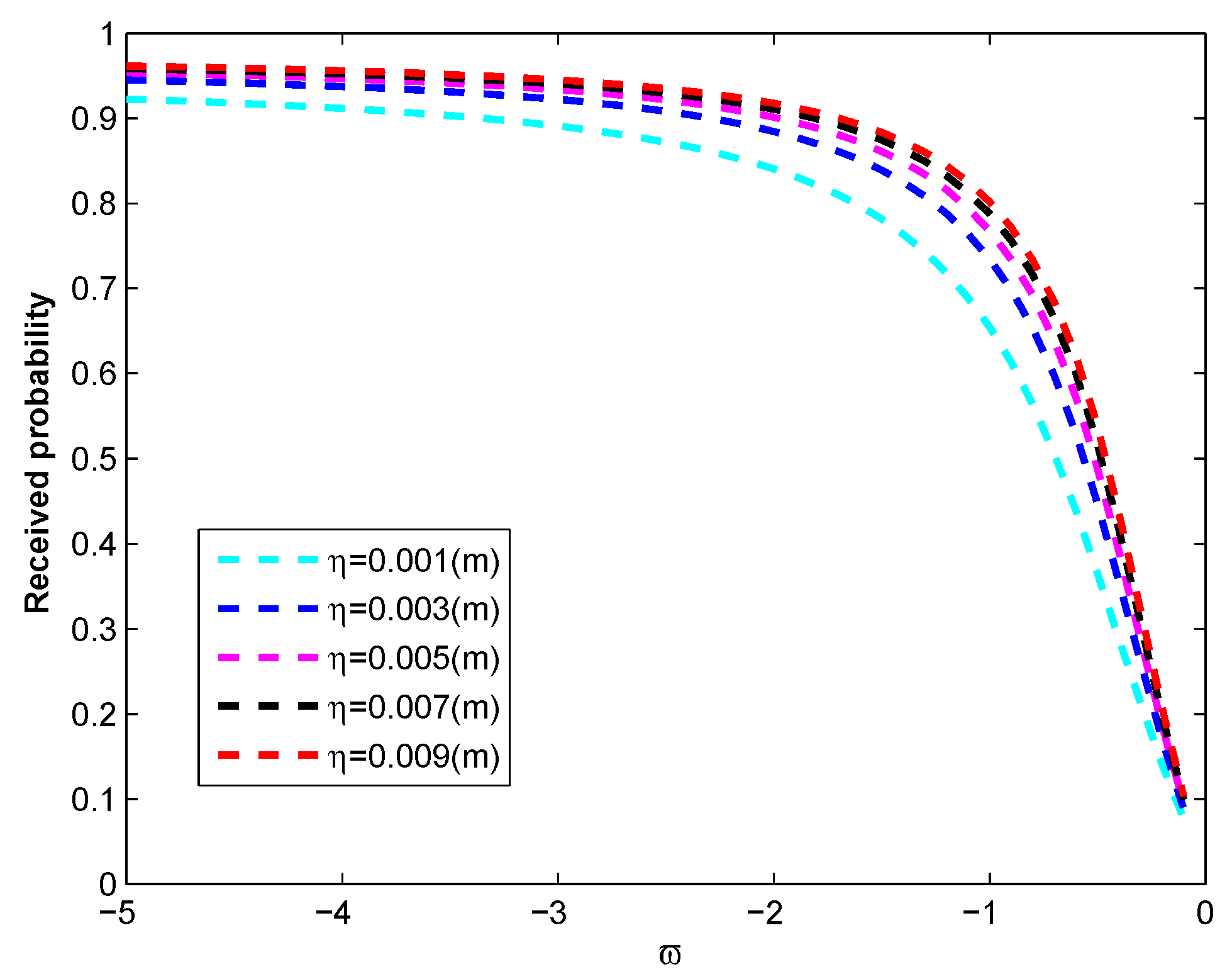
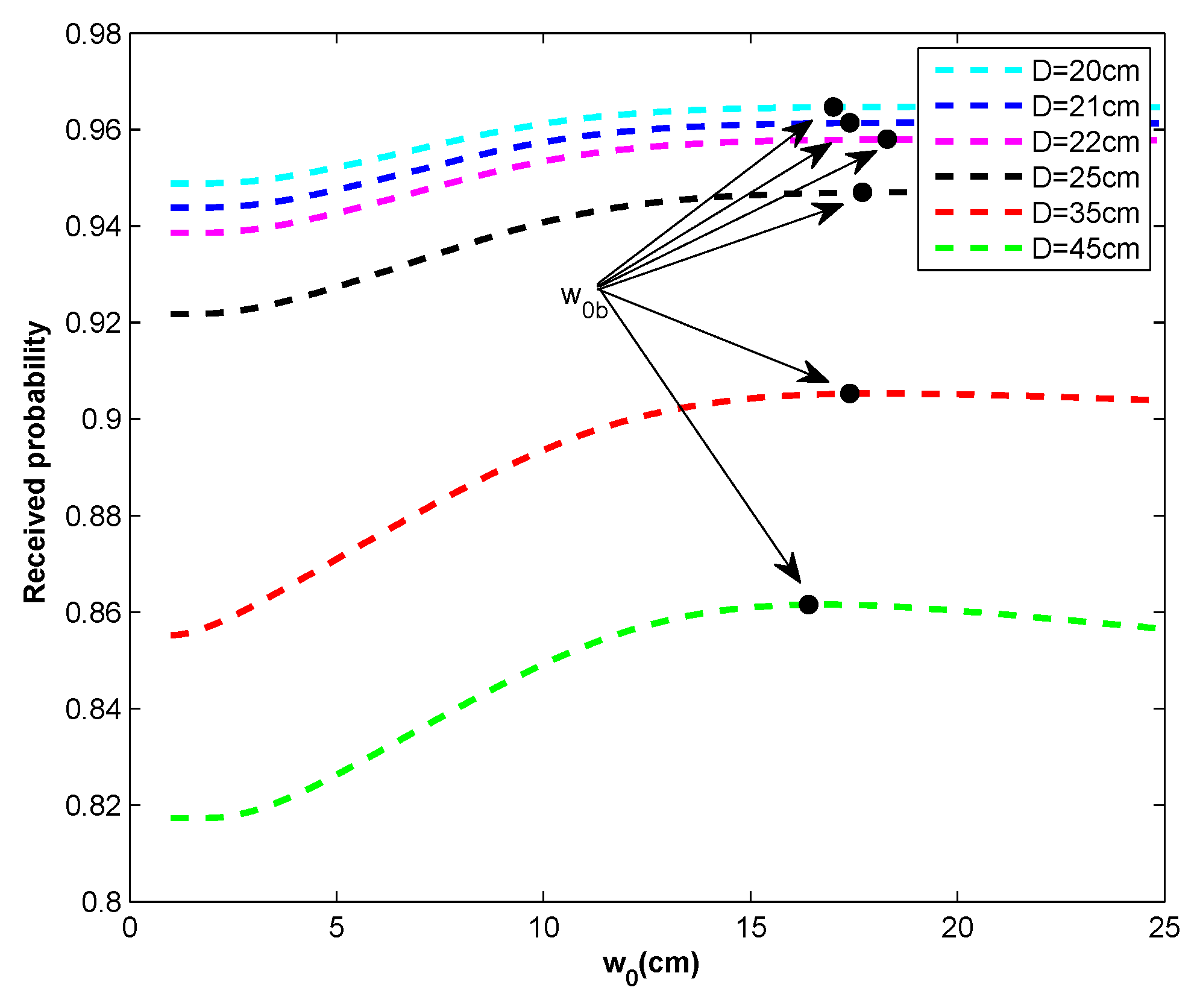
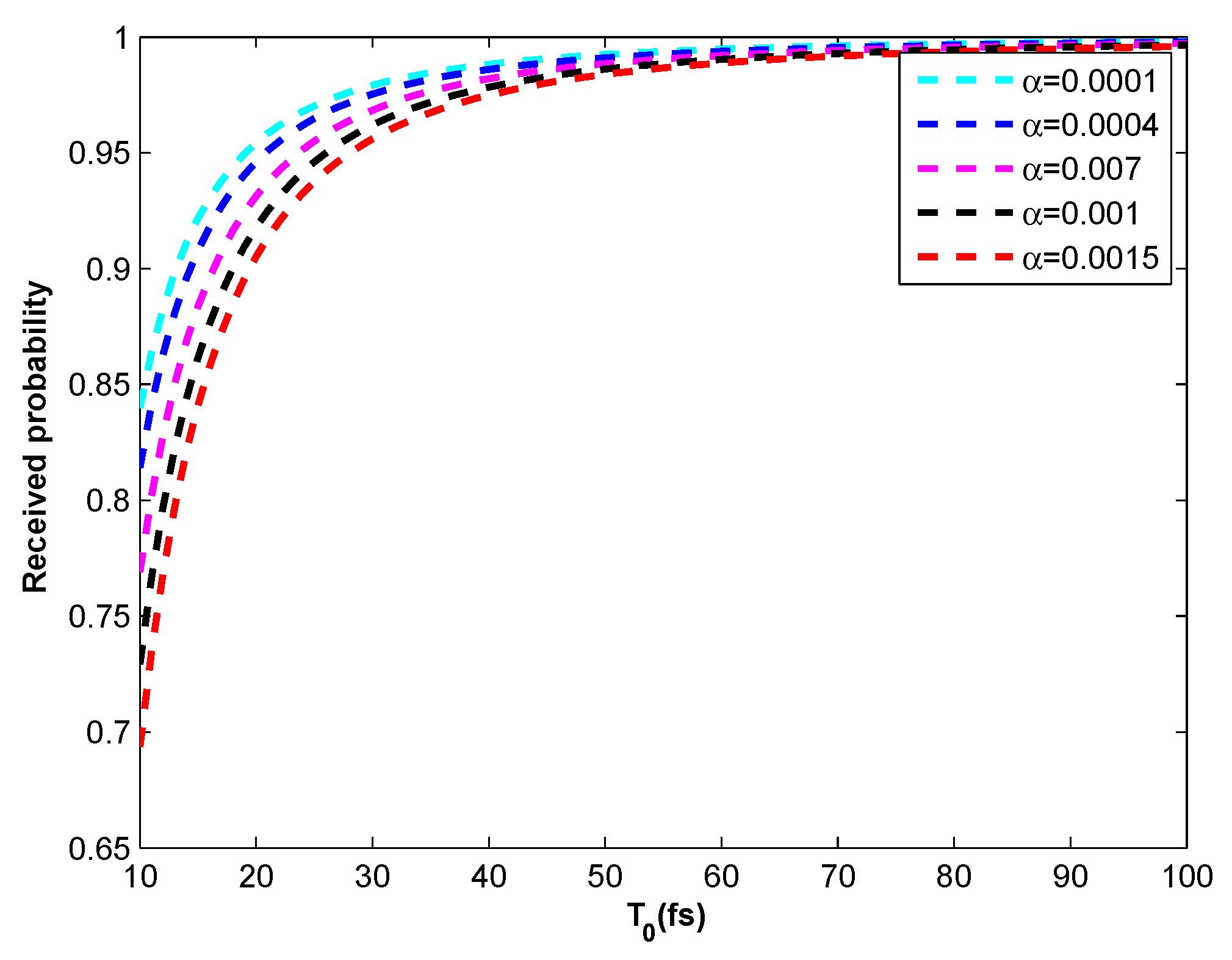
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paterson, C. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys. Rev. Lett. 2005, 94, 153901. [Google Scholar] [CrossRef] [PubMed]
- Wei, M.; Wang, J.; Zhang, Y.; Hu, Z. Orbital-angular-momentum photons for optical communication in non-Kolmogorov atmospheric turbulence. Opt. Commun. 2018, 10, 89–93. [Google Scholar] [CrossRef]
- Wei, M.; Wang, J.; Zhang, Y.; Hu, Z. Universal decay of quantumness for photonic qubits carrying orbital angular momentum through atmospheric Turbulence. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.; Shan, L.; Li, Y.; Yu, L. Effects of moderate to strong turbulence on the Hankel-Bessel–Gaussian pulse beam with orbital angular momentum in the marine atmosphere. Opt. Express 2017, 25, 33469–33479. [Google Scholar] [CrossRef]
- Lu, W.; Liu, L.; Sun, J.F. Influence of temperature and salinity fluctuations on propagation behaviour of partially coherent beams in oceanic turbulence. J. Opt. A Pure Appl. Opt. 2006, 8, 1052–1058. [Google Scholar] [CrossRef]
- Wu, C.; Ko, J.; Rzasa, J.R.; Paulson, D.A.; Davis, C.C. Phase and amplitude beam shaping with two deformable mirrors implementing input plane and Fourier plane phase modifications. Appl. Opt. 2018, 57, 2337–2345. [Google Scholar] [CrossRef] [PubMed]
- Fried, D.L. Branch point problem in adaptive optics. J. Opt. Soc. Am. A 1998, 15, 2759–2768. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, B.; Gao, Z.; Zhao, G.; Duan, Z. Evolution behavior of Gaussian Schell-model vortex beams propagating through oceanic turbulence. Opt. Express 2014, 22, 17723–17734. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Yin, H. Evolution properties of partially coherent flat-topped vortex hollow beam in oceanic turbulence. Appl. Opt. 2015, 54, 10510–10516. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, J.; Wang, A.; Lv, W.; Zhu, L.; Li, S.; Wang, J. Demonstration of data-carrying orbital angular momentum-based underwater wireless optical multicasting link. Opt. Express 2017, 25, 28743–28751. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Wang, G.; Luo, X.; Yin, H. Propagation properties of partially coherent four-petal Gaussian vortex beams in oceanic turbulence. Laser Phys. 2017, 27, 016001. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, D. Propagation of a stochastic electromagnetic vortex beam in the oceanic turbulence. Opt. Laser Technol. 2014, 57, 189–193. [Google Scholar] [CrossRef]
- Li, Y.; Yu, L.; Zhang, Y. Influence of anisotropic turbulence on the orbital angular momentum modes of Hermite-Gaussian vortex beam in the ocean. Opt. Express 2017, 25, 12203–12215. [Google Scholar] [CrossRef] [PubMed]
- Willner, A.E.; Zhao, Z.; Ren, Y.; Li, L.; Xie, G.; Song, H.; Liu, C.; Zhang, R.; Bao, C.; Pang, K. Underwater optical communications using orbital angular momentum-based spatial division multiplexing. Opt. Commun. 2018, 408, 21–25. [Google Scholar] [CrossRef]
- Hernandez-Figueroa, H.E.; Zamboni-Rached, M.; Recami, E. (Eds.) Localized Wave; Wiley-Interscience, IEEE Press: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ciattoni, A.; Conti, C.; Porto, P.D. Vector electromagnetic X waves. Phys. Rev. E 2004, 69, 036608. [Google Scholar] [CrossRef]
- Ornigotti, M.; Conti, C.; Szameit, A. Effect of orbital angular momentum on nondiffracting ultrashort optical pulses. Phys. Rev. Lett. 2015, 115, 100401. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, Y.; Zhu, Y. Influence of oceanic turbulence on propagation of the Gaussian pulsed X wave carrying orbital angular momentum. Opt. Commun. 2018, 428, 57–62. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Y.; Li, Y.; Hu, Z. Beam wander of Gaussian-Schell model beams propagating through oceanic turbulence. Opt. Commun. 2016, 371, 59–66. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: Washington, DC, USA, 2005. [Google Scholar]
- Korotkova, O. Random Light Beams Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 6th ed.; Academic Press: Beijing, China, 2000. [Google Scholar]
- Kelly, D.; Andrews, L.C. Temporal broadening and scintillations of ultrashort optical pulses. Waves Random Media 1999, 9, 307–325. [Google Scholar] [CrossRef]
- Karp, S.; Gagliardi, R.M.; Moran, S.E.; Stotts, L.B. Optical Channels; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Young, C.Y.; Andrews, L.C.; Ishimaru, A. Time-of-arrival fluctuations of a space-time Gaussian pulse in weak optical turbulence: An analytic solution. Appl. Opt. 1998, 37, 7655–7660. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Zhu, Y.; Zhang, L.; Hu, Z.; Zhang, Y. Effects of non-Kolmogorov turbulence on the spiral spectrum of Hypergeometric-Gaussian laser beams. Opt. Express 2015, 23, 9137. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, S.; Zhu, Y.; Zhang, Y. Received Probability of Vortex Modes Carried by Localized Wave of Bessel–Gaussian Amplitude Envelope in Turbulent Seawater. J. Mar. Sci. Eng. 2019, 7, 203. https://doi.org/10.3390/jmse7070203
Deng S, Zhu Y, Zhang Y. Received Probability of Vortex Modes Carried by Localized Wave of Bessel–Gaussian Amplitude Envelope in Turbulent Seawater. Journal of Marine Science and Engineering. 2019; 7(7):203. https://doi.org/10.3390/jmse7070203
Chicago/Turabian StyleDeng, Shibao, Yun Zhu, and Yixin Zhang. 2019. "Received Probability of Vortex Modes Carried by Localized Wave of Bessel–Gaussian Amplitude Envelope in Turbulent Seawater" Journal of Marine Science and Engineering 7, no. 7: 203. https://doi.org/10.3390/jmse7070203
APA StyleDeng, S., Zhu, Y., & Zhang, Y. (2019). Received Probability of Vortex Modes Carried by Localized Wave of Bessel–Gaussian Amplitude Envelope in Turbulent Seawater. Journal of Marine Science and Engineering, 7(7), 203. https://doi.org/10.3390/jmse7070203



