Experimental Study on Toe Scouring at Sloping Walls with Gravel Foreshores
Abstract
:1. Introduction
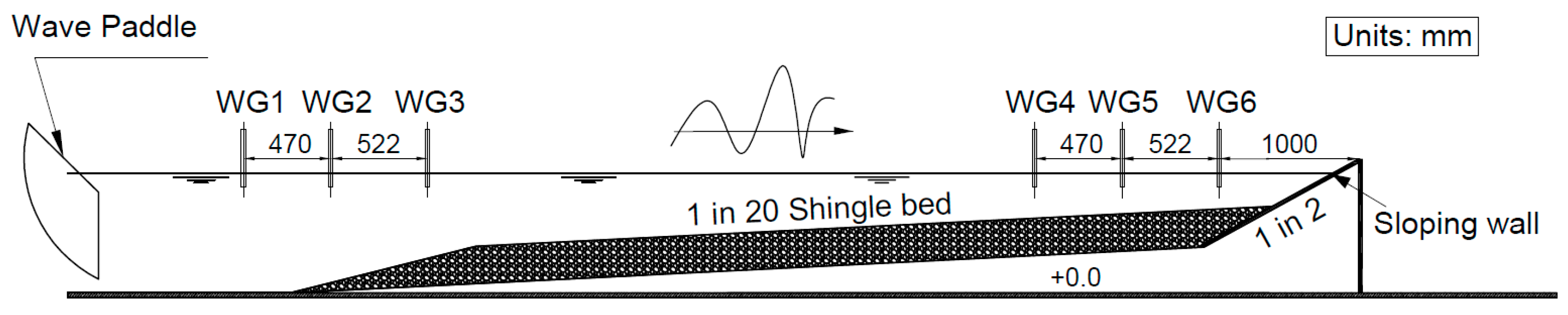
2. Laboratory Set-Up
3. Results and Discussion
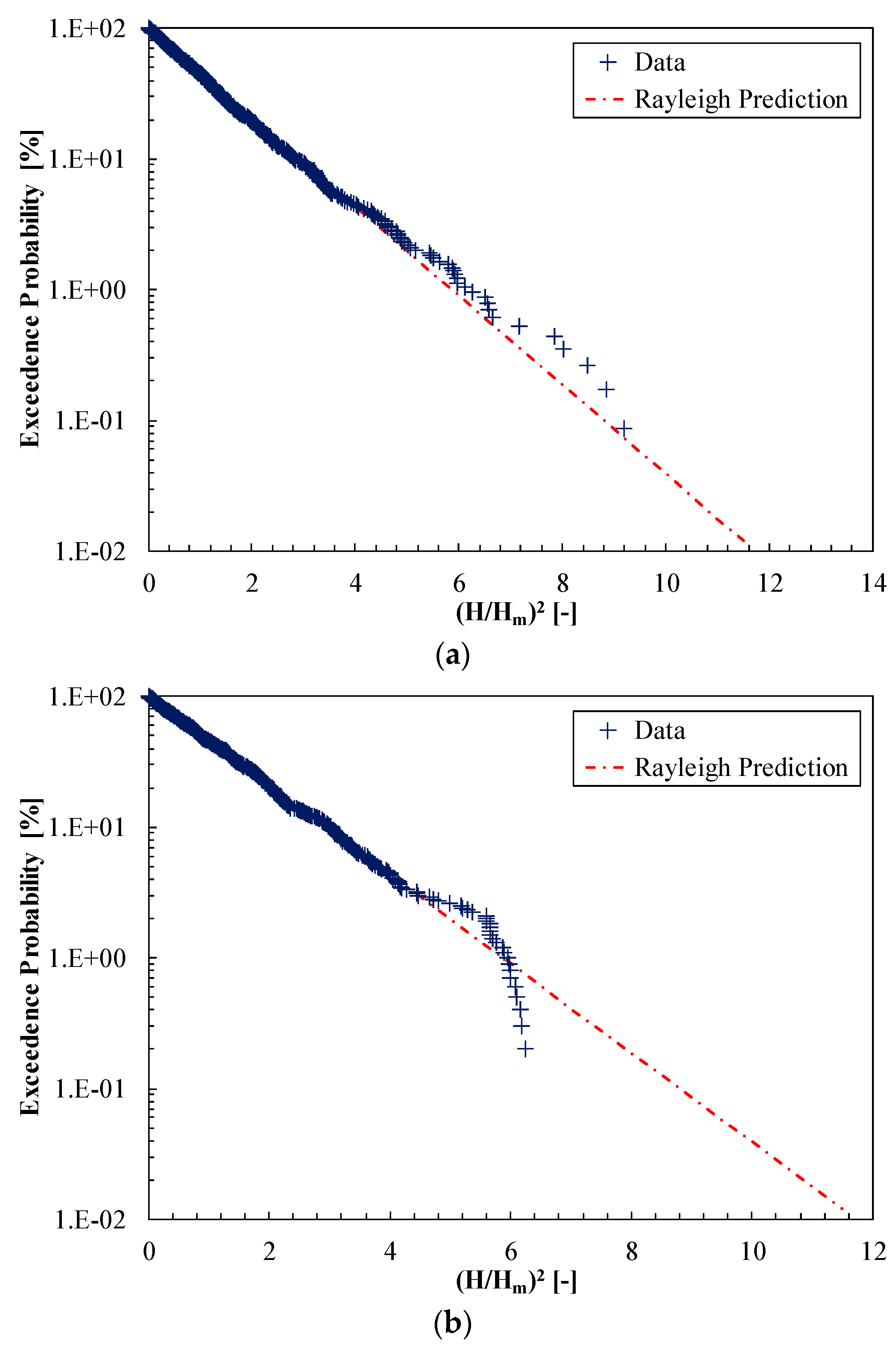
3.1. Inshore Wave Conditions
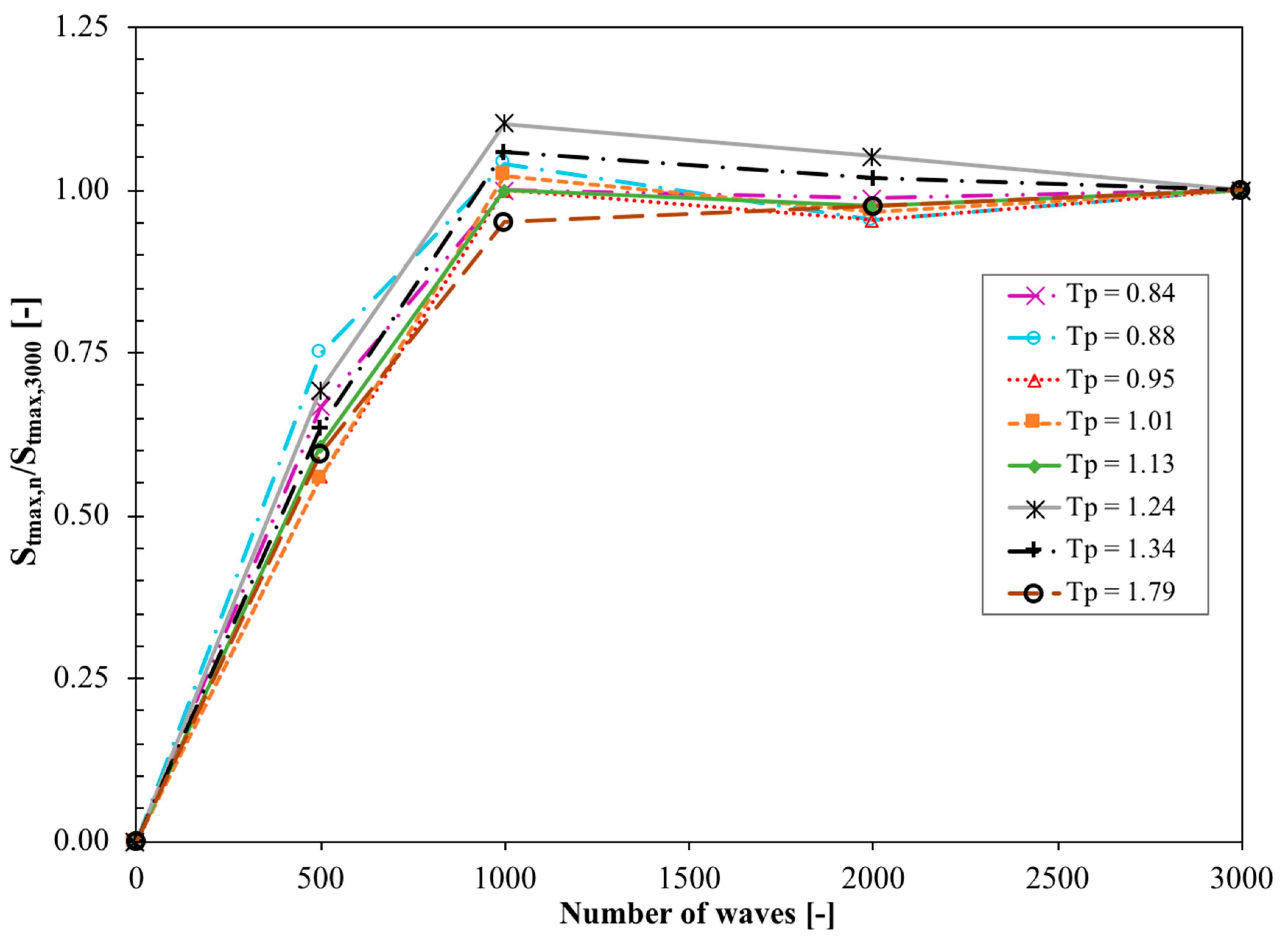
3.2. Relationship between Development of Scour Depth and Storm Duration
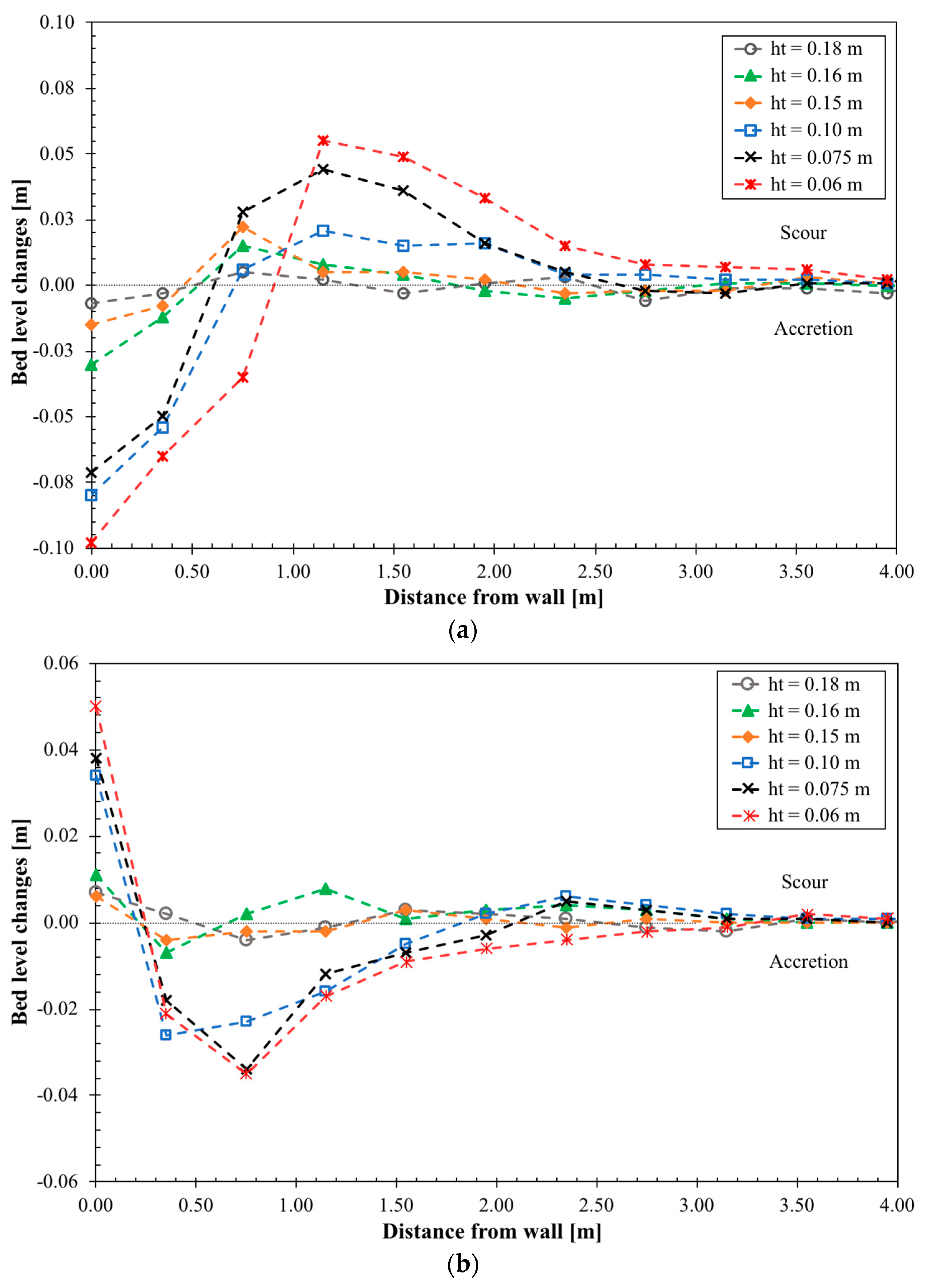
3.3. Variation of Bed Level for a Sloping Wall with a Shingle Foreshore
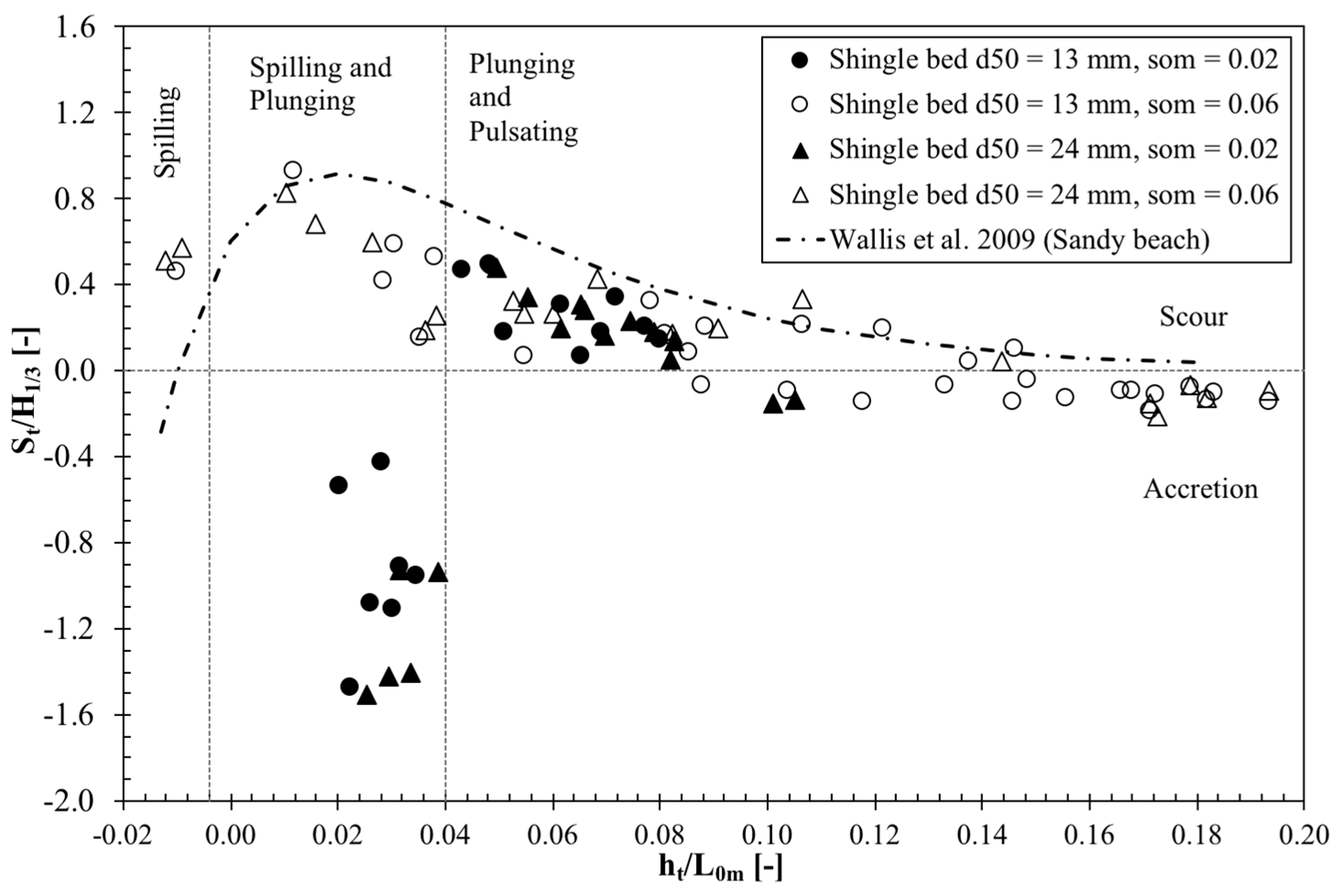
3.4. Variation of Toe Scour Depth with Relative Water Depth
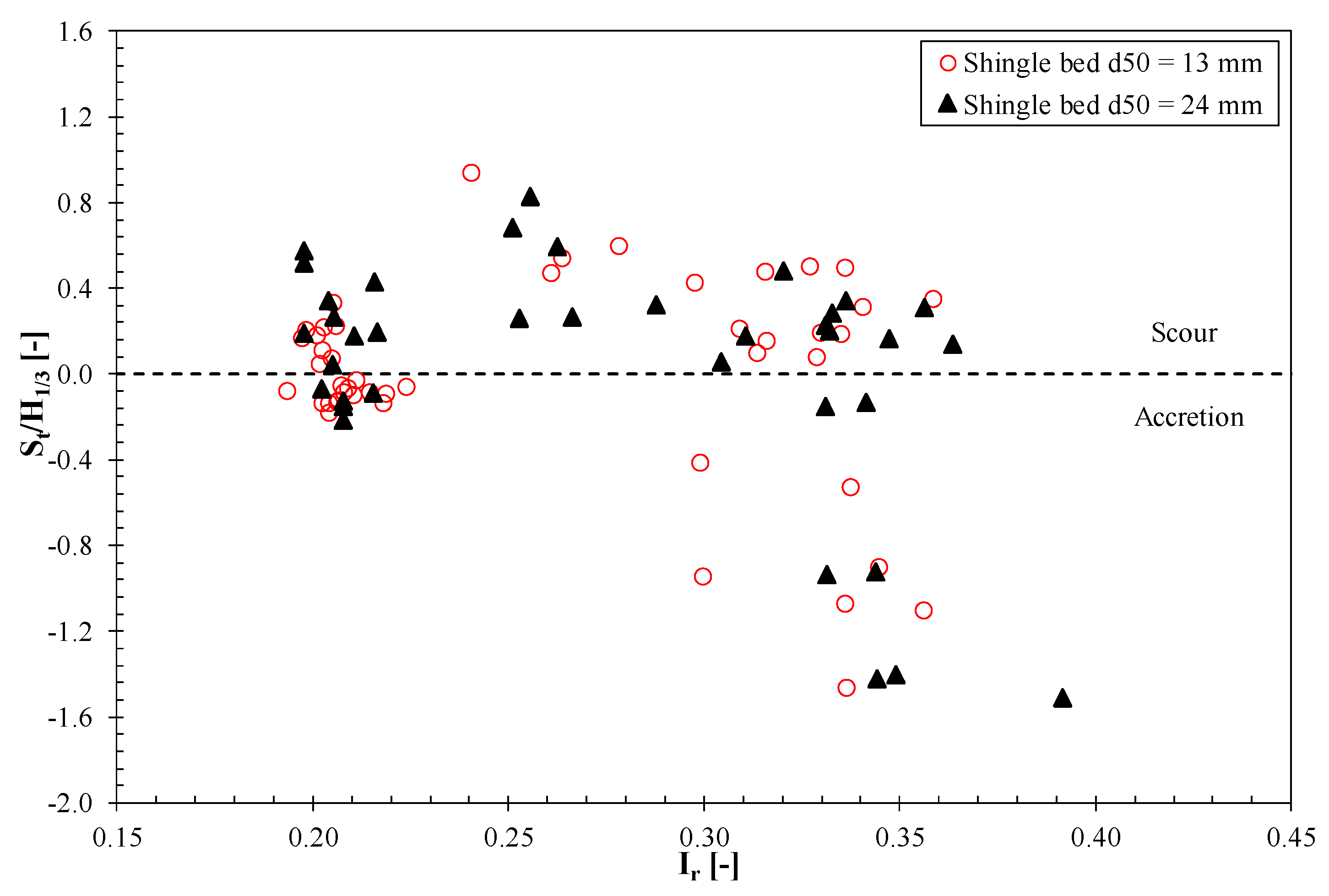
3.5. Variation of Toe Scour Depth with Iribarren Number
3.6. Variation of Toe Scour Depth with Relative Toe Water Depth and Iribarren Number
- 0.20 < Ir < 0.30 and
- Ir > 0.30
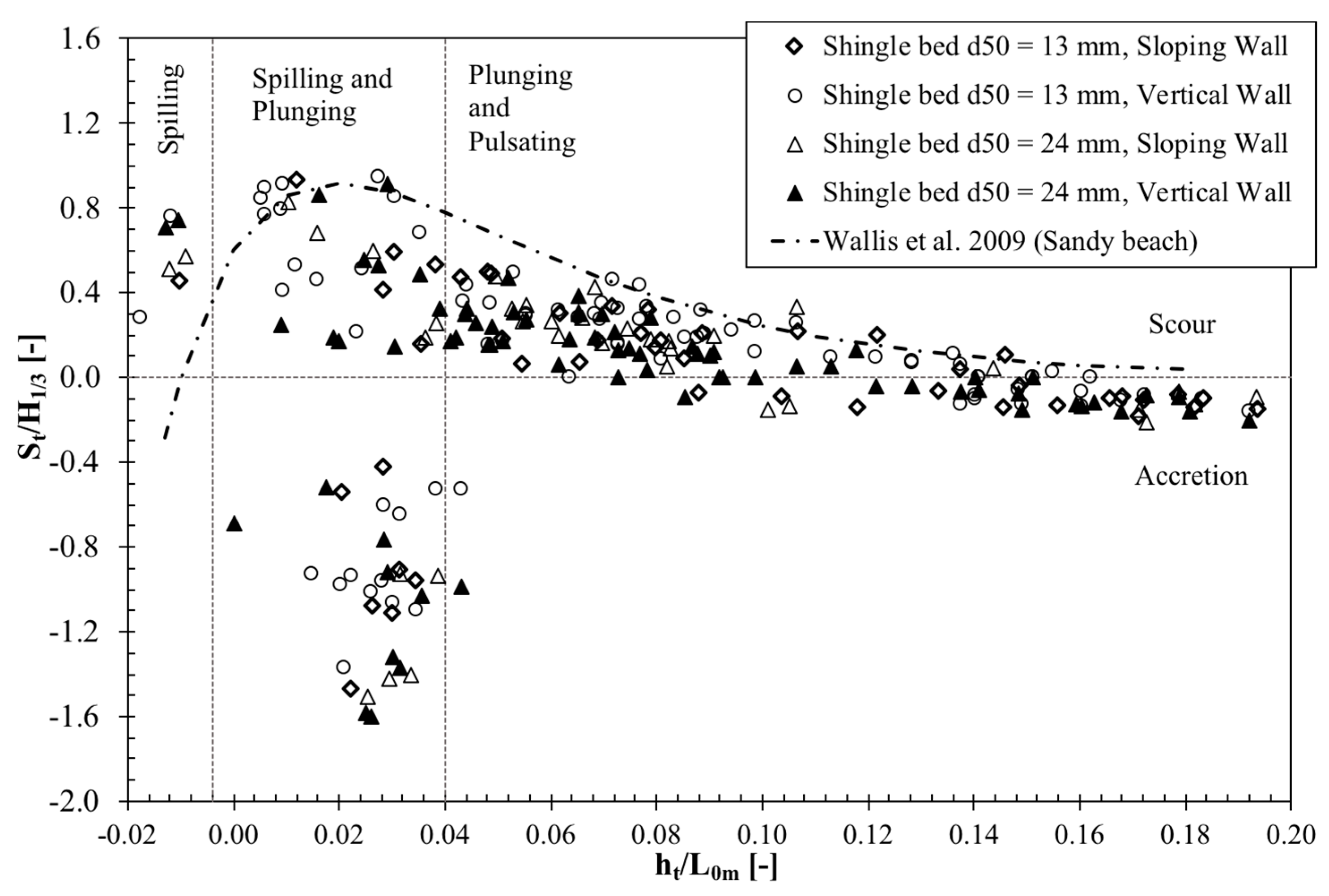
3.7. Variation of Toe Scour Depth with Wall Slope
4. Conclusions
- —
- The results of this study showed that the relative toe scour depth at a sloping structure on a shingle beach, is influenced by the relative toe water depth and Iribarren number.
- —
- Within the experimental limitations, the maximum toe scour depths were observed for the experiments under the spilling and plunging wave attack (0.005 ≤ ht/L0m ≤ 0.04).
- —
- It was found that the scour depths at the sloping walls within this study do not remarkably differ from those reported at vertical walls with similar permeable foreshore slopes, which indicates that the scour depths are independent of the slope of the structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Müller, G.; Allsop, W.; Bruce, T.; Kortenhaus, A.; Pearce, A.; Sutherland, J. The occurrence and effects of wave impacts. Proc. ICE Marit. Eng. 2008, 160, 167–173. [Google Scholar] [CrossRef]
- Pearson, J.M. Overtopping and Toe Scour at Vertical Seawalls. In Proceedings of the 9th International Conference on Coasts, Marine structures and Breakwaters: Adapting to Change, Scotland, UK, 16–18 September 2009; Institution of Civil Engineers, Thomas Telford Ltd.: Edinburgh, UK, 2010; pp. 598–608. [Google Scholar]
- Powell, K.A. Toe Scour at Sea Walls Subject to Wave Action: A Literature Review; Report SR 119; HR Wallingford: Wallingford, UK, 1987. [Google Scholar]
- Fowler, J.E. Scour Problems and Methods for Prediction of Maximum Scour at Vertical Seawalls; Technical Report CERC-92-16; US Army Corps of Engineers Waterways Experiment Station, Coastal Engineering Research Center: Vicksburg, MS, USA, 1992. [Google Scholar]
- Sutherland, J.; Brampton, A.H.; Motyka, G.; Blanco, B.; Whitehouse, R.J.W. Beach Lowering in Front of Coastal Structures—Research Scoping Study; Report FD1916/TR; Defra—Flood Management Division: London, UK, 2003. Available online: http://sciencesearch.defra.gov.uk/ (accessed on 14 February 2017).
- Cohen-Shacham, E.; Walters, G.; Janzen, C.; Maginnis, S. Nature-Based Solutions to Address Global Societal Challenges; IUCN: Gland, Switzerland, 2016. [Google Scholar]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D. Sea level change. In Climate Change 2013: The Physical Science Basis Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Wallis, M.; Whitehouse, R.; Lyness, N. Development of guidance for the management of the toe of coastal defence structures. In Proceedings of the Presented in the 44th Defra Flood and Coastal Management Conference, Telford, UK, 30 June –2 July 2009. [Google Scholar]
- Xie, S.L. Scouring Patterns in Front of Vertical Breakwaters and Their Influences on the stability of the Foundation of the Breakwaters. Master’s Thesis, Department of Civil Engineering, Delft University of Technology, Delft, The Netherlands, 1981. [Google Scholar]
- Kraus, N.C.; Smith, J.M. SUPERTANK Laboratory Data Collection Project. Volume 1: Main Text; Technical Report CERC-94-3; US Army Corps of Engineers Waterways Experiment Station, Coastal Engineering Research Center: Vicksburg, MS, USA, 1994; pp. 2191–2204. [Google Scholar]
- Pearce, A.; Sutherland, J.; Müller, G.; Rycroft, D.; Whitehouse, R. Scour at a seawall-field measurements and physical modelling. In Proceedings of the 30th International Conference on Coastal Engineering, ASCE, San Diego, CA, USA, 2–8 September 2006. [Google Scholar]
- Sutherland, J.; Obhrai, C.; Whitehouse, R.; Pearce, A. Laboratory tests of scour at a seawall. In Proceedings of the 3rd International Conference on Scour and Erosion, CURNET, Technical University of Denmark, Gouda, The Netherlands, 3–5 July 2007. [Google Scholar]
- Jayaratne, R.; Premaratne, B.; Adewale, A.; Mikami, T.; Matsuba, S.; Shibayama, T.; Esteban, M.; Nistor, I. Failure Mechanisms and Local Scour at Coastal Structures Induced by Tsunami. Coast. Eng. J. 2016, 58, 1640017. [Google Scholar] [CrossRef]
- Pourzangbar, A.; Saber, A.; Yeganeh-Bakhtiary, A.; Ahari, L.R. Predicting scour depth at seawalls using GP and ANNs. J. Hydroinform. 2017, 19, 349–363. [Google Scholar] [CrossRef]
- Tahersima, M.; Yeganeh-Bakhtiary, A.; Hajivalie, F. Scour pattern in front of vertical breakwater with wave overtopping. J. Coast. Res. 2011, 64, 598. [Google Scholar]
- Tofany, N.; Ahmad, M.; Kartono, A.; Mamat, M.; Mohd-Lokman, H. Numerical modeling of the hydrodynamics of standing wave and scouring in front of impermeable breakwaters with different steepnesses. Ocean Eng. 2014, 88, 255–270. [Google Scholar] [CrossRef]
- Sutherland, J.; Brampton, A.H.; Obrai, C.; Dunn, S.; Whitehouse, R.J.W. Understanding the Lowering of Beaches in Front of Coastal Defence Structures, Stage 2—Research Scoping Study; Report FD1927/TR; Defra—Flood Management Division: London, UK, 2008. Available online: http://sciencesearch.defra.gov.uk/ (accessed on 20 February 2017).
- Powell, K.A.; Lowe, J.P. The scouring of sediments at the toe of seawalls. In Proceedings of the Hornafjordor International Coastal Symposium, Hofn, Iceland, 20–24 June 1994; pp. 749–755. [Google Scholar]
- Jayaratne, R.; Mendoza, E.; Silva, R.; Gutiérrez, F. Laboratory Modelling of Scour on Seawalls. In Proceedings of the Presented in the International Conference on Coastal Structures, Boston, MA, USA, 9–11 September 2015. [Google Scholar]
- Salauddin, M.; Pearson, J.M. Wave overtopping and toe scouring at a plain vertical seawall with shingle foreshore: A Physical model study. Ocean Eng. 2019, 171, 286–299. [Google Scholar] [CrossRef]
- Powell, K.A. Predicting Short Term Profile Response for Shingle Beaches; Report SR 219; HR Wallingford: Wallingford, UK, 1990. [Google Scholar]
- Eurotop. EurOtop II—Manual on Wave Overtopping of Sea Defences and Related Structures: An Overtopping Manual Largely Based on European Research, But for Worldwide Application. 2016. in press. Available online: www.overtopping-manual.com (accessed on 21 January 2017).
- Wolters, G.; Van Gent, M.; Allsop, N.W.H.; Hamm, L.; Mühlestein, D. HYDRALAB III: Guidelines for physical model testing of rubble mound breakwaters. In Proceedings of the 9th International Conference on Coasts, Marine Structures and Breakwaters: Adapting to Change, Edinburgh, UK, 16–18 September 2009; pp. 659–670. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. Coast. Eng. 1980, 1, 154–172. [Google Scholar]
- Klopman, G.; Van der Meer, J.W. Random wave measurements in front of reflective structures. J. Waterw. Port Coast Ocean Eng. 1990, 125, 39–45. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Experimental study of 2D scour and its protection at a rubble-mound breakwater. Coast. Eng. 2000, 40, 59–87. [Google Scholar] [CrossRef]
- Sherman, D.J. Gravel beaches. Natl. Geogr. Res. Explor. 1991, 7, 442–452. [Google Scholar]

| Structural and Bed Configuration | Toe Water Depth, ht [mm] | Crest Freeboard, Rc [mm] | Wave Height, Hm0 [mm] | Wave Steepness, sop [-] | Wave Period, Tp [s] |
|---|---|---|---|---|---|
| Sloping wall on a shingle bed d50 = 13 mm | 60 | 190 | 50–160 | 0.02 | 1.27–2.26 |
| 0.05 | 0.80–1.43 | ||||
| 75 | 245 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 100 | 150 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 150 | 100 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 180 | 140 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 200 | 50 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| Sloping wall on a shingle bed d50 = 24 mm | 60 | 190 | 50–160 | 0.02 | 1.27–2.26 |
| 0.05 | 0.80–1.43 | ||||
| 75 | 245 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 100 | 150 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 150 | 100 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 180 | 140 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 | ||||
| 200 | 50 | 50–160 | 0.02 | 1.27–2.26 | |
| 0.05 | 0.80–1.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salauddin, M.; Pearson, J.M. Experimental Study on Toe Scouring at Sloping Walls with Gravel Foreshores. J. Mar. Sci. Eng. 2019, 7, 198. https://doi.org/10.3390/jmse7070198
Salauddin M, Pearson JM. Experimental Study on Toe Scouring at Sloping Walls with Gravel Foreshores. Journal of Marine Science and Engineering. 2019; 7(7):198. https://doi.org/10.3390/jmse7070198
Chicago/Turabian StyleSalauddin, M., and J. M. Pearson. 2019. "Experimental Study on Toe Scouring at Sloping Walls with Gravel Foreshores" Journal of Marine Science and Engineering 7, no. 7: 198. https://doi.org/10.3390/jmse7070198





