Large-Scale Electric Propulsion Systems in Ships Using an Active Front-End Rectifier
Abstract
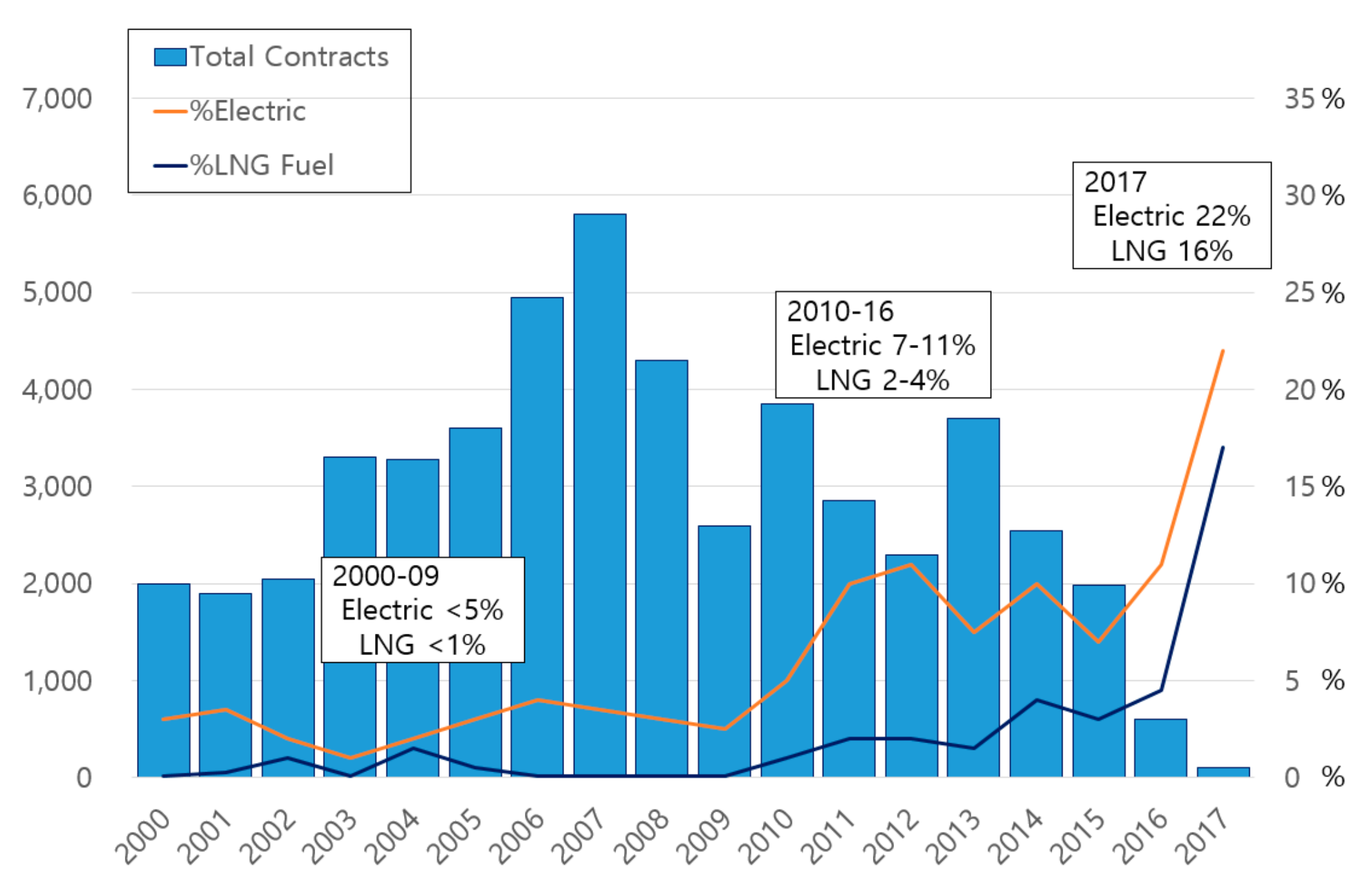
1. Introduction
2. Conventional Methods for Marine Electrical Prolusion Systems
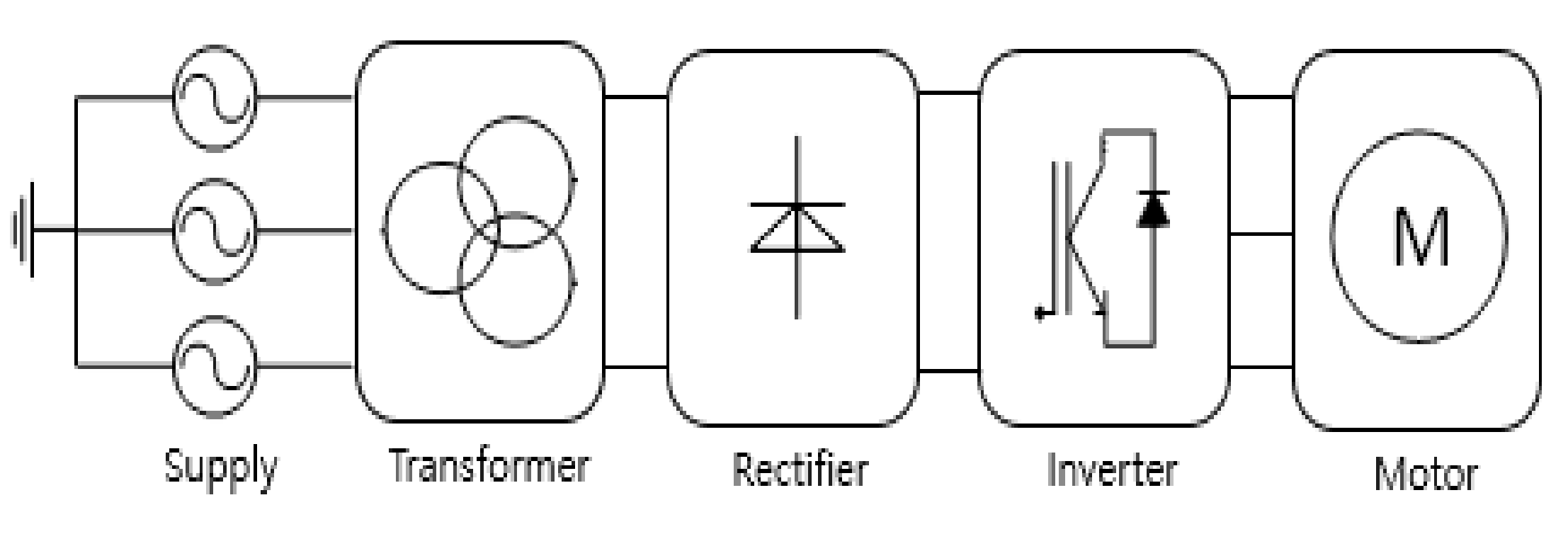
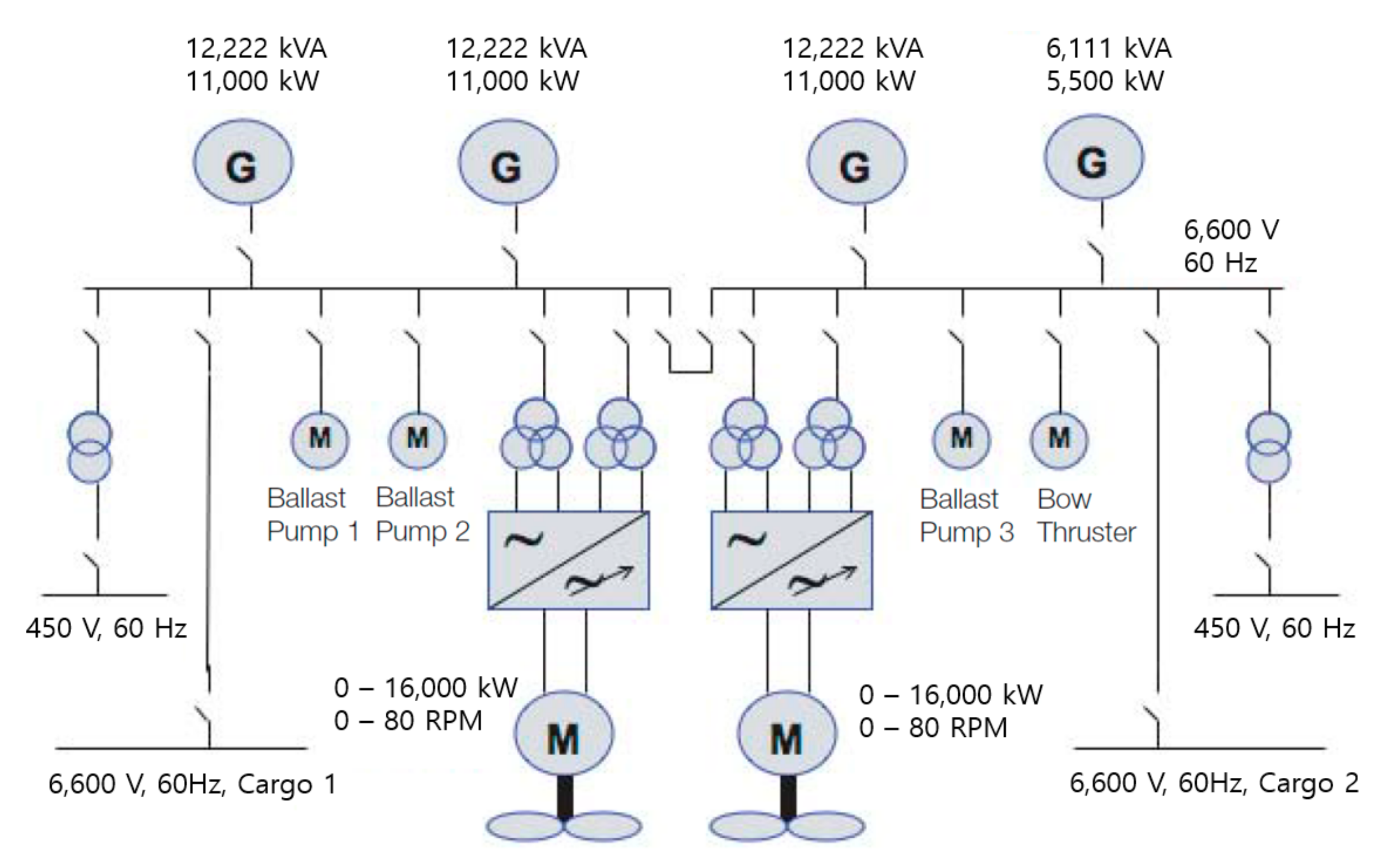
2.1. Background
2.2. DFE Rectification Method in Large-Scale Electric Propulsion Systems
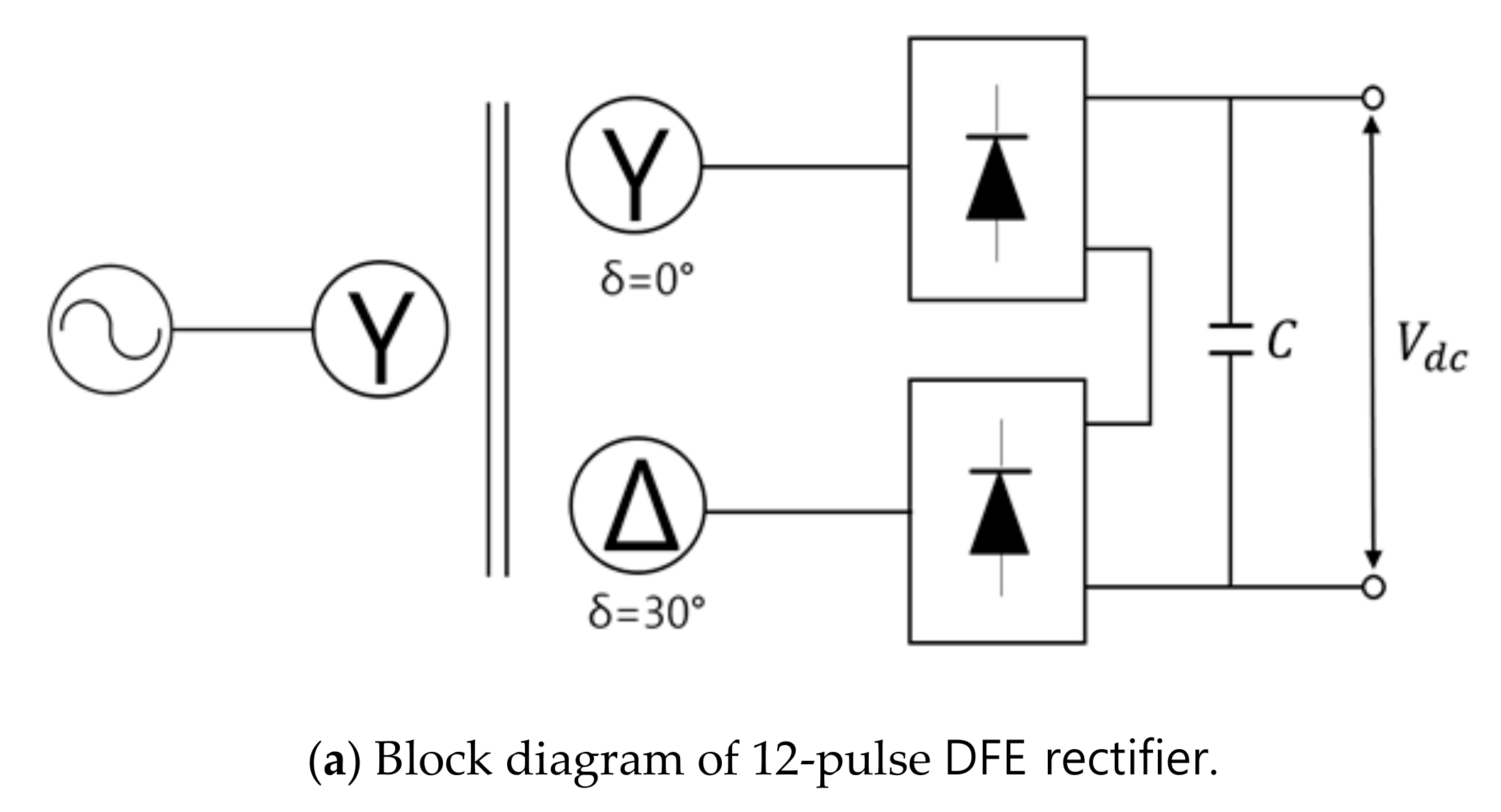
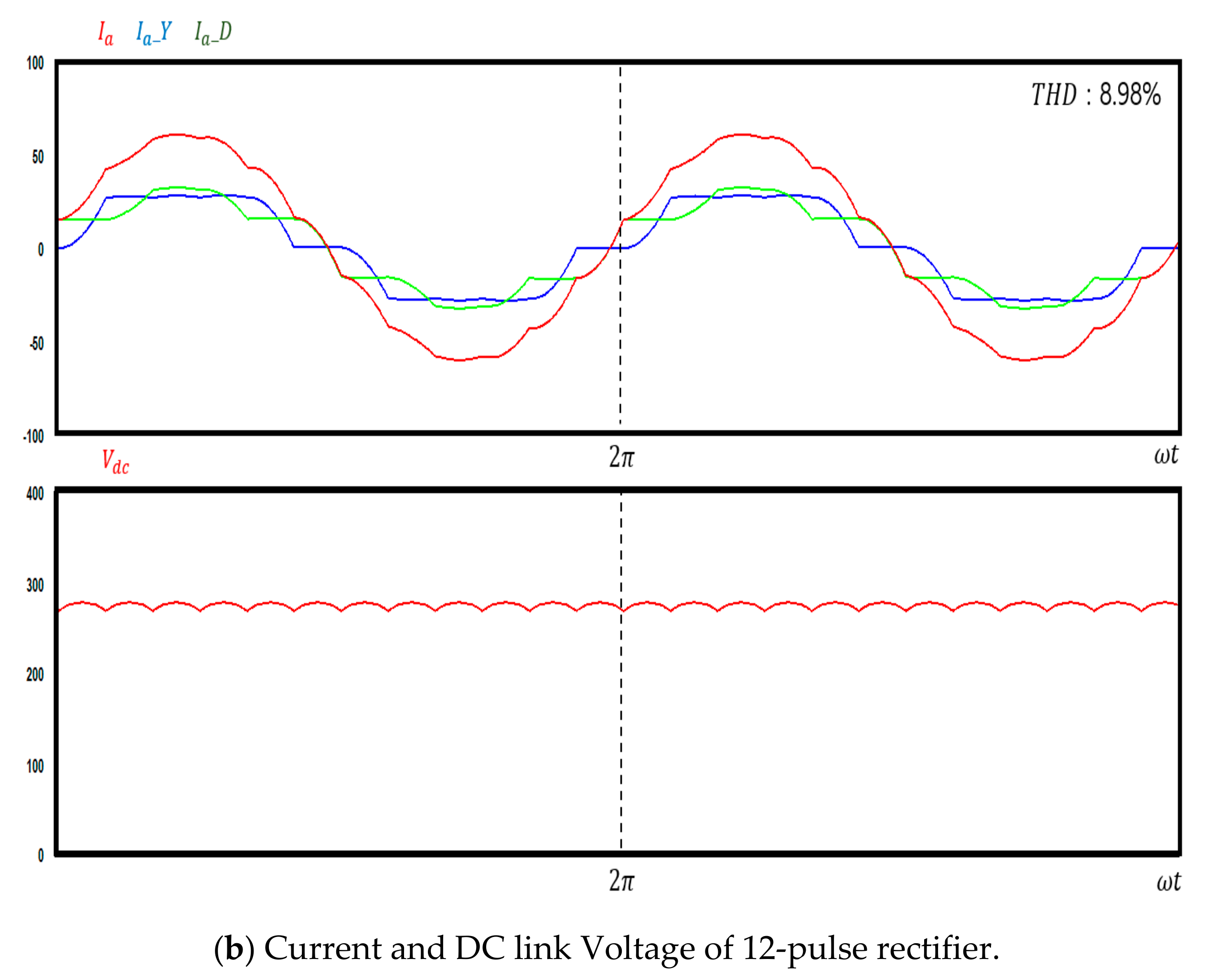
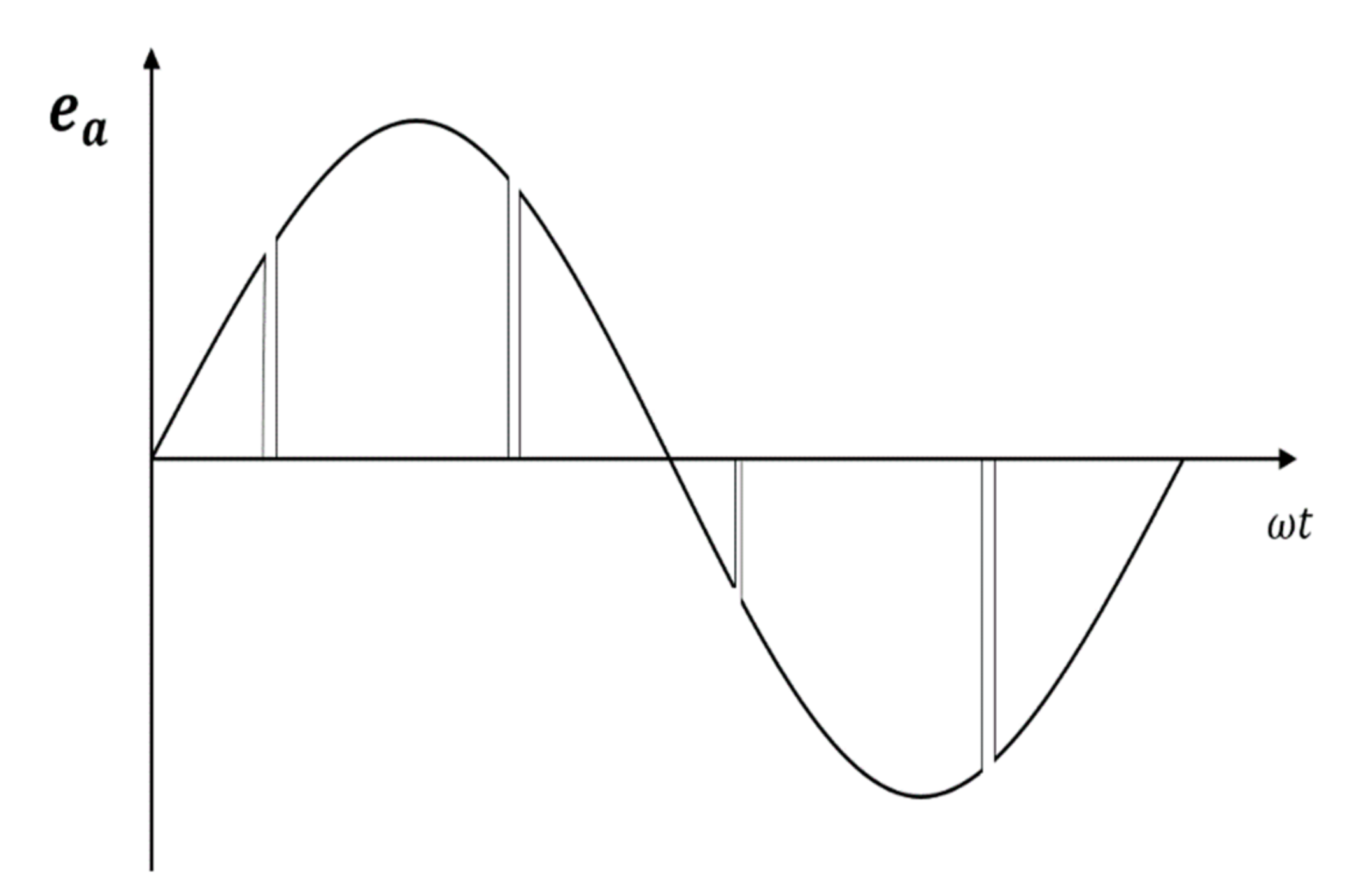
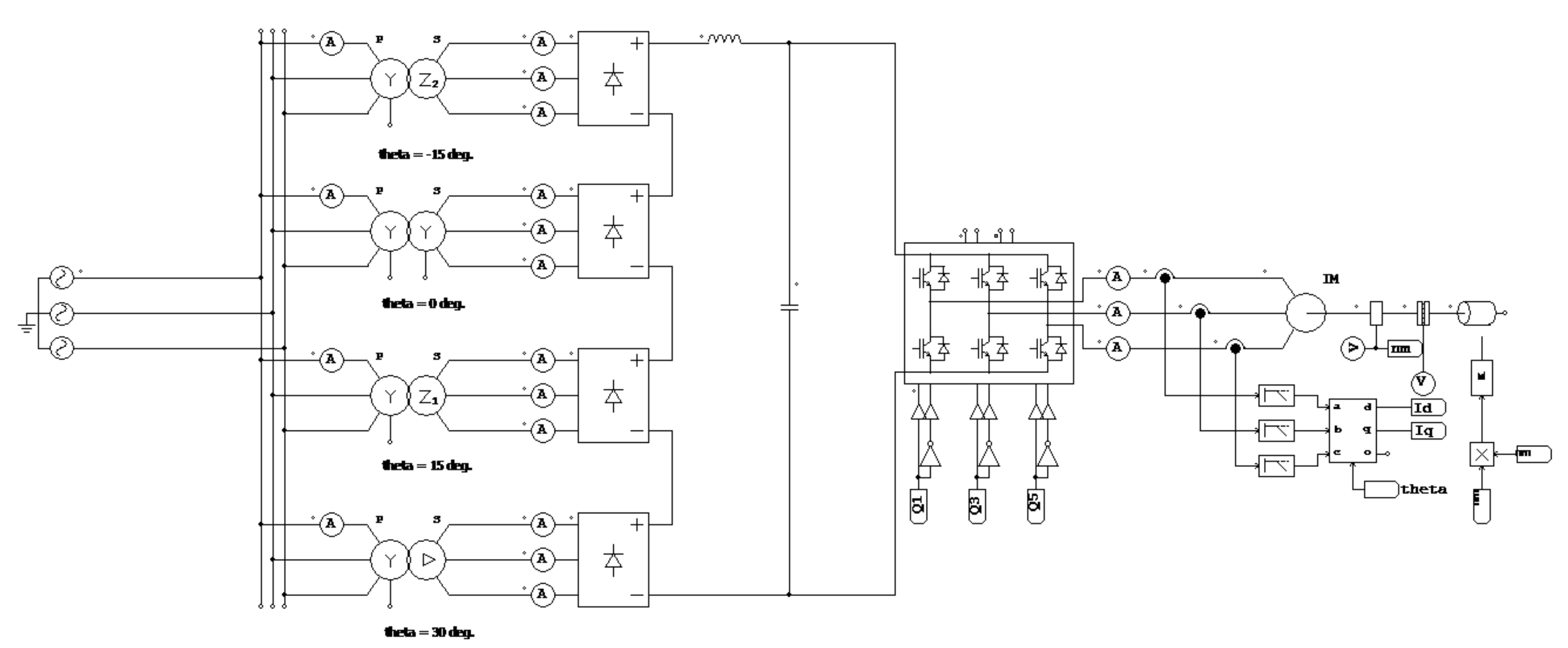
2.2.1. 12-Pulse Rectifier
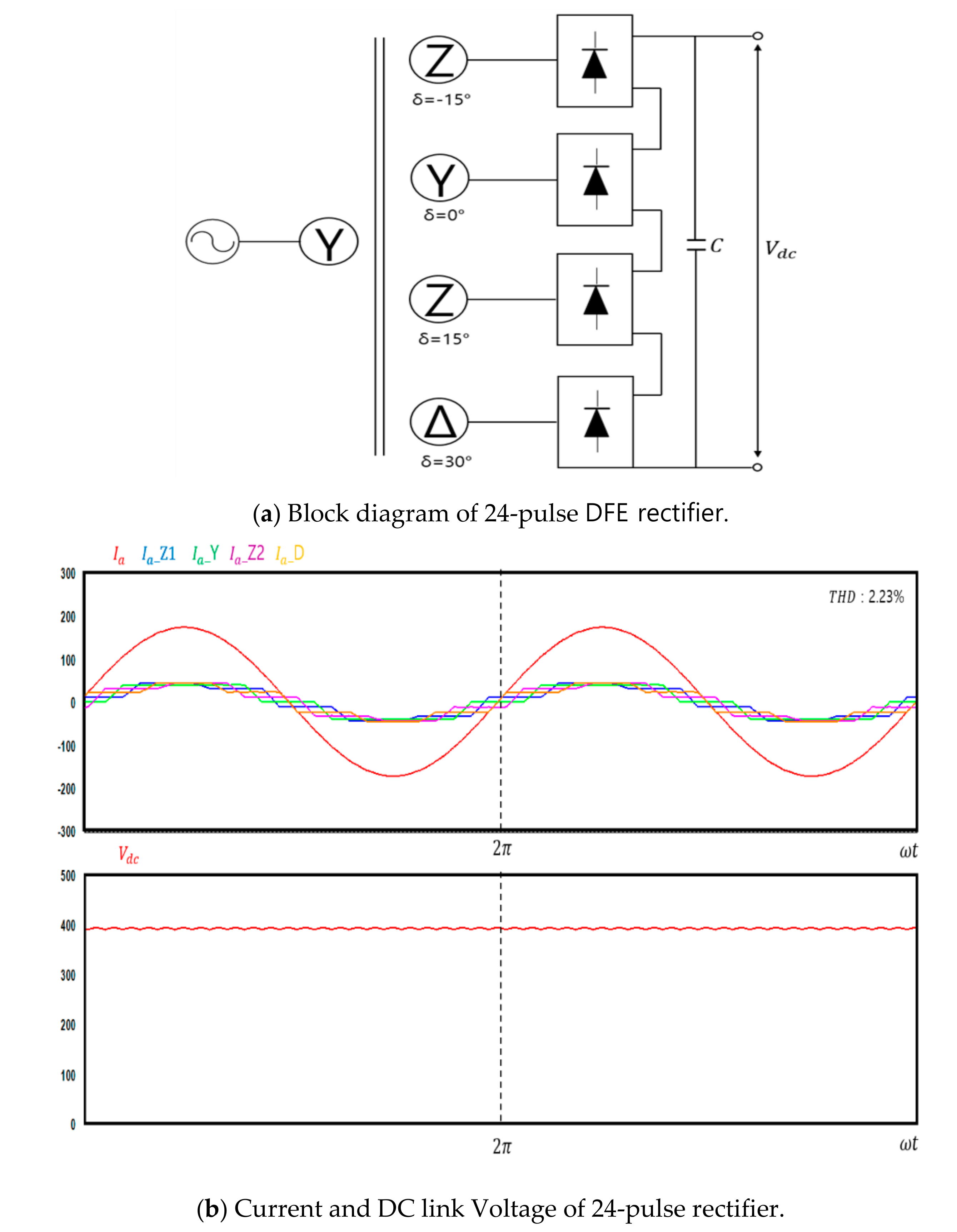
2.2.2. 24-Pulse Rectifier
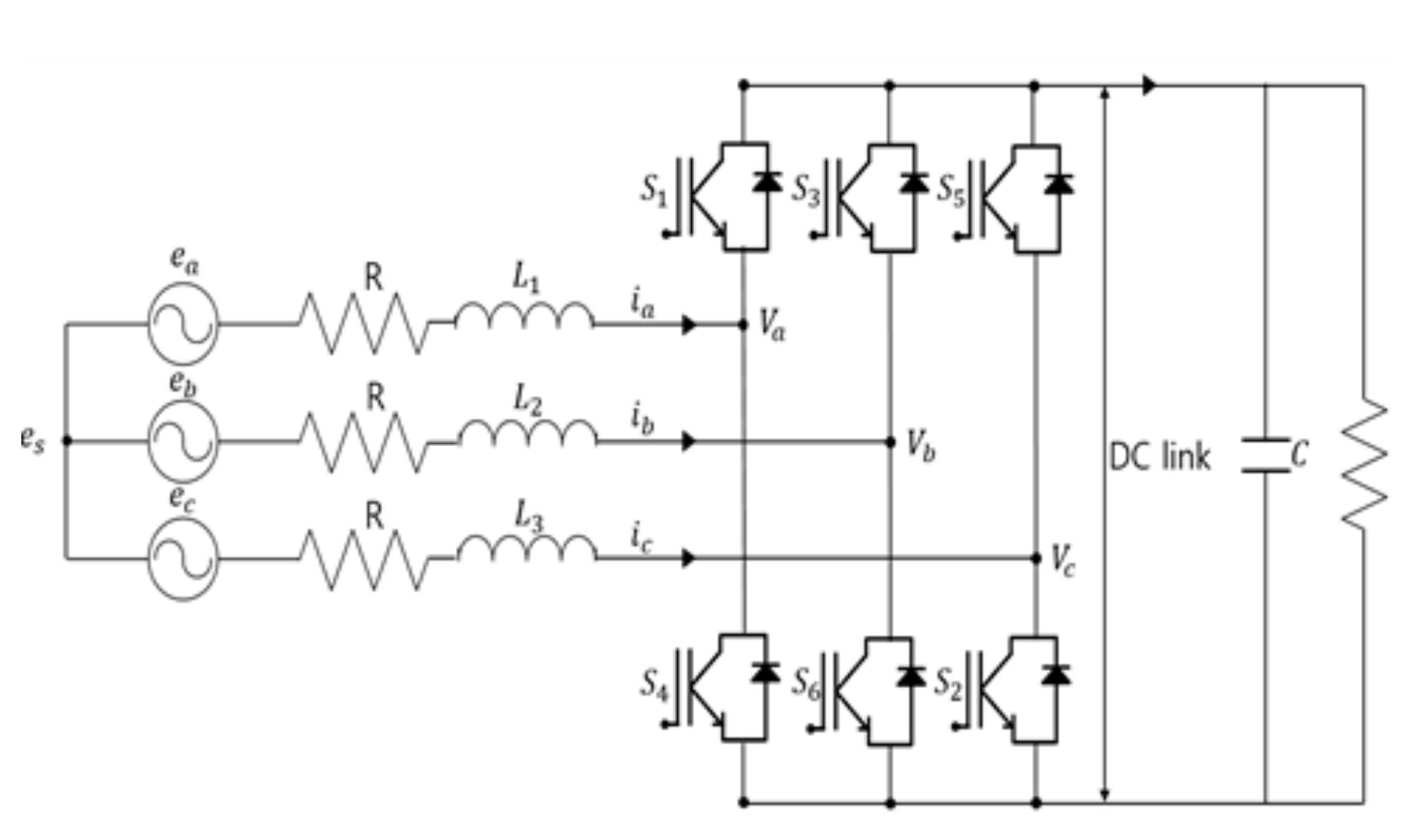
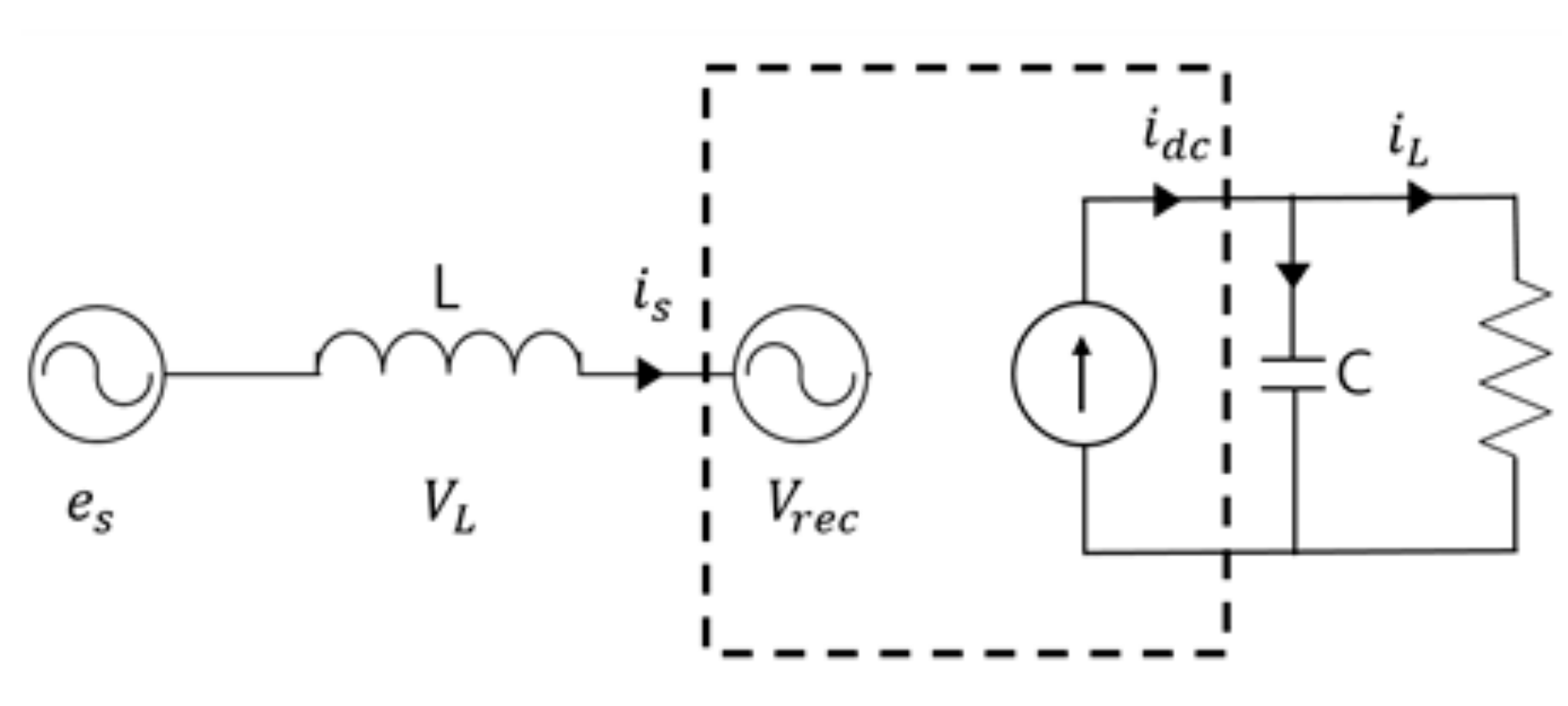
2.3. AFE Rectification Method in Large-Scale Electric Propulsion Systems
3. Large-Scale Electric Propulsion System Using an Improved AFE Rectifier
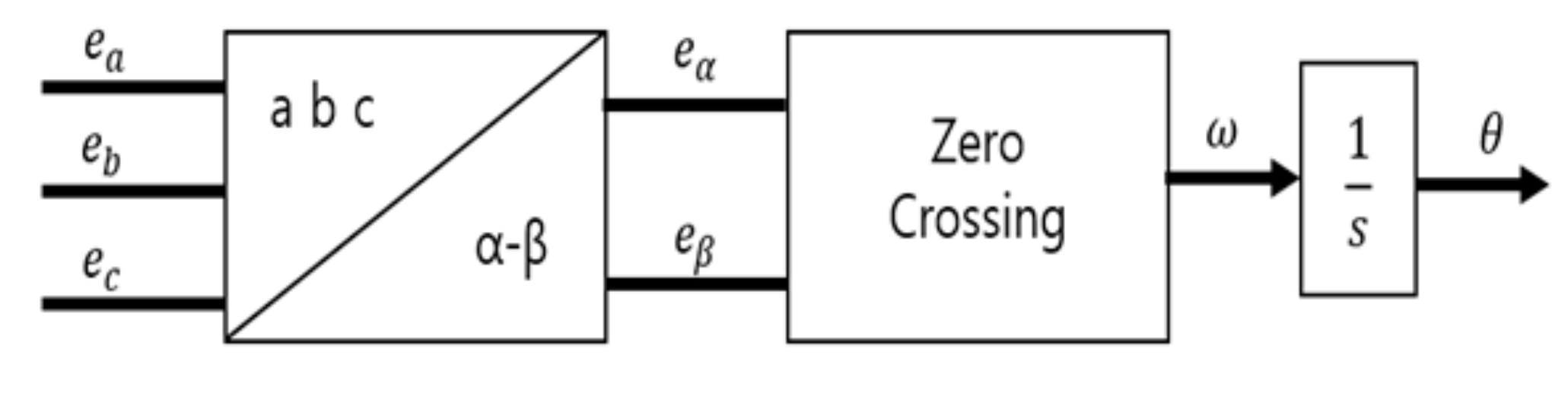
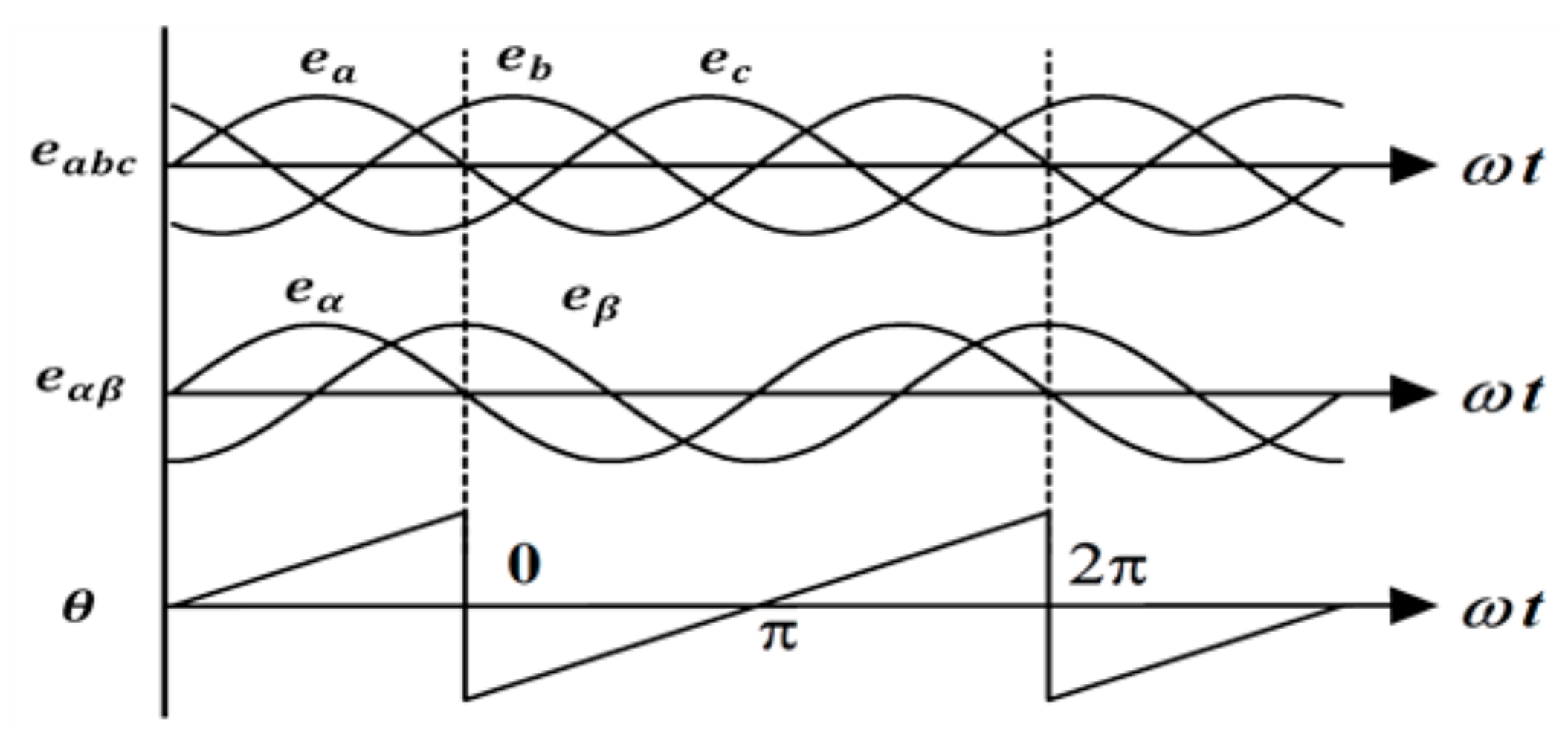
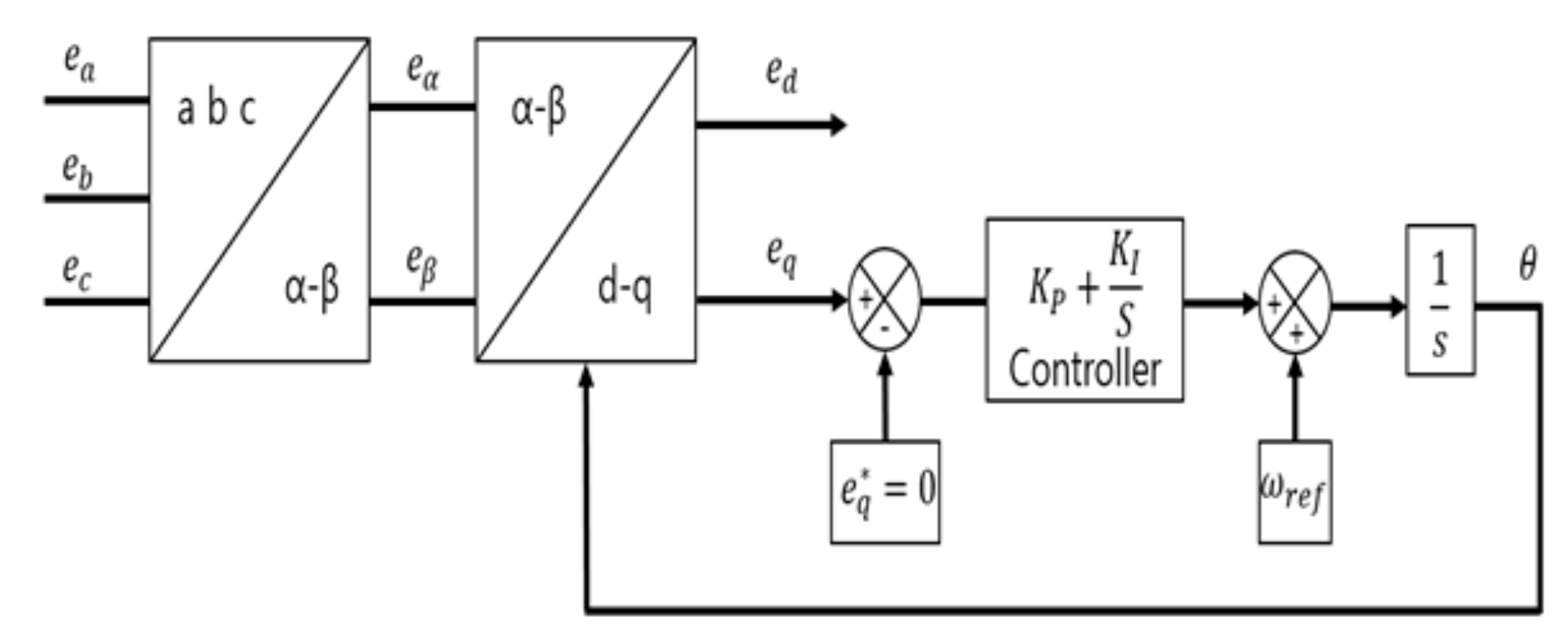
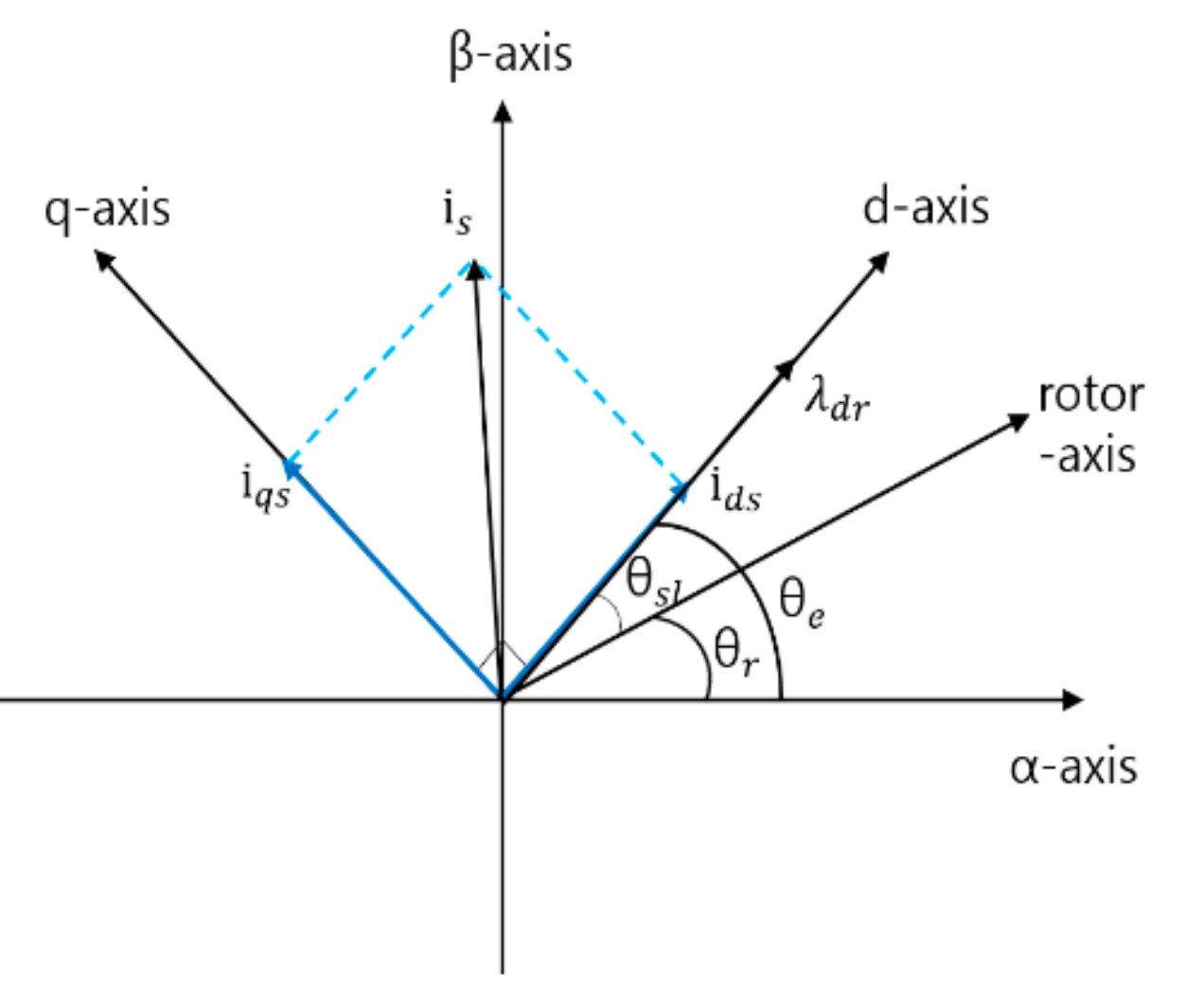
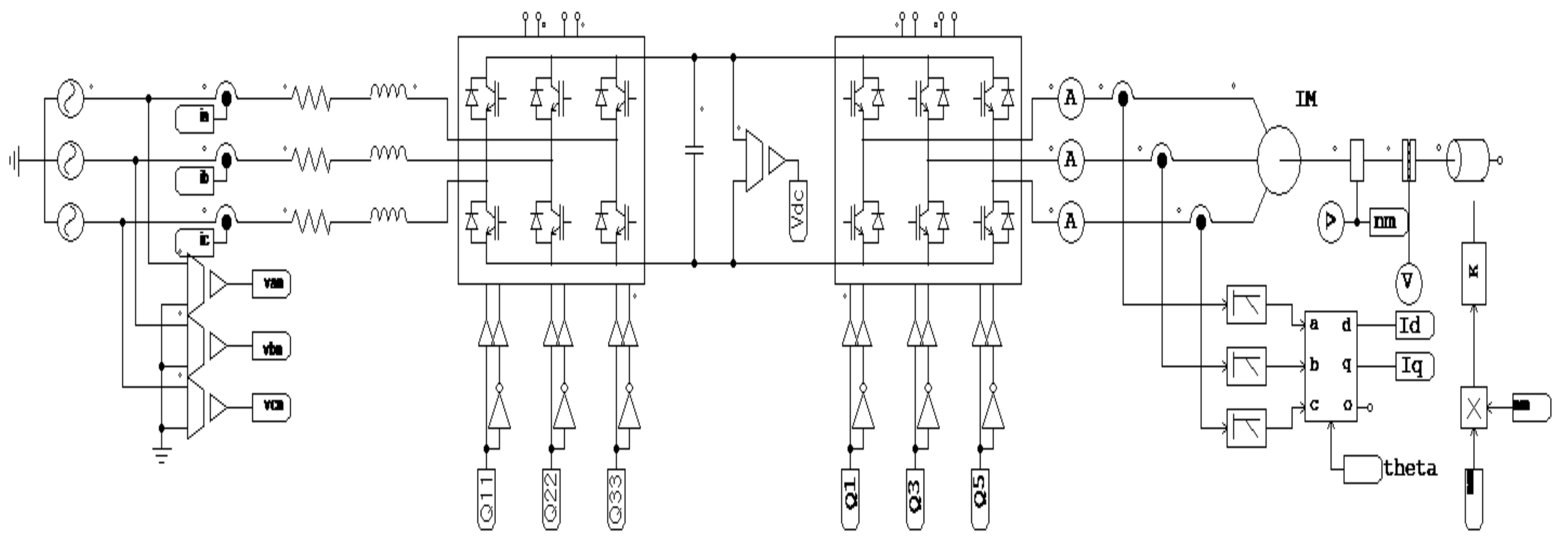
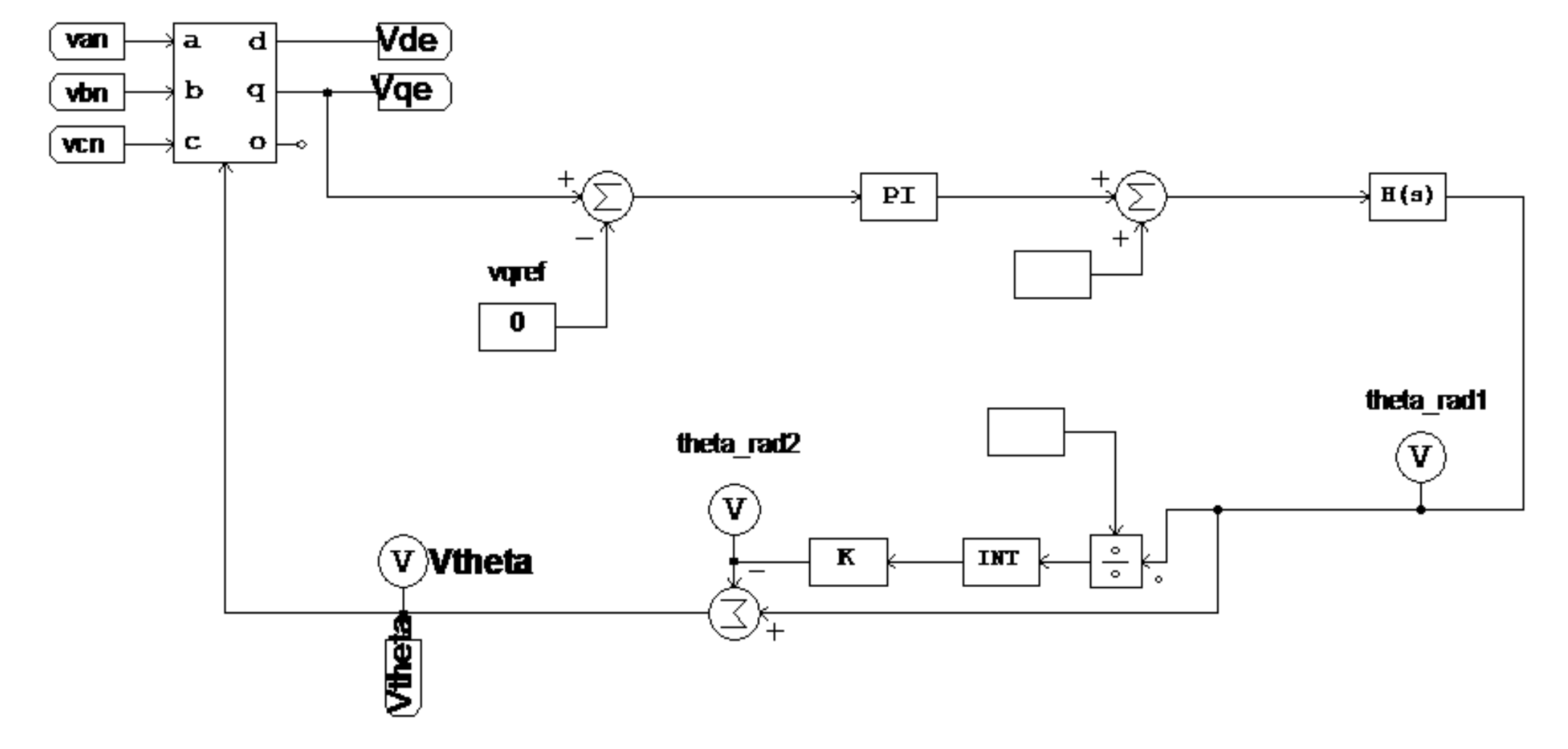
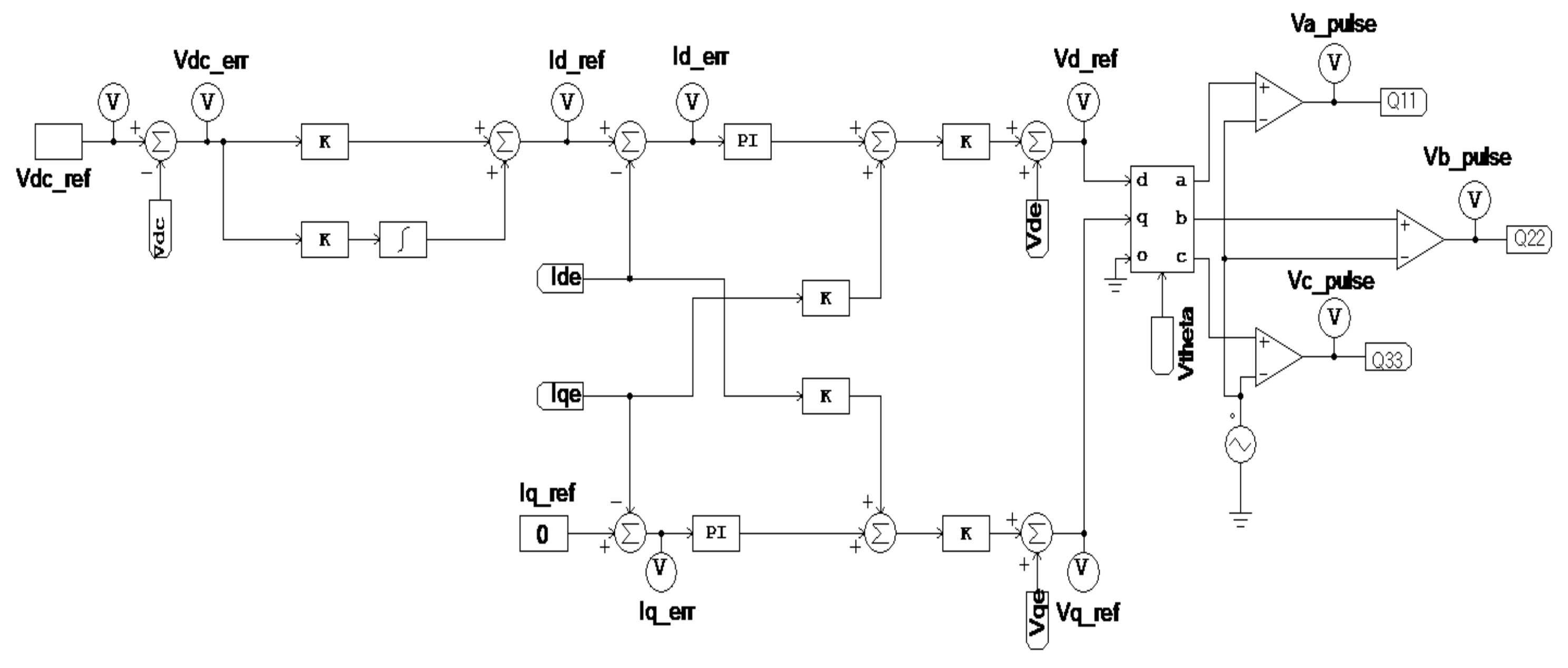
3.1. Improved AFE Rectifier Control
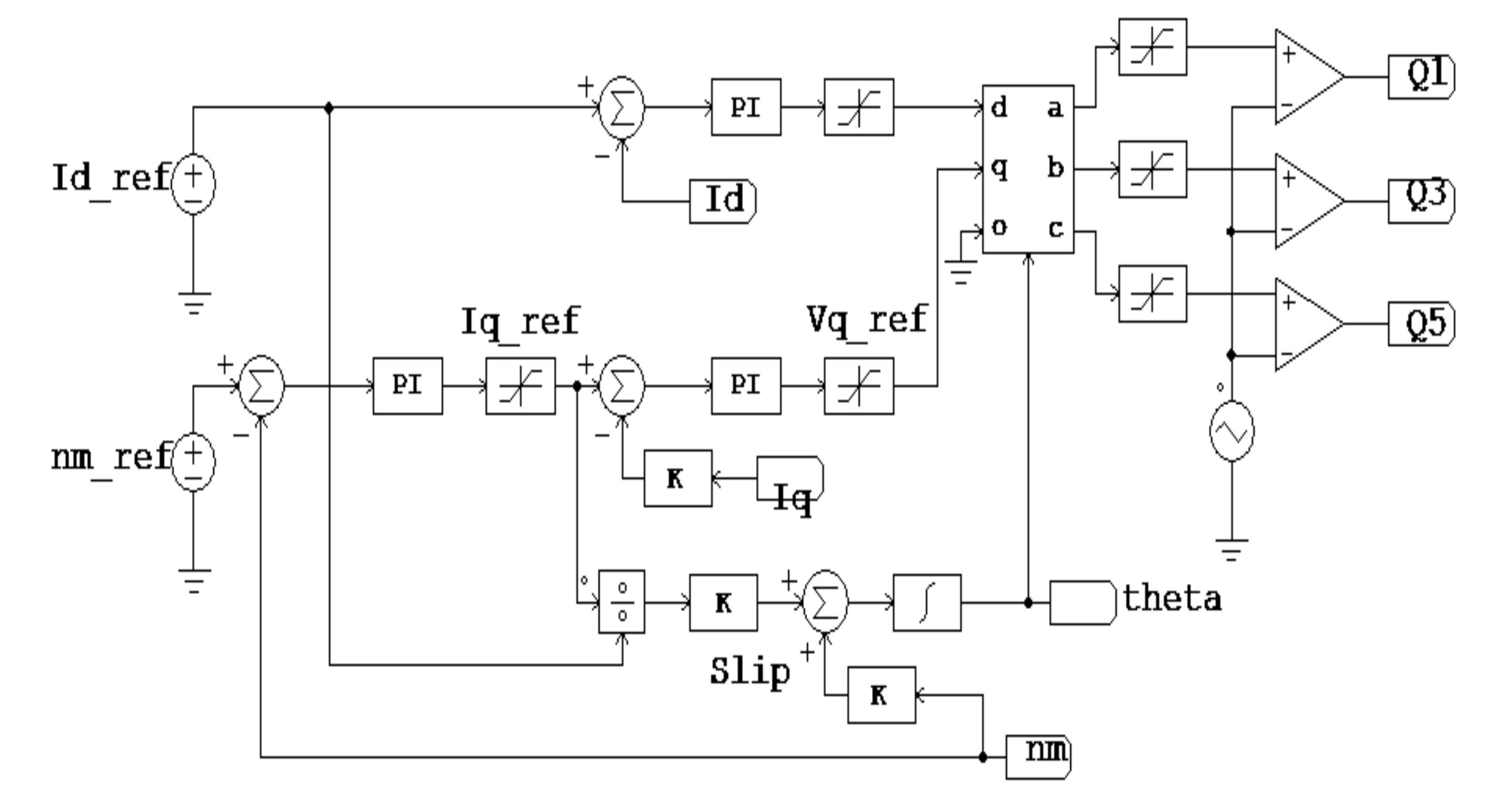
3.2. Controlling the Propulsion Motor Speed of a Large-Scale Electric Propulsion System Using the Improved AFE Rectifier
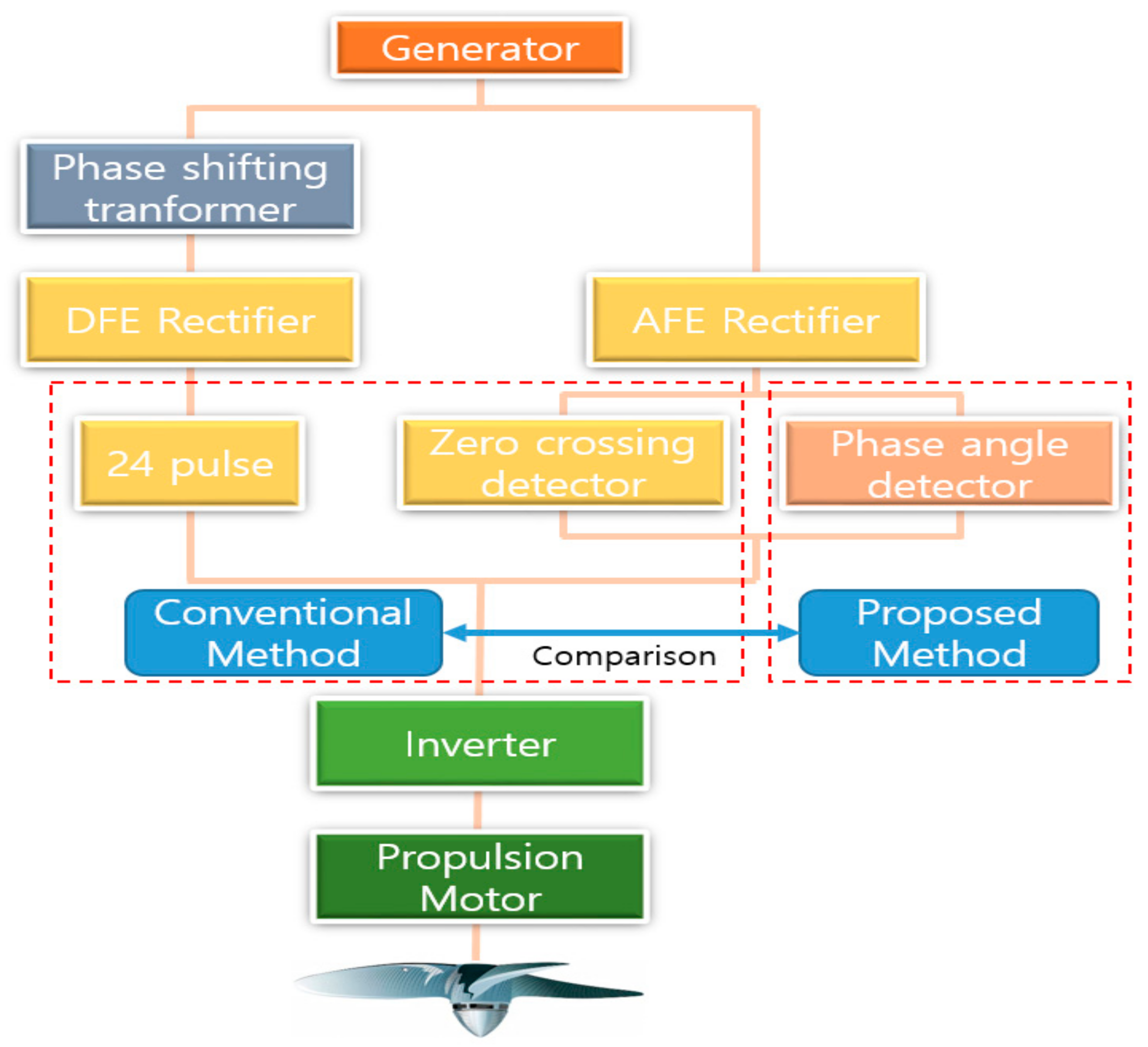
4. Methodology
5. Analysis Simulations of the Operating Characteristics of Large-Scale Electric Propulsion Systems According to Rectification Method
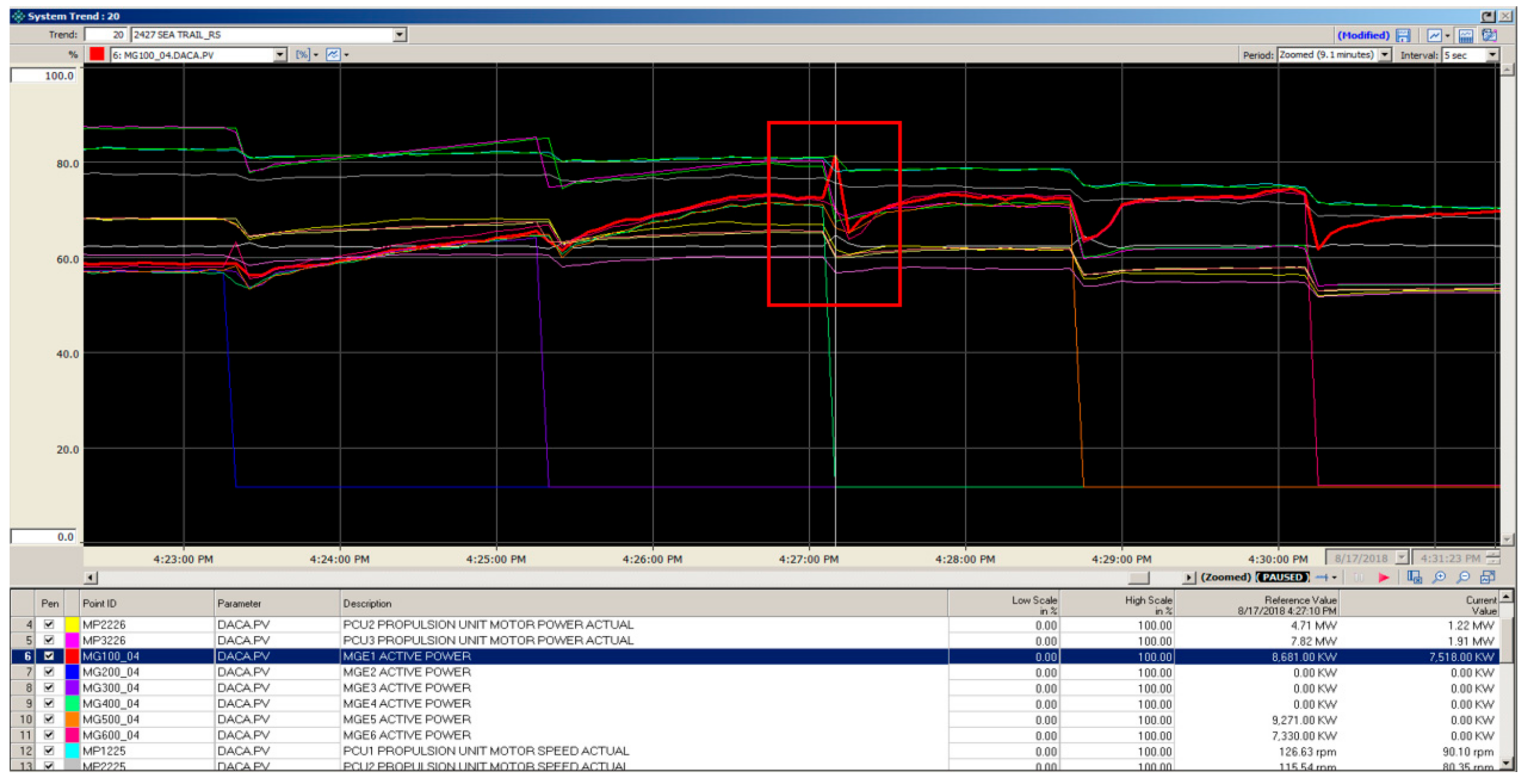
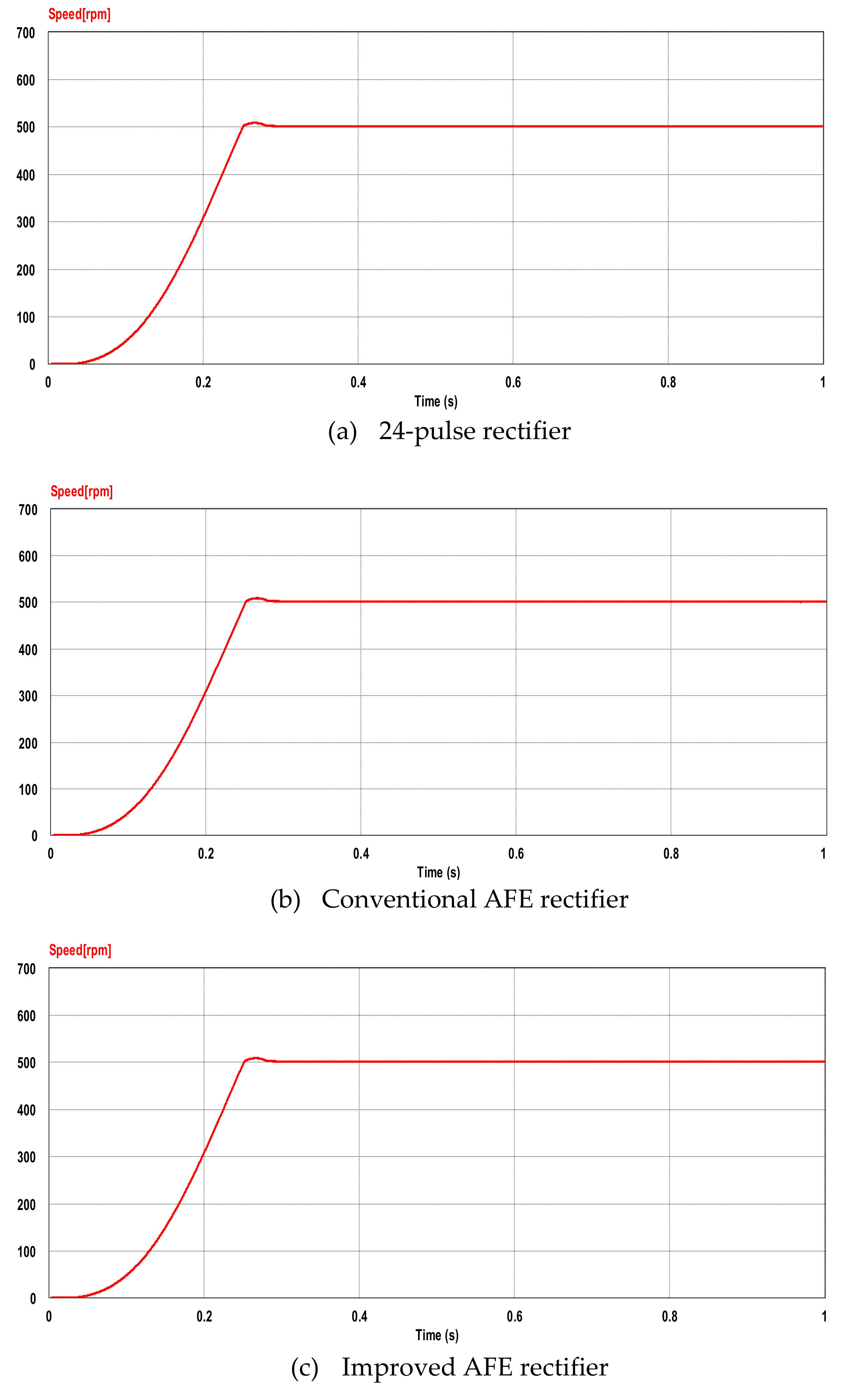
5.1. Speed Response Characteristics of the Propulsion Motor
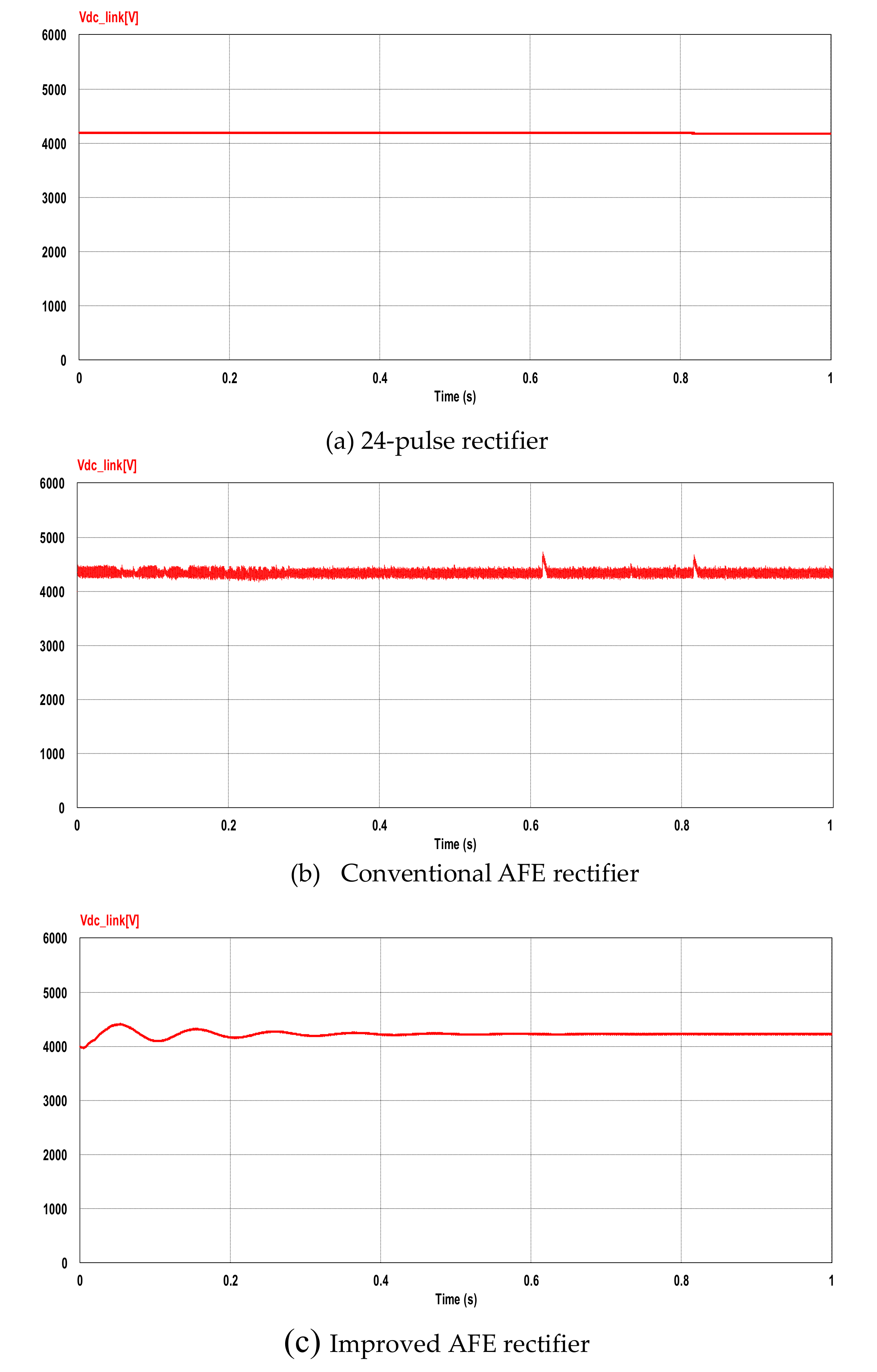
5.2. Comparison of the DC Output Voltage Waveform in the DC Link
5.3. Comparison of the Total Harmonic Distortion in the Voltage of the Power Source
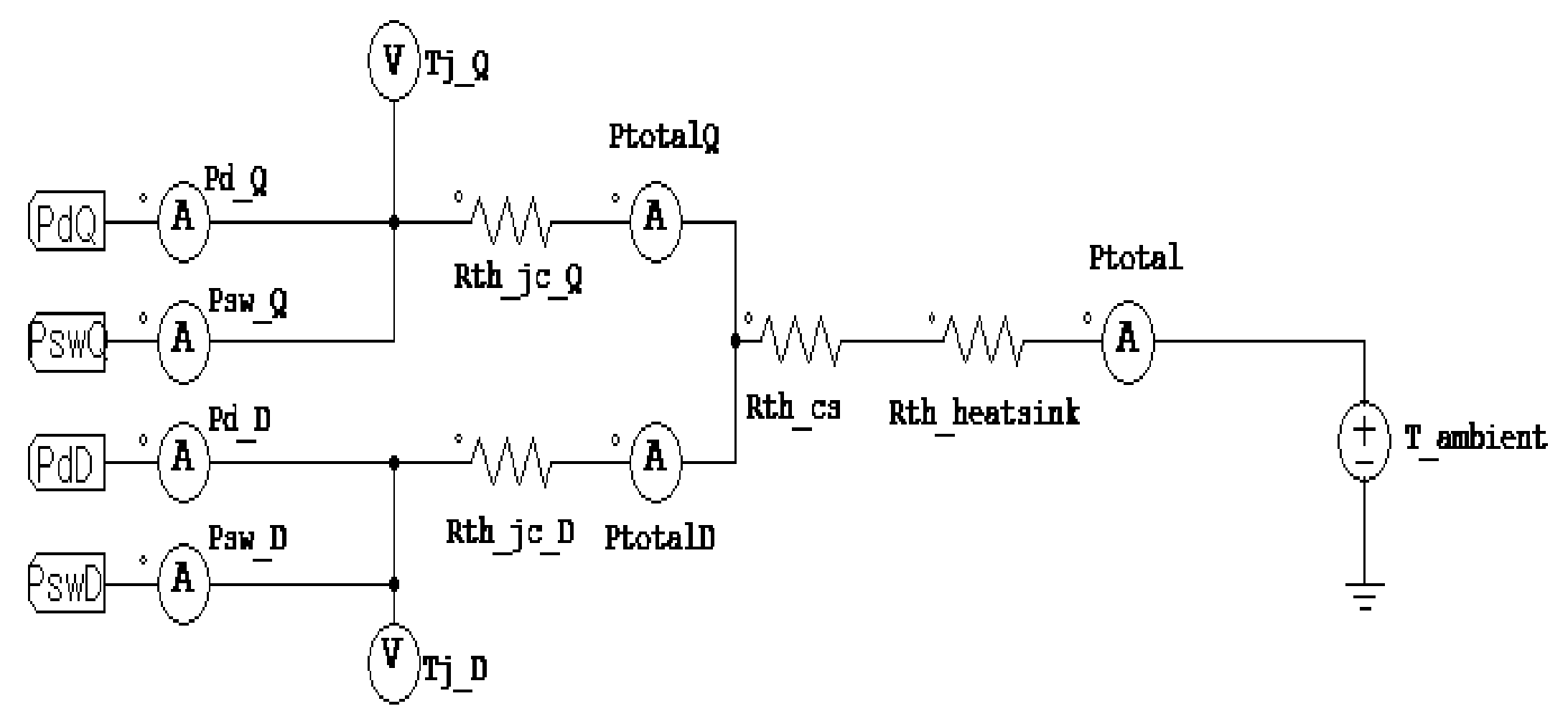
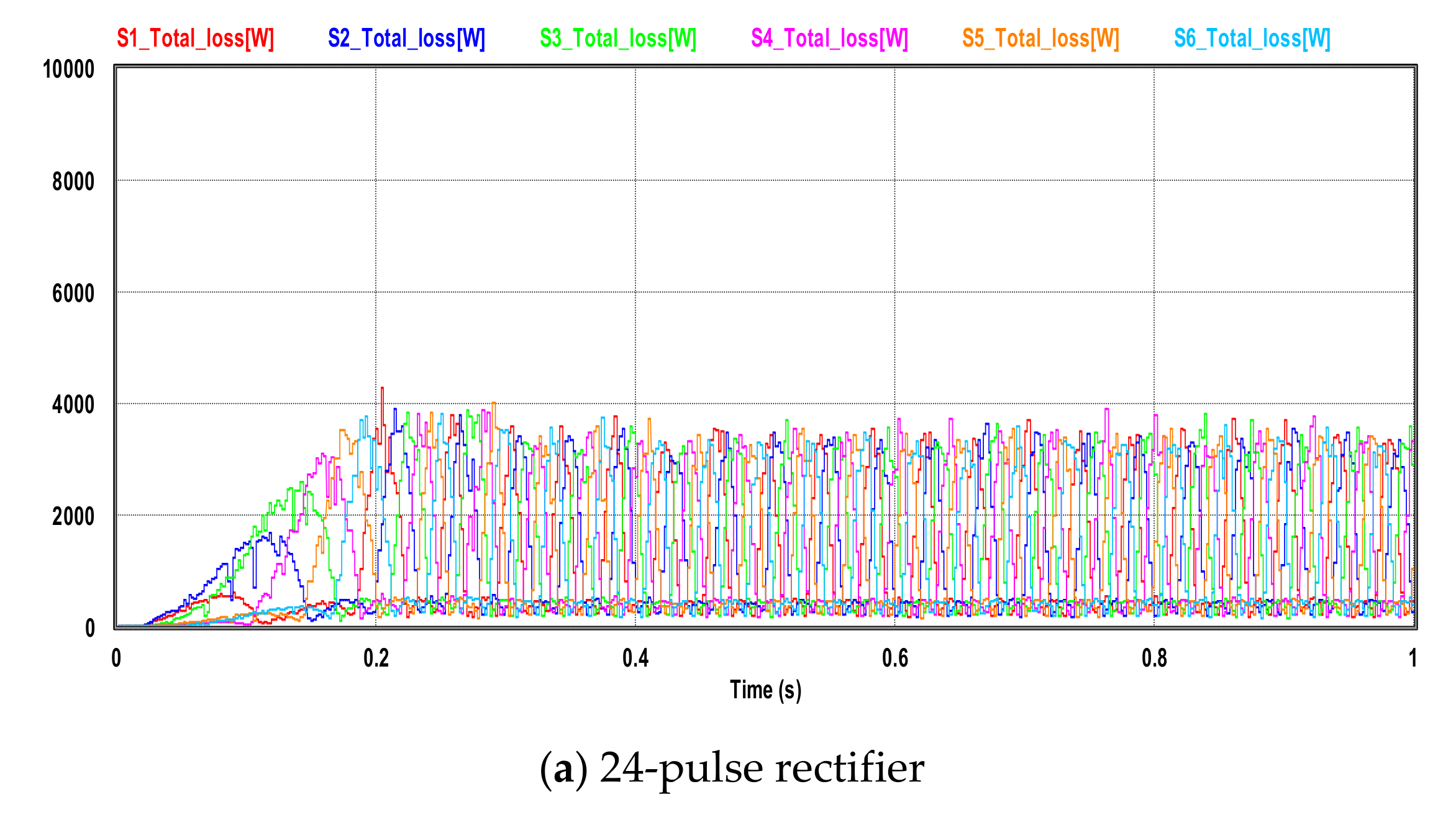
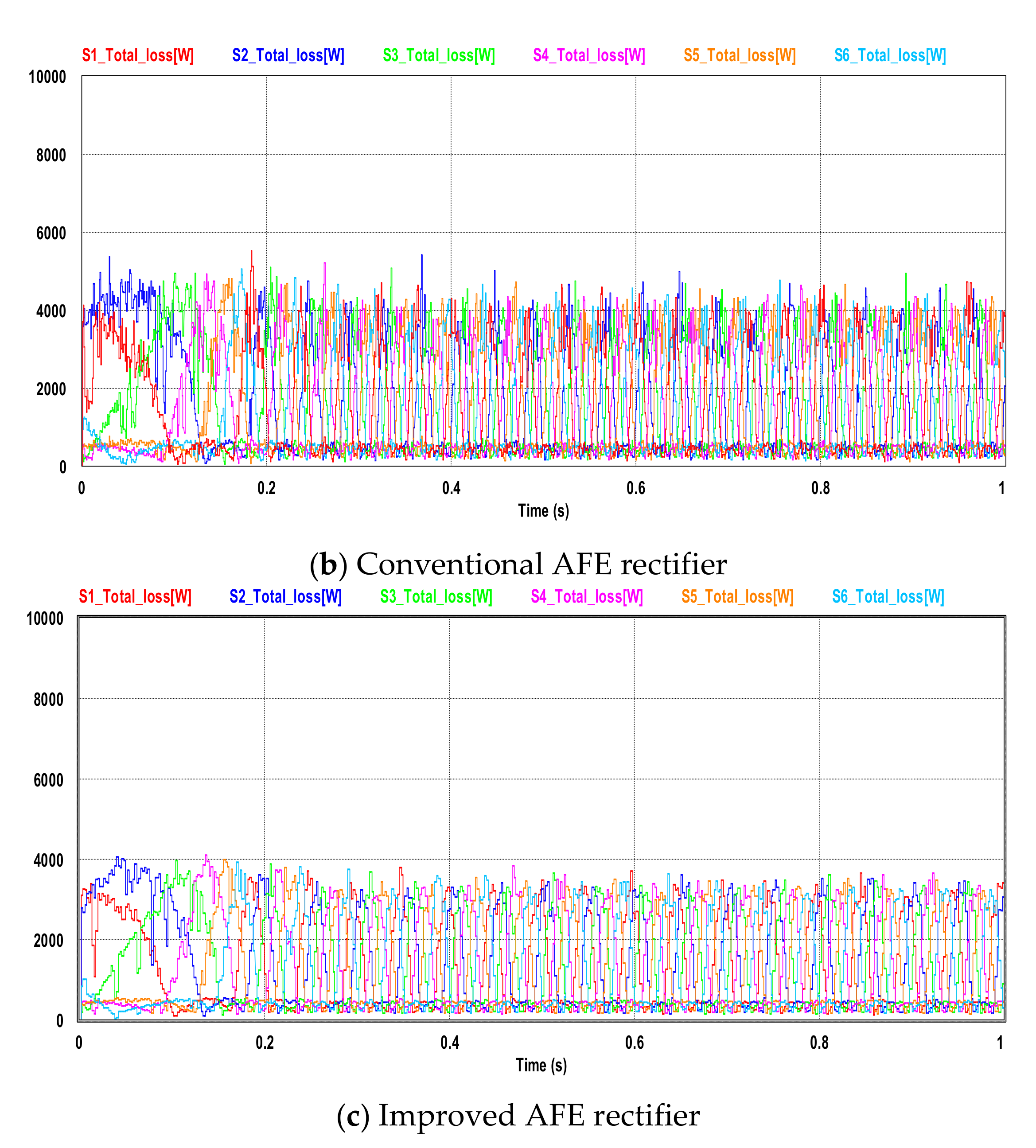
5.4. Comparison of the Heat Loss in the Inverter Switching Element
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Maritime Organization. Marine Environment Protection Committee 72nd Session. Available online: http://www.imo.org/en/MediaCentre/MeetingSummaries/MEPC/Pages/MEPC-72nd-session.aspx (accessed on 13 April 2018).
- International Maritime Organization. Marine Environment Protection Committee. Available online: http://www.imo.org/en/MediaCentre/HotTopics/Pages/Sulphur-2020.aspx (accessed on 23 June 2016).
- ABB Group. System Project Guide for Passenger. Available online: https://library.e.abb.com/public/608df0ae42ea2ce8c1257abd004ff506/ABB_System_Project_Guide_Passenger_Vessels.pdf (accessed on 1 February 2011).
- Hansen, J.F.; Wendt, F. History and State of the Art in Commercial Electric Ship Propulsion, Integrated Power Systems, and Future Trends. Proc. IEEE 2015, 103, 2229–2242. [Google Scholar] [CrossRef]
- McCoy, T.J. Trends in Ship Electric Propulsion. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; pp. 343–346. [Google Scholar]
- Skjong, E.; Cunningham, J.; Johansen, T.A.; Rodskar, E.; Molinas, M.; Volden, R. Past, Present, and Future Challenges of the Marine Vessel’s Electrical Power System. IEEE Trans. Transp. Electrif. 2016, 2, 522–537. [Google Scholar] [CrossRef]
- Vasquez, C.A. Methodology to Select the Electric Propulsion System for Platform Supply Vessels. Master’s Thesis, Universidade de Sao Paulo, Sao Paulo, Brazil, 2014. [Google Scholar]
- Clarksons Research. Available online: https://clarksonsresearch.wordpress.com/tag/propulsion/ (accessed on 31 March 2017).
- Ajioka, Y. Electric Propulsion Systems for Ships. Hitachi Rev. 2013, 62, 231–232. [Google Scholar]
- Ådnanes, A.K. Maritime Electrical Installations and Diesel Electric Propulsion; ABB AS: Oslo, Norway, 2003; 86. [Google Scholar]
- McCoy, T.J.; Amy, J.V. The State-of-the-Art of Integrated Electric Power and Propulsion Systems and Technologies on Ships. In Proceedings of the IEEE Electric Ship Technologies Symposium ESTS, Baltimore, MA, USA, 20–22 April 2009; pp. 340–344. [Google Scholar]
- Hoevenaars, T.; Evans, I.C.; Lawson, A. New Marine Harmonic Standards. IEEE Ind. Appl. Mag. 2010, 16, 16–25. [Google Scholar] [CrossRef]
- Verboomen, J.; Van Hertem, D.; Schavemaker, P.H.; Kling, W.L.; Belmans, R. Phase shifting transformers: Principles and applications. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005. [Google Scholar]
- Kim, J.S.; Choi, J.H.; Yoon, K.K.; Seo, D.H. Harmonic Reduction of Electric Propulsion Ship using New Rectification Scheme. J. Korean Inst. Inf. Commun. Eng. 2012, 16, 2230–2236. [Google Scholar] [CrossRef]
- Kim, J.S. Harmonic Reduction of Electric Propulsion Ship by Multipulse Drive. J. Korean Inst. Marit. Inf. Commun. Sci. 2010, 15, 425–431. [Google Scholar]
- Sun, J.; Bing, Z.; Karimi, K.J. Input Impedance Modeling of Multipulse Rectifiers by Harmonic Linearization. IEEE Trans. Power Electron. 2009, 24, 2812–2820. [Google Scholar]
- Akagi, H.; Isozaki, K. A Hybrid Active Filter for a Three-Phase 12-Pulse Diode Rectifier Used as the Front End of a Medium-Voltage Motor Drive. IEEE Trans. Power Electron. 2012, 27, 69–77. [Google Scholar] [CrossRef]
- Kamath, G.R.; Runyan, B.; Wood, R. A Compact Autotransformer Based 12-Pulse Rectifier Circuit. In Proceedings of the 27th Annual Conference of the IEEE Industrial Electronics Society, Denver, CO, USA, 29 November–2 December 2001; pp. 1344–1349. [Google Scholar]
- Skibinski, G.L.; Guskov, N.; Zhou, D. Cost Effective Multi-Pulse Transformer Solutions for Harmonic Mitigation in AC Drives. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; pp. 1488–1497. [Google Scholar]
- Wen, J.; Qin, H.; Wang, S.; Zhou, B. Basic Connections and Strategies of Isolated Phase-Shifting Transformers for Multipulse Rectifiers: A Review. In Proceedings of the 2012 Asia-Pacific Symposium on Electromagnetic Compatibility APEMC 2012, Singapore, 21–24 May 2012; pp. 105–108. [Google Scholar]
- Kim, S.Y.; Choe, S.; Ko, S.; Kim, S.; Sul, S.K. Electric Propulsion Naval Ships with Energy Storage Modules through AFE Converters. J. Power Electron. 2014, 14, 402–412. [Google Scholar] [CrossRef][Green Version]
- Kim, S.Y.; Cho, B.G.; Sul, S.K. Consideration of Active-Front-End Rectifier for Electric Propulsion Navy Ship. In Proceedings of the 2013 IEEE Energy Conversion Congress & Expo, Denver, CO, USA, 15–19 September 2013; pp. 13–19. [Google Scholar]
- Applied Materials. Available online: http://www.appliedmaterials.com/nanochip/nanochip-fab-solutions/december-2013/power-struggle (accessed on 8 March 2013).
- Gupta, A.; Rajev, T.; Sachin, M. Review on Zero Crossing Detector. India IJECT J. 2012, 7109, 366–368. [Google Scholar]
- Irmak, E.; Colak, I.; Kaplan, O.; Guler, N. Design and Application of a Novel Zero-Crossing Detector Circuit. In Proceedings of the International Conference on Power Engineering Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–4. [Google Scholar]
- Vainio, O.; Ovaska, S.J. Noise Reduction in Zero Crossing Detection by Predictive Digital Filtering. IEEE Trans. Ind. Electron. 1995, 42, 58–62. [Google Scholar] [CrossRef]
- Wall, R.W. Simple Methods for Detecting Zero Crossing. In Proceedings of the 29th Annual Conference of the IEEE Industrial Electronics Society (IEEE Cat. No.03CH37468), Roanoke, VA, USA, 2–6 November 2003; Volume 3, pp. 2477–2481. [Google Scholar]
- Parvez, M.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. An Improved Active-Front-End Rectifier Using Model Predictive Control. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 122–127. [Google Scholar]
- Chomat, M. Operation of Active Front-End Rectifier in Electric Drive under Unbalanced Voltage Supply. Electr. Mach. Drives 2012, 10, 195–216. [Google Scholar]
- Chung, S.K. Phase-Locked Loop for Grid-Connected Three-Phase Power Conversion Systems. IEE Proc. Electr. Power Appl. 2000, 147, 213–219. [Google Scholar] [CrossRef]
- Trivedi, M.S.; Mujumdar, U.B. Study and Simulation of Parks Transform PLL for robust single phase grid connected system. Int. J. Recent Innov. Trends Comput. Commun. 2015, 3, 149–152. [Google Scholar]
- Guo, X.Q.; Wu, W.Y.; Gu, H.R. Phase Locked Loop and Synchronization Methods for Grid- Interfaced Converters: A Review. Prz. Elektrotechniczny 2011, 87, 182–187. [Google Scholar]
- Salamah, A.M.; Finney, S.J.; Willians, B.W. Three-phase Phase-locked loop for Distorted Utilities. IET Electr. Power Appl. 2001, 67, 263–270. [Google Scholar]
- Wiechmann, E.P.; Aqueveque, P.; Burgos, R.; Rodriguez, J. On the Efficiency of Voltage Source and Current Source Inverters for High-Power Drives. IEEE Trans. Ind. Electron. 2008, 55, 1771–1782. [Google Scholar] [CrossRef]
- Wu, B. High-Power Converters and AC Drives, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006; pp. 251–316. [Google Scholar]
- Al-Falahi, M.D.A.; Tarasiuk, T.; Jayasinghe, S.G.; Jin, Z.; Enshaei, H.; Guerrero, J.M. Ac Ship Microgrids: Control and Power Management Optimization. Energies 2018, 11, 1458. [Google Scholar] [CrossRef]
- Zahedi, B.; Norum, L.E. Modeling and Simulation of All-Electric Ships with Low-Voltage DC Hybrid Power Systems. IEEE Trans. Power Electron. 2013, 28, 4525–4537. [Google Scholar] [CrossRef]
- Thantirige, K.; Rathore, A.K.; Panda, S.K.; Jayasignhe, G.; Zagrodnik, M.A.; Gupta, A.K. Medium Voltage Multilevel Converters for Ship Electric Propulsion Drives. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Archen, Germany, 3–5 March 2015. [Google Scholar]
- Sofras, E.; Prousalidis, J. Developing a New Methodology for Evaluating Diesel—Electric Propulsion. J. Mar. Eng. Technol. 2014, 13, 63–92. [Google Scholar] [CrossRef][Green Version]
- ABB GROUP. Available online: http://pdf.nauticexpo.com/pdf/abb-marine/abb-lngcarrier-brochure-final/30709-44457.html (accessed on 1 May 2009).
- Prousalidis, J.; Antonopoulos, G.; Mouzakis, P.; Sofras, E. On Resolving Reactive Power Problems in Ship Electrical Energy Systems. J. Mar. Eng. Technol. 2015, 14, 124–136. [Google Scholar] [CrossRef][Green Version]
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Sul, S.K. Control of Electric Machine Drives Systems; Hongleung Science: Seoul, Korea, 2016; pp. 306–326. [Google Scholar]
- ABB. ABB HiPak IGBT Module 5SNA 1200G450350 Datasheet. Available online: https://new.abb.com/semiconductors/integrated-gate-commutated-thyristors- (accessed on 8 January 2019).
- IEEE. IEEE Std 519-2014 IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE: New York, NY, USA, 2014; pp. 5–9. [Google Scholar]

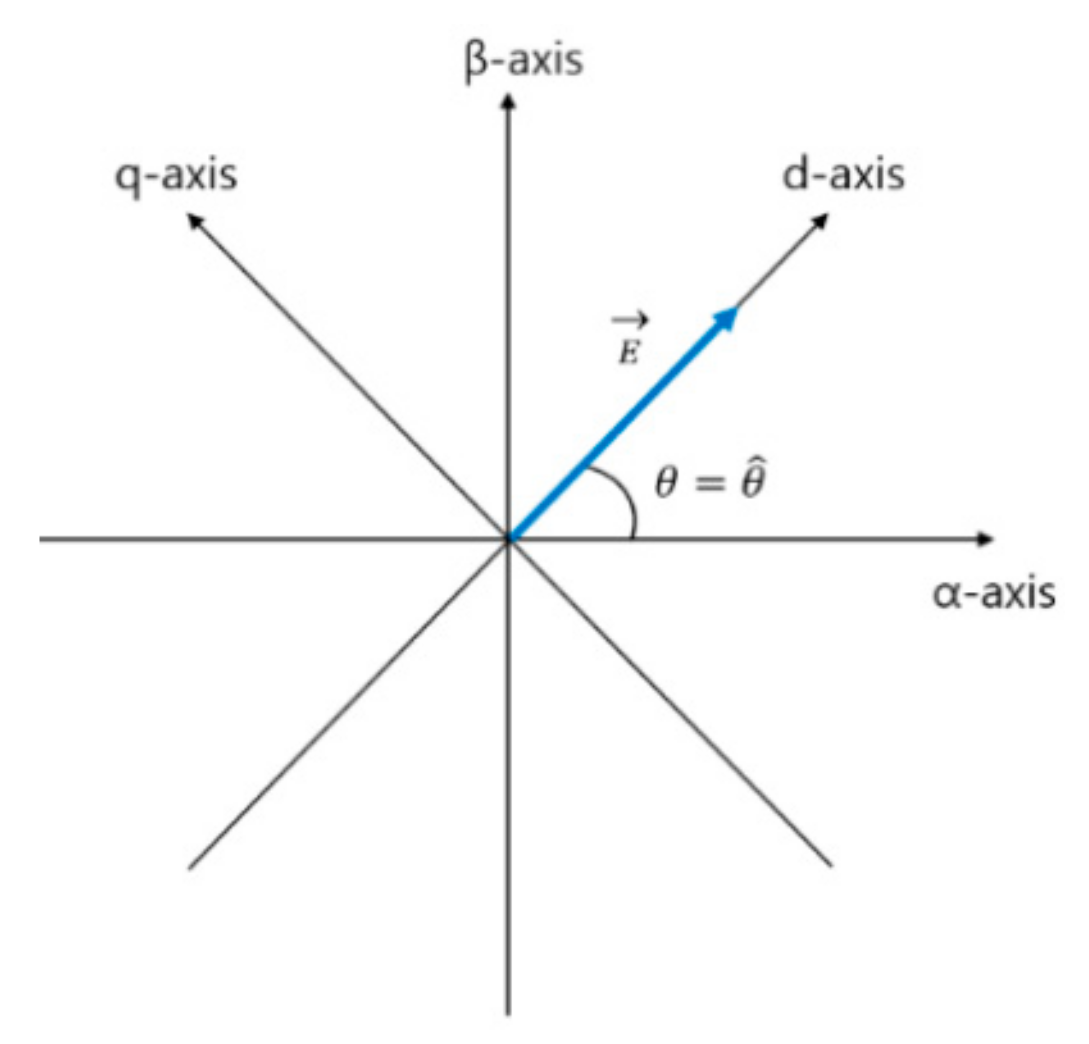
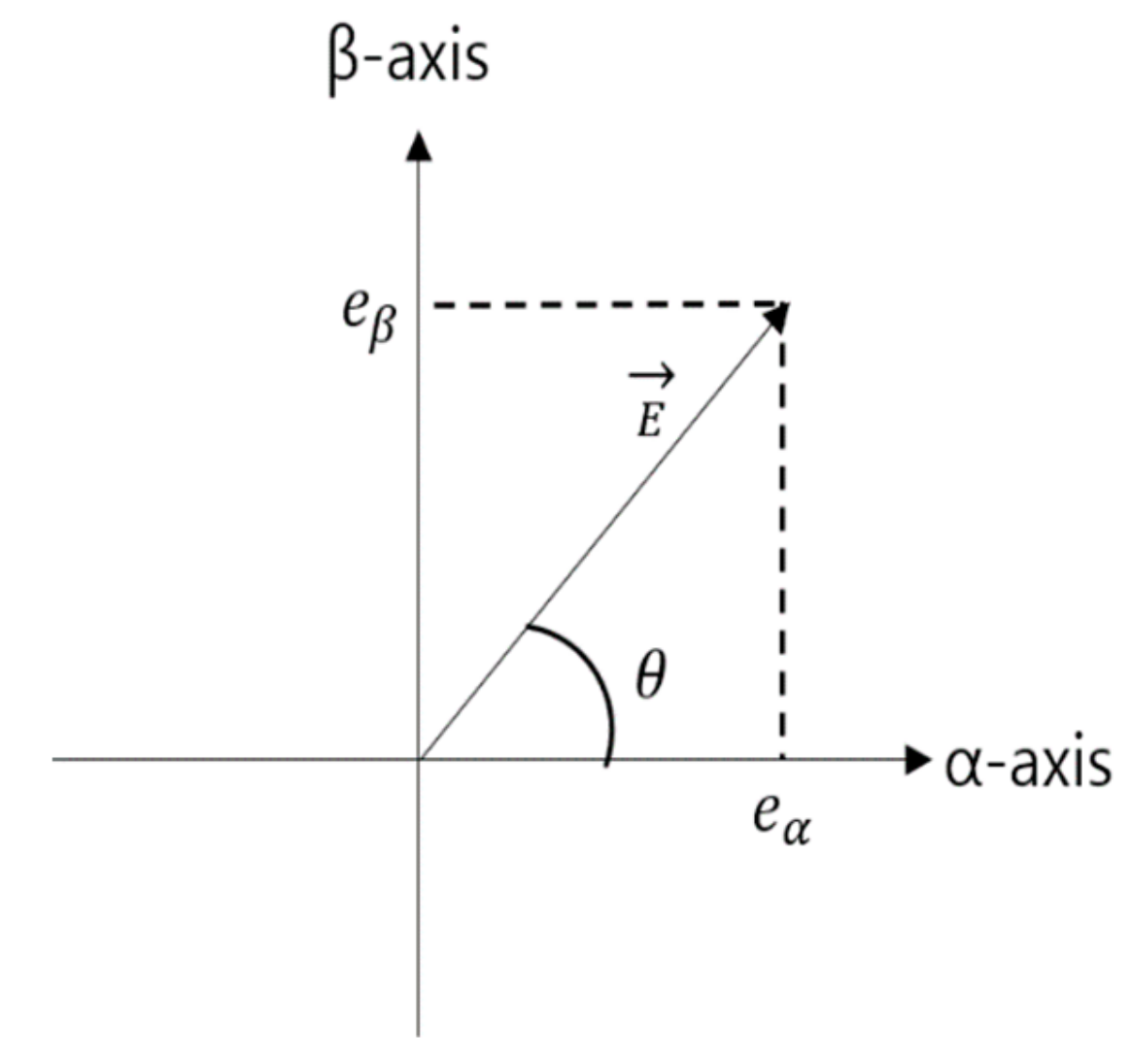
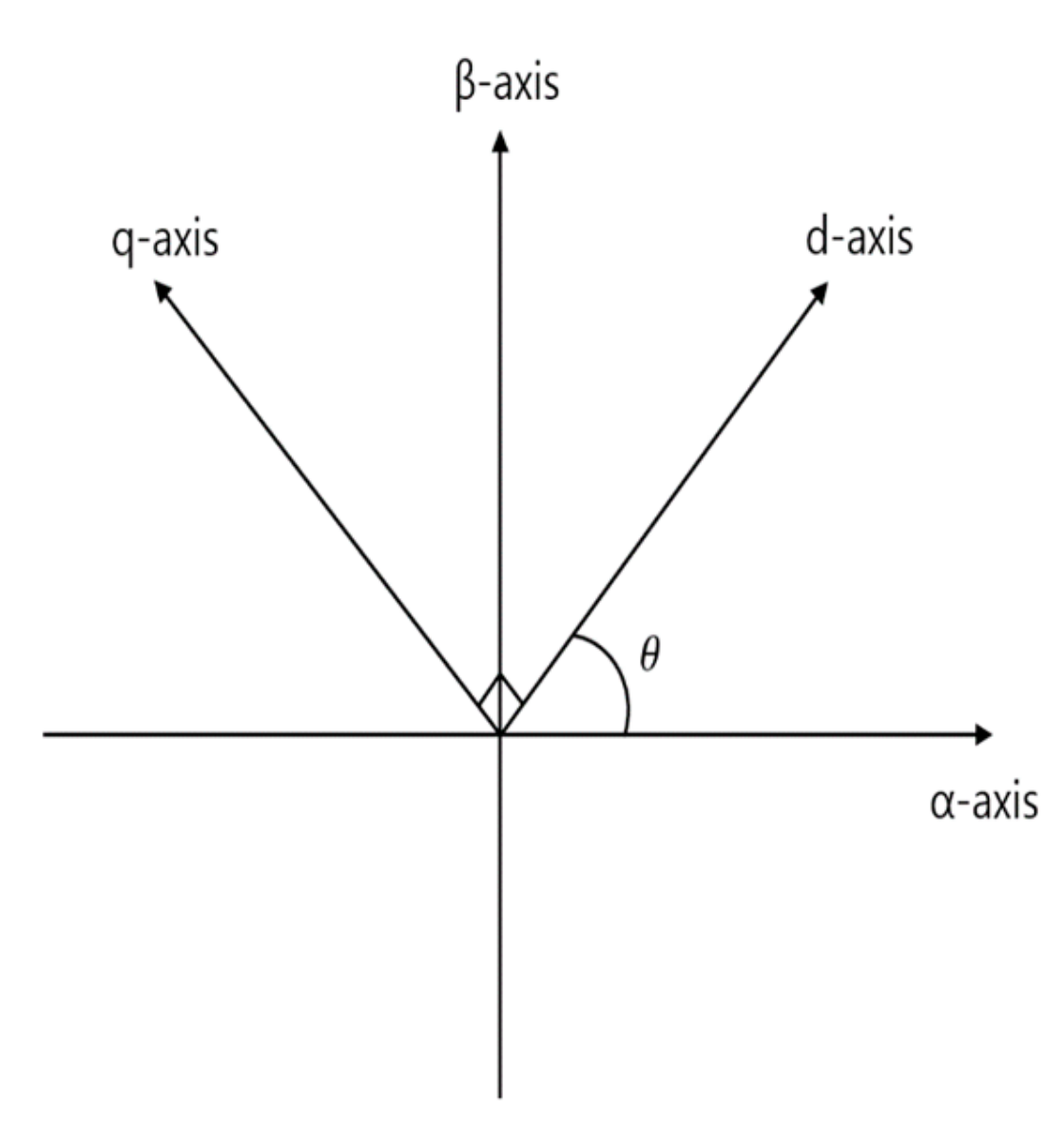
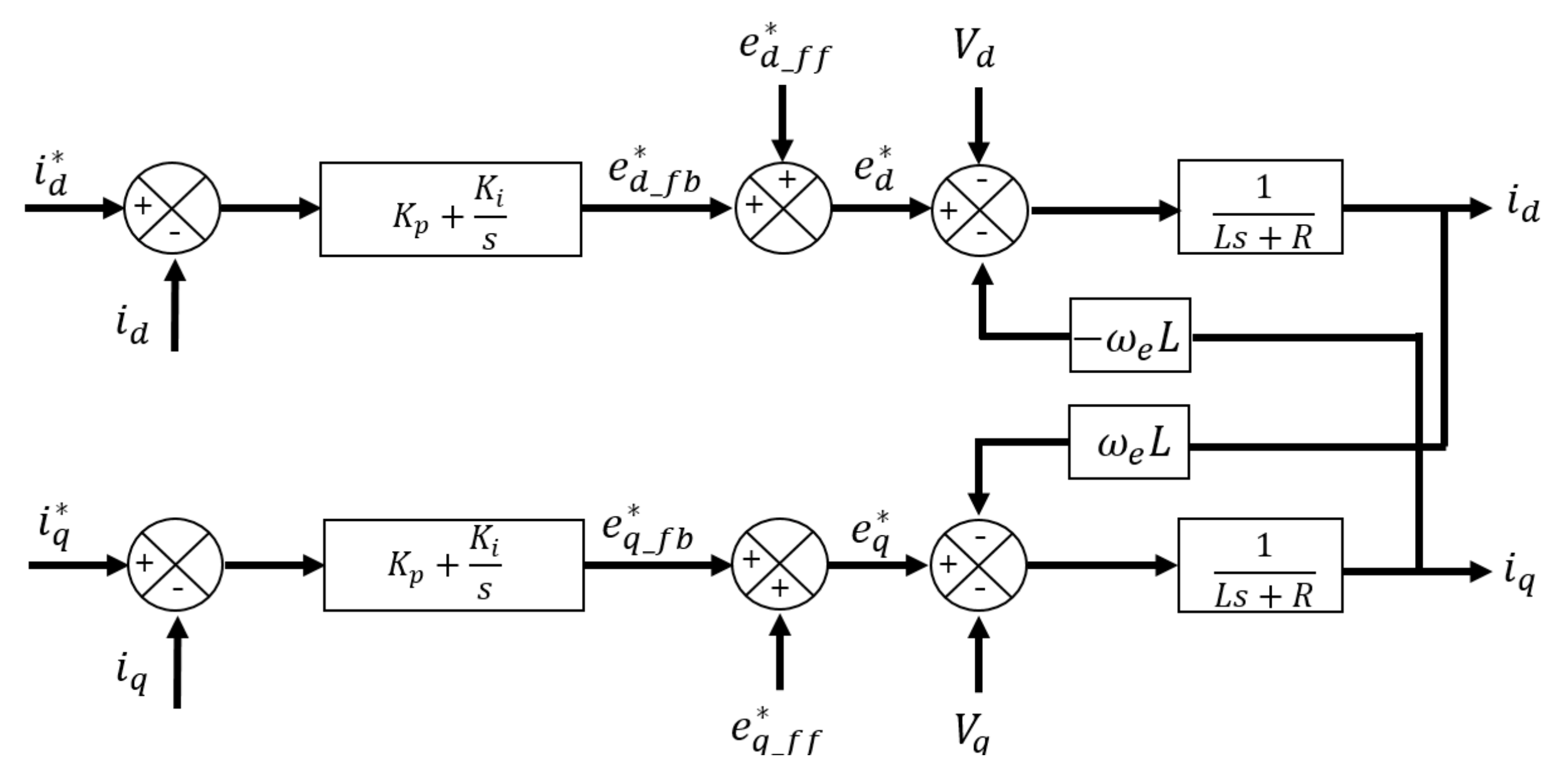

| Component | 24-Pulse DFE Rectifier | AFE Rectifier |
|---|---|---|
| Propulsion Motor | 2 pcs 41,679 kg × 2 = 83,358kg | 2 pcs 41,679 kg × 2 = 83,358 kg |
| Phase Shifting Transformer | 4 pcs 11,940 kg × 4 = 47,760kg | - |
| Rectifier | 8pcs 4730 kg × 8 = 37,840kg | 4pcs 3760 kg × 4 = 15,040 kg |
| Inverter | 4 pcs 3760 kg × 4 = 15,040kg | 4 pcs 3,760 kg × 4 = 15,040 kg |
| Total Weight | 183,998 kg | 113,438 kg |
| Rectifier Type | Total Harmonic Distortion (THD) |
|---|---|
| 6-Pulse | 25~27% |
| 12-Pulse | 8~11% |
| 18-Pulse | 4~5% |
| 24-Pulse | 2~3% |
| AFE | 4~5% |
| Item | Value | Item | Value |
|---|---|---|---|
| Rated Power | 6000 Kw | 0.0167 Ω | |
| Rated Voltage | 3300 V | 1.49 mH | |
| Rated Current | 1200 A | 0.07 Ω | |
| Rated Speed | 650.8 rpm | 0.35 mH | |
| Frequency | 60 Hz | 48 mH | |
| Number of Poles | 10 | 169 Kg/m2 |
| Model | ABB Hi-Pak 5SNA 1200G450350 |
|---|---|
| Collector-emitter voltage | 4500 V |
| DC collector current | 1200 A |
| Peak collector current | 2400 A |
| DC forward current | 1200 A |
| Conventional AFE | 24 Pulse | Improved AFE | |
|---|---|---|---|
| Diode loss average [W] | 514 | 453 | 445 |
| IGBT loss average [W] | 3717 | 3321 | 3350 |
| Total loss average [W] | 4231 | 3774 | 3795 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, H.; Kim, J.; Yoon, K. Large-Scale Electric Propulsion Systems in Ships Using an Active Front-End Rectifier. J. Mar. Sci. Eng. 2019, 7, 168. https://doi.org/10.3390/jmse7060168
Jeon H, Kim J, Yoon K. Large-Scale Electric Propulsion Systems in Ships Using an Active Front-End Rectifier. Journal of Marine Science and Engineering. 2019; 7(6):168. https://doi.org/10.3390/jmse7060168
Chicago/Turabian StyleJeon, Hyeonmin, Jongsu Kim, and Kyoungkuk Yoon. 2019. "Large-Scale Electric Propulsion Systems in Ships Using an Active Front-End Rectifier" Journal of Marine Science and Engineering 7, no. 6: 168. https://doi.org/10.3390/jmse7060168
APA StyleJeon, H., Kim, J., & Yoon, K. (2019). Large-Scale Electric Propulsion Systems in Ships Using an Active Front-End Rectifier. Journal of Marine Science and Engineering, 7(6), 168. https://doi.org/10.3390/jmse7060168







