Weather-Routing System Based on METOC Navigation Risk Assessment
Abstract
:1. Introduction
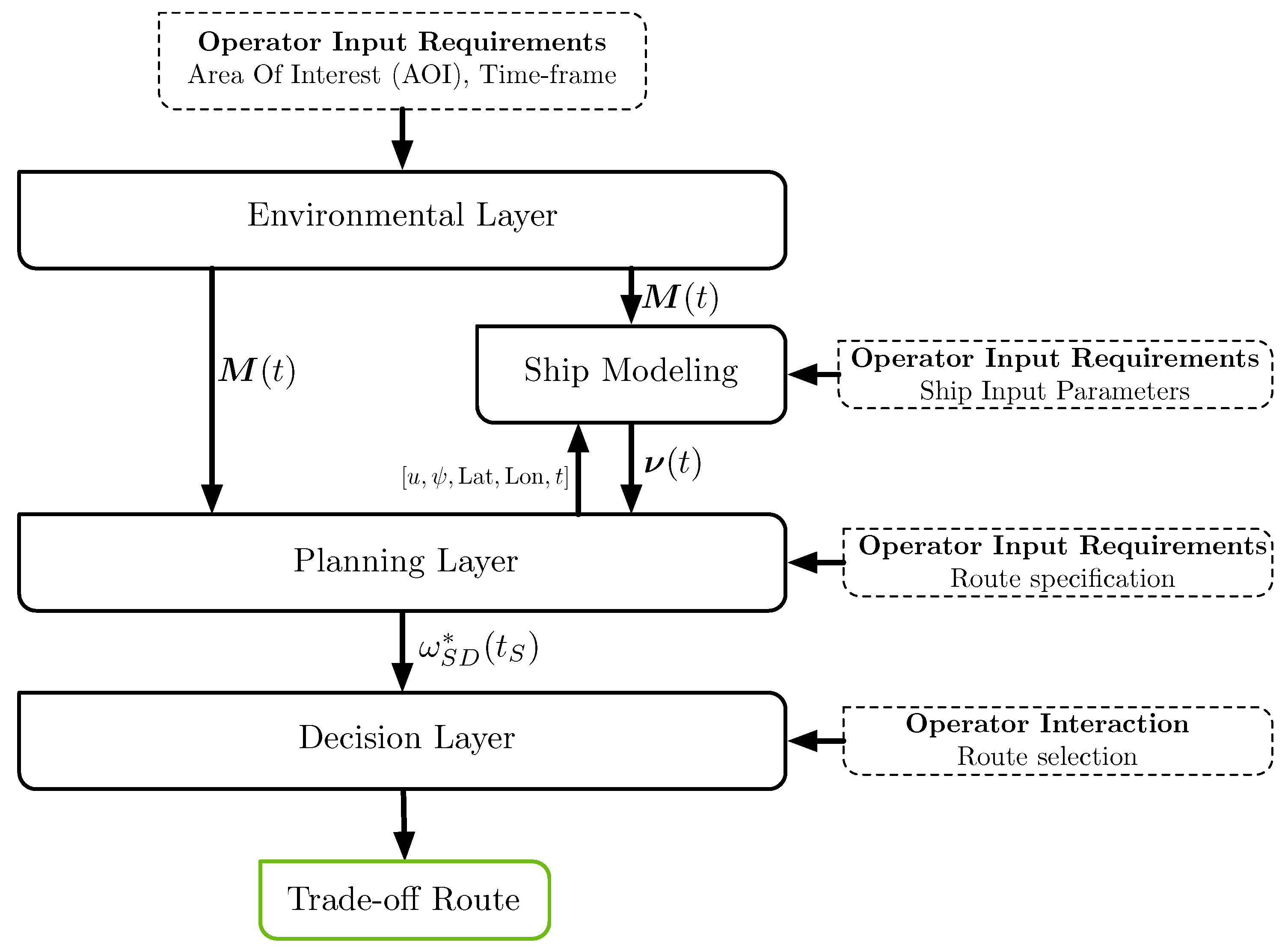
2. Multi-Criteria Weather-Routing Framework
2.1. Environmental Layer
2.2. Ship Modeling
2.3. Planning Layer
- Estimate of the still/calm water resistance, , at the speed of interest.
- Estimate of the added resistance caused by the interaction of the ship with the waves, , at the speed of interest.
- surf-riding and broaching-to;
- successive high-wave attack;
- synchronous rolling;
- reduction of intact-stability when riding a wave crest amidships.
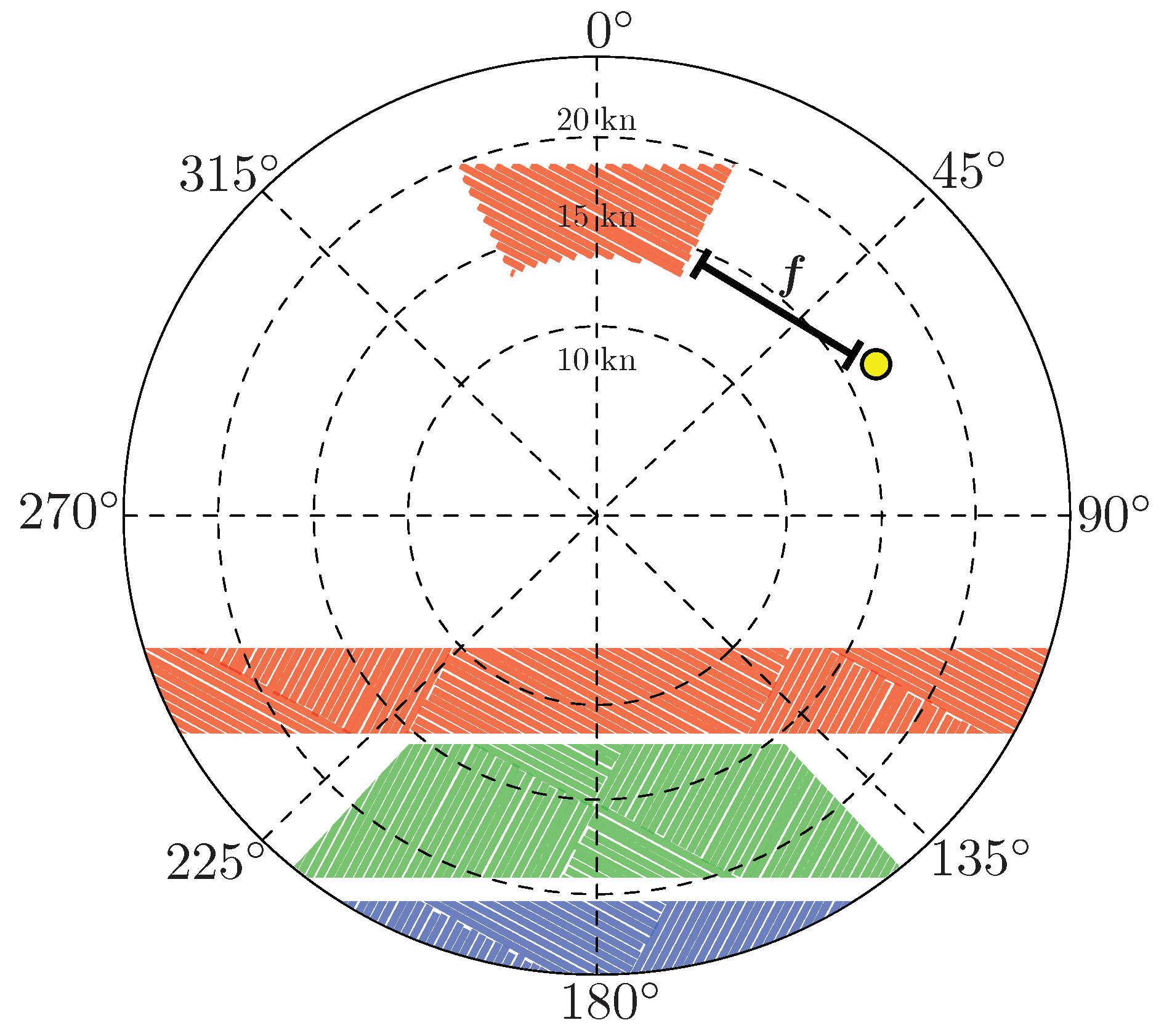
2.4. Decision Layer
3. Results: Testing the Proposed System in a Real Scenario
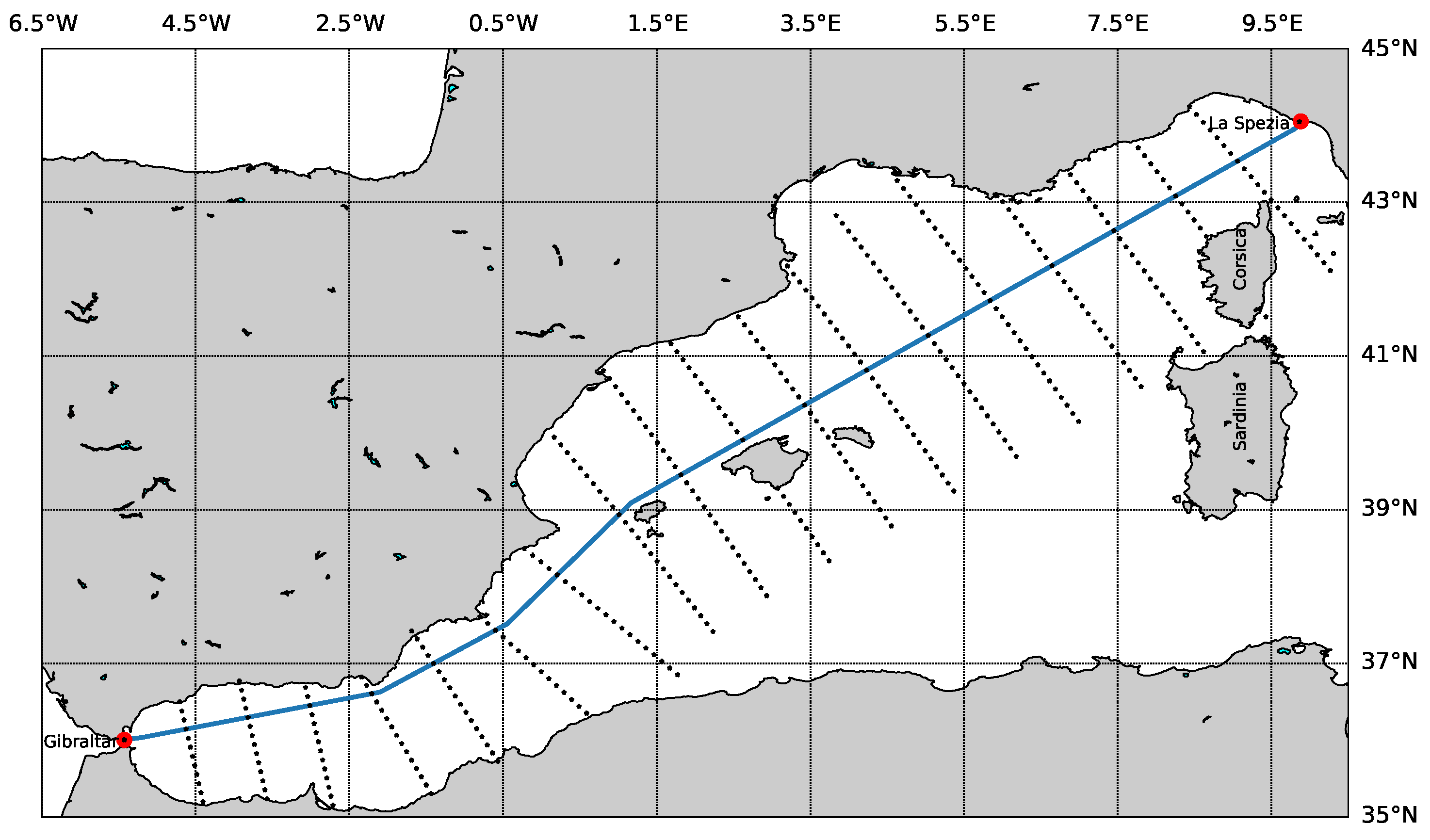
3.1. Scenario Setup
- AOI longitude range: from W to E.
- AOI latitude range: from N to N.
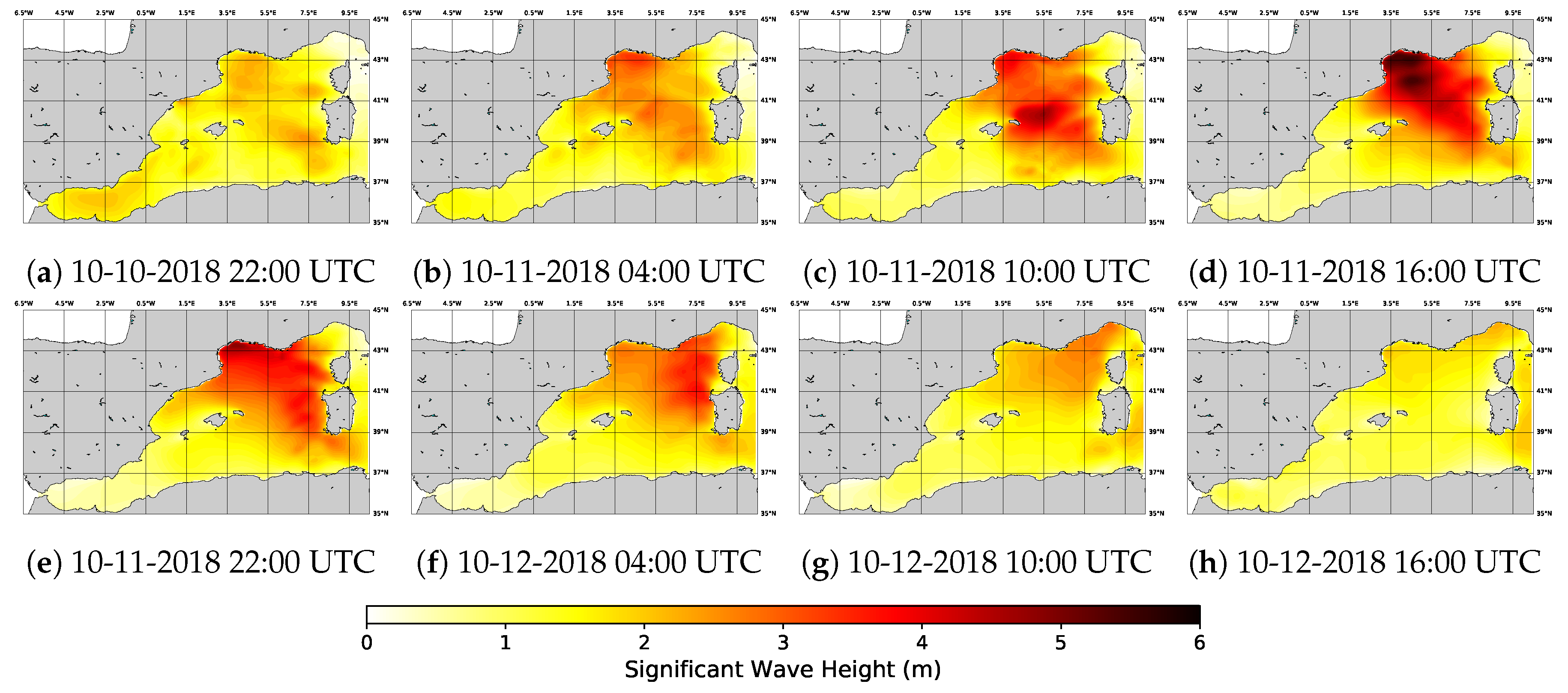
- ETD: 10 October 2018 22:00 UTC.
3.2. Environmental Layer Setup
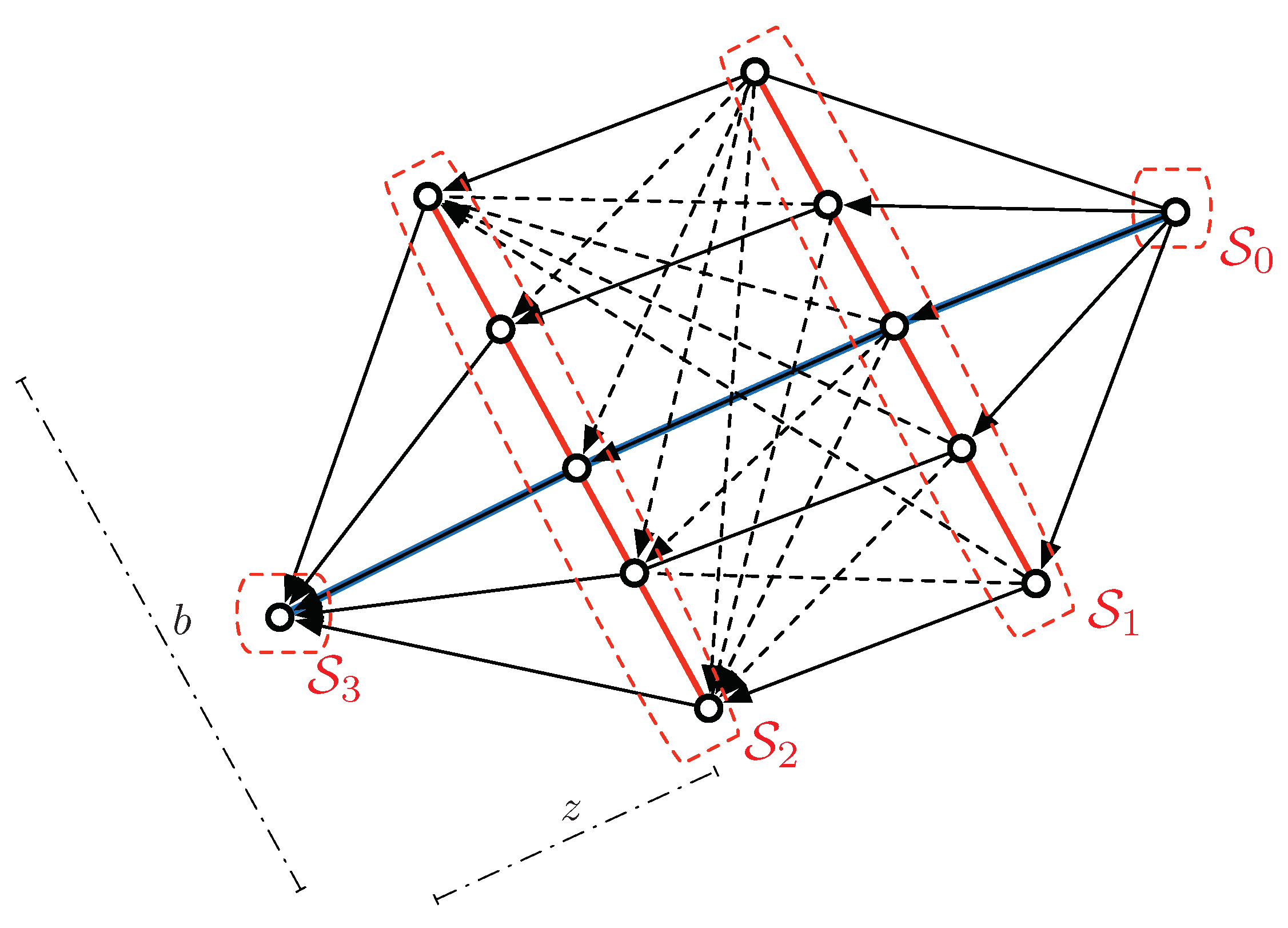
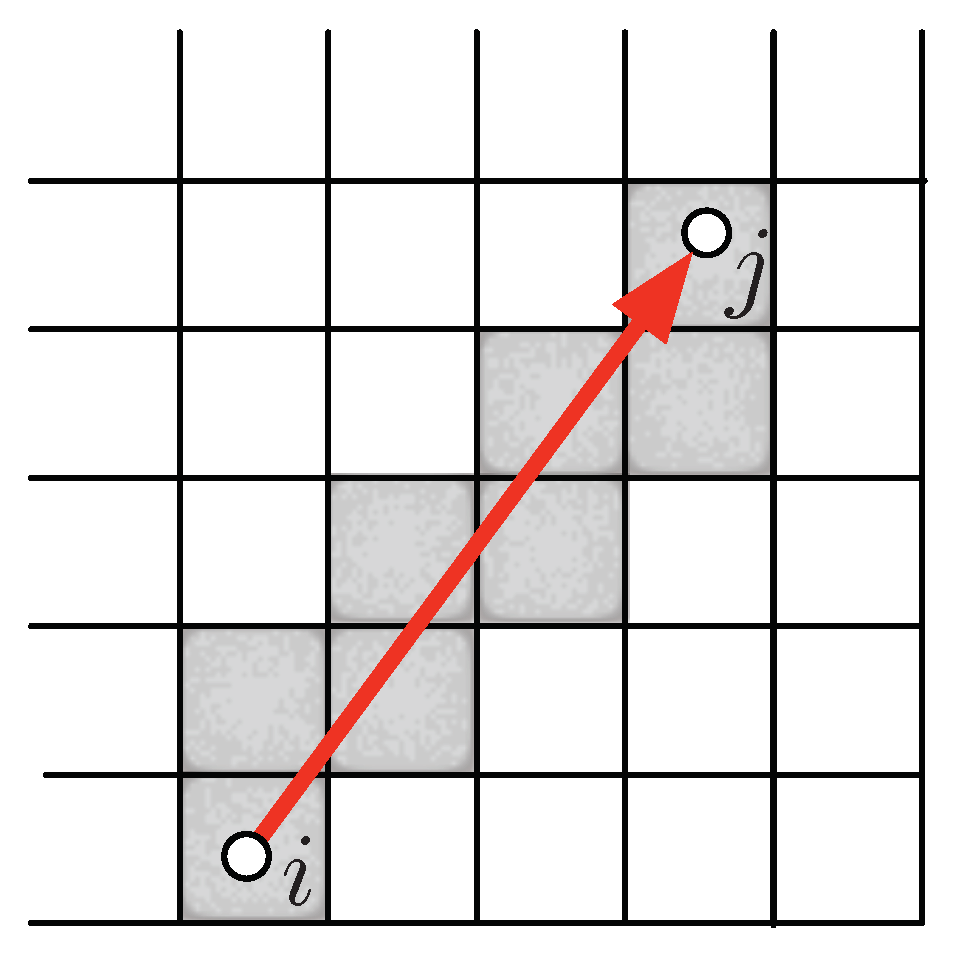
3.3. Planning Layer Setup: Navigation Graph Construction
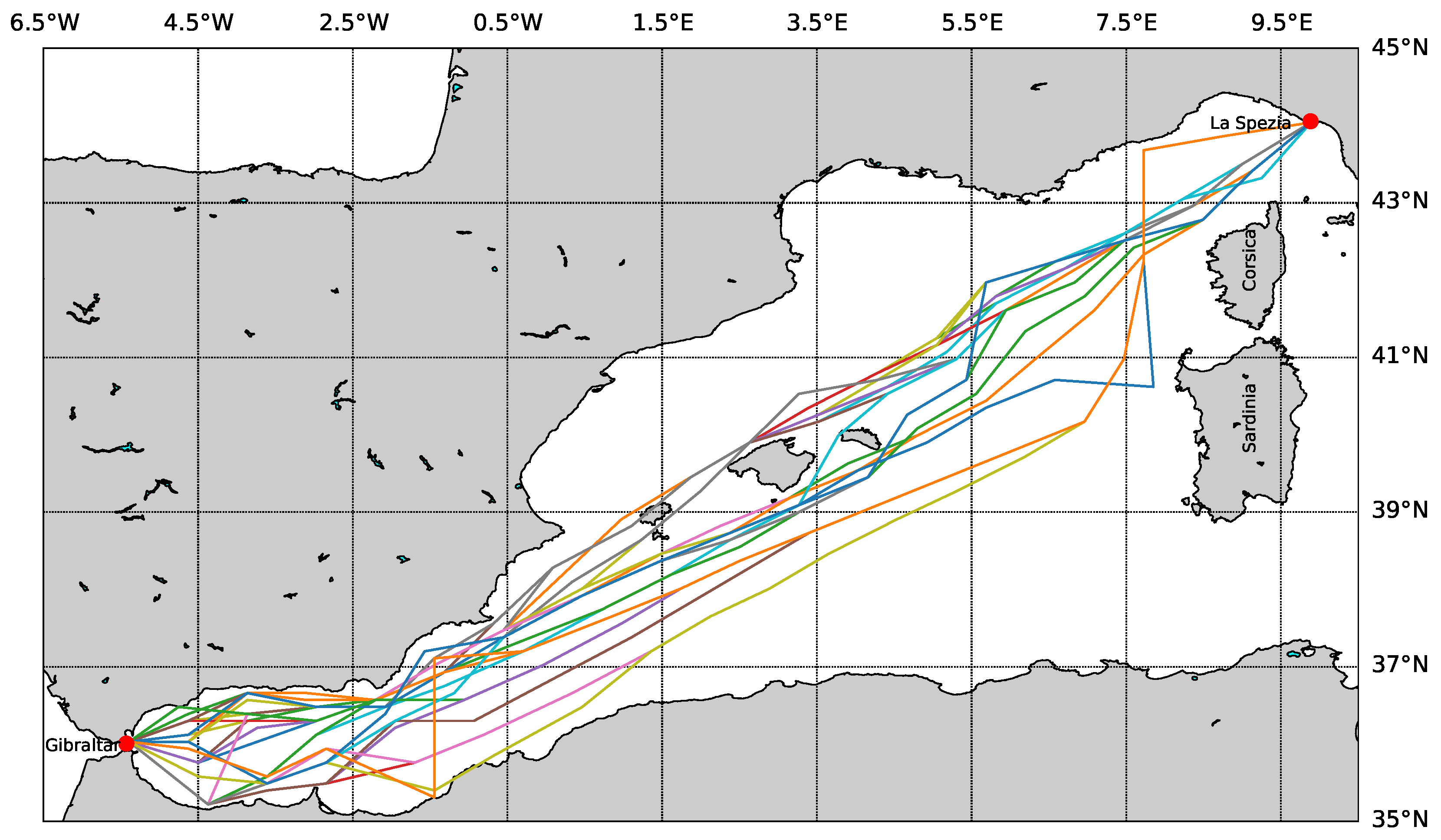
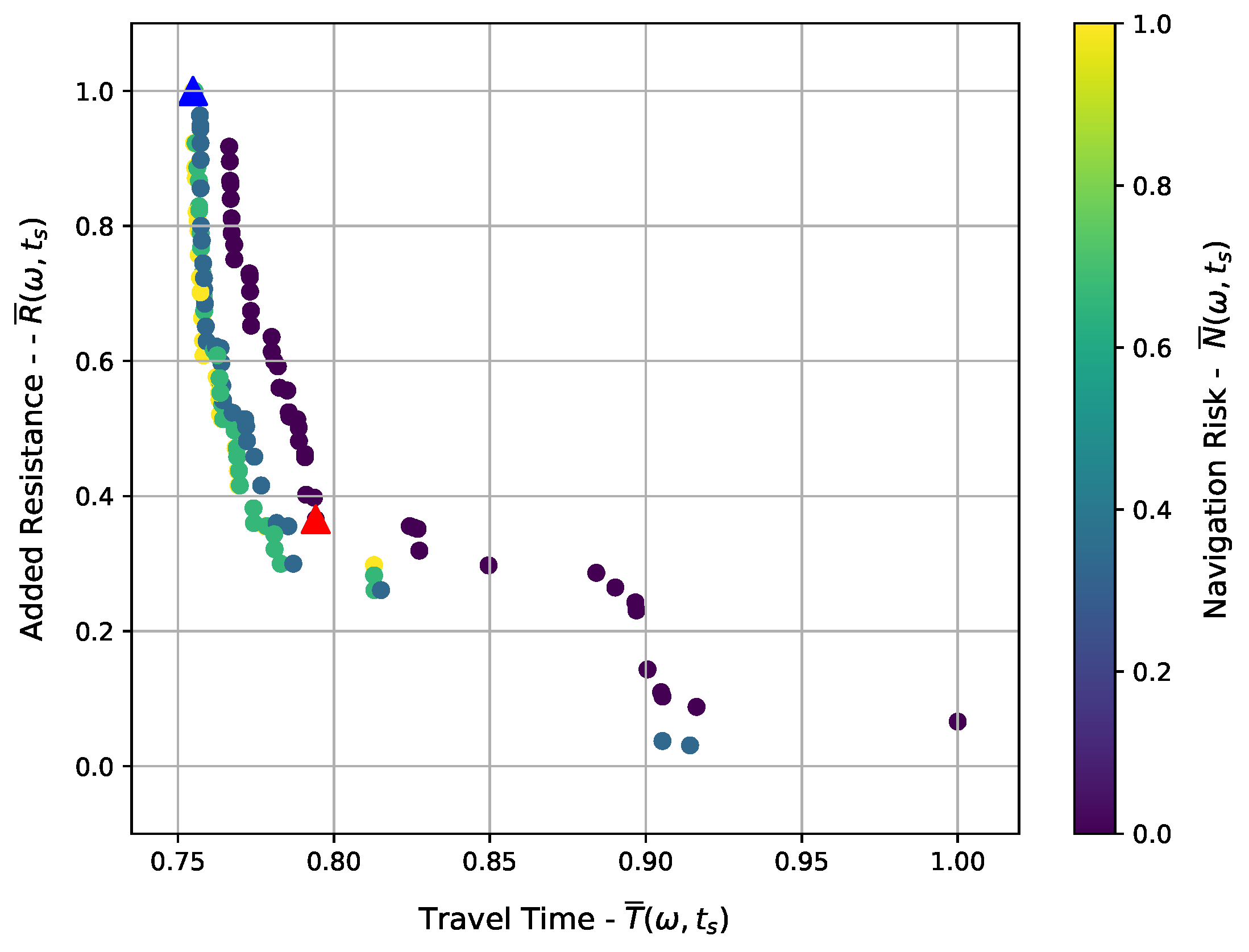
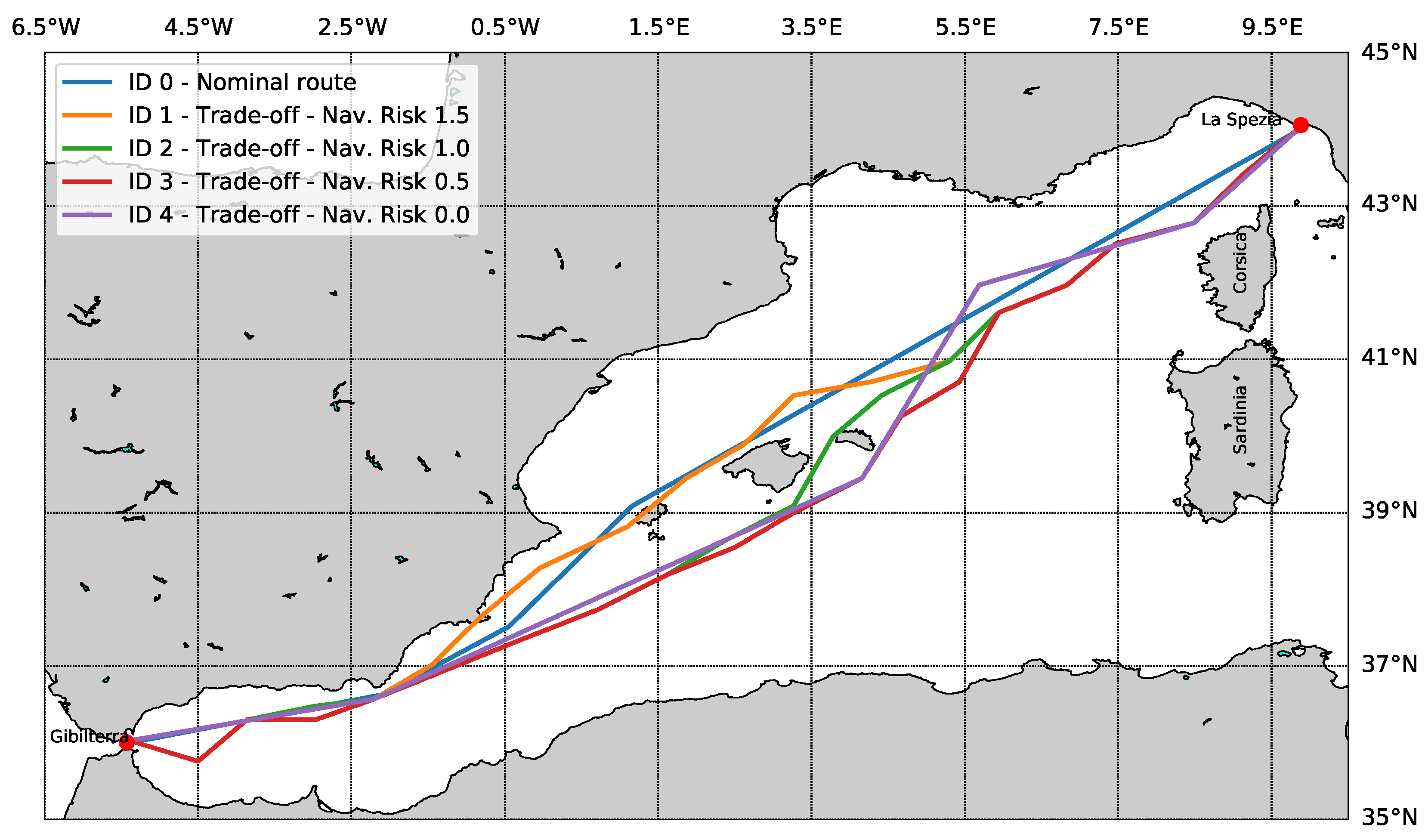
3.4. Output of Planning Layer
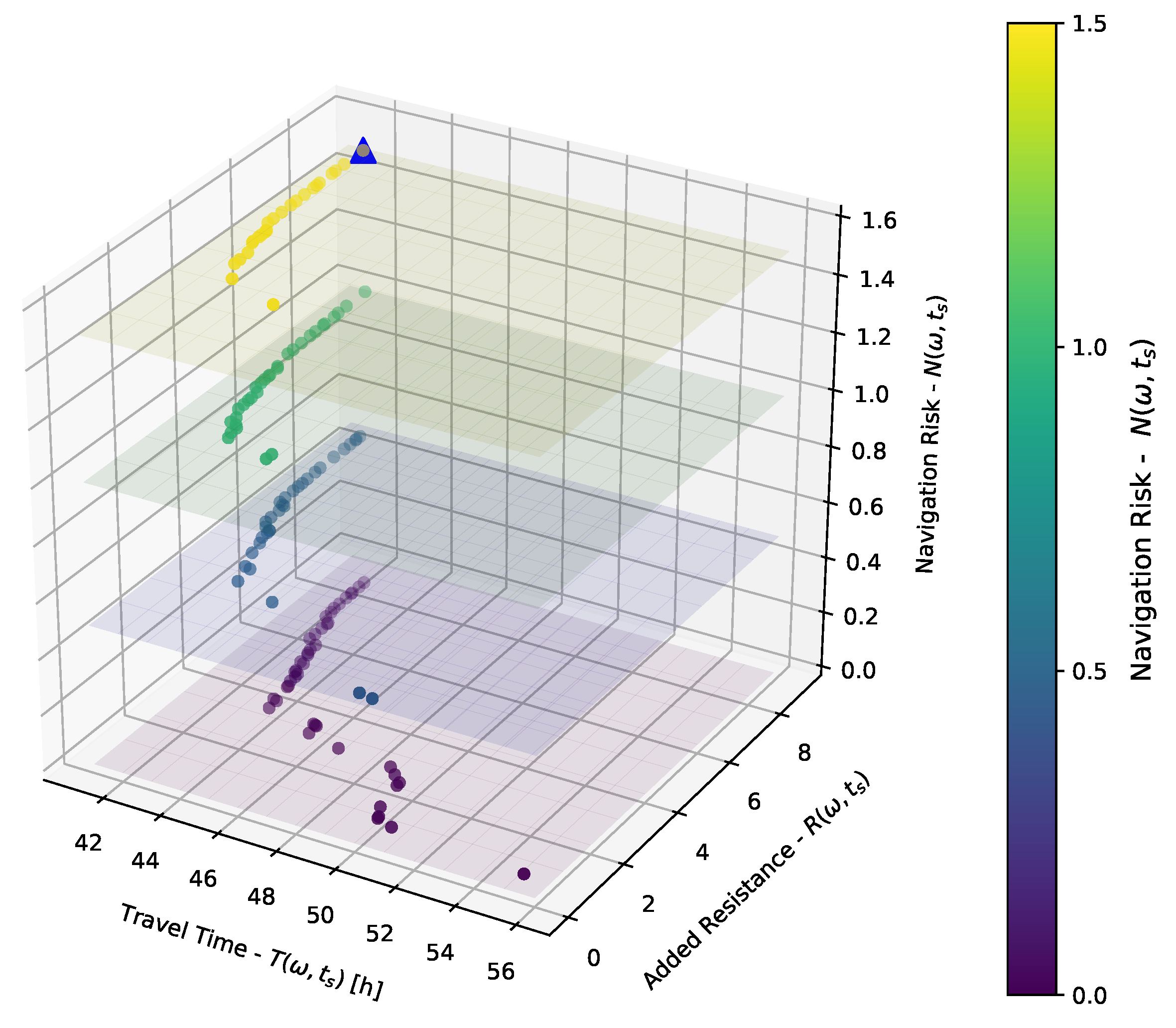
3.5. Output of Decision Layer
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perera, L.P.; Soares, C.G. Weather routing and safe ship handling in the future of shipping. Ocean Eng. 2017, 130, 684–695. [Google Scholar] [CrossRef]
- Zwierzewicz, Z. Algorithms for the Ship Trajectory Planning and Its Tracking in the Collision A voidance Process. IFAC Proc. Vol. 2001, 34, 523–529. [Google Scholar] [CrossRef]
- Mannarini, G.; Pinardi, N.; Coppini, G.; Oddo, P.; Iafrati, A. VISIR-I: Small vessels, least-time nautical routes using wave forecasts. Geosci. Model Dev. 2015, 8, 7911–7981. [Google Scholar] [CrossRef]
- Sidoti, D.; Avvari, G.V.; Mishra, M.; Zhang, L.; Nadella, B.K.; Peak, J.E.; Hansen, J.A.; Pattipati, K.R. A Multiobjective Path-Planning Algorithm with Time Windows for Asset Routing in a Dynamic Weather-Impacted Environment. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 3256–3271. [Google Scholar] [CrossRef]
- Fabbri, T.; Vicen-Bueno, R.; Grasso, R.; Pallotta, G.; Millefiori, L.M.; Cazzanti, L. Optimization of surveillance vessel network planning in maritime command and control systems by fusing METOC and AIS vessel traffic information. In Proceedings of the OCEANS 2015—Genova, Genoa, Italy, 18–21 May 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Fang, M.C.; Lin, Y.H. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements (II): Optimized routings. Appl. Ocean Res. 2015, 50, 130–140. [Google Scholar] [CrossRef]
- Krata, P.; Szlapczynska, J. Ship weather routing optimization with dynamic constraints based on reliable synchronous roll prediction. Ocean Eng. 2018, 150, 124–137. [Google Scholar] [CrossRef]
- IMO. Revised Guidance To The Master For Avoiding Dangerous Situations In Adverse Weather And Sea Conditions; Technical Report; International Maritime Organization (IMO): London, UK, 2007. [Google Scholar]
- Krata, P.; Szlapczynska, J. Weather Hazard Avoidance in Modeling Safety of Motor-Driven Ship for Multicriteria Weather Routing. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2012, 6, 71–78. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Krata, P. Determining and visualizing safe motion parameters of a ship navigating in severe weather conditions. Ocean Eng. 2018, 158, 263–274. [Google Scholar] [CrossRef]
- Dipartimento di Ingegneria Civile, Chimica e Ambientale (DICCA). MeteOcean—DICCA. 2018. Available online: http://www.dicca.unige.it/meteocean/ (accessed on 1 June 2018).
- Thompson, I. Fatigue damage variation within a class of naval ships. Ocean Eng. 2018, 165, 123–130. [Google Scholar] [CrossRef]
- Vantorre, M.; Eloot, K.; Delefortrie, G.; Lataire, E.; Candries, M.; Verwilligen, J. Maneuvering in Shallow and Confined Water. In Encyclopedia of Maritime and Offshore Engineering; American Cancer Society: Atlanta, GA, USA, 2017; pp. 1–17. [Google Scholar] [CrossRef]
- U.S. Army Engineer Waterways Experiment Station, Coastal Engineering Research Center. Direct Methods for Calculating Wavelength; Coastal Engineering Technical Note CETN-1-17; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1985. [Google Scholar]
- Perez, T. Ship Motion Control: Course Keeping and Roll Stabilisation Using Rudder and Fins, 1st ed.; Springer Publishing Company: London, UK, 2010. [Google Scholar]
- Lin, Y.H.; Fang, M.C.; Yeung, R.W. The optimization of ship weather-routing algorithm based on the composite influence of multi-dynamic elements. Appl. Ocean Res. 2013, 43, 184–194. [Google Scholar] [CrossRef]
- Bijlsma, S. Minimal Time Route Computation for Ships with Pre-Specified Voyage Fuel Consumption. J. Navig. 2008, 61, 723–733. [Google Scholar] [CrossRef]
- Shao, W.; Zhou, P.; Thong, S.K. Development of a novel forward dynamic programming method for weather routing. J. Mar. Sci. Technol. 2012, 17, 239–251. [Google Scholar] [CrossRef]
- Zyczkowski, M.; Szlapczynski, R. Multi-Objective Weather Routing of Sailing Vessels. Pol. Marit. Res. 2017, 24. [Google Scholar] [CrossRef]
- Padhy, C.; Sen, D.; Bhaskaran, P. Application of wave model for weather routing of ships in the North Indian Ocean. Nat. Hazards 2007, 44, 373–385. [Google Scholar] [CrossRef]
- Walther, L.; Rizvanolli, A.; Wendebourg, M.; Jahn, C. Modeling and Optimization Algorithms in Ship Weather Routing. Int. J. E Navig. Marit. Econ. 2016, 4, 31–45. [Google Scholar] [CrossRef]
- Martins, E.Q.V. On a multicriteria shortest path problem. Eur. J. Oper. Res. 1984, 16, 236–245. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Maritime Data Systems. Searoutes.com. 2018. Available online: https://www.searoutes.com (accessed on 1 June 2018).
- Loeches, J.; Vicen-Bueno, R.; Mentaschi, L. METOC-driven Vessel Interdiction System (MVIS): Supporting decision making in Command and Control (C2) systems. In Proceedings of the OCEANS 2015—Genova, Genoa, Italy, 18–21 May 2015; pp. 1–6. [Google Scholar]
- Zyczkowski, M.; Krata, P.; Szlapczynski, R. Multi-Objective Weather Routing of Sailboats Considering Wave Resistance. Pol. Marit. Res. 2018, 25, 4–12. [Google Scholar] [CrossRef]
- Lu, R.; Turan, O.; Boulougouris, E.; Banks, C.; Incecik, A. A semi-empirical ship operational performance prediction model for voyage optimization towards energy efficient shipping. Ocean Eng. 2015, 110, 18–28. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Chiu, P.W.; Bloebaum, C.L. Hyper-Radial Visualization (HRV) method with range-based preferences for multi-objective decision making. Struct. Multidiscip. Optim. 2009, 40, 97. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Developing and validating a forecast/hindcast system for the Mediterranean Sea. J. Coast. Res. 2013, 2, 1551–1556. [Google Scholar] [CrossRef]
- National Weather Service—Environmental Modeling Center. Wavewatch III Model. 2018. Available online: http://polar.ncep.noaa.gov/waves/wavewatch/ (accessed on 1 June 2018).
- EMODnet Bathymetry—The European Marine Observation And Data Network. EMODnet—Understading the Topography of the European Seas. 2018. Available online: http://www.emodnet-bathymetry.eu/ (accessed on 1 June 2018).
- Hunt, J.N. Direct solution of wave dispersion equation. J. Waterw. Port Coast. Ocean Eng. 1979, WW4, 457–459. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
| Property | Symbol | Units | Value | |
|---|---|---|---|---|
| Ship parameters | Length | |||
| Beam width | B | |||
| Draft | ||||
| Max Speed | kn | |||
| Metacentric height | ||||
| Displacement | ||||
| Navigation parameters | Speed | u | kn | |
| Heading | respect to N |
| Parameter | Symbol | Units | Data Provider |
|---|---|---|---|
| Significant wave height | DICCA-MeteOcean [11] | ||
| Wave period | T | DICCA-MeteOcean [11] | |
| Wavelength | Hunt’s method [33] function of T and d. | ||
| Wave direction | respect to North | DICCA-MeteOcean [11] | |
| Wind speed | DICCA-MeteOcean [11] | ||
| Wind direction | respect to North | DICCA-MeteOcean [11] | |
| Depth | d | EMODNet [32] |
| Property | Symbol | Value | Units |
|---|---|---|---|
| Number of stages | m | 20 | - |
| Stage length | b | ||
| Number of nodes per stage | q | 31 | - |
| Number of valid nodes | 388 | - | |
| Number of valid edges | 7589 | - | |
| Average edge length |
| ID | Travel Time [h] | Added Resistance | Navigation Risk |
|---|---|---|---|
| 0 | |||
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabbri, T.; Vicen-Bueno, R. Weather-Routing System Based on METOC Navigation Risk Assessment. J. Mar. Sci. Eng. 2019, 7, 127. https://doi.org/10.3390/jmse7050127
Fabbri T, Vicen-Bueno R. Weather-Routing System Based on METOC Navigation Risk Assessment. Journal of Marine Science and Engineering. 2019; 7(5):127. https://doi.org/10.3390/jmse7050127
Chicago/Turabian StyleFabbri, Tommaso, and Raul Vicen-Bueno. 2019. "Weather-Routing System Based on METOC Navigation Risk Assessment" Journal of Marine Science and Engineering 7, no. 5: 127. https://doi.org/10.3390/jmse7050127
APA StyleFabbri, T., & Vicen-Bueno, R. (2019). Weather-Routing System Based on METOC Navigation Risk Assessment. Journal of Marine Science and Engineering, 7(5), 127. https://doi.org/10.3390/jmse7050127





