Seagrass Resource Assessment Using WorldView-2 Imagery in the Redfish Bay, Texas
Abstract
:1. Introduction
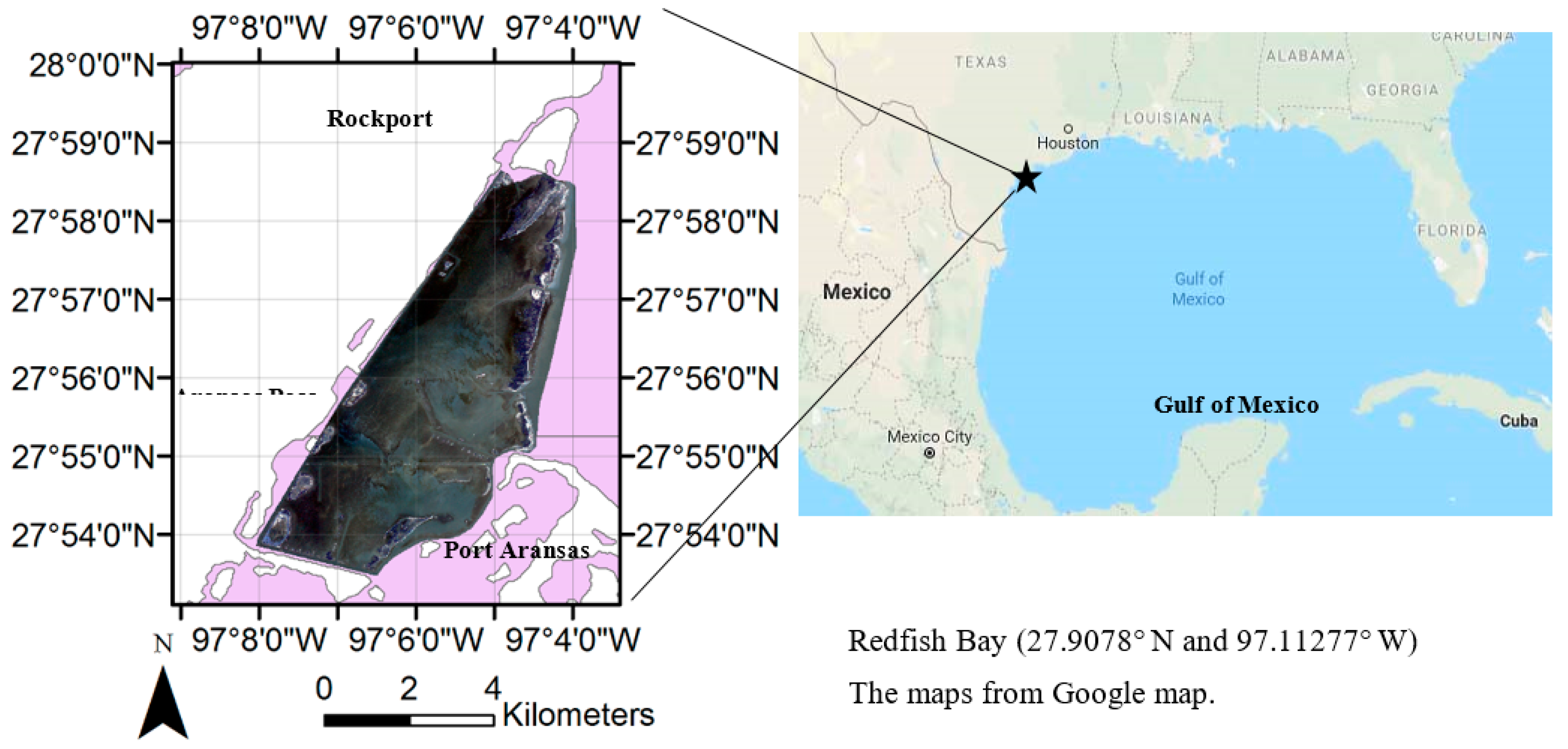
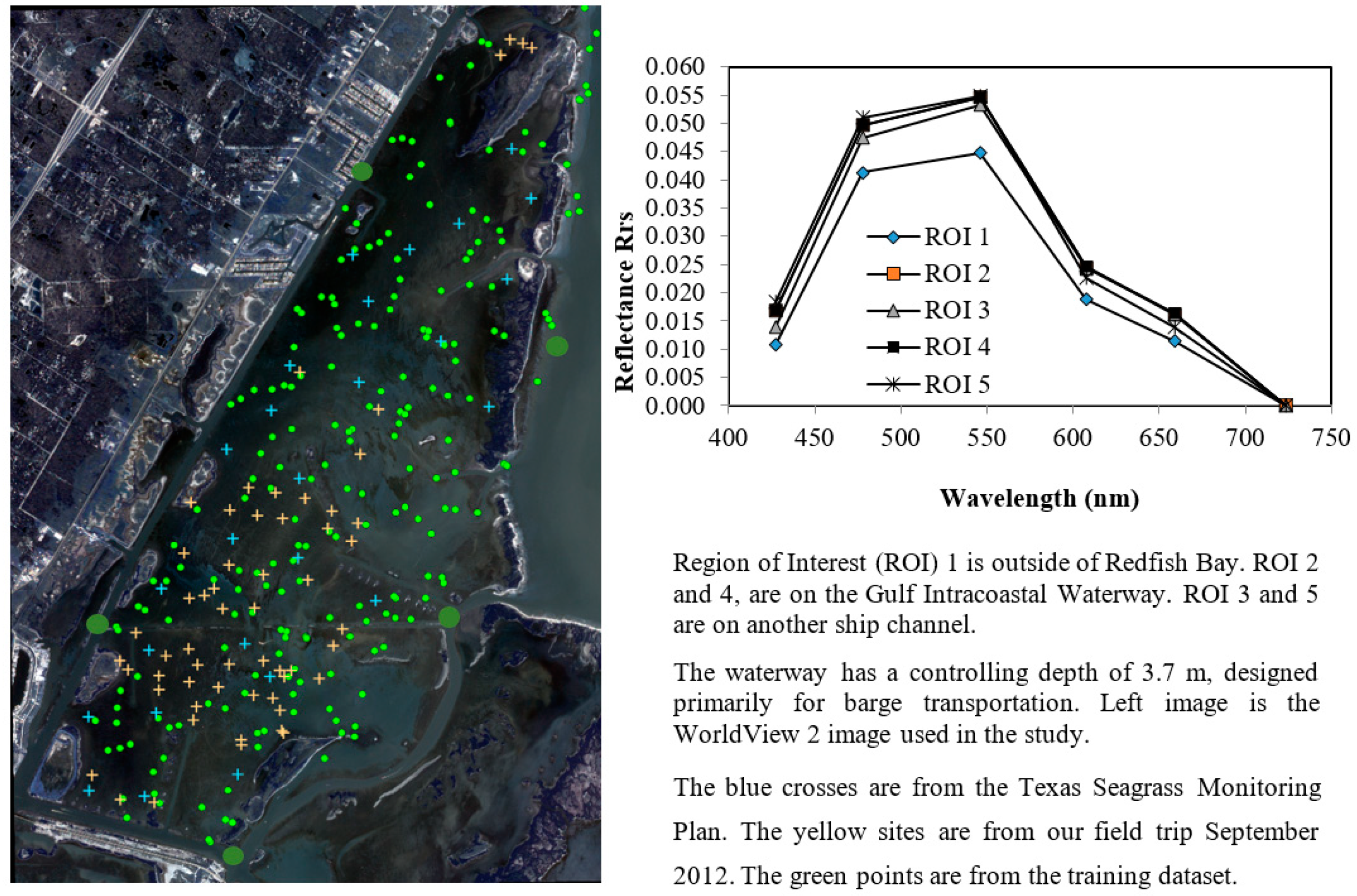
2. Experiment Site and Satellite Data
3. Methods for Data PROCESSING and Classification
3.1. Satellite Data Processing for Bottom Reflectance
3.1.1. Land and Cloud Masking
3.1.2. Sun Glint Correction
3.1.3. Atmospheric Correction
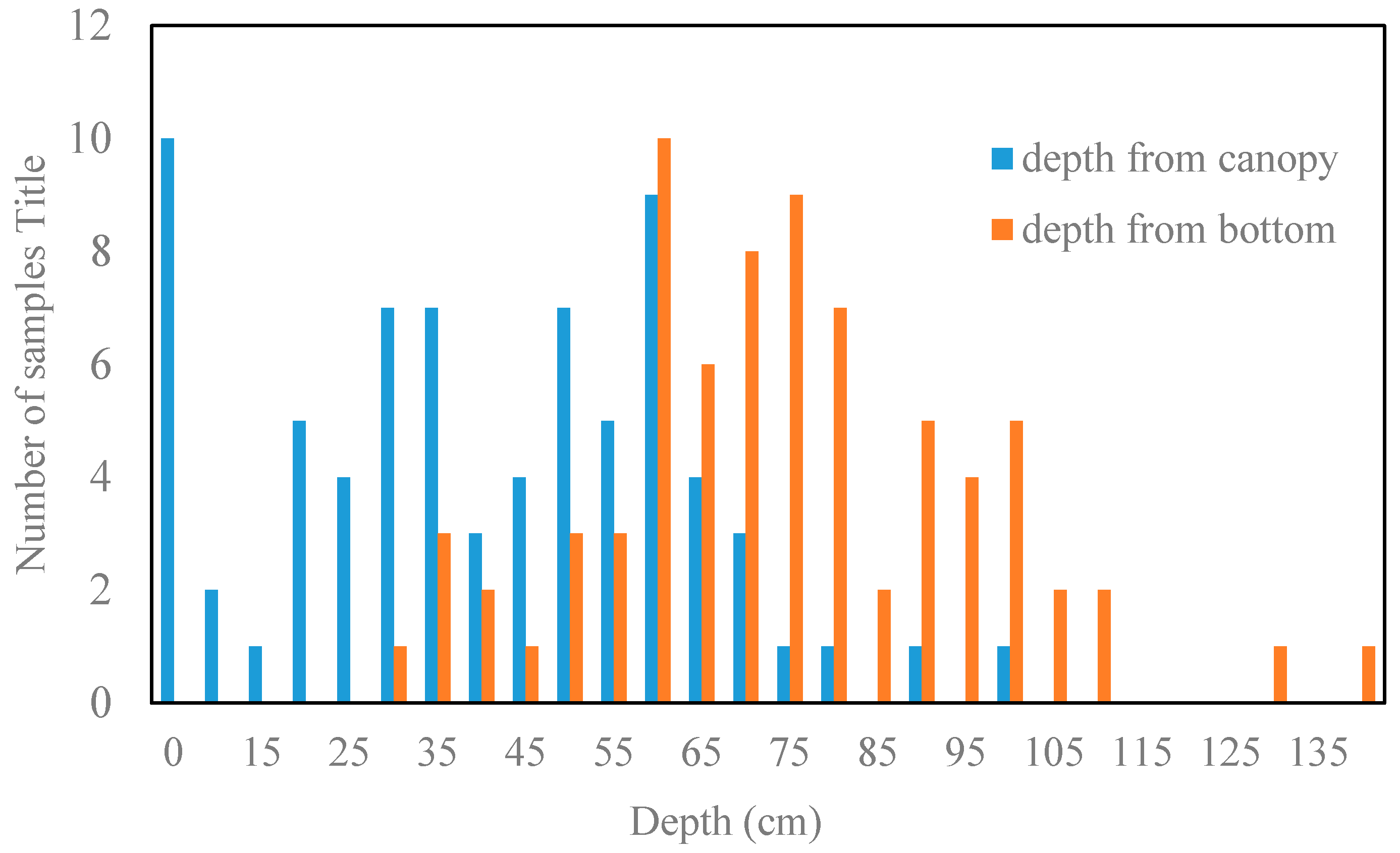
3.1.4. Water Column Correction
3.2. Classification and Accuracy Assessment
3.2.1. Band Selection
3.2.2. Method and Parameters Selection of Segmentation
3.2.3. Classification on Segmented Image Objects
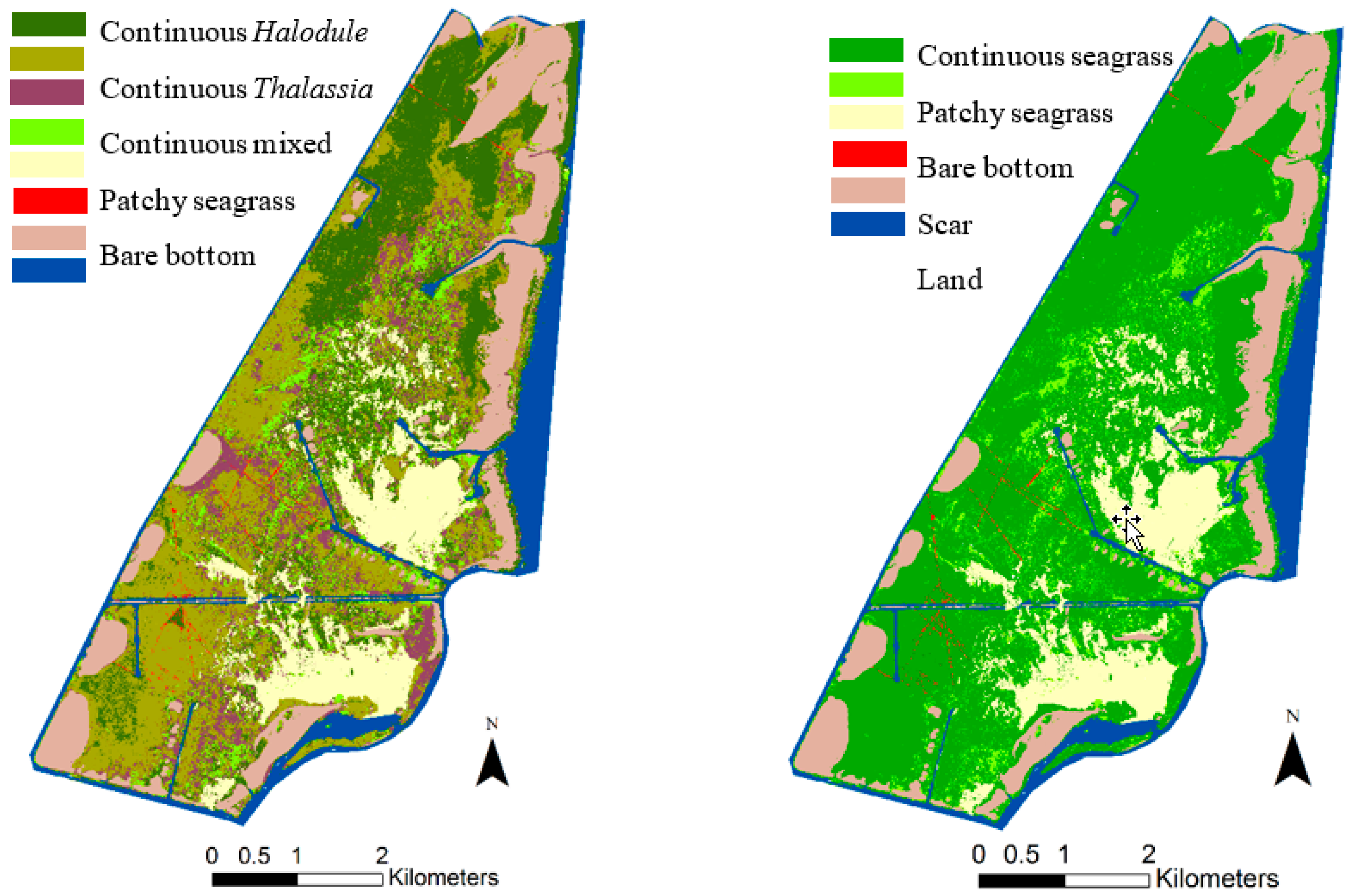
3.2.4. Results and Accuracy Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hemminga, M.A.; Duarte, C.M. Seagrass Ecology; Cambridge University Press: London, UK, 2000. [Google Scholar]
- Orth, R.J.; Carruthers, T.J.B.; Dennison, W.C.; Duarte, C.M.; Fourqurean, J.W.; Heck, K.L.; Hughes, A.R.; Kendrick, G.A.; Kenworthy, W.J.; Olyarnik, S.; et al. A Global Crisis for Seagrass Ecosystems. BioScience 2006, 56, 987–996. [Google Scholar] [CrossRef] [Green Version]
- Short, F.; Carruthers, T.; Dennison, W.; Waycott, M. Global seagrass distribution and diversity: A bioregional model. J. Exp. Mar. Biol. Ecol. 2007, 350, 3–20. [Google Scholar] [CrossRef]
- Alongi, D.M. Coastal Ecosystem Processes (Marine Science); CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Ferguson, R.L.; Wood, L.L.; Graham, D.B. Monitoring spatial change in seagrass habitat with aerial photography. Photogramm. Eng. Remote Sens. 1993, 59, 1033–1038. [Google Scholar]
- Pasqualini, V.; Pergent-Martinia, C.; Pergenta, G.; Agreila, M.; Skoufasb, G.; Sourbesc, L.; Tsirikad, A. Use of SPOT 5 for mapping seagrasses: An application to Posidonia oceanica. Remote Sens. Environ. 2005, 94, 39–45. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Zimmerman, R.C.; Burdige, D.; Drake, L. Benthic ecology from space: Optics and net primary production in seagrass and benthic algae across the Great Bahama Bank. Mar. Ecol. Prog. Ser. 2010, 411, 1–15. [Google Scholar] [CrossRef]
- Traganos, D.; Aggarwal, B.; Poursanidis, D.; Topouzelis, K.; Chrysoulakis, N.; Reinartz, P. Towards Global-Scale Seagrass Mapping and Monitoring Using Sentinel-2 on Google Earth Engine: The Case Study of the Aegean and Ionian Seas. Remote Sens. 2018, 10, 1227. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Zimmerman, R.C. Ocean color remote sensing of seagrass and bathymetry in the Bahamas Banks by high-resolution airborne imagery. Limnol. Oceanogr. 2003, 48, 444–455. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.D.; Sundman, L.K.; Davis, C.O.; Bowles, J.H.; Downes, T.V.; Leathers, R.A.; Montes, M.J.; Bissett, W.P.; Kohler, D.D.R.; Reid, R.P.; et al. Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables. Appl. Opt. 2005, 44, 3576–3592. [Google Scholar] [CrossRef] [PubMed]
- Valle, M.; Pal, V.; Lafon, V.; Dehouck, A.; Garmendia, J.M.; Borja, A.; Chust, G. Mapping estuarine habitats using airborne hyperspectral imagery, with special focus on seagrass meadows. Estuar. Coast. Shelf Sci. 2015, 164, 433–442. [Google Scholar] [CrossRef]
- Mishra, D.R.; Narumalani, S.; Rundquist, D.; Lawson, M. High-Resolution Ocean Color Remote Sensing of Benthic Habitats: A Case Study at the Roatan Island, Honduras. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1592–1604. [Google Scholar] [CrossRef]
- Green, K.; Lopez, C. Using Object-Oriented Classification of ADS40 Data to Map the Benthic Habitats of the State of Texas. Photogramm. Eng. Remote Sens. 2007, 73, 861–865. [Google Scholar]
- Reshitnyk, L.; Costa, M.P.F.; Robinson, C.L.K.; Dearden, P. Evaluation of WorldView-2 and acoustic remote sensing for mapping benthic habitats in temperate coastal Pacific waters. Remote Sens. Environ. 2014, 153, 7–23. [Google Scholar] [CrossRef]
- Eugenio, F.; Marcello, J.; Martin, J. High-Resolution Maps of Bathymetry and Benthic Habitats in Shallow-Water Environments Using Multispectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3539–3549. [Google Scholar] [CrossRef] [Green Version]
- Koedsin, W.; Intararuang, W.; Ritchie, R.J.; Huete, A. An Integrated Field and Remote Sensing Method for Mapping Seagrass Species, Cover, and Biomass in Southern Thailand. Remote Sens. 2016, 8, 292. [Google Scholar] [CrossRef]
- Duffy, J.P.; Pratt, L.; Anderson, K.; Land, P.E.; Shutler, J.D. Spatial assessment of intertidal seagrass meadows using optical imaging systems and a lightweight drone. Estuar. Coast. Shelf Sci. 2018, 200, 169–180. [Google Scholar] [CrossRef]
- Zhao, D.; Jiang, H.; Yang, T.; Cai, Y.; Xu, D.; An, S. Remote sensing of aquatic vegetation distribution in Taihu Lake using an improved classification tree with modified thresholds. J. Environ. Manag. 2012, 95, 98–107. [Google Scholar] [CrossRef]
- Hedley, J.D.; Russell, B.J.; Randolph, K.; Pérez-Castro, M.Á.; Vásquez-Elizondo, R.M.; Enríquez, S.; Dierssen, H.M. Remote Sensing of Seagrass Leaf Area Index and Species: The Capability of a Model Inversion Method Assessed by Sensitivity Analysis and Hyperspectral Data of Florida Bay. Front. Mar. Sci. 2017, 4, 362. [Google Scholar] [CrossRef]
- Hossain, M.S.; Bujang, J.S.; Zakaria, M.H.; Hashim, M. The application of remote sensing to seagrass ecosystems: An overview and future research prospects. Int. J. Remote Sens. 2015, 36, 61–114. [Google Scholar] [CrossRef]
- Pulich, W., Jr.; Blair, C.; White, W.A. Current Status and Historical Trends of Seagrass in the Corpus Christi Bay National Estuary Program Study Area. Publication CCBNEP-20; Texas Natural Resource Conservation Commission: Austin, TX, USA, 1997.
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogram. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Lillesand, T.M.; Kiefer, R.W.; Chipman, J.W. Remote Sensing and Image Interpretation, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Beyer, T.G.; Rasser, M.; Morehead, S. Development of a Comprehensive Habitat Map for the Mission Aransas NERR Using the NERRS Habitat Classification Scheme: Matagorda Island, Texas; Mission-Aransas National Estuarine Research Reserve: Aransas, TX, USA, 2007. [Google Scholar]
- Asquith, W.H.; Mosier, J.G.; Bush, P.W. Status, Trends and Changes in Freshwater Inflows to Bay Systems in the Corpus Christi Bay National Estuary Program Study Area. Publication CCBNEP-17; Corpus Christi Bay National Estuary Program: Corpus Christi, TX, USA, 1997. [Google Scholar]
- Fry, B.; Parker, P.L. Animal diet in Texas seagrass meadows: δ13C evidence for the importance of benthic plants. Estuar. Coast. Mar. Sci. 1979, 8, 499–509. [Google Scholar] [CrossRef]
- Pulich, W., Jr. Chapter 1 Introduction. In Seagrass Conservation Plan for Texas–1999; Texas Parks and Wildlife: Austin, TX, USA, 1999. [Google Scholar]
- U.S. Environmental Protection Agency (EPA). The Ecological Condition of Estuaries in the Gulf of Mexico (EPA 620-R-98-004); U.S. Environmental Protection Agency: Washington, DC, USA, 1999.
- Dunton, K.H. Seasonal growth and biomass of the subtropical seagrass Halodule wrightii in relation to continuous measurements of underwater irradiance. Mar. Biol. 1994, 120, 479–489. [Google Scholar] [CrossRef]
- Burfeind, D.D.; Stunz, G.W. The effects of boat propeller scarring intensity on nekton abundance in subtropical seagrass meadows. Mar. Biol. 2006, 148, 953–962. [Google Scholar] [CrossRef]
- Bukata, R.P.; Jerome, J.H.; Kondratyev, K.Y.; Pozdnyakov, D.V. Optical Properties and Remote Sensing Inland Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Martin, S. An Introduction to Ocean Remote Sensing; Cambridge University: London, UK, 2004. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Kay, S.; Hedley, J.D.; Lavender, S. Sun glint correction of high and low spatial resolution images of aquatic scene: A review of methods for visible and near-infrared wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef]
- Hochberg, E.; Andrefout, S.; Tyler, M. Sea surface correction of high spatial resolution Ikonos images to improve bottom mapping in near-shore environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Hedley, J.; Harborne, A.; Mumby, P. Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Stumpf, R.P.; Pennock, J.R. Calibration of a general optical equation for remote sensing of suspended sediments in a moderately turbid estuary. J. Geophys. Res. 1989, 94, 14363–14371. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Evans, R.H.; Gordon, H.R. Coastal zone color scanner ‘system calibration’: A retrospective examination. J. Geophys. Res. 1994, 99, 7293–7307. [Google Scholar] [CrossRef]
- Elterman, L. UV, Visible, and IR Attenuation for Altitudes to 50 km; AFCRL-68-0153, Environmental Research Papers, No. 285; Air Force Cambridge Research Laboratories: Bedford, MA, USA, 1968. [Google Scholar]
- Updike, T.; Comp, C. Radiometric Use of WorldView-2 Imagery, Technical Note, DigitalGlobe, 1 November 2010. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/104/Radiometric_Use_of_WorldView-2_Imagery.pdf (accessed on 6 April 2019).
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral Bathymetry Using a Simple Physically Based Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569–1578. [Google Scholar] [CrossRef]
- Ji, W.; Civco, D.L.; Kennard, W.C. Satellite remote bathymetry: A new mechanisms for modeling. Photogram. Eng. Remote Sens. 1992, 58, 545–549. [Google Scholar]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. Measurement of seagrass standing crop using satellite and digital airborne remote sensing. Mar. Ecol. Prog. Ser. 1997, 159, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Lafon, V.; Froidefond, J.M.; Lahet, F.; Castaing, P. SPOT shallow water bathymetry of a moderately turbid tidal inlet based on field measurements. Remote Sens. Environ. 2002, 81, 136–148. [Google Scholar] [CrossRef]
- Schweizer, D.; Armstrong, R.A.; Posada, J. Remote sensing characterization of benthic habitats and submerged vegetation biomass in Los Roques Archpelago National Park, Venezuela. Int. J. Remote Sens. 2005, 26, 2657–2667. [Google Scholar] [CrossRef]
- Mertes, L.A.K.; Dekker, A.G.; Brakenridge, G.R.; Birkett, C.M.; Letourneau, G. Rivers and Lakes. In Remote Sensing for Natural Resource Management and Environmental Monitoring; Ustin, S.L., Ed.; John Wiley and Sons: New York, NY, USA, 2004; pp. 345–400. [Google Scholar]
- Davis, C.O.; Lamela, G.M.; Donato, T.F.; Bachmann, C.M. Coastal Margins and Estuaries. In Remote Sensing for Natural Resource Management and Environmental Monitoring; Ustin, S.L., Ed.; John Wiley and Sons: New York, NY, USA, 2004; pp. 401–446. [Google Scholar]
- Richardson, L.L.; LeDrew, E.F. Remote Sensing and the Science, Monitoring, and Management of Aquatic Coastal Ecosystems. In Remote Sensing of Aquatic Coastal Ecosystem Processes: Science and Management Applications; Richardson, L.L., LeDrew, E.F., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 1–7. [Google Scholar]
- Zaneveld, J.R.V.; Twardowski, M.J.; Barnard, A.; Lewis, M.R. Introduction to radiative transfer. In Remote Sensing of Coastal Aquatic Environments: Technologies, Techniques and Applications; Miller, R.L., Del Castillo, C.E., McKee, B.A., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 1–20. [Google Scholar]
- Lee, Z.P.; Carder, K.L. Hyperspectral Remote Sensing. In Remote Sensing of Coastal Aquatic Environments: Technologies, Techniques and Applications; Miller, R.L., Del Castillo, C.E., McKee, B.A., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 181–204. [Google Scholar]
- Lee, Z.P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 1. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef]
- Austin, R.W.; Petzold, T.J. Spectral dependence of diffuse attenuation coefficient of light in ocean waters. Opt. Eng. 1986, 25, 471–479. [Google Scholar] [CrossRef]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (case 1 waters). J. Geophys. Res. 1988, 93, 10749–10768. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Steward, R.G.; Peacock, T.G.; Davis, C.O.; Patch, J.S. An empirical algorithm for light absorption by ocean water based on color. J. Geophys. Res. 1998, 103, 27967–27978. [Google Scholar] [CrossRef] [Green Version]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters: Its dependence on sun angle as influenced by the molecular scattering contribution. Appl. Opt. 1991, 30, 4427–4438. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Gordon, H.R.; Smith, R.C.; Zaneveld, J.R.V. Introduction to ocean optics. Proc. SPIE 1980, 208, 1–43. [Google Scholar]
- Sathyendranath, S.; Prieur, L.; Morel, A. A three-component model of ocean colour and its application to remote sensing of phytoplankton pigments in coastal waters. Int. J. Remote Sens. 1989, 10, 1373–1394. [Google Scholar] [CrossRef]
- Lee, Z.P.; Darecki, M.; Carder, K.L.; Davis, C.O.; Stramski, D.; Rhea, W.J. Diffuse attenuation coefficient of downwelling irradiance: An evaluation of remote sensing methods. J. Geophys. Res. 2005, 110, C02017. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters II. Bi-directional aspects. Appl. Opt. 1993, 32, 6864–6879. [Google Scholar] [CrossRef]
- Wilson, C.J.; Dunton, K.H. Assessment of Seagrass Habitat Quality and Plant Physiological Condition in Texas Coastal Waters; The University of Texas at Austin Marine Science Institute: Port Aransas, TX, USA, 2012. [Google Scholar]
- Wood, J.S. Hyperspectral Analysis of Seagrass in Redfish Bay, Texas. Ph.D. Dissertation, Texas A&M University-Corpus Christi, Corpus Christi, TX, USA, 2012. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Mann, K.H. Ecology of Coastal Waters with Implication for Management, 2nd ed.; Blackwall Science: Malden, MA, USA, 2000. [Google Scholar]
- Borowitzka, M.A.; Lethbridge, R.C. Seagrass epiphytes. In Biology of Seagrasses, Aquatic Plant Studies; Larkum, A.W.D., McComb, A.J., Shepard, S.A., Eds.; Elsevier: New York, NY, USA, 1989; pp. 458–499. [Google Scholar]
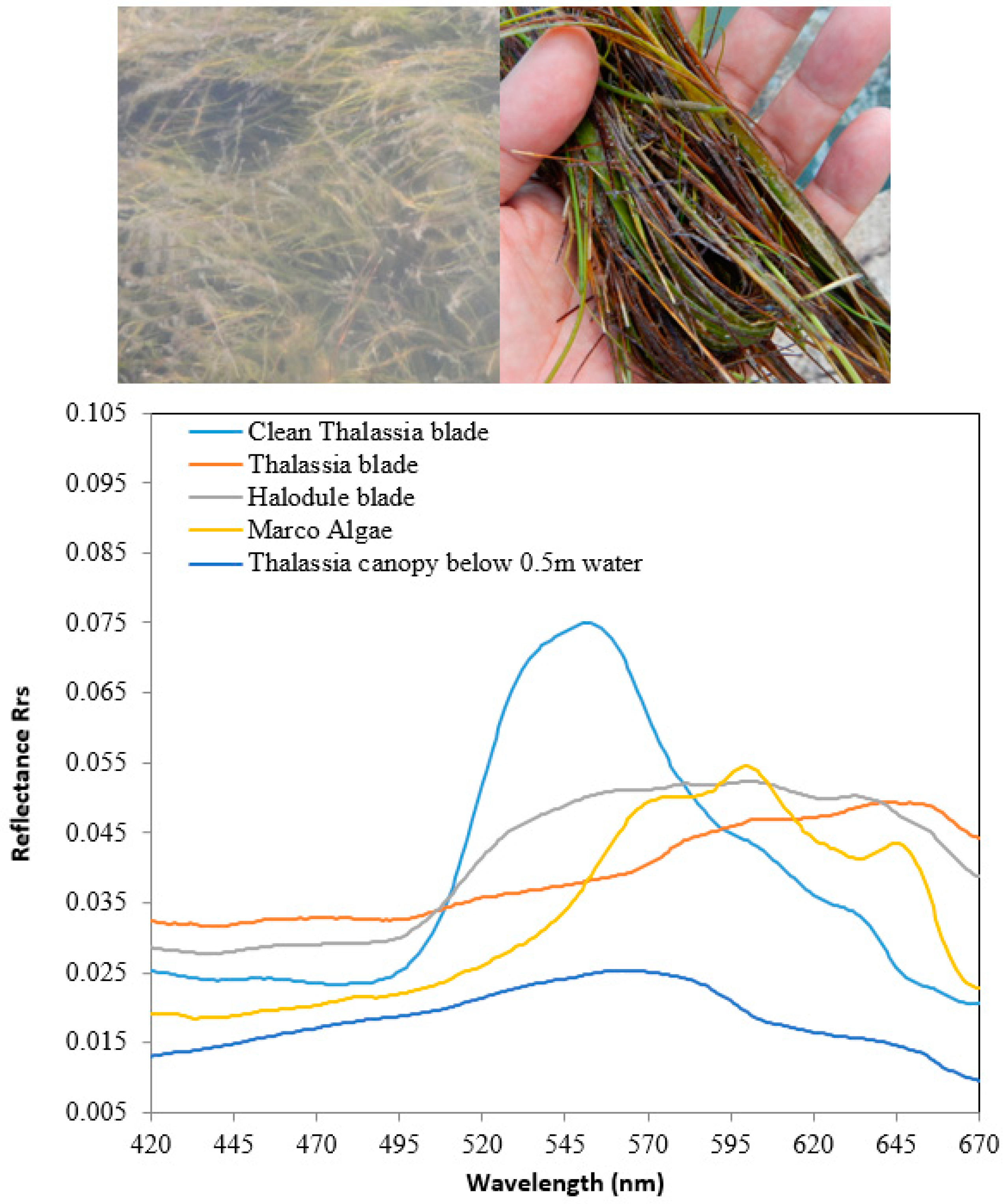
- Fyfe, S.K. Spatial and temporal variation in spectral reflectance: Are seagrass species spectrally distinct? Limnol. Oceanogr. 2003, 48, 464–479. [Google Scholar] [CrossRef] [Green Version]
- Thorhaug, A.; Richardson, A.D.; Berlyn, G.P. Spectral reflectance of the seagrasses: Thalassia testudinum, Halodule wrightii, Syringodium filiforme and five marine algae. Int. J. Remote Sens. 2007, 28, 1487–1501. [Google Scholar] [CrossRef]
- Cowper, S.W. The drift algae community of seagrass beds in Redfish Bay, Texas. Contrib. Mar. Sci. 1978, 21, 125–132. [Google Scholar]

| λ (nm) | ESun | corr | ||||
|---|---|---|---|---|---|---|
| 427.3 Coastal | 0.2845 | 0.0028 | 175.8223 | 0.020755 | 0.662284 | 6.277835 |
| 477.9 Blue | 0.1795 | 0.0085 | 197.4242 | 0.018484 | 0.756456 | 4.376088 |
| 546.2 Green | 0.1039 | 0.0295 | 185.641 | 0.019657 | 0.793434 | 2.243893 |
| 607.8 Yellow | 0.0673 | 0.0042 | 173.8479 | 0.02099 | 0.898054 | 1.462551 |
| 658.8 Red | 0.0485 | 0.0018 | 155.9456 | 0.0234 | 0.928669 | 0.951924 |
| 723.7 Red Edge | 0.0332 | 0.0058 | 134.207 | 0.02719 | 0.938348 | 0.554454 |
| 831.3 NIR 1 | 0.0189 | 0.0020 | 106.973 | 0.034113 | 0.967996 | 0.254318 |
| 908.0 NIR 2 | 0.0133 | 0.0000 | 86.12866 | 0.042369 | 0.981286 | 0.144913 |
| Λ (nm) | (m−1) | (m−1) | (m−1) | (m−1) | |
|---|---|---|---|---|---|
| 427.3 Coastal | 0.0048 | 0.0043 | 1.5849 | 0.2984 | 0.0065 |
| 477.9 Blue | 0.0121 | 0.0027 | 1.1055 | 0.2169 | 0.0047 |
| 546.2 Green | 0.0511 | 0.0015 | 0.6174 | 0.1655 | 0.0034 |
| 607.8 Yellow | 0.2629 | 0.0010 | 0.5130 | 0.3579 | 0.0027 |
| 658.8 Red | 0.3930 | 0.0007 | 0.6797 | 0.5189 | 0.0023 |
| 723.7 Red Edge | 1.7500 | 0.0005 | 0.1449 | 1.7768 | 0.0021 |
| Class | Thalassia | Halodule | Mixed | Patchy | Bare | User’s Accuracy |
|---|---|---|---|---|---|---|
| Thalassia | 26 | 1 | 6 | 0 | 1 | 76% |
| Halodule | 4 | 4 | 6 | 2 | 1 | 24% |
| Mixed | 6 | 2 | 4 | 0 | 0 | 33% |
| Patchy | 0 | 0 | 0 | 3 | 0 | 100% |
| Bare | 1 | 0 | 0 | 0 | 15 | 94% |
| Producer’s Accuracy | 70% | 57% | 2 5% | 60% | 88% | 63% (49.5%) |
| Class | Continuous | Patchy | Bare | User’s Accuracy |
|---|---|---|---|---|
| Continuous | 59 | 2 | 2 | 94% |
| Patchy | 0 | 3 | 0 | 100% |
| Bare | 1 | 0 | 15 | 94% |
| Producer’s Accuracy | 98% | 60% | 88% | 94% (84.6%) |
| Variables | Spectral Responses | ||||
|---|---|---|---|---|---|
| Depth (m) | Change | Blue | Green | Yellow | Red |
| 0.25 | 1% reflectance of deep water sites | 0.00053 | 0.00045 | 0.00020 | 0.00015 |
| 1 cm depth | 0.0034 | 0.0031 | 0.0014 | 0.0010 | |
| Ratio (depth: reflectance) | 6.41 | 6.99 | 6.89 | 6.49 | |
| 0.50 | 1% reflectance of deep water sites | 0.00135 | 0.00111 | 0.00050 | 0.00040 |
| 1 cm depth | 0.0049 | 0.0045 | 0.0021 | 0.0015 | |
| Ratio (depth: reflectance) | 3.63 | 4.05 | 4.09 | 3.86 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Huang, Y. Seagrass Resource Assessment Using WorldView-2 Imagery in the Redfish Bay, Texas. J. Mar. Sci. Eng. 2019, 7, 98. https://doi.org/10.3390/jmse7040098
Su L, Huang Y. Seagrass Resource Assessment Using WorldView-2 Imagery in the Redfish Bay, Texas. Journal of Marine Science and Engineering. 2019; 7(4):98. https://doi.org/10.3390/jmse7040098
Chicago/Turabian StyleSu, Lihong, and Yuxia Huang. 2019. "Seagrass Resource Assessment Using WorldView-2 Imagery in the Redfish Bay, Texas" Journal of Marine Science and Engineering 7, no. 4: 98. https://doi.org/10.3390/jmse7040098
APA StyleSu, L., & Huang, Y. (2019). Seagrass Resource Assessment Using WorldView-2 Imagery in the Redfish Bay, Texas. Journal of Marine Science and Engineering, 7(4), 98. https://doi.org/10.3390/jmse7040098





