A Comprehensive Study of the Wave Impact Loads on an Inclined Plate
Abstract
:1. Introduction
2. Methods
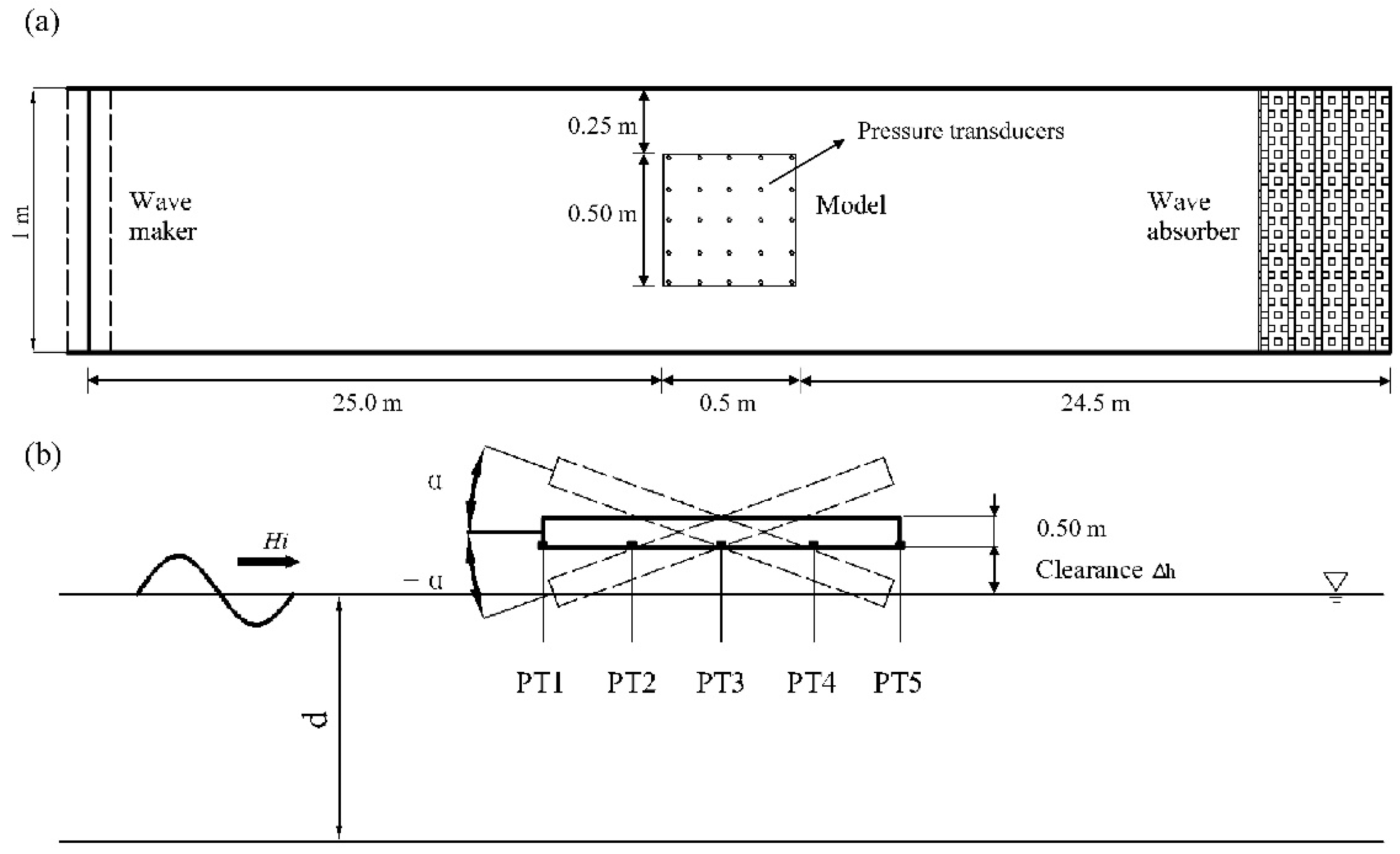
2.1. Experimental Set-Up
2.2. Irregular Wave Generation
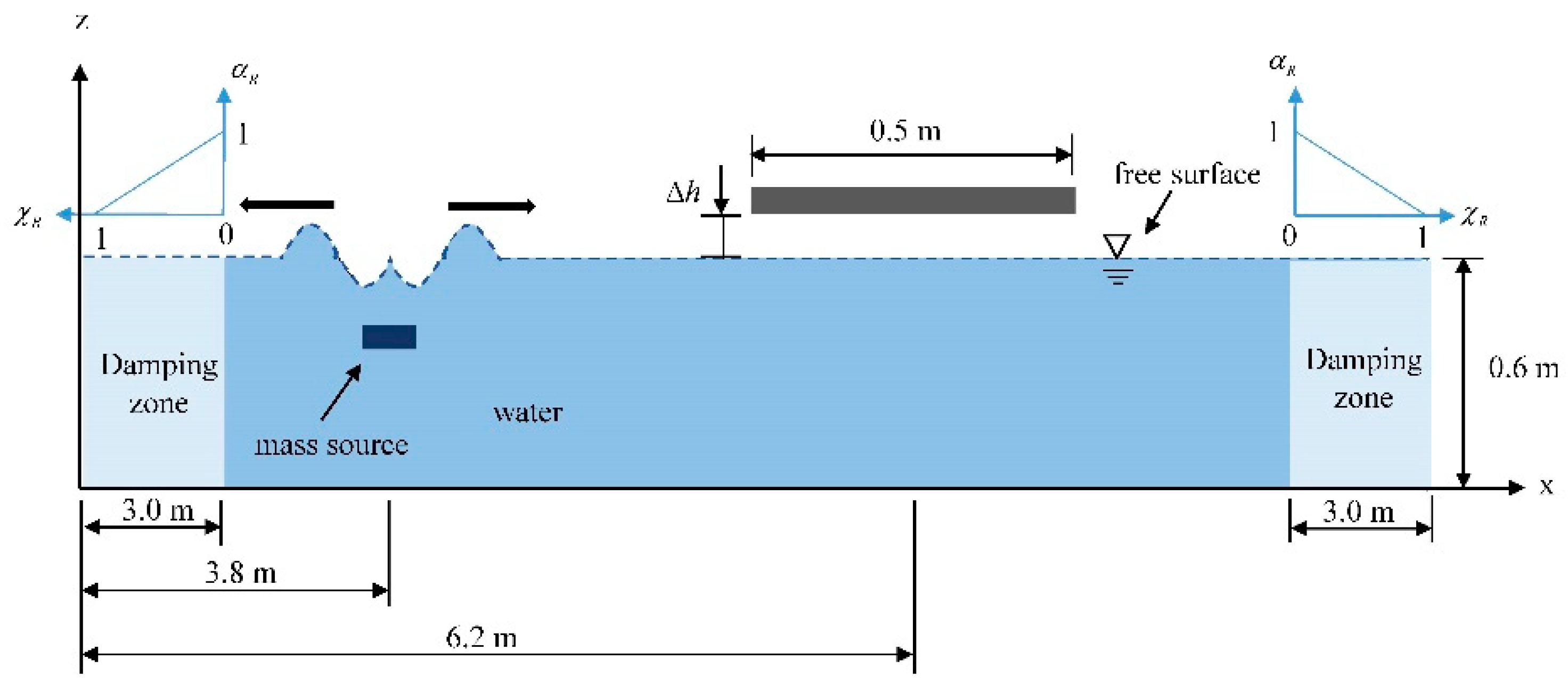
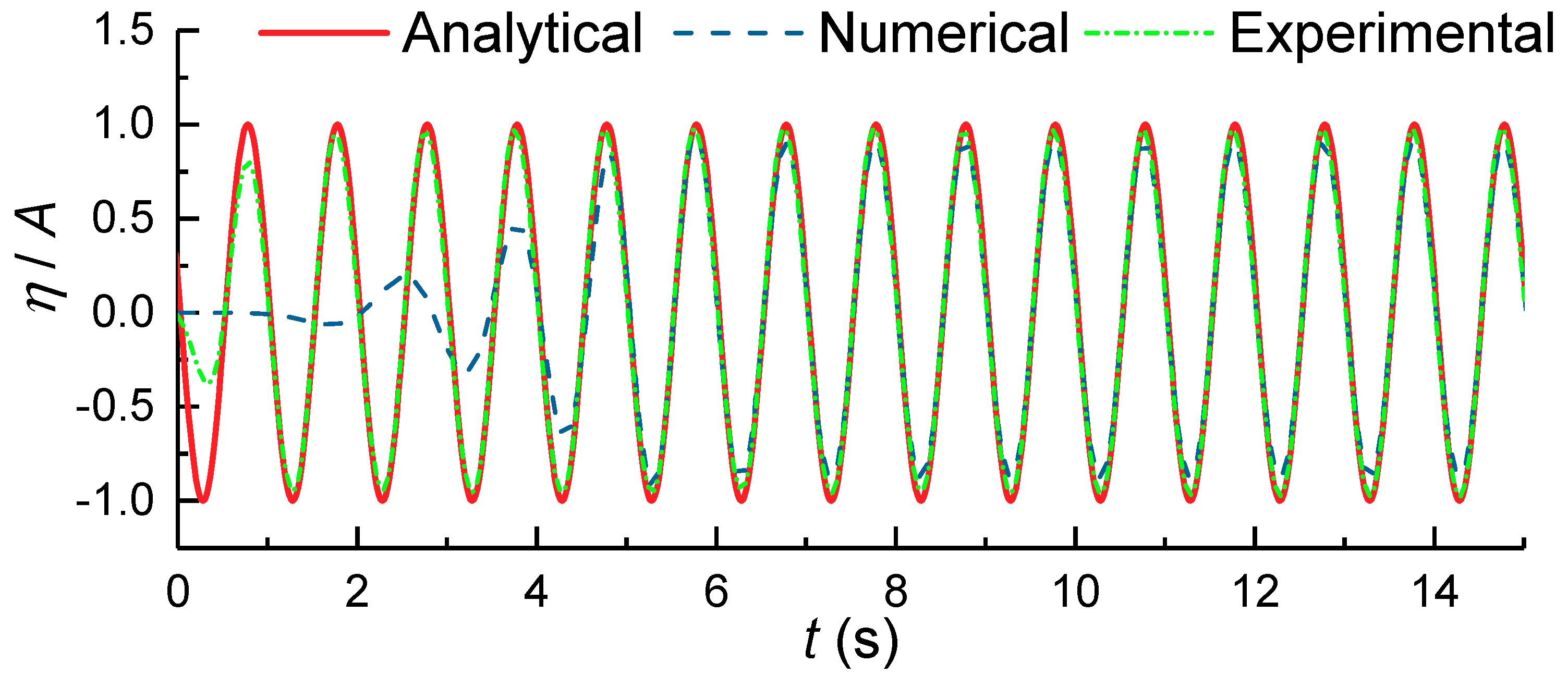
2.3. Numerical Model
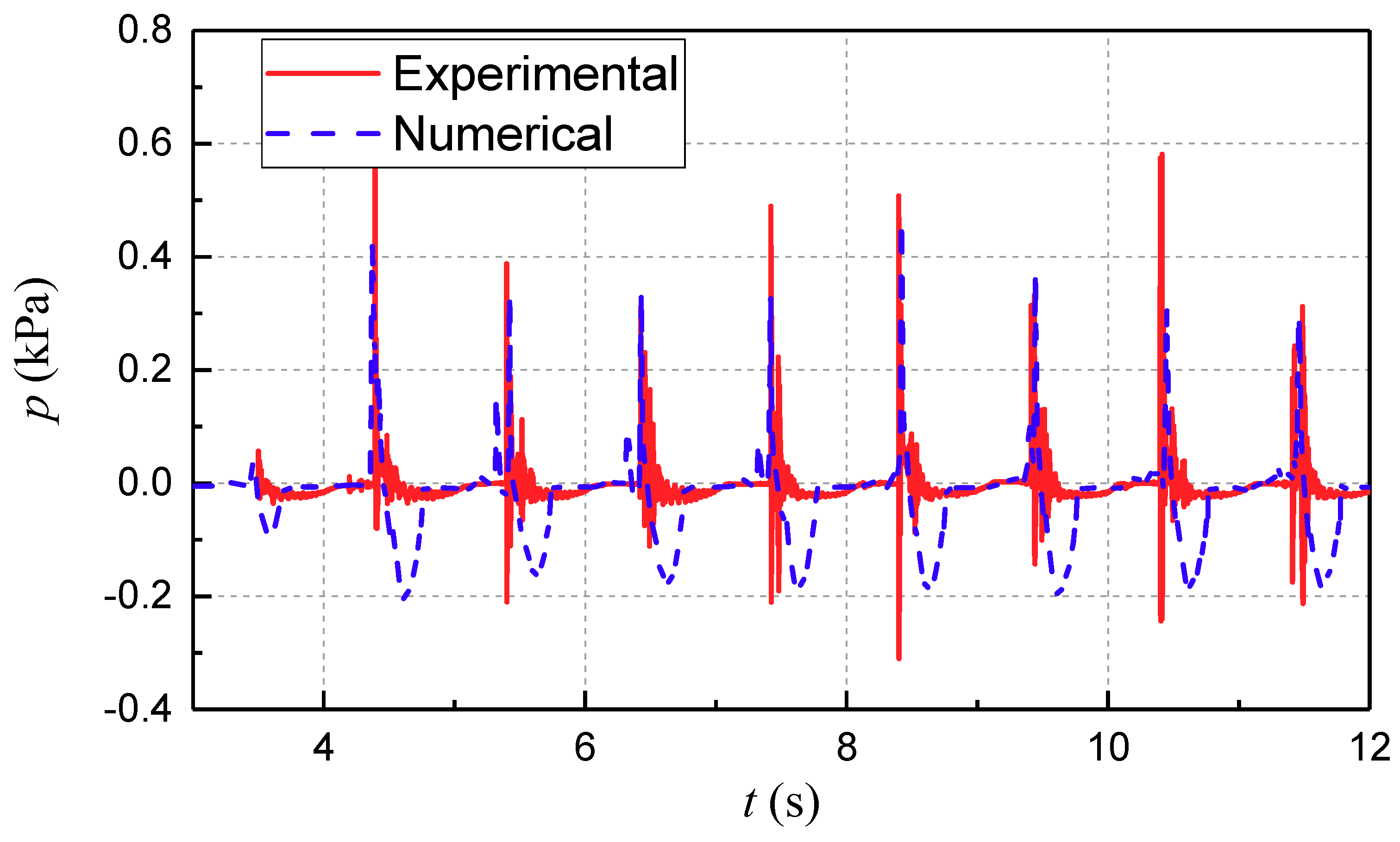
3. Results and Discussion
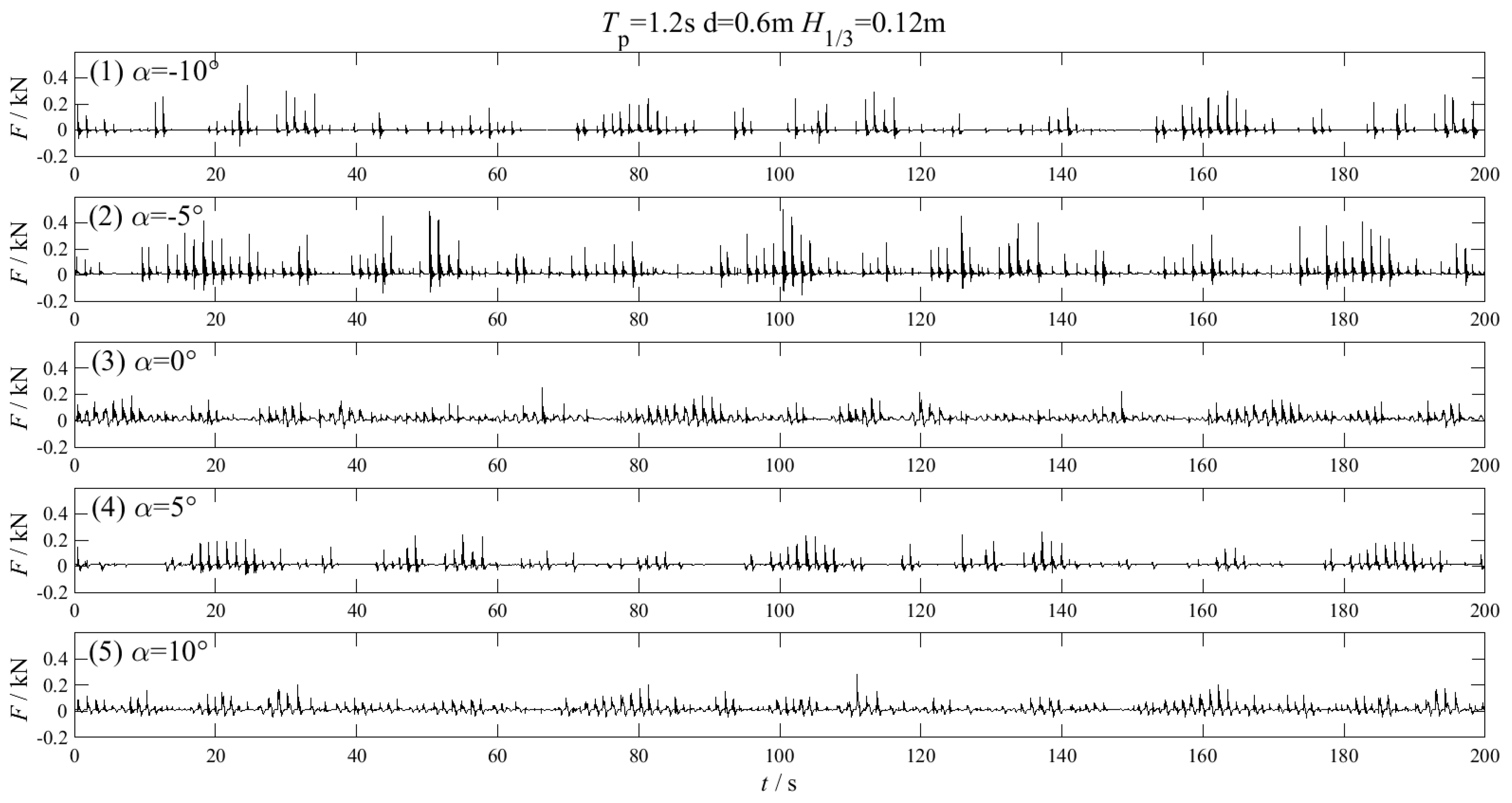
3.1. Parametric Studies of the Wave Uplift Force with Regular Waves
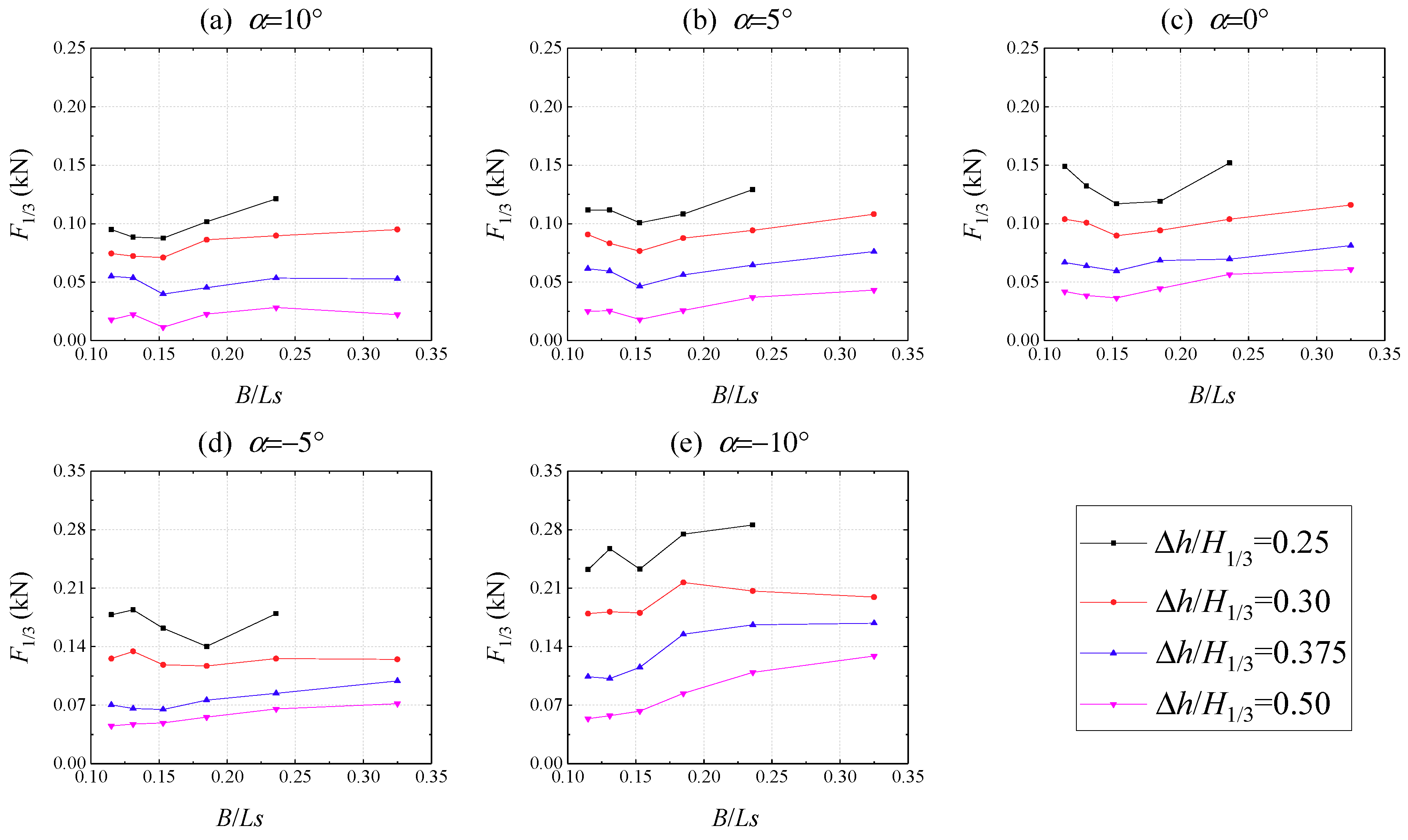
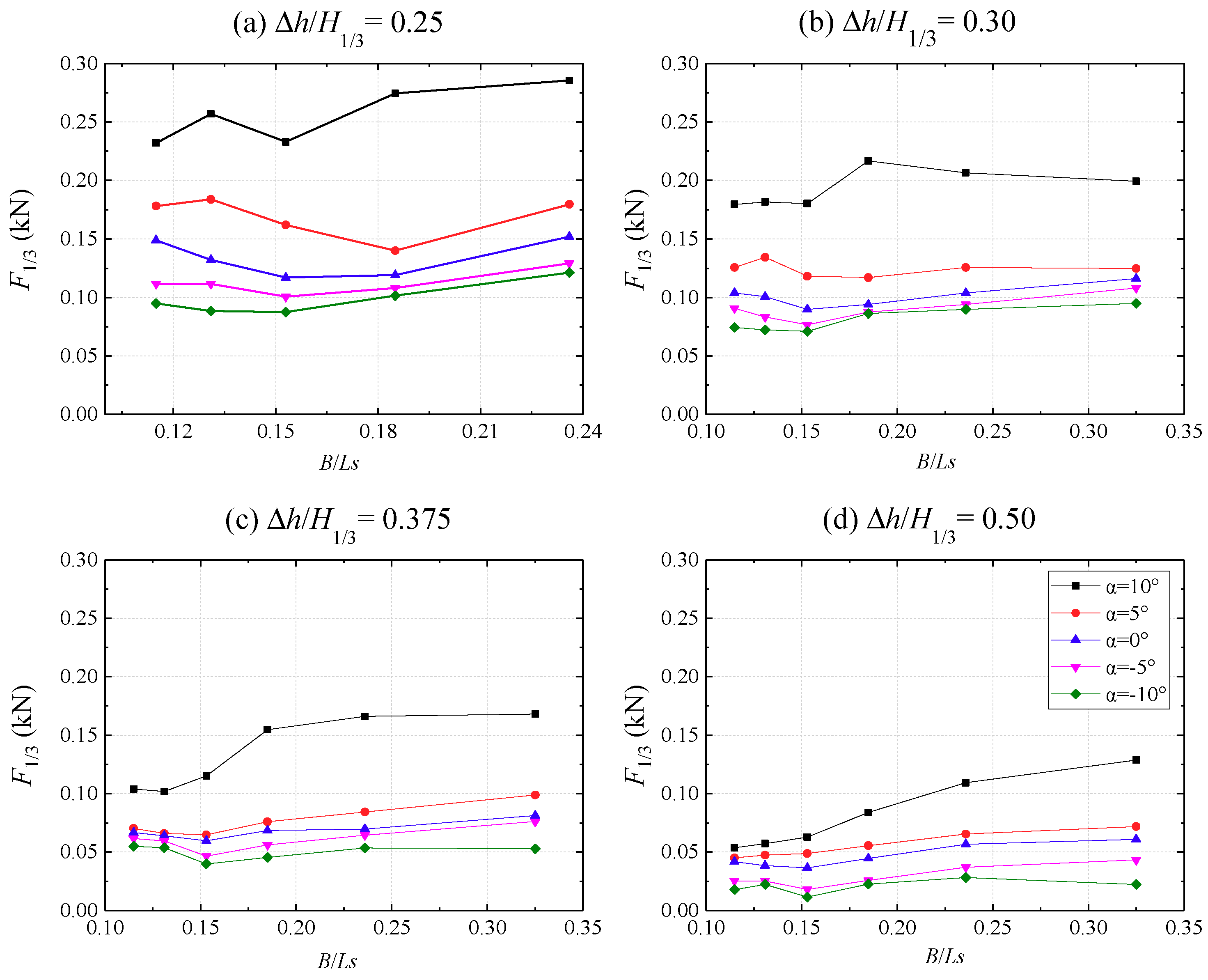
3.2. Parametric Studies of the Wave Uplift Force with Irregular Waves
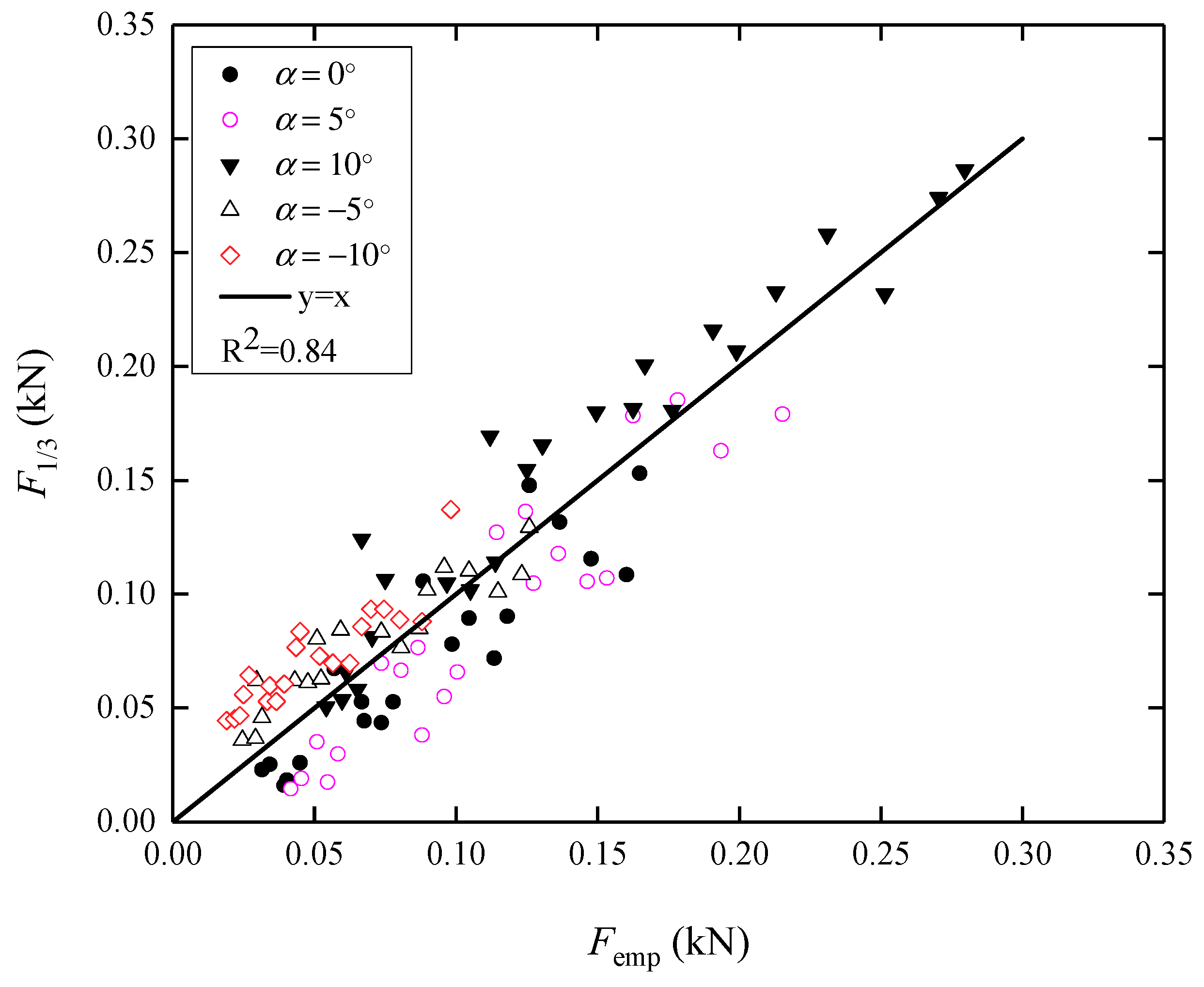
3.3. Prediction Model of Wave Uplift Force
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ren, B.; Wang, Y. Numerical simulation of random wave slamming on structures in the splash zone. Ocean Eng. 2004, 31, 547–560. [Google Scholar] [CrossRef]
- Von Karman, T. The Impact on Seaplane Floats during Landing; Technical Report Archive & Image Library: Tucson, AZ, USA, 1929. [Google Scholar]
- Wagner, H. Über Stoß- und gleitvorgänge an der oberfläche von flüssigkeiten. ZAMM J. Appl. Math. Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Korobkin, A.A.; Pukhnachov, V.V. Initial-stage of water impact. Annu. Rev. Fluid Mech. 1988, 20, 159–185. [Google Scholar] [CrossRef]
- Baarholm, R.; Faltinsen, O.M. Wave impact underneath horizontal decks. J. Mar. Sci. Technol. 2004, 9, 1–13. [Google Scholar] [CrossRef]
- Nikfarjam, M.; Yaakob, O.; Seif, M.; Koto, J. Investigation of wedge water-entry under symmetric impact loads by experimental tests. Lat. Am. J. Solids Struct. 2017, 14, 861–873. [Google Scholar] [CrossRef]
- Ghadimi, P.; Dashtimanesh, A.; Djeddi, S.R. Study of water entry of circular cylinder by using analytical and numerical solutions. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 225–232. [Google Scholar] [CrossRef]
- Shao, J.R.; Yang, Y.; Gong, H.F.; Liu, M.B. Numerical simulation of water entry with improved SPH method. Int. J. Comput. Methods 2019, 16, 1846004. [Google Scholar] [CrossRef]
- Cheng, Y.; Ji, C.; Zhai, G.; Oleg, G. Numerical investigation of water entry of a wedge into waves with current effects using a fully nonlinear HOBEM. Ocean Eng. 2018, 153, 33–52. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, G.; Ji, C.; Zhai, G.J.; Oleg, G. Current effects on nonlinear wave slamming by an Oscillating Wave Surge Converter. Eng. Anal. Bound. Elem. 2018, 96, 150–168. [Google Scholar] [CrossRef]
- Mayer, H.C.; Krechetnikov, R. Flat plate impact on water. J. Fluid Mech. 2018, 850, 1066–1116. [Google Scholar] [CrossRef]
- Baarholm, R.; Faltinsen, O.M.; Herfjord, K. Wave impact on decks of floating platforms. Pract. Des. Ships Other Float. Struct. 2001, 1, 621–627. [Google Scholar]
- Faltinsen, O. Water entry of a wedge by hydroelastic orthotropic plate theory. J. Ship Res. 1999, 43, 180–193. [Google Scholar]
- Wang, H. Water wave pressure on horizontal plate. J. Hydraul. Div. 1970, 96, 1997–2017. [Google Scholar]
- Huera-Huarte, F.J.; Jeon, D.; Gharib, M. Experimental investigation of water slamming loads on panels. Ocean Eng. 2011, 38, 1347–1355. [Google Scholar] [CrossRef]
- Rao, C.; Wan, D. Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method. J. Hydrodyn. 2018, 30, 70–78. [Google Scholar] [CrossRef]
- Goda, Y. A comparative review on the functional forms of directional wave spectrum. Coast. Eng. J. 1999, 41, 1–20. [Google Scholar] [CrossRef]
- Wang, D.; Sun, J.; Gui, J.; Ma, Z.; Ning, D. A numerical piston-type wave-maker toolbox for the open-source library OpenFOAM. J. Hydrodyn. 2017, 5, 774–781. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow (Hemisphere Series in Computational Methods in Mechanics and Thermal Sciences); CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Hirt, C.W.; Nichlos, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Shorter, P.J. Wave propagation and damping in linear viscoelastic laminates. J. Acoust. Soc. Am. 2004, 115, 17–25. [Google Scholar] [CrossRef]
- Weller, H.G. A New Approach to VOF-Based Interface Capturing Methods for Incompressible and Compressible Flow; Report TR/HGW/04; OpenCFD Ltd: Caversham, UK, 2008. [Google Scholar]
- Lin, P.Z.; Liu, P.L.-F. Internal wave-maker for navier-stokes equation models. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Sun, J.; Sun, Z.; Liang, S.; Zheng, K. Spectral analysis of random wave uplift force on a horizontal deck. J. Hydrodyn. 2011, 2, 81–88. [Google Scholar] [CrossRef]
- Dias, F.; Ghidaglia, J.M. Slamming: Recent progress in the evaluation of impact pressures. Annu. Rev. Fluid Mech. 2018, 50, 243–273. [Google Scholar] [CrossRef]
- USACE. Coastal Engineering Manual—Part 6, Chapter 5; USACE: New Orleans District, LA, USA, 2006. [Google Scholar]
- Kaplan, P.; Murray, J.J.; Yu, W.C. Theoretical analysis of wave impact forces on platform deck structures. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Copenhagen, Denmark, 18–22 June 1995; pp. 189–198. [Google Scholar]
- Cuomo, G.; Tirindelli, M.; Allsop, N.W.H. Wave-in-deck loads on exposed jetties. Coast. Eng. 2007, 54, 657–679. [Google Scholar] [CrossRef]
- Det Norske Veritas. Recommended Practice—Environmental Conditions and Environmental Loads; Det Norske Veritas: Hovik, Norway, 2010. [Google Scholar]

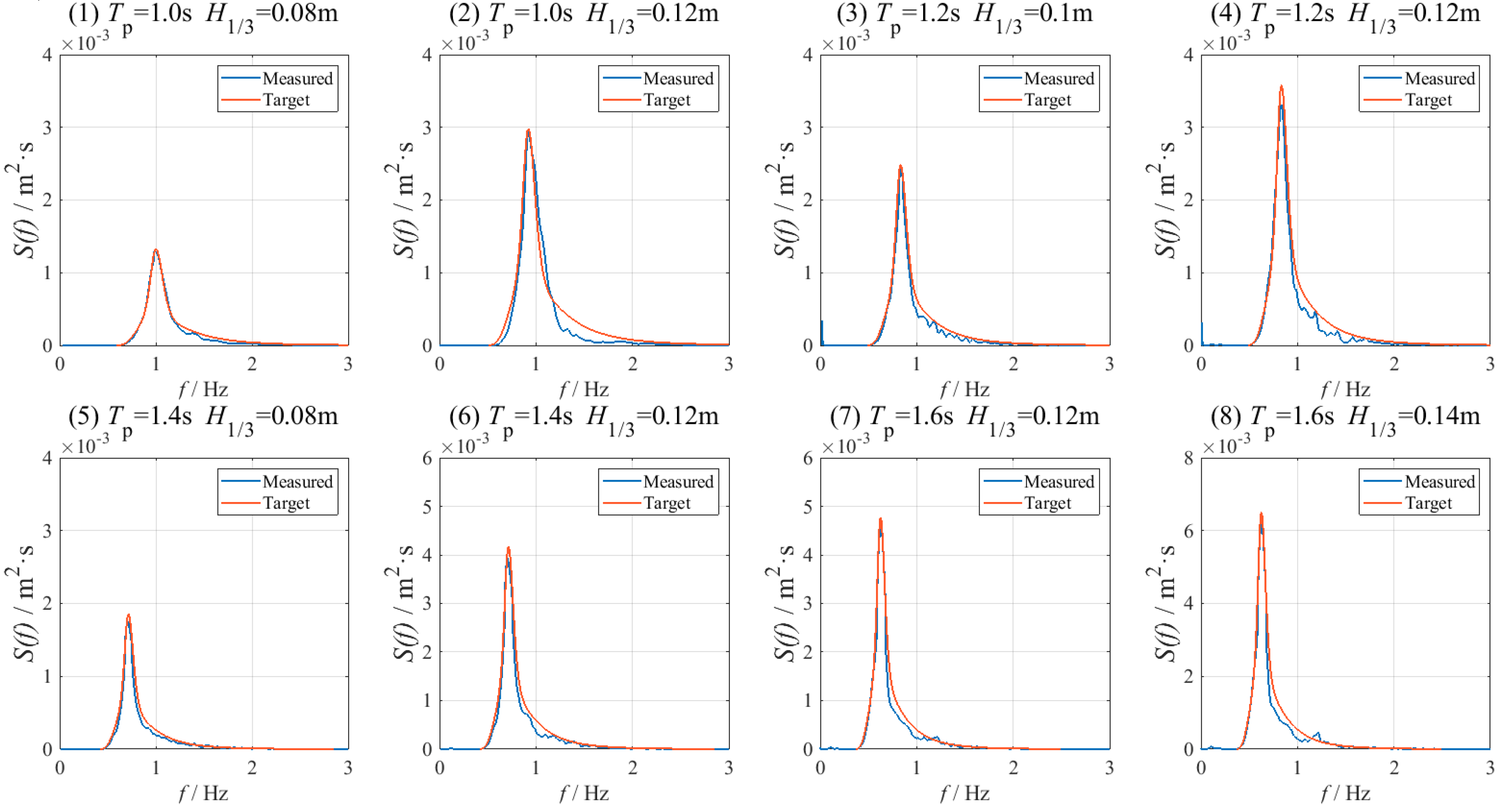
| Maximum Impact Pressure (kPa) | T = 1.0 s | T = 1.2 s | T = 1.4 s | T = 1.6 s | T = 1.8 s | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Angle | n | N | E | N | E | N | E | N | E | N | E |
| −10° | 1 | 0.72 | 0.71 | 2.56 | 1.59 | 2.47 | 0.49 | 2.32 | 0.24 | 0.85 | 0.49 |
| 2 | 6.99 | 8.55 | 6.59 | 8.66 | 2.84 | 1.60 | 1.22 | 2.44 | 1.22 | 1.59 | |
| 3 | 1.08 | 2.17 | 0.98 | 1.59 | 0.62 | 1.23 | 1.10 | 0.98 | 0.73 | 0.73 | |
| 4 | 0.36 | 0.72 | 0.73 | 1.59 | 0.49 | 0.49 | 0.85 | 0.24 | 0.49 | 0.37 | |
| 5 | 0.36 | 0.72 | 0.24 | 0.61 | 2.59 | 4.32 | 0.61 | 0.00 | 0.49 | 0.37 | |
| −5° | 1 | 4.46 | 2.29 | 2.20 | 1.22 | 2.10 | 1.23 | 1.71 | 0.73 | 0.73 | 0.73 |
| 2 | 1.81 | 0.84 | 6.22 | 3.41 | 3.95 | 5.80 | 3.54 | 4.88 | 5.00 | 7.07 | |
| 3 | 2.53 | 3.01 | 1.59 | 2.20 | 0.74 | 1.48 | 1.10 | 1.22 | 0.37 | 2.20 | |
| 4 | 0.36 | 2.29 | 1.46 | 1.22 | 0.74 | 1.36 | 1.22 | 0.61 | 0.24 | 0.61 | |
| 5 | 0.00 | 0.72 | 0.12 | 1.10 | 0.12 | 0.86 | 0.49 | 0.37 | 0.24 | 1.10 | |
| 0° | 1 | 3.49 | 5.18 | 0.85 | 1.83 | 1.98 | 4.44 | 5.00 | 3.41 | 1.46 | 1.34 |
| 2 | 0.48 | 0.96 | 1.34 | 1.95 | 4.94 | 4.32 | 5.61 | 3.90 | 1.95 | 1.95 | |
| 3 | 0.72 | 1.33 | 2.68 | 2.20 | 2.10 | 1.98 | 3.05 | 1.34 | 5.24 | 5.85 | |
| 4 | 2.53 | 4.10 | 1.59 | 2.93 | 1.11 | 1.36 | 2.56 | 4.02 | 2.20 | 2.68 | |
| 5 | 0.60 | 0.96 | 0.61 | 1.95 | 3.95 | 4.32 | 1.59 | 3.90 | 1.34 | 2.80 | |
| 5° | 1 | 3.49 | 4.58 | 0.73 | 2.32 | 2.59 | 6.54 | 5.98 | 5.12 | 4.27 | 2.93 |
| 2 | 1.20 | 1.69 | 1.34 | 2.32 | 5.06 | 5.80 | 6.95 | 5.00 | 5.12 | 4.27 | |
| 3 | 1.20 | 1.20 | 2.56 | 2.44 | 5.06 | 3.95 | 4.51 | 1.59 | 4.88 | 4.27 | |
| 4 | 1.81 | 1.45 | 2.56 | 3.29 | 2.47 | 3.46 | 2.93 | 0.61 | 5.00 | 6.34 | |
| 5 | 1.08 | 1.69 | 0.73 | 2.32 | 4.57 | 5.80 | 1.22 | 4.63 | 3.66 | 4.63 | |
| 10° | 1 | 4.70 | 3.98 | 3.66 | 2.56 | 3.33 | 2.84 | 3.54 | 1.95 | 1.71 | 2.56 |
| 2 | 5.42 | 5.06 | 7.07 | 6.22 | 6.30 | 6.42 | 4.39 | 3.29 | 4.15 | 4.88 | |
| 3 | 5.78 | 7.35 | 5.49 | 5.24 | 6.05 | 5.43 | 5.61 | 3.41 | 3.05 | 2.68 | |
| 4 | 5.78 | 6.14 | 7.93 | 8.66 | 4.20 | 3.46 | 3.54 | 1.71 | 5.12 | 3.54 | |
| 5 | 4.82 | 5.06 | 4.39 | 6.22 | 7.16 | 6.30 | 2.44 | 3.17 | 3.78 | 4.88 | |
| Angle | −10° | −5° | 0° | 5° | 10° |
|---|---|---|---|---|---|
| R2 | 0.78 | 0.85 | 0.81 | 0.85 | 0.89 |
| σ (×10−2) | 2.45 | 1.60 | 2.40 | 2.85 | 2.48 |
| Sensitive Factor | H1/3 | Ls | ∆h | d | B | α |
|---|---|---|---|---|---|---|
| ±5% | 0.69 | −0.16 | −0.02 | 0.02 | −0.17 | 0.37 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Zhou, T.; Ren, N.; Zhai, G. A Comprehensive Study of the Wave Impact Loads on an Inclined Plate. J. Mar. Sci. Eng. 2019, 7, 103. https://doi.org/10.3390/jmse7040103
Ma Z, Zhou T, Ren N, Zhai G. A Comprehensive Study of the Wave Impact Loads on an Inclined Plate. Journal of Marine Science and Engineering. 2019; 7(4):103. https://doi.org/10.3390/jmse7040103
Chicago/Turabian StyleMa, Zhe, Ting Zhou, Nianxin Ren, and Gangjun Zhai. 2019. "A Comprehensive Study of the Wave Impact Loads on an Inclined Plate" Journal of Marine Science and Engineering 7, no. 4: 103. https://doi.org/10.3390/jmse7040103
APA StyleMa, Z., Zhou, T., Ren, N., & Zhai, G. (2019). A Comprehensive Study of the Wave Impact Loads on an Inclined Plate. Journal of Marine Science and Engineering, 7(4), 103. https://doi.org/10.3390/jmse7040103





