Comparison of Physical to Numerical Mixing with Different Tracer Advection Schemes in Estuarine Environments
Abstract
1. Introduction
1.1. Physical Mixing
1.2. Numerical Mixing
2. Methodology
2.1. Numerical Model Description
2.2. Different Tracer Advection Scheme Choices in COAWST Model
2.2.1. Multidimensional Positive Definite Advection Transport Algorithm (MPDATA)
2.2.2. Third-order Upstream-biased Horizontal Scheme (U3H)
2.2.3. High-order Spatial Interpolation at the Middle Temporal Level (HSIMT)
2.3. Estimating Physical and Numerical Mixing
2.3.1. Physical Mixing
2.3.2. Numerical Mixing
3. Model Simulations
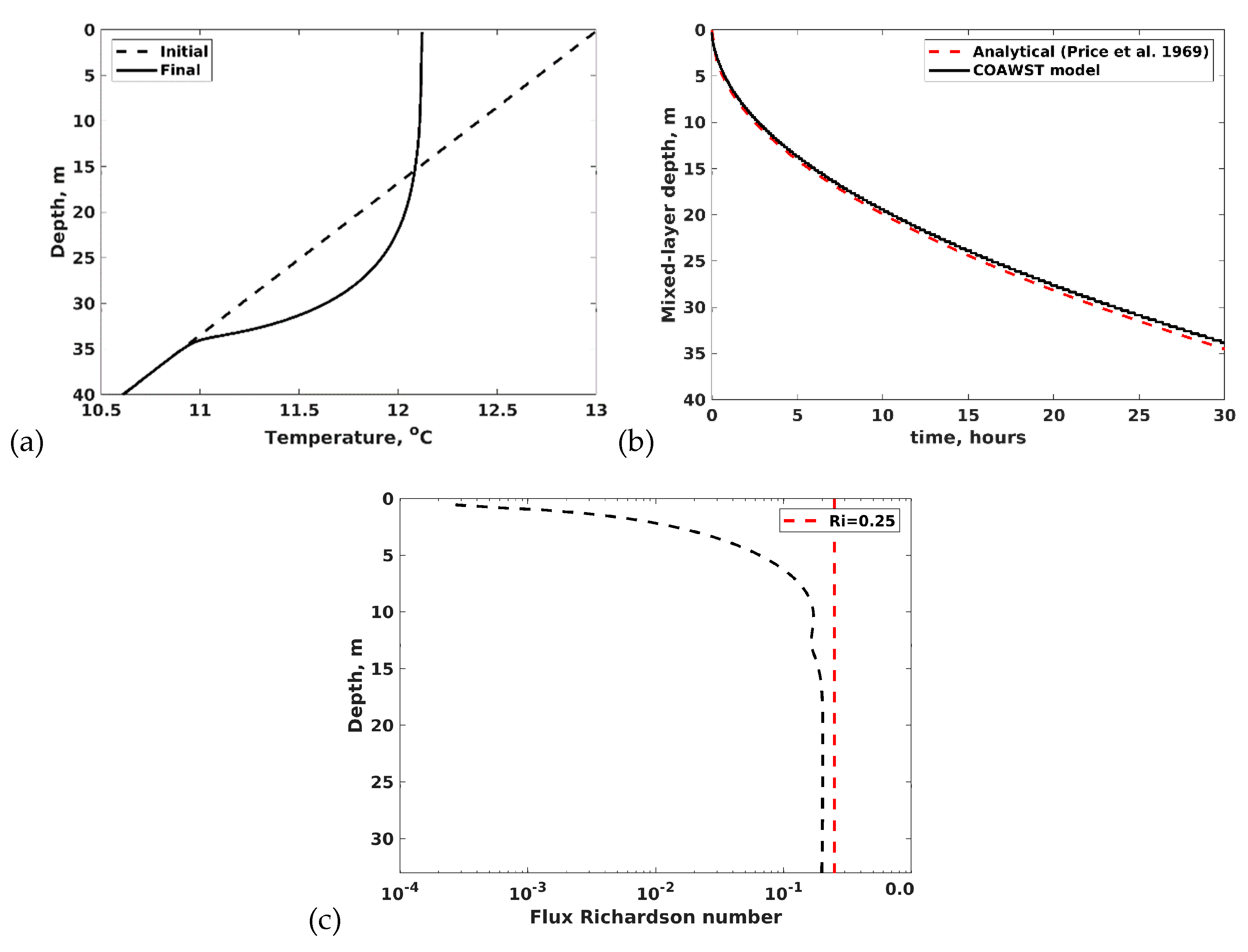
3.1. Test Case 1: Wind-induced Mixed-layer Deepening
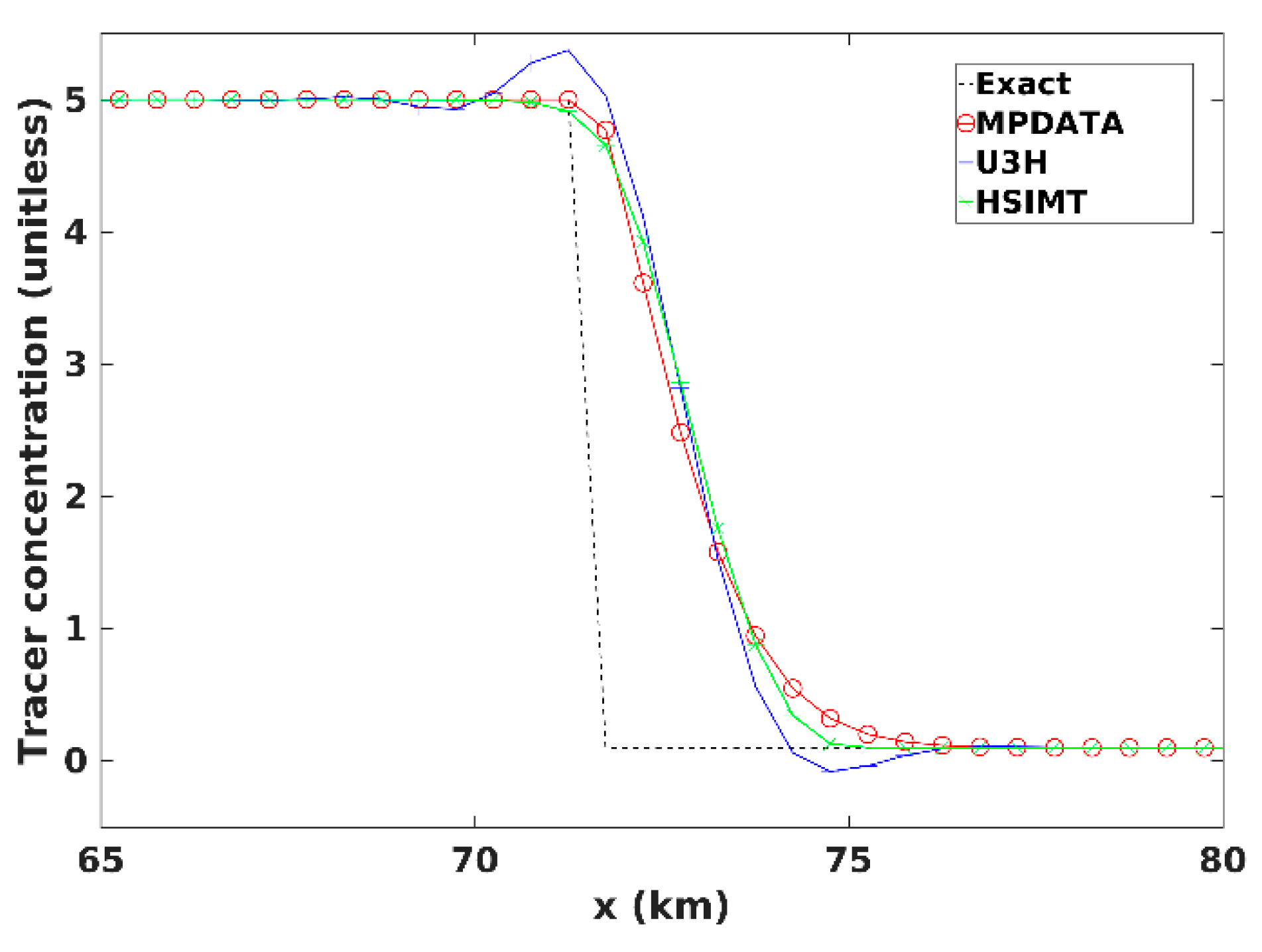
3.2. Test Case 2: Horizontal Tracer Patch Propagation
3.3. Test Case 3: Lock Exchange Problem
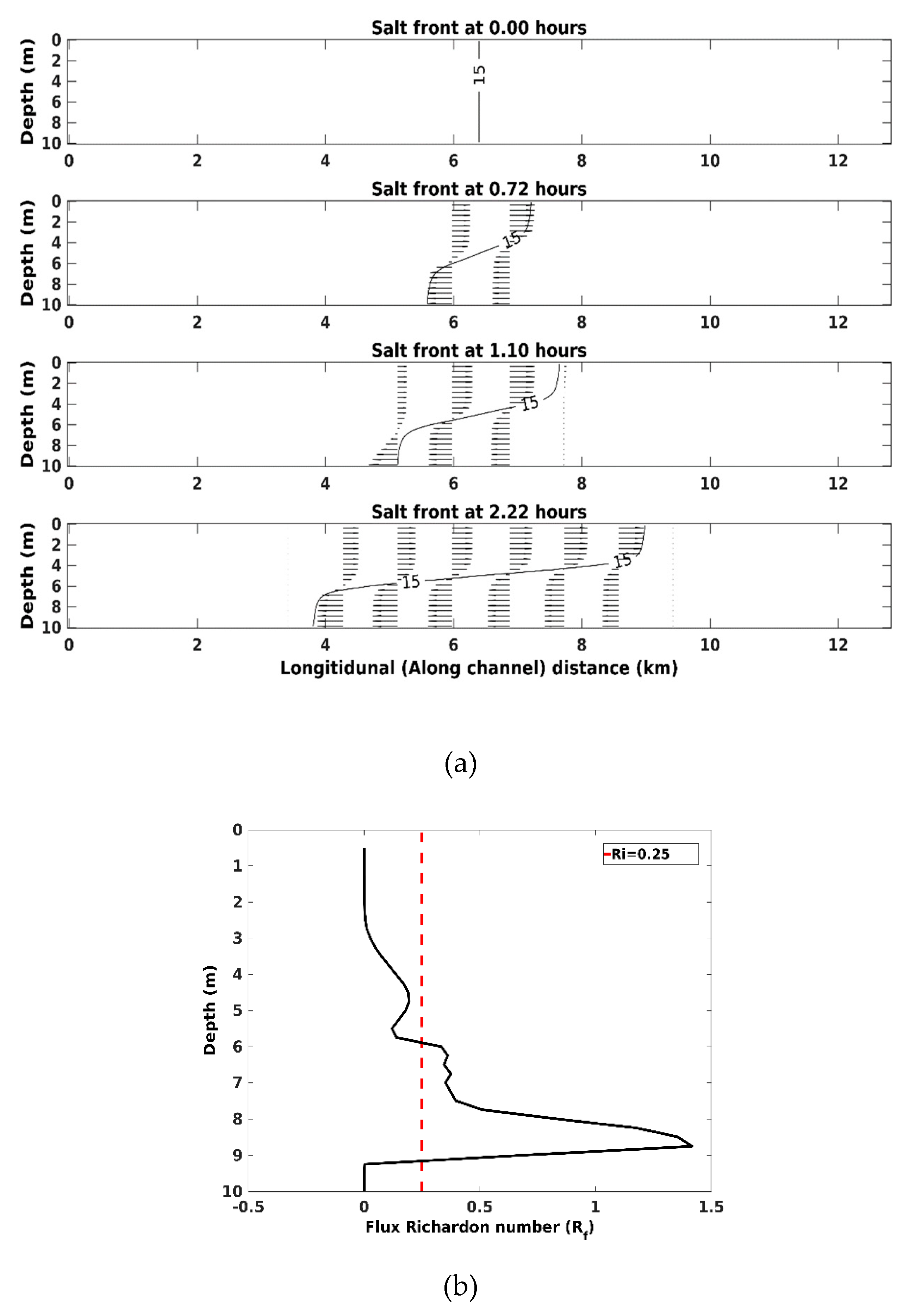
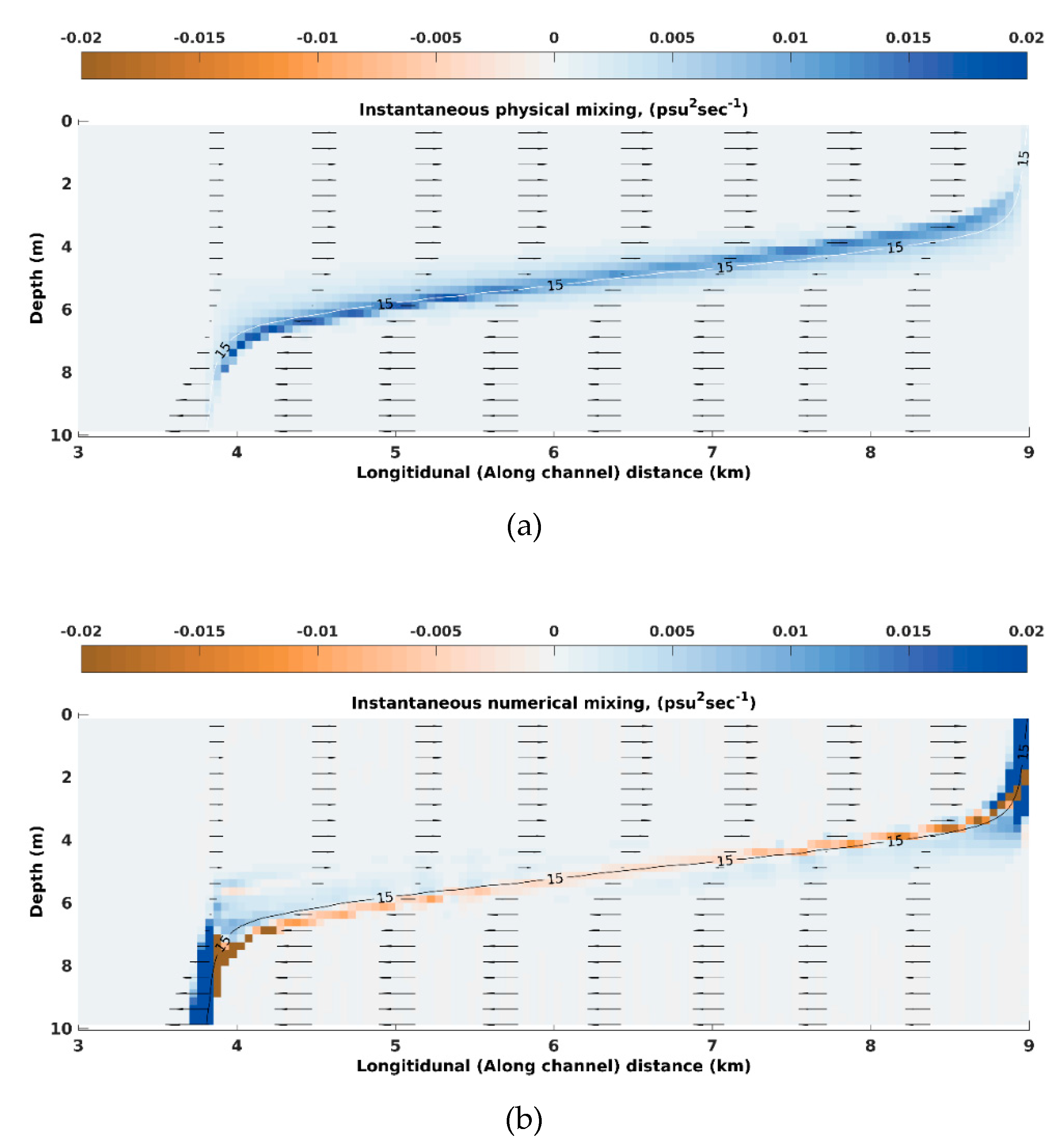
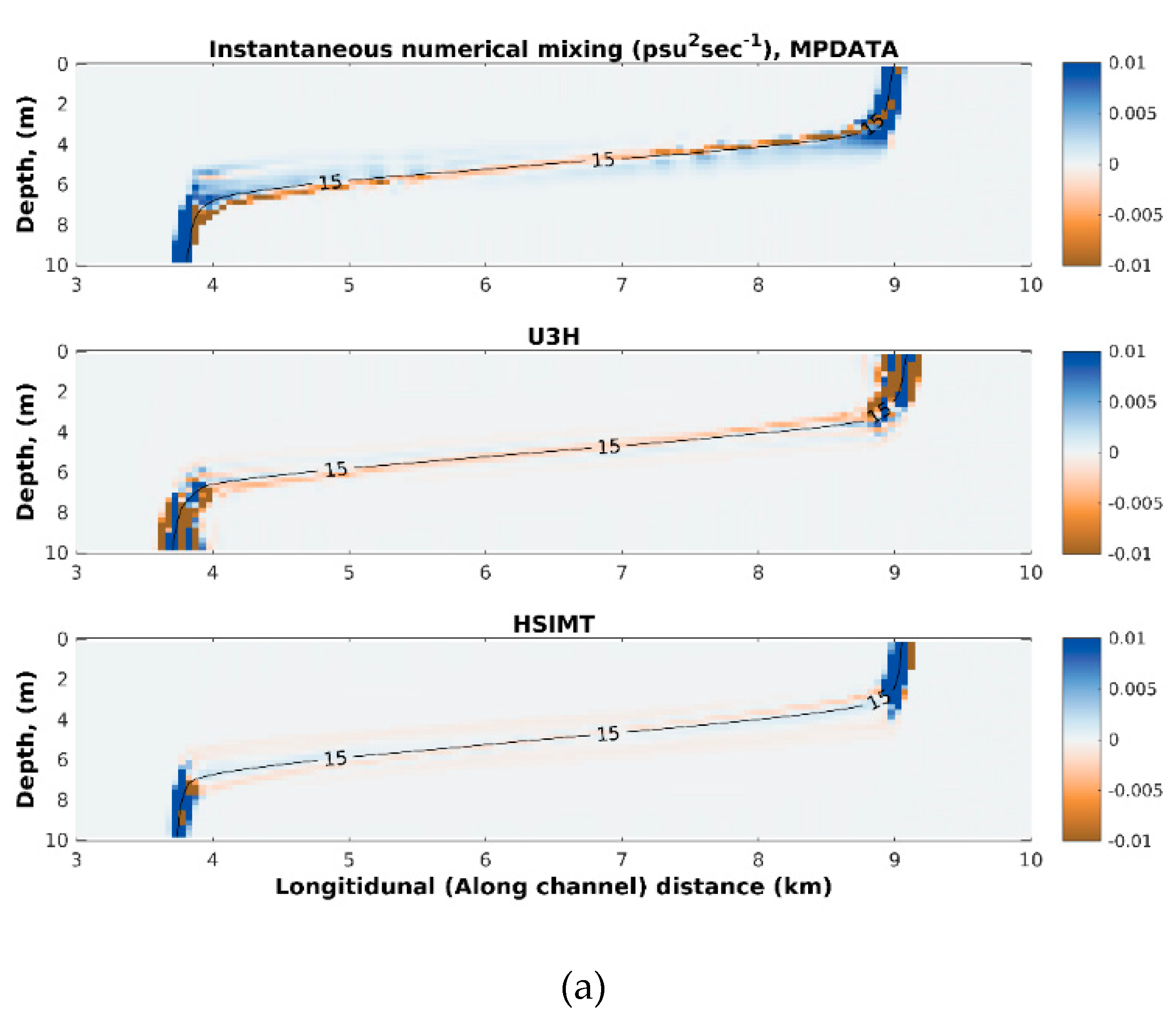
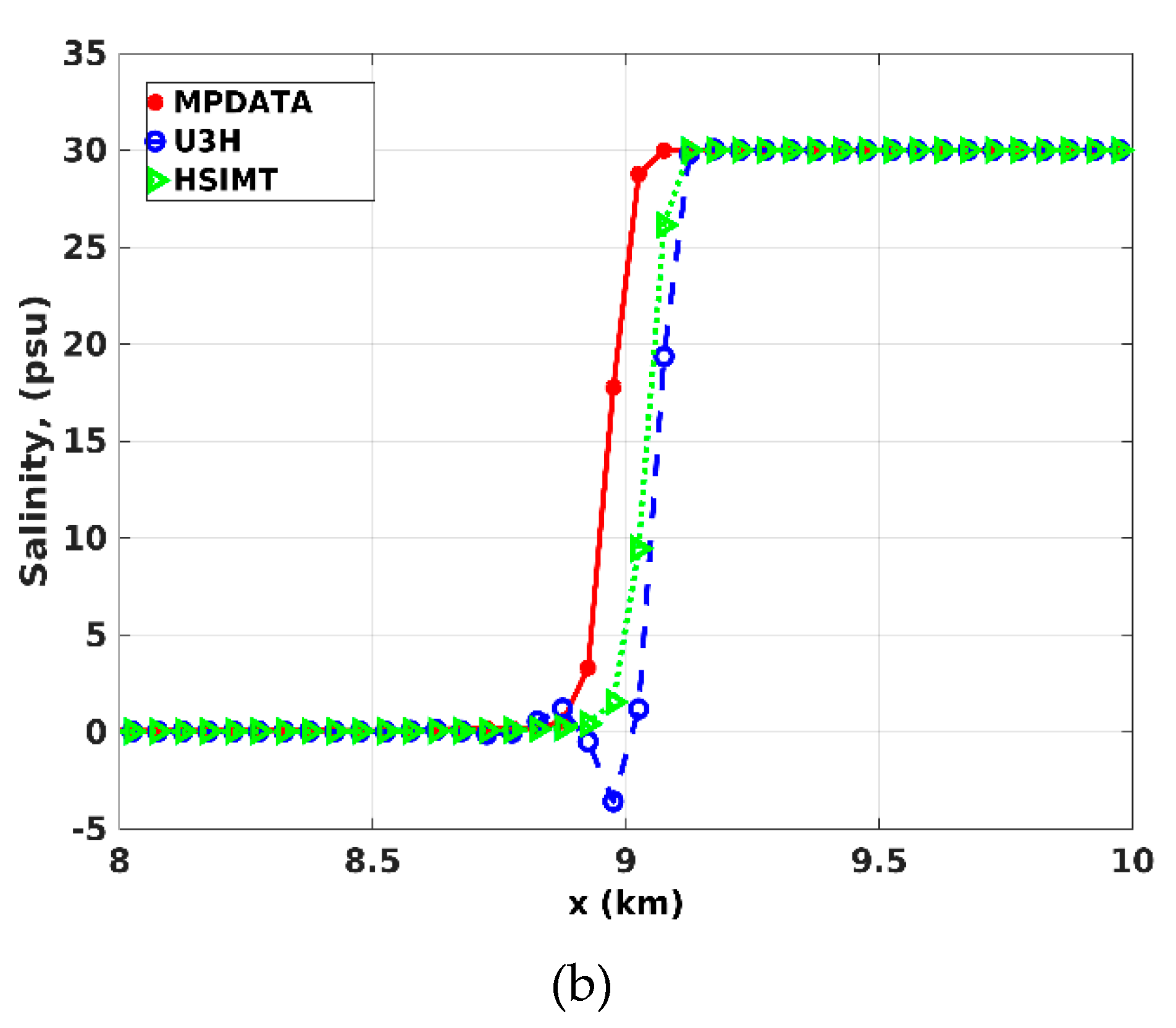
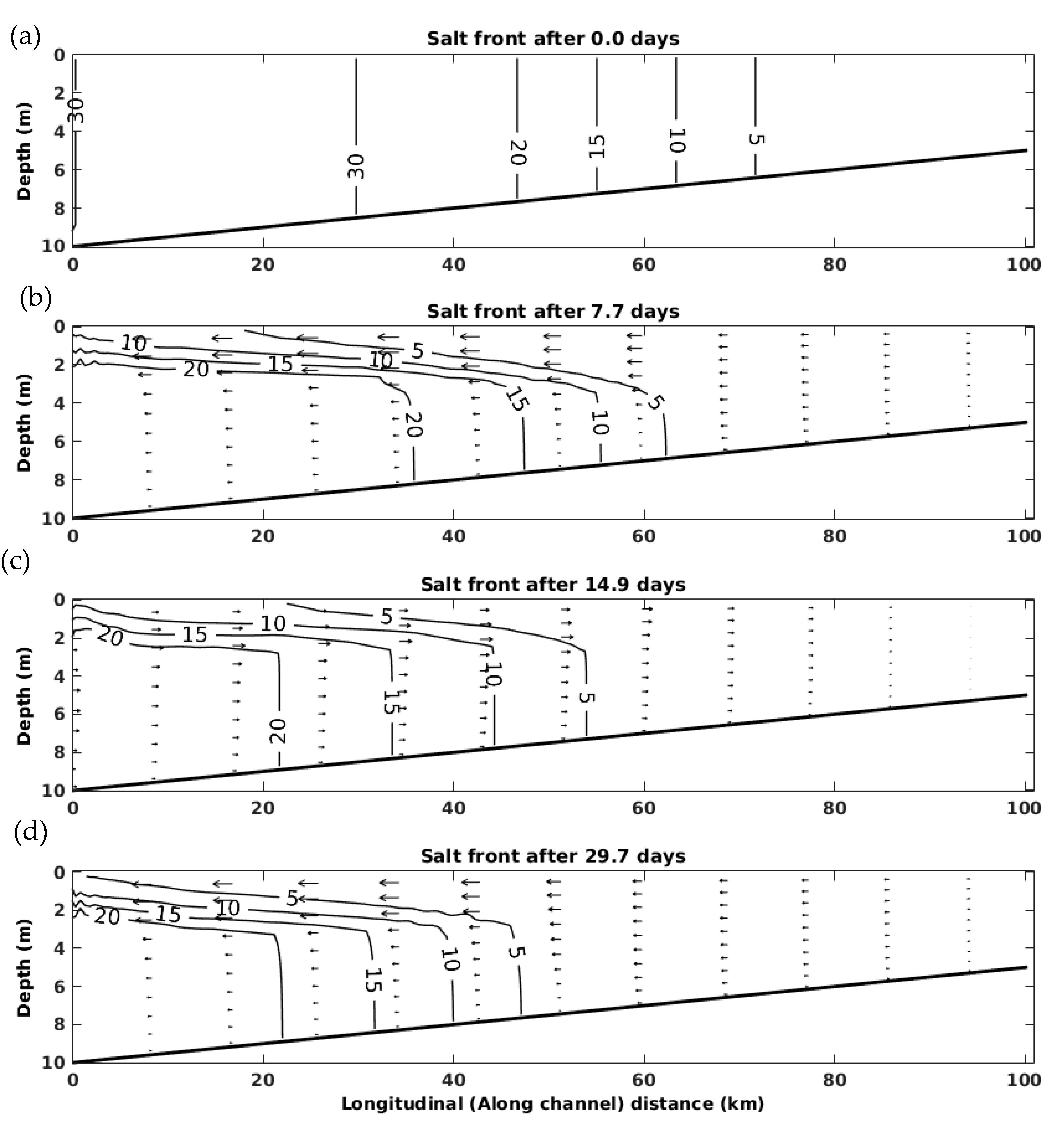
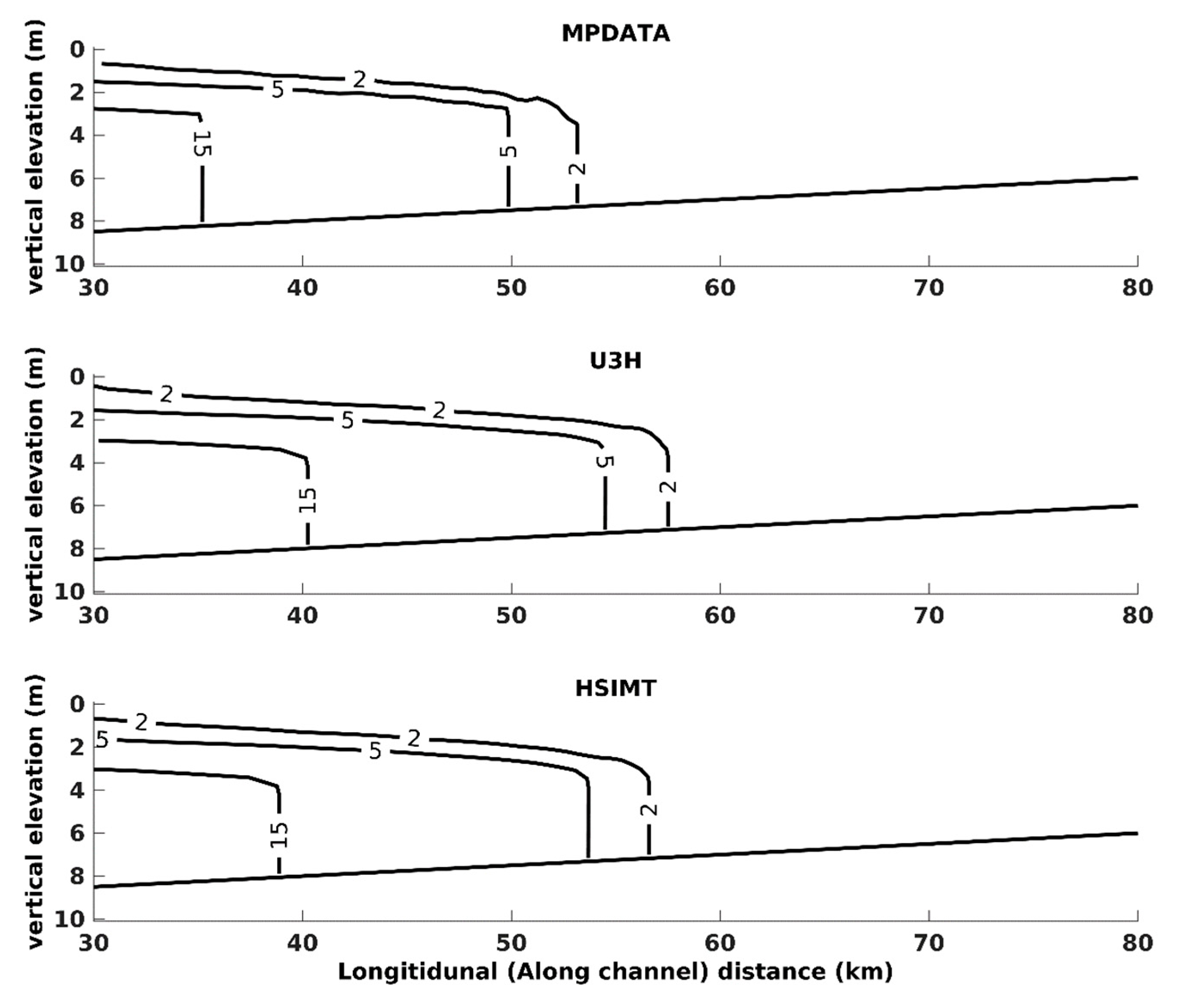
3.4. Test Case 4: Estuary Test Case with a Rectangular Geometry
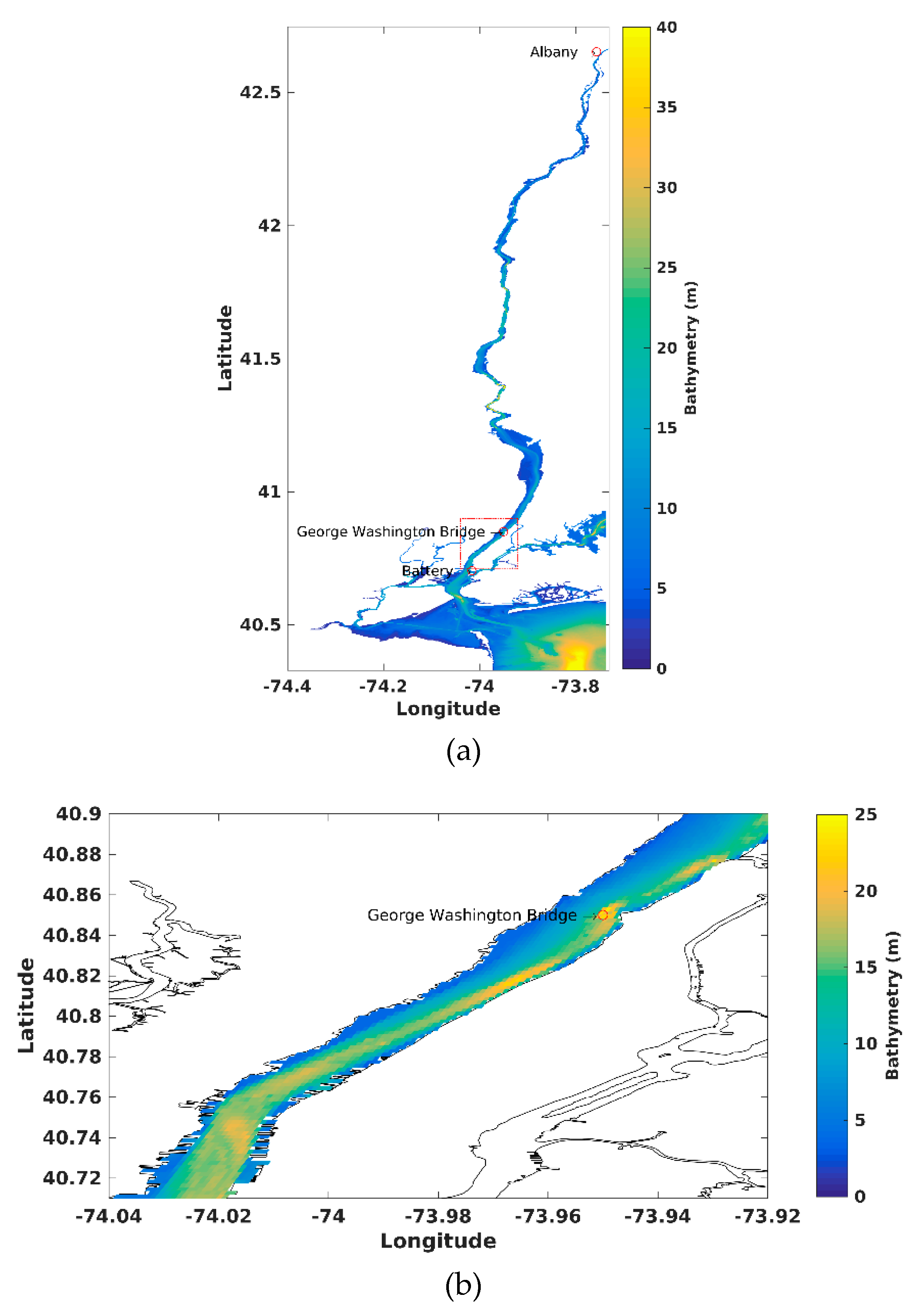
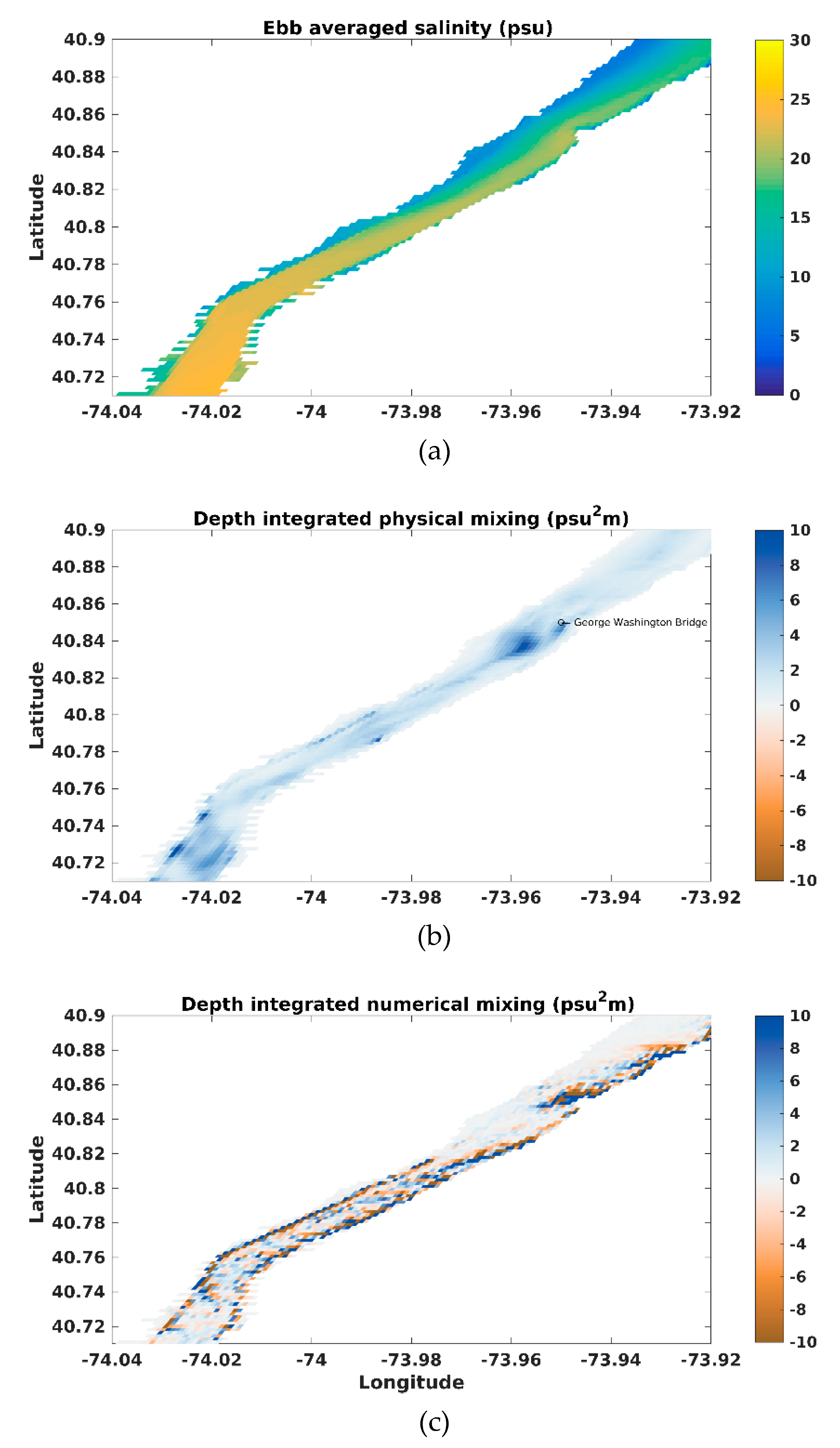
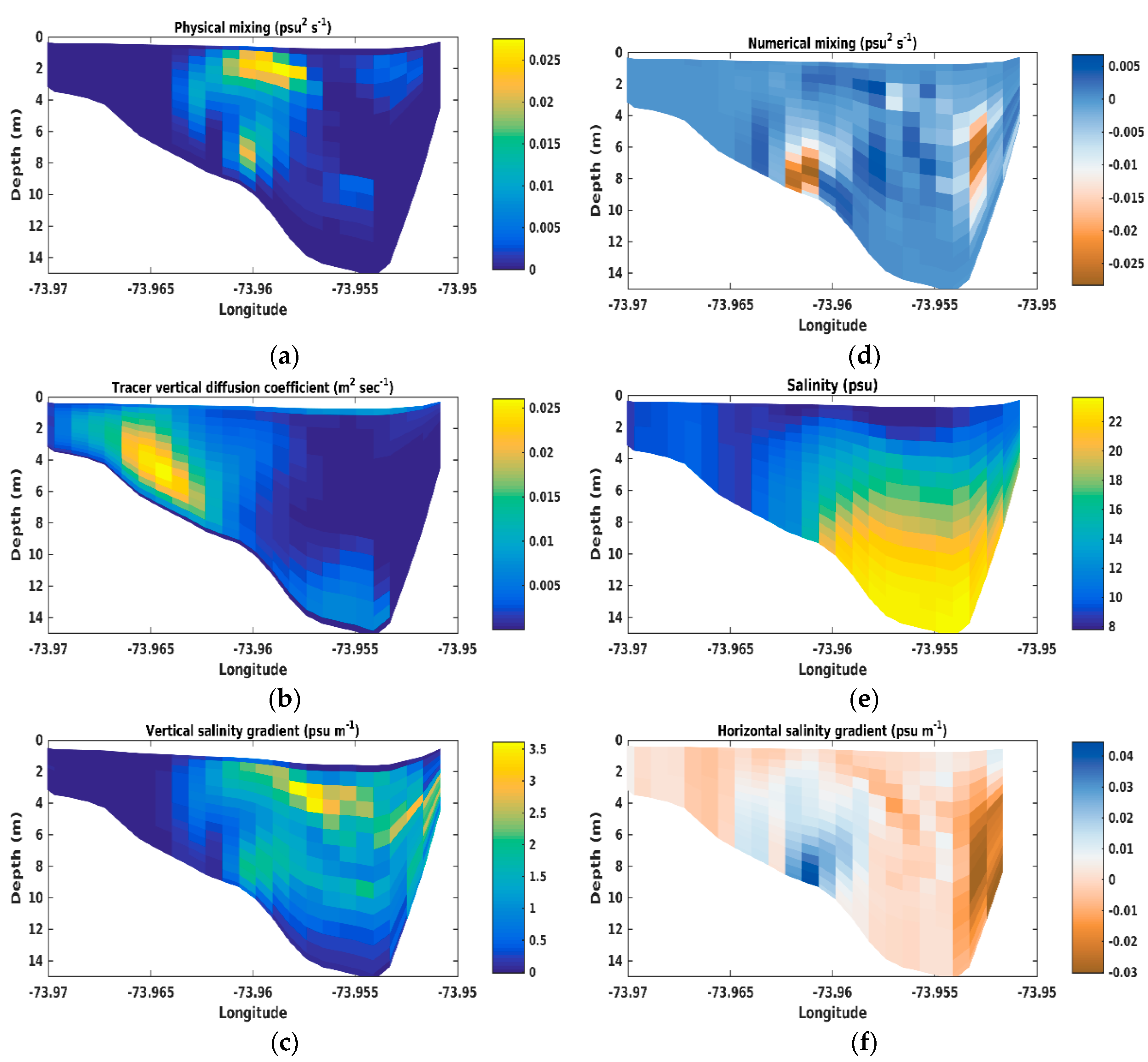
3.5. Realistic Application of Hudson River Estuary
4. Discussion
4.1. Effect of Grid Resolution on Mixing
4.2. Effect of Advection Schemes on Mixing
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MacDonald, D.G.; Geyer, W.R. Turbulent energy production and entrainment at a highly stratified estuarine front. J. Geophys. Res. 2004, 109, C05004. [Google Scholar] [CrossRef]
- Cifuentes, L.A.; Schemel, L.E.; Sharp, J.H. Qualitative and Numerical Analyses of the Effects of River Inflow Variations on Mixing Diagrams in Estuaries. Coast. Shelf Sci. 1990, 30, 411–427. [Google Scholar] [CrossRef]
- Hansen, D.V.; Rattray, M. Gravitational circulation in straits and estuaries. J. Mar. Res. 1965, 23, 104–122. [Google Scholar]
- Geyer, W.R. Influence of Wind on Dynamics and Flushing of Shallow Estuaries. Estuar. Coast. Shelf Sci. 1997, 44, 713–722. [Google Scholar] [CrossRef]
- Gordon, C.M.; Dohne, C.F. Some observations of Turbulent Flow in a Tidal Estuary. J. Geophys. Res. 1973, 78, 1971–1978. [Google Scholar] [CrossRef]
- Stacey, M.T. Turbulent Mixing and Residual Circulation in a Partially Stratified Estuary. Ph.D. Thesis, Department of Civil Engineering, Stanford University, Stanford, CA, USA, 1996. [Google Scholar]
- Trowbridge, J.H.; Geyer, W.R.; Bowen, M.M.; Williams, A.J., III. Near-bottom turbulence measurements in a partially mixed estuary: Turbulent energy balance, velocity structure, and along-channel momentum balance. J. Phys. Oceanogr. 1999, 29, 3056–3072. [Google Scholar] [CrossRef]
- Geyer, W.R.; Malcolm, E.; Scully, M.E.; David, K.; Ralston, D.K. Quantifying vertical mixing in estuaries. Environ. Fluid Mech. 2008, 8, 495–509. [Google Scholar] [CrossRef]
- Scully, M.E.; Geyer, W.R.; Trowbridge, J.H. The influence of stratification and nonlocal turbulent production on estuarine turbulence: An assessment of turbulence closure with field observations. J. Phys. Oceanogr. 2011, 41, 166–185. [Google Scholar] [CrossRef]
- Holleman, R.C.; Geyer, W.R.; Ralston, D.K. Stratified Turbulence and Mixing Efficiency in a Salt Wedge Estuary. J. Phys. Oceanogr. 2016, 46, 1769–1783. [Google Scholar] [CrossRef]
- Nunes Vaz, R.A.; Simpson, J.H. Turbulence closure modeling of estuarine stratification. J. Geophys. Res. 1994, 99, 143–160. [Google Scholar] [CrossRef]
- Simpson, J.H.; Brown, J.; Matthews, J.; Allen, G. Tidal straining, density currents, and stirring in the control of estuarine stratification. Estuaries 1990, 13, 125–132. [Google Scholar] [CrossRef]
- Simpson, J.H.; Sharples, J. Dynamically-active models in the prediction of estuarine stratification. In Dynamics and Exchanges in Estuaries and the Coastal Zone; Prandle, D., Ed.; Springer: New York, NY, USA, 1991; pp. 101–103. [Google Scholar]
- Nunes Vaz, R.A.; Lenon, G.W.; de Silva Samarasinghe, J.R. The negative role of turbulence in estuarine mass transport. Estuar. Coast. Shelf Sci. 1989, 28, 361–377. [Google Scholar] [CrossRef]
- Zhou, M. Influence of bottom stress on the two-layer flow induced by gravity currents in estuaries. Estuar. Coast. Shelf Sci. 1998, 46, 811–825. [Google Scholar] [CrossRef]
- Chatwin, P.C. Some remarks on the maintenance of the salinity distribution in estuaries. Estuar. Coast. Mar. Sci. 1976, 4, 555–566. [Google Scholar] [CrossRef]
- MacCready, P. Toward a Unified Theory of Tidally-Averaged Estuarine Salinity Structure. Estuaries 2004, 27, 561–570. [Google Scholar] [CrossRef]
- Umlauf, L.; Burchard, H. A generic length-scale equation for geophysical turbulence models. J. Mar. Res. 2003, 61, 235–265. [Google Scholar] [CrossRef]
- Burchard, H.; Petersen, O. Models of turbulence in the marine environment. A comparative study of two-equation turbulence models. J. Mar. Syst. 1999, 21, 29–53. [Google Scholar] [CrossRef]
- Burchard, H.; Petersen, O.; Rippeth, T. Comparing the performance of the Mellor–Yamada and the k–ε two-equation turbulence models. J. Geophys. Res. 1998, 103, 10543–10554. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Arango, H.G.; Signell, R.P. Performance of four turbulence closure models implemented using a generic length scale method. Ocean Model. 2005, 8, 81–113. [Google Scholar] [CrossRef]
- Soufflet, Y.; Marchesiello, P.; Lemarié, F.; Jouanno, J.; Capet, X.; Debreu, L.; Benshila, R. On effective resolution in ocean models. Ocean Model. 2006, 98, 36–50. [Google Scholar] [CrossRef]
- Leveque, R.J. Numerical Methods for Conservation Laws; Birkhauser Verlag: Boston, MA, USA, 1992. [Google Scholar]
- Ilicak, M. Quantifying spatial distribution of spurious mixing in ocean models. Ocean Model. 2016, 108, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Gibson, A.H.; Hogg, A.M.; Kiss, A.E.; Shakespeare, C.J.; Adcroft, A.J. Attribution of horizontal and vertical contributions to spurious mixing in an Arbitrary Lagrangian-Eulerian ocean model. Ocean Model. 2017, 119, 45–56. [Google Scholar] [CrossRef]
- Klingbeil, K.; Mohammadi-Aragh, M.; Gräwe, U.; Burchard, H. Quantification of spurious dissipation and mixing Discrete Variance Decay in a Finite-Volume framework. Ocean Model. 2014, 81, 49–64. [Google Scholar] [CrossRef]
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Arango, H.G.; Dietrich, D.; Ezer, T.; Ghil, M.; Haidvogel, D.B.; Ma, C.-C.; Mehra, A.; Paiva, A.M.; Sirkes, Z. DAMEE-NAB: The base experiments. Dyn. Atmos. Ocean. 2000, 32, 155–183. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.G.; Hedstrom, K.; Beckmann, A.; Malanotte-Rizzoli, P.; Shchepetkin, A.F. Model evaluation experiments in the North Atlantic Basin: Simulations in nonlinear terrain-following coordinates. Dyn. Atmos. Ocean. 2000, 32, 239–281. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The Regional Ocean Modeling System: A split-explicit, free-surface, topography-following coordinates ocean model. J. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.G.; Budgell, W.P.; Cornuelle, B.D.; Churchitser, E.; Di Lorenzo, E.; Fennel, K.; Geyer, W.R.; Hermann, A.J.; Lanerolle, L.; et al. Ocean forecasting in terrain following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2008, 227, 3595–3624. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K. A simple positive definite advection scheme with small implicit diffusion. Mon. Weather Rev. 1983, 111, 479–486. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K. A fully multidimensional positive definite advection transport algorithm with small implicit diffusion. J. Comput. Phys. 1984, 54, 325–362. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. Quasi-monotone advection schemes based on explicit locally adaptive dissipation. Mon. Weather Rev. 1998, 126, 1541–1580. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, J. Advection scheme with 3rd high-order spatial interpolation at the middle temporal level and its application to saltwater intrusion in the Changjiang Estuary. Ocean Model. 2010, 33, 33–514. [Google Scholar] [CrossRef]
- Sweby, P.K. High resolution schemes using flux limiters for hyperbolic conservation laws. Society of Industrial and Applied Mathematics. J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Burchard, H.; Rennau, H. Comparative quantification of physically and numerically induced mixing in ocean models. Ocean Model. 2008, 20, 293–311. [Google Scholar] [CrossRef]
- Kato, H.; Phillips, O.M. On the penetration of a turbulent layer into a stratified fluid. J. Fluid Mech. 1969, 37, 643–655. [Google Scholar] [CrossRef]
- Trowbridge, J.H. A simple description of the deepening and structure of a stably stratified flow driven by a surface stress. J. Geophys. Res. 1992, 97, 15529–15543. [Google Scholar] [CrossRef]
- Burchard, H.; Bolding, K. Comparative analysis of four second-moment turbulence closure models for the oceanic mixed layer. J. Phys. Oceanogr. 2001, 31, 1943–1968. [Google Scholar] [CrossRef]
- Warner, J.C.; Geyer, W.R.; Lerczak, J.A. Numerical modeling of an estuary: A comprehensive skill assessment. Geophys. Res. Lett. 2005, 40, 5451–5455. [Google Scholar] [CrossRef]
- Price, J.F. On the scale of stress-driven entrainment experiments. J. Fluid Mech. 1979, 90, 509–529. [Google Scholar] [CrossRef]
- Ralston, D.K.; Warner, J.C.; Geyer, W.R.; Wall, G.R. Sediment transport due to extreme events: The Hudson River estuary after tropical storms Irene and Lee. Geophys. Res. Lett. 2013, 40, 5451–5455. [Google Scholar] [CrossRef]
- Geyer, R.W.; Ralston, D.K. Estuarine Frontogenesis. J. Phys. Oceanogr. 2014, 45, 546–561. [Google Scholar] [CrossRef]
- Wang, T.; Geyer, R.W.; MacCready, P. Total Exchange Flow, Entrainment, and Diffusive Salt Flux in Estuaries. J. Phys. Oceanogr. 2017, 47, 1205–1220. [Google Scholar] [CrossRef]
- Ralston, D.K.; Cowles, G.W.; Geyer, W.R.; Holleman, R.C. Turbulent and numerical mixing in a salt wedge estuary: Dependence on grid resolution, bottom roughness, and turbulence closure. J. Geophys. Res. Ocean. 2017, 122, 692–712. [Google Scholar] [CrossRef]
- Harten, A. On High-Order Accurate Interpolation for Non-Oscillatory Shock Capturing Schemes. In Oscillation Theory, Computation, and Methods of Compensated Compactness; The IMA Volumes in Mathematics and Its Applications; Dafermos, C., Ericksen, J.L., Kinderlehrer, D., Slemrod, M., Eds.; Springer: New York, NY, USA, 1986; Volume 2. [Google Scholar]
- Simpson, J.E.; Britter, R.E. The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 1979, 94, 477–495. [Google Scholar] [CrossRef]
- Kalra, T.S.; Warner, J.C. Idealized COAWST Model Cases for Studying the Comparison of Physical to Numerical Mixing with Different Tracer Advection Schemes in Estuarine Environments; U.S. Geological Survey Data Release; USGS: Reston, VA, USA, 2019.
- Warner, J.C.; Kalra, T.S. Numerical Model of Salinity Transport and Mixing in the Hudson River Estuary; U.S. Geological Survey Data Release; USGS: Reston, VA, USA, 2019.
| Advection Scheme | Mphys/Mtotal | Mnum/Mtotal | Mtotal | Vtotal |
|---|---|---|---|---|
| Test Case 1: MPDATA | 1.0 | 0.0 | 0.25 | −0.25 |
| Test Case 1: U3H | 1.0 | 0.0 | 0.25 | −0.25 |
| Test Case 1: HSIMT | 1.0 | 0.0 | 0.25 | −0.25 |
| Test Case 2: MPDATA | 0.0 | 1.0 | 0.002 | −0.002 |
| Test Case 2: U3H | 0.0 | 1.0 | 0.0003 | −0.0003 |
| Test Case 2: HSIMT | 0.0 | 1.0 | 0.002 | −0.002 |
| Test Case 3: MPDATA | 0.086 | 0.914 | 17.994 | −18.968 |
| Test Case 3: U3H | 0.112 | 0.888 | 15.168 | −16.211 |
| Test Case 3: HSIMT | 0.076 | 0.923 | 18.721 | −19.597 |
| Test Case 4: MPDATA | 0.991 | 0.009 | 211.619 | −171.377 |
| Test Case 4: U3H | 0.998 | 0.002 | 235.329 | −188.808 |
| Test Case 4: HSIMT | 0.996 | 0.014 | 225.643 | −182.531 |
| Advection Scheme | |
|---|---|
| Test case 2: | 0.164 |
| Test case 2: | 0.009 |
| Test case 2: | 0.161 |
| Test case 3: | 0.40 |
| Test case 3: | 0.22 |
| Test case 3: | 0.35 |
| Mphys/Mtotal | Mnum/Mtotal | Mtotal | |
|---|---|---|---|
| 50 m, MPDATA | 0.086 | 0.914 | 17.994 |
| 50 m, U3H | 0.112 | 0.888 | 15.168 |
| 50 m, HSIMT | 0.076 | 0.923 | 18.721 |
| 25 m, MPDATA | 0.111 | 0.889 | 15.936 |
| 25 m, U3H | 0.138 | 0.862 | 14.066 |
| 25 m, HSIMT | 0.113 | 0.886 | 15.742 |
| 12.5 m, MPDATA | 0.134 | 0.866 | 14.565 |
| 12.5 m, U3H | 0.182 | 0.818 | 12.733 |
| 12.5 m, HSIMT | 0.145 | 0.854 | 14.018 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalra, T.S.; Li, X.; Warner, J.C.; Geyer, W.R.; Wu, H. Comparison of Physical to Numerical Mixing with Different Tracer Advection Schemes in Estuarine Environments. J. Mar. Sci. Eng. 2019, 7, 338. https://doi.org/10.3390/jmse7100338
Kalra TS, Li X, Warner JC, Geyer WR, Wu H. Comparison of Physical to Numerical Mixing with Different Tracer Advection Schemes in Estuarine Environments. Journal of Marine Science and Engineering. 2019; 7(10):338. https://doi.org/10.3390/jmse7100338
Chicago/Turabian StyleKalra, Tarandeep S., Xiangyu Li, John C. Warner, Wayne R. Geyer, and Hui Wu. 2019. "Comparison of Physical to Numerical Mixing with Different Tracer Advection Schemes in Estuarine Environments" Journal of Marine Science and Engineering 7, no. 10: 338. https://doi.org/10.3390/jmse7100338
APA StyleKalra, T. S., Li, X., Warner, J. C., Geyer, W. R., & Wu, H. (2019). Comparison of Physical to Numerical Mixing with Different Tracer Advection Schemes in Estuarine Environments. Journal of Marine Science and Engineering, 7(10), 338. https://doi.org/10.3390/jmse7100338





