Iterative Frequency-Domain Response of Floating Offshore Wind Turbines with Parametric Drag
Abstract
1. Introduction
1.1. Coupled Aero-Hydro-Servo-Elastic Dynamics
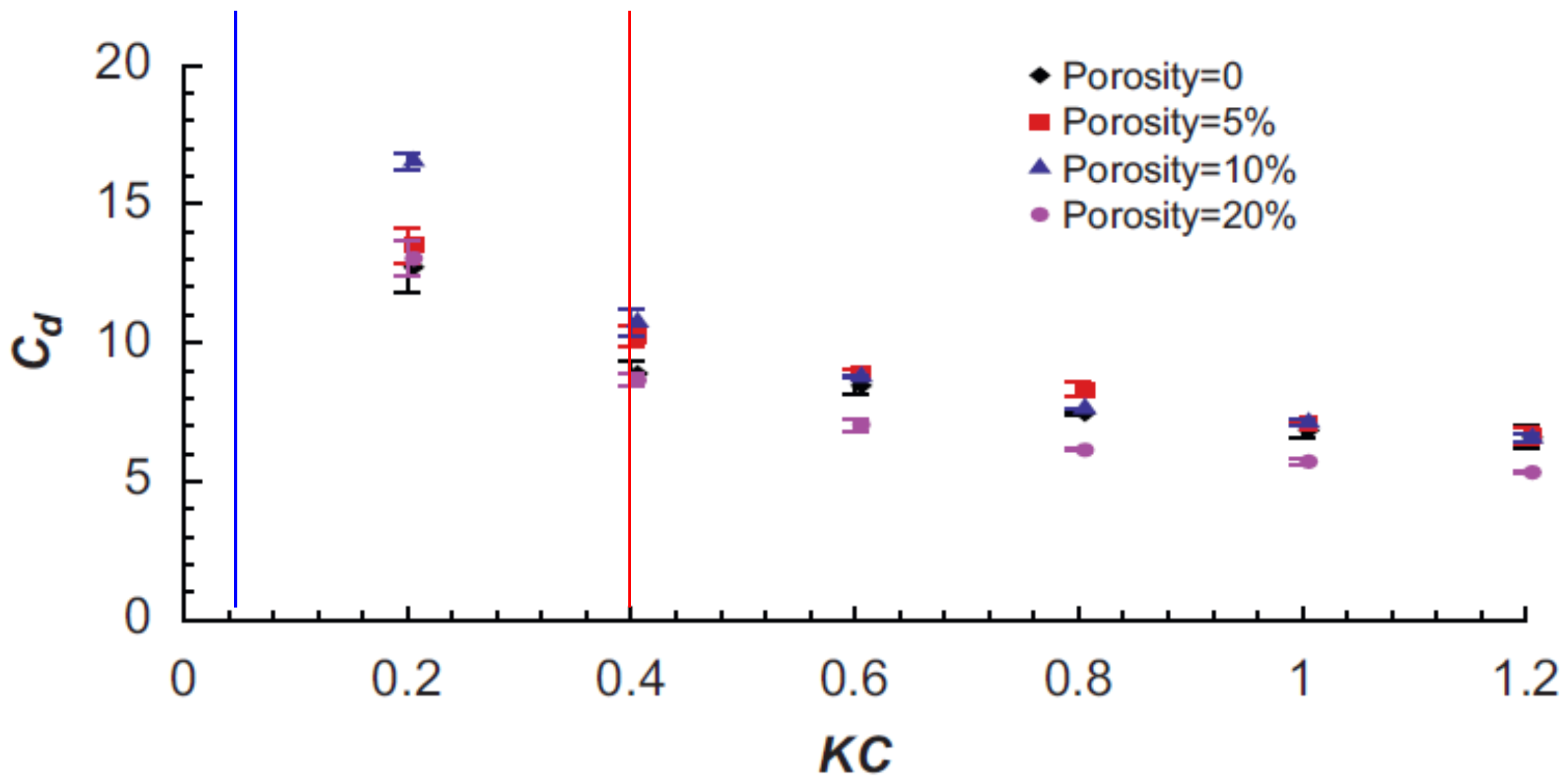
1.2. Hydrodynamic Viscous Drag
2. Numerical Simulation Methods
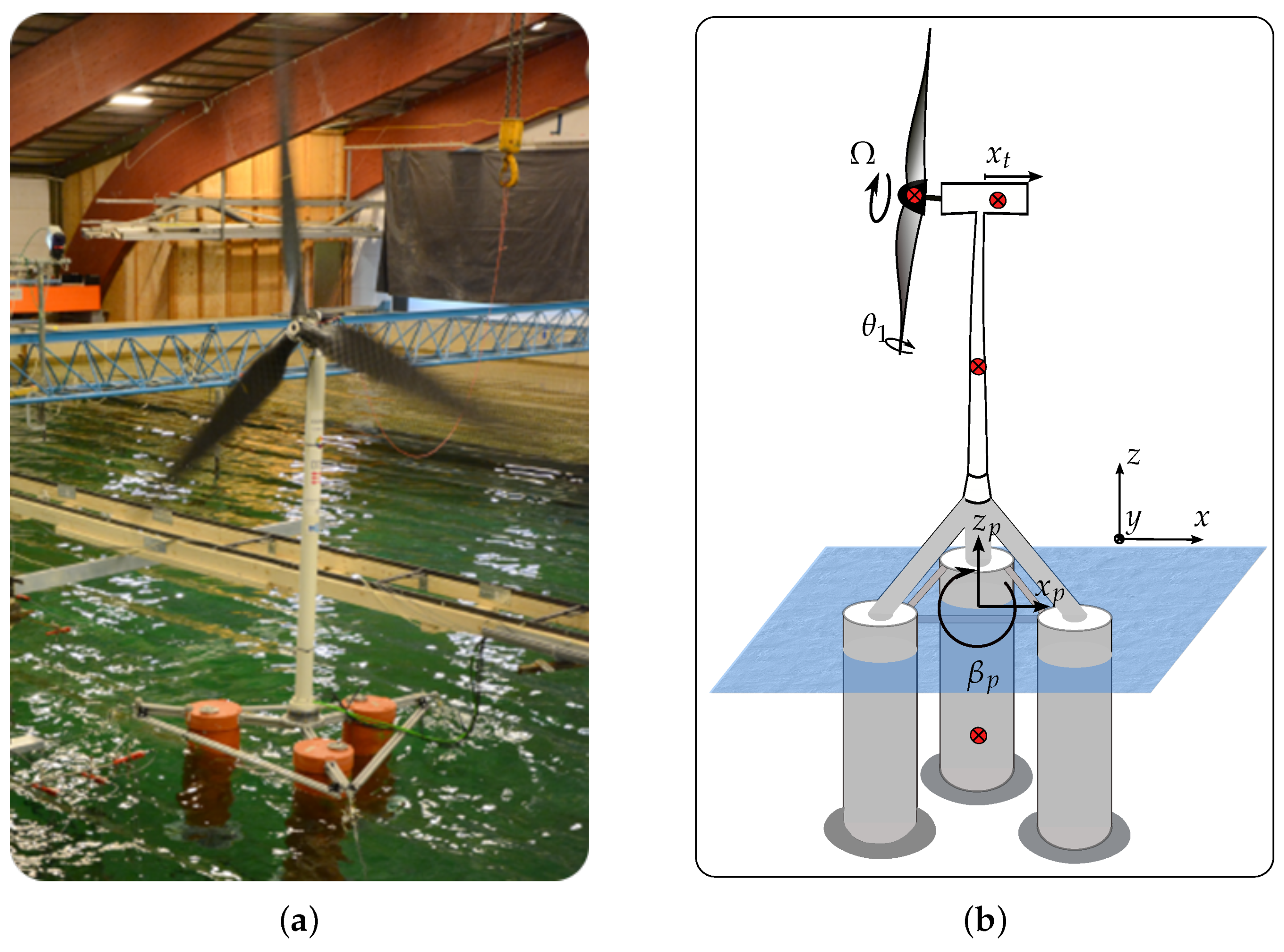
2.1. Reference Design
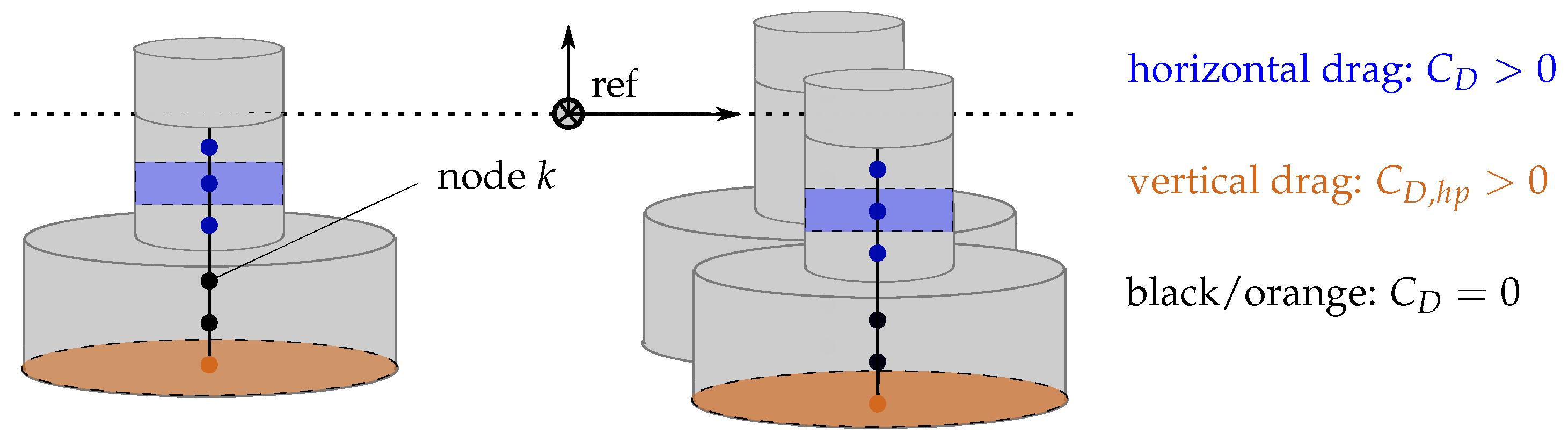
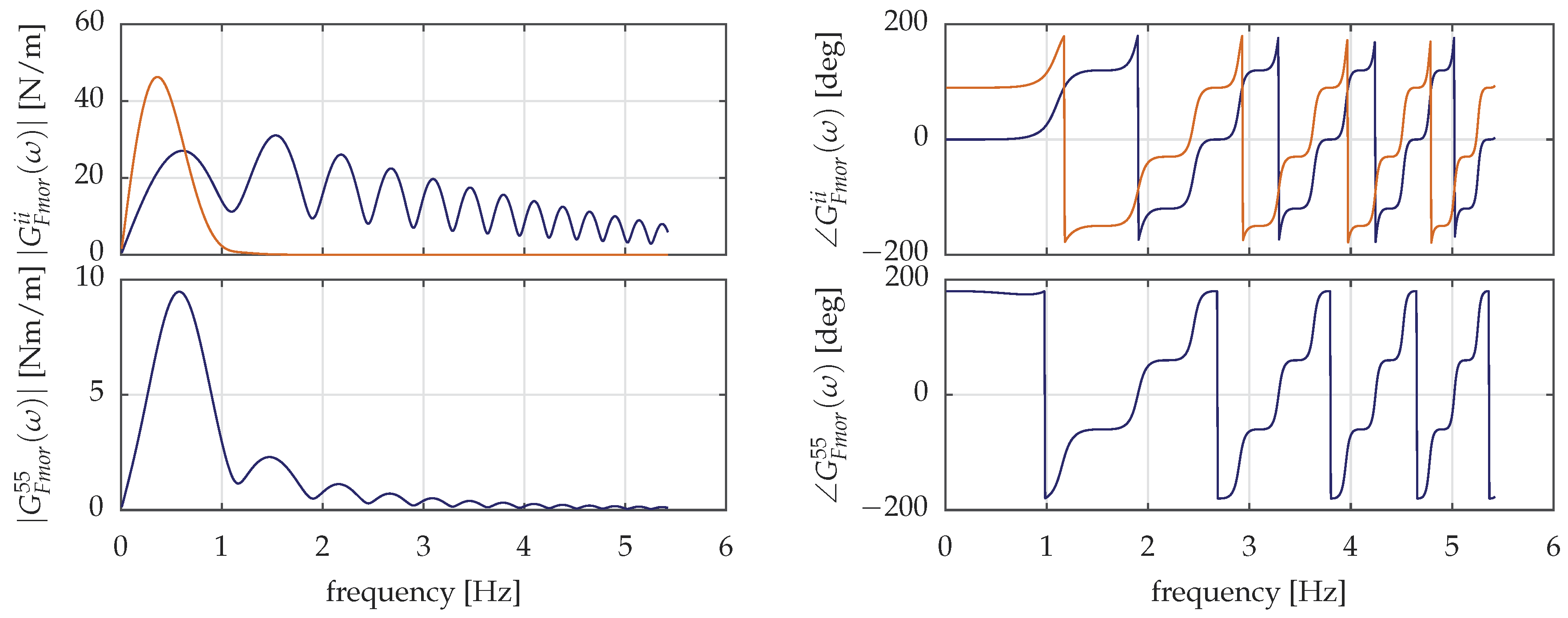
2.2. Generalized Morison’s Equation
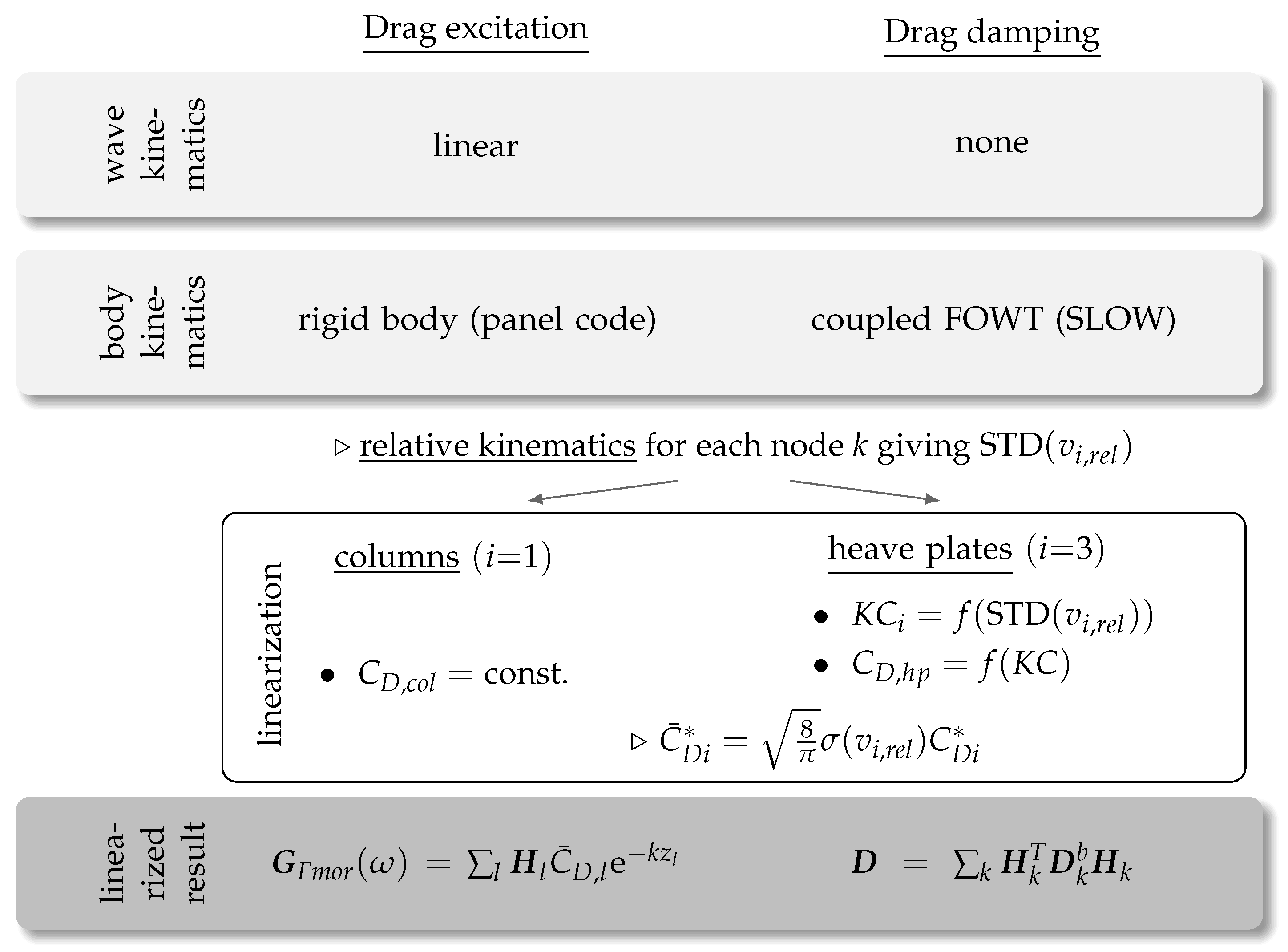
2.3. Linearized Viscous Drag Model
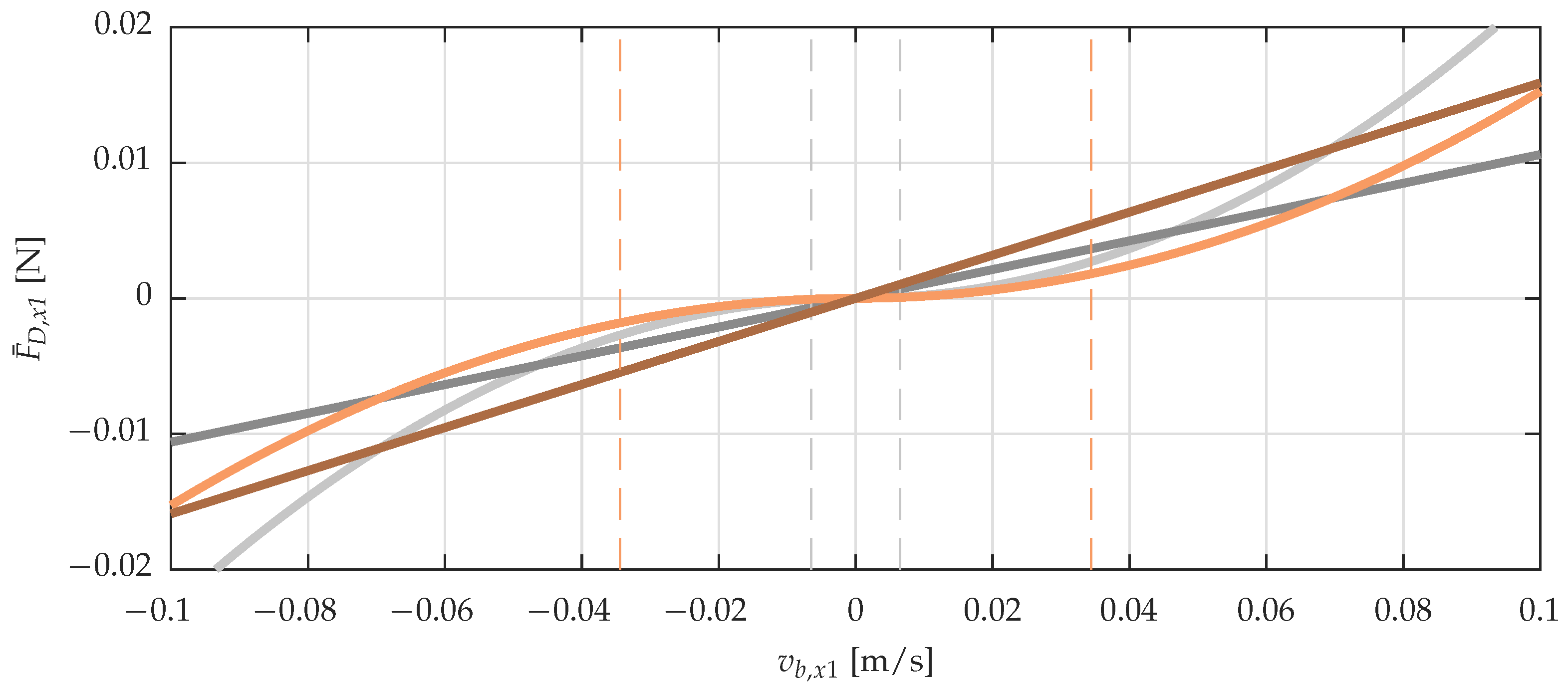
2.3.1. Drag Linearization
2.3.2. Drag Excitation
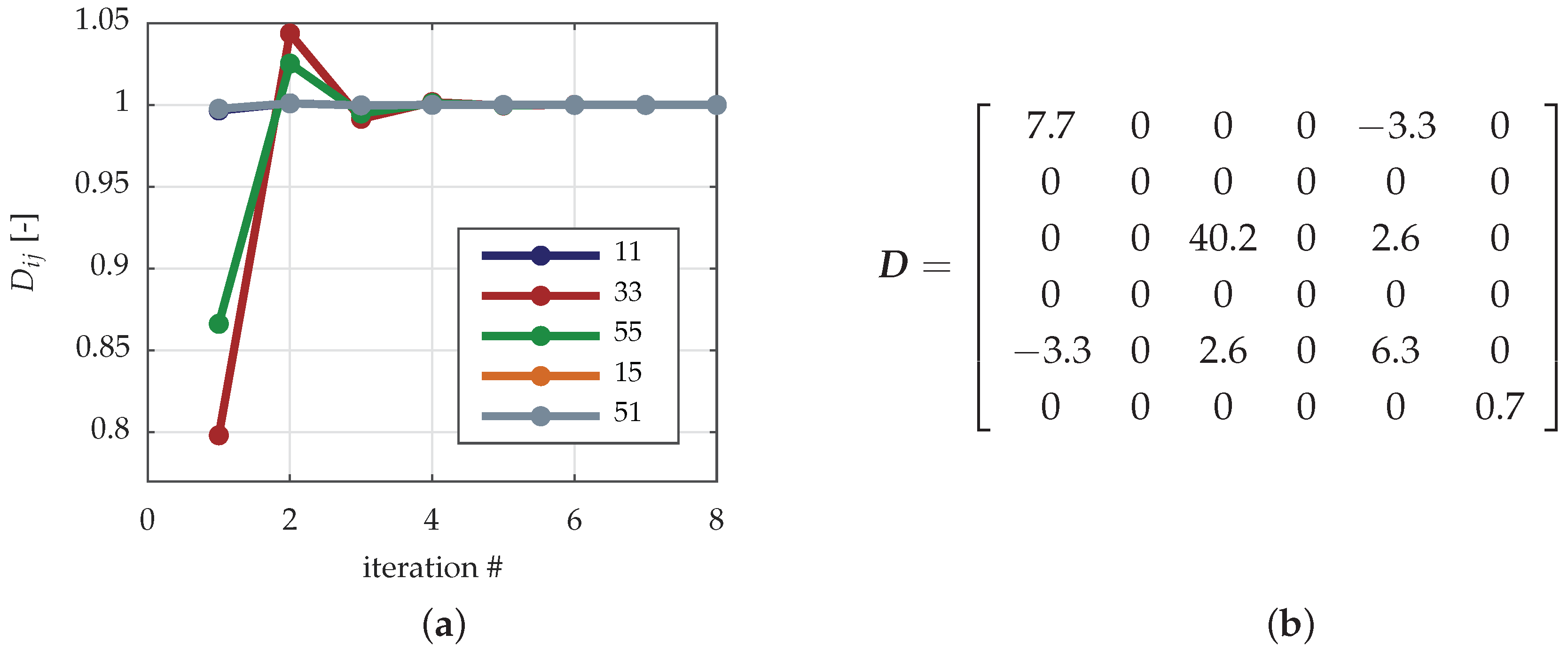
2.3.3. Drag Damping
2.4. Low-Order Aero-Hydro-Servo-Elastic Model
| ● Structural dynamics: | 6 DOFs, 2D motion, |
| ● Aerodynamics: | Quasi-static, rotationally sampled turbulence, |
| ● Hydrodynamics: | 1st-order coefficients, Morison viscous drag, parametric heave plate drag, simplified radiation, 2nd-order slow-drift approximation, |
| ● Mooring dynamics: | Quasi-static, |
| ● Control: | Model-based Proportional-Integral (PI), |
| ● Solution: | Time-domain & frequency-domain. |
3. Results
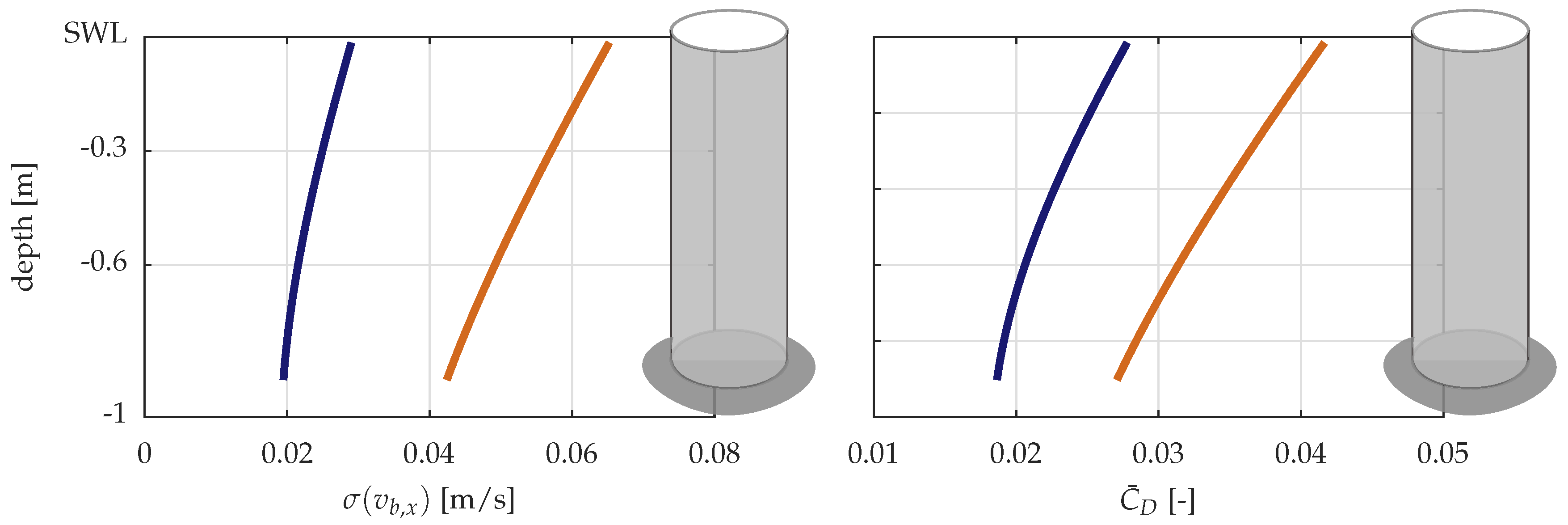
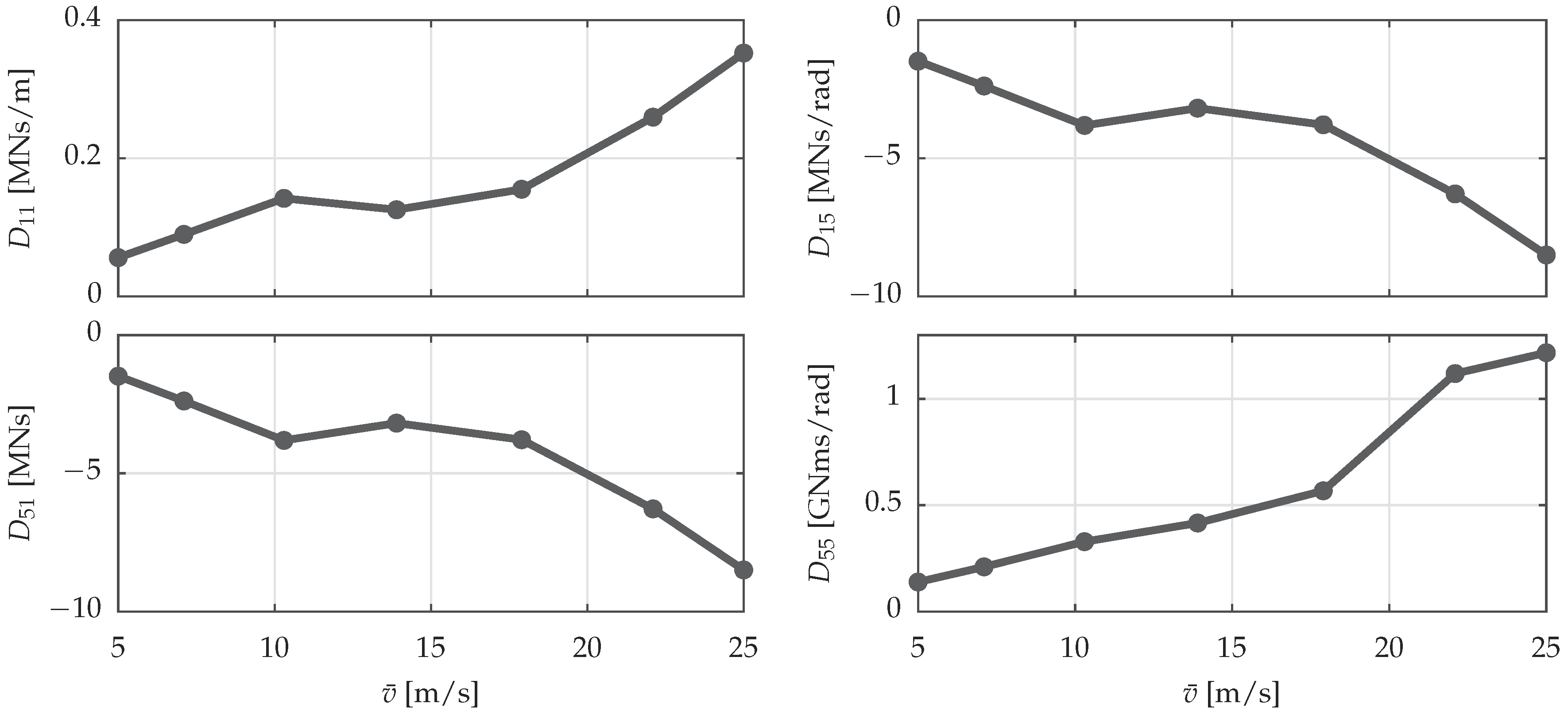
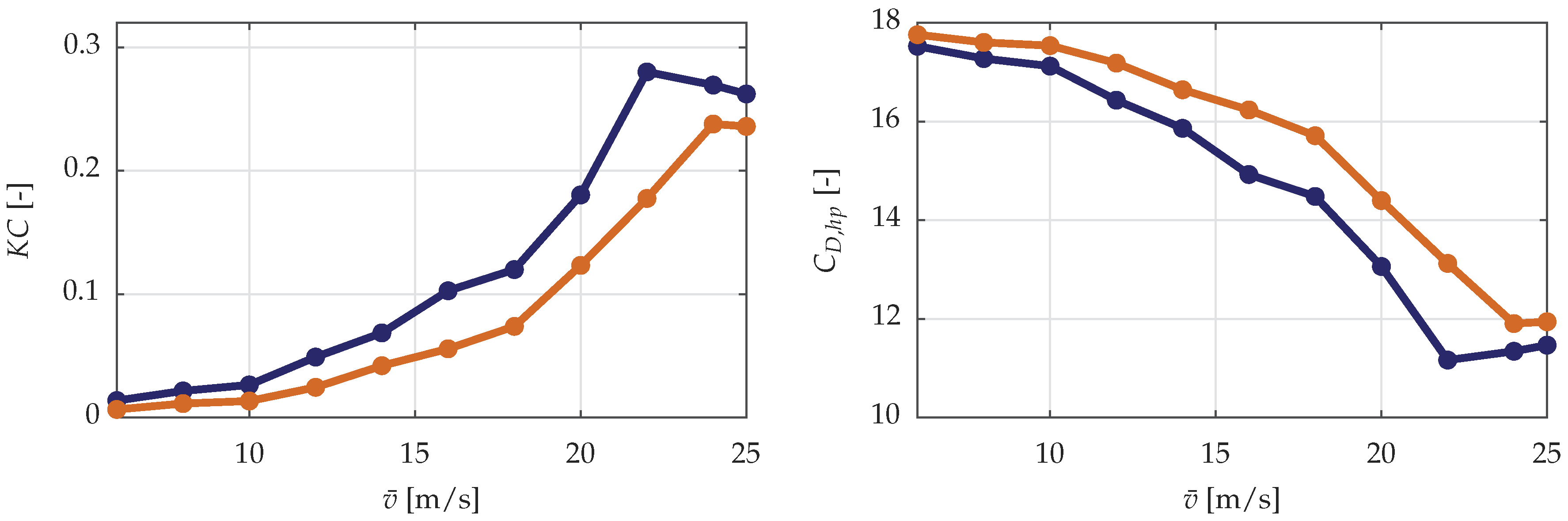
3.1. Parametric Drag
3.2. Solution Procedure
3.3. Iterative Solution
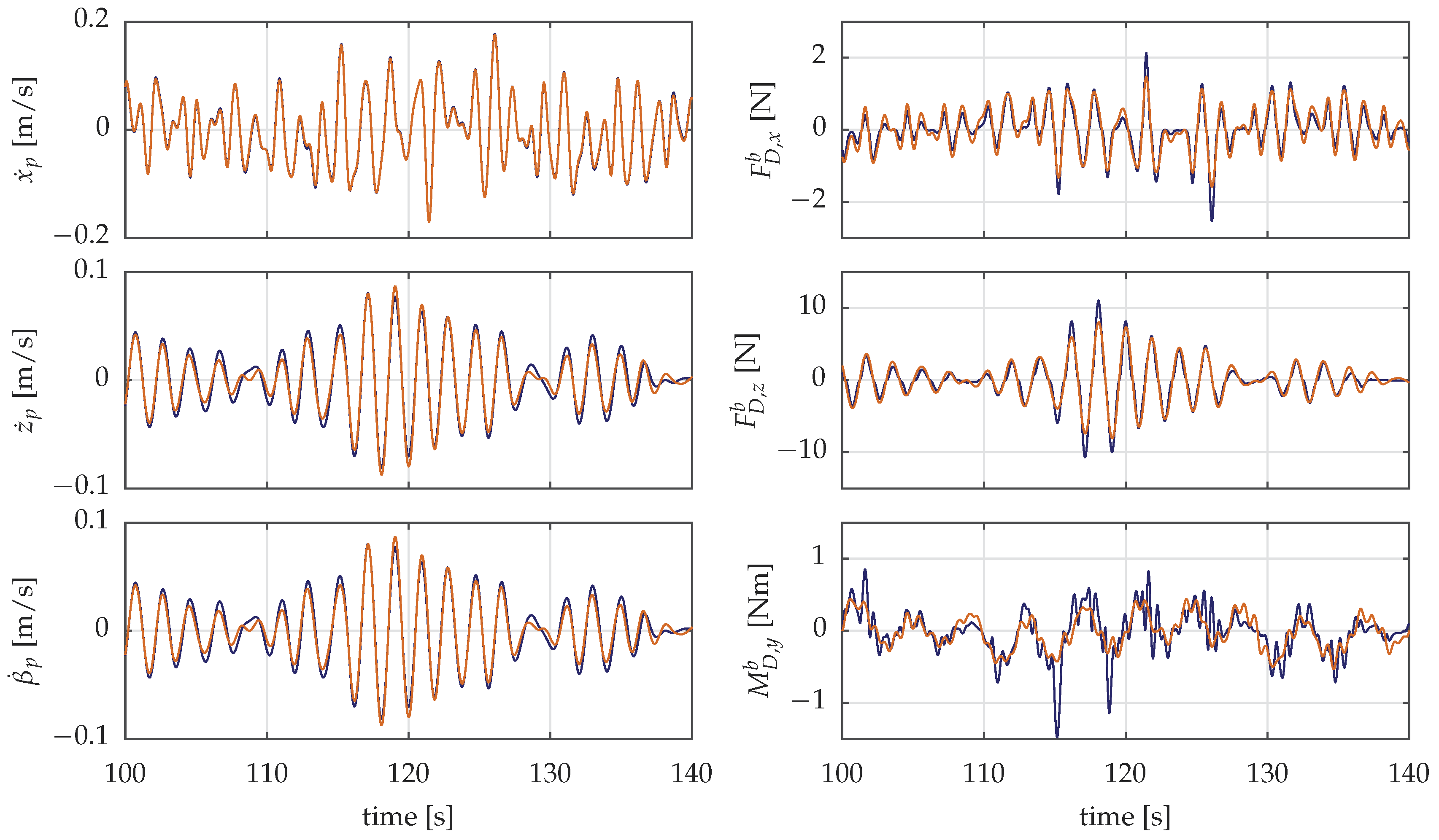
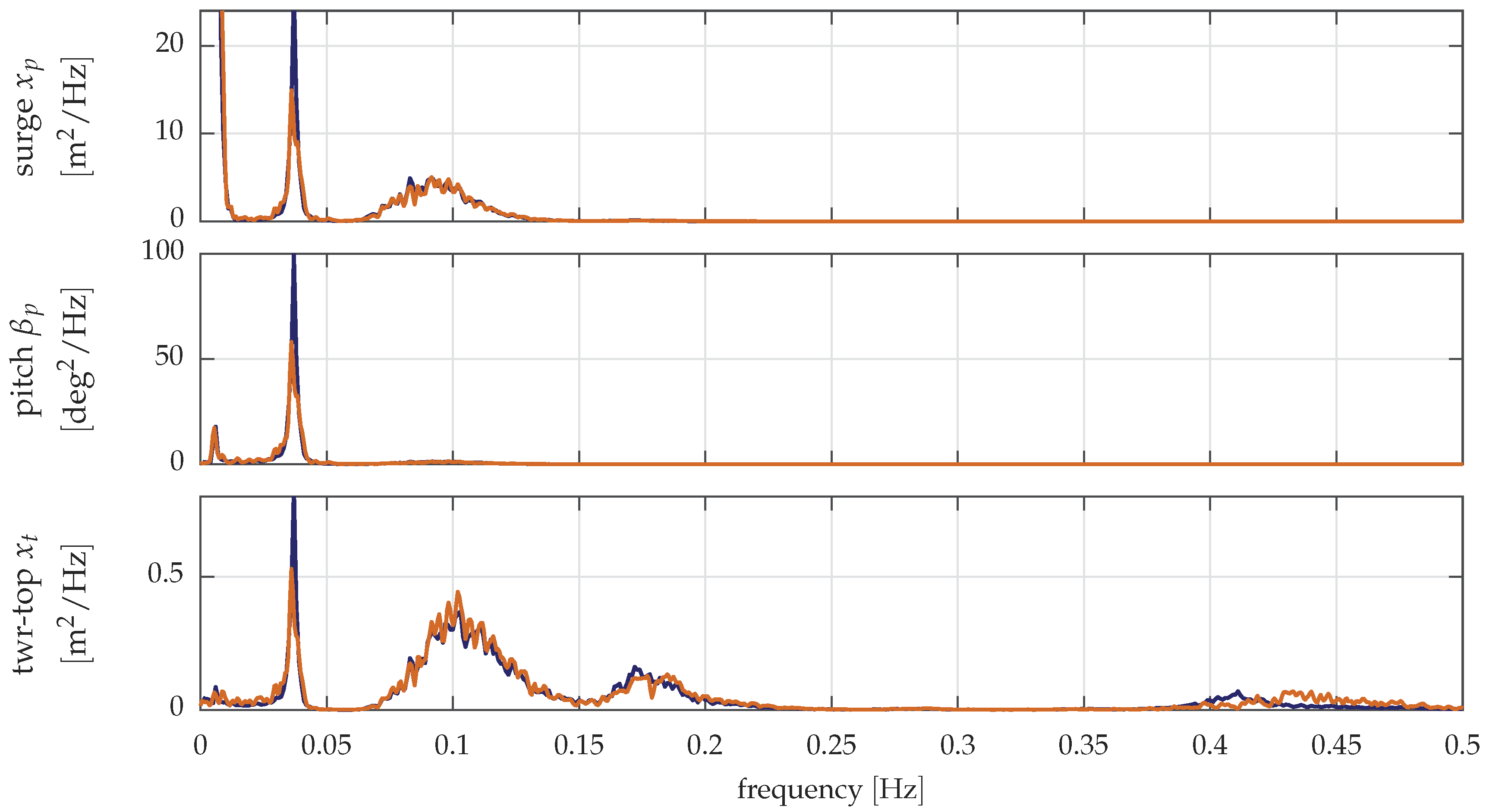
3.4. Verification
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tande, J.O.G.; Merz, K.; Paulsen, U.S.; Svendsen, H.G. Floating offshore turbines. Wiley Interdiscip. Rev. Energy Environ. 2015, 4, 213–228. [Google Scholar] [CrossRef]
- Larsen, T.J.; Hanson, T.D. A method to avoid negative damped low frequent tower vibrations for a floating, pitch controlled wind turbine. J. Phys. Conf. Ser. 2007, 75. [Google Scholar] [CrossRef]
- Veen, G.V.D.; Couchman, Y.; Bowyer, R. Control of floating wind turbines. In Proceedings of the American Control Conference, Montréal, QC, Canada, 27–29 June 2012; pp. 3148–3153. [Google Scholar] [CrossRef]
- Lemmer, F.; Schlipf, D.; Cheng, P.W. Control design methods for floating wind turbines for optimal disturbance rejection. J. Phys. Conf. Ser. 2016, 753. [Google Scholar] [CrossRef]
- Yu, W.; Lemmer, F.; Bredmose, H.; Borg, M.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Stoklund Larsen, T.; Fjelstrup, T.; Lomholt, A.; Boehm, L.; et al. The TripleSpar Campaign: Implementation and test of a blade pitch controller on a scaled floating wind turbine model. Energy Procedia 2017, 137, 323–338. [Google Scholar] [CrossRef]
- Jonkman, J. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2007. [Google Scholar]
- Vaal, J.B.D.; Hansen, M.O.L.; Moan, T. Effect of wind turbine surge motion on rotor thrust. Wind Energy 2014, 17, 105–121. [Google Scholar] [CrossRef]
- Manolas, D. Hydro-Aero-Elastic Analysis of Offshore Wind Turbines. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2015. [Google Scholar]
- Sant, T.; Bonnici, D.; Farrugia, R.; Micallef, D. Measurements and modelling of the power performance of a model floating wind turbine under controlled conditions. Wind Energy 2015, 18, 811–834. [Google Scholar] [CrossRef]
- Bayati, I.; Belloli, M.; Bernini, L.; Zasso, A. A formulation for the unsteady aerodynamics of floating wind turbines, with focus on the global system dynamics. In Proceedings of the ASME 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar] [CrossRef]
- Leble, V.; Barakos, G. Demonstration of a coupled floating offshore wind turbine analysis with high-fidelity methods. J. Fluids Struct. 2016, 62, 272–293. [Google Scholar] [CrossRef]
- Matha, D. Impact of Aerodynamics and Mooring System on Dynamic Response Of Floating Wind Turbines. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2016. [Google Scholar]
- Lin, L.; Vassalos, D.; Dai, S. CFD simulation of aerodynamic performance of floating offshore wind turbine compared with BEM method. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2016; pp. 568–575. [Google Scholar]
- Farrugia, R.; Sant, T.; Micallef, D. A study on the aerodynamics of a floating wind turbine rotor. Renew. Energy 2016, 86, 770–784. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. A CFD study of coupled aerodynamic-hydrodynamic loads on a semisubmersible floating offshore wind turbine. Wind Energy 2017, 21, 70–85. [Google Scholar] [CrossRef]
- Wen, B.; Tian, X.; Dong, X.; Peng, Z.; Zhang, W. On the power coefficient overshoot of an offshore floating wind turbine in surge oscillations (early view). Wind Energy 2018. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, Q.; Incecik, A.; Peyrard, C. Aeroelastic analysis of a floating offshore wind turbine in platform-induced surge motion using a fully coupled CFD-MBD method. Wind Energy 2018, 7, 1–20. [Google Scholar] [CrossRef]
- Journée, J.; Massie, W.W. Offshore Hydromechanics, 1st ed.; Delft University of Technology: Delft, The Netherlands, 2001. [Google Scholar]
- Fossen, T. Handbook of Marine Craft Hydrodynamics and Motion Control, 1st ed.; John Wiley and Sons: New York, NY, USA, 2011. [Google Scholar]
- Cummins, W. The impulse response function and ship motion. In Proceedings of the Symposium on Ship Theory, Hamburg, Germany, 25–27 January 1962. [Google Scholar]
- Morison, J.R. The Force Distribution Exerted by Surface Waves on Piles; Technical Report; University of California, Institute of Engineering Research: Berkeley, CA, USA, 1953. [Google Scholar]
- Robertson, A.; Wendt, F.; Jonkman, J.M.; Popko, W.; Dagher, H.J.; Gueydon, S.; Qvist, J.; Vittori, F.; Azcona, J.; Uzunoglu, E.; et al. OC5 project phase II: Validation of global loads of the DeepCwind floating semisubmersible wind turbine. Energy Procedia 2017, 137, 38–57. [Google Scholar] [CrossRef]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; Technical Report; National Renewable Energy Laboratory: Boulder, CO, USA, 2014.
- Philippe, M.; Courbois, A.; Babarit, A.; Ferrant, P.; Bonnefoy, F.; Rousset, J.M. Comparison of simulation and tank test results of a semi-submersible floating wind turbine under wind and wave loads. In Proceedings of the ASME 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; ASME: Nantes, France, 2013. [Google Scholar] [CrossRef]
- Berthelsen, P.A.; Bachynski, E.; Karimirad, M.; Thys, M. Real-time hybrid model tests of a braceless semi-submersible wind turbine. part III: Calibration of a numerical model. In Proceedings of the ASME 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; ASME: Busan, Korea, 2016. [Google Scholar] [CrossRef]
- Karimirad, M.; Bachynski, E.; Berthelsen, P.A.; Ormberg, H. Comparison of real-time hybrid model testing of a braceless semi- submersible wind turbine and numerical simulations. In Proceedings of the ASME 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; ASME: Trondheim, Norway, 2017. [Google Scholar] [CrossRef]
- Benitz, M.; Schmidt, D.P.; Lackner, M.; Stewart, G.; Jonkman, J.; Robertson, A. Validation of hydrodynamic load models using CFD for the OC4-DeepCwind semisubmersible. In Proceedings of the ASME 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar] [CrossRef]
- Lemmer, F.; Yu, W.; Cheng, P.W.; Pegalajar-Jurado, A.; Borg, M.; Mikkelsen, R.; Bredmose, H. The TripleSpar campaign: Validation of a reduced-order simulation model for floating wind turbines. In Proceedings of the ASME 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018; ASME: Madrid, Spain, 2018. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- DNV-GL. DNVGL-RP-C205: Environmental Conditions and Environmental Loads Recommended Practice; Technical Report; DNV-GL: Høvik, Norway, 2017. [Google Scholar]
- Sumer, B.M.; Fredsøe, J. Hydrodynamics Around Cylindrical Structures, 1st ed.; World Scientific: Singapore, 1997. [Google Scholar]
- Tao, L.; Dray, D. Hydrodynamic performance of solid and porous heave plates. Ocean Eng. 2008, 35, 1006–1014. [Google Scholar] [CrossRef]
- Lemmer, F.; Amann, F.; Raach, S.; Schlipf, D. Definition of the SWE-TripleSpar Floating Platform for the DTU 10MW Reference Wind Turbine; Technical Report; University of Stuttgart: Stuttgart, Germany, 2016. [Google Scholar]
- Borgman, L.E. The spectral density for ocean wave forces. In Proceedings of the Santa Barbara Coastal Engineering Conference, Santa Barbara, CA, USA, 11 October 1965; pp. 147–182. [Google Scholar]
- Pegalajar-Jurado, A.; Borg, M.; Bredmose, H. An efficient frequency-domain model for quick load analysis of floating offshore wind turbines (pre-print). Wind Energy Sci. 2018. [Google Scholar] [CrossRef]
- Langley, R. On the time domain simulation of second order wave forces and induced responses. Appl. Ocean Res. 1986, 8, 134–143. [Google Scholar] [CrossRef]
- Lupton, R. Frequency-Domain Modelling of Floating Wind Turbines. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2014. [Google Scholar]
- NWTC. NWTC Information Portal (FAST V8); NWTC: Boulder, CO, USA, 2016. [Google Scholar]
- Bredmose, H.; Lemmer, F.; Borg, M.; Pegalajar-Jurado, A.; Mikkelsen, R.F.; Stoklund Larsen, T.; Fjelstrup, T.; Yu, W.; Lomholt, A.K.; Boehm, L.; et al. The TripleSpar campaign: Model tests of a 10 MW floating wind turbine with waves, wind and pitch control. Energy Procedia 2017, 137, 58–76. [Google Scholar] [CrossRef]
- INNWIND.EU. Available online: http://www.innwind.eu/ (accessed on 18 August 2018).
- Stuttgarter Lehrstuhl für Windenergie (SWE), Institut für Flugzeugbau, Universität Stuttgart. Available online: http://www.ifb.uni-stuttgart.de/windenergie/downloads (accessed on 18 August 2018).
- Jonkman, J.; Robertson, A.; Hayman, G. HydroDyn User’s Guide and Theory Manual; Technical Report; National Renewable Energy Laboratory: Boulder, CO, USA, 2014.
- Wolfram, J. On alternative approaches to linearization and Morison’s equation for wave forces. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 2957–2974. [Google Scholar] [CrossRef]
- Lemmer, F.; Raach, S.; Schlipf, D.; Cheng, P.W. Parametric wave excitation model for floating wind turbines. Energy Procedia 2016, 94, 290–305. [Google Scholar] [CrossRef]
- Lemmer, F.; Müller, K.; Pegalajar-Jurado, A.; Borg, M.; Bredmose, H. LIFES50+ D4.1: Simple Numerical Models for Upscaled Design; Technical Report; University of Stuttgart: Stuttgart, Germany, 2016. [Google Scholar]
- Yu, W.; Lemmer, F.; Schlipf, D.; Cheng, P.W.; Visser, B.; Links, H.; Gupta, N.; Dankemann, S.; Couñago, B.; Serna, J. Evaluation of control methods for floating offshore wind turbines. Energy Procedia 2018, in press. [Google Scholar]
- Schiehlen, W.; Eberhard, P. Applied Dynamics, 1st ed.; Springer International Publishing: New York, NY, USA, 2014. [Google Scholar]
- Schwertassek, R.; Wallrapp, O.; Shabana, A.A. Flexible multibody simulation and choice of shape functions. Nonlinear Dyn. 1999, 20, 361–380. [Google Scholar] [CrossRef]
- Taghipour, R.; Pérez, T.; Moan, T. Hybrid frequency-time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Krieger, A.; Ramachandran, G.K.V.; Vita, L.; Gómez Alonso, P.; Berque, J.; Aguirre-Suso, G. LIFES50+ D7.2 Design Basis; Technical Report; DNV-GL: Høvik, Norway, 2016. [Google Scholar]
- Naess, A.; Moan, T. Stochastic Dynamics of Marine Structures; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
| Platform draft [m] | 54.5 | Number of mooring lines | 3 | Rated rotor speed [rpm] | 9.6 |
| Platform column radius [m] | 7.5 | Mooring line length [m] | 610.0 | Rotor diameter [m] | 178.3 |
| Platform column spacing (to centerline) [m] | 26.0 | Water depth [m] | 180.0 | Turbine mass [ kg] (incl. tower) | 1.1 |
| Platform mass [ kg] | 28.3 | Rated wind speed [] | 11.4 | Hub height [m] | 119.0 |
| Wind Speed | [m/s] | 5.0 | 7.1 | 10.3 | 13.9 | 17.9 | 22.1 | 25 |
| Significant Wave Height | [m] | 1.4 | 1.7 | 2.2 | 3.0 | 4.3 | 6.2 | 8.3 |
| Peak Spectral Period | [s] | 7.0 | 8.0 | 8.0 | 9.5 | 10.0 | 12.5 | 12.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemmer, F.; Yu, W.; Cheng, P.W. Iterative Frequency-Domain Response of Floating Offshore Wind Turbines with Parametric Drag. J. Mar. Sci. Eng. 2018, 6, 118. https://doi.org/10.3390/jmse6040118
Lemmer F, Yu W, Cheng PW. Iterative Frequency-Domain Response of Floating Offshore Wind Turbines with Parametric Drag. Journal of Marine Science and Engineering. 2018; 6(4):118. https://doi.org/10.3390/jmse6040118
Chicago/Turabian StyleLemmer, Frank, Wei Yu, and Po Wen Cheng. 2018. "Iterative Frequency-Domain Response of Floating Offshore Wind Turbines with Parametric Drag" Journal of Marine Science and Engineering 6, no. 4: 118. https://doi.org/10.3390/jmse6040118
APA StyleLemmer, F., Yu, W., & Cheng, P. W. (2018). Iterative Frequency-Domain Response of Floating Offshore Wind Turbines with Parametric Drag. Journal of Marine Science and Engineering, 6(4), 118. https://doi.org/10.3390/jmse6040118





