Residence Time of a Highly Urbanized Estuary: Jamaica Bay, New York
Abstract
:1. Introduction
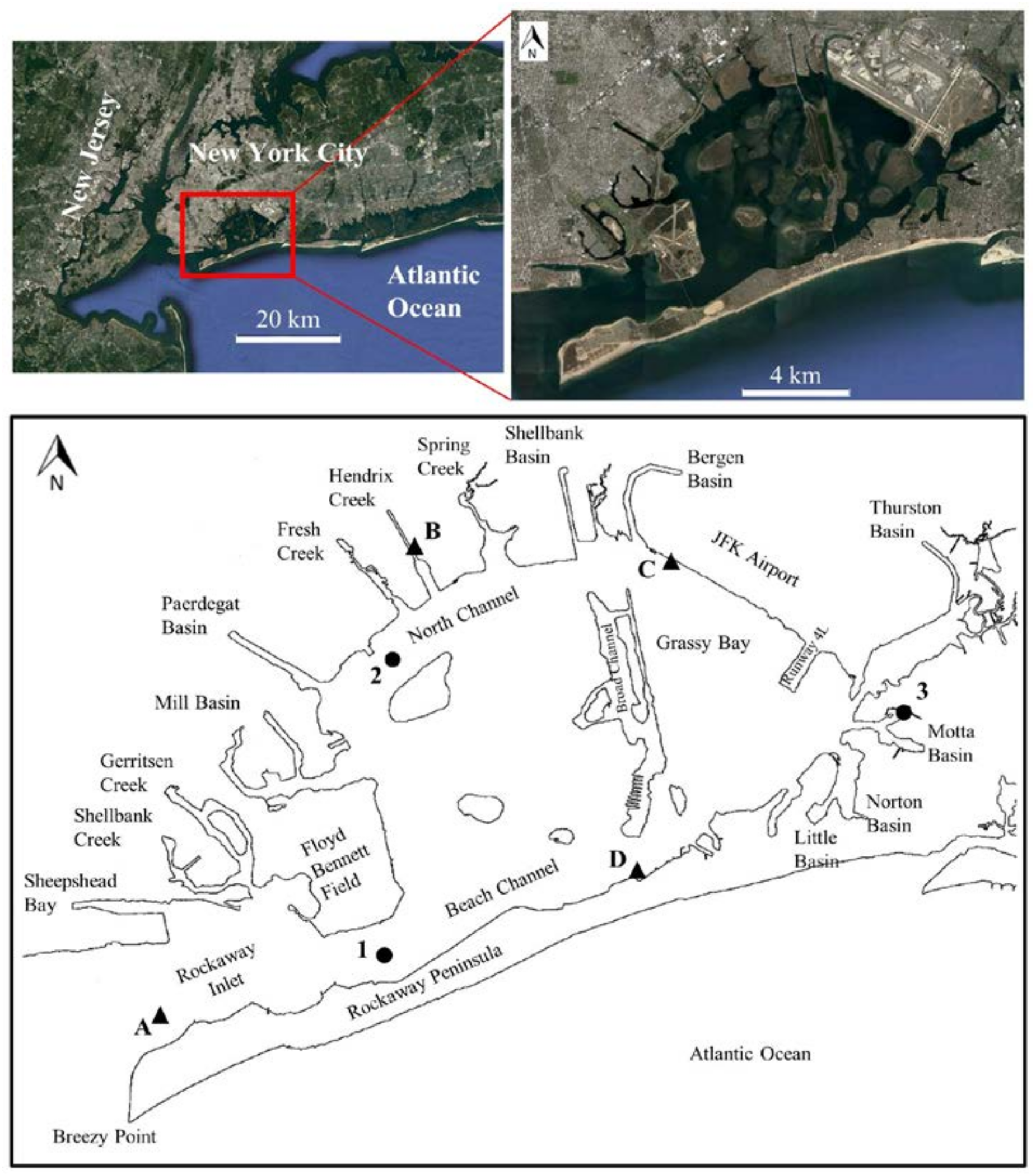
2. Study Area
3. Methods
3.1. Three-Dimensional Tracer Simulation
3.1.1. Computational Models
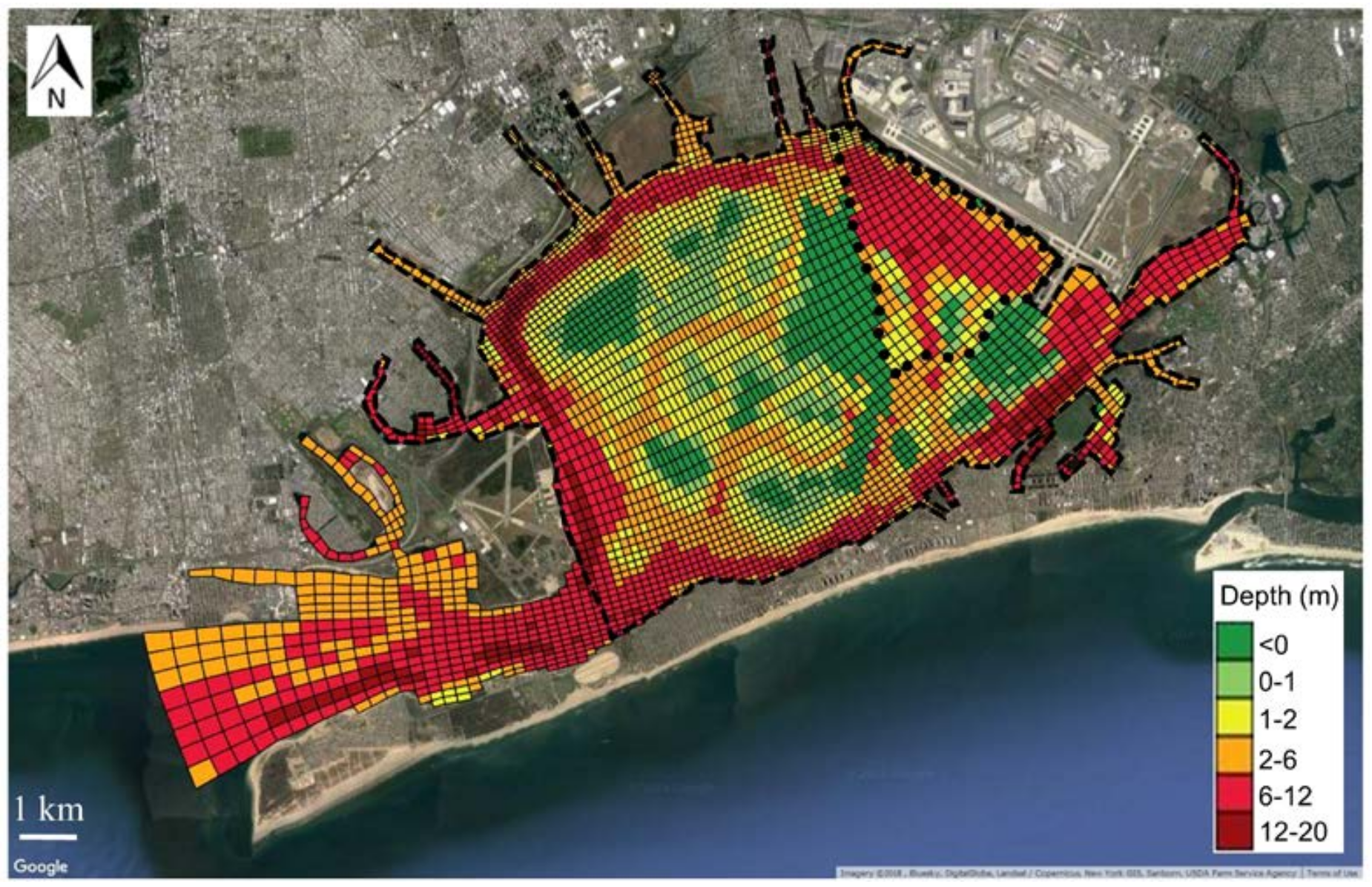
3.1.2. Computational Grid
3.1.3. Boundary Conditions
3.1.4. Mean Residence Time
3.2. Theoretical Tidal Prism Method
4. Model Validation
5. Numerical Experiments
6. Results and Discussion
6.1. Mean Residence Time in the Study Area
6.2. Influence of Wind and Freshwater Discharge
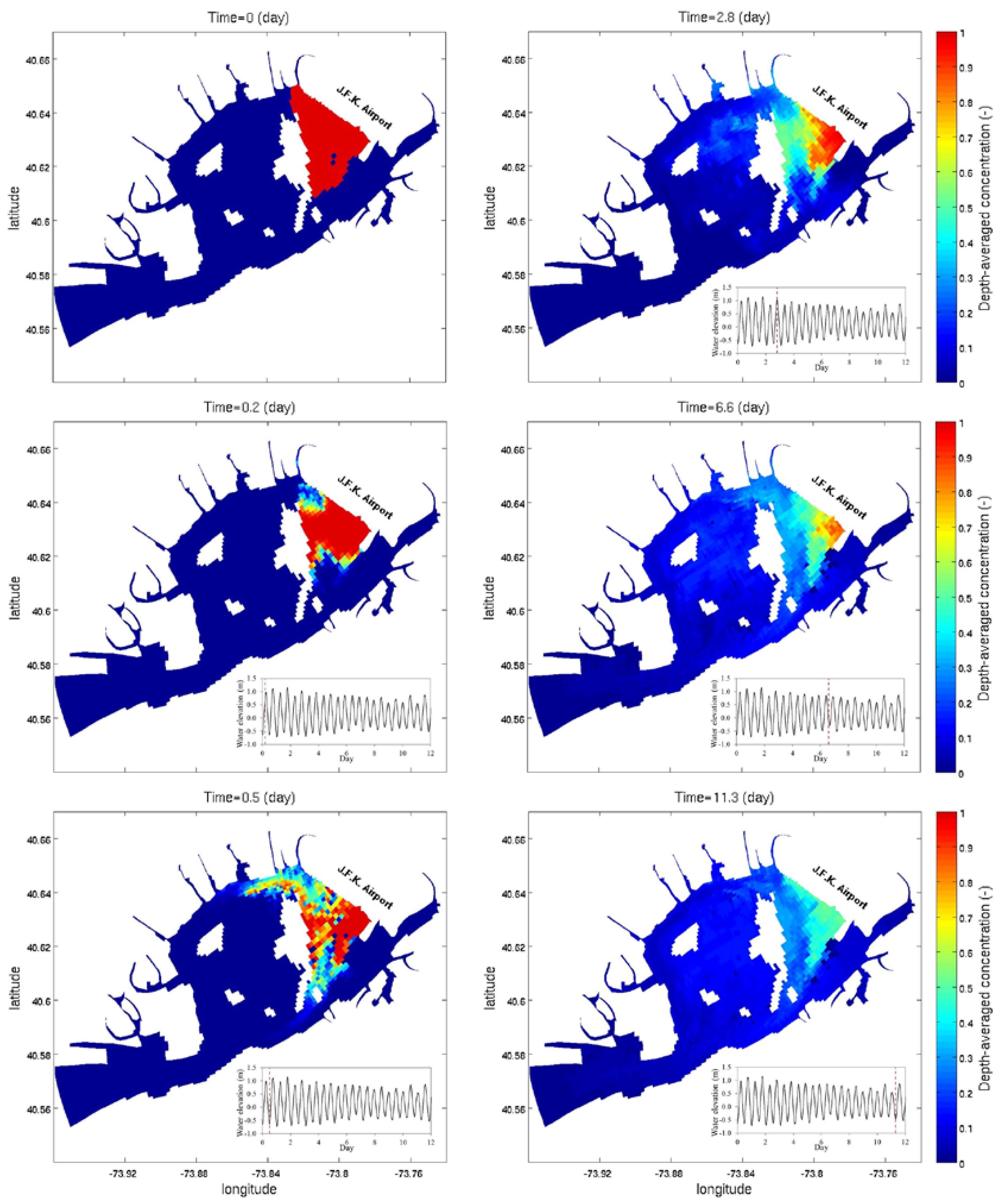
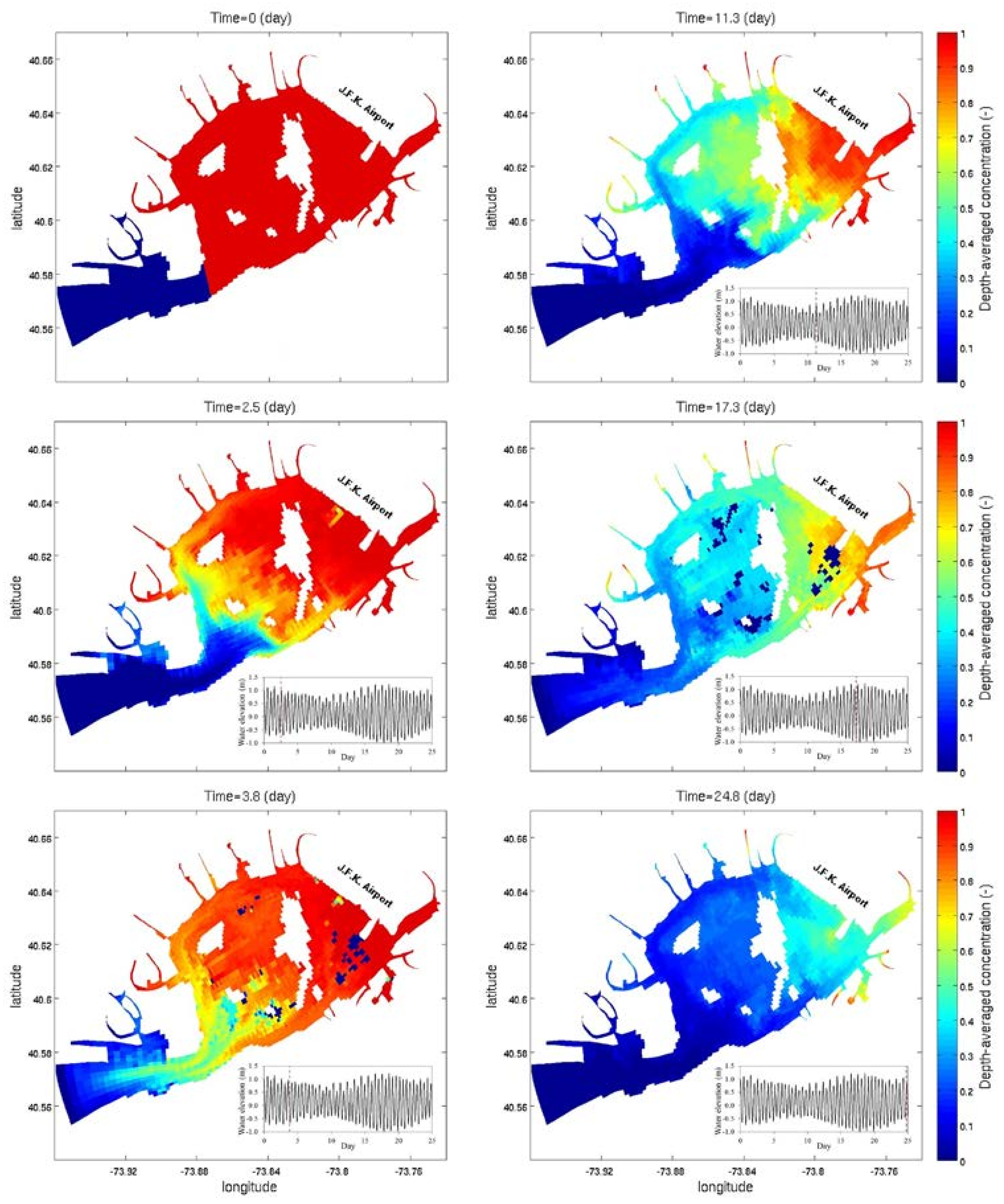
6.3. Spatial Distribution of Tracer Concentration
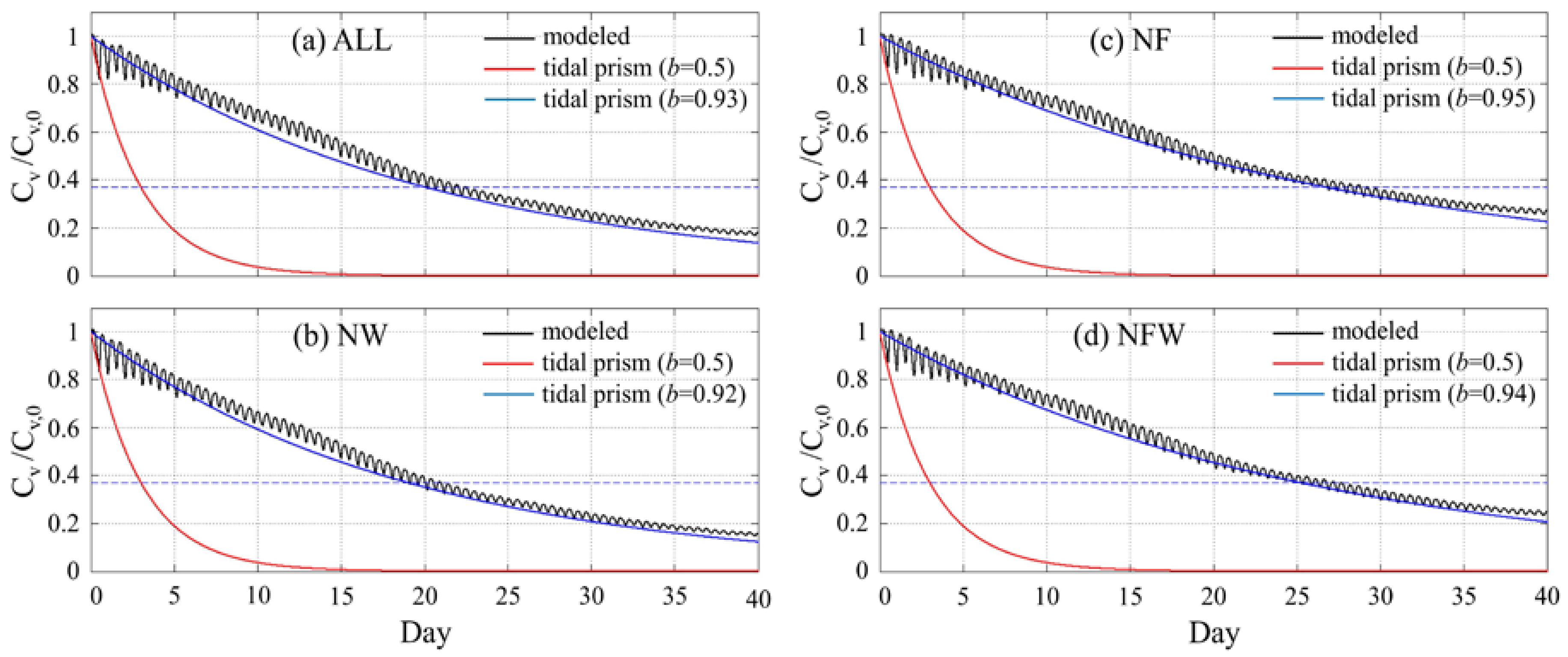
6.4. Results from Tidal Prism Method
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dronkers, J.; Zimmerman, J.T.F. Some principles of mixing in tidal lagoons. In Proceedings of the International Symposium on Coastal Lagoons, Bordeaux, France, 9–14 September 1981; pp. 107–117. [Google Scholar]
- De Brauwere, A.; de Brye, B.; Blaise, S.; Deleersnijder, E. Residence time, exposure time and connectivity in the Scheldt Estuary. J. Mar. Syst. 2011, 84, 85–95. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- Patgaonkara, R.S.; Vethamonya, P.; Lokeshb, K.S.; Babu, M.T. Residence time of pollutants discharged in the Gulf of Kachchh, northwestern Arabian Sea. Mar. Poll. Bull. 2012, 64, 1659–1666. [Google Scholar] [CrossRef] [PubMed]
- Bum, B.K.; Pick, F.R. Factors regulating phytoplankton and zooplankton biomass in temperate rivers. Limnol. Oceanogr. 1996, 41, 1572–1577. [Google Scholar] [CrossRef]
- Engelhardt, C.; Krüger, A.; Sukhodolov, A.; Nicklisch, A. A study of phytoplankton spatial distributions, flow structure and characteristics of mixing in a river reach with groynes. J. Plankton Res. 2004, 26, 1351–1366. [Google Scholar] [CrossRef]
- Bricelj, V.M.; Lonsdale, D.J. Aureococcus anophagefferens: Causes and ecological consequences of brown tides in US mid-Atlantic coastal water. Limnol. Oceanogr. 1997, 42, 1023–1038. [Google Scholar] [CrossRef]
- Ralston, D.K.; Brosnahan, M.L.; Fox, S.E.; Lee, K.D.; Anderson, D.M. Temperature and Residence Time Controls on an Estuarine Harmful Algal Bloom: Modeling Hydrodynamics and Alexandrium fundyense in Nauset Estuary. Estuaries Coasts 2015, 38, 2240–2258. [Google Scholar] [CrossRef] [PubMed]
- Painchaud, J.; Lefaivre, D.; Therriault, J.-C.; Legendre, L. Bacterial dynamics in the upper St. Lawrence estuary. Limnol. Oceanogr. 1996, 41, 1610–1618. [Google Scholar] [CrossRef]
- Andrews, J.C.; Müller, H. Space-time variability of nutrients in a lagoonal patch reef. Limnol. Oceanogr. 1983, 28, 215–227. [Google Scholar] [CrossRef]
- Uncles, R.J.; Frickers, P.E.; Harris, C. Dissolved nutrients in the Tweed Estuary, UK: Inputs, distributions and effects of residence time. Sci. Total Environ. 2003, 314, 727–736. [Google Scholar] [CrossRef]
- Stommel, H.; Farmer, H.G. On the Nature of Estuarine Circulation; Technical Report; No. N6onr-27701 (NR-083-004); Office of Naval Research: Arlington, VA, USA, 1952. [Google Scholar]
- Möller, O.O.; Castaing, P.; Salomon, J.C.; Lazure, P. The influence of local and non-local forcing effects on the subtidal circulation of Patos Lagoon. Estuaries 2001, 24, 297–311. [Google Scholar] [CrossRef]
- Defne, Z.; Ganju, N.K. Quantifying the residence time and flushing characteristics of a shallow, back-barrier estuary: Application of hydrodynamic and particle tracking models. Estuaries Coasts 2015, 38, 1719–1734. [Google Scholar] [CrossRef]
- Liu, W.-C.; Chen, W.-B.; Hsu, M.-H. Using a three-dimensional particle-tracking model to estimate the residence time and age of water in a tidal estuary. Comput. Geosci. 2011, 37, 1148–1161. [Google Scholar] [CrossRef]
- New York City Department of Environmental Protection. New York Harbor Water Quality Report; New York City Department of Environmental Protection: New York, NY, USA, 2009.
- Wallace, R.B.; Gobler, C.J. Factors controlling blooms of microalgae and macroalgae (Ulva rigida) in a eutrophic, urban estuary: Jamaica Bay, NY, USA. Estuaries Coasts 2015, 38, 519–533. [Google Scholar] [CrossRef]
- Horton, R.; Bader, D.; Kushnir, Y.; Little, C.; Blake, R.; Rosenzweig, C. New York City Panel on Climate Change 2015 Report Chapter 1: Climate Observations and Projections. Ann. N. Y. Acad. Sci. 2015, 1336, 18–35. [Google Scholar] [CrossRef] [PubMed]
- Swanson, L.; Dorsch, M.; Giampieri, M.; Orton, P.; Parris, A.; Sanderson, E. Chapter 4: Biophysical Systems of Jamaica Bay. In Prospects for Resilience: Insights from New York City’s Jamaica Bay; Sanderson, E., Solecki, W., Waldman, J., Parris, A., Eds.; Island Press: Washington, DC, USA, 2016. [Google Scholar]
- Barry A. Vittor & Associates, Inc. Norton Basin Restoration Project, Baseline Data Collection at Project and Reference Sites—2000; Final Report to U.S. Army Corps of Engineers, New York District; Barry A. Vittor & Associates, Inc.: Kingston, NY, USA, 2001. [Google Scholar]
- Benotti, M.J.; Abbene, M.; Terracciano, S.A. Nitrogen Loading in Jamaica Bay, Long Island, New York: Predevelopment to 2005; Scientific Investigations Report; U.S. Department of the Interior, U.S. Geological Survey: Reston, VA, USA, 2007.
- Thomann, R.V.; Mueller, J.A. Principles of Surface Water Quality Modeling and Control; Harper & Row: New York, NY, USA, 1987. [Google Scholar]
- Dyer, K.R. Estuaries: A Physical Introduction, 2nd ed.; John Wiley: Chichester, NY, USA, 1997. [Google Scholar]
- Banas, N.S.; Hickey, B.M. Mapping exchange and residence time in a model of Willapa Bay, Washington, a branching, macrotidal estuary. J. Geophys. Res. 2005, 110, C11. [Google Scholar] [CrossRef]
- Oliveira, A.; Fortunato, A.B.; Rego, J. Effect of morphological changes on the hydrodynamics and flushing properties of the Óbidos lagoon (Portugal). Cont. Shelf Res. 2006, 26, 917–942. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, H.; Liu, G.; Zhang, J. Simulation of water exchange in Jiaozhou Bay by average residence time approach. Estuar. Coast. Shelf Sci. 2004, 61, 25–35. [Google Scholar] [CrossRef]
- Arega, F.; Armstrong, S.; Badr, A.W. Modeling of residence time in the East Scott Creek Estuary, South Carolina, USA. J. Hydro. Environ. Res. 2008, 2, 99–108. [Google Scholar] [CrossRef]
- Takeoka, H. Fundamental concepts of exchange and transport time scales in a coastal sea. Cont. Shelf Res. 1984, 3, 311–326. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and residence time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- New York City Department of Environmental Protection. Jamaica Bay Watershed Protection Plan Volume I—Regional Profile; New York City Department of Environmental Protection: New York, NY, USA, 2007.
- New York City Department of Environmental Protection. New York Harbor Water Quality Report; New York City Department of Environmental Protection: New York, NY, USA, 2016.
- Blumberg, A.F.; Mellor, G.L. A Coastal Ocean Numerical Model. Mathematical Modelling of Estuarine Physics; Sundermann, J., Holz, K.P., Eds.; Springer: Berlin, Germany, 1980; pp. 203–219. [Google Scholar]
- Blumberg, A.F.; Mellor, G.L. A Description of a Three Dimensional Coastal Ocean Circulation Model. Three-Dimensional Coastal Ocean Models. Coastal and Estuarine Sciences; Heaps, N., Ed.; American Geophysical Union: Washington, DC, USA, 1987; Volume 4, pp. 1–16. [Google Scholar]
- Oey, L.-Y.; Mellor, G.L.; Hires, R.I. A Three Dimensional Simulation of the Hudson-Raritan Estuary. J. Phys. Oceanogr. 1985, 15, 1693–1709. [Google Scholar] [CrossRef]
- Galperin, B.; Mellor, G.L. A time-dependent, three-dimensional model of the Delaware Bay and River system. Estuar. Coast. Shelf Sci. 1990, 31, 255–281. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Khan, L.A.; St. John, J.P. Three-Dimensional hydrodynamic model of New York harbor region. J. Hydraul. Eng. 1999, 125, 799–816. [Google Scholar] [CrossRef]
- Georgas, N.; Blumberg, A. Establishing confidence in marine forecast systems: The design and skill assessment of the New York Harbor observation and prediction system, version 3 (NYHOPS v3). In Proceedings of the 11th International Conference on Estuarine and Coastal Modeling, Seattle, WA, USA, 4–6 November 2009; pp. 660–685. [Google Scholar]
- Orton, P.M.; Georgas, N.; Blumberg, A.; Pullen, J. Detailed modeling of recent severe storm tides in estuaries of the New York City region. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Orton, P.M.; Talke, S.A.; Jay, D.A.; Yin, L.; Blumberg, A.F.; Georgas, N.; Zhao, H.; Roberts, H.J.; MacManus, K. Channel Shallowing as Mitigation of Coastal Flooding. J. Mar. Sci. Eng. 2015, 3, 654–673. [Google Scholar] [CrossRef]
- Orton, P.M.; Hall, T.M.; Talke, S.; Blumberg, A.F.; Georgas, N.; Vinogradov, S. A Validated Tropical-Extratropical Flood Hazard Assessment for New York Harbor. J. Geophys. Res. 2016, 121, 8904–8929. [Google Scholar] [CrossRef]
- Marsooli, R.; Orton, P.M.; Georgas, N.; Blumberg, A.F. Three-Dimensional Hydrodynamic Modeling of Storm Tide Mitigation by Coastal Wetlands. Coast. Eng. 2016, 111, 83–94. [Google Scholar] [CrossRef]
- Marsooli, R.; Orton, P.M.; Mellor, G.; Georgas, N.; Blumberg, A.F. A Coupled Circulation-Wave Model for Numerical Simulation of Storm Tides and Waves. J. Atmos. Ocean. Technol. 2017, 34, 1449–1467. [Google Scholar] [CrossRef]
- Simons, T.J. Verification of Numerical Models of Lake Ontario, Part I. Circulation in Spring and Early Summer. J. Phys. Oceanogr. 1974, 4, 507–523. [Google Scholar] [CrossRef]
- Madala, R.V.; Piacsek, S.A. A Semi-Implicit Numerical Model for Baroclinic Oceans. J. Comput. Phys. 1977, 23, 167–178. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations; I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Blumberg, A.; Georgas, N.; Yin, L.; Herrington, T.; Orton, P. Street scale modeling of storm surge inundation along the New Jersey Hudson River waterfront. J. Atmos. Ocean. Technol. 2015, 32, 1486–1497. [Google Scholar] [CrossRef]
- Hudson River Foundation (HRF). Defining Restoration Objectives and Design Criteria for Self-Sustaining Oyster Reefs in Jamaica Bay; Final Programmatic Report Prepared for the National Fish and Wildlife Foundation by Hudson River Foundation, HDR|HydroQual, and SUNY Stony Brook; Project Number: 2005-0333-015; HDR|HydroQual: Mahwah, NJ, USA, 2012; 69p. [Google Scholar]
- Danielson, J.J.; Poppenga, S.K.; Brock, J.C.; Evans, G.A.; Tyler, D.J.; Gesch, D.B.; Thatcher, C.A.; Barras, J.A. Topobathymetric elevation model development using a new methodology: Coastal National Elevation Database. J. Coast. Res. 2016, 76, 75–89. [Google Scholar] [CrossRef]
- Flood, R. High-Resolution Bathymetric and Backscatter Mapping in Jamaica Bay; Final Report to the National Park Service; School of Marine and Atmospheric Sciences, Stony Brook University: Stony Brook, NY, USA, 2011. [Google Scholar]
- O’Neil-Dunne, J.P.M.; MacFaden, S.W.; Forgione, H.M.; Lu, J.W.T. Urban Ecological Land-Cover Mapping for New York City; Final Report to the Natural Areas Conservancy; Spatial Informatics Group, University of Vermont, Natural Areas Conservancy, and New York City Department of Parks & Recreation: New York, NY, USA, 2014; p. 21. [Google Scholar]
- EEA, Inc. Jamaica Bay Eutrophication Study: Biological Productivity Study; Report Prepared for the New York City Department of Environmental Protection; EEA, Inc.: Garden City, NY, USA, 1997. [Google Scholar]
- Hartig, E.K.; Gornitz, V.; Kolker, A.; Mushacke, F.; Fallon, D. Anthropogenic and climate change impacts on salt marshes of Jamaica Bay, New York City. Wetlands 2002, 22, 71–89. [Google Scholar] [CrossRef]
- Georgas, N.; Yin, L.; Jiang, Y.; Wang, Y.; Howell, P.; Saba, V.; Schulte, J.; Orton, P.; Wen, B. An open-access, multi-decadal, three-dimensional, hydrodynamic hindcast dataset for the Long Island Sound and New York/New Jersey Harbor Estuaries. J. Mar. Sci. Eng. 2016, 4, 48. [Google Scholar] [CrossRef]
- Ahsan, A.K.M.Q.; Blumberg, A.F. Three-Dimensional Hydrothermal Model of Onondaga Lake, New York. J. Hydraul. Eng. 1999, 125, 912–923. [Google Scholar] [CrossRef]
- Abdelrhman, M.A. Modeling How a Hurricane Barrier in New Bedford Harbor, Massachusetts, Affects the Hydrodynamics and Residence Time. Estuaries 2002, 25, 177–196. [Google Scholar] [CrossRef]
- Li, K. Concepts and Applications of Water Transport Time Scales for Coastal Inlet Systems; Report ERDC/CHL CHETN-IV-77; US Army Corps of Engineering: Washington, DC, USA, 2010.
- Sanford, L.P.; Boicourt, W.C.; Rives, S.R. Model for Estimating Tidal Flushing of Small Embayments. J. Waterw. Port Coast. Ocean Eng. 1992, 118, 635–654. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
- Warner, J.C.; Geyer, W.R.; Lerczak, J.A. Numerical modeling of an estuary: A comprehensive skill assessment. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Warner, J.C.; Geyer, W.R.; Arango, H.G. Using a composite grid approach in a complex coastal domain to estimate estuarine residence time. Comput. Geosci. 2010, 36, 921–935. [Google Scholar] [CrossRef]
- Li, Y.; Li, M. Effects of winds on stratification and circulation in a partially mixed estuary. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Scully, M.E.; Friedrichs, C.; Brubaker, J. Control of estuarine stratification and mixing by wind-induced straining of the estuarine density field. Estuaries 2005, 28, 321–326. [Google Scholar] [CrossRef]
- Brocchini, M.; Calantoni, J.; Postacchini, M.; Sheremet, A.; Staples, T.; Smith, J.; Reed, A.H.; Braithwaite, E.F., III; Lorenzoni, C.; Russo, A.; et al. Comparison between the wintertime and summertime dynamics of the Misa River estuary. Mar. Geol. 2017, 385, 27–40. [Google Scholar] [CrossRef]
- Geyer, W.R.; Chant, R.; Houghton, R. Tidal and spring-neap variations in horizontal dispersion in a partially mixed estuary. J. Geophys. Res. 2008, 113, C07023. [Google Scholar] [CrossRef]
- Gómez, A.G.; Ondiviela, B.; Fernández, M.; Juanes, J.A. Atlas of susceptibility to pollution in marinas. Application to the Spanish coast. Mar. Poll. Bull. 2017, 114, 239–246. [Google Scholar] [CrossRef] [PubMed]
- De Brito, A.N., Jr.; Fragoso, C.R., Jr.; Larson, M. Tidal exchange in a choked coastal lagoon: A study of Mundaú Lagoon in northeastern Brazil. Reg. Stud. Mar. Sci. 2018, 17, 133–142. [Google Scholar] [CrossRef]
- Oliveira, A.; Kjerfve, B. Environmental Responses of a Tropical Coastal Lagoon System to Hydrological Variability: Mundaú-Manguaba, Brazil. Estuar. Coast. Shelf Sci. 1993, 37, 575–591. [Google Scholar] [CrossRef]
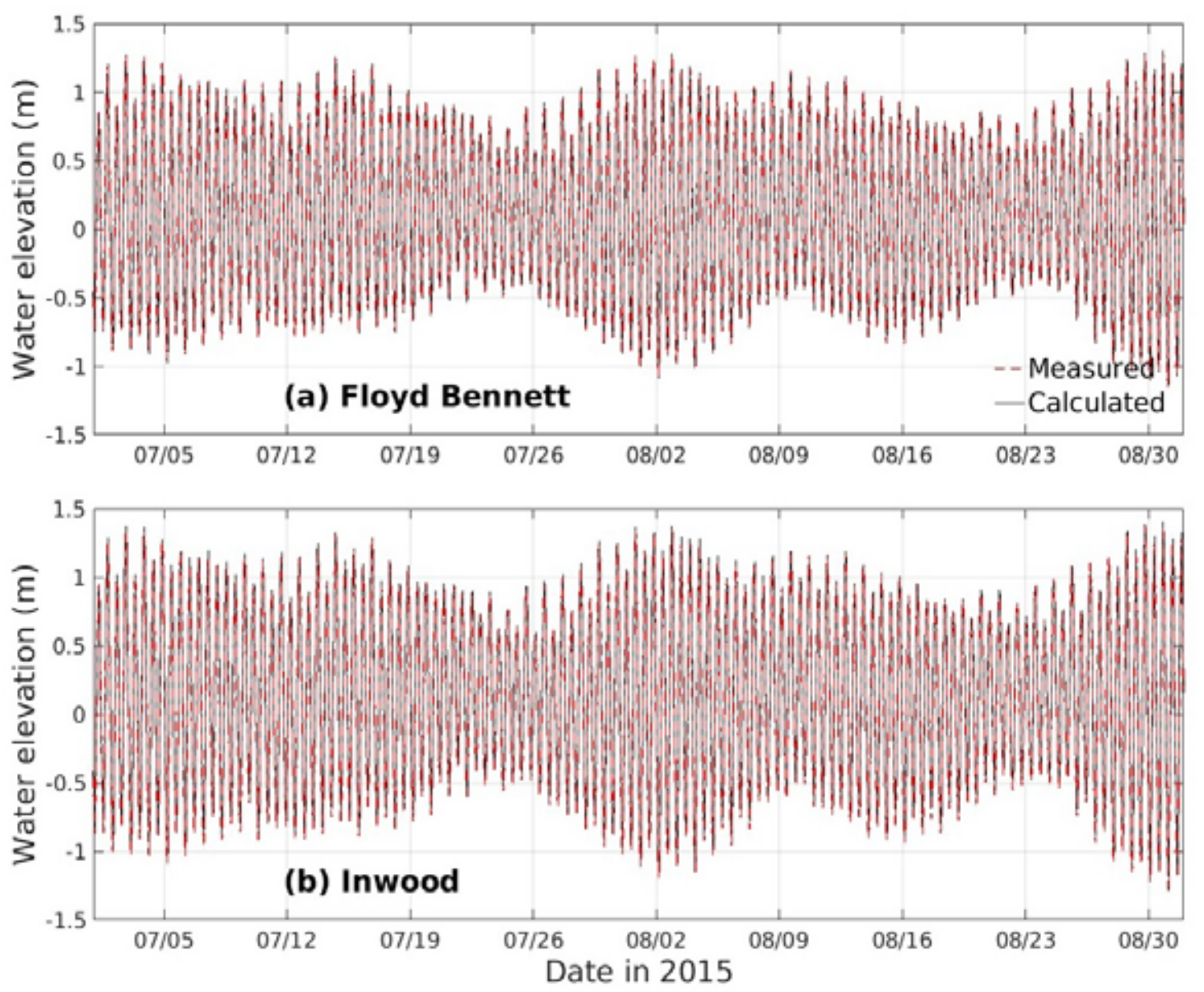
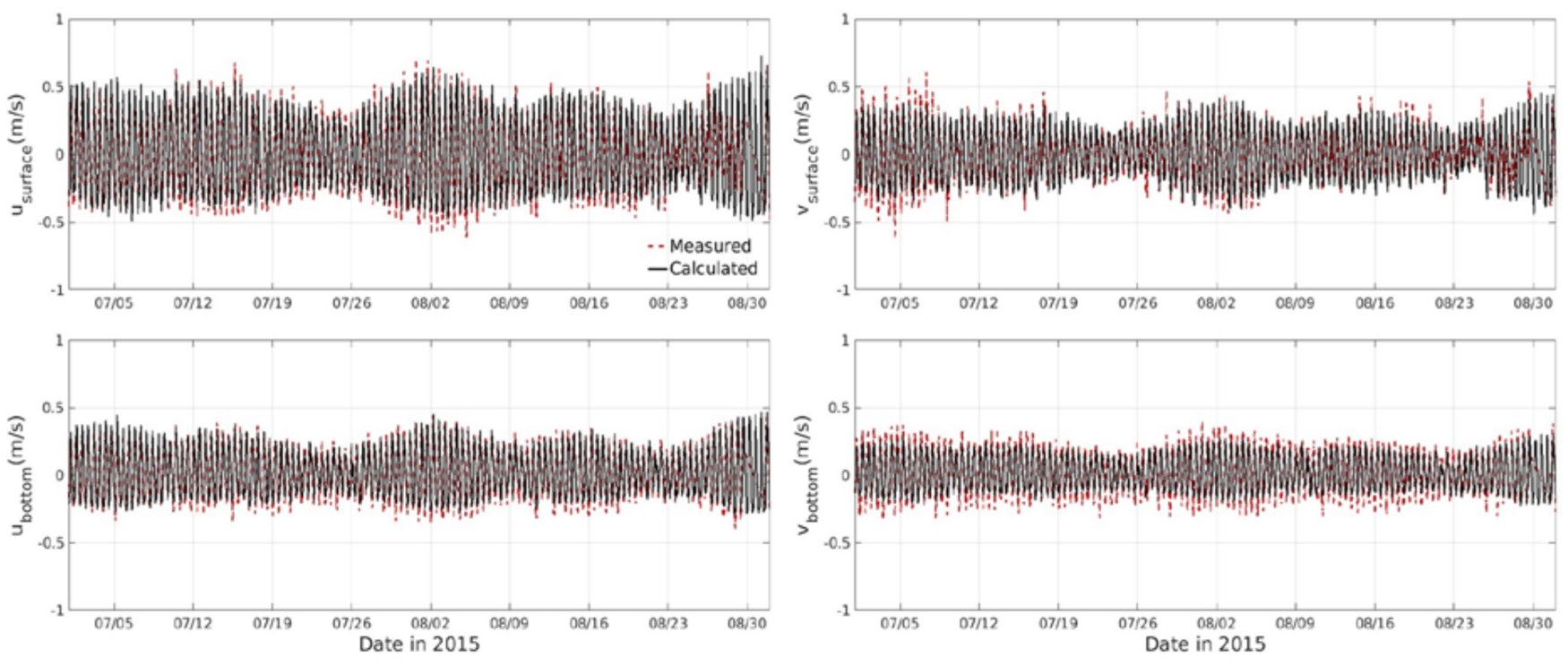
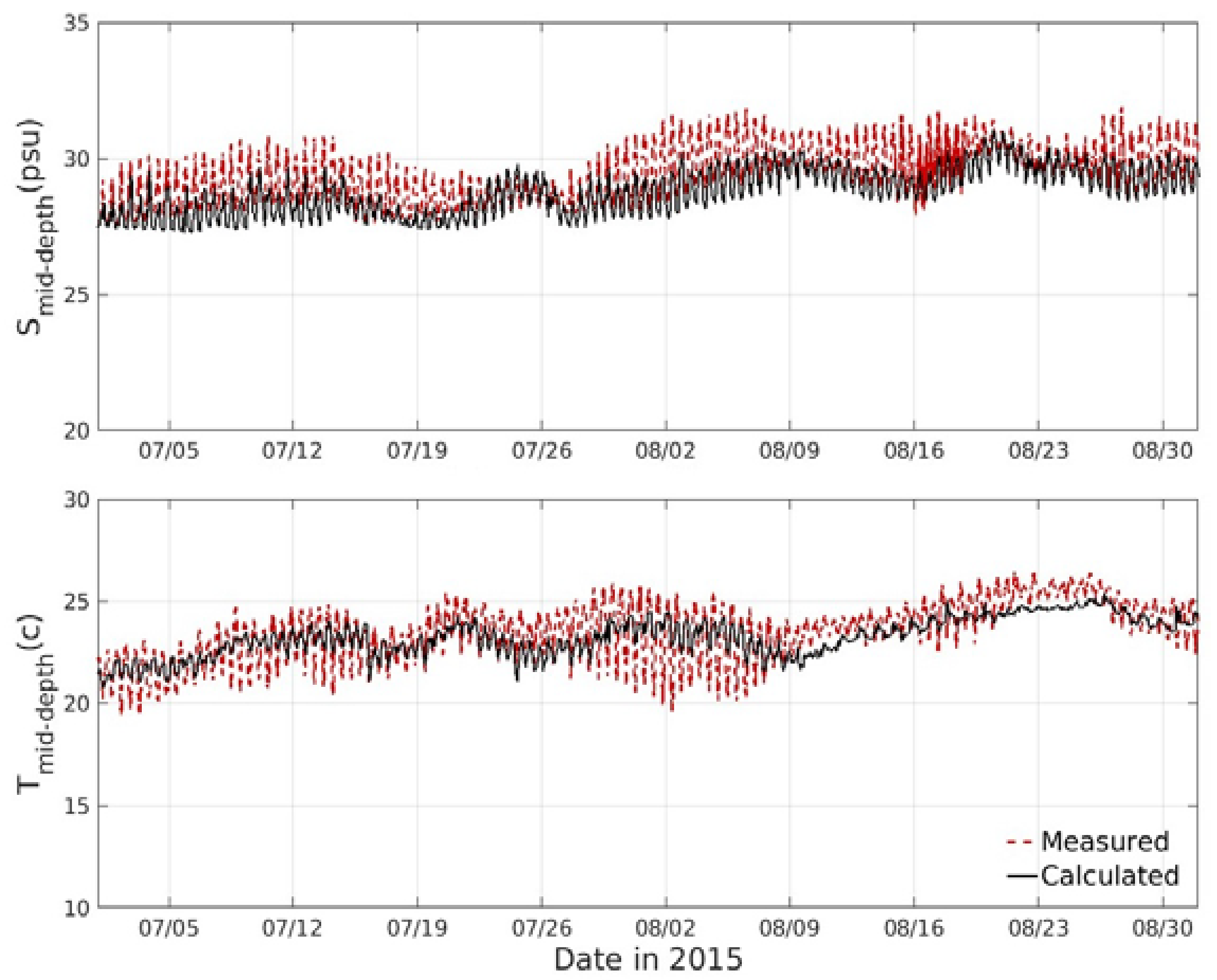

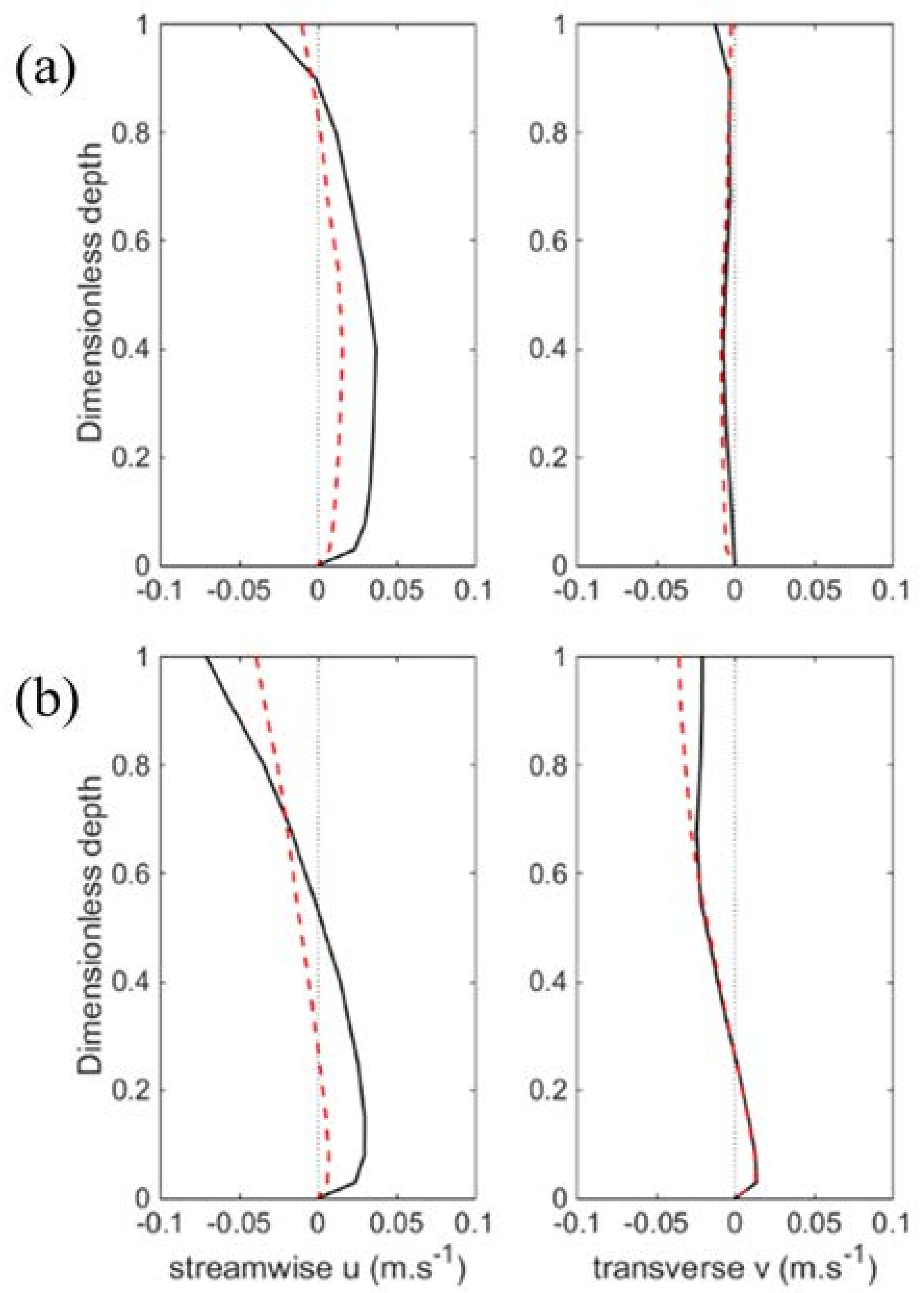
| Site | RMSE | Bias | Skill | |
|---|---|---|---|---|
| water elevation (m) | 1 | 0.04 | 0 | 1 |
| water elevation (m) | 3 | 0.04 | 0.03 | 1 |
| usurface (m s−1) | 2 | 0.1 | 0.01 | 0.96 |
| ubottom (m s−1) | 2 | 0.06 | −0.01 | 0.97 |
| vsurface (m s−1) | 2 | 0.09 | −0.01 | 0.93 |
| vbottom (m s−1) | 2 | 0.06 | −0.01 | 0.95 |
| salinity (psu) | 1 | 0.83 | −0.68 | 0.81 |
| temperature (°C) | 1 | 0.94 | −0.29 | 0.83 |
| Model | Forcing | ||
|---|---|---|---|
| Tidal | Wind | Freshwater Discharge | |
| ALL (all forcing) | √ | √ | √ |
| NW (no wind) | √ | × | √ |
| NF (no freshwater) | √ | √ | × |
| NFW (no freshwater/wind) | √ | × | × |
| Region | Model | Tracer Release Time | ||
|---|---|---|---|---|
| Low Tide | High Tide | Averaged | ||
| Jamaica Bay | ALL | 20.14 | 15.75 | 17.94 |
| NW | 19.10 | 14.72 | 16.91 | |
| NF | 26.87 | 18.36 | 22.61 | |
| NFW | 25.31 | 17.81 | 21.56 | |
| Grassy Bay | ALL | 11.28 | 10.02 | 10.65 |
| NW | 11.25 | 9.55 | 10.40 | |
| NF | 13.91 | 12.13 | 13.02 | |
| NFW | 15.48 | 13.66 | 14.57 | |
| Region | Tracer Release Time | Model ALL | Model ALLfts | ∆Tr (%) |
|---|---|---|---|---|
| Jamaica Bay | Low tide | 20.14 | 19.08 | −5.3 |
| High tide | 15.75 | 14.70 | −6.7 | |
| Averaged | 17.94 | 16.89 | −5.8 | |
| Grassy Bay | Low Tide | 11.28 | 10.81 | −4.2 |
| High Tide | 10.02 | 9.49 | −5.3 | |
| Averaged | 10.65 | 10.15 | −4.7 |
| Region | Model | Low Tide | High Tide | Averaged |
|---|---|---|---|---|
| Jamaica Bay | ALL | 0.93 | 0.91 | 0.92 |
| NW | 0.92 | 0.90 | 0.91 | |
| NF | 0.95 | 0.92 | 0.94 | |
| NFW | 0.94 | 0.92 | 0.93 | |
| Grassy Bay | ALL | 0.84 | 0.82 | 0.83 |
| NW | 0.84 | 0.81 | 0.83 | |
| NF | 0.87 | 0.85 | 0.86 | |
| NFW | 0.88 | 0.87 | 0.88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marsooli, R.; Orton, P.M.; Fitzpatrick, J.; Smith, H. Residence Time of a Highly Urbanized Estuary: Jamaica Bay, New York. J. Mar. Sci. Eng. 2018, 6, 44. https://doi.org/10.3390/jmse6020044
Marsooli R, Orton PM, Fitzpatrick J, Smith H. Residence Time of a Highly Urbanized Estuary: Jamaica Bay, New York. Journal of Marine Science and Engineering. 2018; 6(2):44. https://doi.org/10.3390/jmse6020044
Chicago/Turabian StyleMarsooli, Reza, Philip M. Orton, James Fitzpatrick, and Heather Smith. 2018. "Residence Time of a Highly Urbanized Estuary: Jamaica Bay, New York" Journal of Marine Science and Engineering 6, no. 2: 44. https://doi.org/10.3390/jmse6020044
APA StyleMarsooli, R., Orton, P. M., Fitzpatrick, J., & Smith, H. (2018). Residence Time of a Highly Urbanized Estuary: Jamaica Bay, New York. Journal of Marine Science and Engineering, 6(2), 44. https://doi.org/10.3390/jmse6020044





