Abstract
Ocean thermal energy conversion (OTEC) harvests the power from the thermal energy in the ocean, which is reserved in the ocean as the temperature difference between warm surface and cold deep seawaters. In the energy conversion, the heat exchangers transfer the thermal energy to the heat engine, which converts it into power. The pressure drops yielded by piping, valve and heat exchangers cause pump loads, which show significant negative power with respect to net power in OTEC. The heat transfer performance and the pressure drop in heat exchanger depend on the types and shapes of each heat transfer area. Generally, heat exchangers with higher friction factors yield higher heat transfer performance and vice versa. However, heat transfer performance and pressure drop are separately evaluated and there is no comprehensive performance evaluation index for OTEC power take-off. Therefore, this research proposes a new simplified overall performance evaluation method for heat exchangers, which can be comprehensively and easily applied and takes into consideration the heat transfer performance and the pressure drop. The evaluation results on plate-type heat exchangers show that the overall performance in each heat exchanger are elucidated and are quantitatively compared.
1. Introduction
Renewable energy represents an indispensable power supply for the sustainable development of infrastructure. One source of renewable energy is ocean thermal energy conversion (OTEC) system. They convert the thermal energy in the ocean, which is reserved as the vertical temperature gradient in the ocean, into electricity. OTEC can supply stable power as a baseload for an island country or remote grid, and the accompanying deep seawater provides the byproducts for many industrial applications such as aquaculture, agriculture, air-conditioning, and so on [1,2].
The thermal efficiency of OTEC is theoretically low due to the low available temperature difference between heat sources. Thus, to increase the thermal efficiency, various cycles have been proposed. These include an open cycle [3], a hybrid cycle that combined OTEC with desalination [4], and Kalina and Uehara cycles [5,6,7], which use an ammonia/water mixture as the working fluid. Furthermore, Anderson and Morisaki theoretically elucidated the effectiveness of the staging-closed cycle [8,9]. Moreover, solar-boosted cycles have been proposed as a way to increase the available temperature difference between the turbine inlet and outlet [8,9,10,11,12]. The optimization evaluation method is proposed based on the Carnot cycle thermal efficiency [13].
Johnson achieved the theoretical exergy efficiency for the open cycle, Rankine cycle, multi-component working cycle, Beck cycle, and the staging cycles and showed that the multi-stage open cycle and multi-component cycle exhibits better performance of exergy efficiency. Lee theoretically showed that the available maximum power when using the Lorentz cycle is almost double that of the Carnot cycle [14].
For the commercialized scale of megawatt-class power generation, an abundant quantity of seawater is required. The accompanying required intake pump power for surface and deep seawaters, which is caused by the pressure drop in the heat source because of the friction inside the piping, valves and heat exchangers, can be the same magnitude of power as the turbine/generator (gross) power, and the power might be able to ignore for the net power [4,15,16]. In general, increases in the flow rate of the heat source increases the performance of the heat exchangers, which then results in increased gross power, as well as an elevated heat source pump load. Therefore, the specific heat source flow rate maximizes the available net power, and the flow rate is as the optimum heat source flow rate in each power plant [17]. In addition, since the system uses the thermal energy stored as the sensible heat of seawater, harnessing the thermal energy from the heat source yields a change in the heat source temperatures. This then causes a reduction in the available temperature difference for the heat engine, which reduces the thermal efficiency of the heat engine. Then, theoretical maximum power output, which is well known in finite-time thermodynamics, can be formulated [18,19,20]. Yasunaga and Ikegami propose a normalization method of thermal efficiency for the performance evaluation [21]. The above studies show the importance of the heat balance in order to reduce the required seawater and also maximize the available power. Ibrahim reported on the effect of the heat transfer performance of heat exchangers on the available power output using irreversible heat exchangers [19]. Ikegami and Bejan considered the seawater intake pumping power in an OTEC system by using an ideal heat engine and introducing reversible heat exchange from the heat source to the heat engine, and identified the thermal efficiency in cases of maximum net power [22].
To achieve effective development of the available power output of an OTEC system, a conflict requirement is necessary that the significant enhancement of heat exchanger performances with reducing the pressure drop. In the design stage of an OTEC system, precise adoption of existing heat exchangers is important. However, in general, separate performance evaluations of the heat exchangers are conducted to measure the heat transfer performance and pressure drop produced by friction. Then, the optimum design is carried out to determine the number of plates to maximize the net power. In the case of the heat exchangers, which are made of titanium, and are the dominant capital expenditure of OTEC, and the net power output per the heat transfer area is maximized [23,24,25]. The result of the optimum design method is a balance between the heat transfer performance of all the heat exchangers, including evaporators and condensers, and the required seawater intake pump power. The optimum design method is an evaluation of the heat exchangers; however, it can only represent the total balance of the system and is not able to express the performance of each heat exchangers independently. For the development of the heat exchangers for OTEC, many plate-type and tube-type heat exchangers have been tested, however, they are separately evaluated for their heat transfer coefficients and friction factors using the existing performance evaluation method. In contrast, the assessment of effectiveness of each heat exchanger’s performance as an evaporator or a condenser in the power generation system has not been evaluated individually.
Therefore, the comprehensive performance evaluation method of a heat exchanger for OTEC power generation, which considers the trade-off of the heat transfer performance and the pressure drop, is required for the selection and design of the heat exchangers, as well as the improvement of heat exchanger performance. Therefore, this study describes the theoretical relationship between the heat transfer performance of heat exchangers, including the pressure drop and power output from the heat engine of OTEC, and proposes a comprehensive performance evaluation index. This method will then be applied to the existing plate-type heat exchangers.
2. Heat Exchanger Performance and Power Output
2.1. Maximum Power Output of a Heat Engine
Figure 1 shows the OTEC power generation system model using a reversible heat engine. The ocean thermal energy is the temperature difference between the surface seawater and the deep seawater. To harvest the thermal energy, both seawaters should continuously flow to the heat exchangers in order to transfer the heat into the heat engine via the heat exchangers. The power output from the heat engine is W, the heat transfer rate of the warm seawater is QW and that of the cold deep seawater is QC, respectively:
where is the mass flow rate of seawater, cp is the specific heat of seawater, and the subscription of W is warm sweater, W,O is the warm seawater outlet after heat exchange with the heat engine, C is the deep seawater and C,O is the deep seawater outlet after the heat exchange. Figure 2 shows the conceptual T − s diagram of an OTEC with a reversible heat engine. In the case of a reversible heat engine, the entropy generation will be zero:
where TH and TL show the high and low temperatures of the heat engine in the reversible heat engine, respectively. The thermal efficiency ηth and the power output W can be calculated as:
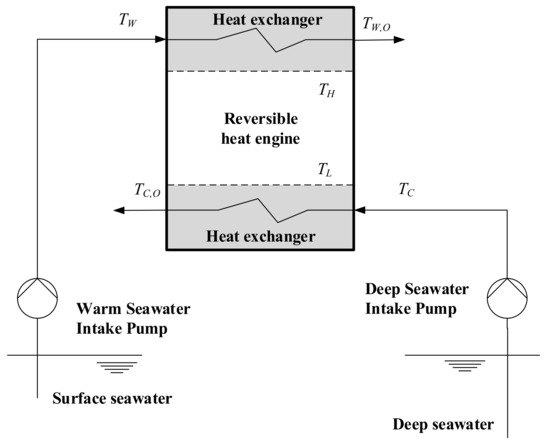
Figure 1.
OTEC power generation system model using a reversible heat engine.
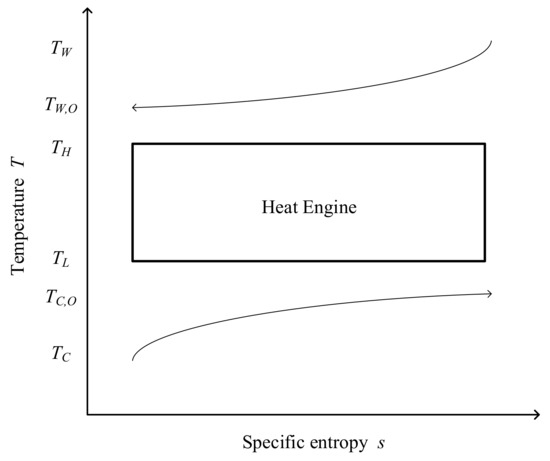
Figure 2.
Conceptual T − s diagram of an OTEC power generation system using a reversible heat engine.
In the heat exchange process via the heat exchangers, the heat flow rate depends on the performance of the heat exchangers. Using an overall heat transfer coefficient U and a logarithmic mean temperature ∆Tm, the heat transfer rates can be expressed as:
where the logarithmic mean temperatures in the case of the counter flow in the heat exchangers are:
From Equations (1) to (10), the work output is one degree of freedom as a function of TW,O or TC,O. Then the work output can be maximized by or . The maximum work considering the heat exchanger performance Wm,NTU is expressed as:
where:
where CHS is the total heat capacity flow rate (CHS = CW + CC, C = ), r is the ratio of the heat capacity flow rate of the surface seawater (r = CW/CHS), and NTU is the net transfer unit defined as follows:
If the NTUs are infinite, the maximum power output Equation (11) will be as follows:
The thermal efficiencies at the maximum power outputs will be calculated as the formula:
Equation (16) is well known as the Curzon-Ahlborn efficiency [26,27,28].
Figure 3 shows the relationship between the ratio of the maximum available power output Wm,NTU/Wm as a function of the net transfer unit in the case in which NTUW and NTUC are identical. According to Figure 3, the ratio of maximum available power will be 63%, 86%, and 95% when NTU is 1.0, 2.0, and 3.0, respectively.
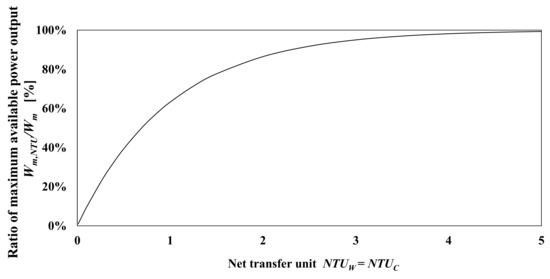
Figure 3.
Dependency of the ratio of maximum available power output and net transfer unit in the case in which NTUW and NTUC are identical.
2.2. Relationship between Net Power and Heat Exchanger Performance
In the OTEC system, the pressure drop due to the friction caused by the flow inside the heat exchanger is not negligible. The seawater intake pumping power P can be calculated as:
where is the seawater density (kg/m3), ηP is the mechanical efficiency of the seawater pumps and ∆P is the pressure drop of the heat exchangers (kPa). Although the total pressure drop of the seawaters are related to each heat exchanger, piping, valve, and the configuration of seawater intake facility, ∆P is assumed that the considerable pressure drop is only inside the heat exchanger in order to directly represent the effect of the performance of the heat exchangers on the net power. Then, the net power output is calculated as:
where PW and PC are the pumping power of the warm surface seawater and the cold deep seawater, respectively. The maximum net power using a reversible heat engine will then be:
According to Equation (19), the heat exchanger in the OTEC system has a significant role and is one of the key pieces of equipment that increases the net power output. For the increase of net power output in the OTEC system, the enhancement of heat transfer performance (positive element), as well as decreasing the pressure drop (negative element) are required. However, the dependency of net power on the heat exchanger is a paradox: a decrease of irreversibility during the heat transfer process and the flow.
3. Basic Performance Evaluation Method
3.1. Basic Heat Exchanger Performance Evaluation Index
In general, the heat exchanger performance and pressure drop are evaluated separately. However, for comparison with the heat exchanger performance in the system, a performance evaluation method is required since the net power is the balance of the positive and negative elements. For example, in the design of the numbers of plates or tubes in the heat exchangers, (1) the net power will be determined by the balance of each heat exchanger comprehensive performance at the constant total heat flow rate, and the velocity changes the overall heat transfer coefficients and pressure drops; and (2) the net power may be reduced in case that the total heat source flow rate is increased. Then, the basic characteristics of the heat exchangers are ascertained and the theoretical maximum net power can be predictable. If a heat exchanger performance evaluation index can reflect such characteristics, it can support the design and development of heat exchangers for use in OTEC.
For the evaluation of the heat exchanger performance in the system, the maximum available power output and the pressure drop are assumed to be a function of the mean velocity of heat source in the heat exchangers. For comparison of a variable heat exchanger, the net power output per heat transfer area in a single path is the most important factor if we consider the effectiveness of the heat exchangers. In optimization studies, the net power output per total heat transfer area has been employed as the optimum function in terms of an economical point of view since the materials of OTEC heat exchangers are normally titanium used as an anti-corrosion material for protection from the seawater [23,24,25]. Hence, the theoretical maximum net power per heat transfer area is expressed as:
where the assumption of Equation (20) is as follows: the efficiency of the heat source pump is assumed to be 100% (ηP = 1) in order to avoid the effect of the efficiency on the heat exchanger performance evaluation: the total performance of the heat exchangers, including the net transfer unit and pressure drop, are the same, and the ratio of warm seawater heat capacity flow rate is 0.5 in order to conduct independent evaluations as a heat exchanger, an evaporator, or a condenser.
Now, to normalize the net power, the ratio of maximum available power output for heat exchanger performance can be calculated using the backwork ratio (BWR), which is generally defined in the gas-turbine cycle [29], as a ratio of the parasitic power of the compressor:
Equation (21) is the theoretical performance evaluation that indicates the ratio of available power output per theoretically maximum available power output using the Carnot cycle with the unit mass flow rate of the heat source in the system. In order to consider the characteristics of Equations (20) and (21), the following performance index for OTEC heat exchanger ω is proposed:
where ω shows the effectiveness of the ratio of available power per heat transfer area in the path of the heat source. Since the net power output per heat transfer area expressed by Equation (20) shows the effectiveness of the net power in a single path of the heat exchanger, ω is defined as the effectiveness of the available thermal energy from the heat source. Therefore, a higher ω represents a lower required seawater flow rate at the same magnitude of the net power output per heat transfer area.
3.2. Assumptions and Evaluation Procedure
The overall heat transfer coefficient U is expressed as:
where αHS is the forced convention heat transfer coefficient of seawater (W/m2K), t is the plate thickness (m), Lpt is the coefficient of thermal conductivity (W/mK), αWF is the heat transfer coefficient of the working fluid (W/m2K) and Rf is the thermal resistance due to fouling (m2K/W). The heat transfer coefficient of the working fluid is the mix of the forced convection with the boiling or condensing heat transfer coefficient. In general, the boiling or condensing heat transfer coefficients are much higher than the forced convection heat transfer coefficient. Thus, this study assumes that the working fluid heat transfer coefficient is much higher than the seawater forced heat transfer coefficient and is constant, which are then applied in the Wilson plot method [30], and then even in an evaporator and a condenser, the effect of superheating and subcooling are negligible. Then, the overall heat transfer coefficient is approximated as an exponential function of seawater mean velocity in the plate heat exchanger. In addition, the thermal resistance due to the fouling is assumed to be negligible.
In the design of the heat exchangers, NTU is held constant by changing the number of plates or tubes if the mean seawater velocity in the path is constant. Therefore, the overall heat transfer coefficient assumes to be approximated by an exponential function of the mean seawater flow rate, which can be correlated by the experiment results.
In the evaluation of the heat exchanger performance, the following steps are applied:
- To make the approximate formula of the overall heat transfer coefficient and pressure drop a function of the mean velocity of seawater by experimentation, which is shown in Figure 4a:
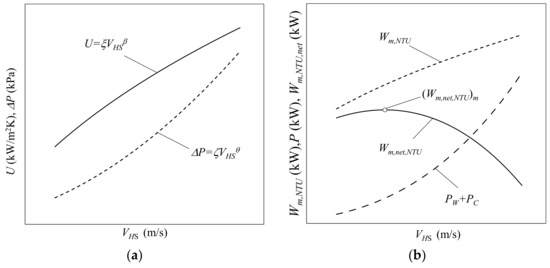 Figure 4. Concept of performance evaluation of a heat exchanger as a function of mean velocity of the heat source. (a) an overall heat transfer coefficient and a pressure drop; and (b) a maximum power output, a required pumping powers and a net power output as a function of mean velocity of the heat source.
Figure 4. Concept of performance evaluation of a heat exchanger as a function of mean velocity of the heat source. (a) an overall heat transfer coefficient and a pressure drop; and (b) a maximum power output, a required pumping powers and a net power output as a function of mean velocity of the heat source. - To calculate the maximum net power output per heat transfer area, which are represented by Equation (20), and the optimum mean velocity of seawater, which maximizes the net power output, in the design seawater temperature condition shown in Figure 4b,
- To calculate ω represented by Equation (23) as the performance index for an OTEC heat exchanger.
The proposed evaluation method can be applied to any type of heat exchangers. Typically, the plate-type and tube-type heat exchangers were applied to OTEC. In the case of the plate-type heat exchanger design, in general, the plate number is the design value once the geometry has been determined. In contrast, the tube-type can change the tube length in the design, which changes the heat transfer are per flow path of the heat sources.
4. Results and Discussion
In this section, the performance of existing plate-type heat exchangers applied to OTEC are evaluated by the proposed performance evaluation method and the procedure using six different plate type heat exchangers [24,31,32,33,34]. Table 1 shows the heat exchanger specifications. By referring to the performance data in this paper, each overall heat transfer coefficient and pressure drop are approximated as the functions of the mean velocity of heat source in the heat exchangers (Equation (25)). The coefficients of Equation (25) are listed on the Table 2. In Table 2, there is a slight discrepancy in the measured velocity range between the overall heat transfer coefficients and pressure drop, and the overall heat transfer coefficient.

Table 1.
Heat exchanger specifications.

Table 2.
Approximation coefficients.
Figure 5 shows the net power output per heat transfer area as a function of the mean velocity of the heat source in the plate. In each PHE, the maximum power output per heat transfer area forms a parabolic path. The maximum power output is the balance of an increase in the maximum power and the heat source pumping power, since the overall heat transfer coefficient increases and the pressure drop increases with the mean velocity of the heat source, respectively. The overall heat transfer coefficient increases with the increase of the mean velocity of the heat source; however, the increase in the pressure drop is higher than the maximum power output. As a result, the net power output forms the parabolic curve. The range of the optimum heat source mean velocities is 0.33 to 2.00 m/s. In the case of Nos. 4, 5 and 6, the optimum heat source mean velocities are out of the range of the overall heat transfer coefficient experimental data or the pressure drop measurement data. However, the maximum points are computed using the approximated formulas, assuming that it is possible to extrapolate and to estimate the optimum points. As shown in Figure 5, a design at too high a mean velocity will cause a negative net power, which is shown in Figure 5 and also in [17,22].
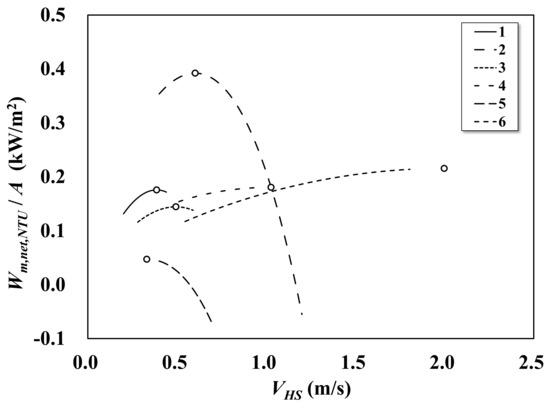
Figure 5.
The net power output per the heat transfer area as function of the mean velocity of heat source in the plate when TW = 30 °C, TC = 5 °C, cp = 4.0 kJ/kgK and = 1025 kg/m3. The open circles show the maximum point of power output, i.e., the optimum mean velocity of the heat source in each plate heat exchanger.
The parameters of the optimum mean heat source velocities, in which the warm seawater temperature is 30 °C and the cold deep seawater temperature is 5 °C, are listed in Table 3. According to Figure 5 and Table 3, the net power output per heat transfer area of No. 1 and No. 4 are the same value of 0.18, while the performance indices for the OTEC heat exchangers ω are 0.36 and 0.15 respectively, and this shows the obvious performance difference. The optimum points shown in Table 3 are constant even when there is a change increment in the number of heat exchanger plates. This is one of the characteristics of the specific heat exchangers.

Table 3.
Optimum mean velocity condition when TW = 30 °C and TC = 5 °C.
Figure 6 shows the ratio of the net power output, and the irreversible loss in the heat exchange process and backwork ratio at the optimum mean heat source velocities, respectively. According to Table 3 and Figure 6, 21% to 72% is the loss during the heat exchange process. This can be reduced by increasing the heat transfer area in the path in the plates. Additionally, 4% to 19% of the power is consumed as the backwork of the seawater pumping power to force a flow through the plate. Consequently, the performance of No. 1 shows the highest ratio of the net power output of 60%, and No. 3 and No. 2 follow that at 52% abd 41%. Others are less than 25%. Regarding the performance index for OTEC heat exchanger ω, which considers the net power by the unit heat transfer area, No. 2 is the highest at almost triple that of No. 1 and No. 3. From Equation (11), the maximum power output is proportional to the mass flow rate of the heat source and, therefore, ω in the No. 2 plate shows the best overall performance.
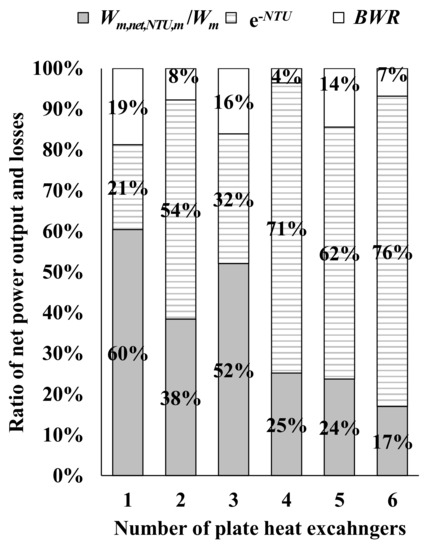
Figure 6.
The ratio of net power, loss in the heat exchange process (e−NTU), and backwork ratio at the optimum mean velocity of heat source in the plate when TW = 30 °C, TC = 5 °C, cp = 4.0 kJ/kgK and = 1025 kg/m3.
5. Conclusions
For the purpose of the development of a comprehensive performance evaluation method for OTEC heat exchangers, it is derived that the theoretical relationship between the heat transfer performance of heat exchangers including the pressure drop and power output from the reversible heat engine. Based on the fundamental relationships that show the paradox of the heat transfer performance and the pressure drop, this study proposes a performance procedure and an index for OTEC heat exchangers. And they show the specific characteristics of each heat exchangers with the heat transfer area in a path. The results of the comparison of the available power output per heat transfer area among six plate heat exchangers then become clear. The results show that the proposed performance index of the heat exchanger for OTEC is able to express the effectiveness of the performance on OTEC system power outputs. Therefore, the proposed evaluation method is applicable to the evaluation of existing heat exchangers as well as to new research and development.
Acknowledgments
We sincerely thank Natsuki Koyama, who is an undergraduate student at Saga University, Japan, and who provided us with assistance with the heat exchanger data analysis.
Author Contributions
T.Y. conceived the performance evaluation method and wrote the paper. T.Y. and T.N. contributed to analyzing and to summarizing the data of heat exchangers using available literature, and T.M. and Y.I. evaluated the method and the procedure.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martin, B.; Okamura, S.; Nakamura, Y.; Yasunaga, T.; Ikegami, Y. Status of the “Kumejima Model” for advanced deep seawater utilization. In Proceedings of the IEE Conference Publications, Kobe, Japan, 6–8 October 2016; pp. 211–216. [Google Scholar]
- Takahashi, M. DOW: Deep Ocean Water as Our Next Natural Resource; Terra Scientific Publishing Company: Tokyo, Japan, 2000; ISBN 488704125x. [Google Scholar]
- Claude, G. Power from the tropical sea. Mech. Eng. 1930, 52, 1039–1044. [Google Scholar]
- Avery, H.W.; Wu, C. Renewable Energy from the Ocean; Oxford University Press: Oxford, UK, 1994; pp. 90–151. ISBN 9780195071993. [Google Scholar]
- Kalina, A.I. Generation of Energy by Means of a Working Fluid, and Regeneration of a Working Fluid. U.S. Patents 4346561, 31 August 1982. [Google Scholar]
- Marston, C.H. Parametric analysis of the Kalina cycle. Trans. ASME J. Eng. Gas Turb. Power 1990, 112, 107–116. [Google Scholar] [CrossRef]
- Uehara, U.; Ikegami, Y.; Nishida, T. OTEC System Using a New Cycle with Absorption and Extraction Process; Physical Chemistry of Aqueous Systems, Begell House, Inc.: Danbury, CT, USA, 1995; pp. 862–869. [Google Scholar]
- Anderson, J.H.; Anderson, J.H., Jr. Thermal power form seawater. Mech. Eng. 1966, 88, 41–46. [Google Scholar]
- Morisaki, T.; Ikegami, Y. Maximum power of a multistage Rankine cycle in low-grade thermal energy conversion. Appl. Ther. Eng. 2014, 69, 78–85. [Google Scholar] [CrossRef]
- Sun, F.; Ikegami, Y.; Arima, H.; Zhou, W. Performance analysis of the low-temperature solar-boosted power generation system—Part I: Comparison between Kalina solar system and Rankine solar system. Trans. ASME J. Sol. Energy Eng. 2013, 135. [Google Scholar] [CrossRef]
- Sun, F.; Ikegami, Y.; Arima, H.; Zhou, W. Performance analysis of the low-temperature solar-boosted power generation system—Part II: Thermodynamic characteristics of the Kalina solar system. Trans. ASME J. Sol. Energy Eng. 2013, 135. [Google Scholar] [CrossRef]
- Bombarda, P.; Invernizzi, C.; Gaia, M. Performance analysis of OTEC plants with multilevel organic Rankine cycle and solar hybridization. Trans. ASME J. Eng. Gas Turb. Power 2013, 135. [Google Scholar] [CrossRef]
- Sinama, F.; Martins, M.; Journoud, A.; Marc, O.; Lucas, F. Thermodynamic analysis and optimization of a 10 MW OTEC Rankine cycle in Reunion Island with the equivalent Gibbs system method and generic optimization program. Appl. Ocean Res. 2015, 53, 54–66. [Google Scholar] [CrossRef]
- Johnson, D.H. The exergy of the ocean thermal resource and analysis of second-law efficiencies of idealized ocean thermal energy conversion power cycles. Energy 1983, 8, 927–946. [Google Scholar] [CrossRef]
- Owens, W.L.; Trimble, L.C. Mini-OTEC operational results. Trans. ASME J. Sol. Energy Eng. 1981, 103, 233–240. [Google Scholar] [CrossRef]
- Mitsui, T.; Ito, F.; Seya, Y.; Nakamoto, Y. Outline of the 100 kW OTEC pilot plant in the Republic of Nauru. IEEE Trans. Power App. Syst. 1983, PAS-102, 3167–3171. [Google Scholar] [CrossRef]
- Yasunaga, T.; Ikegami, Y.; Monde, M. Performance test of OTEC with ammonia/water as working fluid using shell and plate type heat exchangers (effect of heat source temperature and flow rate). Trans. JAME B 2008, 74, 445–452. [Google Scholar] [CrossRef][Green Version]
- Bejan, A. Advanced Engineering Thermodynamics; Wiley: New York, NY, USA, 1998; ISBN 0471677639. [Google Scholar]
- Ibrahim, O.M. Effect of irreversibility and economics on the performance of a heat engine. Trans. ASME J. Sol. Energy Eng. 1992, 114, 267–271. [Google Scholar] [CrossRef]
- Wu, C. Performance bound for real OTEC heat engines. Ocean Eng. 1987, 14, 349–354. [Google Scholar] [CrossRef]
- Yasunaga, T.; Ikegami, Y. Application of finite-time thermodynamics for evaluation method on heat engine. Energy Procedia 2017, 129, 995–1001. [Google Scholar] [CrossRef]
- Ikegami, Y.; Bejan, A. On the thermodynamic optimization of power plants with heat transfer and fluid flow irreversibility. Trans. ASME J. Sol. Energy Eng. 1998, 120, 139–144. [Google Scholar] [CrossRef]
- Owens, W.L. Optimization of closed-cycle OTEC system. In Proceedings of the ASME/JSME Thermal Engineering Joint Conference, Honolulu, HI, USA, 20–24 March 1980; Volume 2, pp. 227–239. [Google Scholar]
- Uehara, H.; Ikegami, Y. Optimization of a closed-cycle OTEC system. Trans. ASME J. Sol. Energy Eng. 1990, 112, 247–256. [Google Scholar] [CrossRef]
- Ikegami, Y.; Uehara, H. Performance analysis of OTEC plants at off-design conditions: Ammonia as working fluid. Trans. ASME J. Sol. Energy Eng. 1992, G0656A, 633–638. [Google Scholar]
- Novikov, I.I. The efficiency of atomic power stations. J. Nuclear Energy II 1958, 7, 125–128. [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Chen, I.; Yan, Z.; Lin, G.; Andersen, B. On the Curzon-Ahlborn efficiency and its connection with the efficiencies of the real heat engines. Energy Convers. Manag. 2001, 42, 173–181. [Google Scholar] [CrossRef]
- Jones, J.B.; Hawkins, G.A. Engineering Thermodynamics an Introductory Textbook, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1986; p. 578. ISBN 0471812021. [Google Scholar]
- Wilson, E.E. A basis for rational design of heat transfer apparatus. Trans. ASME J. Heat Trans. 1915, 37, 47–82. [Google Scholar]
- Kushibe, M.; Ikegami, Y.; Monde, M.; Uehara, H. Evaporation heat transfer of ammonia and pressure drop of warm water for plate type evaporator. Trans. JSRAE 2005, 22, 403–415. [Google Scholar]
- Nakaoka, T.; Urata, K.; Ikegami, Y.; Nishida, T.; Ohhara, J.; Horita, M. Heat transfer coefficient and pressure drop of plate-type condenser using OTEC (using NH3/H2O as working fluid). OTEC 2009, 15, 1–8. [Google Scholar]
- Uehara, H.; Nakaoka, T.; Miyara, A.; Murakami, H.; Dilao, C.O.; Miyazaki, K. A shell and plate type condenser. In Proceedings of the 2nd International Symposium on Condenser and Condensation, Bath, UK, 28–30 March 1990; pp. 347–356. [Google Scholar]
- Uehara, H.; Nakaoka, T.; Hagiwara, K. Plate type condenser (cold water side heat transfer coefficient and friction factor). Refrigeration 1984, 59, 3–9. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).