An Integrated Numerical Model for the Design of Coastal Protection Structures
Abstract
:1. Introduction
2. Model Description
2.1. Nearshore Wave Transformation Module–WAVE_L
- A sponge layer boundary condition is used to absorb the outgoing waves at the four sides of the domain [27].
- The presence of vertical structures is incorporated by introducing a total reflection boundary condition (Uw = (Uw. Vw) = 0 normal to the boundary, where Uw is the mean velocity vector; for a rectilinear grid, the above is equivalent to Uw = 0 or Vw = 0).
- The presence of submerged structures is incorporated as in [31].
- The presence of floating structures is incorporated as in [32].
2.2. Wave-Induced Circulation Module—WICIR
- if (d + ζ)i,j > hcr and (d + ζ)i − 1,j ≤ hcr and Ui,j > 0 → Ui,j = 0
- if (d + ζ)i,j > hcr and (d + ζ)i,j − 1 ≤ hcr and Vi,j > 0 → Vi,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i − 1,j ≤ hcr → Ui,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i,j − 1 ≤ hcr → Vi,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i − 1,j > hcr and Ui,j < 0 → Ui,j = 0
- if (d + ζ)i,j ≤ hcr and (d + ζ)i,j − 1 > hcr and Vi,j < 0 → Vi,j = 0
2.3. Sediment Transport Module—SEDTR
3. Model Applications
3.1. Comparison with Experimental Data
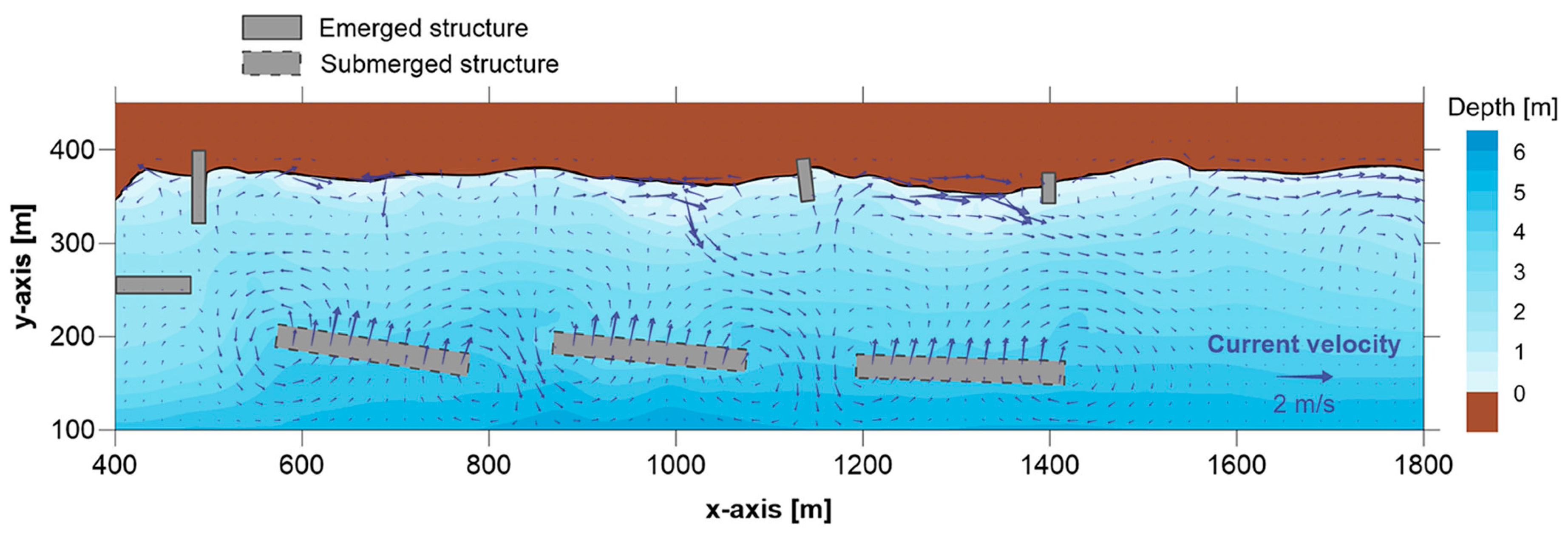
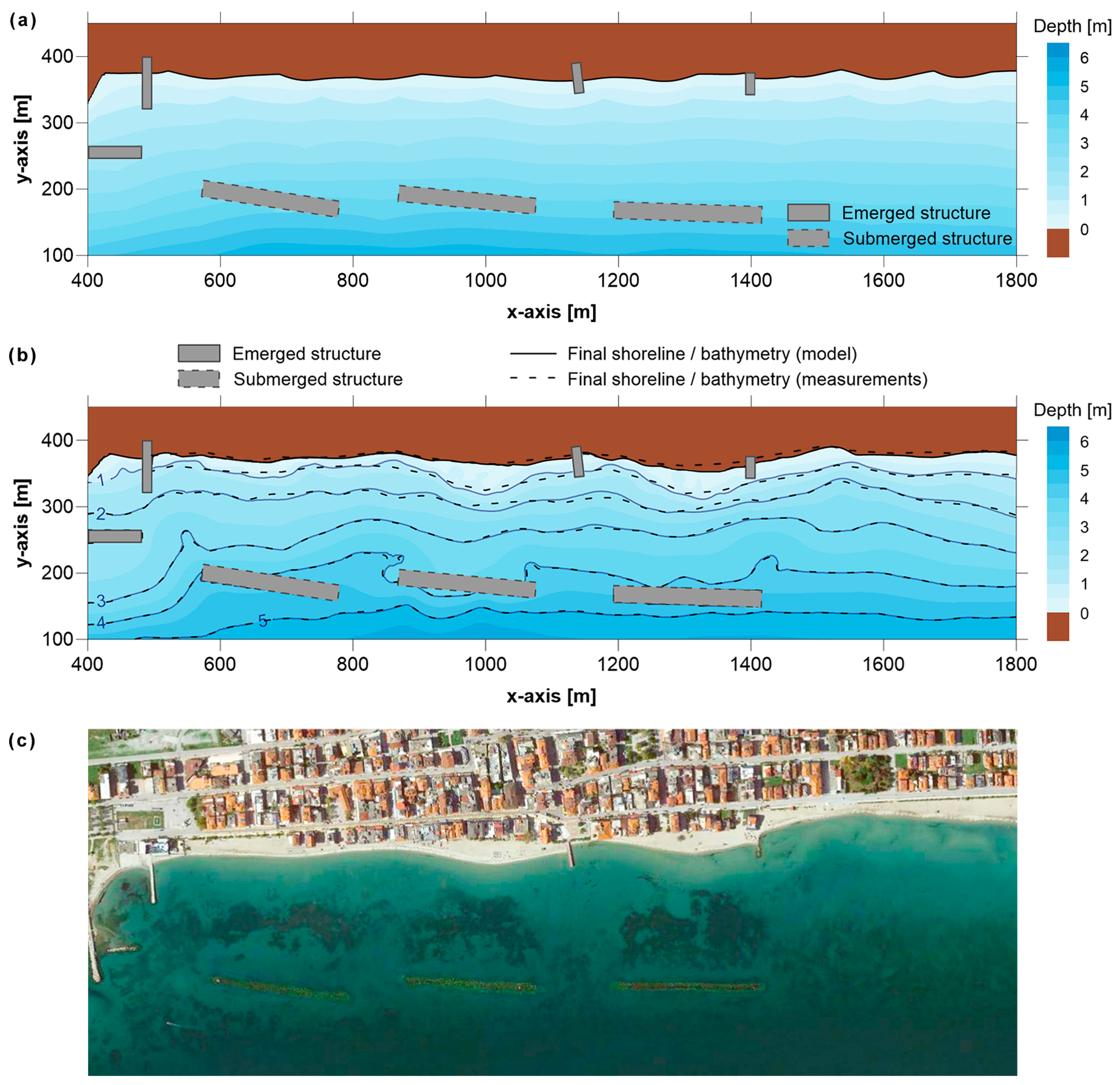
3.2. Application to Paralia Katerinis Beach (Greece)—Coastal Protection with Submerged Breakwaters
4. Results and Discussion
4.1. Comparison with Experimental Data
4.2. Application to Paralia Katerinis Beach (Greece)—Coastal Protection with Submerged Breakwaters
4.3. General Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Note
- Rakha, K.A. A Quasi-3D phase-resolving hydrodynamic and sediment transport model. Coast. Eng. 1998, 34, 277–311. [Google Scholar] [CrossRef]
- Karambas, T.V.; Koutitas, C. Surf and swash zone morphology evolution induced by nonlinear waves. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 102–113. [Google Scholar] [CrossRef]
- Karambas, T.V.; Karathanassi, E.K. Longshore sediment transport by nonlinear waves and currents. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 277–286. [Google Scholar] [CrossRef]
- Karambas, T.V. Prediction of sediment transport in the swash-zone by using a nonlinear wave model. Cont. Shelf Res. 2006, 26, 599–609. [Google Scholar] [CrossRef]
- Karambas, T.V.; Samaras, A.G. Soft shore protection methods: The use of advanced numerical models in the evaluation of beach nourishment. Ocean Eng. 2014, 92, 129–136. [Google Scholar] [CrossRef]
- Gallerano, F.; Cannata, G.; De Gaudenzi, O.; Scarpone, S. Modeling bed evolution using weakly coupled phase-resolving wave model and wave-averaged sediment transport model. Coast. Eng. J. 2016, 58, 58. [Google Scholar] [CrossRef]
- Gallerano, F.; Cannata, G.; Lasaponara, F. A new numerical model for simulations of wave transformation, breaking and long-shore currents in complex coastal regions. Int. J. Numer. Methods Fluids 2016, 80, 571–613. [Google Scholar] [CrossRef]
- Klonaris, G.T.; Memos, C.D.; Drønen, N.K.; Deigaard, R. Boussinesq-type modeling of sediment transport and coastal morphology. Coast. Eng. J. 2017, 59, 59. [Google Scholar] [CrossRef]
- Watanabe, A.; Maruyama, K.; Shimizu, T.; Sakakiyama, T. Numerical prediction model of three-dimensional beach deformation around a structure. Coast. Eng. J. 1986, 29, 179–194. [Google Scholar]
- Nicholson, J.; Broker, I.; Roelvink, J.A.; Price, D.; Tanguy, J.M.; Moreno, L. Intercomparison of coastal area morphodynamic models. Coast. Eng. 1997, 31, 97–123. [Google Scholar] [CrossRef]
- Zyserman, J.A.; Johnson, H.K. Modelling morphological processes in the vicinity of shore-parallel breakwaters. Coast. Eng. 2002, 45, 261–284. [Google Scholar] [CrossRef]
- Postacchini, M.; Russo, A.; Carniel, S.; Brocchini, M. Assessing the hydro-morphodynamic response of a beach protected by detached, impermeable, submerged breakwaters: A numerical approach. J. Coast. Res. 2016, 32, 590–602. [Google Scholar] [CrossRef]
- Roelvink, J.A.; Uittenbogaard, R.E.; Liek, G.J. Morphological modelling of the impact of coastal structures. In Coastal Structures ‘99, Proceedings of the International Conference Coastal Structures ‘99, Santander, Spain, June 1999; Losada, I.J., Balkema, A.A., Eds.; CRC Press: Boca Raton, FL, USA, 2000; pp. 865–871. [Google Scholar]
- Johnson, H.K. Coastal area morphological modelling in the vicinity of groins. In Proceedings of the 29th International Conference on Coastal Engineering, Lisbon, Portugal, 19–24 September 2004; pp. 2646–2658. [Google Scholar]
- Ding, Y.; Wang, S.Y.; Jia, Y. Development and validation of a quasi-three-dimensional coastal area morphological model. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 462–476. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.S.Y. Development and application of a coastal and estuarine morphological process modeling system. J. Coast. Res. 2008, 127–140. [Google Scholar] [CrossRef]
- Leont’yev, I.O. Modelling of morphological changes due to coastal structures. Coast. Eng. 1999, 38, 143–166. [Google Scholar] [CrossRef]
- Nam, P.T.; Larson, M.; Hanson, H.; Hoan, L.X. A numerical model of beach morphological evolution due to waves and currents in the vicinity of coastal structures. Coast. Eng. 2011, 58, 863–876. [Google Scholar] [CrossRef]
- Camenen, B.; Larson, M. A Unified Sediment Transport Formulation for Coastal Inlet Application; ERDC/CH: CR-07-1; US Army Corps of Engineers, Engineering Research and Development Center: Vicksburg, MS, USA, 2007; p. 247. [Google Scholar]
- Camenen, B.; Larson, M. A general formula for noncohesive suspended sediment transport. J. Coast. Res. 2008, 24, 615–627. [Google Scholar] [CrossRef]
- Ming, D.; Chiew, Y. Shoreline changes behind detached breakwater. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 63–70. [Google Scholar] [CrossRef]
- Badiei, P.; Kamphuis, J.; Hamilton, D. Physical experiments on the effects of groins on shore morphology. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; pp. 1782–1796. [Google Scholar]
- Copeland, G.J.M. A practical alternative to the “mild-slope” wave equation. Coast. Eng. 1985, 9, 125–149. [Google Scholar] [CrossRef]
- Watanabe, A.; Maruyama, K. Numerical modelling of nearshore wave field under combined refraction, diffraction and breaking. Coast. Eng. Japan 1986, 29, 19–39. [Google Scholar]
- Battjes, J.A. Modelling of turbulence in the surf zone. In Proceedings of the Symposium on Modelling Techniques, San Francisco, CA, USA, 3–5 September 1975; ASCE: San Francisco, CA, USA, 1975; pp. 1050–1061. [Google Scholar]
- Battjes, J.A.; Janssen, J.P.F.M. Energy loss and set-up due to breaking of random waves. In Proceedings of the 16th International Conference on Coastal Engineering, Hamburg, Germany, 27 August–3 September 1978; pp. 569–587. [Google Scholar]
- Larsen, J.; Dancy, H. Open boundaries in short wave simulations—A new approach. Coast. Eng. 1983, 7, 285–297. [Google Scholar] [CrossRef]
- Lee, C.; Suh, K.D. Internal generation of waves for time-dependent mild-slope equations. Coast. Eng. 1998, 34, 35–57. [Google Scholar] [CrossRef]
- Karambas, T.V.; Bowers, E.C. Representation of partial wave reflection and transmission for rubble mound coastal structures. WIT Trans. Ecol. Environ. 1996, 12, 415–423. [Google Scholar]
- Bruun, P. Design and Construction of Mounds for Breakwaters and Coastal Protection; Elsevier: Amsterdam, The Netherland, 1985; Volume 37. [Google Scholar]
- Kriezi, E.; Karambas, T. Modelling wave deformation due to submerged breakwaters. Marit. Eng. Proc. Inst. Civ. Eng. 2010, 163, 19–29. [Google Scholar] [CrossRef]
- Koutandos, E.V.; Karambas, T.V.; Koutitas, C.G. Floating breakwater response to waves action using a Boussinesq model coupled with a 2DV elliptic solver. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 243–255. [Google Scholar] [CrossRef]
- Copeland, G.J.M. Practical radiation stress calculations connected with equations of wave propagation. Coast. Eng. 1985, 9, 195–219. [Google Scholar] [CrossRef]
- Kobayashi, N.; Agarwal, A.; Johnson, B.D. Longshore current and sediment transport on beaches. J. Waterw. Port Coast. Ocean Eng. 2007, 133, 296–304. [Google Scholar] [CrossRef]
- Stive, M.J.F.; Wind, H.G. Cross-shore mean flow in the surf zone. Coast. Eng. 1986, 10, 325–340. [Google Scholar] [CrossRef]
- De Vriend, H.J.; Stive, M.J.F. Quasi-3D modelling of nearshore currents. Coast. Eng. 1987, 11, 565–601. [Google Scholar] [CrossRef]
- Baba, Y.; Camenen, B. Importance of the Swash Longshore Sediment Transport in Morphodynamic Models. In Proceedings of the Coastal Sediments ‘07 6th International Symposium on Coastal Engineering and Science of Coastal Sediment Process, Louisiana, LA, USA, 13–17 May 2007; Kraus, N.C., Rosati, J.D., Eds.; ASCE: San Francisco, CA, USA, 2012. [Google Scholar]
- Militello, A.; Reed, C.W.; Zundel, A.K.; Kraus, N.C. Two-Dimensional Depth-Averaged Circulation Model M2D: Version 2.0, Report 1, Technical Documentation and User’s Guide; ERDC/CHL TR-04-2; US Army Corps of Engineers, Engineering Research and Development Center: Vicksburg, MS, USA, 2004; p. 134. [Google Scholar]
- Camenen, B.; Larson, M. Phase-lag effects in sheet flow transport. Coast. Eng. 2006, 53, 531–542. [Google Scholar] [CrossRef]
- Isobe, M.; Horikawa, K. Study on water particle velocities of shoaling and breaking waves. Coast. Eng. Japan 1982, 25, 109–123. [Google Scholar]
- Kobayashi, N.; Tega, Y. Sand Suspension and Transport on Equilibrium Beach. J. Waterw. Port Coast. Ocean Eng. 2002, 128, 238–248. [Google Scholar] [CrossRef]
- Nam, P.T.; Larson, M.; Hanson, H.; Hoan, L.X. A numerical model of nearshore waves, currents, and sediment transport. Coast. Eng. 2009, 56, 1084–1096. [Google Scholar] [CrossRef]
- Larson, M.; Wamsley, T.V. A formula for longshore sediment transport in the swash. In Proceedings of the Coastal Sediments ‘07 6th International Symposium on Coastal Engineering and Science of Coastal Sediment Process, Louisiana, LA, USA, 13–17 May 2007; Kraus, N.C., Rosati, J.D., Eds.; ASCE: Reston, VA, USA, 2007; pp. 1924–1937. [Google Scholar]
- Leont’yev, I.O. Numerical modelling of beach erosion during storm event. Coast. Eng. 1996, 29, 187–200. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Physical Modeling. In Handbook of Coastal and Ocean Engineering; Herbich, J., Ed.; Gulf Publishing Company: Huston, TX, USA, 1991; Volume 2, pp. 1049–1066. [Google Scholar]
- Christopoulos, S. Coastal Protection Works of Paralia Katerinis; Technical Report; Municipality of Katerini: Katerini, Greece, 2014.
- Google Earth, Image ©2017 TerraMetrics, Data SIO, NOAA, U.S. Navy, NGA, GEBCO. 2017.

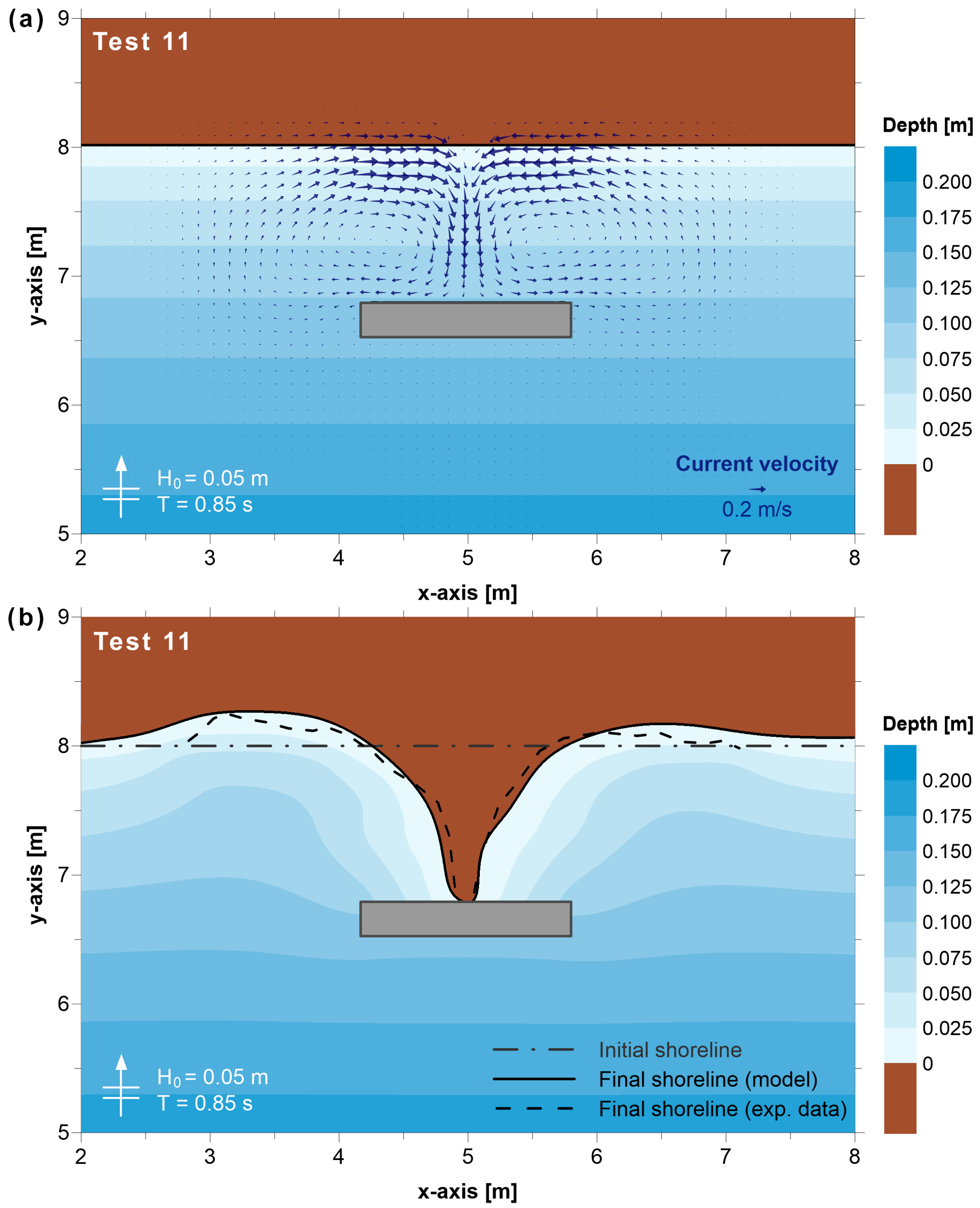
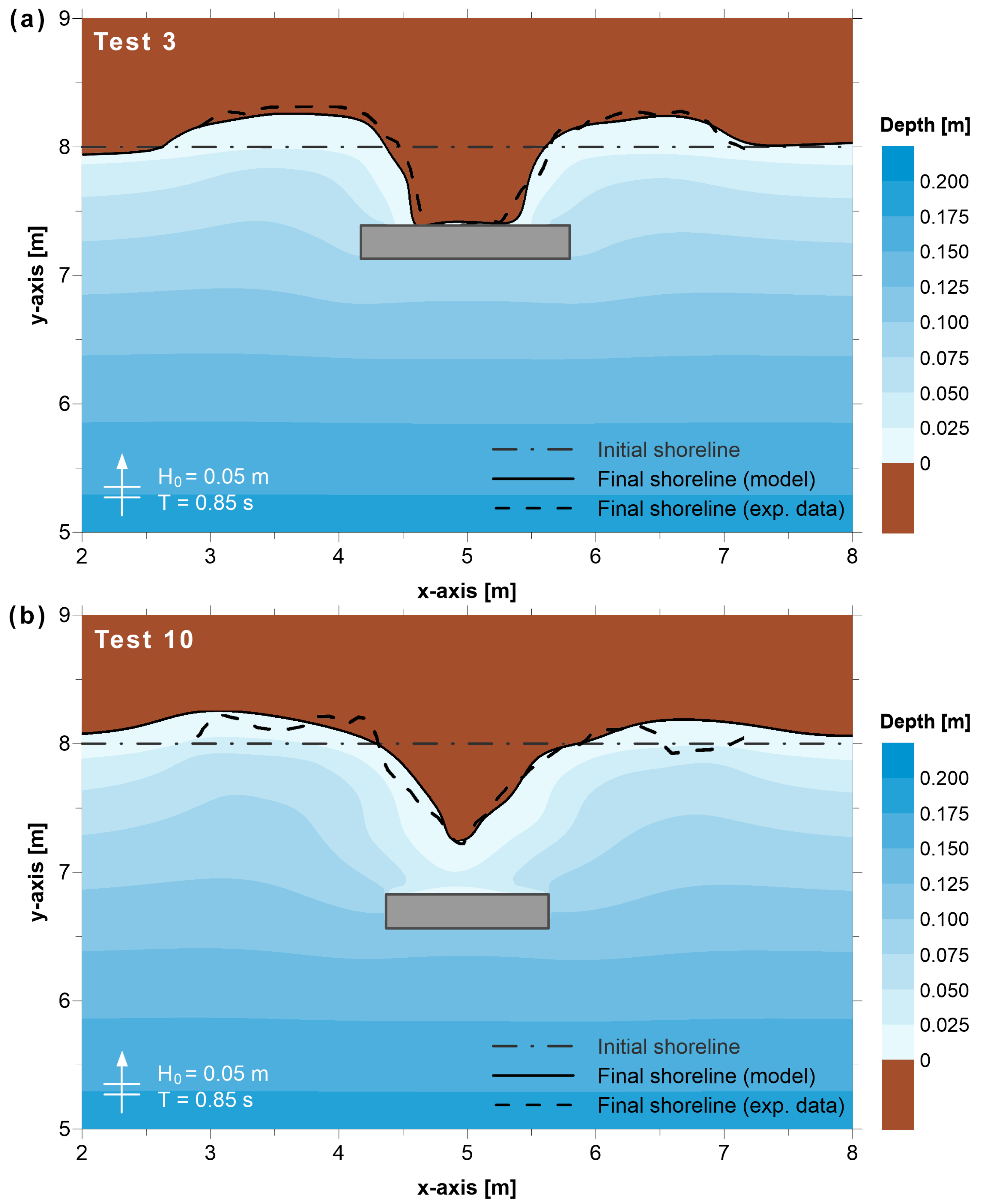
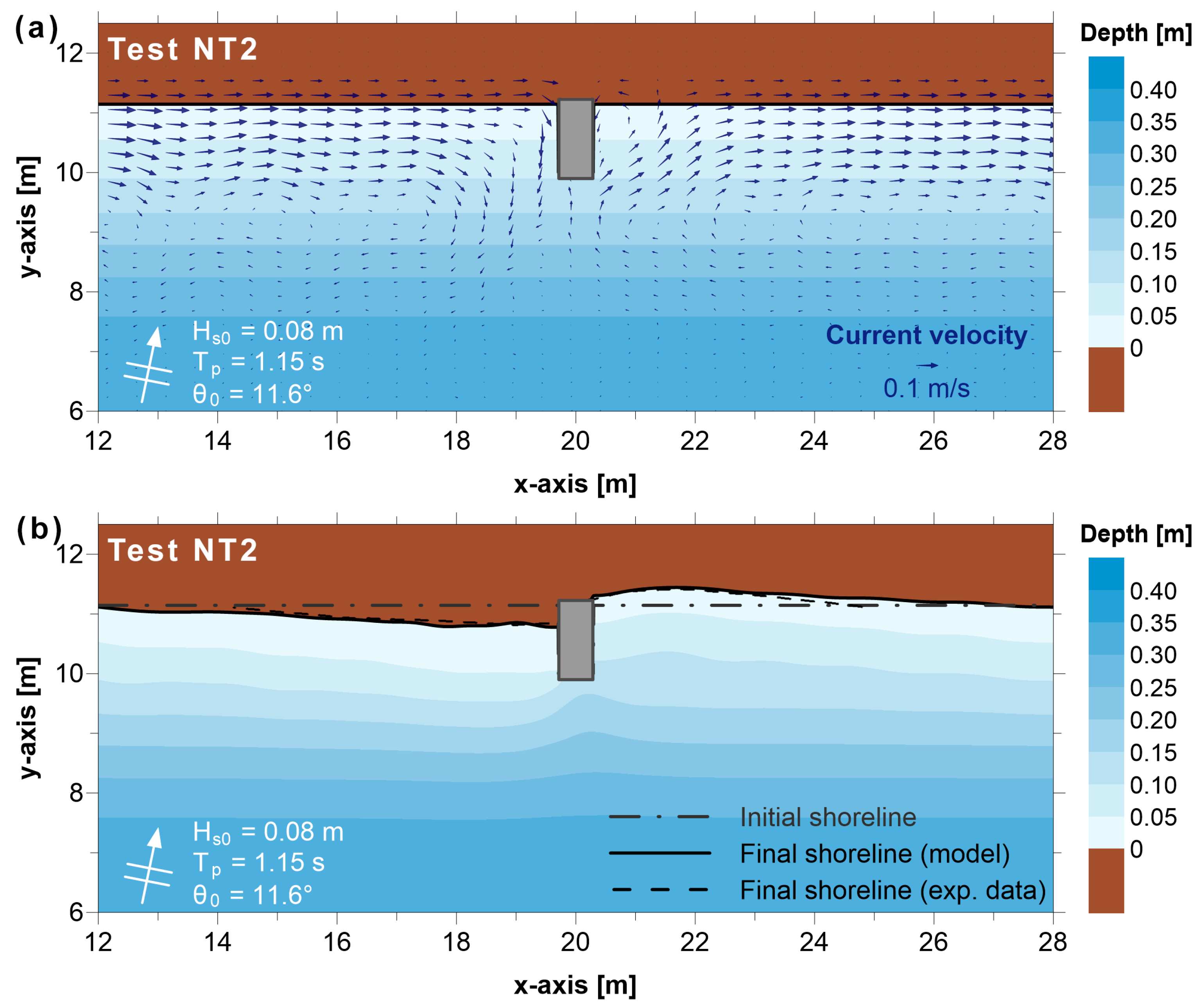
| Test | B = Breakwater Length (m) | X = Distance from the Initial Shoreline (m) | B/X | Formation of Salient/Tombolo |
|---|---|---|---|---|
| 3 | 1.5 | 0.6 | 2.50 | tombolo |
| 10 | 1.2 | 1.2 | 1.00 | salient |
| 11 | 1.5 | 1.2 | 1.25 | tombolo |
| Wave Direction | Significant Wave Height Hs (m) | Peak Wave Period Tp (s) | Annual Frequency of Occurence f (%) |
|---|---|---|---|
| SE-S | 1.34 | 5.4 | 12.70 |
| E | 1.09 | 4.4 | 1.12 |
| NE | 0.94 | 4.6 | 1.17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karambas, T.V.; Samaras, A.G. An Integrated Numerical Model for the Design of Coastal Protection Structures. J. Mar. Sci. Eng. 2017, 5, 50. https://doi.org/10.3390/jmse5040050
Karambas TV, Samaras AG. An Integrated Numerical Model for the Design of Coastal Protection Structures. Journal of Marine Science and Engineering. 2017; 5(4):50. https://doi.org/10.3390/jmse5040050
Chicago/Turabian StyleKarambas, Theophanis V., and Achilleas G. Samaras. 2017. "An Integrated Numerical Model for the Design of Coastal Protection Structures" Journal of Marine Science and Engineering 5, no. 4: 50. https://doi.org/10.3390/jmse5040050
APA StyleKarambas, T. V., & Samaras, A. G. (2017). An Integrated Numerical Model for the Design of Coastal Protection Structures. Journal of Marine Science and Engineering, 5(4), 50. https://doi.org/10.3390/jmse5040050






