Evaluating the Reliability of Counting Bacteria Using Epifluorescence Microscopy
Abstract
:1. Introduction
- To determine the total number of DAPI-stained bacterial cells from all countable fields of view using epifluorescence microscopy and to visually describe the spatial distribution of DAPI-stained bacterial cells on a glass slide.
- To test the accuracy and reliability of the values of the measures of central tendency, such as the arithmetic mean, median and harmonic mean, estimated by counting bacteria in randomly selected fields of view and using the bootstrapping technique to estimate variance.
- To determine the minimum number of random fields of view and the minimum number of bacterial cells that need to be selected and counted to obtain an arithmetic mean value for reliable estimation of the total bacterial number in a natural marine biofilm sample.
2. Materials and Methods
2.1. Biofilm Collection
2.2. Sample Preparation for Staining
2.3. Enumeration of Bacteria and Preparation of the Count Matrix
2.4. Data Analysis
2.4.1. Calculation of Measures of Central Tendency
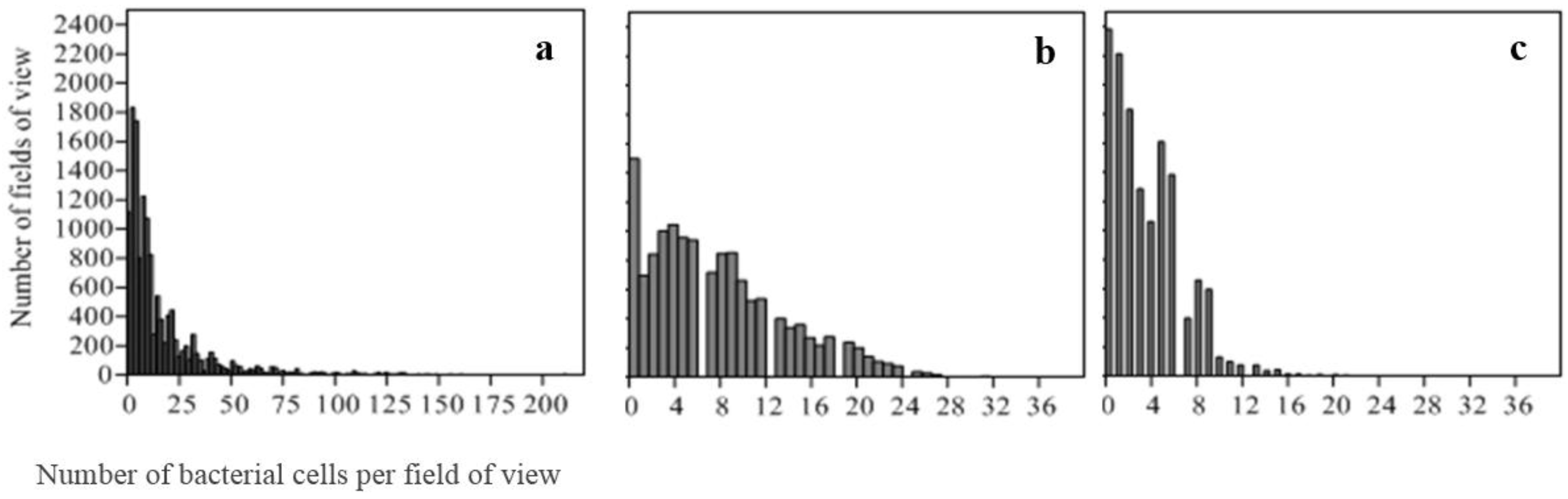
2.4.2. Distribution of Bacterial Counts
2.4.3. Bootstrapping
2.4.4. Assessing the Accuracy and Reliability of the Estimated Statistical Measures
3. Results
3.1. Measures of Central Tendency and Count Data Distribution
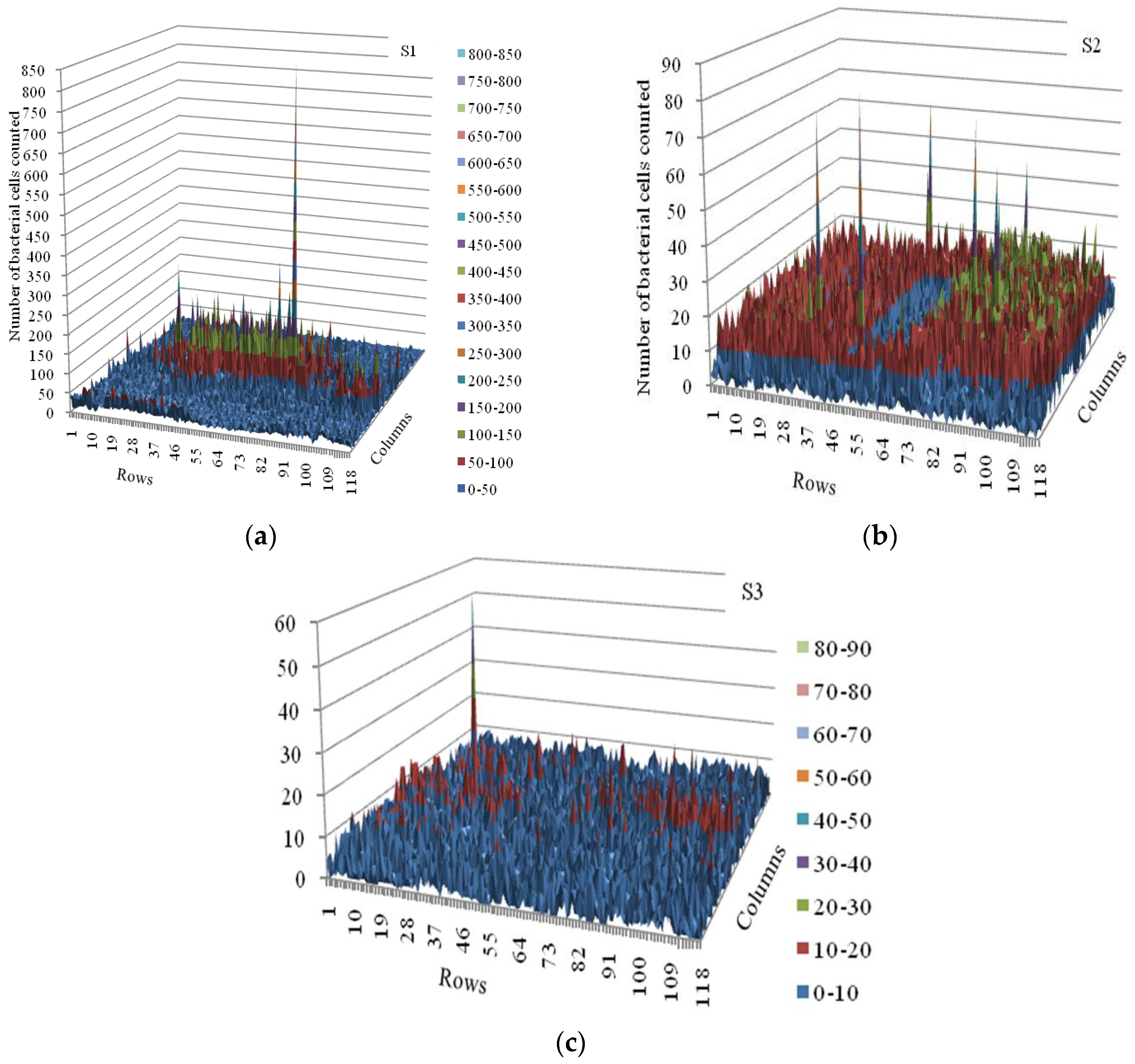
3.2. Spatial Distribution of Bacterial Counts
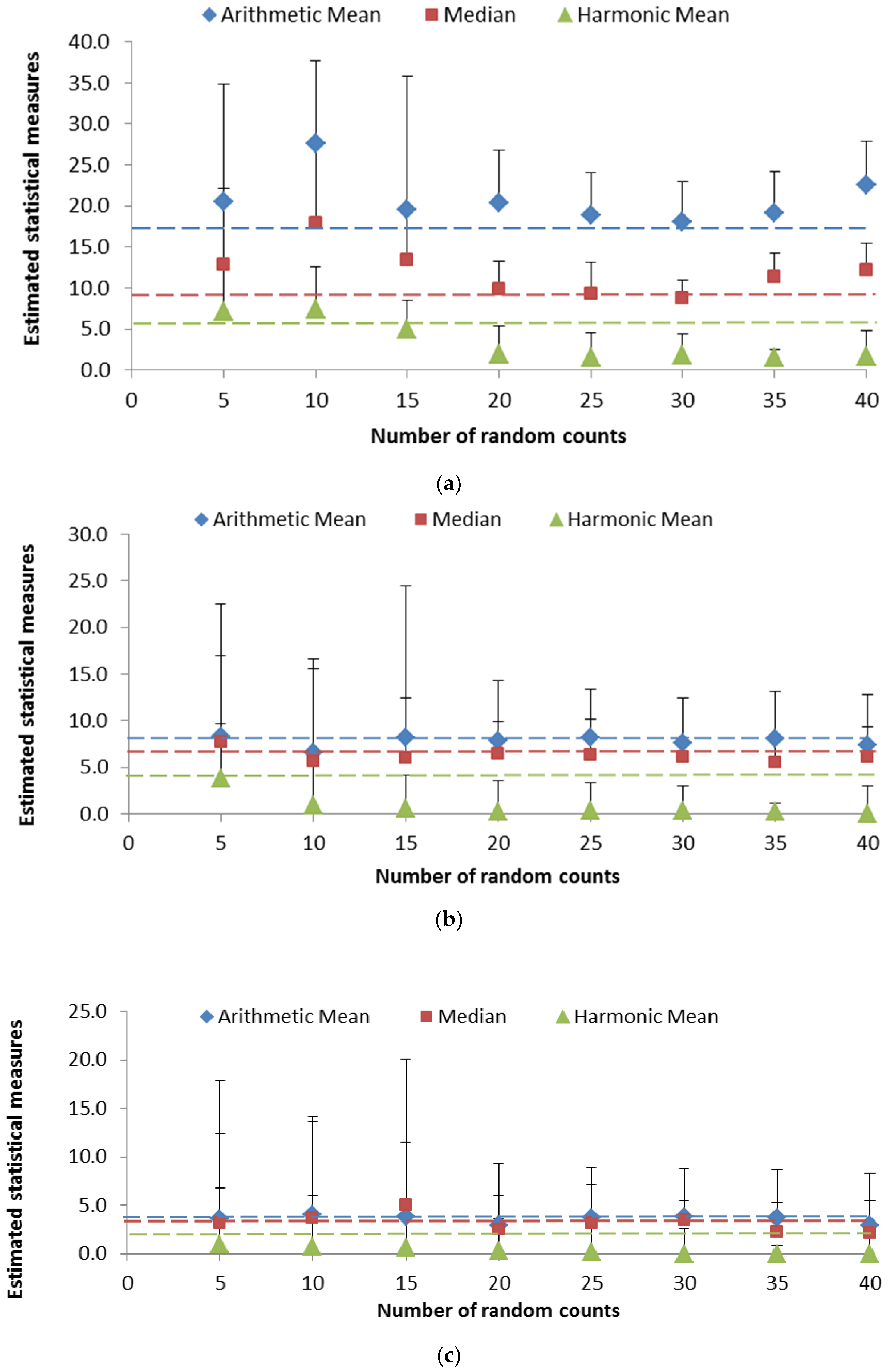
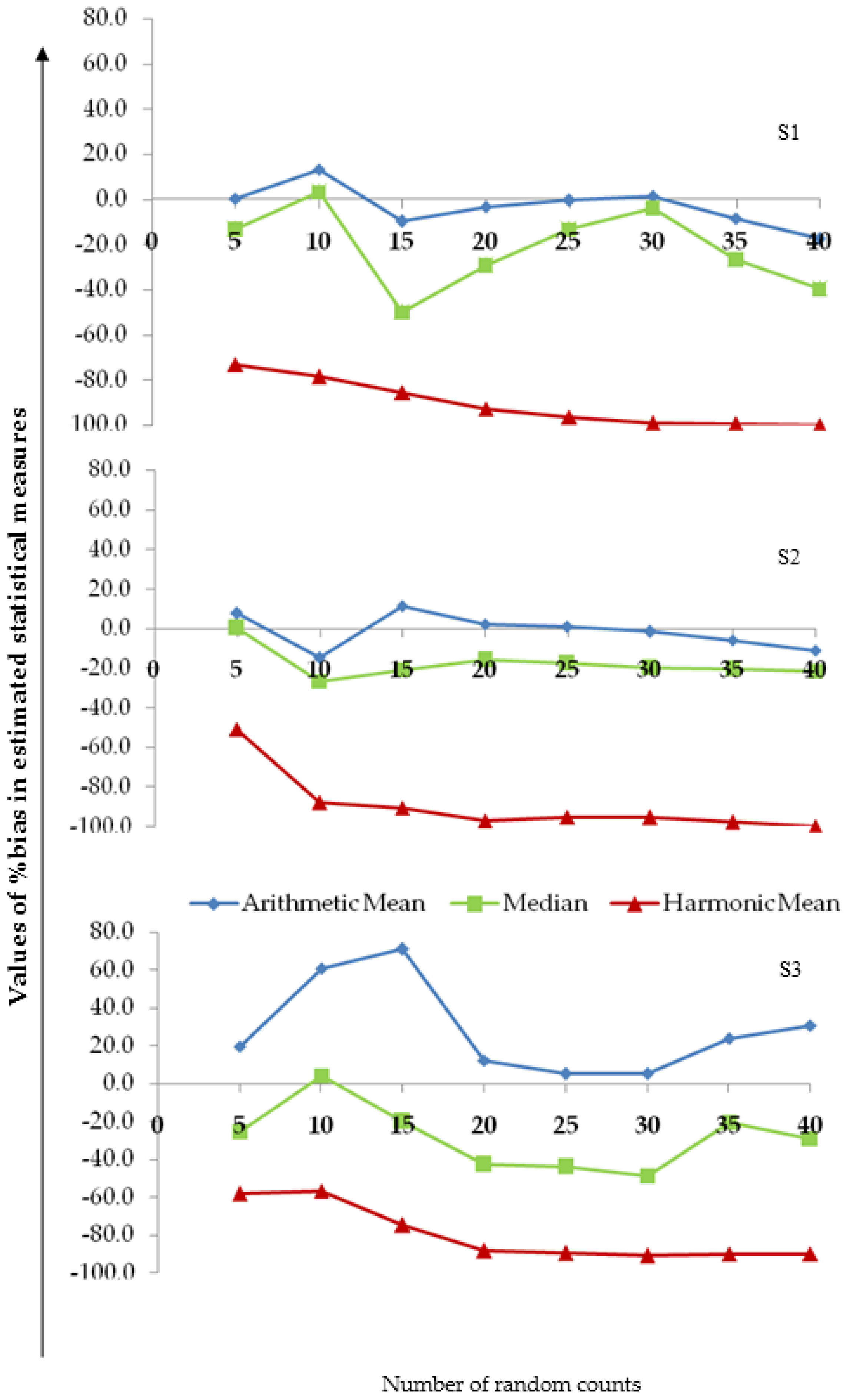
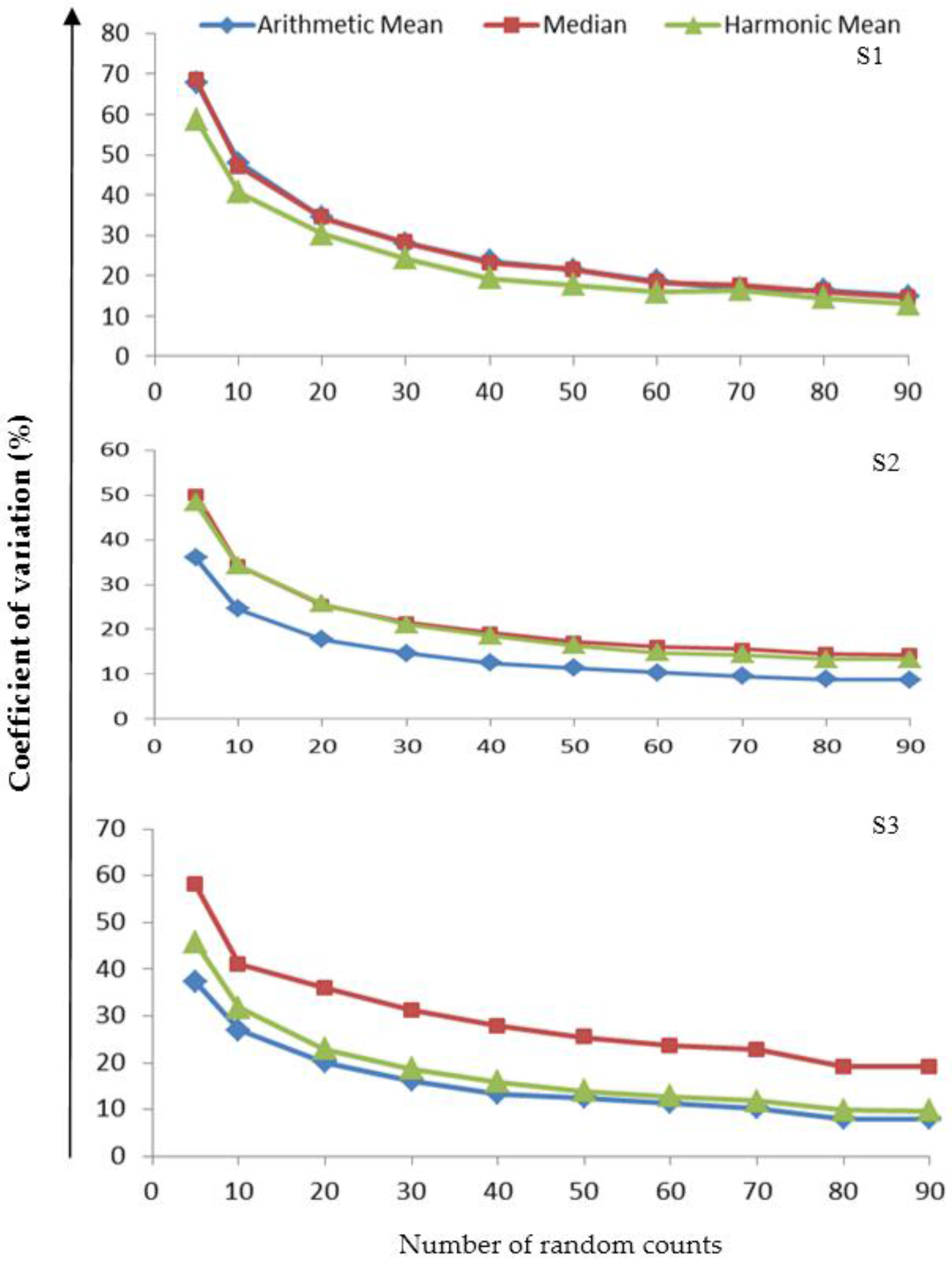
3.3. Variability in the Measures of Central Tendency
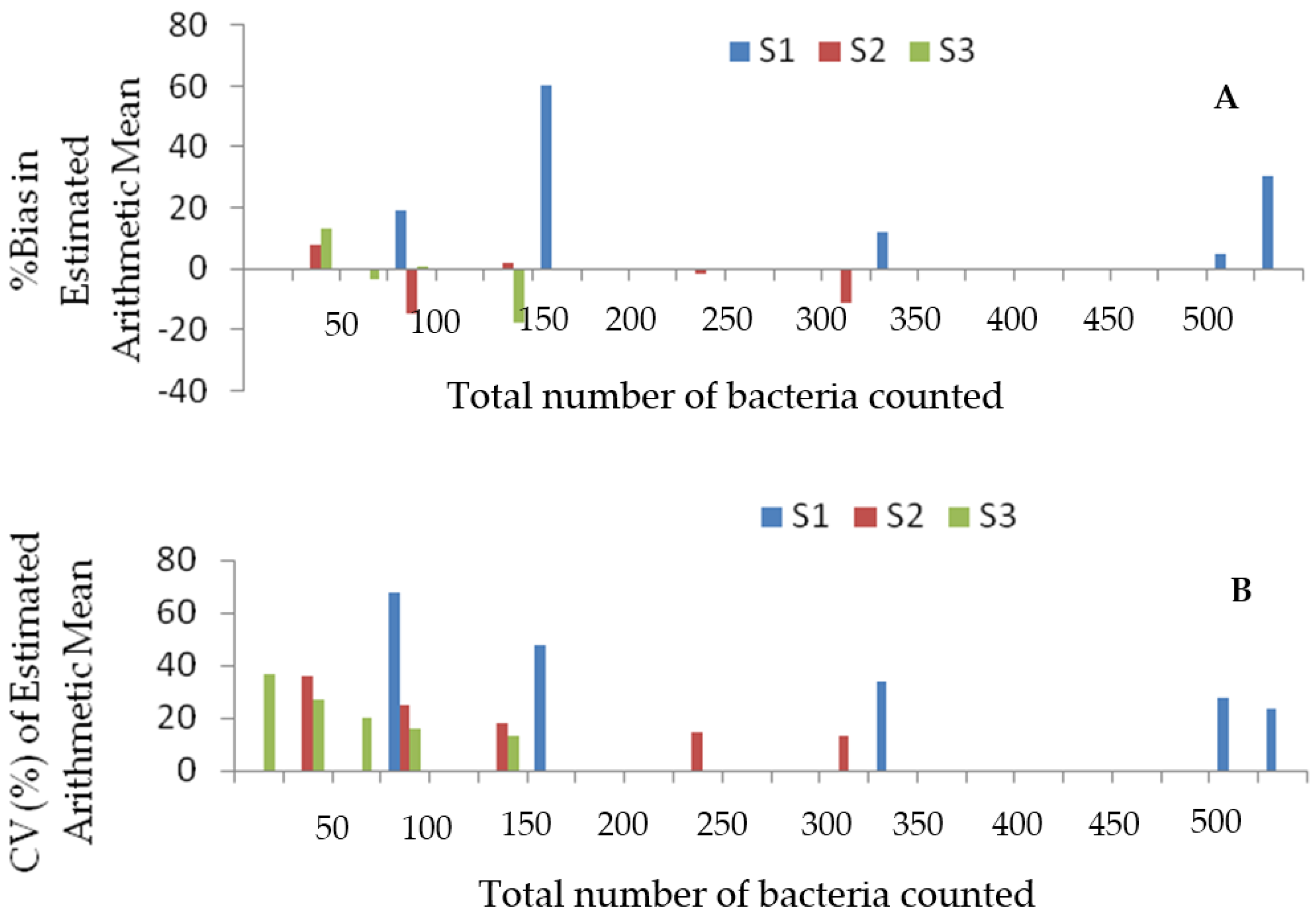
3.4. Assessing the Reliability of the Measures of Central Tendency
3.5. Assessment of the Photo-Fading Effect
4. Discussion
4.1. Distribution of Bacterial Counts
4.2. Accuracy and Reliability of the Arithmetic Mean
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Sample Types | Substrate Used for Counting * | Number of Randomly Selected Fields of View | Number of Bacteria per Field of View | Total Minimum Number of Bacteria per Sample | Reference |
|---|---|---|---|---|---|
| Laboratory culture | MS | 4 | Unknown | 100 | Matsunaga et al. [48] |
| Seawater | NMF | 5 | 50 to 150 | Unknown | DeLong et al. [68] |
| Natural biofilms | MS | 5 | Unknown | Unknown | Chiu et al. [49] |
| In-vitro cultured biofilm | PP | 5 | Unknown | Unknown | Chiu et al. [69] |
| In-vitro cultured biofilm | MW | 5 | Unknown | Unknown | Camps et al. [66] |
| In-vitro cultured biofilm | NMF | 5 | Unknown | Unknown | Nasrolahi et al. [63] |
| Laboratory culture | NMF | 8 to 20 | Unknown | Unknown | Yu et al. [55] |
| Agricultural field | NMF | 8 to 20 | Unknown | Unknown | Yu et al. [55] |
| Lake water | NMF | 10 | Unknown | 1000 | Porter & Feig [1] |
| Laboratory culture | NMF | 10 | Unknown | Unknown | Hicks et al. [50] |
| Aquaculture pond | NMF | 10 | Unknown | Unknown | Hicks et al. [50] |
| Artificial greenhouse pond | NMF | 10 | Unknown | Unknown | Hicks et al. [50] |
| Seawater | NMF | 10 | Unknown | 400 | Lovejoy et al. [51] |
| Drinking water | NMF | 10 | Unknown | 400 | McMath et al. [52] |
| Lake water | NMF | 10 to 20 | Unknown | 1500 | Glöckner et al. [56] |
| Seawater | NMF | 10 to 20 | Unknown | Unknown | Davidson et al. [59] |
| Seawater | NMF | 10 to 20 | Unknown | 400 | Lunau et al. [60] |
| Lake water | NMF | 10 | Unknown | Unknown | Berman et al. [70] |
| Lake water | NMF | 10 | Unknown | 200 | Søndergaard & Danielsen [71] |
| Marine sponge tissue extracts | NMF | 10 | Unknown | Unknown | Harder et al. [54] |
| Seawater | NMF | 10 | Unknown | Unknown | Grossart et al. [72] |
| Lake water | NMF | 10 | Unknown | Unknown | Kondo et al. [73] |
| Waste gas biofilter | NMF | ≥10 | Unknown | 1000 | Friedrich et al. [53] |
| Laboratory culture | NMF | 12 | Unknown | Unknown | Seo et al. [5] |
| Pond water | NMF | 12 | Unknown | Unknown | Seo et al. [5] |
| Natural biofilms | NMF | 12 | Unknown | Unknown | Seo et al. [5] |
| Lake water | NMF | 12 | Unknown | Unknown | Seo et al. [5] |
| Plant roots | NMF | 12 | Unknown | Unknown | Seo et al. [5] |
| Leaf litters | NMF | 12 | Unknown | Unknown | Seo et al. [5] |
| Sand | NMF | 15 | Unknown | 200 | Eppstein & Rossel [74] |
| Tidal sediments | NMF | 15 | Unknown | 200 | Yu et al. [55] |
| Laboratory culture | NMF | 18 | Unknown | Unknown | Monfort & Baleux [64] |
| Lake water | NMF | 18 | Unknown | Unknown | Monfort & Baleux [64] |
| Brackish water | NMF | 18 | Unknown | Unknown | Monfort & Baleux [64] |
| Laboratory culture | NMF | 20 | Unknown | Unknown | Mesa et al. [57] |
| Lake water | NMF | 20 | Unknown | 500 | Pinhassi & Berman [58] |
| Seawater | NMF | 20 | Unknown | 500 | Pinhassi & Berman [58] |
| Soil | NMF | 20 | Unknown | 1000 | Braun et al. [61] |
| Seawater | NMF | 20 | Unknown | 400 | Shibata et al. [62] |
| Natural biofilms | MS | 20 | Unknown | Unknown | Dobretsov et al. [14] |
| In-vitro cultured biofilm | NMF | 25 | Unknown | 1250 | Leroy et al. [75] |
| Seawater | NMF | 30 | Unknown | Unknown | Hassanshahian et al. [67] |
| Laboratory culture | NMF | 30 | Unknown | Unknown | Saby et al. [65] |
| River water | NMF | 30 | Unknown | Unknown | Saby et al. [65] |
| Drinking water | NMF | 30 | Unknown | Unknown | Saby et al. [65] |
| Seawater | NMF | ≥30 | 20 to 50 | 600 | Garabétian et al. [76] |
| Freshwater | NMF | ≥30 | 20 to 50 | 600 | Garabétian et al. [76] |
| Stream sediment | NMF | 34 | Unknown | Unknown | Diederichs et al. [77] |
| Laboratory culture | NMF | 50 | 20 to 40 | Unknown | Davidson et al. [59] |
| Whey | NMF | 50 | 20 to 40 | Unknown | Corich et al. [78] |
| Seawater | NMF | 260 | Unknown | Unknown | Sekar et al. [79] |
| Seawater | NMF | Unknown | 15 to 30 | Unknown | Sherr et al. [80] |
| Laboratory culture | NMF | Unknown | Unknown | 100 | Pace & Bailiff [81] |
| Wastewater | NMF | Unknown | Unknown | 100 | Garren & Azam [82] |
| Seawater | NMF | Unknown | Unknown | 100 | Garren & Azam [82] |
| Freshwater | NMF | Unknown | Unknown | 100 | Garren & Azam [82] |
| Seawater | NMF | Unknown | Unknown | 200 | Karner & Fuhrman [83] |
| Lake water | NMF | Unknown | Unknown | 400 | Alfreider et al. [84] |
| Seawater | NMF | Unknown | Unknown | 400 | Garneau et al. [85] |
| Laboratory culture | NMF | Unknown | Unknown | 1000 | Ogawa et al. [86] |
| River water | NMF | Unknown | Unknown | 1000 | Ogawa et al. [86] |
References
- Porter, K.G.; Feig, Y.S. The use of DAPI for identifying and counting aquatic microflora. Limnol. Oceanogr. 1980, 25, 943–948. [Google Scholar] [CrossRef]
- Kirchman, D.; Sigda, J.; Kapuscinski, R.; Mitchell, R. Statistical analysis of the direct count method for enumerating bacteria. Appl. Environ. Microb. 1982, 44, 376–382. [Google Scholar]
- Montagna, P.A. Sampling design and enumeration statistics for bacteria extracted from marine sediments. Appl. Environ. Microb. 1982, 43, 1366–1372. [Google Scholar]
- Kepner, R.L.; Pratt, J.R. Use of fluorochromes for direct enumeration of total bacteria in environmental samples: Past and present. Microbiol. Rev. 1994, 58, 603–615. [Google Scholar] [PubMed]
- Seo, E.Y.; Ahn, T.S.; Zo, Y.G. Agreement, precision, and accuracy of epifluorescence microscopy methods for enumeration of total bacterial numbers. Appl. Environ. Microb. 2010, 76, 1981–1991. [Google Scholar] [CrossRef] [PubMed]
- Dobretsov, S.; Thomason, J.C. The development of marine biofilms on two commercial non-biocidal coatings: A comparison between silicone and fluoropolymer technologies. Biofouling 2011, 27, 869–880. [Google Scholar] [CrossRef] [PubMed]
- Dobretsov, S.; Abed, R.M.M. Microscopy of biofilms. In Biofouling Methods, 1st ed.; Dobretsov, S., Thomason, J.C., Williams, D.N., Eds.; John Wiley & Sons Ltd: Oxford, UK, 2014; pp. 3–9. [Google Scholar]
- Cassé, F.; Swain, G.W. The development of microfouling on four commercial antifouling coatings under static and dynamic immersion. Int. Biodeter. Biodegr. 2006, 57, 179–185. [Google Scholar] [CrossRef]
- Mitbavkar, S.; Anil, A.C. Seasonal variations in the fouling diatom community structure from a monsoon influenced tropical estuary. Biofouling 2008, 24, 415–426. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, E.; Bonnet, C.; Lemarchand, K. Biofouling growth in cold estuarine waters and evaluation of some chitosan and copper anti-fouling paints. Int. J. Mol. Sci. 2009, 10, 3209–3223. [Google Scholar] [CrossRef] [PubMed]
- Briand, J.F.; Djeridia, I.; Jamet, D.; Coupe, S.; Bressy, C.; Molmeret, M.; le Berre, B.; Rimet, F.; Bouchez, A.; Blach, Y. Pioneer marine biofilms on artificial surfaces including antifouling coatings immersed in two contrasting French Mediterranean coast sites. Biofouling 2012, 28, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Camps, M.; Barani, A.; Gregori, G.; Bouchez, A.; le Berre, B.; Bressy, C.; Blache, Y.; Briand, J.F. Antifouling coatings influence both abundance and community structure of colonizing biofilms: A case study in the Northwestern Mediterranean sea. Appl. Environ. Microbiol. 2014, 80, 4821–4831. [Google Scholar] [CrossRef] [PubMed]
- Molino, P.J.; Childs, S.; Eason Hubbard, M.R.; Carey, J.M.; Burgman, M.A.; Wetherbee, R. Development of the primary bacterial microfouling layer on antifouling and fouling release coatings in temperate and tropical environments in Eastern Australia. Biofouling 2009, 25, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Dobretsov, S.; Abed, R.M.M.; Voolstra, C.R. The effect of surface colour on the formation of marine micro- and macrofouling communities. Biofouling 2013, 29, 617–627. [Google Scholar] [CrossRef] [PubMed]
- ZoBell, C.E. Marine Microbiology: A Monograph on Hydrobacteriology; Chronica Botanica Co.: Waltham, MA, USA, 1946. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research, 1st ed.; W.H. Freeman and Company: San Francisco, CA, USA, 1969; pp. 222–223. [Google Scholar]
- Lisle, J.T.; Hamilton, M.A.; Willse, A.R.; McFeters, G.A. Comparison of fluorescence microscopy and solid-phase cytometry methods for counting bacteria in water. Appl. Environ. Microbiol. 2004, 70, 5343–5348. [Google Scholar] [CrossRef] [PubMed]
- Chae, G.T.; Stimsonb, J.; Emelkoc, M.B.; Blowesb, D.W.; Ptacekb, C.J.; Mesquitac, M.M. Statistical assessment of the accuracy and precision of bacteria- and virus-sized microsphere enumerations by epifluorescence microscopy. Water Res. 2008, 42, 1431–1440. [Google Scholar] [CrossRef] [PubMed]
- Engelbart, D.C. Augmenting Human Intellect: A Conceptual Framework; Summary Report AFOSR-3223 under Contract AF 49 (638)-1024, SRI Project 3578 for Air Force Office of Scientific Research; Stanford Research Institute: Menlo Park, CA, USA, 1962. [Google Scholar]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1986, 54–75. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap, 1st ed.; Chapman & Hall: New York, NY, USA, 1993; pp. 10–391. [Google Scholar]
- Picard, N.; Chagneau, P.; Mortier, F.; Bar-Hen, A. Finding confidence limits on population growth rates: Bootstrap and analytic methods. Math. Biosci. 2009, 219, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Calmette, G.; Drummond, G.B.; Vowler, S.L. Making do with what we have: use your bootstraps. Adv. Physiol. Educ. 2012, 36, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Hall, P.; Park, B.U.; Samworth, R.J. Choice of neighbor order in nearest-neighbor classification. Ann. Stat. 2008, 36, 2135–2152. [Google Scholar] [CrossRef]
- Busschaert, P.; Geeraerd, A.H.; Uyttendaele, M.; van Impe, J.F. Estimating distributions out of qualitative and (semi) quantitative microbiological contamination data for use in risk assessment. Int. J. Food Microbiol. 2010, 138, 260–269. [Google Scholar] [CrossRef] [PubMed]
- Muthukrishnan, T.; Abed, R.M.M.; Dobretsov, S.; Kidd, B.; Finnie, A.A. Long-Term Microfouling on Commercial Biocidal Fouling Control Coatings. Biofouling 2014, 30, 1155–1164. [Google Scholar] [CrossRef] [PubMed]
- Martin, G.R.; Ruhl, K.J. Regionalization of harmonic-mean streamflows in Kentucky. US Geological Survey: Reston, VA, USA, 1993. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Jongenburger, I.; Reij, M.W.; Boer, E.P.J.; Zwietering, M.H.; Gorris, L.G.M. Modelling homogeneous and heterogeneous microbial contaminations in a powdered food product. Int. J. Food Microbiol. 2012, 157, 35–44. [Google Scholar] [CrossRef] [PubMed]
- Alexander, N. Review: analysis of parasite and other skewed counts. Trop Med. Int. Health 2012, 17, 684–693. [Google Scholar] [CrossRef] [PubMed]
- Hood, G.M. PopTools version 3.2.5. Available online: http://www.poptools.org (accessed on 25 May 2012).
- Baranyi, J.; Pin, C.; Ross, T. Validating and comparing predictive models. Int. J. Food Microbiol. 1999, 48, 159–166. [Google Scholar] [CrossRef]
- Lund, J.W.G.; Kipling, C.; le Cren, E.S. The inverted microscope method of estimating algal numbers and the statistical basis of estimations by counting. Hydrobiologia 1958, 11, 143–170. [Google Scholar] [CrossRef]
- Venrick, E.L. The statistics of subsampling. Limnol. Oceanogr. 1971, 16, 811–818. [Google Scholar] [CrossRef]
- Ashby, R.E.; Rhodes-Roberts, M.E. The use of analysis of variance to examine the variations between samples of marine bacterial populations. J. Appl. Bacteriol. 1976, 41, 439–451. [Google Scholar] [CrossRef] [PubMed]
- Kaper, J.B.; Mills, A.L.; Colwell, R.R. Evaluation of the accuracy and precision of enumerating aerobic heterotrophs in water samples by the spread plate method. Appl. Environ. Microbiol. 1978, 35, 756–761. [Google Scholar] [PubMed]
- Palmer, F.E.; Methot, R.D., Jr.; Staley, J.T. Patchiness in the distribution of planktonic heterotrophic bacteria in lakes. Appl. Environ. Microbiol. 1976, 31, 1003–1005. [Google Scholar] [PubMed]
- Fletcher, M. The question of passive versus active attachment mechanisms in non-specific bactterial adhesion. In Microbial Adhesion to Surfaces; Berkeley, R.C.W., Lynch, J.M., Melling, J., Rutter, P.R., Vincent, B., Eds.; Ellis Horwood Ltd.: Chichester, UK, 1980; pp. 197–210. [Google Scholar]
- Marshall, K.C. Mechanism of adhesion of marine bacteria to surfaces. In Proceedings of the Third International Congress on Marine Corrosion and Fouling, Gaithersburg, MD, USA, 2–7 October 1972; Acker, R.F., Brown, B.F., DePalma, J.R., Iverson, W.P., Eds.; National Bureau of Standards Special Publication: Gaithersburg, MD, USA, 1973; pp. 625–634. [Google Scholar]
- Fletcher, M.; Floodgate, G.D. An electron-microscopic demonstration of an acidic polysaccharide involved in the adhesion of a marine bacterium to solid surfaces. J. Gen. Microbiol. 1973, 74, 325–334. [Google Scholar] [CrossRef]
- Costerton, J.W.; Geesey, G.G.; Cheng, K.J. How bacteria stick. Sci. Am. 1978, 238, 86–95. [Google Scholar] [CrossRef] [PubMed]
- Velji, M.; Albright, L. The dispersion of adhered marine bacteria by pyrophosphate and ultrasound prior to direct counting. In Proceedings of the 2nd Colloque International de Bacteriologie Marine, Brest, France, 1–5 October 1984; pp. 1–5.
- Schijven, J.F.; Hassanizadeh, S.M. Removal of viruses by soil passage: Overview of modeling, processes and parameters. Crit. Rev. Env. Sci. Tech. 2000, 30, 49–127. [Google Scholar] [CrossRef]
- Saiers, J.E.; Lenhart, J.J. Colloid mobilization and transport within unsaturated porous media under transient-flow conditions. Water Resour. Res. 2003, 39, 1019. [Google Scholar] [CrossRef]
- Bell, W.; Mitchell, R. Chemotactic and growth responses of marine bacteria to algal extracellular products. Biol. Bull. 1972, 143, 265–277. [Google Scholar] [CrossRef]
- Azam, F.; Ammerman, J.W. Growth of free-living marine bacteria around sources of dissolved organic matter. EOS Trans. Am. Geophys. Union 1982, 63, 54. [Google Scholar]
- Matsunaga, T.; Tomoda, R.; Nakajima, T.; Wake, H. Photoelectrochemical sterilization of microbial cells by semiconductor powders. FEMS Microbiol. Lett. 1985, 29, 211–214. [Google Scholar] [CrossRef]
- Chiu, C.H.; Lu, T.Y.; Tseng, Y.Y.; Pan, T.M. The effects of Lactobacillus-fermented milk on lipid metabolism in hamsters fed on high-cholesterol diet. Appl. Microbiol. Biot. 2006, 71, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Hicks, R.E.; Amann, R.I.; Stahl, D.A. Dual staining of natural bacterioplankton with 4′,6-diamidino-2-phenylindole and fluorescent oligonucleotide probes targeting kingdom-level 16s rRNA sequences. Appl. Environ. Microbiol. 1992, 58, 2158–2163. [Google Scholar] [PubMed]
- Lovejoy, C.; Legendre, L.; Klein, B.; Tremblay, J.; Ingram, R.; Therriault, J. Bacterial Activity during Early Winter Mixing (Gulf of St. Lawrence, Canada). Aquat. Microb. Ecol. 1996, 10, 1–13. [Google Scholar] [CrossRef]
- Mcmath, S.M.; Sumpter, C.; Holt, D.M.; Delanoue, A.; Chamberlain, A.H.L. The Fate of Environmental Coliforms in a Model Water Distribution System. Lett. Appl. Microbiol. 1999, 28, 93–97. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, U.; Langenhove, H.V.; Altendorf, K.; Lipski, A. Microbial Community and Physicochemical Analysis of an Industrial Waste Gas Biofilter and Design of 16S RRNA-Targeting Oligonucleotide Probes. Environ. Microbiol. 2003, 5, 439. [Google Scholar] [CrossRef]
- Harder, T.; Lau, S.C.K.; Tam, W.-Y.; Qian, P.-Y. A Bacterial Culture-Independent Method to Investigate Chemically Mediated Control of Bacterial Epibiosis in Marine Invertebrates by Using TRFLP Analysis and Natural Bacterial Populations. FEMS Microbiol. Ecol. 2004, 47, 93–99. [Google Scholar] [CrossRef]
- Yu, W.; Dodds, W.K.; Banks, M.K.; Skalsky, J.; Strauss, E.A. Optimal staining and sample storage time for direct microscopic enumeration of total and active bacteria in soil with two fluorescent dyes. Appl. Environ. Microbiol. 1995, 61, 3367–3372. [Google Scholar] [PubMed]
- Glöckner, F.O.; Fuchs, B.M.; Amann, R. Bacterioplankton compositions of lakes and oceans: A first comparison based on fluorescence in situ hybridization. Appl. Environ. Microbiol. 1999, 65, 3721–3726. [Google Scholar] [PubMed]
- Mesa, M.M.; Macías, M.; Cantero, D.; Barja, F. Use of the direct epifluorescent filter technique for the enumeration of viable and total acetic acid bacteria from vinegar fermentation. J. Fluoresc. 2003, 13, 261–265. [Google Scholar] [CrossRef]
- Pinhassi, J.; Berman, T. Differential growth response of colony-forming α-and γ-proteobacteria in dilution culture and nutrient addition experiments from Lake Kinneret (Israel), the Eastern Mediterranean Sea, and the Gulf of Eilat. Appl. Environ. Microbiol. 2003, 69, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Davidson, P.M.; Roth, L.A.; Gambrel-Lenarz, S.A. Coliform and other indicator bacteria. In Standard Methods for the Examination of Dairy Products, 17th ed.; Wehr, H.M., Frank, J.F., Eds.; American Public Health Association: Washington, DC, USA, 2004; pp. 187–226. [Google Scholar]
- Lunau, M.; Lemke, A.; Walther, K.; Martens-Habbena, W.; Simon, M. An improved method for counting bacteria from sediments and turbid environments by epifluorescence microscopy. Environ. Microbiol. 2005, 7, 961–968. [Google Scholar] [CrossRef] [PubMed]
- Braun, B.; Böckelmann, U.; Grohmann, E.; Szewzyk, U. Polyphasic characterization of the bacterial community in an urban soil profile with in situ and culture-dependent methods. Appl. Soil Ecol. 2006, 31, 267–279. [Google Scholar] [CrossRef]
- Shibata, A.; Goto, Y.; Saito, H.; Kikuchi, T.; Toda, T.; Taguchi, S. Comparison of SYBR Green I and SYBR Gold stains for enumerating bacteria and viruses by epifluorescence microscopy. Aquat. Microb. Ecol. 2006, 43, 221–231. [Google Scholar] [CrossRef]
- Nasrolahi, A.; Stratil, S.B.; Jacob, K.J.; Wahl, M. A Protective Coat of Microorganisms on Macroalgae: Inhibitory Effects of Bacterial Biofilms and Epibiotic Microbial Assemblages on Barnacle Attachment. FEMS Microbiol. Ecol. 2012, 81, 583–595. [Google Scholar] [CrossRef] [PubMed]
- Monfort, P.; Baleux, B. Comparison of Flow Cytometry and Epifluorescence Microscopy for Counting Bacteria in Aquatic Ecosystems. Cytometry 1992, 13, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Saby, S.; Sibille, I.; Mathieu, L.; Paquin, J.L.; Block, J.C. Influence of water chlorination on the counting of bacteria with DAPI (4′,6-diamidino-2-phenylindole). Appl. Environ. Microbiol. 1997, 63, 1564–1569. [Google Scholar] [PubMed]
- Camps, M.; Briand, J.-F.; Guentas-Dombrowsky, L.; Culioli, G.; Bazire, A.; Blache, Y. Antifouling Activity of Commercial Biocides vs. Natural and Natural-Derived Products Assessed by Marine Bacteria Adhesion Bioassay. Mar. Poll Bull. 2011, 62, 1032–1040. [Google Scholar] [CrossRef] [PubMed]
- Hassanshahian, M.; Emtiazi, G.; Caruso, G.; Cappello, S. Bioremediation (Bioaugmentation/Biostimulation) Trials of Oil Polluted Seawater: A Mesocosm Simulation Study. Mar. Environ. Res. 2014, 95, 28–38. [Google Scholar] [CrossRef] [PubMed]
- DeLong, E.F.; Taylor, L.T.; Marsh, T.J.; Preston, C.M. Visualization and enumeration of marine planktonic archaea and bacteria by using polyribonucleotide probes and fluorescent in situ hybridization. Appl. Environ. Microbiol. 1999, 65, 5554–5563. [Google Scholar] [PubMed]
- Chiu, J.M.-Y.; Thiyagarajan, V.; Pechenik, J.A.; Hung, O.-S.; Qian, P.-Y. Influence of Bacteria and Diatoms in Biofilms on Metamorphosis of the Marine Slipper Limpet Crepidula Onyx. Mar. Biol. 2007, 151, 1417–1431. [Google Scholar] [CrossRef]
- Berman, T.; Kaplan, B.; Chava, S.; Viner, Y.; Sherr, B.; Sherr, E. Metabolically Active Bacteria in Lake Kinneret. Aquat. Microb. Ecol. 2001, 23, 213–224. [Google Scholar] [CrossRef]
- Sondergaard, M. Active Bacteria (CTC) in Temperate Lakes: Temporal and Cross-System Variations. J. Plankton Res. 2001, 23, 1195–1206. [Google Scholar] [CrossRef]
- Grossart, H.-P.; Levold, F.; Allgaier, M.; Simon, M.; Brinkhoff, T. Marine Diatom Species Harbour Distinct Bacterial Communities. Environ. Microbiol. 2005, 7, 860–873. [Google Scholar] [CrossRef] [PubMed]
- Kondo, R.; Osawa, K.; Mochizuki, L.; Fujioka, Y.; Butani, J. Abundance and Diversity of Sulphate-Reducing Bacterioplankton in Lake Suigetsu, a Meromictic Lake in Fukui, Japan. Plankton Benthos Res. 2006, 1, 165–177. [Google Scholar] [CrossRef]
- Epstein, S.; Rossel, J. Enumeration of Sandy Sediment Bacteria: Search for Optimal Protocol. Mar. Ecol. Prog. Ser. 1995, 117, 289–298. [Google Scholar] [CrossRef]
- Leroy, C.; Delbarre-Ladrat, C.; Ghillebaert, F.; Rochet, M.; Compère, C.; Combes, D. A Marine Bacterial Adhesion Microplate Test Using the DAPI Fluorescent Dye: a New Method to Screen Antifouling Agents. Lett. Appl. Microbiol. 2007, 44, 372–378. [Google Scholar] [CrossRef] [PubMed]
- Garabétian, F.; Petit, M.; Lavandier, P. Does Storage Affect Epifluorescence Microscopic Counts of Total Bacteria in Freshwater Samples? Comptes Rendus Acad. Sci. Ser. III Sci. Vie 1999, 322, 779–784. [Google Scholar] [CrossRef]
- Diederichs, S.; Beardsley, C.; Cleven, E.-J. Detection of Ingested Bacteria in Benthic Ciliates Using Fluorescence In Situ Hybridization. Syst. Appl. Microbiol. 2003, 26, 624–630. [Google Scholar] [CrossRef] [PubMed]
- Corich, V.; Soldati, E.; Giacomini, A. Optimization of fluorescence microscopy techniques for the detection of total and viable lactic acid bacteria in whey starter cultures. Ann. Microbiol 2004, 54, 335–342. [Google Scholar]
- Sekar, R.; Deines, P.; Machell, J.; Osborn, A.; Biggs, C.; Boxall, J. Bacterial Water Quality and Network Hydraulic Characteristics: a Field Study of a Small, Looped Water Distribution System Using Culture-Independent Molecular Methods. J. Appl. Microbiol. 2012, 112, 1220–1234. [Google Scholar] [CrossRef] [PubMed]
- Sherr, E.; Sherr, B.; Sigmon, C. Activity of Marine Bacteria under Incubated and in Situ Conditions. Aquat. Microb. Ecol. 1999, 20, 213–223. [Google Scholar] [CrossRef]
- Pace, M.; Bailiff, M. Evaluation of a Fluorescent Microsphere Technique for Measuring Grazing Rates of Phagotrophic Microorganisms. Mar. Ecol. Prog. Ser. 1987, 40, 185–193. [Google Scholar] [CrossRef]
- Garren, M.; Azam, F. New Method for Counting Bacteria Associated with Coral Mucus. Appl. Environ. Microbiol. 2010, 76, 6128–6133. [Google Scholar] [CrossRef] [PubMed]
- Karner, M.; Fuhrman, J.A. Determination of active marine bacterioplankton: a comparison of universal 16S rRNA probes, autoradiography, and nucleoid staining. Appl. Environ. Microbiol. 1997, 63, 1208–1213. [Google Scholar] [PubMed]
- Alfreider, A.; Pernthaler, J.; Amann, R.; Sattler, B.; Glockner, F.; Wille, A.; Psenner, R. Community analysis of the bacterial assemblages in the winter cover and pelagic layers of a high mountain lake by in situ hybridization. Appl. Environ. Microbiol. 1996, 62, 2138–2144. [Google Scholar] [PubMed]
- Garneau, M.-È.; Vincent, W.F.; Terrado, R.; Lovejoy, C. Importance of Particle-Associated Bacterial Heterotrophy in a Coastal Arctic Ecosystem. J. Marine Syst. 2009, 75, 185–197. [Google Scholar] [CrossRef]
- Ogawa, M.; Tani, K.; Yamaguchi, N.; Nasu, M. Development of Multicolour Digital Image Analysis System to Enumerate Actively Respiring Bacteria in Natural River Water. J. Appl. Microbiol. 2003, 95, 120–128. [Google Scholar] [CrossRef] [PubMed]
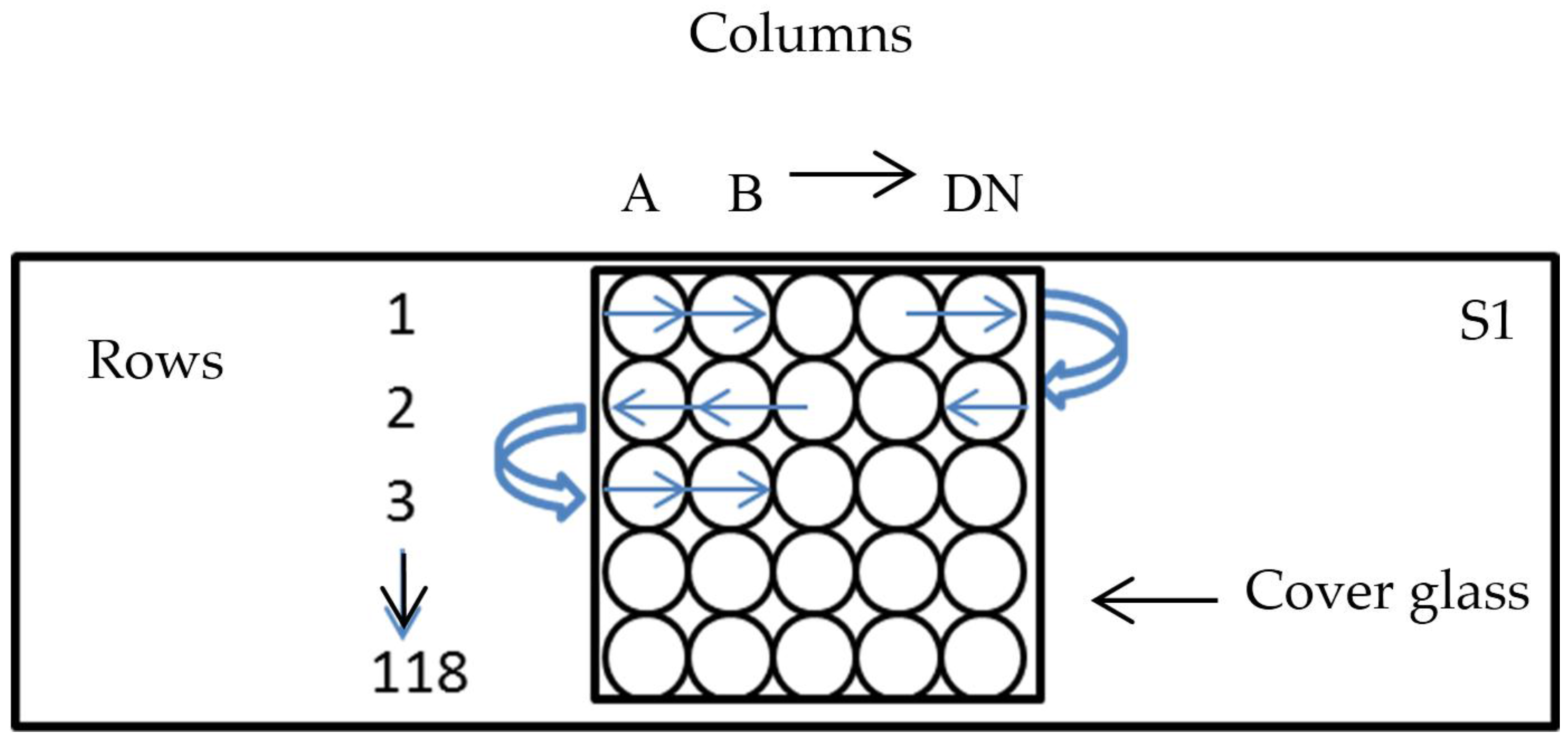

| Sample | Sample Preparation | Total Volume (µL) of Sample on Glass Slide | Total Volume (µL) of DAPI Solution Added | Total Volume (µL) of Stained Sample Counted | ||
|---|---|---|---|---|---|---|
| Volume (µL) of Biofilm Suspension | Volume (µL) of Sterile Nuclease-Free Water | Total Volume (µL) of Sample in Eppendorf Tube | ||||
| S1 | 100 | 0 | 100 | 3 | 6 | 9 |
| S2 | 1 (from S1) | 9 | 10 | 3 | 6 | 9 |
| S3 | 1 (from S2) | 9 | 10 | 3 | 6 | 9 |
| S4 * | 1 (from S1) | 9 | 10 | 3 | 6 | 9 |
| Sample * | Total No. of Bacterial Cells Counted | Arithmetic Mean | Median | Harmonic Mean |
|---|---|---|---|---|
| S1 | 240,005 | 17.24 | 9.00 | 5.34 |
| S2 | 107,188 | 7.70 | 6.00 | 4.12 |
| S3 | 50,087 | 3.60 | 3.00 | 2.07 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muthukrishnan, T.; Govender, A.; Dobretsov, S.; Abed, R.M.M. Evaluating the Reliability of Counting Bacteria Using Epifluorescence Microscopy. J. Mar. Sci. Eng. 2017, 5, 4. https://doi.org/10.3390/jmse5010004
Muthukrishnan T, Govender A, Dobretsov S, Abed RMM. Evaluating the Reliability of Counting Bacteria Using Epifluorescence Microscopy. Journal of Marine Science and Engineering. 2017; 5(1):4. https://doi.org/10.3390/jmse5010004
Chicago/Turabian StyleMuthukrishnan, Thirumahal, Anesh Govender, Sergey Dobretsov, and Raeid M.M. Abed. 2017. "Evaluating the Reliability of Counting Bacteria Using Epifluorescence Microscopy" Journal of Marine Science and Engineering 5, no. 1: 4. https://doi.org/10.3390/jmse5010004
APA StyleMuthukrishnan, T., Govender, A., Dobretsov, S., & Abed, R. M. M. (2017). Evaluating the Reliability of Counting Bacteria Using Epifluorescence Microscopy. Journal of Marine Science and Engineering, 5(1), 4. https://doi.org/10.3390/jmse5010004







