Abstract
Wave and current energy can be harnessed in the East China Sea and South China Sea; however, both areas are subject to high frequencies of typhoon events. To improve the safety of the ocean energy conversion device, a Floating Ocean Energy Conversion Device (FOECD) with a single mooring system is proposed, which can be towed to avoid severe ocean conditions or for regular maintenance. In this paper, the structure of the FOECD is introduced, and it includes a catamaran platform, an oscillating buoy part, a current turbine blade, hydraulic energy storage and an electrical generation part. The numerical study models the large catamaran platform as a single, large buoy, while the four floating buoys were modeled simply as small buoys. Theoretical models on wave energy power capture and efficiency were established. To improve the suitability of the buoy for use in the FOECD and its power harvesting capability, a numerical simulation of the four buoy geometries was undertaken. The shape profiles examined in this paper are cylindrical, turbinate (V-shaped and U-shaped cone with cylinder), and combined cylinder-hemisphere buoys. Simulation results reveal that the suitability of a turbinate buoy is the best of the four types. Further simulation models were carried out by adjusting the tip radius of the turbinate buoy. Three performance criteria including suitability, power harvesting capability and energy capture efficiency were analyzed. It reveals that the turbinate buoy has almost the same power harvesting capabilities and energy capture efficiency, while its suitability is far better than that of a cylindrical buoy.
1. Introduction
As a type of sustainable and renewable energy, ocean wave energy is widely distributed in the world. In recent years, sustainable energy generation has become increasingly important due to the expected limitations in conventional energy resources and the drive to reduce pollution [1]. Among renewable energy resources, the possibility of extracting energy from the ocean has intrigued people for centuries. Many devices have been developed for ocean energy conversion, and numerous ocean energy generation systems have emerged [2,3,4,5,6,7]. Wave energy in China is distributed in the East China Sea and South China Sea; hence, most wave energy convertors (including test devices) are deployed in these two areas [8,9]. However, the East China Sea and South China Sea are typhoon-prone areas. The wave amplitude can reach up to 10 meters or more when typhoons occur, which led to many Wave Energy Convertors (WECs) being damaged or even destroyed [10]. There are two approaches to ensure the safety of WECs: the first is improving the survivability performance of the WEC under extreme weather and the other is to design movable WECs, which can be towed into bays to avoid huge wave impact [11]. Many works have been done to improve the wave resistance performance. For example, in each joint of the Pelamis WEC, there are spring and damp arrays to decrease the wave impact [12]. Salter’s Ducks with rigid structures move like “ducks” to improve the wave energy capture efficiency and decrease the wave impact. The Lancaster Flexible Bag has the shape of “bags” to react against a rigid spine [13,14,15]. To avoid having to retune power take-off (PTO) damping for different incident wave frequencies, an optimization over appropriate sea spectra data sets can be used. Devices using direct drive energy generation, such as the Lysekil device, make use of the motion of a submerged, positively buoyant structure reacting against a bottom-mounted mooring system [15,16,17,18,19]. The other concept, where the wave energy conversion system is movable, is convenient because it can be towed into bays to avoid possible damage caused by typhoons or other severe seas. This paper focuses on the latter solution and proposes a Floating Ocean Energy Conversion Device (FOECD) capable of both wave and current energy capture. Here, the design of the FOECD is introduced, and the performance criteria including capture power, efficiency and the suitability of the oscillating buoy are discussed.
2. Design of FOECD
The FOCED designed by the Ningbo Institute of Technology (NIT), Zhejiang University, to be deployed in the East China Sea near Ningbo City, is shown in Figure 1, which also includes: the floating buoy and linking parts, the current energy capture parts, the hydraulic energy conversion and transmission parts, the hydraulic energy storage parts, the electric generation and control parts, the marine current energy conversion device and the floating catamaran platform itself. Due to the fact that most ocean energy generation systems can be easily destroyed by heavy seas, the platform can be towed back to avoid severe sea conditions. The working principle of FOECD for coupling the conversion of current energy and wave energy generation is shown in Figure 2. When there is only wave energy, the floating buoys oscillate up and down around the axis; piston pumps absorb low-pressure hydraulic oil from the oil tank and pump high-pressure hydraulic oil to the accumulator. When there is only current energy, current turbine blades rotate in a certain direction and the rotor pump will rotate at a high speed though step-up gears. This absorbs low-pressure hydraulic oil and pumps high-pressure oil, and the high-pressure oil line is the same as that of the wave energy conversion. When wave and current occur at the same time, both the piston pump and rotor pump work together, and two high-pressure oil branches are gathered in one single line. High-pressure hydraulic oil is initially stored in the hydraulic accumulator. When the oil pressure reaches a certain high value threshold, the high-pressure oil is released, opening a proportional flow control valve from the accumulator to the hydraulic motor to drive the electric generator, which will rotate with a near-constant design speed. If the hydraulic oil pressure drops to a certain low value, the proportional valve will be shut off completely, and thus the wave energy inputs will be conserved in the accumulator cyclically. By doing this, the cycle of converting continuous wave energy inputs into a stable and steady electrical output is complete, and electricity is charged into batteries for storage.
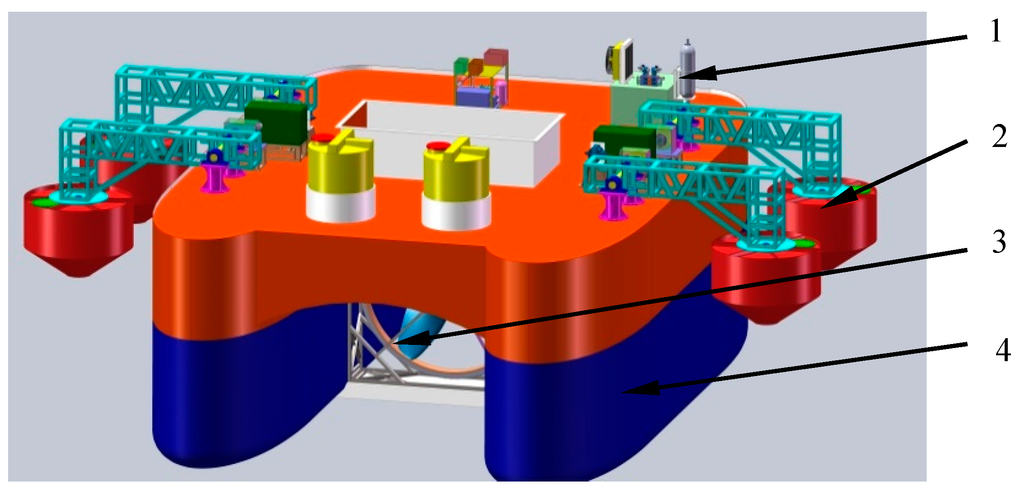
Figure 1.
Schematic of floating platform of offshore ocean energy converter. 1. Hydraulic energy storage and generation parts; 2. Floating buoy and link parts; 3. Current energy capture part; 4. Movable catamaran platform.
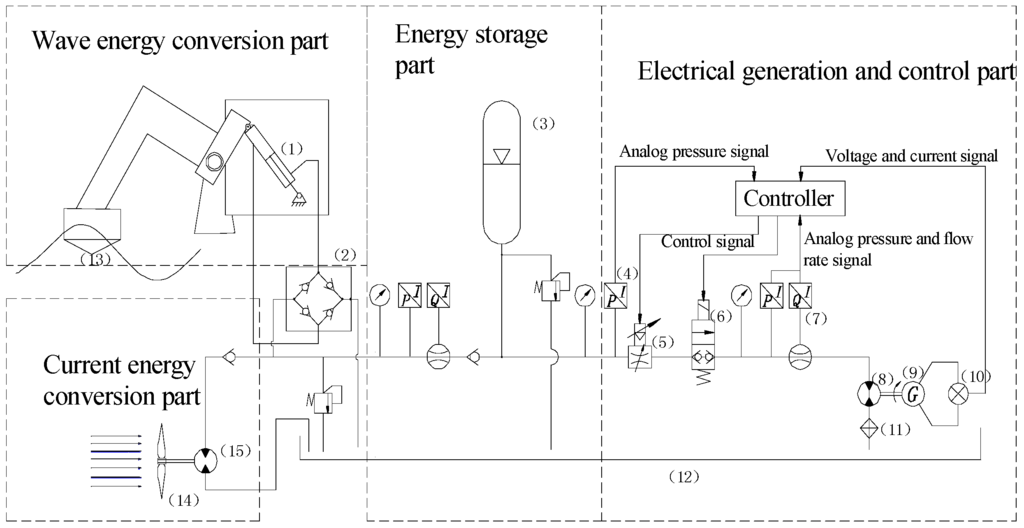
Figure 2.
The system schematic of coupling of wave energy and current energy generation with hydraulic energy storage and pressure control. 1. Piston pump; 2. One-way valve manifold; 3. Accumulator; 4. Pressure sensor; 5. Two-way electro-hydraulic proportional flow control valve; 6. Solenoid valve; 7. Flow sensor; 8. Hydraulic motor; 9. Electrical generator; 10. Load; 11. Oil filter; 12. Oil tank; 13. Oscillating buoy; 14. Current capture turbine blade; 15. Hydraulic pump.
The schematic of the FOECD consists of the following main sub-system loops: wave energy capture, current energy capture, hydraulic energy storage, electrical generation and control, as shown in Figure 2. The wave energy capture part includes oscillation buoys (13) and piston pumps (1) to convert mechanical energy into hydraulic energy. Four check valves are used to establish a hydraulic bridge circuit (2), which is used to convert the two opposite hydraulic oil flows into a single direction supply. The current energy capture part includes three turbine blades (14), the speeder and the rotor pump (15), and the turbine blades are assembled on the horizontal shaft. The hydraulic energy storage part mainly consists of the accumulator (3), the unloading circuit, the pressure instruments and flow meter sensors. The electrical generation part consists of the hydraulic motor and electrical generator, and the control part includes the pressure sensor, the flow meter and the proportional flow control valve, which is used to regulate the pressure drop and the flow rate of the hydraulic oil through the motor. Some main scales and characters of FOECD are as follows:
- The total length, width and height of the floating platform are 14 m, 13 m and 5.5 m, respectively. The platform body has three layers: the bottom cabins are water tanks to adjust the draught of the catamaran platform; the middle layer is the displaced oil circle and water circle; the upper layer is the control room.
- The floating platform can rise and sink with a range of 3 m by pumping water from the water tank, which is also convenient for checking oscillating buoys and current turbine blades.
- Considering the turbine blades’ need to face the direction of water flow, single-anchor mooring is adopted in the FOECD. When the current direction changes, the platform can adjust its position automatically under the current force.
- The floating platform can be towed to bay or other safe places to avoid typhoons or other severe sea conditions. It can also be conveniently dragged into port for maintenance.
- The platform can be towed to areas with abundant ocean energy considering the wave energy and current energy is changeable over a year. It can also be towed to areas near an island to supply electrical power for people who live in the island.
Considering there are two different energy capture theory and design on wave energy and current energy in FOECD, we discuss the wave energy capture part only without regards to the current energy capture part in the paper.
3. Theoretical Model of FOECD
In Figure 1, when FOECD is semi-submerged in ocean waters with a single mooring system, it has heave, sway, bow and rolling movements under the action of free surface waves. The floating buoy arrays have the same movements because they articulate with the platform. Since the power generation is determined by the relative motion between the floating buoy and platform, it is somehow too difficult and not necessary to model the detailed movement equations of the floating platform under the constraint of a single mooring system. Because floating buoy arrays rotate around the catamaran floating platform, they are simplified as oscillating in a vertical direction relative to the catamaran floating platform. Here, both the floating buoy and catamaran platform are simplified as buoys oscillating in free surface waves, while the catamaran platform is simplified as a big cuboid buoy and buoy arrays are simplified as small buoys. Since the radius of the buoy is only 1.1 m, which is far smaller than the wave length, the buoy is considered as a point absorbing the wave energy capture device. Other assumptions are as follows:
- The fluid is an incompressible ideal fluid.
- The water depth is sufficiently large relative to the wavelength, and therefore the wave is set as a linear regular wave [17,18,19,20].
It is apparent that the oscillating amplitude of the buoy is decided by system damping through the natural frequency of buoy. When the natural frequency of the buoy is equal to the frequency of the incident wave, resonance occurs between the buoy and wave. The total energy and average power are expressed, respectively, as
where is the circular frequency of wave (), is the wave period, is the buoy mass, is the added mass of the buoy, i.e., the mass of the water excited by the heaving motion; is the water density, is the water plane area of the buoy, is the wave force amplitude, is the gravity acceleration. is the oscillating amplitude of the buoy and can be expressed as follows:
where is the dimensionless system damping factor in the vertical direction. The equations of added mass and water plane area for three types of buoys including a cuboid buoy, vertical cylindrical buoy and cone buoy are shown in Table 1. For a buoy with a certain shape, circular frequency in the vertical direction is determined, and the circular frequency ratio of is obtained. The value of is found by checking chart curves between and [20].

Table 1.
Added mass and surface waterplane area for several buoy shapes. 1
Considering that both the radius and draught of the cylindrical buoy are much smaller than the wavelength (i.e., , , it can be seen that . Two wave force amplitudes for the big cuboid buoy () and small floating buoy () are as follows:
where is the wave amplitude, is the wavelength () and is the draught of the buoy.
Through simultaneous Equations (3)–(5), the oscillating amplitude for the big cuboid buoy and small floating buoy are found as follows, respectively,
where , and and are extracted from McCormick, 2013 [20].
The relative oscillating amplitude between the big cuboid buoy and small floating buoy () is
Considering the coupling force between the two buoys, a minimum value is selected to find
Due to the four small floating buoys in the FOECD, the theoretical wave energy capture power for four buoys is
The total energy of the incident wave for the small floating buoy with a radius of in the field width S (S = 2R) is
Then the theoretical power harvesting efficiency of the small floating buoy is
4. Proposition of Buoy Shape
Due to the single anchor, the force acting on the mooring system of the FOECD is almost equal to the wave and current force acting on the catamaran platform. On one hand, the horizontal force component acting on the platform is proportional to the vertical cross-sectional area of the platform and buoys. Besides the floating platform itself, the wave and current forces acting on the buoys have an apparent influence on the stability and safety performance for the platform (it is named as suitability in the paper). On the other hand, the power capture of buoy is mainly determined by the oscillating amplitude and the scale of the buoy. So, to improve the power capture performance and suitability of the buoy, the shape and scale of the buoy have been studied by many researchers. Stansby et al. proposed a line absorber consisting of three cylindrical floats, which have high crest capture widths for wave energy conversion across a broad band of frequencies [21]. Ramadan proposed a new design of float and the analytical analysis of its performance [22]. The float consists of two parts: a hollow cylinder and an inverted cup fixed to its bottom. This float is initially submerged in water with sufficient submergence. Water rises up due to the wave action and the float will follow the water motion which reduces the slamming of the float. When the water level drops, the water enclosed in the inverted cup is exposed to a negative pressure which helps the float down to follow the water wave motion without slamming [22]. Hu et al. established simulation models of several floating tanks including a horizontal cylinder and floating cylinder-hemisphere combined in extreme free surface waves [23]. Orazov et al. designed a novel buoy-type ocean wave energy converter, which has the potential to improve the energy harvesting capabilities of these converters. The scheme uses the incident waves to modulate the mass of the device in a manner which amplifies its resonant response. They established a simple one-degree-of-freedom model for the wave energy converter. The model is then used to show that the excitation scheme improves the power harvesting capabilities by 25%–65% even when the amplitude restrictions are present [24]. Yage You proposed a floating wave energy conversion with a bionic-shaped buoy named “egal” [10]. Lin Jiangbo, Li Fuwei et al. have compared several types of floating buoys including a cuboid buoy, spherical buoy, cone buoy and cylindrical buoy through the method of simulations and experiments [25,26,27,28].
A certain buoy type has its own character because of different ocean environments, different wave energy capture methods and different structural platforms, and it is hard to determine which buoy type is the best. Typically, the cylindrical buoy has the merit of high wave energy capture efficiency and the conical buoy has the merit of good suitability. Combining the two merits and structural character, a novel buoy is adopted in the design for the FOECD. The buoy has a V-shaped and U-shaped cone attached to the end of a cylinder, and we name it the turbinate buoy due to its shape.
5. Suitability and Power Harvesting Capability Performance Simulation for Turbinate Buoy
To ensure the safety of the floating platform, it is necessary to analyze the suitability of the floating buoy. The maximum Von Mises stress and deformation is calculated for the wave acting on the buoy in the horizontal direction to judge the suitability of the small floating buoys. In the condition of the same wave period, wave amplitude and wave length, a lower stress means better suitability. Similarly, the maximum stress and deformation when waves act on the buoy in the vertical direction relate to the power harvesting performance of the buoy, and a larger stress gives a better power harvesting performance. In the simulation model, the radius of the cylinder part is fixed as 1.1 m and the total height is 3 m for the turbinate buoy. Simulation models were established for four types of buoys including a cylindrical buoy, a turbinate buoy with a point bottom, a turbinate buoy with a flat bottom and a cylinder-hemisphere combined buoy.
5.1. Suitability Analysis for Turbinate Buoy
The Navier-Stokes (N-S) equation and the Froude-Krylov (F-K) theory were selected in the simulation model [21], and the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) method is selected in the calculation. The aim of the simulation was to calculate the maximum stress, deformation and strain of the buoy. A single-direction fluid-solid coupling analysis model was used with an ANSYS workbench software tool, and the fluid coupling field was 10 m × 8 m × 6 m (shown in Figure 3). To calculate the fluid pressure and velocity assigned to the fluid field, the pressure applied on the buoy surface is initially found, and then the stress and strain of the buoy are calculated under the impact of the wave. Due to viscous damping having an apparent influence on the wave impact coefficient acting on the buoy, the N-S equation and F-K theory were selected in the simulation model. In the N-S calculation, the SIMPLE method was selected, which is suitable for solving unstable turbulence fields. Some assumptions and simplifications were made as follows:
- (1)
- The current flow is constant and the flow velocity is 2 m/s.
- (2)
- To simplify the calculation, the floating platform is fixed and the fluid direction is horizontal or vertical.
- (3)
- The body of the buoy is semi-submerged in sea water with a draught of 1.8 m.
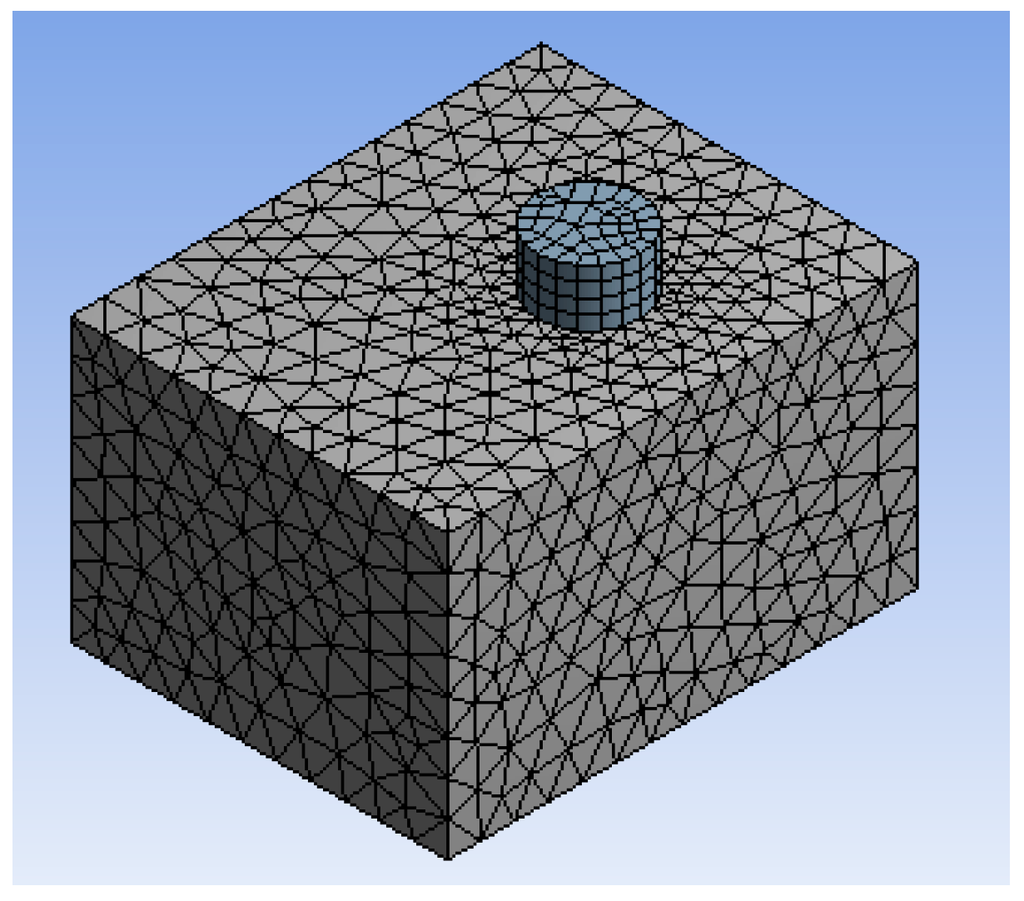
Figure 3.
Mesh for floating buoy and fluid field.
The Von Mises stress and deformation diagram of the four buoys are shown in Figure 4. In the figure, on the condition of the same water flow and the same cross area of the buoy, the cylindrical buoy has the maximum stress and deformation of the four buoys, while the turbinate buoy has minimum stress and deformation.
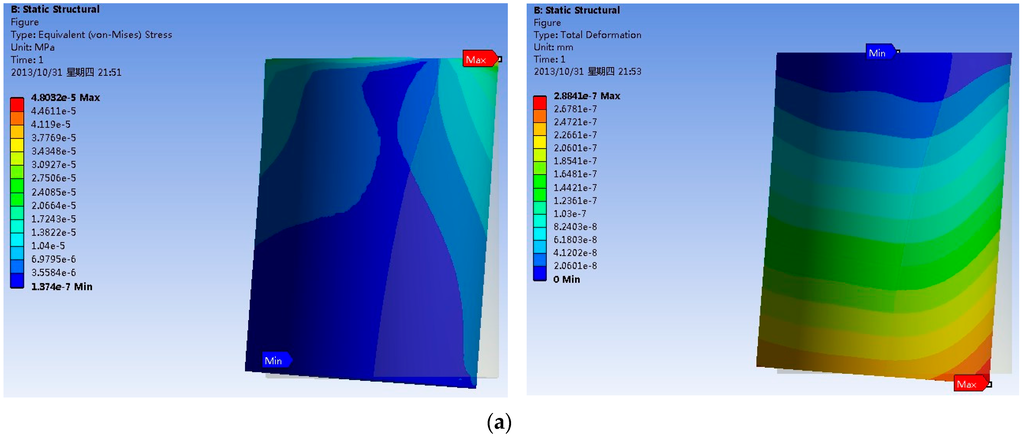
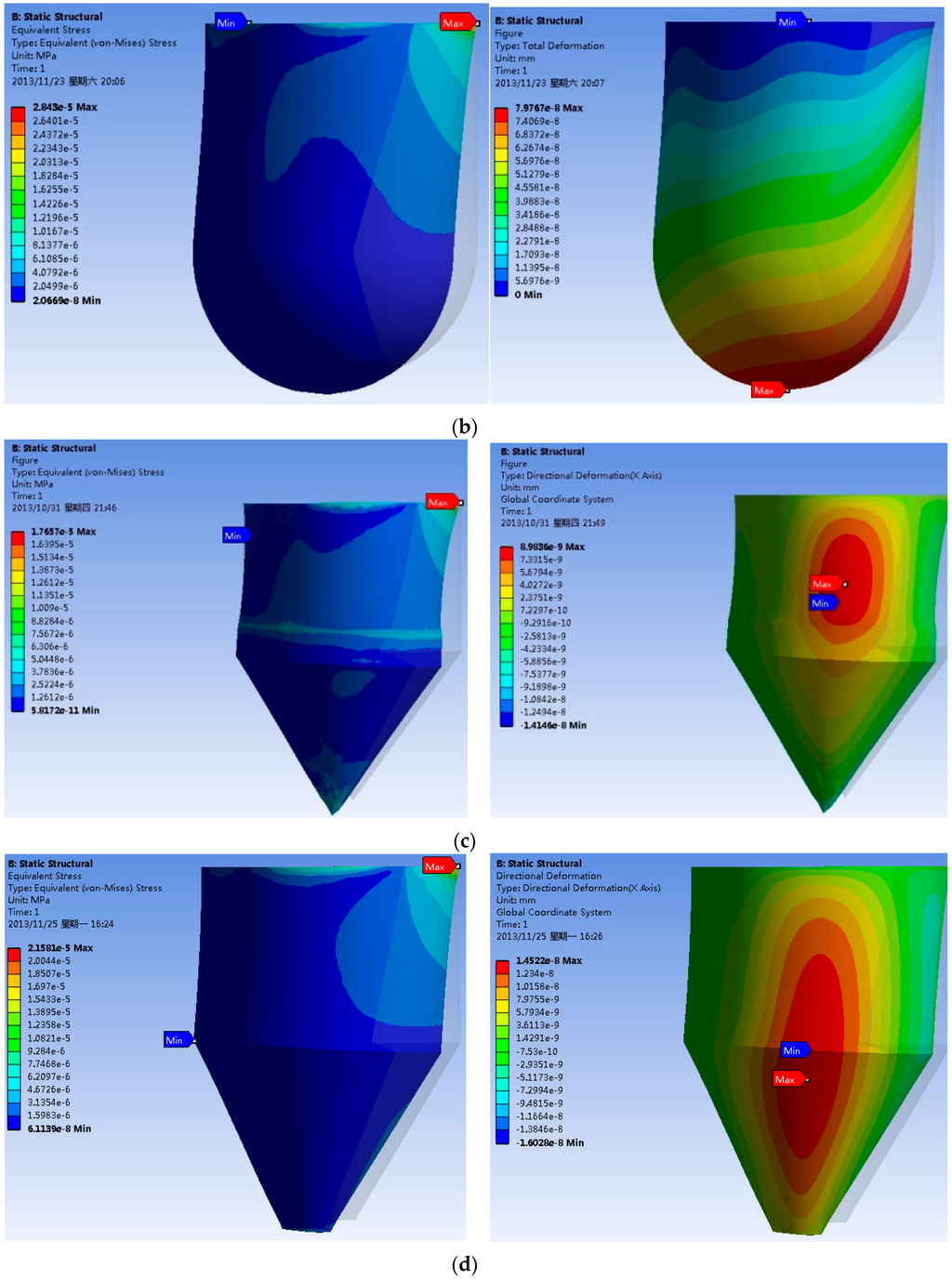
Figure 4.
Von Mises stress and deformation of four types of buoys. (a) cylindrical buoy; (b) cylinder-hemisphere combined buoy; (c) turbinate buoy with point tip; (d) turbinate buoy with tip radius at 0.2 m.
Figure 5 shows the comparisons of the Von Mises stress (), total deformation () and maximum impact force acting on the buoys in the horizontal direction () for each of the four buoy types. In the figure, the two turbinate buoys have the lowest Von Mises stress, deformation and impact force, with values 20%–80% less than those of the cylindrical buoy and cylinder-hemisphere combined buoy. It illustrates that the turbinate buoy has the best suitability. To optimize the turbinate buoy, the tip radius of the circular cone is adjusted from 0 m to 1.1 m with a span of 0.05 m. Through the same simulation method, the curves of , and are shown in Figure 6, Figure 7 and Figure 8, respectively.
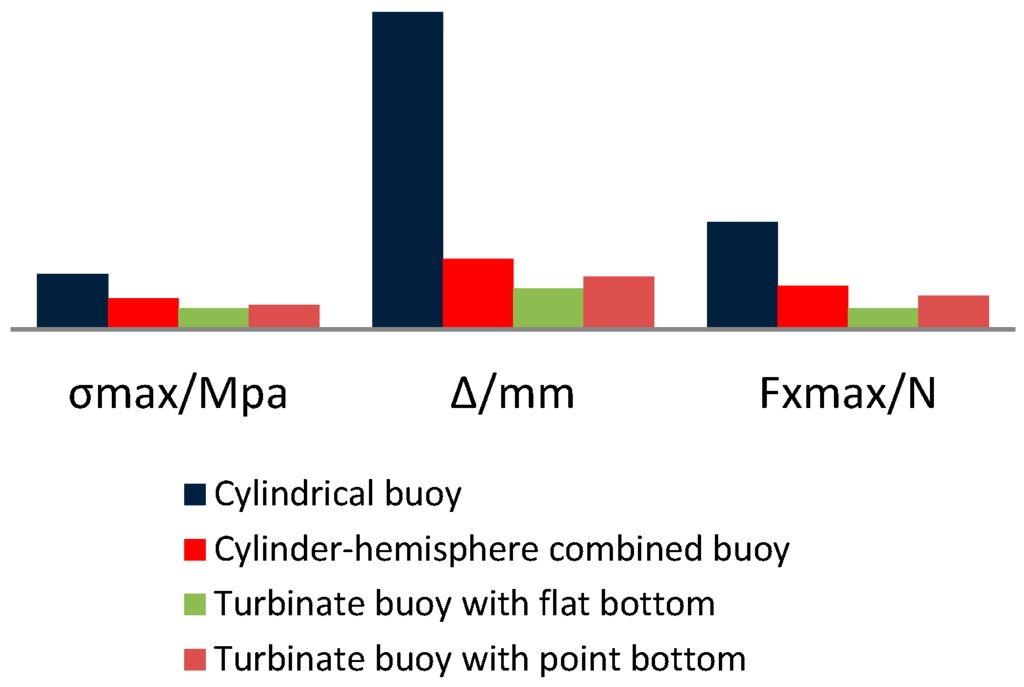
Figure 5.
Suitability comparison diagram of four kinds of buoys.
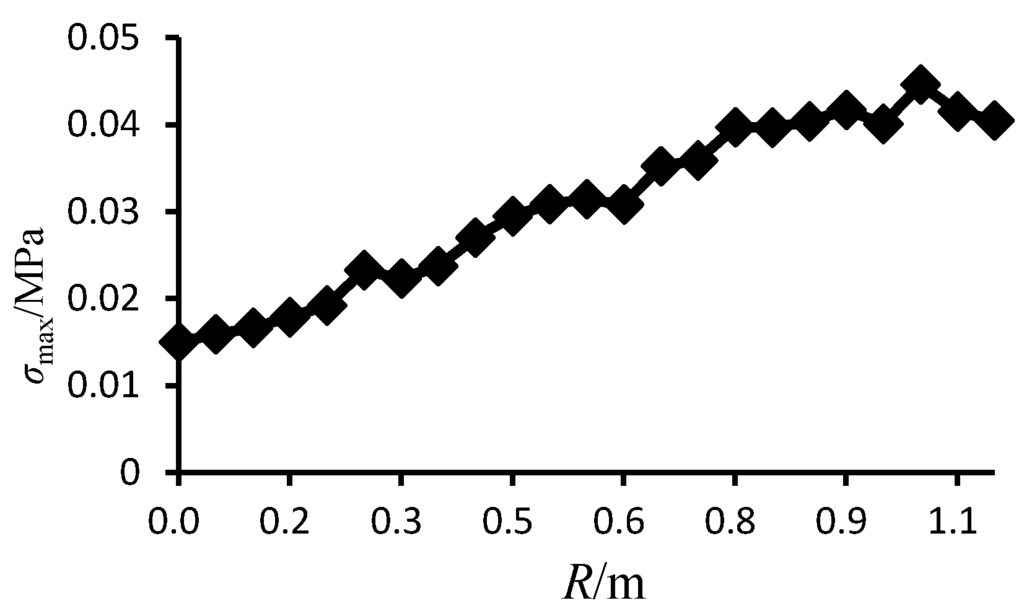
Figure 6.
Maximum stress through varying tip radius of cone.
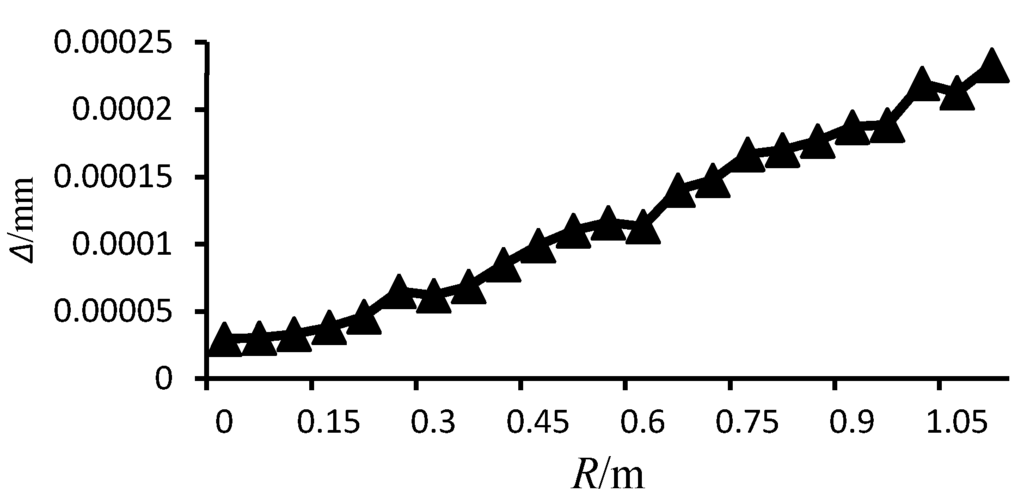
Figure 7.
Maximum deformation through varying tip radius of cone.
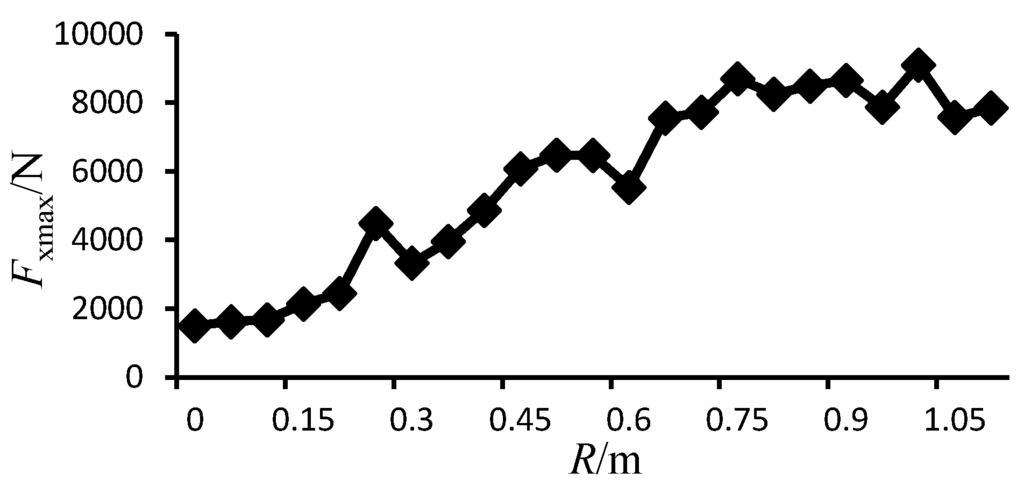
Figure 8.
Maximum horizontal impact force through varying tip radius of cone.
In the three figures, , and increase with the increasing tip radius of the circular cone, but the trends are not entirely consistent. When the tip radius of the cone increases from 0 to 0.75 m, , and generally increase linearly. When the tip radius increases from 0.75 m to 1.1 m, continually increases while and remain stable. The main reason is because the decrease of the tip radius of the cone causes the taper of the circular cone to increase. This leads the component force in the vertical direction to increase while the horizontal component force has no apparent changes.
5.2. Analysis of Power Harvesting Capabilities and Efficiency
In the theoretical power harvesting model, i.e., Equations (8) and (9), it is clear that the relative oscillation amplitude of the floating buoy is proportional to the wave force (), and the average captured power is mainly determined by both the relative oscillation amplitude of the floating buoy and the wave force. While the taper of the circular cone has an apparent influence on the wave force and oscillation amplitude of the buoy, an analysis of the Von Mises stress, deformation and force in the vertical direction is needed for the small floating buoy. In the simulation model, the flow velocity is 2 m/s and the direction is from the bottom to top of the fluid field. The tip radius of the circular cone is adjusted from 0 m to 1.1 m with a span of 0.05 m. The same simulation method is adopted in the analysis of the stress, deformation and total force in the vertical direction of the turbinate buoy. Figure 9 shows the maximum force curve acting on the buoy in the vertical direction with the varying tip radius of the circular cone. The figure reveals that by increasing the tip radius of the circular cone from 0 m to 0.75 m, the maximum force remains stable. A further increase of the tip radius from 0.75 m to 1.1 m causes the maximum force to increase exponentially.
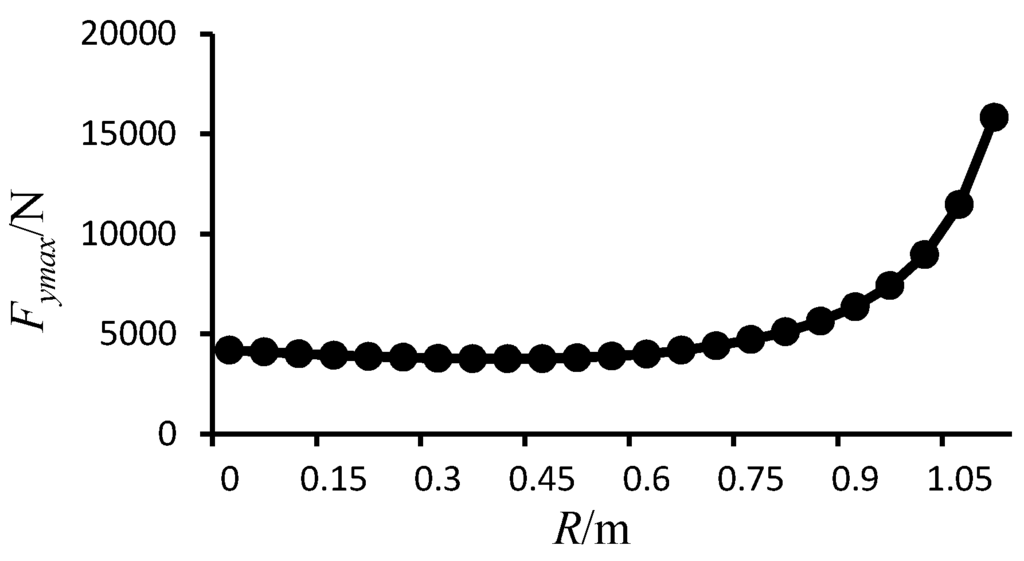
Figure 9.
Maximum vertical impact force through varying tip radius.
All the certain parameter values were substituted into Equation (8) and the relative oscillating amplitude of the floating buoy was found. Figure 10 shows the curve of the relative oscillating amplitude through the varying tip radius of the circular cone. In the figure, when the tip radius of the circular cone increases from 0 m to 0.4 m, the relative oscillating amplitude remains stable within a certain range; when the tip radius increases from 0.4 m to 1.1 m, the relative oscillating amplitude decreases continually. Furthermore, the average harvest power and the efficiency of the turbinate buoy were found by substituting certain parameter values into Equations (9) and (11), which are shown in Figure 11 and Figure 12, correspondingly. In Figure 12, the average harvest power of the buoy has no obvious change when the tip radius of the circular cone increases from 0 m to 1.1 m, and the harvest power only rises from 3.5 kW to 3.7 kW. It reveals that the shape and scale of the circular cone for the buoy has no apparent influence on the power harvesting capabilities. In Figure 12, the power harvest efficiency is kept at a stable range (17%–20%), which means the tip radius of the circular cone has no apparent influence on the power harvesting capabilities as well.
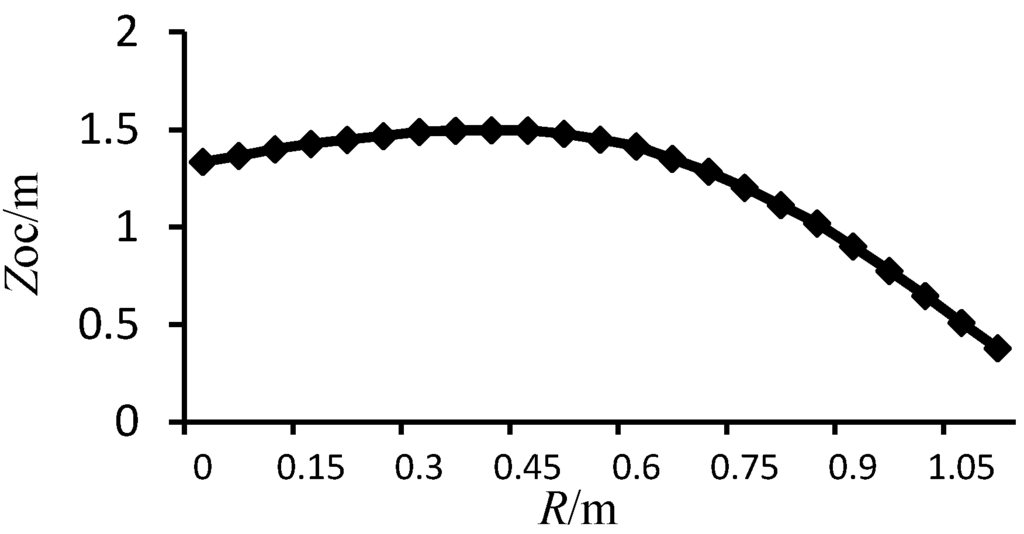
Figure 10.
Relative oscillating amplitude through varying tip radius of cone.
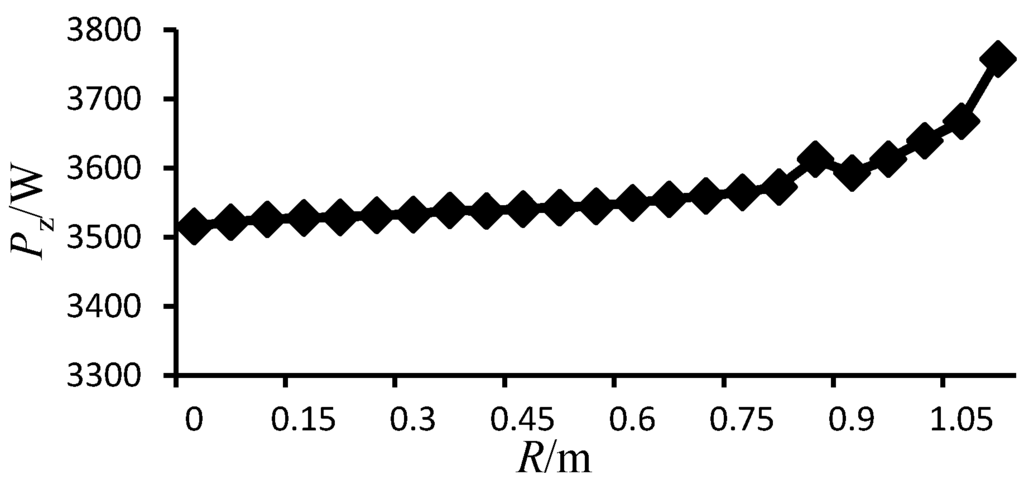
Figure 11.
Harvest power curve through varying tip radius of cone.
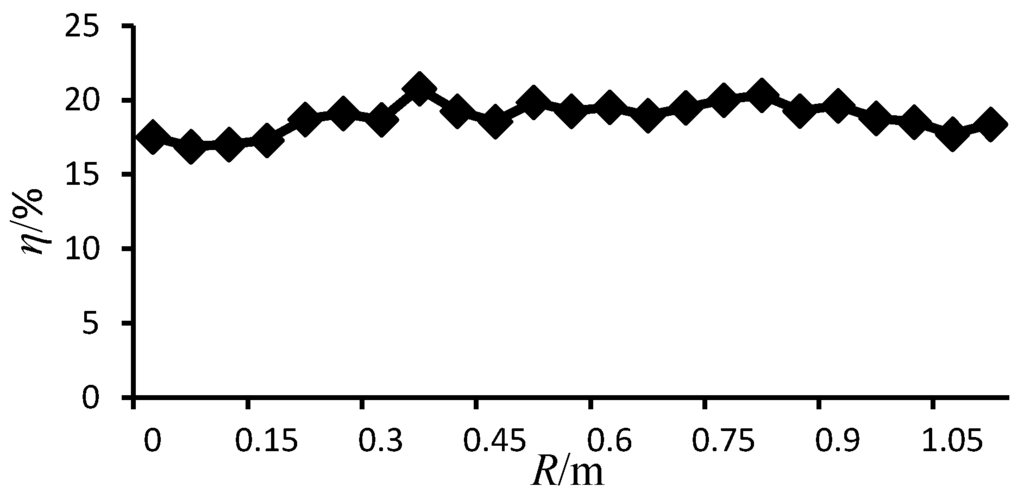
Figure 12.
Power harvest efficiency through varying tip radius of cone.
6. Establishment of FOECD
Mainly under the support of projects funded by the State Oceanic Administration, China, a physical prototype platform of the FOECD was designed and built by Ningbo Institute of Technology, Zhejiang University (NIT), to be deployed in the East China Sea near Ningbo City, which is shown in Figure 13. The main performance and parameters are as follows:
- The total length, width and height of the floating platform are 14 m, 13 m and 5.5 m, respectively.
- The rated electrical generator is 25 kW, which includes current energy generation (15 kW) and wave energy generation (10 kW).
- The wave energy capture part is composed of four turbinate buoys, each with a diameter of 2.2 m. The current capture part has three blades with a horizontal shaft which has a diameter of 4 m. The FOECD starts to work when the wave amplitude is higher than 1.2 m or the current velocity is higher than 0.8 m/s.
- To ensure safe mooring, an iron chain is used. The total length of the chain is 80 m and the anchor weight is 1.5 t. The power of the electric motor used in Capstan is 5 kW.

Figure 13.
Physical prototype platform of FOECD.
The experimental tests and improvement of the performance are still ongoing.
7. Conclusions
In this paper, the structures of a FOECD including the catamaran platform, the oscillating buoy part, and the wave and current energy conversion were introduced. Only the hydrodynamic performance of the oscillating buoy is discussed and the other performance criteria, such as the suitability of the catamaran platform and the power harvesting capability of the current turbine blades, are neglected. In the theoretical model, the catamaran platform and floating buoys were simplified as a big cuboid buoy and small buoys, respectively, i.e., the device is simplified as dual buoys. Two theoretical models of the FOECD for evaluating wave energy power harvest and efficiency were established. To improve the suitability and power harvesting capability, simulation models were created for four different profiles of small buoys. This included a cylindrical buoy, a turbinate buoy with a point bottom, a turbinate buoy with a flat bottom, and a combined cylinder-hemisphere buoy. Simulation results reveal that the suitability of the turbinate buoy is the best from the four types of buoys. Further analysis was done on the turbinate buoy, and simulation models were established by adjusting the tip radius of the cone for the turbinate buoy. Three performance measures including suitability, power harvesting capability and energy capture efficiency were analyzed. It has been revealed that when the buoy shape is changed from cylindrical to turbinate, the influence on power harvesting capabilities and energy capture efficiency is almost negligible, while the suitability of the FOECD is improved by a large degree.
As a FOECD with a single mooring system is convenient both for towing and for capturing wave energy and current energy, such a system could be used to supply electrical energy for islands. It is, however, limited to small-scale power harvest platforms because of the single mooring anchor.
Acknowledgments
The paper is supported by projects funded by the State Oceanic Administration, China (NBME2011CL02), Zhejiang Natural Science Fund, China (LY13E090007), Marine Economic Development Demonstration Area Projects, China (2012) and Ningbo major scientific and technological projects (2012C10041), China.
Author Contributions
In the paper, Ruiyin Song and Meiqin Zhang designed the wave energy conversion part and established the simulation model; Xiaohua Qian and Xiancheng Wang established the hydraulic energy storage and electrical generation part; Yong Ming Dai proposed the control strategy and modifications for this paper; Junhua Chen established the current energy conversion part.
Conflicts of Interest
The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results. Therefore, the authors declare there are no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FOECD | Floating Ocean Energy Conversion Device |
| PTO | Power Take Off |
| NIT | Ningbo Institute of Technology, Zhejiang University |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| N-S | Navier-Stokes |
| F-K | Froude-Krylov |
References
- Truong, D.Q.; Ahn, K.K. Wave prediction based on a modified grey model MGM(1,1) for real-time control of wave energy converters in irregular waves. Renew. Energy 2012, 43, 242–255. [Google Scholar] [CrossRef]
- Babarit, A. A database of capture width ratio of wave energy converters. Renew. Energy 2015, 80, 610–628. [Google Scholar] [CrossRef]
- Myers, L.E.; Bahaj, A.S. An experimental investigation simulating flow effects in first generation marine current energy converter arrays. Renew. Energy 2012, 37, 28–36. [Google Scholar] [CrossRef]
- Rourke, F.O.; Boyle, F.; Reynolds, A. Marine current energy devices: Current status and possible future applications in Ireland. Renew. Sustain. Energy Rev. 2010, 14, 1026–1036. [Google Scholar] [CrossRef]
- De Andres, A.; Guanche, R.; Vidal, C.; Losada, I.J. Adaptability of a generic wave energy converter to different climate conditions. Renew. Energy 2015, 78, 322–333. [Google Scholar] [CrossRef]
- Jama, M.A.; Noura, H.; Wahyudie, A.; Assi, A. Enhancing the performance of heaving wave energy converters using model-free control approach. Renew. Energy 2015, 83, 931–941. [Google Scholar] [CrossRef]
- Siegel, S.G.; Jeans, T.; McLaughlin, T.E. Deep ocean wave energy conversion using a cycloidal turbine. Appl. Ocean Res. 2011, 33, 110–119. [Google Scholar] [CrossRef]
- Zhang, D.; Li, W.; Lin, Y. Wave energy in China: Current status and perspectives. Renew. Energy 2009, 34, 2089–2092. [Google Scholar] [CrossRef]
- Wu, S.; Liu, C.; Chen, X. Offshore wave energy resource assessment in the East China Sea. Renew. Energy 2015, 76, 628–636. [Google Scholar] [CrossRef]
- You, Y.; Sheng, S.; Wu, B.; He, Y. Wave energy technology in China. Phil. Trans. R. Soc. A 2012, 370, 472–480. [Google Scholar] [CrossRef] [PubMed]
- Tiron, R.; Mallon, F.; Dias, F.; Reynaud, E.G. The challenging life of wave energy devices at sea: A few points to consider. Renew. Sustain. Energy Rev. 2015, 43, 1263–1272. [Google Scholar] [CrossRef]
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Phil. Trans. R. Soc. A 2012, 370, 365–380. [Google Scholar] [CrossRef] [PubMed]
- Hearn, G.E.; Donati, E.; Mahendran, I.K. Prediction, measurement and comparison of fluid-structure interaction using mathematical and experimental results. Appl. Math. Model. 1983, 7, 41–47. [Google Scholar] [CrossRef]
- Renzi, E.; Doherty, K.; Henryb, A.; Dias, F. How does Oyster work? The simple interpretation of Oyster mathematics. Eur. J. Mech. B Fluids 2014, 47, 124–131. [Google Scholar] [CrossRef]
- Guanche, R.; Gomez, V.; Vidal, C.; Eguino, I. Numerical analysis and performance optimization of a submerged wave energy point absorber. Ocean Eng. 2013, 59, 214–230. [Google Scholar] [CrossRef]
- Mueller, M.A. Electrical generators for direct drive wave energy conversion. IEE Proc. Gener. Transm. Distrib. 2002, 149, 446–456. [Google Scholar] [CrossRef]
- Leijon, M.; Boström, C.; Danielsson, O.; Gustafsson, S.; Haikonen, K.; Langhamer, O.; Strömstedt, E.; Stålberg, M.; Sundberg, J.; Svensson, O.; et al. Wave energy from the North Sea: Experiences from the Lysekil research site. Surv. Geophys. 2008, 29, 221–224. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, P.; Li, D.; Jiao, Y. An overview of ocean renewable energy in China. Renew. Sustain. Energy Rev. 2011, 15, 91–111. [Google Scholar] [CrossRef]
- Henriques, J.C.C.; Lopes, M.F.P.; Gomes, R.P.F.; Gato, L.M.C.; Falcão, A.F.O. On the annual wave energy absorption by two-body heaving WECs with latching control. Renew. Energy 2012, 45, 31–40. [Google Scholar] [CrossRef]
- McCormick, M.E. Ocean Wave Energy Conversation; Dover Publications, Inc: New York, NY, USA, 2013; pp. 42–58. [Google Scholar]
- Stansby, P.; Moreno, E.C.; Stallard, T.; Maggi, A. Three-float broad-band resonant line absorber with surge for wave energy conversion. Renew. Energy 2015, 78, 132–140. [Google Scholar] [CrossRef]
- Ramadan, A.; Mohamed, M.H.; Abdien, S.M.; Marzouk, S.Y.; El Feky, A.; El Baz, A.R. Analytical investigation and experimental validation of an inverted cup float used for wave energy conversion. Energy 2014, 70, 539–546. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Causon, D.M.; Mingham, C.G.; Qian, L. Numerical simulation of floating bodies in extreme free surface waves. Nat. Hazard. Earth Syst. Sci. 2011, 11, 519–527. [Google Scholar] [CrossRef]
- Orazov, B.; O’Reilly, O.M.; Savas, O. On the dynamics of a novel ocean wave energy converter. J. Sound Vib. 2010, 329, 5058–5069. [Google Scholar] [CrossRef]
- Lin, J. Dynamic Analysis and Emulation of Float-Type Wave Power Generation Boat. Master’s Thesis, Yanshan University, Qinghuangdao, China, April 2005. [Google Scholar]
- Li, F. The Influence of Buoy Shape on Efficiency of Oscillating Buoy Wave Energy Converter. Master’s Thesis, Harbin Institute of Technology, Harbin, China, June 2011. [Google Scholar]
- Hao, N. The Structure Design and Optimization Analysis of Full Hydraulic Floating Type Wave Power Device. Master’s Thesis, Shandong University, Jinan, China, April 2012. [Google Scholar]
- Gao, R. Study on Combined Oscillating Floater Buoy Wave Energy Converter. Master’s Thesis, Ocean University of China, Qingdao, China, June 2012. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).