Channel Shallowing as Mitigation of Coastal Flooding
Abstract
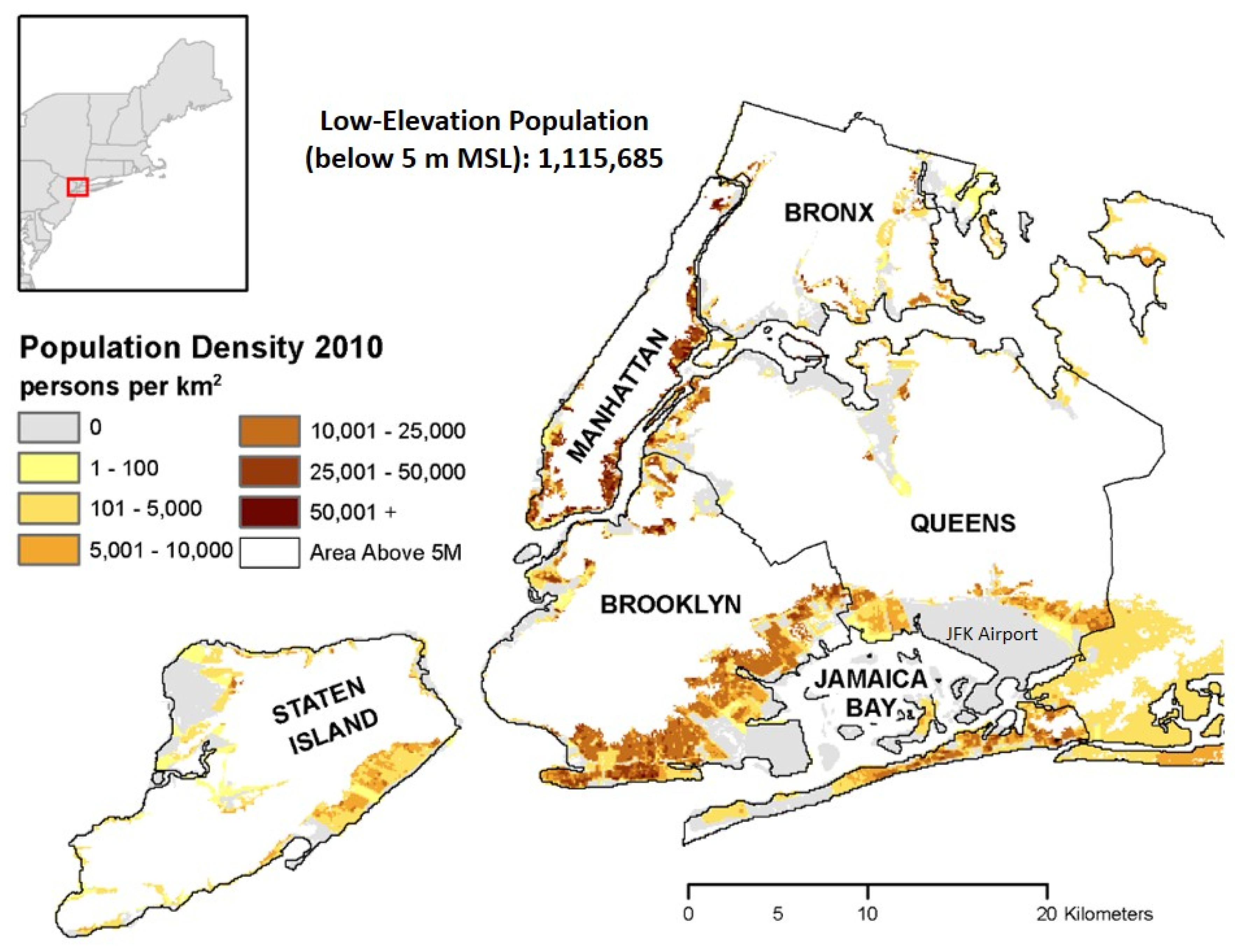
:1. Introduction
2. Methods
2.1. Hydrodynamic Modeling
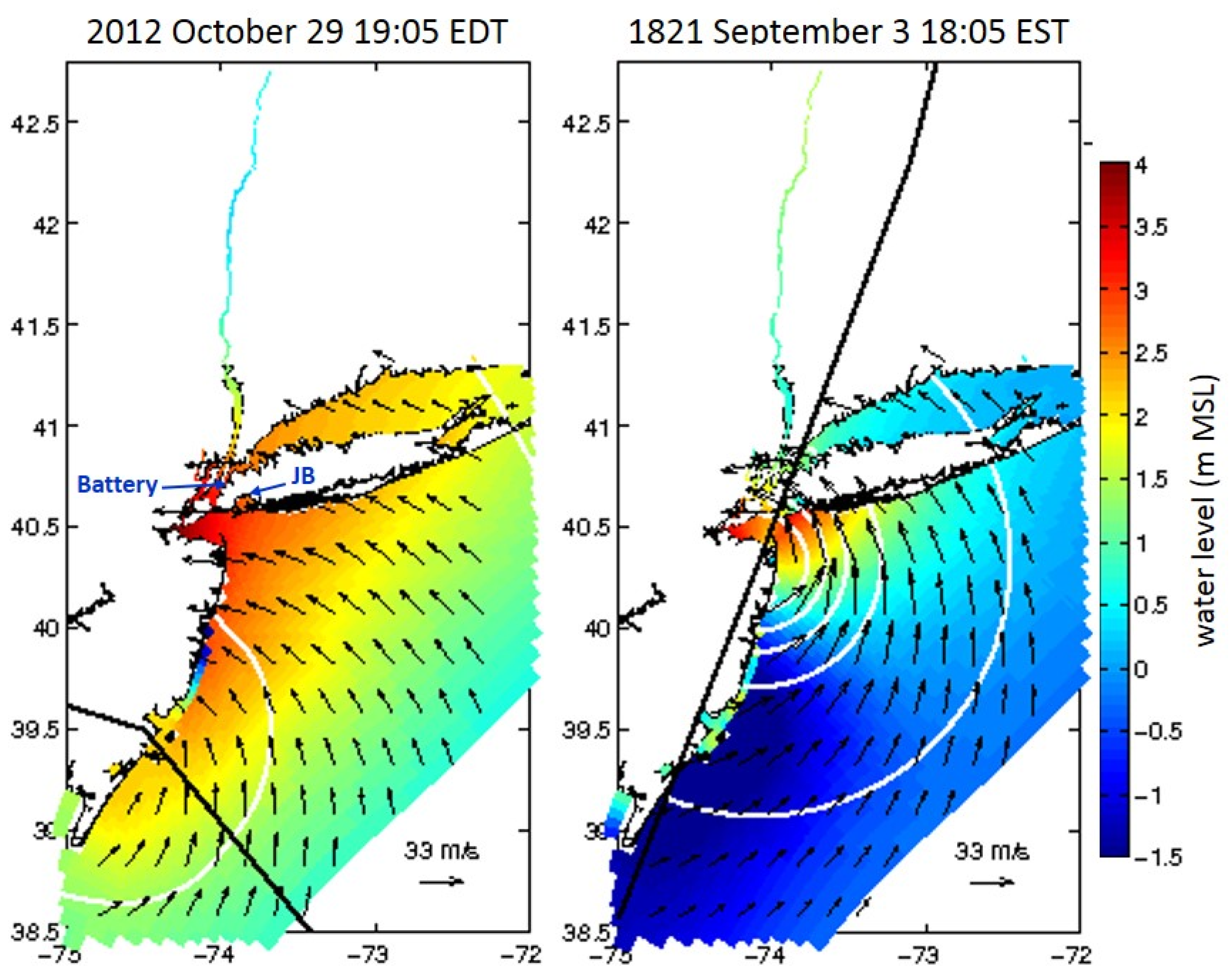
2.2. Storms and Forcing Data
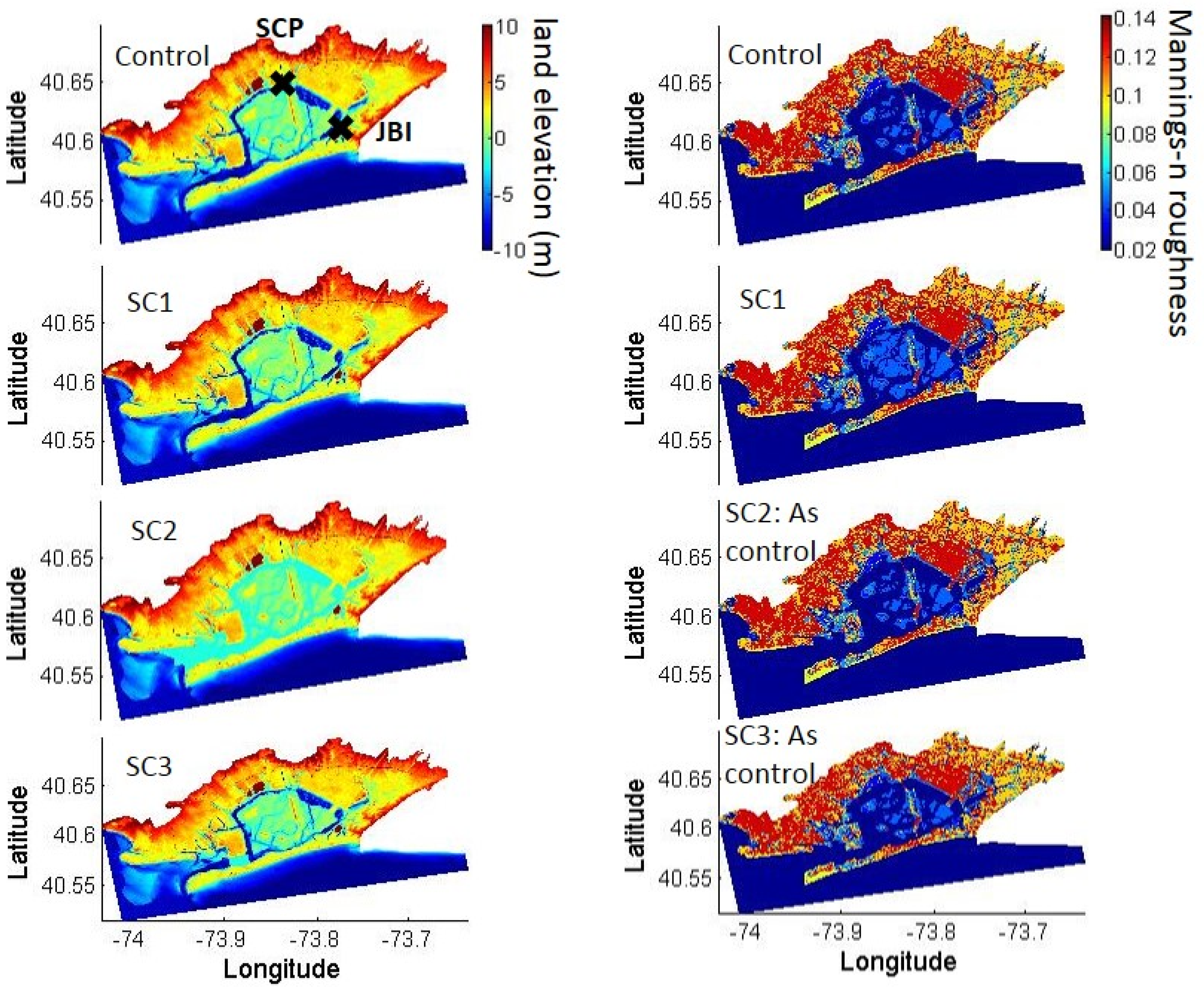
2.3. Landscape Scenarios
- CONTROL: Present-day landscape and land cover;
- SC1: “Wetland restoration”: Restoring the 1879 wetland footprint and bathymetry, while not altering areas of present-day deep channels or neighborhoods;
- SC2: “Full shallowing”: Shallowing deep (>2m) channels to 2 m depth below Mean Low Water;
- SC3: “Inlet shallowing”: As SC2, but shallowing only the narrowest region in the inlet;
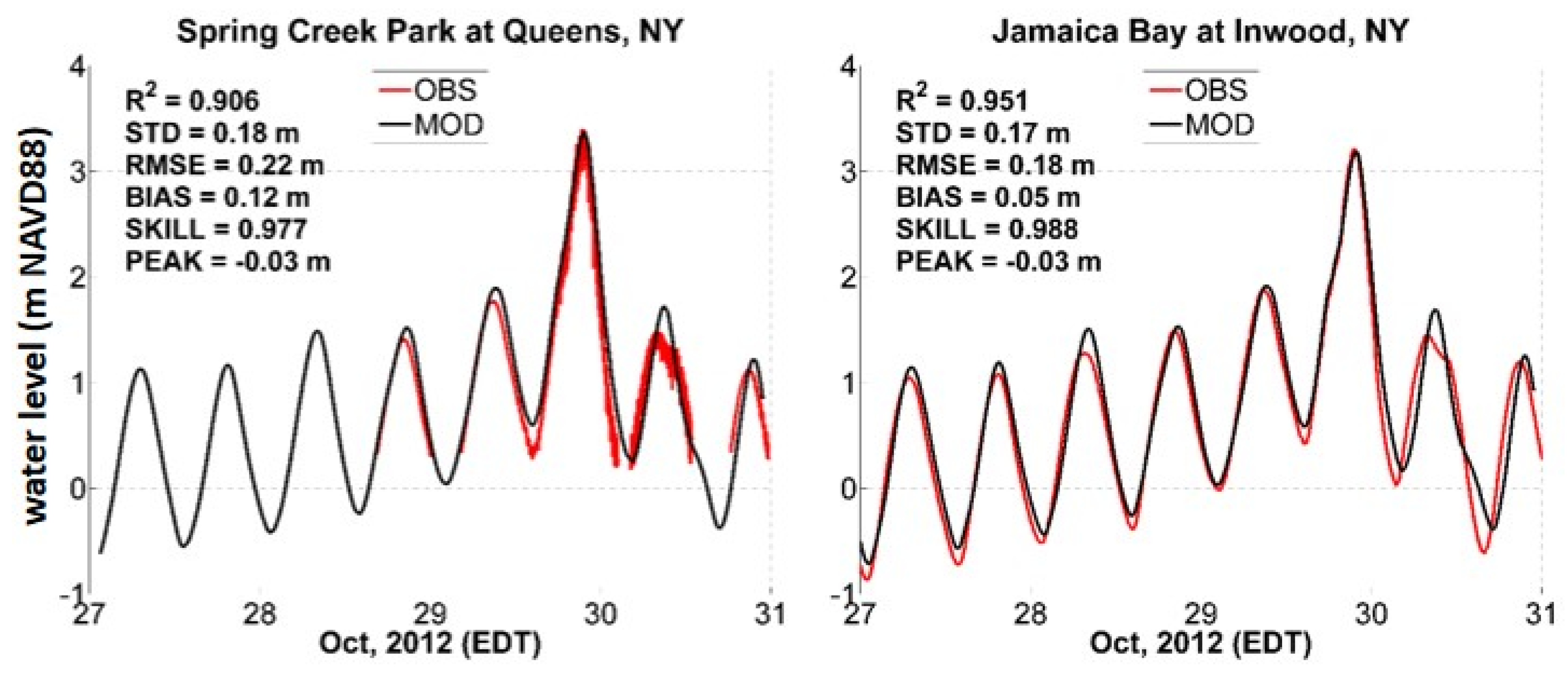
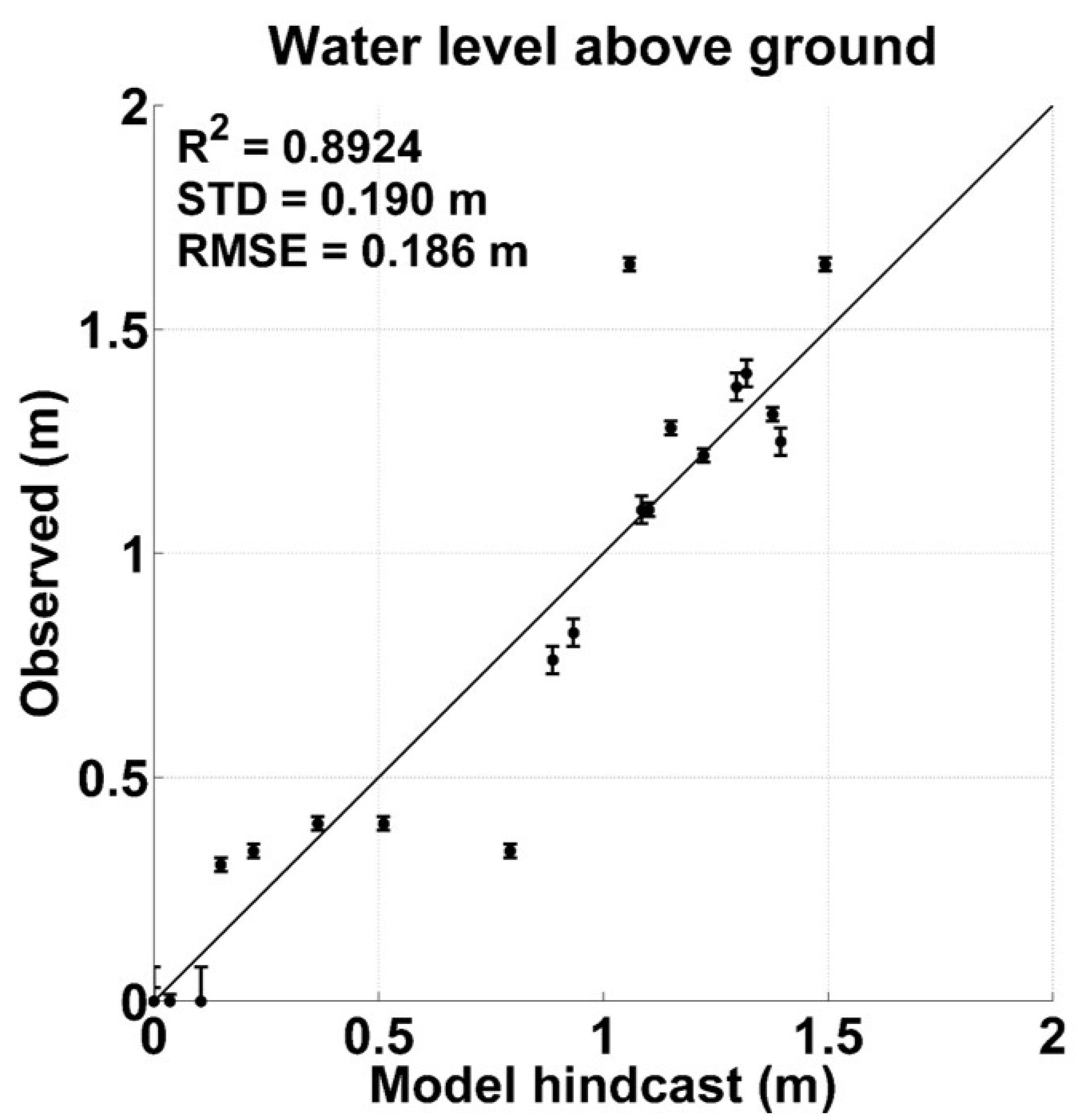
2.4. Model Validation
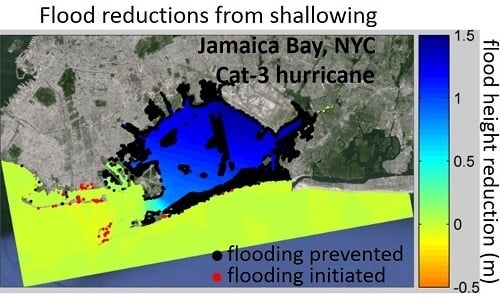
3. Results
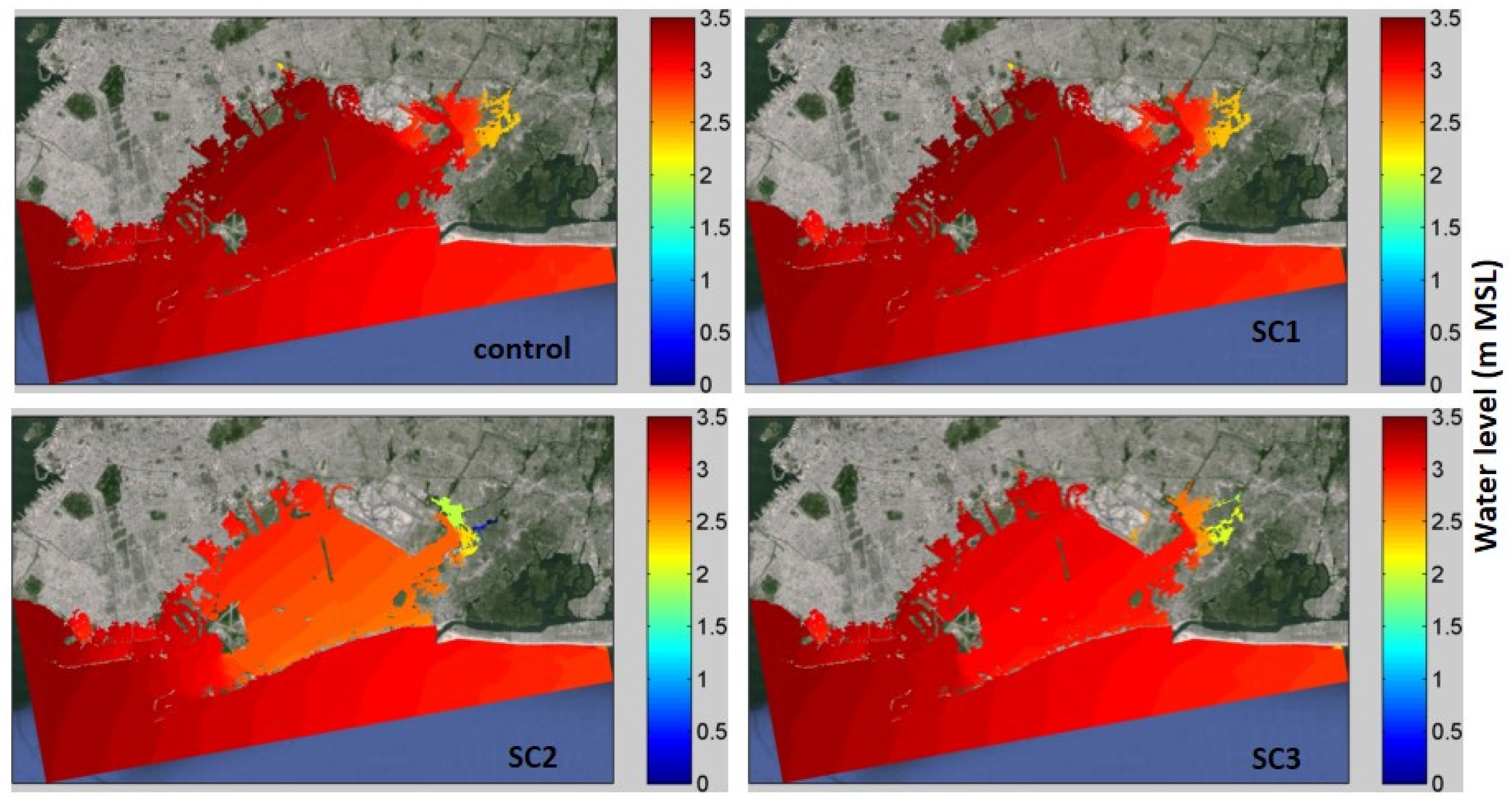
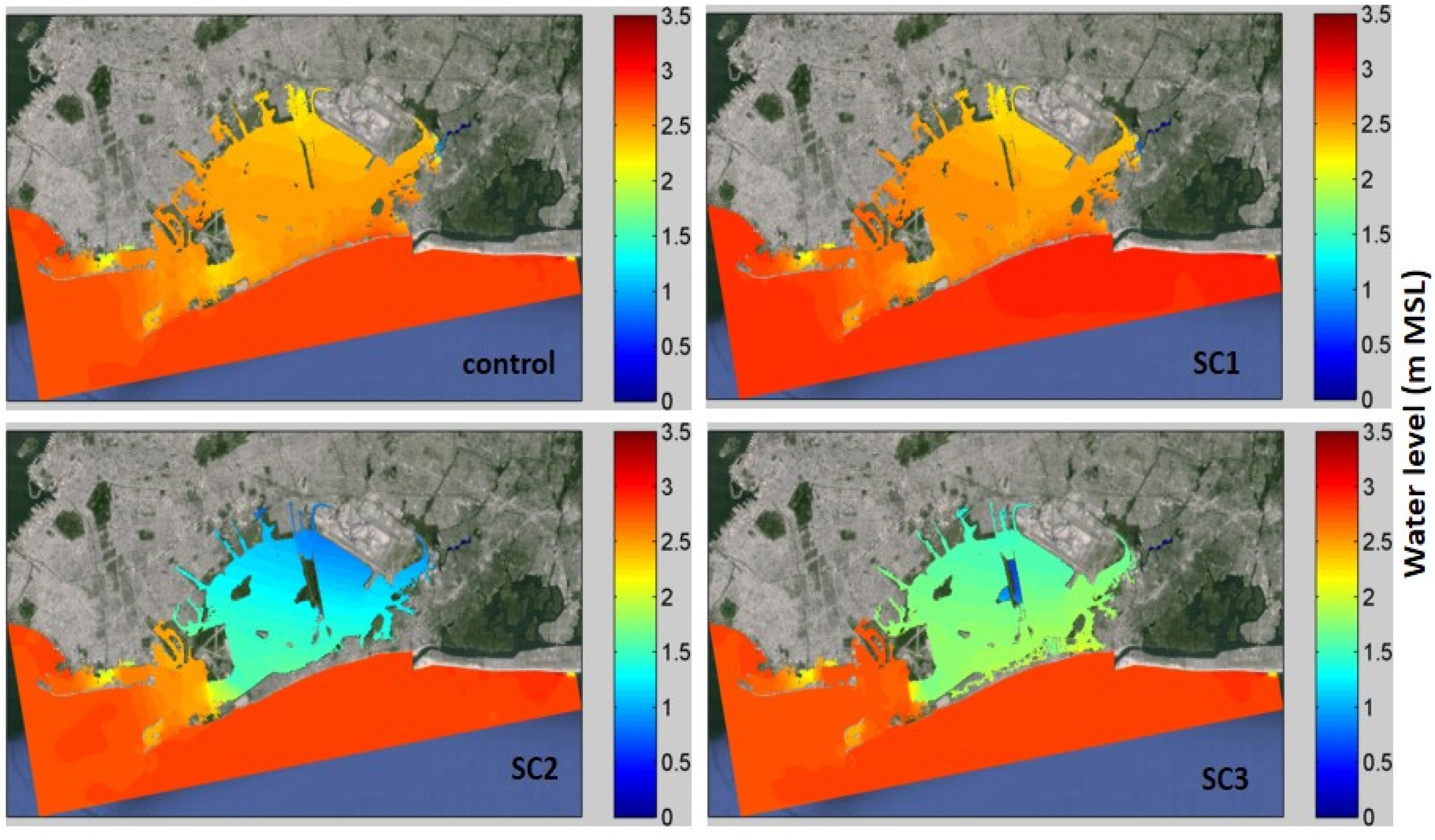
| Storm Events | Scenario | Bay-Average | JBI Station | ||||
|---|---|---|---|---|---|---|---|
| Peak Water Level (m a) | Reduction (m) | Reduction Percentage (%) | Peak Water Level (m a) | Peak Surge b (m) | Peak Tide c (m) | ||
| Hurricane Sandy 2012 | Control | 3.39 | -- | -- | 3.27 | 2.38 | 1.03 |
| SC1 | 3.38 | 0.01 | 0.3 | 3.25 | 2.33 | 1.01 | |
| SC2 | 2.89 | 0.50 | 14.7 | 2.77 | 2.23 | 0.58 | |
| SC3 | 3.16 | 0.23 | 6.8 | 3.06 | 2.32 | 0.76 | |
| Hurricane 1821 | Control | 2.54 | -- | -- | 2.60 | 2.87 | 0.78 |
| SC1 | 2.48 | 0.06 | 2.4 | 2.50 | 2.73 | 0.74 | |
| SC2 | 1.38 | 1.16 | 45.7 | 1.27 | 1.46 | 0.49 | |
| SC3 | 1.79 | 0.75 | 29.5 | 1.85 | 2.20 | 0.64 | |
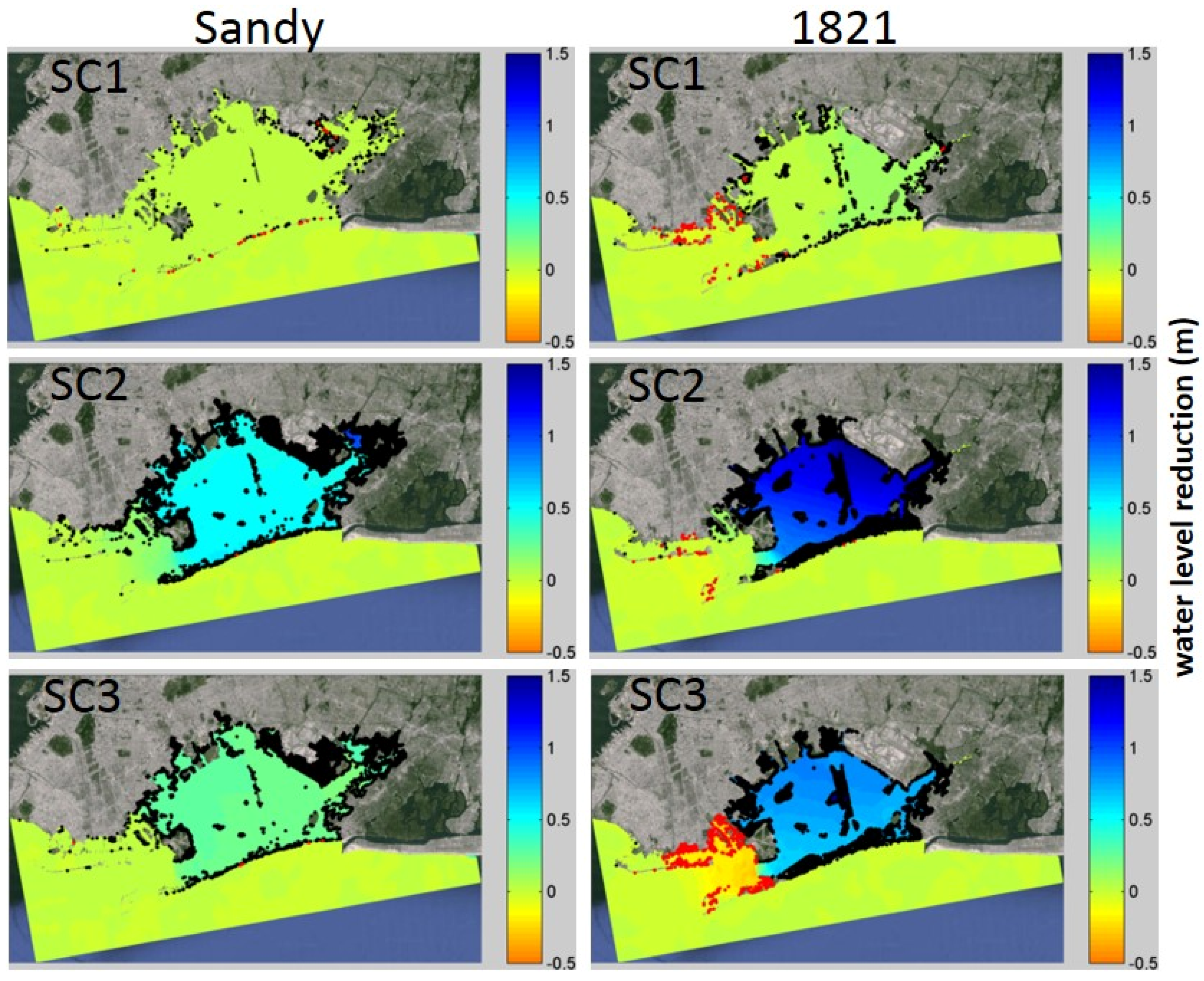
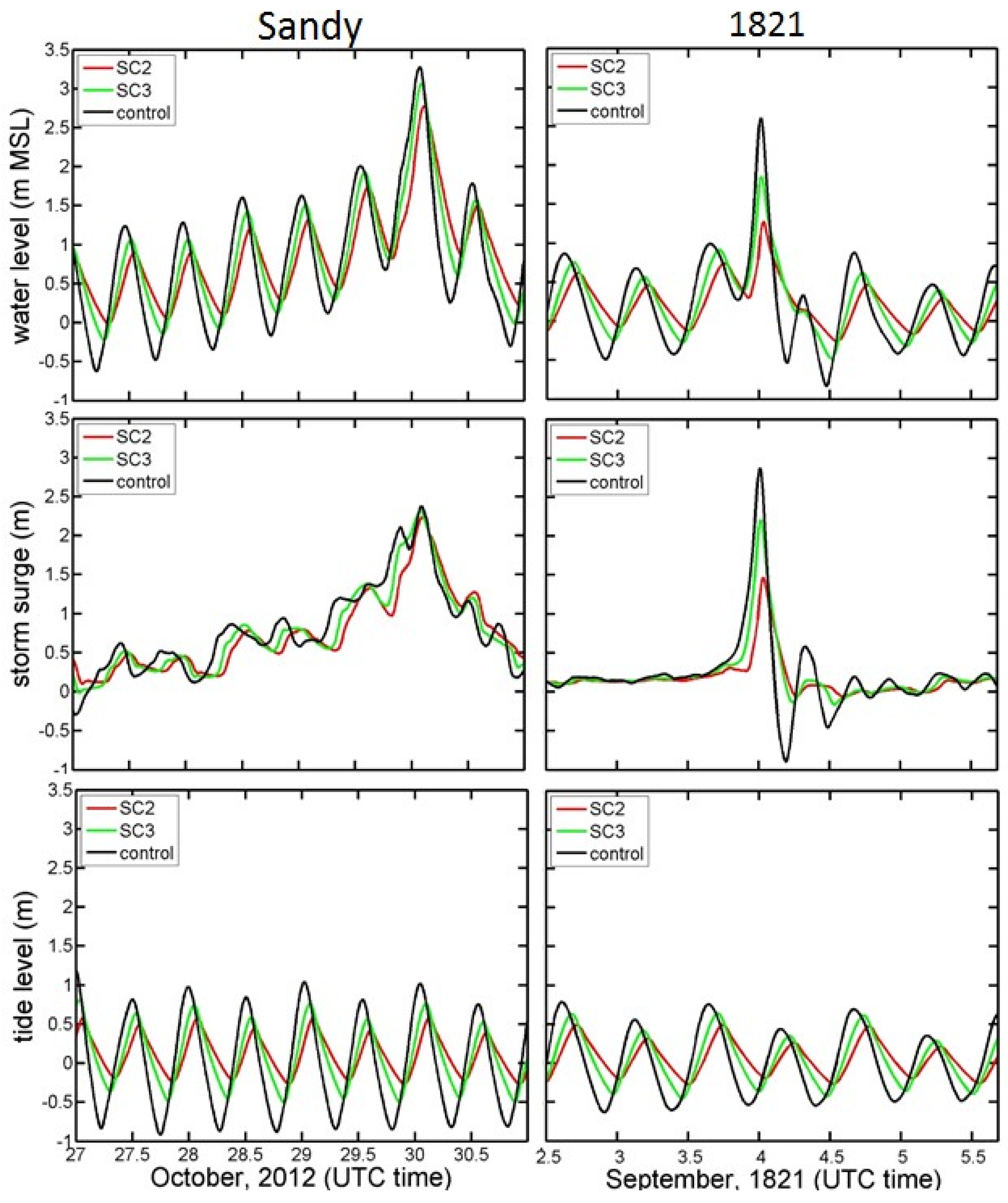
4. Discussion
4.1. Physics of Channel Depth and Storm Tides
4.2. Broader Considerations for Shallowing as Mitigation of Coastal Flooding
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bridges, T.S.; Wagner, P.W.; Burks-Copes, K.A.; Bates, M.E.; Collier, Z.A.; Fischenich, C.J.; Gailani, J.Z.; Leuck, L.D.; Piercy, C.D.; Rosati, J.D. Use of Natural and Nature-Based Features (NNBF) for Coastal Resilience; Engineer Research and Development Center, Vicksburg MS Environmental Lab: Vicksburg, MS, USA, 2015. [Google Scholar]
- Hanson, H.; Brampton, A.; Capobianco, M.; Dette, H.; Hamm, L.; Laustrup, C.; Lechuga, A.; Spanhoff, R. Beach nourishment projects, practices, and objectives—A European overview. Coast. Eng. 2002, 47, 81–111. [Google Scholar] [CrossRef]
- City of New York. A Stronger, More Resilient New York; City of New York: New York, NY, 2013; p. 445.
- Orton, P.; Vinogradov, S.; Georgas, N.; Blumberg, A.; Lin, N.; Gornitz, V.; Little, C.; Jacob, K.; Horton, R. New York City Panel on Climate Change 2015 Report Chapter 4: Dynamic Coastal Flood Modeling. Ann. N. Y. Acad. Sci. 2015, 1336, 56–66. [Google Scholar] [CrossRef] [PubMed]
- Swanson, R.; West-Valle, A.; Decker, C. Recreation vs. waste disposal: The use and management of Jamaica Bay. Long Isl. Hist. J. 1992, 5, 21–41. [Google Scholar]
- Swanson, R.L.; Wilson, R.E. Increased tidal ranges coinciding with Jamaica Bay development contribute to marsh flooding. J. Coast. Res. 2008, 1565–1569. [Google Scholar] [CrossRef]
- NYC-DEP. Jamaica Bay Watershed Protection Plan; New York City Department of Environmental Protection (DEP): New York, NY, USA, 2007; Volume 1, p. 128.
- USACE. Fact Sheet: Jamaica Bay Marsh Islands. Available online: http://www.nan.usace.army. mil/Missions/CivilWorks/ProjectsinNewYork/EldersPointJamaicaBaySaltMarshIslands.aspx (accessed on 13 July 2015).
- NYC-DEP. Jamaica Bay Watershed Protection Plan, One-Year Progress Report; New York City Department of Environmental Protection: New York, NY, USA, 2008; p. 64.
- Corps of Engineers. Interim Survey Report, Morgan City, Louisiana and Vicinity: Serial no. 63; U.S. Army Corps of Engineers District: New Orleans, LA, USA, 1963. [Google Scholar]
- Wamsley, T.V.; Cialone, M.A.; Smith, J.M.; Atkinson, J.H.; Rosati, J.D. The potential of wetlands in reducing storm surge. Ocean Eng. 2010, 37, 59–68. [Google Scholar] [CrossRef]
- Scileppi, E.; Donnelly, J.P. Sedimentary evidence of hurricane strikes in western Long Island, New York. Geochem. Geophys. Geosyst. 2007, 8. [Google Scholar] [CrossRef]
- Swiss Re. The big one: The East Coast’s USD 100 billion hurricane event; Swiss Re America Holding Corporation: Armonk, NY, USA, 2014; p. 21. [Google Scholar]
- Doxsey-Whitfield, E.; MacManus, K.; Adamo, S.B.; Pistolesi, L.; Squires, J.; Borkovska, O.; Baptista, S.R. Taking advantage of the improved availability of census data: A first look at the Gridded Population of the World, Version 4 (GPWv4). Appl. Geogr. 2015, in press. [Google Scholar]
- Columbia University Center for International Earth Science Information Network (CIESIN). New York City, 5 meter Low Elevation Coastal Zone Population Estimates. Available online: http://www.ciesin.columbia.edu/data/nyc5mlecz2010/nyc5mlecz2010.zip (accessed on 13 July 2015).
- Blumberg, A.F.; Georgas, N. Quantifying uncertainty in estuarine and coastal ocean circulation modeling. J. Hydraul. Engin. 2008, 134, 403–415. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Khan, L.A.; St John, J. Three-dimensional hydrodynamic model of New York Harbor region. J. Hydraul. Eng. 1999, 125, 799–816. [Google Scholar] [CrossRef]
- Georgas, N.; Blumberg, A.F. Establishing Confidence in Marine Forecast Systems: The Design and Skill Assessment of the New York Harbor Observation and Prediction System, Version 3 (NYHOPS v3). In Proceedings of the Eleventh International Conference in Estuarine and Coastal Modeling (ECM11), Seattle, WA, USA, 4–6 November 2009.
- Georgas, N.; Blumberg, A.; Herrington, T. An operational coastal wave forecasting model for New Jersey and Long Island waters. Shore Beach 2007, 75, 30–35. [Google Scholar]
- Blumberg, A.; Georgas, N.; Yin, L.; Herrington, T.; Orton, P. Street scale modeling of storm surge inundation along the New Jersey Hudson River waterfront. J. Atmos. Oceanic Technol. 2015, 32. [Google Scholar] [CrossRef]
- FEMA. Region II Coastal Storm Surge Study: Overview; Federal Emergency Management Agency: Washington, DC, USA, 2014; p. 15.
- Georgas, N.; Orton, P.; Blumberg, A.; Cohen, L.; Zarrilli, D.; Yin, L. The impact of tidal phase on Hurricane Sandy's flooding around New York City and Long Island Sound. J. Extreme Events 2014, 1, 1450006. [Google Scholar] [CrossRef]
- Bunya, S.; Dietrich, J.C.; Westerink, J.J.; Ebersole, B.A.; Smith, J.M.; Atkinson, J.H.; Jensen, R.; Resio, D.T.; Luettich, R.A.; Dawson, C.; et al. A high-resolution coupled riverine flow, tide, wind, wind wave, and storm surge model for Southern Louisiana and Mississippi. Part I: Model development and validation. Mon. Weather. Rev. 2010, 138, 345. [Google Scholar] [CrossRef]
- Mattocks, C.; Forbes, C. A real-time, event-triggered storm surge forecasting system for the state of North Carolina. Ocean Model. 2008, 25, 95–119. [Google Scholar] [CrossRef]
- Talke, S.; Orton, P.; Jay, D. Increasing storm tides at New York City. Geophys. Res. Lett. 2014, 41, 1844–2013. [Google Scholar] [CrossRef]
- Kussman, A.S. Report on the Hurricane of September 3, 1821; U.S. Weather Bureau: New York, NY, USA, 1957; p. 54.
- Boose, E.R.; Chamberlin, K.E.; Foster, D.R. Landscape and regional impacts of hurricanes in New England. Ecol. Monogr. 2001, 71, 27–48. [Google Scholar] [CrossRef]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather. Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Jelesnianski, C.; Chen, J.; Shaffer, W.; Oceanic, U.S.N.; Administration, A.; Service, U.S.N.W. SLOSH: Sea, lake, and overland surges from hurricanes; US Dept. of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 1992.
- USC & GS. Jamaica Bay and Rockaway Inlet, Long Island, New York; United States Coast and Geodetic Survey: Washington, DC, USA, 1879.
- Orton, P.; Georgas, N.; Blumberg, A.; Pullen, J. Detailed modeling of recent severe storm tides in estuaries of the New York City region. J. Geophys. Res. 2012, 117, C09030. [Google Scholar] [CrossRef]
- Wang, H.V.; Loftis, J.D.; Liu, Z.; Forrest, D.; Zhang, J. The storm surge and sub-grid inundation modeling in New York City during Hurricane Sandy. J. Mar. Sci. Eng. 2014, 2, 226–246. [Google Scholar] [CrossRef]
- Forbes, C.; Rhome, J.; Mattocks, C.; Taylor, A. Predicting the storm surge threat of Hurricane Sandy with the National Weather Service SLOSH model. J. Mar. Sci. Eng. 2014, 2, 437–476. [Google Scholar] [CrossRef]
- Loder, N.; Irish, J.; Cialone, M.; Wamsley, T. Sensitivity of hurricane surge to morphological parameters of coastal wetlands. Estuar. Coast. Shelf Sci. 2009, 84, 625–636. [Google Scholar] [CrossRef]
- Shepard, C.C.; Crain, C.M.; Beck, M.W. The protective role of coastal marshes: A systematic review and meta-analysis. PLoS ONE 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Resio, D.T.; Westerink, J.J. Modeling the physics of storm surges. Phys. Today 2008, 61, 33–38. [Google Scholar] [CrossRef]
- Ianniello, J. Tidally induced residual currents in estuaries of constant breadth and depth. J. Mar. Res. 1977, 35, 755–786. [Google Scholar]
- Friedrichs, C.T.; Aubrey, D.G. Tidal propagation in strongly convergent channels. J. Geophys. Res. 1994, 99, 3321–3336. [Google Scholar] [CrossRef]
- Dronkers, J.J. Tidal computations in rivers and coastal waters; North Holland Publishing: Amsterdam, The Netherlands, 1964; p. 296. [Google Scholar]
- Jay, D.A. Green’s law revisited: Tidal long-wave propagation in channels with strong topography. J. Geophys. Res. 1991, 96, 20585–20598. [Google Scholar] [CrossRef]
- Aretxabaleta, A.L.; Butman, B.; Ganju, N.K. Water level response in back-barrier bays unchanged following Hurricane Sandy. Geophys. Res. Lett. 2014, 41, 3163–3171. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Gravois, U.; Zachry, B.C.; Westerink, J.J.; Hope, M.E.; Dietrich, J.C.; Powell, M.D.; Cox, A.T.; Luettich, R.A.; Dean, R.G. Origin of the Hurricane Ike forerunner surge. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Burchard, H. Combined effects of wind, tide, and horizontal density gradients on stratification in estuaries and coastal seas. J. Phys. Oceanogr. 2009, 39, 2117–2136. [Google Scholar] [CrossRef]
- Seavitt, C.; Alexander, K.; Alessi, D.; Sands, E. Shifting Sands: Sedimentary Cycles for Jamaica Bay, New York; Catherine Seavitt Nordenson: New York, NY, USA, 2015; p. 218. [Google Scholar]
- Shaffer, G.P.; Day, J.W., Jr.; Mack, S.; Kemp, G.P.; van Heerden, I.; Poirrier, M.A.; Westphal, K.A.; FitzGerald, D.; Milanes, A.; Morris, C.A. The MRGO Navigation Project: A massive human-induced environmental, economic, and storm disaster. J. Coast. Res. 2009, 54, 206–224. [Google Scholar] [CrossRef]
- Chant, R.J.; Fugate, D.; Garvey, E. The shaping of an estuarine superfund site: Roles of evolving dynamics and geomorphology. Estuar. Coasts 2011, 34, 90–105. [Google Scholar] [CrossRef]
- Horton, R.; Little, C.; Gornitz, V.; Bader, D.; Oppenheimer, M. New York City Panel on Climate Change 2015 report Chapter 2: Sea level rise and coastal storms. Ann. N. Y. Acad. Sci. 2015, 1336, 36–44. [Google Scholar] [CrossRef] [PubMed]
- USACE. Hudson-Raritan Estuary Comprehensive Restoration Plan Potential Restoration Opportunities Project Summary Sheets: Jamaica Bay, United States Army Corps of Engineers; USCAE: New York, NY, USA, 2014; p. 138. [Google Scholar]
- Hapke, C.J.; Stockdon, H.F.; Schwab, W.C.; Foley, M.K. Changing the paradigm of response to coastal storms. Eos Trans. Am. Geophys. Union 2013, 94, 189–190. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orton, P.M.; Talke, S.A.; Jay, D.A.; Yin, L.; Blumberg, A.F.; Georgas, N.; Zhao, H.; Roberts, H.J.; MacManus, K. Channel Shallowing as Mitigation of Coastal Flooding. J. Mar. Sci. Eng. 2015, 3, 654-673. https://doi.org/10.3390/jmse3030654
Orton PM, Talke SA, Jay DA, Yin L, Blumberg AF, Georgas N, Zhao H, Roberts HJ, MacManus K. Channel Shallowing as Mitigation of Coastal Flooding. Journal of Marine Science and Engineering. 2015; 3(3):654-673. https://doi.org/10.3390/jmse3030654
Chicago/Turabian StyleOrton, Philip M., Stefan A. Talke, David A. Jay, Larry Yin, Alan F. Blumberg, Nickitas Georgas, Haihong Zhao, Hugh J. Roberts, and Kytt MacManus. 2015. "Channel Shallowing as Mitigation of Coastal Flooding" Journal of Marine Science and Engineering 3, no. 3: 654-673. https://doi.org/10.3390/jmse3030654
APA StyleOrton, P. M., Talke, S. A., Jay, D. A., Yin, L., Blumberg, A. F., Georgas, N., Zhao, H., Roberts, H. J., & MacManus, K. (2015). Channel Shallowing as Mitigation of Coastal Flooding. Journal of Marine Science and Engineering, 3(3), 654-673. https://doi.org/10.3390/jmse3030654