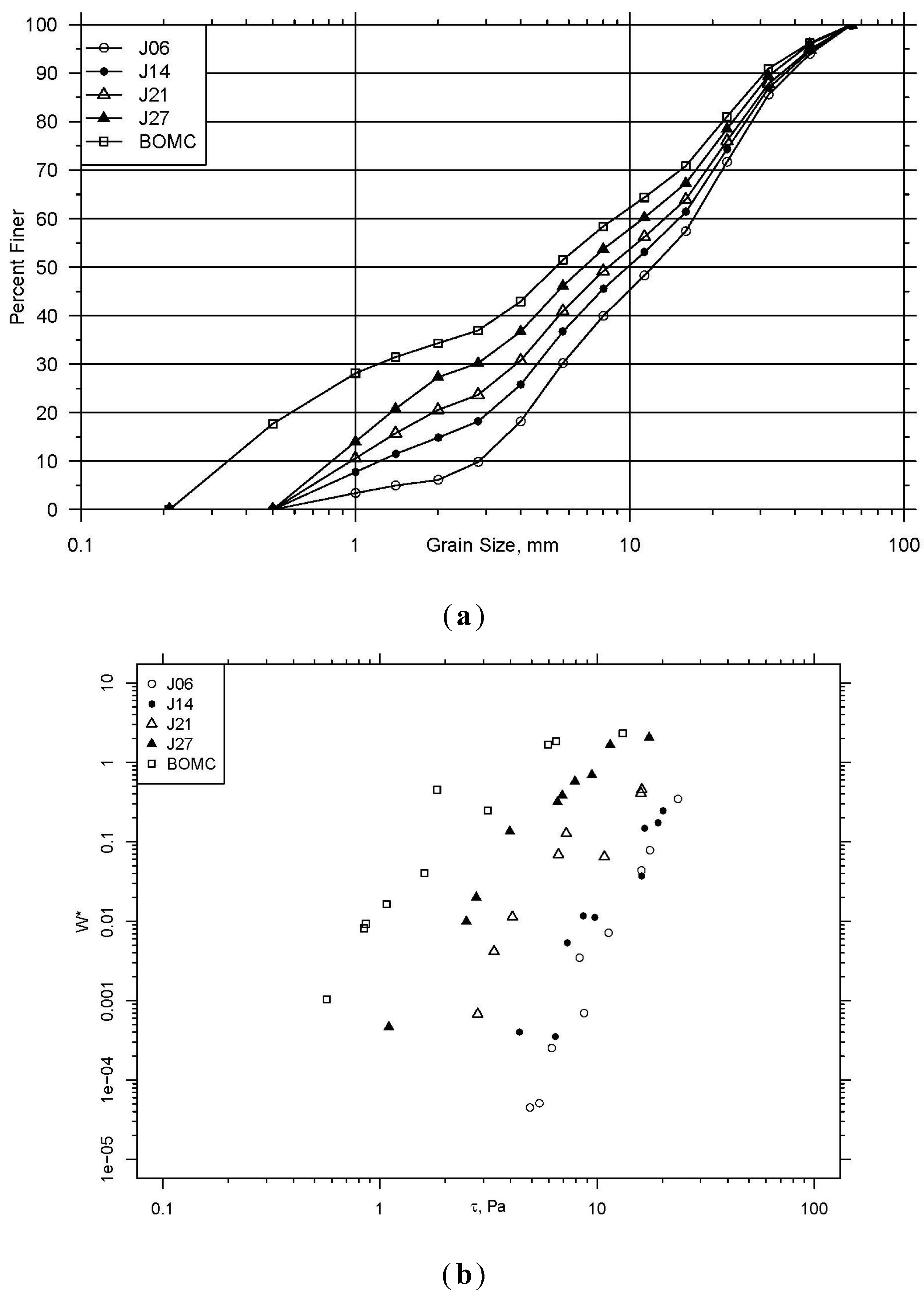
The results that follow are in three sections. The first briefly describes the dataset and provides visualizations and analysis. These also serve as illustrations of the data. The remaining two sections describe the results of the bulk and fractional transport models.
3.1.2. Bulk Transport
The bulk transport model fitted to the observations is similar to the analysis performed in previous work (Schmelter
et al. [
4,
12] for a single sediment size, in which a multi-fraction sediment mixture is modeled using a single fraction model. The total transport rate, integrated across all grain sizes, is the observation and prediction in such an analysis. The reference shear stress and variance inferred from this model represent the integrated or bulk behavior of the sediment mixture as an ensemble. Each different sediment mixture was analyzed in the model described by Equation (7). The inferred reference stresses and variances are summarized in
Table 1.
Table 1.
Data summary for sediment mixtures. Inferred bulk transport posterior means for τr, in Pa and σ in m3/m/s, number of observational runs for each sediment, and the proportion sand in both the surface and total mixture.
Table 1.
Data summary for sediment mixtures. Inferred bulk transport posterior means for τr, in Pa and σ in m3/m/s, number of observational runs for each sediment, and the proportion sand in both the surface and total mixture.
| Parameter | Sediment Mixture |
|---|
| J06 | J14 | J21 | J27 | BOMC |
|---|
| τ | 8.90 | 7.14 | 3.46 | 1.82 | 0.73 |
| σ | 0.74 | 1.26 | 1.23 | 1.11 | 1.04 |
| Observations | 10 | 9 | 8 | 10 | 10 |
| Surface sand proportion | 0.0013 | 0.0130 | 0.0728 | 0.1990 | 0.4789 |
| Total sand proportion | 0.0612 | 0.1484 | 0.2056 | 0.2730 | 0.3432 |
Typical prior parameterizations for reference stress and standard deviation parameters in the likelihood of both the bulk and fractional transport models are generally vague and were used in all models.
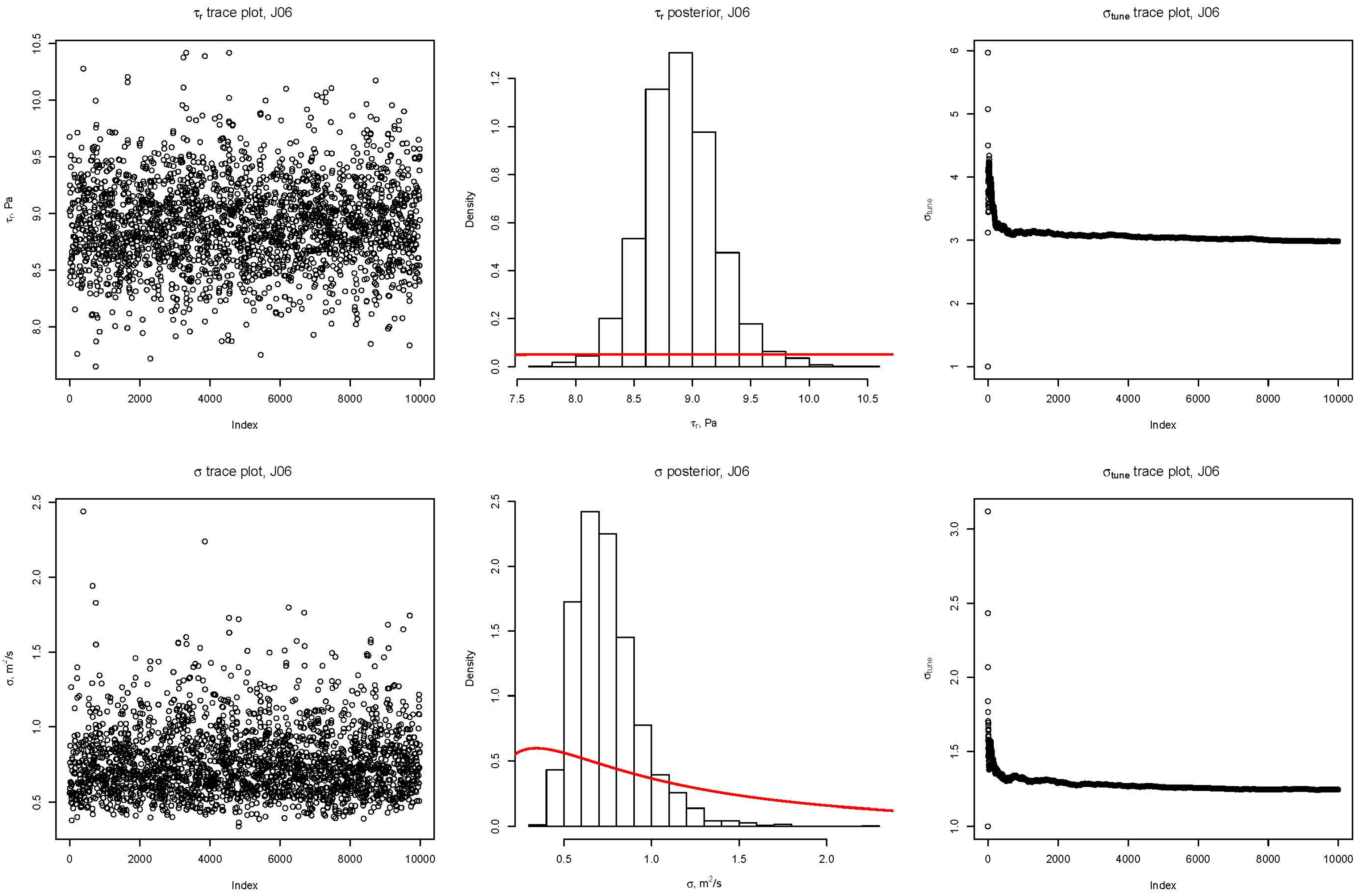
Figure 2.
Trace plots for J06 sediment. Results are representative of all bulk sediments. Red line represents the prior distribution used in the model.
Figure 2.
Trace plots for J06 sediment. Results are representative of all bulk sediments. Red line represents the prior distribution used in the model.
Figure 2 displays the diagnostic plots that resulted from the bulk transport model run for the J06 sediment. The left-most column shows the MCMC trace plots up to the maximum value of 10,000 samples. In these columns we see good mixing of the chains. Further, convergence was rapid and there appears to be minimal autocorrelation among the data points (partial autocorrelation plots were created and inspected, but are not included here), another indicator of valid MCMC results. The middle column shows the posterior histograms after discarding the first 2000 samples as “burn-in”. The right-most column shows the tuning variance adaptation trace plot. There are large fluctuations in the trace plot followed quickly by convergence to a stable tuning variance value. Trace plots for additional sediment exhibited similar characteristics, but are not included here.
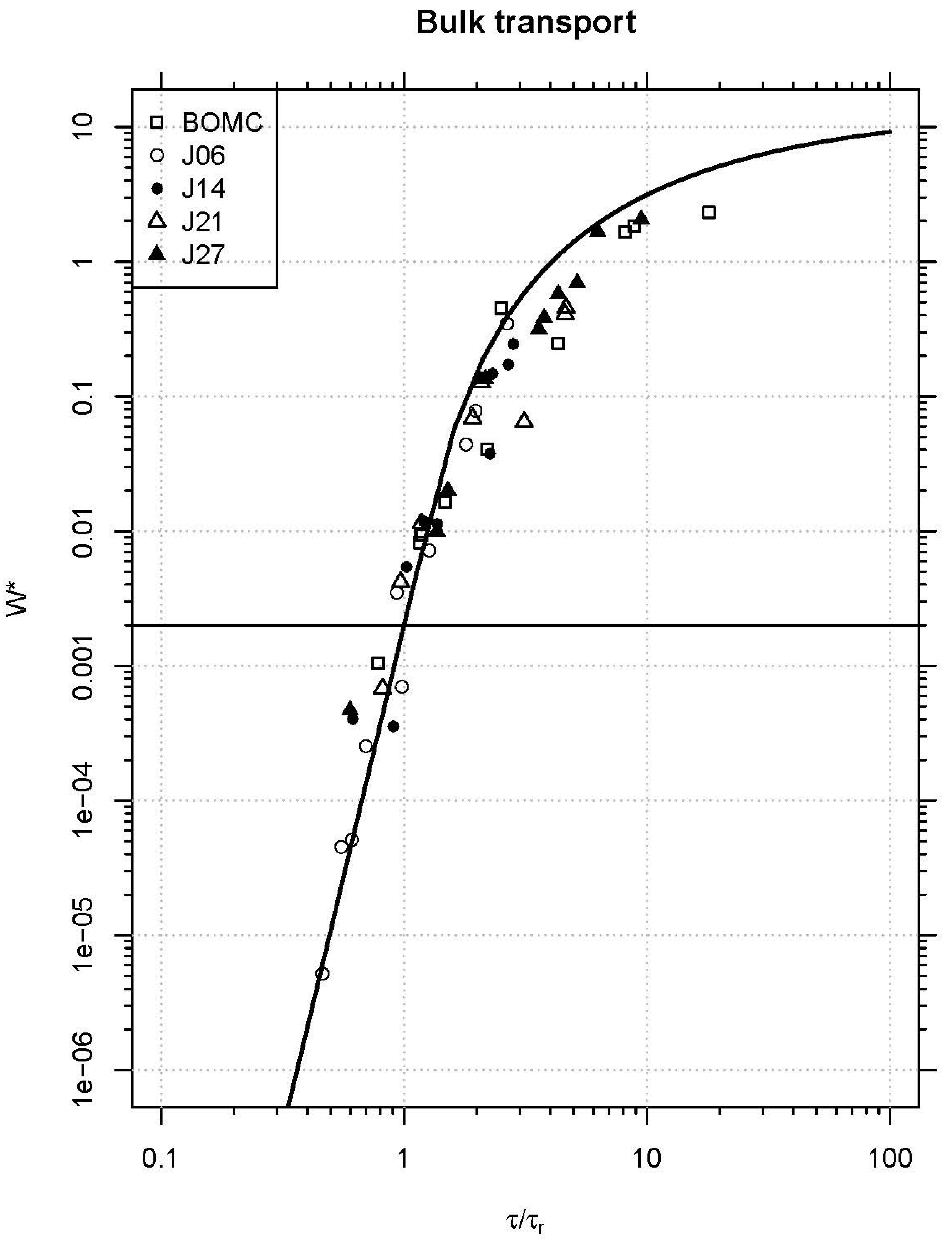
Figure 3 shows the similarity collapse of the bulk transport data. If a single transport function applies to all mixtures, then dividing each stress by the reference stress should collapse all transport observations about a common trend. The similarity collapse relies on the inferred reference stresses for each bulk sediment mixture, which are included in
Table 1 along with the inferred variances and number of observations for each sediment. The mean inferred reference stresses provides the normalizing constant to make all the transport observations collapse into a single series of points. The resulting similarity collapse for the bulk transport model demonstrates that when each sediment mixture and transport observation is scaled by the inferred reference stress, then all of the points collapse into a single relationship. The line in
Figure 3 (the calibrated Wilcock-Crowe Equation (1) for the bulk transport data) fits the data very well for
W* values less than 0.01. Transport rates appear to be over predicted for
W* values greater than 0.03, indicating a model deficiency in the case of bulk sediment transport.
Figure 3.
Similarity collapse for bulk transport rates. The bold line is the calibrated Wilcock-Crowe Equation (1) for the bulk transport data. W* = 0.002 is the reference value that corresponds to the reference shear stress τr.
Figure 3.
Similarity collapse for bulk transport rates. The bold line is the calibrated Wilcock-Crowe Equation (1) for the bulk transport data. W* = 0.002 is the reference value that corresponds to the reference shear stress τr.
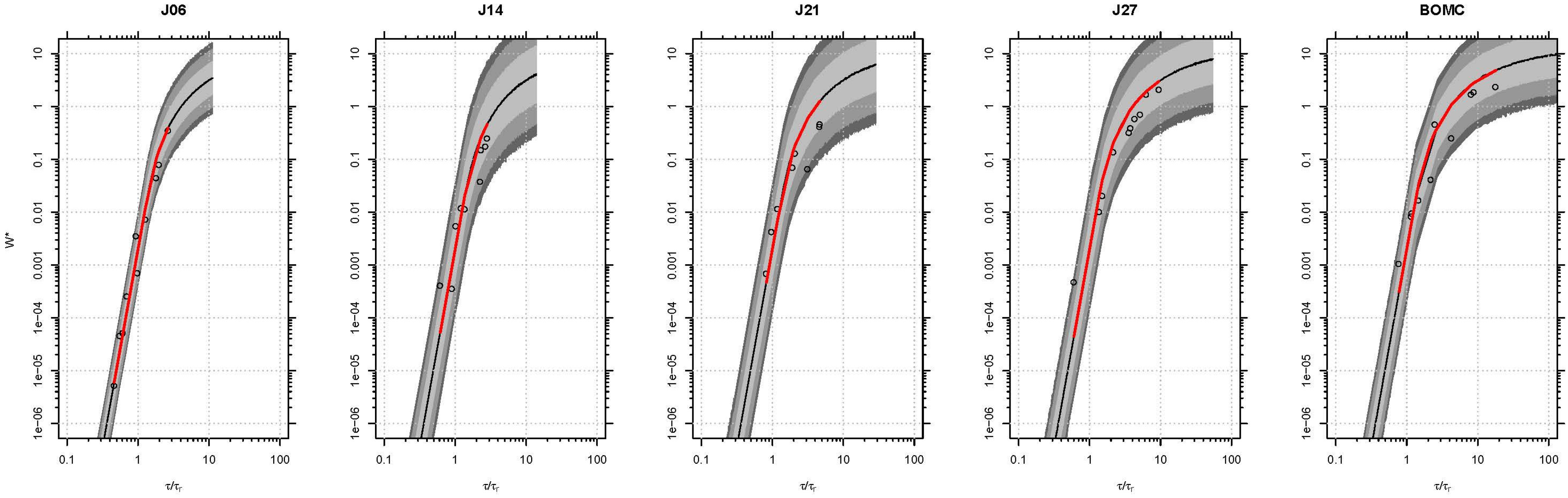
Individual posterior predictive distributions (PPDs) were calculated for each sediment mixture, and these PPDs are included as
Figure 4. As a validation/check of Bayesian parameter estimates, a non-linear least squares regression was fitted to the observed data, and the resulting rating curves are represented by the red lines. This overlay demonstrates that parameter inference resulting from the Bayesian and nonlinear least squares (NLS) approaches agree, so this serves as a type of validation that the Bayesian model was correctly implemented in the code.
Figure 4 also illustrates one of the primary differences defined in the Bayesian approach. Individually, the transport rating curves may also suggest systematic over-prediction evidenced by the individual rating curves for J21 and J27, though it is less convincing than the evidence provided by the similarity collapse in
Figure 3.
Figure 4.
Bulk rating curves. Red line shows the NLS prediction. Color coded darkest to lightest for the 95%, 90%, and 68% credible intervals.
Figure 4.
Bulk rating curves. Red line shows the NLS prediction. Color coded darkest to lightest for the 95%, 90%, and 68% credible intervals.
3.1.3. Fractional Transport
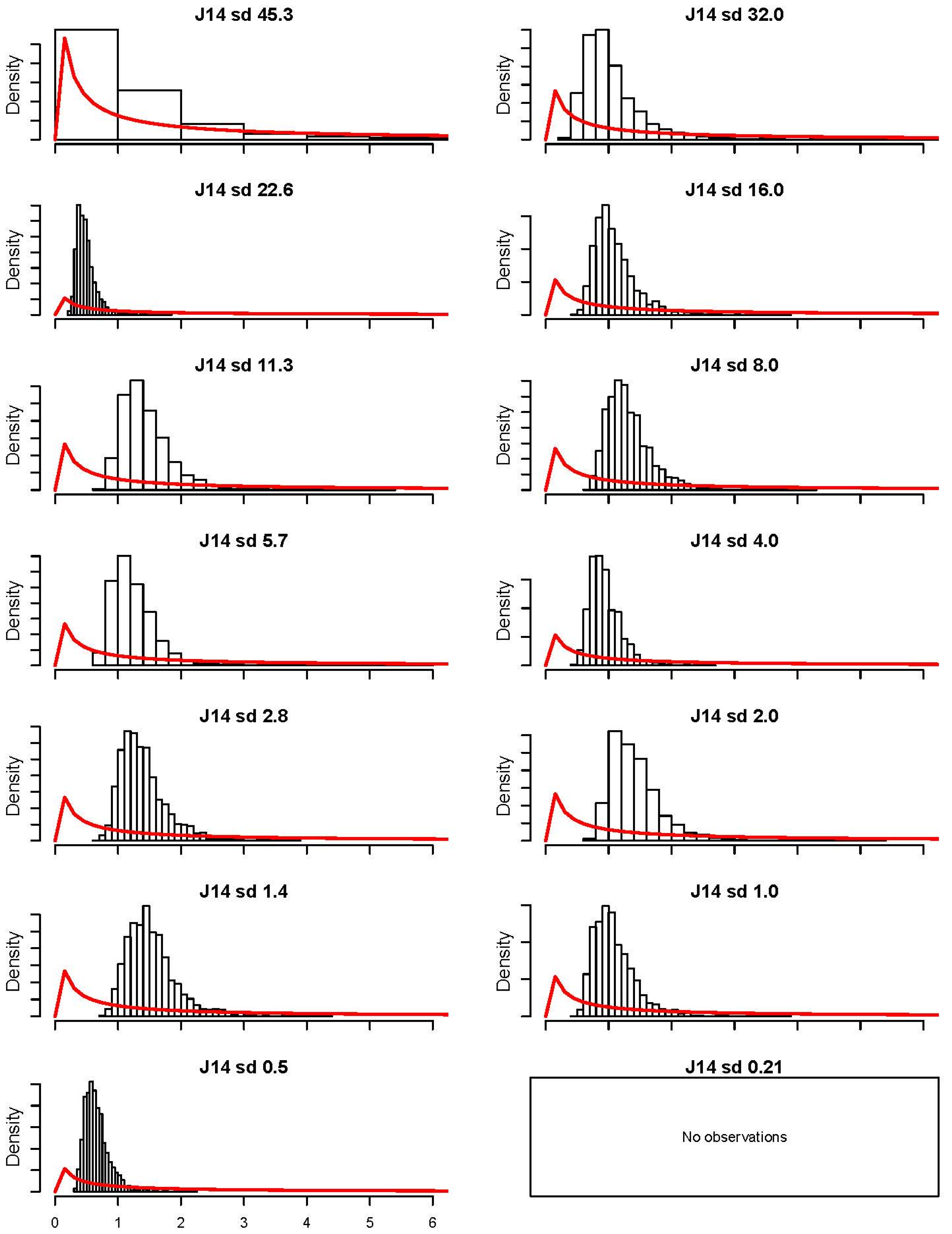
Figure 5 and
Figure 6 show the posterior distributions for the fractional model fitted to the J14 sediment mixture. The distributions are plotted by size fraction, along with the prior distribution plotted as a solid (red) line for reference. Compared to the prior information supplied, which was a uniform distribution over the interval (0,20], the information provided by the observations, even where there were very few observations as is the case for the coarser grain sizes, such as 45.3 mm, (
Table 2) indicates that there is still significant learning about the reference stress. One weakness of the current model, however, is that flume experiments that did not result in any movement of a particular grain size (e.g., larger grains at small τ) are not accounted for in the model. That is, only those instances where sediment moved are considered a data point, even though there is important information contained in experiments with nonmoving fractions. The current model does not use any of the information contained in zero-transport experimental runs. This is possible by specifying a lower limit in the prior distribution based on the experimental runs with no transport for some fractions. Those conditions produce a shear stress that is necessarily smaller than the reference stress for immobile fractions. Finally, incorporating this information into the model in a more formal way (
i.e., developing a model that accounts for zero transport events) would be a valuable improvement in future research.
Figure 5.
Fractional posterior distributions of τr;j for J14. Red line represents the prior distribution used in the model.
Figure 5.
Fractional posterior distributions of τr;j for J14. Red line represents the prior distribution used in the model.
Figure 6.
Fractional posterior distributions of σj for J14. Red line represents the prior distribution used in the model.
Figure 6.
Fractional posterior distributions of σj for J14. Red line represents the prior distribution used in the model.
Table 2.
Inferred fractional transport posterior means for τr,j (Pa).
Table 2.
Inferred fractional transport posterior means for τr,j (Pa).
| Size (mm) | Sediment Mixture |
|---|
| J06 | J14 | J21 | J27 | BOMC |
|---|
| τr,j (Pa) | # Obs. | τr,j (Pa) | # Obs. | τr,j (Pa) | # Obs. | τr,j (Pa) | # Obs. | τr,j (Pa) | # Obs. |
|---|
| 45.3 | 14.40 | 3 | 13.87 | 2 | 13.13 | 1 | 8.14 | 1 | 8.42 | 1 |
| 32.0 | 11.33 | 4 | 11.15 | 4 | 7.45 | 2 | 7.00 | 4 | 7.07 | 2 |
| 22.6 | 10.27 | 6 | 9.67 | 7 | 7.48 | 5 | 5.38 | 6 | 3.59 | 4 |
| 16.0 | 9.08 | 7 | 7.25 | 8 | 5.39 | 6 | 3.57 | 6 | 3.86 | 4 |
| 11.3 | 9.39 | 7 | 7.31 | 9 | 4.80 | 6 | 3.08 | 7 | 3.46 | 4 |
| 8.0 | 8.65 | 9 | 7.46 | 9 | 4.04 | 8 | 2.83 | 9 | 2.31 | 5 |
| 5.7 | 7.90 | 10 | 6.38 | 9 | 3.09 | 8 | 2.19 | 9 | 1.94 | 6 |
| 4.0 | 7.71 | 10 | 5.60 | 9 | 2.87 | 8 | 1.48 | 10 | 1.79 | 6 |
| 2.8 | 8.99 | 10 | 7.41 | 9 | 3.47 | 8 | 1.97 | 10 | 1.31 | 8 |
| 2.0 | 8.96 | 9 | 6.83 | 9 | 3.07 | 8 | 1.51 | 10 | 1.03 | 9 |
| 1.4 | 9.53 | 8 | 7.12 | 9 | 3.21 | 8 | 1.56 | 10 | 1.01 | 10 |
| 1.0 | na | 0 | 5.02 | 8 | 2.57 | 8 | 1.35 | 10 | 0.74 | 10 |
| 0.5 | 6.77 | 4 | 4.18 | 8 | 2.63 | 8 | 1.43 | 10 | 0.61 | 10 |
| 0.21 | na | 0 | na | 0 | na | 0 | na | 0 | 0.62 | 10 |
The original derivation of the Wilcock-Crowe equations was based on reference stress values that were fitted by eye in Wilcock and Crowe [
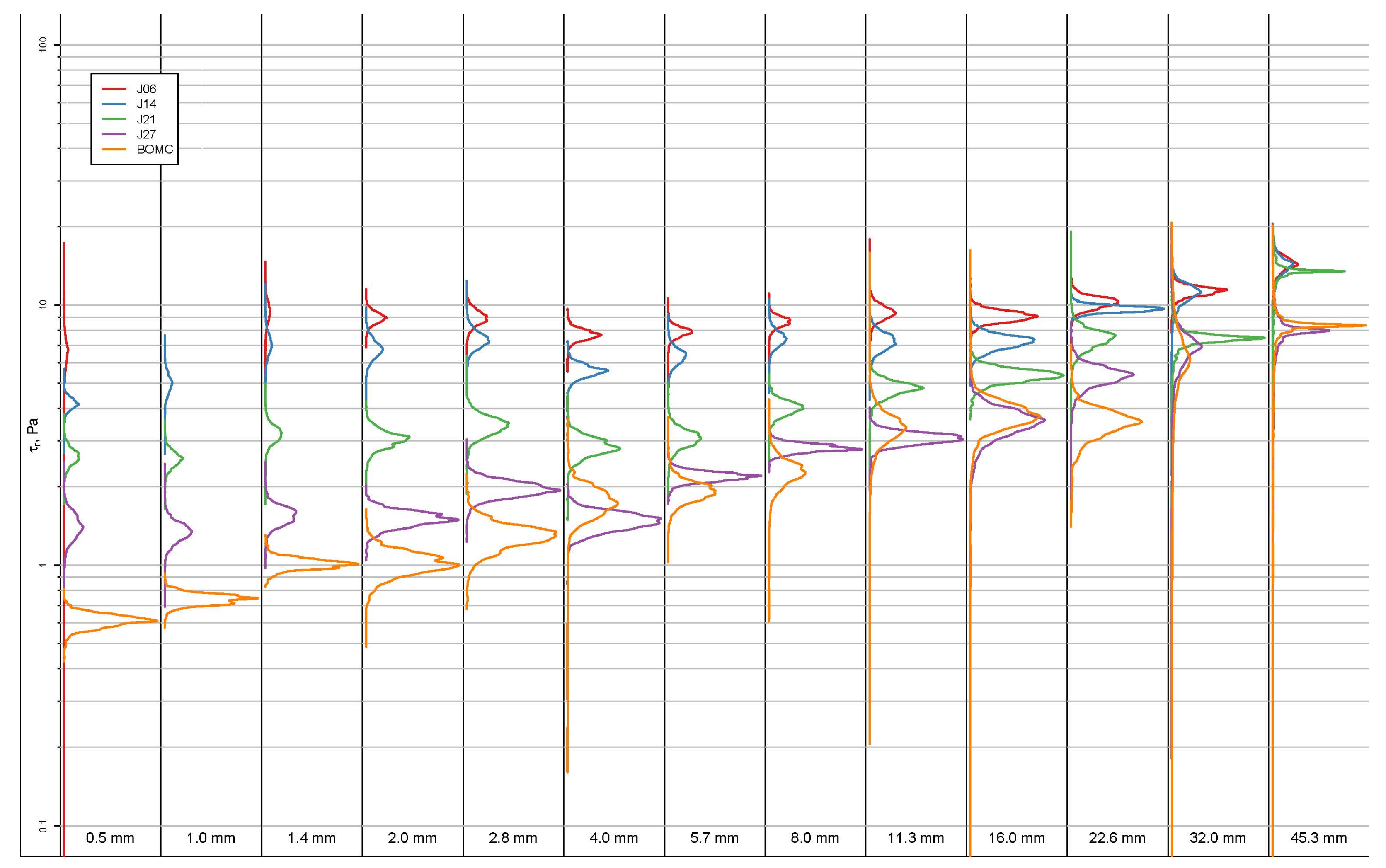
6] because it was observed that optimized solutions for the parameters did not provide as good a fit visually and seemed to be overly influenced by outliers. The Bayesian model produces estimates of reference shear. The point values (means) are shown in
Table 2, and the graphical representation of the posteriors is shown in
Figure 7. From these densities, the inference can be visualized in a number of ways.
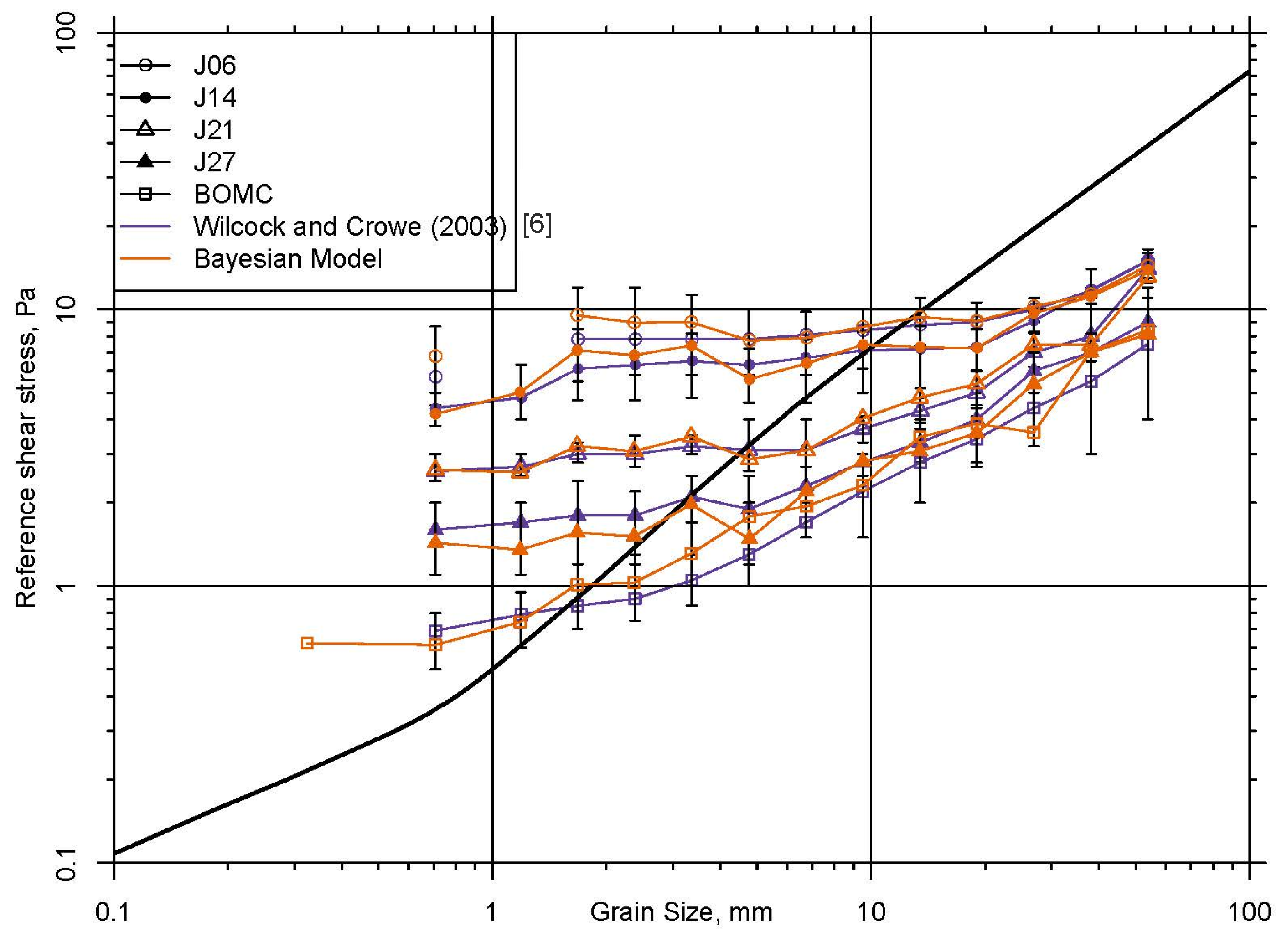
Figure 8 shows the original Wilcock and Crowe [
6] point estimates for reference stress, as well as error bars for each point value, along with the posterior mean values referenced in
Table 2.
Figure 7.
Inferred densities for reference shear stress.
Figure 7.
Inferred densities for reference shear stress.
Figure 8.
Comparison of original reference stress curves from Wilcock and Crowe [
6] to inferred curves from Bayesian model. Error bars are those from [
6]. The solid black line shows the standard Shields Curve for incipient motion of uni-size sediment.
Figure 8.
Comparison of original reference stress curves from Wilcock and Crowe [
6] to inferred curves from Bayesian model. Error bars are those from [
6]. The solid black line shows the standard Shields Curve for incipient motion of uni-size sediment.
Reference shear stress are more widely separated among the mixtures for finer grain sizes. The mixtures with less sand are generally flatter, indicating a condition of equal mobility in which all particles begin to move at the same shear stress. Sandier mixtures exhibit a larger variation in reference shear stress and, in general, fall below the mixtures with less sand, indicating the effect of sand on reducing mobility and increasing transport rate. Also shown on
Figure 8 is the traditional Shields curve for incipient motion of uni-size sediment (solid black line). The reference shear stress for different size fractions in a mixture is clearly different than for uni-size beds.
Figure 9 shows each sediment mixture broken out individually with the posterior distribution of reference stress overlain by the original estimates of reference stress, with their associated uncertainty estimates, from [
6].
There are some structural differences in the individual model results from this analysis. For example, inferred reference stresses for sediment mixture J27 shows a dip in the 4.0 mm size. The reference stresses from [
6] show a much smaller decrease for this size fraction, but it is not as prominent as the results from the Bayesian model. On the whole, the original results shown in
Figure 5 of Wilcock and Crowe [
6] are more monotonic than the results of the current analysis. One underlying goal of Wilcock and Crowe [
6] was to further investigate the effect of sand content on transport and it was assumed that increased sand contents correlated with increased transport rates. With an overarching theory of increased transport with sand content, one would believe the relationship to be positive monotonic, so the bumps and deviations in the inferred reference stresses may be experimental noise.
The overall positive monotonic theoretical relationship for sand content and transport, while not directly inferred from the analysis, is still likely given the variability of the parameters.
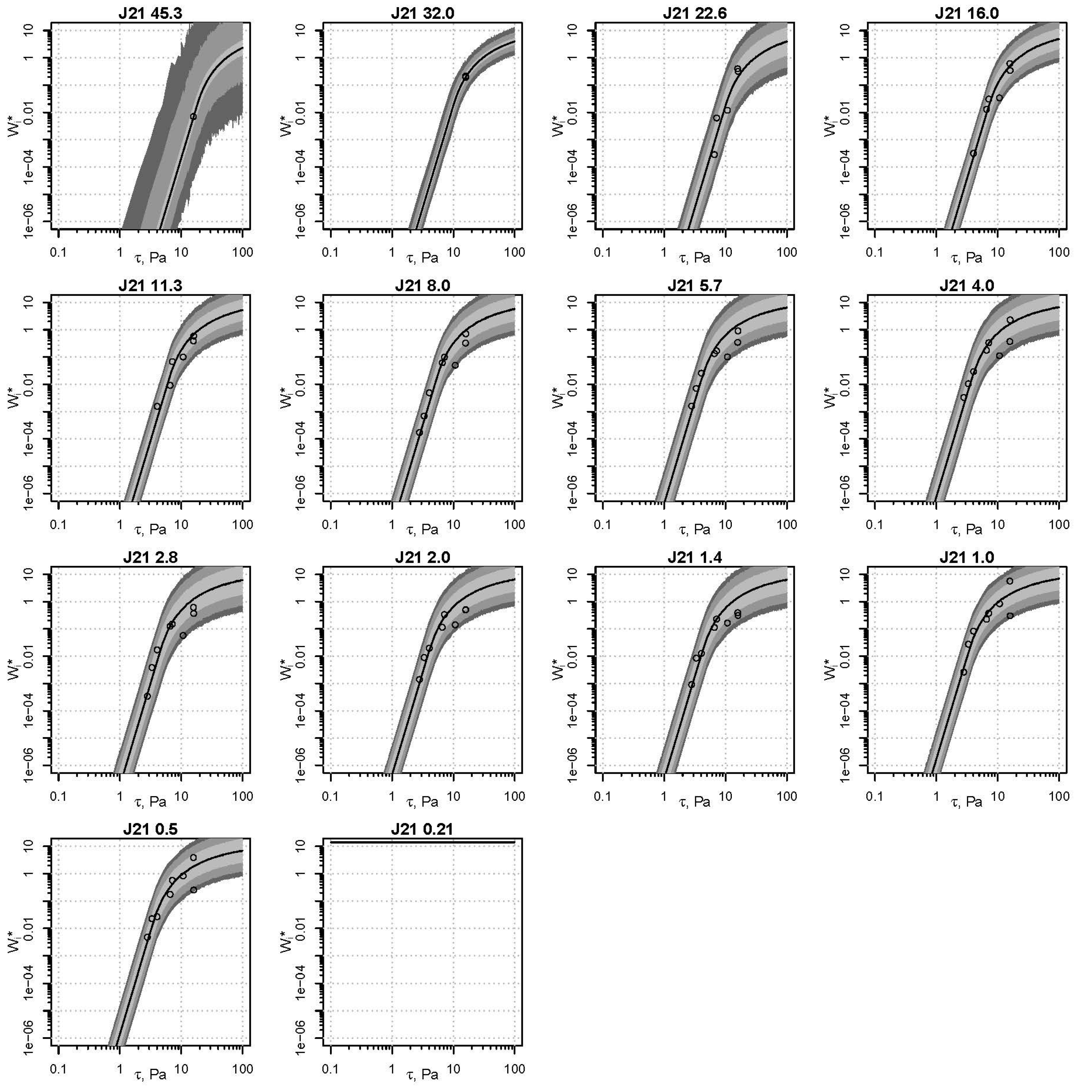
Figure 10 shows an example the fractional rating curves for the J21 sediment. The results in this and related figures [
25] indicate that the model is generally able to infer a reference stress distribution that produces predictions consistent with the observations. While the rating curves generally seem to be appropriate, there is one suspect rating curve, that for the 32.0 mm size fraction. This size fraction had only two closely spaced observations, such that the posterior distribution is surprisingly narrow compared to the 45.3 mm posterior of the same figure, which has only one observation. The variance for the 32.0 mm fraction is evidently not representative of the true process. This shortcoming is not unique to a Bayesian approach, but is a general limitation and constraint that accompany these data. To compensate for this, a more specific prior for the variance parameter could be specified.
Figure 9.
Individual sediment comparisons of original reference stress curves from Wilcock and Crowe [
6] to inferred curves from Bayesian Model. Error bars are those from Wilcock and Crowe [
6]. Credible intervals are color coded from darkest to lightest for 95%, 90%, and 68%. The 0.707 mm value was jittered so as to not overplot for J06. The solid black line shows the standard Shields Curve for incipient motion of uni-size sediment.
Figure 9.
Individual sediment comparisons of original reference stress curves from Wilcock and Crowe [
6] to inferred curves from Bayesian Model. Error bars are those from Wilcock and Crowe [
6]. Credible intervals are color coded from darkest to lightest for 95%, 90%, and 68%. The 0.707 mm value was jittered so as to not overplot for J06. The solid black line shows the standard Shields Curve for incipient motion of uni-size sediment.
Figure 10.
Posterior predictive distribution for J21, color coded darkest to lightest for the 95%, 90%, and 68% credible intervals.
Figure 10.
Posterior predictive distribution for J21, color coded darkest to lightest for the 95%, 90%, and 68% credible intervals.
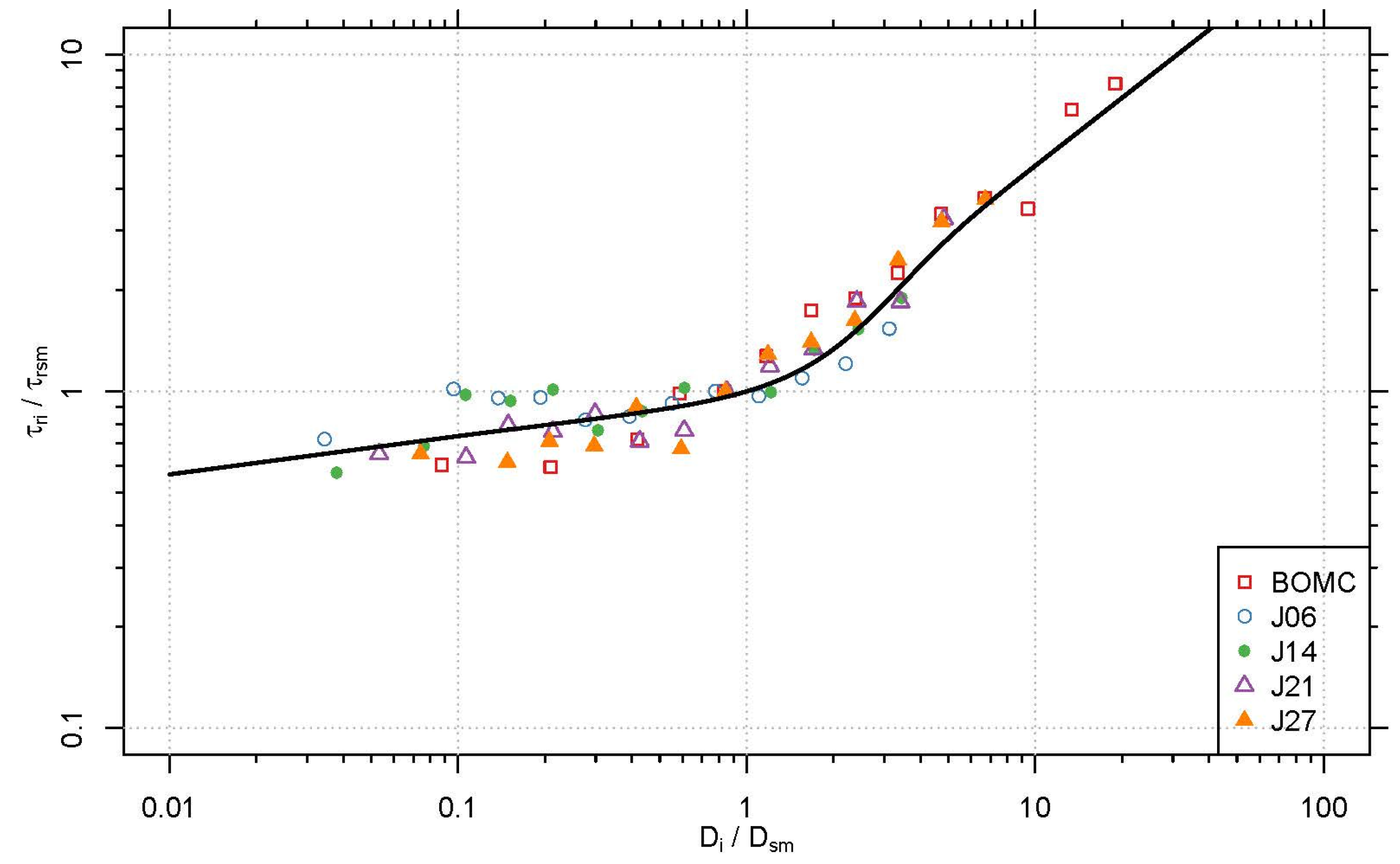
The inferred reference stresses in
Table 2 can be used to construct a plot of the Wilcock-Crowe hiding function, which plots the ratio of the reference stress for a given size fraction to the reference stress of the surface geometric mean particle size against the ratio of the grain diameter of a given size fraction to the ratio of the geometric mean surface grain diameter. Thus,
Figure 11 shows how the reference stress for a given size fraction can collapse into a single relation when scaled by the geometric mean particle size reference stress and diameter. This relationship was a central finding of Wilcock and Crowe ([
6],
Figure 4) and resulted from the manually calibrated reference stresses. In this research, the reference stresses were inferred from the Bayesian multi-fraction model and yield a similar trend.
Another central result from Wilcock and Crowe ([
6],
Figure 5) was the observation that the reference shear stress of the entire sediment mixture varies with sand content. It was observed that the reference stress of the geometric mean particle size of the mixture—the grain size used to scale the hiding function—decreased with increasing sand content and a model to describe this change in reference stress was proposed
with the published result
Figure 11.
Hiding function using inferred mean surface size reference stresses give valid results when compared to the manually-estimated parameter values used to construct the original similarity collapse of
Figure 6 in Wilcock and Crowe [
6].
Figure 11.
Hiding function using inferred mean surface size reference stresses give valid results when compared to the manually-estimated parameter values used to construct the original similarity collapse of
Figure 6 in Wilcock and Crowe [
6].
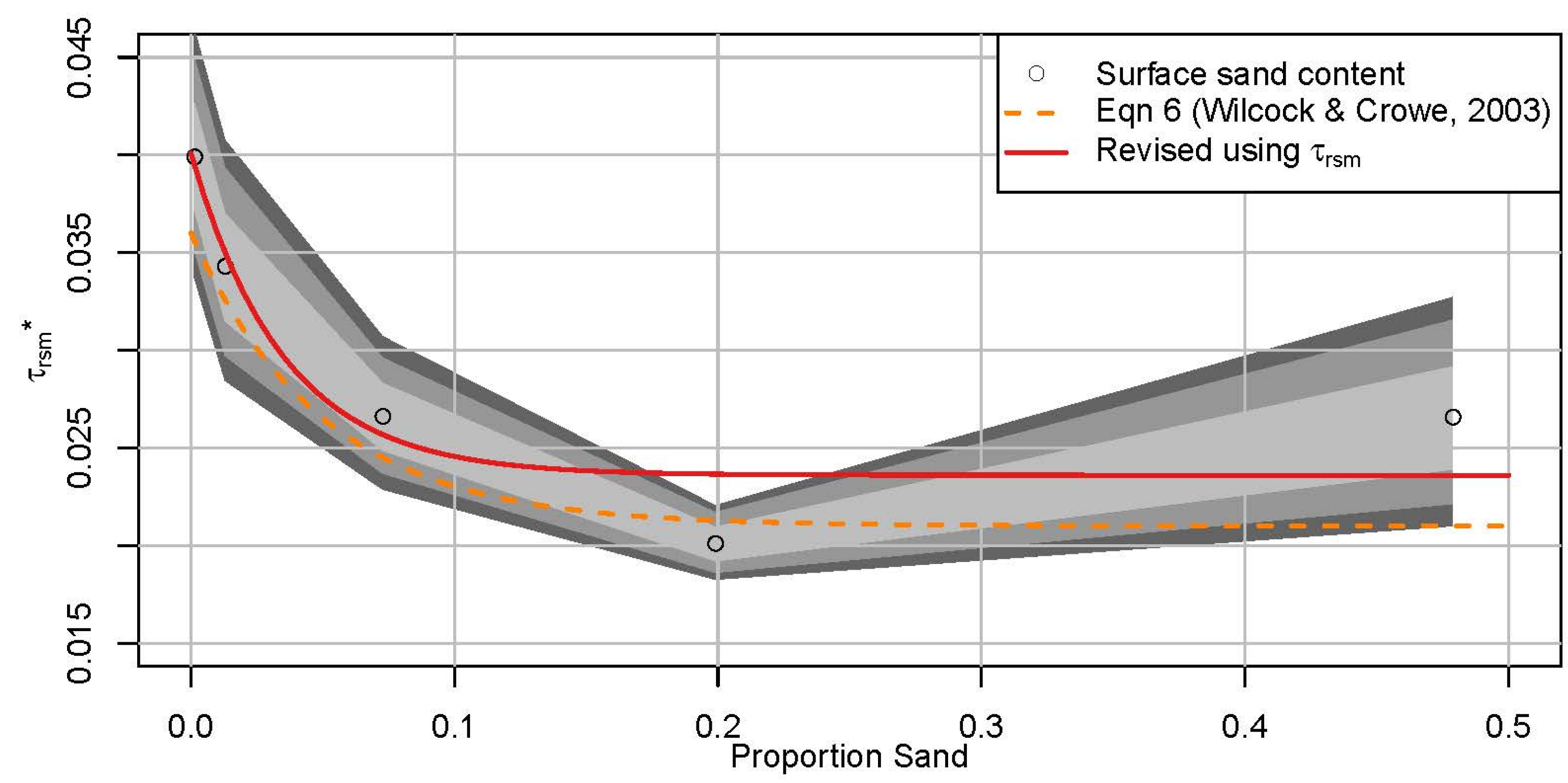
Figure 5 of [
6] was updated using the inferred parameter values for reference stress and is included as
Figure 12. The original formulation for describing the change in the reference stress of the mean particle size class is plotted as a dashed line in
Figure 12. Because there is significant variability in the right-most point (corresponding to the inferred mean reference stress for BOMC), a new relationship was fitted to these data points using NLS:
Figure 12.
Reference Shields stresses for the mean size of the bed surface plotted against proportion sand on the bed surface, with credible intervals, color coded darkest to lightest for 95%, 90%, and 68%.
Figure 12.
Reference Shields stresses for the mean size of the bed surface plotted against proportion sand on the bed surface, with credible intervals, color coded darkest to lightest for 95%, 90%, and 68%.
While a new equation can be fitted to the plotted points, this does not change the fact that there the right-most point exerts leverage and requires the entire flat portion of Equation (15) and
Figure 12 to be elevated. The posterior distribution of the geometric mean surface grain size reference stress was used to construct a credible interval, plotted in
Figure 12. Here we see that the variation in the reference stress alone could account for significant spread in the resulting Equations (13) through (15).
Another central result from Wilcock and Crowe ([
6],
Figure 5) was the observation that the reference shear stress of the entire sediment mixture varies with sand content. It was observed that the reference stress of the geometric mean particle size of the mixture—the grain size used to scale the hiding function—decreased with increasing sand content and a model to describe this change in reference stress was proposed
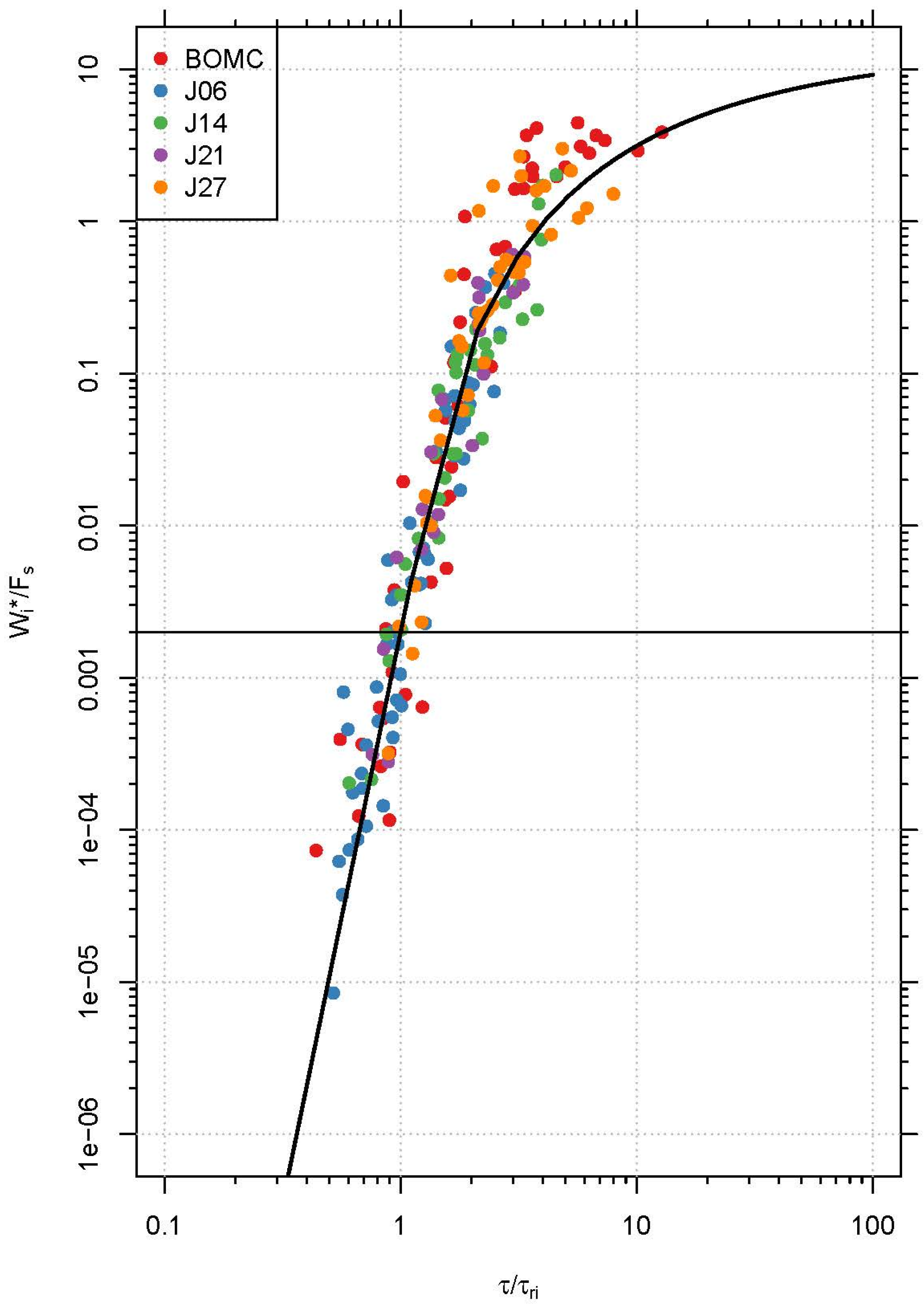
Figure 13 shows the fractional similarity collapse constructed using the inferred reference stresses for each grain size class and sediment mixture. This figure is comparable to
Figure 6 of Wilcock and Crowe [
6] and demonstrates that the estimated parameters from the Bayesian model are able to give valid results when compared to the manually-estimated parameter values used to construct the original similarity collapse of
Figure 6 in Wilcock and Crowe [
6].
Figure 13.
Fractional similarity collapse for multifraction observations and model prediction. The bold line though the data is the calibrated multifraction Wilcock-Crowe Equations (2)–(6) for the multifraction transport data). W* = 0.002 is the reference value that corresponds to the reference shear stress τr.
Figure 13.
Fractional similarity collapse for multifraction observations and model prediction. The bold line though the data is the calibrated multifraction Wilcock-Crowe Equations (2)–(6) for the multifraction transport data). W* = 0.002 is the reference value that corresponds to the reference shear stress τr.