Research on Calibration Methods and Experiments for Six-Component Force Sensors
Abstract
1. Introduction
- The innovative design and implementation of an efficient six-component force sensor calibration device and method based on a dual-rotation mechanism to improve the degrees of freedom, efficiency, and accuracy of calibration.
- Systematic validation of the proposed calibration method’s high accuracy and engineering applicability through rotational arm tests with a KCS standard ship model, thereby providing reliable measurement support for hydrodynamic model testing.
2. Methodology
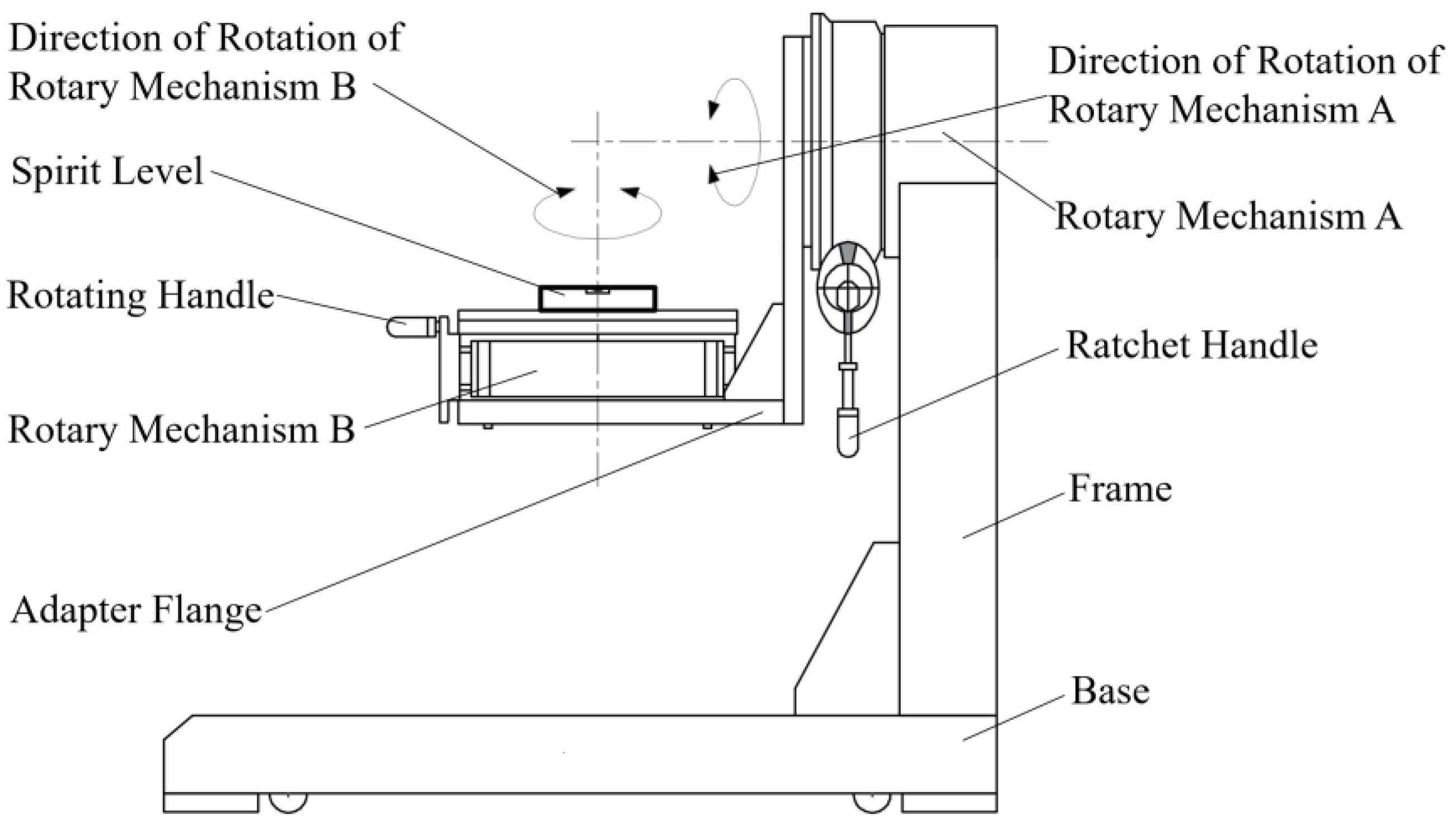
2.1. Calibration Device Design
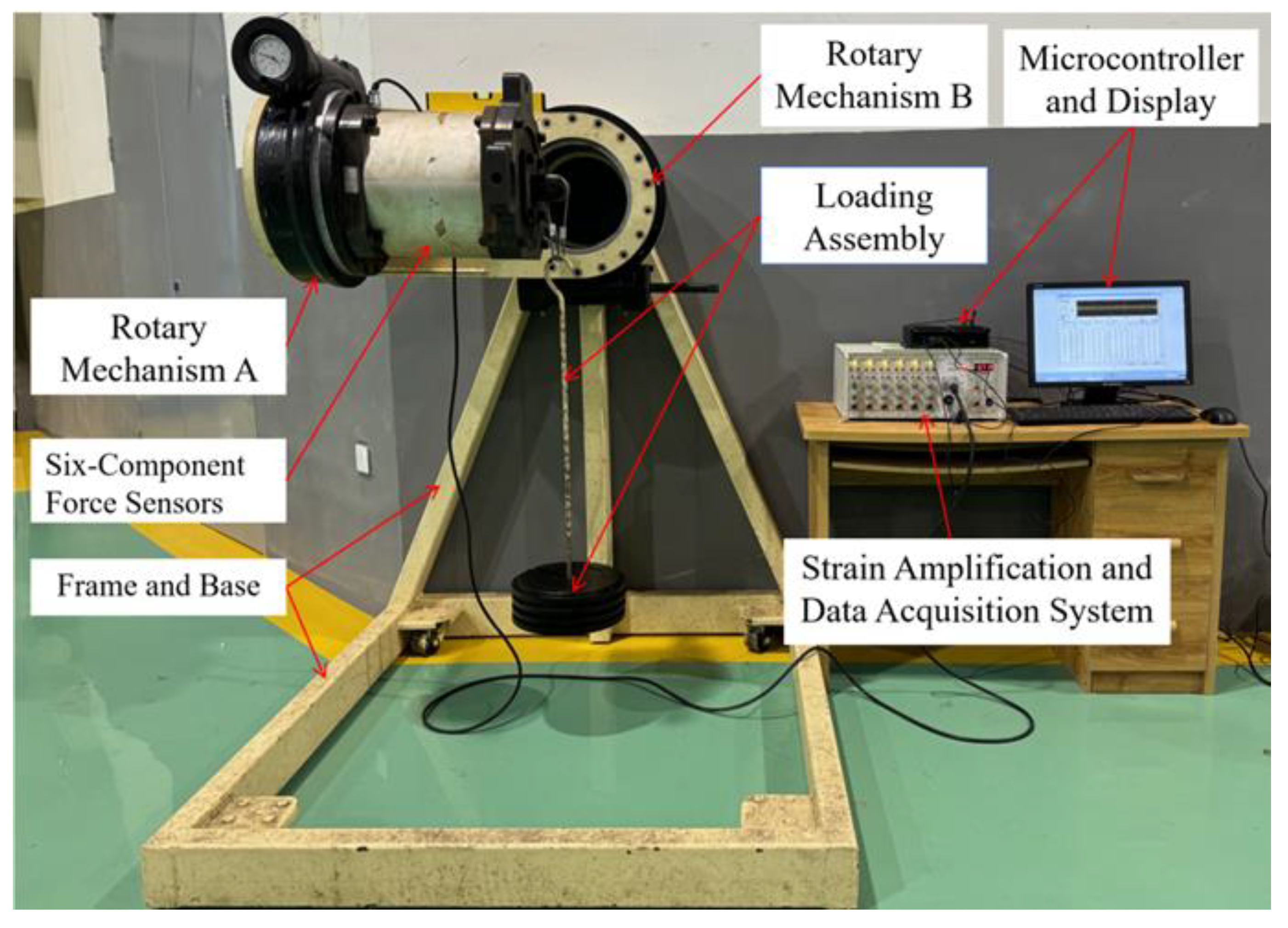
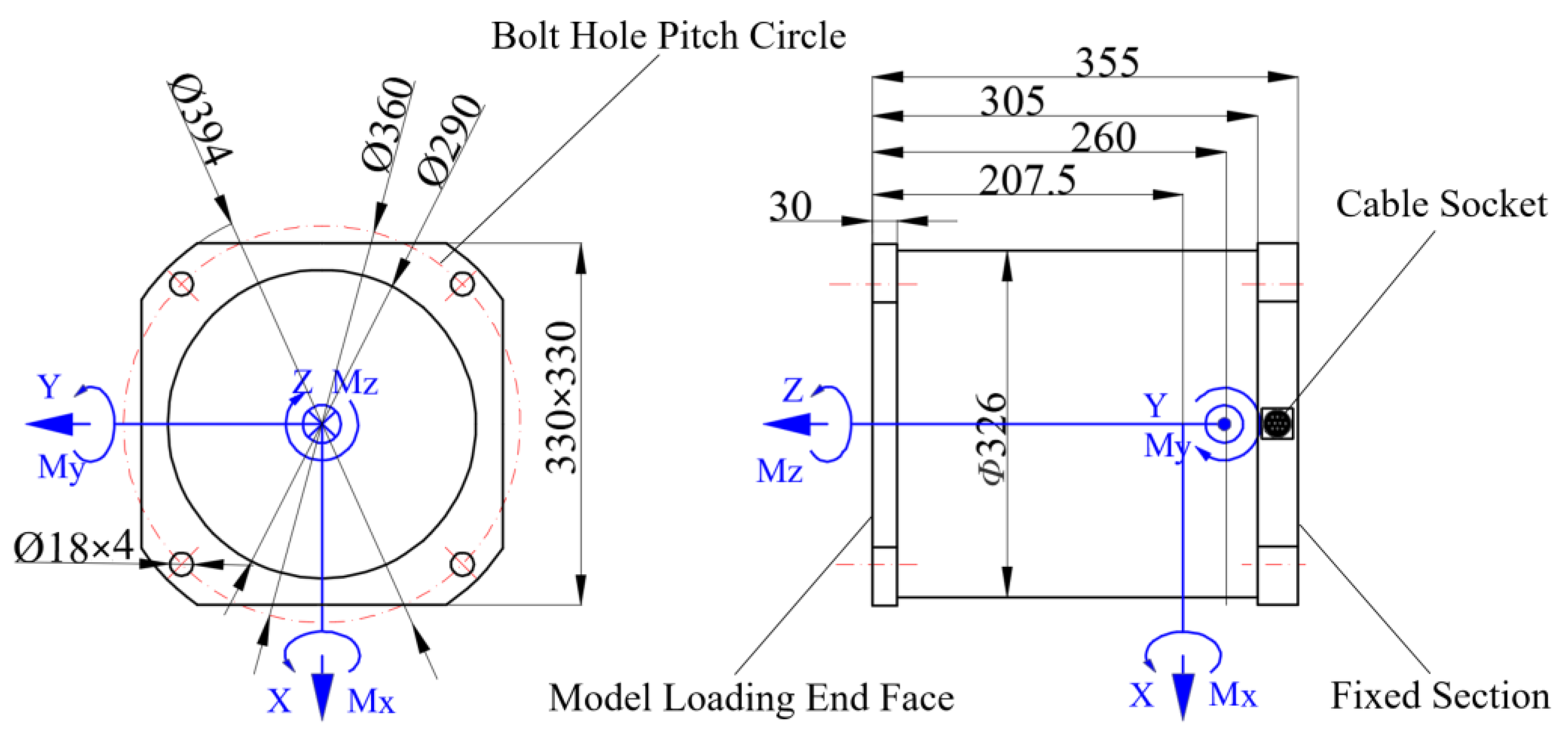
2.2. Calibration System Composition
2.3. Calibration Example
3. Results
3.1. Data Processing
3.2. Coefficient Matrix Verification
4. Experimental Cases
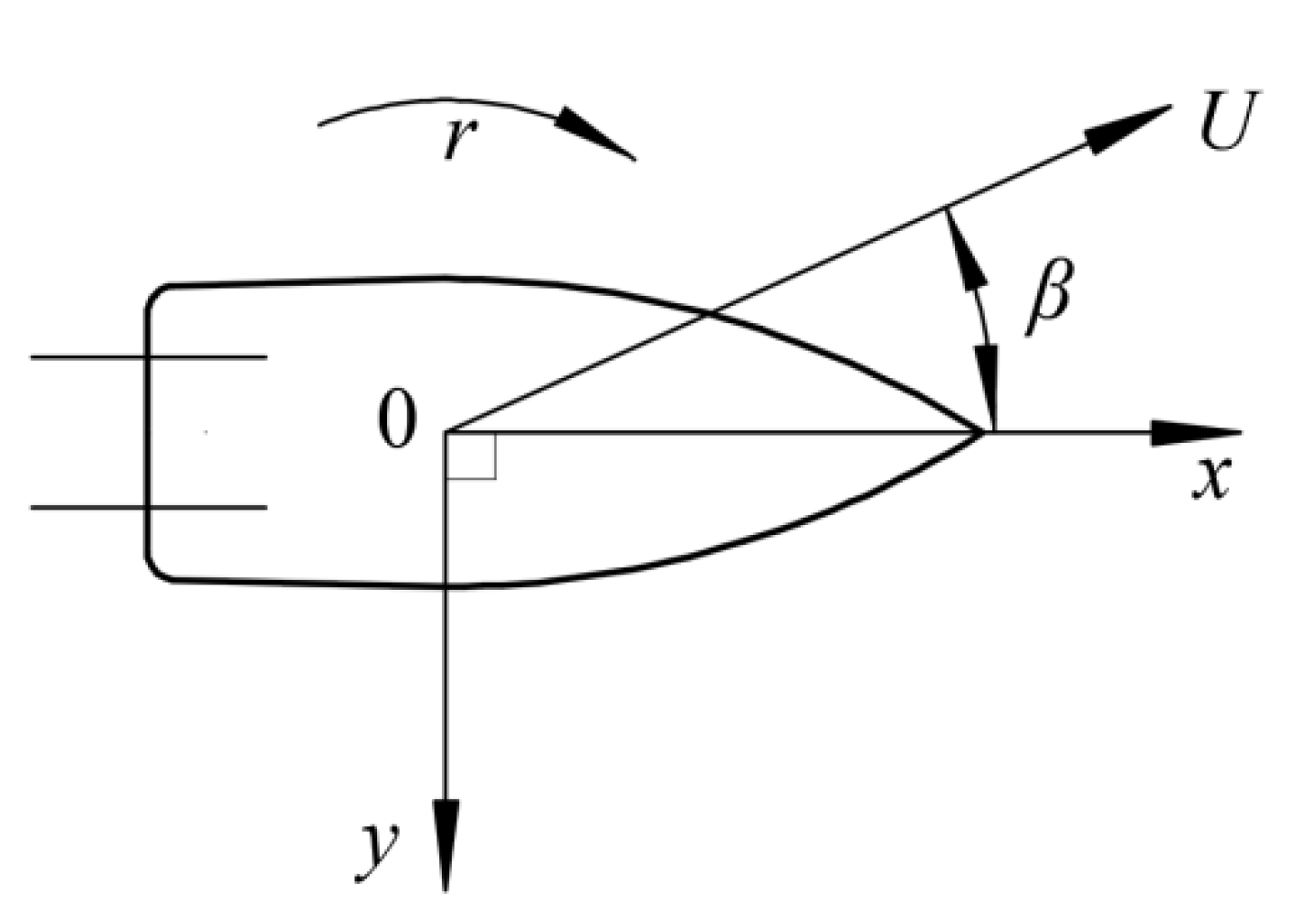
4.1. Experimental Design
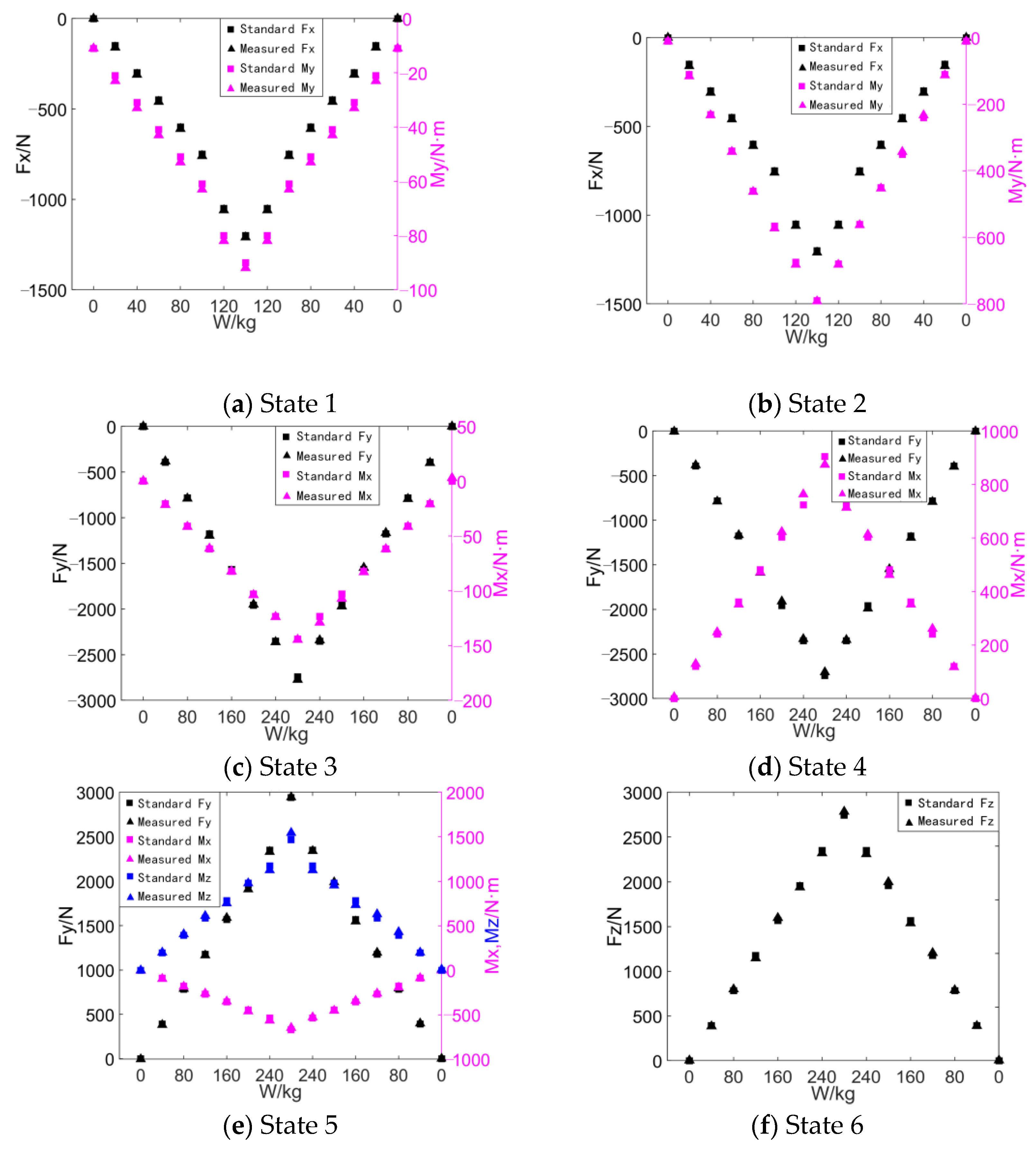
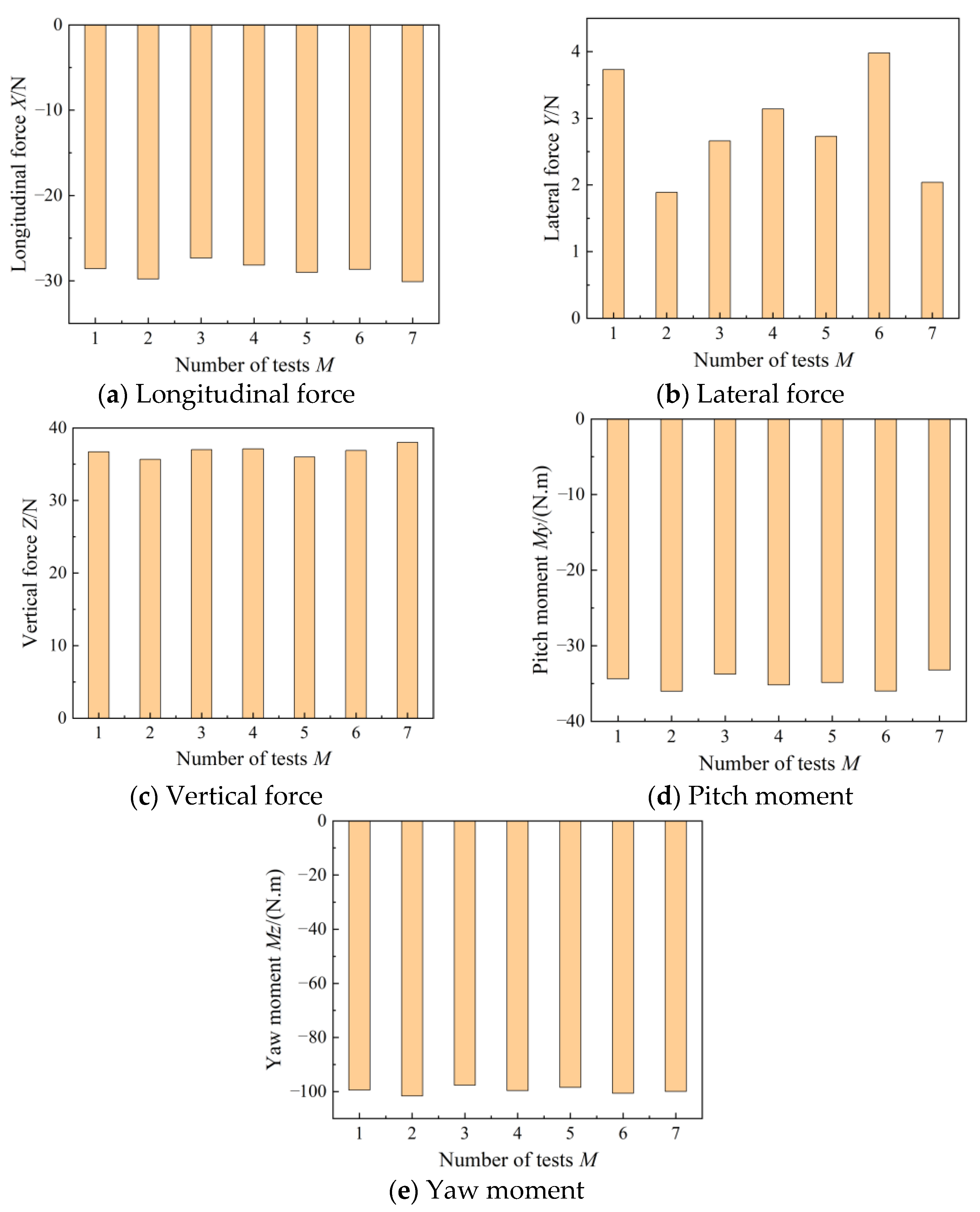
4.2. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, B.; Yun, Y.; Sun, J.; Yang, Z.; Huang, B. Rotating Arm Tank Test and Single-Plane Force Study of a Full-Form Submarine. J. Zhejiang Univ. (Eng. Ed.) 2023, 57, 773–783. [Google Scholar]
- Jiao, J.; Ren, H.; Soares, C.G. A review of large-scale model at-sea measurements for ship hydrodynamics and structural loads. Ocean Eng. 2021, 227, 108863. [Google Scholar] [CrossRef]
- Pranesh, S.B.; Rajput, N.S.; Sathianarayanan, D.; Palaniappan, M.; Ramadass, G.A. CFD analysis of the hull form of a manned submersible for minimizing resistance. J. Ocean Eng. Mar. Energy 2022, 9, 125–143. [Google Scholar] [CrossRef]
- Zhao, B.; Yun, Y.; Hu, F.; Sun, J.; Wu, D.; Huang, B. Hydrodynamic coefficients of the DARPA SUBOFF AFF-8 in rotating arm maneuver: Part I: Test technology and validation. Ocean Eng. 2022, 266, 113148. [Google Scholar] [CrossRef]
- Zhao, B.; Yun, Y.; Hu, F.; Sun, J.; Wu, D.; Huang, B. Hydrodynamic coefficients of the DARPA SUBOFF AFF-8 in rotating arm maneuver-Part II: Test results and discussion. Ocean Eng. 2023, 268, 113466. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Adhikari, S. Experimental validation of soil-structure interaction of offshore wind turbines. Soil Dyn. Earthq. Eng. 2011, 31, 805–816. [Google Scholar] [CrossRef]
- Kim, W.J.; Van, S.H.; Kim, D.H. Measurement of flows around modern commercial ship models. Exp. Fluids 2001, 31, 567–578. [Google Scholar] [CrossRef]
- Yasukawa, H.; Hasnan, M.; Matsuda, A. Validation of 6-DOF motion simulations for ship turning in regular waves. J. Mar. Sci. Technol. 2021, 26, 1096–1111. [Google Scholar] [CrossRef]
- Zhao, B.; Jiang, H.; Sun, J.; Zhang, D. Research on the Hydrodynamic Performance of a Pentamaran in Calm Water and Regular Waves. Appl. Sci. 2023, 13, 4461. [Google Scholar] [CrossRef]
- Tavakolpour-Saleh, A.R.; Setoodeh, A.R.; Gholamzadeh, M. A novel multi-component strain-gauge external balance for wind tunnel tests: Simulation and experiment. Sens. Actuators A Phys. 2016, 247, 172–186. [Google Scholar] [CrossRef]
- Nouri, N.M.; Mostafapour, K.; Kamran, M.; Bohadori, R. Design methodology of a six-component balance for measuring forces and moments in water tunnel tests. Measurement 2014, 58, 544–555. [Google Scholar] [CrossRef]
- Butler, D.; Smith, S.M.; Brandner, P.A.; Clarke, D.B.; Pearce, B.W. Static calibration and dynamic behaviour of a six-component force balance for variable pressure water tunnel facilities. Exp. Tech. 2021, 45, 157–167. [Google Scholar] [CrossRef]
- Nouri, N.M.; Kamran, M.; Mostafapur, K.; Bahadori, R. Design and fabrication of a force-moment measurement system for testing of the models in a water tunnel. Modares Mech. Eng. 2015, 14, 291. [Google Scholar]
- Yan, N.; Kühnel, M.; Vasilyan, S.; Fröhlich, T. Torsion balance-based system for high-precision force measurement in horizontal plane: Part I. Development concept. Meas. Sci. Technol. 2018, 29, 84001. [Google Scholar] [CrossRef]
- Persi, E.; Petaccia, G.; Fenocchi, A.; Manenti, S.; Ghilardi, P.; Sibilla, S. Hydrodynamic coefficients of yawed cylinders in open-channel flow. Flow Meas. Instrum. 2019, 65, 288–296. [Google Scholar] [CrossRef]
- Avin, O.; Raveh, D.E.; Drachinsky, A.; Ben-Shmuel, Y.; Tur, M. An experimental benchmark of a very flexible wing. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 and 19–21 January 2021. [Google Scholar]
- Liang, Q.; Zhang, D.; Coppola, G.; Wang, Y.; Wei, S.; Ge, Y. Multi-dimensional MEMS/micro sensor for force and moment sensing: A review. IEEE Sens. J. 2014, 14, 2643–2657. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Samardžić, M.; Ćurčić, D.; Rajić, Z.; Ocokoljić, G. Wind tunnel measurement of small values of rolling moment using six-component strain gauge balance. Measurement 2018, 116, 438–450. [Google Scholar] [CrossRef]
- Nanda, S.R.; Kulkarni, V.; Sahoo, N. Design of artificial neuro-fuzzy based methodology for six component force balance. Procedia Eng. 2016, 144, 528–536. [Google Scholar] [CrossRef]
- Reis, M.L.; Mello, O.; Uyeno, S. Calibration uncertainty of an external six-component wind tunnel balance. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Booth, D.; King, D.; Galway, R.; Mole, P. Calibration of a six component air flow through balance. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Huang, B.; Wang, X.; Li, C.; Yi, J.; Lu, R.; Tao, J. Development and calibration of an air-floating six-axis force measurement platform using self-calibration. Rev. Sci. Instrum. 2016, 87, 095002. [Google Scholar] [CrossRef]
- Ulbrich, N.M.; Volden, T. Wind Tunnel Strain-Gage Balance Calibration Data Analysis using a Weighted Least Squares Approach. In Proceedings of the 33rd AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Parker, P.; Morton, M.; Draper, N.; Line, W. A single-vector force calibration method featuring the modern design of experiments. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar]
- Nanda, S.R.; Kulkarni, V.; Sahoo, N.; Menezes, V. Sensitivity studies of ANFIS based force recovery technique towards prediction of aerodynamic load. Flow Meas. Instrum. 2021, 80, 101969. [Google Scholar] [CrossRef]
- Kamran, M.; Nouri, N.M. Model testing system for surface-piercing propellers in a water tunnel: Design and in situ calibration methodology. Measurement 2022, 199, 111200. [Google Scholar] [CrossRef]
- Yu, A.; Wan, D.; Chen, G. Verification and validation for the resistance of a KRISO container ship in calm water. In Proceedings of the 29th International Ocean and Polar Engineering Conference (ISOPE), Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- ITTC-Recommended Procedures and Guidelines 7.5-02-02-02.1. Example for Uncertainty Analysis of Resistance Tests in Towing Tanks. 29th ITTC, Quality Systems Group. 2021. Available online: https://www.ittc.info/media/10176/75-02-02-021.pdf (accessed on 13 July 2024).
- SIMMAN 2014. Available online: https://simman2014.dk/about-simman2014/ (accessed on 13 July 2024).
- SIMMAN 2019. Available online: https://web.archive.org/web/20211021062834/http://simman2019.kr/contents/Purpose.php (accessed on 13 July 2024).


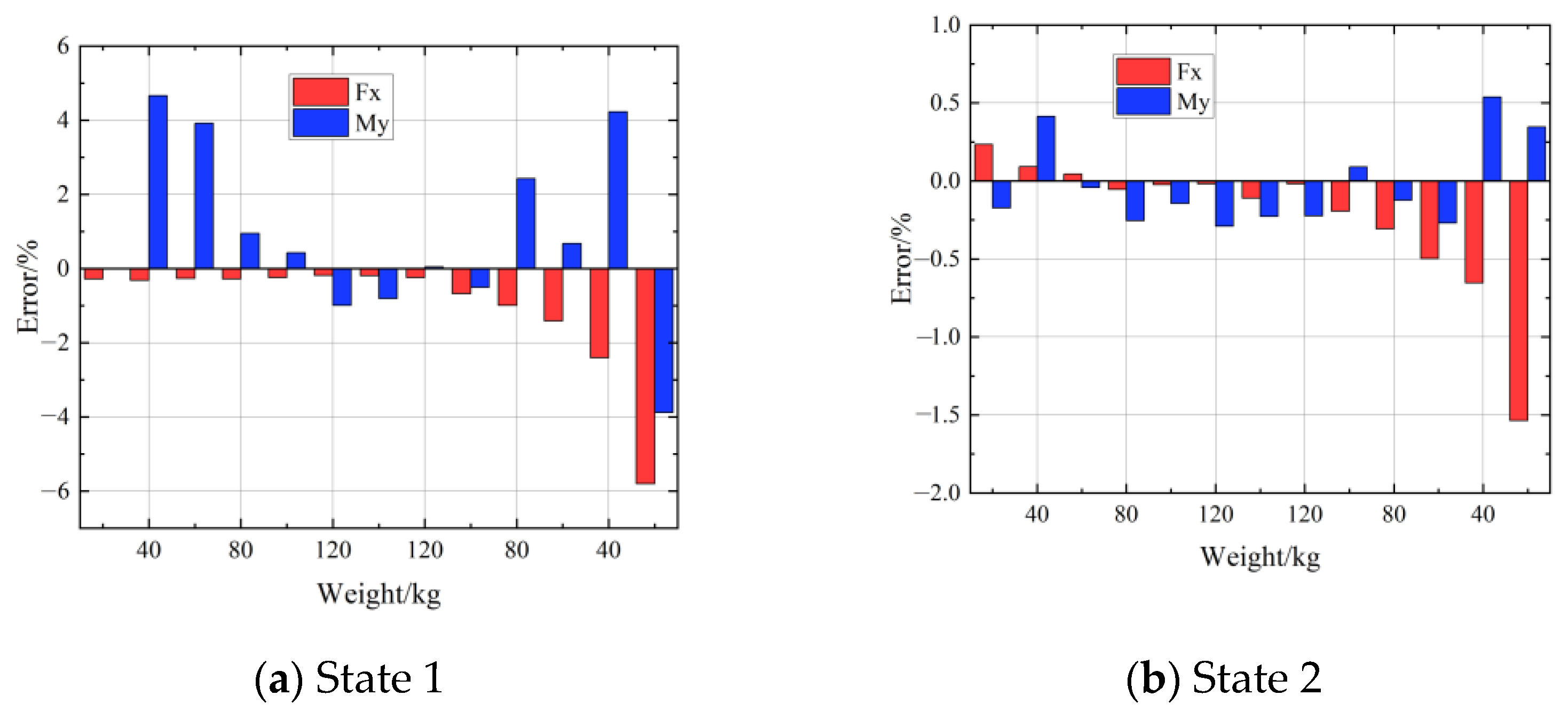
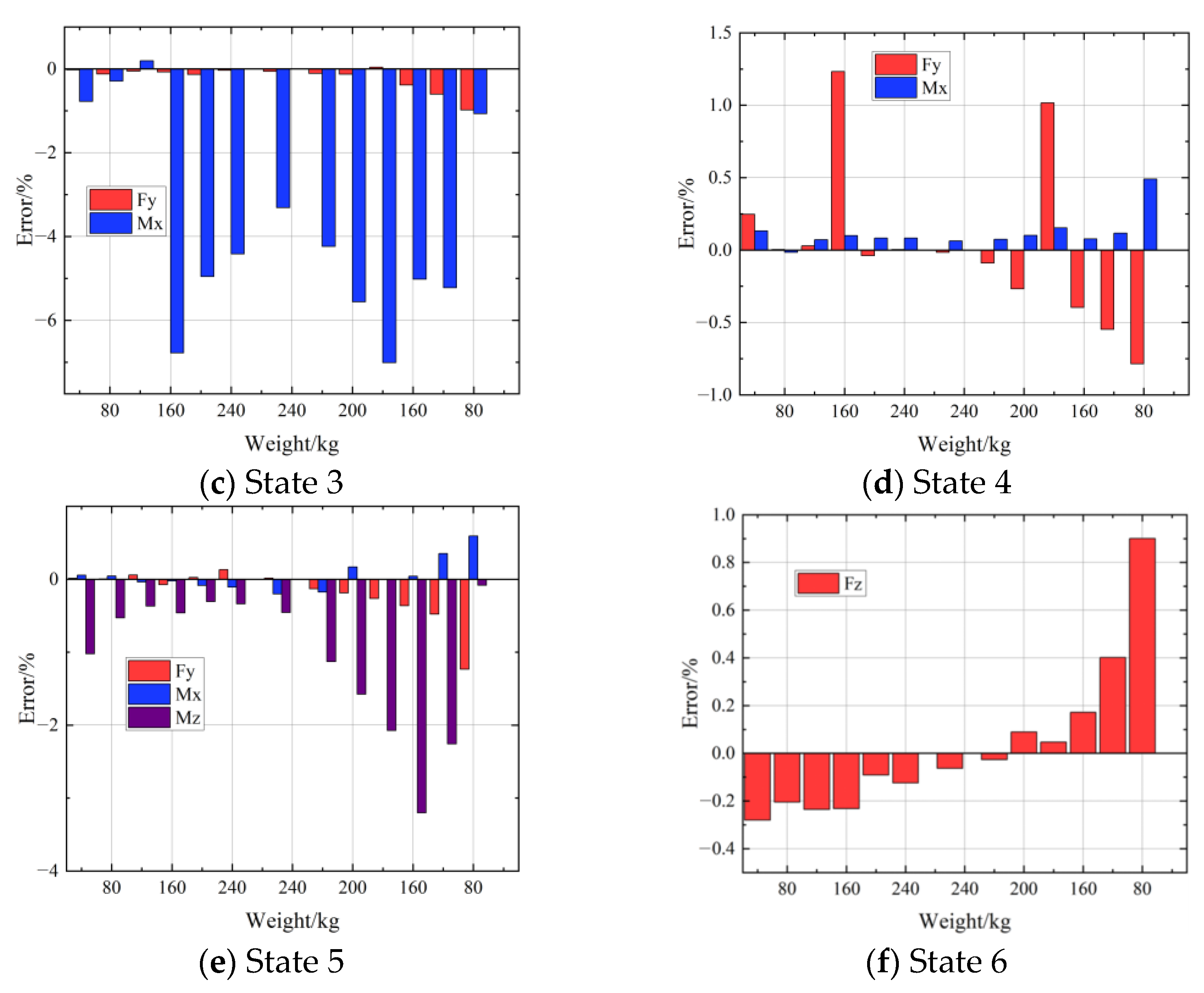


| States | Forces/N | Moments/(N·m) | W/kg | ||||
|---|---|---|---|---|---|---|---|
| Fx | Fy | Fz | Mx | My | Mz | ||
| 1 | -Wg | 0 | 0 | 0 | -Wgl1 | 0 | 0~140 |
| 2 | -Wg | 0 | 0 | 0 | -Wgl2 | 0 | 0~140 |
| 3 | 0 | -Wg | 0 | -Wgl3 | 0 | 0 | 0~300 |
| 4 | 0 | -Wg | 0 | Wgl4 | 0 | 0 | 0~300 |
| 5 | 0 | Wg | 0 | -Wgl5 | 0 | Wgl6 | 0~300 |
| 6 | 0 | 0 | Wg | 0 | 0 | 0 | 0~300 |
| Force/Moment | SDev | P(M) |
|---|---|---|
| Fx | 0.865 | 0.671 |
| Fy | 0.743 | 0.544 |
| Fz | 0.754 | 0.537 |
| My | 0.976 | 0.753 |
| Mz | 1.224 | 0.916 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhao, B.; Liang, X.; Lin, Q. Research on Calibration Methods and Experiments for Six-Component Force Sensors. J. Mar. Sci. Eng. 2025, 13, 1811. https://doi.org/10.3390/jmse13091811
Zhao H, Zhao B, Liang X, Lin Q. Research on Calibration Methods and Experiments for Six-Component Force Sensors. Journal of Marine Science and Engineering. 2025; 13(9):1811. https://doi.org/10.3390/jmse13091811
Chicago/Turabian StyleZhao, Hongyang, Bowen Zhao, Xu Liang, and Qianbin Lin. 2025. "Research on Calibration Methods and Experiments for Six-Component Force Sensors" Journal of Marine Science and Engineering 13, no. 9: 1811. https://doi.org/10.3390/jmse13091811
APA StyleZhao, H., Zhao, B., Liang, X., & Lin, Q. (2025). Research on Calibration Methods and Experiments for Six-Component Force Sensors. Journal of Marine Science and Engineering, 13(9), 1811. https://doi.org/10.3390/jmse13091811






