DNN Predictive Model for Estimating the Metacetric Height of Small Fishing Vessels in South Korea at the Early Design Stages
Abstract
1. Introduction
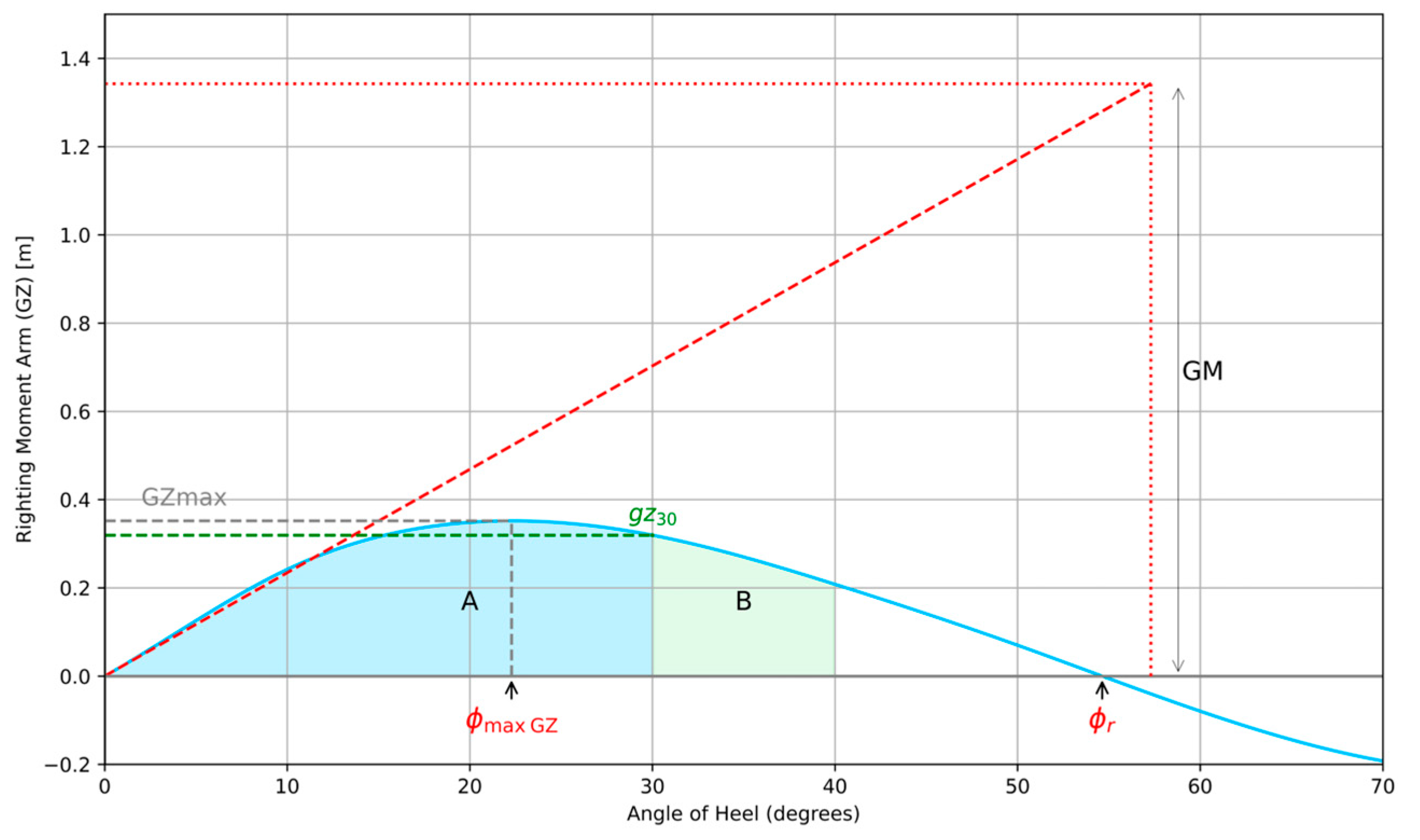
2. Ship Stability Regulations
2.1. The IMO Regulations on Small Fishing Vessels Stability
2.2. The Korea Domestic Regulations on Small Fishing Vessels Stability
3. Ship Model Data
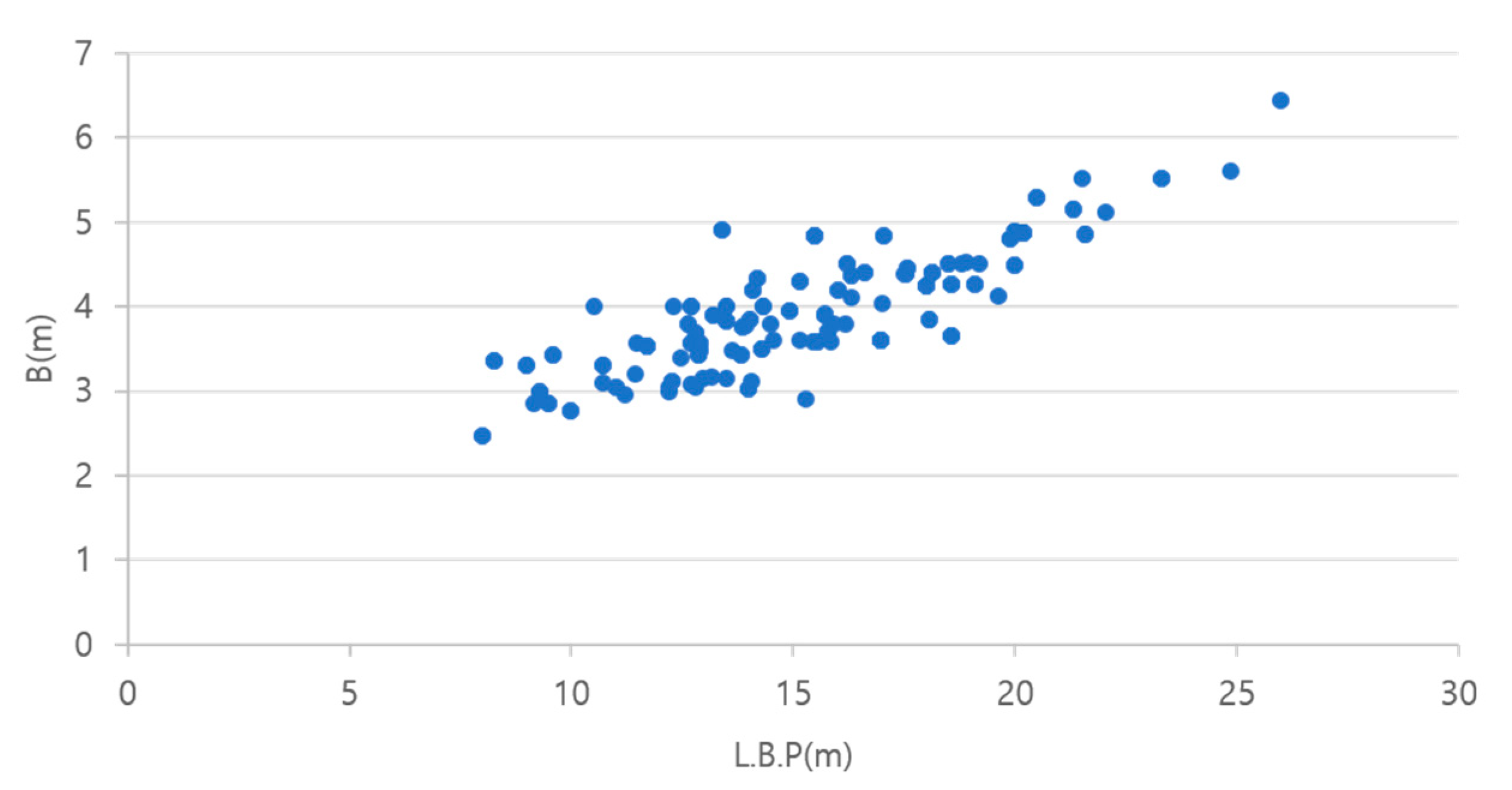
3.1. Vessel Specification Data
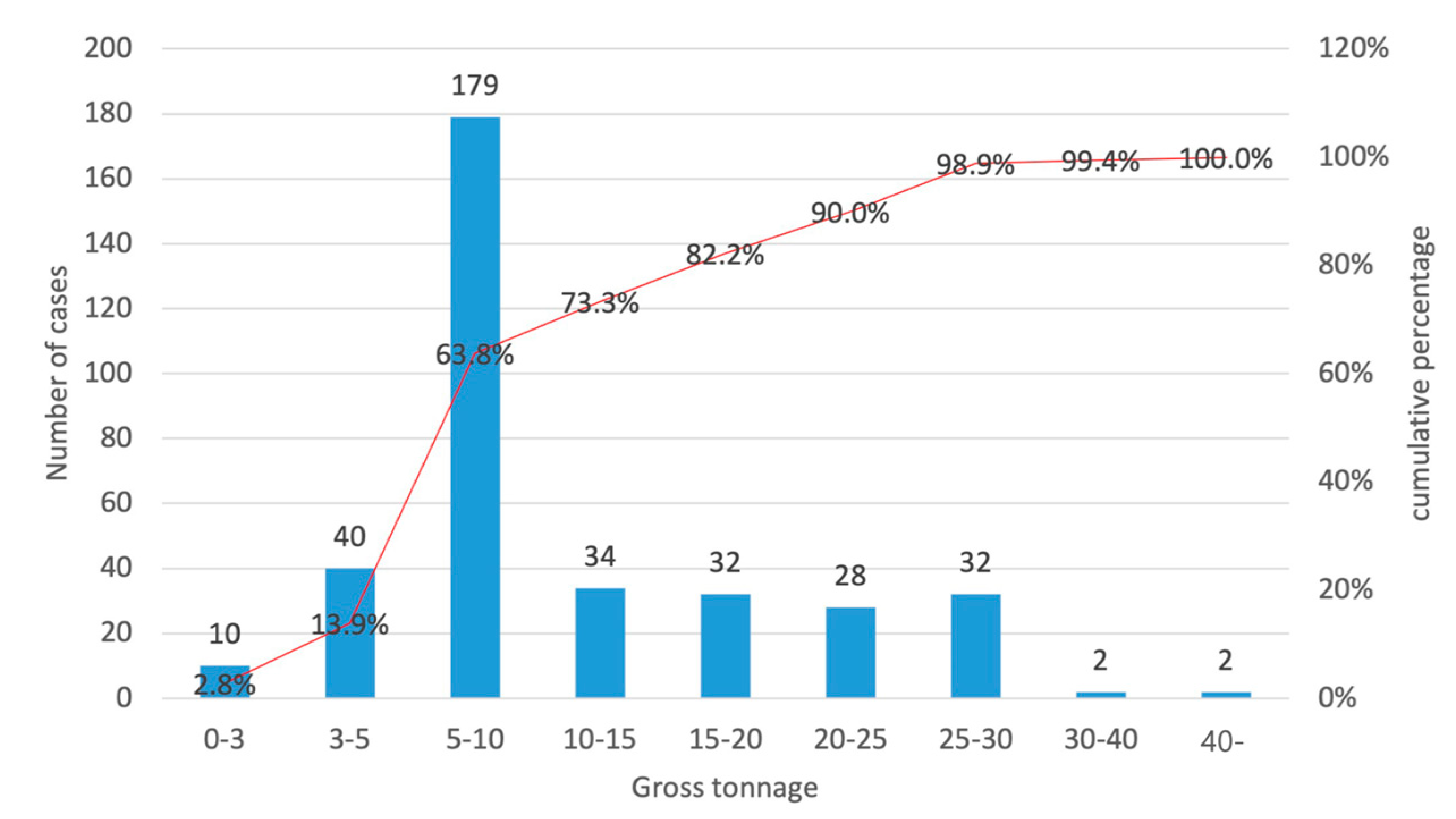
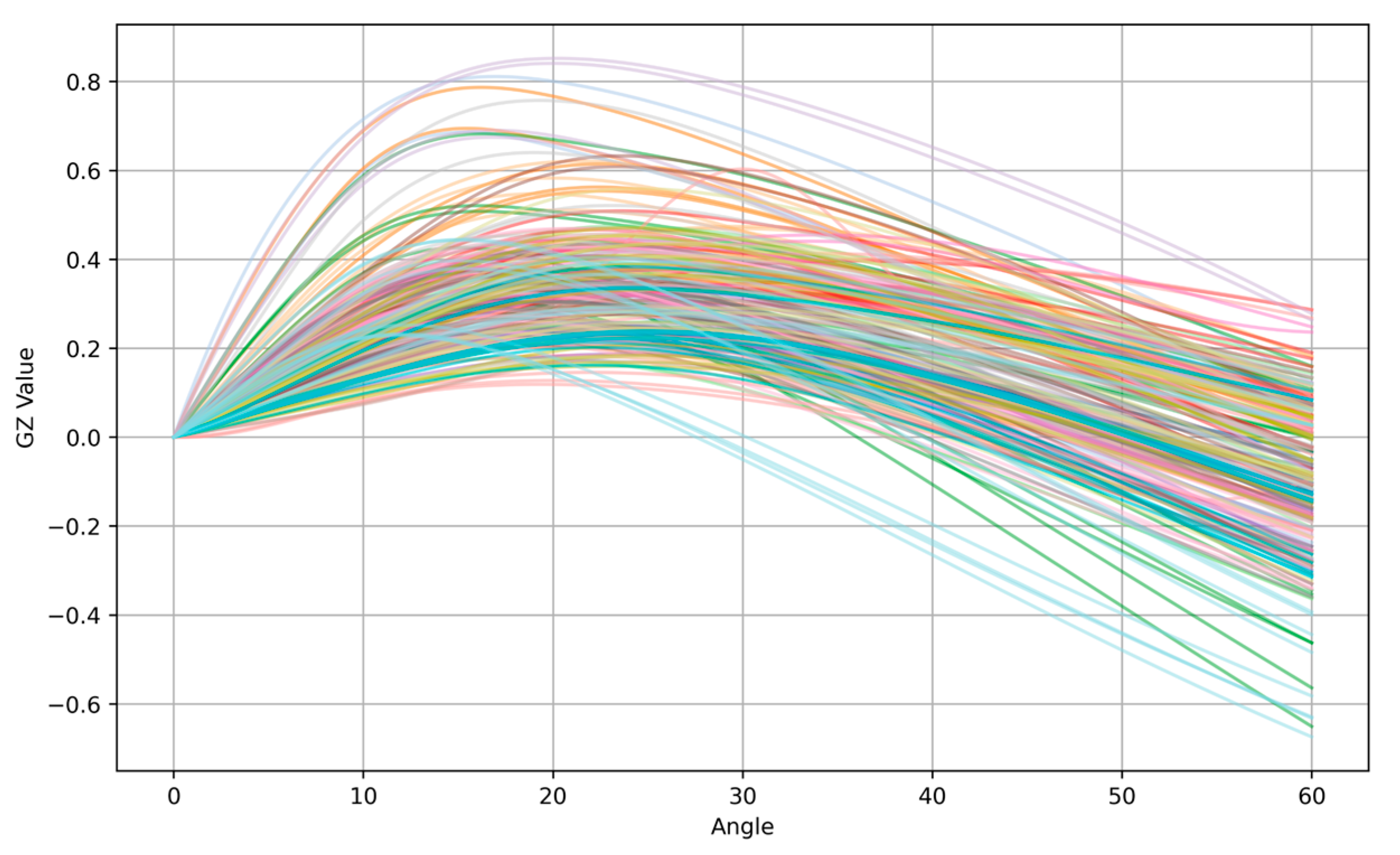
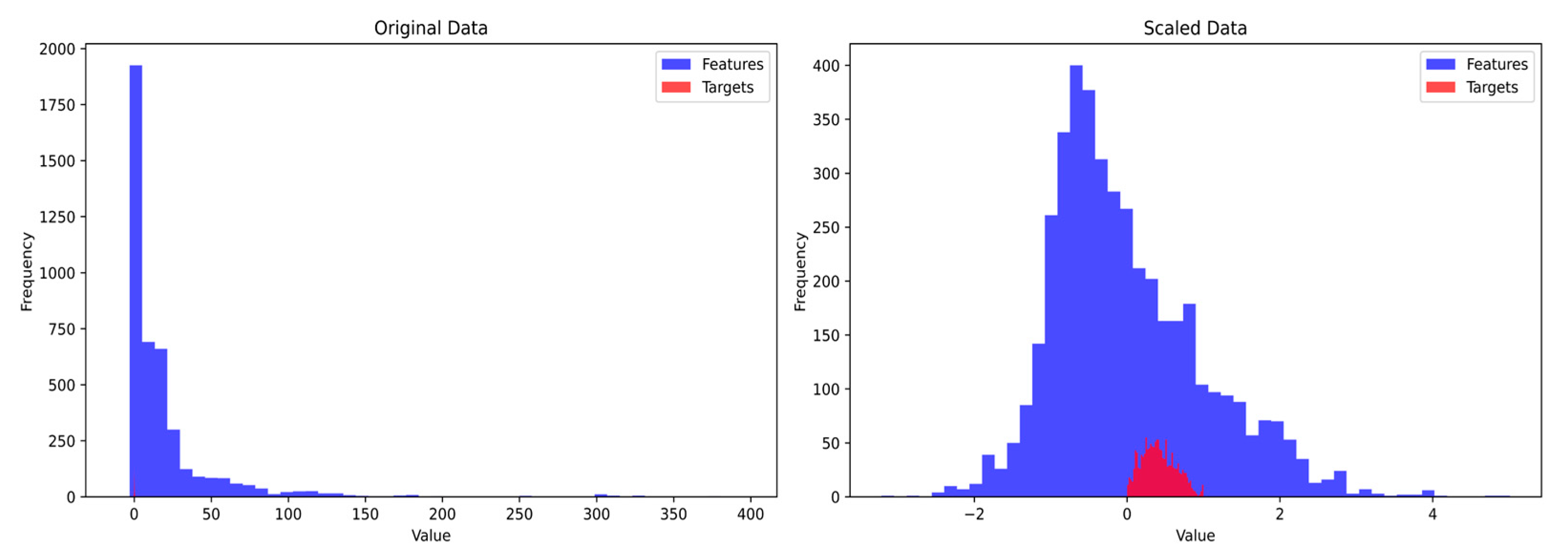
3.2. Ship Stability Data Distribution
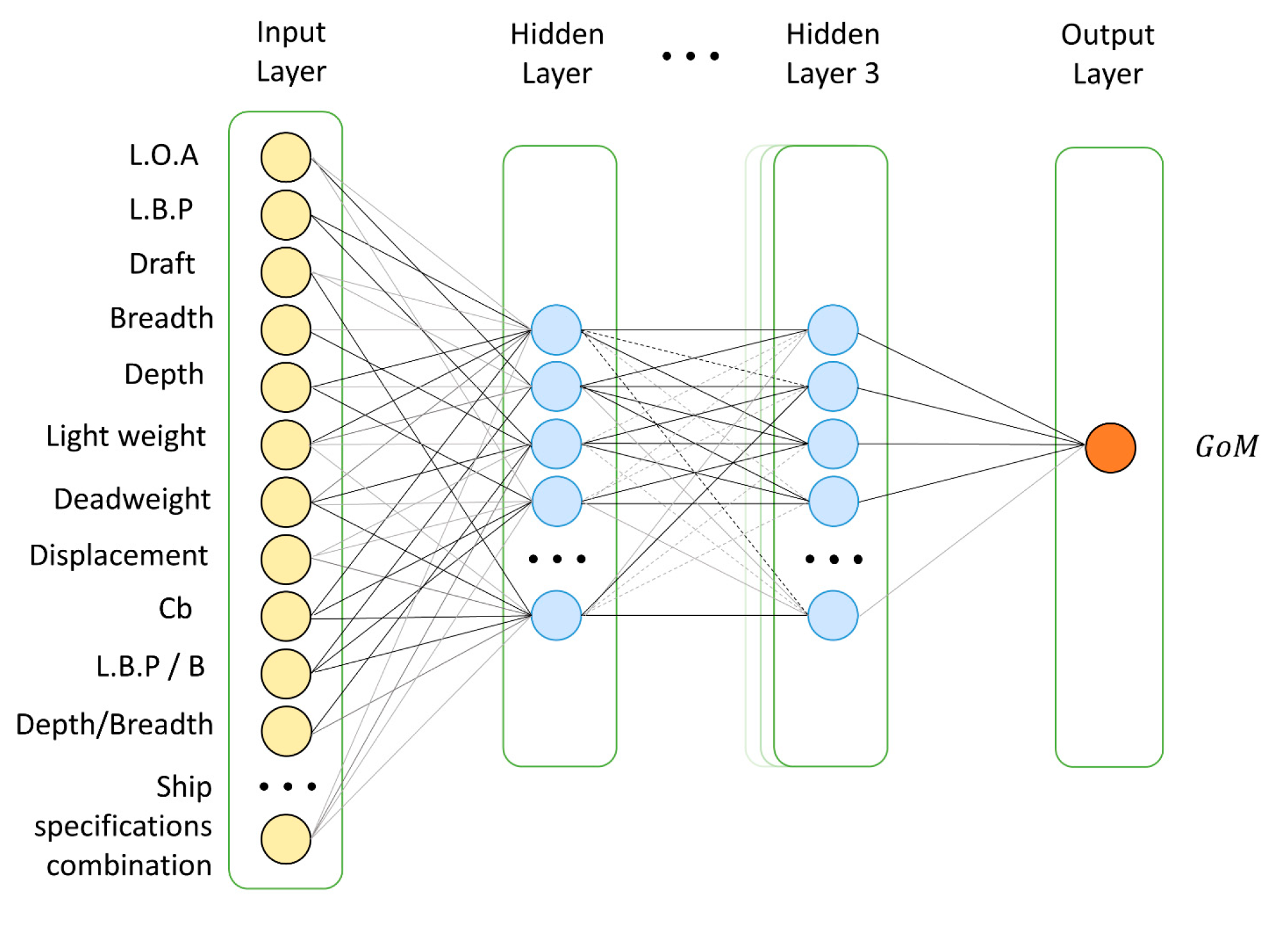
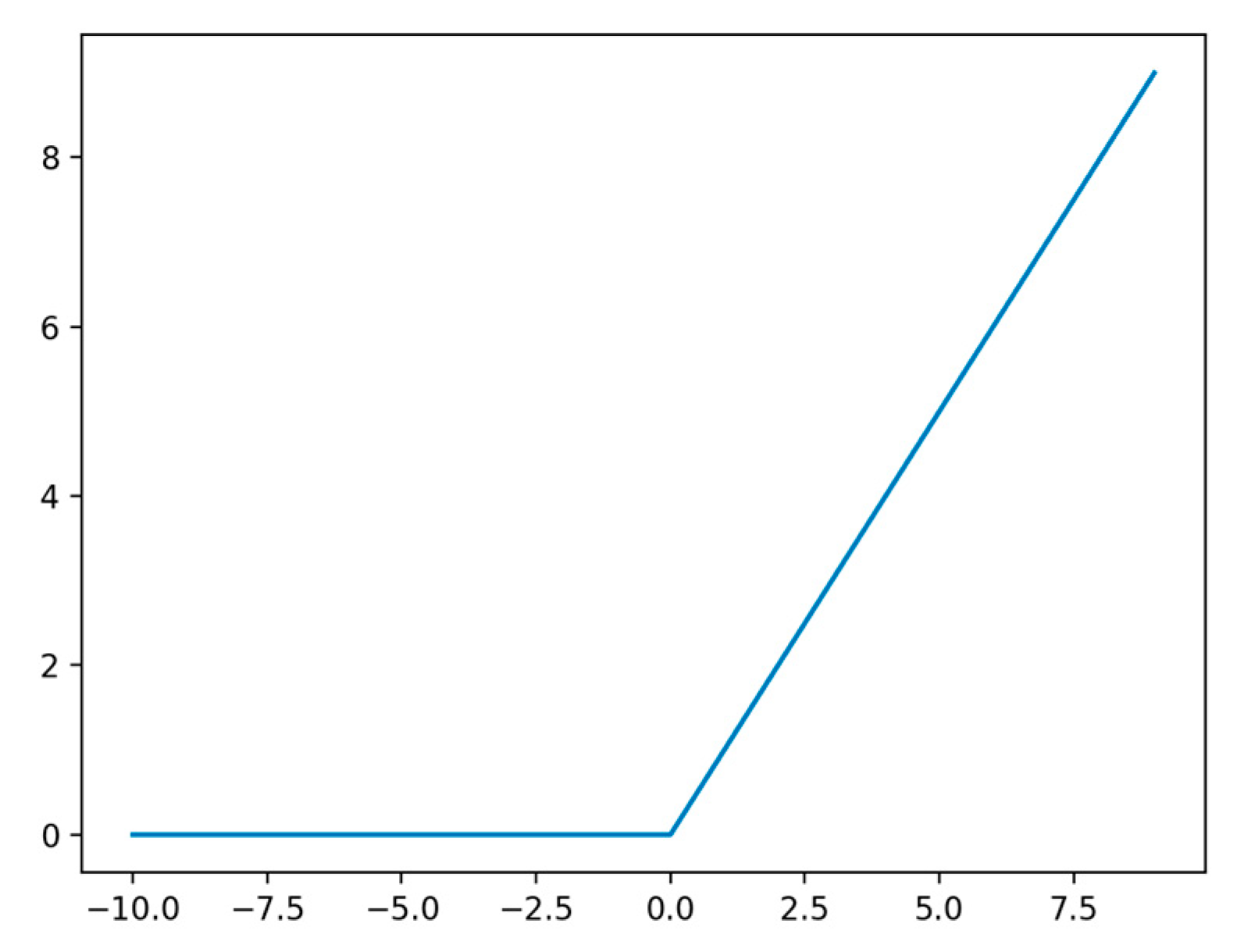
4. DNN Model for Estimating the Metacentric Height
4.1. DNN Structure
4.2. Data Preprocessing
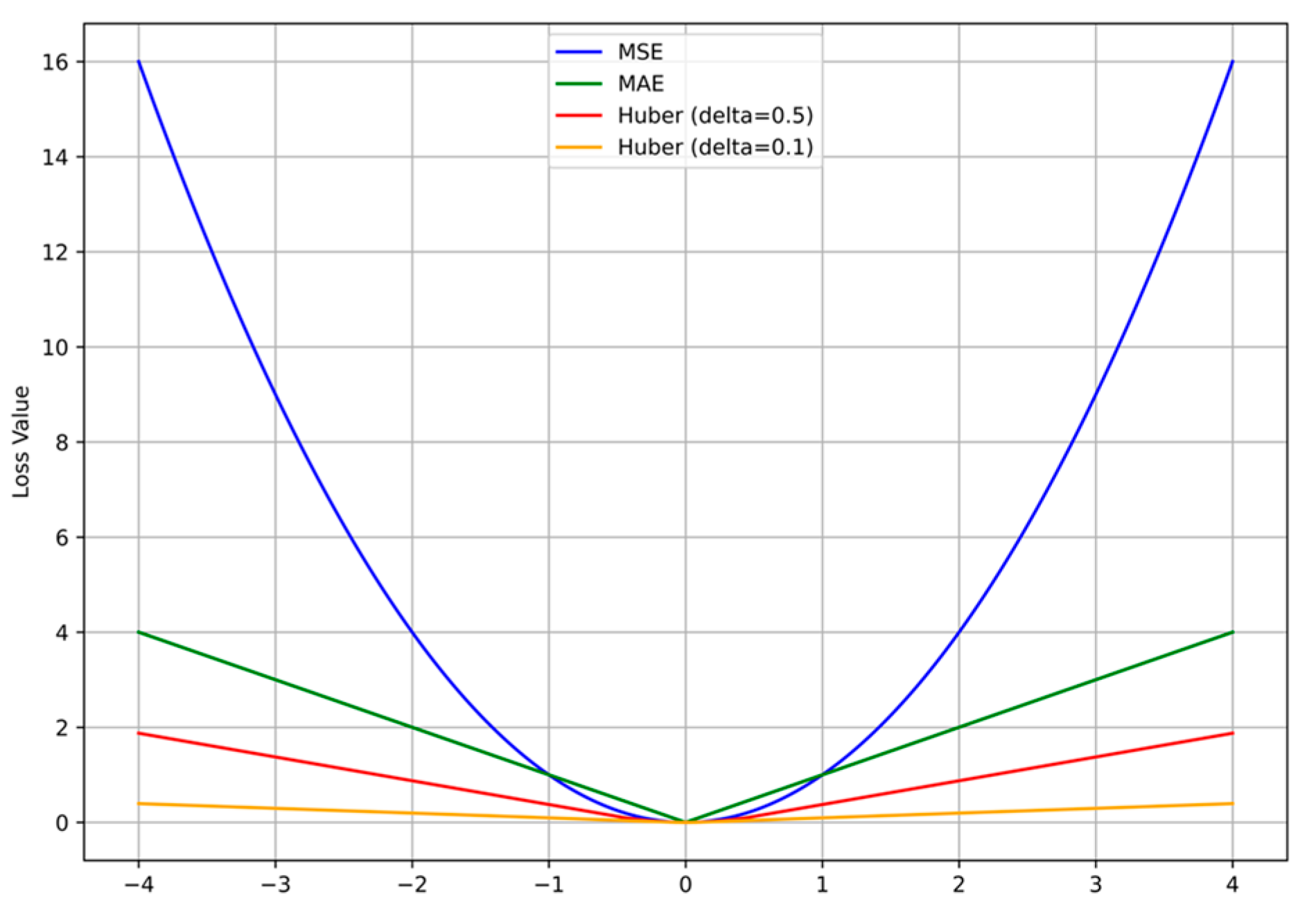
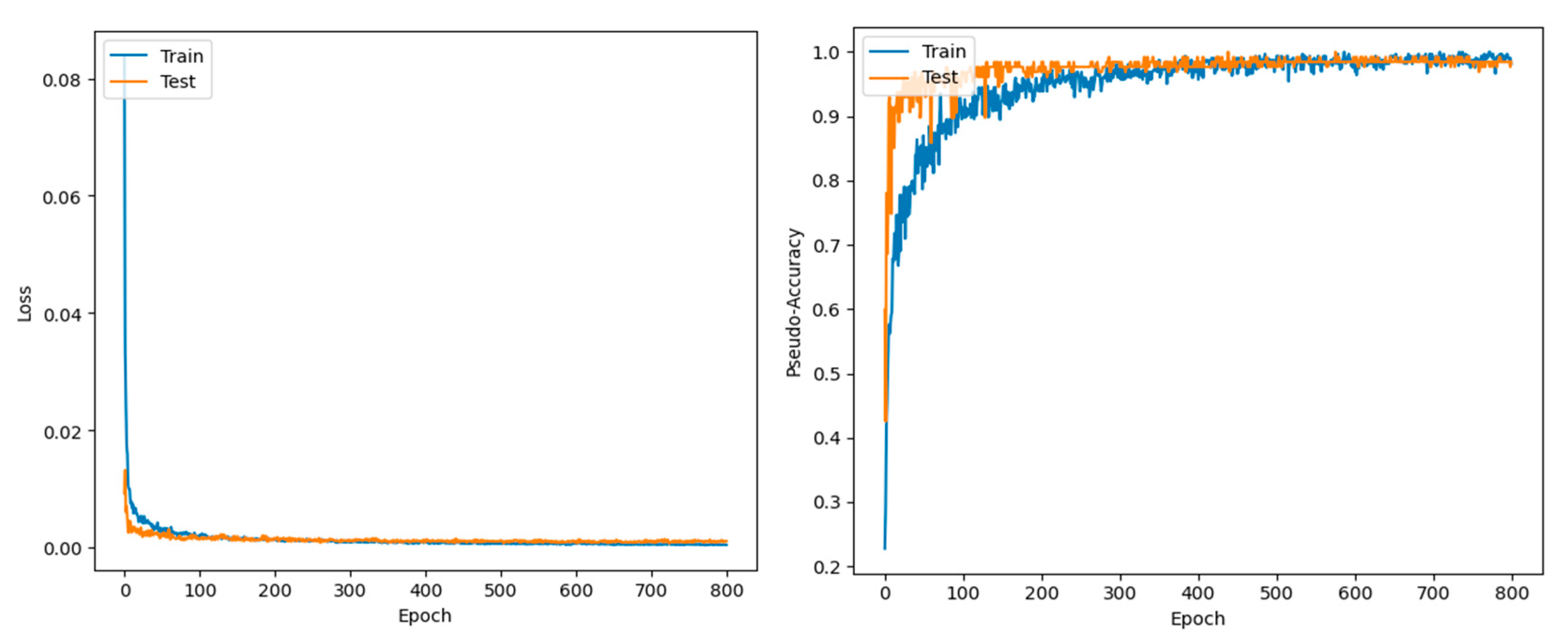
4.3. Training Process
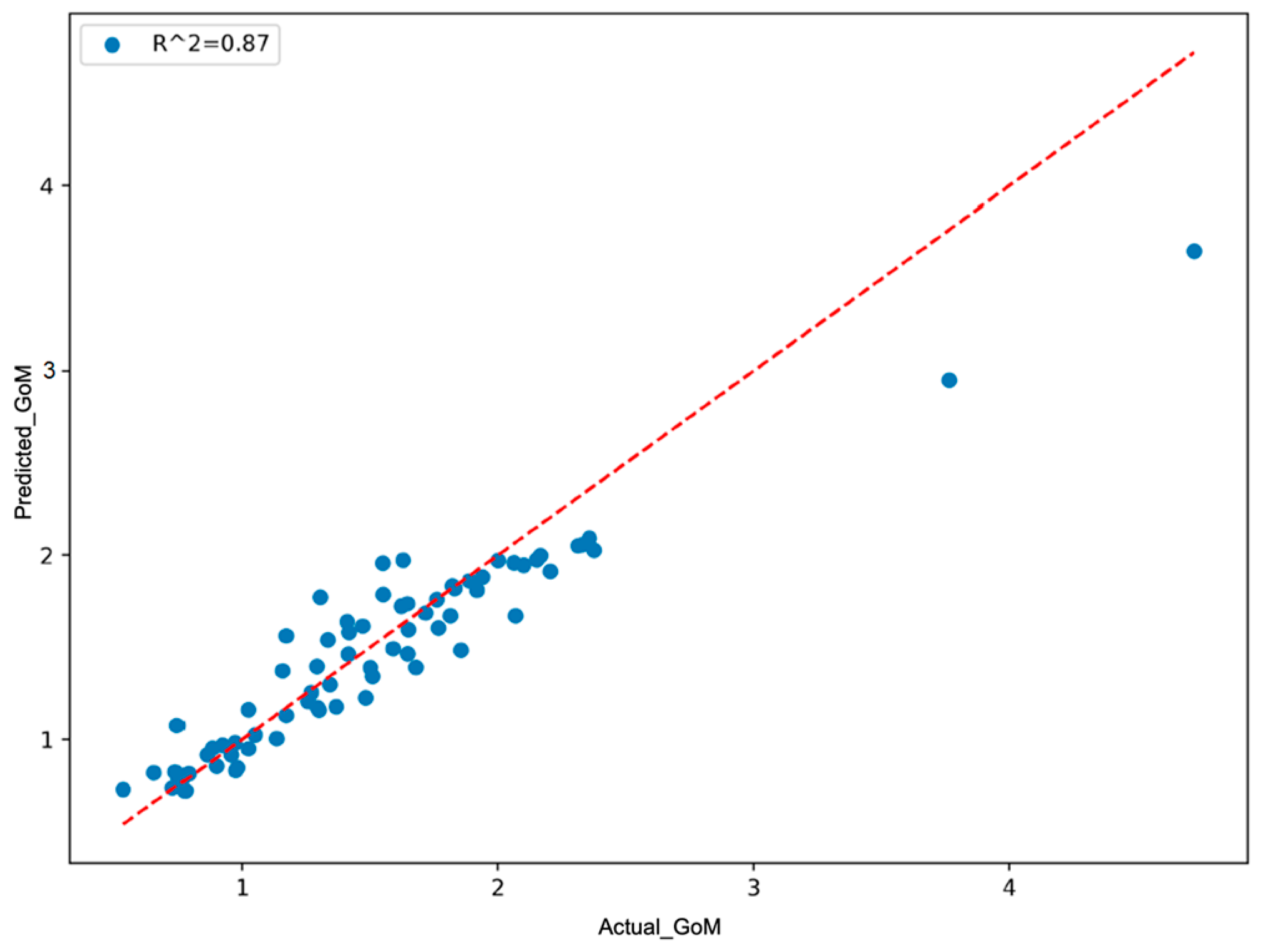
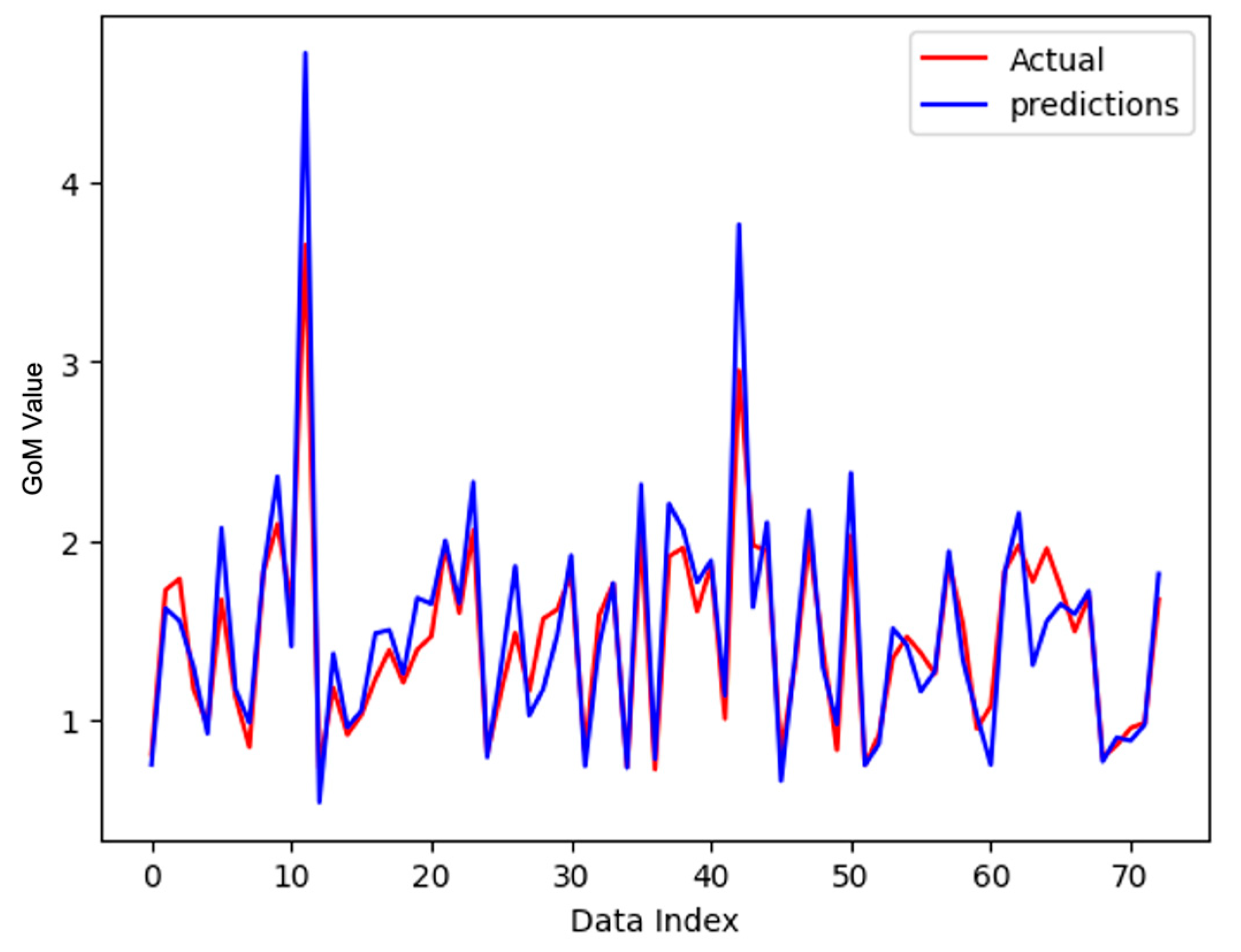
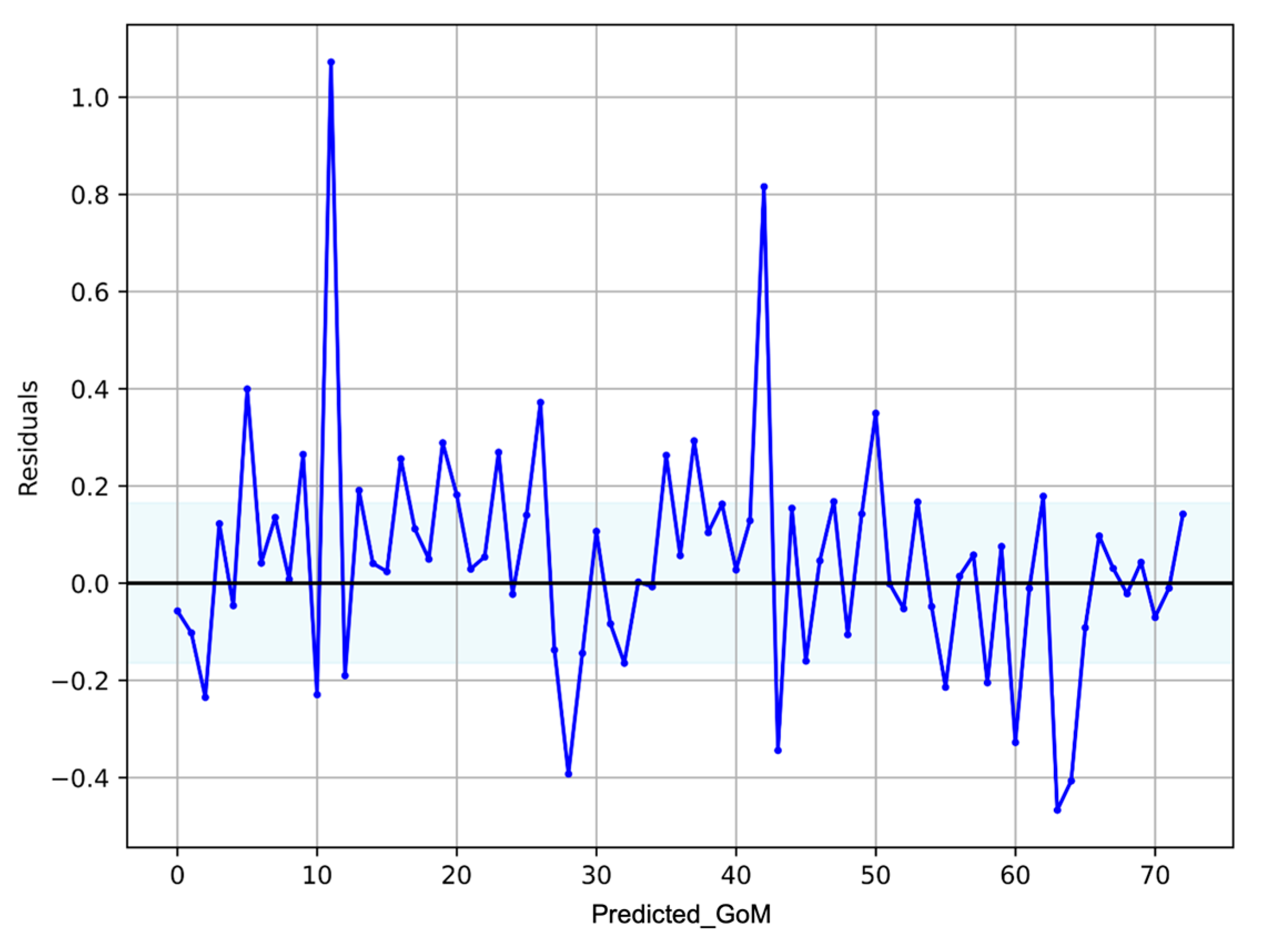
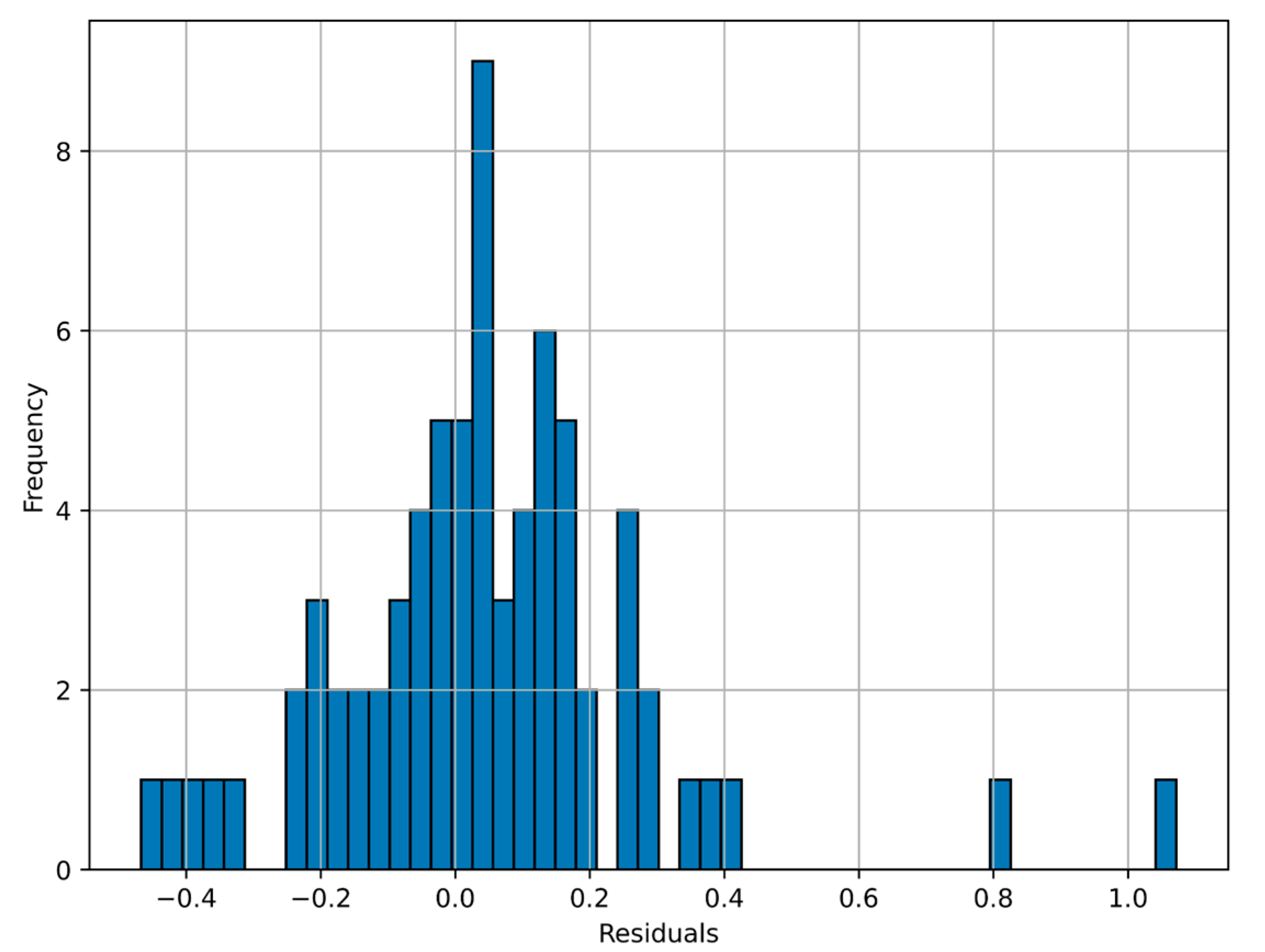
4.4. Model Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- International Labour Office; International Maritime Organization; Food and Agriculture Organization of the Uniited Nations. Safety Recommendations for Decked Fishing Vessels of Less than 12 Metres in Length and Undecked Fishing Vessels; International Labour Organization: Genève, Switzerland, 2012; ISBN 978-92-5-107397-1. [Google Scholar]
- Enforcement Rules of the Fishing Vessel Safety Operation Act. Available online: https://www.law.go.kr/admRulInfoP.do?admRulSeq=2000000100025 (accessed on 1 September 2025).
- Melo, R.F.; Figueiredo, N.M.d.; Tobias, M.S.G.; Afonso, P. A Machine Learning Predictive Model for Ship Fuel Consumption. Appl. Sci. 2024, 14, 7534. [Google Scholar] [CrossRef]
- Ren, Y.; Li, X.; Xu, H. Extracting Ship’s Size from SAR Images by Deep Learning. In Artificial Intelligence Oceanography; Li, X., Wang, F., Eds.; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Latinopoulos, C.; Zavvos, E.; Kaklis, D.; Leemen, V.; Halatsis, A. Marine Voyage Optimization and Weather Routing with Deep Reinforcement Learning. J. Mar. Sci. Eng. 2025, 13, 902. [Google Scholar] [CrossRef]
- Balas, E.A.; Balas, C.E. Maritime Risk Assessment: A Cutting-Edge Hybrid Model Integrating Automated Machine Learning and Deep Learning with Hydrodynamic and Monte Carlo Simulations. J. Mar. Sci. Eng. 2025, 13, 939. [Google Scholar] [CrossRef]
- Chen, Z.S.; Lam, J.S.L.; Xiao, Z. Prediction of harbour vessel emissions based on machine learning approach. Transp. Res. Part D Transp. Environ. 2024, 131, 104214. [Google Scholar] [CrossRef]
- Hasan, S.M.; Islam, M.S.; Awal, Z.I. A Machine Learning Framework for Predicting Efficient Ship Design Parameters. In Proceedings of the 14th International Conference on Marine Technology (MARTEC), Johor Bahru, Malaysia, 24–26 September 2024. [Google Scholar]
- He, G.; Xue, J.; Zhao, C.; Cui, T.; Liu, C. Deep learning based short-term motion prediction of floating wind turbine under shutdown condition. Appl. Ocean Res. 2024, 151, 1014147. [Google Scholar] [CrossRef]
- Terada, D.; Tamashima, M.; Nakao, I.; Matsuda, A. Estimation of metacentric height using onboard monitoring roll data based on time series analysis. J. Mar. Sci. Technol. 2018, 24, 285–296. [Google Scholar] [CrossRef]
- Krata, P.; Wawrzyński, W. Method for ship’s rolling period prediction with regard to non-linearity of GZ curve. J. Theor. Appl. Mech. 2016, 4, 1329–1343. [Google Scholar] [CrossRef]
- Wilczynski, V.; Knowles, P.; Diehl, W. Uncertainty Analysis of a Vessel’s Metacentric Height. In Proceedings of the Conference: Probabilistic Safety Assessment and Management—1998, New York, NY, USA, 13–18 September 1998. [Google Scholar]
- Ruponen, P.; Manderbacka, T.; Lindroth, D. On the calculation of the righting lever curve for a damaged ship. Ocean Eng. 2018, 149, 313–324. [Google Scholar] [CrossRef]
- Perrault, D. Correlations of GZ Curve Parameters. In Proceedings of the 15th International Ship Stability Workshop, Stockholm, Sweden, 13–15 June 2016; pp. 1–7. [Google Scholar]
- Kim, D.J.; Yeo, D.J. Estimation of drafts and metacentric heights of small fishing vessels according to loading conditions. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 199–212. [Google Scholar] [CrossRef]
- Nam-Kyun, I.M.; Hun, C.H.O.E. A quantitative methodology for evaluating the ship stability using the index for marine ship intact stability assessment model. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 246–259. [Google Scholar]
- Woo, D.; Choe, H.; Im, N.-K. Analysis of the Relationship between GM and IMO Intact Stability Parameters to Propose Simple Evaluation Methodology. J. Mar. Sci. Eng. 2021, 9, 735. [Google Scholar] [CrossRef]
- Woo, D.; Im, N.-K. A Methodology for Simply Evaluating the Safety of a Passenger Ship Stability Using the Index for the Intact Stability Appraisal Module. Sensors 2022, 22, 1938. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Taimuri, G.; Zhang, J.; Hirdaris, S. A deep learning method for the prediction of 6-DoF ship motions in real conditions. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2023, 237, 887–905. [Google Scholar] [CrossRef]
- Wang, L.; Liao, S.; Wang, S.; Jia, B.; Yin, J.; Li, R. Real-time prediction of metacentric height of ro-ro passenger ships in Qiongzhou strait based on improved RBF neural network. Ocean Eng. 2024, 312, 119067. [Google Scholar] [CrossRef]
| Criteria | Minimum Requirement | |
|---|---|---|
| G0M (metacentric height) | 0.35 m (0.15 m for vessels ≥ 70 m in length or with significant upper structures) | |
| GZ (Righting Lever) at 30° heel angle | 0.2 m | |
| Angle Max GZ | 25° | |
| GZ Curve Area | Between 0° and 30° | 0.055 m-rad |
| Between 0° and 40° or 1 | 0.090 m-rad | |
| Between 30° and 40° or | 0.030 m-rad | |
| Vessel Type | Criteria | ||
|---|---|---|---|
| Vessels 24 m or more but less than 40 m in length | ≤ G0M | ||
| Vessels 40 m or more in length | 0.35 m ≤ G0M (0.15 m for vessels with traditional superstructures or those 70 m or more in length) | ||
| 0.2 m | |||
| Maximum GZ Angle | 25° | ||
| GZ Area | 0–30° | 0.055 m-rad | |
| 0–40° | 0.090 m-rad | ||
| Weather Criterion | 30–40° | 0.030 m-rad | |
| Area Ratio (b/a) | 1 | ||
| Heel angle under steady wind | Limit of heel angle or not exceeding 16° | ||
| No | Features (Unit) |
|---|---|
| 1 | LOA (m) |
| 2 | LBP (m) |
| 3 | Draft (m) |
| 4 | Breadth (m) |
| 5 | Depth (m) |
| 6 | Light Weight Tonnage (ton) |
| 7 | Dead Weight Tonnage (ton) |
| 8 | Displacement (ton) |
| 9 | Cb (-) |
| 10 | LBP × B (m × m) |
| 11 | LBP × D (m × m) |
| 12 | B × d (m × m) |
| 13 | L/B (-) |
| 14 | B/d (-) |
| 15 | L/d (-) |
| 16 | D/B (-) |
| Hyperparameter | Value |
|---|---|
| Train:Test | 8:02 |
| Hidden Layer | 128:256:128 |
| Dropout | 0.3 |
| Loss Function | Huber |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Batch size | 32 |
| epoch | 1000 |
| Metric | Description | Value |
|---|---|---|
| score | Coefficient of determination | 0.8701 |
| MSE | Mean Squared Error | 0.0577 |
| RMSE | Root Mean Squared Error | 0.2402 |
| MAE | Mean Absolute Error | 0.1647 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, Y.; Im, N. DNN Predictive Model for Estimating the Metacetric Height of Small Fishing Vessels in South Korea at the Early Design Stages. J. Mar. Sci. Eng. 2025, 13, 1779. https://doi.org/10.3390/jmse13091779
Jeong Y, Im N. DNN Predictive Model for Estimating the Metacetric Height of Small Fishing Vessels in South Korea at the Early Design Stages. Journal of Marine Science and Engineering. 2025; 13(9):1779. https://doi.org/10.3390/jmse13091779
Chicago/Turabian StyleJeong, Yeonju, and Namkyun Im. 2025. "DNN Predictive Model for Estimating the Metacetric Height of Small Fishing Vessels in South Korea at the Early Design Stages" Journal of Marine Science and Engineering 13, no. 9: 1779. https://doi.org/10.3390/jmse13091779
APA StyleJeong, Y., & Im, N. (2025). DNN Predictive Model for Estimating the Metacetric Height of Small Fishing Vessels in South Korea at the Early Design Stages. Journal of Marine Science and Engineering, 13(9), 1779. https://doi.org/10.3390/jmse13091779






