Autonomous Inspection Strategies and Simulation for Large Aquaculture Net Cages Based on Deep Visual Perception
Abstract
1. Introduction
2. Simulation Scenarios and Underwater Robots
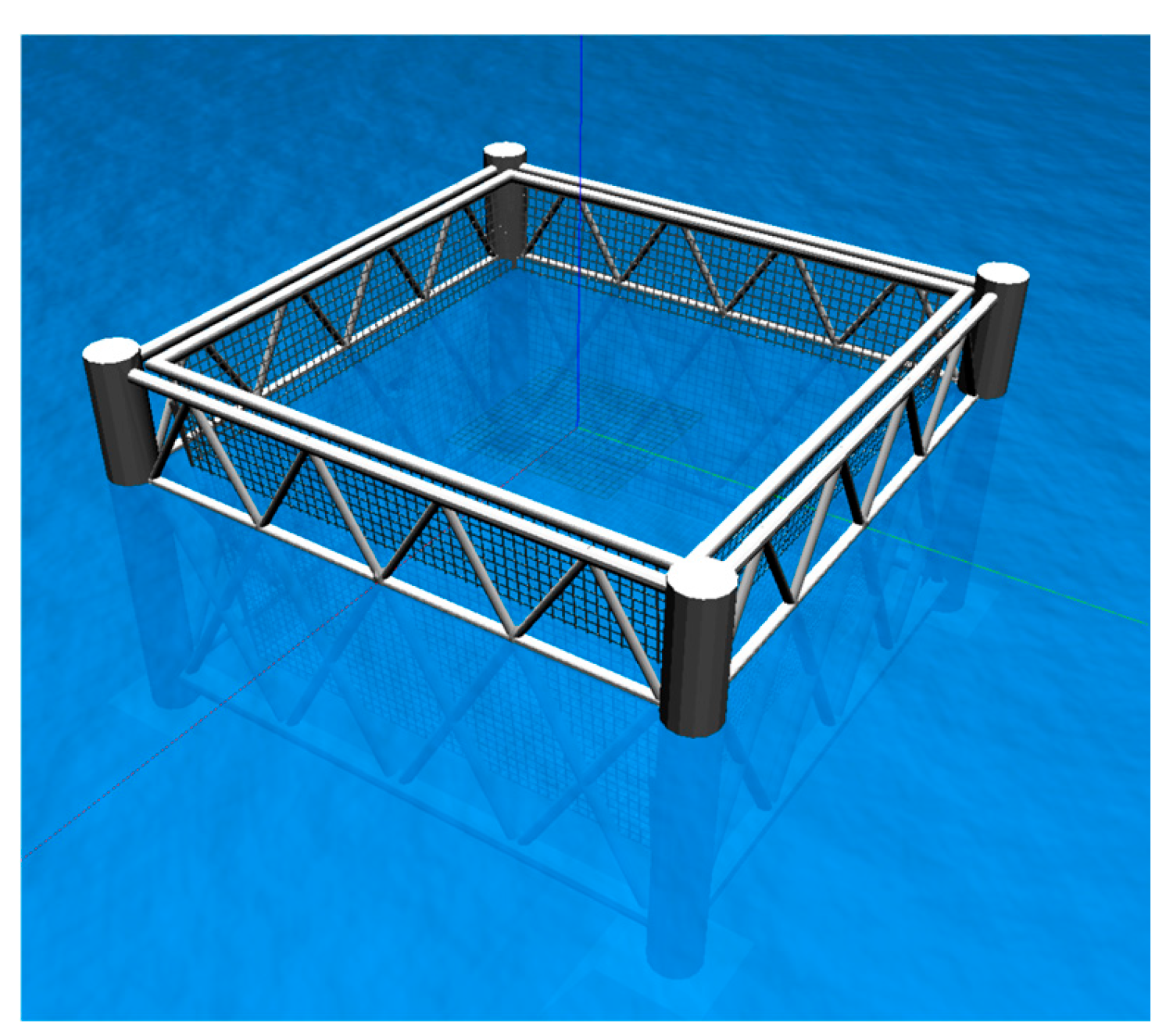
2.1. Simulation Scenarios
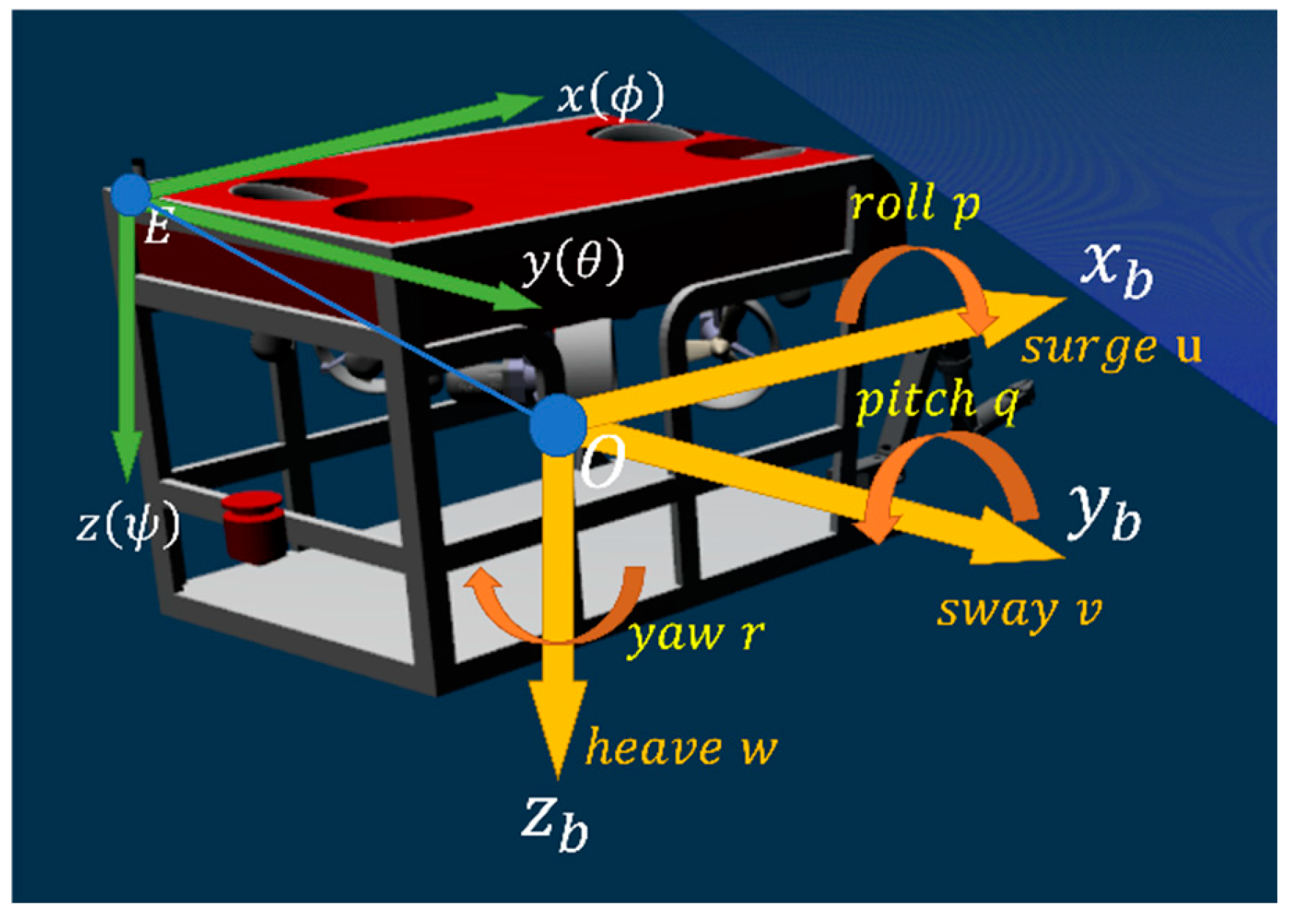
2.2. Underwater Robots
2.2.1. Main Parameters and Sensors
2.2.2. Hydrodynamic Load and Motion Equation of the Underwater Robot
3. Autonomous Inspection Strategy
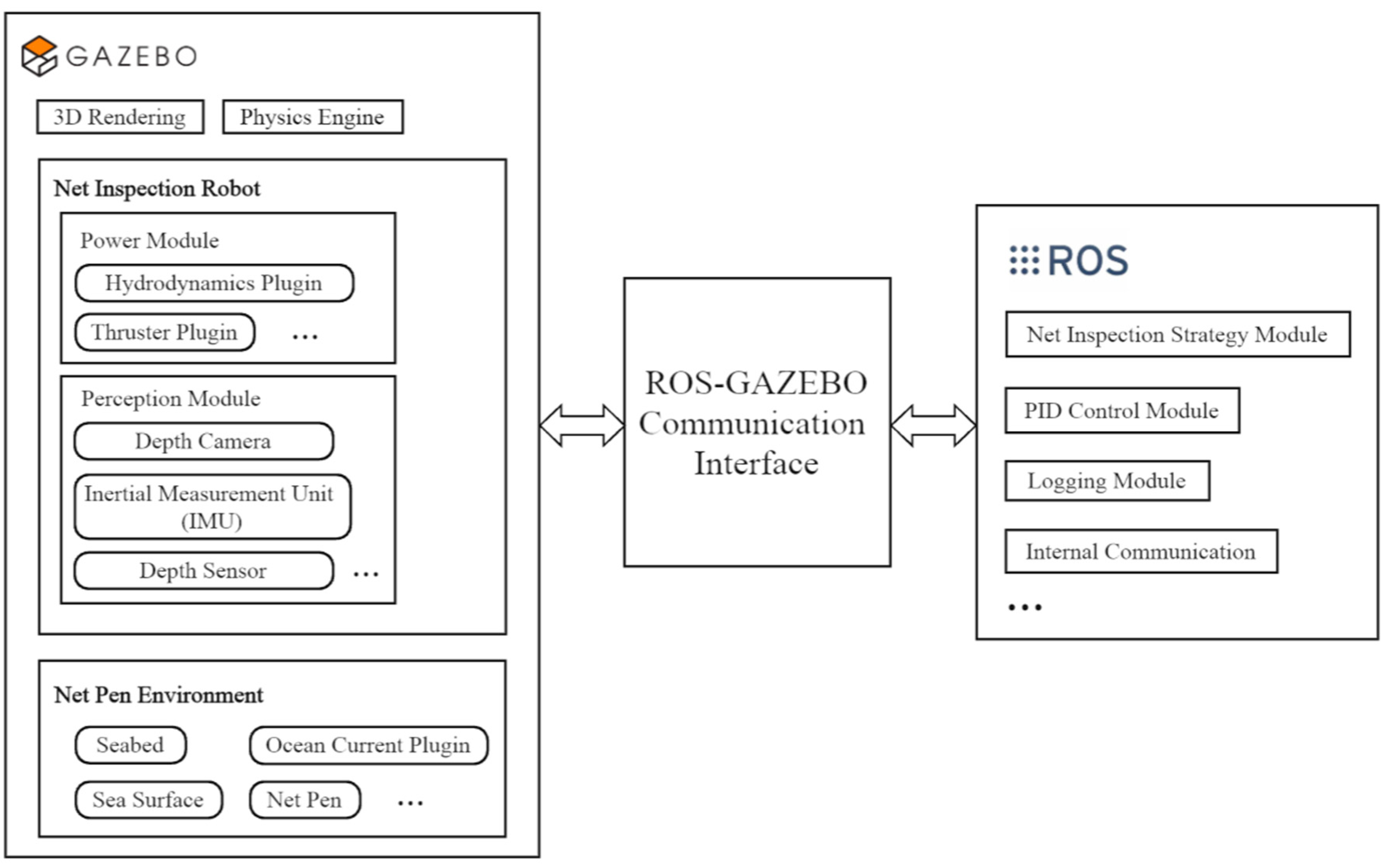
3.1. Simulators for Autonomous Inspection with Underwater Robots
3.2. Autonomous Inspection Strategy for Underwater Robots
- (1)
- The Forward State is the AUV’s primary inspection mode. In this state, the right-side depth camera collects depth information from the fish net. Using the Net Distance Controller, Net Angle Controller, and Depth Controller, the AUV maintains a constant depth and follows a trajectory parallel to the net, advancing at a fixed speed along a path at a specified distance from the net.
- (2)
- The Turning State is triggered when the AUV needs to make a large-angle rotation. The Yaw Controller compares the current yaw angle with the desired angle and adjusts the AUV’s orientation accordingly. Once the target angle is reached, the AUV transitions back to the Forward State to continue its inspection.
- (3)
- The Reset State is the AUV’s automatic net-search mode, activated in the event of strong interference. The Yaw Controller uses data from the IMU to reorient the AUV and return it to the vicinity of the net. Once the AUV determines its coordinates relative to the net, it seamlessly resumes the Forward State.

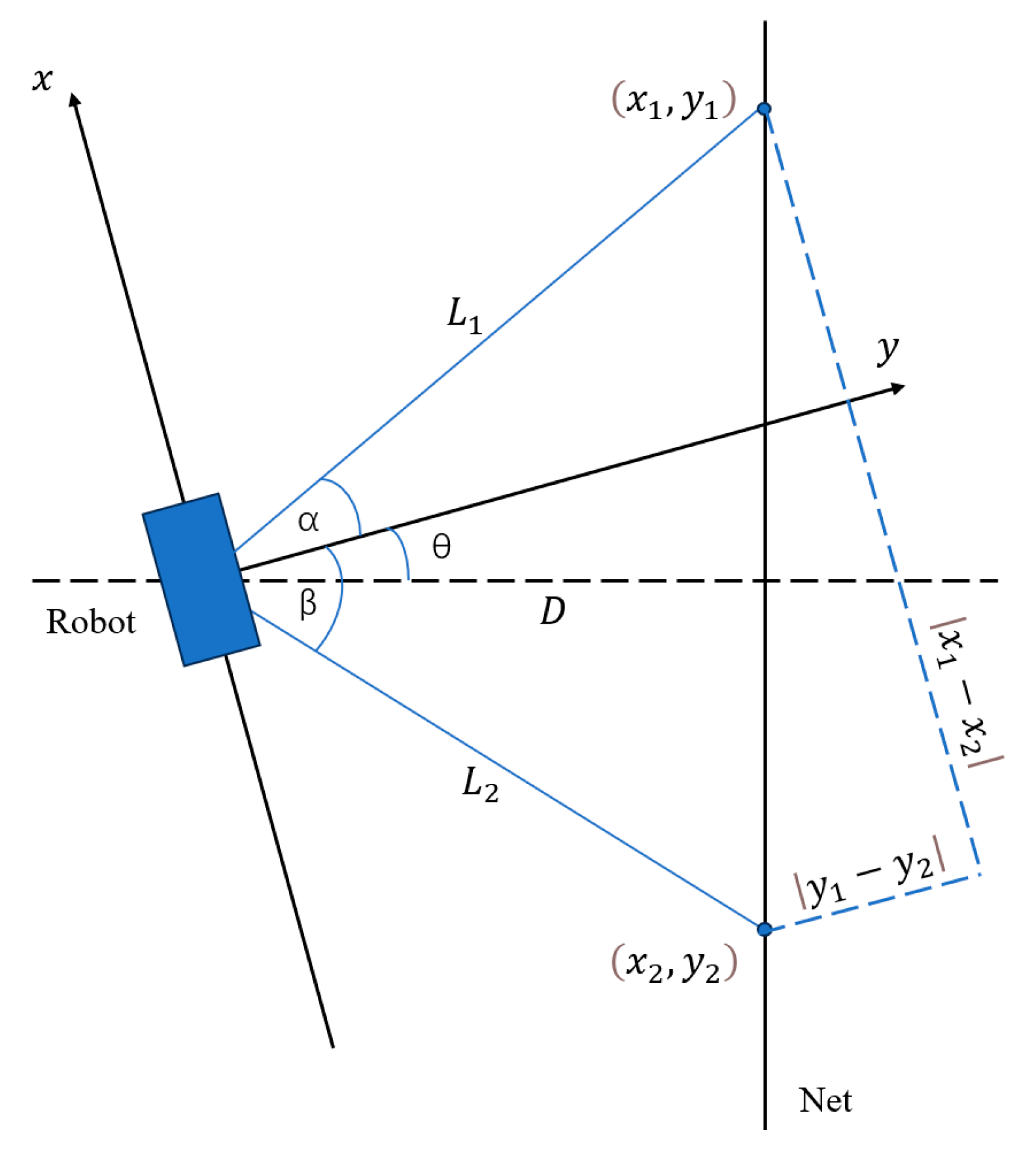
3.3. Distance and Orientation Measurement via Deep Vision
3.4. PID-Based Autonomous Inspection Control Method
3.4.1. Velocity PID Control
3.4.2. Thrust PID Control
4. Results and Discussion
4.1. AUV Inspection Simulation Results in Static Water
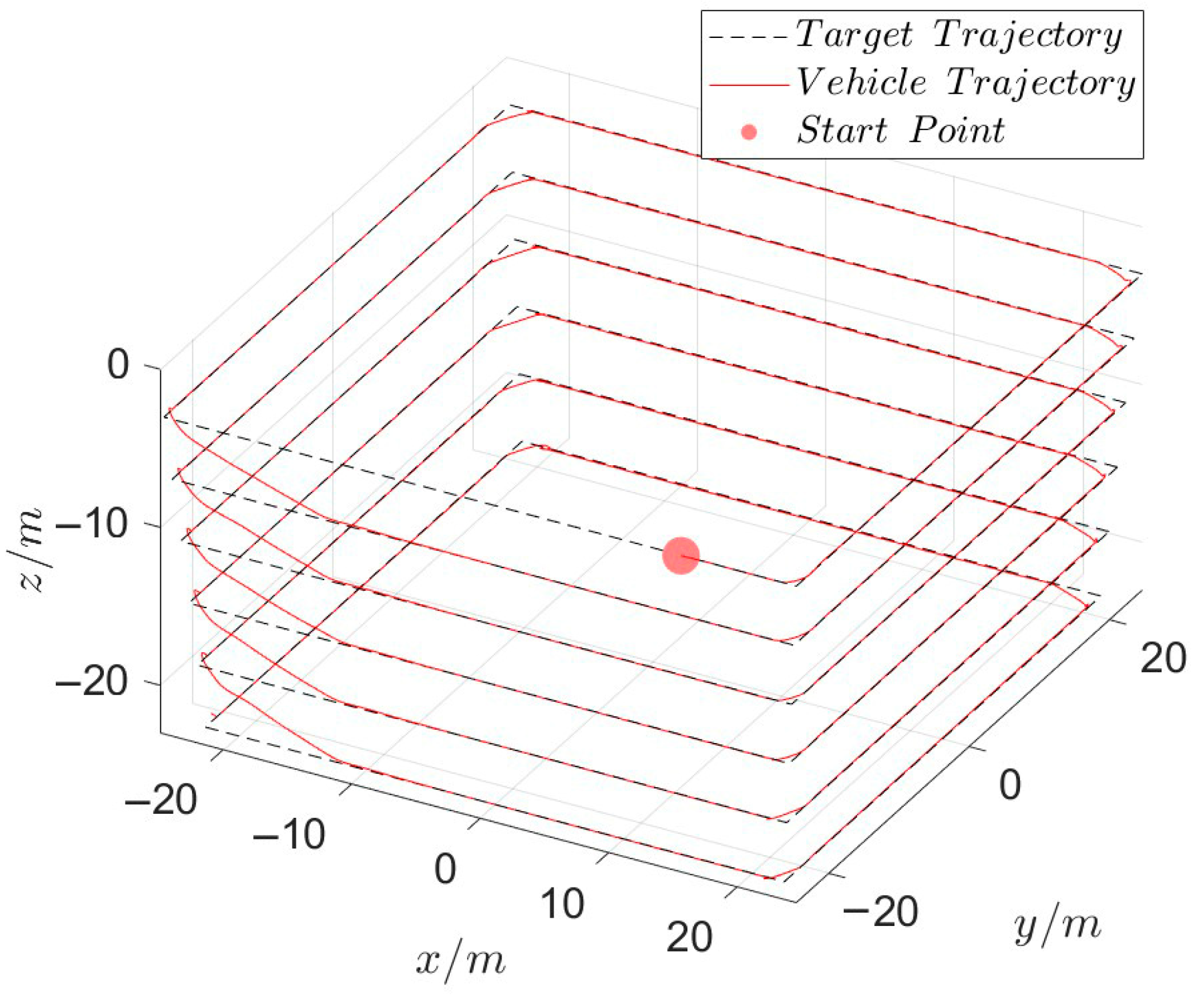
4.1.1. AUV Inspection Path
4.1.2. Yaw Angle, Depth, Net Distance, and Relative Angle of Attack
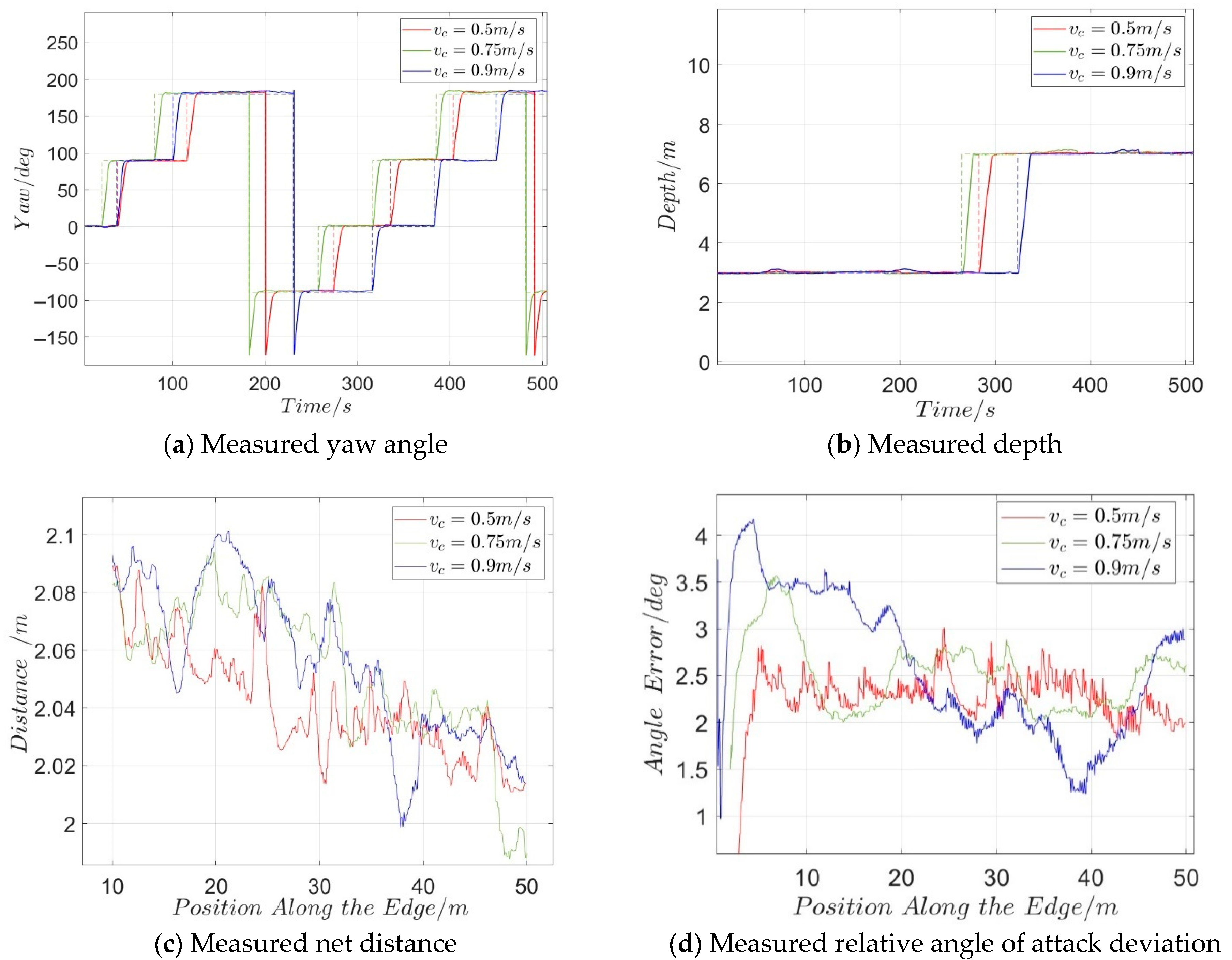
4.2. AUV Inspection Simulation Results Under Different Ocean Currents
4.3. AUV Inspection Simulation Results at Different Speeds
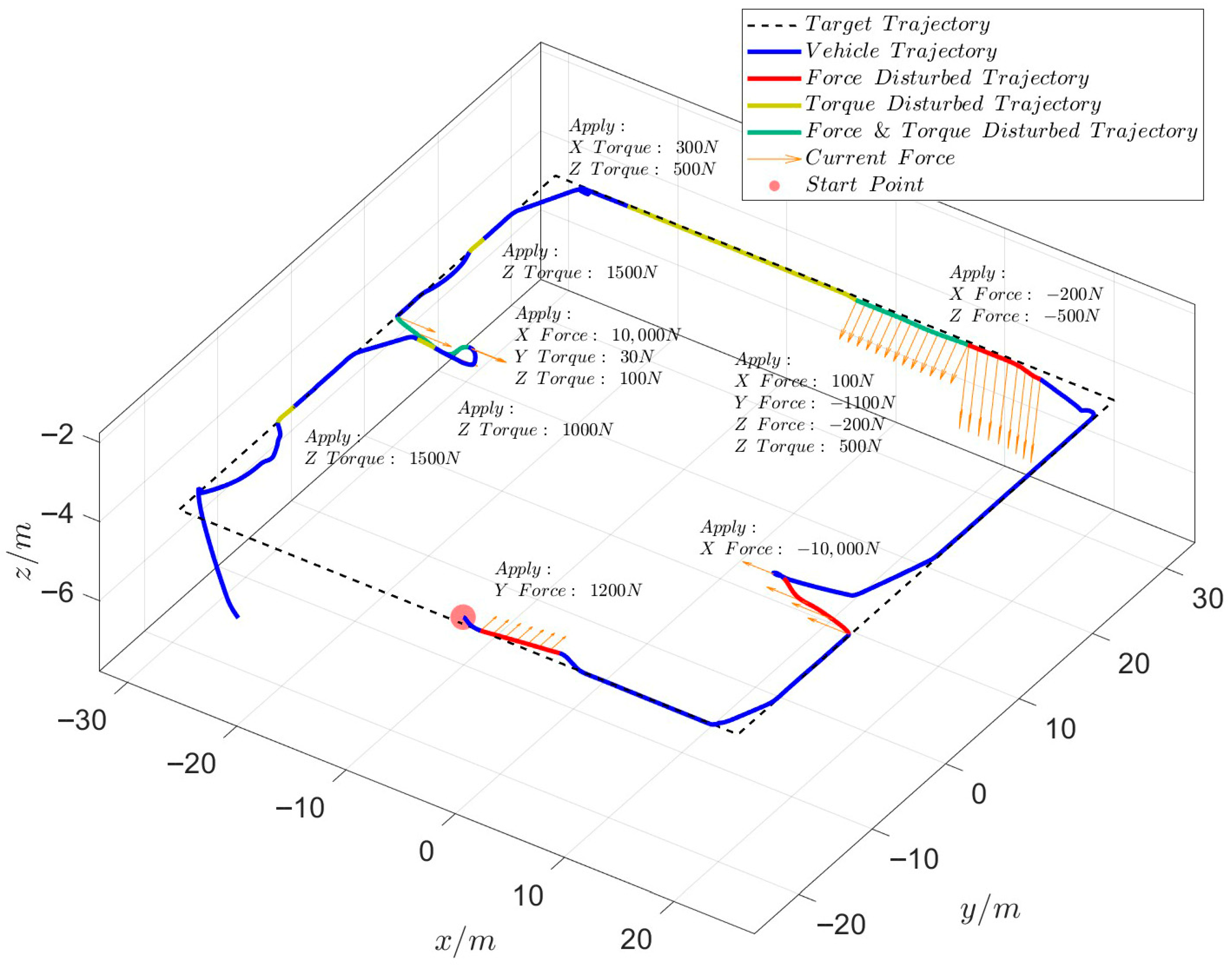
4.4. AUV Inspection Simulation Results Under Sudden External Forces
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Hydrodynamic Parameters of RexROV [22]
Appendix A.2. Pid Controller Parameter
| Controller Names | Lower Limit | Upper Limit | |||
|---|---|---|---|---|---|
| Depth controller | |||||
| Right net panel controller | |||||
| Net panel angle controller | |||||
| Yaw angle controller |
| DOF | x | y | z | ϕ | θ | ψ |
|---|---|---|---|---|---|---|
References
- Yu, J.; Wang, Y. Evolution of Deep-Sea Fisheries Policies in China: Review, Performance and Prospects. Fish. Manag. Ecol. 2023, 30, 109–120. [Google Scholar] [CrossRef]
- Yu, J.; Yan, T. Analyzing Industrialization of Deep-Sea Cage Mariculture in China: Review and Performance. Rev. Fish. Sci. Aquac. 2023, 31, 483–496. [Google Scholar] [CrossRef]
- Dong, S.-L.; Dong, Y.W.; Huang, L.-Y.; Zhou, Y.-G.; Cao, L.; Tian, X.-L.; Han, L.-M.; Li, D.-H. Advancements and Hurdles of Deeper-Offshore Aquaculture in China. Rev. Aquac. 2024, 16, 644–655. [Google Scholar] [CrossRef]
- Atalah, J.; Sanchez-Jerez, P. Global Assessment of Ecological Risks Associated with Farmed Fish Escapes. Glob. Ecol. Conserv. 2020, 21, e00842. [Google Scholar] [CrossRef]
- Gao, Q.F.; Dong, S.L. Cage Farming of Fish in Open Waters. In Aquaculture Ecology; Dong, S.L., Tian, X.L., Gao, Q.F., Dong, Y.W., Eds.; Springer: Singapore, 2023. [Google Scholar]
- Akram, W.; Casavola, A.; Kapetanović, N.; Miškovic, N. A Visual Servoing Scheme for Autonomous Aquaculture Net Pens Inspection Using ROV. Sensors 2022, 22, 3525. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Kim, A. Visibility Enhancement for Underwater Visual SLAM Based on Underwater Light Scattering Model. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 710–717. [Google Scholar] [CrossRef]
- Nauert, F.; Kampmann, P. Inspection and Maintenance of Industrial Infrastructure with Autonomous Underwater Robots. Front. Robot. AI 2023, 10, 1240276. [Google Scholar] [CrossRef] [PubMed]
- Ioannou, G.; Forti, N.; Millefiori, L.M.; Carniel, S.; Renga, A.; Tomasicchio, G.; Binda, S.; Braca, P. Underwater Inspection and Monitoring: Technologies for Autonomous Operations. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 4–16. [Google Scholar] [CrossRef]
- Yang, J.; Ni, J.; Xi, M.; Wen, J.; Li, Y. Intelligent Path Planning of Underwater Robot Based on Reinforcement Learning. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1983–1996. [Google Scholar] [CrossRef]
- Cepeda, M.F.S.; Machado, M.d.S.F.; Barbosa, F.H.S.; Moreira, D.S.S.; Almansa, M.J.L.; de Souza, M.I.L.; Caprace, J.-D. Exploring Autonomous and Remotely Operated Vehicles in Offshore Structure Inspections. J. Mar. Sci. Eng. 2023, 11, 2172. [Google Scholar] [CrossRef]
- Sandoy, S.S.; Schjolberg, I. Experimental Verification of Underwater Positioning System in Aquaculture. In Proceedings of the OCEANS 2017-Aberdeen, Aberdeen, UK, 19–22 June 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Amundsen, H.B.; Caharija, W.; Pettersen, K.Y. Autonomous ROV Inspections of Aquaculture Net Pens Using DVL. IEEE J. Ocean. Eng. 2022, 47, 1–19. [Google Scholar] [CrossRef]
- Stenså, O.A. Choice and Design of 6 Degree-of-Freedom Observer for ROVs Operating in Fish Farms in the Presence of Time-Varying Environmental Disturbances; Norwegian University of Science and Technology: Trondheim, Noorwegen, 2023. [Google Scholar]
- Bjerkeng, M.; Kirkhus, T.; Caharija, W.; Thielemann, J.T.; Amundsen, H.B.; Ohrem, S.J.; Grøtli, E.I. ROV Navigation in a Fish Cage with Laser-Camera Triangulation. J. Mar. Sci. Eng. 2021, 9, 79. [Google Scholar] [CrossRef]
- López-Barajas, S.; Sanz, P.J.; Marín-Prades, R.; Gómez-Espinosa, A.; González-García, J.; Echagüe, J. Inspection Operations and Hole Detection in Fish Net Cages through a Hybrid Underwater Intervention System Using Deep Learning Techniques. J. Mar. Sci. Eng. 2024, 12, 80. [Google Scholar] [CrossRef]
- Yan, C. Research on Autonomous Net Inspection of Marine Pastures Based on Reinforcement Learning. Master’s Thesis, Dalian Ocean University, Dalian, China, 2023. [Google Scholar]
- Manhaes, M.M.M.; Scherer, S.A.; Voss, M.; Douat, L.R.; Rauschenbach, T. UUV Simulator: A Gazebo-Based Package for Underwater Intervention and Multi-Robot Simulation. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Farley, A.; Wang, J.; Marshall, J.A. How to Pick a Mobile Robot Simulator: A Quantitative Comparison of CoppeliaSim, Gazebo, MORSE and Webots with a Focus on Accuracy of Motion. Simul. Model. Pract. Theory 2022, 120, 102629. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and Use Paradigms for Gazebo, an Open-Source Multi-Robot Simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Xing, W.; Huang, X.; Li, G.; Pang, G.; Yuan, T. Construction of a Dynamics Simulation System for Net Cleaning Robot Based on Gazebo. South China Fish. Sci. 2024, 20, 1–10. [Google Scholar] [CrossRef]
- Berg, V. Development and Commissioning of a DP System for ROV SF 30k. Master’s Thesis, Department of Marine Technology, Institutt for Marin Teknikk, Trondheim, Norway, 2012. [Google Scholar]






| Current Speeds | MSE of Measured Net Distance | MSE of Measured Relative Angle of Attack Deviation |
|---|---|---|
| 0.5 m/s | ||
| 0.75 m/s | ||
| 0.9 m/s |
| Cruising Speeds | MSE of Measured Net Distance | MSE of Measured Relative Angle of Attack Deviation |
|---|---|---|
| 0.75 m/s | ||
| 1.0 m/s | ||
| 1.25 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, K.; Li, C.; Sun, Q.; Liu, Y.; Ye, H.; Xu, Y. Autonomous Inspection Strategies and Simulation for Large Aquaculture Net Cages Based on Deep Visual Perception. J. Mar. Sci. Eng. 2025, 13, 1736. https://doi.org/10.3390/jmse13091736
Cai K, Li C, Sun Q, Liu Y, Ye H, Xu Y. Autonomous Inspection Strategies and Simulation for Large Aquaculture Net Cages Based on Deep Visual Perception. Journal of Marine Science and Engineering. 2025; 13(9):1736. https://doi.org/10.3390/jmse13091736
Chicago/Turabian StyleCai, Keru, Cong Li, Qian Sun, Yijun Liu, Hongyi Ye, and Yuwang Xu. 2025. "Autonomous Inspection Strategies and Simulation for Large Aquaculture Net Cages Based on Deep Visual Perception" Journal of Marine Science and Engineering 13, no. 9: 1736. https://doi.org/10.3390/jmse13091736
APA StyleCai, K., Li, C., Sun, Q., Liu, Y., Ye, H., & Xu, Y. (2025). Autonomous Inspection Strategies and Simulation for Large Aquaculture Net Cages Based on Deep Visual Perception. Journal of Marine Science and Engineering, 13(9), 1736. https://doi.org/10.3390/jmse13091736







