A High-Efficiency Task Allocation Algorithm for Multiple Unmanned Aerial Vehicles in Offshore Wind Power Under Energy Constraints
Abstract
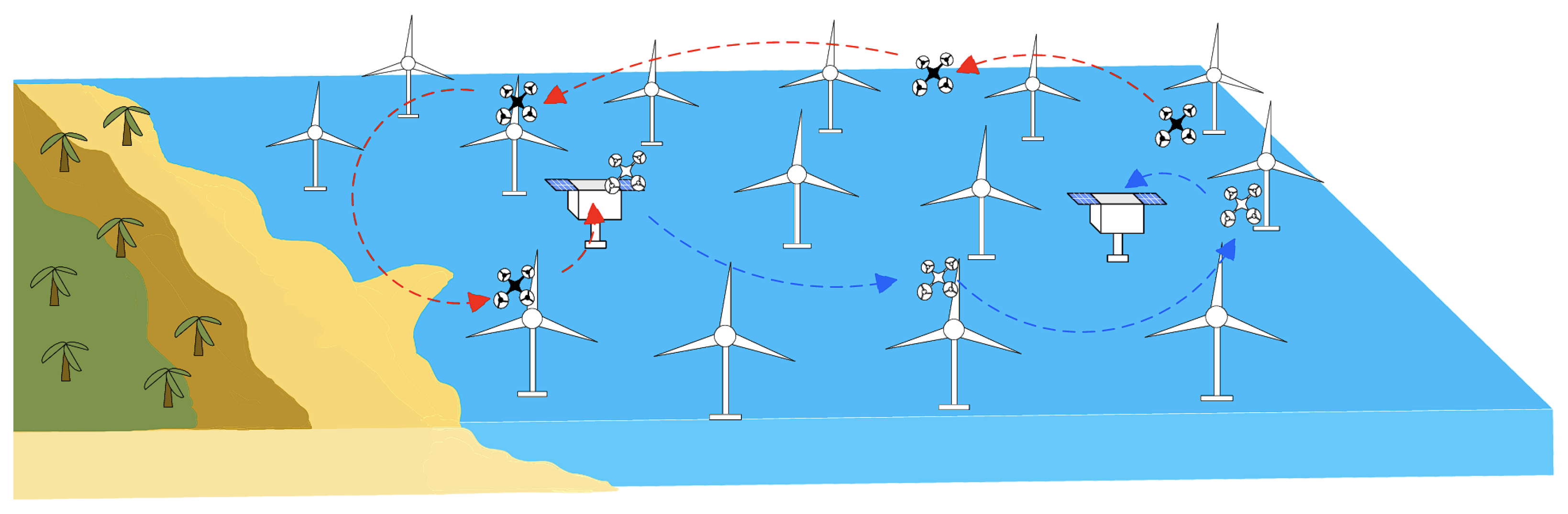
1. Introduction
- An improved Particle Swarm optimization algorithm (IPSO) is proposed to optimize the location of charging stations. An innovative UAV task allocation optimization algorithm is developed by adopting the dynamic elite group double population mechanism genetic algorithm (DDGA), which has good high-quality disorientation and excellent global search ability.
- The location optimization function of the charging station and the task allocation optimization model of UAVs with multiple charging stations under energy constraints are established, enabling UAVs to charge dynamically at different locations and optimize task execution. This model balances factors such as task completion time, workload allocation among UAVs, and energy consumption, ensuring that UAVs effectively perform tasks while maintaining the optimal battery power through the strategic use of the charging station.
- We conduct simulation experiments on the position optimization of charging stations and the task allocation of UAVs with multiple charging stations under energy constraints to verify the proposed task allocation model and optimization algorithm. These experiments proved the effectiveness of the proposed solution in real-world scenarios and compared the performance of the UAV system under different conditions.
2. Multi-Station UAV Cooperative Task Allocation Model
2.1. Optimization of Charging Station Locations
2.1.1. Minimize the Safe Charging Distance
2.1.2. The Balance of the Pre-Allocated Task Distance of the Charging Station
2.1.3. The Balance of the Pre-Allocation of the Number of Task Points
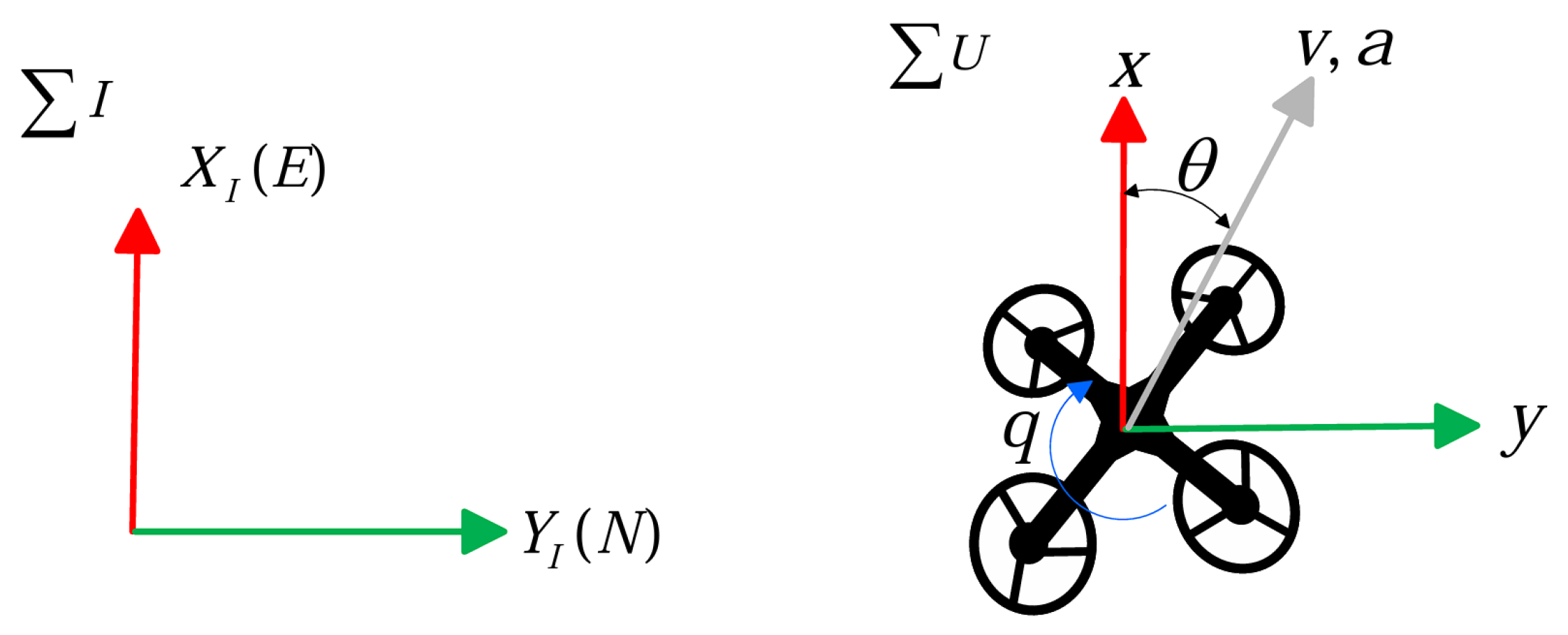
2.2. Kinematics Model and Performance Constraints of Four-Rotor UAV
2.2.1. Kinematic Model
2.2.2. Constraint Conditions
2.2.3. Nonlinear Charging Time Model
2.3. UAV Inspection Model with Charging Constraint
3. Proposed Method
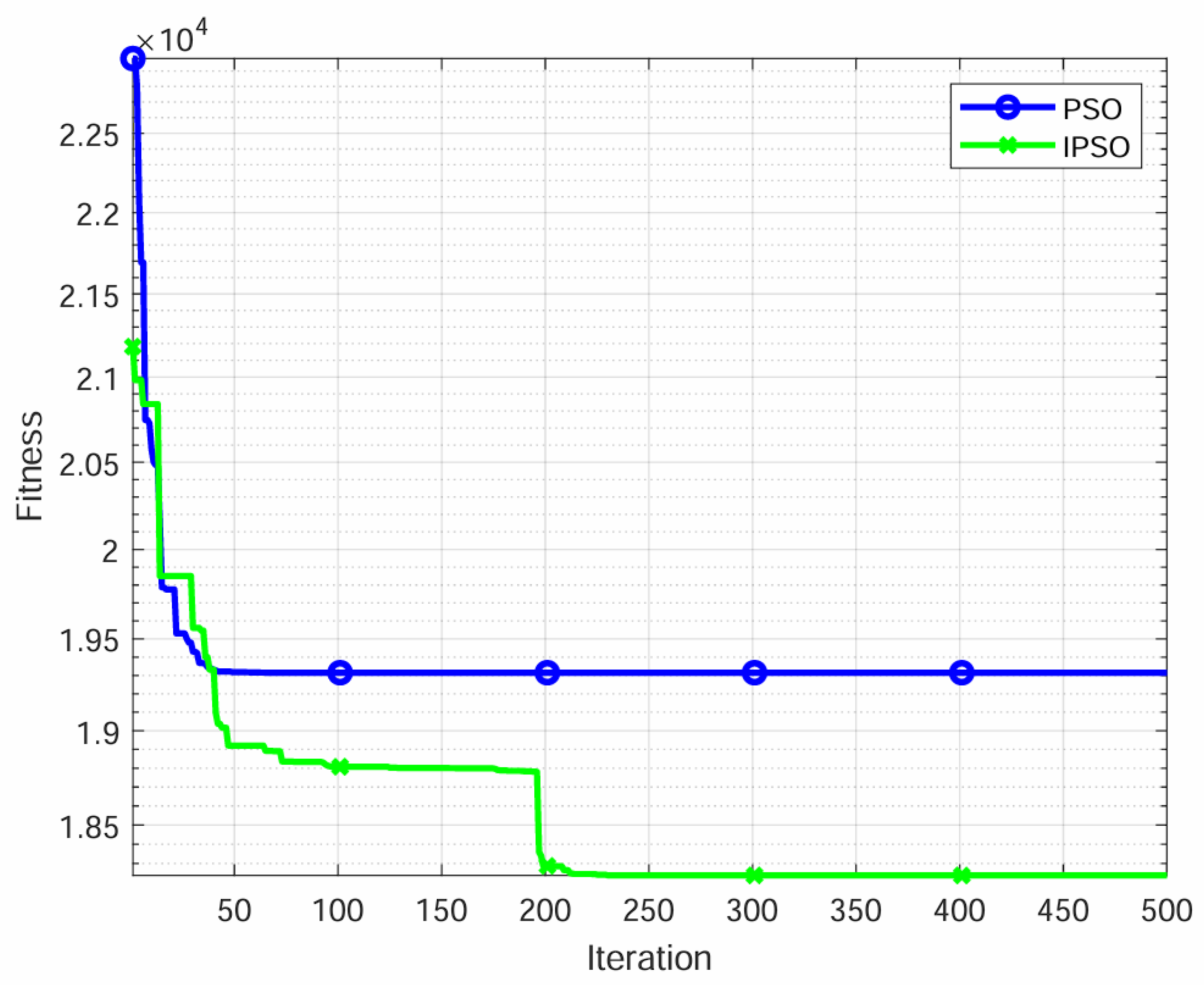
3.1. Optimized Charging Station Location Algorithm Based on IPSO
| Algorithm 1: IPSO algorithm |
 |
3.2. Multi-Uav Task Allocation Algorithm Based on DDGA
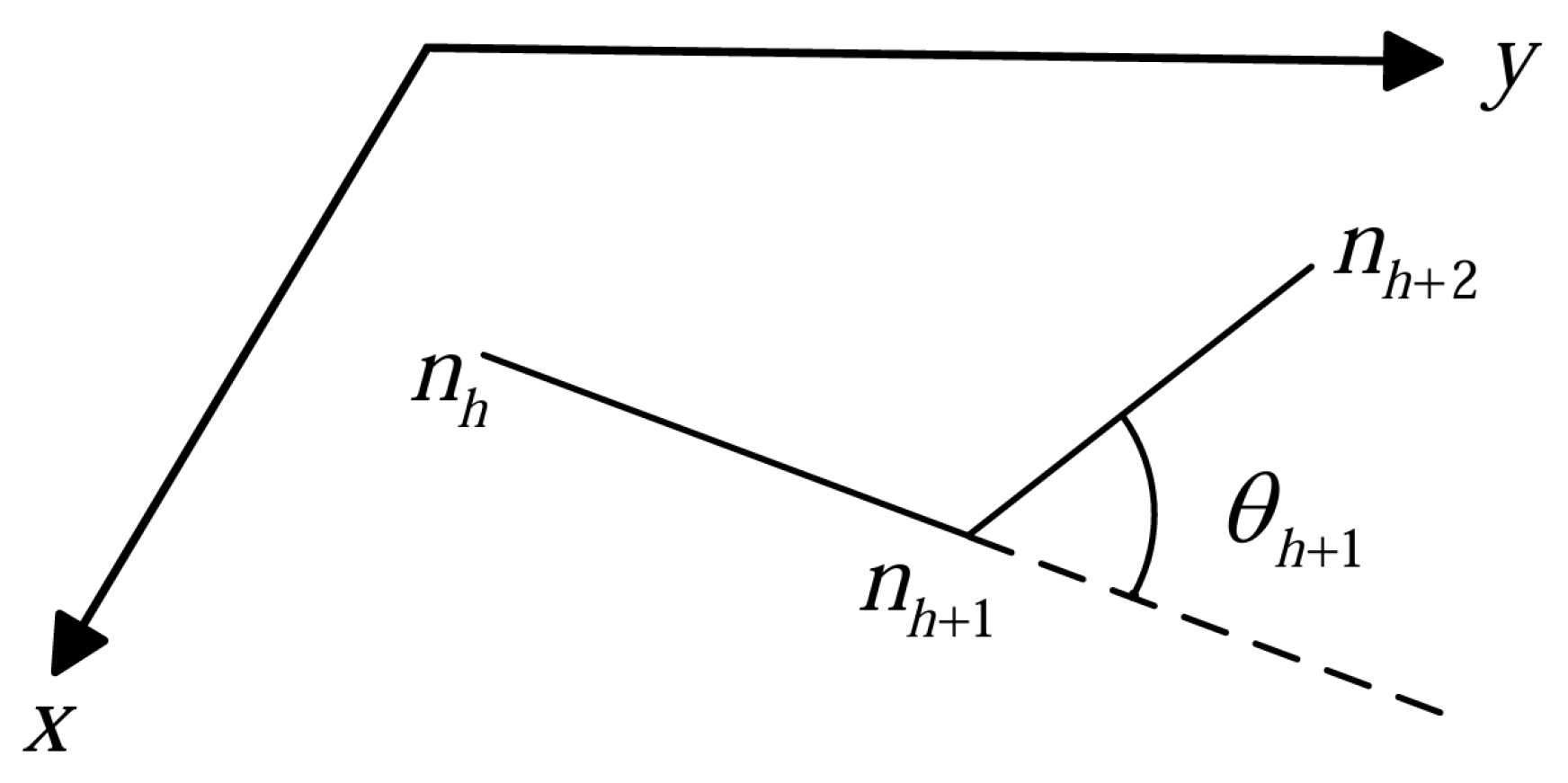
3.2.1. Coding
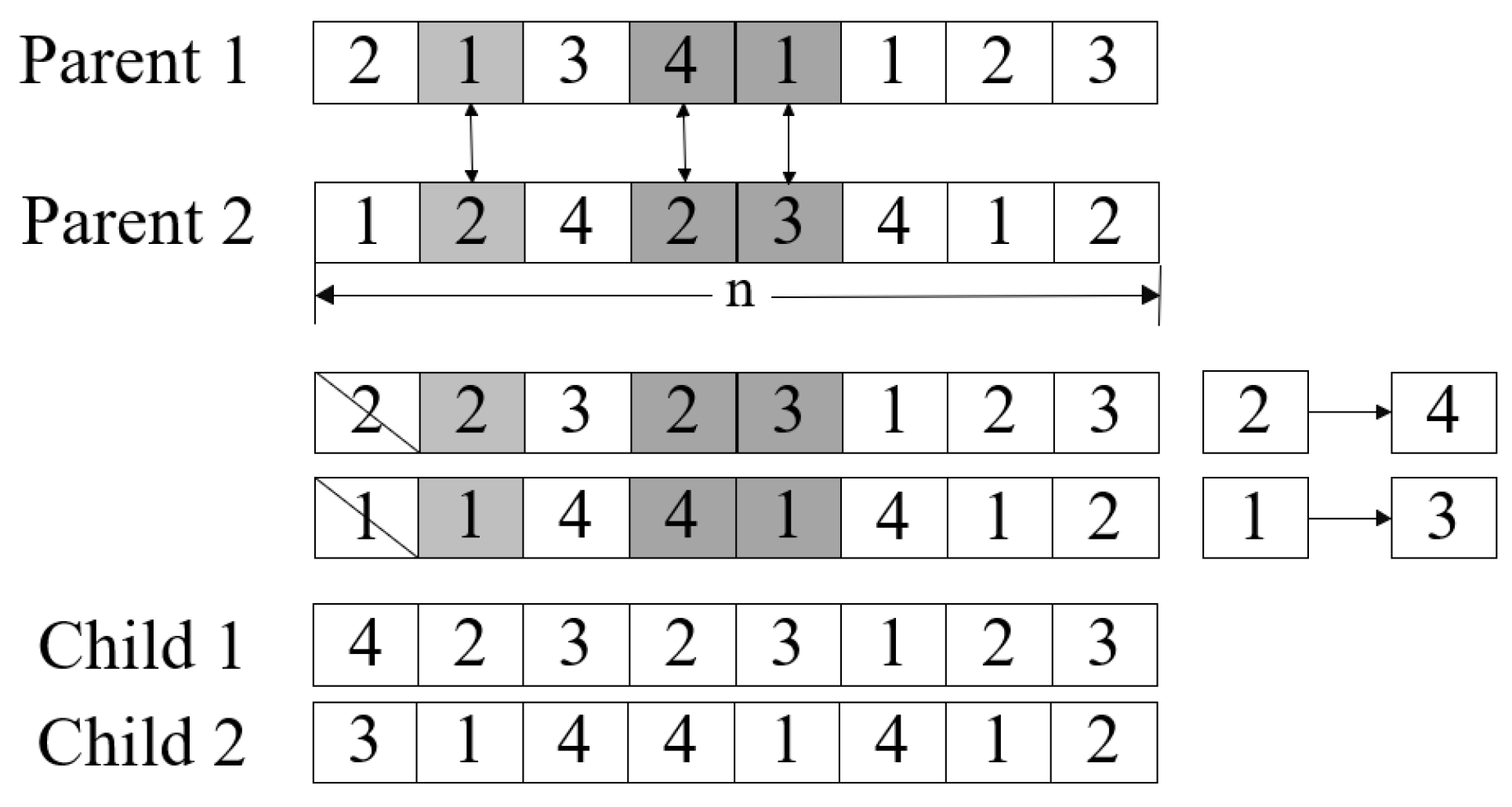
3.2.2. Crossover Operation
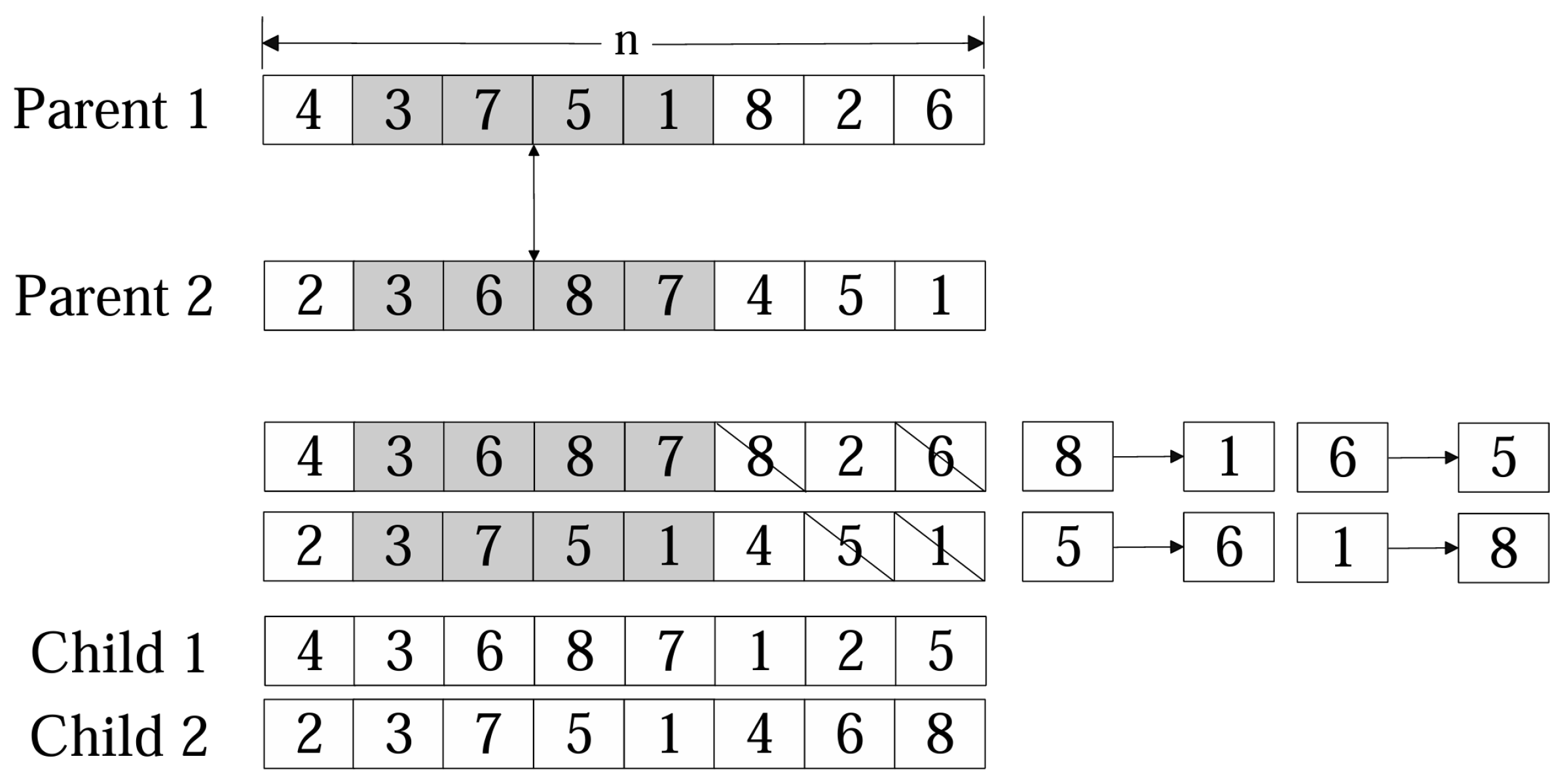
- The A segment of the chromosome contains information about the task allocation of UAVs. For this segment, after the initial crossover, genetic testing ensures that each UAV identifier exists in the chromosome. Avoid the situation where UAVs have no task. In the crossover operation, a uniform crossover strategy is adopted, guided by a predefined crossover probability P. For each gene position, a chaotic random number is generated to determine whether a crossover should occur. If the chaotic random number exceeds P, the genes at the corresponding position in the two parent chromosomes are exchanged; otherwise, the genes remain unchanged. An illustrative example of this uniform crossover process is presented in Figure 6.
- The B segment of the chromosome contains information about the execution sequence of the task points of the UAV. For chromosome B, we use PMX to ensure that every gene occurs once and only once, preventing intra-chromosome repetition. A sample partial crossover is depicted in Figure 7.
3.2.3. Mutation Operation
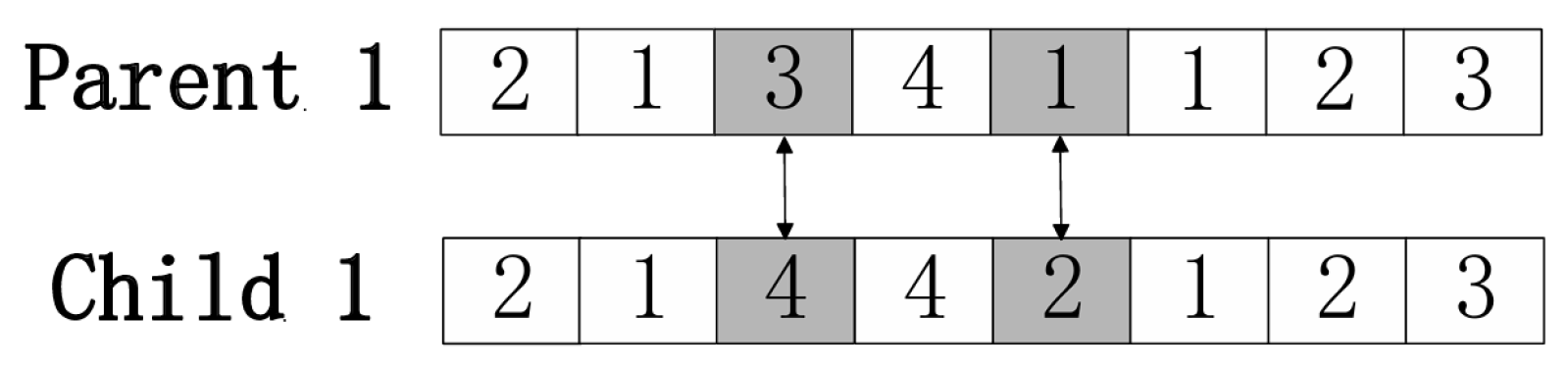
- In segment A, mutation is carried out using a random scheme (Figure 8): x gene positions are sampled uniformly and replaced with admissible unmanned system identifiers.
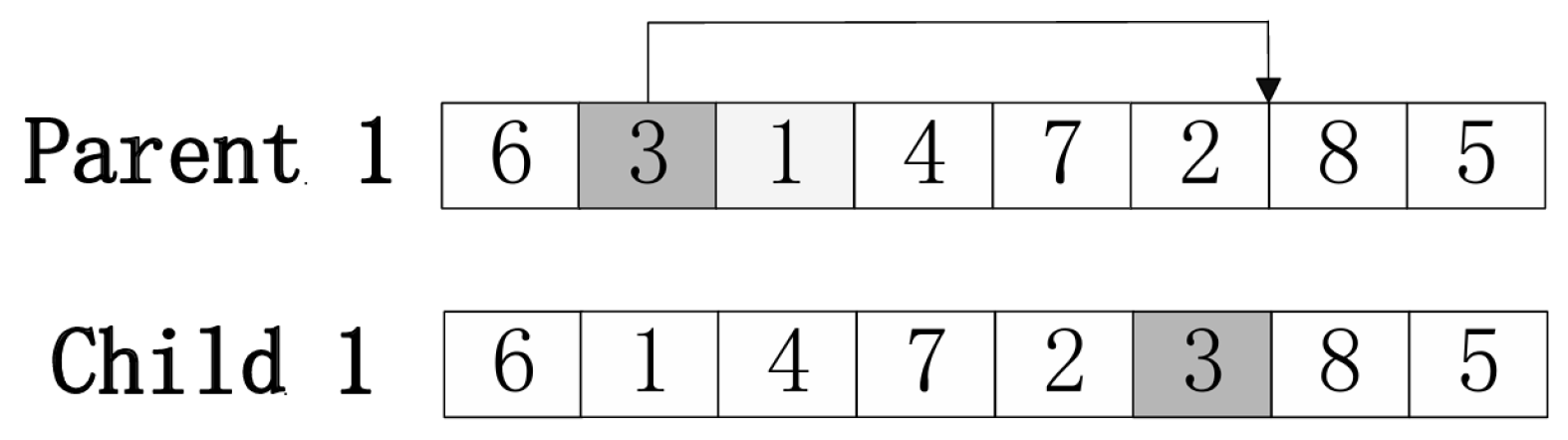
- For segment B, insertion mutation is used, as illustrated in Figure 9; one gene is randomly selected from the segment and reinserted at a different random index within that segment.
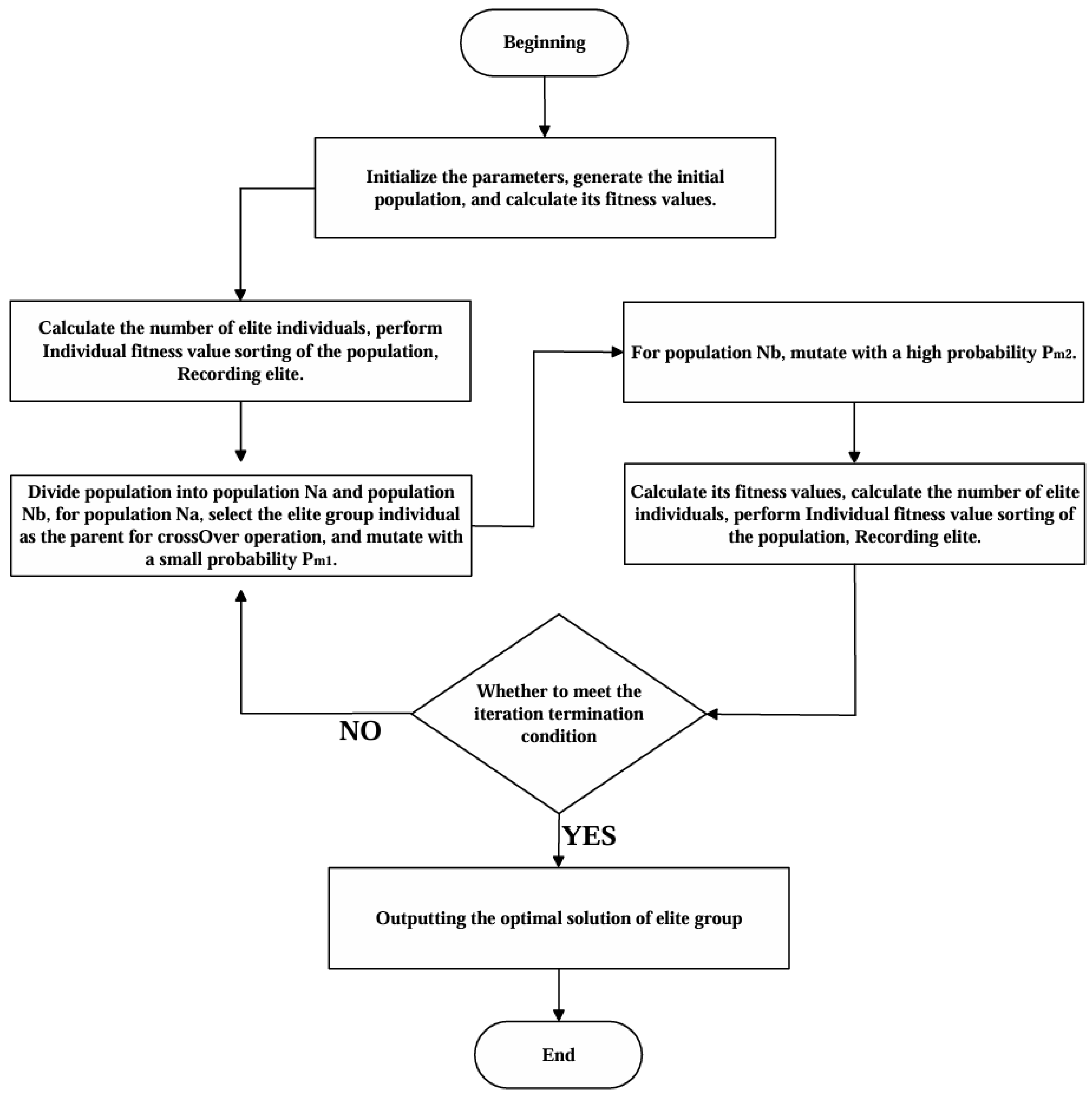
3.2.4. Proposed DDGA
3.2.5. Algorithm Step
4. Case Study
4.1. Simulation Cases for Charging Station Location
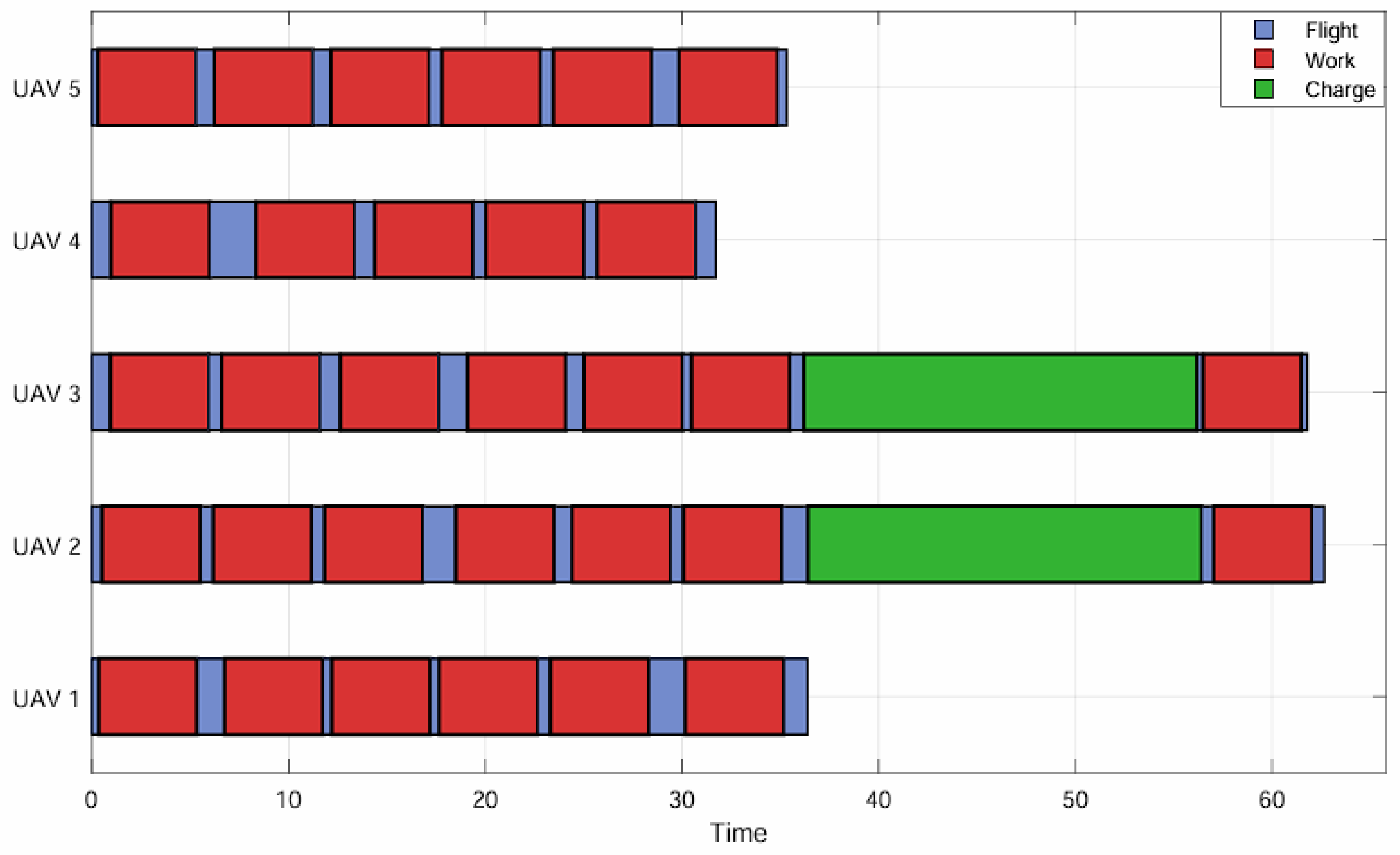
4.2. Simulation Cases for Cooperative Task Allocation
5. Evaluation and Validation
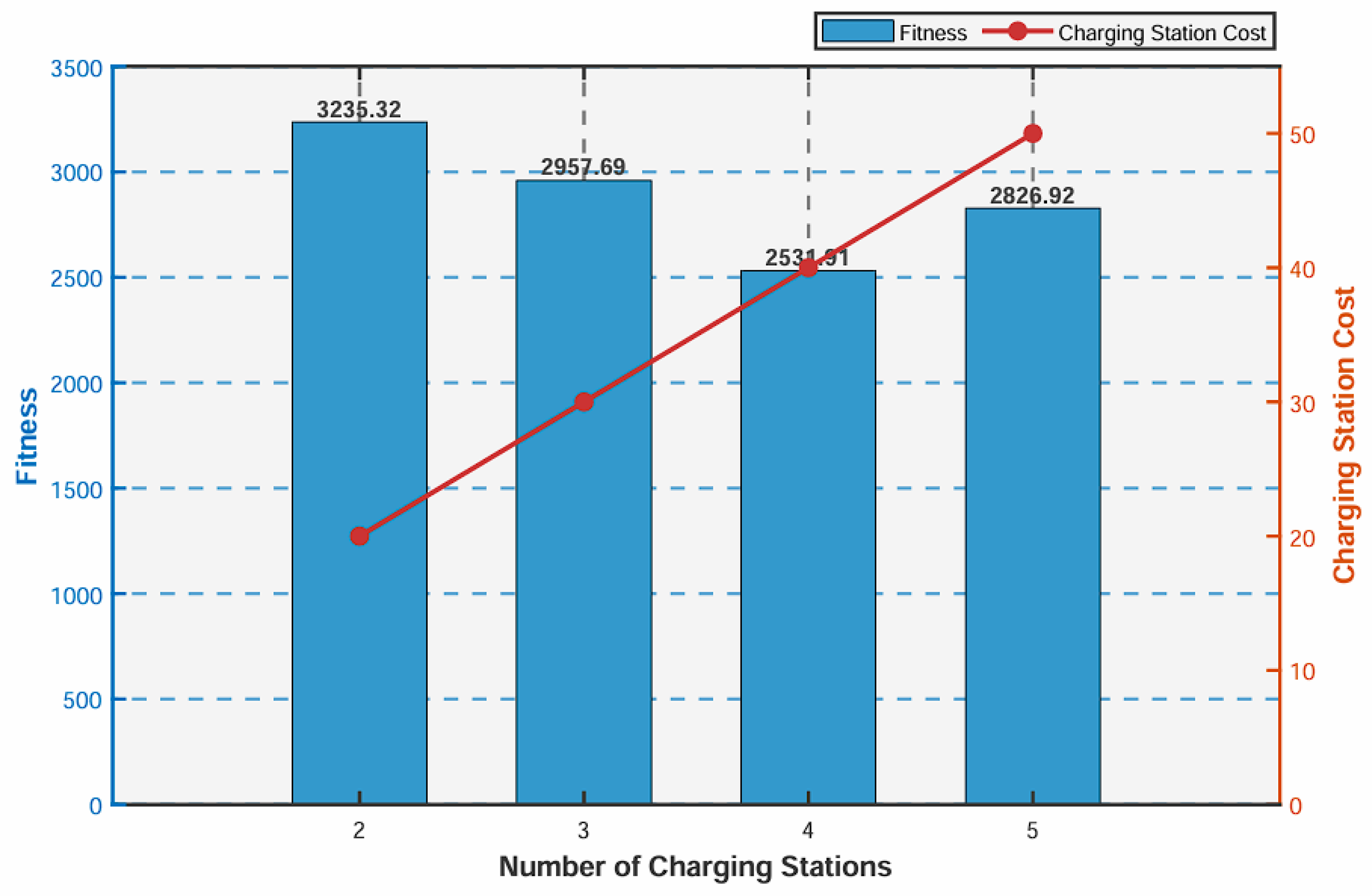
5.1. Sensitive Analysis
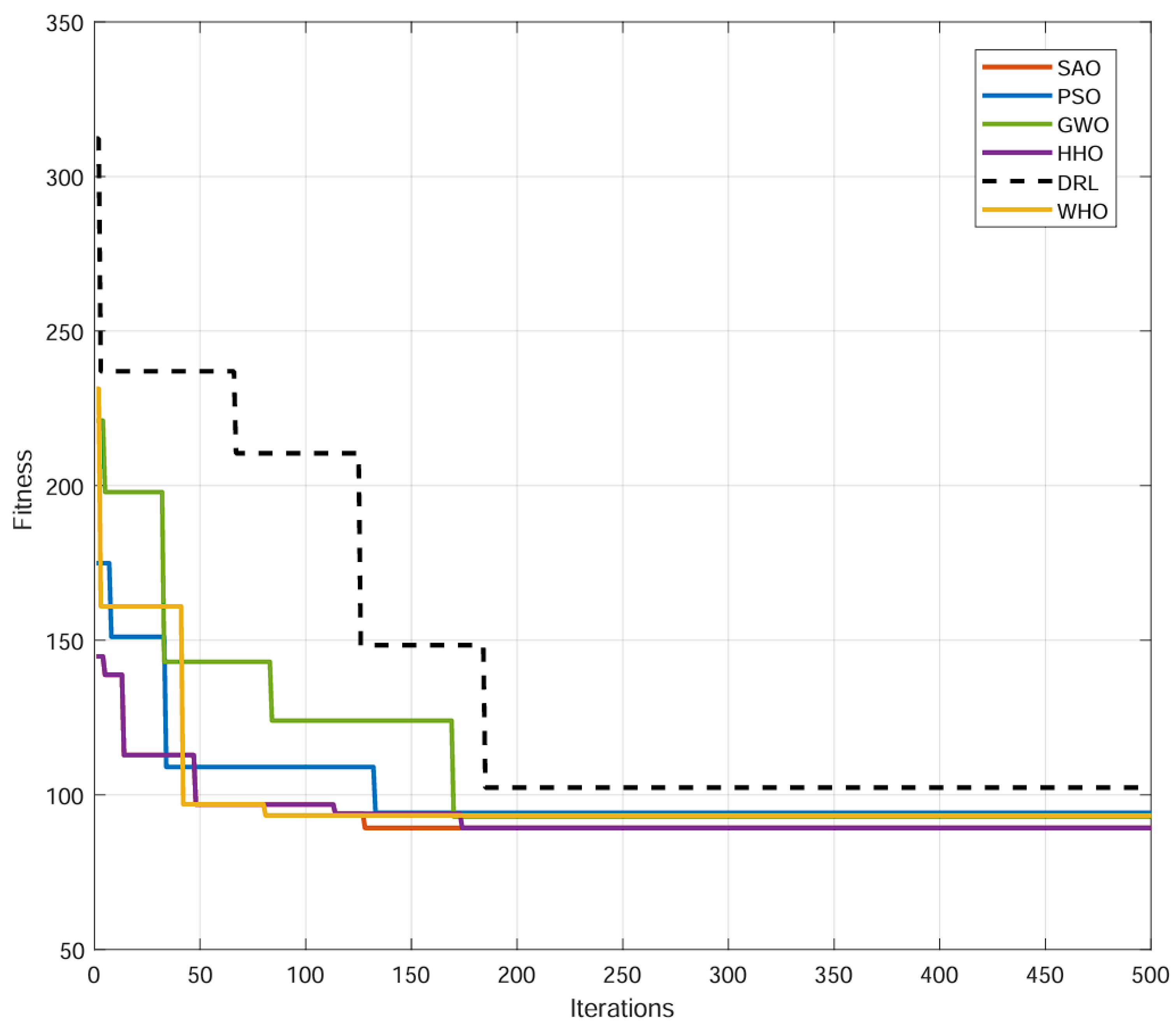
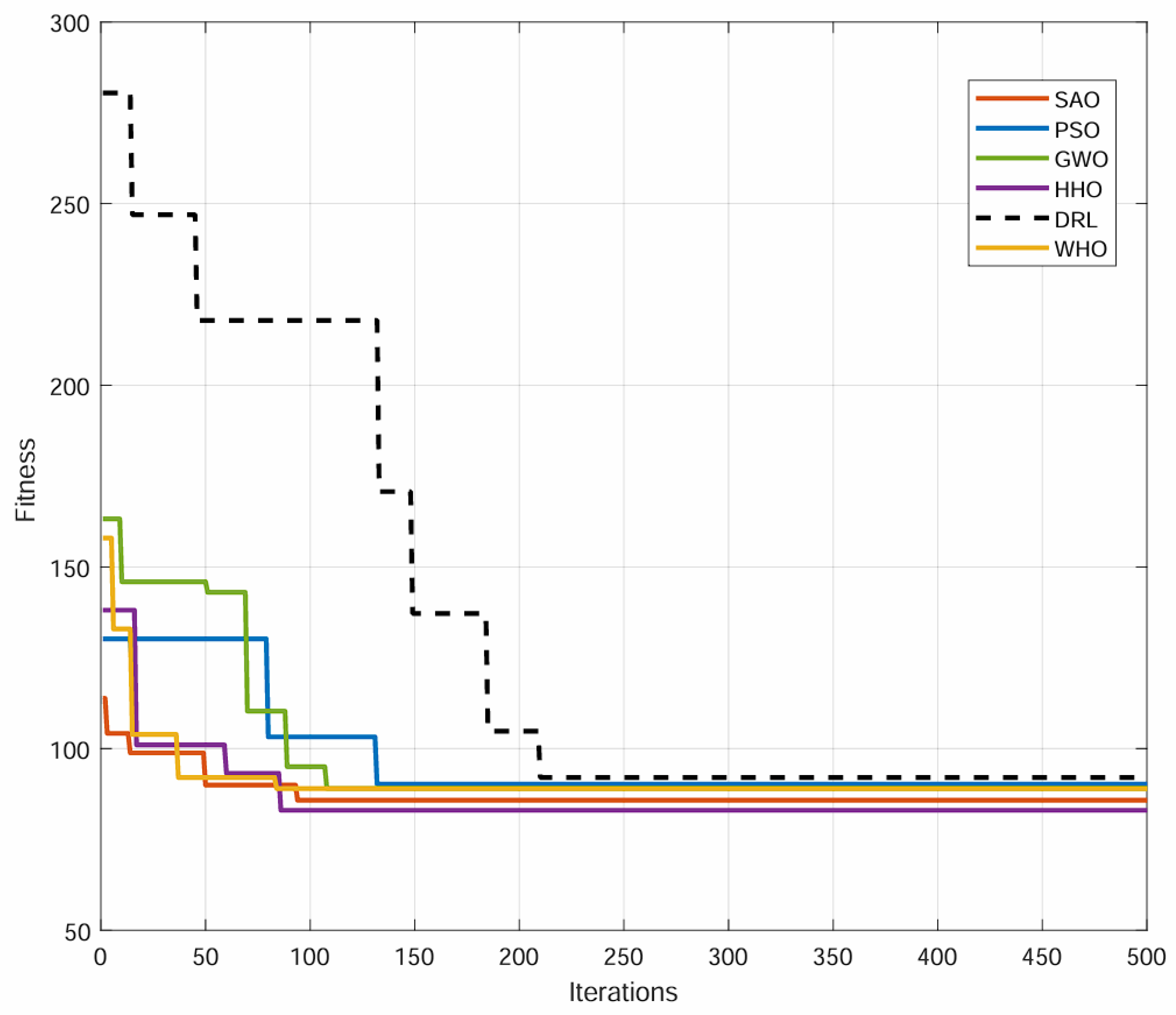
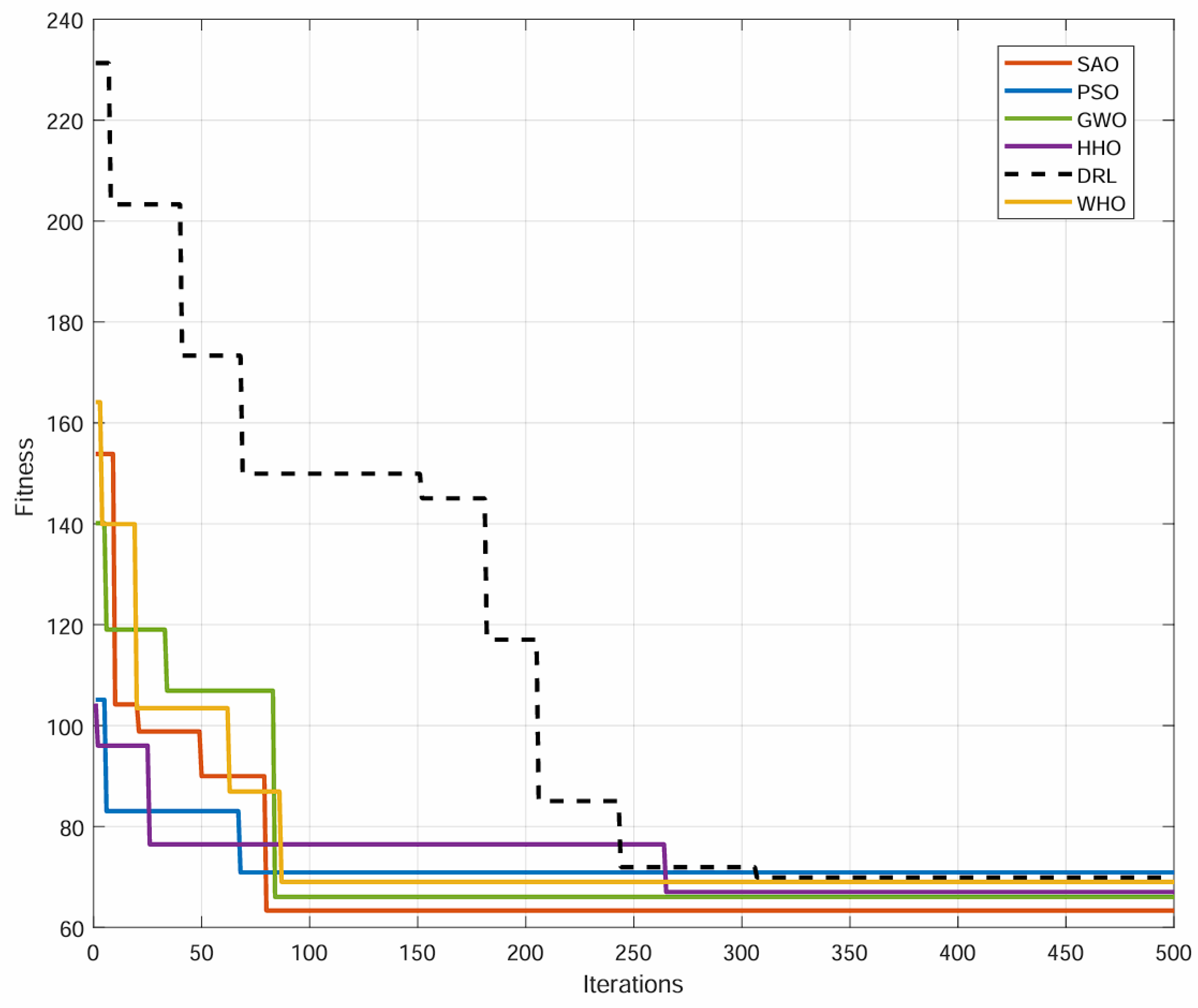
5.2. Comparison Analysis
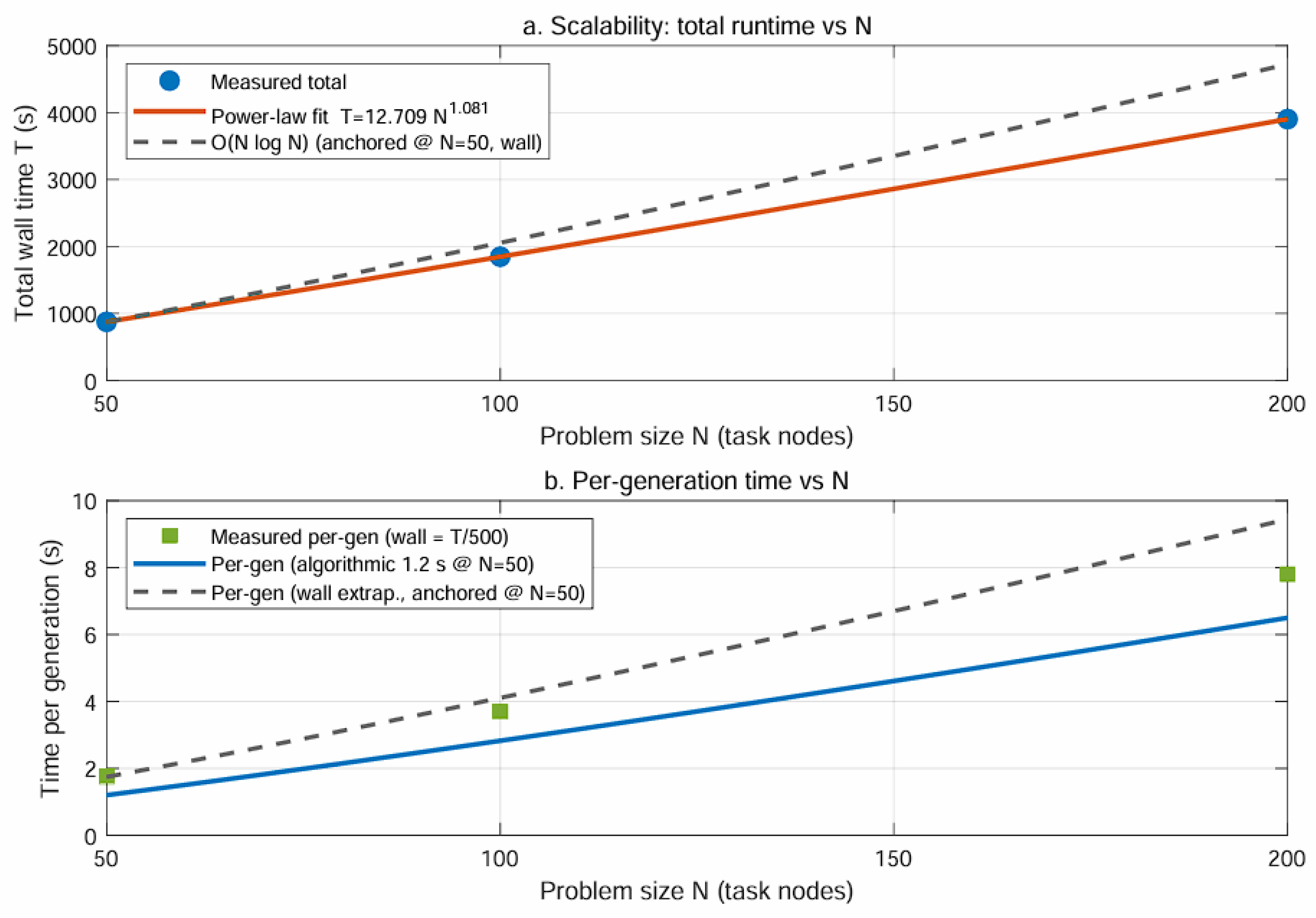
5.3. Scalability Testing
6. Conclusions
- The IPSO algorithm is proposed based on the establishment of the location optimization model of charging stations, aiming to ensure the flight safety of UAVs and the low-cost location of charging stations, and to optimize the pre-inspection time, preparing for later task allocation research. Through the enhanced search strategy based on elite reverse learning, the global search ability of the PSO algorithm has been improved, and the performance of the algorithm has been enhanced. The simulation results show that the IPSO algorithm is superior to the original PSO algorithm.
- This work presents an offshore UAV-swarm task allocation model with energy limitations and intricate constraints, optimized for inspection time cost. We devise DDGA, a GA improvement that integrates a dual-population architecture and an elite group, augments performance via piecewise coding and genetic operators, and refines adaptive elite preservation. Experiments in scenarios where charging chambers are more numerous than, fewer than, or equal to the UAVs validate the method and highlight its superiority through comparative tests.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, L.; Li, M.; Wang, X.; Chen, Y.; Chen, T. Indo-Pacific finless porpoises presence in response to pile driving on the Jinwan Offshore Wind Farm, China. Front. Mar. Sci. 2023, 10, 1005374. [Google Scholar] [CrossRef]
- Reid, K.; Baker, G.B.; Woehler, E.J. An ecological risk assessment for the impacts of offshore wind farms on birds in Australia. Austral Ecol. 2023, 48, 1. [Google Scholar] [CrossRef]
- Liu, Y.; Hajj, M.; Bao, Y. Review of robot-based damage assessment for offshore wind turbines. Renew. Sustain. Energy Rev. 2022, 158, 112187. [Google Scholar] [CrossRef]
- Gohar, I.; Yew, W.K.; Halimi, A.; See, J. Review of state-of-the-art surface defect detection on wind turbine blades through aerial imagery: Challenges and recommendations. Eng. Appl. Artif. Intell. 2025, 144, 109970. [Google Scholar] [CrossRef]
- Tremps, L.; Yeter, B.; Kolios, A. Review and analysis of the failure risk mitigation via monitoring for monopile offshore wind structures. Energy Rep. 2024, 11, 5407–5420. [Google Scholar] [CrossRef]
- Cyp, H.G.; Jovanova, J. From Heights to the Deep Sea, a Review of Robots Interacting with Offshore Structures. Robot. Rep. 2024, 2, 85–100. [Google Scholar] [CrossRef]
- Zhang, K.; Pakrashi, V.; Murphy, J.; Hao, G. Inspection of Floating Offshore Wind Turbines Using Multi-Rotor Unmanned Aerial Vehicles: Literature Review and Trends. Sensors 2022, 24, 911. [Google Scholar] [CrossRef]
- Omara, A.; Nasser, A.; Alsayed, A.; Nabawy, M.R.A. Remote Wind Turbine Inspections: Exploring the Potential of Multimodal Drones. Drones 2025, 9, 4. [Google Scholar] [CrossRef]
- Rahman, M.; Sarkar, N.I.; Lutui, R. A Survey on Multi-UAV Path Planning: Classification, Algorithms, Open Research Problems, and Future Directions. Drones 2025, 9, 263. [Google Scholar] [CrossRef]
- Foster, A.J.I.; Gianni, M.; Aly, A.; Samani, H.; Sharma, S. Multi-Robot Coverage Path Planning for the Inspection of Offshore Wind Farms: A Review. Drones 2024, 8, 10. [Google Scholar] [CrossRef]
- Rendle, E.J.; Hunt, E.L.; Bicknell, A.W.J. A three-step approach for co-locating nature-based solutions within offshore wind farms. Front. Ecol. Evol. 2023, 11, 2296. [Google Scholar] [CrossRef]
- Methratta, E.T.; Silva, A.; Lipsky, A.; Ford, K.; Christel, D.; Pfeiffer, L. Science Priorities for Offshore Wind and Fisheries Research in the Northeast U.S. Continental Shelf Ecosystem: Perspectives from Scientists at the National Marine Fisheries Service. Mar. Coast. Fish. 2023, 3, e10242. [Google Scholar] [CrossRef]
- Han, S. Survey on UAV Deployment and Trajectory in Wireless Communication Networks: Applications and Challenges. Information 2022, 13, 389. [Google Scholar] [CrossRef]
- Messaoudi, K.; Oubbati, O.S.; Rachedi, A.; Lakas, A.; Bendouma, T.; Chaib, N. A survey of UAV-based data collection: Challenges, solutions and future perspectives. J. Netw. Comput. Appl. 2023, 216, 103670. [Google Scholar] [CrossRef]
- Mukerjee, L.; Yadav, M.; Choraria, A.; Tendolkar, A.; Hariharan, A.; Manohara Pai, M.M. Aerodock (a smart, autonomous charging and docking station for unmanned aerial vehicles). J. Phys. Conf. Ser. 2022, 2161, 012058. [Google Scholar] [CrossRef]
- Diller, J.; Han, Q. Energy-Aware Drone Path Finding with a Fixed-Trajectory Ground Vehicle. ACM J. Auton. Transp. Syst. 2025, 2, 1–33. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Z.; Chu, J.; Wang, H.; Sun, S. Long-term path planning with optimal deployment of a charging station for monitoring photovoltaic solar farms. Sci. Rep. 2024, 14, 17279. [Google Scholar] [CrossRef]
- Salameh, H.B.; Othman, A.; Alhafnawi, M. Optimized charging-station placement and UAV trajectory for enhanced uncertain target detection in intelligent UAV tracking systems. Int. J. Cogn. Comput. Eng. 2024, 5, 367–378. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Chen, J. Adaptive path planning method for UAVs in complex environments. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103133. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Wang, Z.; Liu, R.; Huang, C.; Shi, Y.; Wang, M.; Chen, H. Efficient multi-UAV path planning in dynamic and complex environments using hybrid polar lights optimization. J. King Saud Univ. Comput. Inf. Sci. 2025, 37, 1319–1578. [Google Scholar] [CrossRef]
- Gabriel, F.C.; Pensado, E.A.; Veiga-López, F.; González-Jorge, H. Efficient offshore wind farm inspections using a support vessel and UAVs. Ocean Eng. 2025, 332, 121416. [Google Scholar] [CrossRef]
- Ghambari, S.; Golabi, M.; Jourdan, L.; Lepagnot, J.; Idoumghar, L. UAV path planning techniques: A survey. RAIRO Oper. Res. 2024, 58, 2951–2989. [Google Scholar] [CrossRef]
- Krishan, K.; Neeraj, K. Region coverage-aware path planning for unmanned aerial vehicles: A systematic review. Phys. Commun. 2023, 59, 102073. [Google Scholar] [CrossRef]
- Serhii, S.; Scislo, L.; Pawlik, M.; Melnychenko, O.; Radiuk, P.; Savenko, O.; Sachenko, A. DyTAM: Accelerating Wind Turbine Inspections with Dynamic UAV Trajectory Adaptation. Energies 2025, 18, 1823. [Google Scholar] [CrossRef]
- Khamis, A.; Hussein, A.; Elmogy, A.M. Multi-robot Task Allocation: A Review of the State-of-the-Art. Stud. Comput. Intell. 2015, 1, 31–52. [Google Scholar]
- Dijkstra, E. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Archetti, C.; Bianchessi, N.; Speranza, M.G. Branch-and-cut algorithms for the split delivery vehicle routing problem. Eur. J. Oper. Res. 2014, 238, 685–698. [Google Scholar] [CrossRef]
- Al-Furhud, M.A.; Ahmed, Z. Experimental Study of a Hybrid Genetic Algorithm for the Multiple Travelling Salesman Problem. Math. Probl. Eng. 2020, 2020, 8864167. [Google Scholar] [CrossRef]
- Duan, X.J.; Liu, H.; Tang, H.; Cai, Q.; Zhang, F.; Han, X. A Novel Hybrid Auction Algorithm for Multi-UAVs Dynamic Task Assignment. IEEE Access 2020, 8, 86207–86222. [Google Scholar] [CrossRef]
- Huang, J.; Du, B.; Zhang, Y.; Quan, Q.; Wang, B.; Mu, L. A Pesticide Spraying Mission Allocation and Path Planning with Multicopters. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2277–2291. [Google Scholar] [CrossRef]
- Peng, Z.B.; Sun, S.; Tong, L.; Fan, Q.; Wang, L.; Liu, D. Optimization of offshore wind farm inspection paths based on K-means-GA. PLoS ONE 2024, 19, e0303533. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.F.; Wang, G. Optimization for total energy consumption of drone inspection based on distance-constrained capacitated vehicle routing problem: A study in wind farm. Expert Syst. Appl. 2024, 255, 124880. [Google Scholar] [CrossRef]
- Chung, H.-M.; Maharjan, S.; Zhang, Y.; Eliassen, F.; Strunz, K. Placement and Routing Optimization for Automated Inspection with UAVs: A Study in Offshore Wind Farm. IEEE Trans. Ind. Inform. 2020, 17, 3032–3043. [Google Scholar] [CrossRef]
- Zhao, S.M.; Hwang, S.-H. Complete coverage path planning scheme for autonomous navigation ROS-based robots. ICT Express 2024, 10, 83–89. [Google Scholar] [CrossRef]
- Zhao, L.; Bai, Y.; Paik, J.K. Optimal coverage path planning for USV-assisted coastal bathymetric survey: Models, solutions, and lake trials. Ocean Eng. 2024, 296, 116921. [Google Scholar] [CrossRef]
- Ismail, A.H.; Song, X.; Ouelhadj, D.; Al-Behadili, M.; Fraess-Ehrfeld, A. Unmanned surface vessel routing and unmanned aerial vehicle swarm scheduling for off-shore wind turbine blade inspection. Expert Syst. Appl. 2025, 284, 127534. [Google Scholar] [CrossRef]
- Zhao, C.; Roberts, A.; Cui, Y.; Johanning, L. Strategic Deployment of Service Vessels for Improved Offshore Wind Farm Maintenance and Availability. Mar. Energy Res. 2024, 1, 10003. [Google Scholar] [CrossRef]
- Fox, H.; Pillai, A.C.; Friedrich, D.; Collu, M.; Dawood, T.; Johanning, L. A Review of Predictive and Prescriptive Offshore Wind Farm Operation and Maintenance. Energies 2022, 15, 504. [Google Scholar] [CrossRef]
- Asim, T.; Islam, S.Z.; Hemmati, A.; Khalid, M.S.U. A Review of Recent Advancements in Offshore Wind Turbine Technology. Energies 2022, 15, 579. [Google Scholar] [CrossRef]
- Mohd, H.N.; Sharma, S.; Khan, A.; Gianni, M.; Rajendran, S.; Sutton, R. Collaborative Unmanned Vehicles for Inspection, Maintenance, and Repairs of Offshore Wind Turbines. Drones 2022, 6, 137. [Google Scholar] [CrossRef]
- Khalid, O.; Hao, G.; MacDonald, H.; Cooperman, A.; McAuliffe, F.D.; Desmond, C. Cost-benefit assessment framework for robotics-driven inspection of floating offshore wind farms. Wind Energy 2024, 27, 152–164. [Google Scholar] [CrossRef]
- Hong, S.; McMorland, J.; Zhang, H.; Collu, M.; Halse, K.H. Floating offshore wind farm installation, challenges and opportunities: A comprehensive survey. Ocean Eng. 2024, 304, 117793. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Li, J.; Zhang, X. Robust extreme learning machine control for offshore nacelle inspection maneuvering of sea-air cooperative vehicles via asynchronous virtual guidance. Ocean Eng. 2025, 331, 121347. [Google Scholar] [CrossRef]
- Li, W.H.; Zhao, T.; Dian, S. Multirobot Coverage Path Planning Based on Deep Q-Network in Unknown Environment. J. Robot. 2022, 2022, 6825902. [Google Scholar] [CrossRef]
- Wei, Y.D.; Feng, J.; Huang, Y.; Liu, K.; Ren, B. Path Planning of Mobile Robot Based on Improved Genetic Algorithm. J. Phys. Conf. Ser. 2022, 2365, 012053. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Tracking and optimizing dynamic systems with particle swarms. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001; pp. 94–100. [Google Scholar]
- Dudeja, C.; Kumar, P. An improved weighted sum–fuzzy Dijkstra’s algorithm for shortest path problem (iWSFDA). Soft Comput. 2022, 26, 3217–3226. [Google Scholar] [CrossRef]
- Yao, B.Z.; Yan, Q.; Zhang, M.; Yang, Y. Improved artificial bee colony algorithm for vehicle routing problem with time windows. PLoS ONE 2017, 12, 1–18. [Google Scholar] [CrossRef]
- Liu, Z.W.; Qiu, C.; Zhang, Z. Sequence-to-Sequence Multi-Agent Reinforcement Learning for Multi-UAV Task Planning in 3D Dynamic Environment. Appl. Sci. 2022, 12, 12181. [Google Scholar] [CrossRef]
- Zhu, T.B.; Xiao, Y.; Zhang, H. Maritime patrol tasks assignment optimization of multiple USVs under endurance constraint. Ocean Eng. 2023, 285, 115445. [Google Scholar] [CrossRef]


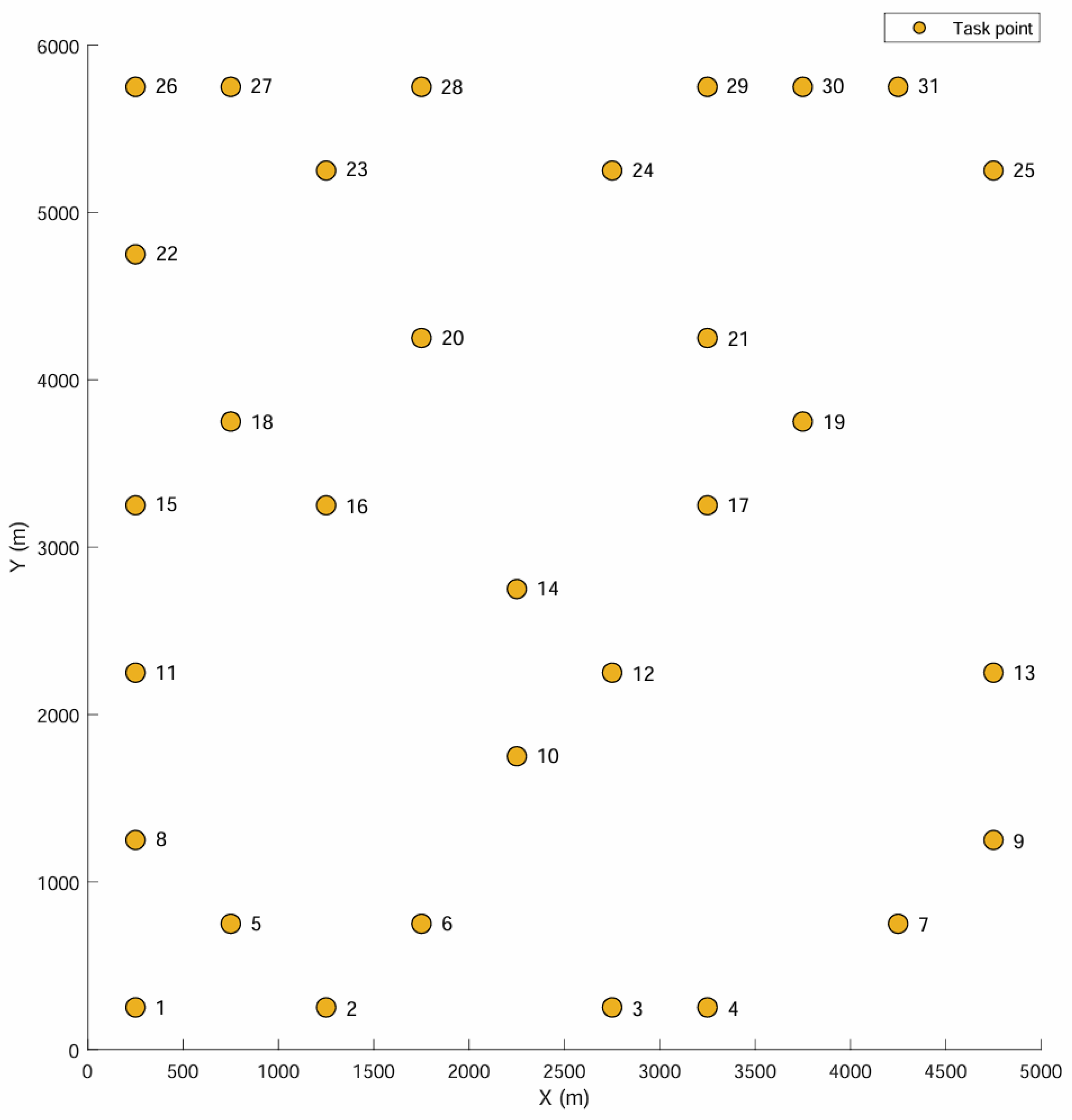
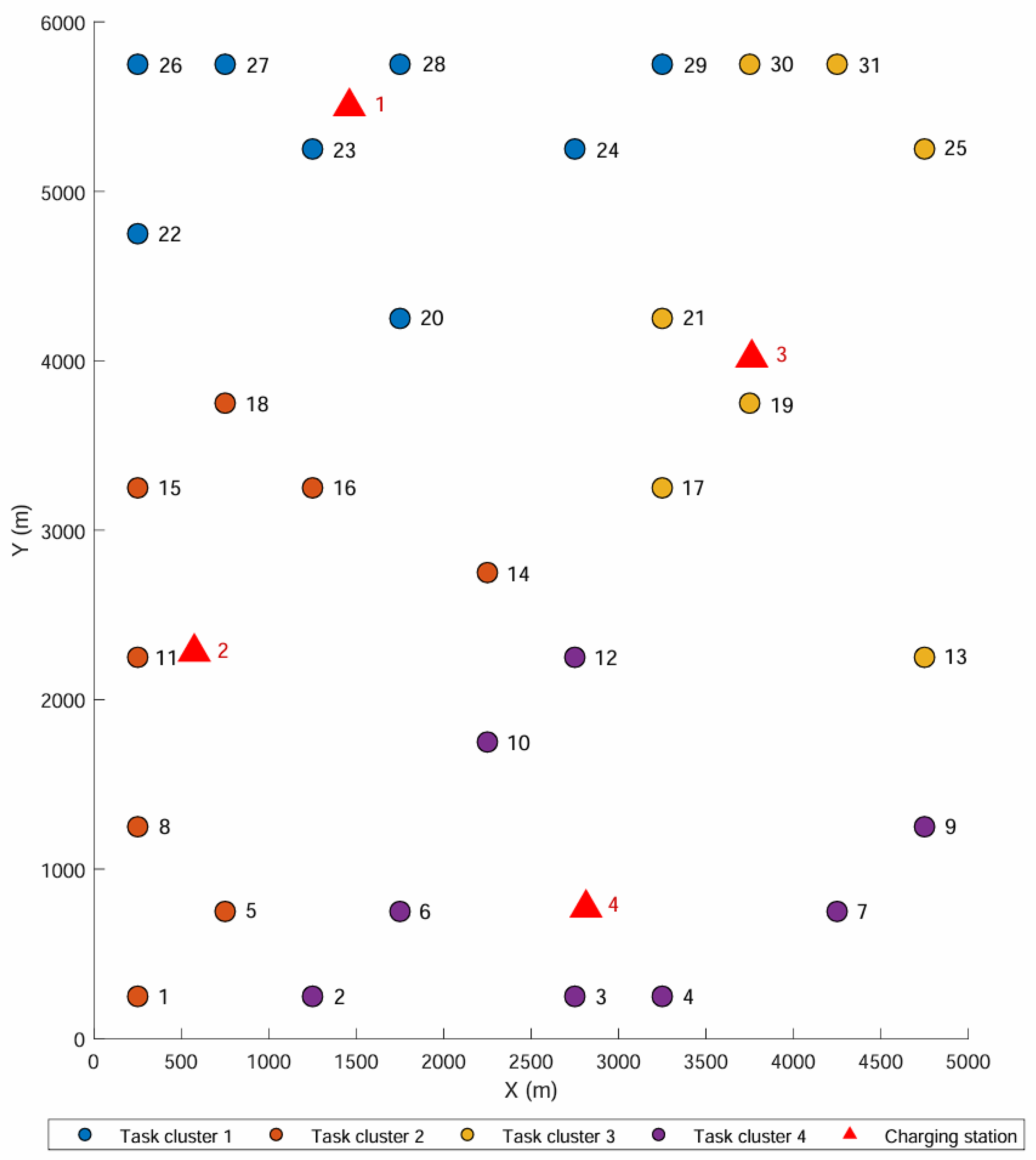
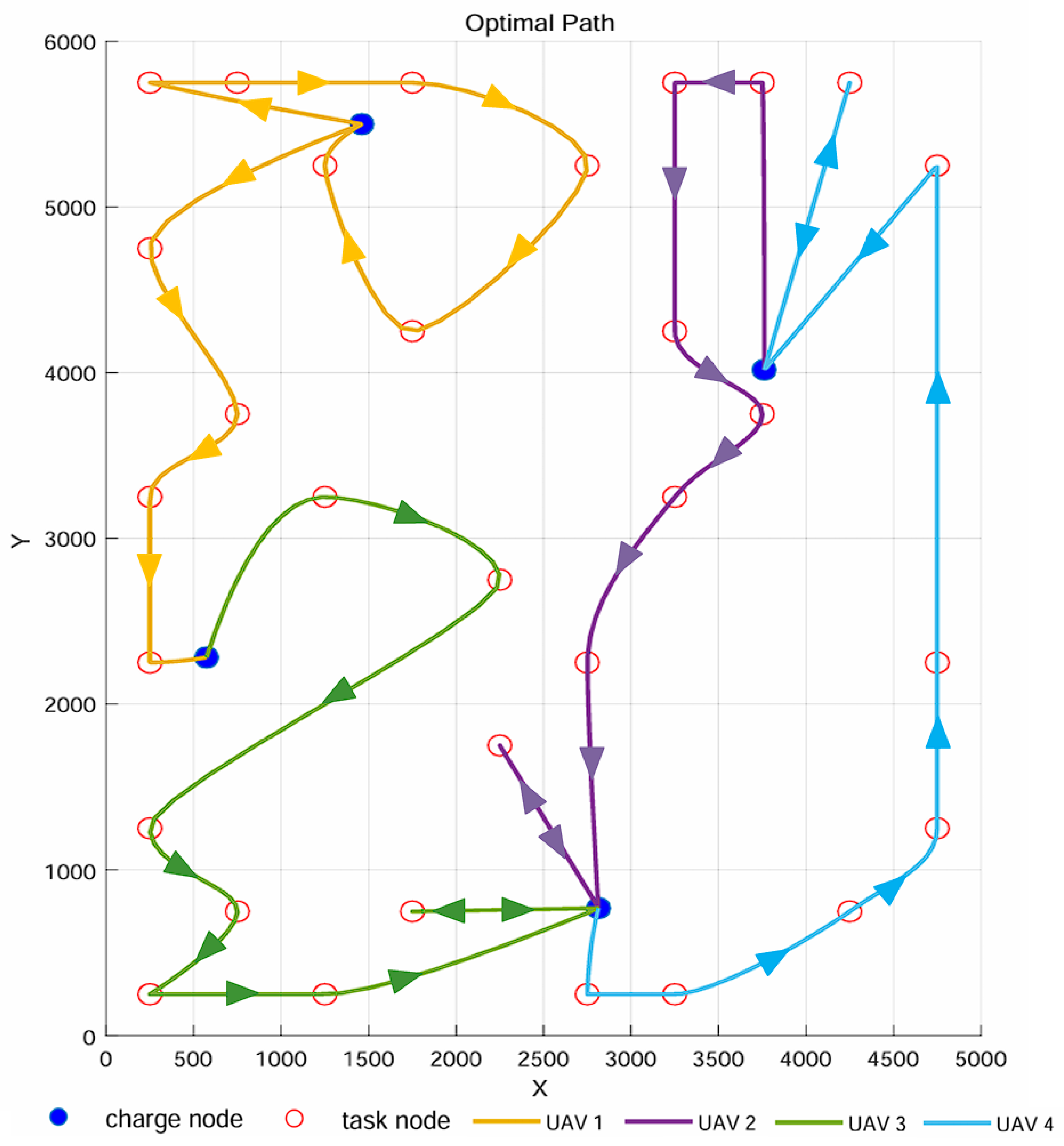
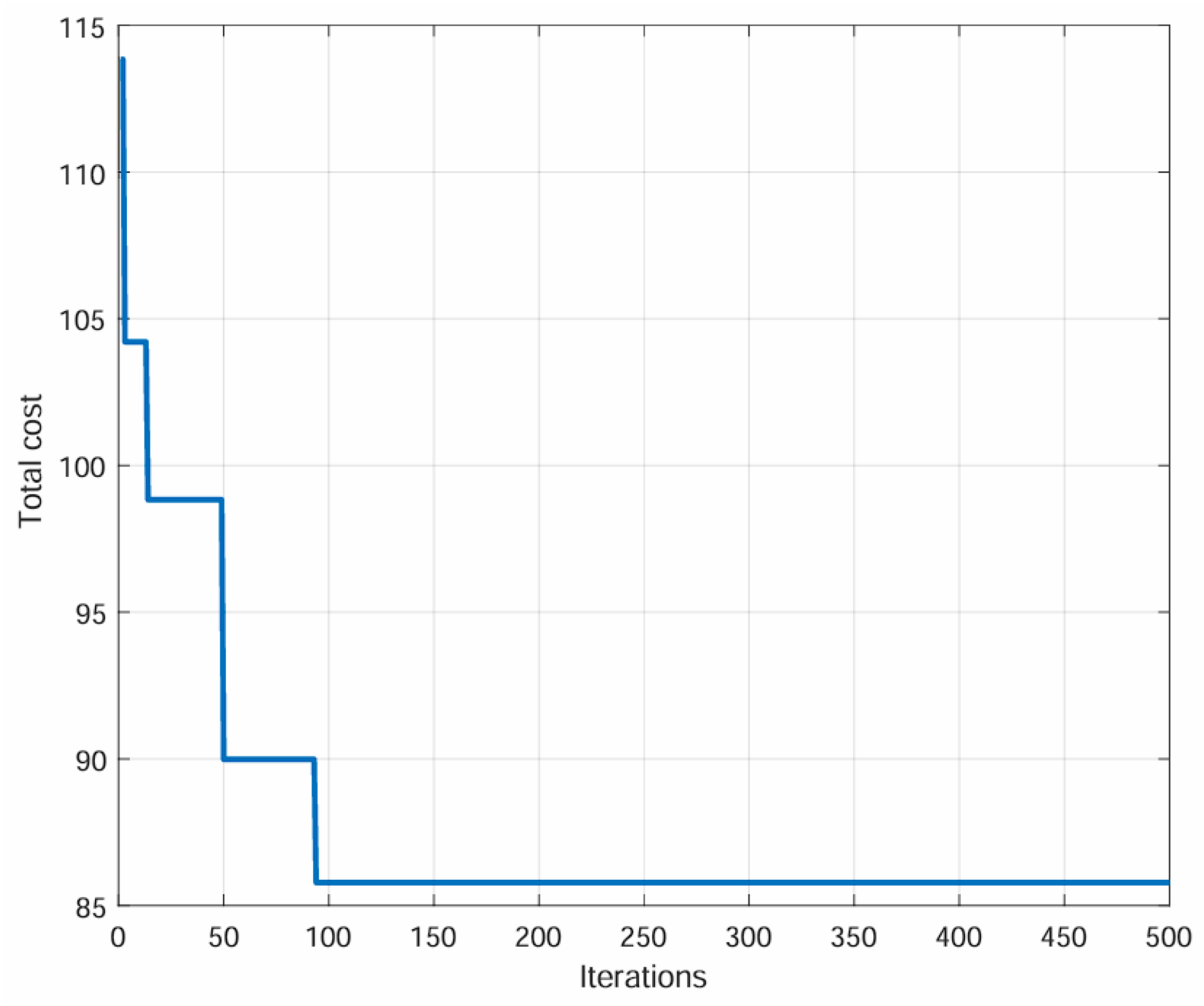
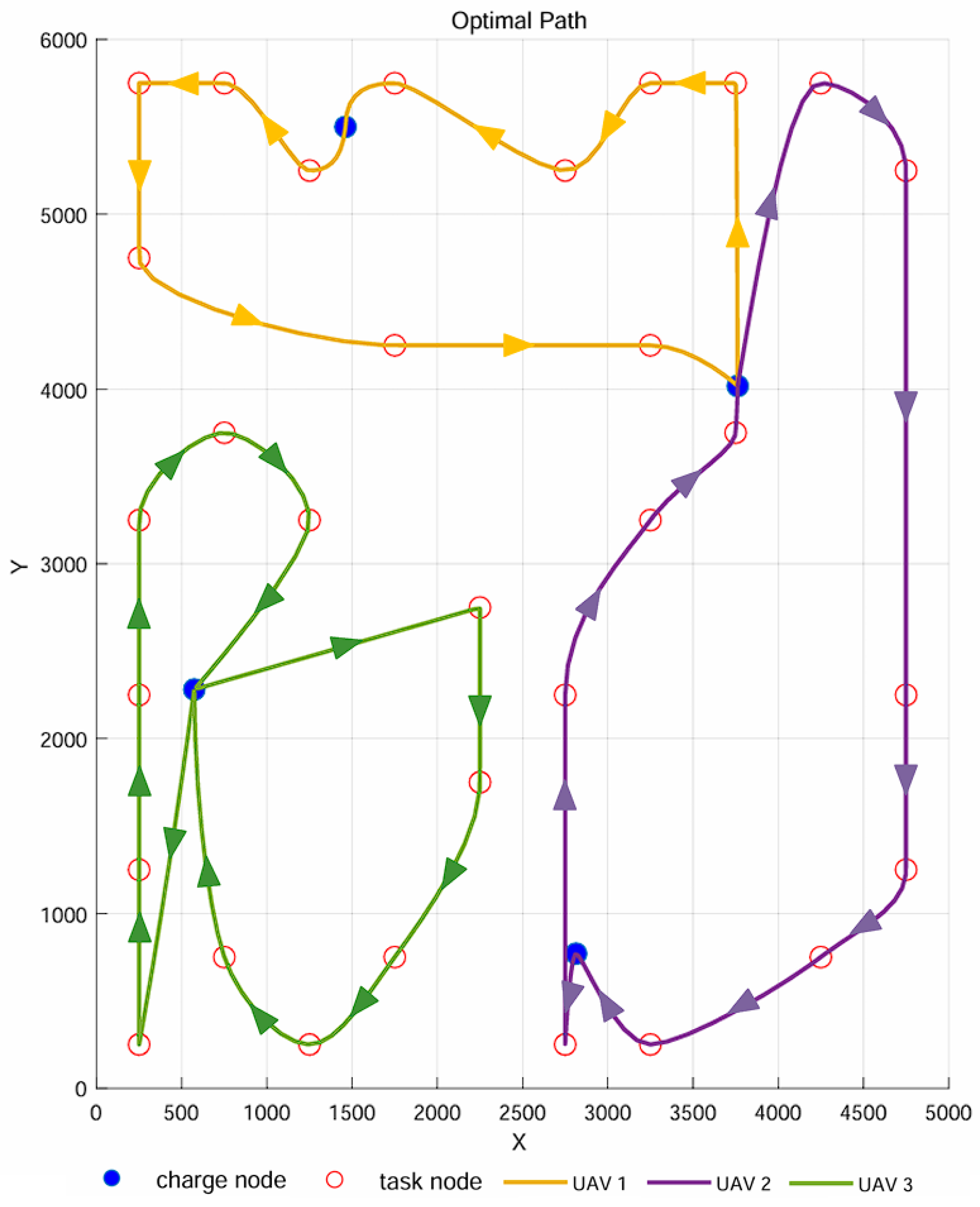
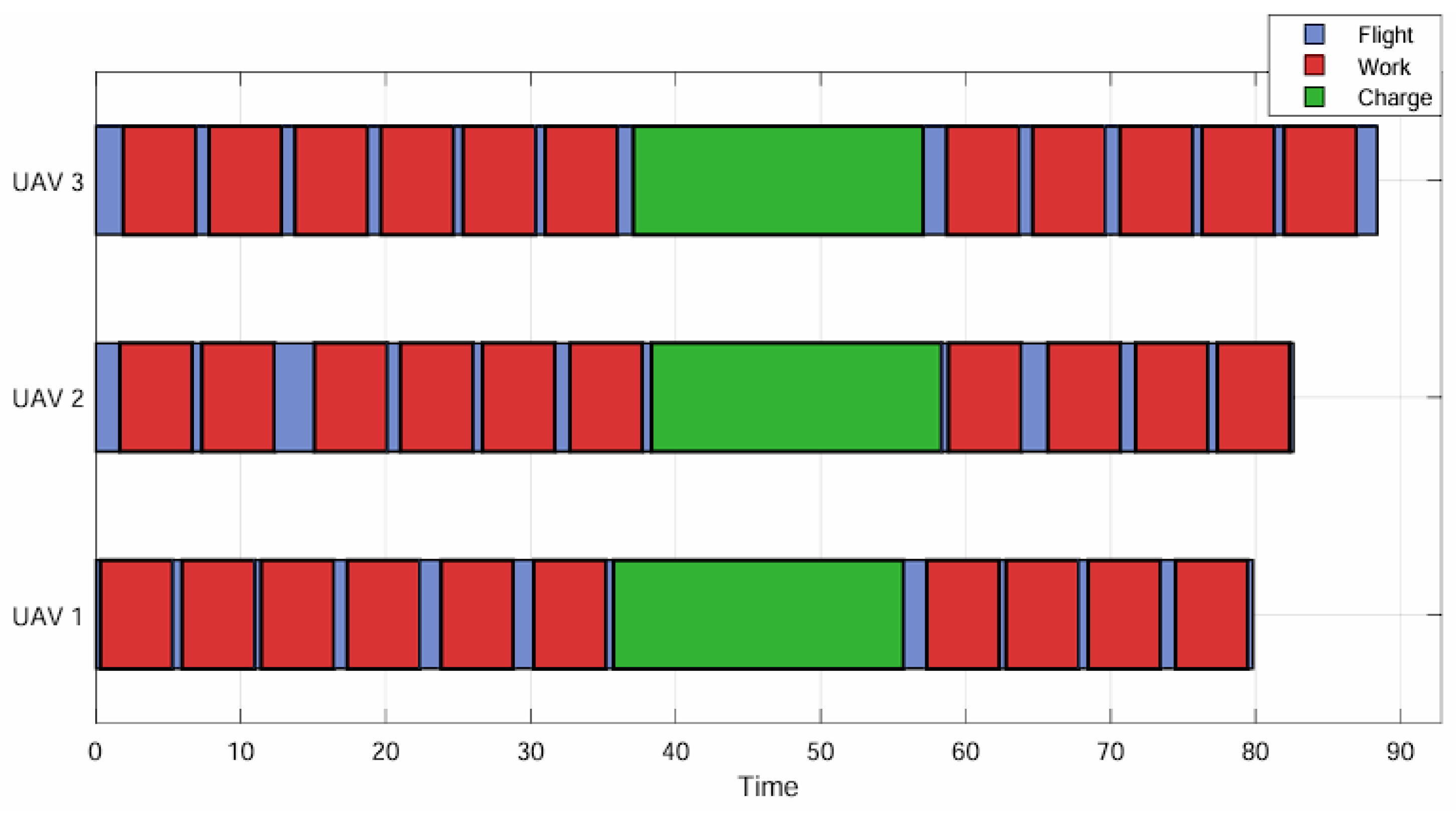



| Number | X | Y | Number | X | Y |
|---|---|---|---|---|---|
| 1 | 1460.81 | 5500 | 3 | 3762.14 | 4017.54 |
| 2 | 573.615 | 2281.21 | 4 | 2814.06 | 769.866 |
| Parameters | Value | |
|---|---|---|
| Algorithm parameters | Maximum number of iterations: MaxIter | 500 |
| Population size: Popsize | 200 | |
| Crossover probability: | 0.8 | |
| Mutation probability: | 0.4 | |
| Mutation probability: | 0.4 | |
| UAV parameters | UAV speed: | 18 m/s |
| The maximum flight endurance time: E | 40 min |
| Task Sequence Identifier | Operating Time of the UAV | |
|---|---|---|
| UAV1 | (32, 28, 24, 27, 31, 30, 26, 22, 19, 15) | 84.42 min |
| UAV2 | (34, 33, 25, 23, 21, 16, 14) | 69.13 min |
| UAV3 | (20, 18, 12, 9, 5, 6, 10, 7) | 71.48 min |
| UAV4 | (8, 11, 13, 17, 29, 35) | 71.92 min |
| UAV number = 3 | AVE | MAX | MIN |
|---|---|---|---|
| DDGA | 85.78 | 97.03 | 82.94 |
| GA-PSO | 94.23 | 101.38 | 89.23 |
| GA-GWO | 92.93 | 99.04 | 87.71 |
| HHO | 89.29 | 97.56 | 84.75 |
| WHO | 93.32 | 98.46 | 88.16 |
| DRL | 102.35 | 113.16 | 89.72 |
| UAV number = 4 | AVE | MAX | MIN |
| DDGA | 84.42 | 90.64 | 81.58 |
| GA-PSO | 90.23 | 97.03 | 87.46 |
| GA-GWO | 89.02 | 93.79 | 83.23 |
| HHO | 83.04 | 92.11 | 81.36 |
| WHO | 89.03 | 96.03 | 82.61 |
| DRL | 92.04 | 103.44 | 89.60 |
| UAV number = 5 | AVE | MAX | MIN |
| DDGA | 63.35 | 69.41 | 59.87 |
| GA-PSO | 70.90 | 78.24 | 65.73 |
| GA-GWO | 66.03 | 73.01 | 63.48 |
| HHO | 67.03 | 74.50 | 60.04 |
| WHO | 69.03 | 78.43 | 61.30 |
| DRL | 69.86 | 83.91 | 65.17 |
| N (A) | (s/gen) | Total (500 gen) (s/min) | Eval/s |
|---|---|---|---|
| 50 | 1.200 | 600.0/10.0 | 166.7 |
| 100 | 2.825 | 1412.6/23.5 | 70.8 |
| 200 | 6.501 | 3250.5/54.2 | 30.8 |
| N (B) | (s/gen) | Total (500 gen) (s/min) | Eval/s |
| 50 | 1.744 | 872.0 / 14.5 | 114.7 |
| 100 | 4.106 | 2053.0 / 34.2 | 48.7 |
| 200 | 9.448 | 4724.0 / 78.7 | 21.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Li, W.; Liu, C.; He, X.; Li, K. A High-Efficiency Task Allocation Algorithm for Multiple Unmanned Aerial Vehicles in Offshore Wind Power Under Energy Constraints. J. Mar. Sci. Eng. 2025, 13, 1711. https://doi.org/10.3390/jmse13091711
Zhang D, Li W, Liu C, He X, Li K. A High-Efficiency Task Allocation Algorithm for Multiple Unmanned Aerial Vehicles in Offshore Wind Power Under Energy Constraints. Journal of Marine Science and Engineering. 2025; 13(9):1711. https://doi.org/10.3390/jmse13091711
Chicago/Turabian StyleZhang, Dongliang, Wankai Li, Chenyu Liu, Xuheng He, and Kaiqi Li. 2025. "A High-Efficiency Task Allocation Algorithm for Multiple Unmanned Aerial Vehicles in Offshore Wind Power Under Energy Constraints" Journal of Marine Science and Engineering 13, no. 9: 1711. https://doi.org/10.3390/jmse13091711
APA StyleZhang, D., Li, W., Liu, C., He, X., & Li, K. (2025). A High-Efficiency Task Allocation Algorithm for Multiple Unmanned Aerial Vehicles in Offshore Wind Power Under Energy Constraints. Journal of Marine Science and Engineering, 13(9), 1711. https://doi.org/10.3390/jmse13091711







