Artificial Texture-Free Measurement: A Graph Cuts-Based Stereo Vision for 3D Wave Reconstruction in Laboratory
Abstract
1. Introduction
- We use SAM (version 1.0) as a preprocessing step for water surface segmentation and replace the photometric or color consistency criterion in generalized stereo vision with the concept of affine consistency.
- Our approach operates solely at the software level and does not require any configurations or restrictions of the light field environment.
- We present a proof of concept validated in controlled laboratory conditions, demonstrating the feasibility of texture-free 3D wave reconstruction with clearly identified limitations and future research directions.
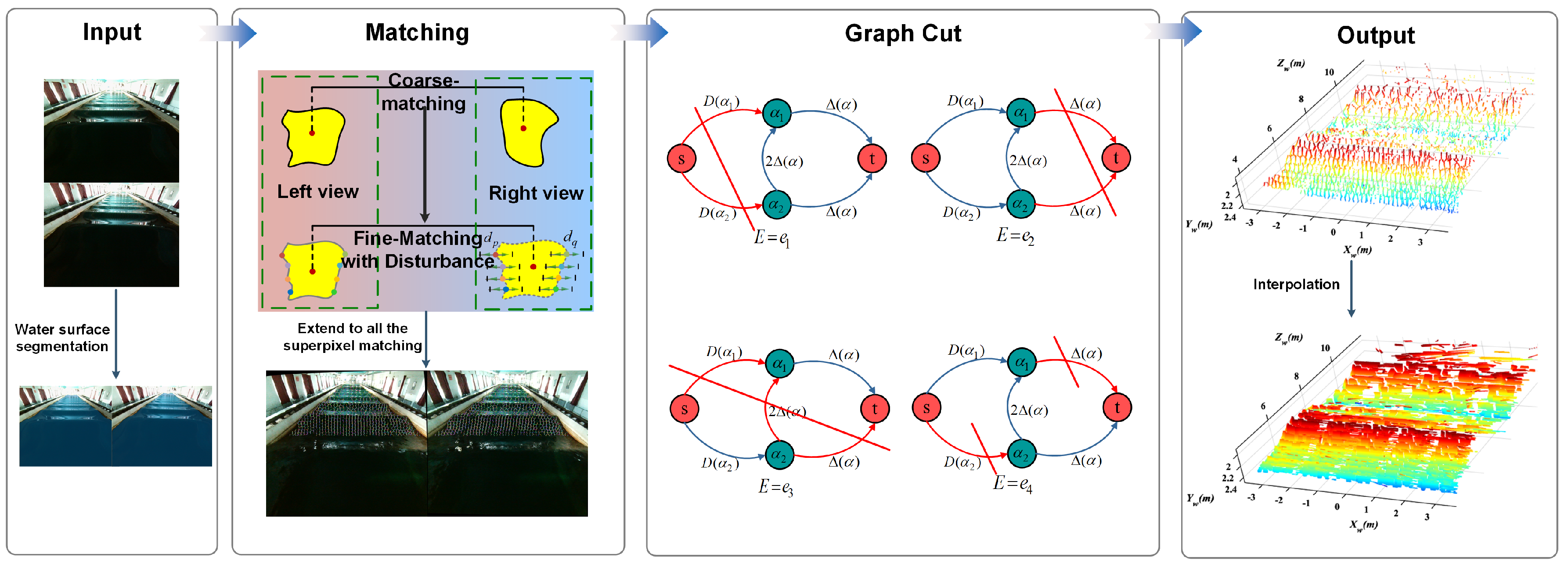
2. Method
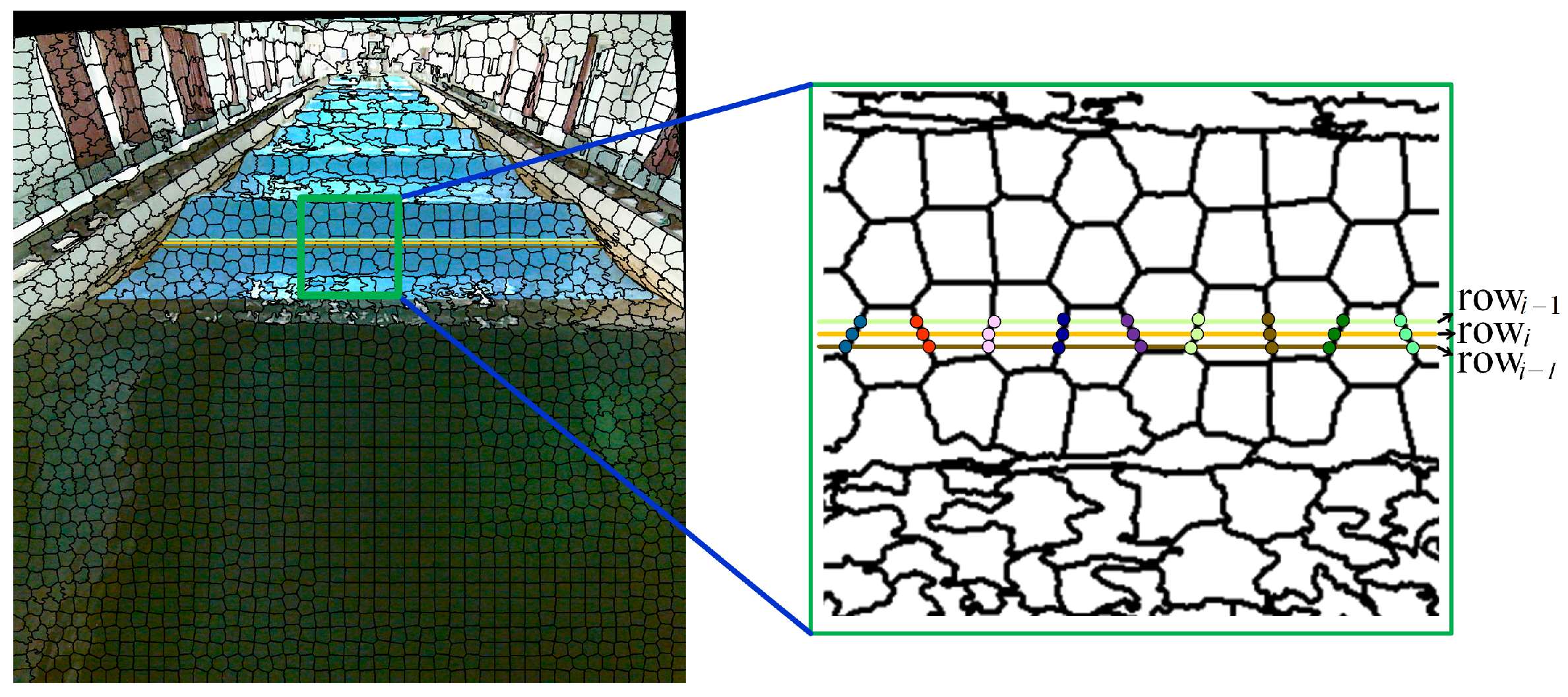
2.1. Affine Consistency as Matching Invariance
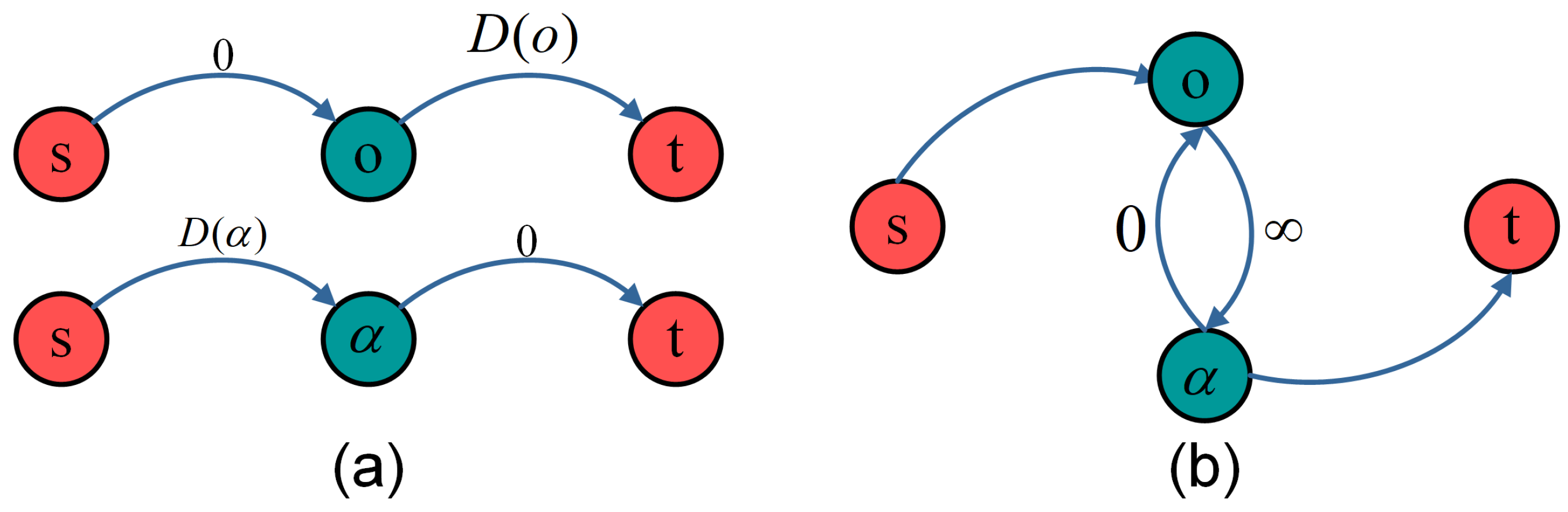
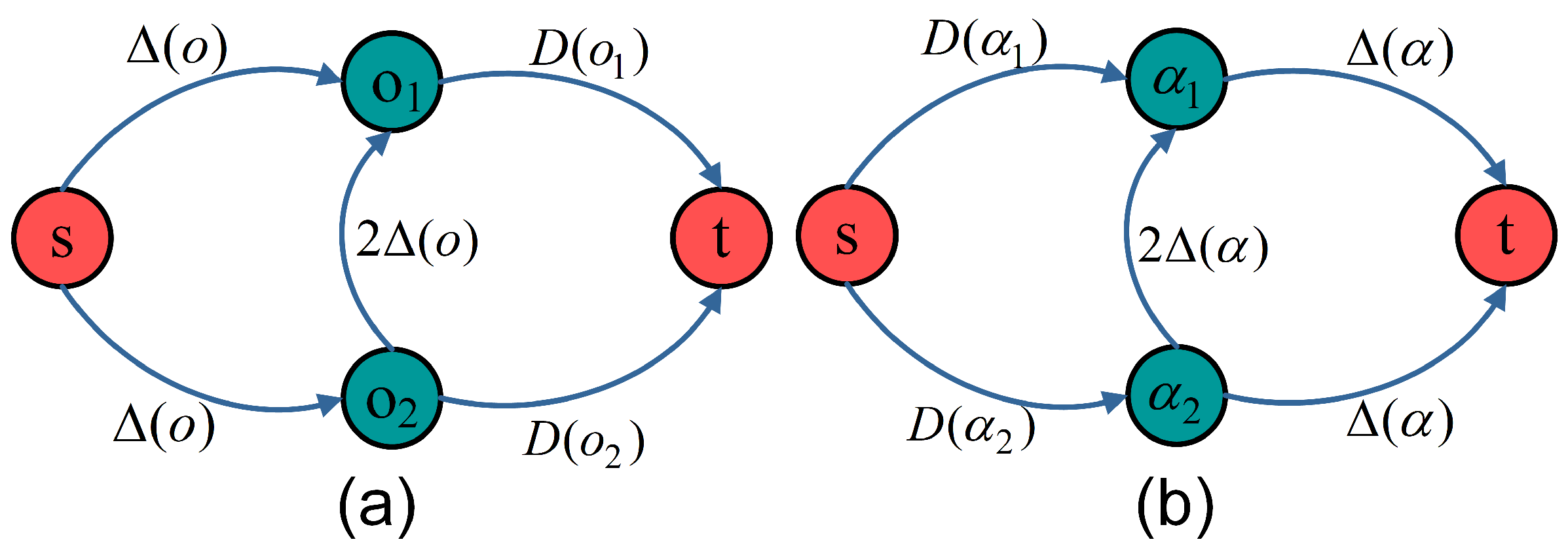
2.2. Fine-Level Matching Framework with Perturbation
| Algorithm 1 The iteration of the perturbation strategy in the graph cuts. |
| Input: The sparse pairs of boundary points within a superpixel; a coarse disparity d; a perturbation range ; number of loops N. Output: All the final disparity within a superpixel. Initialization: , make in a random order, set the map of the perturbations . While : For each : Build the graph cuts network For each : , Calculate data and smoothness by (3) and (4) Add the edge weights and uniqueness to the network End for Compute the minimal cost of If : Update based the decisions of Done[:] = False Else: Done[] = True End for If Done[:] == True: Return perturbations of all boundary pairs End while |
3. Experiment
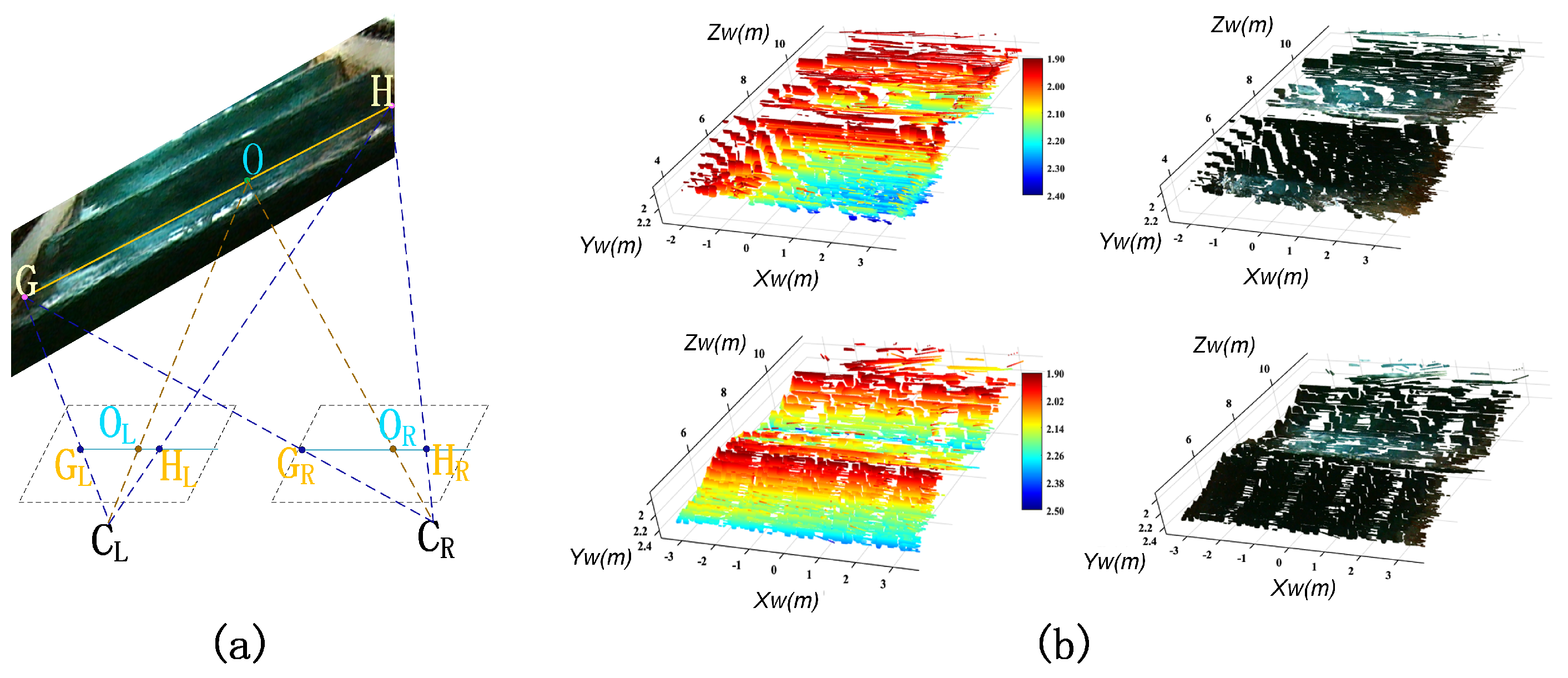
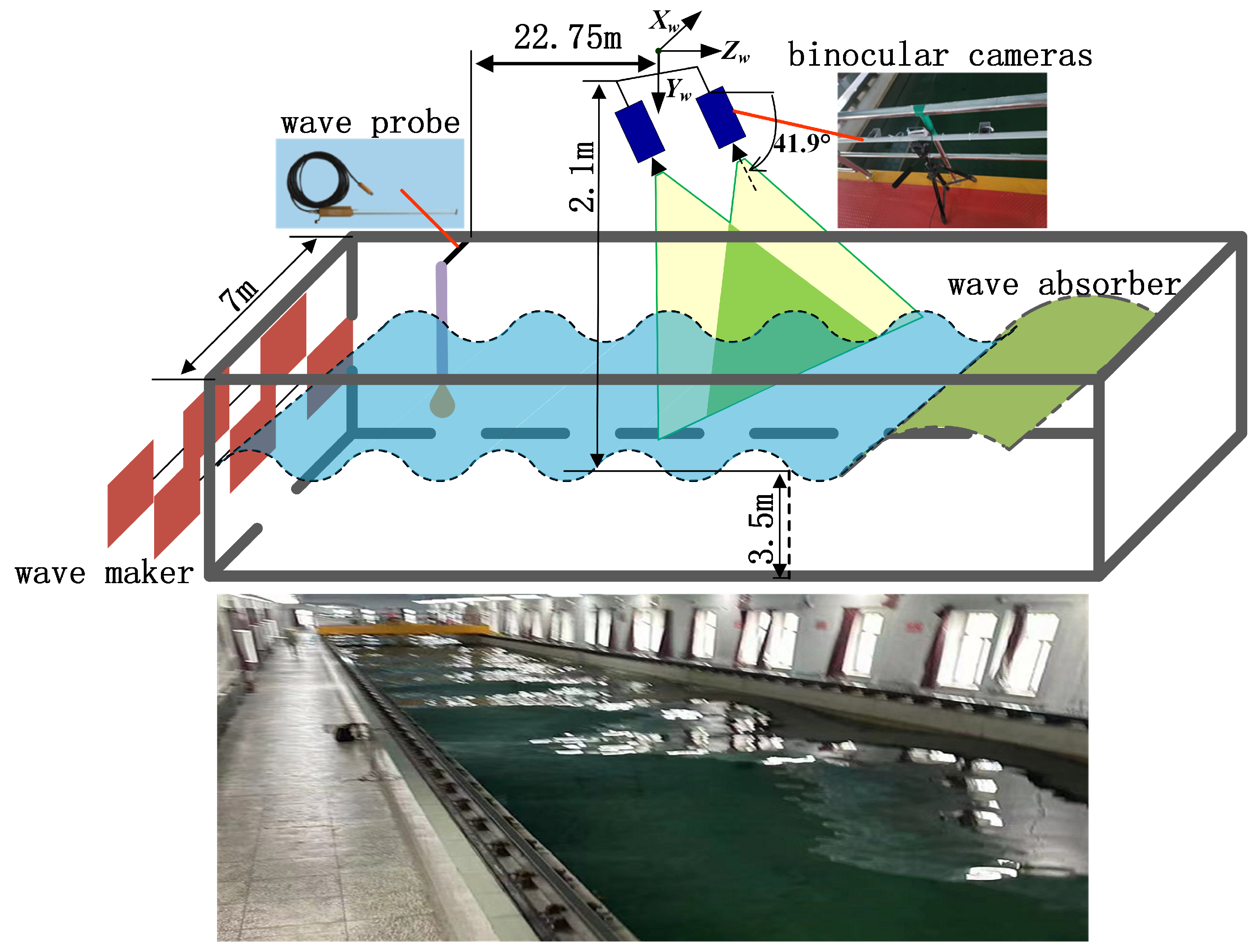
3.1. Experimental Setup
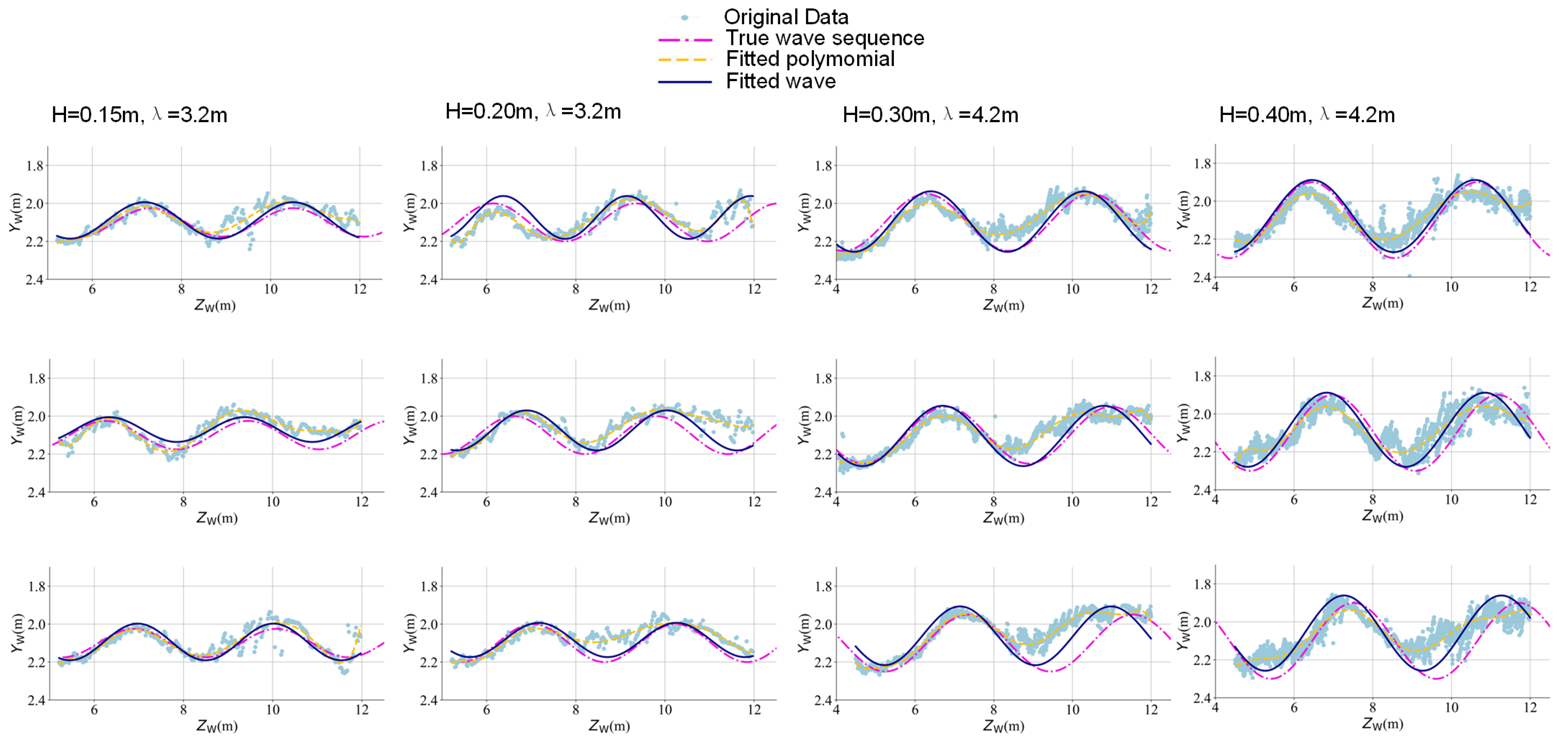
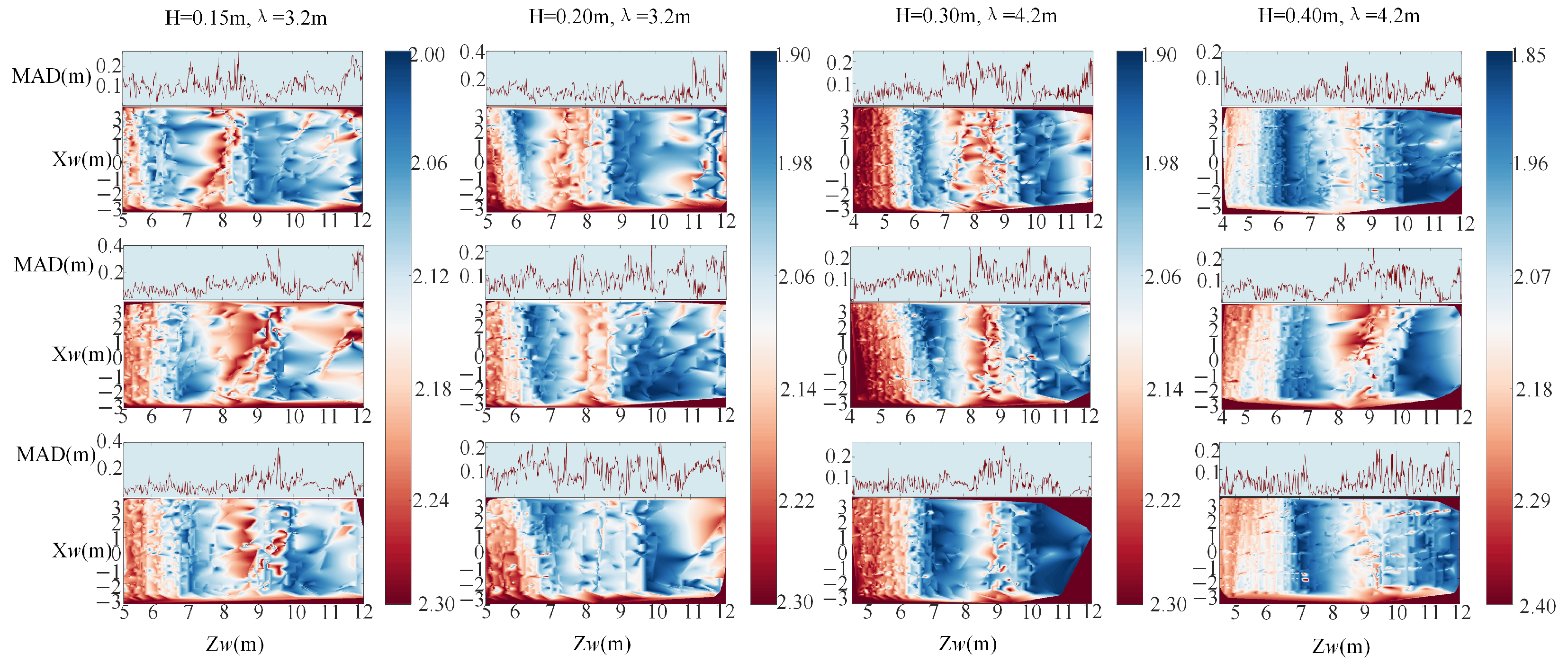
3.2. Experimental Results
3.3. Parameter Selection and Theoretical Justification
3.4. Limitations and Scope
3.5. Discussion
4. Conclusions and Future Work
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Swan, C.; Sheikh, R. The interaction between steep waves and a surface-piercing column. Phil. Trans. R. Soc. A 2015, 373, 20140114. [Google Scholar] [CrossRef]
- Douglas, S.; Cornett, A.; Nistor, I. Image-based measurement of wave interactions with rubble mound breakwaters. J. Mar. Sci. Eng. 2020, 8, 472. [Google Scholar] [CrossRef]
- Mou, T.; Shen, Z.; Xue, G. Task-driven learning downsampling network based phase-resolved wave fields reconstruction with remote optical observations. J. Mar. Sci. Eng. 2024, 12, 1082. [Google Scholar] [CrossRef]
- Pan, Z.; Hou, J.; Yu, L. Optimization RGB-D 3D reconstruction algorithm based on dynamic SLAM. IEEE Trans. Instrum. Meas. 2023, 72, 5008413. [Google Scholar] [CrossRef]
- Zhou, P.; Cheng, Y.; Zhu, J.; Hu, J. High-dynamic-range 3D shape measurement with adaptive speckle projection through segmentation-based mapping. IEEE Trans. Instrum. Meas. 2022, 72, 5003512. [Google Scholar]
- Ou, Y.; Fan, J.; Zhou, C.; Tian, S.; Cheng, L.; Tan, M. Binocular structured light 3D reconstruction system for low-light underwater environments: Design, modeling, and laser-based calibration. IEEE Trans. Instrum. Meas. 2023, 72, 5010314. [Google Scholar] [CrossRef]
- Hu, Y.; Rao, W.; Qi, L.; Dong, J.; Cai, J.; Fan, H. A refractive stereo structured-light 3D measurement system for immersed object. IEEE Trans. Instrum. Meas. 2022, 72, 5003613. [Google Scholar]
- Zhu, S.; Liu, J.; Guo, A.; Li, H. Non-contact measurement method for reconstructing three-dimensional scour depth field based on binocular vision technology in laboratory. Measurement 2022, 200, 111556. [Google Scholar] [CrossRef]
- Bergamasco, F.; Torsello, A.; Sclavo, M.; Barbariol, F.; Benetazzo, A. WASS: An open-source pipeline for 3D stereo reconstruction of ocean waves. Comput. Geosci. 2017, 107, 28–36. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Wolrige, S.H.; Howe, D.; Majidiyan, H. Intelligent computerized video analysis for automated data extraction in wave structure interaction; a wave basin case study. J. Mar. Sci. Eng. 2025, 13, 617. [Google Scholar] [CrossRef]
- Sun, D.; Gao, G.; Huang, L.; Liu, Y.; Liu, D. Extraction of water bodies from high-resolution remote sensing imagery based on a deep semantic segmentation network. Sci. Rep. 2024, 14, 14604. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, X.; Zhang, Y. HA-Net: A lake water body extraction network based on hybrid-scale attention and transfer learning. Remote Sens. 2021, 13, 4121. [Google Scholar] [CrossRef]
- Fitzpatrick, A.; Mathews, R.P.; Singhvi, A.; Arbabian, A. Multi-modal sensor fusion towards three-dimensional airborne sonar imaging in hydrodynamic conditions. Commun. Eng. 2023, 2, 16. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, Q.; Cai, C.; Wang, X.; Qiao, R. From points to waves: Fast ocean wave spatial–temporal fields estimation using ensemble transform Kalman filter with optical measurement. Coast. Eng. 2025, 197, 104690. [Google Scholar] [CrossRef]
- Gomit, G.; Chatellier, L.; Calluaud, D.; David, L.; Fréchou, D.; Boucheron, R.; Perelman, O.; Hubert, C. Large-scale free surface measurement for the analysis of ship waves in a towing tank. Exp. Fluids 2015, 56, 184. [Google Scholar] [CrossRef]
- Caplier, C.; Rousseaux, G.; Calluaud, D.; David, L. Energy distribution in shallow water ship wakes from a spectral analysis of the wave field. Phys. Fluids 2016, 28, 107104. [Google Scholar] [CrossRef]
- Ferreira, E.; Chandler, J.; Wackrow, R.; Shiono, K. Automated extraction of free surface topography using SfM-MVS photogrammetry. Flow Meas. Instrum. 2017, 54, 243–249. [Google Scholar] [CrossRef]
- Fleming, A.; Winship, B.; Macfarlane, G. Application of photogrammetry for spatial free surface elevation and velocity measurement in wave flumes. Pro. IMechE 2019, 233, 905–917. [Google Scholar] [CrossRef]
- Han, B.; Endreny, T.A. River surface water topography mapping at sub-millimeter resolution and precision with close range photogrammetry: Laboratory scale application. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 602–608. [Google Scholar] [CrossRef]
- Li, D.; Xiao, L.; Wei, H.; Li, J.; Liu, M. Spatial-temporal measurement of waves in laboratory based on binocular stereo vision and image processing. Coastal Eng. 2022, 177, 104200. [Google Scholar] [CrossRef]
- van Meerkerk, M.; Poelma, C.; Westerweel, J. Scanning stereo-PLIF method for free surface measurements in large 3D domains. Exp. Fluids 2020, 61, 19. [Google Scholar] [CrossRef]
- Bung, D.B.; Crookston, B.M.; Valero, D. Turbulent free-surface monitoring with an RGB-D sensor: The hydraulic jump case. J. Hydraul. Res. 2021, 59, 779–790. [Google Scholar] [CrossRef]
- Evers, F.M. Videometric water surface tracking of spatial impulse wave propagation. J. Vis. 2018, 21, 903–907. [Google Scholar] [CrossRef]
- Viriyakijja, K.; Chinnarasri, C. Wave flume measurement using image analysis. Aquat. Procedia 2015, 4, 522–531. [Google Scholar] [CrossRef]
- Hernández, I.D.; Hernández-Fontes, J.V.; Vitola, M.A.; Silva, M.C.; Esperança, P.T. Water elevation measurements using binary image analysis for 2D hydrodynamic experiments. Ocean Eng. 2018, 157, 325–338. [Google Scholar] [CrossRef]
- Du, H.; Li, M.; Meng, J. Study of fluid edge detection and tracking method in glass flume based on image processing technology. Adv. Eng. Softw. 2017, 112, 117–123. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.; et al. Segment anything. arXiv 2023, arXiv:2304.02643. [Google Scholar] [PubMed]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef]
- Williams, J.; Schönlieb, C.; Swinfield, T.; Lee, J.; Cai, X.; Qie, L.; Coomes, D.A. 3D segmentation of trees through a flexible multiclass graph cut algorithm. IEEE Trans. Geosci. Remote Sens. 2019, 58, 754–776. [Google Scholar] [CrossRef]
- Lu, B.; Sun, L.; Yu, L.; Dong, X. An improved graph cut algorithm in stereo matching. Displays 2021, 69, 102052. [Google Scholar] [CrossRef]
- Barath, D.; Matas, J. Graph-cut RANSAC: Local optimization on spatially coherent structures. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 4961–4974. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, V.; Monasse, P.; Tan, P. Kolmogorov and Zabih’s graph cuts stereo matching algorithm. Image Process. Line 2014, 4, 220–251. [Google Scholar] [CrossRef]
- Yang, Q.; Ahuja, N. Stereo matching using epipolar distance transform. IEEE Trans. Image Process. 2012, 21, 4410–4419. [Google Scholar] [CrossRef]
- Kim, J.; Park, C.; Min, K. Fast vision-based wave height measurement for dynamic characterization of tuned liquid column dampers. Measurement 2016, 89, 189–196. [Google Scholar] [CrossRef]
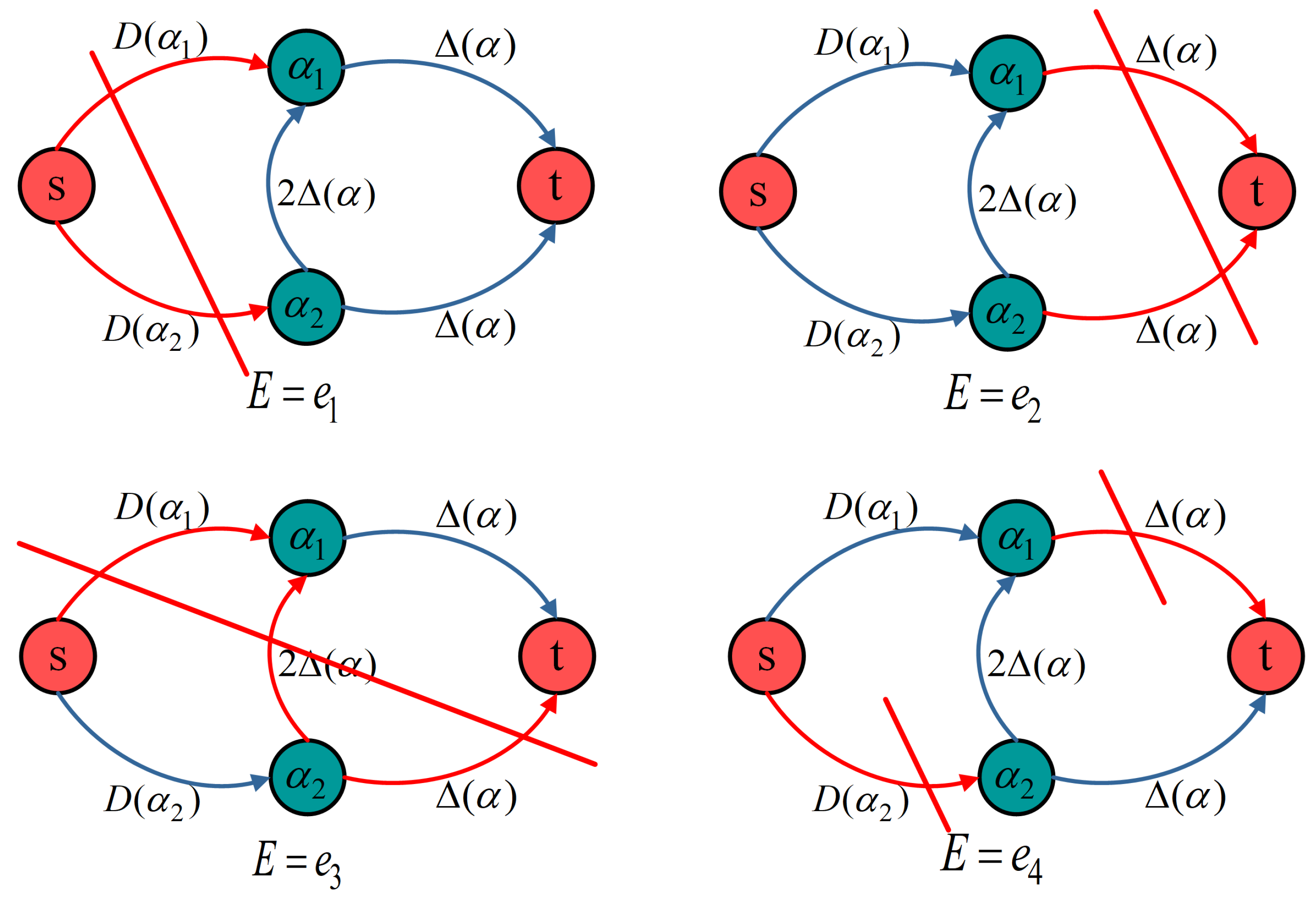
| Cases | Trigger | Original State | Updated State |
|---|---|---|---|
| Case1 | |||
| Case2 | |||
| Case3 | |||
| Case4 |
| No. | Frames | Wavelength (m) | Wave Height (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Stereo | Truth | Error | Stereo | Truth | Error | ||||
| 1 | 3.0516 | 3.20 | 04.64% | 0.1326 | 0.15 | 11.60% | 0.3829 | 0.6985 | |
| 3.0470 | 3.20 | 04.78% | 0.1669 | 0.15 | 11.27% | 0.5847 | 0.6613 | ||
| 3.3414 | 3.20 | 04.42% | 0.1550 | 0.15 | 03.33% | 0.5045 | 0.7226 | ||
| 2 | 2.9351 | 3.20 | 08.28% | 0.1897 | 0.20 | 05.15% | 0.0758 | 0.1569 | |
| 2.9697 | 3.20 | 07.19% | 0.1824 | 0.20 | 08.08% | 0.2917 | 0.5837 | ||
| 3.0857 | 3.20 | 03.57% | 0.1805 | 0.20 | 09.75% | 0.3090 | 0.6201 | ||
| No. | Frames | Wavelength (m) | Wave Height (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Stereo | Truth | Error | Stereo | Truth | Error | ||||
| 3 | 3.9815 | 4.2 | 05.20% | 0.3121 | 0.30 | 04.03% | 0.6616 | 0.7227 | |
| 4.0902 | 4.2 | 02.61% | 0.2815 | 0.30 | 06.17% | 0.6428 | 0.8732 | ||
| 4.0639 | 4.2 | 03.24% | 0.3095 | 0.30 | 03.17% | 0.1774 | 0.9555 | ||
| 4 | 4.1528 | 4.2 | 01.12% | 0.3847 | 0.40 | 03.83% | 0.7483 | 0.8029 | |
| 4.1154 | 4.2 | 02.01% | 0.4253 | 0.40 | 06.33% | 0.6755 | 0.6619 | ||
| 4.0758 | 4.2 | 02.76% | 0.3760 | 0.40 | 06.00% | 0.4479 | 0.7608 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zhu, Q. Artificial Texture-Free Measurement: A Graph Cuts-Based Stereo Vision for 3D Wave Reconstruction in Laboratory. J. Mar. Sci. Eng. 2025, 13, 1699. https://doi.org/10.3390/jmse13091699
Wang F, Zhu Q. Artificial Texture-Free Measurement: A Graph Cuts-Based Stereo Vision for 3D Wave Reconstruction in Laboratory. Journal of Marine Science and Engineering. 2025; 13(9):1699. https://doi.org/10.3390/jmse13091699
Chicago/Turabian StyleWang, Feng, and Qidan Zhu. 2025. "Artificial Texture-Free Measurement: A Graph Cuts-Based Stereo Vision for 3D Wave Reconstruction in Laboratory" Journal of Marine Science and Engineering 13, no. 9: 1699. https://doi.org/10.3390/jmse13091699
APA StyleWang, F., & Zhu, Q. (2025). Artificial Texture-Free Measurement: A Graph Cuts-Based Stereo Vision for 3D Wave Reconstruction in Laboratory. Journal of Marine Science and Engineering, 13(9), 1699. https://doi.org/10.3390/jmse13091699





