GPSFlow/Hydrate: A New Numerical Simulator for Modeling Subsurface Multicomponent and Multiphase Flow Behavior of Hydrate-Bearing Geologic Systems
Abstract
1. Introduction
2. GPSFlow/Hydrate Simulator
2.1. GPSFlow Software
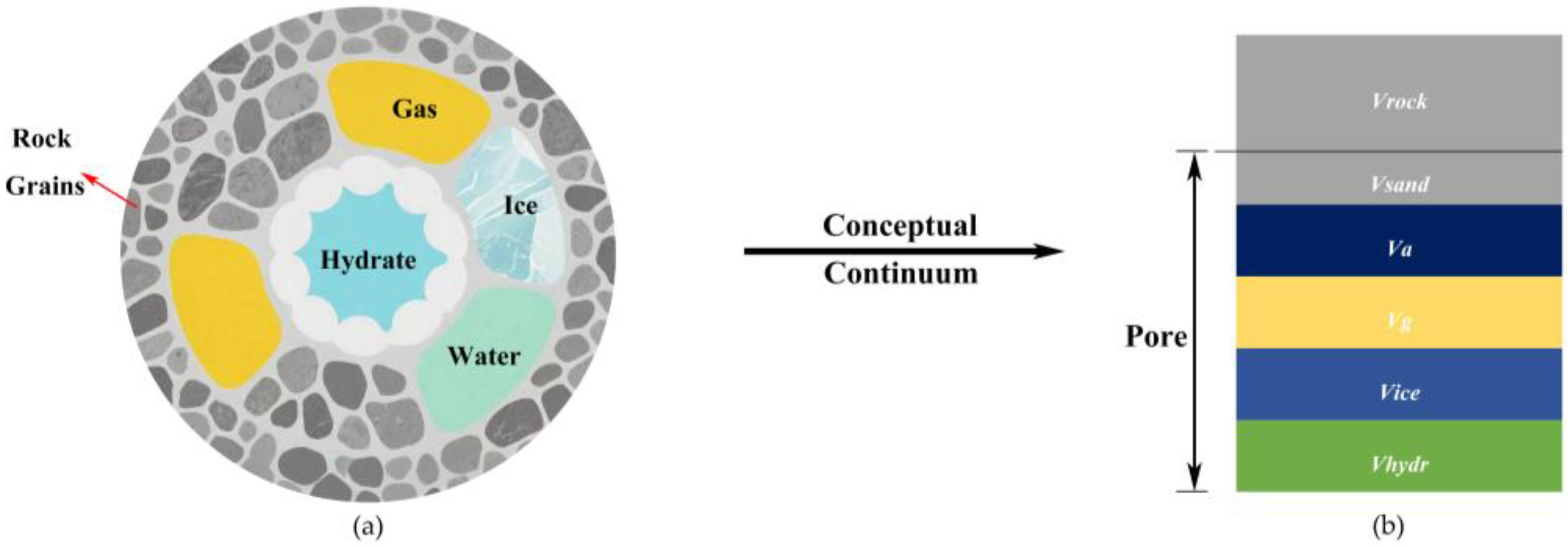
2.2. Mathematical Model
2.2.1. Governing Equations
2.2.2. Sand Flow
2.2.3. Phase Equilibrium for Multiple Gas
2.2.4. Thermophysical Properties of Gases
2.3. Numerical Design Approach
2.3.1. Equation of States and Primary Variables
2.3.2. Space and Time Discretization
2.3.3. Numerical Solutions
2.3.4. Solution of Linear Equations
2.3.5. Parallel Computing
2.3.6. Workflow Path
- Initialization: At the start of the simulation, default settings are applied, and input files containing various module configurations—such as rock properties, hydrate information, initial conditions, equation-solving parameters, and computing parameters—are read to initialize the flow system. The simulator is capable of generating computational grids and employs domain decomposition techniques to allocate grid elements and their connections to different computing units (CPUs/computing cores).
- Time-Stepping Iteration: This step constitutes the core computational process of the simulator. It involves assembling and solving the Jacobian matrix, calculating secondary variables within the equation of state, and solving linear equations. These operations are iteratively performed to advance the simulation through discrete time steps.
- Result Generation: Upon completion, at user defined times of the simulation, or reaching the maximum simulated time step, the simulator generates output files. These include log files, restart files, hydrate information, and user-defined files, which provide comprehensive data on the simulation outcomes.
3. Verifications: Comparison of Different Numerical Simulators
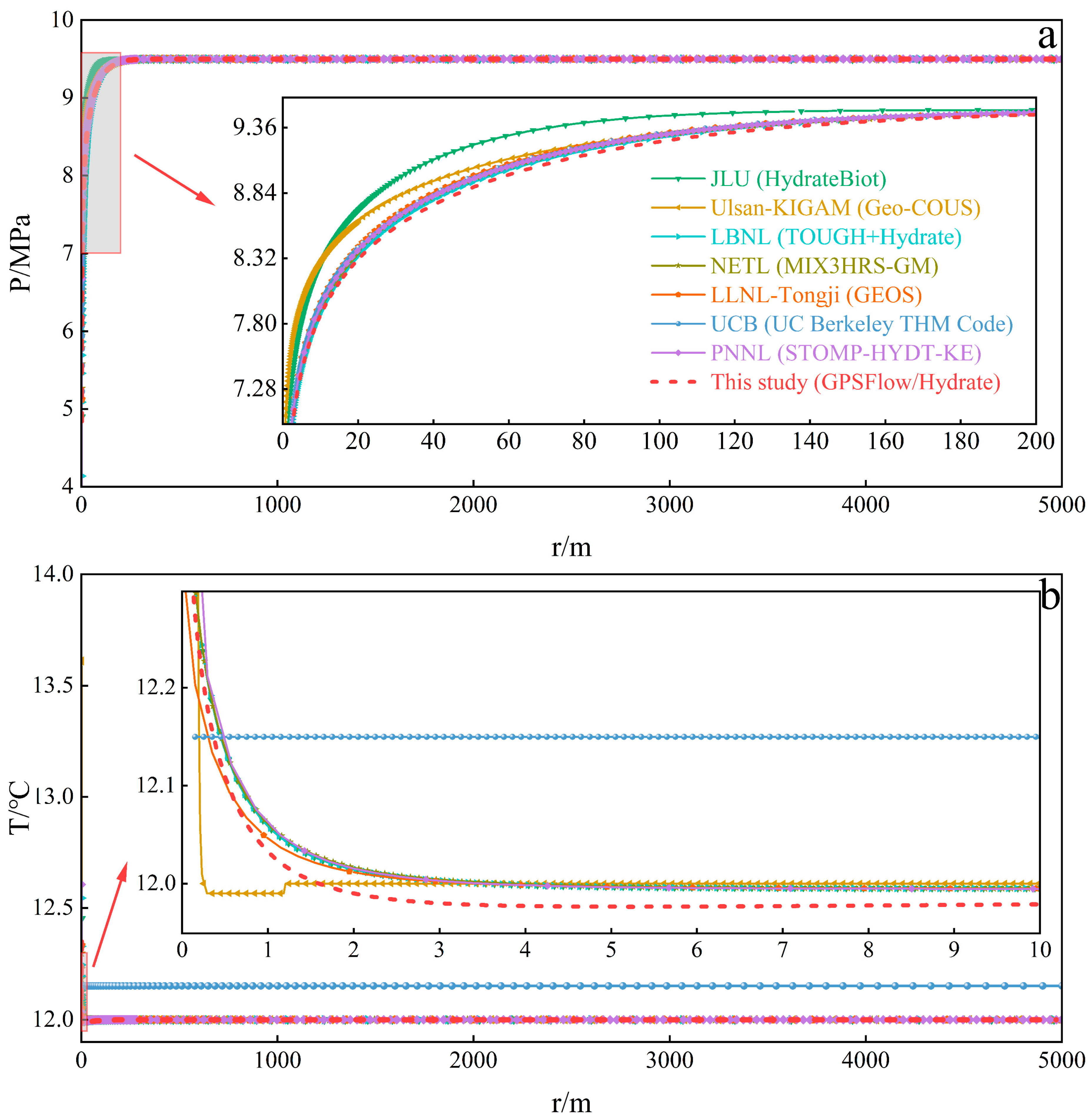
3.1. Case 1: BP3—Depressurization and Thermal Stimulation
3.2. Case 2: BP4—Depressurization of a Pure Liquid Phase
4. Applications
4.1. Case 3: One-Dimensional Numerical Simulation in Modeling the Behavior of Sand Flow
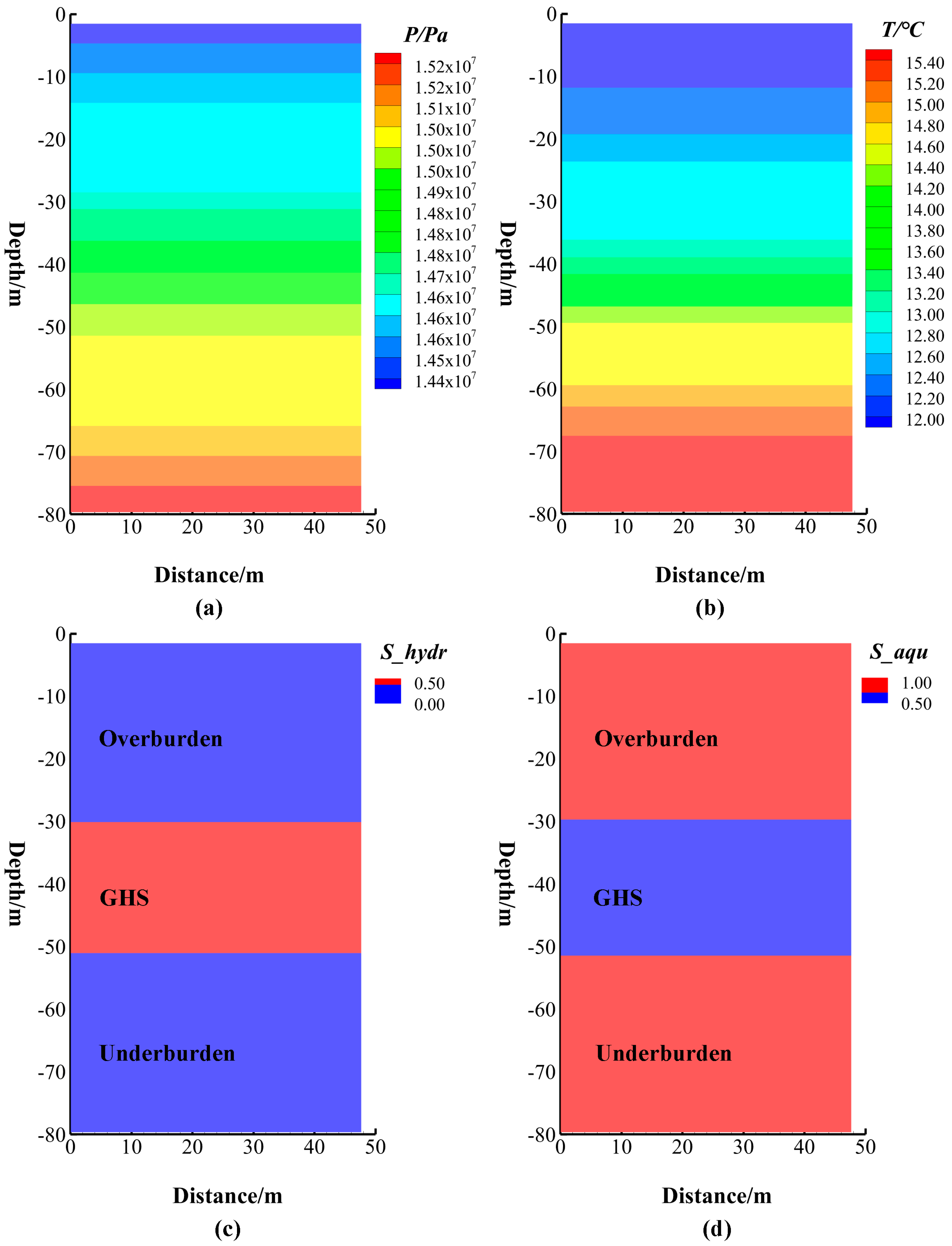
4.2. Three-Dimensional Numerical Simulation in Modeling the Behavior of Gas Hydrate
4.2.1. Spatial Evolution and Gas Production Characteristics of Reservoir Parameters
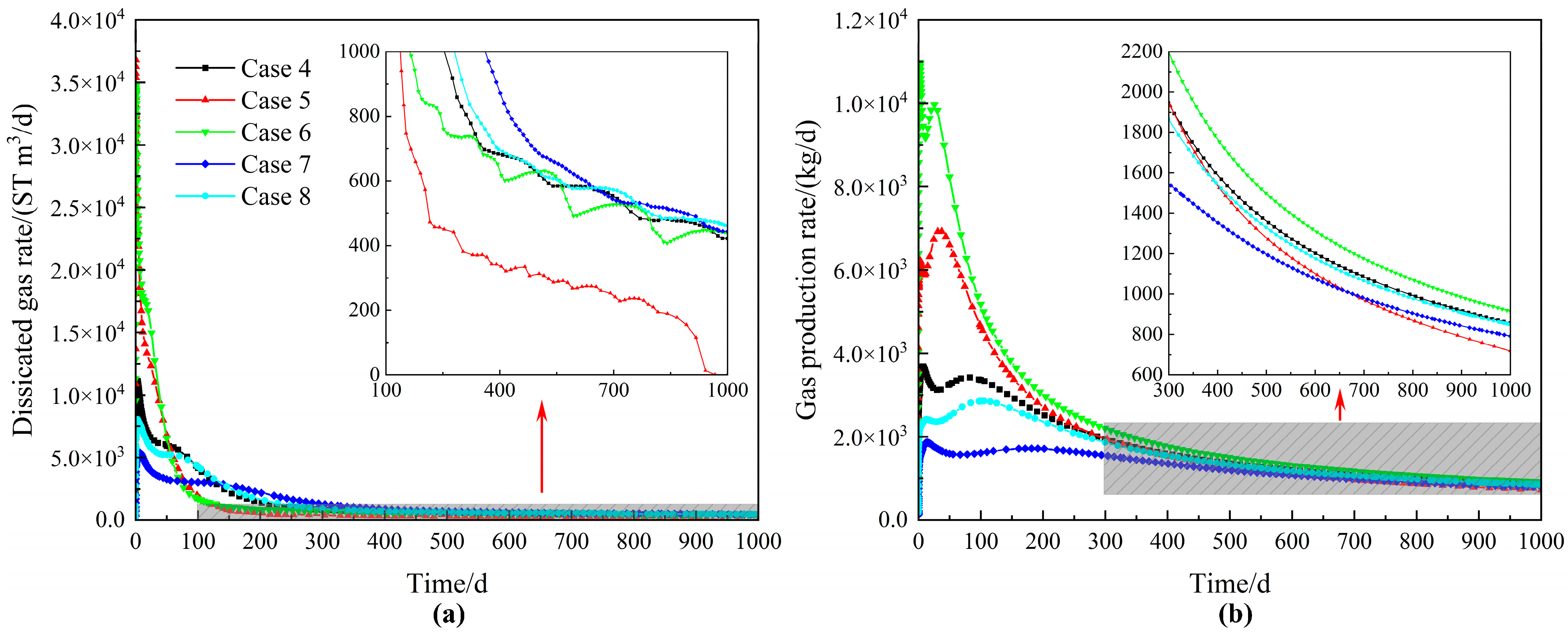
4.2.2. Sensitivity Analysis of Parameters
4.2.3. Parallel Computing Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NGH | Natural gas hydrate |
| CH4-hydrate | Methane hydrate |
| CO2-hydrate | Carbon dioxide hydrate |
| IGHCCS2 | The Second International Gas Hydrate Code Comparison Study |
| 1D | One-dimensional |
| 3D | Three-dimensional |
| MPI | Message Passing Interface |
| OpenMP | Open Multi-Processing |
| EOS | Equations of state |
| PV | Primary variables |
| FIM | Fully implicit method |
| IMPES | Implicit pressure–explicit saturation method |
| AIM | Adaptive implicit method |
| BP | Benchmark problem |
| GHS | Gas hydrate-bearing sediments |
Appendix A
Appendix A.1
| Institutes and Teams | Simulators |
|---|---|
| Cambridge-JOGMEC (MH21 Research Consortium) University of California, Berkeley (UCB) | Berkeley-Cambridge THM model—COMSOL FEM Code |
| GEOMAR Helmholtz Center for Ocean Research Kiel (GEOMAR) | SuGaR-THMC |
| Jilin University (JLU) | HydrateBiot |
| Korea Advanced Institute of Science and Technology | K-Hydrate + FLAC2D/FLAC3D |
| Korea Institute of Geoscience and Mineral Resources University of Ulsan (Ulsan-COUS) | Geo-COUS |
| Kyoto University | COMVI-MH |
| Lawrence Berkeley National Laboratory (LBNL) | TOUGH + HYDRATE + Millstone |
| Lawrence Livermore National Laboratory-Tongji University (LLNL-Tongji) | GEOS |
| National Energy Technology Laboratory (NETL) | MIX3HRS-GM |
| Pacific Northwest National Laboratory (PNNL) | STOMP-HYDT-KE + GeoMech |
| Sandia National Laboratories (SNL) | PFLOTRAN |
| National Oceanography Center Southampton, University of Southampton | CODE_BRIGHT + Hydrate-CASM |
| University of Texas at Austin (UT) | UT_HYD |
Appendix A.2
| State | Phase Combination | PV 1 | PV 2 (opt) | PV 3 | PV 4 (Kinetics *) | PV 5 (opt) | PV 6 (opt) | PV 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | Gas | P_gas | S_sand | Y_gas1 | S_hydrate * | Y_gas2 | Xinhibitor | T |
| 2 | Aqueous | P | S_sand | X_gas1 | S_hydrate * | X_gas2 | Xinhibitor | T |
| 3 | Aqueous, Gas | P_gas | S_sand | S_aqueous | S_hydrate * | Y_gas2 | Xinhibitor | T |
| 4 | Ice, Gas | P_gas | S_sand | S_ice | S_hydrate * | Y_gas2 | Xinhibitor | T |
| 5 | Aqueous, Hydrate | P | S_sand | S_aqueous | X_gas1 * | X_gas2 | Xinhibitor | T |
| 6 | Ice, Hydrate | P | S_sand | S_ice | S_gas * | Y_gas2 | Xinhibitor | T |
| 7 | Aqueous, Gas, Hydrate | S_gas P_gas * | S_sand | S_aqueous | S_gas * | Y_gas2 | Xinhibitor | T |
| 8 | Aqueous, Ice, Gas | P_gas | S_sand | S_aqueous | S_hydrate * | Y_gas2 | Xinhibitor | S_gas |
| 9 | Aqueous, Ice, Hydrate | P | S_sand | S_aqueous | S_gas * | X_gas2 | Xinhibitor | S_ice |
| 10 | Ice, Gas, Hydrate | S_gas P_gas * | S_sand | S_ice S_gas * | S_ice * | Y_gas2 | Xinhibitor | T |
| 11 | Aqueous, Ice, Gas, Hydrate | S_gas P_gas * | S_sand | S_aqueous | S_gas * | Y_gas2 | Xinhibitor | S_ice |
| 12 | Gas, Hydrate | P_gas | S_sand | S_gas | S_ice * | Y_gas2 | Xinhibitor | T |
| 13 | Aqueous, Ice | P | S_sand | S_aqueous | S_gas * | X_gas2 | Xinhibitor | X_gas1 |
References
- Merey, Ş. Prediction of Methane, Water and Ice Properties for Numerical Gas Hydrate Simulations. Celal Bayar Üniversitesi Fen Bilim. Derg. 2018, 14, 177–186. [Google Scholar] [CrossRef]
- Shahnazar, S.; Hasan, N. Gas hydrate formation condition: Review on experimental and modeling approaches. Fluid Phase Equilibria 2014, 379, 72–85. [Google Scholar] [CrossRef]
- Sun, Y.H.; Ma, X.L.; Guo, W.; Jia, R.; Li, B. Numerical simulation of the short- and long-term production behavior of the first offshore gas hydrate production test in the South China Sea. J. Pet. Sci. Eng. 2019, 181, 106196. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.-S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Zhang, W.; Tian, S. Numerical simulation of gas production from natural gas hydrate deposits with multi-branch wells: Influence of reservoir properties. Energy 2022, 238, 121738. [Google Scholar] [CrossRef]
- Kurihara, M.; Sato, A.; Funatsu, K.; Ouchi, H.; Yamamoto, K.; Numasawa, M.; Ebinuma, T.; Narita, H.; Masuda, Y.; Dallimore, S.R.; et al. Analysis of Production Data for 2007/2008 Mallik Gas Hydrate Production Tests in Canada. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar]
- Boswell, R.; Schoderbek, D.; Collett, T.S.; Ohtsuki, S.; White, M.; Anderson, B.J. The Iġnik Sikumi Field Experiment, Alaska North Slope: Design, Operations, and Implications for CO2-CH4 Exchange in Gas Hydrate Reservoirs. Energy Fuels 2017, 31, 140–153. [Google Scholar] [CrossRef]
- Uchida, S.; Klar, A.; Yamamoto, K. Sand production model in gas hydrate-bearing sediments. Int. J. Rock Mech. Min. Sci. 2016, 86, 303–316. [Google Scholar] [CrossRef]
- Li, J.F.; Ye, J.L.; Qin, X.W.; Qiu, H.J.; Wu, N.Y.; Lu, H.L.; Xie, W.W.; Lu, J.A.; Peng, F.; Xu, Z.Q.; et al. The first offshore natural gas hydrate production test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, T.; Yuan, Y.; Feng, G.; Xia, Y.; Xin, X. Numerical analysis of sand production during natural gas extraction from unconsolidated hydrate-bearing sediments. J. Nat. Gas Sci. Eng. 2020, 76, 103229. [Google Scholar] [CrossRef]
- Ebinuma, T. Method for Dumping and Disposing of Carbon Dioxide Gas and Apparatus Therefor. U.S. Patent US5261490A, 16 November 1993. [Google Scholar]
- Ogaki, K.; Takano, K.; Sangawa, H.; Matsubara, T.; Nakano, S. Methane exploitation by carbon dioxide from gas hydrates. Phase equilibria for CO2-CH4 mixed hydrate system. J. Chem. Eng. Jpn. 1996, 29, 478–483. [Google Scholar] [CrossRef]
- Zhang, X.H.; Lu, X.B.; Li, P. A comprehensive review in natural gas hydrate recovery methods. Sci. Sin.-Phys. Mech. Astron. 2019, 49, 38–59. [Google Scholar] [CrossRef]
- Park, Y.; Kim, D.-Y.; Lee, J.-W.; Huh, D.-G.; Park, K.-P.; Lee, J.; Lee, H. Sequestering carbon dioxide into complex structures of naturally occurring gas hydrates. Proc. Natl. Acad. Sci. USA 2006, 103, 12690–12694. [Google Scholar] [CrossRef]
- Ahn, Y.-H.; Kang, H.; Koh, D.-Y.; Lee, H. Production of Natural Gas Hydrate by Using Air and Carbon Dioxide. World Academy of Science, Engineering and Technology. Int. J. Chem. Mol. Nucl. Mater. Metall. Eng. 2015, 9, 808–812. [Google Scholar]
- Kurihara, M.; Sato, A.; Ouchi, H.; Narita, H.; Masuda, Y.; Saeki, T.; Fujii, T. Prediction of Gas Productivity From Eastern Nankai Trough Methane-Hydrate Reservoirs. SPE Reserv. Eval. Eng. 2009, 12, 477–499. [Google Scholar] [CrossRef]
- White, M.; Oostrom, M. STOMP Subsurface Transport Over Multiple Phases, Version 4.0, Users Guide; Technical Information Service, U.S. Department of Commerce: Springfield, VA, USA, 2006. [Google Scholar] [CrossRef]
- White, M.D. STOMP-HYDT-KE A Numerical Simulator for the Production of Natural Gas Hydrate using Guest Molecule Exchange with CO2 and N2; PNNL: Richland, WA, USA, 2012. [Google Scholar]
- Wan, Y.; Wu, N.; Chen, Q.; Li, W.; Hu, G.; Huang, L.; Ouyang, W. Coupled thermal-hydrodynamic-mechanical–chemical numerical simulation for gas production from hydrate-bearing sediments based on hybrid finite volume and finite element method. Comput. Geotech. 2022, 145, 104692. [Google Scholar] [CrossRef]
- Wilder, J.W.; Moridis, G.J.; Wilson, S.J.; Kurihara, M.; Masuda, Y.; Anderson, B.J.; Collett, T.; Hunter, R.B.; Narita, H.; Pooladi-Darvish, M.; et al. An International Effort To Compare Gas Hydrate Reservoir Simulators. In Proceedings of the 6th International Conference on Gas Hydrates (ICGH 2008), Vancouver, BC, Canada, 6–10 July 2008. [Google Scholar]
- White, M.D.; Kneafsey, T.J.; Seol, Y.; Waite, W.F.; Uchida, S.; Lin, J.S.; Myshakin, E.M.; Gai, X.; Gupta, S.; Reagan, M.T.; et al. An international code comparison study on coupled thermal, hydrologic and geomechanical processes of natural gas hydrate-bearing sediments. Mar. Pet. Geol. 2020, 120, 104566. [Google Scholar] [CrossRef]
- Howe, S.J. Production Modeling and Economic Evaluation of a Potential Gas Hydrate Pilot Production Program on the North Slope of Alaska. 2004. Available online: http://hdl.handle.net/11122/6032 (accessed on 27 April 2024).
- Wan, Y. QIMGHyd-THMC User’s Manual: A Thermal-Hydraulic-Chemical-Mechanical Coupled Simulator for the Simulation of Behavior in Natural Gas Hydrate Bearing Sediments; Qingdao, China, 2022. [Google Scholar]
- Yan, C.L.; Ren, X.; Cheng, Y.F.; Song, B.J.; Li, Y.; Tian, W.Q. Geomechanical issues in the exploitation of natural gas hydrate. Gondwana Res. 2020, 81, 403–422. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Z.; Zhao, Y.; Zuo, J.; Li, P.; Liang, W.; Wang, B.; Chen, X.; Lei, H.; Jin, G. Coupled thermal–hydrodynamic–mechanical numerical simulation of natural gas hydrate horizontal well depressurization production: Method and application in the South China Sea. Nat. Gas Ind. B 2022, 9, 548–560. [Google Scholar] [CrossRef]
- Loret, B. Sand Production During Hydrate Dissociation and Erosion of Earth Dams: Constitutive and Field Equations. In Fluid Injection in Deformable Geological Formations: Energy Related Issues; Loret, B., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 369–463. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, J.; Yang, M. Fundamentals of Natural Gas Hydrates Exploitation; Science Press: Beijing, China, 2021. [Google Scholar]
- Zhang, K. User’s Guide for GPSFlow-A Hybrid Parallel Computing General Purpose Subsurface Flow Simulator; Berkeley, CA, USA, 2022. [Google Scholar]
- Xu, B. User’s Manual for GPSFlow/Hydrate-A Numerical Simulator for Modeling Subsurface Multicomponent and Multiphase Flow Behavior of Hydrate-Bearing Geologic Systems; Guangzhou, China, 2023. [Google Scholar]
- Moridis, G.J.; Queiruga, A.F.; Reagan, M.T. Simulation of Gas Production from Multilayered Hydrate-Bearing Media with Fully Coupled Flow, Thermal, Chemical and Geomechanical Processes Using TOUGH + Millstone. Part 1: Numerical Modeling of Hydrates. Transp. Porous Media 2019, 128, 405–430. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Zhao, Y.; Wang, H.; Li, S.; Jia, J. Numerical investigation of the flow characteristics of Bingham fluid on a slope with corrected smooth particle hydrodynamics. Front. Environ. Sci. 2022, 10, 1060703. [Google Scholar] [CrossRef]
- Wang, W.; Fan, S.; Liang, D.; Li, Y. A model for estimating flow assurance of hydrate slurry in pipelines. J. Nat. Gas Chem. 2010, 19, 380–384. [Google Scholar] [CrossRef]
- Nuland, S.; Tande, M. Hydrate Slurry Flow Modeling. In Proceedings of the 12th International Conference on Multiphase Production Technology, Barcelona, Spain, 25–27 May 2005. [Google Scholar]
- Kamath, V.A. Study of Heat Transfer Characteristics During Dissociation of Gas Hydrates in Porous Media Univ. of Pittsburgh, Pittsburgh, PA. United States. 1984. Available online: https://www.osti.gov/biblio/5753228 (accessed on 4 March 2023).
- Moridis, G.J. Numerical Studies of Gas Production From Methane Hydrates. SPE J. 2003, 8, 359–370. [Google Scholar] [CrossRef]
- Shi, B. Gas Hydrate Treatment Technology; Petroleum Industry Press: Beijing, China, 2021. [Google Scholar]
- Chen, G.-J.; Guo, T.-M. A new approach to gas hydrate modelling. Chem. Eng. J. 1998, 71, 145–151. [Google Scholar] [CrossRef]
- Sloan, J.; Carolyn, K. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- NIST. Thermophysical Properties of Fluid Systems. 2022. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 3 April 2022).
- Moridis, G.J. User’s Manual for the HYDRATE Option of TOUGH+ v1.5: A Code for the Simulation of System Behavior in Hydrate-Bearing Geologic Media; Earth Sciences Division, Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2014. [Google Scholar]
- Stone, H.L. Estimation of Three-Phase Relative Permeability And Residual Oil Data. J. Can. Pet. Technol. 1973, 12, 53–61. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, D.; Zheng, T. Numerical simulations of the synthetic processes and consequences of secondary hydrates during depressurization of a horizontal well in the hydrates production. Energy 2023, 263, 125675. [Google Scholar] [CrossRef]













| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Grain density | 2600.0 kg/m3 | Grain specific heat | 1000.0 J/(kg·°C) |
| Porosity | 0.3 | Wet thermal conductivity | 2.18 W/(m·K) |
| Pore compressibility | 10−9 Pa−1 | Dry thermal conductivity | 2.0 W/(m·K) |
| Intrinsic permeability (depressurization) | m2 | Intrinsic permeability (thermal) | m2 |
| Relative permeability | Stone model [41]: | ||
| Capillary pressure | van Genuchten model [42]: | ||
| Numerical simulators for comparison | GEOMAR (SuGaR-THMC) SNL (PFLOTRAN) JLU (HydrateBiot) Ulsan-KIGAM (Geo-COUS) LBNL (TOUGH + Hydrate) UT (UT_HYD) NETL (MIX3HRS-GM) LLNL-Tongji (GEOS) UCB (UC Berkeley THM Code) PNNL (STOMP-HYDT-KE) GPSFlow/Hydrate | ||
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Grain density | 2600.0 kg/m3 | Grain specific heat | 1000.0 J/(kg·°C) |
| Porosity | 0.3 | Wet thermal conductivity | 3.1 W/(m·K) |
| Intrinsic permeability | m2 | Dry thermal conductivity | 1.0 W/(m·K) |
| Fluid type | 2-Bingham fluid | Threshold pressure gradient | 1.0 MPa |
| Relative permeability | |||
| Capillary pressure | van Genuchten model | ||
| Numerical simulators for comparison | JLU (HydrateBiot) Ulsan-KIGAM (Geo-COUS) LBNL (TOUGH + Hydrate) NETL (MIX3HRS-GM) LLNL-Tongji (GEOS) UCB (UC Berkeley THM Code) PNNL (STOMP-HYDT-KE) GPSFlow/Hydrate | ||
| Parameters | Value | Parameters | Value | ||
|---|---|---|---|---|---|
| Thickness | Overburden: | 30.0 m | Overburden: | 0.42 | |
| GHS: | 21.1 m | Porosity | GHS: | 0.40 | |
| Underburden: | 30.0 m | Underburden: | 0.38 | ||
| Intrinsic permeability 1 | × 10−16 m2 (Isotropic, overburden and underburden) | Rock grain density | 2600.0 kg/m3 | ||
| Geothermal gradient | 46.95 °C/km | Dry/Wet thermal conductivity | 1.0/3.1 W/(m·℃) | ||
| Gas composition | CH4 | Hydration number | 6.0 | ||
| Pressure at the base of GHS | 15.14 MPa | Temperature at the base of GHS | 14.23 °C | ||
| Relative permeability model | Capillary pressure model | subject to the restriction: | |||
| Case | Intrinsic Permeability (m2) | Initial Conditions | Wellbore Conditions |
|---|---|---|---|
| Case 4 | × 10−13 | Phases: Aqueous and Hydrate | Phase: Aqueous |
| Case 5 | Phases: Aqueous and Hydrate | Phase: Aqueous | |
| Case 6 | × 10−13 | Phases: Aqueous and Hydrate | Phase: Aqueous |
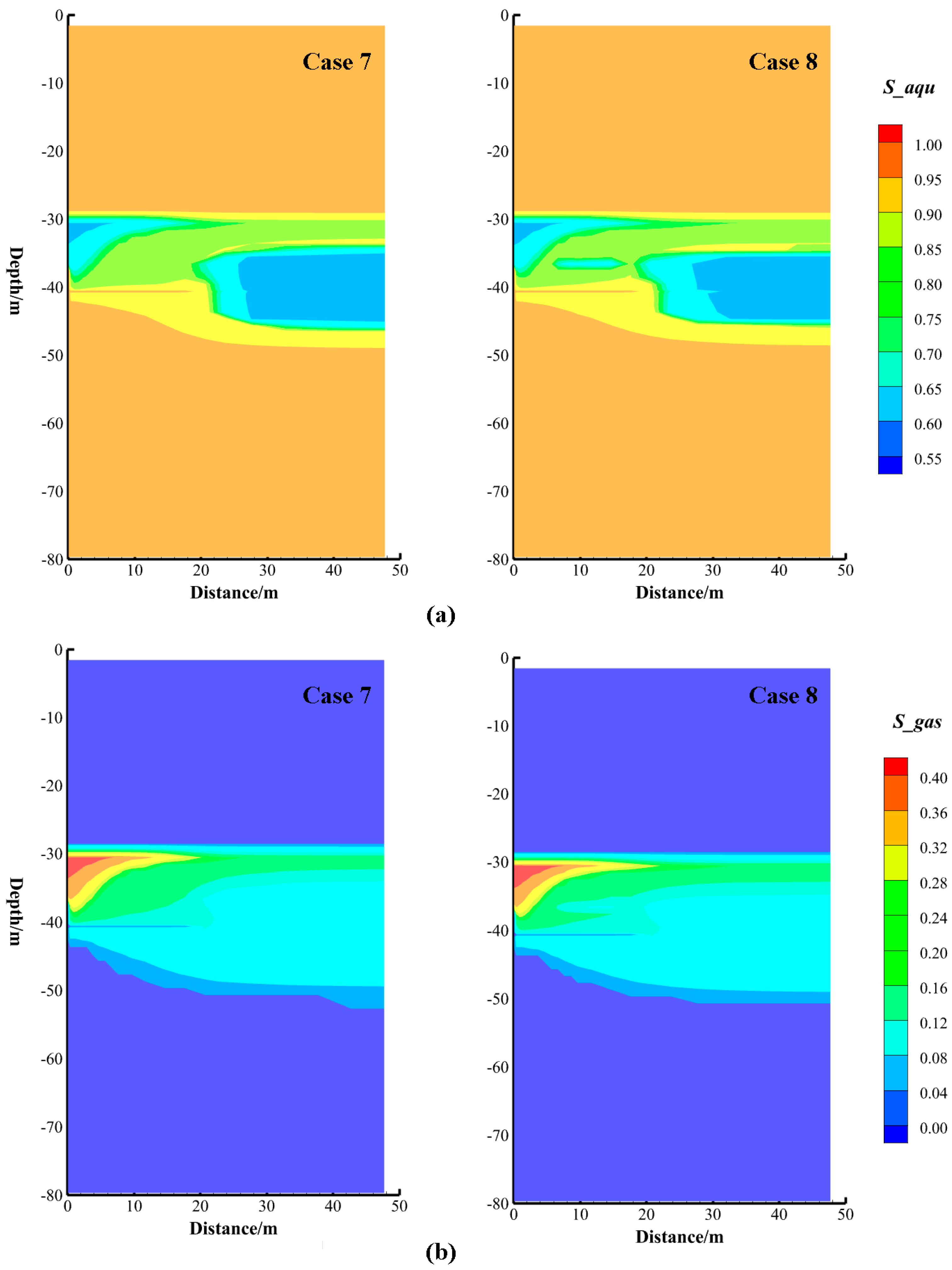
| Case 7 | × 10−14 | Phases: Aqueous and Hydrate | Phase: Aqueous |
| Case 8 | × 10−14 | Phases: Aqueous and Hydrate | Phase: Aqueous |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Zhang, K. GPSFlow/Hydrate: A New Numerical Simulator for Modeling Subsurface Multicomponent and Multiphase Flow Behavior of Hydrate-Bearing Geologic Systems. J. Mar. Sci. Eng. 2025, 13, 1622. https://doi.org/10.3390/jmse13091622
Xu B, Zhang K. GPSFlow/Hydrate: A New Numerical Simulator for Modeling Subsurface Multicomponent and Multiphase Flow Behavior of Hydrate-Bearing Geologic Systems. Journal of Marine Science and Engineering. 2025; 13(9):1622. https://doi.org/10.3390/jmse13091622
Chicago/Turabian StyleXu, Bingbo, and Keni Zhang. 2025. "GPSFlow/Hydrate: A New Numerical Simulator for Modeling Subsurface Multicomponent and Multiphase Flow Behavior of Hydrate-Bearing Geologic Systems" Journal of Marine Science and Engineering 13, no. 9: 1622. https://doi.org/10.3390/jmse13091622
APA StyleXu, B., & Zhang, K. (2025). GPSFlow/Hydrate: A New Numerical Simulator for Modeling Subsurface Multicomponent and Multiphase Flow Behavior of Hydrate-Bearing Geologic Systems. Journal of Marine Science and Engineering, 13(9), 1622. https://doi.org/10.3390/jmse13091622






