Upper-Bound Stability Analysis of Cracked Embankment Slopes with Inclined Interlayers Subject to Pore Water Pressure
Abstract
1. Introduction
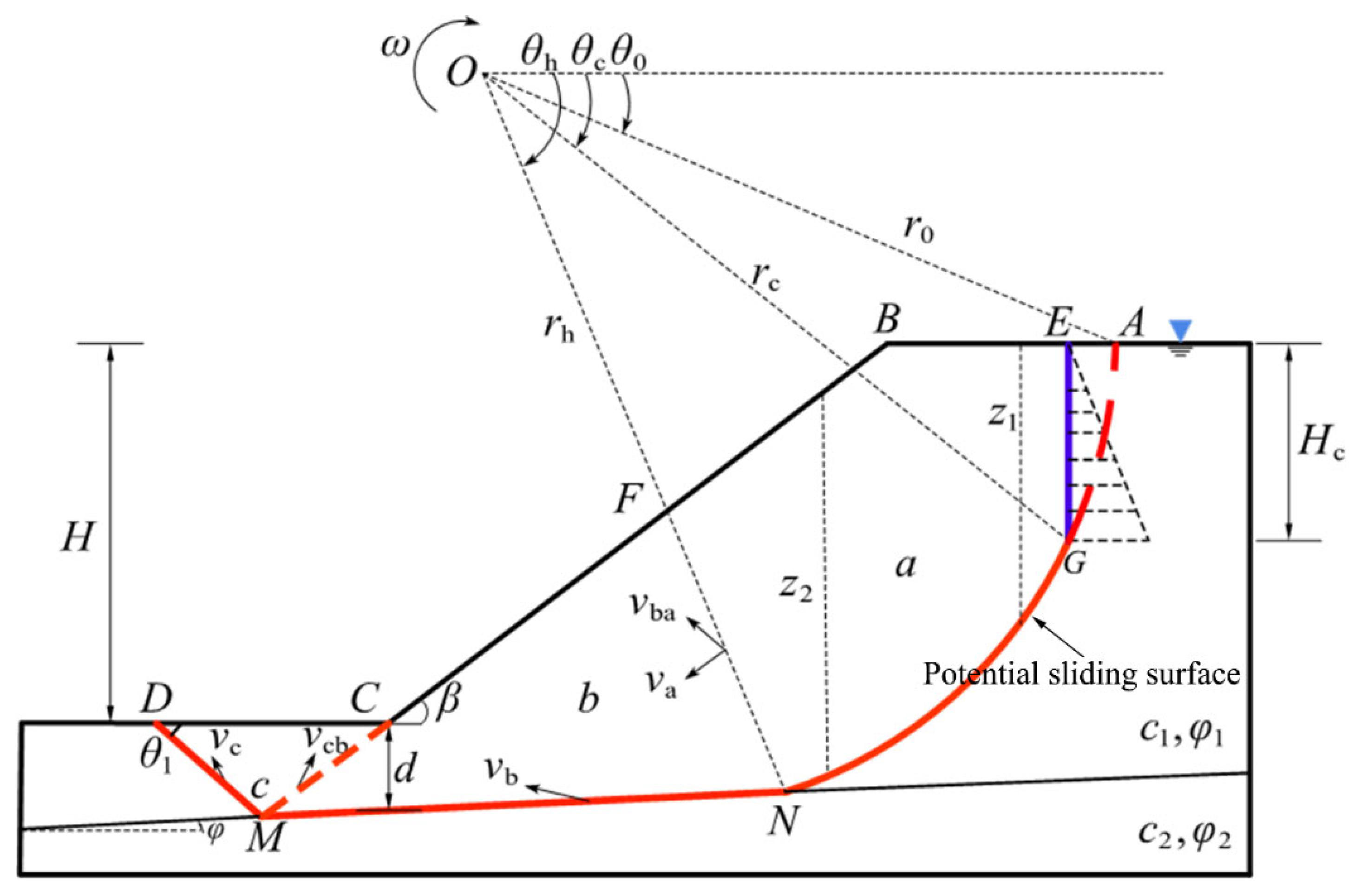
2. Composite Failure Mechanism
- (1)
- The midpoint velocity of discontinuity NF is selected as the reference to establish the velocity relationship between sliding blocks a and b;
- (2)
- The angle between discontinuity NF and the weak interlayer surface is assumed as an arbitrary value θh + δ, with θh being treated as an optimization parameter;
- (3)
- The sliding surface at the slope toe is modified by setting the shear surface at the intersection of the slope toe and weak interlayer parallel to the slope face, ensuring compliance with velocity compatibility conditions.
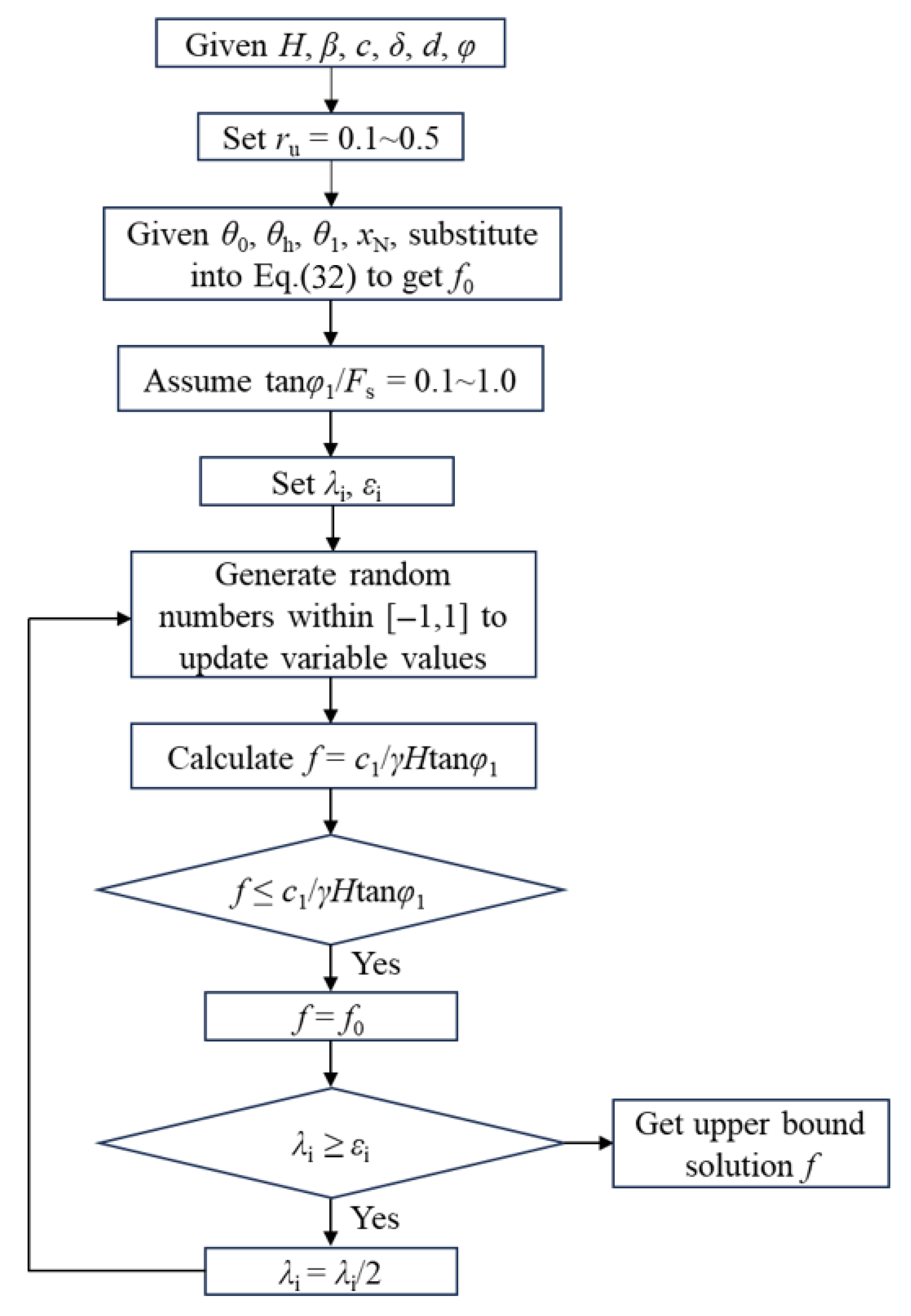
3. Upper-Bound Theorem Derivation
- (1)
- The soil is idealized as a perfectly plastic material, neglecting phenomena such as strain softening, and follows the Mohr–Coulomb failure criterion with an associated flow rule;
- (2)
- The deformation of the soil at the limit state is assumed to be small, and the slope is sufficiently long to be treated as a plane strain problem;
- (3)
- The slope is under steady-state seepage conditions, considering only hydrostatic pressure. The pore water pressure distribution within the soil is vertical, and its magnitude at any point corresponds to the vertical distance from that point to the groundwater level.
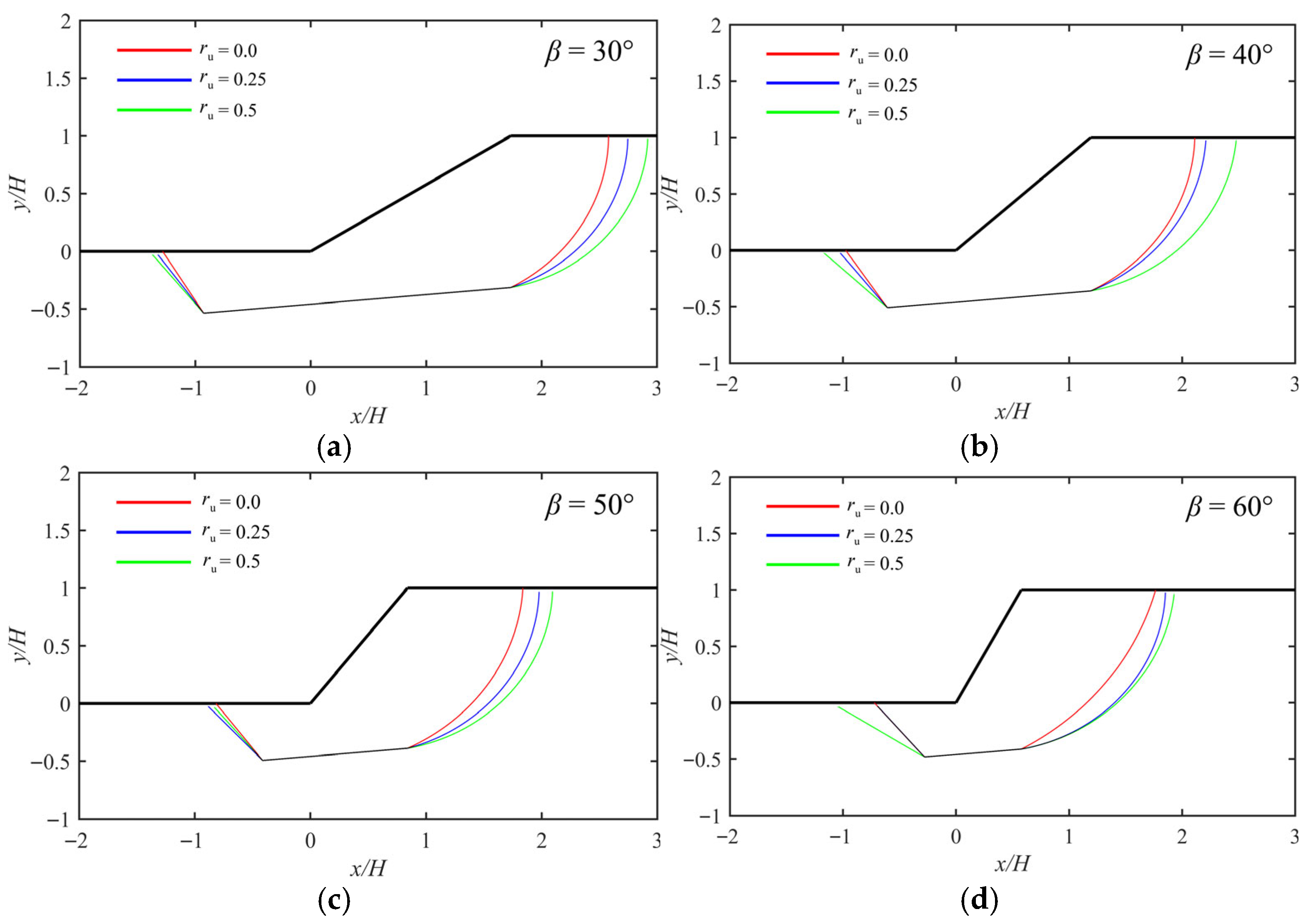
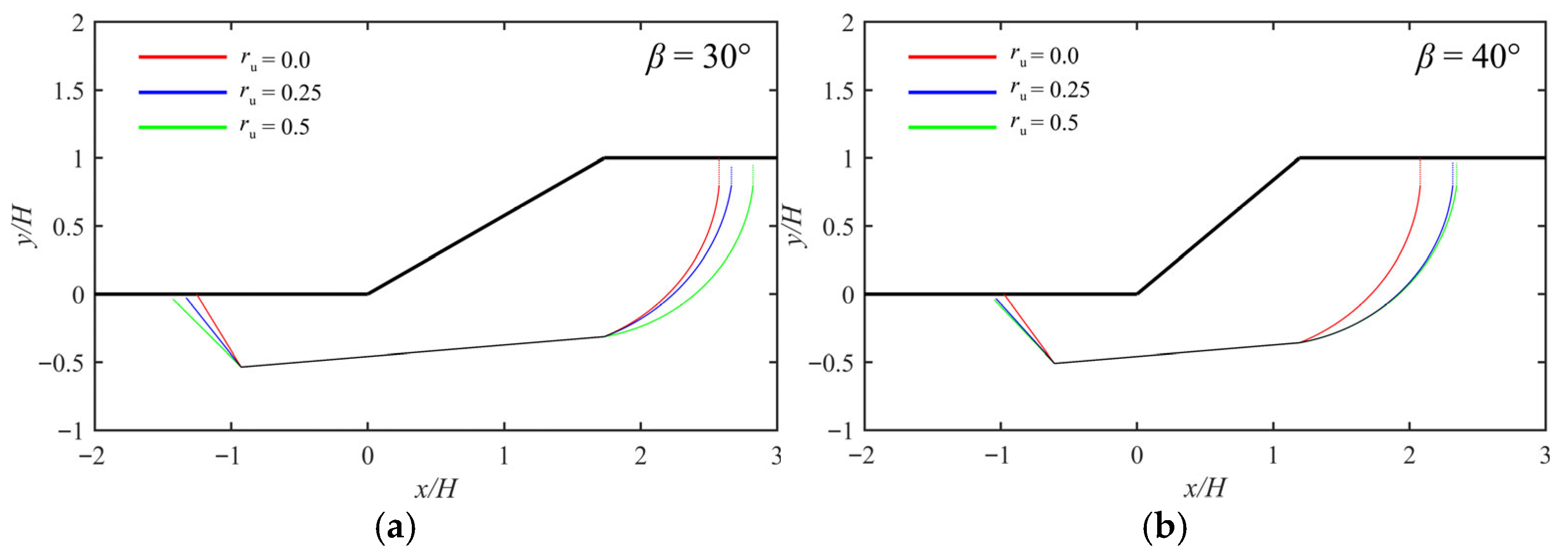
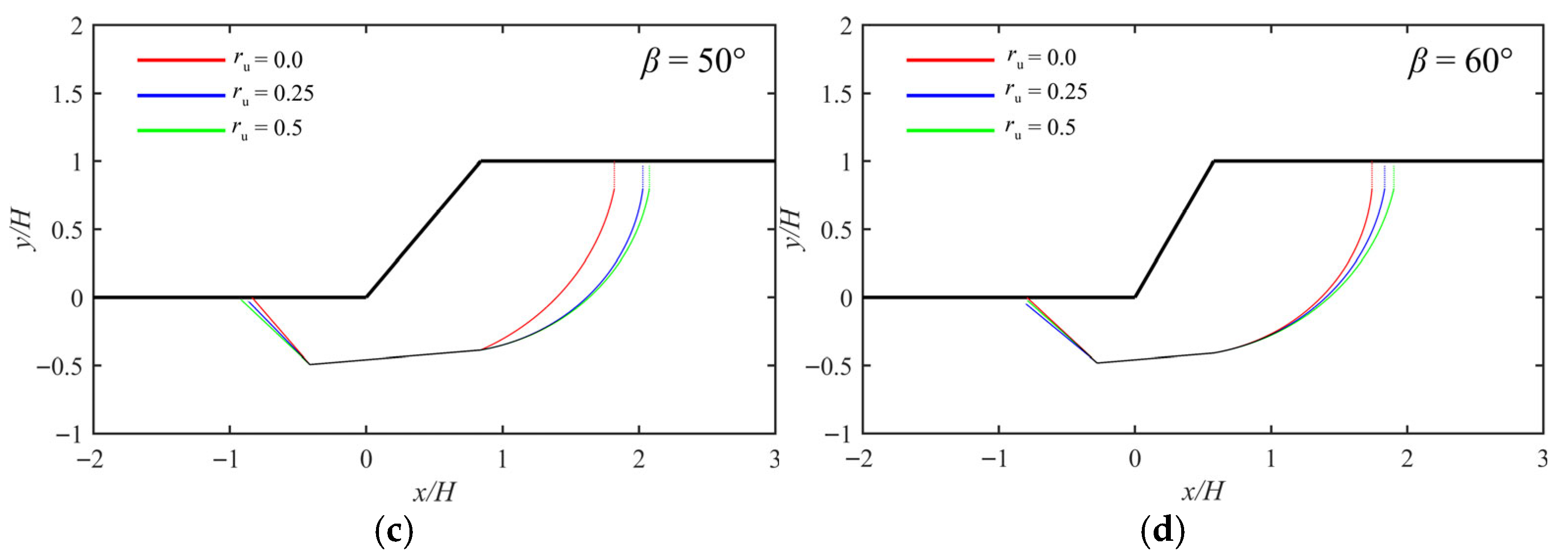
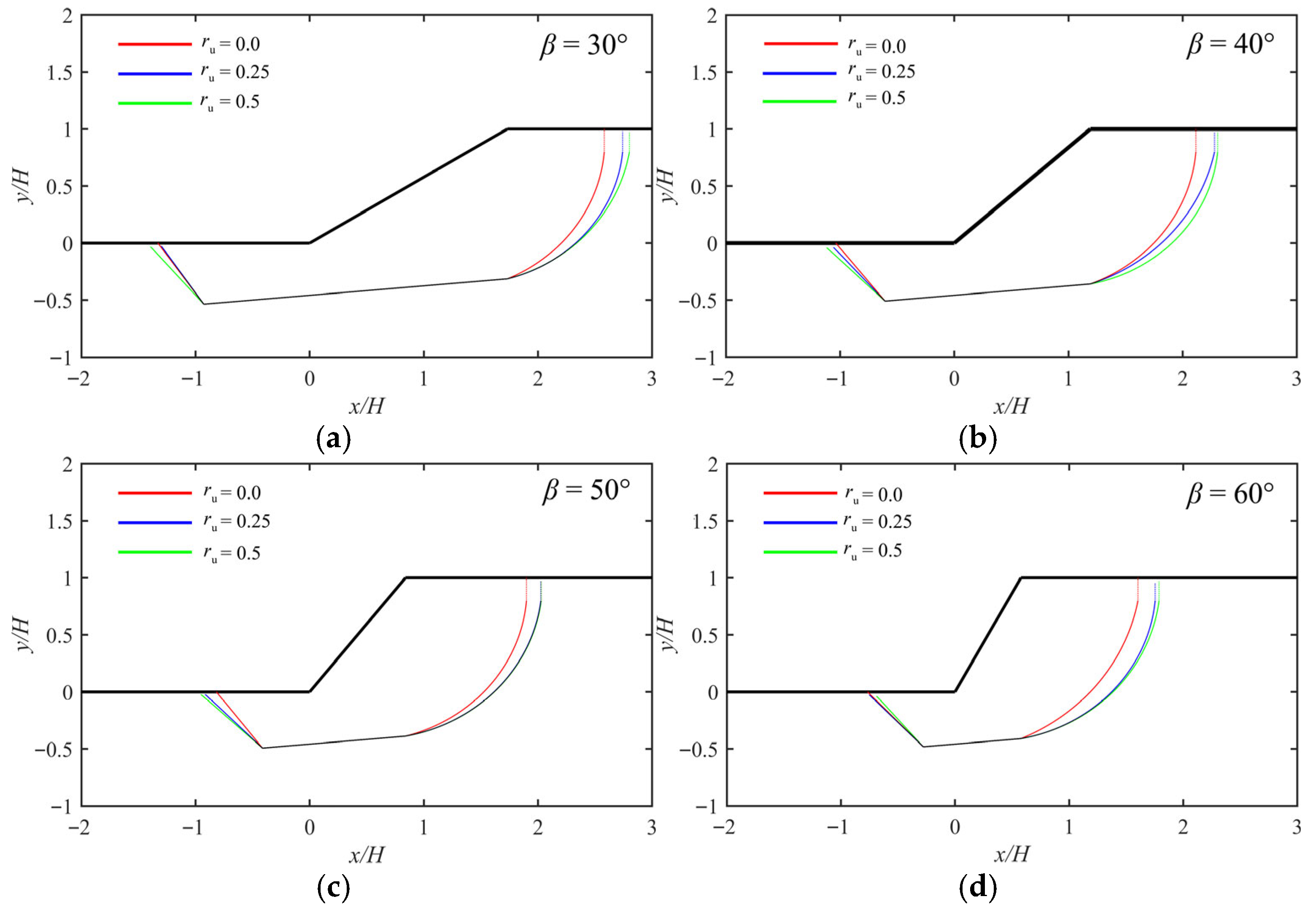
4. Results and Discussion
4.1. Comparative Analysis
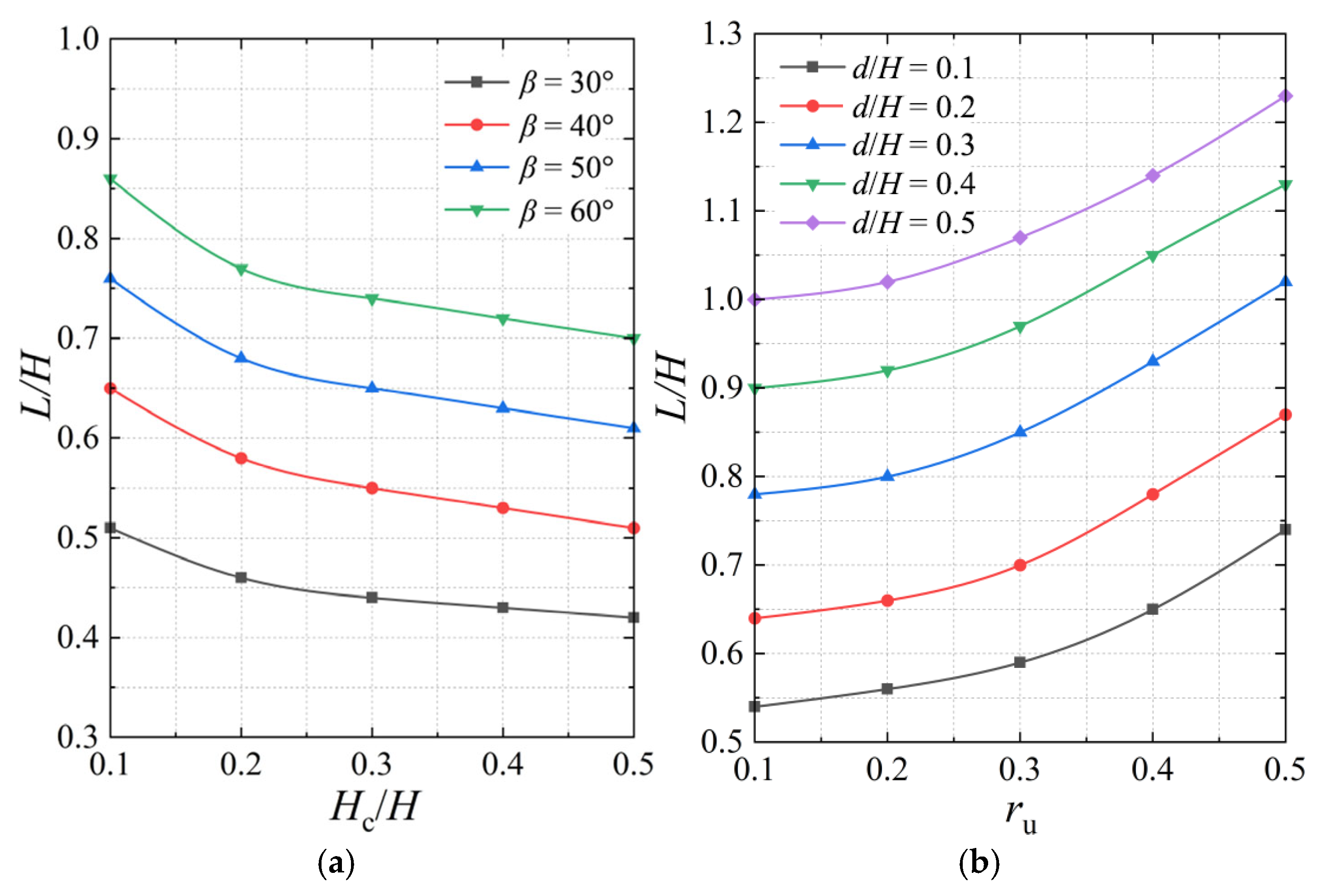
4.2. Critical Crack Location L/H
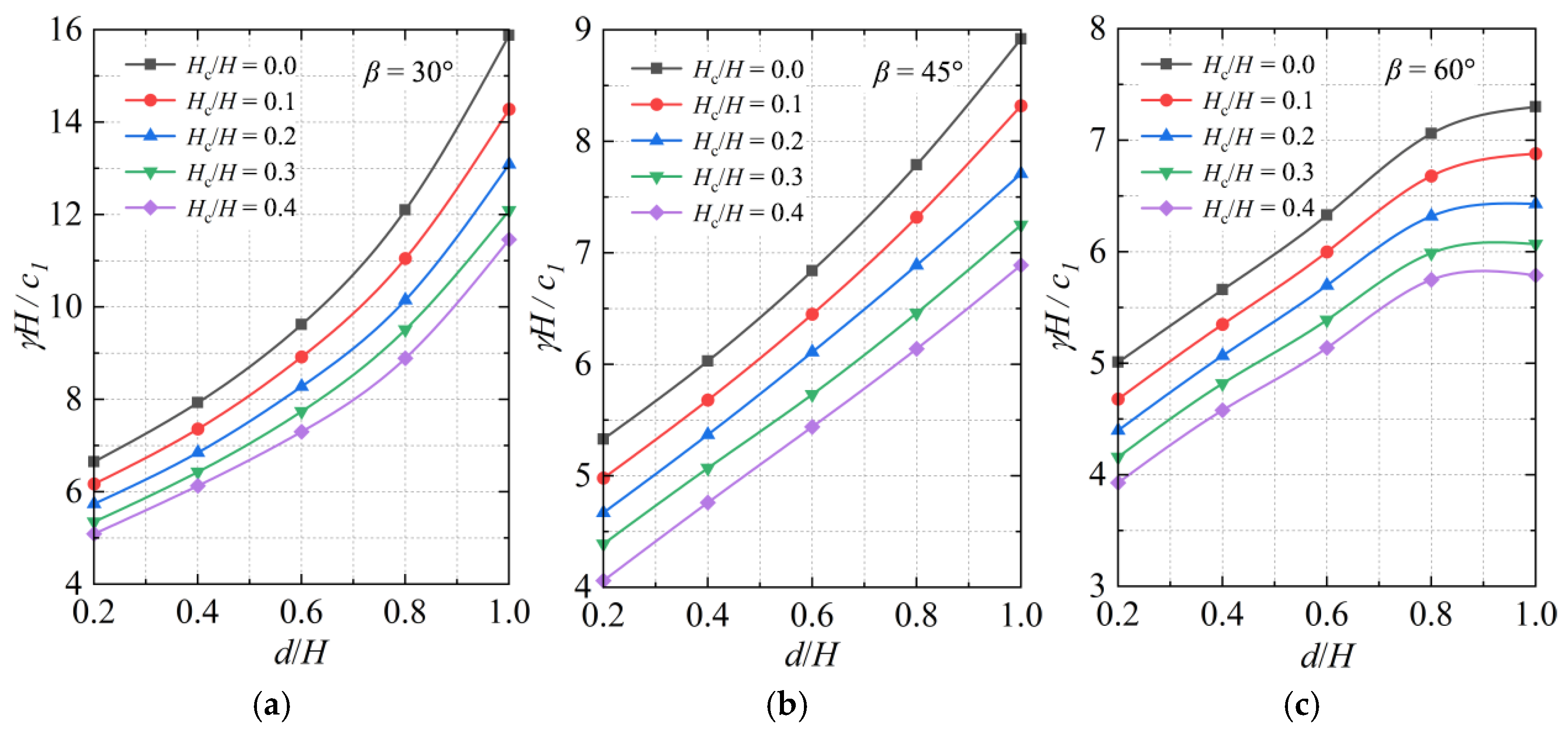
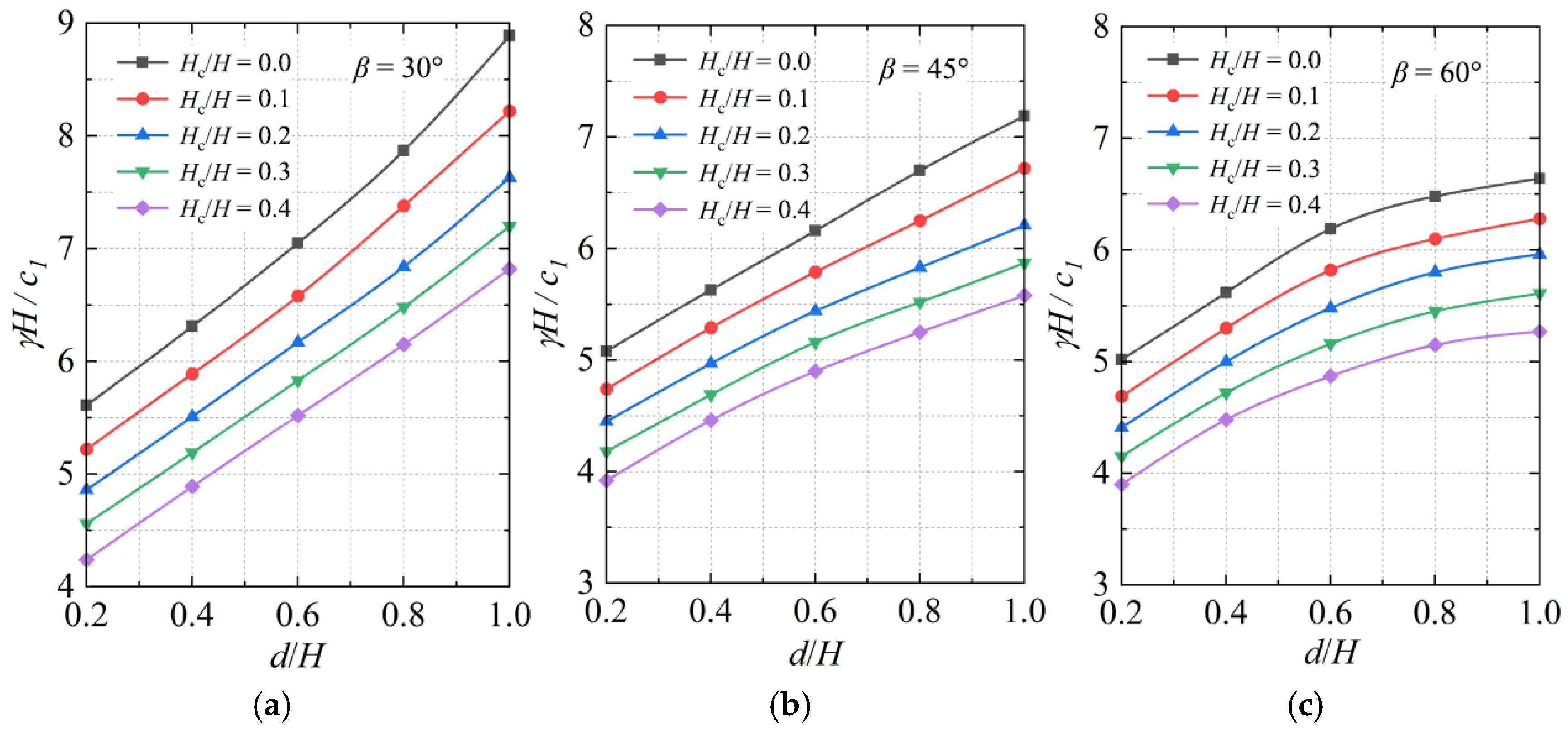
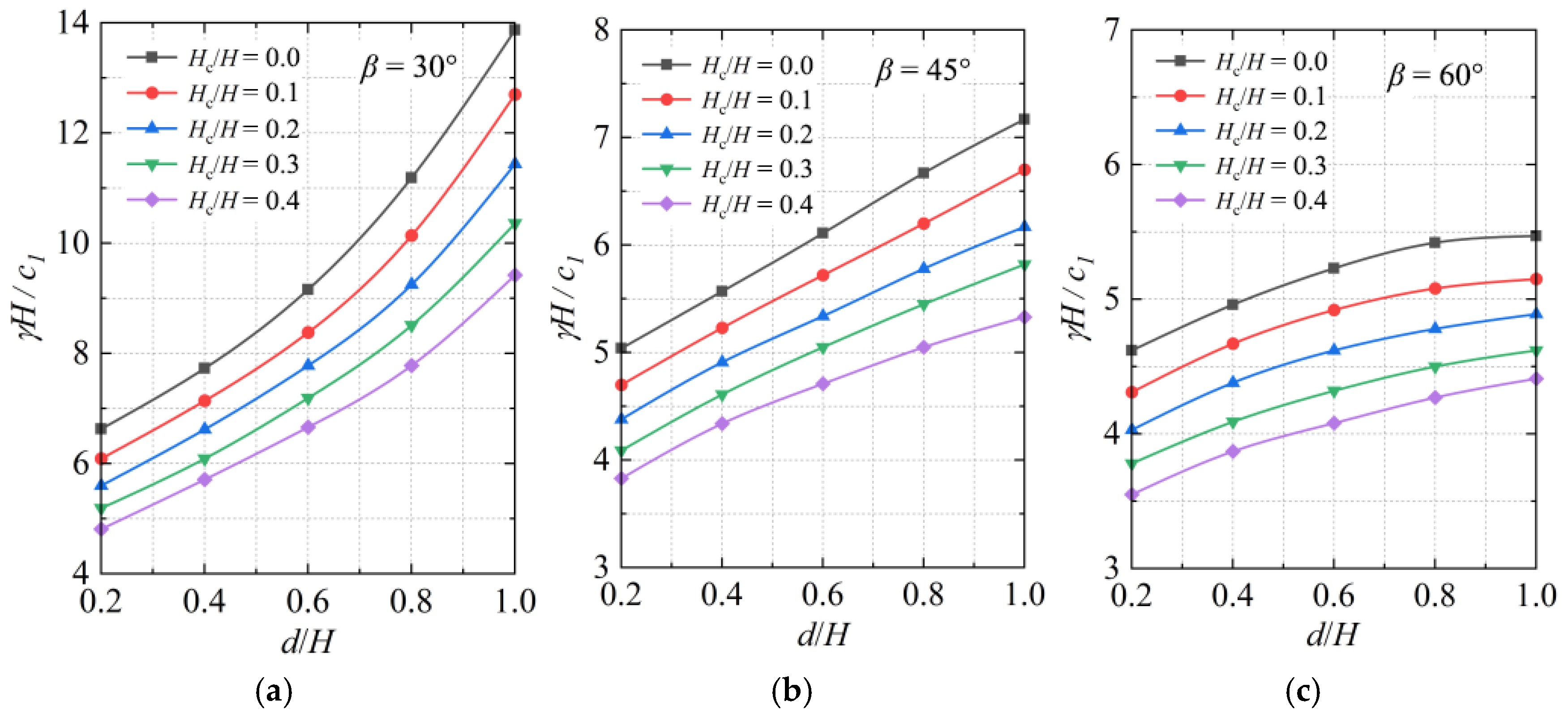
4.3. Stability Number Ns
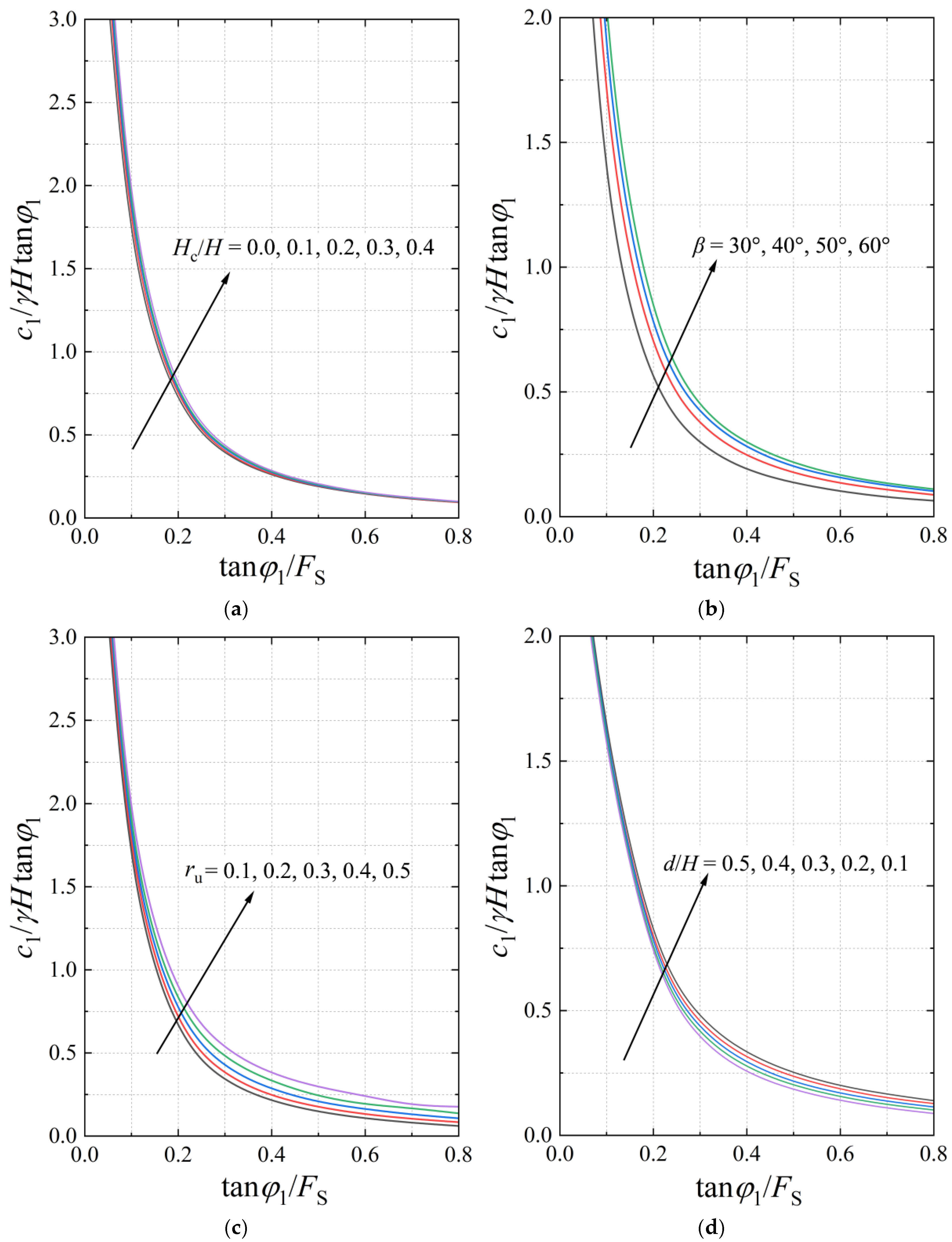
4.4. Safety Factors FS
4.5. Critical Failure Surface
5. Conclusions
- (1)
- Increased crack depth Hc shifts the crack location toward the crest edge, whereas a larger slope angle β, higher pore pressure ru, or increased embedment depth d cause opposite migration.
- (2)
- The stability number γH/c1 decreases by 7–13% when the pore water pressure coefficient ru increases from 0.25 to 0.5 under constant conditions. For slopes with β = 30°, γH/c1 decreases by 26–36% as ru rises from 0 to 0.25, while for β = 60°, the reduction rate diminishes to 23–28%. Additionally, γH/c1 decreases by 3–8% with Hc/H increasing from 0 to 0.4, and it increases by 5–15% when d/H increases from 0.1 to 0.5, though this increasing trend weakens by 30–40% for β = 60° compared with β = 30°.
- (3)
- The safety factor Fs decreases with increases in the pore water pressure coefficient ru, crack depth Hc, and slope angle β. When ru increases from 0.1 to 0.5, the safety factor decreases by approximately 12 percentage points for a given interlayer embedment depth (d/H = 0.2). On the positive side, Fs increases with higher interlayer embedment depth d and higher cohesion ratio c2/c1, with the latter leading to increases of 6% to 21% when c2/c1 rises from 0 to 0.5, though this is only about 6% for β = 60°.
- (4)
- For embankment slopes with inclined interlayers and no cracks, the emergence of pore water pressure significantly increases both the depth and extent of the critical sliding surface. However, steeper slopes reduce the depth and range of this critical sliding surface. When a vertical tension crack exists at the crest, the influence of the pore water pressure coefficient on the sliding surface depth and range diminishes compared with no-crack conditions. Furthermore, a lower cohesion ratio c2/c1 extends the critical sliding surface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.-F.; Chen, C.-F.; Zhao, H.-Y. An Approach to Assess the Stability of Unsaturated Multilayered Coastal-Embankment Slope during Rainfall Infiltration. J. Mar. Sci. Eng. 2019, 7, 165. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef]
- Oumeraci, H. Review and analysis of vertical breakwater failures-lessons learned. Coast. Eng. 1994, 22, 3–29. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, X.; Qiu, F. Stability analysis of unsaturated soil slopes with cracks under rainfall infiltration conditions. Comput. Geotech. 2024, 165, 105907. [Google Scholar] [CrossRef]
- Konrad, J.M.; Ayad, R. An idealized framework for the analysis of cohesive soils undergoing desiccation. Can. Geotech. J. 1997, 34, 477–488. [Google Scholar] [CrossRef]
- Utili, S.; Castellanza, R.; Galli, A.; Sentenac, P. Novel approach for health monitoring of earthen embankments. J. Geotech. Geoenviron. 2015, 141, 04014111. [Google Scholar] [CrossRef]
- Rahardjo, H.; Lim, T.T.; Chang, M.F.; Fredlund, D.G. Shear-strength characteristics of a residual soil. Can. Geotech. J. 1995, 32, 60–77. [Google Scholar] [CrossRef]
- Vanicek, I.; Vanicek, M. Earth Structures: In Transport, Water and Environmental Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Huang, M.; Wang, H.; Liu, Y. Rotation-translation combined mechanism for stability analysis of slopes with weak interlayer under rainfall condition. Chin. J. Geotech. Eng. 2012, 34, 1561–1567. (In Chinese) [Google Scholar]
- Ogila, W.A.M. Analysis and assessment of slope instability along international mountainous road in north Africa. Nat. Hazards 2021, 106, 2479–2517. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, X.; Sun, R.; Cui, C.; Gu, H.; Qiu, Y. A novel analytical approach for 3D stability of unsaturated soil slopes with cracks under rainfall infiltration. Eng. Fail. Anal. 2025, 175, 109575. [Google Scholar] [CrossRef]
- Huang, M.; Wang, H.; Sheng, D.; Liu, Y. Rotational–translational mechanism for the upper bound stability analysis of slopes with weak interlayer. Comput. Geotech. 2013, 53, 133–141. [Google Scholar] [CrossRef]
- He, Y.; Liu, Y.; Zhang, Y.; Yuan, R. Stability assessment of three-dimensional slopes with cracks. Eng. Geol. 2019, 252, 136–144. [Google Scholar] [CrossRef]
- Shen, L.; Han, X.; Fei, L.; Ding, R. Case study on Feasibility and Performance of Embankment over Soft Soils with Beam-type Capped Piles. KSCE J. Civ. Eng. 2025, 29, 100208. [Google Scholar] [CrossRef]
- He, Y.; Yu, J.; Yuan, R.; Fang, Y. Stability Analysis of the Soil Slope with Cracks Considering the Upper Slope Inclination. China J. Highw. Transport. 2021, 34, 45–54. (In Chinese) [Google Scholar]
- Zhou, H.; Zheng, G.; Yang, X.; Diao, Y.; Gong, L.; Cheng, X. Displacement of Pile-Reinforced Slopes with a Weak Layer Subjected to Seismic Loads. Math. Probl. Eng. 2016, 2016, 1527659. [Google Scholar] [CrossRef]
- Li, C.; Jiang, P. Failure mechanism of two-layered slopes subjected to the surcharge load. Int. J. Geomech. 2020, 20, 06019024. [Google Scholar] [CrossRef]
- Fredlund, D.; Krahn, J. Comparison of slope stability methods of analysis. Can. Geotech. J. 1977, 14, 429–439. [Google Scholar] [CrossRef]
- Huang, C.; Tsai, C.; Chen, Y. Generalized method for three-dimensional slope stability analysis. J. Geotech. Geoenviron. 2002, 128, 836–848. [Google Scholar] [CrossRef]
- Chang, M. Three-dimensional stability analysis of the Kettleman Hills landfill slope failure based on observed sliding-block mechanism. Comput. Geotech. 2005, 32, 587–599. [Google Scholar] [CrossRef]
- Deng, D.; Li, L.; Zhao, L. Critical position of tensile cracks and stability analysis in slope near river. J. Cent. South Univ. (Sci. Technol.) 2013, 44, 3873–3883. (In Chinese) [Google Scholar]
- Utili, S. Investigation by limit analysis on the stability of slopes with cracks. Géotechnique 2013, 63, 140–154. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Yi, J.; Liu, Z.; Yu, Z.; Liu, H. Upper bound stability analysis of cracked embankment fill on soil with spatially varying shear strength. Geotech. Geol. Eng. 2025, 43, 112. [Google Scholar] [CrossRef]
- Baker, R. Tensile strength, tension cracks, and stability of slopes. Soils. Found. 1981, 21, 1–17. [Google Scholar]
- Leshchinsky, D. Slope stability analysis: Generalized approach. J. Geotech. Eng. 1990, 116, 851–867. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, J. Limit analysis of slope stability by rigid finite-element method and linear programming considering rotational failure. Int. J. Geomech. 2012, 13, 827–839. [Google Scholar] [CrossRef]
- Tang, Z.; Li, L.; Zhao, L.; Zhou, F. Stability analysis of slopes with weak interlayer based on upper bound limit analysis. J. Railw. Sci. Eng. 2014, 11, 60–64. (In Chinese) [Google Scholar]
- Zheng, G.; Zhao, J.; Zhou, H.; Yang, X. Stability analysis of weak interlayer slopes reinforced with piles under seismic load. J. Chongqing Univ. 2019, 42, 47–55. (In Chinese) [Google Scholar]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis for limit design. Q. Appl. Math. 1952, 10, 157–164. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity; Elsevier: Rotterdam, The Netherlands, 1975. [Google Scholar]
- Zhang, H.; Li, C.; Chen, W.; Xie, N.; Wang, G.; Yao, W.; Jiang, X.; Long, J. Upper-bound limit analysis of the multi-layer slope stability and failure mode based on generalized horizontal slice method. J. Earth Sci. 2024, 35, 929–940. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.; Li, D.; Chen, Q.; Lin, L.; Zhang, S.; Jia, W. System reliability analysis of bedrock-soil layer slopes subject to seismic action based on the upper bound limit analysis method. Geomat. Nat. Haz. Risk. 2025, 16, 2442020. [Google Scholar] [CrossRef]
- Zuo, J.-Y.; Wang, B.-T.; Li, W.-W.; Zhang, H.-X. Upper-bound solution for the stability analysis of layered slopes. J. Eng. Mech. 2022, 148, 04022007. [Google Scholar] [CrossRef]
- Chen, Y.; Lai, Y.; Zhang, M.; Zhang, M.; Li, H.; Zhang, Y. Upper-bound optimized solution of unsaturated soil slope stability under steady and unsteady flows. Comput. Geotech. 2023, 164, 105815. [Google Scholar] [CrossRef]
- Michalowski, R. Slope stability analysis: A kinematical approach. Géotechnique 1995, 45, 283–293. [Google Scholar] [CrossRef]
- Bishop, A.-W. The use of pore-pressure coefficients in practice. Géotechnique 1954, 4, 148–152. [Google Scholar] [CrossRef]
- Kim, J.; Salgado, R.; Lee, J. Stability analysis of complex soil slopes using limit analysis. J. Geotech. Geoenviron. 2002, 128, 546–557. [Google Scholar] [CrossRef]
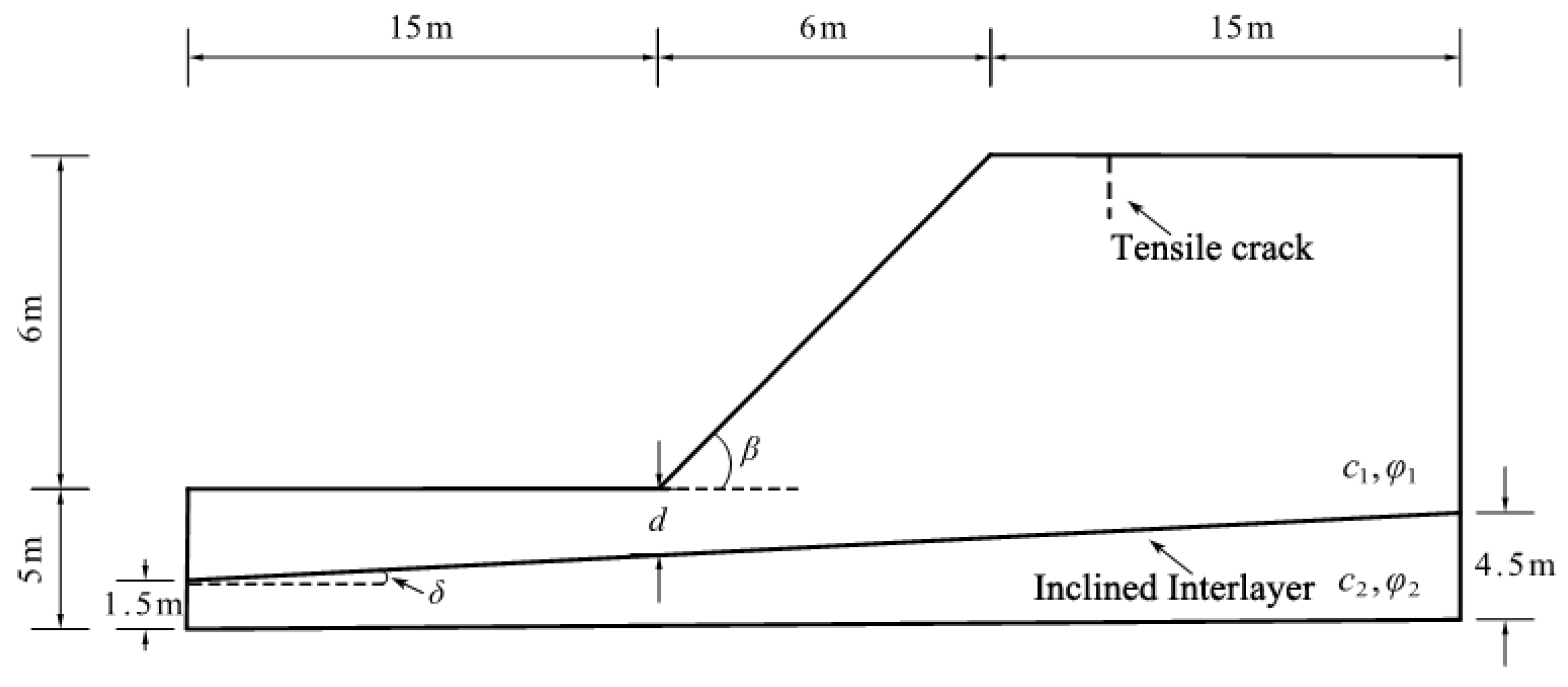








| c1/kPa | c2/kPa | φ1/(°) | φ2/(°) | γ/(kN/m3) | β/(°) | δ/(°) | d/m | H/m | Hc/m |
|---|---|---|---|---|---|---|---|---|---|
| 20 | 12 | 10 | 5 | 20 | 45 | 4.76 | 2.7 | 6 | 0.6 |
| Analytical Methods | FS |
|---|---|
| Lower-bound limit analysis method [37] | 1.07 |
| Upper-bound limit analysis method [37] | 1.16 |
| Morgenstern–Price method | 1.12 |
| This study | 1.14 |
| Group | Pore Water Pressure Coefficient | φ2/φ1 | c2/c1 |
|---|---|---|---|
| I II III | ru = 0.25 | 1.0 0.5 0.5 | 0.0 0.0 0.5 |
| IV V VI | ru = 0.5 | 1.0 0.5 0.5 | 0.0 0.0 0.5 |
| Hc/H | β/(°) | ru = 0 | ru = 0.25 | Reduction Rate/% |
|---|---|---|---|---|
| d/H = 0.4 | ||||
| 0.0 | 30 | 10.83 | 7.93 | 26.78 |
| 0.1 | 10.50 | 7.36 | 29.90 | |
| 0.2 | 10.17 | 6.85 | 32.65 | |
| 0.3 | 9.85 | 6.43 | 34.72 | |
| 0.4 | 9.59 | 6.13 | 36.08 | |
| 0.0 | 45 | 7.78 | 6.03 | 22.49 |
| 0.1 | 7.56 | 5.68 | 24.87 | |
| 0.2 | 7.39 | 5.37 | 27.33 | |
| 0.3 | 7.25 | 5.07 | 30.07 | |
| 0.4 | 7.07 | 4.76 | 32.67 | |
| 0.0 | 60 | 7.35 | 5.66 | 22.99 |
| 0.1 | 7.10 | 5.35 | 24.65 | |
| 0.2 | 6.91 | 5.07 | 26.63 | |
| 0.3 | 6.68 | 4.82 | 27.84 | |
| 0.4 | 6.43 | 4.58 | 28.77 | |
| Hc/H | β/(°) | (ru = 0.25, Group III) | (ru = 0.5, Group VI) | Reduction Rate/% | |||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | A | B | ||
| d/H = 0.2 | d/H = 1.0 | d/H = 0.2 | d/H = 1.0 | ||||
| 0.0 | 30 | 7.99 | 11.22 | 7.44 | 9.18 | 6.88 | 18.18 |
| 0.1 | 7.44 | 10.46 | 6.87 | 8.42 | 7.66 | 19.50 | |
| 0.2 | 6.97 | 9.7 | 6.39 | 7.79 | 8.32 | 19.69 | |
| 0.3 | 6.56 | 9.02 | 5.96 | 7.25 | 9.15 | 19.62 | |
| 0.4 | 6.23 | 8.53 | 5.54 | 6.76 | 11.08 | 20.75 | |
| 0.0 | 45 | 6.41 | 8.28 | 5.9 | 6.4 | 7.96 | 22.71 |
| 0.1 | 6.02 | 7.7 | 5.45 | 5.98 | 9.47 | 22.34 | |
| 0.2 | 5.64 | 7.26 | 5.06 | 5.58 | 10.28 | 23.14 | |
| 0.3 | 5.32 | 6.84 | 4.68 | 5.29 | 12.03 | 22.66 | |
| 0.4 | 4.98 | 6.42 | 4.35 | 4.99 | 12.65 | 22.27 | |
| 0.0 | 60 | 5.78 | 7.33 | 4.83 | 5.42 | 16.44 | 26.06 |
| 0.1 | 5.43 | 6.89 | 4.49 | 5.11 | 17.31 | 25.83 | |
| 0.2 | 5.11 | 6.42 | 4.2 | 4.83 | 17.81 | 24.77 | |
| 0.3 | 4.81 | 6.05 | 3.95 | 4.63 | 17.88 | 23.47 | |
| 0.4 | 4.52 | 5.68 | 3.76 | 4.42 | 16.81 | 22.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yu, Z.; Yi, J. Upper-Bound Stability Analysis of Cracked Embankment Slopes with Inclined Interlayers Subject to Pore Water Pressure. J. Mar. Sci. Eng. 2025, 13, 1594. https://doi.org/10.3390/jmse13081594
Zhang J, Yu Z, Yi J. Upper-Bound Stability Analysis of Cracked Embankment Slopes with Inclined Interlayers Subject to Pore Water Pressure. Journal of Marine Science and Engineering. 2025; 13(8):1594. https://doi.org/10.3390/jmse13081594
Chicago/Turabian StyleZhang, Jingwu, Zehao Yu, and Jinxiang Yi. 2025. "Upper-Bound Stability Analysis of Cracked Embankment Slopes with Inclined Interlayers Subject to Pore Water Pressure" Journal of Marine Science and Engineering 13, no. 8: 1594. https://doi.org/10.3390/jmse13081594
APA StyleZhang, J., Yu, Z., & Yi, J. (2025). Upper-Bound Stability Analysis of Cracked Embankment Slopes with Inclined Interlayers Subject to Pore Water Pressure. Journal of Marine Science and Engineering, 13(8), 1594. https://doi.org/10.3390/jmse13081594





