Estimation of Growth and Carrying Capacity of Porphyra spp. Under Aquaculture Conditions on the Southern Coast of Korea Using Dynamic Energy Budget (DEB)
Abstract
1. Introduction
2. Materials and Methods
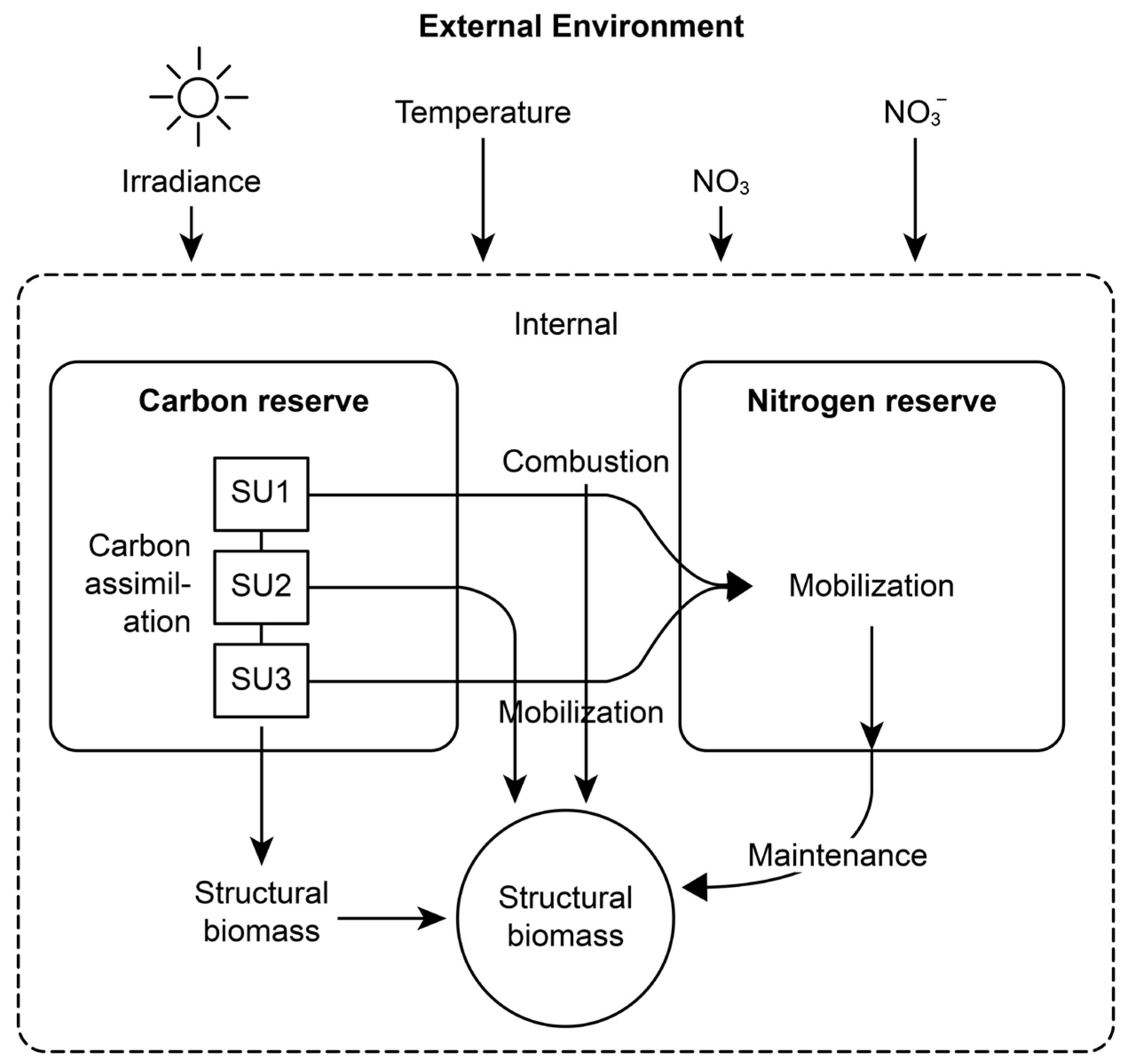
2.1. Model Assumptions and Framework
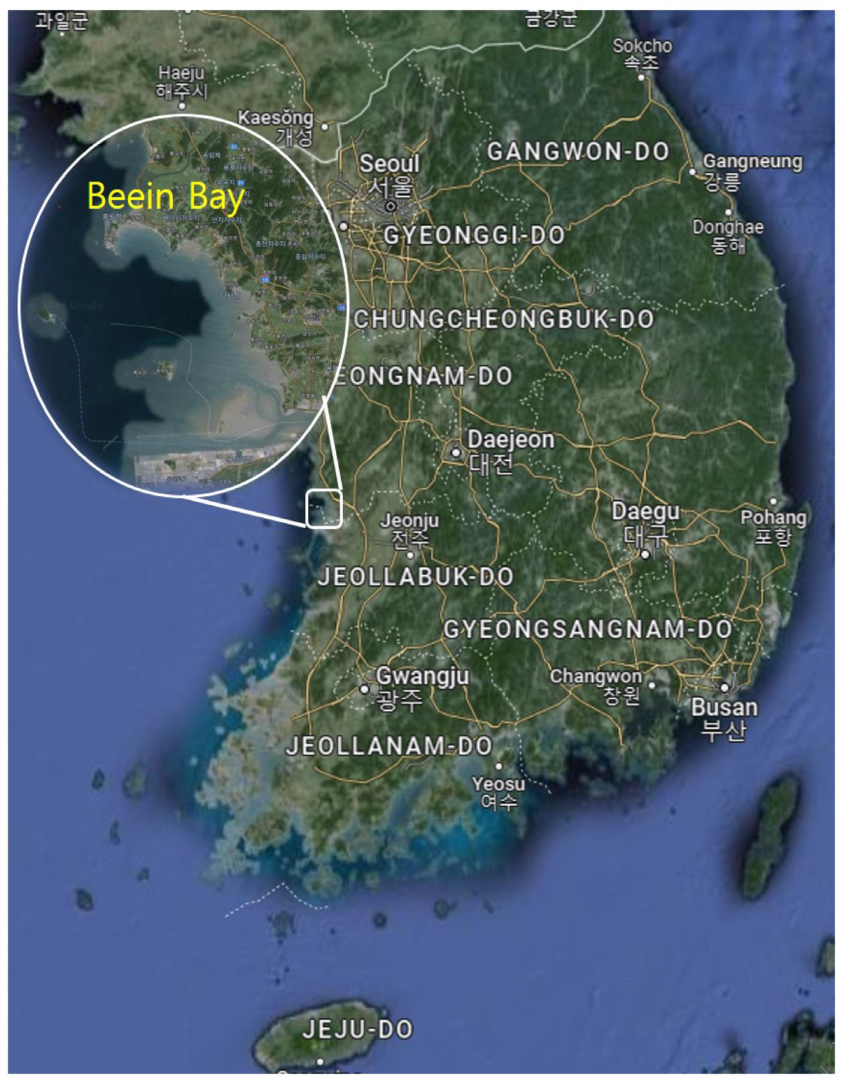
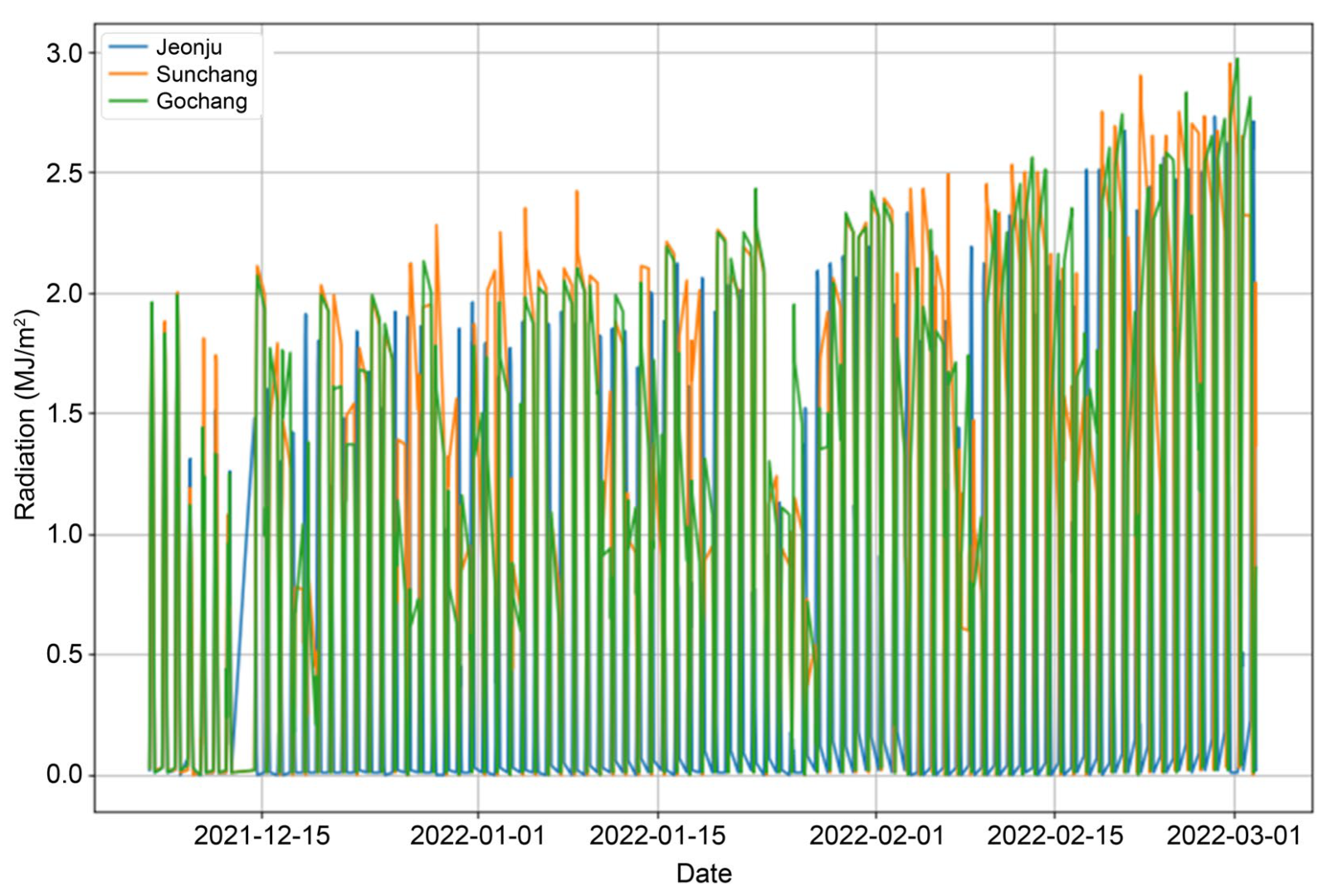
2.2. Study Site and Environmental Forcing
2.3. Core Equations and Parameterization
2.4. Numerical Scheme
2.5. Flux Diagnostics and Growth Limitation Analysis
3. Research Results
3.1. Numerical Stability Assessment
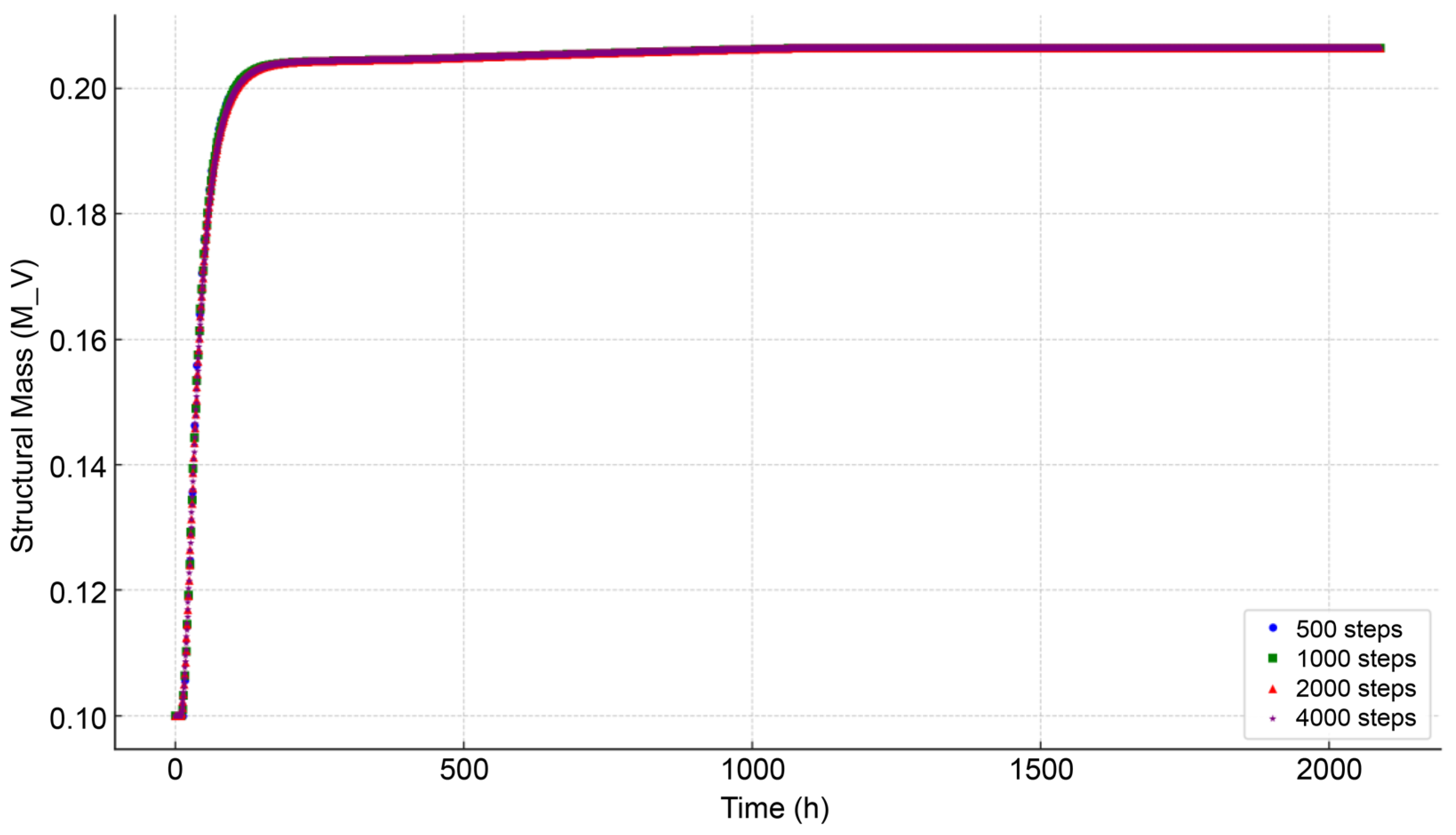
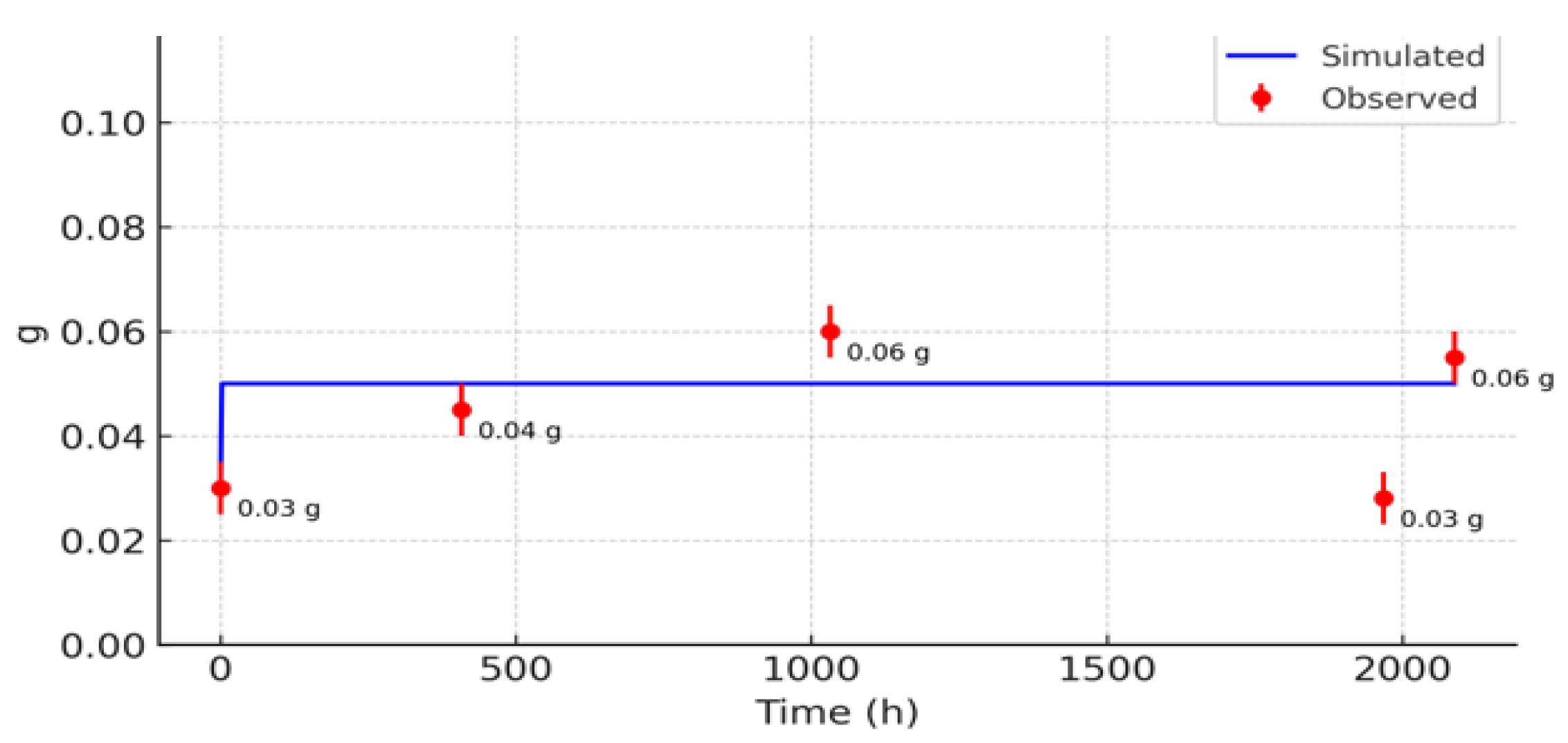
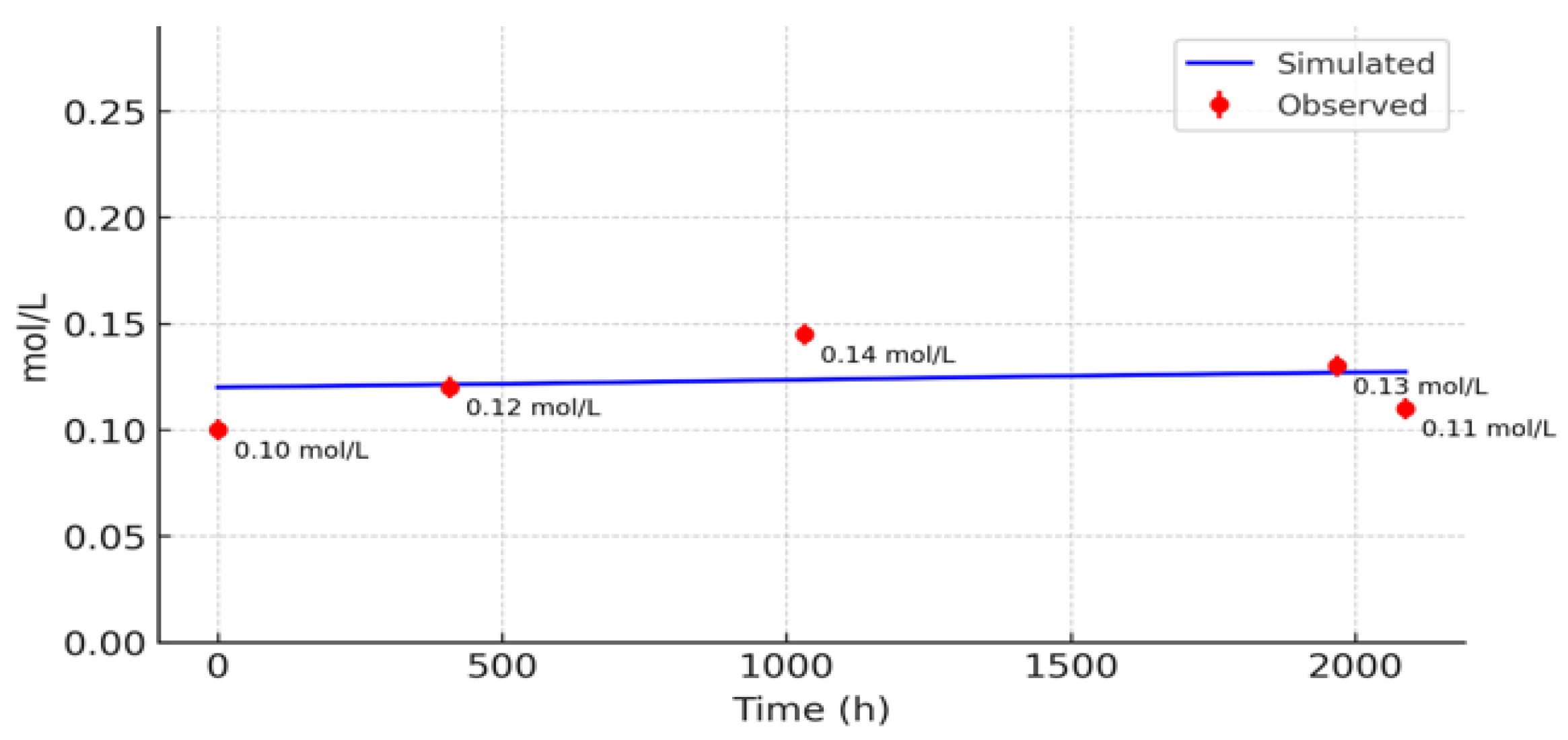
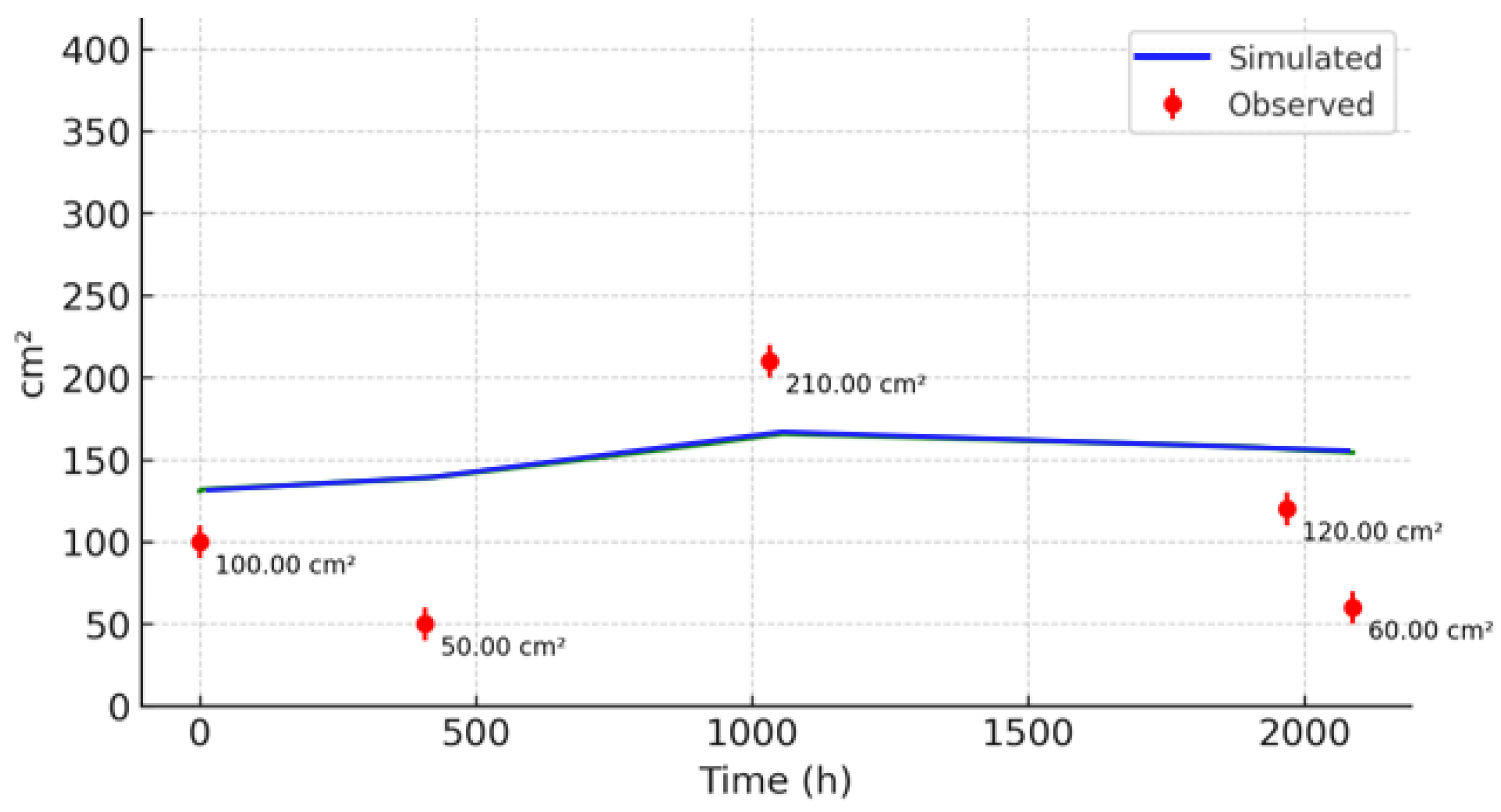
3.2. Comparison with Observed Data



3.3. Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEB | Dynamic Energy Budget |
| IMTA | Integrated multi-trophic aquaculture |
| RMSE | Root-mean-square error |
| SU | Synthesizing unit |
References
- FAO. The State of World Fisheries and Aquaculture 2022. In Towards Blue Transformation; Food and Agriculture Organization of the United Nations: Rome, Italy, 2022. [Google Scholar]
- Duarte, P.; Ferreira, J.G. A model for the simulation of macroalgal population dynamics and productivity. Ecol. Model. 1997, 98, 199–214. [Google Scholar] [CrossRef]
- Krause-Jensen, D.; Duarte, C.M. Substantial role of macroalgae in marine carbon sequestration. Nat. Geosci. 2016, 9, 737–742. [Google Scholar] [CrossRef]
- Alleway, H.K.; Gillies, C.L.; Bishop, M.J.; Gentry, R.R.; Theuerkauf, S.J.; Jones, R. The ecosystem services of marine aquaculture: Valuing benefits to people and nature. BioScience 2019, 69, 59–68. [Google Scholar] [CrossRef]
- Gentry, R.R.; Lester, S.E.; Kappel, C.V.; Bell, T.W.; Stevens, J.; Gains, S.D. Exploring the potential for marine aquaculture to contribute to ecosystem services. Rev. Aquacult. 2019, 12, 499–512. [Google Scholar] [CrossRef]
- Froehlich, H.E.; Afflerbach, J.C.; Frazier, M.; Halpern, B.S. Blue growth potential to mitigate climate change through seaweed offsetting. Nat. Geosci. 2019, 12, 998–1000. [Google Scholar] [CrossRef]
- Ministry of Oceans and Fisheries. Korean Statistical Yearbook of Oceans and Fisheries; Ministry of Oceans and Fisheries: Sejong, Republic of Korea, 2023. [Google Scholar]
- Buschmann, A.H.; Camus, C.; Infante, J.; Neori, A.; Israel, Á.; Hernández-González, M.C.; Pereda, S.V.; Gomez-Pinchetti, J.L.; Golberg, A.; Tadmor-Shalev, N.; et al. Seaweed production: Overview of the global state of exploitation, farming and emerging research activity. Eur. J. Phycol. 2017, 52, 391–406. [Google Scholar] [CrossRef]
- Kim, J.K.; Yarish, C.; Hwang, E.K.; Park, M.; Kim, Y. Seaweed aquaculture: Cultivation technology, challenges and its ecosystem services. Algae 2017, 32, 1–13. [Google Scholar] [CrossRef]
- Kim, J.K.; Kraemer, G.P.; Neefus, C.D.; Chung, I.K.; Yarish, C. Effects of temperature and ammonium on growth, pigment production and nitrogen uptake by four species of Porphyra (Bangiales, Rhodophyta) native to the New England coast. J. Appl. Phycol. 2007, 19, 431–440. [Google Scholar] [CrossRef]
- Sohn, C.H.; Kim, J.H.; Lee, Y.S. Seasonal nitrogen dynamics and their effects on Porphyra spp. productivity in Korean coastal waters. Algae 2019, 34, 211–224. [Google Scholar]
- Harrison, P.J.; Hurd, C.L. Nutrient physiology of seaweeds: Application to aquaculture. Cah. Biol. Mar. 2001, 42, 71–82. [Google Scholar]
- Chen, X.; Yang, B.; Du, X.; Li, Q.; Li, Z.; Yang, Y.; Jiang, Z.; Zhu, Y.; Ni, H.; Miao, X. Rapid prediction of Porphyra photosynthetic pigments based on colorimetric parameters. Front. Sustain. Food Syst. 2025, 9, 1553250. [Google Scholar] [CrossRef]
- Zhang, W.; Pan, M.; Wang, P.; Xue, J.; Zhou, X.; Sun, W.; Hu, Y.; Shen, Z. Comparative analysis of XGB, CNN, and ResNet models for predicting moisture content in Porphyra yezoensis using near-infrared spectroscopy. Foods 2024, 13, 3023. [Google Scholar] [CrossRef]
- Soto, D.; Aguilar-Manjarrez, J.; Hishamunda, N. (Eds.) Building an Ecosystem Approach to Aquaculture. Proceedings of the FAO/Universitat de les Illes Balears Expert Workshop, Palma de Mallorca, Spain, 7–11 May 2007; FAO Fisheries and Aquaculture Proceeding No. 14; Food Agriculture Organization of the United Nations: Rome, Italy, 2008. [Google Scholar]
- Grant, J.; Bacher, C.; Cranford, P.J.; Guyondet, T.; Carreau, M. A spatially explicit ecosystem model of seston depletion in dense mussel culture. J. Mar. Syst. 2008, 73, 155–168. [Google Scholar] [CrossRef]
- Petrell, R.J.; Tabrizi, K.M.; Harrison, P.J.; Druehl, L.D. Mathematical model of Laminaria production near salmon farm. J. Appl. Phycol. 1993, 5, 1–14. [Google Scholar] [CrossRef]
- Kooijman, S.A.L.M. Dynamic Energy Budget Theory for Metabolic Organisation; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Lika, K.; Kearney, M.R.; Kooijman, S.A.L.M. The covariation method for estimating DEB model parameters I: Philosophy. J. Sea Res. 2011, 66, 270–277. [Google Scholar] [CrossRef]
- van der Meer, J. An introduction to dynamic energy budget (DEB) models with special emphasis on parameter estimation. J. Sea Res. 2006, 56, 85–102. [Google Scholar] [CrossRef]
- Pu, T.; Keretz, S.S.; Elgin, A.K.; Godwin, C.J.; Rowe, M.D.; Carrick, H.J.; Glyshaw, P.W.; Pietscher, R.M.; Vanderploeg, H.A. Dynamic energy budget (DEB) parameter estimation for the globally invasive Quagga Mussel (Dreissena rostriformis bugensis). Ecol. Model. 2025, 505, 111100. [Google Scholar] [CrossRef]
- Lanjouw, M.; Jansen, H.M.; van der Meer, J. Exploring aquaculture related traits of the grooved carpet shell (Ruditapes decussatus) in relation to other bivalve species using Dynamic Energy Budget theory. Ecol. Model. 2024, 498, 110883. [Google Scholar] [CrossRef]
- Venolia, C.T.; Lavaud, R.; Green-Gavrielidis, L.A.; Thornber, C.; Humphries, A.T. Modeling the growth of sugar kelp (Saccharina latissima) using DEB theory. Ecol. Modell. 2020, 430, 109151. [Google Scholar] [CrossRef]
- Lavaud, R.; Filgueira, R.; Nadeau, A.; Steeves, L.; Guyondet, T. A dynamic energy budget model for the macroalga Ulva lactuca. Ecol. Modell. 2020, 418, 108922. [Google Scholar] [CrossRef]
- Filgueira, R.; Grant, J.; Strand, Ø. A comparison of shellfish carrying capacity determination tools: A case study in Sungo Bay, China. Aquaculture 2014, 434, 484–494. [Google Scholar]
- Axelsson, L.; Mercado, J.; Figueroa, F. Utilization of HCO3− at high pH by the brown macroalga Laminaria saccharina. Eur. J. Phycol. 2000, 35, 53–59. [Google Scholar] [CrossRef]
- Ahn, O.; Petrell, R.J.; Harrison, P.J. Ammonium and nitrate uptake by Laminaria saccharina and Nereocystis luetkeana originating from a salmon sea cage farm. J. Appl. Phycol. 1998, 10, 333–340. [Google Scholar] [CrossRef]
- Bolton, J.J.; Lüning, K. Optimal growth and maximal survival temperatures of Atlantic Laminaria species in culture. Mar. Biol. 1982, 66, 89–94. [Google Scholar] [CrossRef]
- Boden, G.T. The effect of depth on summer growth of Laminaria saccharina (Phaeophyta). Phycologia 1979, 18, 405–408. [Google Scholar] [CrossRef]
- MOF; NIFS; GIST; KIOST. National Report on the Carbon Absorption and Ecosystem Services of Seaweed Farming in Korea; Ministry of Oceans and Fisheries: Busan, Republic of Korea, 2021. (In Korean) [Google Scholar]
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving differential equations in R: deSolve package. J. Stat. Softw. 2010, 33, 1–25. [Google Scholar] [CrossRef]
- Brown, M.T.; Nyman, M.A.; Keogh, J.A.; Chin, N.K.M. Seasonal growth of the giant kelp Macrocystis pyrifera in New Zealand. Mar. Biol. 1997, 129, 417–424. [Google Scholar] [CrossRef]
- Bell, L.E.; Kroeker, K.J. Standing crop, turnover, and production dynamics of Macrocystis pyrifera and understory species in high-latitude giant kelp forests. J. Phycol. 2022, 58, 773–788. [Google Scholar] [CrossRef]
- Handa, A.; Forbord, S.; Wang, X.; Broch, O.J.; Dahle, S.W.; Størseth, T.R.; Reitan, K.I.; Olsen, Y.; Skjermo, J. Seasonal- and depth-dependent growth of Saccharina latissima near salmon aquaculture. Aquaculture 2013, 414, 191–201. [Google Scholar] [CrossRef]
- Johansson, G.; Snoeijs, P. Macroalgal photosynthetic responses to light in relation to thallus morphology and depth zonation. Mar. Ecol. Prog. Ser. 2002, 244, 63–72. [Google Scholar] [CrossRef]
- Broch, O.J.; Slagstad, D. Modelling seasonal growth and composition of the kelp Saccharina latissima. J. Appl. Phycol. 2012, 24, 759–776. [Google Scholar] [CrossRef]
- Heinrich, S.; Valentin, K.; Frickenhaus, S.; John, U.; Wiencke, C. Transcriptomic analysis of acclimation to temperature and light stress in Saccharina latissima (Phaeophyceae). PLoS ONE 2012, 7, e44342. [Google Scholar] [CrossRef]
- van Oort, P.A.J.; Verhagen, A.; van der Werf, A.K. Can seaweeds feed the world? Modelling global offshore seaweed production potential. Ecol. Model. 2023, 484, 110486. [Google Scholar] [CrossRef]
- Brady-Campbell, M.M.; Campbell, D.B.; Harlin, M.M. Productivity of kelp (Laminaria spp.) near the southern limit in the NW Atlantic. Mar. Ecol. Prog. Ser. 1984, 18, 79–88. [Google Scholar] [CrossRef]
- Gerard, V.A. Ecotypic differentiation in light-related traits of the kelp Macrocystis pyrifera. Mar. Biol. 1988, 97, 25–36. [Google Scholar] [CrossRef]

| Environmental Data | Value | Unit |
|---|---|---|
| Temperature | 8.3–9.2 | °C |
| Salinity | 28.9–31.7 | PSU |
| DIN | 1.67–11.19 | µM |
| DIP | 0.05–0.79 | µM |
| Light intensity | 0.952–1.4 | μmol m−2 s−1 |
| Rainfall | 0 | mm |
| Growth rate | 0.405–1.206 | d−1 |
| Blade area | 31.3–199.7 | m2 |
| Biomass | 0.071–0.2 | g |
| Carbon content | 0.026–0.05 | G |
| Nitrogen content | 0.002–0.008 | g |
| C/N ratio | 6.57–16.88 | - |
| Chlorophyll | 0.54–3.21 | µg L−1 |
| Primary production | 0.12–2500 | µgC L−1 h−1 |
| CO2 | 0.119–1.5 | µM |
| NO3 | 0.02–0.143 | µM |
| Parameter | Description | Value | Unit | Source |
|---|---|---|---|---|
| j_E_Cm | Max specific carbon assimilation rate | 0.002 | mol L−1 h−1 | This study |
| j_EN_Am | Max specific nitrogen assimilation rate | 0.00015 | mol L−1 h−1 | This study |
| K_N | Half-saturation constant for NO3− uptake | 0.8 | mol L−1 | This study |
| j_CO2_m | Max CO2 uptake rate | 0.102 | mol L−1 h−1 | Calibrated |
| K_max | Max carrying capacity | 1 | g | This study |
| max_blade_area | Max blade area | 100 | cm2 | This study |
| max_m_Ei | Max reserve mass | 0.08 | g | This study |
| K_c | Half-saturation constant for CO2 | 0.0000001 | mol L−1 | [23] |
| ρ_PSU | Photosynthetic unit density | 0.5 | - | [23] |
| b1 | Photon binding probability | 0.5 | - | [23] |
| alpha_K | Light saturation constant | 0.2 | - | This study |
| α_l | Photon cross-section | 1 | m2 mol−1 | [23] |
| k_I | Photosynthate dissociation rate | 0.075 | h−1 | [23] |
| y_IC | Yield of C reserve per photon | 10 | mol C mol−1 photon | [23] |
| y_CO2C | Yield of C reserve per CO2 | 1 | mol C mol−1 CO2 | [23] |
| y_IO2 | Yield of O2 per photon | 0.125 | mol O2 mol−1 photon | [23] |
| kappa | Fraction of mobilized energy to soma | 0.2 | - | This study |
| k_EN | N reserve turnover rate | 0.05 | h−1 | This study |
| k_EC | C reserve turnover rate | 0.1 | h−1 | This study |
| k_M | Maintenance rate coefficient | 0.02 | h−1 | [18] |
| j_E_VM | Volume-specific maintenance (N) | 0.000004 | mol L−1 h−1 | [23] |
| j_E_CM | Volume-specific maintenance (C) | 0.05 | mol L−1 h−1 | [23] |
| y_EV | Yield of N reserve to structure | 0.06 | mol N mol−1 V | [23] |
| y_EC_V | Yield of C reserve to structure | 0.5 | mol C mol−1 V | [23] |
| κ_Ei | Fraction of rejection flux to reserve | 1 | - | [23] |
| T_A | Arrhenius temperature | 6000 | K | [18] |
| T_0 | Reference temperature | 278.15 | K | [18] |
| T_H | Upper boundary of tolerance | 288.15 | K | This study |
| T_L | Lower boundary of tolerance | 275.15 | K | This study |
| T_AH | Arrhenius temp above T_H | 15,000 | K | [18] |
| T_AL | Arrhenius temp below T_L | 4391.9 | K | [18] |
| w_V | Molar weight of structure | 29.89 | g mol−1 | [18] |
| w_EC | Molar weight of C reserve | 54 | g mol−1 | [18] |
| w_EN | Molar weight of N reserve | 17 | g mol−1 | [18] |
| w_O2 | Molar weight of O2 | 32 | g mol−1 | [18] |
| K_decay | Decay coefficient (exp model) | 0.3 | - | Calibrated |
| T_decay | Temp stress threshold | 0.01 | - | Calibrated |
| I_decay | Light stress threshold | 0.001 | - | Calibrated |
| decay_coeff | Overall decay rate | 0.12 | - | Calibrated |
| Time Step Count | RMSE (vs. 4000 Step) |
|---|---|
| 500 | 5.29 × 10−4 |
| 1000 | 2.14 × 10−4 |
| 2000 | 6.96 × 10−5 |
| 4000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tac, D.H.; Park, S.E.; Lee, J.Y. Estimation of Growth and Carrying Capacity of Porphyra spp. Under Aquaculture Conditions on the Southern Coast of Korea Using Dynamic Energy Budget (DEB). J. Mar. Sci. Eng. 2025, 13, 1586. https://doi.org/10.3390/jmse13081586
Tac DH, Park SE, Lee JY. Estimation of Growth and Carrying Capacity of Porphyra spp. Under Aquaculture Conditions on the Southern Coast of Korea Using Dynamic Energy Budget (DEB). Journal of Marine Science and Engineering. 2025; 13(8):1586. https://doi.org/10.3390/jmse13081586
Chicago/Turabian StyleTac, Dae Ho, Sung Eun Park, and Ji Young Lee. 2025. "Estimation of Growth and Carrying Capacity of Porphyra spp. Under Aquaculture Conditions on the Southern Coast of Korea Using Dynamic Energy Budget (DEB)" Journal of Marine Science and Engineering 13, no. 8: 1586. https://doi.org/10.3390/jmse13081586
APA StyleTac, D. H., Park, S. E., & Lee, J. Y. (2025). Estimation of Growth and Carrying Capacity of Porphyra spp. Under Aquaculture Conditions on the Southern Coast of Korea Using Dynamic Energy Budget (DEB). Journal of Marine Science and Engineering, 13(8), 1586. https://doi.org/10.3390/jmse13081586







