Multi-Agent Reinforcement Learning-Based Cooperative Encirclement Control of Autonomous Surface Vehicles Against Multiple Targets

Abstract

Autonomous surface vehicles (ASVs) have been widely applied in ocean engineering due to their small size, low cost, and high mobility. However, more relevant encirclement control methods with many-to-one are simple and do not consider the system dynamics. This article proposes a cooperative encirclement control method for ASVs against multiple targets based on multi-agent reinforcement learning. Firstly, a dynamic target allocation algorithm is designed based on location information of both vehicles and targets, enabling vehicles to select encirclement targets in real-time according to relative distances. Subsequently, the whole encirclement process is divided into multiple stages, and a multi-stage reward function is developed based on curriculum learning to guide ASVs in completing encirclement tasks progressively, from simpler to more complex scenarios. Then, the actor and critic networks incorporating long short-term memory are constructed, respectively, and a multi-agent soft actor-critic reinforcement learning algorithm is employed to train ASVs, enhancing cooperative target encirclement maneuvers. Finally, the effectiveness and superiority of the proposed method is validated through a six-on-two encirclement simulation.

1. Introduction

In recent years, autonomous surface vehicles (ASVs) have garnered unprecedented attention and experienced rapid development in both military and civilian domains [1,2]. With the continuous advancement of vehicle intelligence, the operation and application of ASVs has expanded from safe environments focused on reconnaissance and surveillance to complex scenarios involving combat and confrontation [3,4]. Target encirclement represents a crucial research direction in cooperative control of multi-ASVs, where non-cooperative targets are enclosed within a specific circular domain, thereby diminishing their threat capabilities [5,6]. However, the targets in real-world scenarios are not stationary, such as pollutant spills, illegal fishing, or autonomous interdiction, which can move and disperse [7]. Sequential encirclement of such targets is frequently ineffective and prone to uncontrolled spreading or escape, leading to excessive duration and mission failure. Therefore, the study of cooperative encirclement for ASVs against multiple targets has significant practical value.

Existing target encirclement control methods can be broadly categorized into three approaches: bio-inspired encirclement [8], differential game-based encirclement [9], and reinforcement learning-based encirclement [10]. To be specific, bio-inspired approaches primarily mimic the dynamic interactions observed between predators and prey in nature. For example, Ref. [11] simulates the cooperative behaviors of biological groups to design a bio-inspired distributed encirclement controller, achieving efficient encirclement for non-cooperative targets. Ref. [12] develops a switching encirclement control strategy using animal group behavior. Ref. [13] designs a bio-inspired optimization algorithm based on orca predation behavior, simulating orcas’ search, encirclement, and attack behaviors. By combining with agent position-based area partitioning and bio-inspired neural networks, Ref. [14] proposes a cooperative encirclement method using an improved crayfish optimization algorithm. However, these methods exhibit limited adaptability to complex environments, and abrupt changes in target behavior often render the system incapable of adjusting the encirclement strategy effectively.

Differential game-based methods construct pursuit-evasion models and derive optimal encirclement strategies by solving Hamilton–Jacobi equations [15,16]. For example, Ref. [17] constructs a cooperative encirclement framework based on differential games, analytically solving via Hamilton–Jacobi–Isaacs equations. Ref. [18] proposes a hybrid differential game-based encirclement guidance method, enabling pursuit-evasion missions under static obstacle constraints. Ref. [19] develops a pursuit-evasion matching framework through global game decomposition. Ref. [20] designs a cooperative control method based on stochastic potential games and multi-agent reinforcement learning that estimates Nash equilibrium strategies using temporal relative motion information. However, as the size of the agent group increases, these methods require extensive assumptions and rules, making them less feasible for real-time control in large-scale scenarios.

Due to the rapid advancement of artificial intelligence technology, deep reinforcement learning has been extensively applied in decision-making, control, and optimization [21,22]. Reinforcement learning-based encirclement methods can optimize encirclement strategies through agent–environment interactions, effectively handling high-dimensional state spaces and demonstrating strong adaptability in complex environments [23,24]. For example, Ref. [25] balances individual and collective benefits through knowledge-embedded encirclement rewards. Ref. [26] establishes an obstacle-assisted cooperative encirclement method based on multi-agent reinforcement learning. Ref. [27] conducts decentralized encirclement training via curriculum learning. Ref. [28] utilizes a centralized training-decentralized execution framework to solve the pursuit evasion problem. Ref. [29] proposes a reinforcement learning-based adaptive encirclement control method under an obstacle environment. Ref. [30] uses virtual barriers and curriculum learning techniques during the training process, improving the generalization capabilities and convergence speed of the capture policy for limited perception ASVs. However, the reward functions employed in these approaches often lead to insufficient learning motivation for individual agents. Some agents may exploit collective rewards and cease optimizing the encirclement strategies, thereby prolonging the training process. Note that most existing studies focus on single-target encirclement, with limited attention paid to multi-target cooperative encirclement scenarios.

Motivated by these research gaps, this article investigates the cooperative encirclement problem for ASVs against multi-targets based on multi-agent reinforcement learning (MARL). By integrating dynamic target allocation and multi-stage reward guidance, the method utilizes a MARL framework to train ASVs for cooperative target encirclement. Simulation results with six-on-two game demonstrate that the encirclement performance of our proposed control method significantly outperforms existing control methods. Main contributions are as follows: (1) A dynamic target allocation algorithm based on proximity principles and encirclement distance is developed to optimize the target selection process for ASVs. (2) A curriculum learning-inspired multi-stage reward function is designed, including search, besiege, and capture, increasing the success rate of target encirclement. (3) A cooperative control solution is proposed by employing a multi-agent soft actor-critic reinforcement learning framework with long short-term memory networks, resulting in more efficient and stable ASV encirclement maneuvers.

The rest of this article is composed of the following sections. Section 2 formulates the encirclement problem of ASVs against multiple targets. The dynamic target assignment, cooperative encirclement reward, and reinforcement learning control are presented in Section 3. Section 4 verifies the performance of the designed control method by simulations. Finally, Section 5 concludes this article.

Notations: Throughout this article, $‖\cdot ‖$ denotes the Euclidean norm of a vector. $t$ denotes the time step. $\mathbb{E}$ denotes the mathematical expectation. $\odot$ denotes the Hadamard product and $\nabla$ denotes the gradient operator.

2. Problem Statement

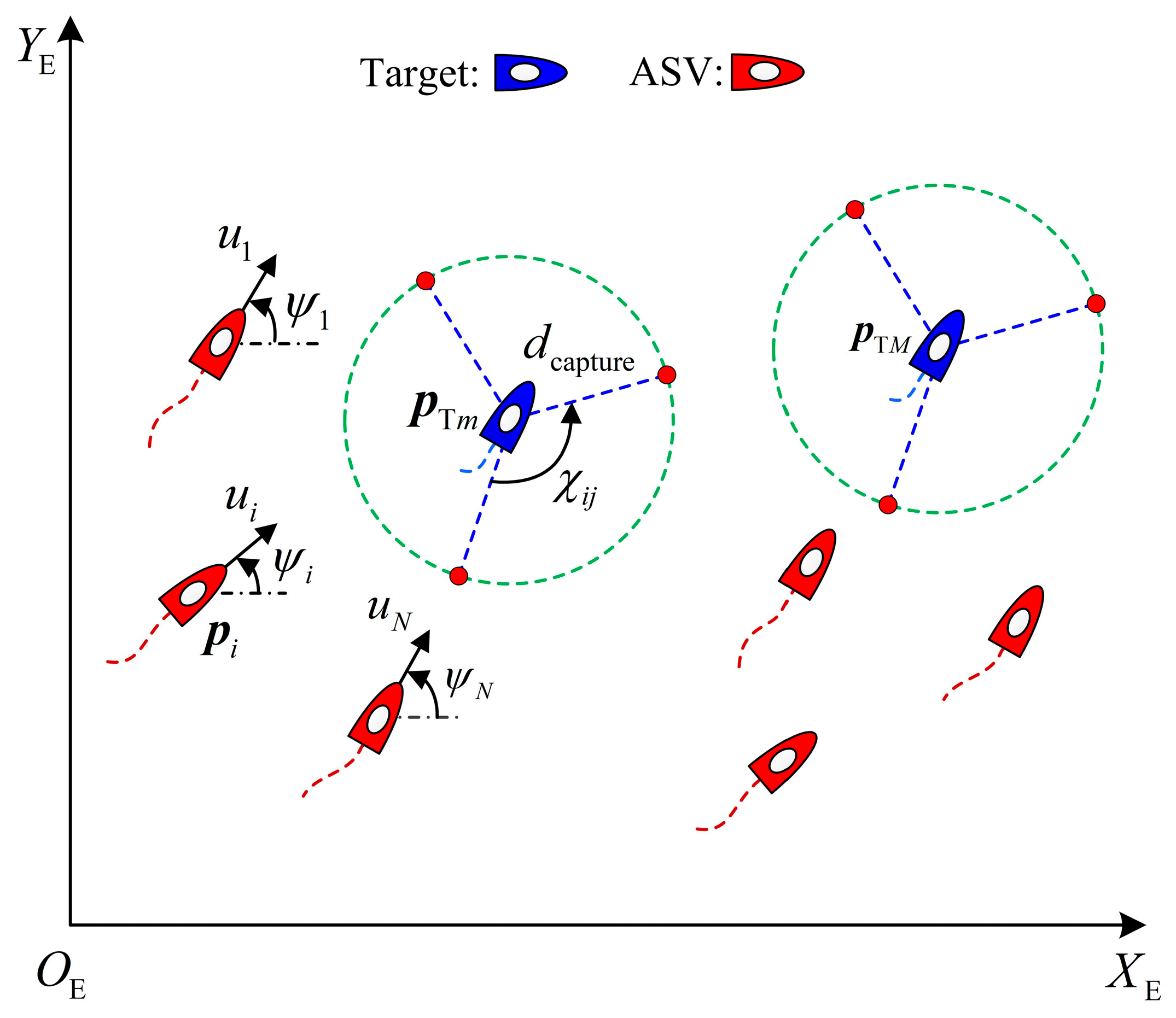
As shown in Figure 1, consider multiple high-speed ASVs and multiple low-speed targets in the horizontal plane. ${\mathit{p}}_i={[x_i,y_i]}^T$ denotes the position of the $i\mathrm{th}$ ASV with $i=1,2,\cdot \cdot \cdot ,N$. ${\mathit{p}}_{\mathrm{T}m}={[x_{\mathrm{T}m},y_{\mathrm{T}m}]}^T$ denotes the position of the $m\mathrm{th}$ target with $m=1,2,\cdot \cdot \cdot ,M$. $d_{\mathrm{capture}}$ denotes the encirclement radius. ${\chi }_{ij}$ denotes encirclement angles formed by adjacent ASVs.

According to Ref. [31], the kinematic and kinetic equation of the $i\mathrm{th}$ ASV can be expressed as

$$\left\{\begin{array}{l}{\dot{\mathit{\eta }}}_i=\mathit{R}({\psi }_i){\mathit{\nu }}_i\\ \mathit{M}{\dot{\mathit{\nu }}}_i=\mathit{f}({\mathit{\nu }}_i)+{\mathit{\tau }}_i+{\mathit{\tau }}_{wi}\end{array}\right.$$

(1)

where ${\mathit{\eta }}_i={[x_i,y_i,{\psi }_i]}^T$ denotes the position and heading angle information of the ASV in the earth-fixed frame. ${\mathit{\nu }}_i={[u_i,v_i,r_i]}^T$ denotes the surge, sway and yaw velocities of the ASV in the body-fixed frame. ${\mathit{\tau }}_i={[{\tau }_{ui},0,{\tau }_{ri}]}^T$ denotes the input of the ASV including surge forces and yaw moments. ${\mathit{\tau }}_{wi}={[{\tau }_{wui},{\tau }_{wvi},{\tau }_{wri}]}^T$ denotes the time-varying environmental disturbances. $\mathit{R}({\psi }_i)$ denotes the rotation matrix from the body-fixed frame to the earth-fixed frame, which can be written as

$$\mathit{R}({\psi }_i)=\left[\begin{array}{ccc}\cos {\psi }_i& -\sin {\psi }_i& 0\\ \sin {\psi }_i& \cos {\psi }_i& 0\\ 0& 0& 1\end{array}\right]$$

(2)

while the inertial matrix $\mathit{M}=\mathrm{diag}\left(m_{ui},m_{vi},m_{ri}\right)$, the nominal dynamics $\mathit{f}({\mathit{\nu }}_i)={[f_{ui},f_{vi},f_{ri}]}^T$, $f_{ui}=m_{vi}{v}_i{r}_i-d_{ui}{u}_i$, $f_{vi}=-m_{ui}{u}_i{r}_i-d_{vi}{v}_i$, $f_{ri}=\left(m_{ui}-m_{vi}\right)u_i{v}_i-d_{ri}{r}_i$, $d_{ui}$, $d_{vi}$ and $d_{ri}$ denote the fluid damping. $m_{ui}$, $m_{vi}$ and $m_{ri}$ denote the inertial component on the three degrees of freedom.

In this article, a MARL-based cooperative encirclement control method is constructed for ASVs to guarantee that vehicles are evenly distributed around the targets with desired distances and angles under the premise of safety. To be specific, the control objective can be formalized as

$$\left\{\begin{array}{l}\underset{t\to \infty }{\lim }{d}_{\min }\le ‖{\mathit{p}}_i-{\mathit{p}}_{\mathrm{T}m}‖\le d_{\mathrm{capture}},i\in {\mathcal{D}}_m\\ \underset{t\to \infty }{\lim }\left|{\chi }_{ij}-{\chi }_{\mathrm{d}}\right|\le {\chi }_0,i,j\in {\mathcal{D}}_m,i\ne j\end{array}\right.$$

(3)

where ${\mathcal{D}}_m$ denotes the encirclement alliance for the $m\mathrm{th}$ target. $d_{\min }$ denotes the minimum distance between the ASV and the target. ${\chi }_{\mathrm{d}}=2\pi /K$ denotes the desired encirclement angle with $K$ being the number of one alliance. ${\chi }_0$ is a small positive constant.

Remark 1. 

In this paper, the encirclement mission of ASVs is not subject to geographical boundary constraints. To guarantee the existence of a feasible solution, we focus exclusively on high-speed ASVs and low-speed targets. Moreover, considering the minimum number of nodes required for a closed loop in the two-dimensional plane, there exists $N\ge 3M$.

Remark 2. 

By virtue of artificial potential field method, the maneuvering strategy of targets based on position information is generated by

$${\mathit{v}}_{\mathrm{T}m}={\displaystyle \sum _{i=1}^N\left(\frac{k_{\mathrm{a}}\left({\mathit{p}}_{\mathrm{T}m}-{\mathit{p}}_i\right)}{‖{\mathit{p}}_i-{\mathit{p}}_{\mathrm{T}m}‖}\right)}$$

(4)

where $k_{\mathrm{a}}>0$.

3. Reinforcement Learning-Based Cooperative Encirclement Control

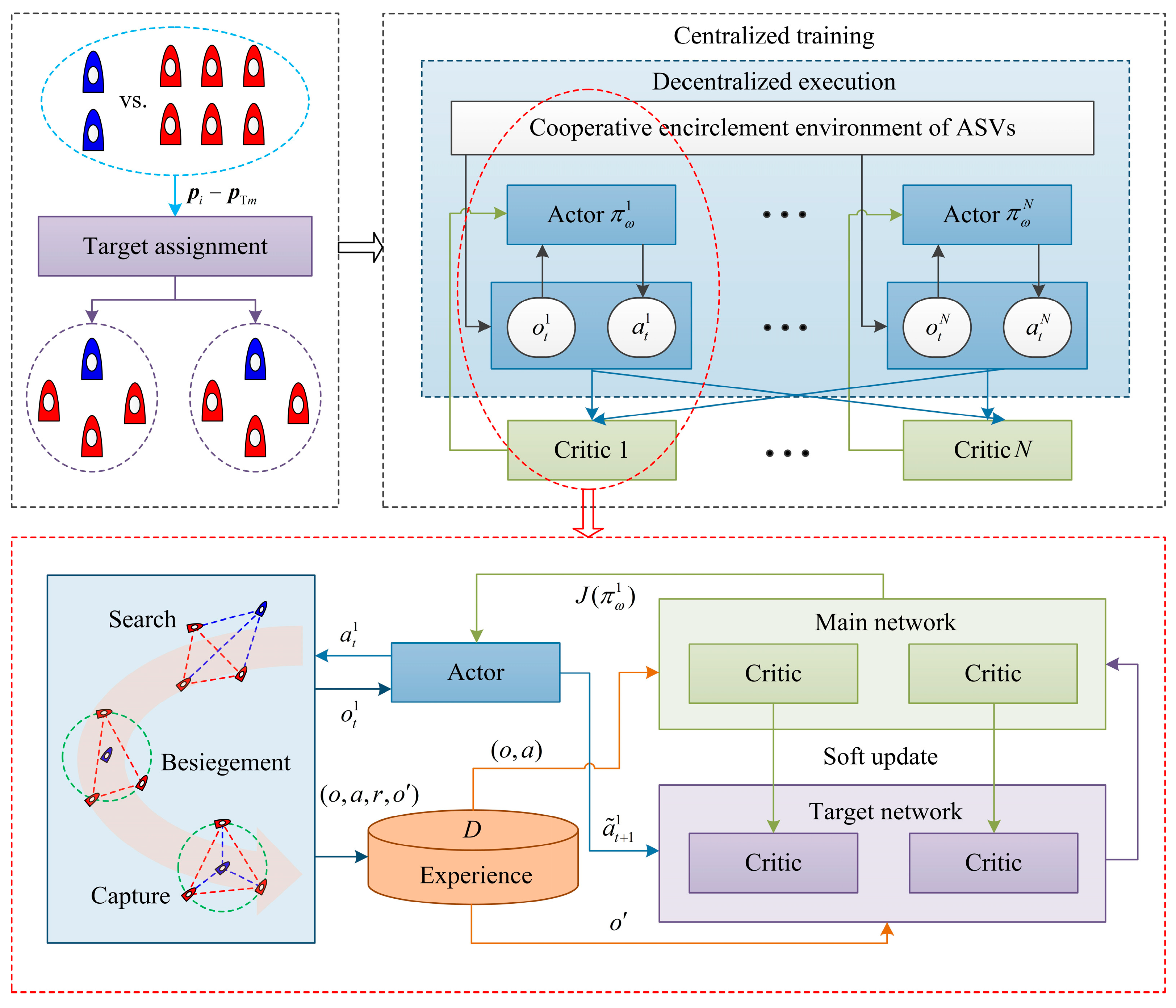
This section presents the proposed cooperative encirclement control design. The entire control architecture is illustrated in Figure 2, which includes dynamic target assignment, cooperative encirclement reward and reinforcement learning control modules. To be specific, the assignment module is used to assign targets to the ASVs based on the shortest encirclement distance. The cooperative encirclement reward module is responsible for guiding ASVs to approach and capture the assigned targets. The multi-agent soft actor-critic reinforcement learning module is used to train ASVs with unknown dynamics, optimizing encirclement performance through agent–environment interactions.

3.1. Dynamic Target Assignment

In this part, a dynamic task allocation algorithm is designed using the total encirclement distance. To obtain the minimal encirclement distance at any time, the position-based objective function is designed as

$$J_{\mathrm{allocat}}=-{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{m=1}^M‖{\mathit{p}}_i-{\mathit{p}}_{\mathrm{T}m}‖{\mathit{H}}_{im}}}$$

(5)

with ${\mathit{H}}_{im}$ satisfying

$$\left\{\begin{array}{l}{\displaystyle \sum _{i=1}^N{\mathit{H}}_{im}\ge K,m=1,\dots ,M}\\ {\displaystyle \sum _{m=1}^M{\mathit{H}}_{im}=1,i=1,\dots ,N}\end{array}\right.$$

(6)

Note that in the cooperative encirclement process, each ASV can choose one target to encircle, while each target requires at least $K$ vehicles to form an effective encirclement. If the ASV is matched with a target, then ${\mathit{H}}_{im}=1$. Otherwise, ${\mathit{H}}_{im}=0$.

The optimal assignment between ASVs and targets at each time step is obtained by solving the maximization of Equation (5). The dynamic task allocation is presented in Algorithm 1, where ${\mathit{H}}^k(k=1,2,\dots ,K)$ denotes assignment matrices that satisfy Equation (6).

Algorithm 1: Target allocation for cooperative encirclement.

Inputs: Target position ${\mathit{p}}_{\mathrm{T}m}$, ASV position ${\mathit{p}}_i$, the number of ASVs/targets $N$ and $M$. Initialization: Optimal allocation relation matrix ${\mathit{H}}_{\mathrm{d}}\leftarrow N\mathrm{one}$, extreme value $J^{\ast }\leftarrow -\infty$. 1:  Calculating the Euclidean distance between ASVs and targets. 2:  for $k=1,2,\dots ,K$ do 3:   $\mathbf{if}{J}^{\ast }<J_{\mathrm{allocat}}({\mathit{H}}^k)$ 4:    $J^{\ast }=J_{\mathrm{allocat}}({\mathit{H}}^k)$ 5:    ${\mathit{H}}_{\mathrm{d}}={\mathit{H}}^k$ 6:   end if 7:  end for Outputs: Optimal allocation relation matrix ${\mathit{H}}_{\mathrm{d}}$.

3.2. Cooperative Encirclement Reward

In this part, to overcome the learning inefficiency caused by sparse rewards, a curriculum learning-based encirclement reward function is developed for one alliance, which divides the whole process into three stages: search, besiegement, and capture, progressively enhancing the cooperative encirclement capability of ASVs.

To be specific, the condition of the search stage is defined as

$${\displaystyle \sum _{i=1}^{N-1}{S}_{{\mathrm{TH}}_i{\mathrm{H}}_{i+1}}}+S_{{\mathrm{TH}}_N{\mathrm{H}}_1}>S_{{\mathrm{H}}_1,\dots ,{\mathrm{H}}_N}$$

(7)

where $S_{(\cdot )}$ denotes the polygonal area formed by connecting all ASVs. The search stage-induced reward is designed as

$$r_{\mathrm{search}}^i=-k_0\left({\displaystyle \sum _{i=1}^{N-1}{S}_{{\mathrm{TH}}_i{\mathrm{H}}_{i+1}}}+S_{{\mathrm{TH}}_N{\mathrm{H}}_1}-S_{{\mathrm{H}}_1,\dots ,{\mathrm{H}}_N}\right)+{\displaystyle \sum _{i=1}^N\left(d_{\mathrm{T}i}(t-1)-d_{\mathrm{T}i}(t)\right)}$$

(8)

where $k_0>0$.

The condition of the besiegement stage is defined as

$$d_{ij}\le k_1\left(d_{\mathrm{T}i}+d_{\mathrm{T}j}\right)$$

(9)

where $0<k_1<1$, $d_{ij}$ denotes the Euclidean distance between two vehicles. The besiegement stage-induced reward is designed as

$$r_{\mathrm{besieged}}^i=-k_2\left(d_{ij}-k_1\left(d_{\mathrm{T}i}+d_{\mathrm{T}j}\right)\right)+k_3\exp \left(-\left|d_{\mathrm{T}i}-d_{\mathrm{capture}}\right|\right)$$

(10)

where $k_2>0$, $k_3>0$, and $j=i+1$.

The condition of the capture stage is defined as

$$\max d_{\mathrm{T}i}\le d_{\mathrm{capture}}$$

(11)

where $\max$ denotes the maximum value. The capture stage-induced reward is designed as

$$\left\{\begin{array}{l}{r}_{\mathrm{capture}}^i=k_4\exp \left(g({\phi }_i)\right)\\ g({\phi }_i)=-\left({\left({\displaystyle \sum _{i=1}^N\sin \left({\phi }_i\right)}\right)}^2+{\left({\displaystyle \sum _{i=1}^N\cos \left({\phi }_i\right)}\right)}^2\right)\end{array}\right.$$

(12)

where $k_4>0$ and ${\phi }_i=\arctan \left((y_i-y_{\mathrm{T}})/(x_i-x_{\mathrm{T}})\right)$.

By combining rewards Equations (8), (10), and (12), the stage-induced reward of cooperative target encirclement is written as

$$r_{\mathrm{encirclement}}^i=\left\{\begin{array}{l}{r}_{\mathrm{search}}^i,{\displaystyle {\sum }_{i=1}^{N-1}{S}_{{\mathrm{TH}}_i{\mathrm{H}}_{i+1}}}+S_{{\mathrm{TH}}_N{\mathrm{H}}_1}>S_{{\mathrm{H}}_1,\dots ,{\mathrm{H}}_N}\\ r_{\mathrm{besieged}}^i,d_{ij}\le k_1\left(d_{\mathrm{T}i}+d_{\mathrm{T}j}\right)\\ r_{\mathrm{capture}}^i,\max d_{\mathrm{T}i}\le d_{\mathrm{capture}}\end{array}\right.$$

(13)

Moreover, to prevent collision among ASVs, the collision avoidance reward is designed as

$$r_{\mathrm{collision}}^i=-k_5\exp \left(-\min d_{ij}\right)-k_6\exp \left(-d_{\mathrm{T}i}\right)$$

(14)

where $k_5>0$ and $k_6>0$.

Moreover, to reduce the control input chattering, the constraint reward is designed as

$$r_{\mathrm{inputs}}^i=-\left(\left|{\tau }_{ui}(t)-{\tau }_{ui}(t-1)\right|+\left|{\tau }_{ri}(t)-{\tau }_{ri}(t-1)\right|\right)$$

(15)

In this context, the cooperative target encirclement reward function for the $i\mathrm{th}$ ASV at time step $t$ can be computed by

$$r_t^i=r_{\mathrm{encirclement}}^i+r_{\mathrm{inputs}}^i+r_{\mathrm{collision}}^i$$

(16)

3.3. Reinforcement Learning Control

By virtue of centralized training with a decentralized execution framework, a maximum entropy-based multi-agent soft actor-critic algorithm is developed for ASVs against multiple targets. In centralized training, the critic network of each ASV evaluates the global encirclement status by incorporating observations and actions from all vehicles, which can alleviate coordination inefficiencies caused by local observations. In distributed execution, the actor network of each ASV independently executes policy without relying on behavioral information from other vehicles, just utilizing its local observations to execute the encirclement strategy.

Firstly, the observation and action of the $i\mathrm{th}$ ASV is defined as

$$\left\{\begin{array}{l}{\mathit{o}}_t^i=[x_i,y_i,u_i,{\psi }_i,x_{\mathrm{T}1},\dots ,x_{\mathrm{T}m},y_{\mathrm{T}1},\dots ,y_{\mathrm{T}m}]\\ {\mathit{a}}_t^i=[{\tau }_{ui},{\tau }_{ri}]\end{array}\right.$$

(17)

which satisfies ${\tau }_{ui}\in [0,100]$ and ${\tau }_{ri}\in [-25,25]$ according to the maneuverability of ASVs.

The actor network ${\pi }_{\omega }^i$ of the $i\mathrm{th}$ ASV fits the policy function $f_{{\omega }^i}({\mathit{o}}_t^i,\xi )$, whose outputs of are the mean and standard deviation of a Gaussian distribution. The action is sampled by reparameterization

$${\mathit{a}}_t^i=f_{{\omega }^i}({\mathit{o}}_t^i,\xi )=\tanh \left({\vartheta }_{{\omega }^i}({\mathit{o}}_t^i)+{\delta }_{{\omega }^i}({\mathit{o}}_t^i)\odot \xi \right)$$

(18)

where $\xi$ denotes the Gaussian noise, ${\vartheta }_{{\omega }^i}({\mathit{o}}_t^i)$ denotes the mean value, ${\delta }_{{\omega }^i}({\mathit{o}}_t^i)$ denotes the standard deviation and ${\omega }^i$ is the parameter of the actor network for the $i\mathrm{th}$ ASV.

Within the reinforcement learning, the maximum entropy mechanism is adopted, enabling ASVs to enhance the random exploration ability of the policy while maximizing cumulative rewards. Consequently, the objective function of actor networks is designed based on the policy entropy and action value function

$$J({\pi }_{\omega }^i)={\mathbb{E}}_D\left[\underset{k=1,2}{\min }{Q}_{{\theta }_k}^i(\mathit{o},\mathit{a})\right]+{\alpha }_{i}H({\pi }_{\omega }^i(\cdot |{\mathit{o}}_t^i))$$

(19)

where $H({\pi }_{\omega }^i(\cdot |{\mathit{o}}_t^i))=-{\mathbb{E}}_D\log ({\pi }_{\omega }^i({\mathit{a}}_t^i|{\mathit{o}}_t^i))$, $\mathit{o}=\{{\mathit{o}}_t^1,{\mathit{o}}_t^2,\cdots ,{\mathit{o}}_t^N\}$, $\mathit{a}=\{{\mathit{a}}_t^1,{\mathit{a}}_t^2,\cdots ,{\mathit{a}}_t^N\}$. $\underset{k=1,2}{\min }{Q}_{{\theta }_k}^i(\mathit{o},\mathit{a})$ represents the smaller value generated by the two critic networks in the main network, where ${\theta }_k$ represents the parameter of two critic networks. $D$ denotes the experience replay buffer, and each set of experience data is stored in the form of tuple $\left\{\mathit{o},\mathit{a},\mathit{r},{\mathit{o}}^{\prime }\right\}$. $\mathit{r}=\{r_t^1,r_t^2,\cdots ,r_t^N\}$ represents the reward set of all ASVs. ${\mathit{o}}^{\prime }$ denotes the observation information set at the next moment. ${\alpha }_i>0$ denotes the regularization coefficient, which is updated by minimizing the loss function

$$L({\alpha }_i)={\mathbb{E}}_D\left[-{\alpha }_i\log ({\pi }_{\omega }^i({\mathit{a}}_t^i|{\mathit{o}}_t^i))-{\alpha }_i{H}_{\mathrm{d}}\right]$$

(20)

where $H_{\mathrm{d}}$ is the predefined entropy threshold.

The critic network of the $i\mathrm{th}$ ASV evaluates the current encirclement status based on the global observation and action information, which is updated by minimizing the following loss function

$$L(Q_{{\theta }_k}^i)={\mathbb{E}}_D\left[{\displaystyle \frac{1}{2}}{\left(Q_{{\theta }_k}^i(\mathit{o},\mathit{a})-y_{\mathrm{d}}^i\right)}^2\right]$$

(21)

with

$$y_{\mathrm{d}}^i=r_t^i+\gamma \left(\underset{k=1,2}{\min }{Q}_{{\overline{\theta }}_k}^i({\mathit{o}}^{\prime },{\tilde{\mathit{a}}}^{\prime })\right.\left.-{\alpha }_i\log \left({\pi }_{\omega }^i({\tilde{\mathit{a}}}_{t+1}^i|{\mathit{o}}_{t+1}^i)\right)\right)$$

(22)

where $\underset{k=1,2}{\min }{Q}_{{\overline{\theta }}_k}^i({\mathit{o}}^{\prime },{\tilde{\mathit{a}}}^{\prime })$ represents the smaller value generated by two target critic networks. ${\overline{\theta }}_k$ denotes the parameters of the target critic network. ${\tilde{\mathit{a}}}^{\prime }=\{{\tilde{\mathit{a}}}_{t+1}^1,{\tilde{\mathit{a}}}_{t+1}^2,\cdots ,{\tilde{\mathit{a}}}_{t+1}^N\}$ with ${\tilde{\mathit{a}}}_{t+1}^i$ being obtained by real-time sampling, that is ${\tilde{\mathit{a}}}_{t+1}^i\sim {\pi }_{\omega }^i(\cdot |{\mathit{o}}_{t+1}^i)$, rather than from the experience replay buffer.

The target network of the $i\mathrm{th}$ ASV is updated using soft update

$${\overline{\theta }}_k^i\leftarrow \sigma {\theta }_k^i+(1-\sigma ){\overline{\theta }}_k^i$$

(23)

where $\sigma$ denotes update rate.

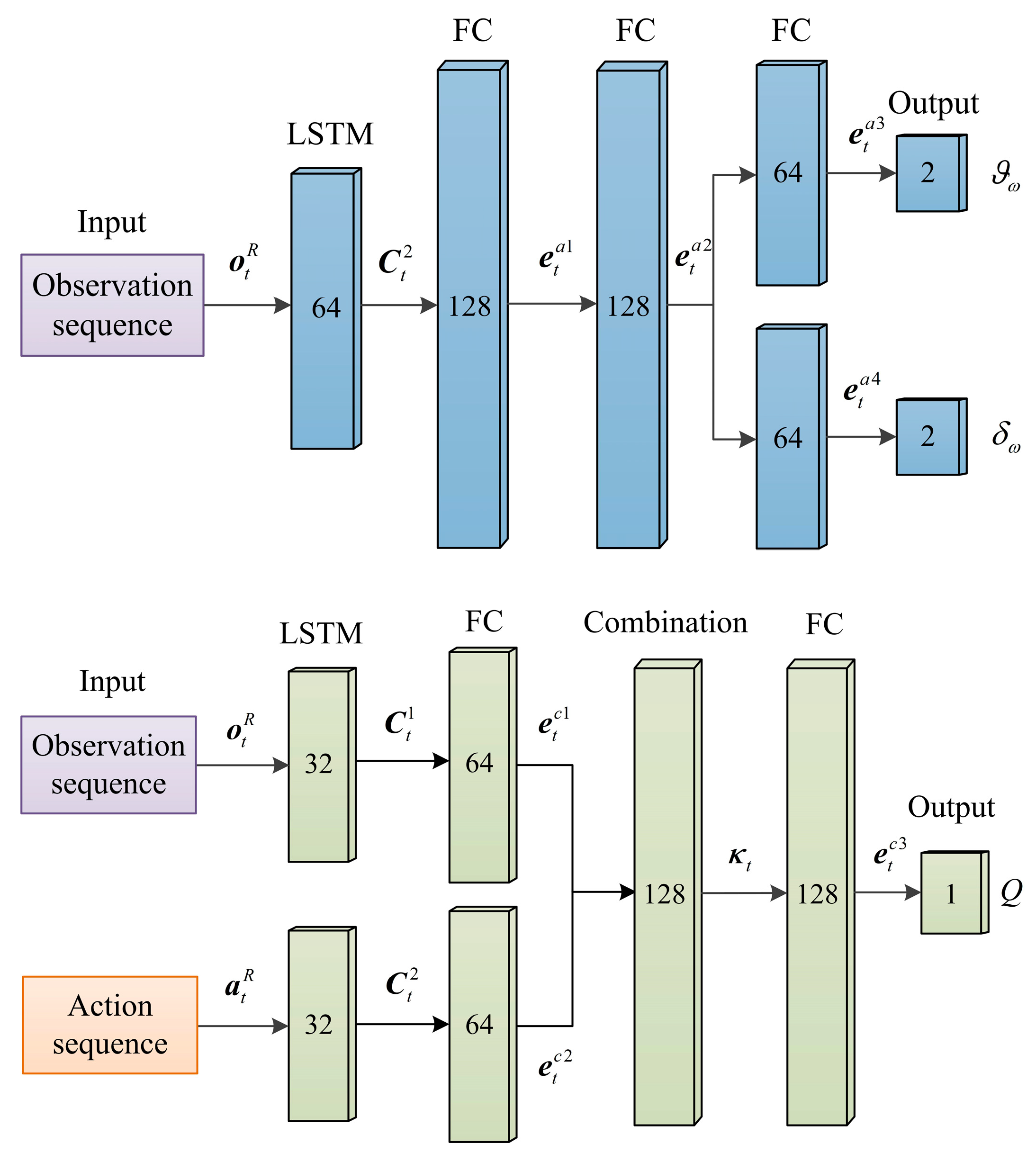
Moreover, to enhance the sequential modeling capability of the deep network structure for historical encirclement information, the actor and critic networks are constructed using long short-term memory (LSTM), as shown in Figure 3, thereby capturing the temporal dependencies in the encirclement process.

The computation process of the actor network is as follows

$$\left\{\begin{array}{l}({\tilde{\mathit{h}}}_t,{\mathit{C}}_t)=\mathrm{LSTM}({\mathit{o}}_t^R,{\tilde{\mathit{h}}}_{t-1},{\mathit{W}}_{a1})\\ {\mathit{e}}_t^{a1}=F_{a1}\left({\mathit{C}}_t,{\mathit{W}}_{a2}\right),{\mathit{e}}_t^{a2}=F_{a2}\left({\mathit{e}}_t^{a1},{\mathit{W}}_{a3}\right)\\ {\mathit{e}}_t^{a3}=F_{a3}\left({\mathit{e}}_t^{a2},{\mathit{W}}_{a4}\right),{\mathit{e}}_t^{a4}=F_{a4}\left({\mathit{e}}_t^{a2},{\mathit{W}}_{a5}\right)\\ {\vartheta }_{\omega }=O_{a1}\left({\mathit{e}}_t^{a3},{\mathit{W}}_{a6}\right),{\delta }_{\omega }=O_{a2}\left({\mathit{e}}_t^{a4},{\mathit{W}}_{a7}\right)\end{array}\right.$$

(24)

where ${\mathit{o}}_t^R$ denotes the historical observation sequence. ${\tilde{\mathit{h}}}_t$ and ${\mathit{C}}_t$ denote the hidden state and cell state generated by the LSTM layer. $F_{a\ast }$ denotes fully connected (FC) layer. ${\mathit{e}}_t^{a\ast }$ denotes the output of the fully connected layer. $O_{a\ast }$ denotes output layer. ${\mathit{W}}_{a\ast }$ denotes learnable network weights.

The computation process of the critic network is as follows

$$\left\{\begin{array}{l}({\mathit{h}}_t^1,{\mathit{C}}_t^1)=\mathrm{LSTM}\text{\_}1({\mathit{o}}_t^R,{\mathit{h}}_{t-1}^1,{\mathit{W}}_{c1})\\ ({\mathit{h}}_t^2,{\mathit{C}}_t^2)=\mathrm{LSTM}\text{\_}2({\mathit{a}}_t^R,{\mathit{h}}_{t-1}^2,{\mathit{W}}_{c2})\\ {\mathit{e}}_t^{c1}=F_{c1}\left({\mathit{C}}_t^1,{\mathit{W}}_{c3}\right),{\mathit{e}}_t^{c2}=F_{c2}\left({\mathit{C}}_t^2,{\mathit{W}}_{c4}\right)\\ {\mathit{\kappa }}_t=\mathcal{T}\left({\mathit{e}}_t^{c1},{\mathit{e}}_t^{c2},{\mathit{W}}_{c5}\right),{\mathit{e}}_t^{c3}=F_{c3}\left({\mathit{\kappa }}_t,{\mathit{W}}_{c6}\right)\\ Q=O_c\left({\mathit{e}}_t^{c3},{\mathit{W}}_{c7}\right)\end{array}\right.$$

(25)

where ${\mathit{a}}_t^R$ denotes the historical action sequence. ${\mathit{h}}_t^{\ast }$ and ${\mathit{C}}_t^{\ast }$ denote the hidden state and cell state generated by the two LSTM layers. $F_{c\ast }$ denotes fully connected layer. ${\mathit{e}}_t^{c\ast }$ denotes the output of the fully connected layer. $\mathcal{T}$ denotes connection layer and ${\mathit{\kappa }}_t$ is its output. $O_c$ denotes output layer. ${\mathit{W}}_{c\ast }$ denotes learnable network weights.

The specific training process is presented in Algorithm 2, where ${\lambda }_{\ast }$ denotes learning rates and satisfies $0<{\lambda }_{\ast }<1$.

Algorithm 2: Cooperative encirclement control via MARL.

Inputs: Actor network parameters ${\omega }^i$, critic network parameters ${\theta }_1^i$ and ${\theta }_2^i$.

Initialization: Target network parameters ${\overline{\theta }}_1^i\leftarrow {\theta }_1^i$ and ${\overline{\theta }}_2^i\leftarrow {\theta }_2^i$, experience replay buffer $D\leftarrow \varnothing$, cooperative encirclement environment.

1:   for $n_1=1,\dots ,F$ do

2:  for $n_2=1,\dots ,Q$ do

3:   Sample action ${\mathit{a}}_t^i\sim {\pi }_{\omega }^i(\cdot |{\mathit{o}}_t^i)$ from policy based on observation ${\mathit{o}}_t^i$

4:   Compute reward $r_t^i$ and obtain ${\mathit{o}}_{t+1}^i$

5:   Store $\left\{\mathit{o},\mathit{a},\mathit{r},{\mathit{o}}^{\prime }\right\}$ into the experience replay buffer $D$

6:  end for

7:  Replay mini-batch samples from $D$

8:  Update network parameters using the gradient descent/ascent and soft update    ${\theta }_k\leftarrow {\theta }_k-{\lambda }_{cr}{\nabla }_{{\theta }_k}L(Q_{{\theta }_K}^i)$ for $k\in \{1,2\}$    $\omega \leftarrow \omega +{\lambda }_{ac}{\nabla }_{\omega }J({\pi }_{\omega }^i)$    ${\alpha }_i\leftarrow {\alpha }_i-{\lambda }_{\alpha }{\nabla }_{\alpha }L({\alpha }_i)$    ${\overline{\theta }}_k^i\leftarrow \sigma {\theta }_k^i+(1-\sigma ){\overline{\theta }}_k^i$ for $k\in \{1,2\}$

9:   end for

Outputs: Network parameters ${\omega }^i$, ${\theta }_1^i$ and ${\theta }_2^i$.

4. Simulation Results

In order to demonstrate the effectiveness of the proposed cooperative encirclement control method, simulation studies together with comprehensive comparisons are conducted. Principal parameters of the ASV are as follows: $m_{ui}=19$, $m_{vi}=35.2$ and $m_{ri}=4.2$. The nominal dynamics is given by $f_{ui}=35.2v_i{r}_i-4u_i$, $f_{vi}=-19u_i{r}_i-1v_i$ and $f_{ri}=-16.2u_i{v}_i-10r_i$ [32]. Time-varying environmental disturbances are added to the ASV model at the beginning of each episode and remain throughout the episode, which are given by

$$\left\{\begin{array}{l}{\dot{\tau }}_{wui}+{\alpha }_{ui}{\tau }_{wui}=m_{ui}G(s)w_{ui}\\ {\dot{\tau }}_{wvi}+{\alpha }_{vi}{\tau }_{wvi}=m_{vi}G(s)w_{vi}\\ {\dot{\tau }}_{wri}+{\alpha }_{ri}{\tau }_{wri}=m_{ri}G(s)w_{ri}\end{array}\right.$$

(26)

where ${\alpha }_{\ast i}$ is a positive constant. $w_{\ast i}$ represents a Gaussian white noise process, $\ast =u,v,r$. $G(s)=0.255s/(s^2+0.485s+{0.8}^2)$ represents the transfer function.

The simulation scenario is as follows. Consider a networked system composed of six ASVs and two targets in the horizontal plane without geographical boundary constraints. If the distance between the ASV and the target is less than 50 m, the target adopts the maneuver strategy given by (4). When the criteria (3) are met, it is determined that the target encirclement mission is completed.

At the beginning of each episode, the positions and heading angles of ASVs are randomly initialized with a specified range. To be specific, $x_i\in [-30,30]$, $y_i\in [-30,30]$, ${\psi }_i\in [0,\pi ]$. The initial positions of the two targets are $(20,100)$ and $(50,100)$, and initial heading angles are both $\pi /4$. Let the encirclement radius be $d_{\mathrm{capture}}=15$ and the minimum distance between ASVs and targets be $d_{\min }=10$. After numerous simulations and parameter adjustments, the reward coefficients are set as $k_0=2$, $k_1=10$, $k_5=100$, and $k_6=100$. The training hyperparameters are listed in

Table 1. Main training hyperparameters.

Hyperparameters	Value
Discount factor $\gamma$	0.99
Maximum training episodes $F$	10,000
Maximum steps per training episodes $Q$	1000
Critic network learning rate ${\lambda }_{\mathrm{cr}}$	0.0003
Actor network learning rate ${\lambda }_{\mathrm{ac}}$	0.0002
Entropy learning rate ${\lambda }_{\mathrm{en}}$	0.0005
Target network update rate $\sigma$	0.0002
Entropy threshold $H_{\mathrm{d}}$	−2
Mini-batch	256
Experience replay buffer size	1,000,000

.

In order to demonstrate the superiority of the proposed stage-induced reward function, the traditional reward method in [33] is deployed to derive comparison results. Specifically, the traditional encirclement reward function is governed by

$$r_{\mathrm{encirclement}}^i=100{\displaystyle \frac{{\chi }_{left}+{\chi }_{right}}{4\pi }}\exp \left(-0.03\sigma (\chi )\right)+r_{\mathrm{guide}}^i$$

(27)

with $r_{\mathrm{guide}}^i=0.5$ if $d_{\mathrm{T}i}\le d_{\mathrm{capture}}$ and $r_{\mathrm{guide}}^i=0.5\exp \left(-0.005d_{\mathrm{capture}}\right)$ if $d_{\mathrm{T}i}>d_{\mathrm{capture}}$, where ${\chi }_{left}$ and ${\chi }_{right}$ are the encirclement angles of the $i\mathrm{th}$ vehicle and the neighbor vehicle, respectively. $\sigma (\chi )$ is the standard deviation of the encirclement angle. Note that the superiority and comparisons of the LSTM can be found in our previous work [34].

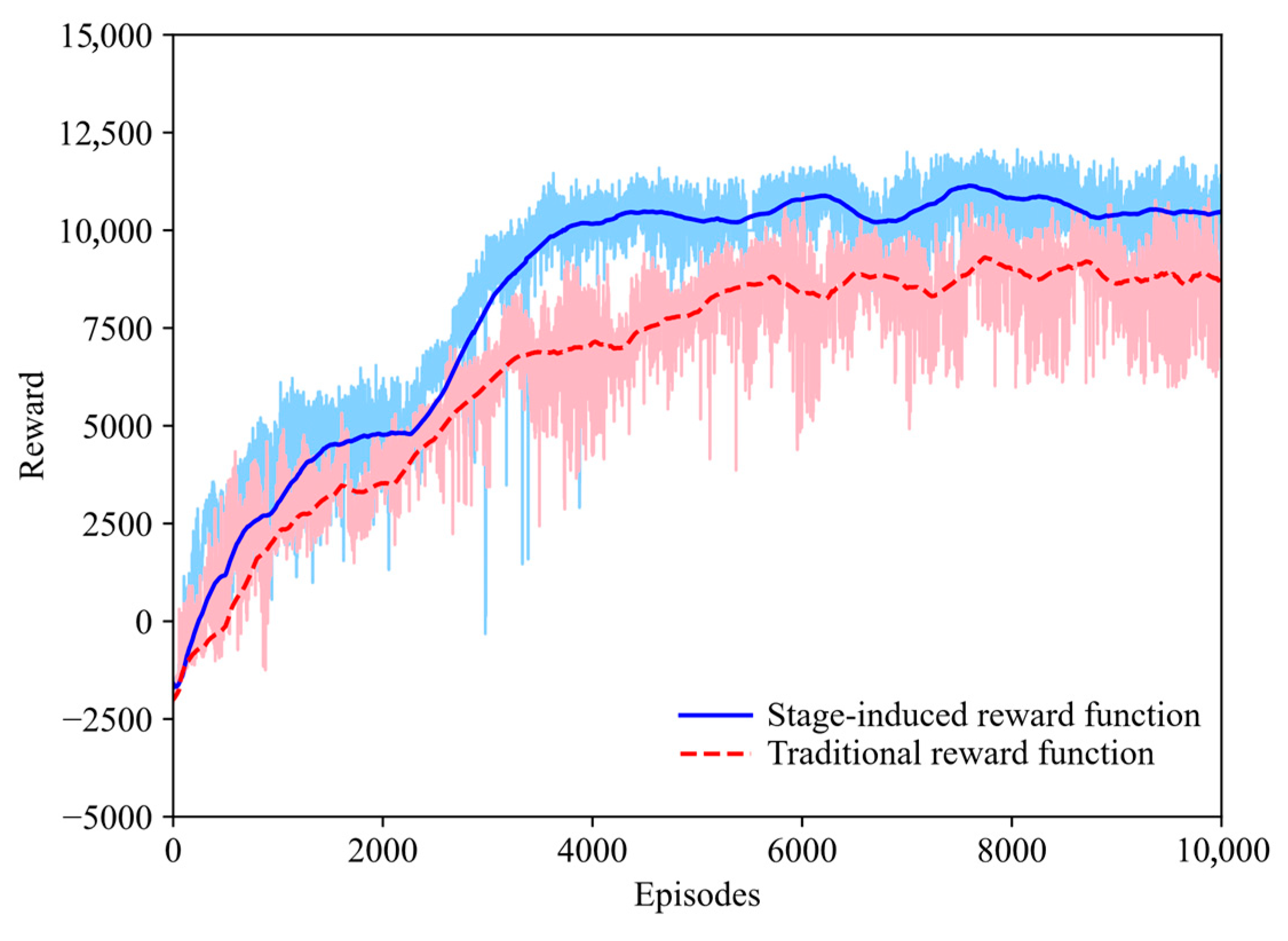
The encirclement performance is evaluated from two aspects, including episode rewards and task success rates. Episode rewards of cooperative target encirclement using different reward functions are shown in Figure 4, where the shaded areas represent the standard deviation. As illustrated, all methods converge within the training steps. However, policy training using the stage-induced reward function clearly exhibits faster convergence and higher reward values, which can be explained by the fact that ASVs using the curriculum rewards gradually learn to search, besiegement and capture, avoiding unnecessary exploration for the dynamic environment. 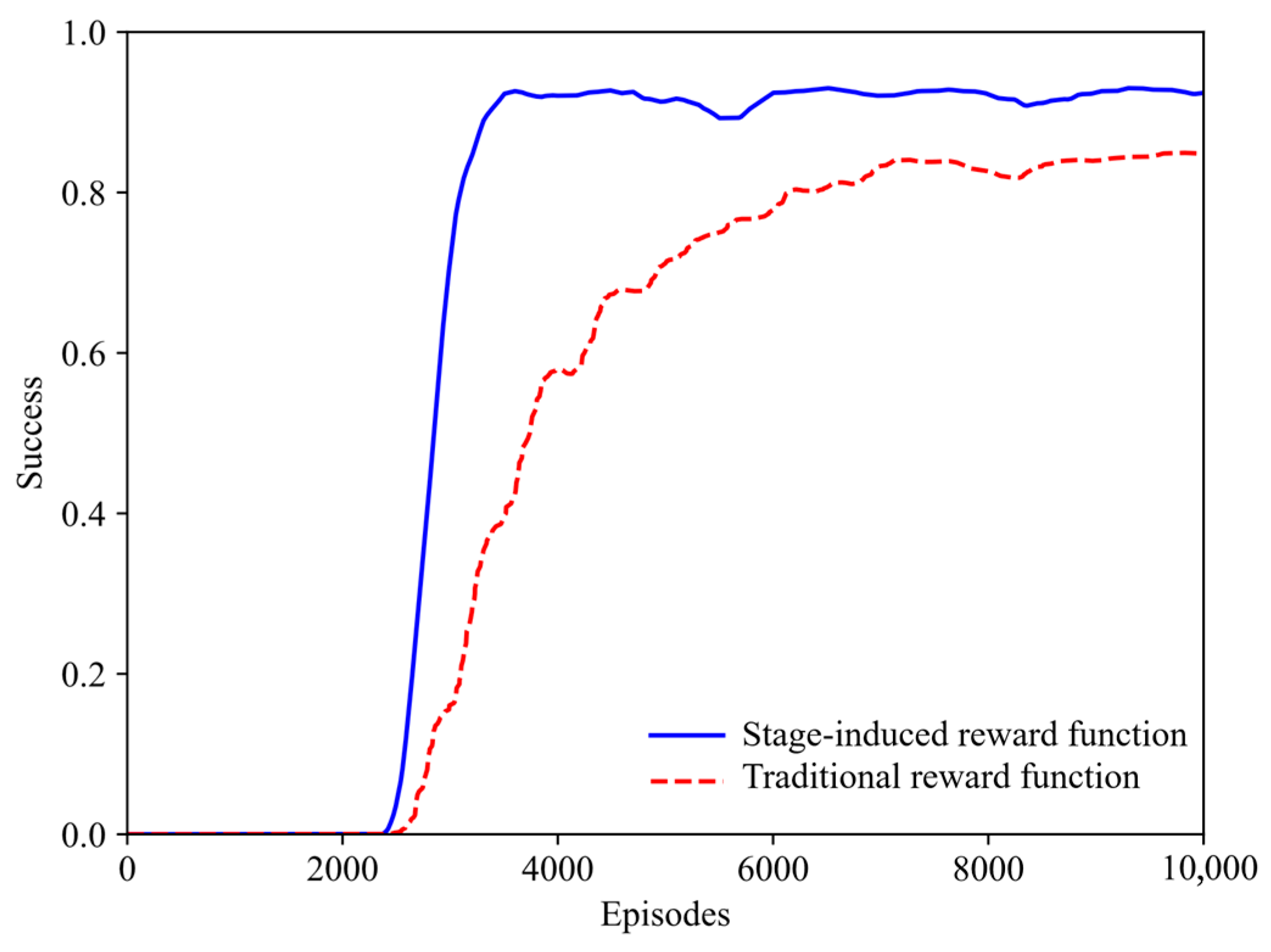Success rate of cooperative target encirclement using different reward functions is shown in Figure 5. During the first 2000 episodes, the success rate is basically close to zero, indicating that the ASVs are in the exploration process and have not developed a successful policy for cooperative target encirclement. After 2500 episodes, with the assistance of curriculum learning, the success rates of encirclement achieved by the stage-induced reward function continue to increase (approaching 90%), while the success rates of the comparison method rise more slowly.

After the training is completed, we save the network parameters with the highest reward value, and conduct a six-on-two cooperative target encirclement test. The vehicles’ initial positions are set as ${\mathit{p}}_1={[-20,-20]}^T$, ${\mathit{p}}_2={[0,-20]}^T$, ${\mathit{p}}_3={[20,-20]}^T$, ${\mathit{p}}_4={[-20,0]}^T$, ${\mathit{p}}_5={[0,0]}^T$, and ${\mathit{p}}_6={[20,0]}^T$. The other values are the same as those in the training process. Note that if the target meets the encirclement condition (3), the encirclement mission will be immediately terminated.

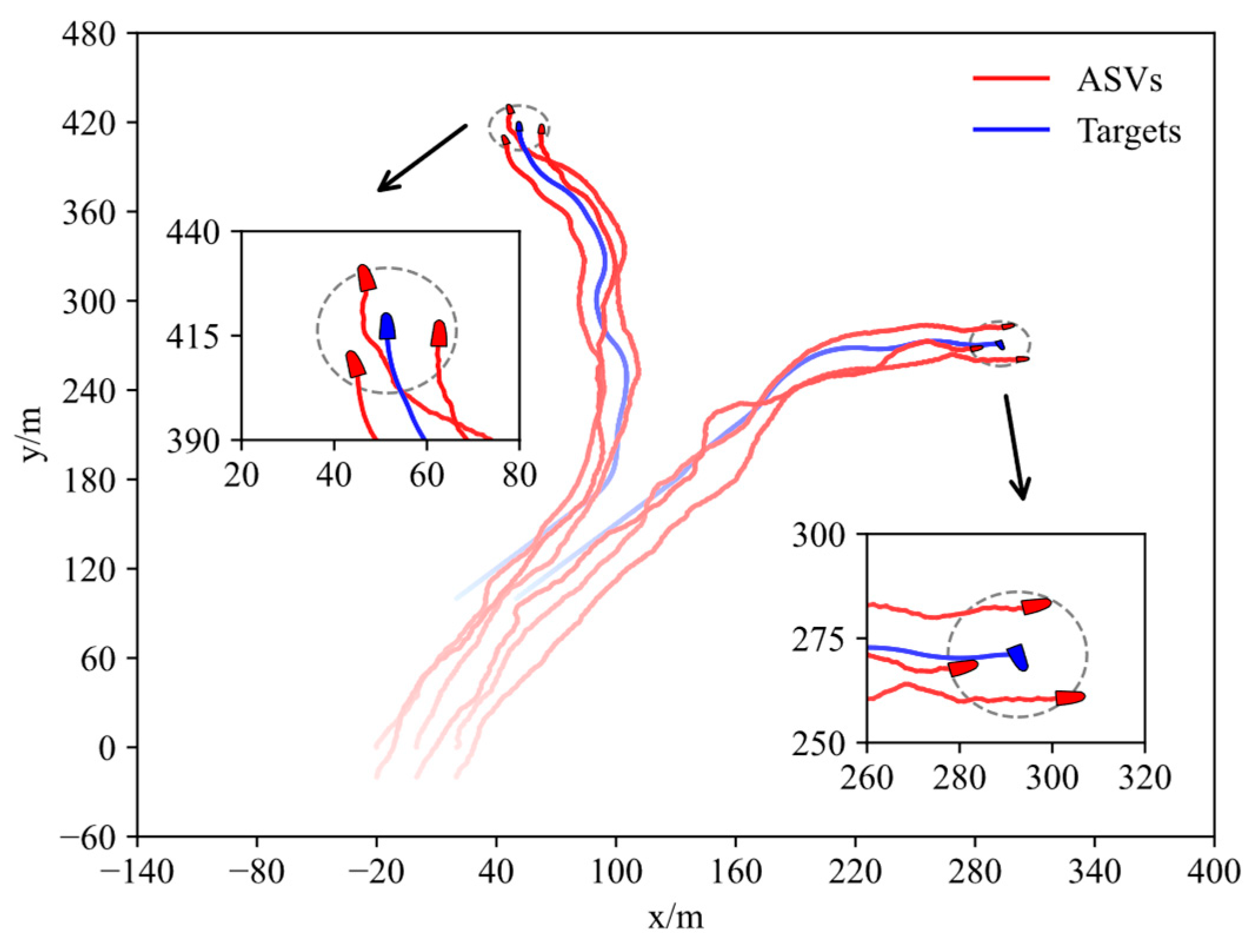
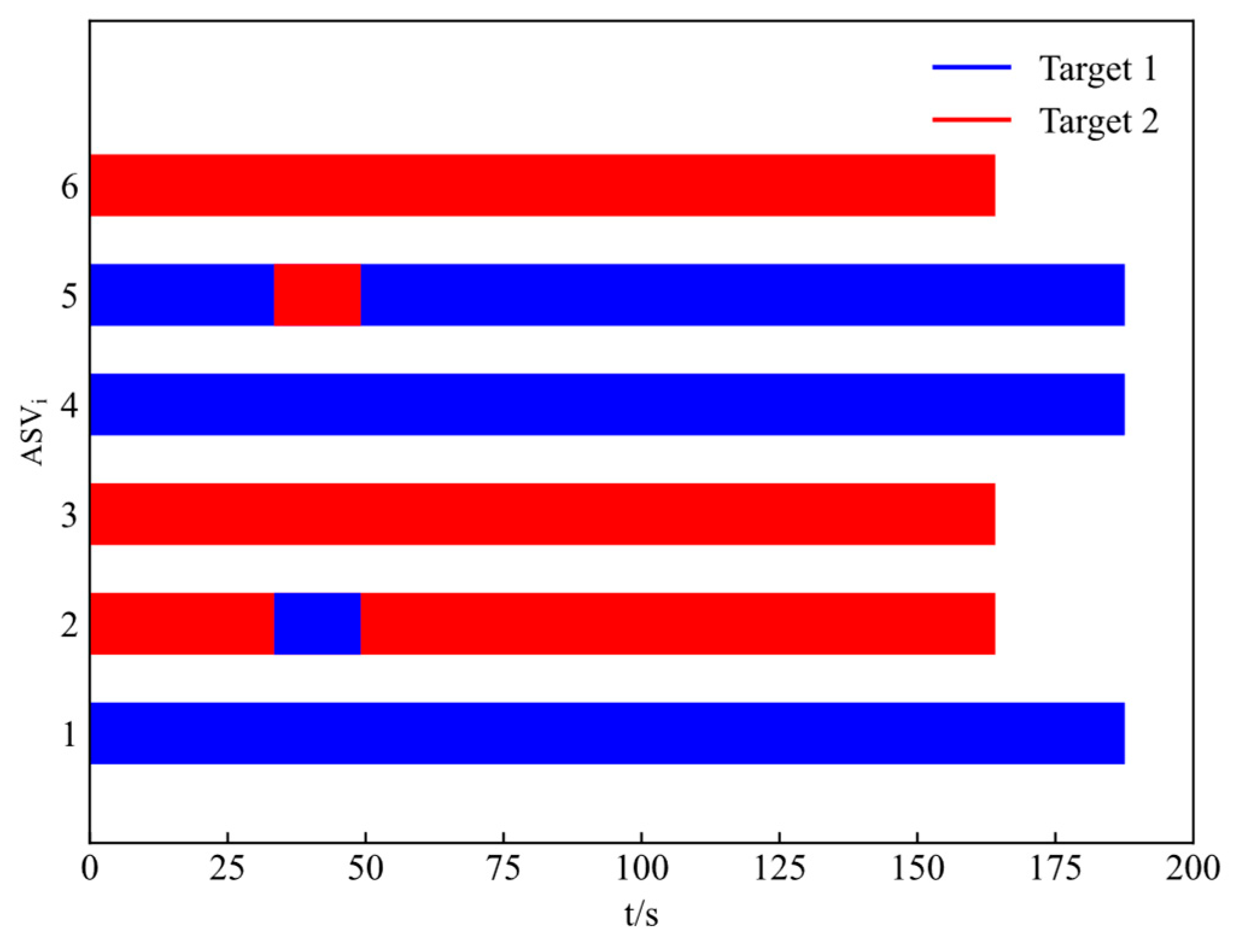
The trajectories of both ASVs and targets throughout the encirclement process are depicted in Figure 6. Notably, six vehicles set off from the initial positions and gradually capture the two moving targets, respectively, forming an encirclement circle. Worth of mention is that six vehicles are gradually divided into two encirclement alliances. Each alliance has three ASVs, and an effective encirclement for the two moving targets is achieved in the end. The target allocation result is shown in Figure 7, where the second ASV and the fifth ASV switch the encirclement target at about 40 s. Finally, the first, fourth, and fifth ASVs encircle the first target, while the second, third, and sixth ASVs encircle the second target. In addition, different encirclement alliances have differential termination times.

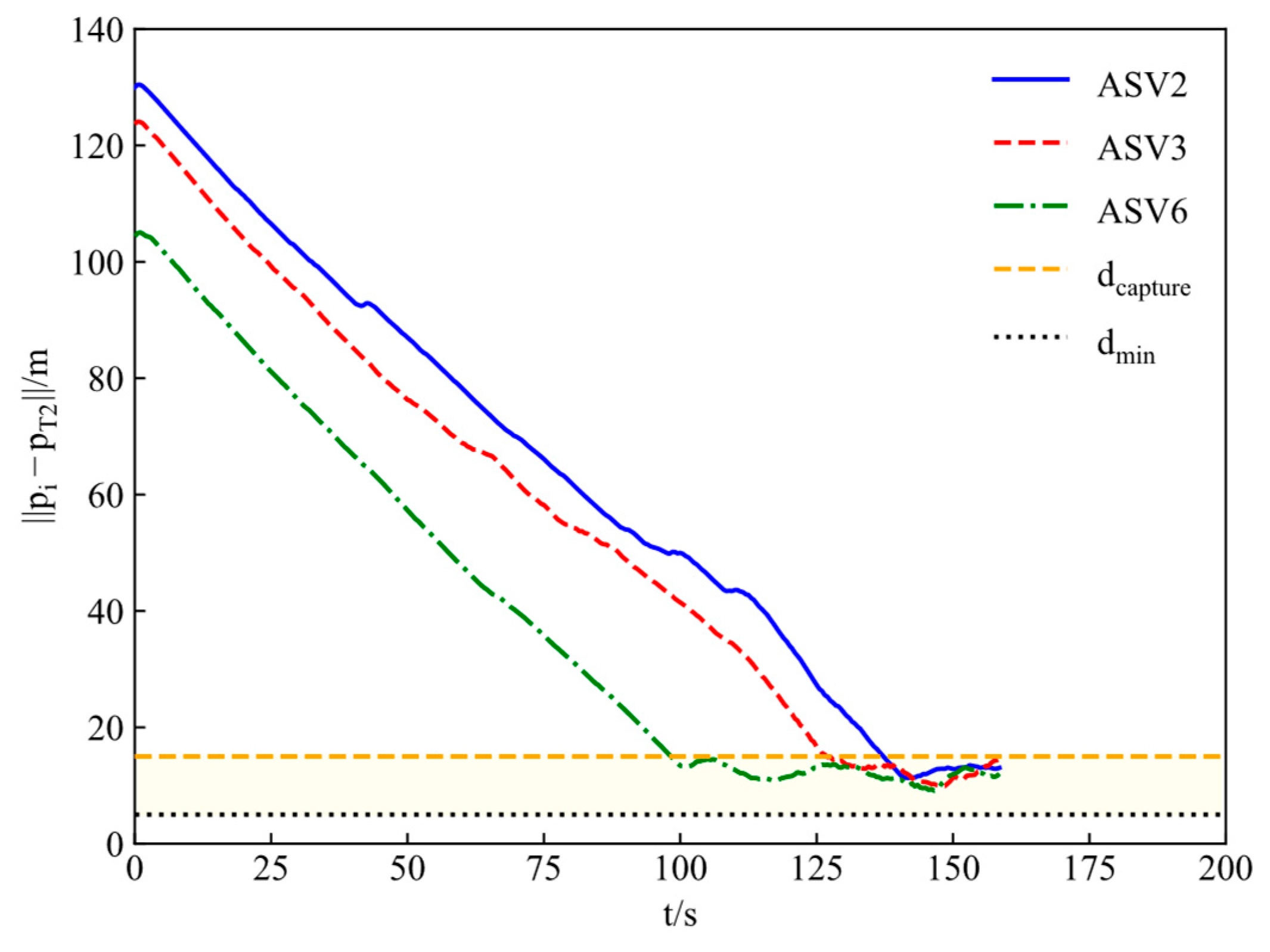
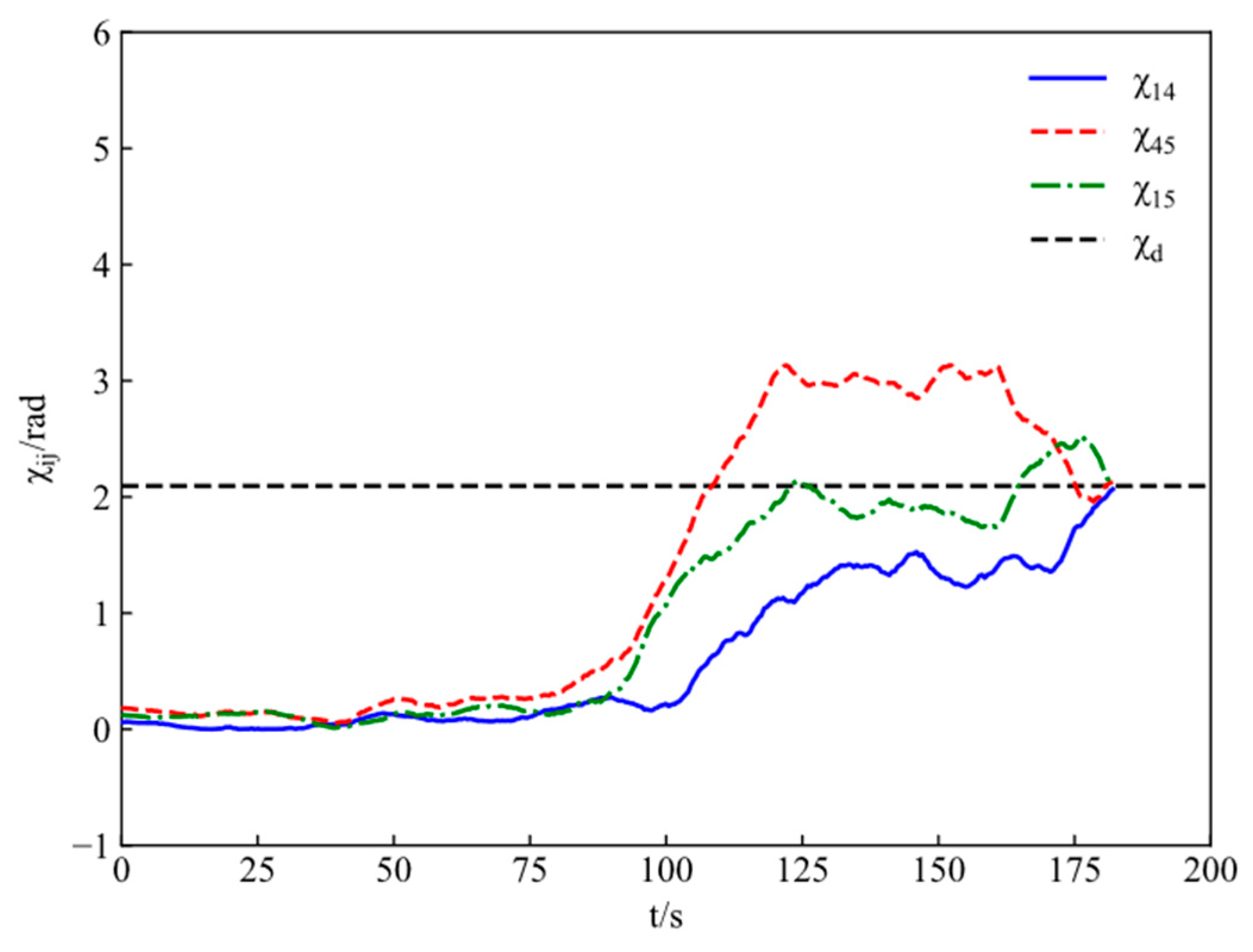
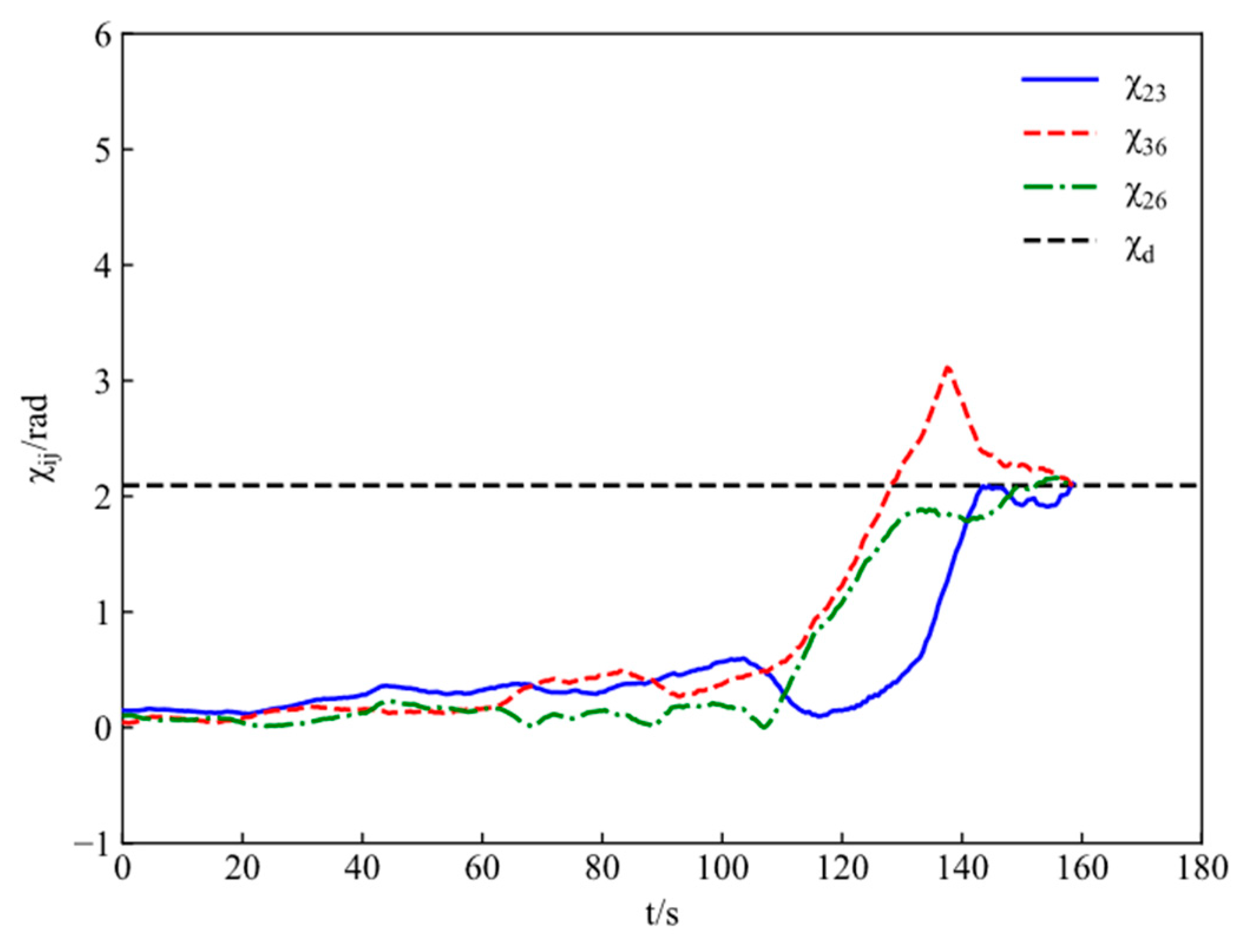
The distances between ASVs and the corresponding targets are shown in Figure 8 and Figure 9. The encirclement angles of adjacent ASVs are shown in Figure 10 and Figure 11. One can conclude that both distances and angles satisfy the desired requirements. Moreover, under the incentive of curriculum rewards, ASVs first meet the distance constraint and then the angle constraint when conducting the cooperative encirclement, achieving the given control objective from the easier to the more difficult. 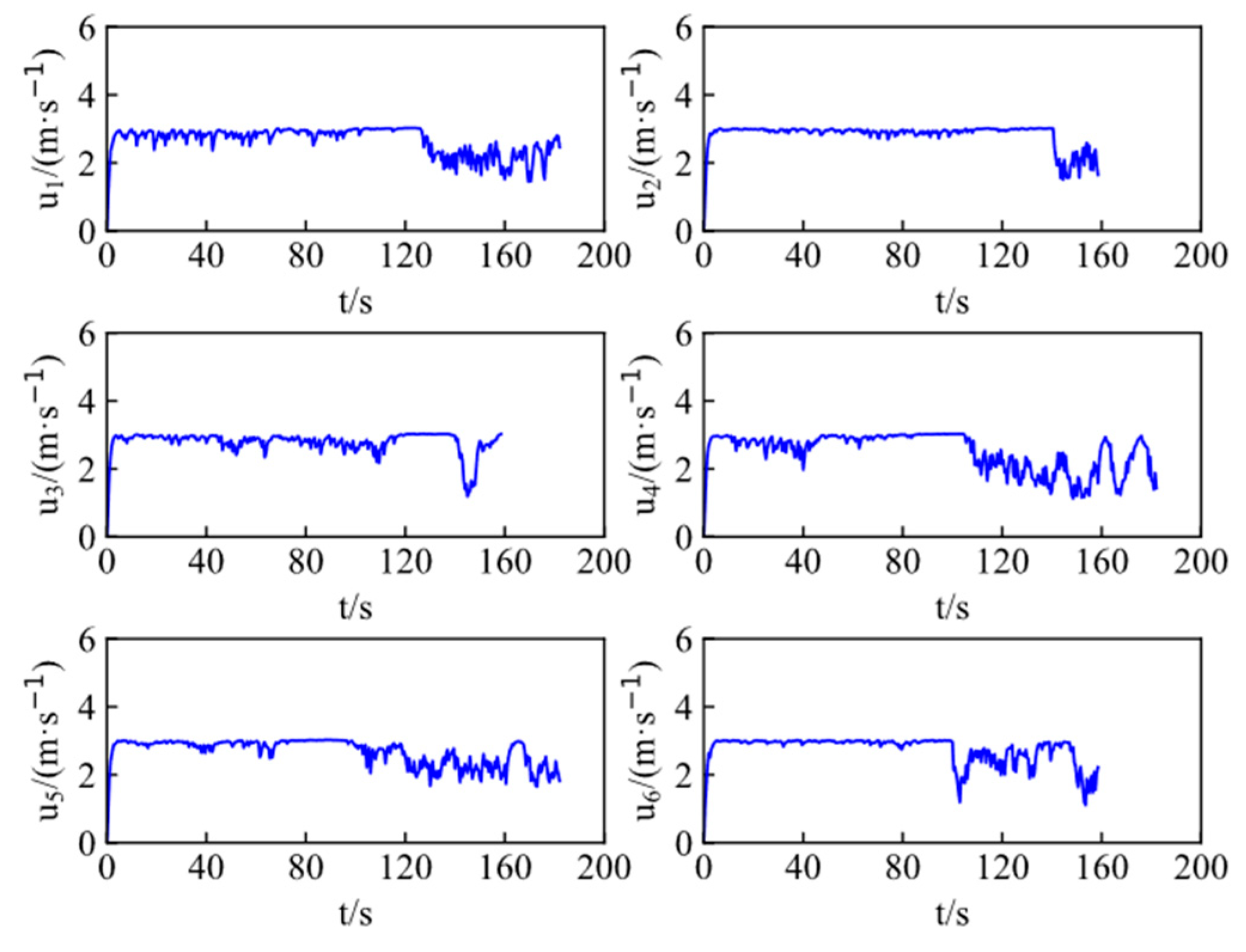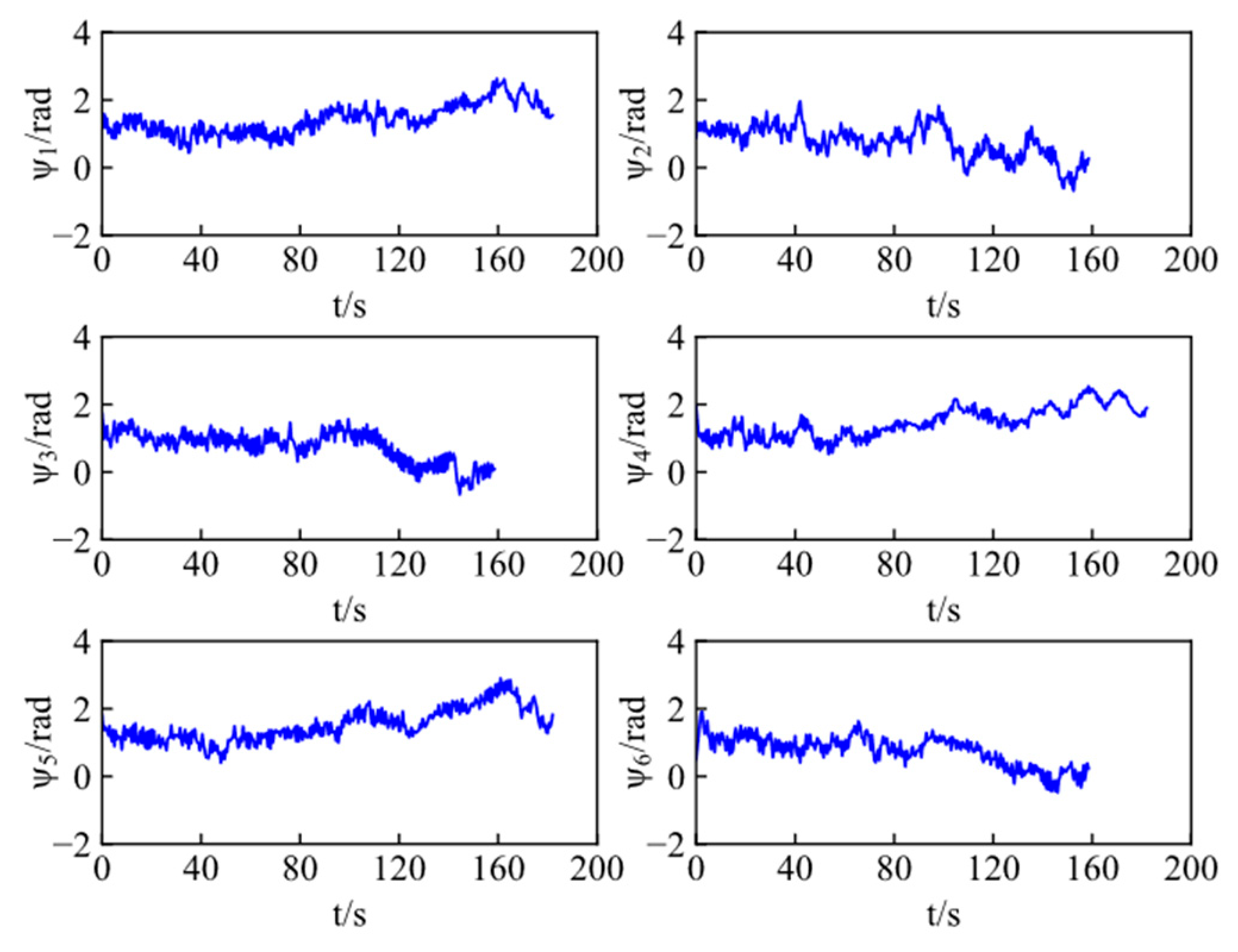Figure 12 and Figure 13 present the velocities and heading angles of ASVs, respectively, where each vehicle adjusts the velocity and angle in real time according to the moving target. 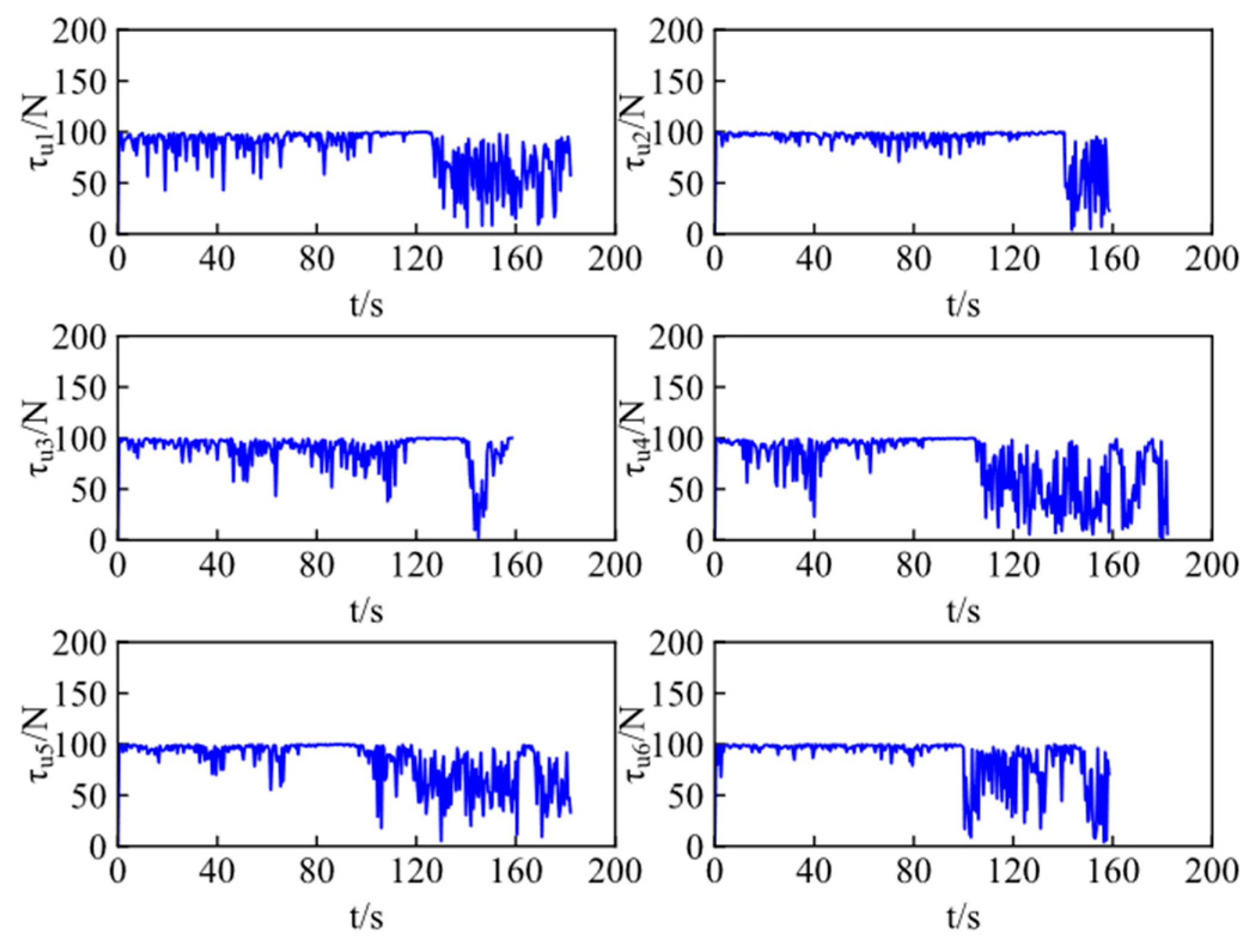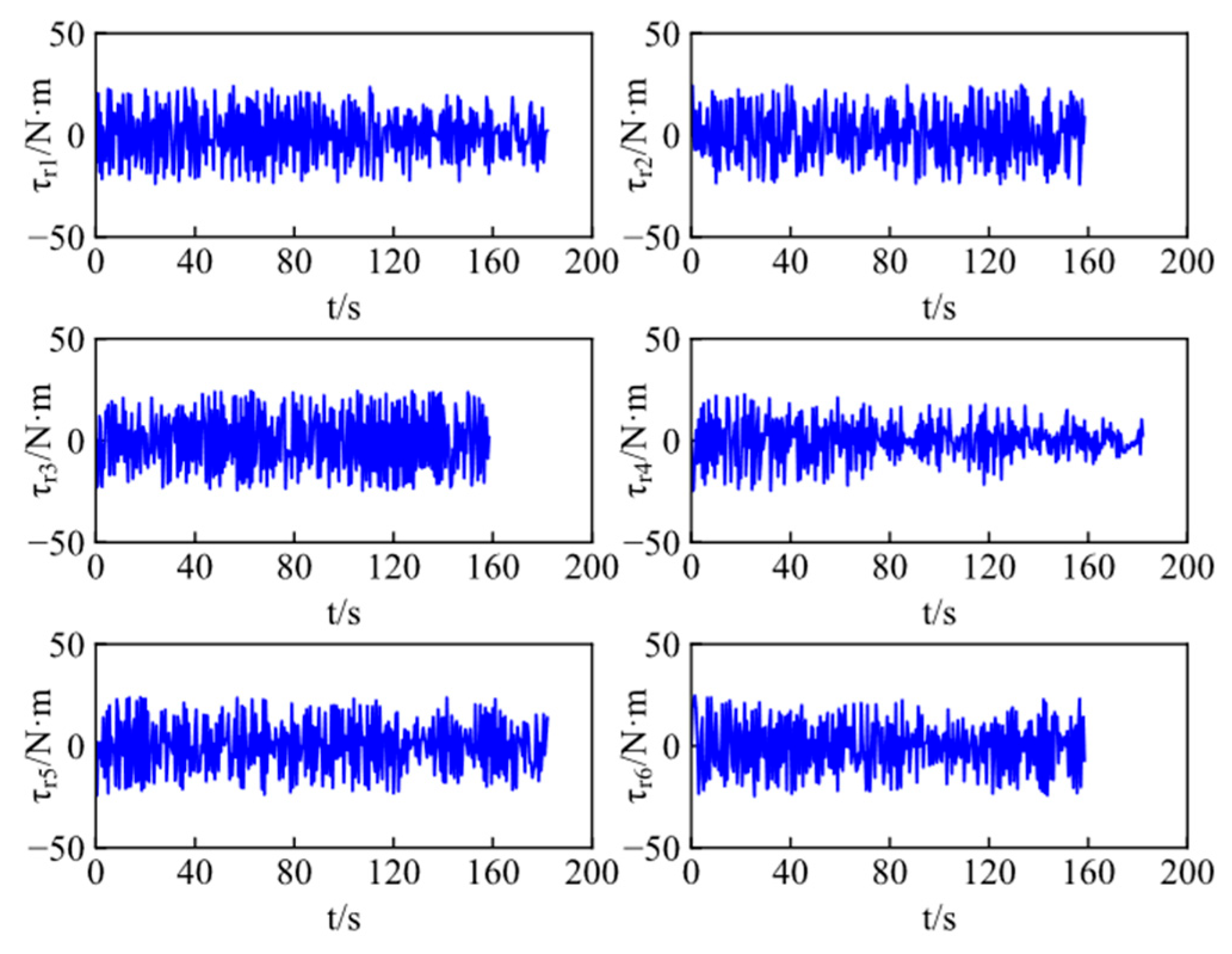Figure 14 and Figure 15 show control inputs of ASVs, including the surge forces and yaw moments, which are bounded and realistic from a practical viewpoint. Both exhibit minor fluctuations during cooperative target encirclement. These fluctuations arise from the time-varying environmental disturbances.

5. Conclusions

This article focuses on the cooperative encirclement problem for multiple ASVs and proposes a multi-target cooperative encirclement control method using MARL. Considering practical mission requirements and operational constraints, the conditions for successful cooperative encirclement by multiple ASVs are established. A dynamic target allocation algorithm, based on the positional information of both vehicles and targets, is designed to optimize target selection in real time. To meet the demands of high-performance cooperative training, a curriculum learning-based multi-stage encirclement reward function is developed, guiding ASVs to approach targets progressively from simpler to more complex tasks. Within a centralized training and decentralized execution framework, a multi-agent soft actor-critic algorithm incorporating long short-term memory is designed to compute the control inputs of vehicles, enabling effective multi-target encirclement. Finally, simulation results validate the effectiveness and superiority of the proposed control method.

Further investigations may aim at the cooperative encirclement of ASVs against unknown targets. It is also desirable to investigate the practical implementation of the proposed method for target encirclement with hardware constraints, communication delays, and measurement errors.