A Study on UAV Path Planning for Navigation Mark Inspection Using Two Improved SOM Algorithms
Abstract
1. Introduction
1.1. Background
1.2. Research Motivation
1.3. Related Work
1.3.1. Navigation Mark Inspection Research
1.3.2. Navigation Mark Inspection Path Planning Methods
1.4. Knowledge Gap and Contributions
- (1)
- An improved ORC_SOM algorithm is proposed. To avoid the algorithm from falling into local optimal solutions, ORC coefficients are introduced, which are combined with local infiltration and generalized competition mechanisms to dynamically adjust the neighborhood radius;
- (2)
- An improved ORCTS_SOM algorithm is proposed. The ORCTS_SOM algorithm, in order to further improve the global optimality finding ability of the ORC_SOM algorithm, incorporates the Tabu Search algorithm (TS) to avoid the algorithm from falling into local optimal solutions;
- (3)
- Validation of the effectiveness of the proposed method based on two different scales of real water coordinates data.
2. Methodology
2.1. Overall Framework
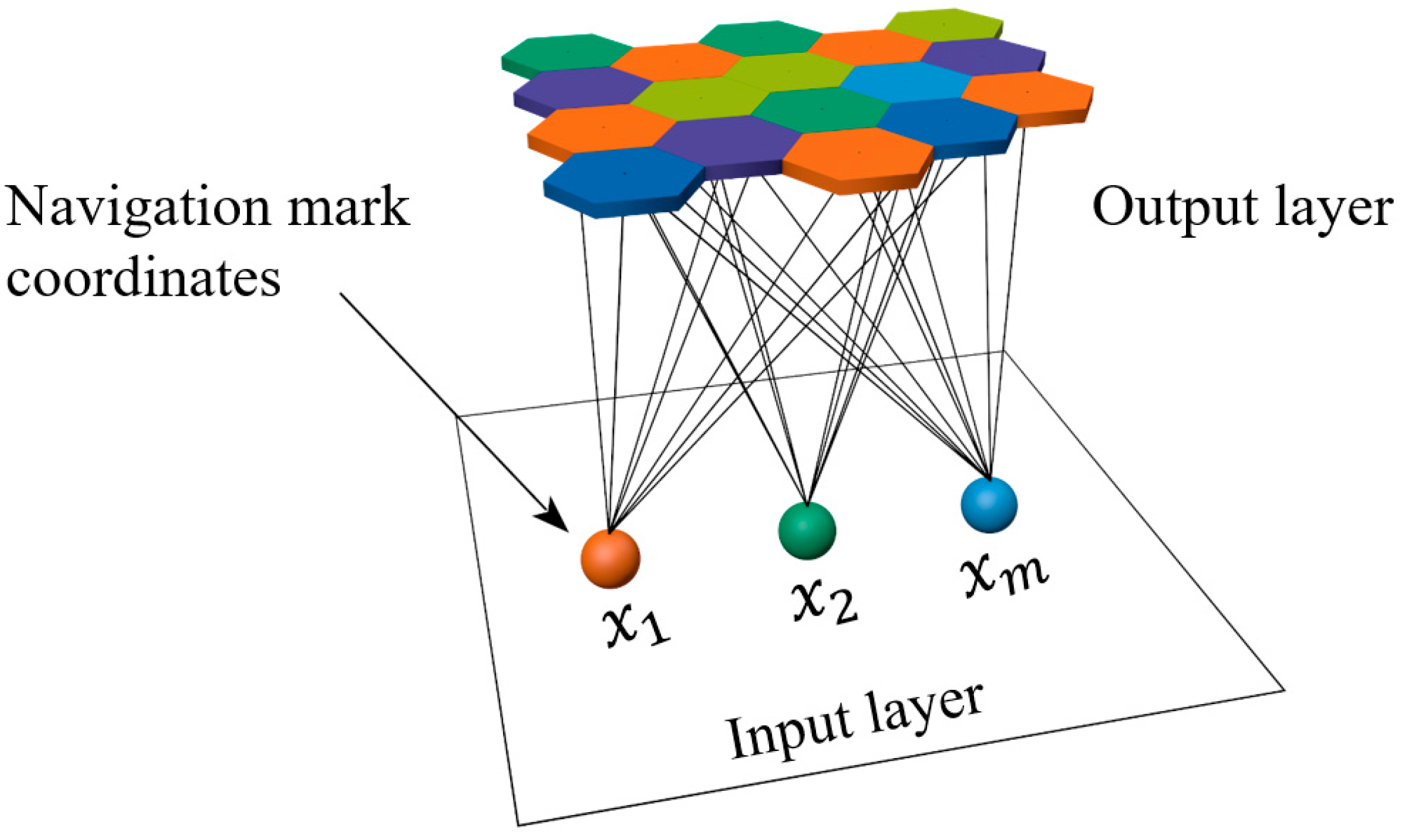
2.2. SOM Algorithm
- (1)
- Data normalization.
- (2)
- Neural network initialization.
- (1)
- Competition stage.
- (2)
- Neighborhood function.
- (3)
- Weighting update.
- (1)
- When the learning rate decays to satisfy the following equation, it indicates that the update of neuron weights has converged to 0, the network stabilizes, and the algorithm ends.
- (2)
- Neighborhood width decays below a threshold; the threshold is taken as one-tenth of the neuron magnification.
- (3)
- Reach the maximum number of iterations.
| Algorithm 1 Traditional SOM framework |
| Input: coordinates of inputted navigation mark X Output: weights of output neurons W, optimized TSP path  |
2.3. ORC_SOM Algorithm
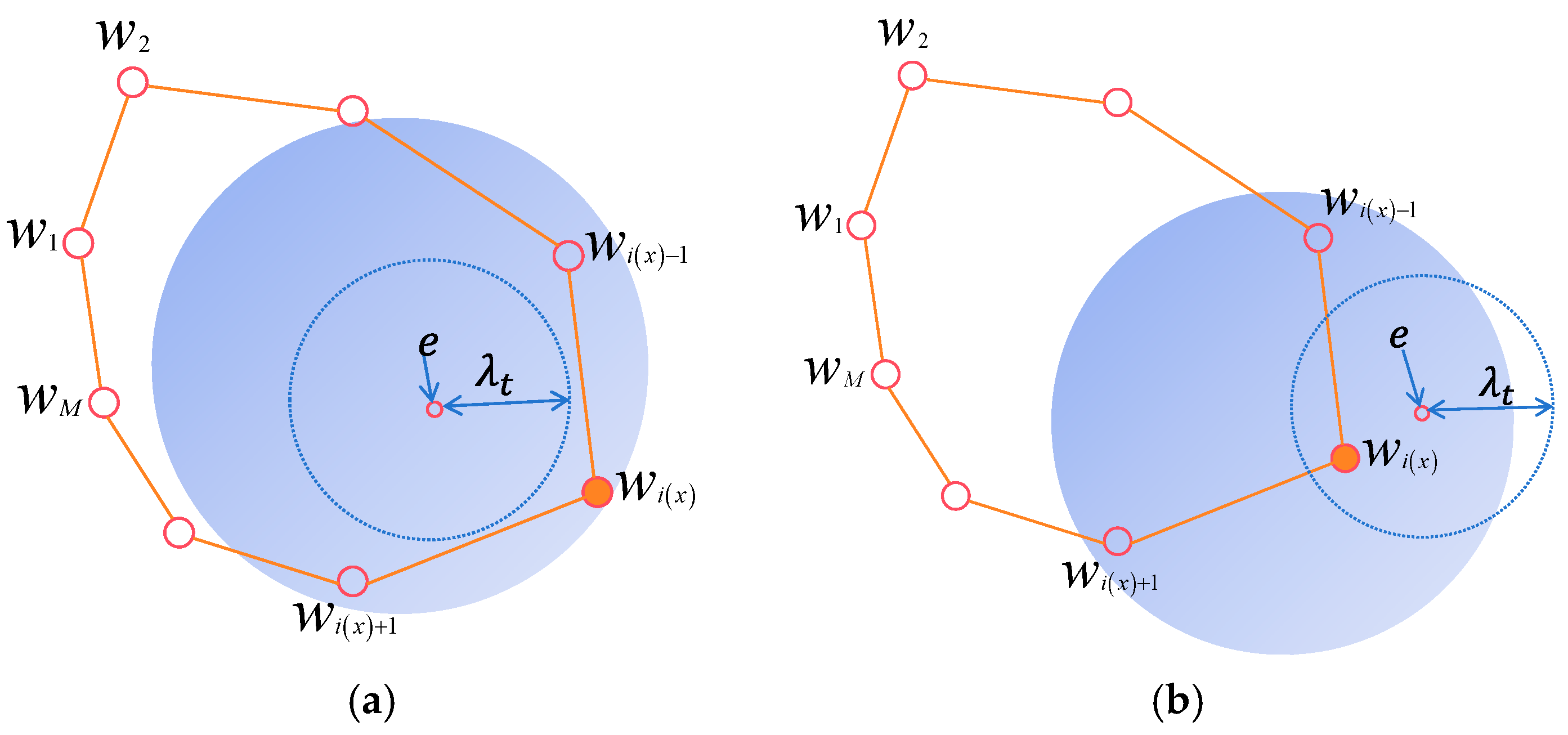
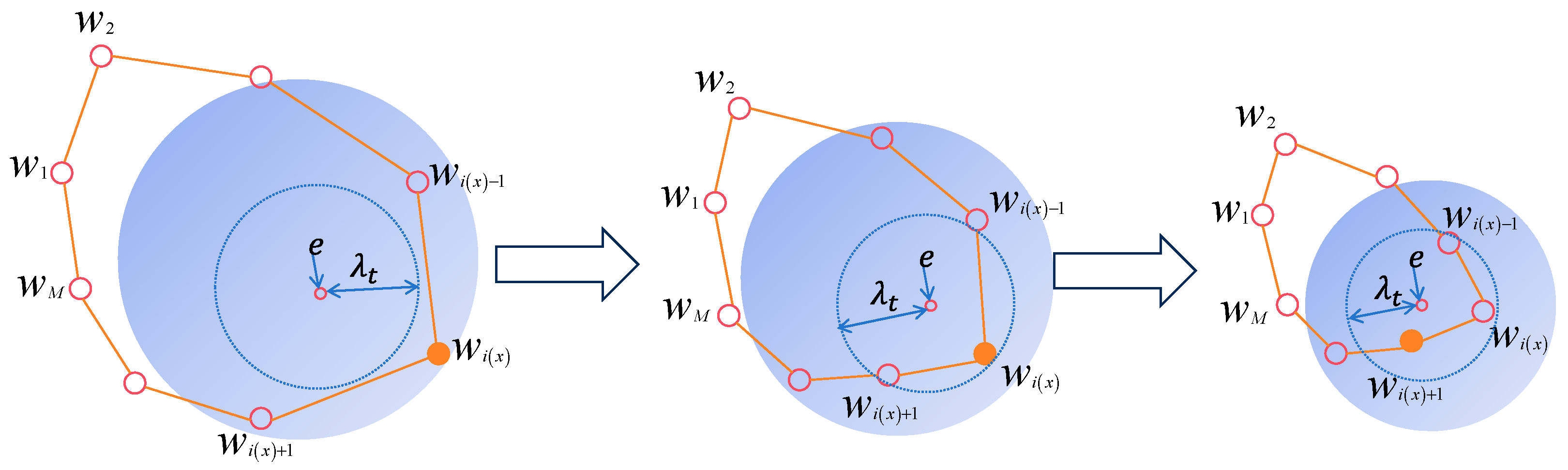
2.3.1. Optimal Radius Coefficient
- (1)
- When , the distance between the inputted navigation mark and the winning neuron is far enough, indicating that the learning is still in the early stage, and needs to emphasize global optimization.
- (2)
- When , the distance between the inputted navigation mark and the winning neuron is very close, the neural network has reached the late stage of learning the spatial distribution of the area around the inputted navigation mark and needs to emphasize the local search.
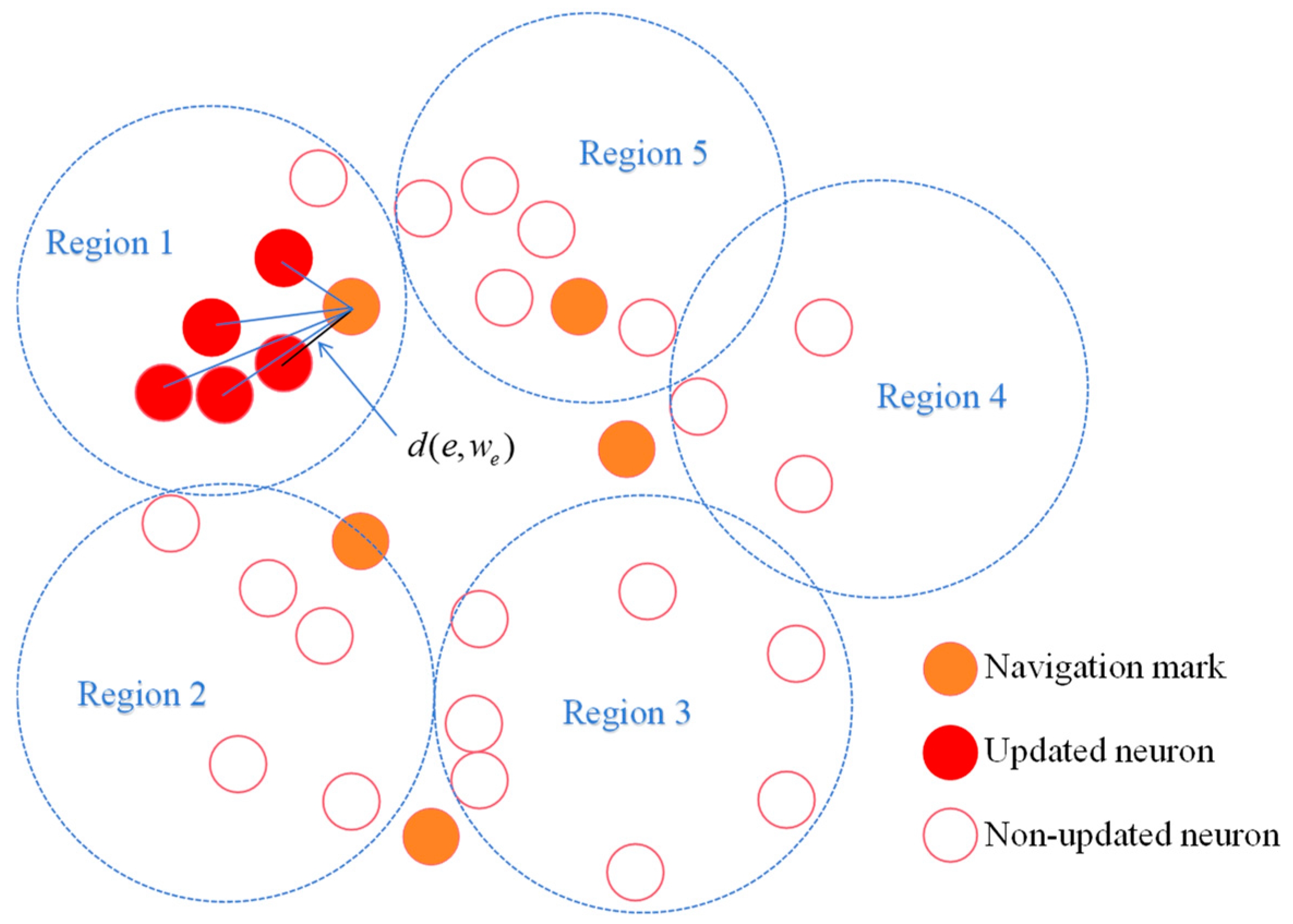
2.3.2. Generalized Competition and Local Infiltration
| Algorithm 2 ORC_SOM framework |
| Input: coordinates of inputted navigation mark X Output: weights of output neurons W, optimized TSP path  |
2.4. ORCTS_SOM Algorithm
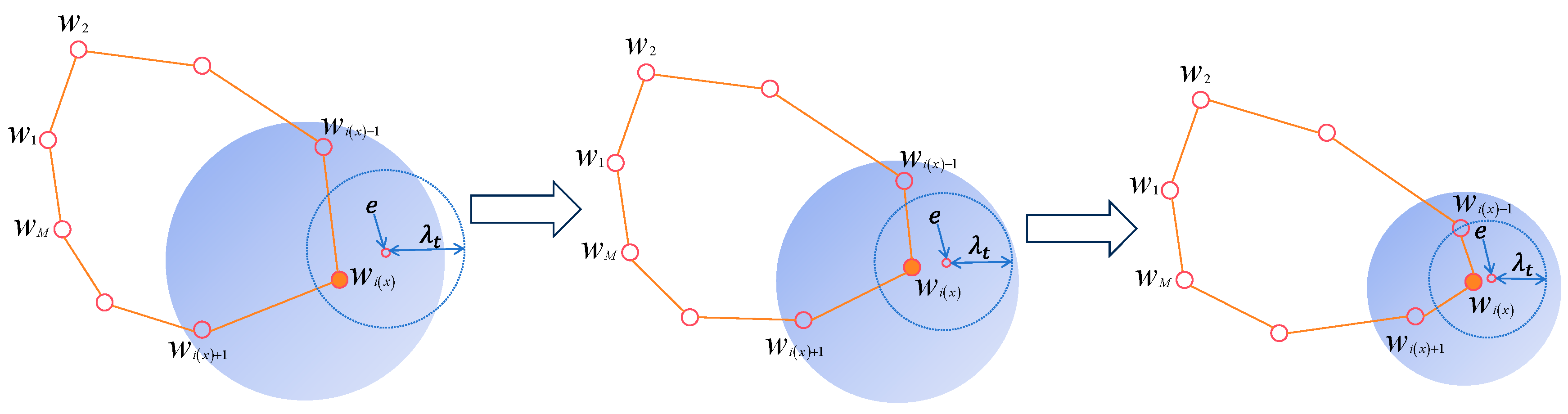
2.4.1. Randomness of Winning Neurons
2.4.2. Inherent Flaws in Random Sampling Mechanisms
- (1)
- Stochastic Selection Inefficiency.
- (2)
- Imbalanced Convergence of Network Topological Structure.
- (3)
- Algorithms easily fall into local optima.
2.4.3. Improved SOM Strategy Based on Tabu Search
- (1)
- System selection control.
- (2)
- Adaptive exploration.
- (3)
- Memory-guided convergence.
| Algorithm 3 ORCTS_SOM framework |
| Input: coordinates of inputted navigation mark X Output: weights of output neurons W, optimized TSP path  |
3. Case Study
3.1. Problem Description
3.2. Data Sources
- (1)
- Spatial scale diversity—incorporating both regional and large-scale navigation environments;
- (2)
- Navigation mark density variation—representing different congestion levels typical in coastal navigation;
- (3)
- Geographical diversity—covering distinct maritime regions with varying navigational challenges.
3.3. Data Processing
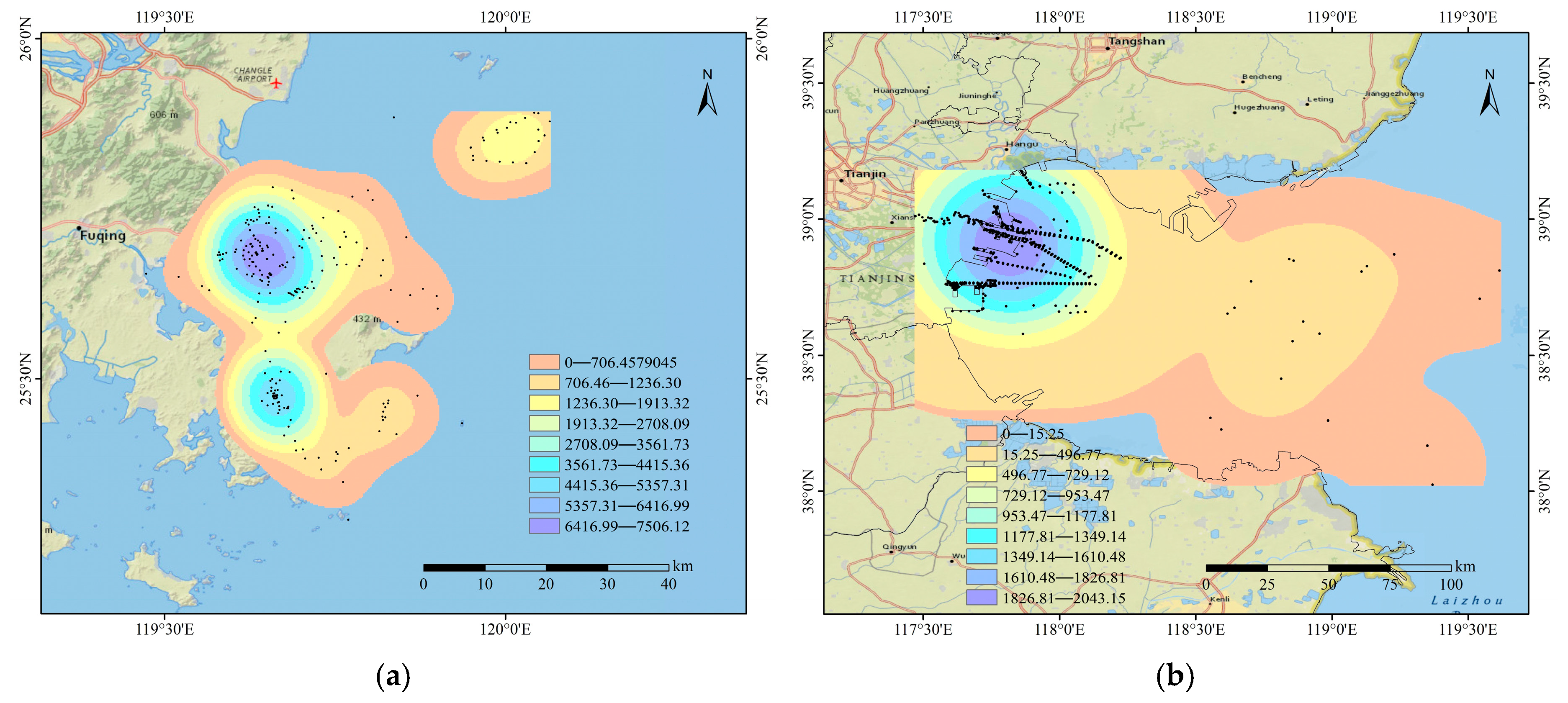
3.4. Data Analysis
4. Experimental Results and Discussion
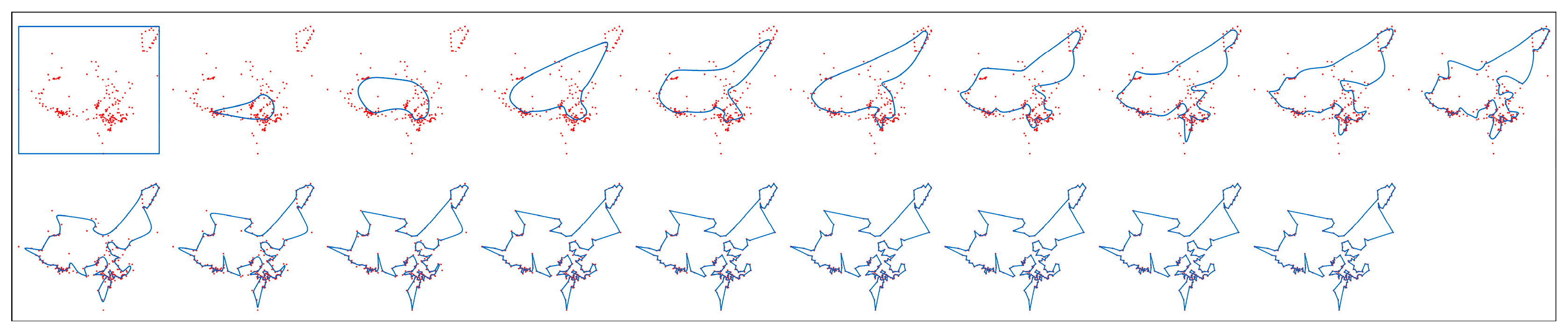
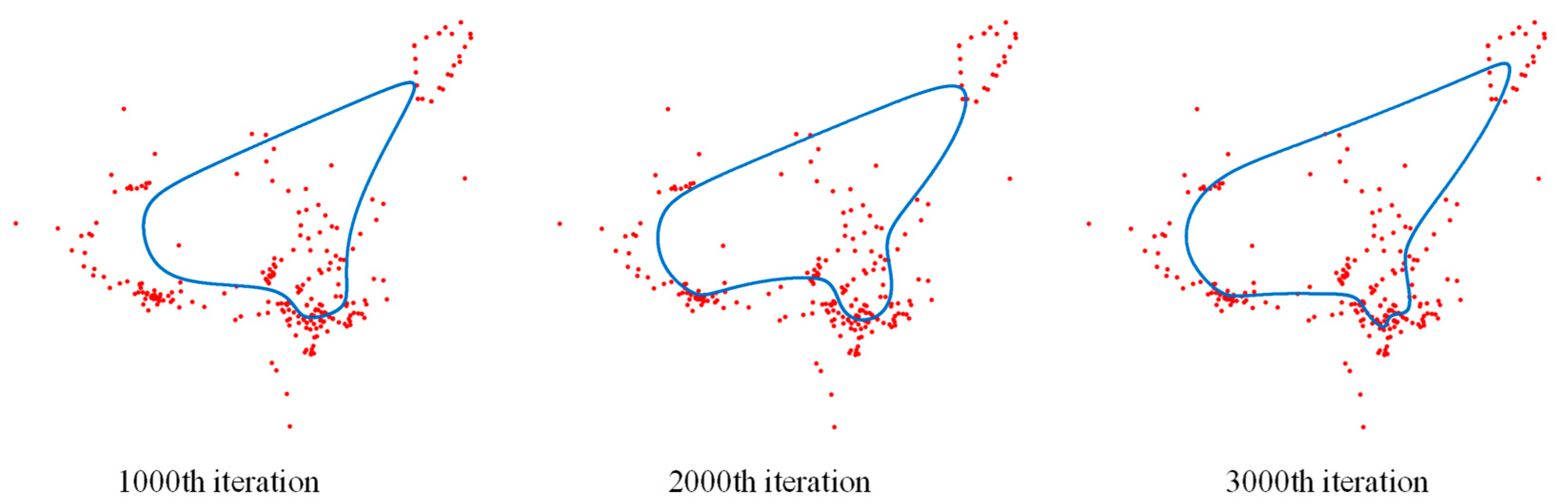
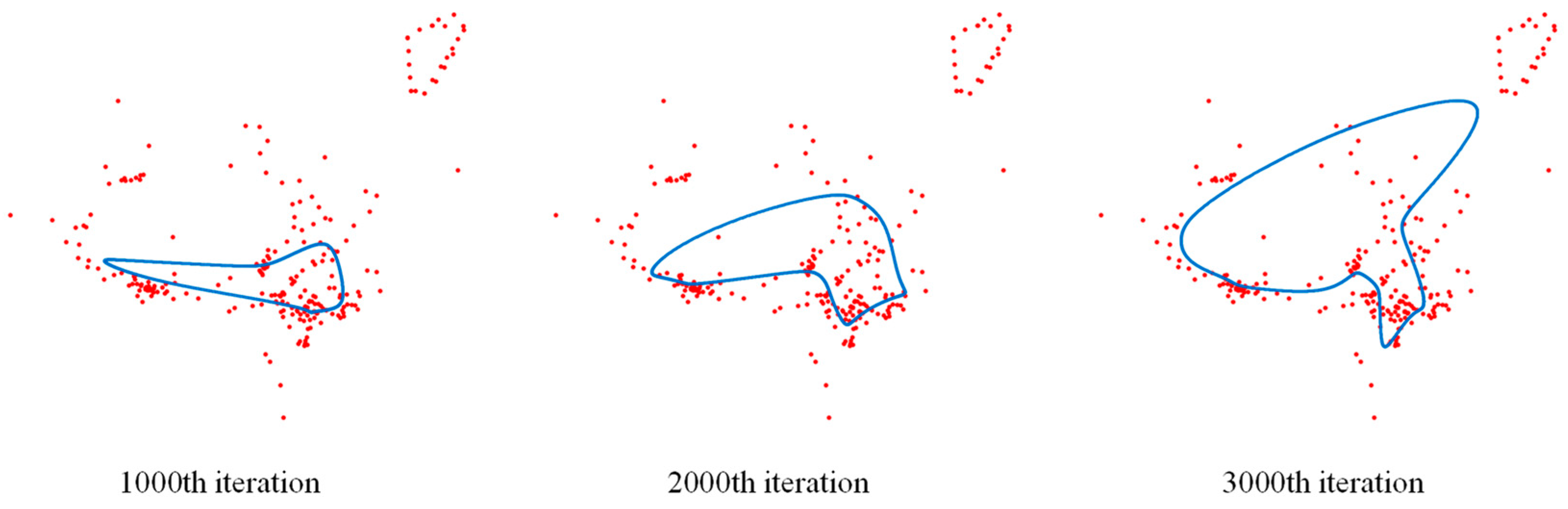
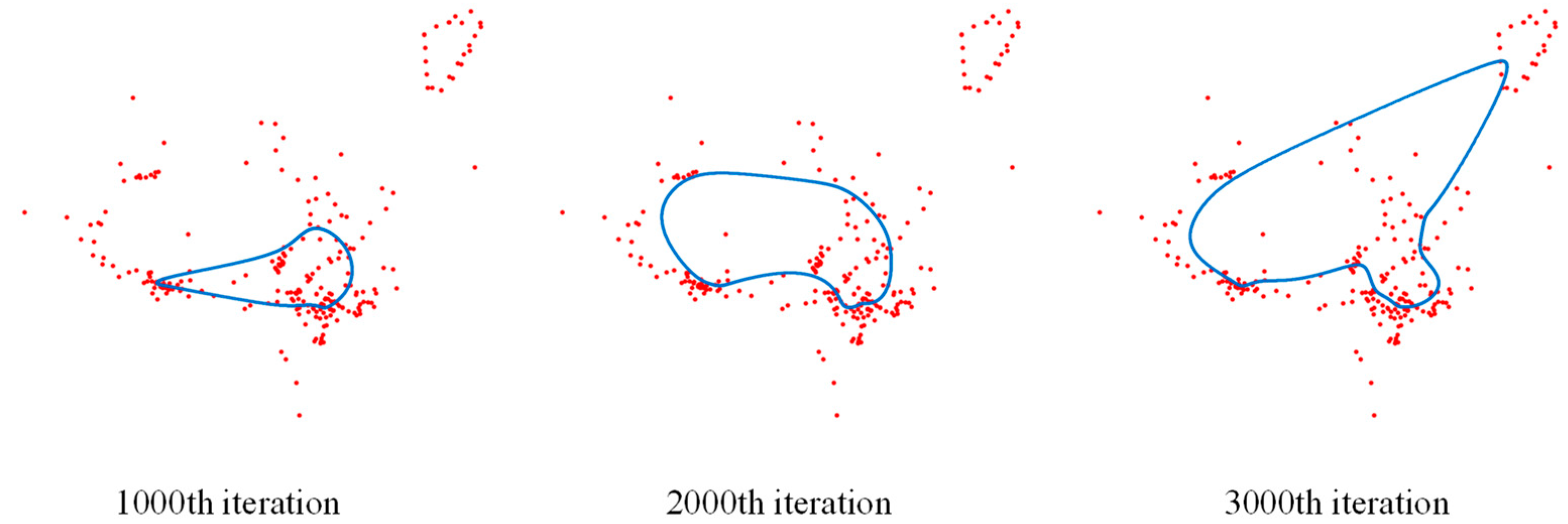
4.1. Path Planning of UAV Navigation Mark Inspection
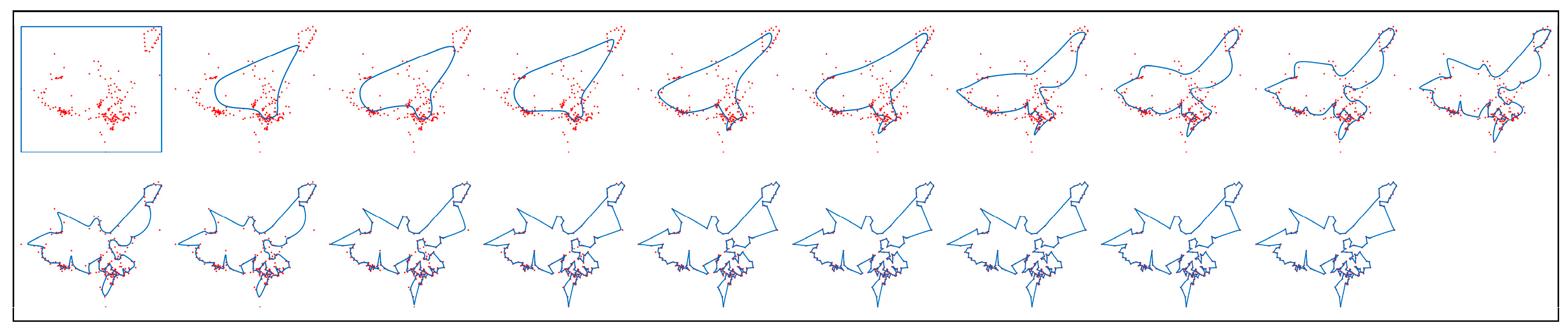
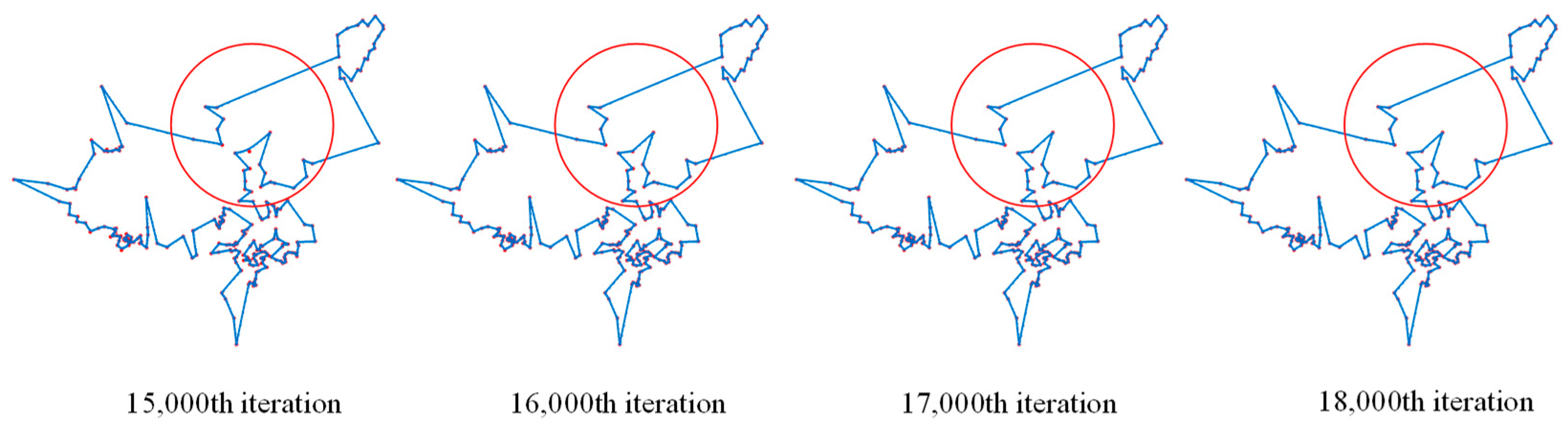
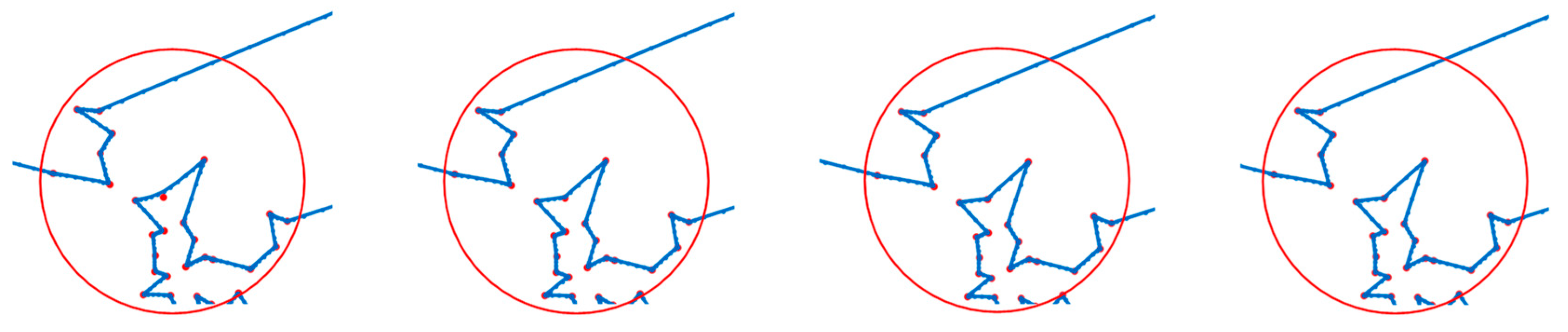
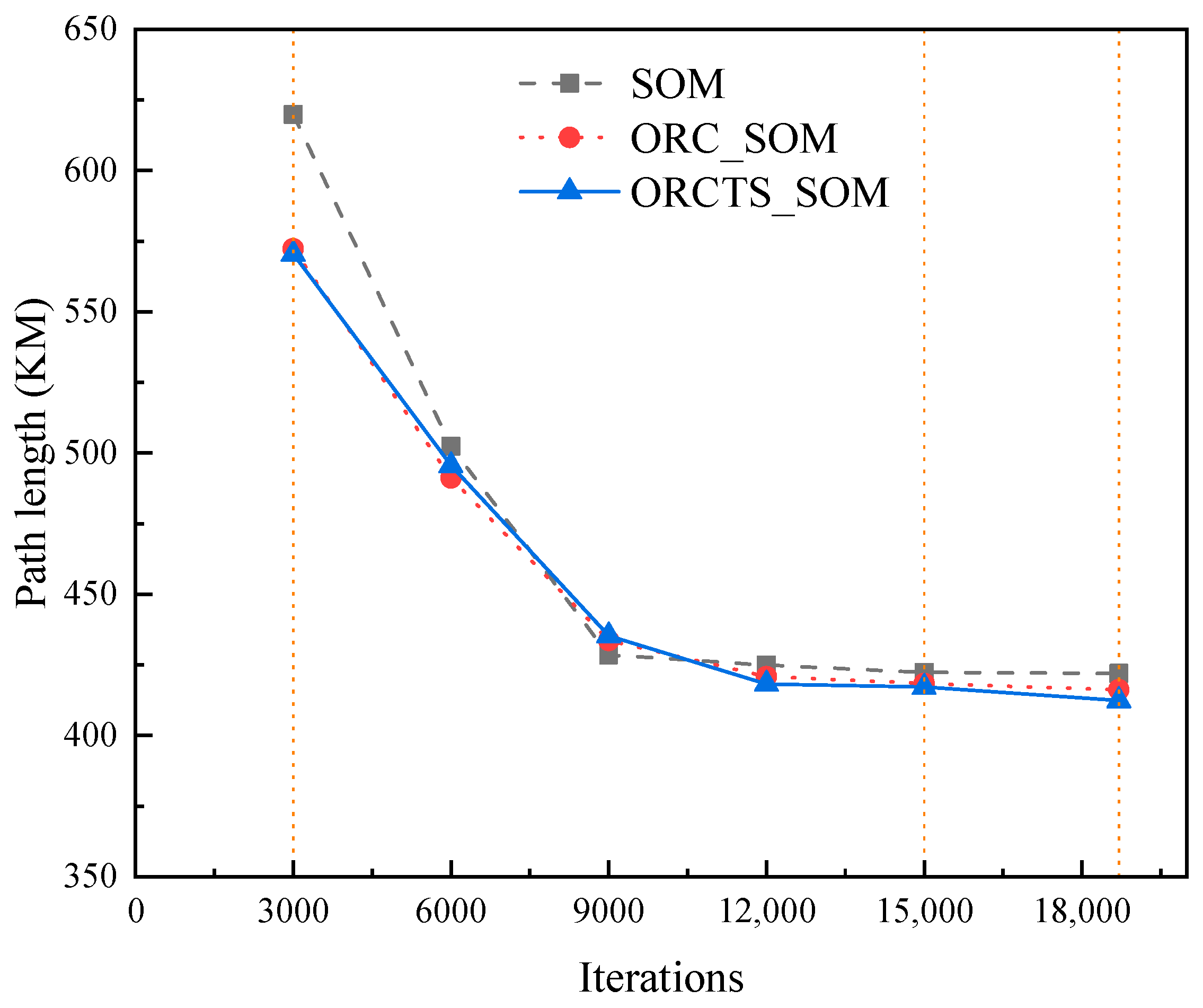
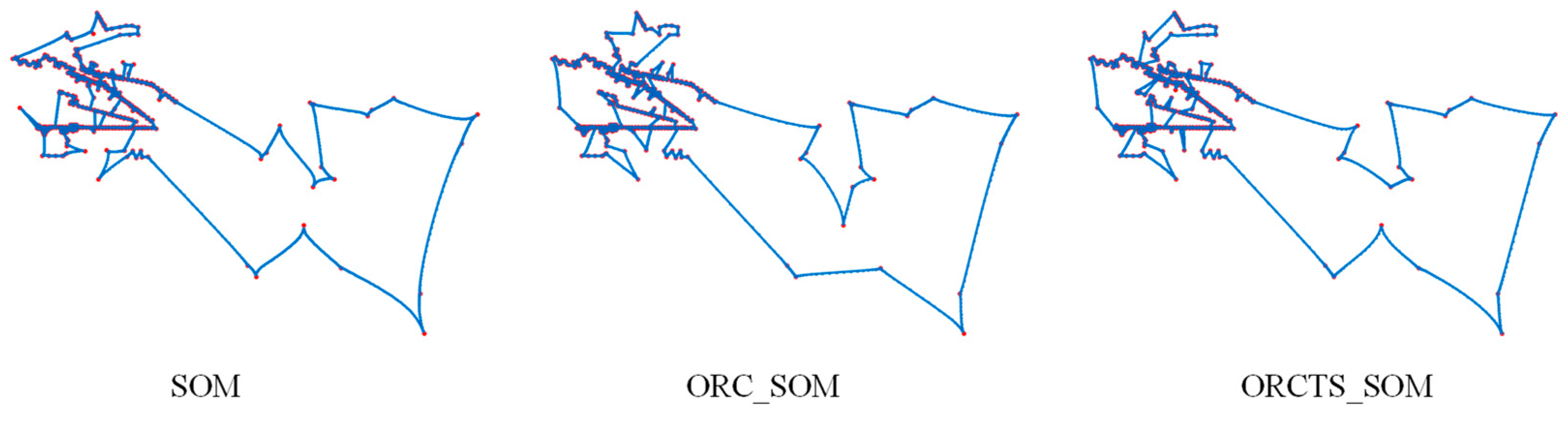
4.1.1. Path Planning of Navigation Mark UAV Inspection in Pingtan Waters
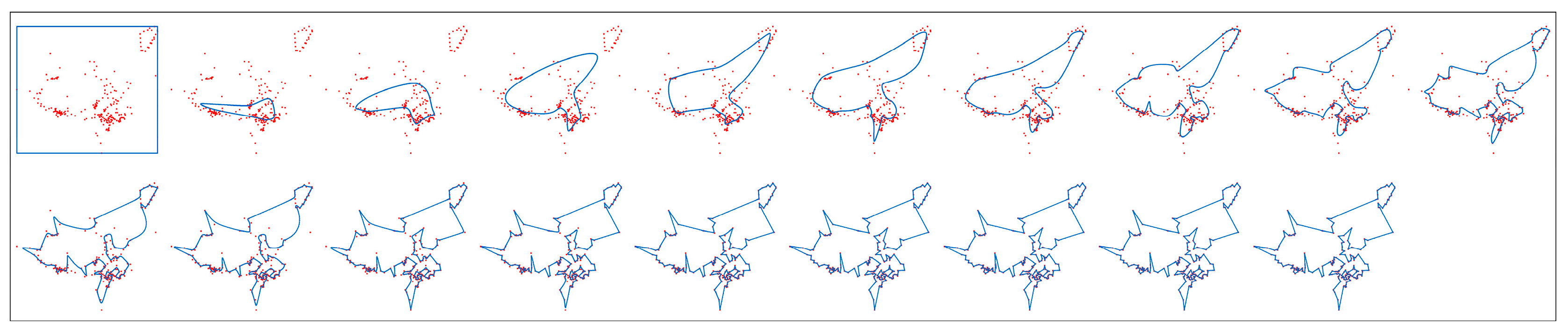
4.1.2. Path Planning of Navigation Mark UAV Inspection in Tianjin Waters
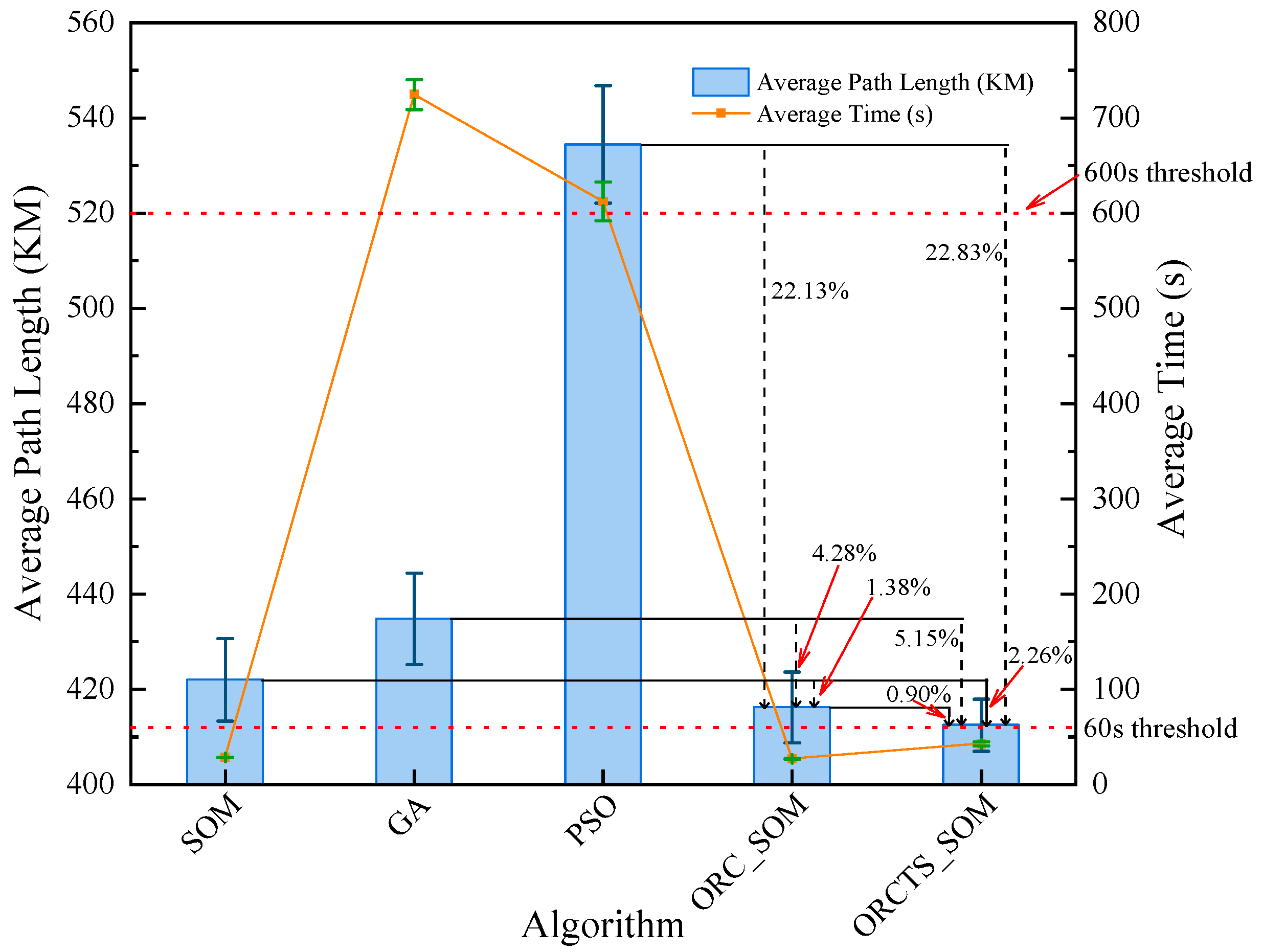
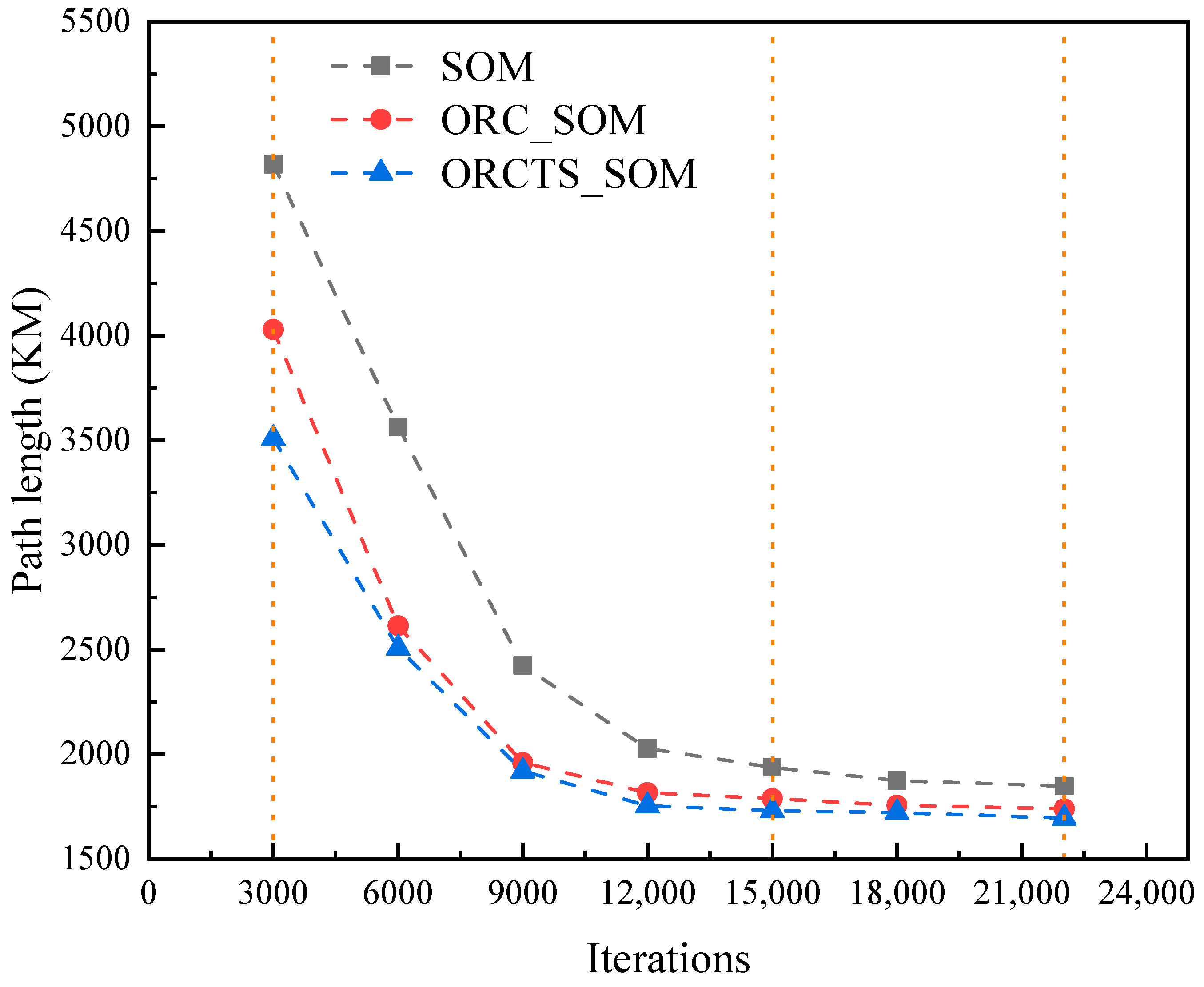
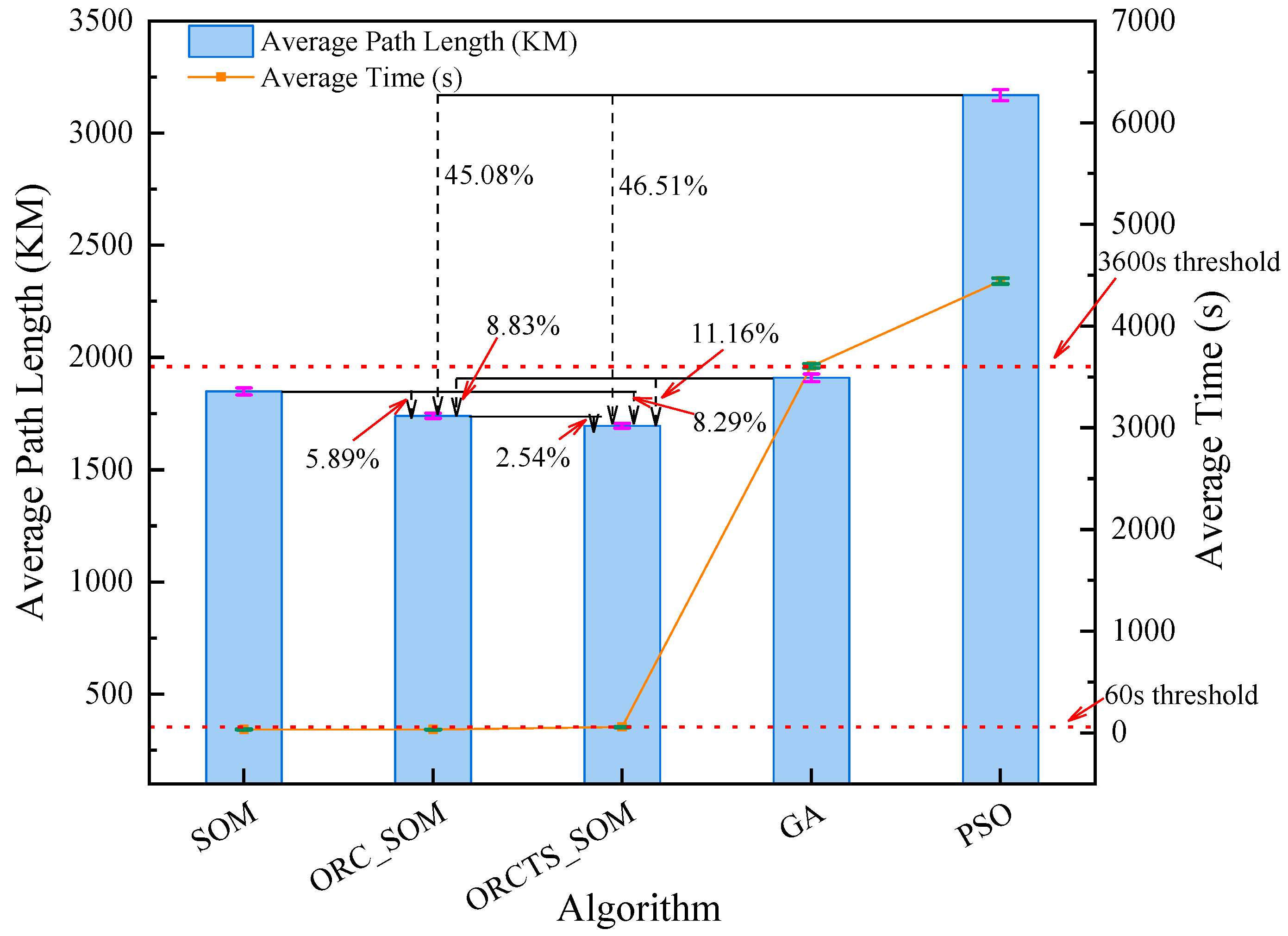
4.2. Discussion of Experimental Results
- (1)
- For small-medium scale navigation mark data in Pingtan waters.
- (2)
- For large scale navigation mark data in Tianjin waters.
5. Conclusions
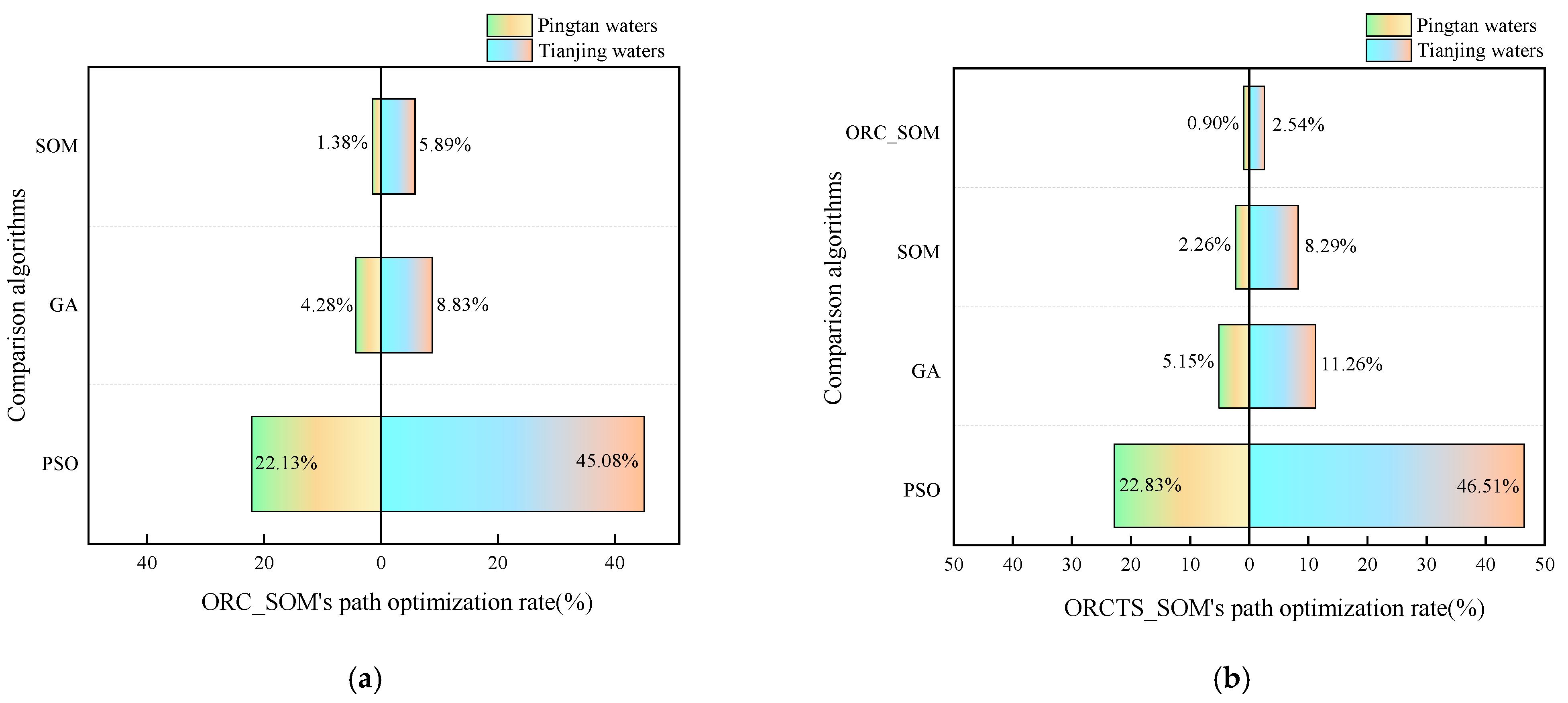
- (1)
- In terms of path optimization rate, ORCTS_SOM optimization is the best, reaching 2.26%~22.83% and 8.29%~46.51%, respectively; ORC_SOM is the second best, reaching 1.38%~22.13% and 5.89%~45.08%, respectively, in which the ORCTS_SOM algorithm improves by 0.90%~2.54% compared to the ORC_SOM algorithm.
- (2)
- In terms of average running time, when practically applied to navigation mark data of different sizes, the response time of the two improved SOM algorithms can be kept within 1 min, which has high running efficiency and fully meets the real-time requirements of UAV navigation mark inspection.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sim, Y.; Chae, C.-J. Enhancing the Function of the Aids to Navigation by Practical Usage of the Deep Learning Algorithm. J. Navig. 2024, 77, 347–358. [Google Scholar] [CrossRef]
- Song, W.; Guo, J.; Wang, Y.; Li, L. An Evaluation of the Development of the Ocean Economy in China Using an Ocean Economic Development Index. Mar. Policy 2021, 132, 104691. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Liu, R.W.; Wu, H.; Han, B.; Zhao, J. Quantifying Arctic oil spilling event risk by integrating an analytic network process and a fuzzy comprehensive evaluation model. Ocean Coast. Manage. 2022, 228, 106326. [Google Scholar] [CrossRef]
- Maghazei, O.; Netland, T. Drones in manufacturing: Exploring opportunities for research and practice. J. Manuf. Technol. Manag. 2020, 31, 1237–1259. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, K.; Xing, W.; Li, H.; Yang, Z. Applications, evolutions, and challenges of drones in maritime transport. J. Mar. Sci. Eng. 2023, 11, 2056. [Google Scholar] [CrossRef]
- Guebsi, R.; Mami, S.; Chokmani, K. Drones in precision agriculture: A comprehensive review of applications, technologies, and challenges. Drones 2024, 8, 686. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Othman, N.Q.H.; Li, Y.; Alsharif, M.H.; Khan, M.A. Unmanned aerial vehicles (UAVs): Practical aspects, applications, open challenges, security issues, and future trends. Intell. Serv. Robot. 2023, 16, 109–137. [Google Scholar] [CrossRef]
- Yan, C.; Xiang, X.; Wang, C. Towards real-time path planning through deep reinforcement learning for a UAV in dynamic environments. J. Intell. Robot. Syst. 2020, 98, 297–309. [Google Scholar] [CrossRef]
- Koulianos, A.; Litke, A. Blockchain technology for secure communication and formation control in smart drone swarms. Future Internet 2023, 15, 344. [Google Scholar] [CrossRef]
- Quero, C.O.; Martinez-Carranza, J. Unmanned aerial systems in search and rescue: A global perspective on current challenges and future applications. Int. J. Disaster Risk Reduct. 2025, 118, 105199. [Google Scholar] [CrossRef]
- Kerle, N.; Nex, F.; Gerke, M.; Duarte, D.; Vetrivel, A. UAV-based structural damage mapping: A review. ISPRS Int. J. Geo-Inf. 2019, 9, 14. [Google Scholar] [CrossRef]
- Shan, J.; Zhu, H.; Yu, R. Feasibility of Accurate Point Cloud Model Reconstruction for Earthquake-Damaged Structures Using UAV-Based Photogrammetry. Struct. Control Health Monit. 2023, 2023, 7743762. [Google Scholar] [CrossRef]
- Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An overview of small unmanned aerial vehicles for air quality measurements: Present applications and future prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, J.; Li, X.; Ahmed, S.H.; Lim, W.Y.B.; Miao, C. Federated learning in the sky: Aerial-ground air quality sensing framework with UAV swarms. IEEE Internet Things J. 2020, 8, 9827–9837. [Google Scholar] [CrossRef]
- Bakirci, M. Efficient air pollution mapping in extensive regions with fully autonomous unmanned aerial vehicles: A numerical perspective. Sci. Total Environ. 2024, 909, 168606. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Lizaga, I.; Zhang, Y.; Ge, X.; Zhang, Z.; Zhang, W.; Huang, Q.; Hu, Z. UAS-based remote sensing for agricultural Monitoring: Current status and perspectives. Comput. Electron. Agric. 2024, 227, 109501. [Google Scholar] [CrossRef]
- Velusamy, P.; Rajendran, S.; Mahendran, R.K.; Naseer, S.; Shafiq, M.; Choi, J.-G. Unmanned Aerial Vehicles (UAV) in precision agriculture: Applications and challenges. Energies 2021, 15, 217. [Google Scholar] [CrossRef]
- Kouadio, L.; El Jarroudi, M.; Belabess, Z.; Laasli, S.-E.; Roni, Z.K.; Amine, I.D.I.; Mokhtari, N.; Mokrini, F.; Junk, J.; Lahlali, R. A review on UAV-based applications for plant disease detection and monitoring. Remote Sens. 2023, 15, 4273. [Google Scholar] [CrossRef]
- Najy, W.; Archetti, C.; Diabat, A. Collaborative truck-and-drone delivery for inventory-routing problems. Transp. Res. Part C Emerg. Technol. 2023, 146, 103791. [Google Scholar] [CrossRef]
- Garg, V.; Niranjan, S.; Prybutok, V.; Pohlen, T.; Gligor, D. Drones in last-mile delivery: A systematic review on Efficiency, Accessibility, and Sustainability. Transp. Res. Part D Transp. Environ. 2023, 123, 103831. [Google Scholar] [CrossRef]
- Li, X.; Tupayachi, J.; Sharmin, A.; Martinez Ferguson, M. Drone-aided delivery methods, challenge, and the future: A methodological review. Drones 2023, 7, 191. [Google Scholar] [CrossRef]
- Mendu, B.; Mbuli, N. State-of-the-Art Review on the Application of Unmanned Aerial Vehicles (UAVs) in Power Line Inspections: Current Innovations, Trends, and Future Prospects. Drones 2025, 9, 265. [Google Scholar] [CrossRef]
- Panigati, T.; Zini, M.; Striccoli, D.; Giordano, P.F.; Tonelli, D.; Limongelli, M.P.; Zonta, D. Drone-based bridge inspections: Current practices and future directions. Autom. Constr. 2025, 173, 106101. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D.; Jachimowicz, A.; Devaney, C. Utilizing UAV and 3D computer vision for visual inspection of a large gravity dam. Front. Built Environ. 2018, 4, 386907. [Google Scholar] [CrossRef]
- Li, B.; Gao, S.; Li, C.; Wan, H. Maritime buoyage inspection system based on an unmanned aerial vehicle and active disturbance rejection control. IEEE Access 2021, 9, 22883–22893. [Google Scholar] [CrossRef]
- Jünger, M.; Reinelt, G.; Rinaldi, G. The traveling salesman problem. Handb. Oper. Res. Manag. Sci. 1995, 7, 225–330. [Google Scholar] [CrossRef]
- Jadczak, R. Traveling salesman problem: Approach to optimality. Przeds. Zarz. 2014, 15, 157–169. [Google Scholar] [CrossRef][Green Version]
- Dahiya, C.; Sangwan, S. Literature review on travelling salesman problem. Int. J. Res. 2018, 5, 1152–1155. Available online: https://journals.pen2print.org/index.php/ijr/article/download/15490/15018 (accessed on 20 June 2025).
- Karp, R.M. Reducibility among combinatorial problems. In 50 Years of Integer Programming 1958–2008: From the Early Years to the State-of-the-Art; Springer: Heidelberg, Germany, 2009; pp. 219–241. [Google Scholar] [CrossRef]
- Pop, P.C.; Cosma, O.; Sabo, C.; Sitar, C.P. A comprehensive survey on the generalized traveling salesman problem. Eur. J. Oper. Res. 2024, 314, 819–835. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, L.; Du, Z.; Lv, Y. Mixed steepest descent algorithm for the traveling salesman problem and application in air logistics. Transp. Res. Part E Logist. Transp. Rev. 2019, 126, 87–102. [Google Scholar] [CrossRef]
- Glocker, M.; von Stryk, O. Hybrid optimal control of motorized traveling salesmen and beyond. IFAC Proc. Vol. 2002, 35, 439–444. [Google Scholar] [CrossRef]
- Dong, X.; Ma, L.; Zhao, X.; Shan, Y.; Wang, J.; Xu, Z. Hybrid genetic algorithm with Wiener process for multi-scale colored balanced traveling salesman problem. Expert Syst. Appl. 2025, 262, 125610. [Google Scholar] [CrossRef]
- Mahmoudinazlou, S.; Kwon, C. A hybrid genetic algorithm for the min-max Multiple Traveling Salesman Problem. Comput. Oper. Res. 2024, 162, 106455. [Google Scholar] [CrossRef]
- Yildiz, B.; Aslan, M.F.; Durdu, A.; Kayabasi, A. Consensus-based virtual leader tracking swarm algorithm with GDRRT*-PSO for path-planning of multiple-UAVs. Swarm Evol. Comput. 2024, 88, 101612. [Google Scholar] [CrossRef]
- Ten Kathen, M.J.; Peralta, F.; Johnson, P.; Flores, I.J.; Reina, D.G. AquaFeL-PSO: An informative path planning for water resources monitoring using autonomous surface vehicles based on multi-modal PSO and federated learning. Ocean Eng. 2024, 311, 118787. [Google Scholar] [CrossRef]
- Ke, C.; Chen, H. Cooperative path planning for air-sea heterogeneous unmanned vehicles using search-and-tracking mission. Ocean Eng. 2022, 262, 112020. [Google Scholar] [CrossRef]
- Heng, H.; Ghazali, M.H.M.; Rahiman, W. Exploring the application of ant colony optimization in path planning for Unmanned Surface Vehicles. Ocean Eng. 2024, 311, 118738. [Google Scholar] [CrossRef]
- Sui, F.; Tang, X.; Dong, Z.; Gan, X.; Luo, P.; Sun, J. ACO+PSO+A*: A bi-layer hybrid algorithm for multi-task path planning of an AUV. Comput. Ind. Eng. 2023, 175, 108905. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, J.; Xu, L.; Wang, J. Cooperative path planning study of distributed multi-mobile robots based on optimised ACO algorithm. Robot. Auton. Syst. 2024, 179, 104748. [Google Scholar] [CrossRef]
- Sui, J.; Ding, S.; Huang, X.; Yu, Y.; Liu, R.; Xia, B.; Ding, Z.; Xu, L.; Zhang, H.; Yu, C.; et al. A survey on deep learning-based algorithms for the traveling salesman problem. Front. Comput. Sci. 2025, 19, 196322. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, C.; Wang, S.; Ruan, Y. Reinforcement learning for the traveling salesman problem: Performance comparison of three algorithms. J. Eng. 2023, 2023, e12303. [Google Scholar] [CrossRef]
- Ling, Z.; Zhou, Y.; Zhang, Y. Solving multiple travelling salesman problem through deep convolutional neural network. IET Cyber-Syst. Robot. 2023, 5, e12084. [Google Scholar] [CrossRef]
- Stohy, A.; Abdelhakam, H.-T.; Ali, S.; Elhenawy, M.; Hassan, A.A.; Masoud, M.; Glaser, S.; Rakotonirainy, A.; Mirjalili, S. Hybrid pointer networks for traveling salesman problems optimization. PLoS ONE 2021, 16, e0260995. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. Event-Driven Based Reinforcement Learning Predictive Controller Design for Three-Phase NPC Converters Using Online Approximator. IEEE Trans. Power Electron. 2024, 40, 4914–4926. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, M.; Yuan, L.; Yu, Y.; Li, Z.; Gu, M. Memory-efficient transformer-based network model for traveling salesman problem. Neural Netw. 2023, 161, 589–597. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Li, M.; Zhang, C.; Chen, H.; Zhong, P.; Li, Z.; Li, J. A self-organizing map approach for constrained multi-objective optimization problems. Complex Intell. Syst. 2022, 8, 5355–5375. [Google Scholar] [CrossRef]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Kuo, R.; Chang, K.; Chien, S. Integration of self-organizing feature maps and genetic-algorithm-based clustering method for market segmentation. J. Organ. Comput. Electron. Commer. 2004, 14, 43–60. [Google Scholar] [CrossRef]
- Begum, M.; Das, B.C.; Hossain, M.Z.; Saha, A.; Papry, K.A. An improved Kohonen self-organizing map clustering algorithm for high-dimensional data sets. Indones. J. Electr. Eng. Comput. Sci. 2021, 24, 600–610. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, N.; Créput, J.-C. A massively parallel neural network approach to large-scale Euclidean traveling salesman problems. Neurocomputing 2017, 240, 137–151. [Google Scholar] [CrossRef]
- Ma, X.; Chen, Y.; Bai, G.; Sha, Y.; Zhu, X. Path planning and task assignment of the multi-AUVs system based on the hybrid bio-inspired SOM algorithm with neural wave structure. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 28. [Google Scholar] [CrossRef]
- Guan, Q.; Hong, X.; Ke, W.; Zhang, L.; Sun, G.; Gong, Y. Kohonen self-organizing map based route planning: A revisit. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar] [CrossRef]
- Zhu, J.; Ye, H.; Yao, L.; Cai, Y. Algorithm for solving traveling salesman problem based on self-organizing mapping network. J. Shanghai Jiaotong Univ. (Sci.) 2024, 29, 463–470. [Google Scholar] [CrossRef]
- Khalid, A.N.; Baki, N.M.R.; Varma, T.S.P.; Khan, A.; Singh, N. Tabu Search Algorithm: Optimizing the Search Runtime. In Proceedings of the 2024 5th International Conference for Emerging Technology (INCET), Belgaum, India, 24–26 May 2024. [Google Scholar] [CrossRef]
- Gouveia, L. Using the Miller-Tucker-Zemlin constraints to formulate a minimal spanning tree problem with hop constraints. Comput. Oper. Res. 1995, 22, 959–970. [Google Scholar] [CrossRef]
- Bektaş, T.; Gouveia, L. Requiem for the Miller-Tucker-Zemlin subtour elimination constraints? Eur. J. Oper. Res. 2014, 236, 820–832. [Google Scholar] [CrossRef]



| Algorithm Category | Algorithm | Time Complexity | Space Complexity | Embedded Adaptability |
|---|---|---|---|---|
| Traditional Heuristics | GA | O (G × P × n2) | O (P × n) | Poor |
| PSO | O (G × S × n2) | O (S × n) | Poor | |
| ACO | O (T × m × n2) | O (m × n2) | Poor | |
| Deep Learning | Double Q-Learning | O (n2 × d × E) | O (n2 × d) | Very Poor |
| Deep CNN-based Methods | O (L × F × H × W) | O (L × F × H × W) | Very Poor | |
| Transformer | O (n2 × d) | O (n2 × d) | Very Poor | |
| Neural Networks | Traditional SOM | O (n2) | O (m × n) | Excellent |
| Hopfield Neural Network | O (n3) | O (n2) | Poor | |
| Graph Neural Network (GNN) | O (n2 × d) | O (n2 × d) | Very Poor | |
| Pointer Network | O (n2 × d) | O (n × d) | Very Poor |
| No. | Name | Latitude | Longitude |
|---|---|---|---|
| 1 | Dongxiang Island Lighthouse | 25°36′10.9″ N | 119°54′04.0″ E |
| 2 | Niushan Lighthouse | 25°26′04.0″ N | 119°56′12.9″ E |
| … | … | … | … |
| 273 | Lantau lamp post | 25°37′47.1″ N | 119°33′57.1″ E |
| 274 | Su’ao lamp post | 25°37′05.6″ N | 119°41′54.3″ E |
| No. | Name | Latitude | Longitude |
|---|---|---|---|
| 1 | Beating RBN-DGPS station | 38°50′11.6″ N | 117°30′17.5″ E |
| 2 | Shanggulin navigation station | 39°6′24″ N | 117°43′12″ E |
| … | … | … | … |
| 741 | Haihe L7 light buoy | 38°59′34.6″ N | 117°40′6.8″ E |
| 742 | Haihe L8 light buoy | 38°59′34.5″ N | 117°40′9.7″ E |
| No. | Latitude (°) | Longitude (°) | X-Axis (Km) | Y-Axis (Km) |
|---|---|---|---|---|
| 1 | 25.6030 | 119.9011 | 34.8769 | 43.2305 |
| 2 | 25.4344 | 119.9369 | 16.1432 | 46.8866 |
| … | … | … | … | … |
| 273 | 25.6298 | 119.5659 | 37.7819 | 9.6105 |
| 274 | 25.6182 | 119.6984 | 36.5162 | 22.9021 |
| No. | Latitude (°) | Longitude (°) | X-Axis (Km) | Y-Axis (Km) |
|---|---|---|---|---|
| 1 | 38.83656 | 117.5049 | −18.3511 | 44.35134 |
| 2 | 39.10667 | 117.72 | 10.88384 | 91.49462 |
| … | … | … | … | … |
| 744 | 38.99294 | 117.6686 | 3.89313 | 71.64635 |
| 745 | 38.99292 | 117.6694 | 4.002595 | 71.6415 |
| Algorithm | Path Length σ (KM) | Computation Time σ (s) |
|---|---|---|
| SOM | 8.68 | 0.26 |
| ORC-SOM | 7.43 | 0.36 |
| ORCTS-SOM | 5.47 | 2.08 |
| PSO | 12.35 | 20.46 |
| GA | 9.62 | 15.69 |
| Algorithm | Path Length σ (KM) | Computation Time σ (s) |
|---|---|---|
| SOM | 15.96 | 1.24 |
| ORC-SOM | 12.18 | 0.29 |
| ORCTS-SOM | 10.33 | 1.07 |
| PSO | 24.72 | 28.35 |
| GA | 16.45 | 19.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Zhu, Z.; Hu, Z.; Cai, L.; Chen, X.; Wang, X. A Study on UAV Path Planning for Navigation Mark Inspection Using Two Improved SOM Algorithms. J. Mar. Sci. Eng. 2025, 13, 1537. https://doi.org/10.3390/jmse13081537
Xu L, Zhu Z, Hu Z, Cai L, Chen X, Wang X. A Study on UAV Path Planning for Navigation Mark Inspection Using Two Improved SOM Algorithms. Journal of Marine Science and Engineering. 2025; 13(8):1537. https://doi.org/10.3390/jmse13081537
Chicago/Turabian StyleXu, Liangkun, Zaiwei Zhu, Zhihui Hu, Liyan Cai, Xinqiang Chen, and Xiaomeng Wang. 2025. "A Study on UAV Path Planning for Navigation Mark Inspection Using Two Improved SOM Algorithms" Journal of Marine Science and Engineering 13, no. 8: 1537. https://doi.org/10.3390/jmse13081537
APA StyleXu, L., Zhu, Z., Hu, Z., Cai, L., Chen, X., & Wang, X. (2025). A Study on UAV Path Planning for Navigation Mark Inspection Using Two Improved SOM Algorithms. Journal of Marine Science and Engineering, 13(8), 1537. https://doi.org/10.3390/jmse13081537







