Nonlinear Effects on the Formation of Large Random Wave Events
Abstract
1. Introduction and Background
2. Methodology and Setup
2.1. Wave Modelling
2.2. Initial Conditions and Setup
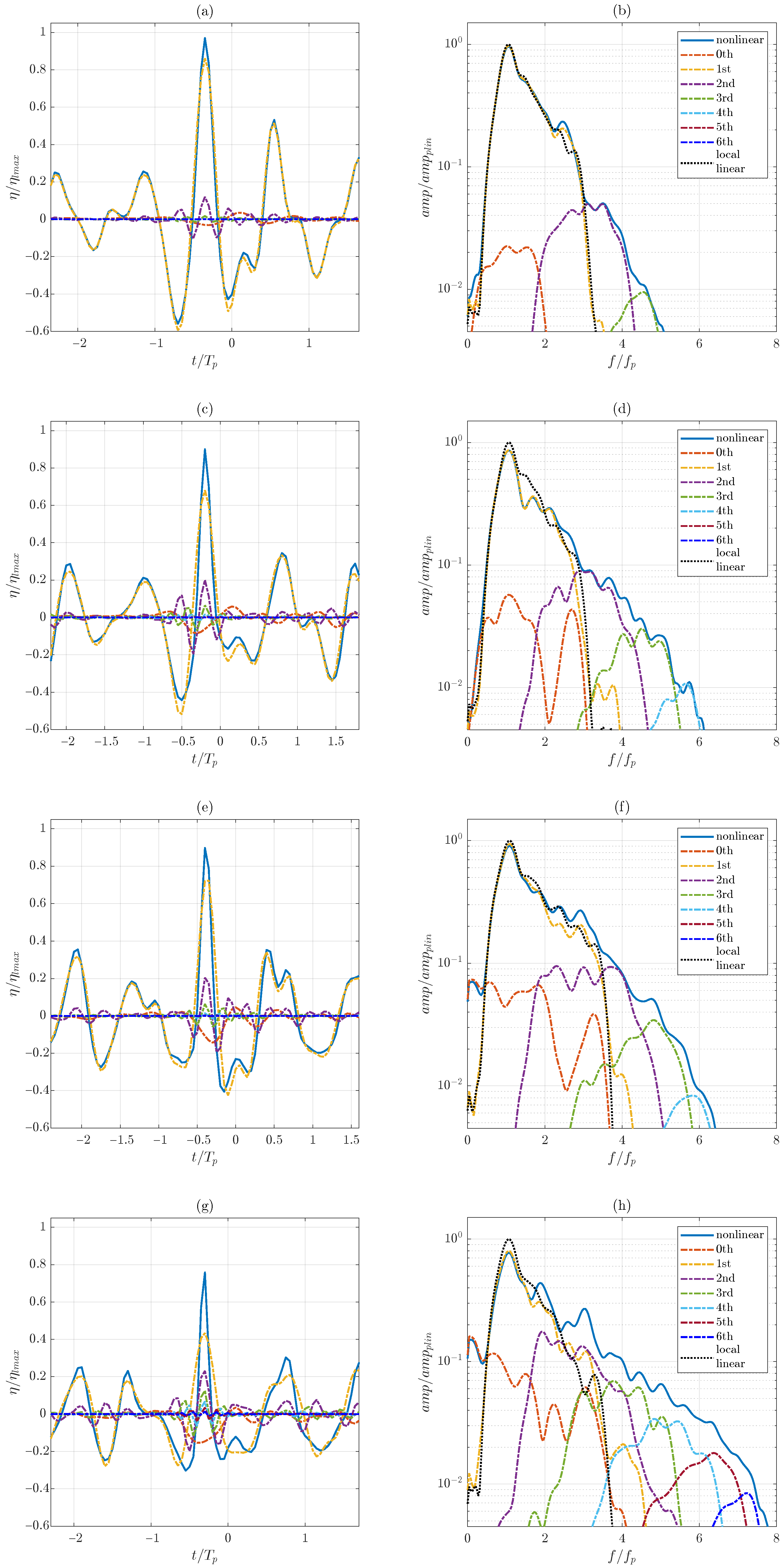
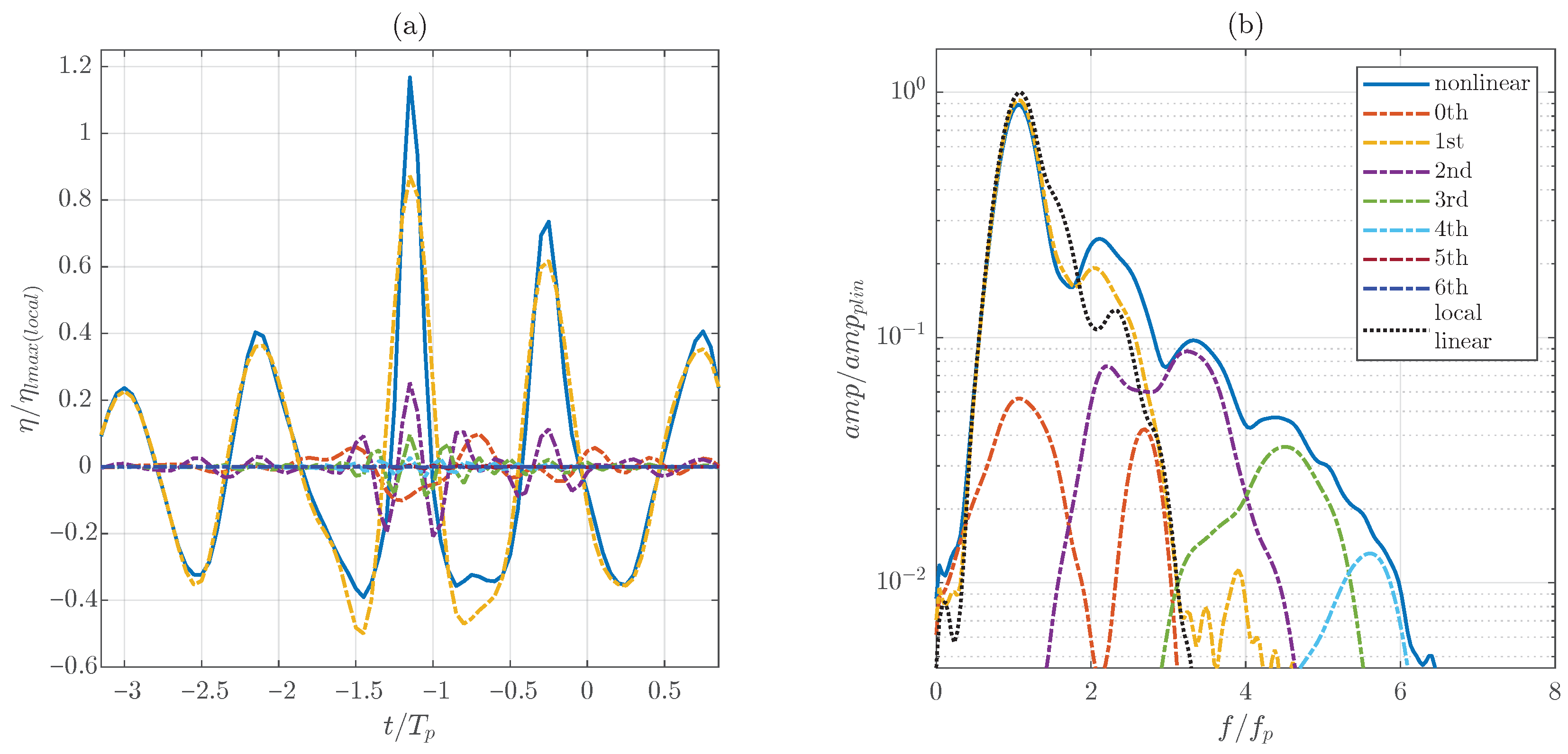
2.3. Nonlinear Harmonic Separation
3. Results
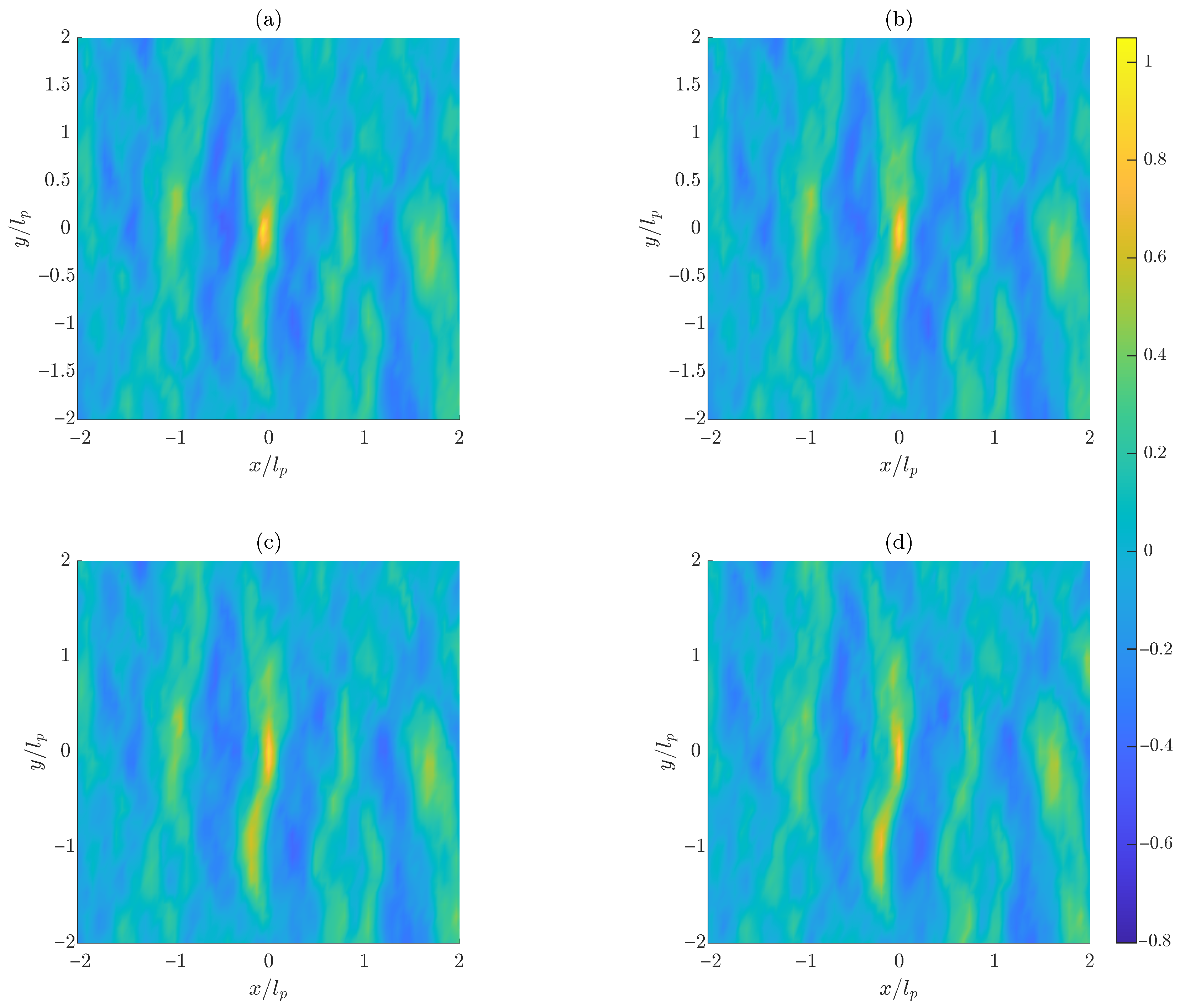
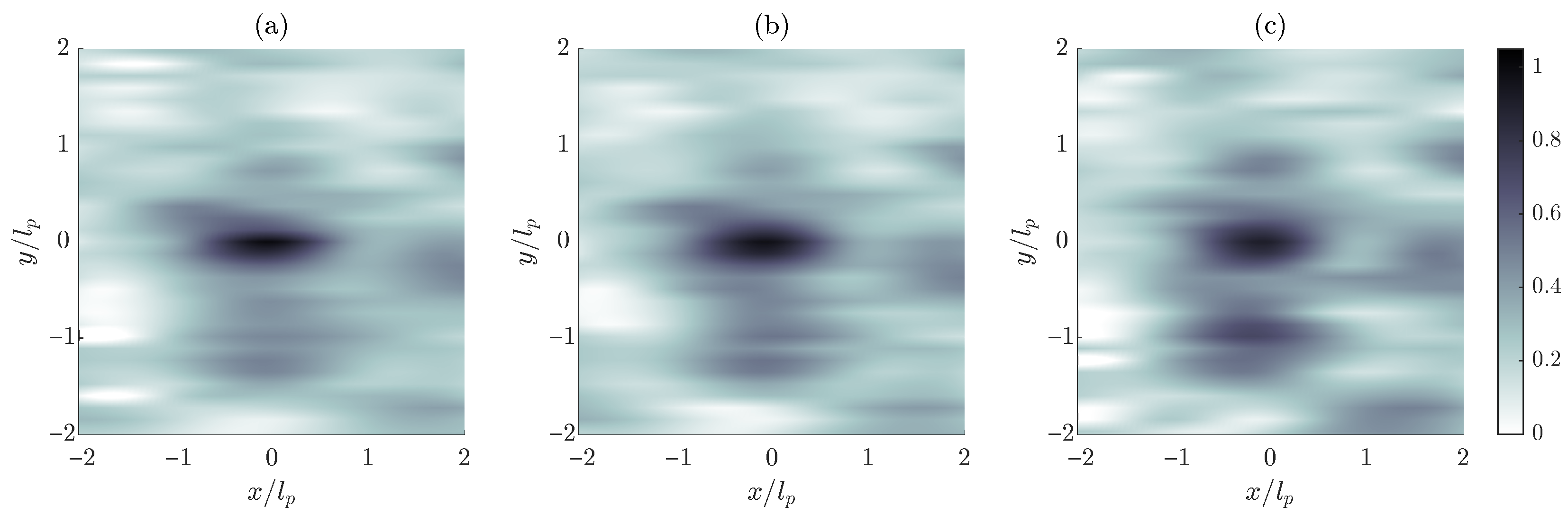
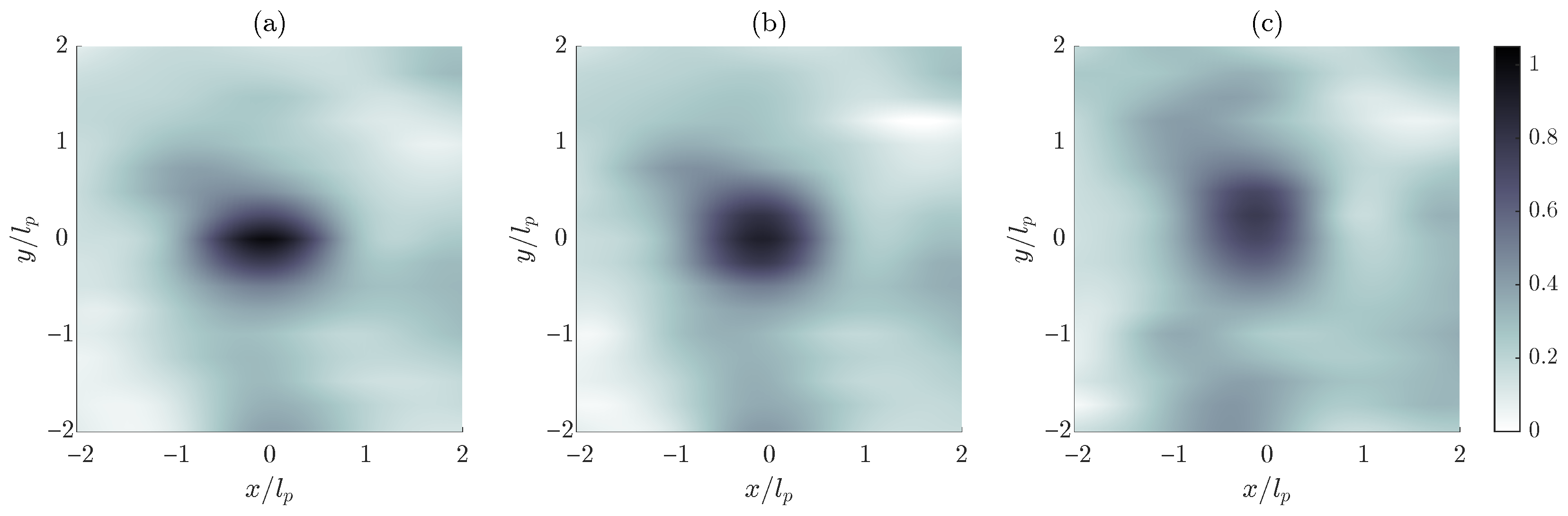
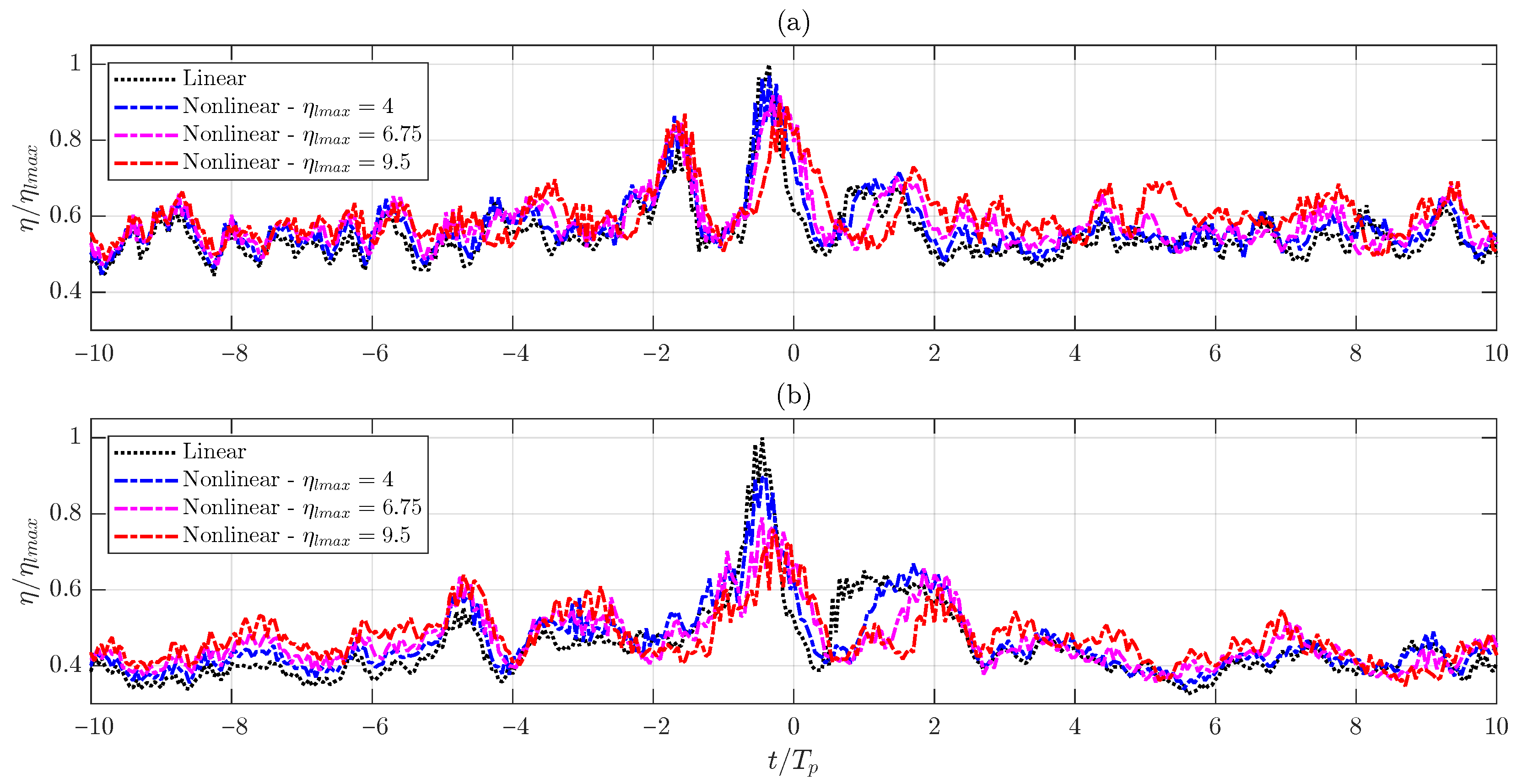
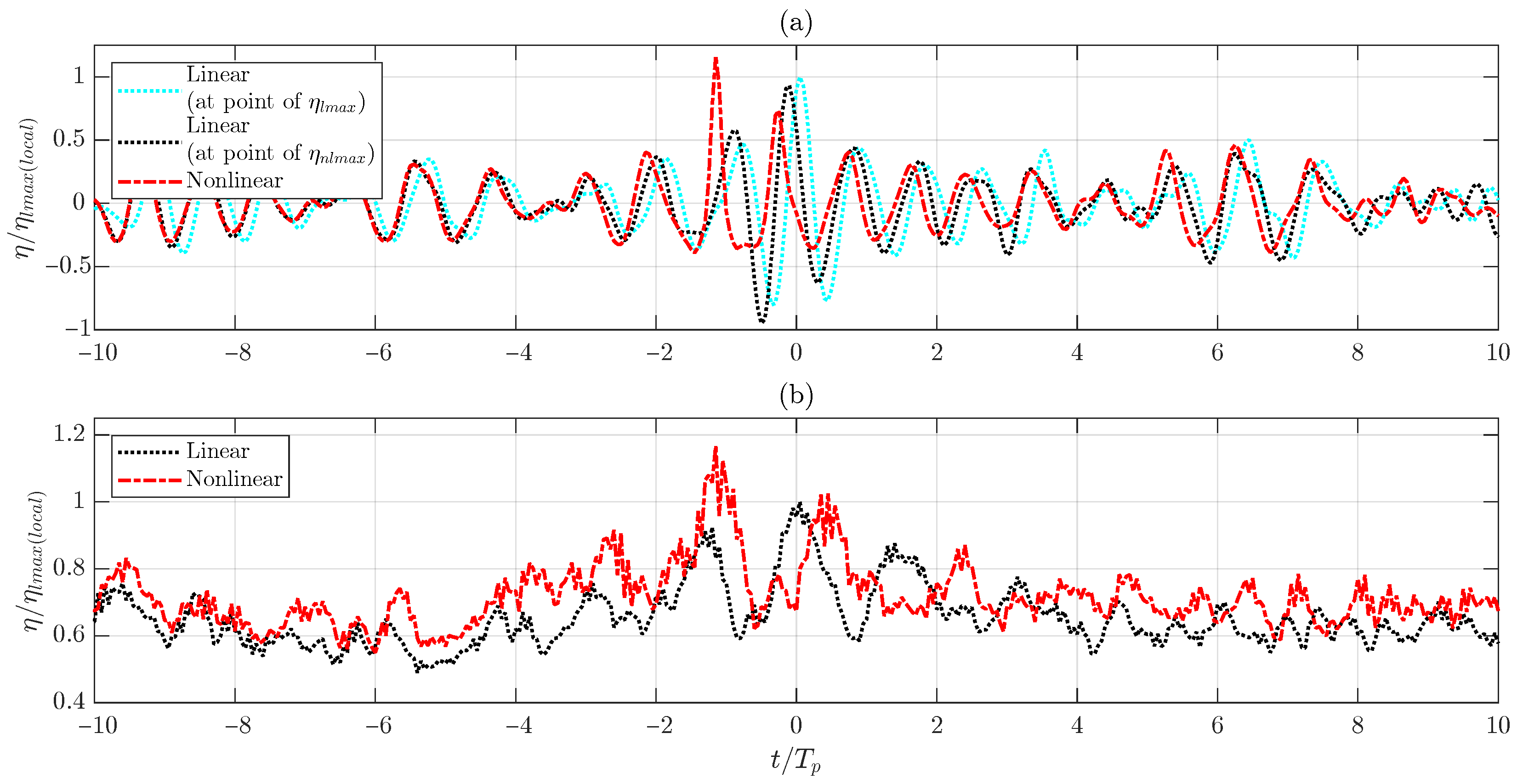
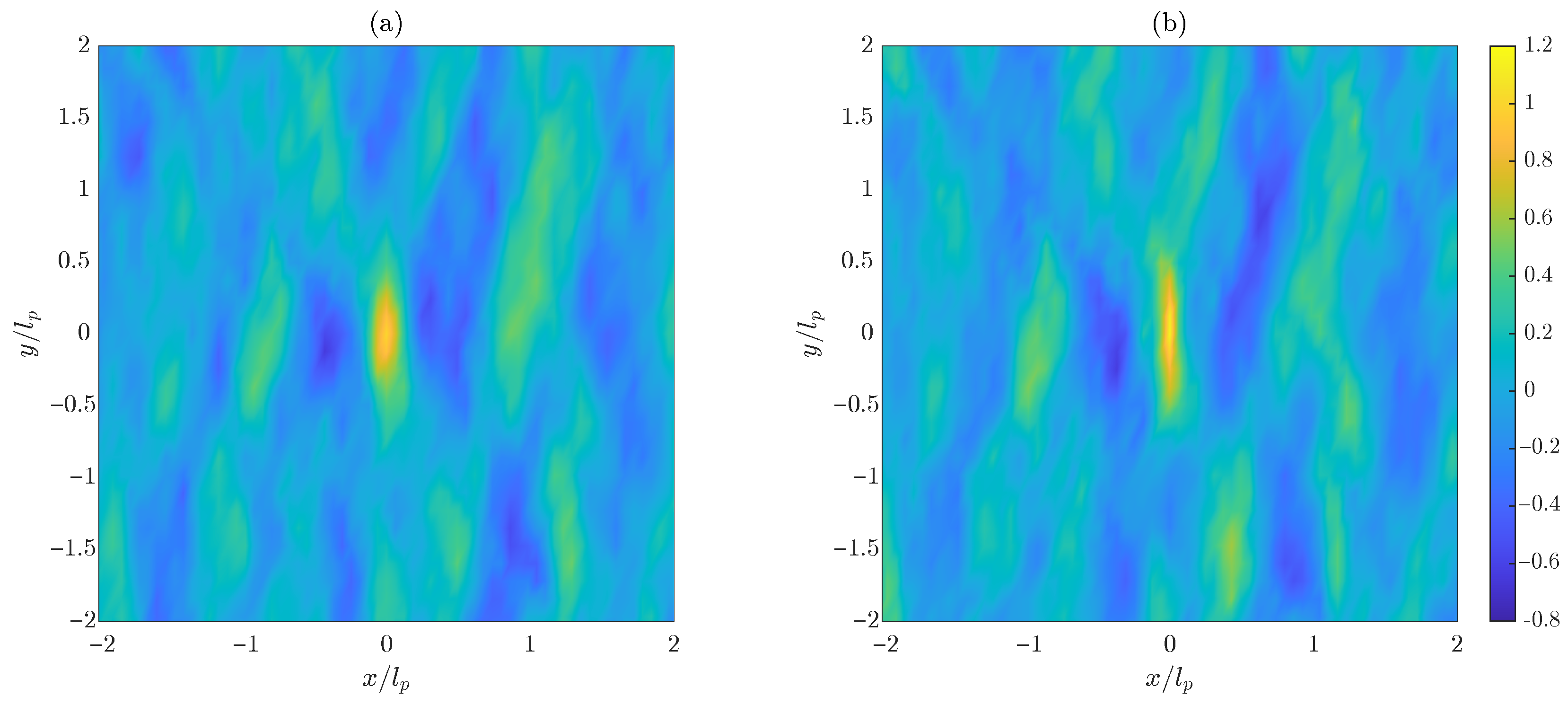
3.1. Changes in the Crest Width
3.2. Time and Frequency Domain Analysis
3.3. Changes in Crest Height
4. Discussion and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Nonlinear Harmonic Separation Scheme
References
- Boccotti, P. Wave Mechanics for Ocean Engineering, 1st ed.; Number 64 in Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Faltinsen, O. Hydrodynamics of marine and offshore structures. J. Hydrodyn. Ser. B 2015, 26, 835–847. [Google Scholar] [CrossRef]
- DNV. RP-C205 Environmental Conditions and Environmental Loads. Technical Report, DNV, 2025. Available online: https://www.dnv.com/energy/standards-guidelines/dnv-rp-c205-environmental-conditions-and-environmental-loads/ (accessed on 2 August 2025).
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Christou, M.; Ewans, K. Field Measurements of Rogue Water Waves. J. Phys. Oceanogr. 2014, 44, 2317–2335. [Google Scholar] [CrossRef]
- Cavaleri, L.; Barbariol, F.; Benetazzo, A.; Bertotti, L.; Bidlot, J.R.; Janssen, P.; Wedi, N. The Draupner Wave: A Fresh Look and the Emerging View. J. Geophys. Res. Ocean 2016, 121, 6061–6075. [Google Scholar] [CrossRef]
- Fedele, F.; Lugni, C.; Chawla, A. The Sinking of the El Faro: Predicting Real World Rogue Waves during Hurricane Joaquin. Sci. Rep. 2017, 7, 11188. [Google Scholar] [CrossRef] [PubMed]
- Dysthe, K.; Krogstad, H.E.; Müller, P. Oceanic Rogue Waves. Annu. Rev. Fluid Mech. 2008, 40, 287–310. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Taylor, P.H.; Draper, S. Nonlinear Dynamics of Wave-Groups in Random Seas: Unexpected Walls of Water in the Open Ocean. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 20150660. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Taylor, P.H.; Draper, S. On the Shape of Large Wave-Groups on Deep Water—The Influence of Bandwidth and Spreading. Phys. Fluids 2016, 28, 106601. [Google Scholar] [CrossRef]
- Gibbs, R.H.; Taylor, P.H. Formation of Walls of Water in `Fully’ Nonlinear Simulations. Appl. Ocean Res. 2005, 27, 142–157. [Google Scholar] [CrossRef]
- Chalikov, D. Freak Waves: Their Occurrence and Probability. Phys. Fluids 2009, 21, 076602. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Le Touzé, D.; Ferrant, P. 3-D HOS Simulations of Extreme Waves in Open Seas. Nat. Hazards Earth Syst. Sci. 2007, 7, 109–122. [Google Scholar] [CrossRef]
- Spiliotopoulos, G.; Katsardi, V. Effects of Nonlinearity on the Crest Shape of Extreme Irregular Sea Waves: Nonlinear Harmonic Separation and Analysis. Phys. Fluids 2024, 36, 106604. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Le Touzé, D.; Ferrant, P. HOS-ocean: Open-source Solver for Nonlinear Waves in Open Ocean Based on High-Order Spectral Method. Comput. Phys. Commun. 2016, 203, 245–254. [Google Scholar] [CrossRef]
- Tromans, P.S.; Anaturk, A.R.; Hagemeijer, P. A New Model For The Kinematics Of Large Ocean Waves-Application As a Design Wave. In Proceedings of the First International Offshore and Polar Engineering Conference, Edinburgh, UK, 11 August 1991. [Google Scholar]
- Boccotti, P. Some New Results on Statistical Properties of Wind Waves. Appl. Ocean Res. 1983, 5, 134–140. [Google Scholar] [CrossRef]
- Katsardi, V.; Swan, C. The Importance of Directionality in the Evolution of Large Waves in Intermediate and Shallow Water. In Proceedings of the 29th International Conference of Coastal Engineering 2006, San Diego, CA, USA, 3–8 September 2007; pp. 157–169. [Google Scholar] [CrossRef]
- Katsardi, V.; Swan, C. The Evolution of Large Non-Breaking Waves in Intermediate and Shallow Water. I. Numerical Calculations of Uni-Directional Seas. Proc. R. Soc. Math. Phys. Eng. Sci. 2011, 467, 778–805. [Google Scholar] [CrossRef]
- Johannessen, T.B.; Swan, C. On the Nonlinear Dynamics of Wave Groups Produced by the Focusing of Surface–Water Waves. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 2003, 459, 1021–1052. [Google Scholar] [CrossRef]
- Walker, D.A.G.; Taylor, P.H.; Eatock Taylor, R. The Shape of Large Surface Waves on the Open Sea and the Draupner New Year Wave. Appl. Ocean. Res. 2004, 26, 73–83. [Google Scholar] [CrossRef]
- Gibson, R.; Swan, C. The Evolution of Large Ocean Waves: The Role of Local and Rapid Spectral Changes. Proc. R. Soc. Math. Phys. Eng. Sci. 2007, 463, 21–48. [Google Scholar] [CrossRef]
- Fitzgerald, C.J.; Taylor, P.H.; Taylor, R.E.; Grice, J.; Zang, J. Phase Manipulation and the Harmonic Components of Ringing Forces on a Surface-Piercing Column. Proc. R. Soc. Math. Phys. Eng. Sci. 2014, 470, 20130847. [Google Scholar] [CrossRef]
- Hann, M.; Greaves, D.; Raby, A. A New Set of Focused Wave Linear Combinations to Extract Non-Linear Wave Harmonics. In Proceedings of the 29th International Workshop on Water Waves and Floating Bodies, Osaka, Japan, 30 March–2 April 2014. [Google Scholar]
- West, B.J.; Brueckner, K.A.; Janda, R.S.; Milder, D.M.; Milton, R.L. A New Numerical Method for Surface Hydrodynamics. J. Geophys. Res. Oceans 1987, 92, 11803–11824. [Google Scholar] [CrossRef]
- Dommermuth, D.G.; Yue, D.K.P. A High-Order Spectral Method for the Study of Nonlinear Gravity Waves. J. Fluid Mech. 1987, 184, 267–288. [Google Scholar] [CrossRef]
- Hasselman, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay During the Joint North Sea Wave Project (JONSWAP); Deutschen Hydrographischen Zeitschrift, Reihe A8. Nr. 12; Deutsches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Mitsuyasu, H.; Tasai, F.; Suhara, T.; Mizuno, S.; Ohkusu, M.; Honda, T.; Rikiishi, K. Observations of the Directional Spectrum of Ocean Waves Using a Cloverleaf Buoy. J. Phys. Oceanogr. 1975, 5, 750–760. [Google Scholar] [CrossRef]
- Forristall, G.Z.; Ewans, K.C. Worldwide Measurements of Directional Wave Spreading. J. Atmos. Ocean. Technol. 1998, 15, 440–469. [Google Scholar] [CrossRef]
- Kumar, V.; Deo, M.; Anand, N.; Chandramohan, P. Estimation of Wave Directional Spreading in Shallow Water. Ocean Eng. 1998, 26, 83–98. [Google Scholar] [CrossRef]
- Boccotti, P.; Arena, F.; Fiamma, V.; Romolo, A.; Barbaro, G. Estimation of Mean Spectral Directions in Random Seas. Ocean Eng. 2011, 38, 509–518. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Perignon, Y. Applicability and limitations of highly non-linear potential flow solvers in the context of water waves. Ocean Eng. 2017, 142, 233–244. [Google Scholar] [CrossRef]
- Fenton, J.D. Nonlinear Wave Theories. In The Sea–Ocean Engineering Science, Part A; Le Méhauté, B., Hanes, D.M., Eds.; Wiley: New York, NY, USA, 1990; Volume 9, pp. 3–25. [Google Scholar]
- Spiliotopoulos, G.; Katsardi, V. Effects of Nonlinearity on the Crest Shape of Extreme Irregular Sea Waves: Effects of Steepness, Water Depth and Directionality. In Proceedings of the The 34th International Ocean and Polar Engineering Conference, Rhodes, Greece, 16–21 June 2024. [Google Scholar]
- Zve, E.; Swan, C.; Hughes, G. Crest-Height Statistics in Finite Water Depth. Part 1: The Role of the Nonlinear Interactions in Uni-Directional Seas. Ocean Eng. 2023, 289, 116369. [Google Scholar] [CrossRef]
- Harleman, D.R.; Nolan, W.C.; Honsinger, V.C. Dynamic Analysis of Offshore Structures. In Proceedings of the Coastal Engineering Proceedings, Mexico City, Mexico, November 1962; Volume 8, pp. 482–499. [Google Scholar] [CrossRef]
- Chatziioannou, K.; Katsardi, V.; Koukouselis, A.; Mistakidis, E. On the Consideration of Wave and Structural Nonlinearities in the Design of Compliant Towers through Dynamic Analysis. J. Ocean. Eng. Mar. Energy 2018, 4, 323–342. [Google Scholar] [CrossRef]
- Gudmestad, O.T. Resonant Motions of Dynamic Offshore Structures in Large Waves. Fluids 2021, 6, 352. [Google Scholar] [CrossRef]



| d | s | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (m) | (rad/m) | (m) | (m) | (m) | |||||
| 4 | ∞ | 0.0402 | ∞ | 2.54 | 0.051 | 0.161 | 10 | 10,000 | 5000 | |
| 6.75 | ∞ | 0.0402 | ∞ | 4.28 | 0.086 | 0.271 | 10 | 10,000 | 5000 | |
| 9.5 | ∞ | 0.0402 | ∞ | 6.03 | 0.121 | 0.382 | 10 | 10,000 | 5000 | |
| 4 | 15 | 0.0576 | 0.864 | 1.77 | 0.051 | 0.230 | 45 | 7000 | 7000 | |
| 6.75 | 15 | 0.0576 | 0.864 | 2.99 | 0.086 | 0.389 | 45 | 7000 | 7000 | |
| 9.5 | 15 | 0.0576 | 0.864 | 4.21 | 0.121 | 0.547 | 45 | 7000 | 7000 |
| Linear | m | m | m | Linear | m | m | m | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.97 | 0.92 | 0.90 | 1 | 0.90 | 0.79 | 0.76 | |
| −0.35 | −0.35 | −0.20 | −0.20 | −0.45 | −0.40 | −0.45 | −0.30 | |
| −0.06 | 0 | +0.18 | +0.31 | −0.12 | 0 | +0.06 | +0.31 | |
| 0 | 0 | 0 | 0 | 0 | 0 | +0.25 | +0.25 |
| Linear | Nonlinear | |
|---|---|---|
| 0.86 | 1.01 | |
| 1 | 1.17 | |
| +0.05 | −1.15 | |
| +26.82 | +26.70 | |
| −11.44 | −11.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spiliotopoulos, G.; Katsardi, V. Nonlinear Effects on the Formation of Large Random Wave Events. J. Mar. Sci. Eng. 2025, 13, 1516. https://doi.org/10.3390/jmse13081516
Spiliotopoulos G, Katsardi V. Nonlinear Effects on the Formation of Large Random Wave Events. Journal of Marine Science and Engineering. 2025; 13(8):1516. https://doi.org/10.3390/jmse13081516
Chicago/Turabian StyleSpiliotopoulos, George, and Vanessa Katsardi. 2025. "Nonlinear Effects on the Formation of Large Random Wave Events" Journal of Marine Science and Engineering 13, no. 8: 1516. https://doi.org/10.3390/jmse13081516
APA StyleSpiliotopoulos, G., & Katsardi, V. (2025). Nonlinear Effects on the Formation of Large Random Wave Events. Journal of Marine Science and Engineering, 13(8), 1516. https://doi.org/10.3390/jmse13081516







