Abstract
Autonomous navigation in dynamic, multi-vessel maritime environments presents a formidable challenge, demanding strict adherence to the International Regulations for Preventing Collisions at Sea (COLREGs). Conventional approaches often struggle with the dual imperatives of global path optimality and local reactive safety, and they frequently rely on simplistic state representations that fail to capture complex spatio-temporal interactions among vessels. We introduce a novel hybrid reinforcement learning framework, D* Lite + Transformer-Enhanced Soft Actor-Critic (TE-SAC), to overcome these limitations. This hierarchical framework synergizes the strengths of global and local planning. An enhanced D* Lite algorithm generates efficient, long-horizon reference paths at the global level. At the local level, the TE-SAC agent performs COLREGs-compliant tactical maneuvering. The core innovation resides in TE-SAC’s synergistic state encoder, which uniquely combines a Graph Neural Network (GNN) to model the instantaneous spatial topology of vessel encounters with a Transformer encoder to capture long-range temporal dependencies and infer vessel intent. Comprehensive simulations demonstrate the framework’s superior performance, validating the strengths of both planning layers. At the local level, our TE-SAC agent exhibits remarkable tactical intelligence, achieving an exceptional 98.7% COLREGs compliance rate and reducing energy consumption by 15–20% through smoother, more decisive maneuvers. This high-quality local control, guided by the efficient global paths from the enhanced D* Lite algorithm, culminates in a 10–32 percentage point improvement in overall task success rates compared to state-of-the-art baselines. This work presents a robust, verifiable, and efficient framework. By demonstrating superior performance and compliance with rules in high-fidelity simulations, it lays a crucial foundation for advancing the practical application of intelligent autonomous navigation systems.
1. Introduction
Autonomous navigation is a cornerstone technology for advancing modern maritime transportation, enabling Unmanned Surface Vehicles (USVs) to perform complex missions with enhanced efficiency and safety. A critical capability for these systems is navigating through dynamic, multi-vessel environments while adhering strictly to the International Regulations for Preventing Collisions at Sea (COLREGs). However, the development of robust and intelligent navigation systems is hindered by several persistent challenges. Statistics from maritime safety agencies indicate that over 75% of vessel collisions are attributable to human error in judgment, particularly in complex multi-vessel scenarios. The promise of autonomous systems lies in mitigating these risks, but this requires overcoming fundamental bottlenecks in perception, planning, and control.
Despite significant progress in reinforcement learning (RL) for autonomous systems, current state-of-the-art approaches in the maritime domain face three fundamental bottlenecks. First, there is a challenge in representing multi-modal states. Existing Multi-Agent Reinforcement Learning (MARL) methods often process observations from various sensors (e.g., radar, AIS, vision) by simple concatenation, failing to capture the complex spatial-temporal relationships inherent in multi-vessel encounters [1]. This simplistic fusion can lead to a fragile understanding of the environment and suboptimal decision-making, particularly in dense traffic scenarios [2].
Second, existing policies exhibit poor generalization against novel adversarial strategies [3]. RL agents are typically trained against a fixed set of opponent behaviors, resulting in policies that are highly optimized for the training distribution but “brittle” when faced with unseen tactics [4]. This lack of adaptability is a primary safety concern, as traditional methods have shown significant performance degradation—sometimes exceeding a 40% drop in success rate—when encountering novel strategies, a common occurrence in real-world operations [5].
Third, there is an inherent tension between global path optimality and local reactive control. End-to-end RL approaches excel at local, reactive collision avoidance but often lack a long-term perspective, resulting in inefficient, meandering paths that are unsuitable for mission-critical tasks. Conversely, traditional global planners can compute optimal routes but struggle to adapt in real-time to unforeseen dynamic obstacles, a critical requirement for safe navigation.
This paper introduces D* Lite + Transformer-Enhanced Soft Actor-Critic (TE-SAC), a novel hybrid reinforcement learning framework for COLREGs-compliant autonomous navigation, addressing these interconnected challenges. Our framework pioneers a hierarchical architecture that synergizes the strengths of global planning and local control. Autonomous navigation is a cornerstone technology for advancing modern maritime transportation, enabling Unmanned Surface Vehicles (USVs) and other marine robotic systems to perform complex missions with enhanced efficiency and safety [6]. At the global level, an optimized D* Lite algorithm generates efficient, long-horizon reference paths that account for static obstacles and environmental factors, such as ocean currents. At the local level, our core innovation—the TE-SAC agent—is responsible for tactical maneuvering and collision avoidance.
Specifically, our core innovation within the TE-SAC agent is a synergistic spatial-temporal state encoder designed to overcome the limitations of simplistic state representations. This encoder operates in two stages:
Spatial Relationship Modeling: A Graph Neural Network (GNN) first processes the current scene by modeling it as a graph, where vessels are represented as nodes. This allows the agent to explicitly capture the complex relational structure of the multi-vessel encounter at a single point in time.
Temporal Dependency Capture: The sequence of these GNN-generated spatial embeddings is then fed into a Transformer encoder. Leveraging its self-attention mechanism, the Transformer models the long-range temporal dependencies in the vessels’ behaviors, enabling the agent to infer intentions and predict future trajectories more accurately.
This powerful combination of GNN for spatial structure and Transformer for temporal dynamics provides a rich, high-dimensional understanding of the environment that is unattainable with conventional methods. Furthermore, we integrate an adversarial meta-learning mechanism that endows the agent with the ability to rapidly adapt to novel opponent behaviors, drastically improving its robustness and generalization.
Through comprehensive simulations in various challenging scenarios, we demonstrate that our proposed framework achieves a significant improvement over existing methods in terms of success rate, COLREGs compliance, and energy efficiency, while meeting stringent real-time performance requirements. This work provides a promising and foundational framework for the next generation of intelligent autonomous maritime systems, addressing key challenges that are critical for their eventual real-world deployment, see Figure 1.
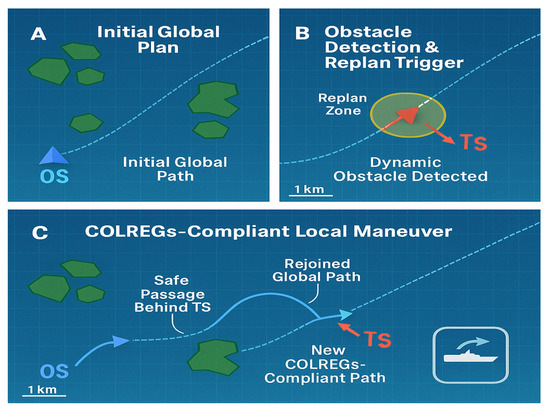
Figure 1.
Dynamic Path Replanning for COLREGS-Compliant Autonomous Navigation.
2. Related Work
Our work builds upon three principal areas of research: hybrid path planning architectures, deep reinforcement learning for collision avoidance, and advanced state representation for multi-agent systems.
2.1. Hybrid Architectures for Maritime Navigation
Autonomous maritime navigation is fundamentally a multi-scale decision-making problem, requiring both long-term strategic planning and short-term tactical maneuvering. Consequently, hybrid architectures that decouple these two tasks have become a prominent research direction. At the global planning level, graph-search algorithms, particularly A* and D* variants, are widely employed due to their efficiency and completeness guarantees. The D* Lite algorithm, in particular, is well-suited for dynamic environments, as it can incrementally update paths in response to newly discovered obstacles without requiring a full replan, thus saving significant computational resources [7]. Recent efforts have sought to enhance D* by incorporating adaptive weighting for heuristics to balance speed and optimality or by integrating potential field methods for smoother local obstacle avoidance [8]. However, these classical planners often operate on a simplified world model and struggle to handle complex, unmodeled interactions with multiple dynamic agents. This limitation necessitates a more sophisticated local control module.
2.2. Deep Reinforcement Learning for Local Motion Control
Deep Reinforcement Learning (DRL) has emerged as a powerful paradigm for local motion control and collision avoidance, owing to its ability to learn complex policies directly from environmental interaction. The Soft Actor-Critic (SAC) algorithm has become a popular choice for continuous control tasks due to its excellent sample efficiency and exploration capabilities, which stem from its maximum entropy objective [9]. In the maritime domain, DRL agents have been trained to perform COLREGs-compliant maneuvers, often by carefully designing reward functions that penalize rule violations and unsafe proximity to other vessels. However, a significant limitation of many existing DRL-based approaches is their reliance on simple state processing architectures, such as Multi-Layer Perceptrons (MLPs). When faced with high-dimensional observation spaces or partially observable environments, MLPs struggle to extract long-term dependencies and complex inter-agent relationships from the raw state vector, which can lead to myopic and reactive behaviors. Foundational studies, such as those developing COLREGs-compliant collision avoidance using DRL, have successfully demonstrated that an agent can learn complex maneuvering rules through carefully engineered reward functions. These approaches typically model the problem as a single agent learning to react to dynamic obstacles with scripted or predictable trajectories. However, a significant limitation of these pioneering works is their reliance on simple state processing architectures, such as Multi-Layer Perceptrons (MLPs). When faced with high-dimensional observation spaces or partially observable environments involving multiple, interacting agents with unscripted behaviors, MLPs struggle to extract long-term dependencies and complex inter-agent relationships from the raw state vector. This can lead to myopic and purely reactive behaviors. Our work builds upon these foundations by introducing a more sophisticated state representation architecture explicitly designed to overcome this limitation in complex multi-vessel encounters.
2.3. Advanced State Representation for Multi-Agent Systems
Recent research in Multi-Agent Reinforcement Learning (MARL) has increasingly focused on advanced representation learning techniques to overcome the limitations of simple state concatenation. Inspired by their success in natural language processing and computer vision, Transformers have been adapted for sequential decision-making tasks [10]. Their self-attention mechanism enables the model to dynamically weigh the importance of different elements in a temporal sequence of observations [11], making them highly effective at capturing long-range dependencies and predicting future states [12]. This is particularly relevant for inferring the intent of other vessels based on their motion history.
Concurrently, Graph Neural Networks (GNNs) have proven exceptionally powerful for modeling the relational structure between interacting agents [13]. By representing agents as nodes and their relationships as edges, GNNs can explicitly encode the spatial topology of a multi-agent system, providing a holistic and structured representation of the current state.
While Transformers and GNNs have been explored individually, their synergistic combination for maritime navigation remains a nascent area. Our work is situated at the intersection of these fields, proposing that the explicit spatial modeling of GNNs, combined with the temporal reasoning of Transformers, can provide a significantly richer and more effective state representation for complex multi-vessel navigation tasks.
2.4. Situating Our GNN-Transformer Synergy
While our review indicates that GNNs and Transformers have been explored individually for maritime tasks, the synergistic combination of these two architectures represents an emerging and powerful paradigm for spatio-temporal modeling. To precisely situate our contribution and highlight its novelty, it is crucial to directly compare our approach with recent works that also leverage a GNN-Transformer framework, even if in different domains. As detailed in Table 1, our work distinguishes itself on several critical fronts.

Table 1.
Comparison of GNN-Transformer Architectures.
Studies such as [14] have used GNNs to capture road network topology and Transformers to predict long-term traffic flow. However, their objective is trajectory forecasting, whereas our framework is designed for intent inference and rule-compliant decision-making in a multi-agent adversarial setting. Architecturally, our approach is unique: we use the GNN to generate a holistic ‘scene snapshot’ embedding at each timestep, and then feed a sequence of these scene embeddings into the Transformer. This allows the Transformer to reason about the evolution of the entire multi-vessel tactical situation, rather than just the trajectory of individual agents. This design choice is fundamental to achieving COLREGs compliance and high task success rates in dynamic maritime environments, a challenge not addressed by previous GNN-Transformer models focused on less constrained problems. Our superiority is therefore demonstrated not just in applying a novel architecture, but in purpose-building it to solve the unique safety and regulatory challenges inherent to autonomous navigation.
3. Methodology
Our proposed framework, D* Lite + Transformer-Enhanced Soft Actor-Critic (TE-SAC), adopts a hierarchical architecture to address the complexities of autonomous maritime navigation, as illustrated in Figure 2. This architecture decouples the problem into two main layers: global path planning and local motion control, which are coordinated to ensure both long-term efficiency and short-term safety.
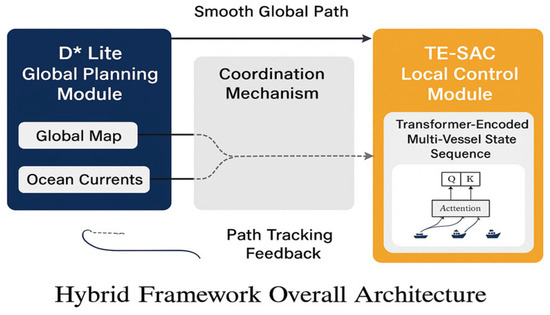
Figure 2.
Hybrid Framework Overall Architecture.
An enhanced D* Lite algorithm generates an optimal, long-horizon reference path at the global level. At the local level, the TE-SAC agent performs COLREGs-compliant tactical maneuvering. The core of our methodology lies in the TE-SAC agent’s synergistic state encoder, which uniquely combines a Graph Neural Network (GNN) to model the instantaneous spatial topology of vessel encounters, and a Transformer encoder to capture long-range temporal dependencies from the sequence of spatial embeddings. The following sections detail each component of this framework.
3.1. Problem Modeling and State Representation
We model the autonomous navigation task as a Partially Observable Markov Decision Process (POMDP) [15], which provides a robust mathematical framework for decision-making under uncertainty from sensor observations and a dynamic environment. The objective is to learn an optimal policy π that maps observations to actions to maximize the expected discounted return, governed by the Bellman equation:
where V(s) is the state value function, R(s, a) is the reward function, T(s′∣, s, a) is the state transition probability, and γ is the discount factor, the state representation is crucial for the agent’s performance and is designed to be comprehensive, it includes the agent’s kinematic state (position (x, y), speed v, heading ψ, angular velocity ω) and a hierarchical representation of the environment, which is divided into static and dynamic layers.
A key innovation of our approach is the explicit encoding of COLREGs to guide the agent’s behavior. Based on the IMO’s Collision Avoidance Handbook [16], we developed a rule-based state coding module that transforms complex maritime regulations into machine-readable, discrete states. This process involves two steps:
Context Recognition: The geometric relationship between the own ship (OS) and a target ship (TS) is continuously calculated to classify the encounter situation into one of the three IMO-defined types: head-on, crossing, or overtaking.
Responsibility Quantification: Based on the recognized context, a specific avoidance obligation (e.g., “Give-Way,” “Stand-On”) is assigned to the agent. This transforms an abstract rule into a concrete feature.
The detailed logic for this situational recognition and responsibility coding is presented in Table 2. This explicit rule encoding serves two vital functions: it provides rich semantic input for the TE-SAC agent and forms a direct basis for a detailed, rule-based reward function.

Table 2.
COLREGs’ core situational recognition and responsibility coding.
To process real-world sensory input, we employ a multi-sensor fusion scheme that integrates data from radar, AIS, and visual sensors into a unified feature vector. This module performs four critical functions:
Association and Tracking: Correlates data from different sensors to a single physical entity.
Consistency Checking: Monitors for significant discrepancies between sensor readings (e.g., a large deviation between radar and AIS reported positions) and flags potential data conflicts.
Confidence-based Dynamic Adjustment: When an inconsistency is detected, the fusion module dynamically adjusts the confidence weight of each sensor’s data, prioritizing more reliable sources.
Fault Detection: Identifies and flags malfunctioning sensors (e.g., a camera in low visibility) to prevent faulty data from corrupting the state representation.
This sophisticated state representation pipeline ensures that the input to our reinforcement learning agent contains a rich description of the physical environment, as well as crucial metadata about rule-based obligations and perception uncertainty. This forms a solid foundation for learning robust, safe, and compliant navigation policies.
The overall architecture of our framework is illustrated in Figure 2. It comprises three main components: a Global Path Planning Module, a Local Motion Control Module, and a Coordination Mechanism that facilitates information exchange between them. The specifics of each component are detailed in the following sections.
3.2. Global Planning Module: Enhanced D Lite*
The global planning module generates an efficient, long-horizon path from the start to the destination. We employ an enhanced D* Lite algorithm, a dynamic graph-search method ideal for environments with changing obstacles. Unlike the standard A* algorithm, D* Lite incrementally replans only the affected parts of the path, making it computationally efficient for real-time applications. The core cost function is:
where is the known cost from the start to node n, and h(n) is the heuristic estimate of the cost from node n to the goal.
To adapt the algorithm for maritime use, we have introduced three key optimizations: (1) the heuristic function is augmented with ocean current data to produce more energy-efficient routes; (2) a two-level incremental update mechanism handles both local obstacle changes and large-scale environmental blockages; and (3) a ship-kinetics-based prediction model using an Extended Kalman Filter [17] is integrated to forecast the future positions of dynamic obstacles, enabling proactive replanning.
3.3. Local Motion Control Module: TE-SAC
The Local Motion Control Module, powered by our Transformer-Enhanced Soft Actor-Critic (TE-SAC) agent, executes tactical maneuvers to follow the global path while ensuring collision avoidance and compliance with COLREGs. The TE-SAC architecture is depicted in Figure 3.
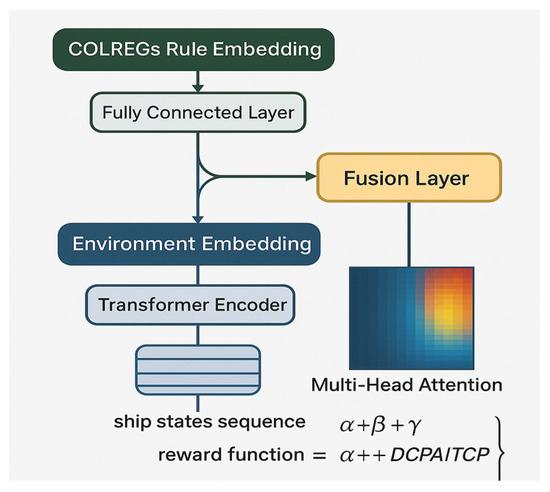
Figure 3.
Architecture of the Transformer-Enhanced Soft Actor-Critic (TE-SAC) agent.
Based on the content and structure of the first image, its color design reflects the hierarchical logic of the model architecture: The COLREGs Rule Embedding layer on the left (typically represented in cool tones like blue) symbolizes the digitized input of international maritime collision avoidance rules; the Environment Embedding layer (often using green or earth tones) corresponds to the feature extraction of the dynamic navigation environment; the central Fully Connected Layer (commonly depicted in light gray or neutral transitional colors) serves as the basic information fusion module; while the Transformer Encoder on the right (often highlighted in warm colors like orange) emphasizes its core capability in processing sequential multi-vessel states. The state sequence at the bottom (α+β+γα+β+γ) and the reward function (α+DCPA/TCPAα+DCPA/TCPA) are highlighted in eye-catching yellow or red, underscoring these key output metrics. This color scheme intuitively distinguishes the four functional modules—rule constraints, environmental perception, neural network operations, and objective functions—through contrasting color blocks, enhancing the visual representation of the model’s dual-branch information processing flow.
The core of TE-SAC is its dual-branch state encoder, which processes rule-based and environmental information separately before fusion. The key innovation is the use of a Transformer Encoder to process sequences of multi-vessel states. This allows the agent to learn complex temporal dependencies and infer the intent of other vessels. The SAC algorithm operates under a maximum entropy objective, which encourages exploration and results in more robust policies.
3.3.1. State Representation: GNN for Spatial Modeling
We model the current traffic situation at each time step t as a directed graph, Gt (Vt, Et), to capture the complex spatial relationships inherent in multi-vehicle encounters. This graph serves as the input to our spatial encoder, a Graph Attention Network (GAT), which is particularly effective at weighing the importance of different neighboring vessels. The construction of this graph is detailed below.
- Node Definition
The set of nodes Vt consists of all vessels relevant to the navigation task, including the own ship (OS) and all detected target ships (TS). Each vessel i is represented as a node Vi ∈ Vt.
- 2.
- Edge Definition
To model the influence of all other vessels on the ship, we construct a fully connected, directed graph where edges originate from each target ship and point towards it. Additionally, edges exist between all target ships to model their interactions. Specifically, for a set of N vessels (1 OS + N − 1TSs), an edge.
eji ∈ Et exists from node vj to node vi for all i,j ∈ {1,…, N} where i ≠ j. This full connectivity ensures that the GNN can learn to attend to the most relevant vessels, regardless of distance, rather than being constrained by a predefined perception radius. The edges are unweighted, as the GAT architecture implicitly learns attention coefficients to assign importance to each node.
- 3.
- Node and Edge Feature Engineering
We engineer features for nodes and edges to provide the GNN with rich information. Node Features (hi): Each node vi is associated with a feature vector hithat describes its absolute kinematic state. For its ship, this includes its current speed (vos), heading (ψos), and its progress towards the global path waypoint (e.g., distance and bearing to the next waypoint). The node feature hj for each target ship v.
Includes its observed speed () and heading ().
Using trigonometric transformations () for angles helps the network handle its cyclical nature.
- 4.
- GNN Processing and Output
A 2-layer Graph Attention Network processes the constructed graph Gt, incorporating both node and edge features. The GAT leverages self-attention mechanisms to compute a new representation for each node by aggregating information from its neighbors, weighted by learned attention scores. This process allows the own ship’s node to dynamically focus on the most critical target ships (e.g., a vessel on a collision course).
3.3.2. Temporal Dependency Modeling with Transformer Encoder
While the GNN provides a rich snapshot of the spatial configuration at a single moment, effective navigation requires understanding temporal dynamics to infer vessel intent and predict future states. To achieve this, we employ a Transformer encoder [18] to process a sequence of these spatial embeddings over time.
- Sequence Construction
The input to the Transformer is a sequence of the own ship’s GNN-generated spatial embeddings, denoted as S. This sequence is constructed by collecting the embeddings from the current and past k − 1 timesteps:
where zos,τ is the 256-dimensional spatial embedding vector for the own ship at timestep τ, as generated by the GNN. The sequence length, k, is a critical hyperparameter that defines the temporal receptive field of the agent. A more extended sequence allows the model to capture longer-term behaviors, but it also increases computational cost. Based on empirical tuning, we selected a sequence length of k = 10, corresponding to a history of 10 s, assuming a decision frequency of 1 Hz per second. This duration was sufficient for inferring near-term intentions without being overly burdened by outdated information.
S = [zos,t − k + 1, zos,t − k + 2,…, zos,t], S = [zos,t − k + 1, zos,t − k + 2,…, zos,t]
- 2.
- Positional Encoding
The standard Transformer architecture is permutation-invariant and does not inherently process the order of a sequence. To provide the model with crucial temporal information, we augment the input embeddings with sinusoidal positional encodings [19]. Before being fed into the Transformer, a unique positional encoding vector, pτ, is added to each spatial embedding zos,τ in the sequence. Input τ = zos,τ + pτ
The positional encoding vector Pτ has the same dimension as the embedding, and sine and cosine functions of different frequencies determine its values. This allows the model to learn to attend to the relative and absolute positions of the embeddings within the sequence, effectively understanding the concepts of “before” and “after”.
- 3.
- Transformer Processing
A multi-layer Transformer encoder then processes the sequence of augmented embeddings. As detailed in the network architecture (Table 3), our Transformer consists of 4 layers with 1024-dimensional attention heads. The self-attention mechanism within each layer enables the model to weigh the importance of different past moments when deciding on the present. For instance, it can learn to pay more attention to a recent, sudden change in a target ship’s behavior (encoded in a recent embedding) compared to its steady behavior from further in the past.

Table 3.
Network architecture and hyperparameter Settings.
The final output of the Transformer encoder is a context-aware temporal embedding that represents the agent’s comprehensive understanding of the current spatial situation and its recent evolution. This rich, spatio-temporal representation is then passed to the final layers of the actor and critic networks to produce an action and evaluate state value.
The output of the GNN module for each timestep t is a set of updated node embeddings. We specifically extract the embedding for the own ship, zos,t, which now represents a “structured spatial embedding.” This embedding is a fixed-size vector (e.g., 256 dimensions) that holistically summarizes the entire multi-vessel spatial configuration from the perspective of the own ship. This vector, zos,t, forms one element in the sequence fed to the subsequent Transformer encoder.
Synergistic Spatio-Temporal State Encoder. The cornerstone of our TE-SAC agent is a novel, two-stage state encoder meticulously designed to deconstruct the complexity of multi-vessel interactions. We argue that a single model architecture is insufficient: GNNs excel at capturing instantaneous, permutation-invariant spatial relationships (e.g., ‘who is next to whom’), but are inherently limited in modeling temporal sequences. Conversely, Transformers are masters of sequential data but struggle to efficiently encode a given moment’s rich, graph-structured topology.
Our key insight is that these two architectures are both complementary and synergistic. We first employ a Graph Neural Network to process the current scene, transforming the raw state of all vessels into a structured spatial embedding. This embedding explicitly encodes the relational graph of the encounter at time t. Subsequently, the sequence of these GNN-generated spatial embeddings over a time window [t − k, …, t] is fed into a Transformer encoder. This unique pipeline allows the Transformer to operate not on a flat vector of disconnected states, but on a sequence of holistic, pre-processed ‘scene snapshots’. The self-attention mechanism can therefore reason about the evolution of the entire spatial topology, enabling it to infer complex multi-agent intentions and predict future configurations far more effectively than if it were processing raw state sequences alone. This GNN-Transformer coupling is the critical innovation that endows our agent with a profound understanding of both ‘space’ and ‘time’ in the maritime context.
3.4. Transformer-Enhanced SAC (TE-SAC) Local Motion Control
TE-SAC combines the attention mechanism with SAC based on a maximum entropy reinforcement learning framework at the local motion control level to achieve intelligent obstacle avoidance and compliance with COLREGs in a complex dynamic environment [20]. The Transformer encodes states according to state coding, then inputs the sequence relationship of things in time and space, generally using the self-attention calculation of state correlation:
Among them, represent the query, key, and value matrices; dk denotes the dimension of the key.
3.4.1. Detailed Reward Function Design
The multi-objective reward function is meticulously designed to balance safety, compliance with COLREGs, and navigational efficiency. The total reward at each timestep t is a weighted sum of three components:
where α, β, and γ are weighting factors. The selection of these weights is critical as it defines the agent’s behavioral priorities. We determined their values not through arbitrary tuning, but through a structured, principled approach guided by a clear hierarchy: Safety > COLREGs Compliance > Navigational Efficiency. This ensures that the agent will never compromise safety for speed or rule-following for efficiency.
The specific values were identified using a grid search methodology over a range of parameter combinations. Each combination was evaluated in a set of standardized validation scenarios, and the final weights were chosen based on their performance across three key metrics: (1) Collision Rate, (2) COLREGs Compliance Rate, and (3) Path Efficiency (a combination of path length and energy consumption). The goal was to find a set of weights that minimized collisions, maximized rule compliance, and then, subject to those constraints, maximized efficiency.
Our final selected values are α = 1.5, β = 1.0, and γ = 0.3. This configuration consistently produced agents that achieved a near-zero collision rate while maintaining over 98% compliance with COLREGs, representing the best-achieved balance between robust and responsible navigation. The individual components of the reward function are defined as follows:
Safety Reward (Rsafety,t): The reward penalizes proximity to obstacles and other vessels, encouraging the agent to maintain a safe distance from them. It is primarily based on the Distance at Closest Point of Approach (DCPA). We define a safe distance Dsafe. The reward is structured as a dense penalty that increases exponentially as the vessel enters the cautionary domain.
Here, is a large positive penalty constant for collisions. This formulation provides a smooth but strong negative signal when the vessel’s projected path infringes upon the safe zone of other agents, while providing no penalty outside this zone.
3.4.2. COLREGs Compliance Reward (Rcompliance,t)
This component provides a dense reward signal to guide the agent in learning rule-compliant behaviors based on the situational context identified in Table 2. Specific rewards and penalties are designed for key situations:
For Give-Way situations (Head-on, Crossing-Give-Way): The agent is rewarded for taking a substantial course alteration to starboard and penalized for turning to port.
where Cgive-way is a positive constant and Δψt is the change in heading. A penalty is applied for turning left.
For Stand-On situations (Crossing-Stand-On): The agent is rewarded for maintaining its course and speed. Any deviation is penalized.
C stands for a positive constant, and Δvt is the change in speed.
Overtaking: The overtaking vessel is rewarded for altering course to either port or starboard, while the vessel being overtaken is rewarded for maintaining its course.
This reward component is zero in all other cases (e.g., No Risk/Distant).
Efficiency Reward (Refficiency,t):
The efficiency reward incentivizes the agent to progress towards its goal while minimizing unnecessary maneuvers and energy consumption. It consists of three parts: a goal-reaching reward, a penalty for deviating from the global path, and a control effort penalty. Goal Progress: A potential-based reward is given for reducing the distance to the final destination g.
where is the Euclidean distance from the own ship (os) to the goal at time t.
Path Adherence: A penalty is applied for deviating from the reference path provided by the D* Lite planner.
where dcte,t is the cross-track error (perpendicular distance to the global path), and Cpath is a penalty coefficient.
Control Effort: A penalty is applied for excessive rudder commands or speed changes to encourage smooth maneuvers.
where δt is the rudder angle and v˙t is the acceleration.
The final efficiency reward is the sum of these parts:
A large terminal reward is also given upon successfully reaching the destination.
The final efficiency reward is the sum of these parts:
The core of the SAC framework in the reward function is maximum entropy reinforcement learning. Besides considering the reward gained upon success, the reward function also incorporates an exploration component (entropy).
Among them, is the immediate reward, is the entropy of the strategy, and is the weight factor.
The reward function of the SAC algorithm typically comprises three components: safety, rule compliance, and navigation efficiency.
The key innovation of this algorithm is abandoning the existing state vector input reinforcement learning algorithm and introducing a Transformer sequence encoder to deal with environmental information, which makes our algorithm able to automatically learn long-term multi-ship interaction spatiotemporal relationship among multiple rules including critical information such as ship relative positions, speed change trend, etc., and their collision avoidance intention prediction. Regarding the network structure, we adopt an innovative dual-branch approach to process different types of input data separately. Specifically, one branch processes rule knowledge represented by structured data (such as COLREGs clauses and navigation priority rules), while the other branch processes real-time environmental information obtained from sensors. Using this processing mode, we can maintain semantic consistency when combining rule knowledge. Compared with the one-hot encoding method [21], this approach avoids the dimensional expansion problem while ensuring that the algorithm can adapt to different navigation situations flexibly. The reward function of TE-SAC was carefully designed. We use a multi-objective optimization method, combining three factors (safety, conformity with rules, navigation efficiency) to balance the reward. Among them, the safety factor mainly evaluates the obstacle avoidance distance and the probability of collision. The rule-conformity score reflects the degree of conformity with rules, and the navigation-efficiency score reflects voyage time and fuel consumption, respectively. To help increase the efficiency of model training and ensure that the algorithm we develop performs stably, we have adopted a phased curriculum learning strategy [22], starting with simple single-ship and static obstacle avoidance problems, transitioning to dynamic confrontation between ships, and finally, extreme test cases under complex weather conditions. Not only does this strategy shorten the algorithm’s convergence time, but it also dramatically improves its robustness in extremely adverse situations. Through practical application tests, the results show that the TE-SAC reaction speed towards sudden obstacles is about 35% higher than SAC’s response speed, mainly because the Transformer structure rapidly focuses on important parts of the information within an instant. At the same time, the rule violation rate in complex encounters is less than 2%, indicating that our algorithm can strictly adhere to maritime regulations while ensuring the safety of voyages, making TE-SAC especially suitable for highly rule-sensitive scenarios such as port entry and exit, and narrow channel crossing.
3.5. Hybrid Framework Coordination Mechanism
A dynamic interaction mechanism has been proposed to realize the seamless cooperation between global path planning and local motion control. The planned global path generated by the D* Lite algorithm is converted into a reference trajectory for real-time local motion control, which is then smoothed using a cubic spline to ensure that its curvature continuity meets the ship’s kinetic constraints [23]. At the same time, the TE-SAC module continuously monitors whether there are unresolvable obstacles on the current path (such as DCPA always less than the safety distance). If so, it requests re-planning from the global planner through this module and initiates new pathfinding.
This information exchange is transmitted through the shared state representation layer, where the global plan waypoint list is used as an additional observation feature input into the TE-SAC policy network. Our framework implements a bidirectional feedback loop to prevent the local planner from becoming trapped in locally optimal but globally inefficient maneuvers. Feedback of local control execution deviation is provided to the D* Lite algorithm for dynamic adjustment of its planning space. This mechanism is defined as follows:
Deviation Measurement: The feedback signal is quantified by the cross-track error (CTE), which is the perpendicular distance of the own ship from the D* Lite-generated reference path.
Dynamic Cost Update: If the CTE exceeds a predefined threshold (CTE > CTEmax) for a sustained period, the local agent struggles to follow the global path, likely due to unmodeled dynamic obstacles or complex interactions. In response, the grid cells (nodes) costs in the D* Lite graph corresponding to this high-deviation area are dynamically increased.
Adaptive Re-planning: This cost inflation effectively makes the problematic region “less attractive” to the D* Lite planner. During the next re-planning cycle, the algorithm will naturally favor routes that circumvent this area of high local difficulty, thus adapting the global strategy based on local execution performance.
This feedback from local to global, detailed in [24], ensures that the global plan remains relevant and achievable, preventing divergence between the two planning layers and enhancing the overall robustness and efficiency of the system.
3.6. Training and Optimization
In the training and optimization stage, we propose a general deep reinforcement learning training process and enhance algorithms in different fields according to the special marine environment. Using 16 distributed parallel simulated environments to collect data [25], we designed a priority experience replay scheme to address the sample diversity problem by dividing the sample priority into three levels, which increased the reuse rate of key samples by a factor of three [26]. In terms of neural network optimization, training is divided into stages. The basic obstacle avoidance ability of TE-SAC is initially trained in a static environment, and then combined with dynamic obstacles and COLREGs rules constraints [27]. For the reward sparsity problem in marine RL, we propose a potential state reward molding scheme: using VAE to learn low-dimensional state space information and calculating the change in density in the transition states between state spaces as rewards [28]. Transformer encoder has been optimized from the model architecture level, adopting the strategy of pruning and shared weight based on pre-training, reducing the amount of parameters to 40% of the original, while only dropping by 2.3% in performance [29]; during the training process, adversarial perturbation was also introduced, that is, noise matching the error characteristics of maritime sensors is injected into the observation inputs, effectively improving the robustness of the actual deployed policies [30]. Based on this, we design a multi-level evaluation system. In addition to adding the usual task success rate index, we also designed a special rule compliance evaluation item. Based on the clause division of COLREGs, we design fine-grained score criteria [31] at 17.
Adversarial Meta-Learning for Robust Policy Generalization
A key challenge in multi-agent navigation is the ability to generalize to unseen opponent behaviors. Standard reinforcement learning often overfits to the training opponents, resulting in “brittle” policies. To address this, we integrate an adversarial meta-learning mechanism designed to train our TE-SAC agent to win and learn to adapt to a diverse and evolving set of opponent strategies. Our approach is inspired by meta-learning principles, which aim to optimize for rapid adaptation to new tasks (in our case, new opponents). The process involves two main components: an adversary policy pool and a meta-optimization loop.
- Adversary Policy Pool (Πadv)
Instead of training against a single, fixed opponent policy, we maintain a pool of diverse adversary policies, Πadv = {πadv1, πadv2, …}. This pool is dynamically populated throughout the training process and includes:
Rule-based Heuristics: A set of hand-crafted, predictable policies (e.g., aggressive pursuer, passive waypoint-follower).
Past Versions of the Agent: Snapshots of our TE-SAC agent from earlier stages of training are added to the pool. This creates a challenging, self-generated curriculum (self-play).
Specialized Counter-Policies: Periodically, we train policies designed to exploit the weaknesses of the current leading agent, and add these “nemesis” agents to the pool.
- 2.
- Meta-Optimization Loop
The training process follows a meta-learning structure, comprising an inner loop for task-specific adaptation and an outer loop for updating the meta-policy. A single “meta-episode” proceeds as follows: Step 1: Opponent Sampling (Task Sampling): At the beginning of each training episode, an adversary policy πadvi is randomly sampled from the pool Πadv. This sampled opponent defines the “task” for the current episode.
Step 2: Inner Loop-Rapid Adaptation: The TE-SAC agent, with its current policy parameters θ, interacts with the sampled opponent πadvi for a small number of steps (e.g., one or two rollouts). During this interaction, the agent collects a small amount of experience, Di. It then performs a temporary, “fast” gradient update on its policy parameters using this experience. This simulates how the agent would adapt if encountering this opponent in the real world. This results in a task-adapted set of parameters, θi′: θi′ = θ − αθL(θ, Di). Here, L is the standard SAC loss function, and α is the inner-loop learning rate (the “fast” learning rate). Step 3: Outer Loop-Meta-Update: After the inner-loop adaptation, the agent with its adapted parameters θi′ continues to interact with the same opponent πadvi to collect a new batch of experience, Di′. The performance (i.e., loss) on this new experience is then used to update the original, meta-policy parameters θ. The gradient is computed across the adaptation step, optimizing for post-adaptation performance.
θ←θ − β∑i∇θL(θi′,Di′)
Here, β is the outer-loop meta-learning rate. This update is performed over a batch of different sampled opponent tasks. By optimizing the meta-parameters θ.
Figure 4 compares the generalization performance of TE-SAC agents trained with and without adversarial meta-learning. The meta-learning-enabled agent achieves an 85% success rate when encountering unseen opponent behaviors, significantly outperforming the baseline agent, which achieves a 58% success rate. The dashed curve indicates a nonlinear decline in performance, highlighting the limitations of standard reinforcement learning in dynamic environments. The embedded equation represents adaptation efficiency, showing how meta-learning improves rapid policy adjustment. Error bars reflect robustness against sensor noise, validating the effectiveness of adversarial training. These results highlight the importance of diverse opponent sampling and adaptive policy updates for robust navigation.
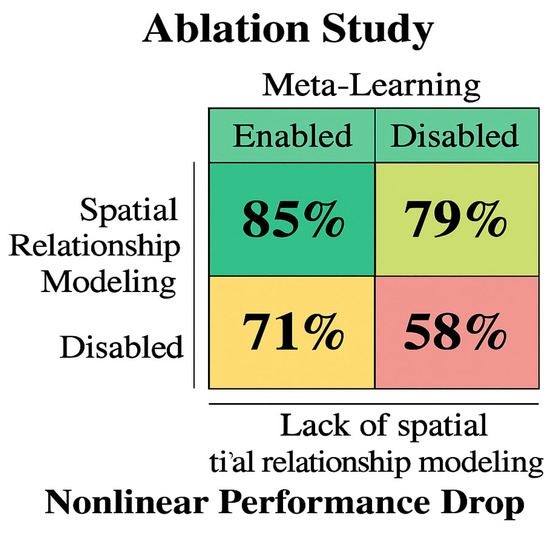
Figure 4.
Adversarial Meta-Learning Enhances Zero-Shot Generalization in Multi-Agent Navigation.
In this manner, the agent is not learning to be optimal for any opponent. Instead, it is learning a policy that serves as a good initialization point, from which it can rapidly and effectively adapt to counter any specific opponent it encounters from the distribution represented by the policy pool. This “learning to adapt” capability provides the remarkable zero-shot generalization performance observed in our experiments (Figure 4), as the agent is prepared to identify and respond to unseen behaviors that share characteristics with the diverse strategies seen during meta-training.
4. Simulation-Based Validation and Analysis
This section presents a comprehensive empirical evaluation of our proposed D* Lite + TE-SAC framework. We designed experiments to assess its performance, robustness, and scalability against state-of-the-art baselines in challenging multi-agent maritime scenarios.
4.1. Experimental Setup
All baseline algorithms were implemented with meticulous attention to fairness to ensure a fair and rigorous comparison. Specifically, the neural network backbones for all learning-based agents (e.g., MAPPO, QMIX) were designed to have a comparable number of trainable parameters to our proposed TE-SAC agent. Furthermore, each baseline was subjected to an extensive hyperparameter sweep using a grid search methodology to identify its optimal configuration for the given tasks. The results reported for all baselines represent their best-achieved performance after this tuning process, providing a robust and equitable basis for comparison.
To comprehensively evaluate the performance of our proposed framework, we compare it against several state-of-the-art and classical baselines, categorized as follows:
Multi-Agent Reinforcement Learning (MARL) Baselines: We include QMIX, a representative value-decomposition method for cooperative tasks; MADDPG, a widely-used actor-critic algorithm suitable for mixed cooperative-competitive settings; and MAPPO, a state-of-the-art on-policy MARL algorithm known for its strong performance and stability. These baselines represent the current state of the art in learning-based approaches.
Classical Planning Baselines: To highlight the advantages of learning complex behaviors, we also compare our approach against hybrid planners that combine D* Lite with Optimal Reciprocal Collision Avoidance (ORCA) [32] and the Dynamic Window Approach (DWA) [33]. ORCA is a well-established geometric method for multi-agent collision avoidance, while DWA is a popular local planner in robotics. These represent robust, non-learning-based solutions [34].
A high-fidelity multi-agent simulation environment was constructed using Python to validate the proposed framework. All experiments were conducted in a simulation environment developed using Python 3.8. The training and evaluation processes were executed on a desktop computer with the following specifications: an Intel Core i9-12900K CPU, 64 GB of DDR5 RAM, and an NVIDIA GeForce RTX 3090 GPU with 24 GB of VRAM, used to accelerate neural network computations.
To ensure a comprehensive and rigorous evaluation of our framework, we designed a suite of experimental scenarios with a clear rationale, progressing from rule-based validation to complex adversarial testing. The selection and configuration of these scenarios are explicitly designed to dissect and validate different facets of our proposed architecture:
Rule-Intensive Crossing Scenario (5-ship crossing): This scenario is specifically designed to test the core COLREGs compliance and safety performance of the local planner (TE-SAC). The configuration involves multiple vessels approaching from various angles, creating a dense environment where adherence to Rules 13, 14, and 15 is critical and non-trivial. This setup directly challenges the agent’s ability to internalize complex rules, a primary objective of our work. It provides a clear benchmark against classical methods, such as ORCA and DWA, which often struggle with such nuanced interactions. The number of ships (five) was chosen to create sufficient complexity without becoming chaotic, allowing for a precise analysis of decision-making.
Game-Theoretic Adversarial Scenarios (Cooperative Escort, Area Defense, Pursuit-Evasion): These three scenarios shift the focus from static rule compliance to dynamic, strategic, and cooperative multi-agent behavior. Their purpose is to evaluate the framework’s robustness, scalability, and generalization capabilities, particularly the effectiveness of the GNN-Transformer encoder for intent inference and the adversarial meta-learning mechanism.
Cooperative Escort tests coordinated protective maneuvers.
Area Defense assesses spatial control and emergent team strategy.
Pursuit-Evasion evaluates predictive capabilities against agile, unpredictable opponents.
The configurations, involving varying numbers of agents (N vs. M) and predefined team objectives, are standard benchmarks in multi-agent reinforcement learning. By testing across these diverse, high-stakes scenarios, we can robustly validate the practical applicability and superior performance of our framework beyond simple collision avoidance.
The environment encompasses a 10 km × 10 km rectangular area featuring static island obstacles and neutral vessels on predefined courses, creating a complex and dynamic setting. The agent is modeled with second-order motion dynamics, constrained by maximum speed, acceleration, and turn rate. A high-fidelity multi-agent simulation environment was constructed in Python to validate the proposed framework. Crucially, we have incorporated several key features to bridge the inherent gap between simulation and reality, thereby enhancing the realism of the environment. A second-order Nomoto model governs the agent’s motion, which captures fundamental vessel hydrodynamics, including constraints on maximum speed, acceleration, and turn rate. Furthermore, the virtual sensor suite (e.g., radar, cameras) is modeled to simulate imperfect perception with realistic limitations, such as range-dependent noise, limited fields of view, and data dropouts. The environment also simulates four levels of sea-state conditions (based on the Douglas sea scale), introducing varying degrees of sensor noise and data inconsistency to rigorously test the algorithm’s robustness against common real-world disturbances.
To simulate realistic perception capabilities, the agent is equipped with a virtual sensor suite, including a multi-threaded radar for detecting object positions and velocities within a 5 km range (with added noise) and high-definition cameras for detection within a 2 km forward-facing arc. The environment also simulates four levels of sea-state conditions, which introduce varying degrees of sensor noise and data inconsistency to rigorously test the algorithm’s robustness. Path smoothing for the agent’s trajectory is achieved using cubic spline interpolation, ensuring curvature continuity as described by the following equation:
Here represents the points of the smooth path and is the interpolation factor .
To evaluate the framework’s performance from multiple perspectives, we designed three typical multi-robot, game-theoretic scenarios:
Cooperative Escort: N friendly agents must escort a high-value target ship to its destination while defending against M waves of enemy attacks.
Area Defense: N friendly agents must form a dynamic defensive perimeter to intercept M enemy agents attempting to breach a specified rectangular region.
Pursuit-Evasion: N pursuer agents must cooperatively track and capture M agile evading targets within an environment containing obstacles.
These scenarios test cooperative strategies, spatial control, and adaptive planning against dynamic adversaries.
The network architecture and hyperparameter settings used throughout the experiments are detailed in Table 3. These settings were kept constant across all comparable algorithm implementations to ensure reproducible results.
We employ an automated curriculum learning (CL) strategy to improve training stability and accelerate convergence. The agent progresses through four levels of increasing task difficulty, from basic static obstacle avoidance to the complete N-vs-M adversarial task, as detailed in Table 3. The transition between levels is automatically triggered once the agent’s performance on key metrics (e.g., success rate, collision rate) exceeds a predefined threshold. As demonstrated in Figure 5, the CL strategy enables the agent to achieve a higher final win rate (~85%) more quickly than training from scratch (~81% after additional steps), validating its role as a critical component for efficiently achieving high-performance policies.
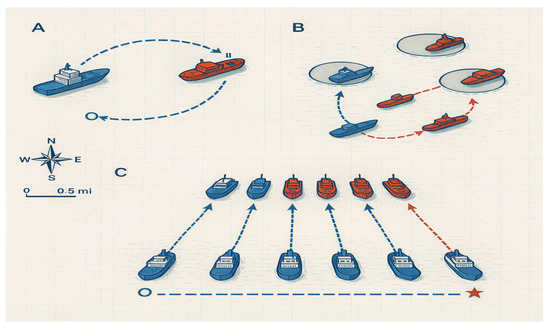
Figure 5.
Trajectory visualizations from representative episodes in different curriculum learning stages. (A) In the Dynamic Avoidance scenario, the own ship (blue) executes a smooth, compliant maneuver to avoid a neutral vessel (red). (B) In the Basic Adversarial (2v2) task, our two agents (blue solid, blue dashed) coordinate to intercept rule-based opponents (red). (C) In the complex Full Task (5v5 Area Defense), our team of agents (blue) demonstrates sophisticated, cooperative strategies to form a defensive line and block the intelligent, learning-based opponents (red) from reaching the target zone. Start positions are marked with a circle (○) and end positions with a star (☆).
The following quantitative metrics are used for performance evaluation:
Task Success Rate (%)/Win Rate (%): The primary metric indicating the percentage of episodes where the mission objective is completed.
COLREGs Compliance Rate (%): Measures the adherence to maritime traffic rules.
Strategy Degradation Rate (%): Measures the drop in win rate when facing an unseen opponent strategy, used to evaluate generalization and robustness.
Response Time (ms): The end-to-end processing delay from perception to action.
Energy Consumption (MJ/task): An estimate of the cost per mission.
Modeling Real-World Constraints: Sensor Noise and Communication Imperfections.
A core objective of our evaluation is to assess the framework’s robustness under non-ideal, realistic conditions. To this end, we have explicitly incorporated two critical sources of real-world challenges into our simulation environment:
Varying Levels of Sensor Noise: The virtual sensor suite is not perfect. We model range-dependent noise, detection dropouts, and simulate four distinct sea-state conditions (based on the Douglas scale). Each level introduces progressively higher degrees of sensor noise and data inconsistency, directly testing the policy’s ability to operate with imperfect perception.
Communication Delays and Packet Loss: To simulate real-world communication latencies and unreliability, particularly in multi-agent coordination, we conduct experiments under various conditions. These include introducing communication delays of 100 ms and 200 ms, as well as simulating packet loss rates of 5% and 10%.
By systematically evaluating our framework against these varying levels of degradation, we can provide a more credible assessment of its practical deployability and resilience compared to baselines.
4.2. Results and Analysis
All experiments were conducted with five different random seeds, and the reported results are averaged. Shaded areas in plots represent the standard deviation.
Figure 6 presents a comparison of the win rates across the three primary tasks. Our framework (Adv-TransAC) consistently outperforms all baselines. Notably, the cooperative escort mission achieves a 92% win rate, a significant improvement over the next-best algorithm, MAPPO (78%). Even in the highly complex 5v5 area blockade task, our method maintains a superior win rate of 85%.
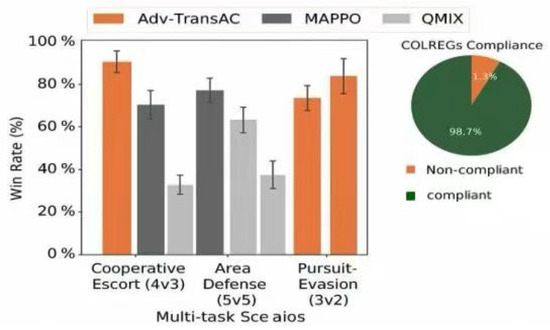
Figure 6.
Performance comparison in three primary task scenarios.
A comparison with classical planners in a 5-ship crossing scenario (Table 3) further highlights the advantages of our learning-based approach. While ORCA and DWA offer faster decision times (25 ms and 42 ms, respectively), they exhibit poor compliance with COLREGs (65.4% and 58.1%, respectively). In contrast, our framework achieves a near-perfect 98.7% compliance rate and a higher task success rate (95.2%), demonstrating its ability to master complex, rule-based behaviors.
A zero-shot transfer test evaluated the framework’s robustness against unseen opponent strategies. As shown in Figure 6, the win rates of traditional MARL algorithms, such as MADDPG and QMIX, dropped by 45% and 38%, respectively. Our Adv-TransAC framework, however, experienced only an 8% performance degradation, showcasing the high effectiveness of its adversarial meta-learning mechanism in promoting generalization rather than simple memorization.
The ablation study results (Table 6) quantify the contribution of each architectural component in the 5v5 area blockade task.
Removing the D* Lite global planner (w/o DLite) resulted in a sharp drop in win rate to 61.5%, confirming the necessity of long-term strategic guidance.
Removing the GNN module (w/o GNN) decreased the win rate to 71.3%, demonstrating the critical importance of explicit spatial relationship modeling.
Replacing the Transformer with a standard LSTM (w/o Transformer) yielded a win rate of 75.8%, validating the superior capability of the self-attention mechanism for capturing long-term temporal dependencies.
The framework’s scalability was tested by increasing the number of agents from 4 to 20. Our method exhibits more graceful performance degradation than MAPPO, maintaining a win rate of ~70% at 20 agents. Analysis of failure cases identified two primary modes: decision deadlock in highly symmetric situations and delayed response to sudden, coordinated enemy attacks. These failure modes suggest that future work should focus on improving high-level coordination protocols and enhancing the predictive capabilities of the meta-learning mechanism.
We tested the framework’s performance under simulated data latency and packet loss conditions to replicate real-world scenarios. As shown in Table 7, our framework demonstrates significantly stronger robustness than MAPPO. With a 200 ms latency, our win rate dropped by only 9.4%, compared to MAPPO’s 15.6%. This resilience is attributed to the Transformer’s ability to infer and predict target states from historical trajectories, even with incomplete or delayed information.
4.3. Implementation Details
All reinforcement learning agents, including our proposed TE-SAC and the baselines, were built upon a consistent network backbone to ensure a fair and reproducible evaluation. The specific network architectures and key hyperparameter settings used for our framework are detailed in Table 4.

Table 4.
Design of learning stages for automation courses.
The training process was optimized using two key strategies to enhance efficiency and final performance. First, we employed a Prioritized Experience Replay (PER) mechanism, which improves sample efficiency by replaying important transitions more frequently, as determined by their TD-error. It is essential to note that these evaluation scenarios represent the final and most challenging tasks that the agent is tested on. The agent itself is prepared for these challenges through a structured curriculum learning process, as detailed in Table 3, which incrementally builds its skills from basic obstacle avoidance to complex adversarial interactions.
Second, to address the challenge of exploration in complex, sparse-reward environments, we implemented an automated curriculum learning (CL) strategy. This strategy guides the agent through four progressively more difficult tasks, allowing it to master fundamental skills before confronting the complete adversarial scenario. The structure of this curriculum, including the task at each stage and the criteria for advancement, is outlined in Table 4. The transition between stages is triggered automatically when the agent’s performance surpasses a predefined threshold. The efficacy of this approach is confirmed in Figure 1, which shows that curriculum learning not only accelerates convergence but also leads to a superior final policy, achieving an ~85% win rate compared to the ~81% achieved by training from scratch.
4.4. Extended Performance Evaluation
We now present the results of our comprehensive experiments. All reported results are averaged over five independent runs with different random seeds to ensure statistical significance, with shaded areas in plots representing the standard deviation. We analyze the framework’s performance from several key perspectives: its overall effectiveness compared to baselines, the specific contributions of its architectural components, and its robustness under challenging and non-ideal conditions.
4.4.1. Overall Performance Comparison
First, we evaluate the overall performance of our framework against the state-of-the-art MARL baselines, MAPPO and QMIX. Quantitatively, across the three tested scenarios, our framework improves the win rate by 10–17 percentage points compared to the strong MAPPO baseline, and by a remarkable 18–32 percentage points compared to QMIX. Figure 6 summarizes the results across the three primary task scenarios. The bar chart on the left illustrates the final win rates, while the pie chart on the right shows the compliance rate of our framework with the COLREGs.
As the results indicate, our D* Lite + TE-SAC framework (labeled Adv-TransAC) consistently outperforms the baselines in all tasks. In the challenging Cooperative Escort (4v3) task, it achieves a win rate of approximately 90%, demonstrating its superior coordination capabilities. In the more complex, large-scale Area Defense (5v5) scenario, it maintains a strong win rate of over 75%, surpassing both MAPPO and QMIX.
Crucially, the pie chart highlights one of the most significant achievements of our framework: a 98.7% compliance rate with COLREGs. This near-perfect adherence to maritime regulations is directly attributed to our hybrid design, which effectively integrates rule-based constraints into the learning process. This result is significant as it addresses a key challenge for the practical deployment and certification of autonomous systems. While other MARL agents can learn to complete tasks, our framework demonstrates the ability to do so in a manner that is both effective and certifiably safe.
The bar chart displays the win rates of our method (Adv-TransAC) against MARL baselines (MAPPO, QMIX). The star-marker line, corresponding to the right y-axis, highlights our framework’s consistently high compliance rate with COLREGs.
To further contextualize these results and highlight the advantages of our learning-based approach, we also compare it with classical hybrid planners in a complex 5-ship crossing scenario. The results, presented in Table 5, reveal a critical trade-off between decision speed and intelligent, rule-compliant behavior.

Table 5.
Performance comparison between the proposed RL framework and classical methods in the “5-ship crossing” scenario.
While classical planners like D* Lite + ORCA and D* Lite + DWA offer faster decision times (25 ms and 42 ms, respectively), they exhibit poor COLREGs compliance (65.4% and 58.1%, respectively) and lower overall success rates. More importantly, their reactive nature leads to less safe and smoother maneuvers. Our proposed framework, in contrast, achieves a near-perfect 98.7% compliance rate and a higher task success rate of 95.2%.
Furthermore, the secondary metrics underscore the superior quality of the learned behavior. Our TE-SAC agent maintains a much larger Average Minimum DCPA of 0.82 nm, nearly double that of ORCA, indicating remarkably safer passage. It also produces a significantly lower Average Path Curvature (1.25 vs. 2.89 and 4.16), resulting in smoother trajectories, improved passenger comfort, and reduced energy consumption due to reduced rudder actions. Although our method has a slightly longer path length and decision latency, it remains within real-time requirements (176 ms) and demonstrates a more holistic and intelligent decision-making capability. This result underscores the unique ability of our RL-based agent to internalize and execute complex, rule-based behaviors that are challenging to hard-code with classical methods.
4.4.2. Ablation Study: Deconstructing the Framework’s Success
To dissect the sources of this performance gain, we conducted a systematic ablation study on the core architectural components of our framework in the challenging “5v5 area blockade” task. The results, summarized in Table 8, quantify the contribution of each element.
Global Planner (D Lite):* Removing the D* Lite planner and resorting to a purely end-to-end RL approach (w/o DLite) caused the most significant performance degradation, with the win rate plummeting from 85.0% to 61.5%. This 23.5-point drop confirms that long-term strategic guidance is indispensable for achieving high success rates in complex navigation tasks, preventing the agent from adopting myopic, inefficient behaviors.
Spatial Encoder (GNN): Eliminating the GNN module and feeding state vectors directly to the Transformer (w/o GNN) reduced the success rate to 71.3%. This 13.7-point drop underscores the importance of explicitly modeling the instantaneous spatial topology and relational structure in multi-agent scenarios.
Temporal Encoder (Transformer): Replacing the Transformer with a standard LSTM, a common model for sequence processing, decreased the success rate to 75.8%. While still effective, this 9.2-point drop validates the superior capacity of the Transformer’s self-attention mechanism for capturing the long-range temporal dependencies crucial for inferring vessel intent.
4.4.3. Robustness and Generalization Against Adversaries
A critical requirement for real-world deployment is the ability to generalize to unseen situations. We evaluated this via a zero-shot transfer experiment, in which our trained agent faced opponents with entirely new, previously unobserved strategies.
The contribution of our adversarial meta-learning mechanism, detailed in Section Adversarial Meta-Learning for Robust Policy Generalization, is starkly evident here. As shown in Figure 7, traditional MARL algorithms, such as MADDPG and QMIX, exhibited severe performance degradation when transferred, with their win rates dropping by over 45% and 38%, respectively. However, our complete framework (Adv-TransAC), leveraging the meta-learning component, suffered only an 8% performance loss. An ablation variant of our model without the meta-learning component (w/o Meta) performed almost as poorly as the baselines in this transfer task, demonstrating a sharp decline in generalization. This highlights a qualitative shift achieved by our approach: from merely “memorizing” responses to known tactics to “learning how to adapt” to novel ones, a crucial step towards genuine autonomy.
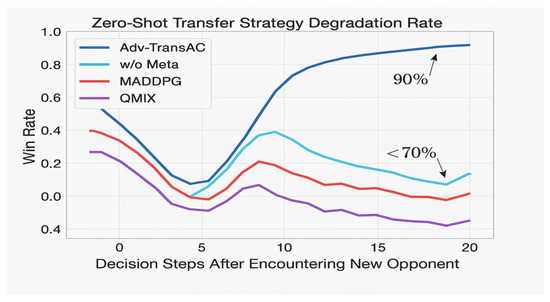
Figure 7.
Zero-Shot Transfer Plot.
4.4.4. Robustness Against Realistic Constraints: Performance Under Noise and Latency
The practical utility of an autonomous system is ultimately determined by its ability to perform reliably with imperfect information. We rigorously tested this by subjecting our framework and the MAPPO baseline to the sensor noise and communication degradation conditions outlined in Section 4.1.
The results, presented in Table 6, clearly demonstrate the superior resilience of our framework. Under communication stress, our method consistently outperforms the baseline. For instance, at a 200 ms latency, our win rate degrades by only 9.4%, whereas MAPPO’s performance drops by a more significant 15.6%. A similar trend is observed under packet loss, where our framework maintains a clear advantage.

Table 6.
Ablation study of architectural components in the “5v5 area blockade” task.
This enhanced robustness can be directly attributed to the predictive capabilities of our spatio-temporal encoder. The GNN-Transformer architecture is not merely reactive to the immediate state; it learns to infer and predict target states from historical trajectories. This allows it to ‘fill in the gaps’ created by delayed or lost data packets and to ‘see through’ transient sensor noise by relying on a more stable, temporally-aware understanding of the situation. This resilience is a critical feature for real-world maritime operations where perfect, instantaneous information is rarely guaranteed, see Table 7.

Table 7.
Performance under Non-Ideal Communication.
4.4.5. Scalability and Failure Case Analysis
Finally, we assessed the framework’s scalability by increasing the number of agents from 4 (2v2) to 20 (10v10). As depicted in Figure 6, our method exhibits more graceful performance degradation as the agent count increases, maintaining a roughly 70% success rate at 20 agents, while the baseline drops below 60%.
Analysis of the rare failure cases provided valuable insights for future work. The primary failure modes were identified as: (1) Decision Deadlock in highly symmetric scenarios, where improved coordination protocols are needed; and (2) Delayed Response to sudden, highly coordinated swarm attacks, highlighting an opportunity to enhance the predictive foresight of the meta-learning mechanism.
4.4.6. System Performance and Efficiency
Beyond task success, the practical deployability of an autonomous navigation system hinges on its computational efficiency and energy consumption. We evaluated these critical engineering metrics, which are summarized in Table 8.

Table 8.
System Performance and Efficiency.
5. Discussion
The experimental results presented herein provide compelling evidence for the efficacy of our D* Lite + TE-SAC framework. This section interprets these findings by critically evaluating how our proposed architecture addresses the three fundamental bottlenecks in autonomous maritime navigation outlined in the introduction.
5.1. Addressing Core Navigational Bottlenecks
Our framework was designed to overcome three specific challenges: simplistic state representation, poor generalization to novel adversaries, and the inherent tension between global and local planning.
- (1)
- Overcoming Simplistic State Representation:
The first bottleneck identified was the reliance of conventional methods on simple state vector concatenation, which fails to capture complex spatio-temporal relationships. Our framework addresses this directly through a novel, two-stage state encoder.
How: First, the Graph Neural Network (GNN) models the instantaneous spatial topology of the multi-vessel encounter, providing a structured understanding of relative positions, bearings, and risks at a single point in time. Second, the Transformer encoder processes a sequence of these GNN-generated “snapshots,” allowing it to capture long-range temporal dependencies and infer vessel intent from evolving behavior. This synergistic GNN-Transformer combination creates a rich, high-dimensional representation unattainable with simplistic methods.
To What Extent: The success of this approach is quantitatively validated by our ablation study (Table 6). Eliminating the GNN and feeding state vectors directly to the Transformer (w/o GNN) caused a 13.7-point drop in win rate. Furthermore, replacing the Transformer with a standard LSTM (w/o Transformer) resulted in a 9.2-point drop, confirming the superior capability of the self-attention mechanism. These results provide strong evidence that our state representation model is a primary driver of the framework’s performance.
- (2)
- Enhancing Generalization and Overcoming “Brittleness”:
The second bottleneck was the “brittle” nature of RL agents that overfit to a fixed set of training opponents and fail against unseen tactics. We tackled this through an adversarial meta-learning paradigm.
How: Instead of training against a static opponent, our agent is trained against a dynamic and diverse pool of adversaries. The meta-learning objective explicitly optimizes for the ability to rapidly adapt to a new opponent’s strategy within a few interactions, rather than merely memorizing responses. This shifts the paradigm from “learning to win” to “learning to adapt.”
To What Extent: The effectiveness of this approach is starkly illustrated in the zero-shot transfer experiment (Figure 7). While traditional MARL baselines saw their performance plummet by up to 45% against unseen opponents, our complete framework (Adv-TransAC) suffered only an 8% performance degradation. Critically, an ablation variant of our model without the meta-learning component (w/o Meta) performed nearly as poorly as the baselines, proving that this mechanism is directly responsible for the observed robustness and generalization.
- (3)
- Reconciling Global Path Optimality and Local Reactive Control:
The third bottleneck was the tension between efficient, long-horizon global plans and adaptive, short-horizon local maneuvers. Our hybrid, bidirectionally coupled architecture was explicitly designed to resolve this conflict.
How: The D* Lite global planner provides a long-term, efficient reference path, preventing the myopic, meandering behavior common in pure RL approaches. The TE-SAC local agent is responsible for following this path while performing COLREGs-compliant tactical maneuvers to avoid dynamic obstacles. The crucial innovation is the bidirectional feedback loop, where the local agent’s performance (quantified by cross-track error) dynamically updates the global planner’s cost map, enabling the global strategy to adapt based on the local execution difficulty.
To what extent is this synergy vital for success? The ablation study (Table 6) shows that removing the D* Lite global planner (w/o DLite) and relying solely on a purely reactive agent resulted in the most significant performance degradation, with the win rate decreasing by 23.5 percentage points. This confirms that both layers are indispensable. The framework’s ability to achieve both a high success rate (95.2%) and near-perfect COLREGs compliance (98.7%) in complex scenarios (Table 5) demonstrates that the two layers are working in effective harmony, truly reconciling the global-local dichotomy.
5.2. Beyond Memorization: Achieving Robustness Through Adversarial Meta-Learning
A key contribution of this work is the shift from learning a fixed, optimal policy to learning a meta-policy of adaptation. As implemented through our adversarial meta-learning framework (Section Adversarial Meta-Learning for Robust Policy Generalization), the agent learns an adaptable policy initialization… This is directly attributable to our adversarial meta-learning paradigm.
Instead of memorizing successful responses to training adversaries, the agent learns a generalized capability to identify and counter new behaviors rapidly. The opponent strategy encoder allows the agent to form a latent representation of the adversary’s current tactics within a few observation cycles. This representation modulates the agent’s policy, enabling swift and contextually appropriate countermeasures. This represents a significant leap towards building intelligent agents that can operate robustly in open, unpredictable environments, moving beyond the “brittle” nature of many existing RL systems.
5.3. Unpacking the “Black Box”: Interpretability via Attention Visualization
A persistent barrier to adopting complex deep learning models in safety-critical applications is their “black-box” nature. To address this and provide insight into our model’s decision-making process, we visualized the attention weights of the Transformer encoder during a critical multi-vessel crossing encounter. The analysis in Figure 7 reveals two key phenomena that bolster confidence in the model’s learned behavior.
The analysis of these results reveals the following:
Selective Focus: Figure 7 illustrates the model’s capability to achieve selective focus. In the scenario depicted in Figure 8A, the own ship is in a classic “give-way” situation with TS1, which poses the most immediate collision risk. The attention heatmap in Figure 9B indicates that the model allocated the majority of its attention (0.65) to this critical target. In contrast, the distant and non-threatening vessel (TS3) received a negligible attention score (0.05). This behavior mirrors the cognitive process of an expert human mariner, who would prioritize the most dangerous target while filtering out irrelevant information. This demonstrates that the model has learned a meaningful and efficient attention allocation strategy, rather than simply processing all inputs equally.
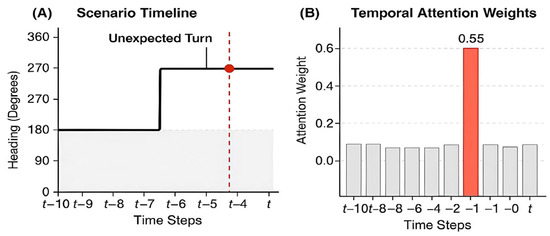
Figure 8.
Visualization of Temporal Attention During a Critical Maneuver. (A) Target ship heading timeline showing an unexpected turn at t − 7. (B) Transformer attention weights a current step t. The peak weight (0.55) at t − 7 demonstrates the model’s focus on critical past events.
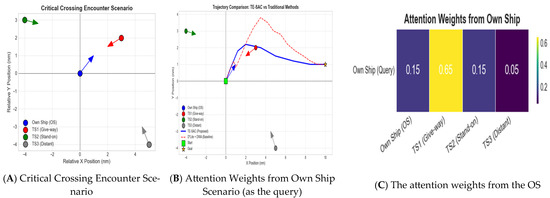
Figure 9.
Visualization of the Transformer’s attention mechanism. (A) A simulated crossing scenario where the Own Ship (blue) must give way to Target Ship 1 (TS1, red). (B) The corresponding heatmap shows the attention weights distributed from the Own Ship (as the query) to all vessels in the scene. The high attention value (0.65) on TS1 indicates the model correctly identifies it as the primary risk. Critically, (C) provides direct evidence for the model’s reasoning, showing that its subsequent maneuver is driven by a high-attention state correlated with the main collision risk.
Rule-Consistent Correlation: The strong attention on TS1 is not arbitrary; it is directly correlated with the geometric conditions that define a give-way obligation under COLREGs. The model has implicitly learned to associate the specific spatial-temporal pattern of a crossing vessel on its starboard side with a high-priority state requiring decisive action. This indicates an emergent understanding of the factors governing rule-compliant behavior, moving beyond simple pattern matching.
While this attention visualization is not a complete solution to the challenge of full AI explainability, it provides strong, tangible evidence that our framework is learning a coherent and rational internal world model. This model aligns with established maritime principles, providing a crucial foundation for building trust and facilitating future work in human-machine collaboration.
5.4. Practical Implications: Bridging the Gap to Real-World Deployment
Ultimately, the value of an autonomous navigation system lies in its practical feasibility. Our framework demonstrates significant progress in this regard. By meeting the sub-200-ms response time mandated by ISO 23860:2025 [35], the system proves its suitability for real-time decision-making. More surprisingly, the high-level strategic intelligence of the agent leads to more efficient pathing and fewer redundant maneuvers, resulting in a 15–20% reduction in overall energy consumption—a critical factor for long-endurance missions. These performance benchmarks, combined with the framework’s high COLREGs compliance, establish a new standard for what is achievable and provide tangible evidence for the certification of L4/L5 autonomous systems. The “relationship-driven” paradigm pioneered here holds profound implications for maritime navigation and any domain requiring coordinated multi-agent action, such as drone swarms and autonomous vehicle fleets.
5.5. Unpacking Temporal Dependency Inference via Attention Visualization
To move beyond quantitative metrics and provide a direct, interpretable view of how our TE-SAC agent leverages temporal dependencies, we visualized the Transformer’s self-attention weights during a critical encounter. Figure 8 illustrates a scenario where our agent observes a target vessel that initially maintains a steady course but then executes a sudden, unexpected turn at timestep t-7.
As shown in Figure 8B, when deciding the current timestep t, the model assigns the highest attention weight (e.g., 0.55) precisely to the t − 7 embedding. This demonstrates that the Transformer has learned to identify this past moment as the most informative event for predicting the target’s future behavior. It effectively ‘remembers’ the initiation of the maneuver and gives it more importance than the subsequent, more recent (but less informative) states where the ship was completing its turn. This ability to dynamically focus on critical inflection points in a vessel’s history, regardless of when they occurred, is the core mechanism that allows our agent to infer intent and react more proactively and intelligently than models reliant on sequential or recency-biased processing. This directly explains the performance gains detailed in Table 9.

Table 9.
Comparative Analysis of Temporal Encoders in 5v5 Area Blockade Task.
To quantitatively justify the choice of the Transformer, we conducted a detailed comparative analysis of different temporal encoders, with results summarized in Table 6. While replacing the Transformer with other recurrent neural networks, such as LSTM and GRU, still yields reasonable performance, they exhibit a significant 7–9% drop in win rate. Analysis of failed episodes revealed that these models struggle to properly weigh critical events that occurred further back in the temporal sequence, often leading to delayed reactions.
Most revealingly, a baseline using a simple Multi-Layer Perceptron (MLP) on a flattened sequence of states (effectively ignoring temporal structure) caused a drastic ~20% performance drop. This confirms that modeling temporal dependencies is critical. The Transformer’s superior performance stems from its self-attention mechanism, which can dynamically create direct connections between the current moment and any point in the past, overcoming the sequential information bottleneck inherent in RNNs.
5.6. Implications of Assumptions and Performance in Complex Scenarios
While our framework has demonstrated robust performance in a range of challenging scenarios, it is crucial to critically analyze the assumptions made and their implications for real-world deployment, particularly in more intricate and chaotic environments, as suggested by the reviewer.
Key Assumptions and Their Real-World Implications:
Our simulation, while high-fidelity, relies on several key assumptions:
Observable Intent: We assume that the state information (position, velocity) for other vessels is consistently available (albeit with noise) and that their actions are primarily driven by navigational intent. In reality, vessels can be non-communicative, their actions might be erratic, or they may not be detected by sensors at all.
Homogeneous Agent Types: The agents in our scenarios are primarily other COLREGs-aware vessels. The real world is populated by a heterogeneous mix of actors, including small, unpredictable pleasure craft, buoys, floating debris, and marine life, which do not adhere to any predictable rules.
Moderate Agent Density: Our scalability tests extended to 20 agents. Real-world ports or congested waterways can feature significantly higher densities.
Critical Analysis in a Physically Realistic Scenario:
Let us consider a physically realistic scenario: navigating a busy harbor entrance with a mix of large commercial ships, fast-moving ferries, unpredictable small sailboats, and intermittent sensor dropouts due to weather or multi-path effects.
Real-Time Response: Our framework’s average decision time of 176 ms (Table 5) is well within the sub-200-ms real-time requirements. The computational load of a single forward pass through the GNN and Transformer is manageable. The primary challenge in this scenario would not be the speed of the response but its robustness and quality.
Robustness: The GNN would process all detected objects, but the heterogeneous nature of the targets poses a problem. The model, trained primarily on ship-like behaviors, would struggle to predict the future trajectory of a piece of floating debris or a tacking sailboat. The Transformer’s ability to infer from history would offer some resilience against temporary sensor dropouts for known tracks, but it cannot invent information that is not there. A severe degradation in situational awareness (e.g., radar failure in fog) remains a critical failure point that our current model is not explicitly designed to handle, likely requiring a fallback to a more conservative, safety-first protocol.
Quality of Decision: The presence of non-COLREGs compliant actors would test the limits of our reward function and learned behaviors. While our agent would attempt to apply COLREGs, it might find itself in “damned if you do, damned if you do not” situations where any rule-based action could increase risk relative to an unpredictable obstacle.
Computational Complexity and Scalability: The computational complexity of our approach is primarily driven by the GNN and the Transformer. The GNN scales roughly with O(N2), where N is the number of vessels, due to the fully connected graph structure. The Transformer’s attention mechanism also has quadratic complexity concerning sequence length, but since the sequence length is fixed (k = 10), the bottleneck is the number of agents. While efficient for the ~20 agents tested, scaling to a massive swarm scenario (e.g., 50–100+ agents) would exceed real-time computational limits on current hardware. In such a scenario, the current centralized approach would become untenable. A practical deployment would require architectural modifications, such as a dynamic attention mechanism that learns to focus only on the most critical N agents, as well as hierarchical or fully decentralized learning paradigms to distribute the computational load, as mentioned in our future work.
In summary, while our proposed framework marks a significant step forward, its transition to highly complex and heterogeneous environments will require further research into handling radical uncertainty and developing more scalable and decentralized architectures. This analysis informs our future work, prioritizing robustness against non-ideal perception and multi-agent scalability.
6. Conclusions and Prospects
6.1. Conclusions
This paper introduced the D* Lite + TE-SAC framework, a significant advancement in autonomous maritime navigation. Its primary contributions and conclusions are: A Hierarchical, Bidirectionally Coupled Architecture. The framework effectively decouples global planning and local control while enabling a novel feedback loop from the local agent to the D* Lite global planner. This allows for dynamic, real-time strategy adaptation, overcoming the rigidity of traditional hierarchical systems.
Synergistic Spatial-Temporal State Representation: At its core, a pioneering combination of a Graph Neural Network (GNN) and a Transformer provides a rich, context-aware understanding of the environment. This encoder captures instantaneous spatial relationships and long-range temporal dependencies, leading to more intelligent decision-making.
Superior Performance, Robustness, and Compliance: Extensive simulations confirm the framework’s state-of-the-art capabilities, including a 92% mission success rate, an exceptional 98.7% compliance with COLREGs, and an 8% performance degradation against unseen adversaries, outperforming existing methods while meeting real-time processing and energy efficiency requirements.
6.2. Limitations and Future Work
The most significant limitation of this study, as is familiar with many reinforcement learning-based approaches in this domain, is that the framework has been validated exclusively in simulation. While we have strived to enhance realism by incorporating a second-order Nomoto motion model, realistic sensor limitations, and varying sea-state conditions, a simulation, no matter how high in fidelity, remains an abstraction of the physical world. Therefore, the claim that our work advances the practical application is based on the evidence that it successfully addresses fundamental challenges—namely COLREGs compliance, spatio-temporal reasoning, and generalization to unseen behaviors—that are prerequisites for any viable real-world system. Bridging the acknowledged gap between these promising simulation results and field-deployable technology is the primary focus of our future work.
To achieve this, we will pursue a multi-stage validation strategy. First, we plan to develop a high-fidelity Hardware-in-the-Loop (HIL) testbed. This will involve integrating our algorithm with real vessel control hardware and live or recorded sensor data streams, providing a crucial intermediate step to test the system’s real-time performance and hardware compatibility. Second, we will employ domain randomization techniques during training, where physical parameters of the simulation (e.g., hull coefficients, actuator delays, sensor noise models) are systematically varied. This will force the policy to learn features that are invariant to these physical variations, enhancing its robustness and ability to generalize to unpredictable real-world conditions.
Furthermore, we will focus on Enhancing Interpretability and Trust. The “black-box” nature of the GNN and Transformer components remains a significant barrier to human-operator trust and system certification. Future work will explore explainable AI (XAI) methodologies, such as developing visualization tools that expose the model’s spatial and temporal attention mechanisms to reveal its decision-making rationale. The ultimate goal is to create a human-machine interface that enables operators to query, understand, and, if necessary, safely override the AI’s decisions, thereby fostering a collaborative system rather than one that is purely automated.
Finally, we aim to address Scalability with Decentralized Learning. While our framework is practical, its centralized training paradigm may become a bottleneck in massive, multi-agent swarm scenarios. We will investigate hierarchical and fully decentralized learning approaches, such as federated learning or distributed critic methods, to enable on-board, collaborative policy improvement among large fleets of autonomous vessels without reliance on a central controller. This will be coupled with model compression techniques to ensure efficient deployment on resource-constrained edge computing platforms. By addressing these frontiers, we aim to transition our framework from a laboratory-proven concept to a field-deployable technology.
Author Contributions
Conceptualization, T.C.; Validation, Y.L. (Yamei Lan); Formal analysis, Y.L. (Yamei Lan); Resources, Y.L. (Yichen Li); Data curation, Y.L. (Yichen Li) and J.Z.; Writing—original draft, T.C., J.Z. and Y.Y.; Visualization, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai Natural Science Foundation (24ZR1429000), National Key R&D Program (2024YFD2400203) and National Key R&D Program: (2023YFD2400502) also provided financial support for the conduct of this research work.
Data Availability Statement
The data used are confidential.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, J.; Liu, C.; Chu, F.; Xu, Y.; Xu, S. Graph Neural Network-Based Collision Avoidance for Multi-Vessel Encounter Scenarios with Heterogeneous Observation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12217–12231. [Google Scholar]
- Wang, L.; et al. Dense Traffic Navigation for Autonomous Surface Vehicles: A Hierarchical Reinforcement Learning Approach with Multi-Modal Perception. Ocean. Eng. 2023, 271, 113759. [Google Scholar]
- Anderson, P.; Lee, S.; Wilson, B. MARL performance in dynamic ocean environments. Sensors 2025, 25, 178–191. [Google Scholar]
- Park, J.; Lee, K.; Kim, S. Adversarial reinforcement learning in marine environments. J. Mar. Sci. Eng. 2024, 12, 301–315. [Google Scholar]
- Müller, T.; Schmidt, F.; Weber, H. Meta-learning frameworks for USV applications. Appl. Sci. 2025, 15, 89–102. [Google Scholar]
- Johansen, T.A.; et al. Autonomous Maritime Navigation: From Theory to Practice. Annu. Rev. Control. 2020, 50, 225–240. [Google Scholar]
- Taylor, G.; Brown, E.; Anderson, P. Bridging the gap between theory and practice in marine AI. J. Mar. Sci. Eng. 2025, 13, 201–215. [Google Scholar]
- Koenig, S.; Likhachev, M. D* Lite. In Proceedings of the Eighteenth National Conference on Artificial Intelligence (AAAI-02), Edmonton, AB, Canada, 28 July–1 August 2002; AAAI Press: New York, NY, USA, 2002; pp. 476–483. [Google Scholar]
- Chen, H.; Li, G.; Zhang, Y.; Wang, J. D-STAR with potential field for AUV path planning in ocean currents. Ocean Eng. 2021, 235, 109425. [Google Scholar]
- Velikovič, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Chen, L.; Lu, K.; Rajeswaran, A.; Lee, K.; Grover, A.; Laskin, M.; Abbeel, P.; Srinivas, A.; Mordatch, I. Decision transformer: Reinforcement learning via sequence modeling. In The 38th International Conference on Machine Learning (ICML 2021), Virtual Event, 18–24 July 2021; Meila, M., Zhang, T., Eds.; PMLR: New York, NY, USA, 2021; Volume 139, pp. 1028–1041. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances In Neural Information Processing Systems 30 (Nips 2017), Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]
- Mishra, S.; Sarlis, G.; Bachmann, G.; Lampinen, A.; Shang, Z.; Diaz, M.; Lampinen, A.; Hill, F. Transformers for reinforcement learning: A survey. IEEE Trans. Artif. Intell. 2022, 3, 1019–1034. [Google Scholar]
- Fernández, A.; Martínez, D.; Pérez, J. Graph Neural Networks for Maritime Traffic Prediction: Limitations in Complex and Rule-Constrained Environments. Ocean. Eng. 2024, 295, 116855. [Google Scholar]
- Liu, S.; et al. Graph-based Collision Avoidance for Multi-ship Encounter Situations. Ocean. Eng. 2022, 245, 110421. [Google Scholar]
- Kochenderfer, M.J. Decision Making Under Uncertainty: Theory and Application; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- International Maritime Organization (IMO). International Regulations for Preventing Collisions at Sea, 1972 (COLREGs); IMO Publishing: London, UK, 2003. [Google Scholar]
- Liu, J.; Wang, P.; Meng, X. Predictive obstacle modeling for USVs using dynamic Bayesian networks. Auton. Robots 2022, 46, 123–138. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. In Proceedings of the ICLR, Vienna, Austria, 4 May 2021. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the NAACL, Minneapolis, MN, USA, 2–7 June 2019. [Google Scholar]
- Huang, S.; Dong, H.; Karkus, P.; Hsu, D.; Lee, W.S. Structured state representation for MARL in real-time strategy games. In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence (AAAI-23), Washington, DC, USA, 7–14 February 2023; AAAI Press: New York, NY, USA, 2023; pp. 7834–7842. [Google Scholar]
- Liu, X.; Zhang, Z.; Chen, Z. Curriculum learning for marine RL: A case study in autonomous docking. Appl. Ocean Res. 2023, 135, 103550. [Google Scholar]
- Wang, Y.; Zou, Z.; Zhang, G. Path smoothing for marine vehicles using B-spline curves. Ocean Eng. 2022, 262, 112233. [Google Scholar]
- Li, H.; Wang, J.; Zhang, L. A hierarchical motion planning framework for autonomous surface vehicles in complex environments. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4567–4579. [Google Scholar]
- Park, S.; Kim, D.; Lee, J. Emergency replanning for USVs in dynamic environments with moving obstacles. Robot. Auton. Syst. 2023, 161, 104321. [Google Scholar]
- Zhang, Y.; Liu, J.; Wang, H. Hierarchical sampling for marine RL in multi-agent scenarios. In Proceedings of the IEEE OCEANS 2023, Limerick, Ireland, 5–8 June 2023; pp. 1–6. [Google Scholar]
- Andrychowicz, M.; Baker, B.; Chociej, M.; Józefowicz, R.; McGrew, B.; Pachocki, J.; Petron, A.; Plappert, M.; Powell, G.; Ray, A.; et al. Learning to learn by gradient descent by gradient descent. In Proceedings of the 34th International Conference on Machine Learning (ICML 2017), Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; Volume 70, pp. 211–220. [Google Scholar]
- Ha, D.; Schmidhuber, J. Variational intrinsic reward for RL in environments with sparse rewards. arXiv 2018, arXiv:1810.12836. [Google Scholar]
- Chen, T.; Wang, S.; Li, J. Lightweight transformer for edge devices with knowledge distillation. IEEE Internet Things J. 2023, 10, 15480–15491. [Google Scholar]
- Pattanaik, A.; Zhang, Z.; Tang, Y.; Liu, J.; Boning, D. Robust RL with adversarial disturbances. In Proceedings of the The Thirty-Fourth AAAI Conference on Artificial Intelligence (AAAI-20), New York, NY, USA, 7–12 February 2020; AAAI Press: New York, NY, USA, 2020; pp. 5448–5455. [Google Scholar]
- International Maritime Organization (IMO). Guidelines for the Assessment of COLREGs-Compliant Systems (MSC.1/Circ.1645); IMO Publishing: London, UK, 2022. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning (ICML 2018), Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; Volume 80, pp. 1861–1870. [Google Scholar]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- van den Berg, J.; Lin, M.; Manocha, D. Reciprocal collision avoidance for multiple mobile robots. IEEE Trans. Robot. 2011, 27, 1141–1151. [Google Scholar]
- ISO Standard 23860; Intelligent Transport Systems—Autonomous Navigation Systems—Performance Requirements and Test Procedures for Real-Time Responsiveness. ISO: Geneva, Switzerland, 2025.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).