Structural Integrity Assessments of an IMO Type C LCO₂ Cargo Tank

Abstract

With the rise of carbon capture and storage, liquefied carbon dioxide (LCO₂) has emerged as a promising medium for large-scale marine transport. This study evaluates the structural integrity of an IMO Type C cargo tank for a medium-range LCO₂ carrier under four conditions: ultimate limit state, accidental limit state, hydrostatic pressure test, and fatigue limit state, based on IGC Code and classification rules. Seventeen load cases were analyzed using finite element methods with multi-step loading to ensure stability. The highest stress occurred at the pump dome–shell junction due to geometric discontinuities, but all stress and buckling criteria were satisfied. The fatigue damage from wave-induced loads was negligible, with low-cycle fatigue from loading/unloading operations governing the fatigue life, which exceeded 31,000 years. The findings confirm the tank’s structural robustness and its suitability for safe, efficient medium-pressure LCO₂ transport.

1. Introduction

As responding to climate change and reducing carbon emissions have emerged as critical global challenges, technologies for carbon capture, utilization, and storage (CCUS) are receiving increasing attention [1,2,3]. In particular, the importance of technologies that can stably transport and store captured CO₂, generated in large quantities from industrial processes and power plants, is being increasingly emphasized. Against this backdrop, Liquefied CO₂ (LCO₂) is considered a suitable form for large-scale transportation due to its advantage of significant volume reduction, and the active development of technologies for maritime transportation of LCO₂ is underway.

Accordingly, the design and safety assurance of LCO₂ carriers and storage systems have emerged as important research topics, and structural integrity assessments of cargo tanks that safely store liquids under low-temperature and high-pressure conditions have become core technical requirements.

Tank systems used for liquid cargo transportation are generally classified into membrane and independent tanks. The membrane-type tank is a widely used design in liquefied gas transportation, using a thin metal sheet as the primary barrier, allowing stable storage even in cryogenic environments. The primary barrier, typically made of durable metals such as stainless steel, directly contains the liquefied gas. To prevent leakage, a secondary barrier is mandatory, and in membrane-type tanks, the ship structure is generally considered the secondary barrier [4]. In addition, a complex insulation system is installed between the hull and the barrier to minimize heat loss and maintain cryogenic conditions. This insulation system is composed of high-performance materials such as polyurethane foam, and although installation and maintenance are complicated, membrane systems are widely used in large-scale liquefied gas carriers due to their excellent space efficiency [5]. Membrane-type tanks are typically operated at low pressures below 0.7 bar, and their design and safety assessments are conducted according to the IMO IGC Code.

The IMO classifies independent tanks into Type A, Type B, and Type C according to design pressure and structural characteristics [6]. Type A tanks have simple structural designs and require partial or full secondary barriers due to relatively higher leakage risks. Type B tanks, designed with probabilistic methods to enhance structural reliability, require limited secondary barriers. Both Type A and Type B tanks are operated under low pressure, not exceeding 0.7 bar. In contrast, Type C tanks are designed as cylindrical or spherical pressure vessels capable of independent operation at high pressures exceeding 2 bar without additional barriers. Due to their structural advantages, Type C tanks can be applied to vessels with minimal modifications and are considered optimal solutions for LCO₂ transportation.

Most prior research on liquefied gas storage systems has focused on membrane or Type B tanks for LNG or ammonia carriers [7,8,9,10,11,12,13]. However, the design and structural considerations of LCO₂ carriers differ significantly from those of LNG carriers.

Because LCO₂ has a relatively higher density compared to LNG, ammonia, and liquefied hydrogen, the optimization of tank design and supporting structures is essential. Furthermore, LCO₂ tanks require independent Type C tank systems capable of safe storage and transportation under low-temperature and high-pressure conditions, considering the higher vapor pressure. IMO Type C tanks applied to LCO₂ carriers demand high structural reliability in these storage conditions, yet quantitative strength assessment studies on such structures remain limited.

Heo et al. [14] conducted a structural strength assessment for IMO Type C tanks based on the IGC Code and classification society rules, calculating design scantlings and verifying structural safety numerically. Kim et al. [15] evaluated the structural safety of a C-type LNG tank using 9% nickel steel at the initial design stage. Experimental studies analyzed elastic behavior under pressure using model tanks. Park et al. [16] and Kim et al. [17] performed thermo–structural coupled analyses considering thermal loads induced by cryogenic cargoes, establishing load cases based on the IGC Code to assess structural integrity and fatigue life. Experimental studies have also measured the actual structural behavior of Type C LNG tanks using strain gauges to verify the reliability of numerical analyses under internal pressure loads [18]. In research on cryogenic liquefied gas tanks for small ships, Lee et al. [19] analyzed the structural behavior of Type C tanks through numerical analysis based on the IGC Code, presenting quantitative responses under thermal and internal pressure conditions. Some studies have examined the effects of insulation methods on the structural integrity of Type C tanks. Sviličić et al. [20] compared vacuum insulation and perlite insulation through finite element analyses, demonstrating that insulation methods cause significant differences in thermal stress and structural response, highlighting the need for integrated analyses including insulation systems in Type C tank designs. Park and Choi [21] analyzed the greenhouse gas emission characteristics of Type C LNG tanks by fuel tank size and boil-off gas treatment method.

Previous studies related to LCO₂ have mainly focused on boil-off gas reliquefaction and energy efficiency improvements [22,23,24,25] or safety and performance evaluations of unloading systems [26,27]. Quantitative strength analyses and fatigue life evaluations of LCO₂ tanks intended for actual maritime transportation have been relatively rare, and comprehensive design assessments reflecting operational conditions have scarcely been reported.

In this study, the structural strength of a C-type tank designed for a medium-range LCO₂ carrier is evaluated under the ultimate limit state (ULS), accidental limit state (ALS), hydrostatic pressure test (HPT), and fatigue limit state (FLS) specified in the IGC Code [28], aiming to verify the safety of the design. Through this work, important basic data for the LCO₂ carrier design can be provided, contributing to the establishment of design guidelines for C-type tanks.

2. Design Criteria

The IGC Code [28] clearly specifies structural safety standards for ships carrying liquefied gases. This section explains the key requirements applied in the design of Type C tanks.

2.1. Design Pressure

The IGC Code requires that the design of Type C tanks incorporate not only conventional pressure vessel design principles but also fracture mechanics and crack propagation theories. This is because an internal pressure rise caused by boil-off gas can lead to tank cracking or explosion, making the determination of design pressure a critical safety factor. According to the IGC Code, the minimum design vapor pressure for Type C tanks is set at 0.2 MPa, aiming to ensure that surface defects do not exceed half the thickness of the tank wall during its service life.

The internal design pressure of a Type C tank is defined as the sum of the internal vapor pressure caused by boil-off gas, determined by Equation (1), and the internal liquid pressure caused by ship motions, calculated by Equation (5). In Equation (2), $∆{\sigma }_A$ represents the allowable membrane stress amplitude, with 55 MPa recommended for steel materials. The allowable stress ${\sigma }_d$ is determined from the yield and tensile strengths of the tank material using Equation (3). The coefficient $C$ for calculating vapor pressure is determined by Equation (4).

$$P_0=0.2+AC{\rho }^{1.5}$$

(1)

$$A=0.00185{\left({\displaystyle \frac{{\sigma }_m}{∆{\sigma }_A}}\right)}^2$$

(2)

$${\sigma }_d=\min \left({\displaystyle \frac{R_u}{A_0}},{\displaystyle \frac{R_y}{B_0}}\right)$$

(3)

$$C=\mathrm{m}\mathrm{a}\mathrm{x} (h_t,0.75b,0.45l)$$

(4)

$$P_{gd}=\left(a_{\beta }g\right)Z_{\beta }\rho$$

(5)

$${\mathit{a}}_{\beta }={\displaystyle \frac{\left[a_x\mathit{i}+a_y\mathit{j}+\left(a_z+g\right)\mathit{k}\right]}{g}}$$

(6)

Internal liquid pressure is calculated by adding the dynamic pressure caused by cargo movement to the static pressure from gravity. The resultant acceleration required to compute the internal liquid pressure is determined using Equation (5). As shown in Figure 1, the dimensionless acceleration $a_{\beta }$ used in Equation (5) represents the acceleration acting on the liquid when the free surface is inclined by $\beta$ due to ship motion. It is assumed that the acceleration acts perpendicular to the inclined free surface. The value of $a_{\beta }$ is calculated by Equation (6). Local pressures caused by sloshing are not included in the internal liquid pressure calculation.

2.2. Acceleration

The IGC Code provides formulas for calculating the acceleration components at the center of gravity of independent tanks due to wave action. These formulas estimate the ship motion accelerations under North Atlantic conditions at a probability level of ${10}^{-8}$.

Each acceleration component is defined as a ratio to gravitational acceleration, and the inclusion of gravity components varies by direction. Longitudinal and transverse accelerations, calculated by Equations (7) and (8), respectively, include the projected gravity components due to pitching and rolling. In contrast, vertical acceleration, determined by Equation (9), only includes the component due to heave motion and does not include gravitational acceleration. Constants $a_0$ and $A_1$ used in acceleration calculations are computed by Equations (10) and (11). The coefficient $K$ is generally taken as one but is calculated by Equation (12) for ships with special loading conditions or hull forms, where $GM$ is the metacentric height.

$$a_x=\pm a_0\sqrt{0.06+A_1^2-0.25A_1}$$

(7)

$$a_y=\pm a_0\sqrt{0.6+2.5{\left({\displaystyle \frac{x}{L}}+0.05\right)}^{2}K{\left(1+{\displaystyle \frac{0.6Kz}{B}}\right)}^2}$$

(8)

$$a_z=\pm a_0\sqrt{1+{\left(5.3-{\displaystyle \frac{45}{L}}\right)}^2{\left({\displaystyle \frac{x}{L}}+0.05\right)}^2{\left({\displaystyle \frac{0.6}{C_B}}\right)}^{1.5}+{\left({\displaystyle \frac{0.6y{K}^{1.5}}{B}}\right)}^2}$$

(9)

$$a_0=0.2{\displaystyle \frac{V}{\sqrt{L}}}+{\displaystyle \frac{34-(600/L)}{L}}$$

(10)

$$A_1=\left(0.7-{\displaystyle \frac{L}{1200}}+{\displaystyle \frac{5z}{L}}\right)\left({\displaystyle \frac{0.6}{C_B}}\right)$$

(11)

$$K=13GM/B$$

(12)

2.3. Shell Thickness

Each classification society specifies minimum thickness requirements for the outer shells of Type C tanks. According to DNV [29], the minimum shell thicknesses for cylindrical, spherical, and hemispherical shells are provided by Equations (13)–(15). The rules also specify that the joint efficiency $v$ is 1.0 for pressure vessels made of carbon steel or carbon–manganese steel with a tensile strength greater than 550 MPa. The nominal design stress ${\sigma }_t$ is determined based on the material yield or tensile strength, as given in Equation (16).

$$s_{cyl}={\displaystyle \frac{p_c{D}_o}{20{\sigma }_{t}v+p_c}}+c$$

(13)

$$s_{con}={\displaystyle \frac{p_c{D}_c}{20{\sigma }_{t}v-p_c}}{\displaystyle \frac{1}{\cos {\alpha }_c}}+c$$

(14)

$$s_{sph}={\displaystyle \frac{p_c{D}_o}{40{\sigma }_{t}v+p_c}}+c$$

(15)

$${\sigma }_t=\mathrm{m}\mathrm{i}\mathrm{n}\left({\displaystyle \frac{R_y}{1.7}},{\displaystyle \frac{R_u}{2.7}}\right)$$

(16)

2.4. Buckling Capacity

The buckling safety of cylindrical shells, conical shells, and hemispherical shells is assessed according to Equations (17)–(20) [30]. Here, $P_{ed}$ represents the external pressure for buckling strength assessment, calculated by Equation (21).

The DNV rules [30] provide minimum buckling pressures as the indicators of buckling strength. Equations (22) and (23) give the external pressures corresponding to elastic instability and membrane yield for cylindrical shells, respectively. Similarly, Equations (24) and (25) provide the corresponding external pressures for hemispherical shells.

$${\displaystyle \frac{P_{cy}^b}{P_{ed}}}\ge 4.0$$

(17)

$${\displaystyle \frac{P_{cy}^m}{P_{ed}}}\ge 3.0$$

(18)

$${\displaystyle \frac{P_{sph}^b}{P_{ed}}}\ge 3.0$$

(19)

$${\displaystyle \frac{P_{sph}^m}{P_{ed}}}\ge 3.0$$

(20)

$$P_{ed}=P_1+P_2+P_3+P_4$$

(21)

$$P_{cy}^b={\displaystyle \frac{2E}{\left(n^2-1\right){\left[1+{\left(\frac{n}{Z}\right)}^2 \right]}^2}}{\displaystyle \frac{t}{D}}+{\displaystyle \frac{2E}{3\left(1-{\nu }^2\right)}}\left[n^2-1+{\displaystyle \frac{2n^2-1-\nu }{{\left(\frac{n}{Z}\right)}^2-1}}\right]{\left({\displaystyle \frac{t}{D}}\right)}^3$$

(22)

$$P_{cy}^m={\displaystyle \frac{R_{y}t}{R}}$$

(23)

$$P_{sph}^b=0.24E{\left({\displaystyle \frac{t}{R}}\right)}^2$$

(24)

$$P_{sph}^m=2{\displaystyle \frac{R_{y}t}{R}}$$

(25)

The buckling strength of the Type C tank was assessed by applying the DNV rules [30] based on the external design pressure defined in the IGC Code. In this buckling assessment, the setting value of the vacuum relief valve ($P_1$) was set to 0.025 MPa. The set pressure of the pressure relief valve ($P_2$) and the external pressure due to environmental conditions ($P_4$) were not considered. The pressure from shell compression ($P_3$) due to insulation, shell weight, and corrosion was set to 0.005 MPa.

2.5. Fatigue Strength

In Type C tanks, cumulative fatigue damage is evaluated by considering both high-cycle fatigue (HCF) induced by wave loads and low-cycle fatigue (LCF) caused by cargo loading and unloading operations. The cumulative fatigue damage $D_F$ is expressed as the sum of HCF and LCF damage, as shown in Equation (26).

$$D_F=D_H+D_L\le 0.1$$

(26)

According to the IGC Code, fatigue failure is considered to occur when the cumulative fatigue damage reaches 1.0. To ensure structural safety, fatigue damage should be limited to 0.5 or lower at locations where crack detection is fully feasible, such as external surfaces, and 0.1 or lower at locations where crack detection is difficult, such as internal structures (e.g., ring stiffeners or ring frames located inside the tank).

3. Numerical Analysis

3.1. Ship and Tank Dimensions

The principal particulars of the 12,000 m³ LCO₂ carrier considered in this study are presented in

Table 1. Nondimensional principal parameters of LCO₂ carrier.

Item	Value
Rule length	15.604
Breadth	2.933
Depth	1.578
Block coefficient	0.732
Ship speed	5.833

. All dimensions used in this paper are non-dimensionalized based on the scantling draft of the vessel. When setting the midship, centerline, and baseline as the origins for the longitudinal, transverse, and vertical axes, respectively, the center of gravity of the tank is located at 2.758 in the longitudinal direction, 0.678 in the transverse direction, and 0.878 in the vertical direction.

The principal dimensions of the tank are presented in

Table 2. Nondimensional principal parameters of LCO₂ tank.

Item	Value
Length	4.422
Distance between saddles	2.222
Target volume	0.038
Molded radii of cylindrical and after-hemispherical shells	0.600
Molded radius of forward-hemispherical shell	0.389

. As shown in Figure 2, the tank mainly consists of a cylindrical shell and a conical shell. The cylindrical and conical shells are terminated at the after and forward ends with hemispherical shells, respectively. A pump dome and a sump are located at the top and bottom of the cylinder, respectively. The tank is supported by two cradles. To prevent local shell damage due to cradle supports, two after-ring frames and one forward-ring frame were installed inside the tank shell for reinforcement. A ring stiffener is positioned between the ring frames.

3.2. Load Cases

Load cases were categorized into ULS, ALS, HPT, and FLS corresponding to the respective limit states. ULS represents the limit state where dynamic pressure is generated inside the tank due to ship motions in rough seas, and ALS considers flooding scenarios resulting from collision accidents. HPT corresponds to the hydrostatic pressure test conducted during tank construction. FLS load cases consider the dynamic pressure generated inside the tank during normal ship operation.

According to the IGC Code [28] and DNV ship rules [31], the ULS load cases were divided into five cases depending on the direction of acceleration due to ship motions. ALS load cases included two collision scenarios under full loading conditions and one flooding case under an empty tank condition. The HPT load case consisted of a single hydrostatic pressure test. Thus, the numbers of load cases corresponding to ULS, ALS, and HPT were five, three, and one, respectively.

For FLS evaluation, the load cases were subdivided into high-cycle fatigue and low-cycle fatigue categories. There were six HCF cases and two LCF cases depending on the acceleration direction and loading/unloading conditions, respectively. Thus, eight load cases corresponded to the FLS limit state. A summary of the 17 load cases considered in this study is provided in

Table 3. Load cases summary.

Limit State	LC	Filling	Condition	Loading Direction	Gravity (g)	Pressure (MPa)			Temp. (°C)	Acceleration (g)
						${\mathit{P}}_0$	${\mathit{P}}_{\mathit{g}\mathit{d}}$	${\mathit{P}}_{\mathit{h}}$	$∆\mathit{T}$	${\mathit{a}}_{\mathit{x}}$	${\mathit{a}}_{\mathit{y}}$	${\mathit{a}}_{\mathit{z}}$
ULS	1-1	Full	Dynamic	Long. forward	1.0	1.90	0.1226	n/a	−55	0.228	n/a	n/a
	1-2	Full	Dynamic	Long. afterward	1.0	1.90	0.1226	n/a	−55	0.228	n/a	n/a
	2-1	Full	Dynamic	Trans. port-side	1.0	1.90	0.1860	n/a	−55	n/a	0.772	n/a
	2-2	Full	Dynamic	Trans. stbd-side	1.0	1.90	0.1860	n/a	−55	n/a	0.772	n/a
	3	Full	Dynamic	Vert. downward	1.0	1.90	0.1448	n/a	−55	n/a	n/a	0.738
ALS	4-1	Full	Collision	Long. forward	1.0	1.90	0.1457	n/a	−55	0.500	n/a	n/a
	4-2	Full	Collision	Long. afterward	1.0	1.90	0.1238	n/a	−55	0.250	n/a	n/a
	5	Empty	Flooding	n/a	1.0	n/a	n/a	0.095	n/a	n/a	n/a	n/a
HPT	6	Full	Static	n/a	1.0	2.85	n/a	n/a	n/a	n/a	n/a	n/a
FLS (HCF)	7-1	Full	Dynamic	Long. forward	1.0	1.50	0.1169	n/a	−55	0.213	n/a	n/a
	7-2	Full	Dynamic	Long. afterward	1.0	1.50	0.1169	n/a	−55	0.213	n/a	n/a
	8-1	Full	Dynamic	Trans. port-side	1.0	1.50	0.1204	n/a	−55	n/a	0.728	n/a
	8-2	Full	Dynamic	Trans. stbd-side	1.0	1.50	0.1204	n/a	−55	n/a	0.728	n/a
	9-1	Full	Dynamic	Vert. downward	1.0	1.50	0.1185	n/a	−55	n/a	n/a	0.735
	9-2	Full	Dynamic	Vert. upward	1.0	1.50	0.1185	n/a	−55	n/a	n/a	0.735
FLS (LCF)	10-1	Full	Static	n/a	1.0	1.50	n/a	n/a	−55	n/a	n/a	n/a
	10-2	Empty	Static	n/a	1.0	1.30	n/a	n/a	n/a	n/a	n/a	n/a

.

All load cases included the self-weight of the tank. The minimum value of the design vapor pressure calculated using Equation (1) slightly exceeded 1.0 MPa, which surpassed the pressure range (0.57–1 MPa) of low-pressure LCO₂ tanks. Thus, the tank considered in this study is suitable for medium-pressure operation within the 1.4–1.9 MPa range. Medium-pressure tanks can operate above the triple point of CO₂ (−56.6 °C/51.8 bar), reducing the risk of dry ice formation and allowing the use of low-temperature carbon steel. In contrast, low-pressure tanks operate near the CO₂ triple point and are subject to solidification risks depending on the operational conditions [32]. The design vapor pressure for ULS and ALS load cases was assumed to be 1.9 MPa, corresponding to the maximum pressure of medium-pressure tanks. For FLS load cases, based on classification society rules and shipyard best practices, the design vapor pressure was set to 1.5 MPa, close to the lower limit of medium-pressure tanks. For the FLS empty condition, 1.3 MPa was applied. For the HPT load case, a design vapor pressure of 2.85 MPa (1.5 times the maximum design pressure) was used according to the IGC Code. Thermal loads were considered for all ULS and ALS load cases except for the flooding case. The ambient temperature around the tank was assumed to be 20 °C, and the LCO₂ temperature was assumed to be −35 °C, leading to a temperature difference of 55 °C.

This study did not perform a separate analysis under a static heel condition of 30°, but it was deemed that the transverse dynamic loading conditions (LC2-1 and LC2-2) sufficiently covered the effect. In these cases, the inclination angle exceeded 30°, and the resultant acceleration exceeded 1 g, adequately reproducing transverse inertial loads.

3.3. Numerical Models

Finite Element Analysis (FEA) models of the C-type tank were developed using HyperMesh [33]. Since LCO₂ is a cryogenic cargo, thermal–mechanical loads needed to be considered, and thus the tank shells were modeled using triangular and quadrilateral shell elements (S3RT and S4RT). Steel plates of the cradle supports were modeled using quadrilateral shell elements (S4R), and the wooden saddles and tank keys were modeled using hexahedral solid elements (C3D8).

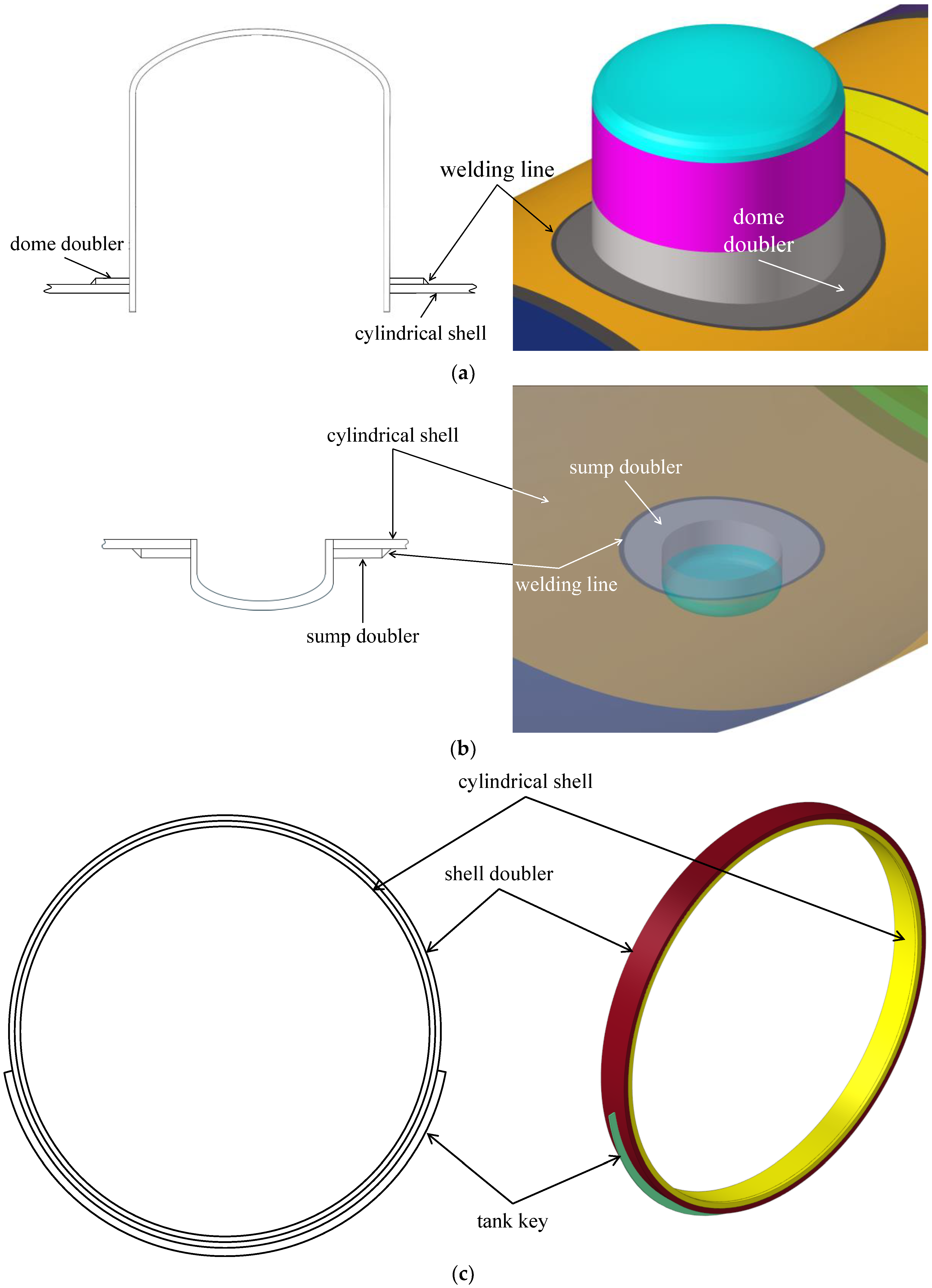
Since the pump dome is welded to the cylindrical shell via a doubler plate, it was modeled by merging nodes along the weld lines between the doubler plate and the cylindrical shell, as shown in Figure 3a. Similar methods were applied to the sump and ring frames with their respective doubler plates, as shown in Figure 3b,c.

According to ABS [34] recommendations, mesh size should be small enough to adequately represent the tank geometry. Thus, two different FEA models were developed for ULS/ALS/HPT load cases and FLS load cases, using different mesh sizes.

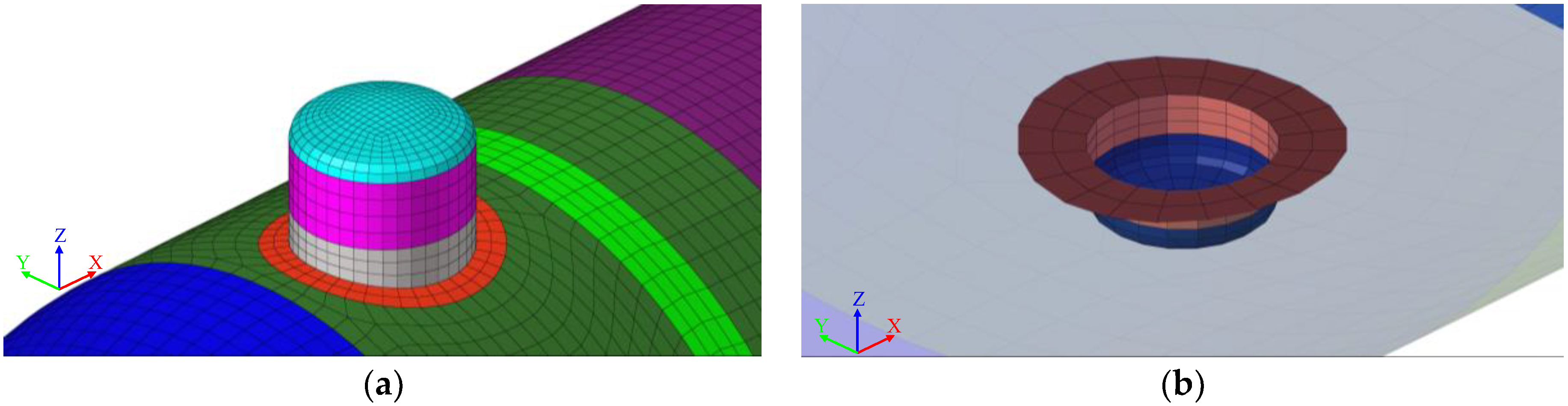
For the ULS, ALS, and HPT cases, 80 elements were generated along the circumference of the cylindrical shell, as shown in Figure 4a. This corresponds to a nominal element size of 400 mm. For the pump dome and sump, where geometric discontinuities are expected to cause stress concentrations, finer meshes of a 200 mm element size were applied.

However, the diameters of the pump dome and sump are approximately 2.5 m and 1 m, respectively, which are significantly smaller than that of the shell. To adequately capture the curvature of the pump dome, 40 elements were generated along its circumference, as shown in Figure 4b. Accordingly, a nominal element size of 200 mm was used for the pump dome. The same element size of 200 mm was applied to the sump.

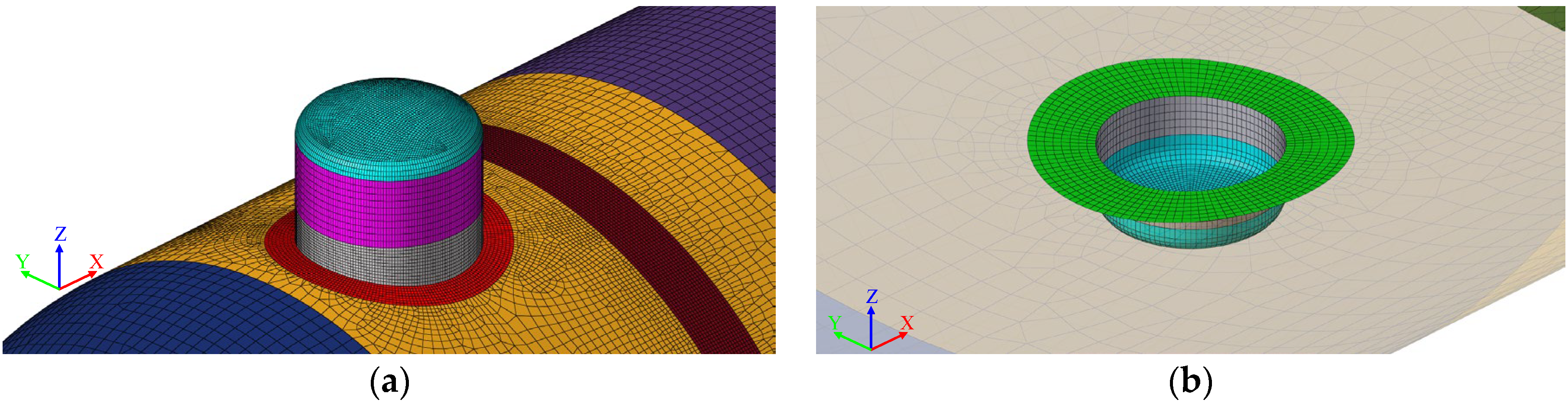
Stress concentration was expected at the junctions where the pump dome and sump connect with the shell due to geometric discontinuities. For FLS evaluation in these regions, the element size was set equal to the shell thickness in accordance with the guidelines provided by DNV [35]. This meshing strategy is illustrated in Figure 5. The element sizes corresponding to the ULS, ALS, HPT, and FLS cases are summarized in

Table 4. Element sizes.

Structural Component	Item	ULS, ALS, and HPT	FLS
Cylindrical shell, conical shell, hemispheres, ring frames, and ring stiffener	Nominal number of elements along circumference	80	160
	Nominal element size (mm)	400	200
Pump dome, sump, and associated doublers	Nominal number of elements along circumference	40	160
	Nominal element size (mm)	200	50

.

The tank material was nickel–manganese alloy steel, and the properties of the wooden saddles were taken from references [36,37], summarized in

Table 5. Mechanical properties of tank and wooden supports.

Item	Tank	Wooden Saddle
Density (ton/m3)	7.85	1.35
Poisson’s ratio	0.3	0.4
Young’s modulus (GPa)	206.0	3.0
Yield strength (MPa)	690.0	102.5 (compressive)
Tensile strength (MPa)	770.0	102.5 (compressive)
Thermal expansion coefficient (°C−1)	1.08 × 10−5	n/a

.

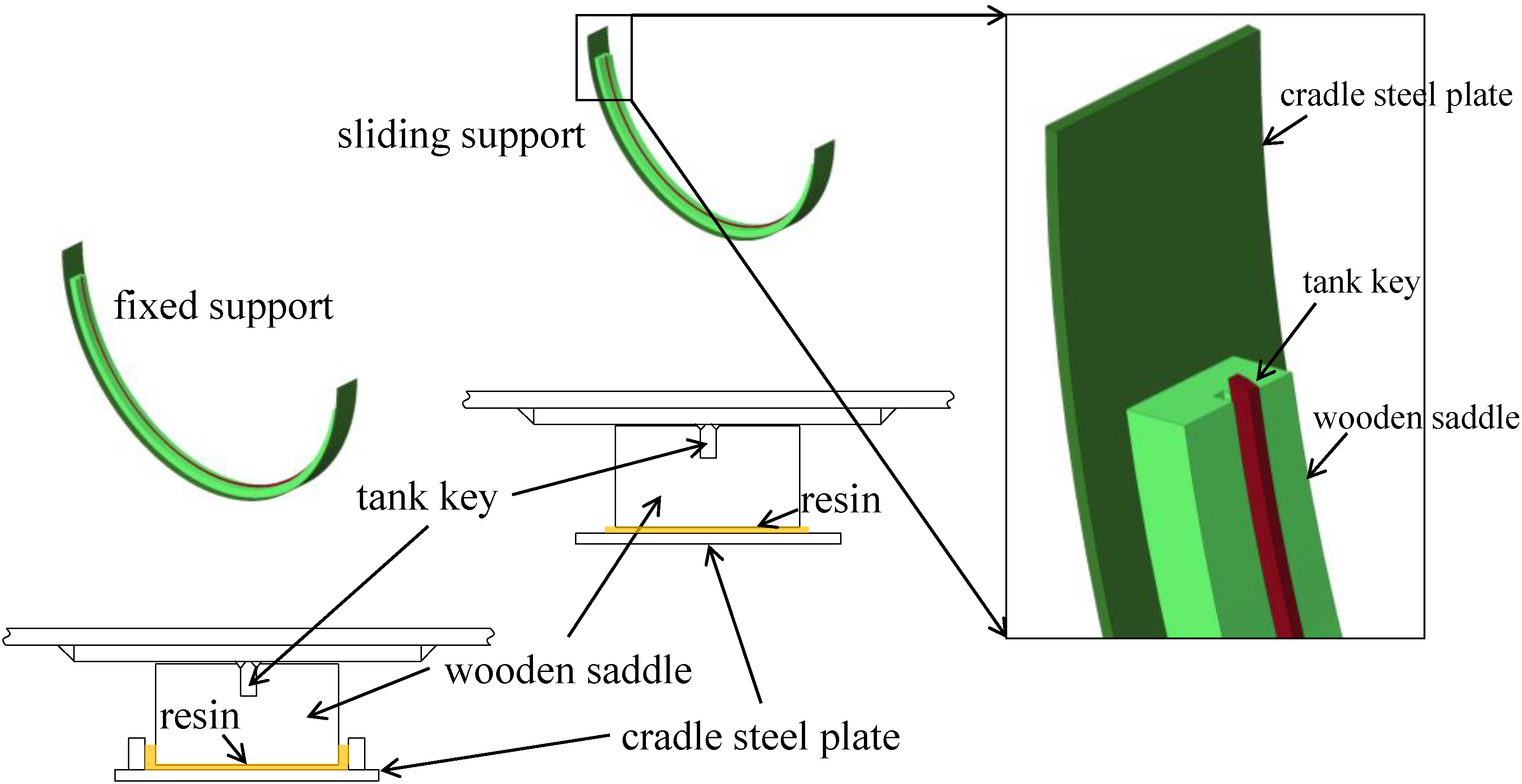
The two cradles were supported by the ship structure, and as shown in Figure 6, the cradle steel plates were bonded to the wooden saddles using resin. The after-cradle steel plate was designed to restrain the longitudinal displacement of the tank shell; therefore, all six degrees of freedom (DOFs) of both the after-cradle steel plate and the wooden saddle were constrained. In contrast, the forward-cradle steel plate was designed to allow sliding of the tank. Accordingly, all six DOFs of the forward-cradle steel plate were constrained, and the wooden saddle was connected to the steel plate using tie contact, resulting in full constraint of the bottom surface of the wooden saddle.

The top surfaces of the wooden saddles on both the after and forward cradles were in contact with the cylindrical shell and conical shell, respectively, and therefore, contact boundary conditions were applied. To restrict the longitudinal movement of the tank in the event that longitudinal inertial forces exceed frictional resistance due to high longitudinal acceleration, contact boundary conditions were also applied between each tank key and the corresponding wooden saddle. According to the classification rules [38], the coefficient of friction at the contact interfaces was set to 0.5 for FLS load cases and 0.2 for ULS, ALS, and HPT load cases. As a result, no boundary conditions were applied directly to the tank itself.

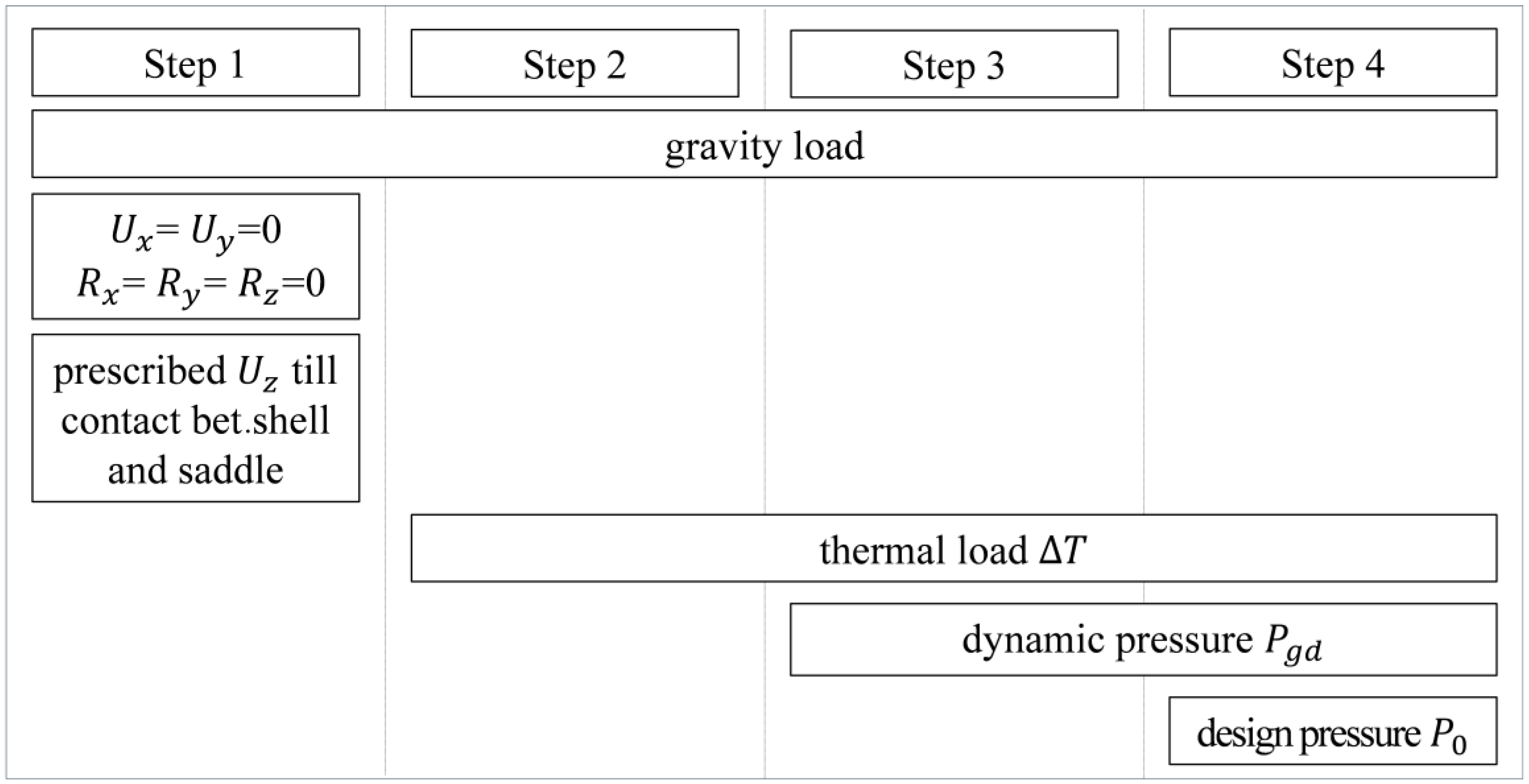
Since no boundary conditions were applied to the tank, convergence issues arose in the analysis due to rigid body motion. To resolve this problem, multiple load steps were implemented. In other words, to avoid the rigid body motion caused by the absence of boundary conditions, a sequential load application scheme consisting of multiple load steps, as shown in Figure 7, was established. This load step procedure was applied to all load cases except for four specific cases where no acceleration acts on the tank during ship operation: ALS LC5, HPT LC6, FLS LC10-1, and LC10-2.

• Step 1: Apply gravitational acceleration to the tank and constrain all degrees of freedom except for vertical displacement. Then, apply a vertical prescribed displacement $U_z$ until contact is established between the tank and the wooden saddles;
• Step 2: While maintaining gravitational acceleration, remove all boundary conditions and apply thermal loads;
• Step 3: With gravitational and thermal loads still applied, apply the dynamic pressure due to the liquid cargo;
• Step 4: Finally, apply the internal vapor pressure while maintaining gravitational, thermal, and dynamic loads.

Since LC5 corresponds to ALS flooding, $P_0$ and $P_{gd}$ in Figure 7 were replaced by $P_h$, and thermal loads were not applied. In the case of HPT LC6, an increased $P_0$ was applied instead of the dynamic pressure $P_{gd}$, and no thermal loads were applied. For LC10-1, thermal loads were applied, but dynamic pressure was not. For LC10-2, neither thermal loads nor dynamic pressure were applied.

3.4. Allowable Stresses for ULS, ALS, and HPT

In the design of Type C tanks, allowable stress criteria specified in the IGC Code were applied, and each stress component must not exceed the defined limits. The allowable design stress ${\sigma }_d$ was determined using Equation (3). Since the tank material used in this study is a nickel alloy, partial safety factors of $A_0$ = 3.0 and $B_0$ = 1.5 were applied.

The IGC Code [28] classifies tank stresses according to the following three criteria:

• Whether the stress is caused by external loads or geometric discontinuities;
• Whether the stress is a general stress (with a negligible stress gradient) or a local stress (including stress concentration);
• Whether the stress component is membrane or bending.

A primary stress is one that arises from internal or external loads, while a secondary stress results from geometric constraints due to surrounding structures. General stress assumes a negligible gradient (nominal stress), whereas a local stress includes concentration effects. Stress components are classified as membrane stress or bending stress.

Primary general membrane stress ${\sigma }_m$ refers to membrane stress induced by external loads without a stress concentration. For a stress to qualify as primary general membrane stress, it must not be redistributed even if it exceeds the material’s yield strength. Primary local membrane stress ${\sigma }_g$ refers to membrane stress caused by external loads that include stress concentration. The stress occurring in the tank shell due to internal pressure is dominated by primary general membrane stress. However, stresses that occur at geometrical discontinuities—such as shell joints, pump domes, and sumps—include primary local membrane stress and secondary local bending stress.

The allowable stresses for each limit state and major structural component, as defined by the IGC Code [28], are summarized in

Table 6. Allowable stress criteria.

Limit State	Component	Criterion	Allowable Stress (MPa)
ULS	Base plate of shell	${\sigma }_m<{\sigma }_d$	256
	Welded zone of shell	${\sigma }_m+{\sigma }_g<1.5{\sigma }_d$	385
	Ring frame and ring stiffener	${\sigma }_m+{\sigma }_g<1.5{\sigma }_d$	385
	Pump dome, sump, and their doublers	${\sigma }_m+{\sigma }_g+{\sigma }_b<3.0{\sigma }_d$	770
ALS	Shell	${\sigma }_m+{\sigma }_g<1.5{\sigma }_d$	385
	Ring frame and ring stiffener	${\sigma }_m+{\sigma }_g<1.5{\sigma }_d$	385
	Pump dome, sump, and their doublers	${\sigma }_m+{\sigma }_g+{\sigma }_b<3.0{\sigma }_d$	770
HPT	All components	${\sigma }_m+{\sigma }_g<0.9R_y$	621

.

3.5. Evaluation Conditions for FLS

DNV [29] recommends both a stochastic approach and a simplified approach for fatigue strength assessment. The stochastic approach requires a seakeeping analysis of the ship to obtain the load response amplitude operator (RAO). In contrast, the simplified approach allows for easier evaluation of fatigue strength by using only the maximum stress corresponding to a probability level of ${10}^{-2}$. For this reason, a simplified approach was adopted in this study to evaluate the fatigue strength of the LCO₂ tank.

In the simplified approach, the stress range $∆\sigma$ induced by long-term wave loading is assumed to follow a two-parameter Weibull distribution, as expressed in Equation (27). The scale parameter $q$ is determined using Equation (28), and the shape parameter $h$ is applied based on the value recommended by DNV [29].

Using the Palmgren–Miner rule [39], the cumulative fatigue damage due to high-cycle fatigue is expressed as an integral of the probability density function, as shown in Equation (29). Here, $n_0$ is the number of stress ranges $\Delta \sigma$ corresponding to the target exceedance probability level. To determine this value, the mean zero upcrossing frequency ${\nu }_0$, which represents the average encounter frequency between waves and the ship, is calculated using Equation (30). By substituting the S-N curve given in Equation (31) into Equation (29) and performing the integration, the result is simplified into Equation (32).

For low-cycle fatigue, cumulative damage is evaluated based on the number of cargo loading and unloading cycles. The number of such cycles over the vessel’s service life is assumed to be 1000, and the LCF-induced cumulative damage is expressed by Equation (33). The number of 1000 loading/unloading cycles was assumed in accordance with the IGC Code, which states that the number of such cycles shall not be less than 1000. The total cumulative damage from HCF and LCF, obtained using Equations (32) and (33), must satisfy the fatigue damage criterion defined in Equation (26).

$$f\left(∆\sigma \right)={\displaystyle \frac{h}{q}}{\left({\displaystyle \frac{∆\sigma }{q}}\right)}^{h-1}\exp \left(-{\left({\displaystyle \frac{∆\sigma }{q}}\right)}^h\right)$$

(27)

$$q={\displaystyle \frac{∆{\sigma }_0}{{\left(\ln n_0\right)}^{1/h}}}$$

(28)

$$D_H={\int }_0^{\infty }{\displaystyle \frac{n_{0}f\left(\mathsf{\Delta }\sigma \right)}{N}}d(∆\sigma )$$

(29)

$${\nu }_0\approx {\displaystyle \frac{1}{4\log L}}$$

(30)

$$\log N=\log \overline{a}-m\log \mathsf{\Delta }\sigma$$

(31)

$$D_H={\displaystyle \frac{n_0}{\overline{a}}}\sum _{i=1}{p}_i{q}_i^m\mathsf{\Gamma }\left(1+{\displaystyle \frac{m}{h_i}}\right)$$

(32)

$$D_L=\sum _{i=1}^{1000}{\displaystyle \frac{1}{N_i}}$$

(33)

The range of the shape parameter h is approximately 0.9 to 1.1, and it varies depending on the location on the vessel. In regions subjected to large accelerations, such as the bow, stern, or port/starboard sides, $h$ tends to approach 1.1. In this study, a conservative value of $h$ = 1.0 was applied. Based on the encounter frequency, the time corresponding to a probability level of ${10}^{-2}$ was calculated to be approximately 0.24 h. Therefore, the value of $n_0$ in Equation (32) was estimated to be around 100 cycles.

For the material constants $\overline{a}$ and $m$ required in Equation (31), the values corresponding to the D-curve in DNV-RP-C203 [35] were used. Specifically, $m_1$ and $m_2$ were set to 3.0 and 5.0, respectively, while ${\mathit{log}\overline{a}}_1$ and ${\mathit{log}\overline{a}}_2$ were taken as 12.164 and 15.606, respectively.

4. Analysis of Results

4.1. Buckling Check

The external pressure $P_{ed}$ used for the buckling strength assessment, calculated according to Equation (21), was 0.03 MPa. The results of the buckling strength evaluation are presented in

Table 7. Buckling strength assessments.

Component	Bending	Membrane
Cylindrical shell	2.317 < 4.0$P_{ed}$	$P_{cy}^m$ = 1.326 < 3.0$P_{ed}$
Conical shell	2.317 < 4.0$P_{ed}$	$P_{cy}^m$ = 1.326
Forward hemisphere	0.860 < 3.0$P_{ed}$	$P_{sph}^m$ = 5.993
After hemisphere	0.785 < 3.0$P_{ed}$	$P_{sph}^m$ = 5.724

, confirming that all components of the tank exhibited sufficient buckling resistance. As per the IGC Code and DNV rules, the buckling evaluation considers only external pressure effects under vacuum conditions. Internal pressure, which stabilizes the shell structure, is not included in the buckling assessment.

4.2. Stress Ratios

A stress analysis was conducted using Abaqus [40]. In this study, instead of extracting directional membrane stresses under multiaxial stress conditions, the von Mises equivalent stress was conservatively regarded as either a membrane stress or a membrane stress including bending stress. Hereafter, the von Mises equivalent stress is referred to simply as the equivalent stress.

In nominal stress regions of the tank shell, the equivalent stress can be considered as a general stress. Specifically, the equivalent stress at the mid-layer can be regarded as the primary general membrane stress ${\sigma }_m$. However, in regions with a stress concentration, it is not possible to clearly distinguish between the primary general membrane stress ${\sigma }_m$ and the primary local membrane stress ${\sigma }_g$. Therefore, in this study, the equivalent stress at the mid-layer was considered as the combined value ${\sigma }_m+{\sigma }_g$. On the other hand, the maximum equivalent stresses obtained at the top and bottom layers were regarded as ${\sigma }_m+{\sigma }_g+{\sigma }_b$, where ${\sigma }_b$ denotes the secondary local bending stress.

The equivalent stress distributions for several ULS, ALS, and HPT load cases with significant stress development are shown in Figure 8. In all cases, high stress concentrations occurred at the junction between the cylindrical shell and the pump dome. As illustrated in Figure 8c, the maximum equivalent stress among all load cases occurred in the HPT load case.

The stress ratio, defined as the ratio of actual stress to allowable stress, is summarized in

Table 8. Stress ratios.

Analysis Case	Load Case	Tank Shell		Ring Frame and Stiffener	Pump Dome, Sump, and Doublers
		Base Plate	Welded Zone
ULS	LC1-1	0.961	0.678	0.370	0.733
	LC1-2	0.961	0.677	0.373	0.732
	LC2-1	0.993	0.701	0.374	0.755
	LC2-2	0.992	0.700	0.385	0.756
	LC3	0.969	0.683	0.401	0.738
ALS	LC4-1	0.647	0.686	0.372	0.742
	LC4-2	0.639	0.678	0.373	0.732
	LC5	0.039	0.057	0.086	0.038
HPT	LC6	n/a	n/a	n/a	0.867

. The maximum stress ratio occurred in the ULS LC2-1 load case. In the ULS load cases, a stress difference of approximately 6% was observed between the base plate and the welded zone of the tank shell; however, due to the difference in allowable stress criteria, the stress ratio at the base plate approached unity. In contrast, in the ALS load cases, the same allowable stress criterion was applied uniformly across the tank shell, resulting in only a small difference in stress ratios between the base plate and the welded zone. For the ring frame and stiffener, the highest stress ratio occurred in the ULS LC3 load case. This is attributed to the fact that the internal supporting structures directly resisted external loads in that case. In the pump dome, sump, and doubler plate regions, although dynamic pressure and thermal loads were not applied in the HPT load case, the resulting membrane stress values were comparable to the sum of membrane and bending stresses in the ULS and ALS load cases. This indicates that the design pressure acts as the most dominant loading condition in determining the structural response of the tank.

4.3. FLS Analysis Results

The difference in maximum principal stresses obtained from the FEAs of two load cases with opposite loading directions (i.e., a pair of load cases) was determined as the stress range $\mathsf{\Delta }\sigma$. For example, LC7-1 and LC7-2 correspond to the forward and backward longitudinal acceleration directions, respectively, and the difference in maximum principal stresses obtained from these two load cases was regarded as $\mathsf{\Delta }\sigma$. The stress ranges were also obtained from LC8-1/LC8-2 and LC9-1/LC9-2 using the same method. Since the two principal angles generated from the load case pairs did not differ significantly, it was considered a reasonably valid assumption to regard the difference in maximum principal stresses as $\mathsf{\Delta }\sigma$.

The occurrence probabilities of the three load case pairs corresponding to HCF (LC7-1/LC7-2, LC8-1/LC8-2, and LC9-1/LC9-2) were assumed to be identical. In other words, the occurrence probability of each load case pair corresponding to HCF was taken as 1/3. On the other hand, the occurrence probability of the load case pair corresponding to LCF (LC10-1/LC10-2) was considered to be 100%.

By examining the distribution of maximum principal stresses, the stress range was calculated at the pump dome, where the highest stress occurred, for both the bottom and top layers, respectively. As shown in

Table 9. Fatigue strength assessment result.

Layer	Load Case	${\mathit{\theta }}_{\mathit{p}}$ (deg)	${\mathit{\sigma }}_{\mathit{p}1}$ (MPa)	$\mathsf{\Delta }{\mathit{\sigma }}_{\mathit{p}1}$ (MPa)
Bottom	LC7-1	0.903	424.469	0.300
	LC7-2	0.903	424.168
Top	LC7-1	0.348	565.907	1.000
	LC7-2	0.350	564.907
Bottom	LC8-1	0.913	425.073	−0.393
	LC8-2	0.894	425.466
Top	LC8-1	0.129	566.601	−0.214
	LC8-2	0.516	566.815
Bottom	LC9-1	0.903	424.068	−1.301
	LC9-2	0.903	425.369
Top	LC9-1	0.346	564.007	−4.000
	LC9-2	0.353	568.007
Bottom	LC10-1	0.903	398.057	104.826
	LC10-2	0.903	293.230
Top	LC10-1	0.353	524.206	68.591
	LC10-2	0.360	455.616

, the maximum principal stress ranges for the load cases corresponding to HCF were negligibly small. Also, the variation in the principal stress angle was not significant.

The stress ranges obtained from the three load case pairs were substituted into Equation (32) to calculate the fatigue life corresponding to HCF. The occurrence probability p for each pair was equally applied as 1/3. The fatigue life corresponding to LCF was obtained using Equation (33). The fatigue damage due to HCF was found to be almost negligible, while the fatigue damage due to LCF was calculated to be 0.001. This corresponds to a fatigue life of 31,661 years based on a design life of 25 years.

5. Conclusions

In this study, a comprehensive strength assessment was conducted for an IMO Type C cargo tank designed for a medium-range LCO₂ carrier. The results of the study are summarized as follows:

• Based on stress analyses under the ULS, ALS, and HPT load cases for the tank designed to meet the buckling strength criteria specified in the IGC Code, a maximum stress ratio of 0.993 was observed at the base plate under the ULS LC2-1 load case, corresponding to a membrane stress of 254.3 MPa. In addition, a local peak stress of 581.3 MPa was found at the junction between the pump dome and the cylindrical shell, which was attributed to the stress concentration caused by geometric discontinuities.
• In the fatigue strength evaluation, fatigue damage induced by wave loads (high-cycle fatigue) was found to be almost negligible, and the overall fatigue life was primarily governed by fatigue damage resulting from cargo loading and unloading operations (low-cycle fatigue). The calculated fatigue life under wave-induced loads was over 31,000 years, which is not intended to represent a practical service life but rather demonstrates quantitatively that wave loads contribute insignificantly to fatigue damage under the current design conditions.
• Even in the HPT case, where only gravitational acceleration and design vapor pressure were applied, a significantly high stress ratio of 0.867 was observed, with a membrane stress of 538.2 MPa. This suggests that the design vapor pressure is the dominant loading condition that induces high stress in the tank structure. Therefore, if stress concentration at geometric discontinuities such as the pump dome can be properly controlled, the medium-pressure (1.4–1.9 MPa) LCO₂ tank design applied in this study may be sufficiently competitive compared to low-pressure tank designs.

Although this study did not aim to perform a formal optimization, the proposed modeling approach and findings are expected to serve as a fundamental reference for the future design optimization of LCO₂ cargo tanks and their supporting structures. For example, while the ULS load cases were derived based on DNV guidelines, greater scientific originality could have been achieved by incorporating acceleration time histories obtained through seakeeping analyses. Similarly, the fatigue evaluation could have benefited from a stochastic fatigue analysis for high-cycle fatigue and a spectrum-based approach for low-cycle fatigue, instead of simplified cumulative methods. These enhanced methods would have yielded more realistic and academically robust results. However, considering the practical scope and constraints of the present study, such advanced analyses were not feasible at this stage and are left for future research. The results of this study are also expected to contribute to the development of LCO₂ transportation infrastructure in line with the future advancement of CCUS technologies. Future research should include additional evaluations of sloshing phenomena under actual operating conditions, thermal fatigue, and structural performance under various environmental conditions.