A Novel iTransformer-Based Approach for AIS Data-Assisted CFAR Detection

Abstract

Detection of small vessels is of great significance for maritime safety assurance, abnormal vessel tracking, illegal fishing supervision, and combating smuggling. However, the radar reflection intensity of small vessels is low, making them difficult to detected with the radar’s constant false-alarm rate (CFAR) algorithm. To enhance the detection capability for small vessels, we propose an improved CFAR scheme. Specifically, we first compared traditional CFAR processing results of radar data with automatic identification system (AIS) data to identify some special targets. These special targets, which possessed AIS information, but remained undetected by radar, enabled an iTransformer model to generate more reasonable CFAR threshold adjustments. iTransformer adaptively lowered the threshold of the areas around these targets until they were detected by radar. This process made it easier to discover the small boats in the surrounding area. Experimental results showed that our method reduces the missed detection rate of small vessels by 73.4% and the false-alarm rate by 60.7% in simulated scenarios, significantly enhancing the CFAR detection capability. Overall, our study provides a new solution for ensuring maritime navigation safety and strengthening illegal supervision, while also offering new technical references for the field of radar detection.

1. Introduction

The accurate detection of small vessels is of paramount importance for maritime security, fisheries management, and collision avoidance [1]. These small vessels are characterized by small radar cross sections, highly random navigation trajectories, and unpredictable appearance patterns. Some even purposefully evade monitoring. These characteristics collectively exacerbate the challenge of supervising such vessels. To address this issue, existing detection methods for small vessels mainly include CFAR detection, infrared thermal imaging, optical camera imaging, and synthetic aperture radar (SAR) [2,3,4]. However, these detection methods are still prone to missed detections when applied to the inspection of small vessels. Among these methods, the CFAR algorithm has been widely used due to its cost-effectiveness, all-weather operability, illumination independence, and long detection range. Thus, CFAR is particularly suitable for long-term and large-area vessels monitoring in fixed sea regions. Improving CFAR detection accuracy for small vessels can effectively enhance maritime safety supervision capacity.

1.1. Related Work

Current detection methodologies for small vessels primarily rely on physical sensing and information fusion technologies. The constant false-alarm rate (CFAR) algorithm dominates radar-based detection due to its all-weather operability and cost-effectiveness, yet it remains susceptible to sea clutter interference in complex environments, leading to missed detections [5]. Synthetic aperture radar (SAR) enables high-resolution vessel contour identification, but suffers from prolonged data update cycles and elevated false-alarm rates in nearshore scenarios [6]. For optical/infrared sensing, optical cameras excel in nearshore surveillance due to high resolution and low cost, though their performance is constrained by weather and lighting conditions [7]. While infrared thermal imaging ensures all-weather detection, its high hardware costs hinder large-scale deployment. Automatic identification system (AIS)-based fusion techniques enhance identification accuracy by cross-correlating signal data with physical detections [8], yet they depend on equipment installation rates and fail to monitor “silent” vessels. In summary, existing methods involve trade-offs among detection efficiency, environmental adaptability, and cost. Overall, CFAR remains the cornerstone for long-term, continuous monitoring of small vessels in fixed maritime areas, balancing practicality and reliability.

The traditional CFAR algorithm estimates the power threshold of surrounding reference cells to determine target presence. Depending on the threshold calculation approach, various CFAR variants have emerged, each tailored to specific sea conditions [9]. The cell averaging (CA) CFAR offers computational simplicity and performs satisfactorily in homogeneous environments. Building on CA CFAR, the smallest-order cell averaging (SOCA) CFAR mitigates strong target interference [10]. It does so by selecting the minimum value from forward/backward training cells. In contrast, the greatest-order cell averaging (GOCA) CFAR divides reference cells into two segments [11]. It uses the maximum value for noise power estimation, which is crucial for clutter-edge scenarios. These improvements have yielded distinct benefits: SOCA has reduced the missed-detection rate, while GOCA has lowered the false-alarm rate. The ordered statistics (OS) CFAR further enhances robustness by sorting reference cells and selecting the median value, though at the cost of higher computational complexity [12]. Overall, these CFAR variants excel in their designated scenarios. However, detection performance deteriorates significantly when applied to mismatched conditions, highlighting their limited adaptability and generalizability in dynamic, complex environments [13,14,15].

To enhance the CFAR algorithm’s ability to dynamically adjust thresholds based on environmental factors and improve small-vessel detection, recent studies have increasingly leveraged deep learning for optimization. In 2019, Chia-Hung Lin et al. proposed DL-CFAR (deep learning-based CFAR), aiming to address the masking effect of CA-CFAR and its variants in multitarget scenarios with lower computational cost [16]. The algorithm uses a deep learning model to learn target structures in distance-Doppler (RD) graphs, removes target patterns to derive pure noise graphs, and thus estimates noise levels more accurately for robust CFAR detection. Subsequently, in 2022, Tzvi Diskin and colleagues introduced CFARnet, a framework that theoretically proved the equivalence between CFAR-constrained Bayesian optimal detectors and the generalized likelihood ratio test (GLRT) [17]. Experiments showed that CFARnet achieved flexible trade-offs between false-alarm rates and detection accuracy. In 2024, Ignacio Roldan et al. developed a data-driven radar detector inspired by computer vision using a 2D CNN backbone [18]. This method employs cross-sensor supervision and unlabeled radar–lidar data to overcome traditional CFAR limitations in complex urban environments with extended targets. These studies demonstrate that deep learning effectively enhances CFAR’s feature extraction and environmental adaptability, improving small-target detection and system robustness. However, current methods still face challenges such as high data dependency, high annotation costs, and limited adaptability to non-uniform environments.

A cutting-edge model for multivariate time-series analysis, iTransformer demonstrates exceptional capabilities in processing multivariate data and conducting robust feature correlation analysis [19]. This implies that it can comprehensively analyze the complex interrelations among various influencing factors in dynamic marine conditions, thereby exhibiting superior adaptability and generalization. This architecture inherits the fundamental modules of the transformer framework, yet it redefines the framework’s design to suit the unique characteristics of time-series data [20]. For multivariate time-series analysis, iTransformer employs a variable-centric strategy. The model captures inter-variable correlations via self-attention mechanisms while leveraging temporal features encoded by the feedforward network to facilitate prediction [21]. This integrated design endows iTransformer with exceptional adaptability to diverse environments, rendering it highly effective in handling non-uniform data.

To enhance the CFAR algorithm’s applicability across complex sea conditions and improve small-vessel detection, we propose an iTransformer-based CFAR improvement that integrates AIS as prior knowledge. Specifically, this method constructs a weakly supervised evaluation index by comparing inputs and outputs of the model to form the loss function, and introduces the Gumbel-softmax algorithm to regulate training dynamics. iTransformer is leveraged to analyze the complex interrelations among diverse sea conditions, radar waveforms, raw CFAR outputs, and AIS data, thereby deriving an adaptively adjusted CFAR threshold. This threshold empowers the CFAR algorithm to achieve more effective small-vessel detection.

1.2. Contributions

To enhance CFAR with iTransformer and integrate AIS as prior knowledge, we conducted the following key work.

• To adapt to real-world scenarios, we performed a comparative analysis between the model inputs (radar signals, AIS data, enhanced CA-CFAR detection results, and spatial encoding) with the improved CFAR threshold outputs. This analysis yielded a weakly supervised evaluation index for constructing the loss function. The design enabled the model to prioritize targets with AIS data, but missed by radar, adaptively reducing detection thresholds around these targets to enhance the detection of other small vessels.
• To avoid falling into local optima and neglecting less influential factors during training, we employed the Gumbel-softmax annealing algorithm. This algorithm regulated the relaxation degree throughout training, enabling extensive exploration in the early stage and focused optimization in the later stage.

2. Methods

The proposed improved CFAR method based on the iTransformer model is shown in Figure 1. This method mainly consists of three parts: the data part, the simulation scene construction part, and the model training part. In the data processing stage, we applied cubic spline interpolation to AIS data to align it with radar data, ensuring that there were corresponding AIS data every minute. Additionally, we stochastically generated position coordinates for AIS-unannotated vessels, which were incorporated into radar waveform modeling. These AIS-unannotated small vessels served as the reference for final validation of the model’s detection performance. In the simulation scenario construction, we modeled sea clutter, obstacle echoes, and vessel echoes based on radar echo simulation principles, then combined and rasterized these waveforms into radar data. The radar waveforms were processed by the original CFAR, and the CFAR processing results and thresholds obtained were encapsulated with the radar and AIS data as the model input. In the model training phase, we augmented the input data with two-channel spatial position information and employed the iTransformer to capture complex correlations among multiple variables in the input data. The iTransformer model output a two-dimensional adaptive threshold distribution. Then, we designed a weakly supervised evaluation system as the loss function to compare the input and output, enabling the model to continuously iterate in the desired learning direction in the absence of labels. Finally, we used the Gumbel-softmax annealing algorithm to adjust the relaxation degree of the entire learning process of the model.

2.1. Construction of Simulated Scenes

We constructed a simulation scenario to facilitate the easier adjustment of parameters for control experiments and verification of model performance. The complete radar echo simulation process is shown in Figure 2. Specifically, we first introduced actual AIS data as the spatial coordinates of vessels with AIS. Then, based on the Monte Carlo method, we added a certain number of obstacles and vessels without AIS information to the samples at each time point. By modeling the radar echoes of vessels, obstacles, and sea clutter, we simulated real radar echo signals as realistically as possible. In addition, we also obtained the threshold and processing results of CFAR before improvement through CA-CFAR processing, which is conducive to helping the model understand how to improve the threshold distribution. The data generated by the above process were rasterized and input as the dataset of the model. The simulated experimental scenario was structured around the core logic of “data-driven modeling–multimodal signal synthesis–spatiotemporal dynamic alignment”, achieving faithful replication of complex marine environments through in situ measurements and physical modeling integration.

The simulated experimental scenario was structured around the core logic of “data-driven modeling–multimodal signal synthesis–spatiotemporal dynamic alignment”, achieving faithful replication of complex marine environments through the integration of in situ measurements and physical modeling. The complete simulation process of the radar echo is shown in Figure 2 [22,23,24]. Sea clutter signal generation is grounded in the statistical properties of empirical data, utilizing a hybrid Rayleigh-K distribution model: Rayleigh distributions simulate homogeneous clutter in high-sea-state regions, while K distributions are introduced in inshore reef areas to characterize spiky amplitude statistics. The texture component is generated via a gamma distribution (parameters co-regulated by topographic gradients and sea state indices), and the speckle component employs zero-mean complex Gaussian processes to model microscale scattering stochasticity. The superposition of the K-distribution and the Rayleigh distribution is shown in Figure 3 [25]. Obstacle echo modeling relies on the geometric theory of diffraction (GTD), partitioning the near-field diffraction zone, interference zone, and far-field shadow zone. Using the method of moments (MoM), the Doppler shift–incidence angle relationship of obstacle scattering fields at the X-band is calculated to physically model multipath interference, interference fringes, and clutter attenuation effects [26]. Since this paragraph pertains to the construction of the simulation environment, and the important theories involved have little relevance to the main innovations of this paper, they will not be elaborated on in the main text. The relevant theoretical content can be found in Appendix A.

2.2. Early Iterative Ideas and Limitations

In earlier work, we proposed using AIS as prior knowledge to adjust CFAR thresholds. During original CFAR detection, the monitored sea area is gridded into cells. The detection threshold for each cell is calculated by referencing the average radar power in a surrounding region. Consequently, adjacent cells share most reference cells during threshold calculation: if one cell has an excessively high threshold, its neighbors often show similar overestimation. When AIS information exists in a cell, but no radar target is detected, this indicates excessively high thresholds in that cell and its vicinity. Thus, we iteratively reduced the thresholds in this region until radar targets were detected and matched with AIS data, as shown in Figure 4. The adjusted thresholds around the cell then became more reasonable, facilitating the identification of AIS-unannotated small vessels.

However, this approach introduced three key challenges. First, defining the spatial scope for threshold reduction was challenging, i.e., how to mathematically characterize the adjustment region. Second, determining the reduction strategy—fixed value across the region or greater reduction near its center—was non-trivial. Finally, 2D CFAR algorithms required accounting for both distance and direction of reference cells, complicating spatial correlation modeling. In summary, relying on simple iterative models for threshold adjustment is subjective and theoretically unsound. Empirically setting model parameters may yield acceptable performance in specific scenarios, but fail entirely in novel contexts. However, this iterative idea itself can effectively enhance the detection capabilities of small ships. Thus, we employed an iTransformer neural network to learn the complex relationships among historical radar data, AIS data, and CFAR detection results. iTransformer has excellent capabilities in analyzing multiple couplings and perceiving spatial characteristics, and can better utilize the laws of analyzing sea conditions to obtain a more reasonable threshold distribution.

2.3. Model Training

We implemented three key improvements to adapt the iTransformer model for non-AIS-transmitting vessel detection scenarios. The architecture of the improved iTransformer model is shown in Figure 5. First, we incorporated spatial position information to help the model learn the complex connections of multichannel input information in the spatial domain. Second, we designed a weakly supervised composite evaluation system to address the shortage of non-AIS-transmitting vessel samples. We constructed the constraint and parameter terms using the general evaluation criteria for radar data detection. These terms were derived through input–output analysis and comparison, reducing reliance on label data. Finally, we adopted the Gumbel-softmax annealing algorithm to achieve differentiable continuous relaxation. By dynamically adjusting the temperature parameter, the algorithm balanced the model’s exploration and convergence capabilities, effectively addressing the problem of traditional methods being prone to local optima during the initial training phase.

2.3.1. Spatial Position Enhancement Mechanism

We added two channels of spatial position encoding information to the original four-channel input variables before flattening, recording the horizontal and vertical coordinates of each grid cell. This ensured that spatial coordinate information was retained even after flattening The multi-head self-attention mechanism can analyze the spatial information of these two channels as variables and establish cross-modal correlations among radar data, AIS information, and spatial coordinates. The spatial position encoding method is shown in Figure 6.

2.3.2. Parameter Term of Weakly Supervised Evaluation System

We constructed a loss function framework that was independent of strong labels by fusing prior AIS knowledge and radar detection results, enabling adaptive optimization of CFAR thresholds. Focused on core detection scenarios with valid AIS data (AIS = 1), the framework guided the model to learn complex spatiotemporal correlation features without labeled data through differentiated reward–penalty mechanisms and dynamic constraint strategies. The weakly supervised evaluation system uses a loss function with synergistic parametric and constraint terms based on four typical detection scenarios for AIS = 1. The parametric terms quantify model performance by defining four scenarios for AIS-enabled vessel detection logic, as follows.

• Correct detection maintenance (case 1): When both pre- and post-improvement CFAR detection results are “1” and AIS = 1, the model stably identifies known vessels. A mild reward weight (0.005) reinforces detection consistency to avoid erroneous elimination of valid targets.
• Missed-detection correction (case 2): If the post-improvement detection is “1,” pre-improvement detection is “0,” and AIS = 1, the model corrects the missed detection of weak-signal targets by traditional CFAR. A high reward weight (1.1) prioritizes optimizing such critical scenarios.
• Uncorrected missed detection (case 3): When both pre- and post-improvement detections are “0” and AIS = 1, the model fails to detect AIS-enabled vessels. A penalty weight (−1.2) forces the model to enhance sensitivity to low-signal-to-noise-ratio targets.
• Erroneous missed detection (case 4): If the post-improvement detection is “0,” pre-improvement detection is “1,” and AIS = 1, the model erroneously eliminates valid detections. The strongest penalty (−1.7) suppresses such severe misjudgments.

The parametric loss is calculated by summing the product of scenario-averaged detection probabilities and weights, defined as:

$$L_{\mathrm{scene}}={\displaystyle \sum _{j=1}^B{\displaystyle \sum _{i=1}^4{w}_i}}\cdot p_{i,j}$$

(1)

Here, $B$ represents the batch size, $w_i$ corresponds to the weights of the four scenarios, and $p_{i,j}$ denotes the detection probability of the j-th sample in the i-th scenario. This design forces the model to prioritize the optimization of the detection stability and missed-detection correction ability for vessels enabled with AIS through the preset reward and punishment logic in the direction we hope for improvement.

2.3.3. Constraint Term of Weakly Supervised Evaluation System

We introduced an exponential constraint term into the system to maintain the target count within a fixed range of $(m,n)$. This approach avoids extreme false alarms or missed detections caused by threshold fluctuations. The range $(m,n)$ was determined based on the average number of AIS-containing cells throughout the training process for computational convenience. The constraint term formula is as follows:

$$f(x)=\left\{\begin{array}{ll}\max \left(1.0-k\times {(m-x)}^{1.5},-1.0\right)\hfill & \mathrm{if} x<m\hfill \\ 1.0\hfill & \mathrm{if} m\le x\le n\hfill \\ \max \left(1.0-k\times {(x-n)}^{1.5},-1.0\right)\hfill & \mathrm{if} x>n\hfill \end{array}\right.$$

(2)

The mathematical function graph of the constraint term is shown in Figure 7. When the detection count falls within the range of $(m,n)$, the constraint term considers the target count as expected and gives a reward (value of 1). When the count is out of this range, the constraint term decreases, and the further it deviates, the faster the decrease becomes, until it reaches the threshold value of −1. This mechanism not only guides the model to constrain the number of detection results but also tolerates a certain degree of deviation in target detection.

2.3.4. Constraint Term of Gumbel-Softmax Annealing Algorithm

We introduced the Gumbel-softmax annealing algorithm [26,27,28] to avoid the local optimum of the model caused by the weakly supervised evaluation system. This approach dynamically adjusted the temperature parameter τ to balance the model’s exploration and convergence capabilities. Its mechanism was deeply integrated into the model architecture to form a “temperature–attention–evaluation” collaborative optimization loop. The specific implementation methods were as follows.

During the initial training phase, a high-temperature strategy ($\tau$ = 1) was adopted to make the decision distribution nearly uniform, forcing the model to widely explore potential correlations between radar echoes and AIS data. In the middle phase, an exponential decay mechanism ($\tau$ = ${\tau }_0\cdot$0.95ᵗ) was introduced to gradually reduce randomness and focus on stable feature correlations. In the later phase, a dynamic response mechanism monitored real-time metrics such as evaluation loss change rate and attention entropy. The formula for local temperature compensation coupling is:

$${\tau }_{\mathrm{effective}}=\tau \cdot \sigma (w\cdot P+b)$$

(3)

A temperature regularization term was introduced to constrain the parameter optimization direction and avoided abnormal temperature fluctuations:

$$L_{\mathrm{reg}}=|\tau -{\tau }_{\mathrm{optimal}}{|}^2$$

(4)

Here, ${\tau }_{\mathrm{optimal}}$ represents the theoretical optimal temperature statistically derived from historical data. Minimizing the regularization term ensured that the temperature parameter converged to a reasonable interval. This balance between the model’s exploration and convergence capabilities was achieved by this optimization. In simulated scenarios, the approach also enabled robust threshold adjustment and detection accuracy. The degrees of influence of case 1 and case 2 on the training process during the process from high temperature to low temperature are shown in Figure 8.

3. Experiments

3.1. Study Area and Experimental Setup

We selected a real-world AIS dataset covering the northern South China Sea (17.793918° N–32.495048° N, 106.4104° E–124.888187° E), focusing on vessel movement characteristics in the Taiwan Strait (a critical East Asian shipping lane) and the southeastern East China Sea–northern South China Sea traditional fishing grounds. The research area—a 10 nm² sea zone (115.64428° E–115.65263° E × 25.14915° N–25.1575° N)—was determined via random sampling to feature moderate vessel density. The AIS data spanned 1–17 December 2024.

The experimental dataset comprised 23,651 independent samples, each corresponding to a marine monitoring scenario at a specific time. Each sample’s six-channel input matrix included mean radar power, CFAR detection thresholds and results, AIS vessel status, longitude–latitude encoding, and topographic feature encoding. To ensure the model fully learned complex inter-channel couplings while avoiding overfitting from temporal continuity, a non-temporal random partitioning strategy was adopted. The dataset was divided into a training set (2556 samples), validation set (548 samples), and test set (547 samples): 70%, 15%, and 15%, respectively. Stratified sampling was used during partitioning to maintain consistent ratios of AIS-present and AIS-absent vessels across datasets.

To validate the rationality of the results, we conducted six repeated experiments on the same dataset. Given that all samples were processed out of order during both dataset partitioning and model training, these experiments can be treated as six independent trials. The dataset included 23,651 sample points (collected at one-minute intervals), with each training cycle comprising 32 samples—a total of 740 training cycles.

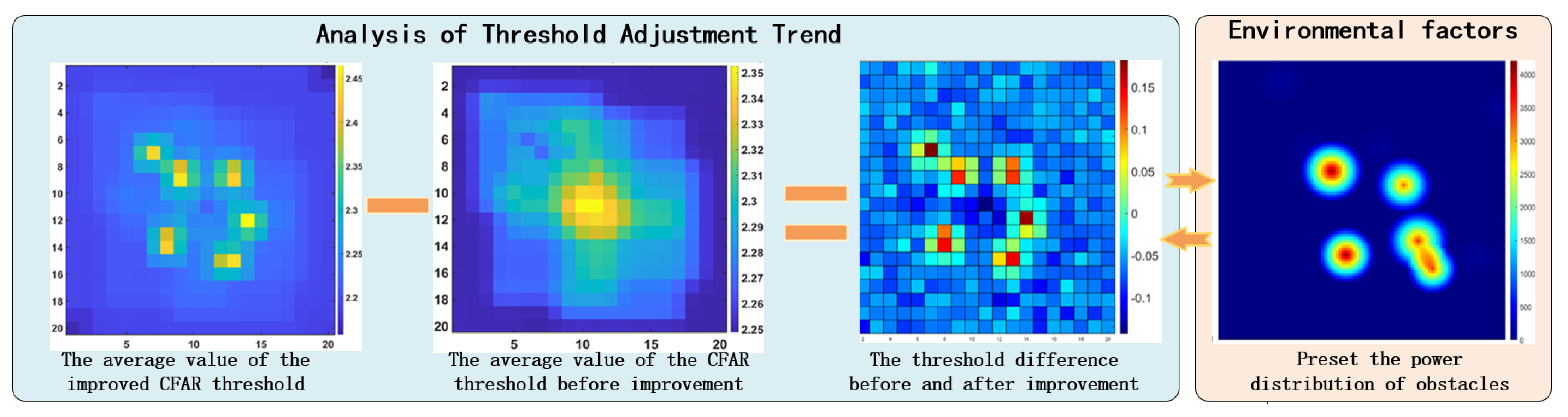
3.2. Comparison of the CFAR Algorithm Before and After Improvement in a Single Sample

As shown in Figure 9, we selected a sample at 14:00 on 8 December 2024 to visually demonstrate the CFAR threshold changes before and after optimization. Compared with the original CFAR threshold, the optimized one shows more distinct distribution features and larger differences in adjacent thresholds. Specifically, significant threshold variations are observed around predefined vessel positions when compared with preassigned coordinates. Analysis of CFAR detection results indicates that the optimized method has significantly alleviated the missed-detection and false-alarm issues present in the original approach.

3.3. Analysis of the Changing Trends of Parameter Terms

As previously discussed, constructing the loss function requires discussing the parameter terms (i.e., the four cases). Figure 10 analyzes the trends of these parameter terms across six training processes. To facilitate observation amid numerous training steps, we averaged values every ten steps before plotting the line graph. Specifically, while correct detection maintenance (case 1) exhibits significant fluctuations, its overall trend remains stable. Uncorrected missed detection (case 3, representing unimproved missed detections post-optimization) and erroneous missed detection (case 4, indicating aggravated missed detections) both decrease markedly after learning, stabilizing near zero by the 400th training step. For missed-detection correction (case 2, reflecting improved missed detections), the number of successful corrections was low initially, but stabilized at slightly below five per sample as training progressed. This aligns with the experimental design of adding six non-AIS vessels per sample, verifying the model’s effectiveness in reducing missed detections. Notably, case 2 counts decreased moderately during mid-training, likely because the higher penalty coefficient for case 4 prioritized avoiding its occurrence. These patterns were consistent across all six experiments, with parameter term trends remaining uniform. This demonstrates that the model is resilient to temporal shuffling and exhibits robust stability.

3.4. Analysis of the Changing Trends of Constraint Terms

We added the previously mentioned constraint term to maintain the quantity of the test results within a reasonable range. Given that the average number of AIS targets across all samples was 5.874, we set the constraint range (m, n) to (5, 12). As illustrated in Figure 11, the initial number of detected targets frequently exceeds the upper limit of this range. However, as training progresses, the count stabilizes within (5, 12), validating the constraint term’s effectiveness during training.

3.5. Analysis of Model Learning Trends

Averaging the CFAR thresholds of all cells across pre- and post-improvement model outputs reveals the overall CFAR threshold pattern, as depicted in Figure 12. This average difference partially reflects the model’s learning of radar echo power patterns in the sea area. Specifically, compared with the initially preset obstacle power distribution, the improved CFAR algorithm yields threshold distributions that more clearly align with actual obstacle locations. Before the improvement, the central sea area showed higher power values in CFAR threshold calculations due to the inclusion of multiple obstacle regions in the reference cells. This inconsistency with actual obstacle distribution was resolved by the improved CFAR algorithm, further verifying the model’s superiority in learning spatial radar echo distribution patterns. However, a notable spatial deviation exists between obstacles in the lower-right sea area and the corresponding high-power regions of the improved radar threshold. This suggests that the model’s learning of echo patterns may be influenced by extraneous factors or that minor local optima occurred during training—both warranting further investigation.

The statistics of the CFAR target detection results and error rates are shown in

Table 1. CFAR object detection results (validation set sample size: 3548).

Detection Method	Total Number of Cells	Average Number of Undetected Cells	Average Number of Cells That Missed Detection
CFAR before improvement	400	3.7152	4.1379
Improved CFAR	400	1.2461	1.1012

and

Table 2. Statistics on false-alarm rate and missed-detection rate.

	False-Alarm Rate	Missed-Detection Rate
CFAR before improvement	0.794%	1.034%
Improved CFAR	0.312%	0.275%
Improvement extent	60.706%	73.404%

. The improved CFAR reduced the average number of cells that were undetected and missed detections from 3.7152/4.1379 to 1.2461/1.1012. The false-alarm rate dropped from 0.794% to 0.312% and the missed-detection rate from 1.034% to 0.275%, showing 60.7% and 73.4% improvements. These results demonstrate the improved CFAR’s significantly enhanced detection accuracy and reliability.

4. Discussion

The experimental results show that the iTransformer model with AIS data information added can effectively enhance the detection ability of the CFAR algorithm for small vessels. The variations in various parameters in the experiment and the overall trend of the improved CFAR thresholds all conform to our expectations. However, several areas for improvement remain in the experimental process.

4.1. Real-World Validation

This experiment was trained and validated in a simulated scenario to enable low-cost annotation for large-scale training. However, simplified sea clutter modeling in simulations fails to fully reproduce the sea clutter in the real scene, and the experiment omitted minor random factors, introducing uncertainties for real-scenario model deployment. To address these limitations, many of the existing similar studies on simulated scenarios chose to conduct predefined experiments in small-scale real scenarios to validate model generalization and robustness [29,30,31]. The addition of real data can make the parameter settings of the model more reasonable. In future work, we will also deploy experiments in a smaller range of real scenarios, using test boats as label targets., thereby enhancing the credibility and authenticity of the experiment.

4.2. Model Training Speed Optimization

The sea area selected in this experiment is moderate and the divided grids are relatively sparse, which can ensure that the sample size of each training sample is within a reasonable range. However, when it is necessary to monitor a broader sea area or divide denser grids, the amount of sample data will significantly increase and the training speed of the iTransformer model will drop sharply. Aiming at the problem of the training speed of similar deep learning models, the current research mainly realizes the improvement in the training speed at the software level through two methods: parallelization strategy coupled with fragmentation optimization technology [32] and data distillation technology [33]. In future research, we will add model parallelism, data parallelism, and gradient compression functions to accelerate the training speed.

4.3. Enhance the Local Detection Ability

We compared the CFAR variation trend with the energy distribution of predefined obstacles and observed local deviations, misalignments, or diffusion despite overall distribution consistency. This may be attributed to the model prioritizing global features at the expense of local accuracy. Existing studies have shown that pyramid attention mechanisms [34], Fourier spectrum gating [35], and adaptive fragmentation strategies [36] effectively address such issues. In future research, we will focus on adaptive fragmentation strategies, implementing finer-grained segment division for abrupt change regions to balance global–local influence and enhance local precision.

5. Conclusions

This study used an iTransformer-based CFAR threshold optimization method by constructing simulated radar echo scenarios that replicate real sea conditions. The experimental results demonstrated the effectiveness of the proposed model. Using six-channel rasterized data, experiments across 23,651 samples validated the model’s performance. The enhanced iTransformer model improved detection efficacy through three key mechanisms: a spatial encoding enhancement, a weakly supervised composite evaluation system, and a dynamic target number constraint. Experimental results showed that the optimized CFAR reduced the average number of missed-detection cells and false-detection cells significantly. Threshold distribution visualization confirmed that the optimized results more clearly reflected the spatial characteristics of predefined obstacles. These findings validate the method’s effectiveness in learning the complex coupling between sea clutter and target signals. Overall, after training, the model’s ability to inspect small vessels was significantly enhanced while taking into account both adaptability and accuracy.