A Fractional Fourier Transform-Based Channel Estimation and Equalization Algorithm for Mud Pulse Telemetry
Abstract
1. Introduction
2. Methods
2.1. The MPT System Model
2.2. Channel Estimation Based on Fractional Fourier Transform
2.3. Channel Equalization Based on Fractional Fourier Transform
- (1)
- Separate the training sequence and data sequence of the baseband data.
- (2)
- Transform the training sequence into fractional Fourier domains of varying orders for least squares channel estimation and select the optimal order.
- (3)
- Set the tap coefficients of the equalizer based on the least squares channel estimation of the optimal order.
- (4)
- Partition the received signal sequence into blocks for the optimal-order fractional Fourier transform.
- (5)
- Apply a multiplicative filter and revert the optimal order back to the time domain.
- (6)
- Convert the segmented processed data into serial data, which can then be fed into a decision feedback equalizer in the time domain for decision making.
3. Simulation and Experiment
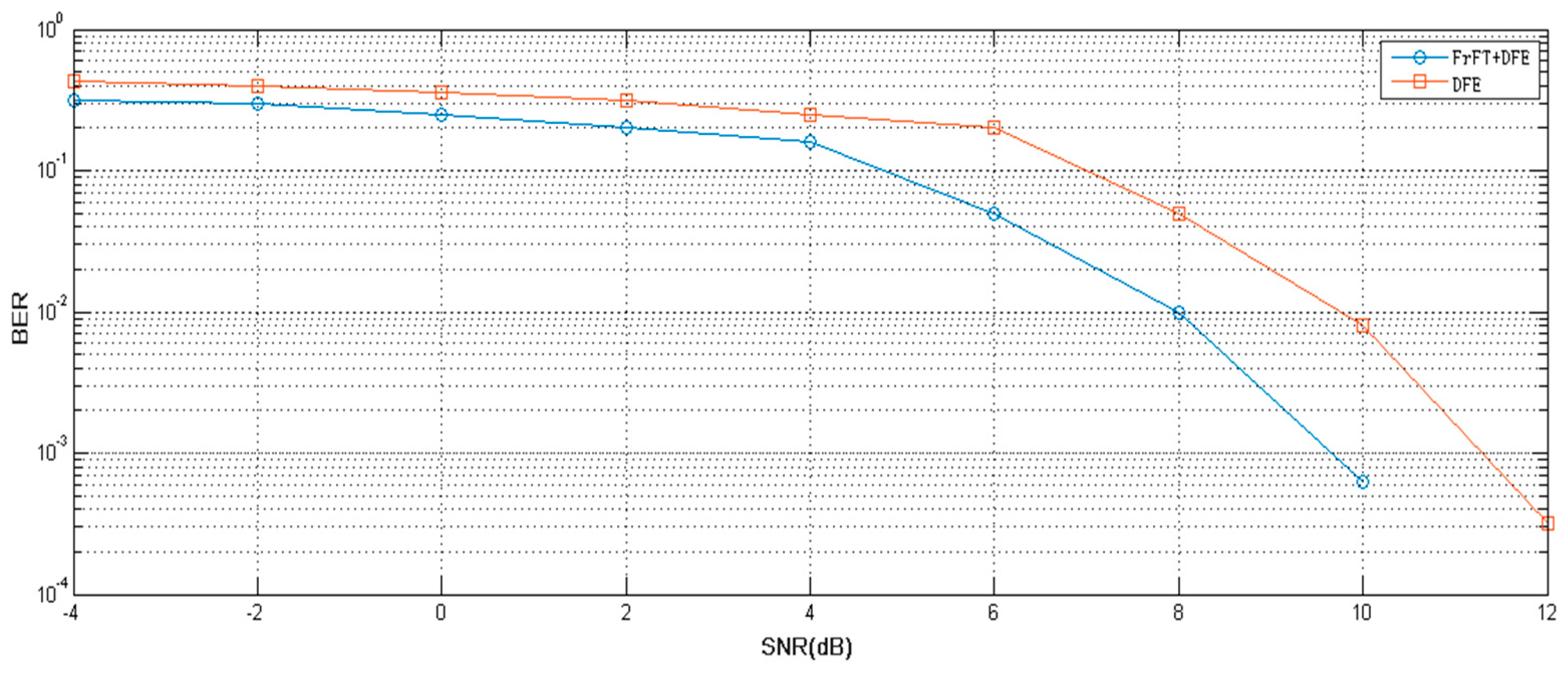
3.1. Simulation Test
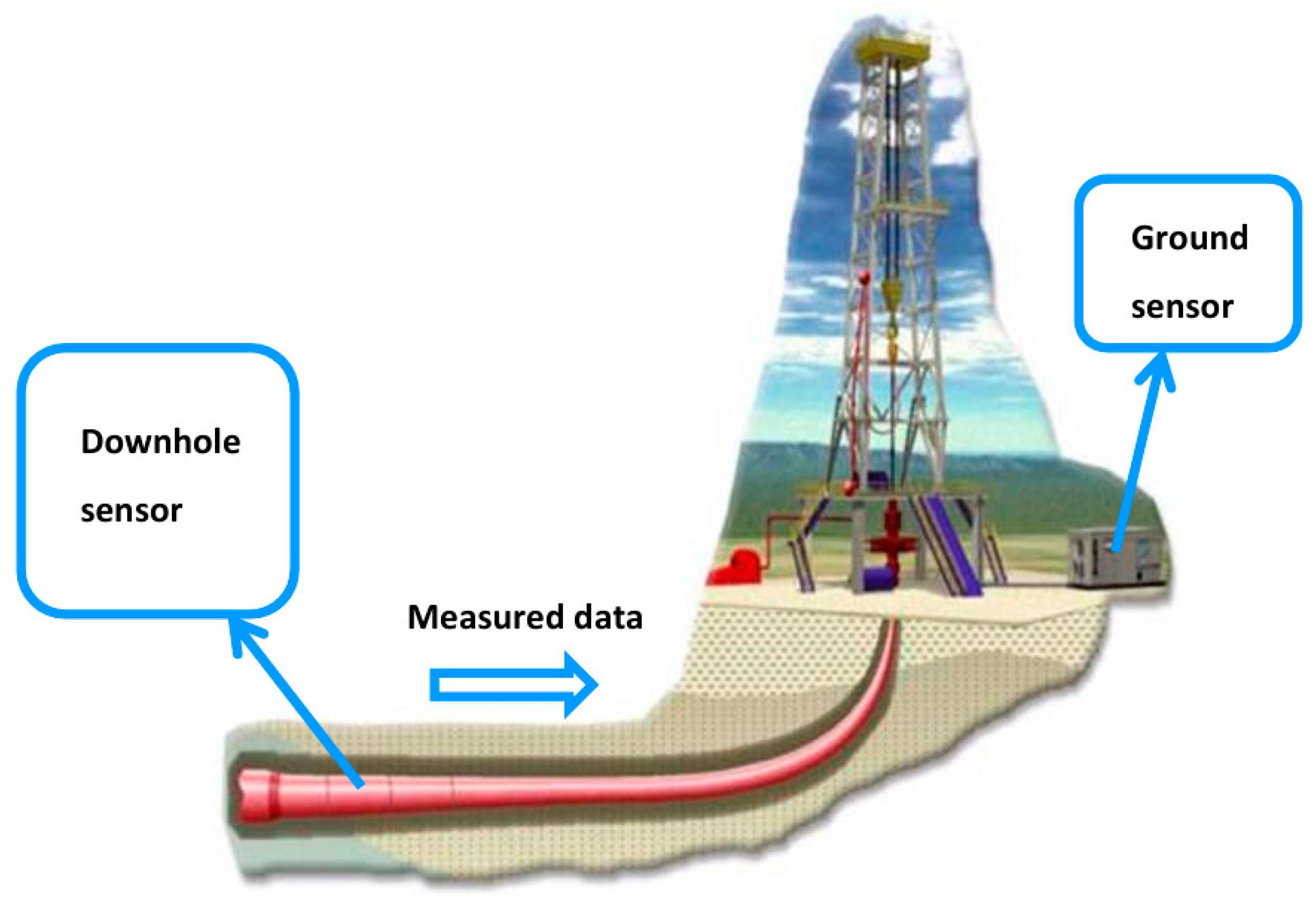
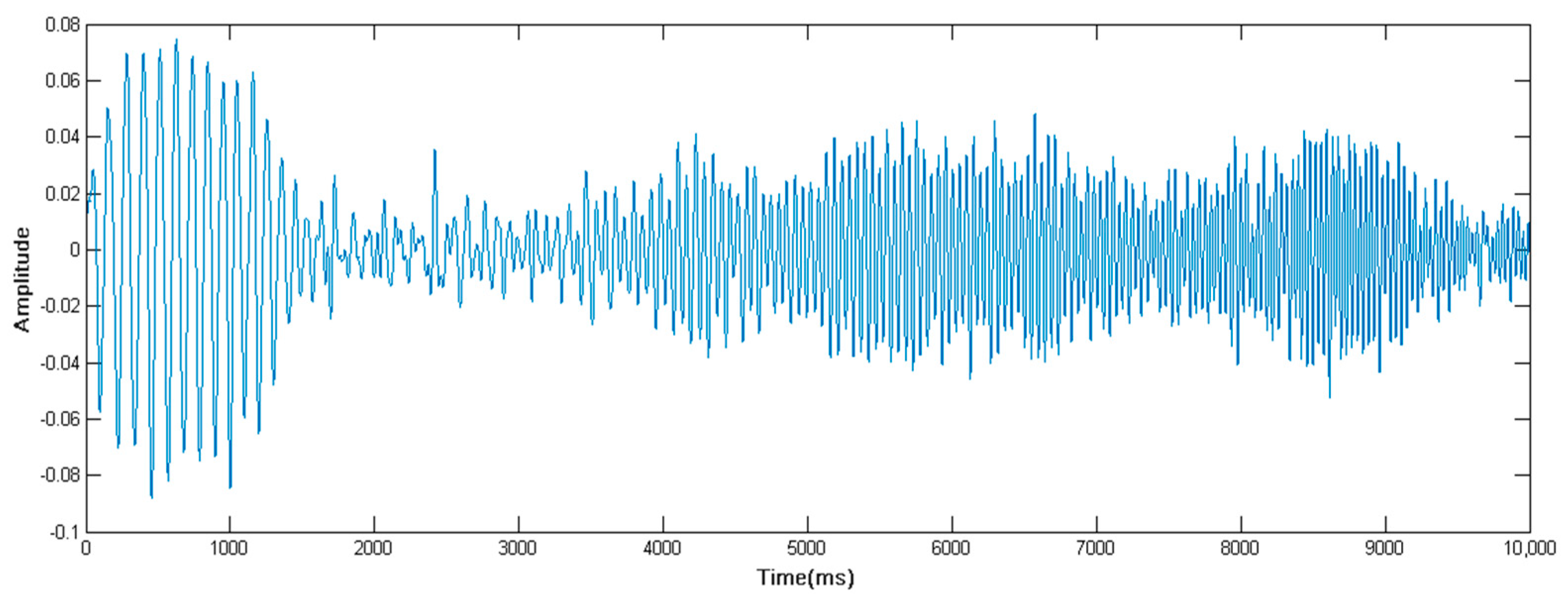
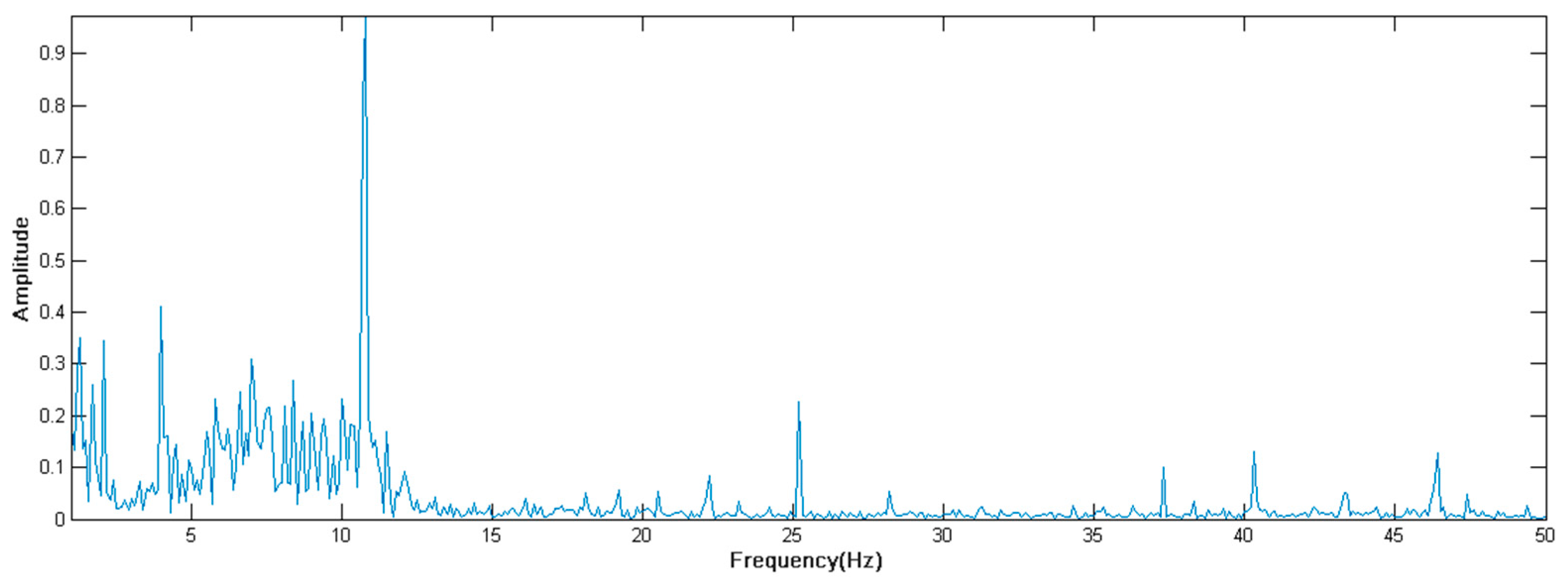
3.2. Real Well Test
4. Discussion and Results
- (1)
- A channel estimation method tailored to the characteristics of mud channels is proposed using FrFT, along with an optimal order search strategy that significantly reduces computational complexity.
- (2)
- A compensation scheme for channel frequency-selective fading is developed using FrFT domain equalization, which enhances the overall communication performance. The BER of experimental results after demodulation has decreased by 90% compared to the traditional DFE method. Moreover, compared with ZF and MMSE equalization, our method obtains a lower BER in real well tests. In general, the BER after demodulation is reduced to below 0.5%, which meets the engineering requirements.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MPT | Mud pulse telemetry |
| FrFT | Fractional Fourier transform |
| FFT | Fast Fourier transform |
| MWD | Measurement while drilling |
| OFDM | Orthogonal Frequency Division Multiplexing |
| SSC | Sweep-Spread carrier |
| RFFI | Radio frequency fingerprint identification |
| ISI | Inter-symbol interference |
| DFE | Decision feedback equalizers |
| RLS | Recursive least squares |
| SC-FDE | Single-carrier frequency-domain equalization |
| LFM | Linear frequency modulation |
| ZF | Zero forcing |
| MMSE | Minimum mean square error |
| RMSE | Root mean squared error |
| AWGN | Additive white Gaussian noise |
| SNR | Signal-to-noise ratio |
| BER | Bit error rate |
| BFSK | Binary frequency shift keying |
References
- Mcdonald, W.J.; Ward, C.E. Borehole telemetry system is key to continuous down-hole drilling measurements. Oil Gas J. 1975, 73, 37. [Google Scholar]
- Gardner, W.R. High data rate MWD mud pulse telemetry. In Proceedings of the United States Department of Energy Natural Gas Conference, Houston, TX, USA, 25 March 1997. [Google Scholar]
- Qu, S.; Zhu, K.; Nie, Z.; Sun, X.; Peng, Y. Analysis of signal transmission for use of logging while drilling. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1001–1005. [Google Scholar]
- Emmerich, W.; Akimov, O.; Brahim, I.B.; Greten, A. Reliable High-speed Mud Pulse Telemetry. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, London, UK, 17–19 March 2015. [Google Scholar]
- Trofimenkoff, F.; Segal, M.; Klassen, A.; Haslett, J. Characterization of EM downhole-to-surface communication links. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2539–2548. [Google Scholar]
- Brooks, R.; Wilson, J. Drilling better wells cheaper and faster. In Proceedings of the Intelligent Energy Conference and Exhibition, Amsterdam, The Netherlands, 25–27 February 2008. [Google Scholar]
- Klotz, C.; Bond, P.R.; Wassermann, I.; Priegnitz, S. A new mud pulse telemetry system for enhanced MWD/LWD applications. In Proceedings of the IADC/SPE Drilling Conference, Orlando, FL, USA, 4–6 March 2008. [Google Scholar]
- Chin, W.; Yinao, S.U.; Sheng, L.; Lin, L.I.; Bian, H.; Shi, R. High-data-rate MWD system for very deep wells. Well Logging Technol. 2014, 38, 713–721. [Google Scholar]
- Qu, F.; Zhang, Z.; Hu, J.; Xu, J.; Wang, S.; Wu, Y. Adaptive dual-sensor noise cancellation method for continuous wave mud pulse telemetry. J. Pet. Sci. Eng. 2017, 162, 386–393. [Google Scholar] [CrossRef]
- Wang, H.; Fan, X.; Chen, Y.; Yang, Y. Wigner-Hough transform based on slice’s entropy and its application to multi-LFM signal detection. J. Syst. Eng. Electron. 2017, 28, 634–642. [Google Scholar]
- Feng, Q.; Wang, R.B. Fractional convolution, correlation theorem and its application in filter design. Signal Image Video Process. 2020, 14, 351–358. [Google Scholar] [CrossRef]
- Miao, H.; Zhang, F.; Tao, R. Fractional Fourier analysis using the mobius inversion formula. IEEE Trans. Signal Process. 2019, 67, 3181–3196. [Google Scholar] [CrossRef]
- Mallouki, N.; Nsiri, B.; Ghanbarisabagh, M.; Hakimi, W.; Ammar, M. Improvement of downlink LTE system performances using nonlinear equalization methods based on SVM and Wiener–Hammerstein. Wirel. Netw. 2017, 23, 2447–2454. [Google Scholar] [CrossRef]
- Lv, C.; Wang, G.; Chen, H.; Zhang, G.; Chen, Z. Estimation of moving thermal boundary condition and temperature field reconstruction of workpieces in drilling process. Hsi-Chiao Tung Ta Hsueh/J. Xi’an Jiaotong Univ. 2019, 53, 18–24+43. [Google Scholar]
- Wang, Q.; Guan, Z.; Zhang, B.; Liu, Y.; Li, C. Multilevel method based on improved radar chart to evaluate acoustic frequency spectrum in periodic pipe structure. J. Pet. Sci. Eng. 2020, 189, 106878. [Google Scholar] [CrossRef]
- Xu, P.Z.; Xiang, W.; Yu, Q.Y. DFrFT-based near-field channel estimation for extremely large-scale MIMO systems. IEEE Commun. Lett. 2024, 28, 5. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Z.; Zhu, C.; Liu, S. Multipath component parameter estimation based on fractional Fourier transform. IEEE Trans. Instrum. Meas. 2025, 74, 5024313. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, Y. Channel estimation based on multi-armed approach for maritime OFDM wireless communications. J. China Univ. Posts Telecommun. 2023, 30, 75–85. [Google Scholar]
- Jia, S.; Zou, S.; Zhang, X.; Tian, D.; Da, L. Multi-block sparse Bayesian learning channel estimation for OFDM underwater acoustic communication based on fractional Fourier transform. Appl. Acoust. 2022, 192, 108721. [Google Scholar] [CrossRef]
- Qi, M.; Su, Y.; Wang, Z.; Lu, K. Research on the integration of sensing and communication based on fractional-order fourier transform. Sensors 2025, 25, 2956. [Google Scholar] [CrossRef]
- Dong, J.; Chen, S.; Sun, G.; Wu, C. A fast method for intra-pulse parameters estimation of polyphase-coded radar signals based on FrFT. Signal Image Video Process. 2024, 18, 8781–8791. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, T.; Wang, R.; Wang, X. Acquisition of binary offset carrier modulation signals in a highly dynamic environment. J. Signal Process. 2022, 38, 2164–2172. [Google Scholar]
- Pan, N.; Mei, L.; Wang, L.; Jiao, L.; Wang, B. Adaptive technologies of hybrid carrier based on WFRFT facing coverage and spectral efficiency balance. Artif. Intell. Commun. Netw. 2021, 356, 177–196. [Google Scholar]
- Li, W.; Jiang, H.; He, H.; Luo, F.; Tang, M. PMD estimation and its enabled feedforward adaptive equalization based on superimposed FrFT training sequences. Opt. Lett. 2021, 46, 1526–1529. [Google Scholar] [CrossRef]
- Pan, C.; Jia, Z.; Yuan, F. FrFT equalization for underwater sweep-spread communication system. Appl. Acoust. 2023, 214, 109671. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, R.; Yuan, Q.; Guo, Z.; Fu, W. KAN-ResNet-enhanced radio frequency fingerprint identification with Zero-forcing equalization. Sensors 2025, 25, 2222. [Google Scholar] [CrossRef]
- Yadav, R.K.; Mishra, H.B.; Mukhopadhyay, S.; Mishra, R. IRS-OTFS systems: Design of reflection coefficients for low-complexity ZF equalizer. IEEE Trans. Veh. Technol. 2024, 73, 15721–15726. [Google Scholar] [CrossRef]
- Zischler, L.A.; Mello, D.A.A. SDM optical systems with MMSE equalizers: Information rates and performance monitoring. J. Light. Technol. 2025, 43, 7119–7129. [Google Scholar] [CrossRef]
- Dong, P.Y.; Xiang, X.; Wang, P.; Liang, Y. A robust MMSE-DEF framework with joint time-frequency domain processing for UAV-to-ground SC-FDE communication systems. Wirel. Netw. 2025, 31, 2955–2974. [Google Scholar]
- Zhang, J.; Sha, Z.; Tu, X.; Zhang, Z.; Zhu, J.; Wei, Y.; Qu, F. Noise Cancellation Method for Mud Pulse Telemetry Based on Discrete Fourier Transform. J. Mar. Sci. Eng. 2025, 13, 75. [Google Scholar] [CrossRef]
- Pagtalunan, J.; Parmar, K.; Kim, S.; Moon, B.; Park, S.S. Experimental study on repeater-free acoustic telemetry for downhole operations. J. Pet. Sci. Eng. 2021, 202, 108551. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, W.; Hu, Q.; Zeng, Z.; Li, Z. Time-varying channel and intrablock carrier frequency offset estimation for OFDM underwater acoustic communication. IEEE Sens. J. 2024, 24, 13. [Google Scholar] [CrossRef]
- Mori, C.; Sawahashi, M.; Miki, N.; Suyama, S. Performance of iterative decision feedback channel estimation in turbo FDE for DFT-spread OFDM. IEICE Trans. Commun. 2025, 108, 294–305. [Google Scholar] [CrossRef]
- Yan, B.M.; Li, Y.; Cheng, W.; Dong, L.; Kou, Q. High-resolution multicomponent LFM parameter estimation based on deep learning. Signal Process. 2025, 227, 109714. [Google Scholar] [CrossRef]
- Li, P.; Pan, W.; Zou, X.; Yan, L. Low-Complexity adaptive frequency-domain nonlinear equalization for Analog RoF mobile fronthaul using FFT/IFFT-assisted channel aggregation. J. Light. Technol. 2022, 40, 1072–1082. [Google Scholar] [CrossRef]


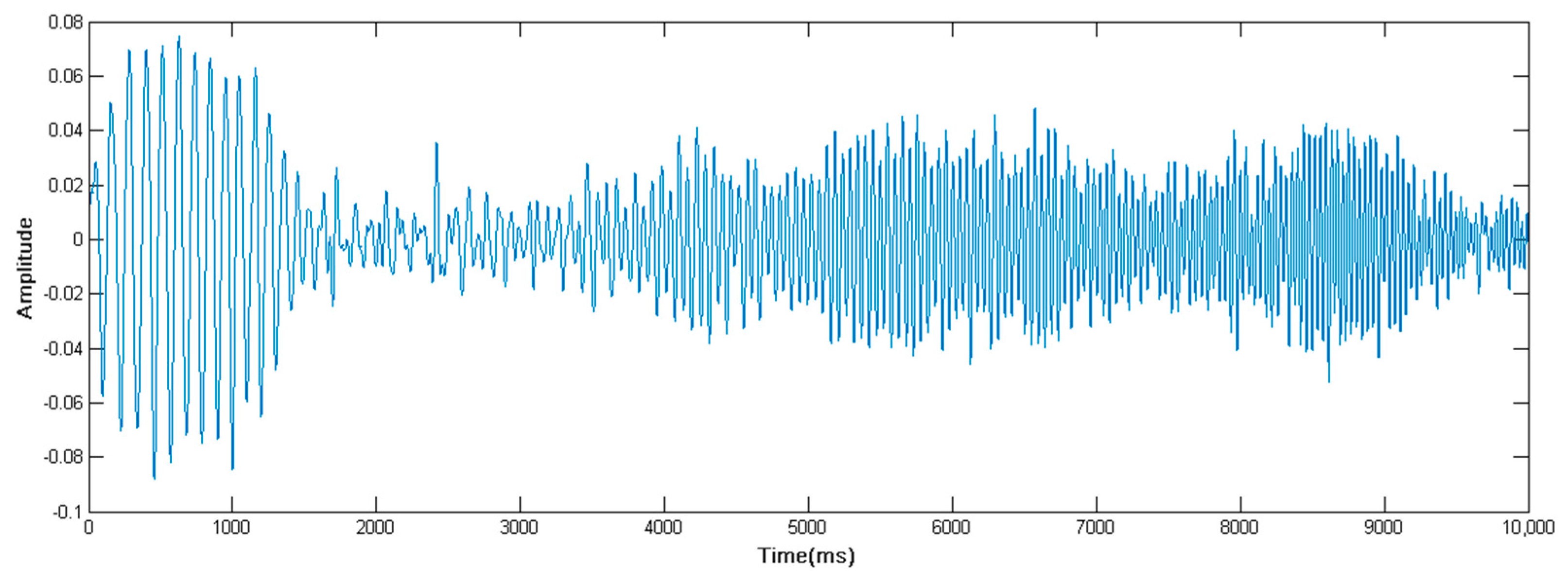
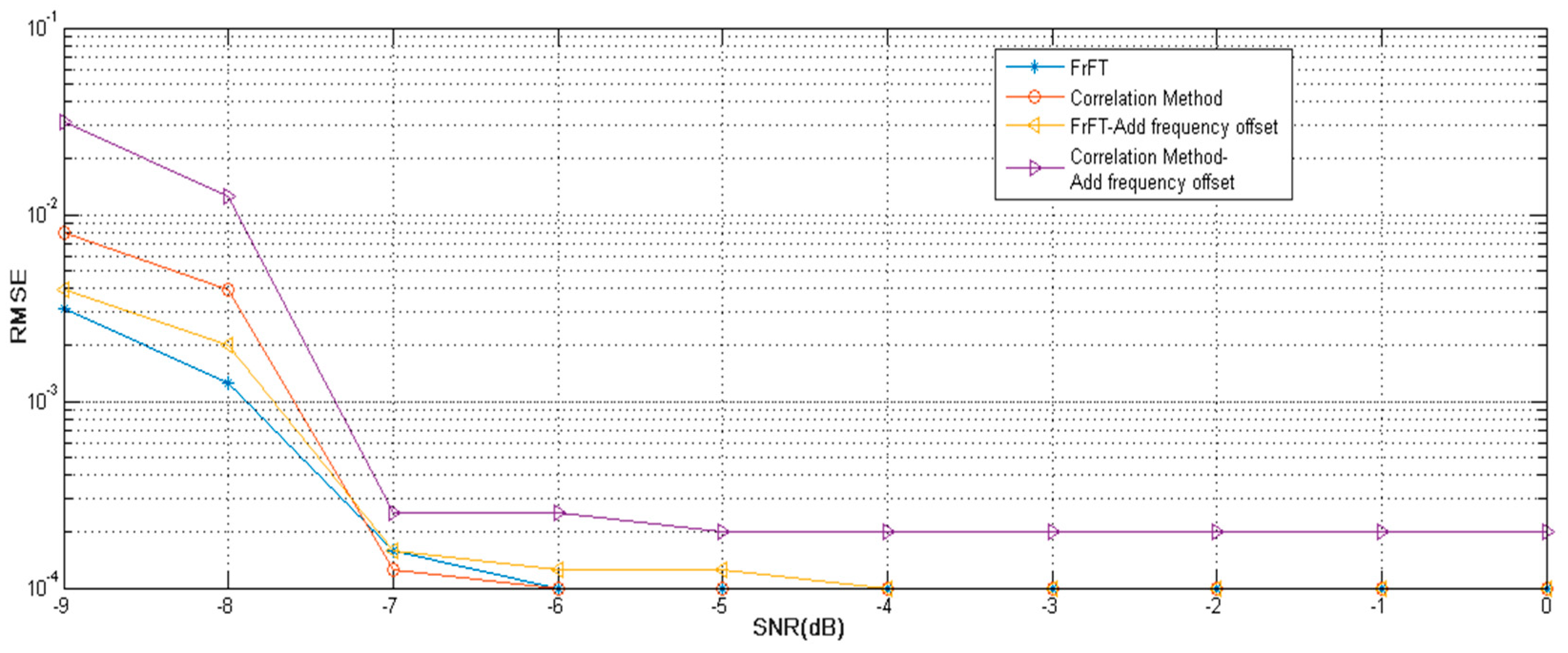
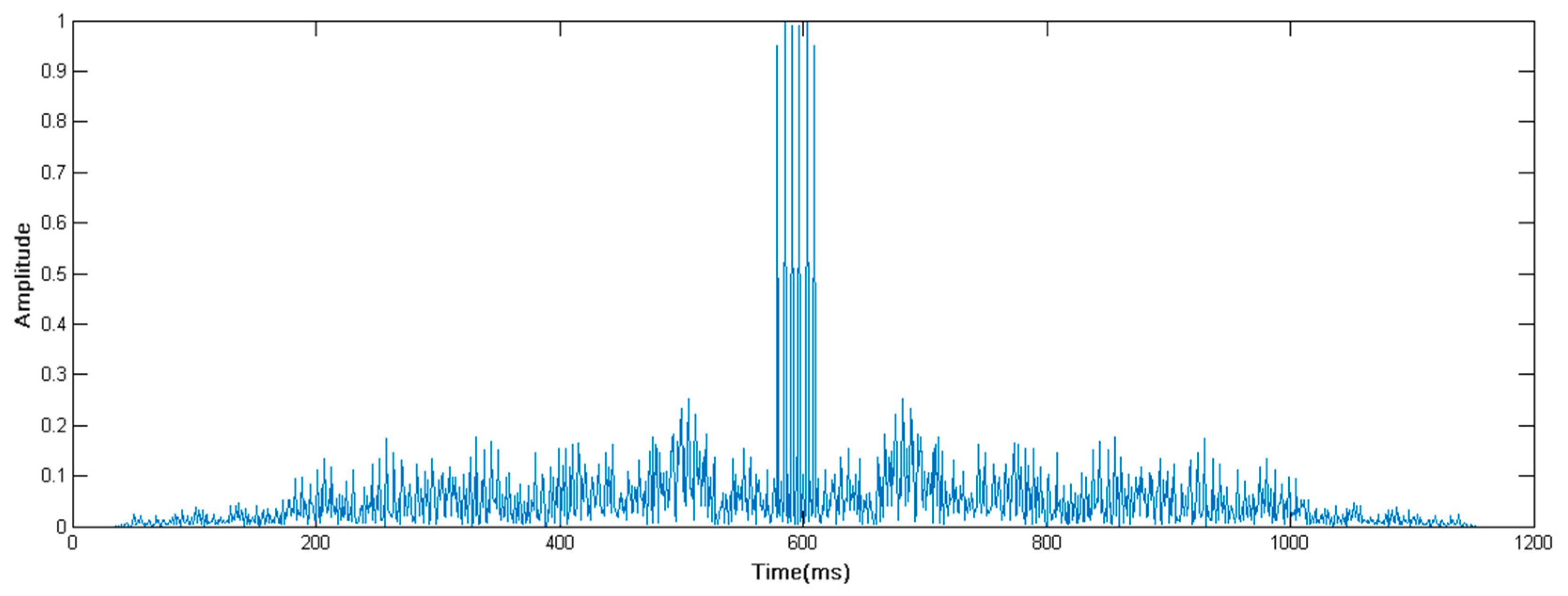
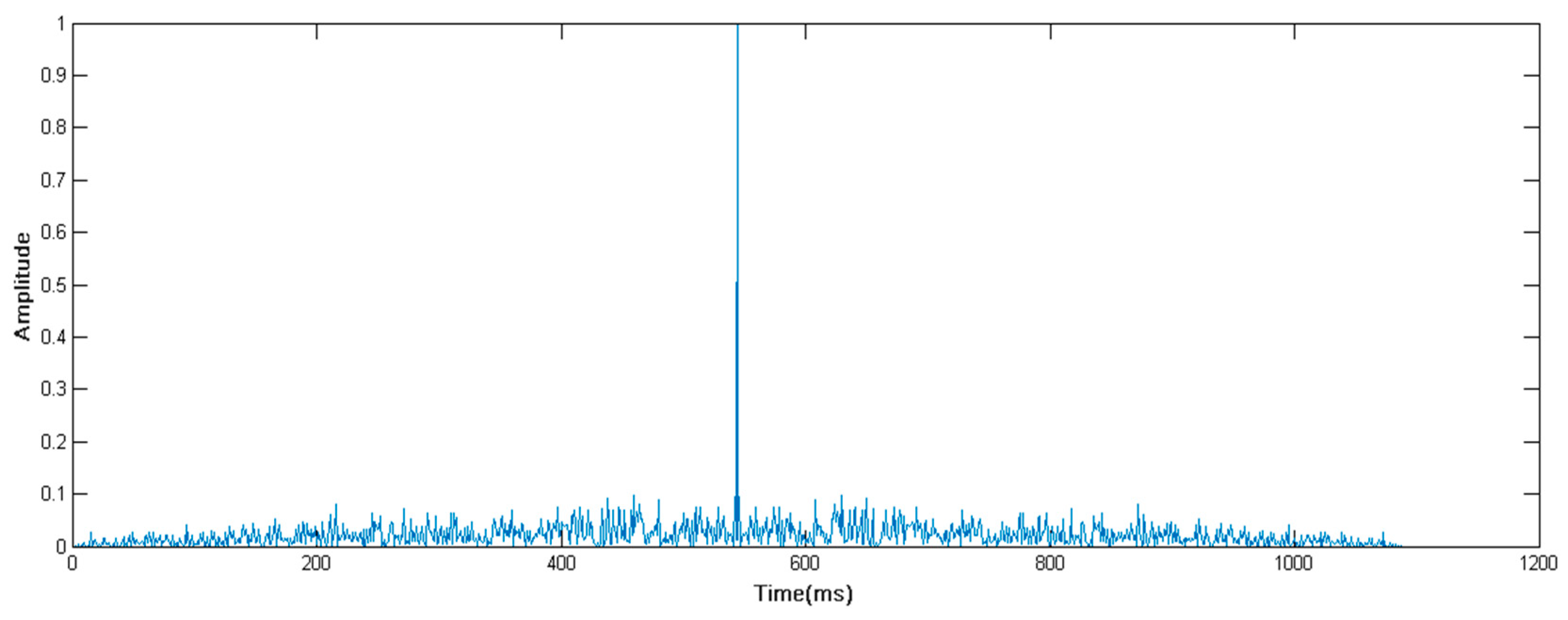

| No. | Modulation Mode | Depths (m) | Data Rate (bit/s) | BER | |
|---|---|---|---|---|---|
| DFE | DFE + FrFT | ||||
| 1 | BFSK | 887 | 8 | 0.004 | 0 |
| 2 | BFSK | 887 | 10 | 0.12 | 0.04 |
| 3 | BFSK | 2515 | 10 | 0 | 0 |
| 4 | BFSK | 2602 | 9 | 0.50 | 0.05 |
| 5 | BFSK | 2632 | 6 | 0.12 | 0.01 |
| 6 | BFSK | 2890 | 12 | 0.14 | 0.03 |
| 7 | BFSK | 2980 | 10 | 0.23 | 0.02 |
| 8 | BFSK | 3016 | 12 | 0.08 | 0 |
| No. | Depths (m) | Data Rate (bit/s) | BER | ||
|---|---|---|---|---|---|
| ZF | MMSE | FrFT | |||
| 1 | 887 | 10 | 0.02 | 0.04 | 0.04 |
| 2 | 2602 | 9 | 0.13 | 0.07 | 0.05 |
| 3 | 2632 | 6 | 0.08 | 0.01 | 0.01 |
| 4 | 2890 | 12 | 0.15 | 0.14 | 0.03 |
| 5 | 2980 | 10 | 0.12 | 0.17 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Sha, Z.; Wan, L.; Su, Y.; Zhu, J.; Qu, F. A Fractional Fourier Transform-Based Channel Estimation and Equalization Algorithm for Mud Pulse Telemetry. J. Mar. Sci. Eng. 2025, 13, 1468. https://doi.org/10.3390/jmse13081468
Zhang J, Sha Z, Wan L, Su Y, Zhu J, Qu F. A Fractional Fourier Transform-Based Channel Estimation and Equalization Algorithm for Mud Pulse Telemetry. Journal of Marine Science and Engineering. 2025; 13(8):1468. https://doi.org/10.3390/jmse13081468
Chicago/Turabian StyleZhang, Jingchen, Zitong Sha, Lei Wan, Yishan Su, Jiang Zhu, and Fengzhong Qu. 2025. "A Fractional Fourier Transform-Based Channel Estimation and Equalization Algorithm for Mud Pulse Telemetry" Journal of Marine Science and Engineering 13, no. 8: 1468. https://doi.org/10.3390/jmse13081468
APA StyleZhang, J., Sha, Z., Wan, L., Su, Y., Zhu, J., & Qu, F. (2025). A Fractional Fourier Transform-Based Channel Estimation and Equalization Algorithm for Mud Pulse Telemetry. Journal of Marine Science and Engineering, 13(8), 1468. https://doi.org/10.3390/jmse13081468









