1. Introduction
Energy is crucial for driving industrial growth, societal development, and technological progress. With the rising use of finite reserve fossil fuels and the escalating pressure of global warming and climate change, the demand for clean renewable energy is increasing. Since the ocean covers 71% of the earth’s surface, water-based energy generation is considered a promising solution for sustainable energy production. However, ocean energy harvesting technology remains less mature than solar and wind energy due to a range of technical and economic challenges.
Among the various methods of water-based energy production, conventional hydropower is the most established, utilizing the gravitational force of flowing or falling water to generate electricity through dams and turbines. Wave energy converters (WECs), on the other hand, harness surface water motion driven by wind, using devices such as oscillating water columns, overtopping structures, and point absorbers. Then, tidal energy is harnessed through tidal stream generators that extract kinetic energy from moving water or tidal barrages that exploit potential energy from differences in water levels. Similarly, ocean current energy utilizes the kinetic energy of marine currents through underwater turbines.
This study develops a novel hybrid ocean energy system to capture energy from both ocean waves and currents simultaneously. The process begins with a comprehensive review of existing wave and current energy technologies, identifying gaps in compact, modular hybrid systems suitable for low-energy environments (
Section 2). This informs a wave resource assessment for the Khobar coastline, Saudi Arabia, using historical data and on-site measurements to characterize local wave conditions (
Section 3). These findings guide the design of a point-absorber buoy and vertical axis water turbine (VAWT), optimized via numerical simulations with ANSYS AQWA and QBLADE, respectively, to ensure resonance with local wave frequencies and efficient current energy capture (
Section 4,
Section 5 and
Section 6). The system’s mechanical components, including a modified mechanical motion rectifier (MMR) and dual-rotor generator, are detailed in
Section 4, followed by prototype fabrication using off-the-shelf and 3D-printed materials (
Section 5). Laboratory and in situ tests validate the system’s performance under combined wave–current conditions (
Section 6). Finally,
Section 7 discusses results, compares them with existing studies, and outlines future research directions.
2. Literature Review
Hybrid marine energy systems have emerged as a response to the limitations of standalone wave and current energy devices. This section reviews the motivation for hybridization, the fundamental operating principles of wave and current systems, prior developments in standalone and hybrid devices, and key challenges that inform the present work.
2.1. Motivation for Hybrid Ocean Energy Systems
While ocean energy offers vast untapped potential, its exploitation is constrained by the variability of individual sources such as waves or tides. Wave energy converters (WECs) often experience reduced performance during calm sea states or seasonal lulls [
1], while tidal and current energy systems, although more predictable, are limited to specific geographic regions.
To address these shortcomings, researchers have explored hybrid systems with multiple and higher degrees of freedom systems such as solar–wave [
2], wind–solar [
3], and wind–tidal [
4] systems. The current study focuses on integrating wave and current energy into a single low-cost, compact system [
5] that combines a heaving buoy and a vertical axis current turbine, linked through a dual-rotor generator and a bi-directional mechanical motion rectifier mechanism capable of capturing energy from both modes without complex coupling systems.
2.2. Principles of Wave and Current Energy Conversion
Wave energy is derived from the vertical displacement of water surfaces caused by wind. WECs generally fall into three categories: oscillating water columns, overtopping devices, and oscillating body devices such as point absorbers and attenuators [
6]. Oscillating water columns drive air turbines via pressure fluctuations, while overtopping devices store water and convert potential energy using turbines. Oscillating body devices extract energy from heaving or pitching motions using mechanical PTO systems [
7].
Tidal energy arises from gravitational interactions between the Earth, moon, and sun, and can be harnessed through barrages or tidal stream turbines. Tidal barrages function similarly to hydroelectric dams but operate bidirectionally due to the nature of tidal flow [
8]. Tidal streams or current turbines extract kinetic energy from moving water via rotors, gearboxes, and generators. In their simplest form, such systems comprise a rotor connected to a gearbox and a generator, with electricity transmitted to shore via subsea cables [
9].
Ocean current energy systems operate similarly to tidal stream devices but target more stable and continuous flows. Vertical axis turbine designs are particularly advantageous in such contexts due to their ability to handle omnidirectional currents without active yaw mechanisms.
2.3. Review of Standalone Wave and Current Energy Devices
Numerous standalone WEC prototypes have been developed to harness heave motion. Youssef et al. [
10] designed a rack-and-pinion buoy system that successfully lit a 3 W lamp in shallow water. Binh et al. [
11] developed a bidirectional gearbox system, while Chandrasekaran et al. [
12] introduced a deep-sea variant with lever-arm transmission. Wang et al. [
13] optimized a buoy for the Penghu Sea using a damping skirt and later proposed a magnetic lead screw (MLS)-based system for improved efficiency and reduced friction losses [
14].
Other notable works include Zhang et al. [
15], who introduced a buoy with turbofan blades and damping plates; Shi et al. [
16], who used a mass-adjustable buoy for wave resonance tuning; and Sakr et al. [
17], who employed a stiffness controller with continuously variable transmission (CVT) for adaptive frequency response. Zheng et al. [
18] used a nonlinear spring PTO to expand the WEC’s operating bandwidth, while Rava et al. [
19] implemented a tethered cable drum system. Vijayasankar et al. [
20] added a mass plate to enhance the natural frequency of a compact point absorber.
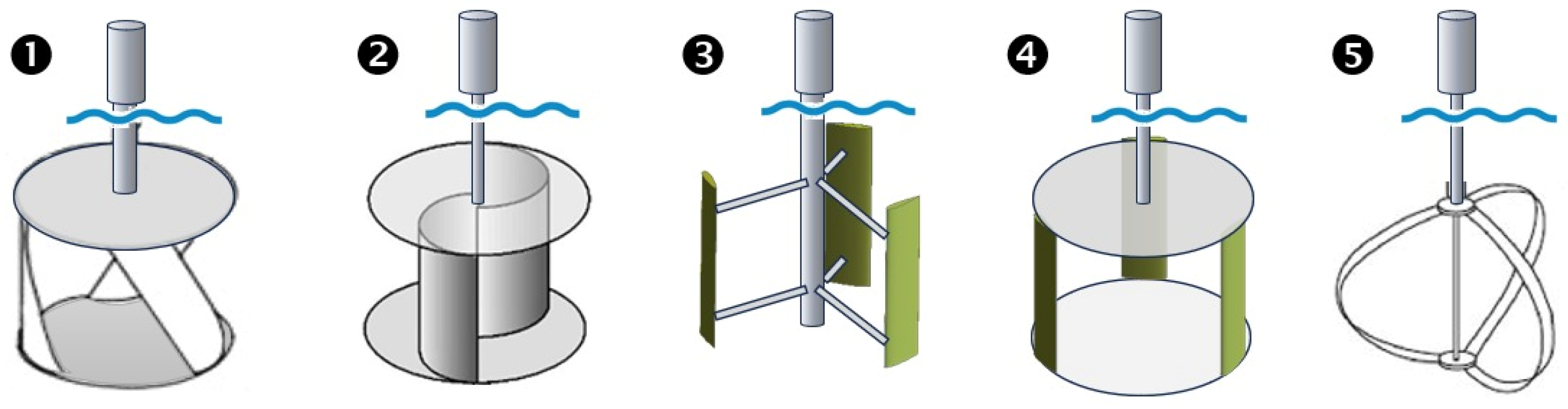
In parallel, vertical axis water turbines (VAWTs) have been developed for capturing current energy. Mutsuda et al. [
21] integrated a small-scale turbine with a fish aggregating device (FAD), achieving outputs up to 20 kW. Behrouzi et al. [
22] proposed a hinged-blade design to reduce drag and achieved 188.8 W at 0.56 m/s. Fernandes et al. [
23] explored autorotation from vortex-induced asymmetry, while Alam et al. [
24] combined Darrieus and Savonius rotors to enhance performance in low-speed flows. A selection of such configurations is illustrated in
Figure 1.
These standalone systems demonstrate the viability of wave and current energy harvesting individually. However, each suffers from inherent limitations in consistency or deployment scope, motivating further integration.
2.4. Existing Hybrid Wave–Current Systems
To overcome the limitations of individual systems, researchers have proposed hybrid wave–current energy converters (HWCECs). Silva et al. [
25] developed a non-coupled platform combining oscillating buoys and a vertical axis turbine, each with separate generators. Chen et al. [
26] introduced a coupled two-body system using a buoy and a heave plate, linked via a planetary gearbox to merge wave and current inputs into a single output shaft.
This design was validated through 1:10 scale testing in wave tanks, achieving 1.226 W under moderate wave and current conditions [
27]. Park et al. [
28] developed a combined swing-plate and rotating-cylinder concept, converting both types of motion using mechanical PTOs.
While these systems show promise, they often involve complex mechanical arrangements, large footprints, or synchronization difficulties. These constraints motivate the development of simpler, more compact designs, particularly those that can operate with minimal mechanical interaction between the subsystems.
2.5. Technical Challenges and Design Considerations
Designing an effective HWCEC involves multiple engineering challenges. Key among them is the integration of two distinct energy sources—one delivering oscillatory, low-frequency linear motion and the other providing continuous rotational input—into a shared PTO. The mismatch in force profiles and frequency characteristics complicates gearbox and rectification design [
27].
Other critical considerations include marine corrosion resistance [
29], buoyancy–stability optimization, and low-friction mechanical transmission. Environmental concerns such as underwater noise [
30], electromagnetic interference, and entanglement risk must also be addressed. While some studies report hybrid systems achieving up to 87% more output than standalone systems [
26], achieving this performance in a cost-effective, scalable way remains a major research challenge.
The present study contributes to this area by proposing a prototype hybrid system that prioritizes mechanical simplicity, compact design, and off-the-shelf manufacturability. Its dual-input generator accepts independent mechanical inputs from a heaving buoy and a vertical axis turbine, operating without complex coupling mechanisms. The main contributions of this study are as follows:
The design and fabrication of a dual-input hybrid ocean energy prototype that can simultaneously harvest wave and current energy with a mechanically decoupled, dual-input generator.
Systematic design optimization using simulation tools (ANSYS AQWA for hydrodynamics, QBLADE for turbine performance) tailored for realistic, modest-resource (low-energy coastal environments) conditions.
Experimental validation in both laboratory and real-world field settings, demonstrating stable performance and practical viability in a low-energy nearshore environment.
Providing a proof-of-concept and deployment pathway for modular hybrid marine energy systems suitable for distributed applications where large-scale devices are impractical.
3. Resource Assessment
This section presents an assessment of wave energy potential relevant to the design and deployment of a hybrid ocean energy harvesting system. It begins by briefly contextualizing the broader wave climate of the Red Sea and Persian Gulf, drawing from existing studies, before focusing on real-time measurements and historical data specific to the Al Khobar coastline. These insights inform the system’s suitability for operation in a nearshore low-to-moderate energy environment.
3.1. Regional Wave Climate Context
Several studies have investigated wave energy availability across Saudi Arabia’s coastal regions, highlighting important contrasts between offshore and nearshore environments. In the Red Sea, offshore locations such as Thual experience wave heights exceeding 4 m and peak periods above 8 s, while nearshore sites exhibit significantly reduced wave energy [
31]. Similarly, wave data from the Persian Gulf reveals that its central and western regions (e.g., Assalouyeh, Boushehr) occasionally reach wave heights over 2 m, with wave power peaking above 3.9 kW/m during high-energy seasons [
32]. In contrast, the eastern region of the Persian Gulf, including the Al Khobar coastline, shows consistently lower wave energy, but with calmer and more predictable conditions. Long-term wave reanalysis at Ras Al Khair further confirms that while extreme wind and swell events do occur offshore, nearshore waters remain significantly more stable in both height and directionality. These findings support the deliberate selection of the Al Khobar coastline as the deployment site for this study. Although not the most energetic location, Khobar’s stable and low-to-moderate wave climate is representative of many real-world sites where small-scale, cost-effective ocean energy solutions are required. Its accessibility and safe nearshore conditions enabled efficient, iterative prototype testing and deployment with minimal resources. This practical context enhances the value of the present work as a proof-of-concept for modular hybrid systems applicable to under-served or low-energy coastal regions.
3.2. Wave Conditions at Al Khobar
To enable design of the hybrid prototype and verify regional model data, wave conditions at the Al Khobar coastline (26.081684° N, 50.154086° E) were analyzed using both reanalysis data and physical site measurements
3.2.1. Historical Oceanographic Data
Wave characteristics at the Al Khobar site were retrieved from the Global Ocean Physics Reanalysis dataset [
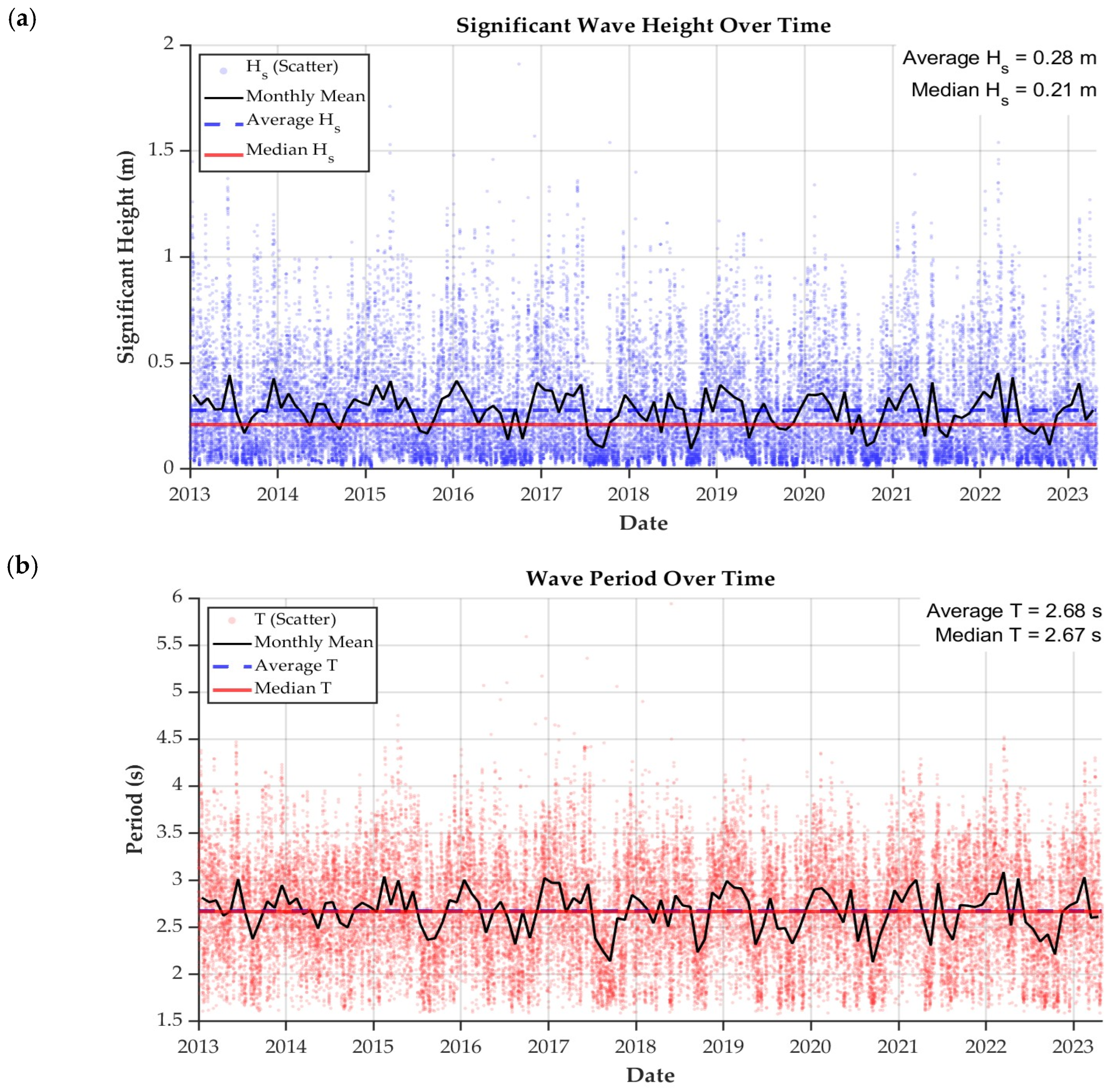
33], provided by Mercator Ocean International through the European Union’s Copernicus Marine Service. This dataset combines satellite observations and in situ measurements to provide high-resolution oceanographic information from 1993 to 2022. The time series data from 2013 to 2023, presented in
Figure 2a,b, show significant wave height and mean wave period, respectively. Significant wave heights ranged from 0.01 m to 1.91 m, while mean periods ranged from 1.58 s to 5.94 s. The average/median values were 0.28/0.21 m for wave height and 2.68/2.67 s for wave period. These values confirm that the site experiences relatively calm and consistent wave conditions.
3.2.2. On-Site Observations and Measurements
Field measurements were conducted at two locations at the Half Moon Bay area of the Khobar coastline south of the city to further characterize real-time wave conditions and support system tuning. A calibrated rod, marked at 5 cm intervals, along with a small buoy, shown in
Figure 3, was used to observe and record the wave motion and wave height using a fixed-position camera.
The recorded video was analyzed using Tracker 5 software [
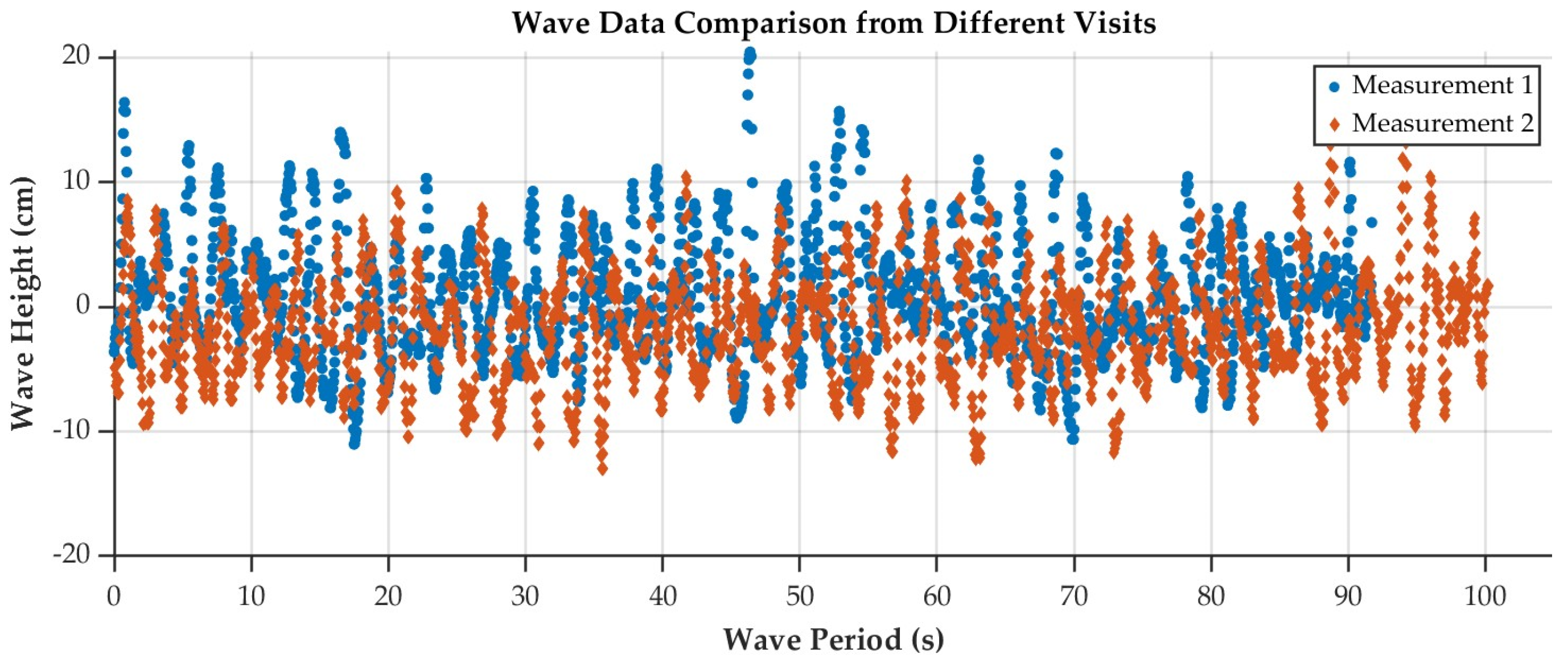
34], which generated a time series of wave elevation and its corresponding frequency spectrum. Observed wave heights ranged from –0.11 m to 0.20 m. The measured wave period was approximately 2.22 s, and the dominant frequency was found to be about 0.45 Hz. These values are consistent with the average and range obtained from the historical dataset, confirming the validity of the measurement approach.
Figure 4 shows the wave height data measurement data from the two separate visits, while
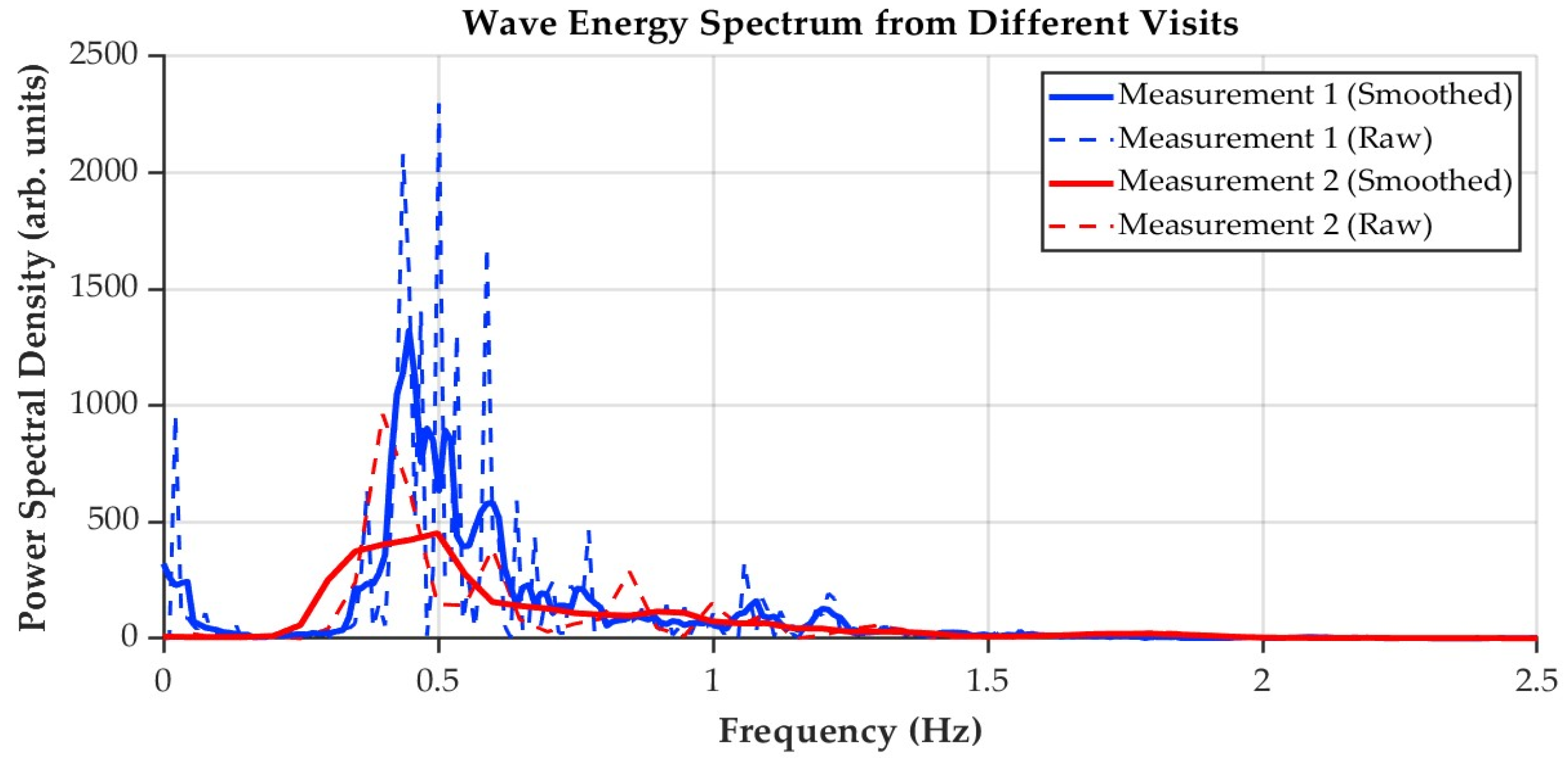
Figure 5 displays the associated frequency spectrum.
3.3. Summary
Historical analysis data indicate that the Khobar coastline experiences an average significant wave height
of 0.28 m and an average wave period
of 2.68 s. Onsite measurements further validated these values, with observed wave heights in a range from −0.11 m to 0.20 m and a dominant wave period of around 2.22 s. Frequency spectrum analysis in
Figure 5 revealed two peaks at 0.39 Hz and 0.5 Hz, which suggested the target natural frequency range for the buoy design. The average wave power density potential of the site can be determined using the following relation:
where
is the water density,
g is the gravitational acceleration,
is the significant wave height, and
is the mean wave period. Based on the measured wave parameters at Khobar, the estimated average wave power density is approximately 103.08 W/m, suggesting potential for small scale ocean energy harvesting and necessitating prototype development and testing.
4. Hybrid System Design and Prototype Development
4.1. Concept Development
The primary design objective was to combine wave and current energy harvesting into a single system such that the oscillating input from a wave-driven buoy after being converted into unidirectional rotation via a specially designed mechanical motion rectifier (MMR) is fed to one rotor of the dual-rotor generator, while the counter-rotating input from the vertical axis water turbine (VAWT) is fed to the other rotor of the dual-rotor generator. With the two counter-rotating rotors, the generator power could be increased many folds depending upon the relative rpm between the two rotors.
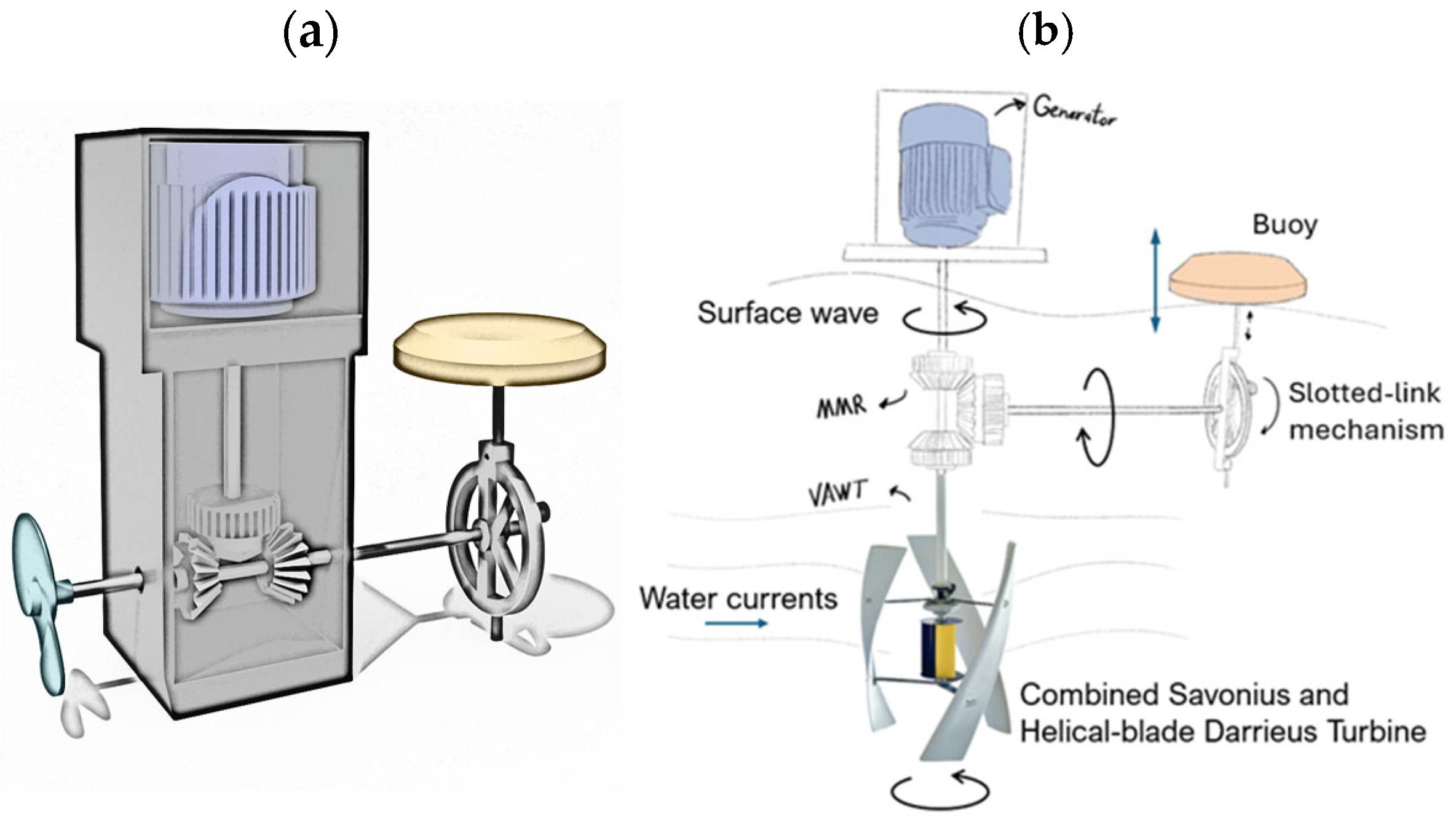
The first design concept (
Figure 6a) had the generator placed on a platform above the water surface, while all the other components, i.e., the MMR, gearbox, turbine shaft, and other linkages, were to be placed in an underwater water-tight compartment. However, the need for a large underwater water-tight compartment meant hydrodynamic blockage of the water currents, which could have had significant negative impact on the performance of the turbine, and, therefore, this idea was later abandoned.
The second design concept (
Figure 6b) was an effort to create a limited underwater footprint with a smaller water-tight compartment to reduce complexity as well as eliminate any flow blockage. Moreover, the original turbine was replaced by combined Savonius–helical blade Darrieus vertical axis water turbine to exploit its omnidirectional character for maximum performance potential. However, it was realized that the potential for mechanical loss in the MMR could be significant, and the complexity and effort to design and manufacture it led to the complete revision of its design.
4.2. Final Prototype Design
Figure 7 shows the different views of the final concept after a series of design changes and trade-offs, along with the key components in its final assembled form that were built and tested. The total cost to build the system, including materials, equipment and instrumentation, was approximately SAR 1500 (USD 400). The key features of the final design include (1) a hollow point-absorber buoy made of polyurethane foam with a lid to hold weights, (2) a helical-blade vertical axis wind turbine (VAWT), (3) a modified MMR with overdrive, and (4) a dual-rotor generator, along with the necessary linkages, bearings, and gear drives. The key innovative features of this design are as follows:
4.2.1. The Modified Mechanical Motion Rectifier (MMR) System with Overdrive
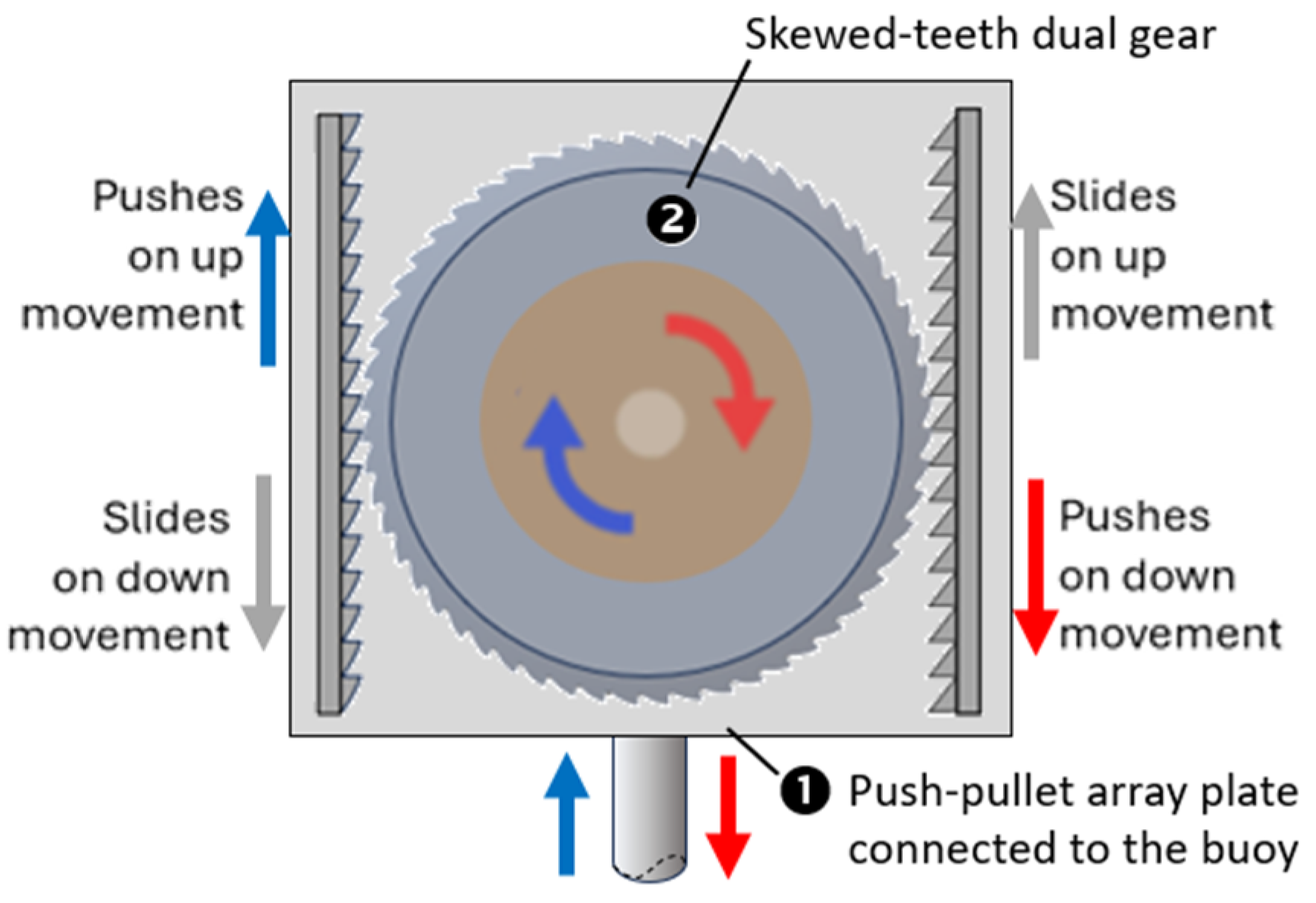
To transform the oscillatory motion of the buoy into unidirectional rotational motion, a specifically designed MMR, as shown in
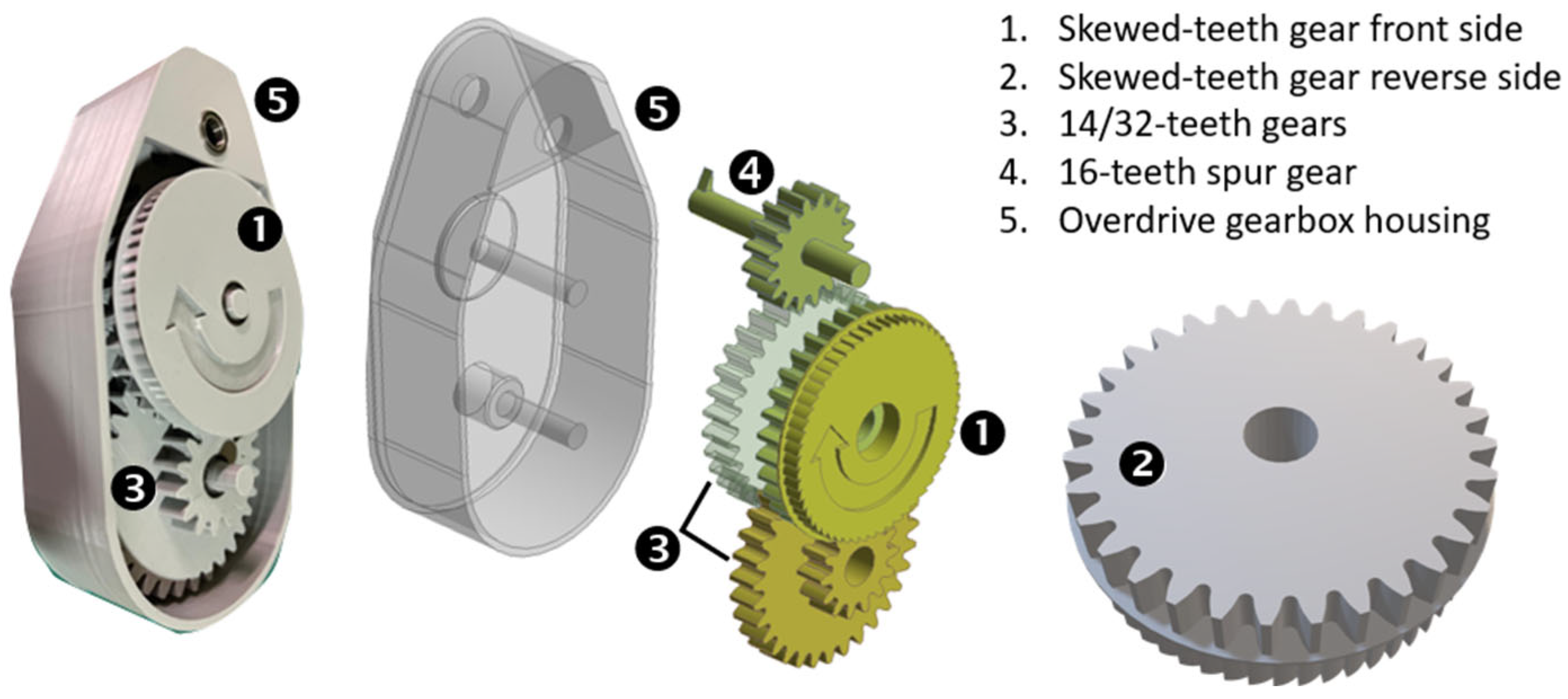
Figure 8, was built. At the heart of the MMR is the skewed-teeth dual gear (
Figure 9). The skewed-teeth side (item 1) engages with the push-pullet array plate, which is attached by a rod to the point-absorber buoy. The other side (back) with regular gears is connected to a 1:10 ratio overdrive gearbox. This arrangement ensures that the one oscillation of the buoy is converted into ten by the modified MMR and overdrive gearbox. This was necessary, as will be explained later, to allow higher rpm input to the dual-rotor generator for reasonable power generation.
The VAWT, modified MMR, overdrive gearbox, dual-rotor generator, and some of the other components were 3D-printed using PLA+ filament. Other structural materials were selected for their resistance to sea water, off-the-shelf availability, lightweight, and mechanical integrity and robustness of the overall assembly.
4.2.2. The Dual-Rotor Generator
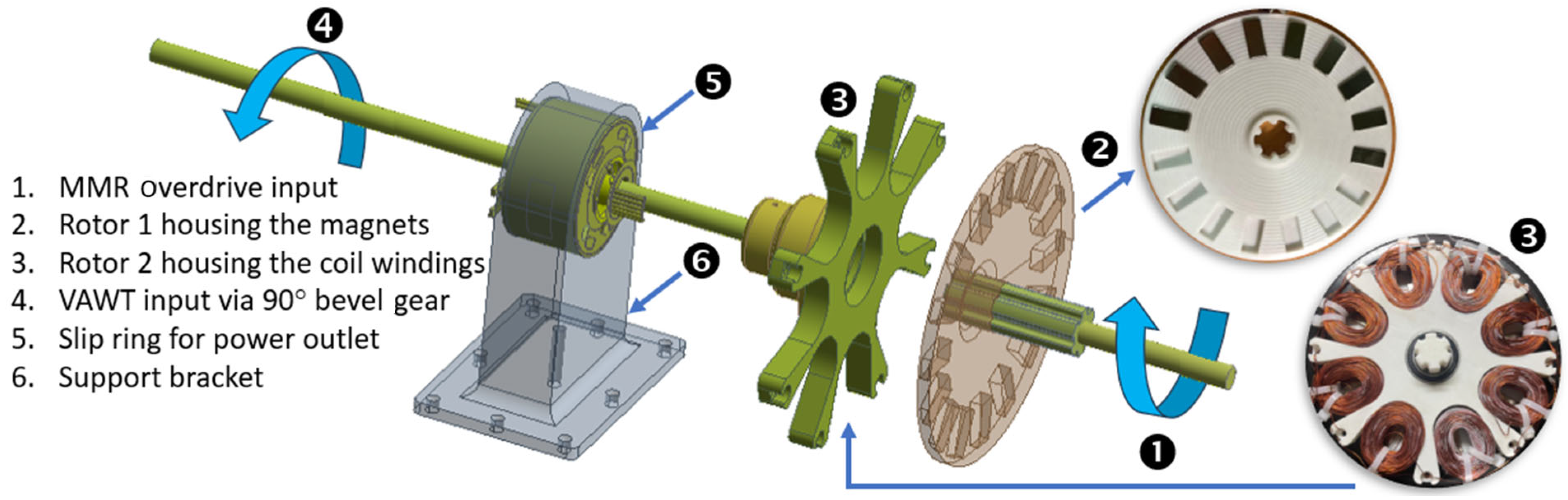
The idea of dual-rotor generator stemmed from two important design constraints. First, the generator should accept input from two diametrically opposed counter-rotating drive shafts. Second, it was anticipated that due to low ocean wave periods and current velocities, the resulting drive shaft rpms would be low; therefore, some means to boost the rpm would be necessary to obtain reasonable generator power output. The former constraint is overcome by the use of a dual-rotor generator.
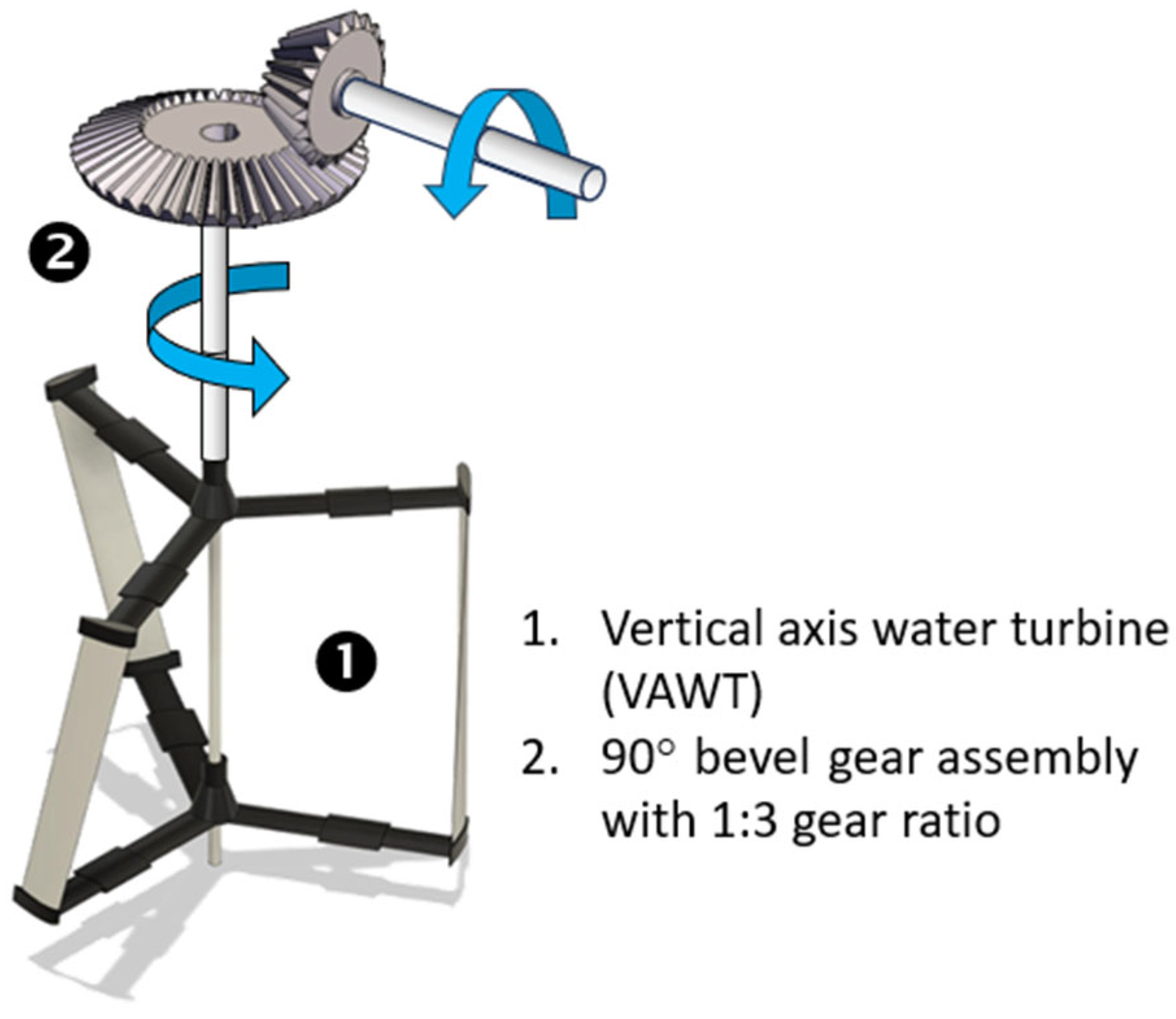
Figure 10 illustrates the dual-rotor generator subassembly along with its different components and rotations. Here, the dual-rotor generator consists of two rotor discs, one housing the permanent magnets and connected to the output shaft from the modified MMR overdrive gearbox and the other containing copper-coil windings driven by the VAWT’s shaft via a 90° bevel gear with a 1:3 ratio. The arrangement is such that the two inputs to the dual-rotor generator are counter-rotating; i.e., the coil windings and the magnets independently counter-rotate. The latter constraint is overcome by providing the boost to rpm by the 1:10 ratio overdrive gear on the magnet side and 1:3 ratio 90° bevel gear on the coil-windings side, resulting in increased electricity generation through enhanced electromagnetic induction at lower relative rpms. It is noted here that the 1:10 overdrive gear ratio was used to boost the buoy rpm (from 30 to 50) to a reasonable value (of around 300 to 500) for voltage and current measurements from the in-house designed and built generator, as well as for validation against an off-the-shelf generator. A full-wave rectifier circuit is used to convert the alternating current into direct current. Finally, a slip ring is used to transfer electrical current from the rotating coil windings to a stationary outlet for power measurements.
4.2.3. The Vertical Axis Water Turbine
Figure 11 illustrates the vertical axis water turbine (VAWT) and 90° bevel gear subassembly. The specific design of the VAWT with skewed blades and Darrieus configuration was chosen for its omni-directional characteristics, as well as the smooth variation of the turbine torque during its complete 360° rotation, as compared to a straight-bladed Darrieus configuration.
4.2.4. Data Acquisition and Recording
An Arduino-based data acquisition system was designed and built to collect real-time voltage and current data from the generator during indoor and in situ tests of the prototype. All readings were stored on an SD card module for post-processing and analysis. The data acquisition and recording system consisted of the Arduino Uno R3 board, REES51 voltage sensor, ACS712 current sensor, Micro SD card reader module, 5V power source, resistors, capacitors, breadboard, and wires.
4.3. The Final Prototype Fabrication
Figure 12 shows the final prototype of the dual-input hybrid wave–current ocean energy system. The upper frame is made up of aluminum sections while the lower frame is made from PVC pipes with adjustable heights. The push-pullet array plate was mounted on a rail mechanism to allow heave motion of the buoy. The VAWT, push-pullet-array plate with the rail mechanism, modified MMR, overdrive, dual-rotor generator and 90° bevel gears were 3D printed using PLA+ filament. The college of engineering workshop and fab-house facilities were used for all other hardware and fabrication tasks.
In the following sections, the design of the point-absorber buoy and the vertical axis water turbine (VAWT) are described in detail. To ensure robust and realistic design, we used ANSYS AQWA for modeling the wave–structure interaction, predicting buoy resonance, and estimating hydrodynamic forces, as it is well validated and widely used in the marine industry. For turbine optimization under low current speeds, QBLADE was selected due to its proven capabilities in aero-hydro-elastic simulation of vertical axis turbines. The use of these industry-standard tools helped in optimizing both subsystems with confidence before prototype fabrication.
5. Point-Absorber Buoy Design
In this section, the objective is to determine the appropriate buoy geometry and characteristics for our system. One of the most critical steps in this process is the accurate estimation of the natural frequency of the buoy. The natural frequency significantly influences the dynamic behavior of the buoy under wave excitation and matching it with the dominant wave frequency helps ensure the optimal performance of the system.
Three different approaches were adopted to estimate the natural frequency of the buoy, thereby identifying the dimensions of the buoy. The first is the theoretical approach in which the following formula [
35] can be used to obtain natural frequency.
where
Awp = (1/4) π
D2 is the water plane area of the buoy,
M33 =
ρ (1/4) π
D2T is the buoy mass based on the submerged volume, and A
33 is the added mass coefficient which can be estimated at the preliminary stage using the following relation:
A33 = 0.167
ρD3. Substitution of these expressions in Equation (2) yields:
The above Equation (3) can be used to determine possible buoy dimensions that have the desired natural frequency. It is important to note that different diameter–draft combinations can yield the same natural frequency. Based on the resource assessment in
Section 3, a natural frequency of 0.5 Hz was selected to match the dominant wave frequency observed at the Al Khobar site. Therefore, using Equation (3), a range of diameter–draft combinations were calculated by the authors for this target natural frequency, as presented in
Table 1.
According to
Table 1, one possible combination of reaching the desired natural frequency of 0.5 Hz is using a buoy of about 1 m draft, with diameter between 0.3 and 0.35 m. However, such buoy dimensions would require greater water depth for tests that are farther away from the coast and, in addition, incur higher projected cost due to larger system size necessitating a more robust structure and motion conversion system. To ensure safe, cost-effective testing and compatibility with readily available components, a smaller buoy was selected without compromising the design’s resonance alignment in scaled conditions. The selected dimensions of cylindrical shape buoy are an outer diameter of 0.35 m, an inner diameter of 0.32 m, and a height of 0.16 m.
For the chosen buoy geometry, different drafts were checked and tested to verify natural frequencies at different submergence depths. Natural periods of the buoy for different drafts were estimated through numerical heave decay simulations using ANSYS AQWA. Detailed hydrodynamic simulation results are presented in
Section 7.
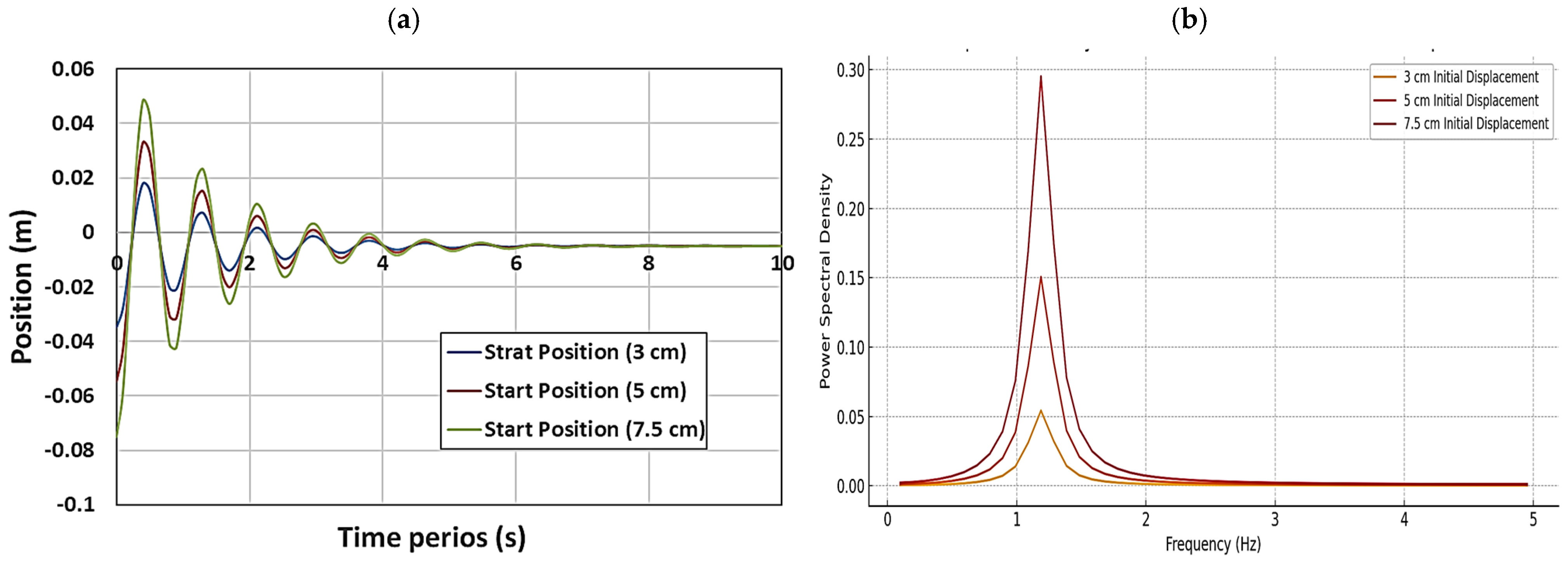
Figure 13 shows: (a) the response of the buoy tested at a draft of 8.5 cm for three different release depths, and (b) the corresponding heave power spectral density.
To explore the natural period of the buoy, free decay experiments were also conducted for different drafts which were achieved by adding weights inside the cylindrical buoy.
Table 2 presents a comparison between the natural periods of the buoy obtained from three different methods: numerical simulation using ANSYS AQWA, experimental data from in situ measurements, and theoretical calculations based on Equation (1). The three approaches are found to yield consistent results thereby confirming the findings and validating the three approaches.
6. Vertical Axis Water Turbine Design
A current turbine design optimized for low water currents as expected near the seashore and shallow water conditions is desirable. A recent study showed that lift-type vertical axis hydro-turbine outperform drag-type one [
36]. Hence, for the current study, a vertical axis water turbine (VAWT) was chosen to determine its potential. Since the turbine is confined within the frame structure, the geometrical constraints on the design included (1) turbine radius
R ≤ 0.2 m and (2) turbine height
H ≤ 0.3 m. Additional design parameters considered to obtain the optimized design included (a) blade profile, (b) blade chord
c, and (c) the circular angle
qc, defined as the relative azimuthal angle between the upper and lower blade tips. The design constraints considered included (a) turbine radius
R ≤ 0.2 m, (b) turbine height
H ≤ 0.3 m, (c) number of blades
N = 2, 3, and 4, (d) blade profile shapes based on symmetrical airfoils: NACA 0015, 0018, or 0021, (e) blade chord 0.04 m ≤
c ≤ 0.12 m (
c = 0.04, 0.08, or 0.12 m), and (f) circular angles
qc = –20°, 0°, or +20°.
The analysis was performed using QBLADE [
37]. Blade section aerodynamic characteristics are obtained using an in-build XFOIL module [
38]. QBLADE has been reliably used for design of hydro-turbines [
39]. The analysis were performed considering water at 20 °C with density 998 kg/m
3 and dynamic viscosity 1.002 × 10
–3 Pa·s, water current velocities ranging from 0.5 m/s to 3.0 m/s at 0.5 m/s increments, and turbine rotational speed ranging from 10 rpm to 900 rpm at 10 rpm increments, which together correspond to turbine tip-speed ratios TSR (=
wR/V) ranging from 0 to 6. Based on these parameters, a total of 27 design configurations were analyzed considering three blades and maximum allowable turbine radius and height of 0.2 m and 0.3 m, respectively.
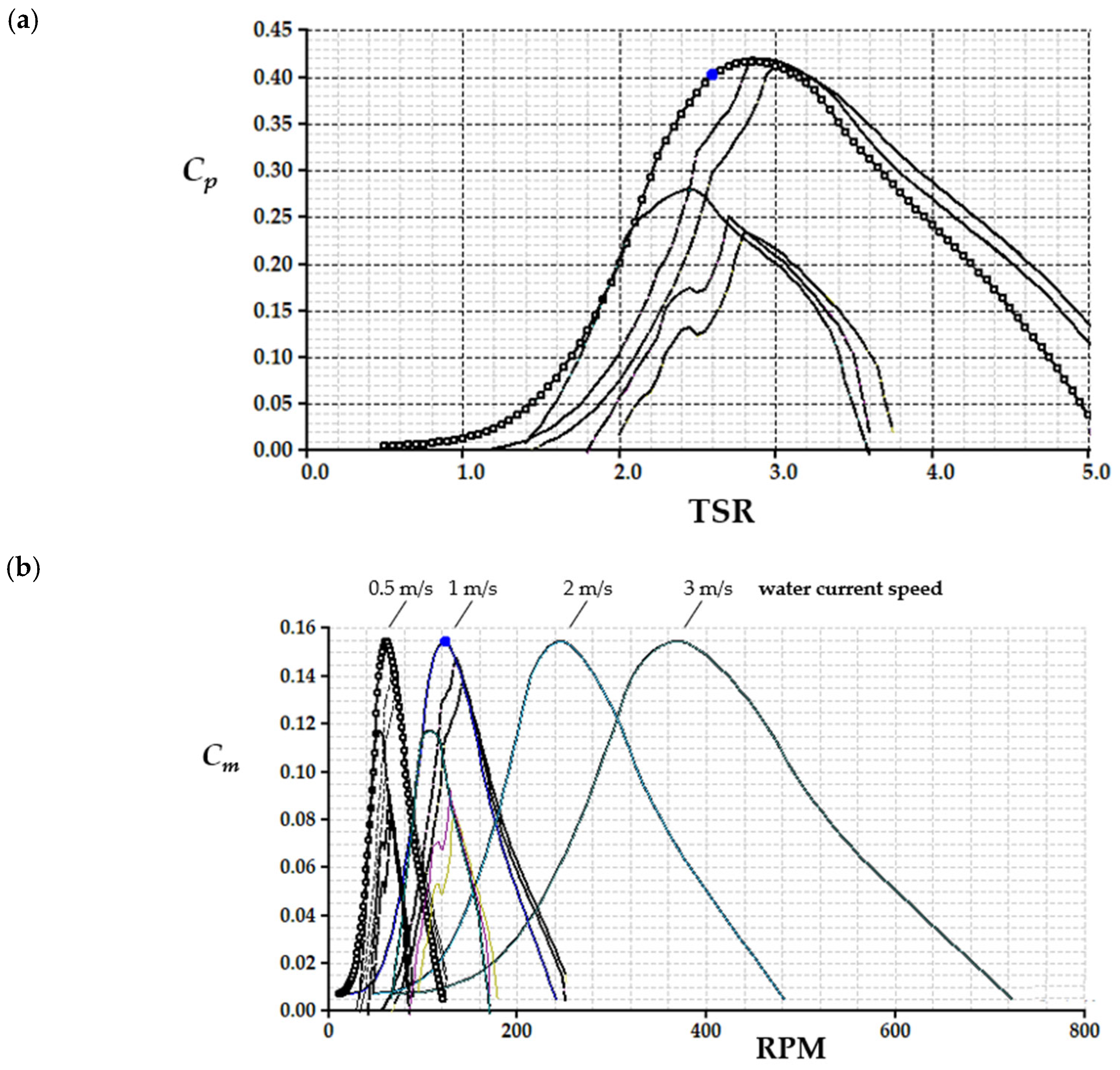
Figure 14 shows comparison of (a) the turbine power and (b) the torque coefficient curves as a function of the tip-speed ratio TSR and RPM, respectively. The results show that the highest turbine power coefficient
Cp = 0.41 is achieved at
TSR = 2.6, corresponding to the highest turbine torque coefficient
Cm = 0.15. These results suggest that the optimal configuration for the VAWT is the one with three blades, radius
R = 0.2 m, height
H = 0.3 m, blade profile based on NACA 0021 airfoil, blade chord
c = 0.04 m, and a circular angle
qc = +20° (forward skew).
Figure 11 shows the geometric rendering of the best configuration selected as the final design. The VAWT blades were connected to the central shaft with the aid of top and bottom struts, having a profile of 16% thick S8036 low Reynolds number laminar flow airfoil for minimum drag due to the struts.
Table 3 lists the performance characteristics of the final VAWT design.
7. Performance Assessment
7.1. Hydrodynamic Performance of Buoy
The simulation of the buoy’s hydrodynamic behavior was performed using ANSYS AQWA [
40]. This platform is particularly effective in analyzing wave-induced motions and predicting the dynamic responses of floating bodies, making it highly suitable for wave energy converter studies [
41]. In this analysis, the hydrodynamic diffraction module was used to compute the wave excitation forces, including both Froude–Krylov and diffraction components, based on linear wave theory. Additionally, the response analysis module was utilized to generate Response Amplitude Operators (RAOs), which provide insights into how the buoy responds at different wave frequencies and submergence depths [
42]. These outputs were essential in identifying resonance zones, estimating natural periods, and optimizing the buoy’s configuration for maximum efficiency under varying sea conditions.
7.1.1. Wave and Fluid Properties
A representative wave profile was defined, using a sinusoidal wave with an amplitude of 0.1 m. The sea water density was set to 1025 kg/m
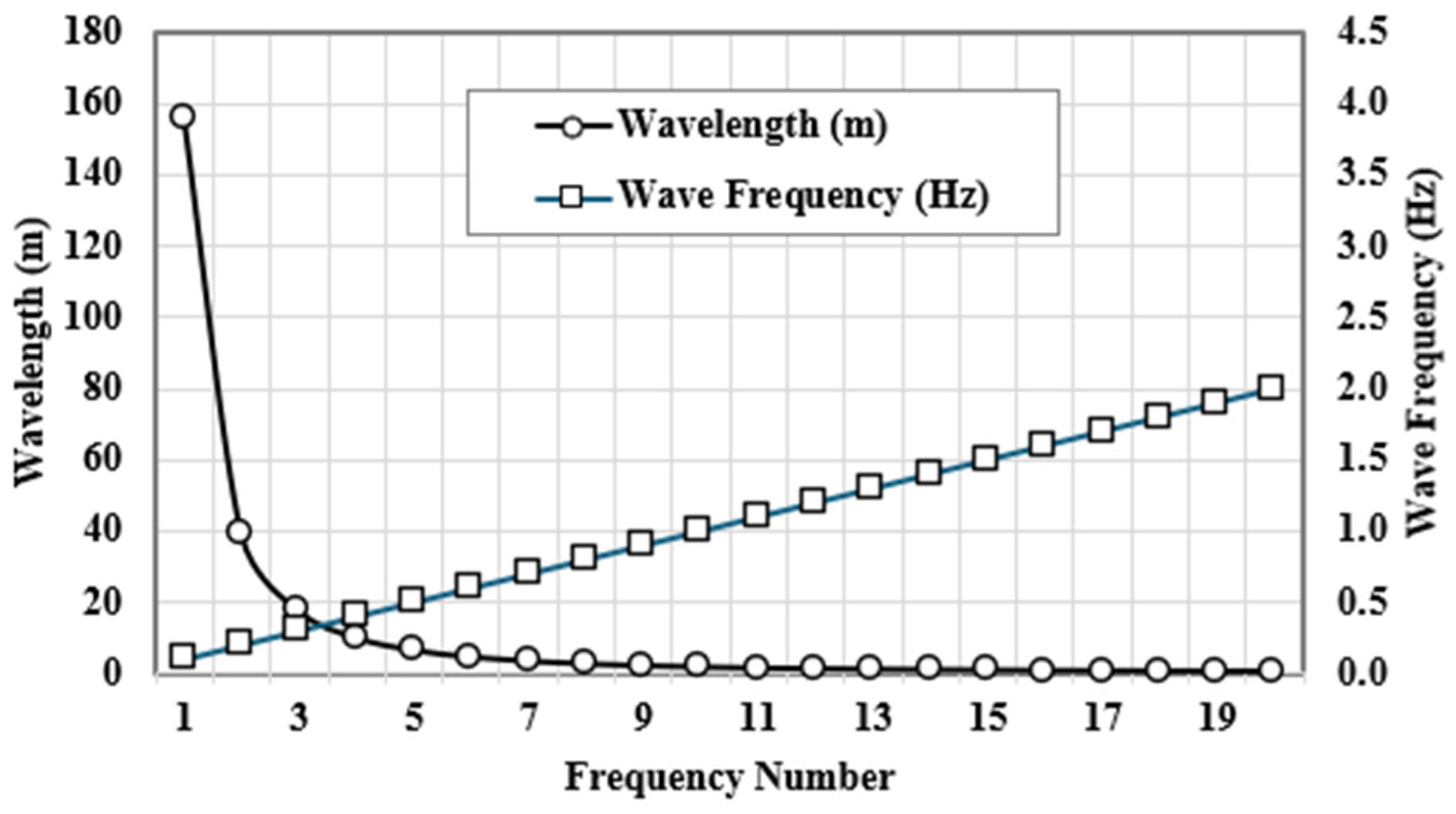
3, along with a water depth of 100 m and water area of 1.02 m × 0.91 m. Wave frequency was varied to study the response under different conditions from 0.1 to 2 Hz, corresponding to 10 s and 0.5 s periods, respectively.
Figure 15 shows plots of wave frequencies and corresponding wavelengths as a function of frequency number based on the hydrodynamic diffraction analysis for a water depth of 100 m.
7.1.2. Mesh Analysis
To ensure accurate simulation results, a structured mesh was generated with an element size of 0.02 m based on grid sensitivity analysis considering suitability for capturing the intricate fluid–structure interactions between the sea waves and the buoy, computational efficiency and result accuracy. The final mesh is made up of 1240 hexahedral elements adapted to the buoy’s geometry and the surrounding fluid domain.
Figure 16 shows ANSYS AQWA simulation of the pressure distribution as head of water on the buoy surface and the mesh.
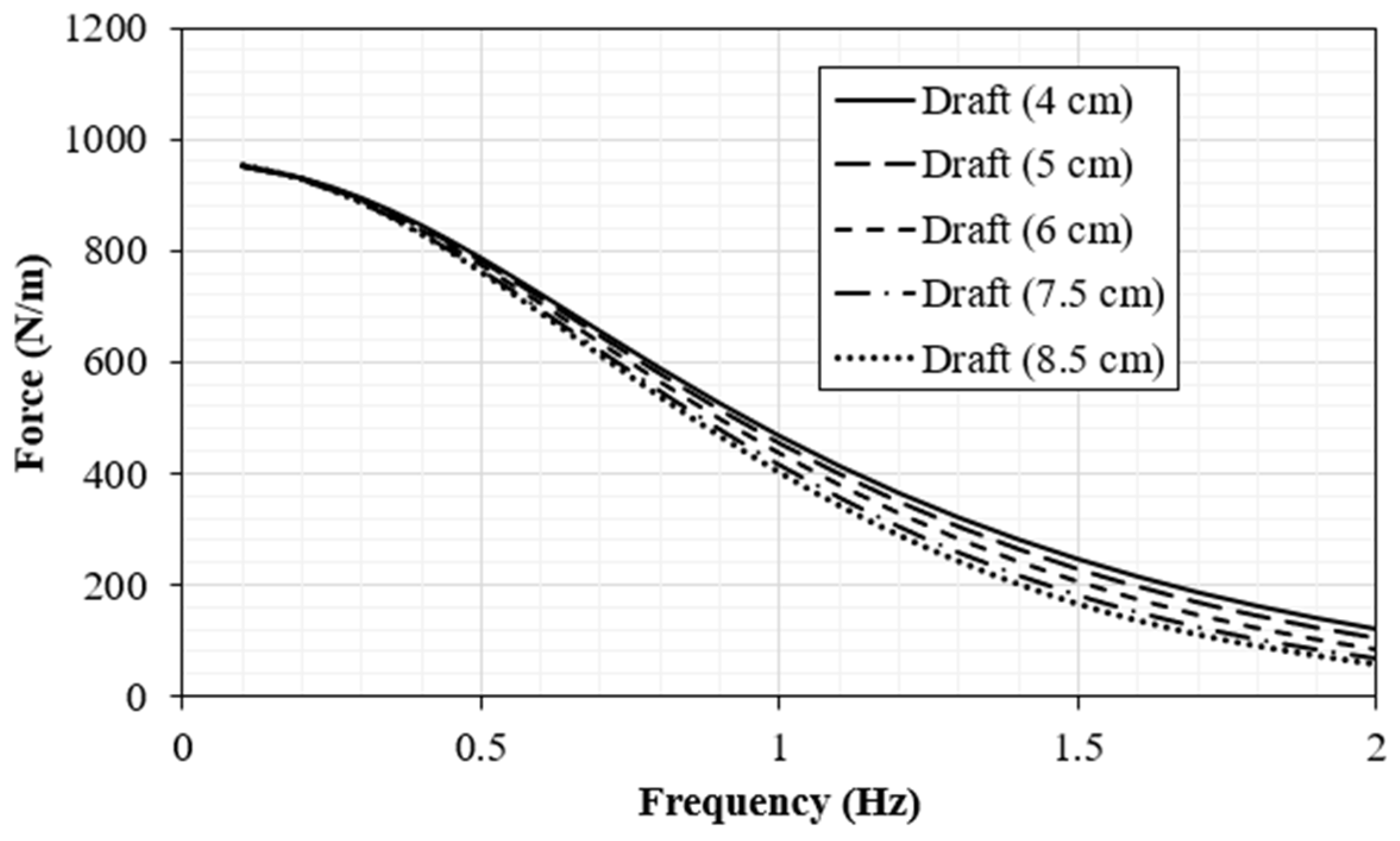
Figure 17 shows a comparison of the diffraction forces and Froude–Krylov forces experienced by the buoy for different drafts under identical wave conditions. The results indicate that these forces decrease as the wave frequency increases, which is typical since low-frequency (longer) waves apply more force. For the cases considered, the 4 cm draft experiences the highest force, indicating stronger interaction with longer waves.
A comparison of the heave Response Amplitude Operators (RAOs) of the buoy for different drafts under identical wave conditions is shown in
Figure 18. By comparing their RAO curves, we can observe how buoy geometry and draft affect its motion behavior as a result of wave excitation at different frequencies. This helps identify which design is more responsive or stable across various sea states, supporting better performance in wave energy applications. The buoy, evaluated across drafts from 4 cm to 8.5 cm, exhibits clear resonance behavior near 1.2 Hz, with the 7.5 cm draft producing the highest RAO value, indicating its natural frequency aligns closely with the incoming wave energy at that point. As the draft increases, the peak shifts slightly and the RAO magnitude decreases, showing the damping effect of greater submergence. The curve flattens more quickly for shallower drafts beyond the peak, reflecting reduced sensitivity to higher frequencies.
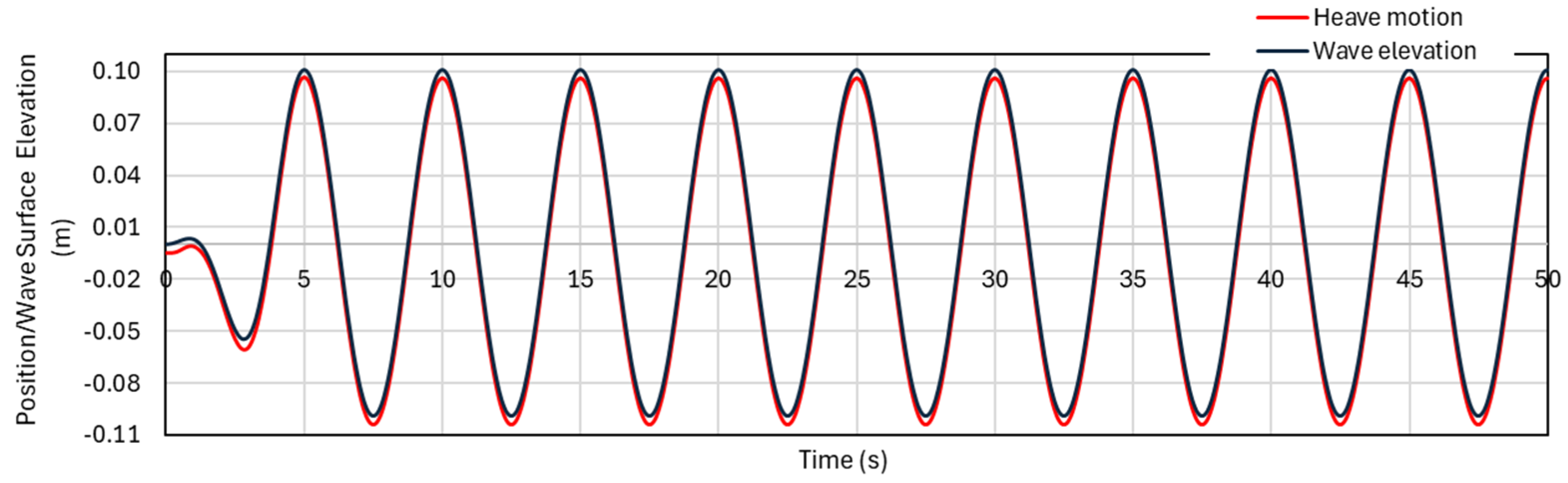
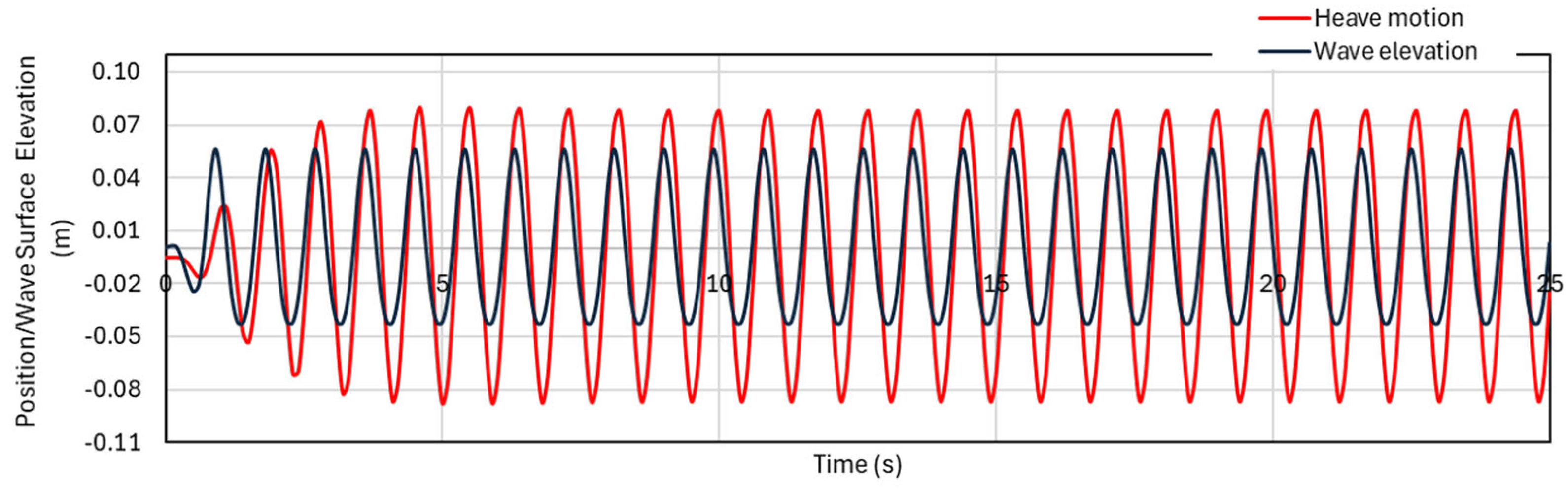
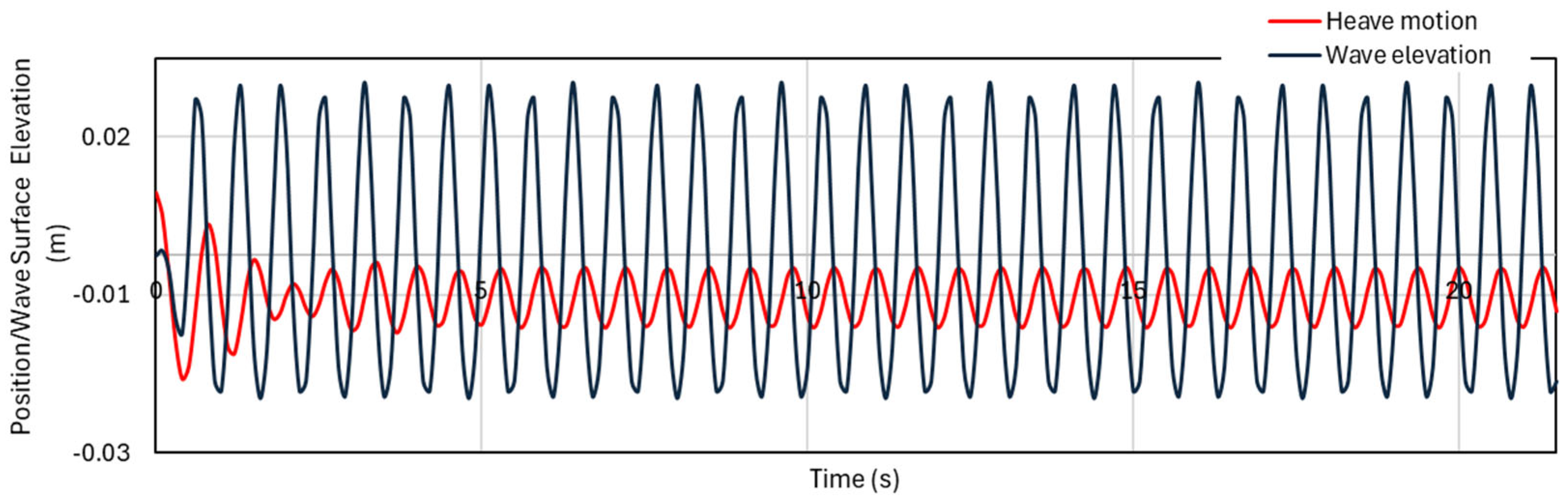
In order to assess the buoy’s dynamic reaction under wave excitation, its heave motion with the wave elevation is compared next. The time-series plot of the buoy heave motion under incident waves with periods of 5 s, 0.9 s, and 0.64 s is shown in
Figure 19,
Figure 20 and
Figure 21. These wave periods were carefully selected to observe the buoy behavior in three different motion types: dominated by inertia, by stiffness, and at resonance. As expected, and as confirmed by the RAO analysis, the buoy shows a much larger response during the resonant period (0.9 s) compared to the wave height. At lower frequencies, the buoy follows the shape of the waves closely, while at higher frequencies, its movement becomes exceedingly small.
7.2. In Situ Experimental Test and Validation
In this section, measurements from the in situ test are presented.
Table 4 lists the buoy mass, the buoy submergence, and the wave frequency recorded during the test. The RMS value of velocity was determined from the ANSYS AQWA simulation.
Figure 22 shows the plot of the measured power from the in situ test, where, on average, the system is generating approximately 0.72 W of power at the buoy rpm of 30, corresponding to the 0.5 Hz wave frequency.
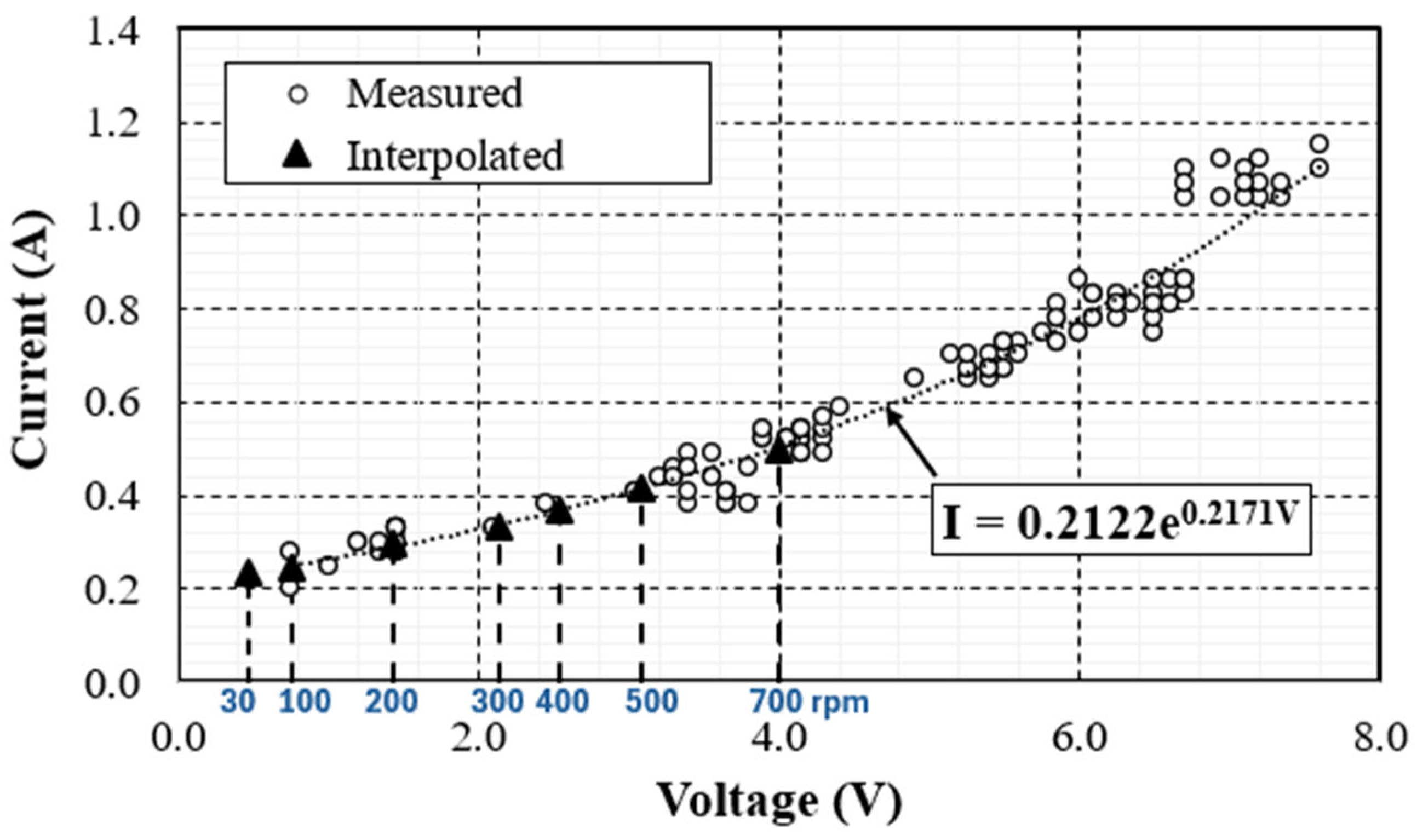
To validate the system’s power output, the voltage and current measurements were compared with the performance data of an off-the-shelf generator available in the market. The generator chosen in this case was the Dunkermotoren model GR 63x25 24V, rated at 48.4 W at 3300 rpm. This generator’s performance was measured using the same Arduino-based data acquisition setup. In this case, a power drill was used to rotate the generator shaft. A marker was taped to the hand drill for taking rpm measurements using a video camera. The Tracker software was used to correlate the current and voltage measurements to the recorded rpm values.
Figure 23 presents the measured and interpolated voltage and current output of the Dunkermotoren generator model GR 63x25 at different rpms.
As mentioned earlier, the overdrive gearbox increases the rpm of the buoy by a factor of 10. Thus, the first rotor of the dual-rotor generator sees an rpm of 300, corresponding to the buoy rpm of 30. Based on
Figure 23, the generic generator yields a power of 0.711 W (2.133 V and 0.333 A) at 300 rpm compared to 0.72 W using the dual-rotor generator. Therefore, one can conclude that the dual-rotor generator measured output is reasonably accurate. Moreover, without the overdrive, the dual-rotor generator will yield a power of approximately 0.11 W, representing only 15.3% of the power generated using the overdrive.
It is also noted here that in the absence of water current during the test, the VAWT did not contribute to generating power. However, based on the VAWT numerical simulation results presented in
Table 3, a water current speed of 1 m/s will result in 124 rpm of the VAWT, which will increase 3-fold due to the 1:3 ratio 90° bevel gear, resulting in 372 rpm of the second rotor of the dual-rotor generator. In this case, the dual-rotor generator will see a combined rpm of 672, resulting in approximately 2 W of power. This represents an 18-fold increase in power generation compared to a system without the dual-rotor generator and the overdrive mechanisms with a power yield of only 0.11 W.
In addition, from
Figure 17, ANSYS AQWA results predict a force response of 800 N/m at 0.5 Hz for the wave amplitude of 0.2 m. This suggests an excitation force of approximately 160 N. With an RMS velocity of 0.444 m/s, the estimated mechanical power is around 71 W. However, from
Section 3.3, the theoretically estimated power output is 103.08 W/m × 0.35 m
36 W. The difference between the two results could be attributed to overestimation of the Froude–Krylov force without consideration for damping, system losses, and phase differences in the analysis. These results suggest that a much higher power potential is available in the point-absorber buoy, and therefore, it remains to be seen how this potential can be fully realized.
Furthermore,
Table 5 presents a comparison of the existing hybrid wave–current energy converter (HWCEC) systems’ features and performance. These systems, although larger in scale than the proposed system, exhibit similar performance if scaled down to the current system.
8. Conclusions
This work presents the design, fabrication, and testing of a small-scale hybrid ocean energy harvesting system utilizing a heaving buoy and a vertical axis water turbine. System development began with a wave resource assessment, confirming the suitability of the Khobar coastline, followed by simulation-driven optimization of the buoy and hydrodynamic validation using ANSYS AQWA. QBlade was used to optimize turbine blade profiles for low-flow conditions, and the prototype used accessible materials with adjustable components for on-site deployment.
The technical innovations that distinguish this project include (1) a custom-designed bi-directional mechanical motion rectifier (MMR), (2) a 1:10 overdrive gearbox, (3) a dual-rotor generator, (4) a slip ring, and (5) a 90° bevel drive with a 1:3 drive ratio. The MMR with overdrive gearbox converts buoy heaves into rotational motion and maintains a single direction of output rotation. The dual-rotor generator accepts independent power input from the buoy and turbine, enabling higher operating rpm without mechanical coupling. This slip ring transfers power from the rotating dual-rotor to a stationary outlet to provide uninterrupted power output.
Several important conclusions can be drawn from this study. First, this hybrid system shows promising power generation potential in nearshore, low-energy environments, aided by overdrive and dual-rotor features. Second, historical data indicate average and median significant wave heights of 0.28 m and 0.21 m and wave periods of 2.68 s and 2.67 s, respectively, for Khobar. Third, in situ tests corroborate these findings, with observed wave heights from –0.11 m to 0.20 m and a dominant period of about 2.22 s. Fourth, frequency analysis reveals peaks at 0.39 Hz and 0.5 Hz, identifying optimal natural frequencies for buoy design. Fifth, force-response analysis suggests that low-rpm, high-torque generators are advantageous for power extraction in such conditions. Sixth, RAO analysis can be used to match buoy resonance with wave periods for improved performance.
The proposed system’s simplicity, modular scalability, and potential environmental benefits, particularly the reduction of CO
2 emissions through increased renewable energy adoption, position it as a promising step toward sustainable marine energy solutions. Although this study does not quantify direct environmental or emissions impacts, deploying such hybrid systems in coastal regions may support sustainability goals by providing clean alternatives for off-grid applications. As highlighted in recent reviews [
43], broader CO
2 mitigation strategies rely on a diverse mix of renewable technologies, with marine energy offering an important complementary role.
Future planned research will address (1) integrating a flywheel and battery storage to stabilize power output, (2) exploring low-rpm, high-torque generators to maximize buoy heave energy, (3) long-term durability testing, (4) modular MMR design for implementation as an array, allowing a mechanism to run multiple low-rpm and high-torque generators at the same time for enhanced power output and extracting maximum available energy, (5) environmental impact assessments, including studies on marine life interactions and system resilience to fouling and corrosion, (6) assessing further enhancement of the hybrid system through incorporation of solar/wind energy harvesting. These steps could bridge the gap to practical, full-scale deployment, contributing to sustainable marine energy solutions.
Author Contributions
Conceptualization, F.S., T.M.S., A.A.B., A.M.A. and O.A.A.; methodology, F.S. and T.M.S.; software, F.S., T.M.S., O.A.A., M.Y.A. and S.A.A.; validation, F.S., A.A.B., A.M.A. and O.A.A.; formal analysis, F.S., T.M.S., O.A.A. and M.Y.A.; investigation, A.A.B., A.M.A., O.A.A., M.Y.A., T.K.A. and S.A.A.; resources, F.S.; data curation, F.S., T.M.S., A.A.B., A.M.A. and O.A.A.; writing—original draft preparation, F.S., T.M.S., M.A.H. and T.K.A.; writing—review and editing, F.S., T.M.S. and M.A.H.; visualization, A.A.B., A.M.A. and O.A.A.; supervision, F.S. and T.M.S.; project administration, F.S. and T.M.S.; funding acquisition, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors would like to acknowledge the support provided by Imam Abdulrahman Bin Faisal University (IAU), in general, and the support provided by the staff of the College of Engineering Mechanical Workshop and Fab-House and the use of the facilities for prototype development, in particular.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, P.; Wu, D. A review of hybrid wave-tidal energy conversion technology. Ocean. Eng. 2024, 303, 117684. [Google Scholar] [CrossRef]
- Jariwala, A.M.; Dash, S.K.; Sahu, U.K.; Chudjuarjeen, S. Design and dynamic emulation of hybrid solar-wind-wave energy converter (SWWEC) for efficient power generation. Sci. Rep. 2024, 14, 22721. [Google Scholar] [CrossRef]
- Karimirad, M. Offshore Energy Structures: For Wind Power, Wave Energy and Hybrid Marine Platforms; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Fan, Y.; Mu, A.; Ma, T. Modeling and control of a hybrid wind-tidal turbine with hydraulic accumulator. Energy 2016, 112, 188–199. [Google Scholar] [CrossRef]
- Khurshid, H.; Mohammed, B.S.; Al-Yacouby, A.M.; Liew, M.S.; Zawawi, W.A.N.A. Analysis of hybrid offshore renewable energy sources for power generation: A literature review of hybrid solar, wind, and waves energy systems. Dev. Built Environ. 2024, 19, 100497. [Google Scholar] [CrossRef]
- Falcão, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Lemonis, G. Wave and Tidal Energy Conversion, in Encyclopedia of Energy; Elsevier: Amsterdam, The Netherlands, 2004; pp. 385–396. [Google Scholar] [CrossRef]
- Bryden, I.G.; Grinsted, T.; Melville, G.T. Assessing the potential of a simple tidal channel to deliver useful energy. Appl. Ocean Res. 2004, 26, 198–204. [Google Scholar] [CrossRef]
- Youssef, J.; Matar, J.; Rahme, P.; Bou-Mosleh, C. A Nearshore Heaving-Buoy Sea Wave Energy Converter for Power Production. Procedia Eng. 2016, 145, 136–143. [Google Scholar] [CrossRef]
- Binh, P.C.; Tri, N.M.; Dung, D.T.; Ahn, K.K.; Kim, S.-J.; Koo, W. Analysis, design and experiment investigation of a novel wave energy converter. IET Gener. Transm. Distrib. 2016, 10, 460–469. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Raghavi, B. Design, Development and Experimentation of Deep Ocean Wave Energy Converter System. Energy Procedia 2015, 79, 634–640. [Google Scholar] [CrossRef]
- Wang, Y.-L. Design of a cylindrical buoy for a wave energy converter. Ocean. Eng. 2015, 108, 350–355. [Google Scholar] [CrossRef]
- Wang, H.; Wu, W.; Cui, L.; Wu, Y.; Zhu, L.; Koutroulis, E. A New Wave Energy Converter for Marine Data Buoy. IEEE Trans. Ind. Electron. 2023, 70, 2076–2084. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Hong, S.; Zhang, M. Design of a new oscillating-buoy type wave energy converter and numerical study on its hydrodynamic performance. Brodogr. Int. J. Nav. Archit. Ocean Eng. Res. Dev. 2023, 74, 145–168. [Google Scholar] [CrossRef]
- Shi, Y.; Lin, J.; Zhuge, Z.; Zheng, R.; Zhang, J. Conceptual Design and Dynamic Analysis of a Wind–Wave Energy Converter with a Mass-Adjustable Buoy. J. Mar. Sci. Eng. 2024, 12, 1460. [Google Scholar] [CrossRef]
- Sakr, A.H.; Metwalli, S.M.; Anis, Y.H. Dynamics of heaving buoy wave energy converters with a stiffness reactive controller. Energies 2020, 14, 44. [Google Scholar] [CrossRef]
- Zheng, Z.; Yao, Z.; Chang, Z.; Yao, T.; Liu, B. A point absorber wave energy converter with nonlinear hardening spring power-take-off systems in regular waves. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2020, 234, 820–829. [Google Scholar] [CrossRef]
- Rava, M.; Dafnakis, P.; Martini, V.; Giorgi, G.; Orlando, V.; Mattiazzo, G.; Bracco, G.; Gulisano, A. Low-Cost Heaving Single-Buoy Wave-Energy Point Absorber Optimization for Sardinia West Coast. J. Mar. Sci. Eng. 2022, 10, 397. [Google Scholar] [CrossRef]
- Vijayasankar, V.; Kumar, S.; Samad, A.; Zuo, L. Analysis of an innovative compact point absorber wave energy converter concept suitable for small-scale power applications. Phys. Fluids 2023, 35, 097140. [Google Scholar] [CrossRef]
- Mutsuda, H.; Rahmawati, S.; Taniguchi, N.; Nakashima, T.; Doi, Y. Harvesting ocean energy with a small-scale tidal-current turbine and fish aggregating device in the Indonesian Archipelagos. Sustain. Energy Technol. Assess. 2019, 35, 160–171. [Google Scholar] [CrossRef]
- Behrouzi, F.; Maimun, A.; Nakisa, M.; Hanafi, M.; Jaswar, J. An innovative vertical axis current turbine design for low current speed. J. Teknol. 2014, 66. [Google Scholar] [CrossRef]
- Fernandes, A.C.; Rostami, A.B. Hydrokinetic energy harvesting by an innovative vertical axis current turbine. Renew. Energy 2015, 81, 694–706. [Google Scholar] [CrossRef]
- Alam, M.J.; Iqbal, M.T. A low cut-in speed marine current turbine. J. Ocean Technol. 2010, 5, 49–61. [Google Scholar]
- Silva, R.N.; Nunes, M.M.; Oliveira, F.L.; Oliveira, T.F.; Brasil, A.C.P.; Pinto, M.S.S. Dynamical analysis of a novel hybrid oceanic tidal-wave energy converter system. Energy 2023, 263, 125933. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, B.; Li, X.; Huang, J.; Wu, X.; Xiong, Q.; Parker, R.G.; Zuo, L. Design, dynamic modeling and wave basin verification of a Hybrid Wave–Current Energy Converter. Appl. Energy 2022, 321, 119320. [Google Scholar] [CrossRef]
- Chen, S.; Jiang, B.; Li, X.; Xiong, Q.; Huang, J.; Zuo, L. Design and Dynamics of Hybrid Wave and Current Energy Converter. In Volume 8: 31st Conference on Mechanical Vibration and Noise; American Society of Mechanical Engineers: Anaheim, CA, USA, 2019. [Google Scholar] [CrossRef]
- Park, M.-S.; Lee, S.-H.; Ko, S.-C. Experimental Capture Width Ratio on Unit Module System of Hybrid Wave Energy Converter for Nearshore. Appl. Sci. 2022, 12, 5845. [Google Scholar] [CrossRef]
- Shifler, D.A. Understanding material interactions in marine environments to promote extended structural life. Corros. Sci. 2005, 47, 2335–2352. [Google Scholar] [CrossRef]
- Copping, A.E.; Hemery, L.G. OES-Environmental 2020 State of The Science Report: Environmental Effects of Marine Renewable Energy Development Around the World; Report for ocean energy systems (OES), OSTI Technical Report; OES: Lisbon, Portugal, 2020. [Google Scholar] [CrossRef]
- Fery, N.; Al-Subhi, A.M.; Zubier, K.M.; Bruss, G. Evaluation of the sea state near Jeddah based on recent observations and model results. J. Oper. Oceanogr. 2024, 8, 1–10. [Google Scholar] [CrossRef]
- Kamranzad, B.; Etemad-shahidi, A.; Chegini, V. Assessment of wave energy variation in the Persian Gulf. Ocean. Eng. 2013, 70, 72–80. [Google Scholar] [CrossRef]
- Global Ocean Physics Reanalysis, E.U. Copernicus Marine Service Information, Marine Data Store. Available online: https://data.marine.copernicus.eu/product/GLOBAL_MULTIYEAR_PHY_001_030/description (accessed on 24 April 2025).
- Brown, D.; Christian, W.; Hanson, R.M. Tracker: Video Analysis and Modeling Tool for Physics Education. Available online: https://opensourcephysics.github.io/tracker-website/ (accessed on 24 April 2025).
- McCormick, M.E. Ocean Wave Energy Conversion; Dover Publications: Mineola, NY, USA, 2007. [Google Scholar]
- Yang, W.; Hou, Y.; Jia, H.; Liu, B.; Xiao, R. Lift-type and drag-type hydro turbine with vertical axis for power generation from water pipelines. Energy 2019, 188, 116070. [Google Scholar] [CrossRef]
- Marten, D. QBlade: A Modern Tool for the Aeroelastic Simulation of Wind Turbines. Ph.D. Thesis, Technische Universität, Berlin, Germany, 2020. [Google Scholar] [CrossRef]
- Drela, M. XFOIL Subsonic Airfoil Development System. Mit.edu. 2013. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 2 January 2025).
- Mahdi, M. Optimal blade Design of a spherical water turbine. e-Prime-Adv. Electr. Eng. Electron. Energy 2024, 7, 100470. [Google Scholar] [CrossRef]
- ANSYS Inc. AQWA Theory Manual; Release 2023 R1; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Devolder, B. Hydrodynamic Modelling of Wave Energy Converter Arrays. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2018. [Google Scholar]
- Akselsen, A.M. Hydrodynamic Analysis of a Floating Renewable Energy Device. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2019. [Google Scholar]
- Geweda, A.E.; Mohamed, E.; Khan, M.Y.; Alquaity, A.B.S. Mitigating CO2 emissions: A review on emerging technologies/strategies for CO2 capture. J. Energy Inst. 2025, 118, 101911. [Google Scholar] [CrossRef]
Figure 1.
Common types of vertical axis water turbines: (1) Gorlov, (2) Savonius, (3) H-Darrieus, (4) Squirrel-cage Darrieus, and (5) Darrieus.
Figure 1.
Common types of vertical axis water turbines: (1) Gorlov, (2) Savonius, (3) H-Darrieus, (4) Squirrel-cage Darrieus, and (5) Darrieus.
Figure 2.
Time series data: (a) significant wave height and (b) wave period from 2013 till 2023.
Figure 2.
Time series data: (a) significant wave height and (b) wave period from 2013 till 2023.
Figure 3.
Calibrated rod and small buoy used for on-site wave motion and height measurements.
Figure 3.
Calibrated rod and small buoy used for on-site wave motion and height measurements.
Figure 4.
On-site wave height data measurements.
Figure 4.
On-site wave height data measurements.
Figure 5.
Frequency spectrum of on-site wave height measurement results.
Figure 5.
Frequency spectrum of on-site wave height measurement results.
Figure 6.
Design evolution showing (a) the first concept and (b) the second concept.
Figure 6.
Design evolution showing (a) the first concept and (b) the second concept.
Figure 7.
The different views of the final complete system in its assembled form.
Figure 7.
The different views of the final complete system in its assembled form.
Figure 8.
The modified mechanical motion rectifier (MMR) system and working concept.
Figure 8.
The modified mechanical motion rectifier (MMR) system and working concept.
Figure 9.
The modified MMR and overdrive gearbox assembly.
Figure 9.
The modified MMR and overdrive gearbox assembly.
Figure 10.
The different components of the dual-rotor generator subassembly.
Figure 10.
The different components of the dual-rotor generator subassembly.
Figure 11.
The VAWT and 90° bevel gear subassembly.
Figure 11.
The VAWT and 90° bevel gear subassembly.
Figure 12.
The system prototype (a) during tests and (b) in final form.
Figure 12.
The system prototype (a) during tests and (b) in final form.
Figure 13.
(a) Heave decay response and (b) Heave power spectral density for three different release depths.
Figure 13.
(a) Heave decay response and (b) Heave power spectral density for three different release depths.
Figure 14.
Comparison of (a) power coefficient and (b) torque coefficient curves of the different VAWT configurations.
Figure 14.
Comparison of (a) power coefficient and (b) torque coefficient curves of the different VAWT configurations.
Figure 15.
Wave frequencies and corresponding wavelengths based on the hydrodynamic diffraction analysis for a water depth of 100 m.
Figure 15.
Wave frequencies and corresponding wavelengths based on the hydrodynamic diffraction analysis for a water depth of 100 m.
Figure 16.
Pressure distribution simulation using ANSYS AQWA.
Figure 16.
Pressure distribution simulation using ANSYS AQWA.
Figure 17.
Diffraction and Froude–Krylov forces acting on the buoy.
Figure 17.
Diffraction and Froude–Krylov forces acting on the buoy.
Figure 18.
Heave RAO of the first buoy.
Figure 18.
Heave RAO of the first buoy.
Figure 19.
Response in heave for an incoming regular wave with period T = 5 s.
Figure 19.
Response in heave for an incoming regular wave with period T = 5 s.
Figure 20.
Response in heave for an incoming regular wave with period T = 0.9 s.
Figure 20.
Response in heave for an incoming regular wave with period T = 0.9 s.
Figure 21.
Response in heave for an incoming regular wave with period T = 0.64 s.
Figure 21.
Response in heave for an incoming regular wave with period T = 0.64 s.
Figure 22.
Power measurement data from in situ test.
Figure 22.
Power measurement data from in situ test.
Figure 23.
Voltage and current measurement of Dunkermotoren generator model GR 63x25.
Figure 23.
Voltage and current measurement of Dunkermotoren generator model GR 63x25.
Table 1.
Predicted Frequency (Hz) for Draft-Diameter Combinations of Buoy.
Table 1.
Predicted Frequency (Hz) for Draft-Diameter Combinations of Buoy.
| | | Diameters (m) |
|---|
| | - | 0.30 | 0.31 | 0.33 | 0.35 |
| Drafts (m) | 0.50 | 0.670 | 0.664 | 0.658 | 0.657 |
| 0.75 | 0.560 | 0.550 | 0.548 | 0.540 |
| 1.00 | 0.501 | 0.501 | 0.498 | 0.497 |
| 1.25 | 0.433 | 0.432 | 0.431 | 0.430 |
Table 2.
Comparison of natural periods of the selected buoy using different approaches.
Table 2.
Comparison of natural periods of the selected buoy using different approaches.
| Draft (cm) | ANSYS AQWA | On-Site Tests | Equation (1) |
|---|
| 4.0 | 0.719 s | 0.728 s | 0.71 s |
| 5.0 | 0.722 s | 0.73 s | 0.72 s |
| 6.0 | 0.775 s | 0.733 s | 0.74 s |
| 7.5 | 0.820 s | 0.766 s | 0.78 s |
| 8.5 | 0.840 s | 0.834 s | 0.80 s |
Table 3.
Performance characteristics of the final VAWT configuration.
Table 3.
Performance characteristics of the final VAWT configuration.
Current
Speed
(m/s) | Turbine
RPM | Turbine
Rotational Speed (rad/s) | Turbine
Power
(W) | Turbine Torque
(N·m) |
|---|
| 0.5 | 62 | 6.5 | 3 | 0.46 |
| 1.0 | 124 | 13.0 | 24 | 1.84 |
| 1.5 | 186 | 19.5 | 81 | 4.20 |
| 2.0 | 248 | 26.0 | 192 | 7.40 |
| 2.5 | 310 | 32.5 | 375 | 11.6 |
| 3.0 | 370 | 39.0 | 650 | 16.6 |
Table 4.
Buoy in situ test and corresponding simulation data.
Table 4.
Buoy in situ test and corresponding simulation data.
| Mass (kg) | Submergence (m) | Amplitude (m) | Frequency (Hz) | RMS Velocity (m/s) |
|---|
| 5 | 0.06 | 0.20 | 0.500 | 0.444 |
Table 5.
Comparison of existing hybrid wave–current energy converter (HWCEC) systems.
Table 5.
Comparison of existing hybrid wave–current energy converter (HWCEC) systems.
| Author | Scale | Output Power | Coupling Type |
|---|
| Chen et al. [1] | Turbine radius: 0.5 m
Buoy diameter: 0.75 m | Tank test: 4.21 W (maximum) | Bevel gear mechanical motion rectifier (MMR) |
| Park et al. [28] | Sectional area in flow direction: 2 m × 3 m. | Average: ∼12.5 W | Horizontal cylinder and swing plate coupled by clutch gears. |
| Current study | Turbine radius: 0.1 m
Buoy diameter: 0.35 m | Field test (buoy only): 1.4 W (maximum)
Simulation (combined): 2.0 W | Modified MMR with overdrive, dual-rotor generator, and bevel gear |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).