Design of Virtual Sensors for a Pyramidal Weathervaning Floating Wind Turbine
Abstract
1. Introduction
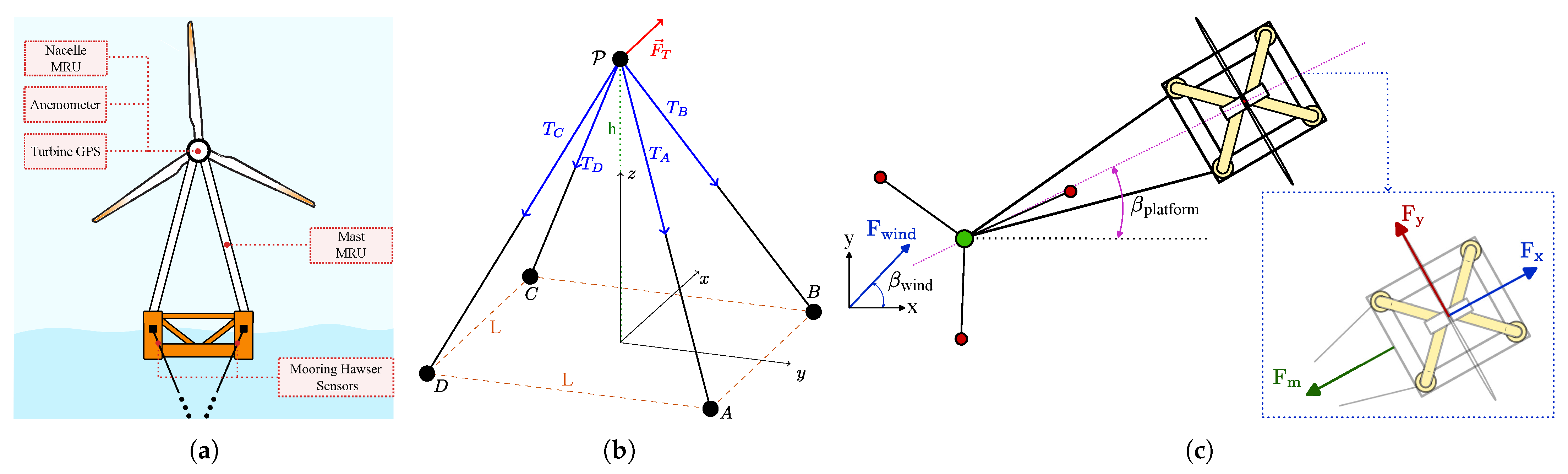
2. Eolink Floating Wind Turbine Concept
3. Methods and Design of the Virtual Sensors
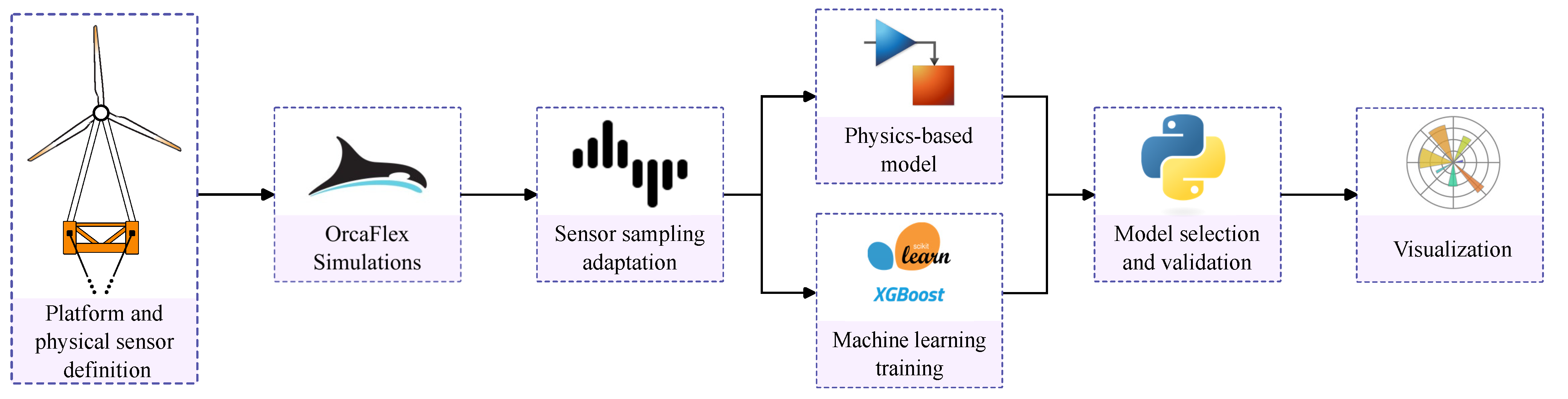
3.1. Methodology
3.2. Assumptions of Physical Sensors Installed
3.3. Load Cases in OrcaFlex and Data Analysis
3.4. Physics Relations for PIML Integration
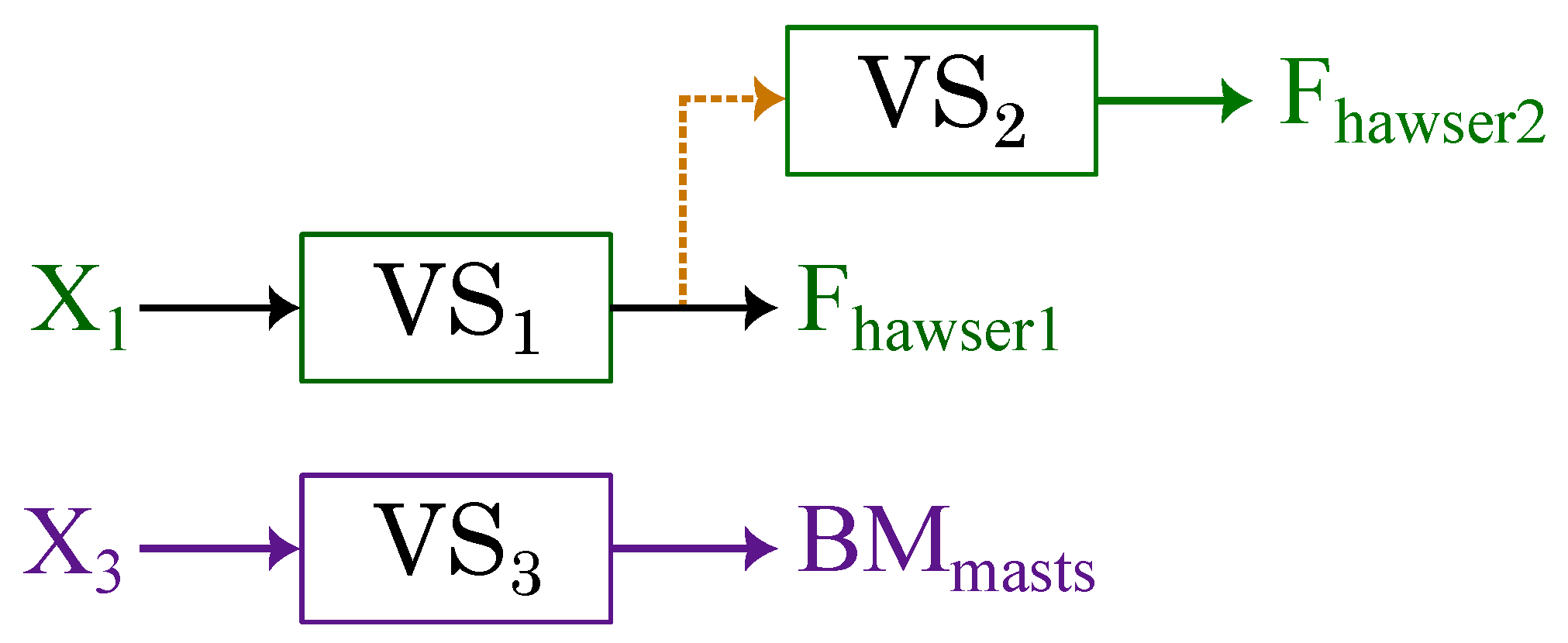
3.5. Supervised and Physics-Informed Machine Learning
4. Results
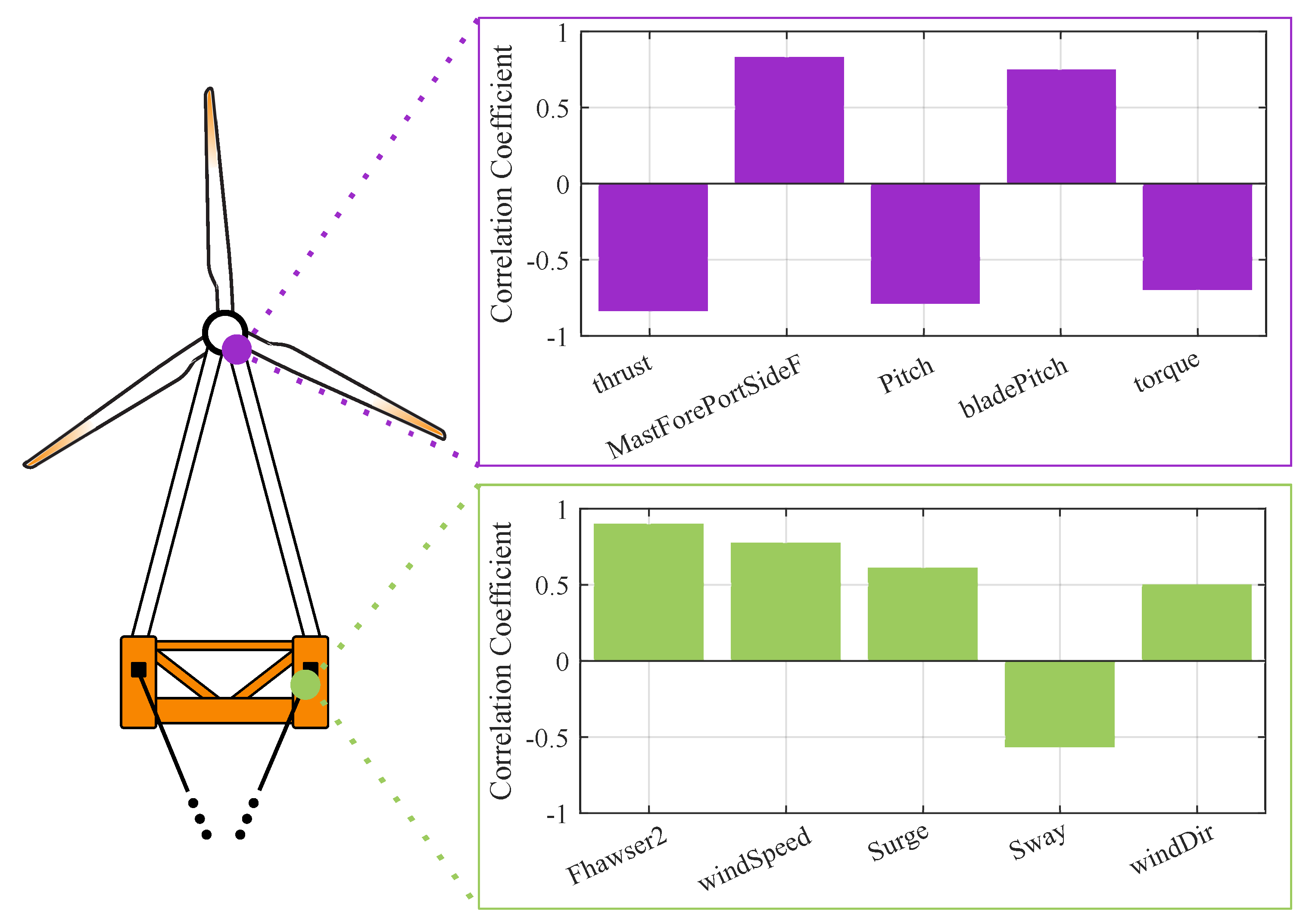
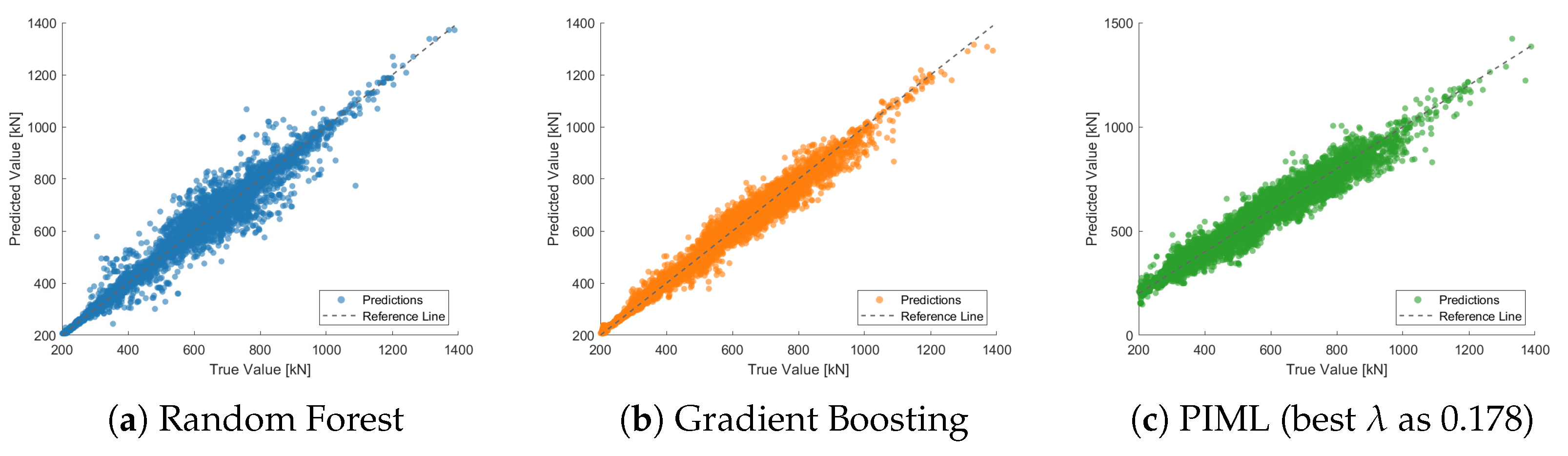
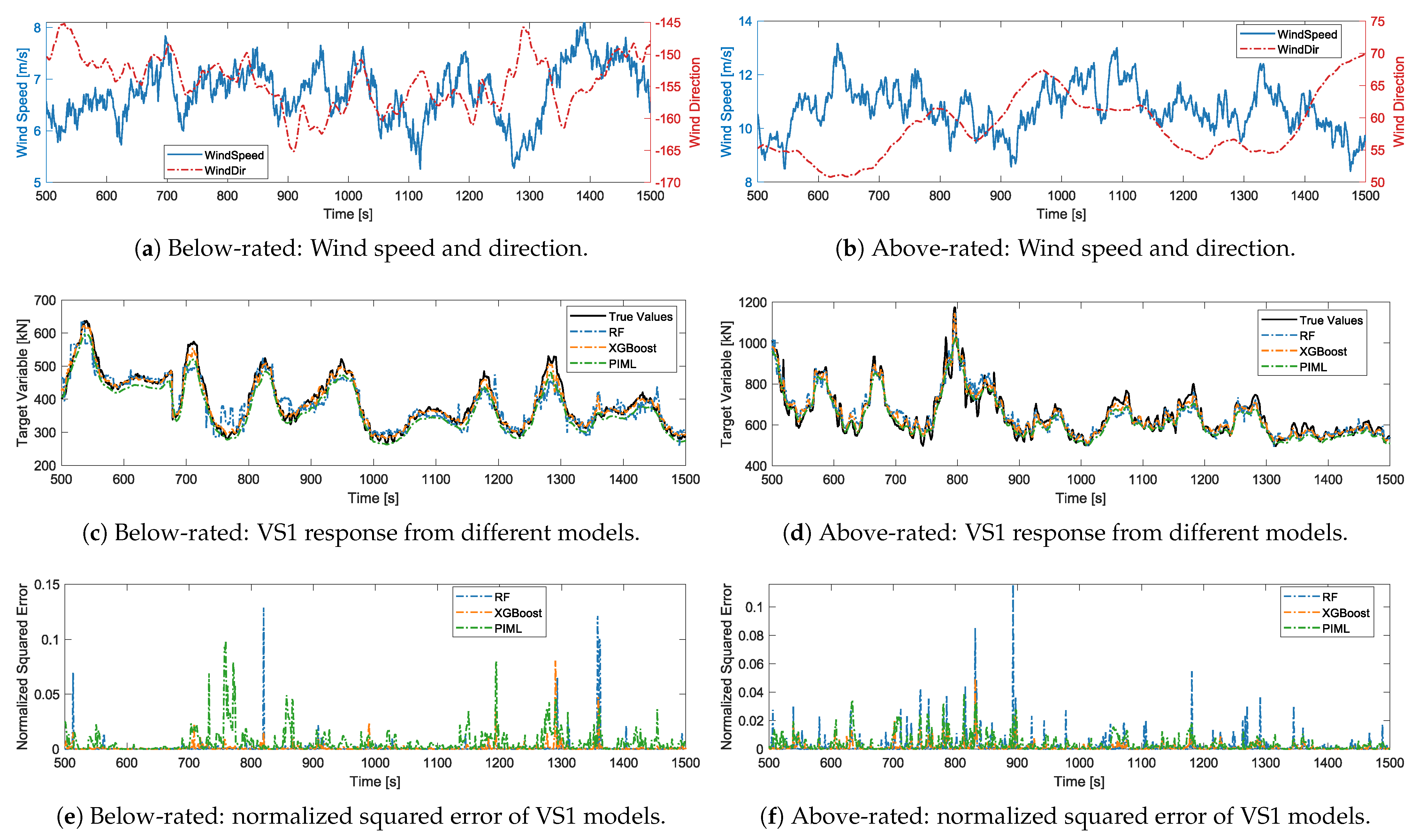
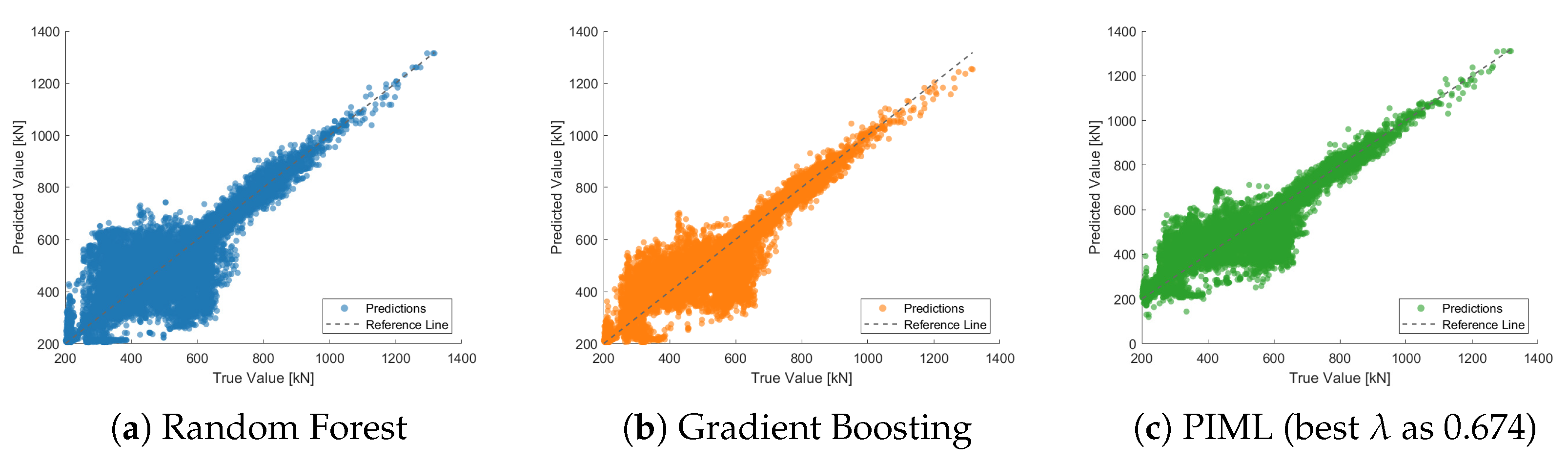
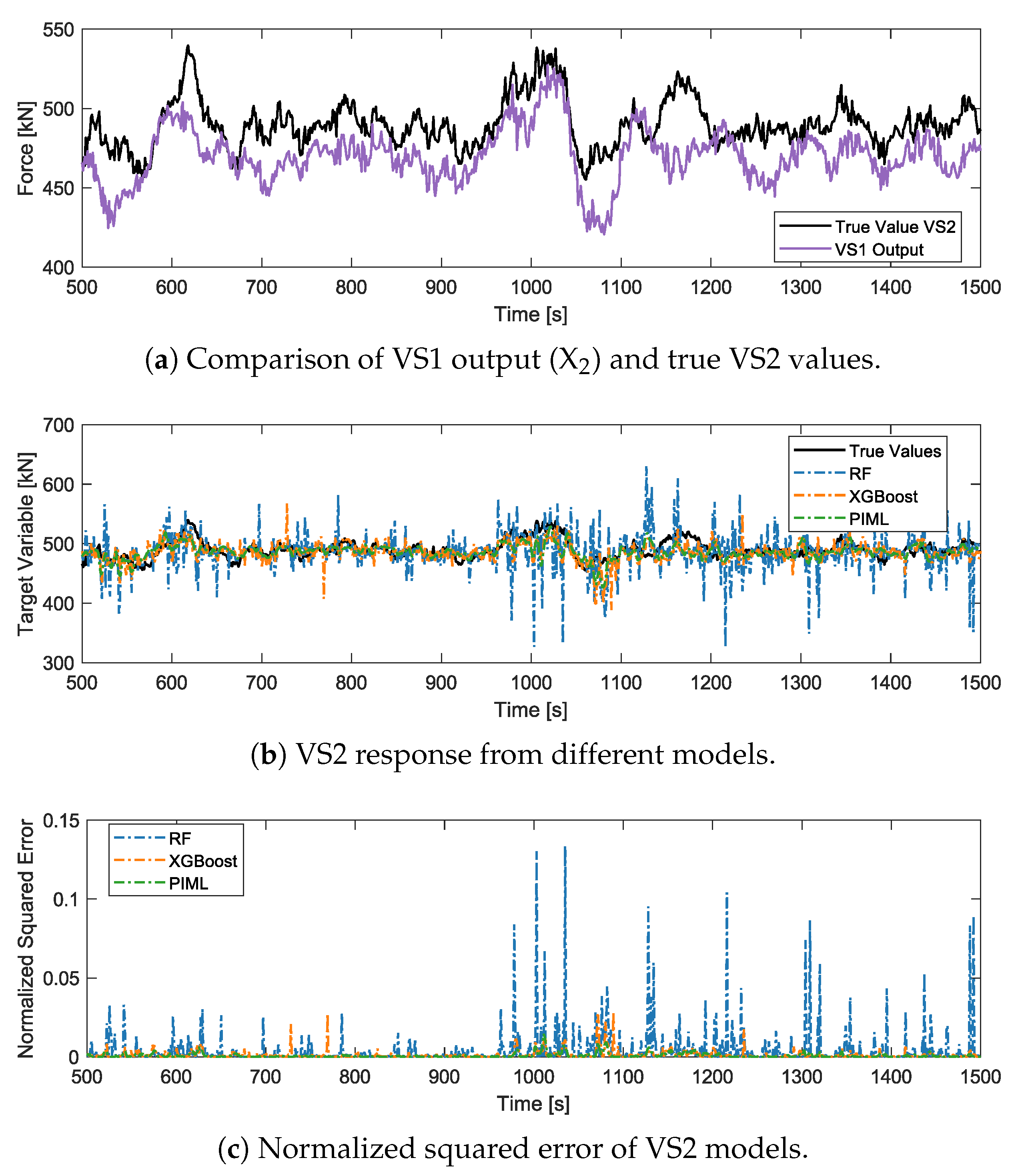
4.1. Mooring Hawsers
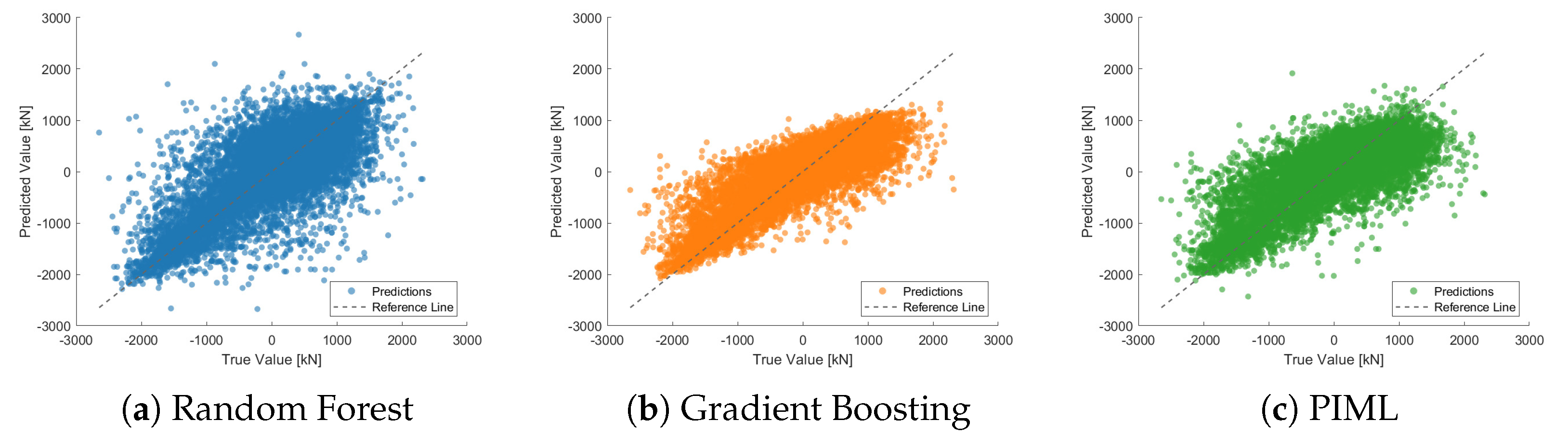
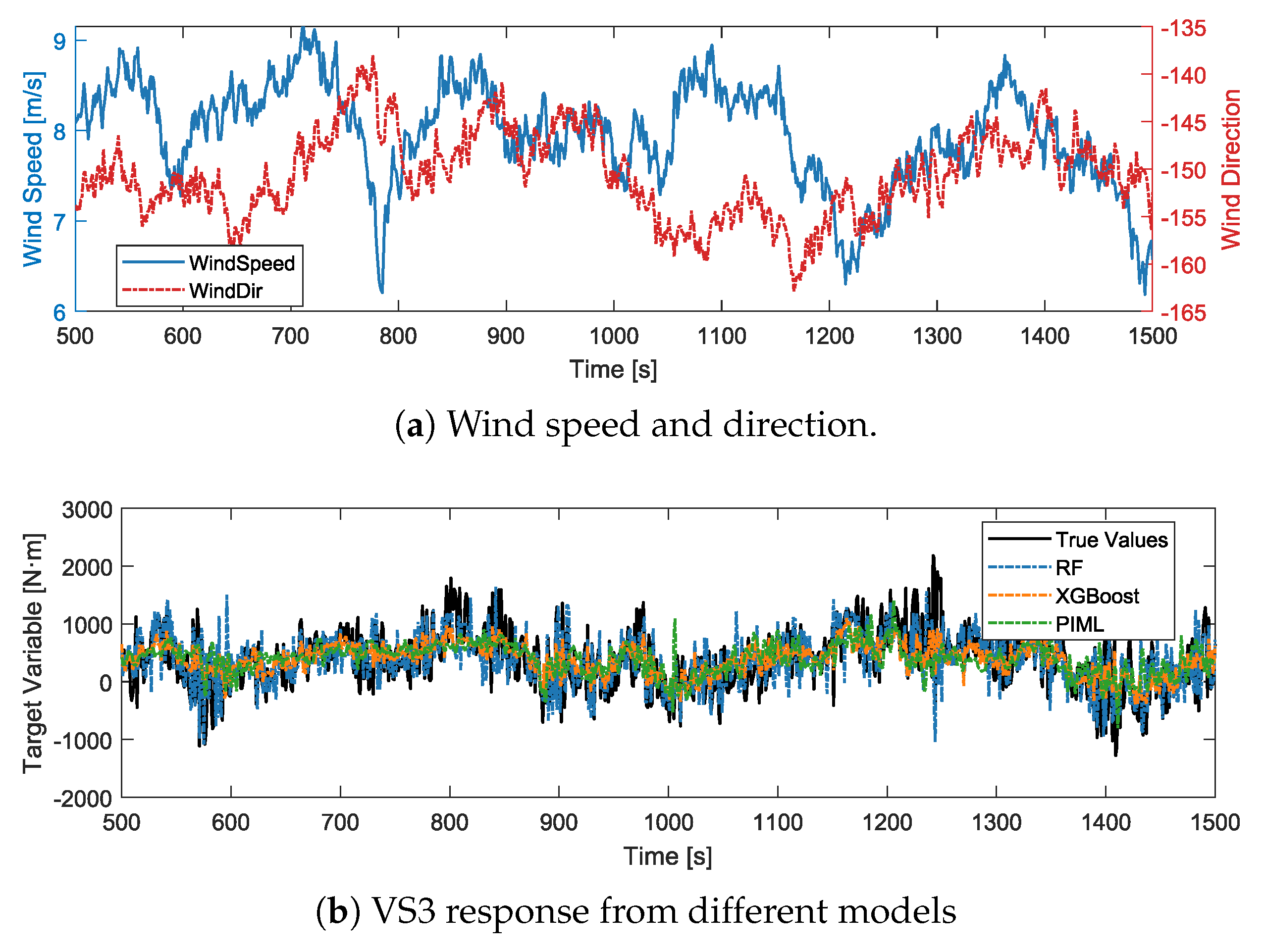
4.2. Mast Joint Bending Moment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FOWT | Floating Offshore Wind Turbine |
| VS | Virtual Sensor |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| MRU | Motion Reference Unit |
| SCADA | Supervisory Control and Data Acquisition |
| RF | Random Forest |
| PIML | Physics-Informed Machine Learning |
| RMSE | Root Mean Square Error |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
| BLOW | Black Sea Offshore Wind |
References
- Edwards, E.C.; Holcombe, A.; Brown, S.; Ransley, E.; Hann, M.; Greaves, D. Evolution of floating offshore wind platforms: A review of at-sea devices. Renew. Sustain. Energy Rev. 2023, 183, 113416. [Google Scholar] [CrossRef]
- del Pozo Gonzalez, H.; Kallinger, M.D.; Rapha, J.I.; Domínguez-García, J.L. Modern Floating Wind Energy Technologies. In Energy Systems Integration for Multi-Energy Systems: From Operation to Planning in the Green Energy Context; Springer: Berlin/Heidelberg, Germany, 2025; pp. 295–316. [Google Scholar]
- Ciuriuc, A.; Rapha, J.I.; Guanche, R.; Domínguez-García, J.L. Digital tools for floating offshore wind turbines (FOWT): A state of the art. Energy Rep. 2022, 8, 1207–1228. [Google Scholar] [CrossRef]
- Kang, J.; Sun, L.; Soares, C.G. Fault Tree Analysis of floating offshore wind turbines. Renew. Energy 2019, 133, 1455–1467. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.M.; Min, Y.T.; Yu, Y.; Lin, C.; Hu, Z.Z. A digital twin-based framework for simulation and monitoring analysis of floating wind turbine structures. Ocean Eng. 2023, 283, 115009. [Google Scholar] [CrossRef]
- Éolink. Our Concept—Éolink. 2025. Available online: https://eolink.fr/en/our-concept/ (accessed on 26 February 2025).
- Bernitsas, M.M.; Papoulias, F.A. Stability of single point mooring systems. Appl. Ocean Res. 1986, 8, 49–58. [Google Scholar] [CrossRef]
- Connolly, A.; Guyot, M.; Le Boulluec, M.; Héry, L.; O’Connor, A. Fully coupled aero-hydro-structural simulation of new floating wind turbine concept. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 51975, p. V001T01A027. [Google Scholar]
- Doisenbant, G.; Le Boulluec, M.; Scolan, Y.M.; Guyot, M. Numerical and experimental modeling of offshore wind energy capture: Application to reduced scale model testing. Wind. Eng. 2018, 42, 108–114. [Google Scholar] [CrossRef]
- Guyot, M.; De Mourgues, C.; Le Bihan, G.; Parenthoine, P.; Templai, J.; Connolly, A.; Le Boulluec, M. Experimental offshore floating wind turbine prototype and numerical analysis during harsh and production events. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, Scotland, 9–14 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59353, p. V001T02A004. [Google Scholar]
- Guyot, M. Floating Wind Turbine Structure. U.S. Patent 9,976,540, 22 May 2018. [Google Scholar]
- Martin, D.; Kühl, N.; Satzger, G. Virtual sensors. Bus. Inf. Syst. Eng. 2021, 63, 315–323. [Google Scholar] [CrossRef]
- Dimitrov, N.; Göçmen, T. Virtual sensors for wind turbines with machine learning-based time series models. Wind. Energy 2022, 25, 1626–1645. [Google Scholar] [CrossRef]
- Hlaing, N.; Morato, P.G.; Santos, F.d.N.; Weijtjens, W.; Devriendt, C.; Rigo, P. Farm-wide virtual load monitoring for offshore wind structures via Bayesian neural networks. Struct. Health Monit. 2024, 23, 1641–1663. [Google Scholar] [CrossRef]
- Mehlan, F.C.; Keller, J.; Nejad, A.R. Virtual sensing of wind turbine hub loads and drivetrain fatigue damage. Forsch. Im Ing. 2023, 87, 207–218. [Google Scholar] [CrossRef]
- Moynihan, B.; Tronci, E.M.; Hughes, M.C.; Moaveni, B.; Hines, E. Virtual sensing via Gaussian Process for bending moment response prediction of an offshore wind turbine using SCADA data. Renew. Energy 2024, 227, 120466. [Google Scholar] [CrossRef]
- Gräfe, M.; Özinan, U.; Cheng, P.W. Lidar-based virtual load sensors for mooring lines using artificial neural networks. Proc. J. Phys. Conf. Ser. 2023, 2626, 012036. [Google Scholar] [CrossRef]
- Gräfe, M.; Pettas, V.; Dimitrov, N.; Cheng, P.W. Machine-learning-based virtual load sensors for mooring lines using simulated motion and lidar measurements. Wind Energy Sci. 2024, 9, 2175–2193. [Google Scholar] [CrossRef]
- Branlard, E.; Jonkman, J.; Brown, C.; Zhang, J. A digital twin solution for floating offshore wind turbines validated using a full-scale prototype. Wind Energy Sci. 2024, 9, 1–24. [Google Scholar] [CrossRef]
- Pacheco-Blazquez, R.; Garcia-Espinosa, J.; Di Capua, D.; Pastor Sanchez, A. A digital twin for assessing the remaining useful life of offshore wind turbine structures. J. Mar. Sci. Eng. 2024, 12, 573. [Google Scholar] [CrossRef]
- Walker, J.; Coraddu, A.; Collu, M.; Oneto, L. Digital twins of the mooring line tension for floating offshore wind turbines to improve monitoring, lifespan, and safety. J. Ocean Eng. Mar. Energy 2022, 8, 1–16. [Google Scholar] [CrossRef]
- Sauder, T.; Mainçon, P.; Lone, E.; Leira, B.J. Estimation of top tensions in mooring lines by sensor fusion. Mar. Struct. 2022, 86, 103309. [Google Scholar] [CrossRef]
- Denil, M.; Matheson, D.; De Freitas, N. Narrowing the gap: Random forests in theory and in practice. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 22–24 June 2014; pp. 665–673. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Patryniak, K.; Collu, M.; Coraddu, A. Rigid body dynamic response of a floating offshore wind turbine to waves: Identification of the instantaneous centre of rotation through analytical and numerical analyses. Renew. Energy 2023, 218, 119378. [Google Scholar] [CrossRef]
- González, H.D.P.; Domínguez-García, J.L. Non-centralized hierarchical model predictive control strategy of floating offshore wind farms for fatigue load reduction. Renew. Energy 2022, 187, 248–256. [Google Scholar] [CrossRef]
- Hall, M. Generalized Quasi-Static Mooring System Modeling with Analytic Jacobians. Energies 2024, 17, 3155. [Google Scholar] [CrossRef]
- Mahfouz, M.Y.; Cheng, P.W. Effect of mooring system stiffness on floating offshore wind turbine loads in a passively self-adjusting floating wind farm. Renew. Energy 2025, 238, 121823. [Google Scholar] [CrossRef]
- del Pozo Gonzalez, H.; Domínguez-García, J.L.; Gomis-Bellmunt, O. Structural motion control of waked floating offshore wind farms. Ocean Eng. 2024, 293, 116709. [Google Scholar] [CrossRef]
| Aspect | Key Insights |
|---|---|
| Application Areas | Gearbox and drivetrain load estimation, mooring-line tension, tower-base bending moments, converter stress, and structural fatigue monitoring. |
| Techniques Used | Kalman filters, linear state-space models, least-squares estimators, physics-informed machine learning, and neural networks integrated with digital twin frameworks. |
| Sensor Inputs | SCADA data, accelerometers, condition monitoring systems (CMS), LiDAR, GPS/inclinometers, and motion reference units (MRUs). |
| VS Outputs | Bearing forces, mooring tension, tower-base bending moments, remaining useful life, and early detection of anomalies. |
| Reported Benefits | Reduces reliance on expensive or hard-to-deploy physical sensors; enables real-time condition monitoring and predictive maintenance for floating offshore wind turbines. |
| Physical Sensor | Sample Frequency | Unit |
|---|---|---|
| Anemometer | 1 | Hz |
| GPS | 1 | Hz |
| Mooring Tension | 5 | Hz |
| Mast/Nacelle MRU | 10 | Hz |
| Wave-Current Data | Constant | – |
| Case | Turbine Condition | Wind Model | Wave Model | Current Model | Misalignment |
|---|---|---|---|---|---|
| 1 | Operational | Turbulent 7 m/s | = 1.0 m, = 5 s | Constant 0.1 m/s | No |
| 2 | Operational | Turbulent 11 m/s | = 2.5 m, = 6 s | Constant 0.2 m/s | Yes |
| 3 | Operational | Turbulent 15 m/s | = 3.5 m, = 7.5 s | Constant 0.2 m/s | No |
| 4 | Operational | Turbulent 9 m/s | = 1.8 m, = 5.5 s | Constant 0.1 m/s | No |
| 5 | Operational | Turbulent 13 m/s | = 3.0 m, = 7 s | Constant 0.2 m/s | Yes |
| 6 | Operational | Dir. change at 9 m/s | = 2.0 m, = 5.5 s | Constant 0.1 m/s | Yes |
| 7 | Operational | Dir. change at 13 m/s | = 3.0 m, = 7 s | Constant 0.2 m/s | Yes |
| 8 | Operational | Step gust to 25 m/s | = 4.0 m, = 8 s | Constant 0.3 m/s | No |
| 9 | Idling (Storm) | Steady 25 m/s | = 6.0 m, = 10 s | Constant 0.6 m/s | Yes |
| 10 | Parked (Survival) | Extreme wind (50-year) | = 8.0 m, = 12 s | Constant 0.9 m/s | Yes |
| 11 | Parked (Survival) | No wind | = 10.0 m, = 15 s | Constant 0.9 m/s | No |
| Input Vector | Variables | Sample Frequency | Output |
|---|---|---|---|
| X1 | Wind Speed Signal | 1 Hz | Fhawser1 |
| Latitude/Longitude | 1 Hz | ||
| Platform Surge | 10 Hz | ||
| X2 | Fhawser1 | 5 Hz | Fhawser2 |
| X3 | Wind Speed Signal | 1 Hz | BMmasts |
| Torque | 1 Hz | ||
| Platform Pitch | 10 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
del Pozo Gonzalez, H.; Kallinger, M.D.; Yalcin, T.; Rapha, J.I.; Domínguez-García, J.L. Design of Virtual Sensors for a Pyramidal Weathervaning Floating Wind Turbine. J. Mar. Sci. Eng. 2025, 13, 1411. https://doi.org/10.3390/jmse13081411
del Pozo Gonzalez H, Kallinger MD, Yalcin T, Rapha JI, Domínguez-García JL. Design of Virtual Sensors for a Pyramidal Weathervaning Floating Wind Turbine. Journal of Marine Science and Engineering. 2025; 13(8):1411. https://doi.org/10.3390/jmse13081411
Chicago/Turabian Styledel Pozo Gonzalez, Hector, Magnus Daniel Kallinger, Tolga Yalcin, José Ignacio Rapha, and Jose Luis Domínguez-García. 2025. "Design of Virtual Sensors for a Pyramidal Weathervaning Floating Wind Turbine" Journal of Marine Science and Engineering 13, no. 8: 1411. https://doi.org/10.3390/jmse13081411
APA Styledel Pozo Gonzalez, H., Kallinger, M. D., Yalcin, T., Rapha, J. I., & Domínguez-García, J. L. (2025). Design of Virtual Sensors for a Pyramidal Weathervaning Floating Wind Turbine. Journal of Marine Science and Engineering, 13(8), 1411. https://doi.org/10.3390/jmse13081411








