Recent Developments in the Nonlinear Hydroelastic Modeling of Sea Ice Interaction with Marine Structures
Abstract
1. Introduction
2. Solutions for Sea Ice–Structure Interaction Problems
2.1. The Governing Analytical Solution in the Fluid Domain
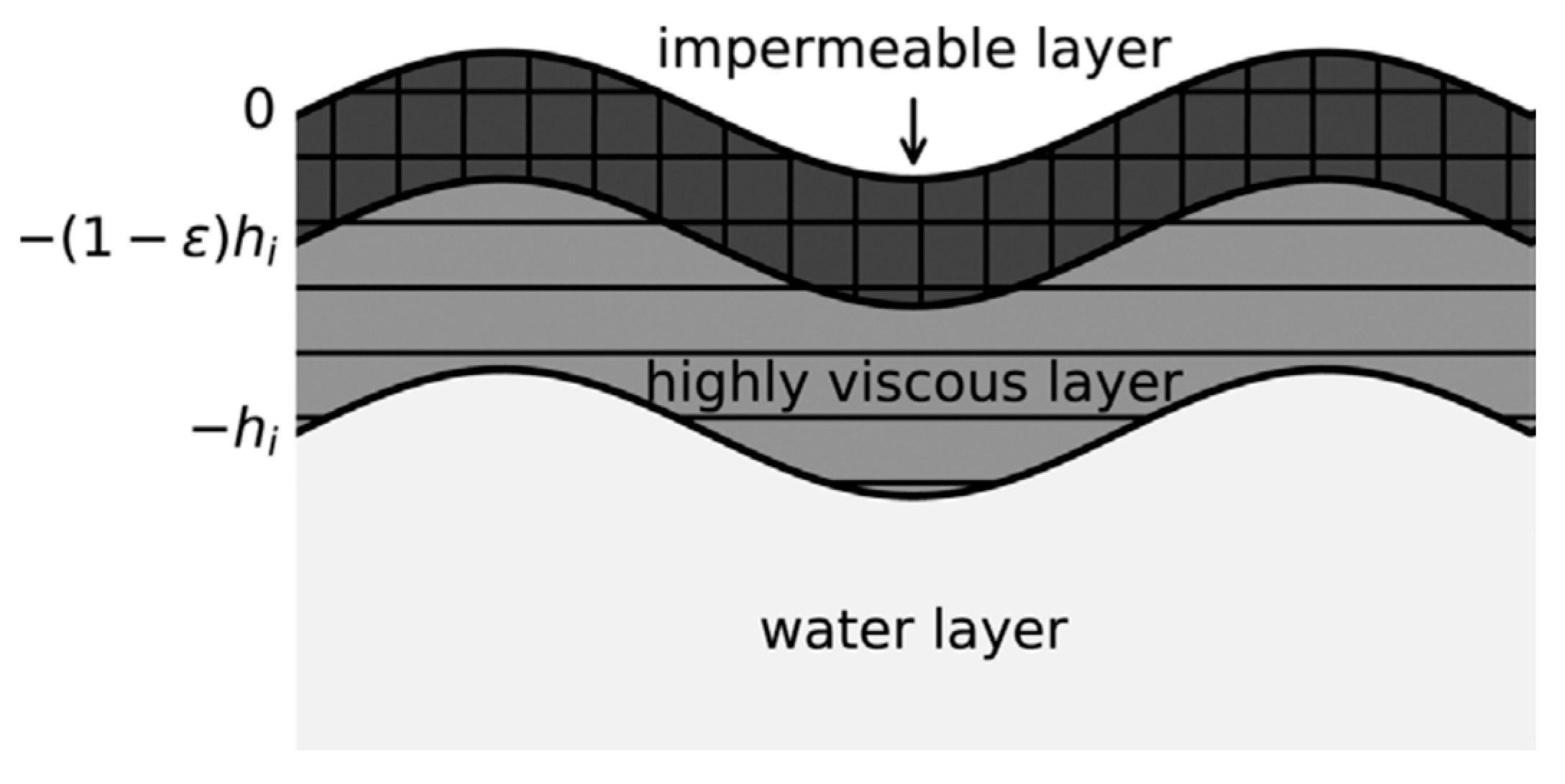
2.2. Fluid–Ice Interaction
2.3. Ice–Structure Interaction
2.4. Experiments
2.5. Numerical Models
3. Conclusions
- More extensive and systematic full-scale measurements, which are crucial to rigorously validate numerical models and experimental findings, bridging the gap between theoretical predictions and real-world performance.
- Development and integration of more sophisticated ice constitutive models that accurately represent the complex failure mechanisms (crushing, bending, shearing) and rheological properties of ice under various strain rates and temperatures.
- Further refinement of fully coupled fluid–ice interaction models to better capture the dynamic interplay between the ship, surrounding water, and ice, including the effects of propeller–ice interaction and maneuvering in ice. Further, incorporating uncertainty quantification methods into numerical simulations to account for the inherent variability in ice properties and environmental conditions provides more robust predictions.
- Investigating underwater ice-boundary data and exploring the application of AI and machine learning techniques for real-time prediction of ice resistance, optimization of ship navigation in ice, and analysis of large datasets from full-scale models. On the other hand, developing more standardized methodologies for both model tests and numerical simulations would ensure comparability and reproducibility of results across different research groups.
- Investigating oil spills in iced water in the Arctic region, which can be considered as one of the challenges for marine transport and offshore activities due to the smoothness of the ice sheet, which is non-symmetric between the top of the ice (smooth) and the bottom underwater interface (low smoothness). Also, oil-polluted ice contains pollution along the vertical, and it indicates that ice could be a non-continuous material with vertical lattice.
- Ensuring consistency between the models and experiments in this review; we suggest using satellite observations of ship wakes in ice to validate research findings against real-world data.
- Moving towards multi-physics and multi-scale modeling approaches that can seamlessly integrate different phenomena (e.g., structural response and ice mechanics) at various scales. Translating research findings into practical tools that can assist ship operators in making informed decisions for safe and efficient navigation in ice-covered waters, including route optimization and speed management.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BIM | Boundary Integral Method |
| BIEM | Boundary Integral Equation Method |
| CFD | Computational Fluid Dynamics |
| DEM | Discrete Element Method |
| NDEM | Non-Smooth Discrete Element Method |
| FEM | Finite Element Method |
| IWSI | Ice–Water–Structure Interaction |
| LBM | Lattice Boltzmann Method |
| MIVET | Model Ice of Virtual Equivalent Thickness |
| RAO | Response Amplitude Operator |
| RPCA | Robust Principal Component Analysis |
| SPH | Smoothed Particle Hydrodynamics |
| VOF | Volume of Fluid |
| ACV | Air-Cushioned Vehicles |
| AI | Artificial Intelligence |
| FLI | Crushing Frequency Lock-in |
| CBR | Continuous Brittle |
| IC | Intermittent Crushing |
References
- Fediuk, R.; Uvarova, T.; Zverev, A.; Smoliakov, A.; Cherkasov, A. Natural effects on offshore structures in the Arctic. IOP Conf. Ser. Mater. Sci. Eng. 2018, 463, 032063. [Google Scholar] [CrossRef]
- Ehlers, S.; Cheng, F.; Jordaan, I.; Kuehnlein, W.; Kujala, P.; Luo, Y.; Freeman, R.; Riska, K.; Sirkar, J.; Oh, Y.-T.; et al. Towards mission-based structural design for arctic regions. Ship Technol. Res. 2017, 64, 115–128. [Google Scholar] [CrossRef]
- Ni, B.; Wang, Y.; Xu, Y.; Chen, W. Numerical Simulation of Ship Collision with Rafted Ice Based on Cohesive Element Method. J. Mar. Sci. Appl. 2024, 23, 127–136. [Google Scholar] [CrossRef]
- Riska, K.; Bridges, R. Limit state design and methodologies in ice class rules for ships and standards for Arctic offshore structures. Mar. Struct. 2019, 63, 462–479. [Google Scholar] [CrossRef]
- Daiyan, H.; Sand, B. Numerical Simulation of the Ice-Structure Interaction in LS-DYNA. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Tuhkuri, J.; Polojärvi, A. A review of discrete element simulation of ice–structure interaction. Philos. Trans. R. Soc. A 2018, 376, 20170335. [Google Scholar] [CrossRef] [PubMed]
- Tsuprik, V.G.; Zanegin, V.G.; Kim, L.V. Mathematical Modelling of Ice-Structure Interaction. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 272, p. 022063. [Google Scholar]
- Yang, B.; Sun, Z.; Zhang, G.; Wang, Q.; Zong, Z.; Li, Z. Numerical estimation of ship resistance in broken ice and investigation on the effect of floe geometry. Mar. Struct. 2021, 75, 102867. [Google Scholar] [CrossRef]
- Huang, L.; Tuhkuri, J.; Igrec, B.; Li, M.; Stagonas, D.; Toffoli, A.; Cardiff, P.; Thomas, G. Ship resistance when operating in floating ice floes: A combined CFD&DEM approach. Mar. Struct. 2020, 74, 102817. [Google Scholar] [CrossRef]
- Duan, K.; Huang, F.; Zhang, S.; Shu, Y.; Dong, S.; Liu, M. Prediction of ship following behavior in ice-covered waters in the Northern Sea Route based on hybrid theory and data-driven approach. Ocean Eng. 2024, 296, 116939. [Google Scholar] [CrossRef]
- Luo, J.M.; Li, X.H.; Yang, Z.W.; Yuan, Y.C. Uncertainty-based assessment of ice loads for ship navigation in ice floe environments. Ocean Eng. 2025, 337, 121904. [Google Scholar] [CrossRef]
- Xue, Y.; Zhong, K.; Ni, B.Y.; Li, Z.; Bergstrom, M.; Ringsberg, J.W.; Huang, L. A combined experimental and numerical approach to predict ship resistance and power demand in broken ice. Ocean Eng. 2024, 292, 116476. [Google Scholar] [CrossRef]
- Shu, Y.; Cui, H.; Song, L.; Gan, L.; Xu, S.; Wu, J.; Zheng, C. Influence of sea ice on ship routes and speed along the Arctic Northeast Passage. Ocean Coast. Manag. 2024, 256, 107320. [Google Scholar] [CrossRef]
- Jiang, J.; He, S.; Jiang, H.; Chen, X.; Ji, S. Research on Sea Ice and Local Ice Load Monitoring System for Polar Cargo Vessels. J. Mar. Sci. Eng. 2025, 13, 808. [Google Scholar] [CrossRef]
- Xu, P.; Chen, B.; Guo, Y.; Wang, H. Numerical Simulation Study on Ice–Water–Ship Interaction Based on FEM-SPH Adaptive Coupling Algorithm. Water 2024, 16, 3249. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, J.; Ji, S.; Tian, Y. Experimental study on the resistance of a transport ship navigating in level ice. J. Mar. Sci. Appl. 2016, 15, 105–111. [Google Scholar] [CrossRef]
- Huang, Y.; Li, W.; Wang, Y.; Wu, B. Experiments on the resistance of a large transport vessel navigating in the Arctic region in pack ice conditions. J. Mar. Sci. Appl. 2016, 15, 269–274. [Google Scholar] [CrossRef]
- Zhu, L.; Xue, Y.; Guo, R.; Zan, Y.; Lu, Y.; Zhang, Y. A Multi-objective Optimization Method for Resistance Performance of an Icebreaker Bow Based on Fully Parameterized Modeling. J. Mar. Sci. Appl. 2025. [Google Scholar] [CrossRef]
- Available online: https://au.pinterest.com/pin/310959549242558457/ (accessed on 25 May 2025).
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Daley, C.; Tuhkuri, J.; Riska, K. The role of discrete failures in local ice loads. Cold Reg. Sci. Technol. 1998, 27, 197–211. [Google Scholar] [CrossRef]
- Ranta, J.; Polojärvi, A.; Tuhkuri, J. Limit mechanisms for ice loads on inclined structures: Buckling. Cold Reg. Sci. Technol. 2018, 147, 34–44. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, L.; Li, S.; Li, Y. A Multi-Yield-Surface Plasticity State-Based Peridynamics Model and its Applications to Simulations of Ice-Structure Interactions. J. Mar. Sci. Appl. 2023, 22, 395–410. [Google Scholar] [CrossRef]
- Shi, C.; Hu, Z.; Luo, Y. An elastic-plastic iceberg material model considering temperature gradient effects and its application to numerical study. J. Mar. Sci. Appl. 2016, 15, 370–375. [Google Scholar] [CrossRef]
- Sayeed, T.; Colbourne, B.; Quinton, B.; Molyneux, D.; Peng, H.; Spencer, D. A review of iceberg and bergy bit hydrodynamic interaction with offshore structures. Cold Reg. Sci. Technol. 2017, 135, 34–50. [Google Scholar] [CrossRef]
- Keijdener, C.; Hendrikse, H.; Metrikine, A. The effect of hydrodynamics on the bending failure of level ice. Cold Reg. Sci. Technol. 2018, 153, 106–119. [Google Scholar] [CrossRef]
- Sandven, S.; Spreen, G.; Heygster, G.; Ardhuin, F.G.; Farrell, S.L.; Dierking, W.; Allard, R.A. Sea Ice Remote Sensing—Recent Developments in Methods and Climate Data Sets. Surv. Geophy. 2023, 44, 1653–1689. [Google Scholar] [CrossRef]
- Itkin, P. Novel methods to study sea ice deformation, linear kinematic features and coherent dynamic clusters from imaging remote sensing data. Cryosphere 2025, 19, 1135–1151. [Google Scholar] [CrossRef]
- Qiu, W.; Li, K.; Zhao, X. Study on the deformation and cracking characteristics of bridge-crossing reservoir ice sheet in cold regions. Cold Reg. Sci. Technol. 2025, 237, 104517. [Google Scholar] [CrossRef]
- Hutchings, J.K.; Roberts, A.; Geiger, C.A.; Menge, J.R. Spatial and temporal characterization of sea-ice deformation. Ann. Glaciol. 2011, 52, 360–368. [Google Scholar] [CrossRef]
- Yang, B.; Wu, J.; Sun, Z.; Yang, B.; Zhang, G. Study on the ice-water interaction problem based on MPS-NDEM coupling model. Eng. Anal. Bound. Elem. 2025, 170, 106055. [Google Scholar] [CrossRef]
- LSTC. LS-DYNA User’s Manual, Version 971 R5; Livermore Soft Technology Corp.: Livermore, CA, USA, 2011. [Google Scholar]
- Siemens PLM Software, Simcenter STAR-CCM+® Documentation Version; Siemens Digital Industries Software: Plano, TX, USA, 2019.
- Chakraborty, R.; Mandal, B.N. Water wave scattering by a nearly circular cylinder submerged beneath an ice-cover. J. Mar. Sci. Appl. 2015, 14, 69–75. [Google Scholar] [CrossRef]
- Bhattacharjee, J.; Guedes Soares, C. Flexural gravity wave over a floating ice sheet near a vertical wall. J. Eng. Math. 2012, 75, 29–48. [Google Scholar] [CrossRef]
- Bergan, P.G.; Cammaert, G.; Skeie, G.; Tharigopula, V. On the potential of computational methods and numerical simulation in ice mechanics. IOP Conf. Ser. Mat. Sci. Eng. 2010, 10, 012102. [Google Scholar] [CrossRef]
- Sand, B. Nonlinear Finite Element Simulations of Ice Forces on Offshore Structures. Ph.D. Thesis, Luleå University of Technology, Luleå, Sweden, 2008. [Google Scholar]
- Kaldjian, M.J. Ice-sheet failure against inclined and conical surfaces. Comput. Struct. 1987, 26, 145–152. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. 3D hydroelastic modelling of fluid–structure interactions of porous flexible structures. J. Fluid Struct. 2022, 112, 103588. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. Hydroelastic Response to Oblique Wave Incidence on a Floating Plate with a Submerged Perforated Base. J. Mar. Sci. Eng. 2022, 10, 1205. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Islam, H.; Guedes Soares, C. Boussinesq Model and CFD Simulations of Non-Linear Wave Diffraction by a Floating Vertical Cylinder. J. Mar. Sci. Eng. 2020, 8, 575. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. Surface Gravity Wave Interaction with a Horizontal Flexible Floating Plate and Submerged Flexible Porous Plate. Ocean Eng. 2021, 237, 109621. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. Hydroelastic behaviour of a submerged horizontal flexible porous structure in three-dimensions. J. Fluid Struct. 2021, 104, 103319. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C.; Meylan, M.H. Three-Dimensional and Oblique Wave-Current Interaction with a Floating Elastic Plate Based on an Analytical Approach. Symmetry 2025, 17, 831. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C.; Sahoo, T. Oblique wave diffraction by a flexible floating structure in the presence of a submerged flexible structure. Geophys. Astrophys. Fluid Dyn. 2014, 108, 615–638. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. Wave-current interaction with a deformable bottom in a three-dimensional channel. Phys. Fluids 2025, 37, 057109. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Amouzadrad, P.; da Silva Bispo, I.B.; Guedes Soares, C. Hydrodynamic Response to Current and Wind on a Large Floating Interconnected Structure. J. Mar. Sci. Eng. 2025, 13, 63. [Google Scholar] [CrossRef]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Numerical Analysis of the effect of current and wind on the dynamics of large floating flexible platform. In Advances in Maritime Technology and Engineering; Soares, C.G., Santos, T.A., Eds.; Taylor & Francis: London, UK, 2024; pp. 341–348. [Google Scholar]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Numerical simulations on the dynamic analysis of a large articulated floating circular platform. In Innovations in the Analysis and Design of Mar. Structures; Garbatov, Y., Soares, C.G., Eds.; Taylor & Francis: London, UK, 2025; pp. 461–466. [Google Scholar]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Effect of current on the hydroelastic behaviour of floating flexible circular structure. Appl. Ocean Res. 2025, 154, 104387. [Google Scholar] [CrossRef]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Hydroelastic Response to the Effect of Current Loads on Floating Flexible Offshore Platform. J. Mar. Sci. Eng. 2023, 11, 437. [Google Scholar] [CrossRef]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Current loads to the hydroelastic response of large interconnected floating platform using analytical approach. In Innovations in the Analysis and Design of Mar. Structures; Garbatov, Y., Soares, C.G., Eds.; Taylor & Francis: London, UK, 2025; pp. 453–460. [Google Scholar]
- Bispo, I.B.S.; Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Motion analysis of a floating horizontal set of interconnected plates based on computer vision target tracking technique. In Advances in the Analysis and Design of Marine Structures; Ringsberg, J.W., Guedes Soares, C., Eds.; Taylor and Francis: London, UK, 2023; pp. 153–159. [Google Scholar]
- Von Bock und Polach, R.; Molyneux, D. Model Ice: A Review of its Capacity and Identification of Knowledge Gaps. In Volume 8: Polar and Arctic Sciences and Technology; Petroleum Technology. Proceedings of the ASME 2017 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; V008T07A017; ASME: New York, NY, USA, 2017. [Google Scholar]
- Zhao, X.; Shen, H.H.; Cheng, S. Modeling ocean wave propagation under sea ice covers. Acta Mech. Sin. 2015, 31, 1–15. [Google Scholar] [CrossRef]
- Ni, B.Y.; Han, D.F.; Di, S.C.; Xue, Y.Z. On the Development of Ice-Water-Structure Interaction. J. Hydrodyn. 2020, 32, 629–652. [Google Scholar] [CrossRef]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Review of recent developments on the hydroelastic response and gap resonance of multi-body floating structures. Ocean Eng. 2024, 313, 119398. [Google Scholar] [CrossRef]
- Amouzadrad, P.; Mohapatra, S.C.; Guedes Soares, C. Review on Sensitivity and Uncertainty Analysis of Hydrodynamic and Hydroelastic Response of Floating Offshore Structures. J. Mar. Sci. Eng. 2025, 13, 1015. [Google Scholar] [CrossRef]
- Kellner, L.; Herrnring, H.; Ring, M. Review of ice load standards and comparison with measurements. In Proceedings of the 36th International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Li, F.; Huang, L. A Review of Computational Simulation Methods for a Ship Advancing in Broken Ice. J. Mar. Sci. Eng. 2022, 10, 165. [Google Scholar] [CrossRef]
- Islam, M.; Mills, J.; Gash, R.; Pearson, W. A literature survey of broken ice-structure interaction modelling methods for ships and offshore platforms. Ocean Eng. 2021, 221, 108527. [Google Scholar] [CrossRef]
- Ni, B.; Xiong, H.; Han, D.; Zeng, L.; Sun, L.; Tan, H. A Review of Ice Deformation and Breaking Under Flexural-Gravity Waves Induced by Moving Loads. J. Mar. Sci. Appl. 2025, 24, 35–52. [Google Scholar] [CrossRef]
- Martin, B.; Ove, E.S.; Sören, E. A simulation-based probabilistic design method for arctic sea transport systems. J. Mar. Sci. Appl. 2016, 15, 349–369. [Google Scholar] [CrossRef]
- Thomson, J.; Ackley, S.; Girard-Ardhuin, F.; Ardhuin, F.; Babanin, A.; Boutin, G.; Brozena, J.; Cheng, S.; Collins, C.; Doble, M.; et al. Overview of the Arctic Sea State and Boundary Layer Physics Program. J. Geophys. Res. Ocean. 2018, 123, 8674–8687. [Google Scholar] [CrossRef]
- Ryan, C.; Huang, L.; Li, Z.; Ringsberg, J.W.; Thomas, G. An Arctic ship performance model for sea routes in ice-infested waters. Appl. Ocean Res. 2021, 117, 102950. [Google Scholar] [CrossRef]
- Long, X.; Liu, S.; Ji, S. Discrete element modelling of relationship between ice breaking length and ice load on conical structure. Ocean Eng. 2020, 201, 107152. [Google Scholar] [CrossRef]
- Hegarty, G.M.; Squire, V.A. A boundary-integral method for the interaction of large-amplitude ocean waves with a compliant floating raft such as a sea-ice floe. J. Eng. Math. 2008, 62, 355–372. [Google Scholar] [CrossRef]
- Părău, E.I.; Vanden-Broeck, J.M. Three-dimensional waves beneath an ice sheet due to a steadily moving pressure. Philos. Trans. R. Soc. 2011, 369, 2973–2988. [Google Scholar] [CrossRef] [PubMed]
- Vanden-Broeck, J.M.; Părău, E.I. Two-dimensional generalized solitary waves and periodic waves under an ice sheet. Philos. Trans. R. Soc. 2011, 369, 2957–2972. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Jiang, D.; Wu, T.; Guo, C.; Wang, C.; Deng, R.; Dai, S. Numerical simulation of an ice-strengthened bulk carrier in brash ice channel. Ocean Eng. 2020, 196, 106830. [Google Scholar] [CrossRef]
- Norouzi, H.R.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; John Wiley & Sons: New York, NK, USA, 2016. [Google Scholar]
- Kämäräinen, J. Theoretical Investigation on the Effect of Fluid Flow Between the Hull of a Ship and Ice Floes on Ice Resistance in Level Ice; Helsinki University of Technology: Espoo, Finland, 2007. [Google Scholar]
- Wang, J.; Wan, D. Application progress of computational fluid dynamic techniques for complex viscous flows in ship and ocean engineering. J. Mar. Sci. Appl. 2020, 19, 1–16. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Cundall, P.; Strack, O. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and non-spherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Sommerfeld, M. Theoretical and Experimental Modelling of Particulate Flows; Technical Report Lecture Series; Von Karman Institute for Fluid Dynamics: Saint-Geneva-Rode, Belgium, 2000; Volume 6, pp. 20–23. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Ni, B.Y.; Huang, Q.; Chen, W.S.; Xue, Y. Numerical simulation of ice load of a ship turning in level ice considering fluid effects. Chin. J. Ship Res. 2020, 15, 1–7. [Google Scholar]
- Jang, H.S.; Hwang, S.Y.; Lee, J.H. Experimental Evaluation and Validation of Pressure Distributions in Ice–Structure Collisions Using a Pendulum Apparatus. J. Mar. Sci. Eng. 2023, 11, 1761. [Google Scholar] [CrossRef]
- Hendrikse, H.; Hammer, T.C.; van den Berg, M.; Willems, T.; Owen, C.C.; van Beek, K.; Ebben, N.J.J.; Puolakka, O.; Polojärvi, A. Experimental data from ice basin tests with vertically sided cylindrical structures. Data Brief 2022, 41, 107877. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, M.; Owen, C.C.; Hendrikse, H. Experimental study on ice-structure interaction phenomena of vertically sided structures. Cold Reg. Sci. Technol. 2022, 201, 103628. [Google Scholar] [CrossRef]
- Von Bock und Polach, F.; Klein, M.; Hartmann, M. A New Model Ice for Wave-Ice Interaction. Water 2021, 13, 3397. [Google Scholar] [CrossRef]
- Klein, M.; Hartmann, M.; von Bock und Polach, F. Note on the Application of Transient Wave Packets for Wave–Ice Interaction Experiments. Water 2021, 13, 1699. [Google Scholar] [CrossRef]
- Yiew, L.J.; Parra, S.M.; Wang, D.; Sree, D.K.K.; Babanin, A.V.; Law, A.W.K. Wave attenuation and dispersion due to floating ice covers. Appl. Ocean Res. 2019, 87, 256–263. [Google Scholar] [CrossRef]
- Dolatshah, A.; Nelli, F.; Bennetts, L.G.; Alberello, A.; Meylan, M.H.; Monty, J.P.; Toffoli, A. Hydroelastic interactions between water waves and floating freshwater ice. Phys. Fluids 2018, 30, 091702. [Google Scholar] [CrossRef]
- Li, H.; Gedikli, E.D.; Lubbad, R.; Nord, T.S. Laboratory study of wave-induced ice-ice collisions using robust principal component analysis and sensor fusion. Cold Reg. Sci. Technol. 2020, 172, 103010. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Choi, K.; Kim, H.S. Investigation of ship resistance characteristics under pack ice conditions. Ocean Eng. 2021, 219, 108264. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Y. Investigations on the ship-ice impact: Part 1. Experimental methodologies. Mar. Struct. 2020, 72, 102772. [Google Scholar] [CrossRef]
- Zong, Z.; Yang, B.; Sun, Z.; Zhang, G. Experimental study of ship resistance in artificial ice floes. Cold Reg. Sci. Technol. 2020, 176, 103102. [Google Scholar] [CrossRef]
- Huang, L.; Ren, K.; Li, M.; Tuković, Ž.; Cardiff, P.; Thomas, G. Fluid-structure interaction of a large ice sheet in waves. Ocean Eng. 2019, 182, 102–111. [Google Scholar] [CrossRef]
- Hartmann, M.C.N.; Onorato, M.; De Vita, F.; Clauss, G.; Ehlers, S.; von Bock und Polach, F.; Schmitz, L.; Hoffmann, N.; Klein, M. Hydroelastic potential flow solver suited for nonlinear wave dynamics in ice-covered waters. Ocean Eng. 2022, 259, 111756. [Google Scholar] [CrossRef]
- Sutherland, G.; Rabault, J.; Christensen, K.H.; Jensen, A. A two-layer model for wave dissipation in sea ice. Appl. Ocean Res. 2019, 88, 111–118. [Google Scholar] [CrossRef]
- Tavakoli, S.; Huang, L.; Azhari, F.; Babanin, A.V. Viscoelastic Wave–Ice Interactions: A Computational Fluid–Solid Dynamic Approach. J. Mar. Sci. Eng. 2022, 10, 1220. [Google Scholar] [CrossRef]
- Xue, Y.Z.; Zeng, L.D.; Ni, B.Y.; Korobkin, A.A.; Khabakhpasheva, T.I. Hydroelastic response of an ice sheet with a lead to a moving load. Phys. Fluids 2021, 33, 037109. [Google Scholar] [CrossRef]
- Khabakhpasheva, T.I.; Korobkin, A.A. Blunt body impact onto viscoelastic floating ice plate with a soft layer on its upper surface. Phys. Fluids 2021, 33, 062105. [Google Scholar] [CrossRef]
- Huang, L.; Thomas, G. Simulation of Wave Interaction With a Circular Ice Floe. J. Offshore Mech. Arct. Eng. 2019, 141, 041302. [Google Scholar] [CrossRef]
- Bian, G.F. Study on the Interaction Process of Sea-Ice and Marine Structures Based on SPH-FEM Coupling Algorithm. Master’s Thesis, Harbin Engineering University, Harbin, China, 2019. [Google Scholar]
- Gui, H.B.; Hu, Z.K. SPH-based numerical simulation of ship propeller under ice impact. J. Ship Mech. 2018, 22, 425–433. [Google Scholar]
- Zhang, N.; Zheng, X.; Ma, Q.; Hu, Z. A numerical study on ice failure process and ice-ship interactions by smoothed particle hydrodynamics. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 796–808. [Google Scholar] [CrossRef]
- Wang, C.; Feng, Z.; Li, X.; Peng, L. Analysis of the ice resistance and ice response of ships sailing in the crushed ice area. Chin. Ship Res. 2018, 13, 73–78. [Google Scholar]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and numerical investigation on self-propulsion performance of polar merchant ship in brash ice channel. Ocean Eng. 2023, 269, 113424. [Google Scholar] [CrossRef]
- Liu, L.; Ji, S. Ice load on floating structure simulated with dilated polyhedral discrete element method in broken ice field. Appl. Ocean Res. 2018, 75, 53–65. [Google Scholar] [CrossRef]
- Guo, W.; Zhao, Q.S.; Tian, Y.K.; Zhang, C.W. Research on total resistance of ice-going ship for different floe ice distributions based on virtual mass method. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 957–966. [Google Scholar] [CrossRef]
- Tang, X.; Zou, M.; Zou, Z.; Li, Z.; Zou, L. A parametric study on the ice resistance of a ship sailing in pack ice based on CFD-DEM method. Ocean Eng. 2022, 265, 112563. [Google Scholar] [CrossRef]
- Zhong, K.; Ni, B.-Y.; Li, Z. Direct measurements and CFD simulations on ice-induced hull pressure of a ship in floe ice fields. Ocean Eng. 2023, 272, 113523. [Google Scholar] [CrossRef]
- Zou, M.; Tang, X.-J.; Zou, L.; Zou, Z.-J.; Zhang, X.-S. Numerical investigations of the restriction effects on a ship navigating in pack-ice channel. Ocean Eng. 2024, 305, 117968. [Google Scholar] [CrossRef]
- Janßen, C.F.; Mierke, D.; Rung, T. On the development of an efficient numerical ice tank for the simulation of fluid-ship-rigid-ice interactions on graphics processing units. Comput. Fluids 2017, 155, 22–32. [Google Scholar] [CrossRef]
- Guo, C.Y.; Zhang, Z.T.; Tian, T.P.; Li, X.-Y.; Zhao, D.-G. Numerical simulation on the resistance performance of ice-going container ship under brash ice conditions. China Ocean Eng. 2018, 32, 546–556. [Google Scholar] [CrossRef]
- Wang, C.; Hu, X.; Tian, T.; Guo, C.; Wang, C. Numerical simulation of ice loads on a ship in broken ice fields using an elastic ice model. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 414–427. [Google Scholar] [CrossRef]
- Song, Y.; Li, S.; Zhang, S. Peridynamic modeling and simulation of thermo-mechanical de-icing process with modified ice failure criterion. Def. Technol. 2021, 17, 15–35. [Google Scholar] [CrossRef]
- Liu, R.W.; Xue, Y.Z.; Lu, X.K.; Cheng, W.X. Simulation of ship navigation in ice rubble based on peridynamics. Ocean Eng. 2018, 148, 286–298. [Google Scholar] [CrossRef]
- Li, F.; Goerlandt, F.; Kujala, P. Numerical simulation of ship performance in level ice: A framework and a model. Appl. Ocean Res. 2020, 102, 102288. [Google Scholar] [CrossRef]
- Yang, B.; Sun, Z.; Zhang, G.; Yang, B.; Lubbad, R. Non-smooth discrete element method analysis of channel width’s effect on ice resistance in broken ice field. Ocean Eng. 2024, 313, 119419. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Zan, Y.; Lu, W.; Bai, X.; Guo, J. Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion. J. Mar. Sci. Technol. 2018, 23, 52–66. [Google Scholar] [CrossRef]
- Polić, D.; Ehlers, S.; Æsøy, V. Propeller torque load and propeller shaft torque response correlation during ice-propeller interaction. J. Mar. Sci. Appl. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Sazonov, K.; Kanevskii, G.; Klubnichkin, A.; Dobrodeev, A. Method to Determine the Propulsion Characteristics of a Ship Moving in Ice. J. Mar. Sci. Appl. 2025, 24, 532–541. [Google Scholar] [CrossRef]
- Zheng, X.; Tian, Z.; Xie, Z.; Zhang, N. Numerical Study of the Ice Breaking Resistance of the Icebreaker in the Yellow River Through Smoothed-Particle Hydrodynamics. J. Mar. Sci. Appl. 2022, 21, 1–14. [Google Scholar] [CrossRef]
- Li, F.; Suominen, M.; Kujala, P. Ship performance in ice channels narrower than ship beam: Model test and numerical investigation. Ocean Eng. 2021, 240, 109922. [Google Scholar] [CrossRef]
- Kim, J.; Yoon, D.H.; Choung, J. Numerical study of ship hydrodynamics on ice resistance during ice sheet breaking. Ocean Eng. 2024, 308, 118285. [Google Scholar] [CrossRef]
- Du, Y.; Sun, L.; Pang, F.; Li, H.; Gao, C. Experimental Research of Hull Vibration of a Full-Scale River Icebreaker. J. Mar. Sci. Appl. 2020, 19, 182–194. [Google Scholar] [CrossRef]
- Sazonov, K.; Dobrodeev, A. Ice resistance assessment for a large size vessel running in a narrow ice channel behind an icebreaker. J. Mar. Sci. Appl. 2021, 20, 446–455. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Y. Investigations on the ship-ice impact: Part 2. spatial and temporal variations of ice load. Ocean Eng. 2021, 240, 109686. [Google Scholar] [CrossRef]
- Hartmann, M.C.N.; von Bock und Polach, F.; Ehlers, S.; Hoffmann, N.; Onorato, M.; Klein, M. Investigation of Nonlinear Wave–Ice Interaction Using Parameter Study and Numerical Simulation. J. Offshore Mech. Arct. Eng. 2020, 142, 021601. [Google Scholar] [CrossRef]












| Methodologies | Descriptions | Applications | References |
|---|---|---|---|
| Smoothed Particle Hydrodynamics (SPH) | Meshless Lagrangian method that simulates ice mechanics and IWSI problems. | Ice–structure interaction, ice–water interaction, and IWSI. | [15,98,99,100] |
| Discrete Element Method (DEM) | Particle-based method that simulates ice dynamics and its interaction with structures. Coupled with CFD to consider water effects. | IWSI problems. | [9,66,70,101,102,103,104,105,106,107] |
| Lattice Boltzmann Method (LBM) | Mesoscopic method for simulating fluid motion. | Simulating interaction between fluid and multi-bodies in IWSI problems. | [108] |
| Finite Element Method (FEM) | Continuum mechanics problems are tackled using a sophisticated technique. This technique enables the simulation of complex, nonlinear wave processes. | Ice–structure interaction (with simplified models for water effects). | [79,92,109,110] |
| Boundary Integral Method (BIM) | 3D method to compute nonlinear wave interactions with an ice sheet. | The first and second-order hydrodynamic solutions for a floating body interacting with waves. | [67,68,95] |
| Computational Fluid Dynamics (CFD) | 3D model to solve the nonlinear Navier–Stokes equations. | Wave–ice interaction, capturing the elastic deformation of the ice sheet. | [91,97] |
| Peridynamics (PD) | Meshless method good at solving fracture problems. | Ice mechanics and ice–structure interaction. | [101,111,112] |
| Experimental Models | In situ tests and model tests. | IWSI problems. kinematics of sea ice. | [80,81,82,83,84,85,86,88,89,90,113] |
| Winkler–Kelvin–Voigt Model | A 1D model to simulate the counterforce of an ice floe to the rigid body impact. | Arctic sea ice nonlinear simulations. | [96] |
| Non-smooth Discrete Element Method (NDEM) | Nonlinear method to solve ship–ice interactions. | Ship resistance in broken ice conditions. | [8,31,114] |
| Key Parameters | Range/Scenarios | Key Findings | Modeling Approaches | Experimental Validation | References |
|---|---|---|---|---|---|
| Ice Thickness |
|
| FEM, CFD-DEM, NDEM, SPH | Ice tank tests using varying thicknesses | [83,88,89,90,113,115] |
| Ship Velocity |
|
| CFD-DEM, SPH, NDEM | Towing experiments, impact tests | [89,106,107,114] |
| Ship Resistance |
|
| DEM, NDEM, CFD-DEM | Resistance tests with synthetic/brash ice | [9,12,90,105,114] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohapatra, S.C.; Amouzadrad, P.; Guedes Soares, C. Recent Developments in the Nonlinear Hydroelastic Modeling of Sea Ice Interaction with Marine Structures. J. Mar. Sci. Eng. 2025, 13, 1410. https://doi.org/10.3390/jmse13081410
Mohapatra SC, Amouzadrad P, Guedes Soares C. Recent Developments in the Nonlinear Hydroelastic Modeling of Sea Ice Interaction with Marine Structures. Journal of Marine Science and Engineering. 2025; 13(8):1410. https://doi.org/10.3390/jmse13081410
Chicago/Turabian StyleMohapatra, Sarat Chandra, Pouria Amouzadrad, and C. Guedes Soares. 2025. "Recent Developments in the Nonlinear Hydroelastic Modeling of Sea Ice Interaction with Marine Structures" Journal of Marine Science and Engineering 13, no. 8: 1410. https://doi.org/10.3390/jmse13081410
APA StyleMohapatra, S. C., Amouzadrad, P., & Guedes Soares, C. (2025). Recent Developments in the Nonlinear Hydroelastic Modeling of Sea Ice Interaction with Marine Structures. Journal of Marine Science and Engineering, 13(8), 1410. https://doi.org/10.3390/jmse13081410








