A New Eco-Physical, Individual-Based Model of Humpback Whale (Megaptera novaeangliae, Borowski, 1781) Swimming and Diving
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Design Overview
- 1.
- The production of a muscular force .
- 2.
- Muscular contractions provoke the sinusoidal movement of the flukes.
- 3.
- A propulsive force is generated in the down phase of the sinusoidal fluke movement [4].
- 4.
- The propulsive force generates an acceleration that induces a forward movement.
2.2. Morphometric Description of Humpback Whale Individuals
| Symbol | Description | Units | a | b | Min. | Max. | Source |
|---|---|---|---|---|---|---|---|
| Body mass | kg | 1 | 1 | 1000 | 50,000 | This paper | |
| Body length | m | 0.41 | 1/3 | 4.1 | 15.0 | [41] | |
| Body surface | m2 | 0.05 | 2/3 | 5.0 | 67.0 | [42] | |
| Body volume | m3 | 9.7 × 10−4 | 1 | 0.97 | 47.6 | This paper | |
| Muscular mass | kg | 0.334 | 1 | 334 | 16,366 | [41] | |
| Total lung capacity | m3 | 68.6 × 10−6 | 1 | 0.07 | 3.36 | [43] | |
| Blood volume | m3 | 127.0 × 10−6 | 1 | 0.13 | 6.22 | [44] | |
| Length of the jaw | m | 89.9 × 10−3 | 1/3 | 0.9 | 3.3 | [39] | |
| Width of the head | m | 68.6 × 10−3 | 1/3 | 0.7 | 2.5 | [39] | |
| VPL | m | 195.7 × 10−3 | 1/3 | 2.0 | 7.2 | [39] |
2.3. Quantifying the Spatial Dynamics of Movement
2.4. Foraging Dynamics Simulated Through Water Engulfment and Flushing Processes
2.5. Oxygen Respiration and Energy Production
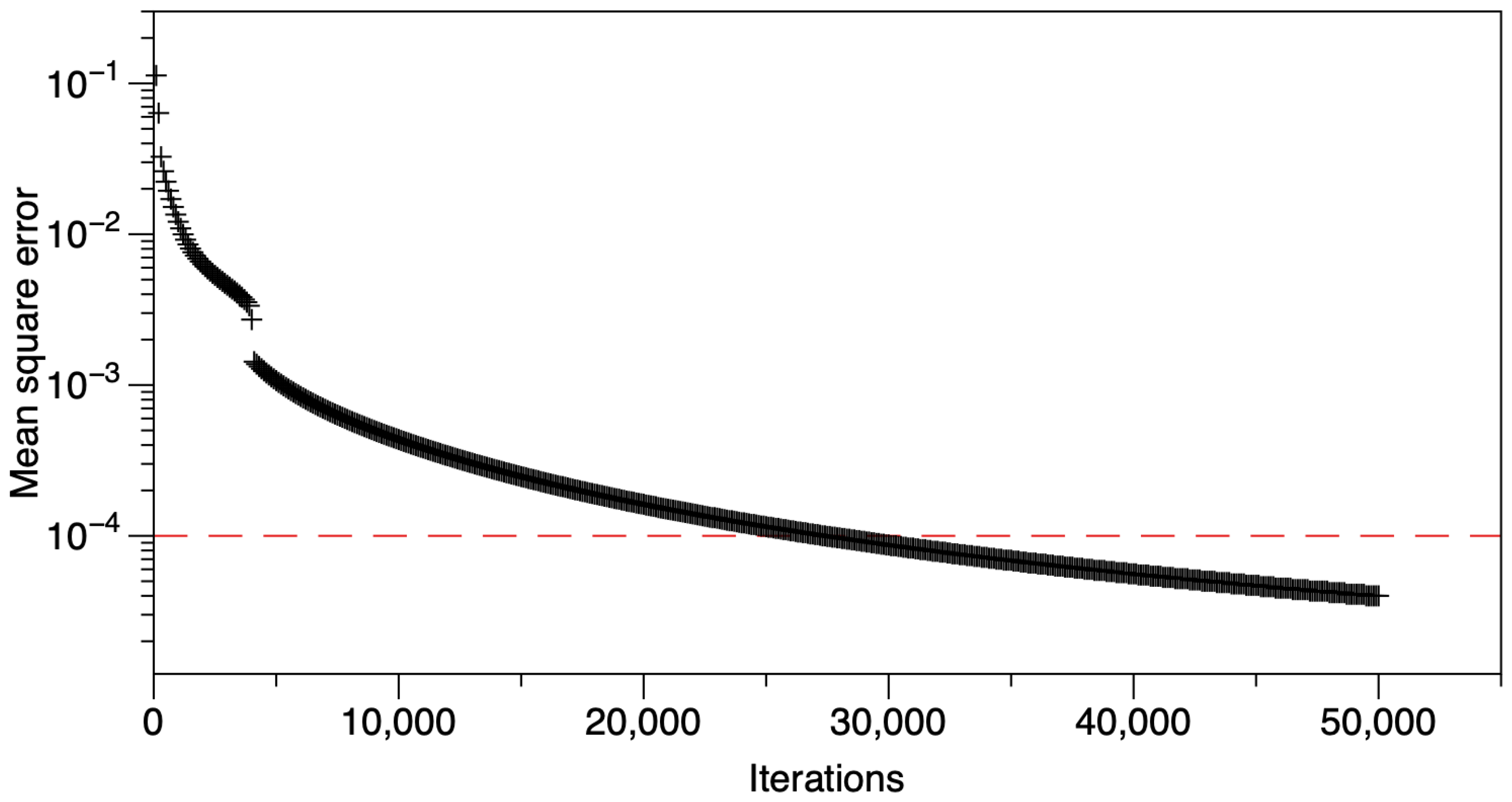
2.6. Perceptron Algorithm
3. Simulations
3.1. Swimming at the Surface
3.2. The Physiological Limits of Humpback Whale Dives
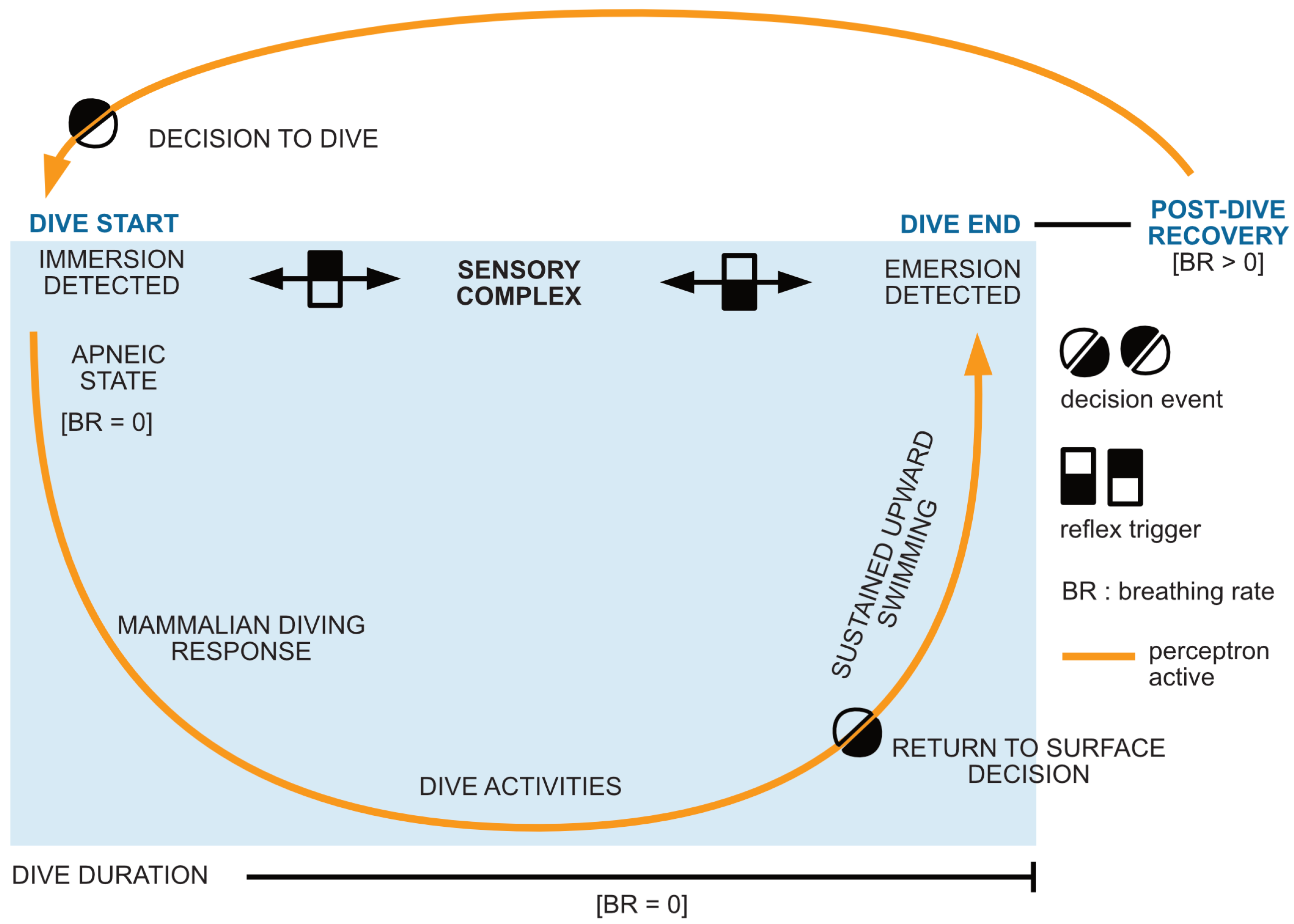
3.3. Diving Limitations, Perception and Decision Autonomy
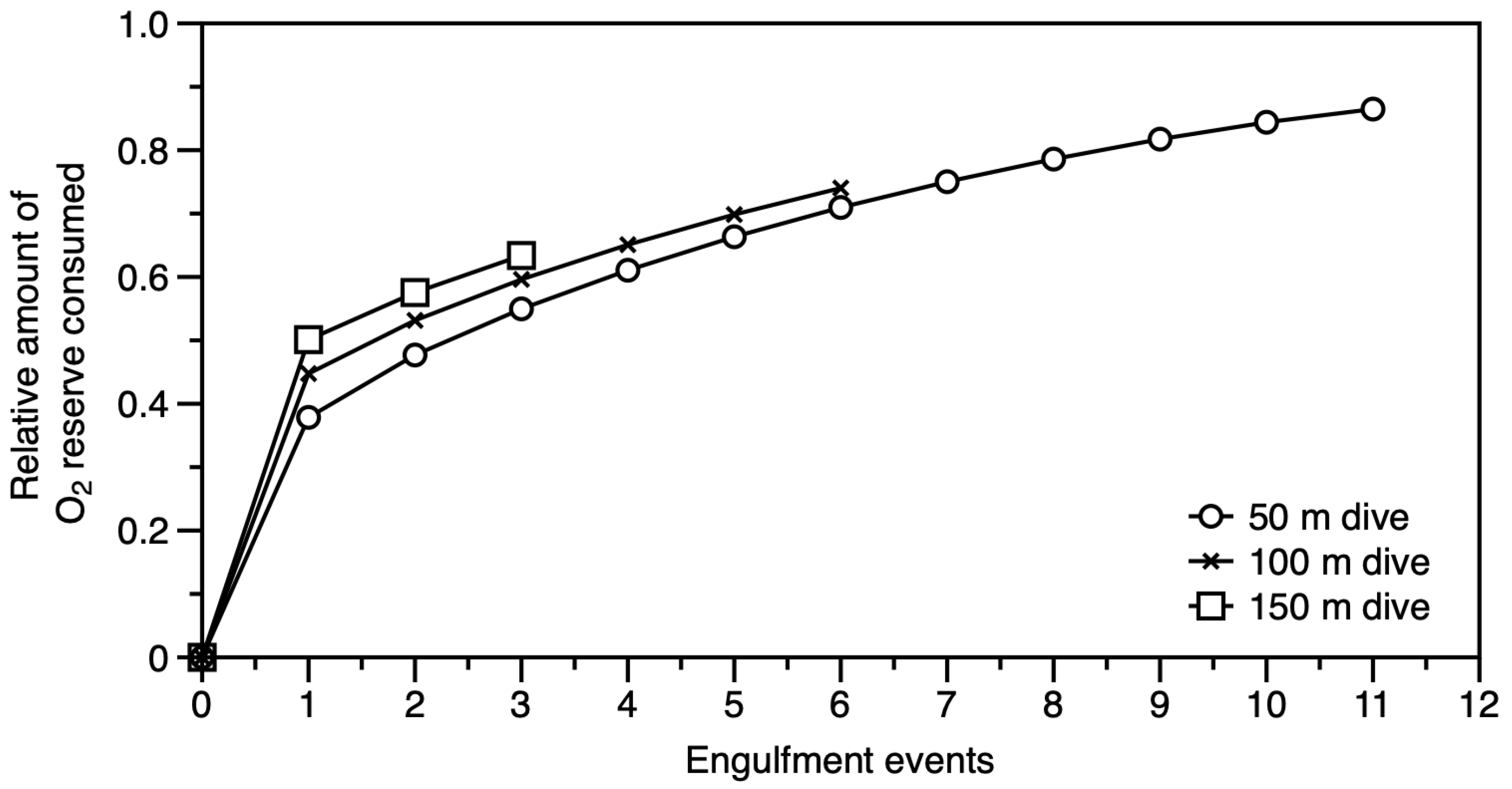
3.4. Exploring the Physiological Costs of Foraging Dives: Engulfment Events and Bubble Net Feeding
4. Discussion
4.1. The Definition of Whale Shape Has Consequences
- Estimates assembled from different publications give inconsistent results;
- Individual variability cannot be apprehended by an ‘average individual’ that possess averaged characteristics for all variables.
4.2. Major Challenges Remain for Quantifying Metabolic Processes
4.3. How Can We Identify Dive Limits Without Reliable Metabolic Information?
4.4. Resolving Behavioral Decisions During a Dive
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Symbols Used
| Symbol | Description | Unit | Eq. | Value |
|---|---|---|---|---|
| t, T | Time, Duration | s | ||
| Time spent at the surface | (time) | (1) | - | |
| , | Oxygen stored at time s, maximum | L(O2) | (1) | - |
| Oxygen accumulation rate | (time)−1 | (1) | - | |
| , | Oxygen consumption rate (traveling, foraging) | L(O2)·(time)−1 | (1) | - |
| , | Travel, foraging periods | (time) | (1) | - |
| Water volumic mass | kg·m−3 | (5) | 1030.0 | |
| Components of the water velocity vector (. is x, y, z) | m·s−1 | (9) | ||
| g | Gravity acceleration constant | m·s−2 | (16), (17) | 9.8067 |
| Whale length | m | (2) | ||
| Whale surface | m2 | (2) | ||
| Whale volume | m3 | (2) | ||
| , | Whale mass, whale muscular mass | kg | (2) | |
| Whale volumic mass | kg·m−3 | 1030.0 | ||
| Whale’s body fineness | dim.less | 5.0 | ||
| , | Total lung volume capacity, blood volume | L | ||
| , | Jaw length, head width | m | (3), (4) | |
| Length of the ventral pouch | m | (4) | ||
| , | Engulfment pouch surface, anterior, posterior | m2 | (4) | |
| , | Engulfment pouch volume, anterior, posterior | m3 | (3) | |
| Exponent to convert ellipsoid axis length to surface | dim.less | (4) | 1.605 | |
| Whale coordinates in the Cartesian system | m | (9) | ||
| Comp. of the whale acceleration vector (. is x, y, z) | m·s−2 | (7) | ||
| Comp. of the whale velocity vector (. is x, y, z) | m·s−1 | (8) | ||
| U | Norm of the whale velocity vector | m·s−1 | (5) | |
| , , | Muscular, propulsive forces and comp. (. is x, y, z) | N | (7) | |
| D, | Drag force and comp. (. is x, y, z) | N | (5), (7) | |
| , | Drag, added mass coefficients | dim.less | (5), (7) | |
| Volume compression factor | dim.less | (6) | [0,1[ | |
| , | Buoyancy force, whale’s weight | N | (7) | |
| Opening angle of the jaw | radian | (10) | ||
| , | Opening closing rates | radian.s−1 | (10) | |
| Prep., open., clos. time phase of engulfment | s | (11), (15) | ||
| Flushing time of engulfed water | s | (18) | ||
| , , | Surf., vol., mass of the engulfment | m2, m3, kg | (11), (14) | |
| , | Oxygen in the lung, capacity | L(O2) | (19), (22) | |
| , | Oxygen dissolved in blood, capacity | L(O2) | (19), (22) | |
| Oxygen bound with hemoglobin in blood | L(O2) | (19) | ||
| , | Oxygen in capillary vessels of muscles, capacity | L(O2) | (19), (22) | |
| Oxygen bound with myoglobin | L(O2) | (19) | ||
| , | Active, basal metabolic rates (oxygen) | L(O2).s−1 | (20), (19) | |
| Breathing rate | L(O2).s−1 | (19) | ||
| , | Transfer rates between L and B, and B and R | s−1 | (19) | |
| Oxygen consumption rate in muscles | s−1 | (19) | ||
| , | Exch. rates between free oxygen and hemoglobin | s−1 | (19) | |
| , | Exch. rates between free oxygen and myoglobin, | s−1 | (19) | |
| , , | Oxygen conversion factors for L, B, O | dim.less | (22) | |
| Efficiency coefficient | dim.less | (23) | 0.20 ∈ [0,1[ | |
| Total oxygen volume | L(O2) | (24) | ||
| , | Average and average optimal velocities | m.s−1 | (24) | |
| , , | Forward init. and at t, and past diving distances | s | (24) | |
| K, y | Constraint and constraint index | dim.less | (25) |
Appendix B. Detailed Results for Simulations Shown
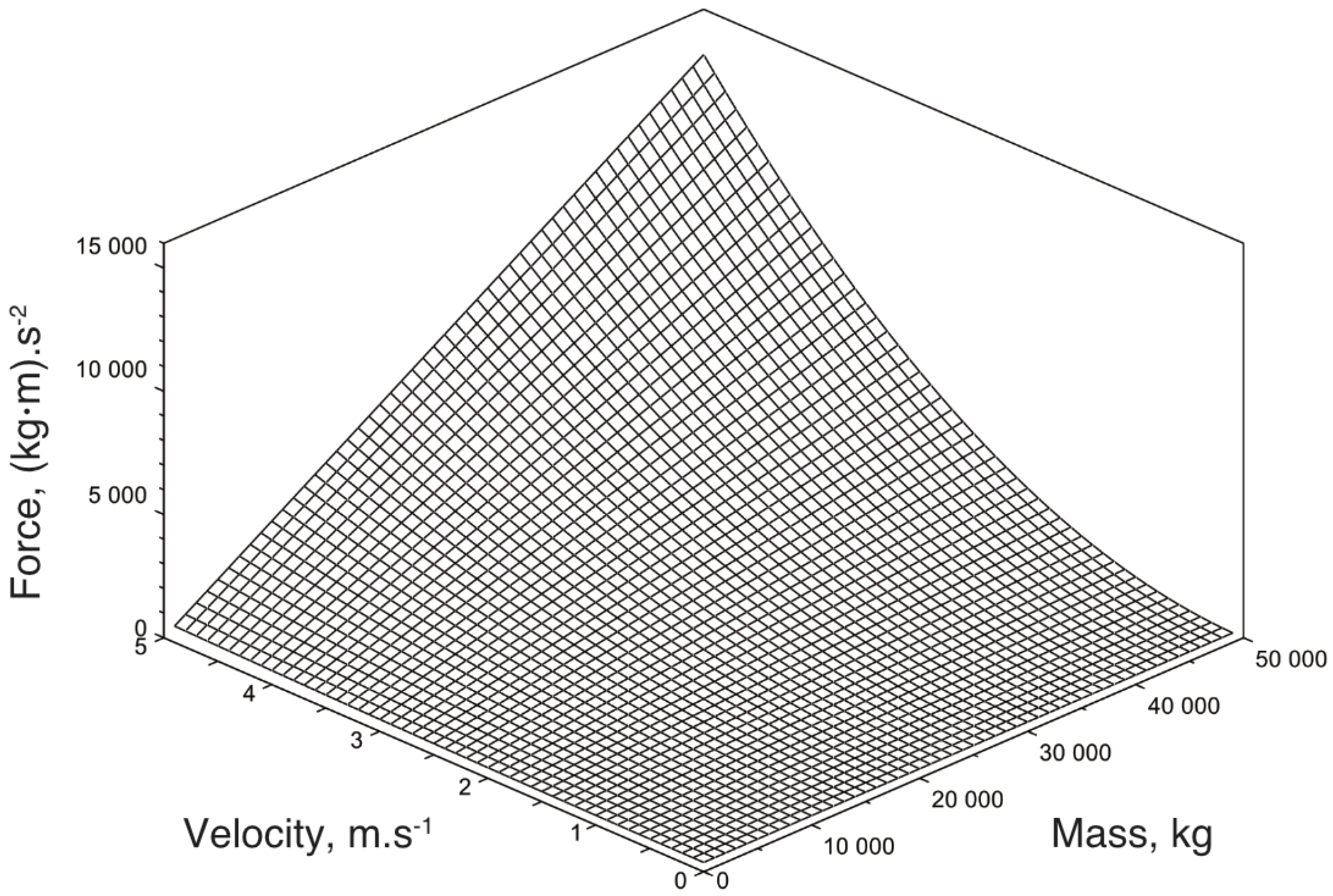
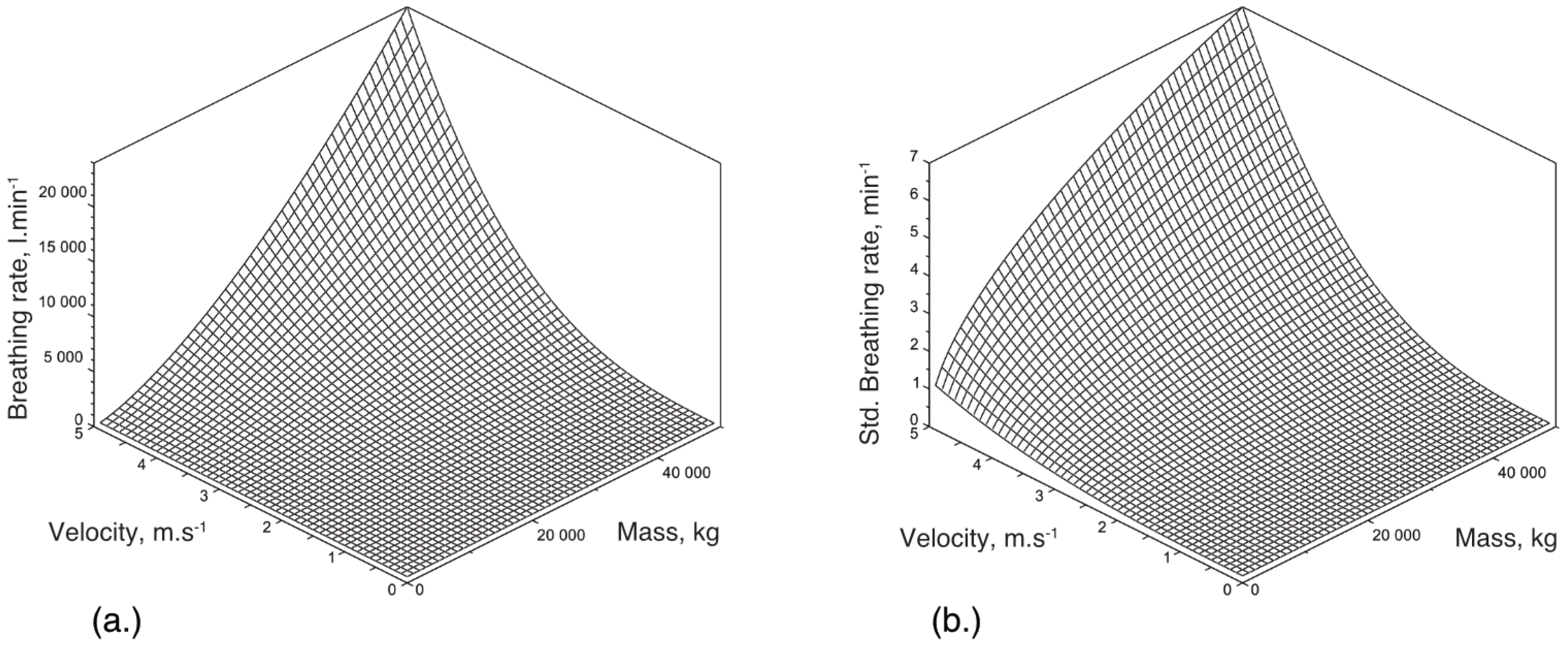
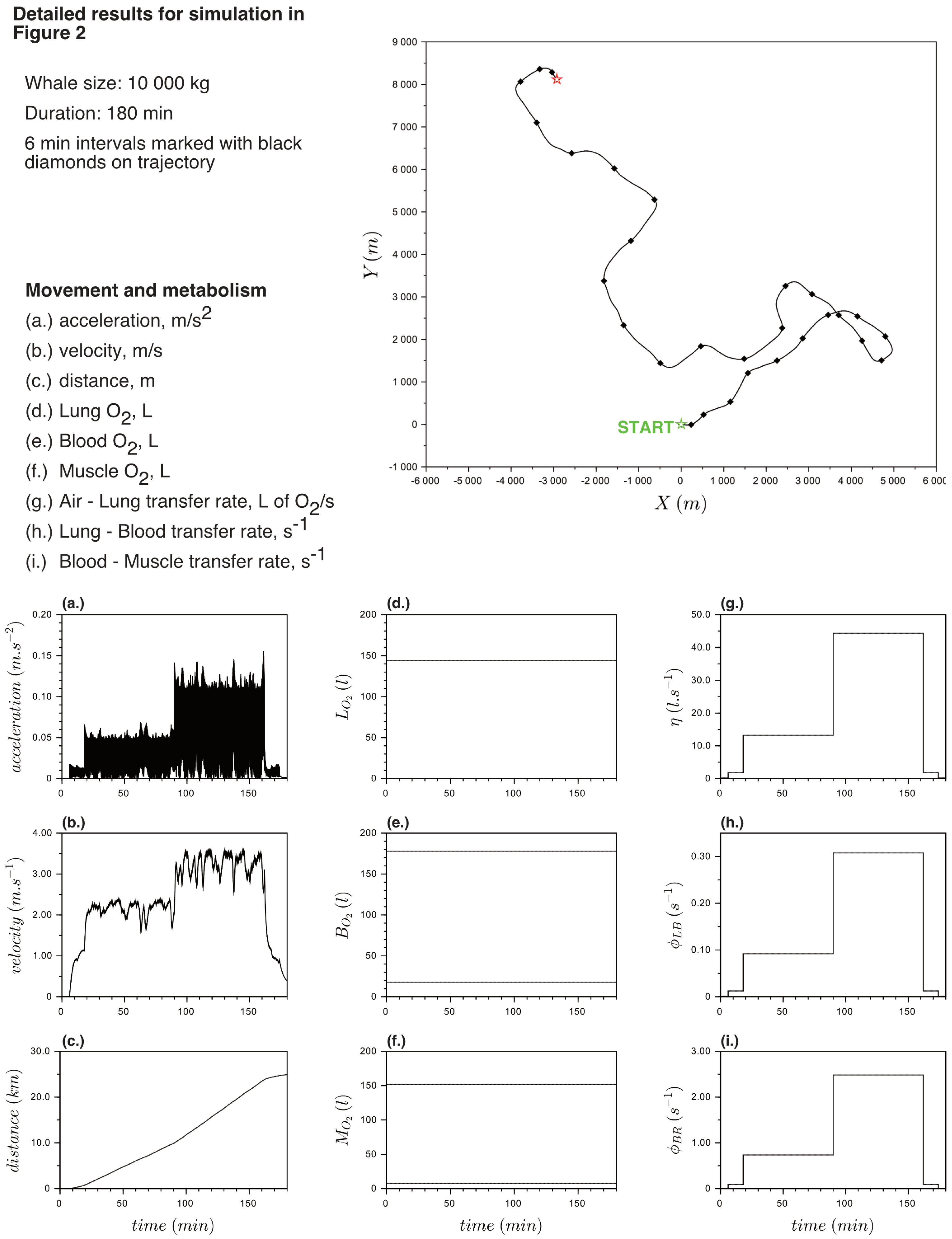
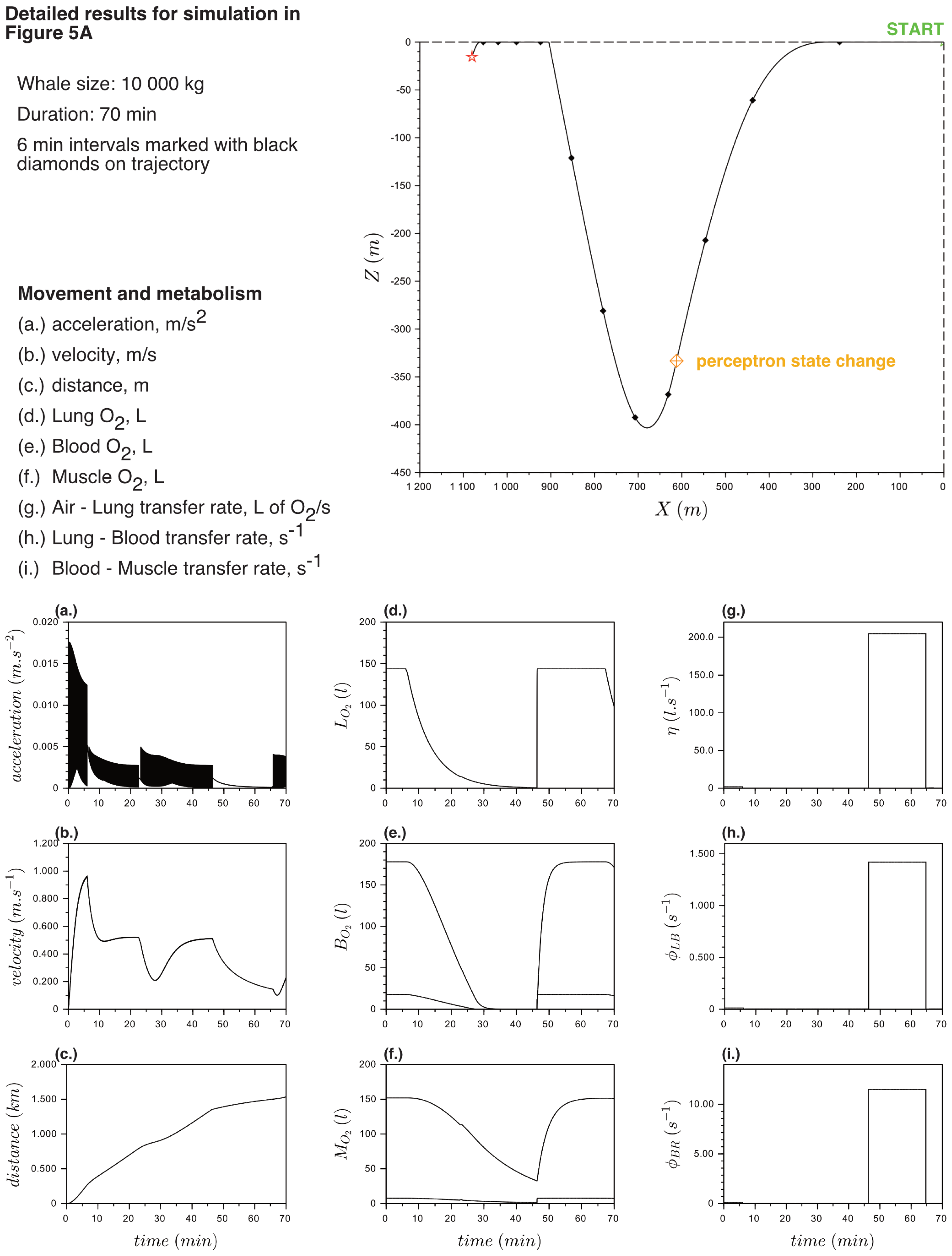

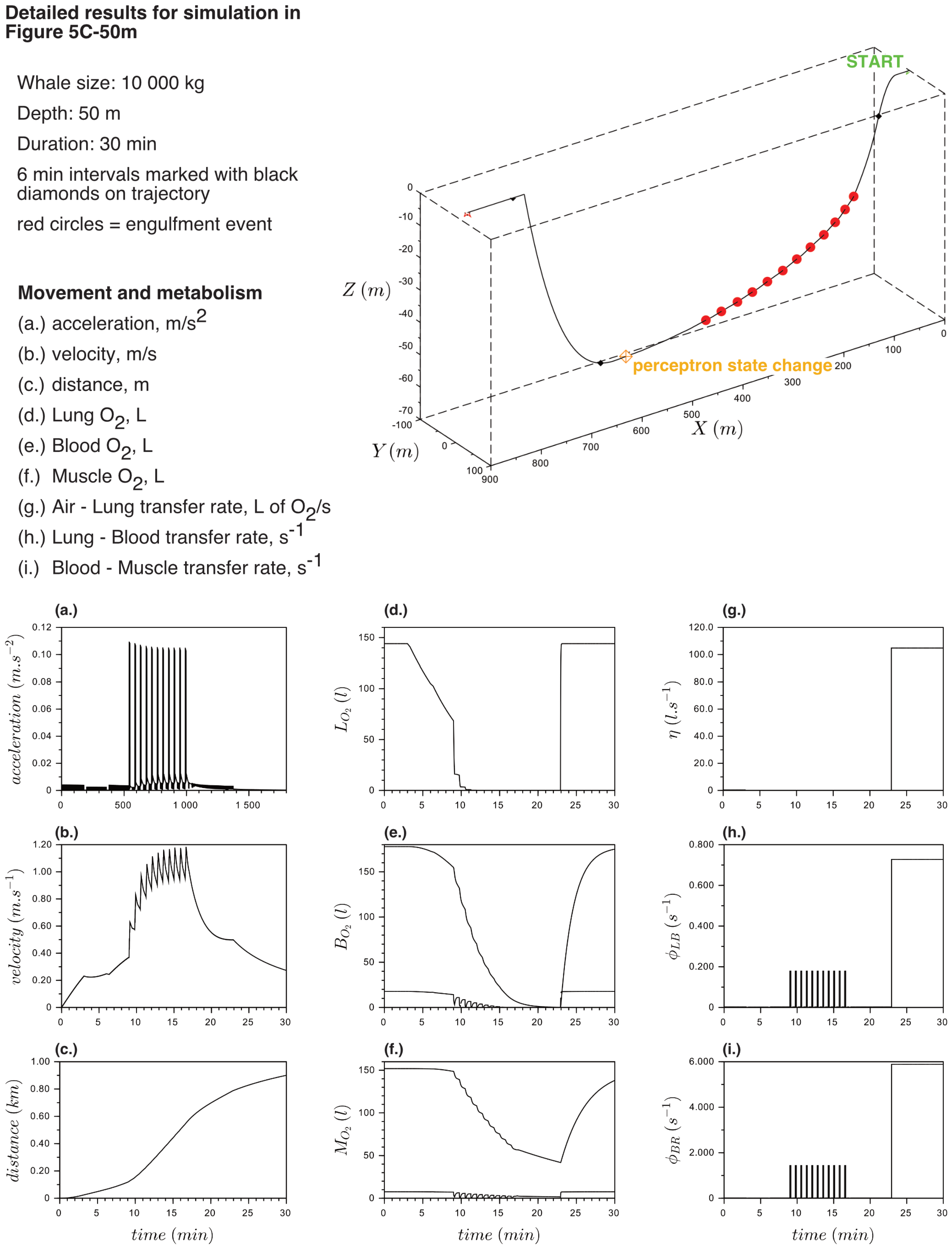
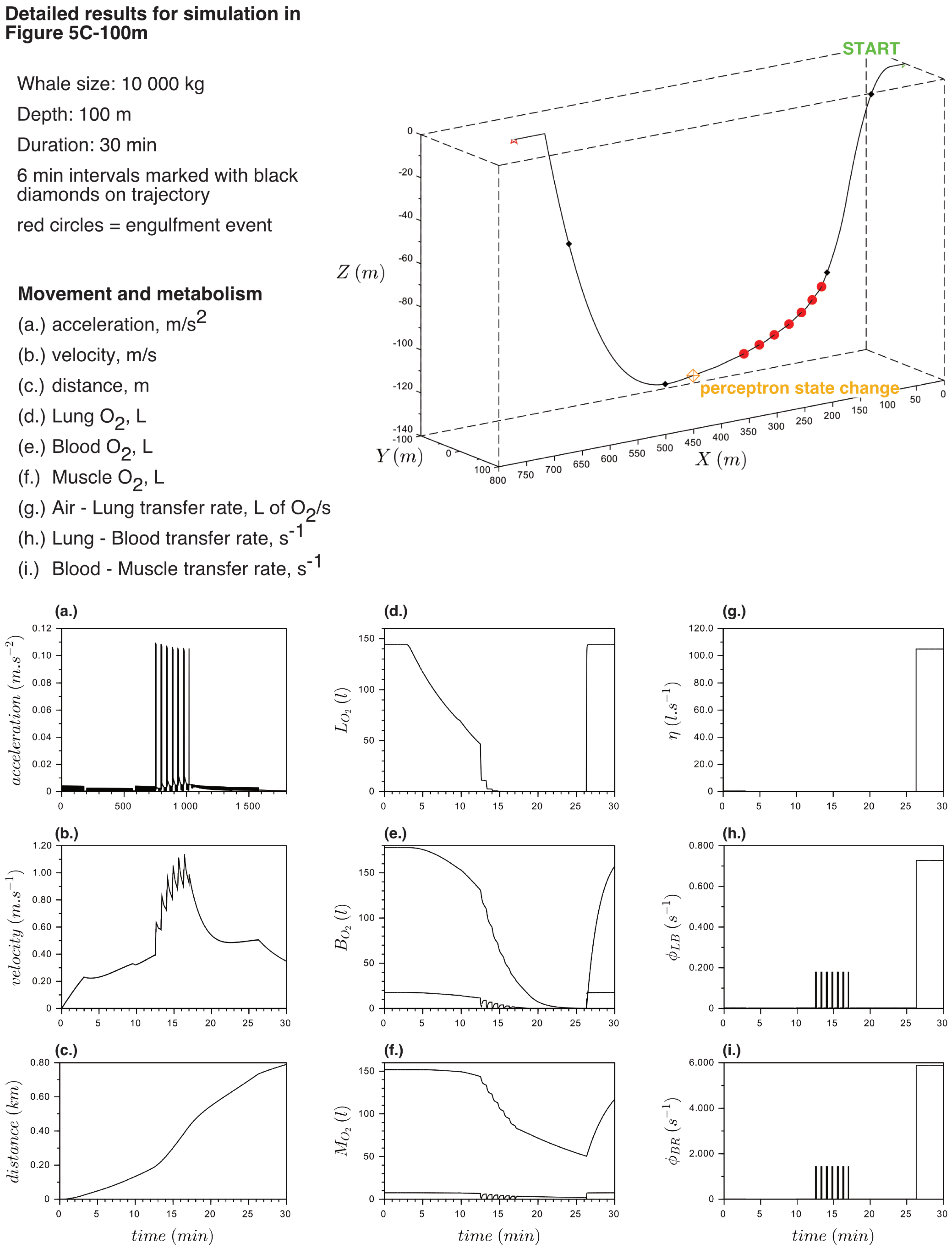

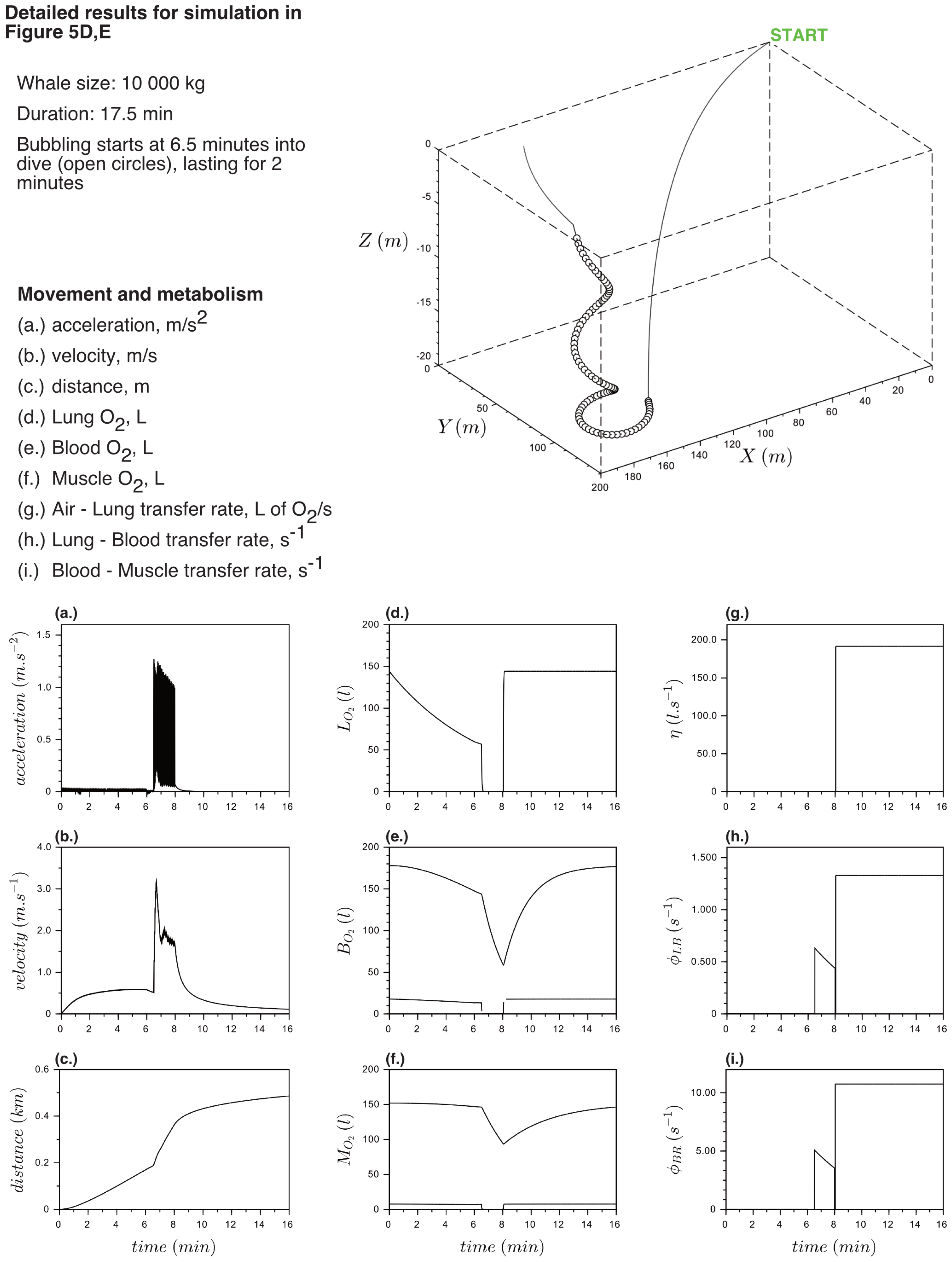
References
- Friedlaender, A.; Tyson, R.; Stimpert, A.; Read, A.; Nowacek, D. Extreme diel variation in the feeding behavior of Humpback whales along the western Antarctic Peninsula during autumn. Mar. Ecol. Prog. Ser. 2013, 494, 281–289. [Google Scholar] [CrossRef]
- Davis, R.; Fuiman, L.; Williams, T.; Horning, M.; Hagey, W. Classification of Weddell seal dives based on 3-dimensional movements and video-recorded observations. Mar. Ecol. Prog. Ser. 2003, 264, 109–122. [Google Scholar] [CrossRef]
- Ponganis, P.J. Diving Mammals. Compr. Physiol. 2011, 1, 447–465. [Google Scholar] [CrossRef] [PubMed]
- Gough, W.T.; Smith, H.J.; Savoca, M.S.; Czapanskiy, M.F.; Fish, F.E.; Potvin, J.; Bierlich, K.C.; Cade, D.E.; Di Clemente, J.; Kennedy, J.; et al. Scaling of oscillatory kinematics and Froude efficiency in baleen whales. J. Exp. Biol. 2021, 224, jeb237586. [Google Scholar] [CrossRef]
- Hunt, K.E.; Moore, M.J.; Rolland, R.M.; Kellar, N.M.; Hall, A.J.; Kershaw, J.; Raverty, S.A.; Davis, C.E.; Yeates, L.C.; Fauquier, D.A.; et al. Overcoming the challenges of studying conservation physiology in large whales: A review of available methods. Conserv. Physiol. 2013, 1, cot006. [Google Scholar] [CrossRef]
- Modest, M.; Irvine, L.; Andrews-Goff, V.; Gough, W.; Johnston, D.; Nowacek, D.; Pallin, L.; Read, A.; Moore, R.T.; Friedlaender, A. First description of migratory behavior of Humpback whales from an Antarctic feeding ground to a tropical calving ground. Anim. Biotelem. 2021, 9, 42. [Google Scholar] [CrossRef]
- Shadwick, R.E.; Potvin, J.; Goldbogen, J.A. Lunge Feeding in Rorqual Whales. Physiology 2019, 34, 409–418. [Google Scholar] [CrossRef]
- Laurie, A. Adaptations to Hydrostatic Pressure in Whales. Nature 1933, 132, 135–136. [Google Scholar] [CrossRef]
- Kleiber, M. Body size and metabolic rate. Physiol. Rev. 1932, 27, 511–541. [Google Scholar] [CrossRef]
- Krogh, A. The supply of oxygen to the tissues and the regulation of the capillary circulation. J. Physiol. 1919, 52, 457–474. [Google Scholar] [CrossRef]
- Hill, A.V. A new mathematical treatment of changes of ionic concentration in muscle and nerve under the action of electric currents, with a theory as to their mode of excitation. J. Physiol. 1910, 40, 190–224. [Google Scholar] [CrossRef] [PubMed]
- Kramer, D.L. The behavioral ecology of air breathing by aquatic animals. Can. J. Zool. 1988, 66, 89–94. [Google Scholar] [CrossRef]
- Dolphin, W.F. Ventilation and dive patterns of Humpback whales, Megaptera novaeangliae, on their Alaskan feeding grounds. Can. J. Zool. 1987, 65, 83–90. [Google Scholar] [CrossRef]
- MacArthur, R.H.; Pianka, E.R. On optimal use of a patchy environment. Am. Nat. 1966, 100, 603–609. [Google Scholar] [CrossRef]
- Houston, A.I.; Carbone, C. The optimal allocation of time during the diving cycle. Behav. Ecol. 1992, 3, 255–265. [Google Scholar] [CrossRef]
- Tyson, R.; Friedlaender, A.; Nowacek, D. Does optimal foraging theory predict the foraging performance of a large air-breathing marine predator? Anim. Behav. 2016, 116, 223–235. [Google Scholar] [CrossRef]
- Davis, R.W. A review of the multi-level adaptations for maximizing aerobic dive duration in marine mammals: From biochemistry to behavior. J. Comp. Physiol. B 2013, 184, 23–53. [Google Scholar] [CrossRef]
- Watanabe, Y.Y.; Goldbogen, J.A. Too big to study? The biologging approach to understanding the behavioural energetics of ocean giants. J. Exp. Biol. 2021, 224, jeb202747. [Google Scholar] [CrossRef]
- Kooyman, G.L. Techniques used in measuring diving capacities of Weddell Seals. Polar Rec. 1965, 12, 391–394. [Google Scholar] [CrossRef]
- Williams, T.M.; Davis, R.W. Physiological resiliency in diving mammals: Insights on hypoxia protection using the Krogh principle to understand COVID-19 symptoms. Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2021, 253, 110849. [Google Scholar] [CrossRef]
- Palacios, D.M.; Irvine, L.M.; Lagerquist, B.A.; Fahlbusch, J.A.; Calambokidis, J.; Tomkiewicz, S.M.; Mate, B.R. A satellite-linked tag for the long-term monitoring of diving behavior in large whales. Anim. Biotelem. 2022, 10, 26. [Google Scholar] [CrossRef]
- Ware, C.; Arsenault, R.; Plumlee, M.; Wiley, D. Visualizing the underwater behavior of Humpback whales. IEEE Comput. Graph. Appl. 2006, 26, 14–18. [Google Scholar] [CrossRef]
- Potvin, J.; Goldbogen, J.A.; Shadwick, R.E. Metabolic Expenditures of Lunge Feeding Rorquals Across Scale: Implications for the Evolution of Filter Feeding and the Limits to Maximum Body Size. PLoS ONE 2012, 7, e44854. [Google Scholar] [CrossRef] [PubMed]
- Goldbogen, J.A.; Calambokidis, J.; Croll, D.A.; McKenna, M.F.; Oleson, E.; Potvin, J.; Pyenson, N.D.; Schorr, G.; Shadwick, R.E.; Tershy, B.R. Scaling of lunge-feeding performance in rorqual whales: Mass-specific energy expenditure increases with body size and progressively limits diving capacity. Funct. Ecol. 2011, 26, 216–226. [Google Scholar] [CrossRef]
- Goldbogen, J.A.; Calambokidis, J.; Croll, D.A.; Harvey, J.T.; Newton, K.M.; Oleson, E.M.; Schorr, G.; Shadwick, R.E. Foraging behavior of Humpback whales: Kinematic and respiratory patterns suggest a high cost for a lunge. J. Exp. Biol. 2008, 211, 3712–3719. [Google Scholar] [CrossRef] [PubMed]
- Kooyman, G.L.; Ponganis, P.J. The physiological basis of diving to depth: Birds and mammals. Annu. Rev. Physiol. 1998, 60, 19–32. [Google Scholar] [CrossRef]
- Stimmelmayr, R.; Horstmann, L.; Person, B.T.; George, J. Chapter 11—Hematology, serum, and urine composition. In The Bowhead Whale, Balaena mysticetu: Biology and Human Interactions; Elsevier: Amsterdam, The Netherlands, 2021; pp. 151–163. [Google Scholar] [CrossRef]
- Castellini, M.A.; Baskurt, O.; Castellini, J.M.; Meiselman, H.J. Blood Rheology in Marine Mammals. Front. Physiol. 2010, 1, 1–8. [Google Scholar] [CrossRef]
- Fahlman, A.; van der Hoop, J.; Moore, M.J.; Levine, G.; Rocho-Levine, J.; Brodsky, M. Estimating energetics in cetaceans from respiratory frequency: Why we need to understand physiology. Biol. Open 2016, 5, 436–442. [Google Scholar] [CrossRef]
- Piscitelli, M.A.; Raverty, S.A.; Lillie, M.A.; Shadwick, R.E. A review of cetacean lung morphology and mechanics: Cetacean lung morphology and mechanics. J. Morphol. 2013, 274, 1425–1440. [Google Scholar] [CrossRef]
- Ommanney, F.D. The vascular networks (retia mirabilia) of the Fin whale (Balaenoptera physalus). Discov. Rep. 1932, 5, 327–362. [Google Scholar]
- Laurie, A. Physiology of Whales. Nature 1935, 135, 823. [Google Scholar] [CrossRef]
- Bosco, G.; Rizzato, A.; Martani, L.; Schiavo, S.; Talamonti, E.; Garetto, G.; Paganini, M.; Camporesi, E.M.; Moon, R.E. Arterial Blood Gas Analysis in Breath-Hold Divers at Depth. Front. Physiol. 2018, 9, 1558. [Google Scholar] [CrossRef] [PubMed]
- Tetzlaff, K.; Lemaitre, F.; Burgstahler, C.; Luetkens, J.A.; Eichhorn, L. Going to Extremes of Lung Physiology–Deep Breath-Hold Diving. Front. Physiol. 2021, 12, 710429. [Google Scholar] [CrossRef] [PubMed]
- Eaton, W.A.; Henry, E.R.; Hofrichter, J.; Mozzarelli, A. Is cooperative oxygen binding by hemoglobin really understood? Nat. Struct. Biol. 1999, 6, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Poole, D.C.; Musch, T.I. Capillary-Mitochondrial Oxygen Transport in Muscle: Paradigm Shifts. Function 2023, 4, zqado13. [Google Scholar] [CrossRef]
- Guarini, J.M.; Coston-Guarini, J. A First Individual-Based Model to Simulate Humpback Whale (Megaptera novaeangliae) Migrations at the Scale of the Global Ocean. J. Mar. Sci. Eng. 2022, 10, 1412. [Google Scholar] [CrossRef]
- Gough, W.T.; Segre, P.S.; Bierlich, K.C.; Cade, D.E.; Potvin, J.; Fish, F.E.; Dale, J.; di Clemente, J.; Friedlaender, A.S.; Johnston, D.W.; et al. Scaling of swimming performance in baleen whales. J. Exp. Biol. 2019, 222, jeb204172. [Google Scholar] [CrossRef]
- Kahane-Rapport, S.R.; Goldbogen, J.A. Allometric scaling of morphology and engulfment capacity in rorqual whales. J. Morphol. 2018, 279, 1256–1268. [Google Scholar] [CrossRef]
- Patial, J.S. A Study on Mensuration with Special Reference to Ellipse and Ellipsoid. J. Res. Appl. Math. 2023, 9, 1–13. [Google Scholar]
- Lockyer, C. Body weights of some species of large whales. ICES J. Mar. Sci. 1976, 36, 259–273. [Google Scholar] [CrossRef]
- Ryg, M.; Lydersen, C.; Knutsen, L.Ø.; Bjørge, A.; Smith, T.G.; ØRitsland, N.A. Scaling of insulation in seals and whales. J. Zool. 1993, 230, 193–206. [Google Scholar] [CrossRef]
- Stephens, P.A.; Carbone, C.; Boyd, I.L.; McNamara, J.M.; Harding, K.C.; Houston, A.I. The Scaling of Diving Time Budgets: Insights from an Optimality Approach. Am. Nat. 2008, 171, 305–314. [Google Scholar] [CrossRef][Green Version]
- Ridgway, S.H.; Bowers, C.A.; Miller, D.; Schultz, M.L.; Jacobs, C.A.; Dooley, C.A. Diving and blood oxygen in the white whale. Can. J. Zool. 1984, 62, 2349–2351. [Google Scholar] [CrossRef]
- Vogel, S. Life in Moving Fluids, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Narazaki, T.; Isojunno, S.; Nowacek, D.P.; Swift, R.; Friedlaender, A.S.; Ramp, C.; Smout, S.; Aoki, K.; Deecke, V.B.; Sato, K.; et al. Body density of Humpback whales (Megaptera novaengliae) in feeding aggregations estimated from hydrodynamic gliding performance. PLoS ONE 2018, 13, e0200287. [Google Scholar] [CrossRef]
- Daniel, T.L. Unsteady Aspects of Aquatic Locomotion. Am. Zool. 1984, 24, 121–134. [Google Scholar] [CrossRef]
- Cade, D.E.; Friedlaender, A.S.; Calambokidis, J.; Goldbogen, J.A. Kinematic Diversity in Rorqual Whale Feeding Mechanisms. Curr. Biol. 2016, 26, 2617–2624. [Google Scholar] [CrossRef] [PubMed]
- Popel, A.S. Theory of oxygen transport to tissue. Crit. Rev. Biomed. Eng. 1989, 17, 257–321. [Google Scholar] [PubMed]
- Helbo, S.; Fago, A. Functional properties of myoglobins from five whale species with different diving capacities. J. Exp. Biol. 2012, 215, 3403–3410. [Google Scholar] [CrossRef]
- Michael Panneton, W. The Mammalian Diving Response: An Enigmatic Reflex to Preserve Life? Physiology 2013, 28, 284–297. [Google Scholar] [CrossRef]
- Hind, A.T.; Gurney, W.S.C. The Metabolic Cost Of Swimming In Marine Homeotherms. J. Exp. Biol. 1997, 200, 531–542. [Google Scholar] [CrossRef]
- Woledge, R.C.; Curtin, N.A.; Homsher, E. Energetic Aspects of Muscle Contraction; Number 41 in Monographs of the Physiological Society; Academic Press: London, UK, 1985; pp. 1–357. [Google Scholar]
- Popescu, M.C.; Balas, V.; Perescu-Popescu, L.; Mastorakis, N. Multilayer Perceptron and Neural Networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Boulila, W.; Driss, M.; Alshanqiti, E.; Al-Sarem, M.; Saeed, F.; Krichen, M. Weight Initialization Techniques for Deep Learning Algorithms in Remote Sensing: Recent Trends and Future Perspectives. In Advances on Smart and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1399, pp. 477–484. [Google Scholar] [CrossRef]
- Laplanche, C.; Marques, T.A.; Thomas, L. Tracking marine mammals in 3D using electronic tag data. Methods Ecol. Evol. 2015, 6, 987–996. [Google Scholar] [CrossRef]
- Wiley, D.; Ware, C.; Bocconcelli, A.; Cholewiak, D.; Friedlaender, A.S.; Thompson, M.A.; Weinrich, M.T. Underwater components of Humpback whale bubble-net feeding behaviour. Behaviour 2011, 148, 575–602. [Google Scholar] [CrossRef]
- Mastick, N.C.; Wiley, D.; Cade, D.E.; Ware, C.; Parks, S.E.; Friedlaender, A.S. The effect of group size on individual behavior of bubble-net feeding Humpback whales in the southern Gulf of Maine. Mar. Mammal Sci. 2022, 38, 959–974. [Google Scholar] [CrossRef]
- Szabo, A.; Bejder, L.; Warick, H.; van Aswegen, M.; Friedlaender, A.S.; Goldbogen, J.; Kendall-Bar, J.M.; Leunissen, E.M.; Angot, M.; Gough, W.T. Solitary Humpback whales manufacture bubble-nets as tools to increase prey intake. R. Soc. Open Sci. 2024, 11, 240328. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.B.; Krebs, J.R. (Eds.) Behavioural Ecology, 4th ed.; Blackwell Science: Oxford, UK, 1997. [Google Scholar]
- Doniol-Valcroze, T.; Lesage, V.; Giard, J.; Michaud, R. Optimal foraging theory predicts diving and feeding strategies of the largest marine predator. Behav. Ecol. 2011, 22, 880–888. [Google Scholar] [CrossRef]
- Friedlaender, A.S.; Johnston, D.W.; Tyson, R.B.; Kaltenberg, A.; Goldbogen, J.A.; Stimpert, A.K.; Curtice, C.; Hazen, E.L.; Halpin, P.N.; Read, A.J.; et al. Multiple-stage decisions in a marine central-place forager. R. Soc. Open Sci. 2016, 3, 160043. [Google Scholar] [CrossRef]
- Pierce, G.J.; Ollason, J.G. Eight Reasons Why Optimal Foraging Theory Is a Complete Waste of Time. Oikos 1987, 49, 111. [Google Scholar] [CrossRef]
- Videsen, S.K.A.; Simon, M.; Christiansen, F.; Friedlaender, A.; Goldbogen, J.; Malte, H.; Segre, P.; Wang, T.; Johnson, M.; Madsen, P.T. Cheap gulp foraging of a giga-predator enables efficient exploitation of sparse prey. Sci. Adv. 2023, 9, eade3889. [Google Scholar] [CrossRef]
- Christiansen, F.; Sironi, M.; Moore, M.J.; Di Martino, M.; Ricciardi, M.; Warick, H.A.; Irschick, D.J.; Gutierrez, R.; Uhart, M.M. Estimating body mass of free-living whales using aerial photogrammetry and 3D volumetrics. Methods Ecol. Evol. 2019, 10, 2034–2044. [Google Scholar] [CrossRef]
- Napoli, C.; Hirtle, N.; Stepanuk, J.; Christiansen, F.; Heywood, E.I.; Grove, T.J.; Stoller, A.; Dodds, F.; Glarou, M.; Rasmussen, M.H.; et al. Drone-based photogrammetry reveals differences in Humpback whale body condition and mass across North Atlantic foraging grounds. Front. Mar. Sci. 2024, 11, 1336455. [Google Scholar] [CrossRef]
- Zhang, D.; van der Hoop, J.M.; Petrov, V.; Rocho-Levine, J.; Moore, M.J.; Shorter, K.A. Simulated and experimental estimates of hydrodynamic drag from bio-logging tags. Mar. Mammal Sci. 2019, 36, 136–157. [Google Scholar] [CrossRef]
- Wu, C.; Nowacek, D.P.; Nousek-McGregor, A.E.; McGregor, R.; Howle, L.E. Computational fluid dynamics of flow regime and hydrodynamic forces generated by a gliding North Atlantic right whale (Eubalaena glacialis). Mar. Mammal Sci. 2021, 37, 826–842. [Google Scholar] [CrossRef]
- Hirtle, N.O.; Stepanuk, J.E.F.; Heywood, E.I.; Christiansen, F.; Thorne, L.H. Integrating 3D models with morphometric measurements to improve volumetric estimates in marine mammals. Methods Ecol. Evol. 2022, 13, 2478–2490. [Google Scholar] [CrossRef]
- Christiansen, F.; Sprogis, K.R.; Gross, J.; Castrillon, J.; Warick, H.A.; Leunissen, E.; Bengtson Nash, S. Variation in outer blubber lipid concentrations does not reflect morphological body condition in Humpback whales. J. Exp. Biol. 2020, 223, jeb213769. [Google Scholar] [CrossRef]
- Sun, T.; Chen, G.; Yang, S.; Wang, Y.; Wang, Y.; Tan, H.; Zhang, L. Design and optimization of a bio-inspired hull shape for AUV by surrogate model technology. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1057–1074. [Google Scholar] [CrossRef]
- Miller, C.; Best, P.; Perryman, W.; Baumgartner, M.; Moore, M. Body shape changes associated with reproductive status, nutritive condition and growth in Right whales Eubalaena glacialis and E. australis. Mar. Ecol. Prog. Ser. 2012, 459, 135–156. [Google Scholar] [CrossRef]
- Williamson, G.R. The true body shape of rorqual whales. J. Zool. 1972, 167, 277–286. [Google Scholar] [CrossRef]
- Goldbogen, J.A.; Cade, D.E.; Wisniewska, D.M.; Potvin, J.; Segre, P.S.; Savoca, M.S.; Hazen, E.L.; Czapanskiy, M.F.; Kahane-Rapport, S.R.; DeRuiter, S.L.; et al. Why whales are big but not bigger: Physiological drivers and ecological limits in the age of ocean giants. Science 2019, 366, 1367–1372. [Google Scholar] [CrossRef]
- Goldbogen, J.A.; Potvin, J.; Shadwick, R.E. Skull and buccal cavity allometry increase mass-specific engulfment capacity in Fin whales. Proc. R. Soc. B Biol. Sci. 2009, 277, 861–868. [Google Scholar] [CrossRef]
- Segre, P.S.; Gough, W.T.; Roualdes, E.A.; Cade, D.E.; Czapanskiy, M.F.; Fahlbusch, J.; Kahane-Rapport, S.R.; Oestreich, W.K.; Bejder, L.; Bierlich, K.C.; et al. Scaling of maneuvering performance in baleen whales: Larger whales outperform expectations. J. Exp. Biol. 2022, 225, jeb243224. [Google Scholar] [CrossRef]
- Zhang, H.; Van Kaick, O.; Dyer, R. Spectral Mesh Processing. Comput. Graph. Forum 2010, 29, 1865–1894. [Google Scholar] [CrossRef]
- Shen, L.; Kim, S.; Saykin, A.J. Fourier method for large-scale surface modeling and registration. Comput. Graph. 2009, 33, 299–311. [Google Scholar] [CrossRef][Green Version]
- Xue, G.; Bai, F.; Guo, L.; Ren, P.; Liu, Y. Research on the effects of complex terrain on the hydrodynamic performance of a deep-sea fishlike exploring and sampling robot moving near the sea bottom. Front. Mar. Sci. 2023, 10, 1091523. [Google Scholar] [CrossRef]
- Scott, C. Misconceptions about Aerobic and Anaerobic Energy Expenditure. J. Int. Soc. Sport. Nutr. 2005, 2, 32–37. [Google Scholar] [CrossRef] [PubMed]
- Rivero, J.L.L. Locomotor muscle fiber heterogeneity and metabolism in the fastest large-bodied rorqual: The Fin whale (Balaenoptera physalus). J. Exp. Biol. 2018, 221, jeb177758. [Google Scholar] [CrossRef] [PubMed]
- Sierra, E.; Fernández, A.; Espinosa de los Monteros, A.; Díaz-Delgado, J.; Bernaldo de Quirós, Y.; García-Álvarez, N.; Arbelo, M.; Herráez, P. Comparative histology of muscle in free ranging cetaceans: Shallow versus deep diving species. Sci. Rep. 2015, 5, 15909. [Google Scholar] [CrossRef] [PubMed]
- Salin, K.; Auer, S.K.; Rey, B.; Selman, C.; Metcalfe, N.B. Variation in the link between oxygen consumption and ATP production, and its relevance for animal performance. Proc. R. Soc. B Biol. Sci. 2015, 282, 20151028. [Google Scholar] [CrossRef]
- Gunnufsen, R. Dive Behaviour and Respiration Rates of Humpback Whales (Megaptera novaeangliae) During Foraging off Northern Norway, with Implications for Metabolic Rate Estimates. Master’s Thesis, The Arctic University of Norway, Faculty of Bioscience, Fisheries and Economics, Tromsø, Norway, 2022. [Google Scholar]
- Roos, M.M.H. Respiratory Behaviour in Migrating Lactating Humpback Whales. Ph.D. Thesis, University of Queensland (Australia), School of Veterinary Science, Brisbane, Australia, 2021. [Google Scholar] [CrossRef]
- Horton, T.W.; Hauser, N.; Cassel, S.; Klaus, K.F.; Fettermann, T.; Key, N. Doctor Drone: Non-invasive Measurement of Humpback Whale Vital Signs Using Unoccupied Aerial System Infrared Thermography. Front. Mar. Sci. 2019, 6, 466. [Google Scholar] [CrossRef]
- Tyson, R.; Friedlaender, A.; Ware, C.; Stimpert, A.; Nowacek, D. Synchronous mother and calf foraging behaviour in humpback whales Megaptera novaeangliae: Insights from multi-sensor suction cup tags. Mar. Ecol. Prog. Ser. 2012, 457, 209–220. [Google Scholar] [CrossRef]
- McKnight, J.C.; Bennett, K.A.; Bronkhorst, M.; Russell, D.J.F.; Balfour, S.; Milne, R.; Bivins, M.; Moss, S.E.W.; Colier, W.; Hall, A.J.; et al. Shining new light on mammalian diving physiology using wearable near-infrared spectroscopy. PLoS ONE 2019, 17, e3000306. [Google Scholar] [CrossRef]
- Fahlman, A.; Moore, M.J.; Garcia-Parraga, D. Respiratory function and mechanics in pinnipeds and cetaceans. J. Exp. Biol. 2017, 220, 1761–1773. [Google Scholar] [CrossRef]
- Reidenberg, J.S. Where does the air go? Anatomy and functions of the respiratory tract in the Humpback whale (Megaptera novaeangliae). Madag. Conserv. Dev. 2018, 13, 91. [Google Scholar] [CrossRef]
- Riggs, A. Bohr Effect in the Hæmoglobins of Marine Mammals. Nature 1961, 190, 94–95. [Google Scholar] [CrossRef] [PubMed]
- Boyd, I.L.; Bowen, W.D.; Iverson, S.J. (Eds.) Marine Mammal Ecology and Conservation: A Handbook of Techniques; Techniques in ecology and conservation series; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Goldbogen, J.A.; Cade, D.E.; Calambokidis, J.; Czapanskiy, M.F.; Fahlbusch, J.; Friedlaender, A.S.; Gough, W.T.; Kahane-Rapport, S.R.; Savoca, M.S.; Ponganis, K.V.; et al. Extreme bradycardia and tachycardia in the world’s largest animal. Proc. Natl. Acad. Sci. USA 2019, 116, 25329–25332. [Google Scholar] [CrossRef] [PubMed]
- Croll, D.A.; Acevedo-Gutierrez, A.; Tershy, B.R.; Urban-Ramirez, J. The diving behavior of Bue and Fin whales: Is dive duration shorter than expected based on oxygen stores? Comp. Biochem. Physiol. Part A Mol. Integr. Physiol. 2001, 129, 797–809. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.; Fedak, M.A. How long should a dive last? A simple model of foraging decisions by breath-hold divers in a patchy environment. Anim. Behav. 2001, 61, 287–296. [Google Scholar] [CrossRef]
- Tian, R.; Yin, D.; Liu, Y.; Seim, I.; Xu, S.; Yang, G. Adaptive Evolution of Energy Metabolism-Related Genes in Hypoxia-Tolerant Mammals. Front. Genet. 2017, 8, 205. [Google Scholar] [CrossRef]
- Ponganis, P.J.; McDonald, B.I. Chapter 5—Cardiovascular physiology in dolphins and other cetaceans. In The Physiology of Dolphins; Elsevier: Amsterdam, The Netherlands, 2024; pp. 77–105. [Google Scholar] [CrossRef]
- Ydenberg, R.; Clark, C.W. Aerobiosis and anaerobiosis during diving by Western Grebes: An optimal foraging approach. J. Theor. Biol. 1989, 139, 437–447. [Google Scholar] [CrossRef]
- Kooyman, G.L.; Wahrenbrock, E.A.; Castellini, M.A.; Davis, R.W.; Sinnett, E.E. Aerobic and anaerobic metabolism during voluntary diving in Weddell seals: Evidence of preferred pathways from blood chemsitry and behavior. J. Comp. Physiol. B 1980, 138, 335–346. [Google Scholar] [CrossRef]
- Carbone, C.; Houston, A. The optimal allocation of time over the dive cycle: An approach based on aerobic and anaerobic respiration. Anim. Behav. 1996, 51, 1247–1255. [Google Scholar] [CrossRef][Green Version]
- McKnight, J.C.; Bønnelycke, E.M.; Balfour, S.; Milne, R.; Moss, S.E.W.; Armstrong, H.C.; Downie, C.; Hall, A.J.; Kershaw, J.L. Cognitive perception of circulating oxygen in seals is the reason they don’t drown. Science 2025, 387, 1276–1280. [Google Scholar] [CrossRef] [PubMed]
- Cade, D.E.; Kahane-Rapport, S.R.; Wallis, B.; Goldbogen, J.A.; Friedlaender, A.S. Evidence for Size-Selective Predation by Antarctic Humpback Whales. Front. Mar. Sci. 2022, 9, 747788. [Google Scholar] [CrossRef]
- Akiyama, Y.; Akamatsu, T.; Rasmussen, M.H.; Iversen, M.R.; Iwata, T.; Goto, Y.; Aoki, K.; Sato, K. Leave or stay? Video-logger revealed foraging efficiency of humpback whales under temporal change in prey density. PLoS ONE 2019, 14, e0211138. [Google Scholar] [CrossRef] [PubMed]
- Braithwaite, J.E.; Meeuwig, J.J.; Hipsey, M.R. Optimal migration energetics of humpback whales and the implications of disturbance. Conserv. Physiol. 2015, 3, cov001. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Gough, W.T.; Cade, D.E.; Czapanskiy, M.F.; Potvin, J.; Fish, F.E.; Kahane-Rapport, S.R.; Savoca, M.S.; Bierlich, K.C.; Johnston, D.W.; Friedlaender, A.S.; et al. Fast and Furious: Energetic Tradeoffs and Scaling of High-Speed Foraging in Rorqual Whales. Integr. Org. Biol. 2022, 4, obac038. [Google Scholar] [CrossRef]
- Peterson, C. On some biological principles. Det Kgl. Dan. Vidensk. Selsk. Biol. Meddeleser 1928, VII, 1–53. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González Félix, M.; Coston-Guarini, J.; Rivière, P.; Guarini, J.-M. A New Eco-Physical, Individual-Based Model of Humpback Whale (Megaptera novaeangliae, Borowski, 1781) Swimming and Diving. J. Mar. Sci. Eng. 2025, 13, 1388. https://doi.org/10.3390/jmse13081388
González Félix M, Coston-Guarini J, Rivière P, Guarini J-M. A New Eco-Physical, Individual-Based Model of Humpback Whale (Megaptera novaeangliae, Borowski, 1781) Swimming and Diving. Journal of Marine Science and Engineering. 2025; 13(8):1388. https://doi.org/10.3390/jmse13081388
Chicago/Turabian StyleGonzález Félix, Marisa, Jennifer Coston-Guarini, Pascal Rivière, and Jean-Marc Guarini. 2025. "A New Eco-Physical, Individual-Based Model of Humpback Whale (Megaptera novaeangliae, Borowski, 1781) Swimming and Diving" Journal of Marine Science and Engineering 13, no. 8: 1388. https://doi.org/10.3390/jmse13081388
APA StyleGonzález Félix, M., Coston-Guarini, J., Rivière, P., & Guarini, J.-M. (2025). A New Eco-Physical, Individual-Based Model of Humpback Whale (Megaptera novaeangliae, Borowski, 1781) Swimming and Diving. Journal of Marine Science and Engineering, 13(8), 1388. https://doi.org/10.3390/jmse13081388






