Optimization Study of the Line Array Layout of Slope–Pendulum Wave Energy Conversion Device
Abstract
1. Introduction
2. Theoretical Model
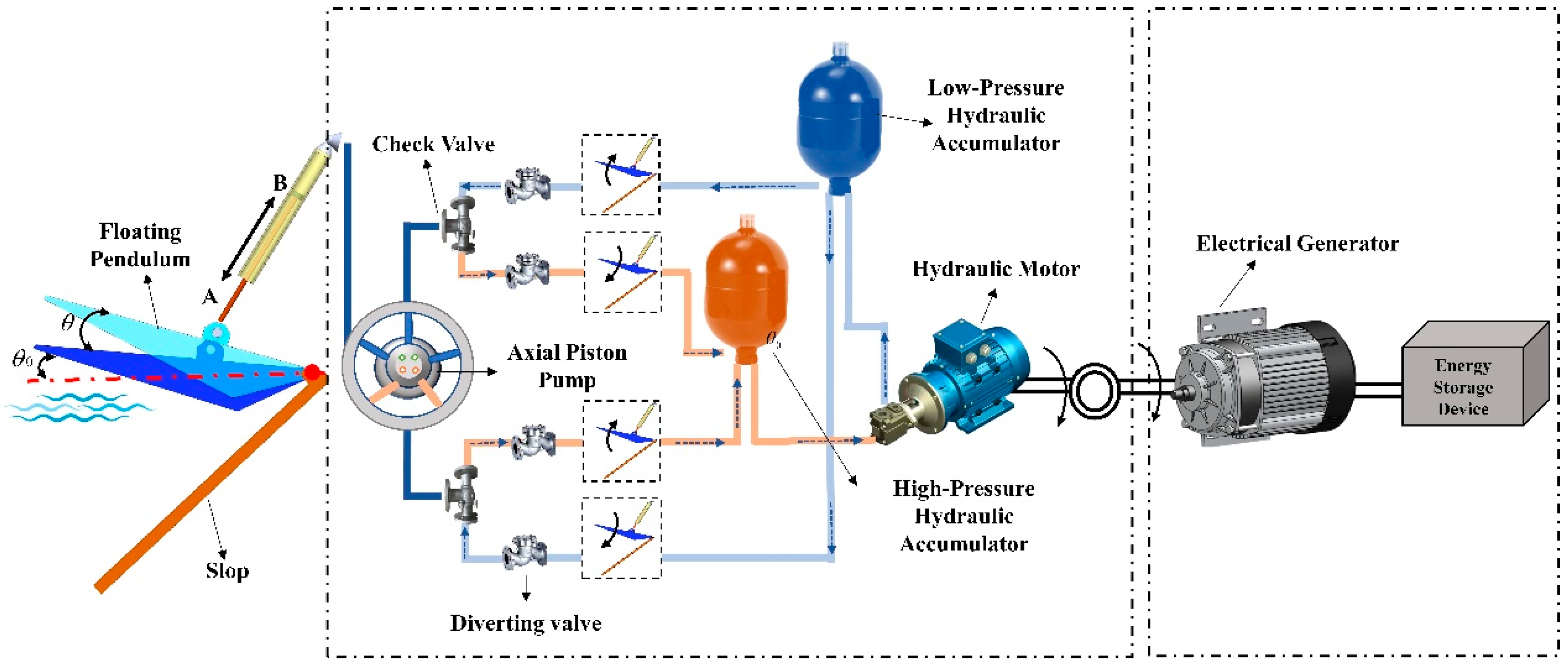
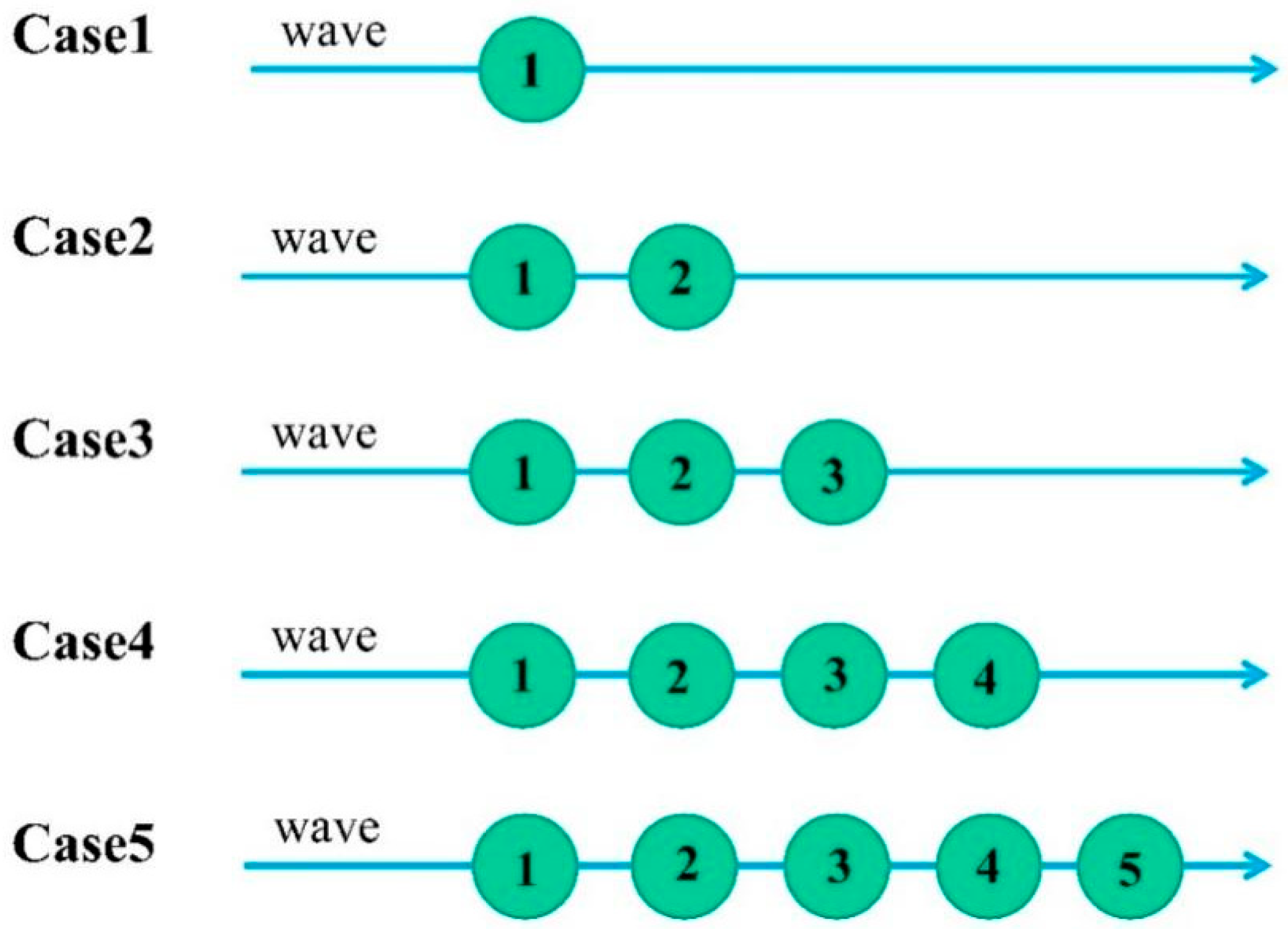
2.1. Individual and Linear Array Layout of S-PWEC
2.2. Motion Response
- , , , and are the column vector of the radiative moments to which the units are subjected, the hydrostatic recovery moment matrix, the wave excitation moment matrix in the longitudinal rocking direction, and the column vector of the displacement response, respectively. is the column vector of the velocity response and is the acceleration response vector in pitch direction.
- is the mass matrix of array wave energy conversion device, is the number of array devices, and represents the additional moment of inertia in the longitudinal direction.
- The wave radiation moment is given as follows:represents the radiation moment on the th pendulum caused by the motion of the th pendulum. is the delay function of the radiative force on the th floating pendulum caused by the motion of the th floating pendulum, characterizing the memory effect of the fluid; this can be solved by the spatial equation of state. represents an integral variable, which is a differential element in time integration.
- The hydrostatic restoring moment is the combined moments of gravity and static buoyancy of the generating unit:where and are the moments of buoyancy and gravity, respectively.
- is the secondary viscous drag moment. In the field operation, the wave energy conversion device undergoes vortex detachment during its interaction with waves, leading to viscous interaction [23]. This is modeled as follows:In Equation (4), is the coefficient of the secondary damping term in viscous moment. can be obtained from the published data or hydrodynamic experiments. is the velocity of the floating plate, is the velocity of the surrounding fluid, and is the moment of the viscous force on the pivot point.
- is the damping torque of the hydraulic power take-off (PTO):where is the pressure difference on the piston in the hydraulic rod, is the force area of the piston in the hydraulic rod, and is the length of the force arm from the hydraulic rod to the floating pendulum.
- is the braking torque of the limiting device, which is achieved by installing springs with large stiffness coefficients at the articulation point. Assuming that the braking torque is proportional to the angular velocity of the floating pendulum, is given bywhere is the large stiffness coefficient of the limit spring, is the limit angle, and the step function. This is given as
- Coupling the above equations yields the overall time-domain equation for the arrayed wave energy conversion device:
- In order to determine the rationality of the array field and the superiority of the wave energy-generating device’s power generation performance, it is necessary to introduce the dimensionless array impact factor . The array impact factor is an important index to measure the performance of array device, which is defined as follows:In Equation (9), is the power generated by a single S-PWEC at normal operation conditions, and is the average of the total power of all S-PWECs at the following array layout:where is the generating power of each S-PWEC.
3. Results & Discussion
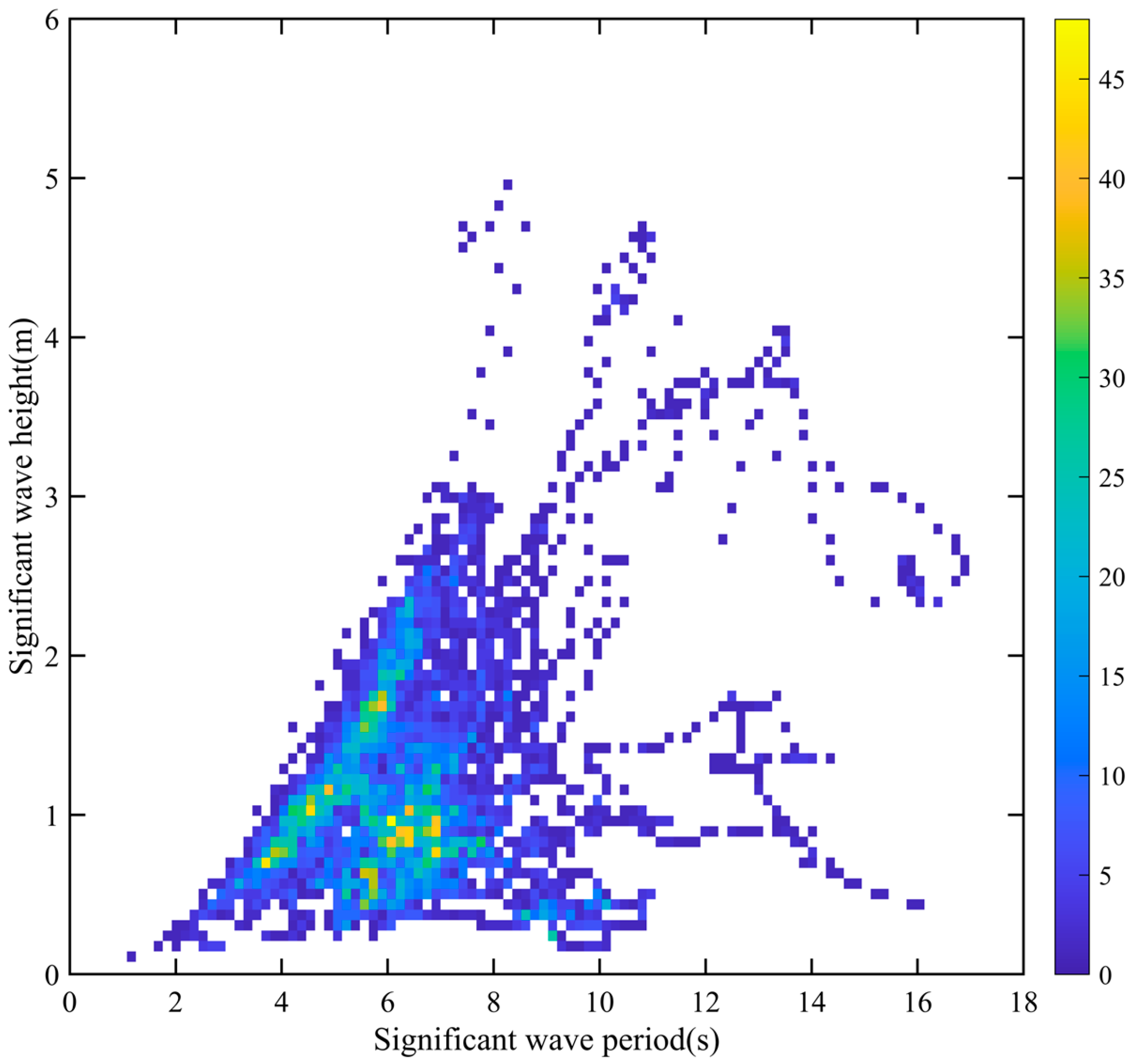
3.1. Setup of Initial Sea State Parameters
3.2. Full-System Modeling for Arrayed S-PWEC
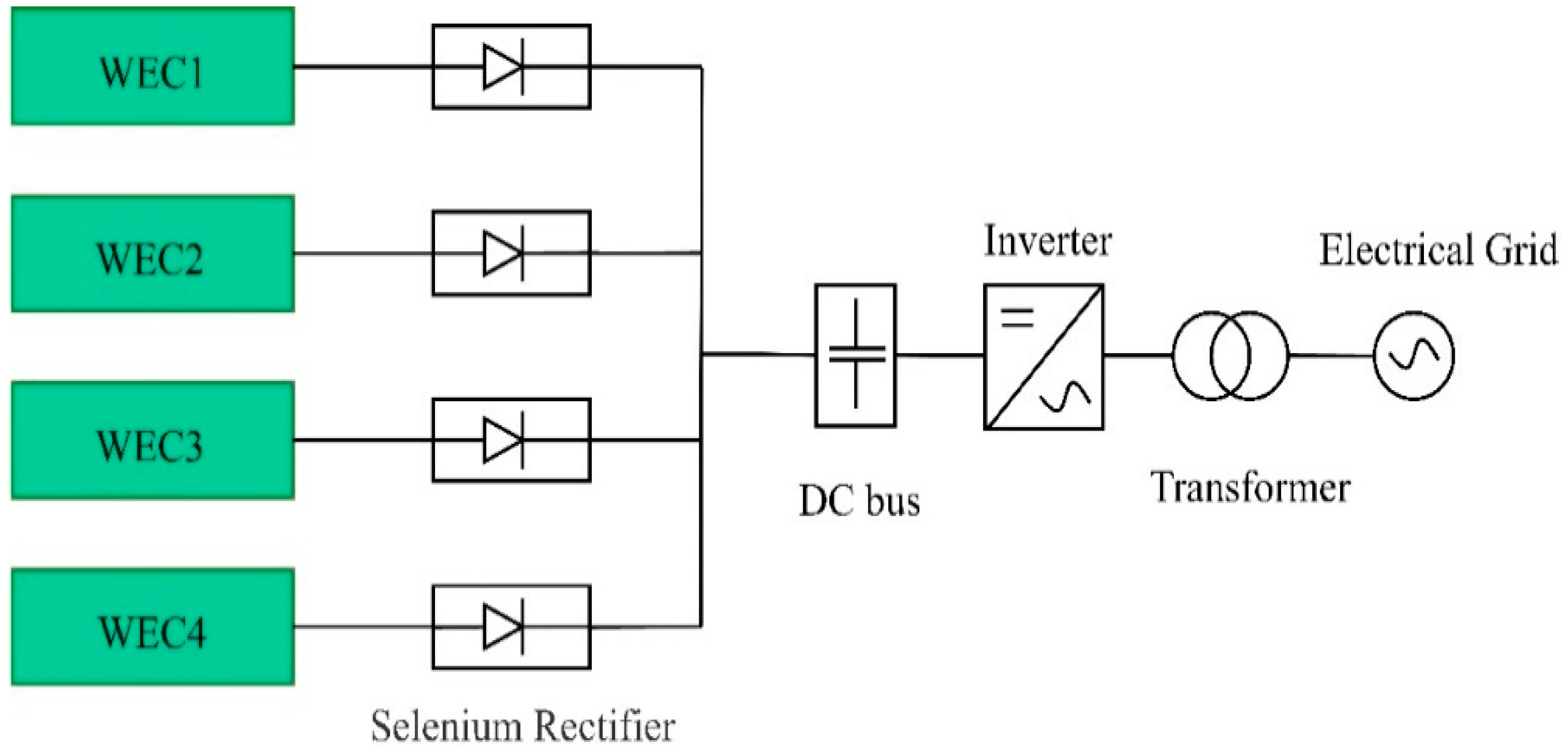
3.2.1. Power Integration System Design
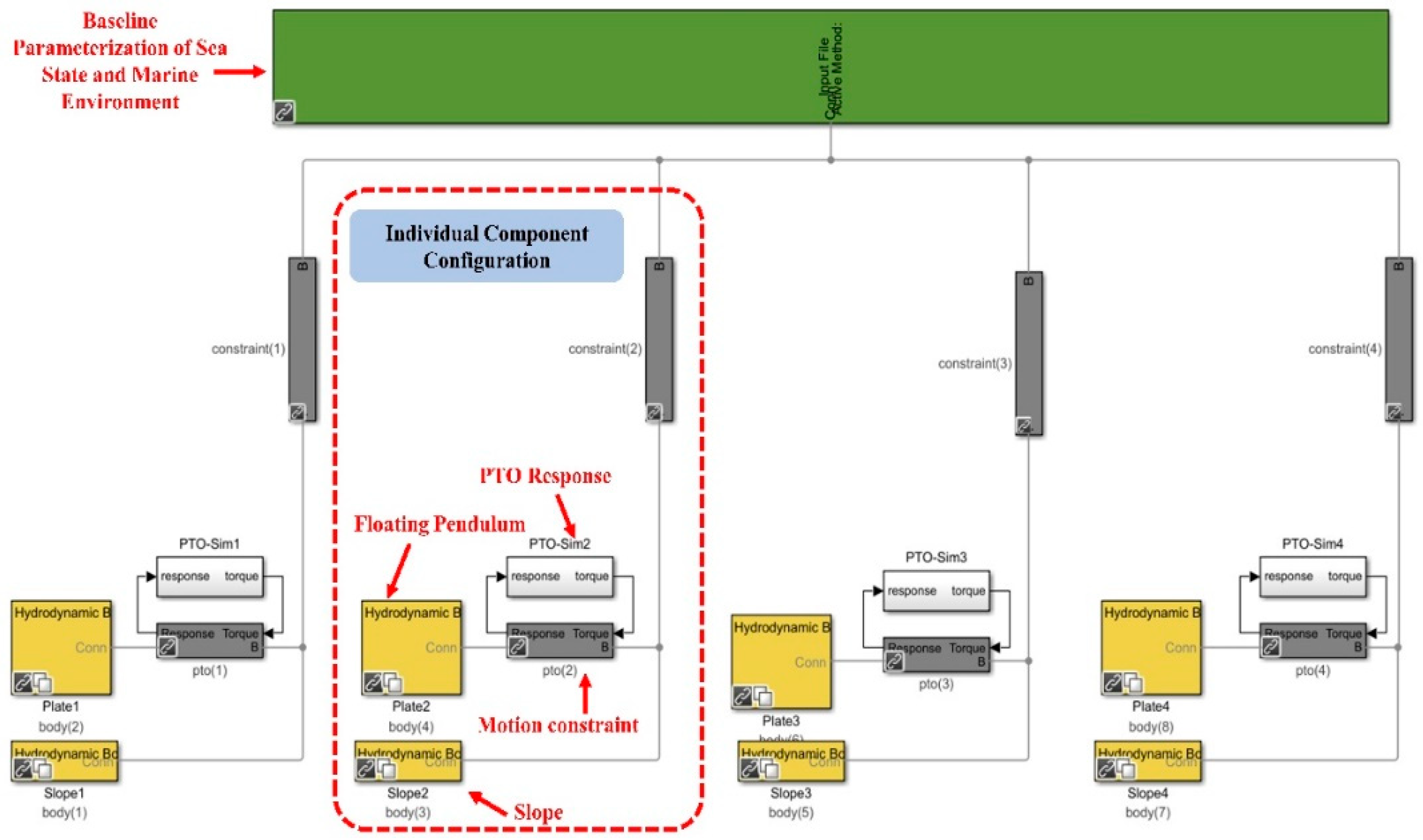
3.2.2. Simulation Platform for Arrayed S-PWEC
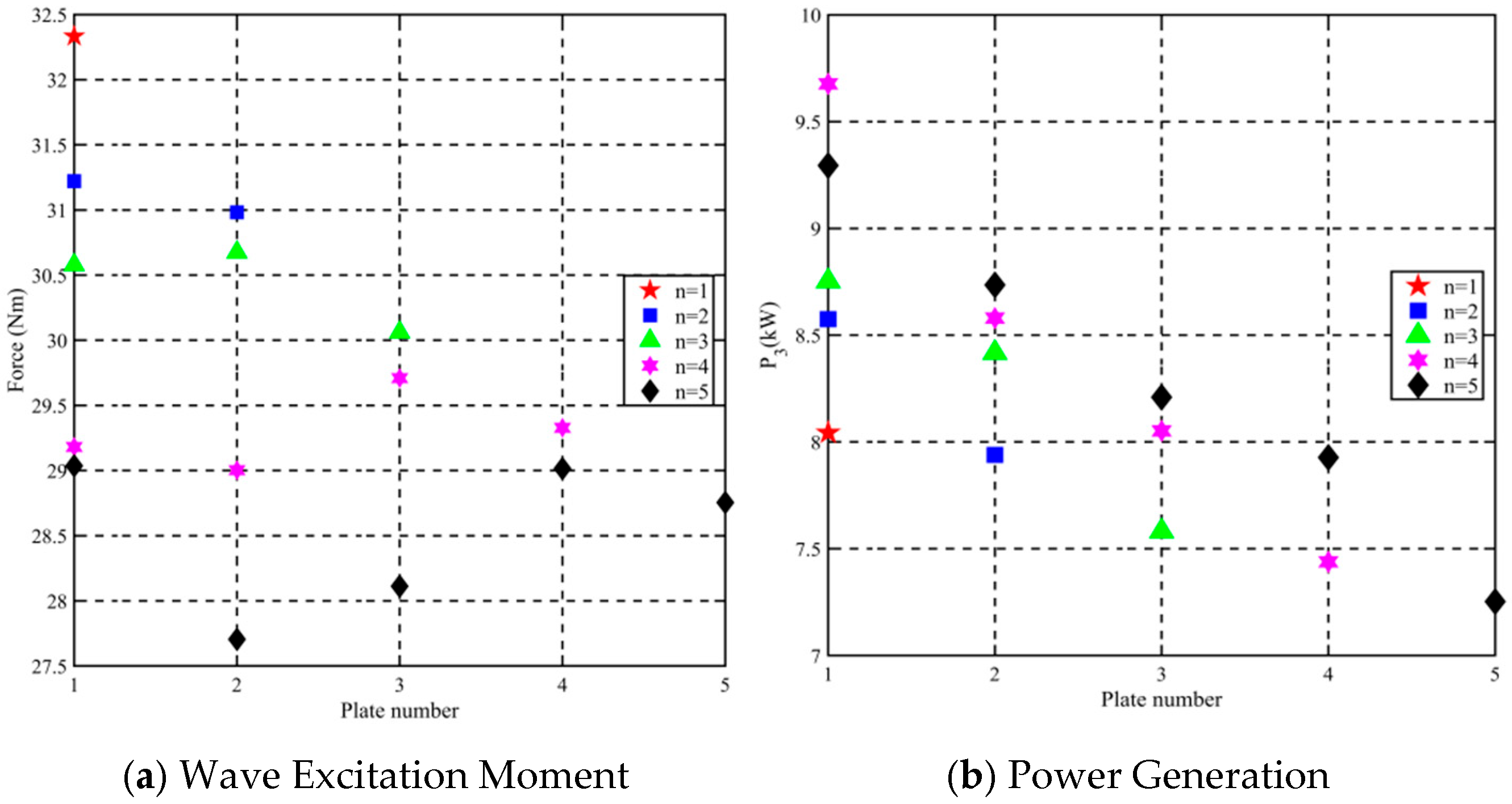
3.3. The Effect of Array Scale on System Output Characteristics
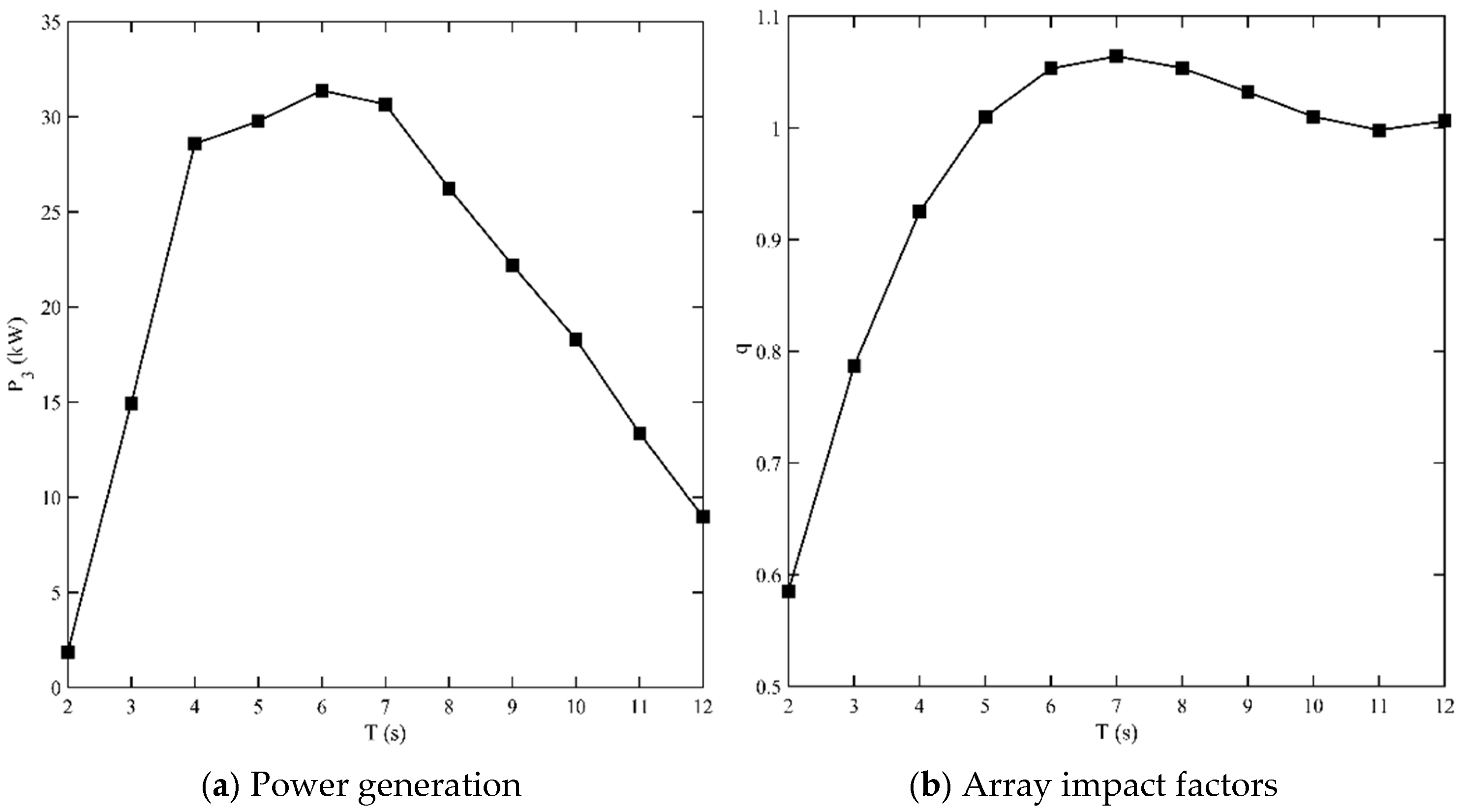
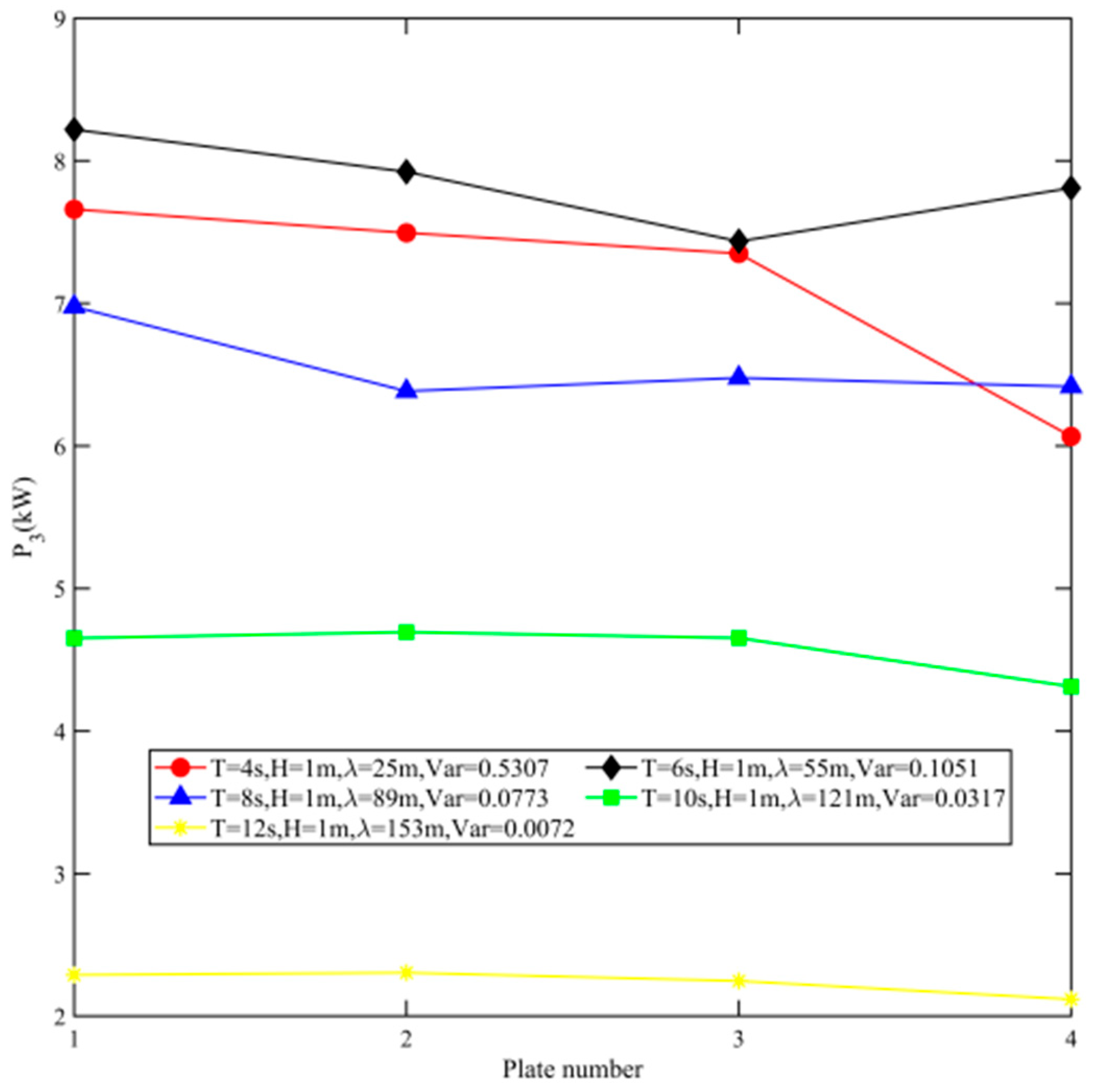
3.4. Power Generation Characterization of Linear Vertical Arrayed S-PWECs
3.5. Characterization of S-PWEC Power Generation by Individuals in an Array
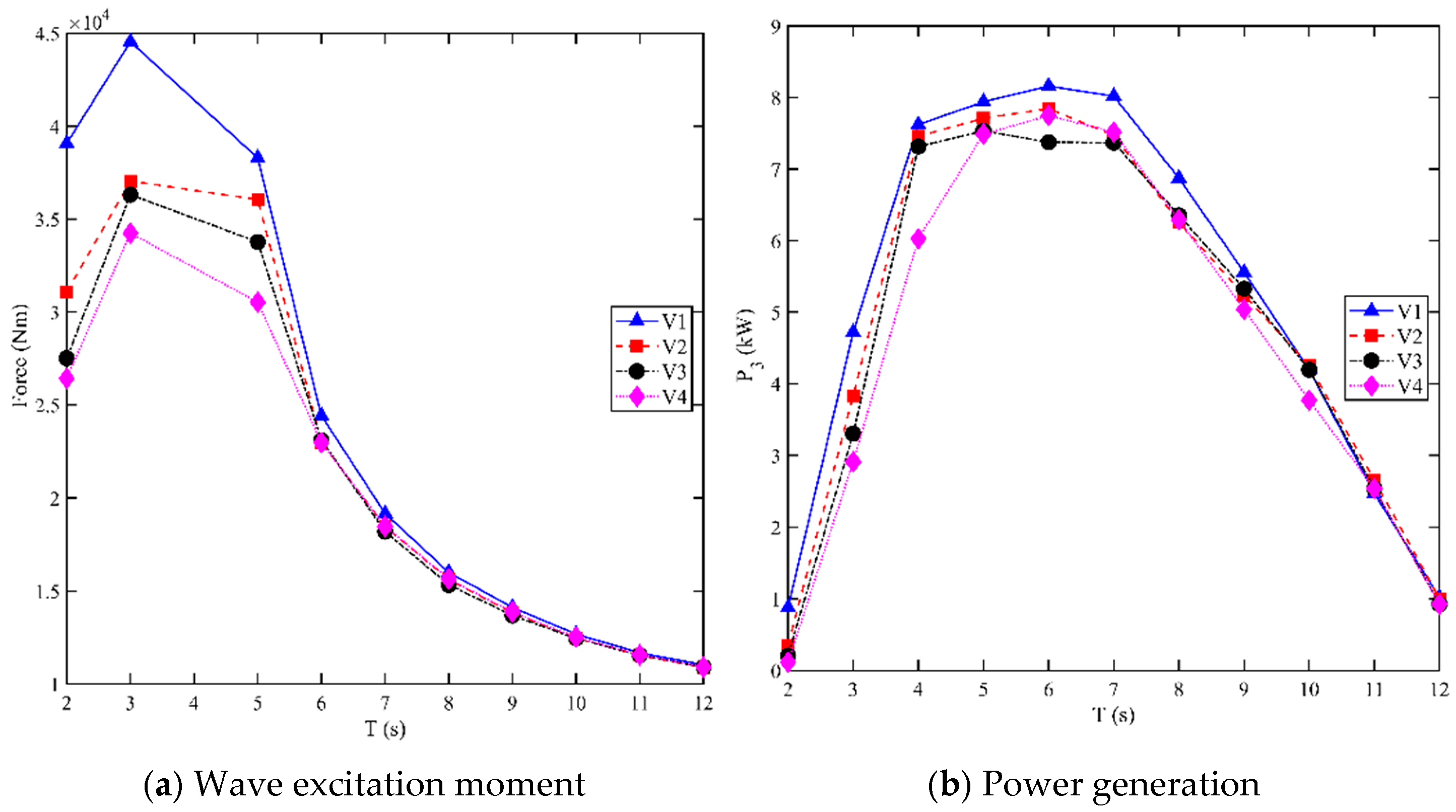
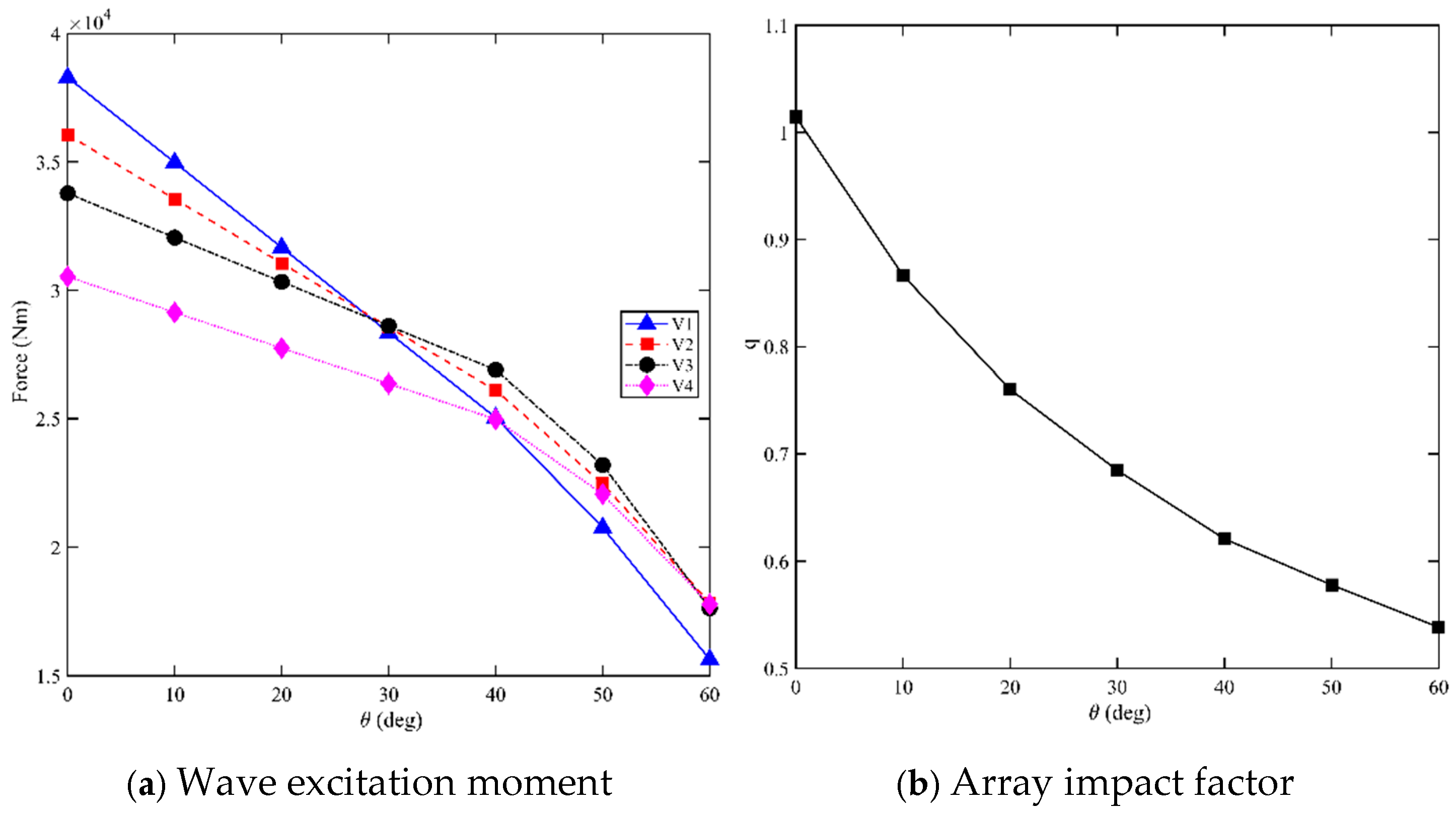
3.6. Effect of Wave Incidence Angle on Power Generation Characteristics
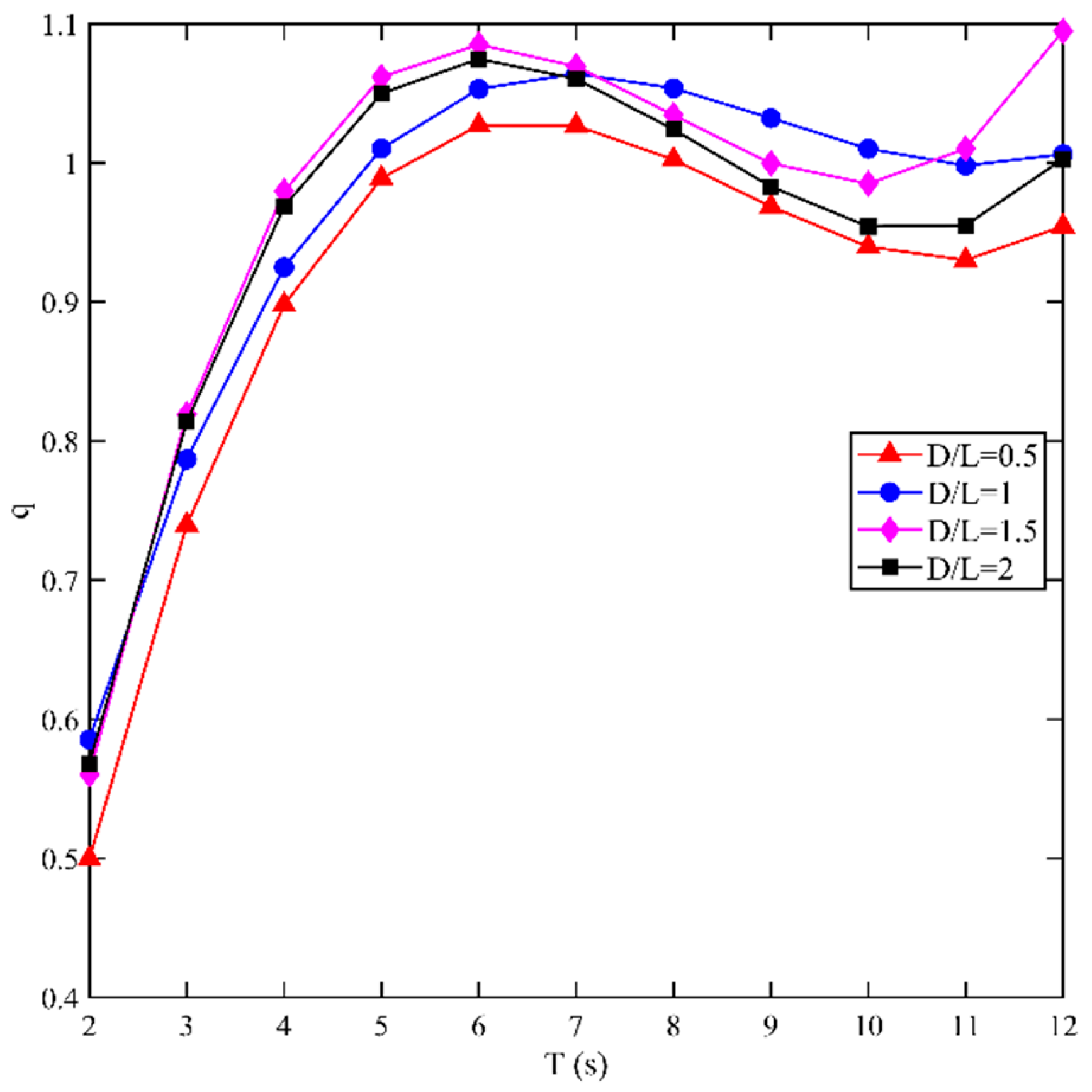
3.7. Influence of S-PWECs Array Spacing on System Power Generation Characteristics
4. Conclusions
- In a linear vertical array configuration, the S-PWEC devices interact with each other. As the number of devices in the array increases, the wave excitation moment and output power of each individual S-PWEC undergo more pronounced variations, suggesting the existence of an optimal array configuration for maximum power output.
- Incident waves arriving from different directions have a great impact on the linear vertical array arrangement. Therefore, the linear vertical array configuration of S-PWEC devices is not suitable for deep-sea areas, but can be used near the shore or near breakwaters where incident waves mostly come from one direction only.
- The spacing arrangement between S-PWEC devices is significantly influenced by sea conditions. Increasing the distance between adjacent S-PWECs under smaller wave periods, and decreasing it when the wave period is large, can effectively enhance the overall power generation of the linear vertical array layout. Among these, the linear vertical array device has the best power generation effect for the Zhejiang Sea area when D/L = 1.5.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Column vector of the radiative moments | |
| Hydrostatic recovery moment matrix | |
| Wave excitation moment matrix in the longitudinal rocking direction | |
| Column vector of the displacement response | |
| Column vector of the velocity response | |
| Acceleration response vector in pitch direction | |
| Mass matrix of array wave energy conversion device | |
| Additional moment of inertia in the longitudinal direction | |
| Wave radiation moment | |
| Delay function of the radiative force | |
| Differential element in time integration | |
| Moments of buoyancy | |
| Moments of gravity | |
| Secondary viscous drag moment | |
| Coefficient of secondary damping term in viscous moment | |
| Velocity of the floating plate | |
| Velocity of the surrounding fluid | |
| Moment of the viscous force on the pivot point | |
| Damping torque of the hydraulic power take-off | |
| Pressure difference on the piston in the hydraulic rod | |
| Force area of the piston in the hydraulic rod | |
| Length of the force arm from the hydraulic rod to the floating pendulum | |
| Braking torque of the limiting device | |
| Large stiffness coefficient of the limit spring | |
| Limit angle | |
| Step function | |
| Array impact factor | |
| Power generated by a single S-PWEC at normal operation conditions | |
| Average of the total power of all S-PWECs at the array layout | |
| Generating power of each S-PWEC |
References
- Cui, Y.; Zhao, H. Marine Renewable Energy Project: The Environmental Implication and Sustainable Technology. Ocean Coast. Manag. 2023, 232, 106415. [Google Scholar] [CrossRef]
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S.; et al. Wave Energy in Europe: Current Status and Perspectives. Renew. Sustain. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Astariz, S.; Iglesias, G. The Economics of Wave Energy: A Review. Renew. Sustain. Energy Rev. 2015, 45, 397–408. [Google Scholar] [CrossRef]
- Mitigation, C.C. IPCC Special Report on Renewable Energy Sources and Climate Change Mitigation. Renew. Energy 2011, 20, 2–24. [Google Scholar]
- Silva, D.; Martinho, P.; Soares, C.G. Wave Energy Distribution along the Portuguese Continental Coast Based on a Thirty Three Years Hindcast. Renew. Energy 2018, 127, 1064–1075. [Google Scholar] [CrossRef]
- Huang, H.S.; Wang, Y.Z.; Tang, Y.F.; Zhang, J. Discussion on Issues Related to Wave Power Generation in the Context of Low Carbonization. China Eng. Consult. 2021. Available online: https://kns.cnki.net/kcms2/article/abstract?v=a4fp6zKrpgahNuMfE8tySoUeeyrBcAYM5IqcatAetCnn570em8Kf7Hrd43ywHqwnvVa48r3diXaTHTa5vN2BujSqHCsao1xYPB_HFczCDb0JV3TKjoityPd5AF_WQGmbzxapEA12Fmp7-g9w9tvf_yh-h42EGJFEuOwDxOQU71Jj-BDIo6hNyQ==&uniplatform=NZKPT&language=CHS (accessed on 11 May 2025).
- Ruehl, K.; Forbush, D.D.; Yu, Y.-H.; Tom, N. Experimental and Numerical Comparisons of a Dual-Flap Floating Oscillating Surge Wave Energy Converter in Regular Waves. Ocean Eng. 2020, 196, 106575. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Hamzah, H.; Hamdoon, O.M.; Yang, H.-S.; Easa, H.; Lee, Y.-H. A Unique Design of a Hybrid Wave Energy Converter. Renew. Energy 2025, 245, 122814. [Google Scholar] [CrossRef]
- Bhaskar, G.; Sarkar, A. Numerical Study on the Performance of a Floating Circular Cross Section U-Tube Type Wave Energy Extractor Unit in the Ocean Environment. Renew. Energy 2025, 245, 122817. [Google Scholar] [CrossRef]
- Ermakov, A.M.; Ali, Z.A.; Mahmoodi, K.; Mason, O.; Ringwood, J.V. Optimisation of Heterogeneous Wave Energy Converter Arrays: A Control Co-Design Strategy. Renew. Energy 2025, 244, 122637. [Google Scholar] [CrossRef]
- Kramer, M. Performance Evaluation of the Wavestar Prototype. In Proceedings of the 9th European Wave and Tidal Conference, Southampton, UK, 5 September 2011. [Google Scholar]
- Han, M.; Shi, H.; Cao, F.; Wei, Z.; Zhu, K.; Wang, C.; Yu, M. Layout Optimization of Wave Energy Converter Arrays in Realistic Wave Climates. Renew. Sustain. Energy Rev. 2025, 218, 115829. [Google Scholar] [CrossRef]
- Shi, H.; Wang, C. Progress and Prospects of China’s Ocean Energy Technology. Sol. Energy 2017, 3, 30–37. [Google Scholar]
- Tay, Z.Y.; Venugopal, V. Hydrodynamic Interactions of Oscillating Wave Surge Converters in an Array under Random Sea State. Ocean Eng. 2017, 145, 382–394. [Google Scholar] [CrossRef]
- Tay, Z.Y. Energy Generation Enhancement of Arrays of Point Absorber Wave Energy Converters via Moonpool’s Resonance Effect. Renew. Energy 2022, 188, 830–848. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; He, H.; Zhang, J.; Chen, H. Dynamic Properties and Energy Conversion Efficiency of A Floating Multi-Body Wave Energy Converter. China Ocean Eng. 2018, 32, 347–357. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, M.; Jin, Y.; Zhou, J. Analysis of power generation performance of seesaw wave energy device array. Sci. Technol. Rev. 2021, 39, 35–41. [Google Scholar]
- Tay, Z.Y.; Htoo, N.L.; Konovessis, D. A Comparison of the Capture Width and Interaction Factors of WEC Arrays That Are Co-Located with Semi-Submersible-, Spar- and Barge-Supported Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2024, 12, 2019. [Google Scholar] [CrossRef]
- Zhong, Q.; Yeung, R.W. On Optimal Energy-Extraction Performance of Arrays of Wave-Energy Converters, with Full Consideration of Wave and Multi-Body Interactions. Ocean Eng. 2022, 250, 110863. [Google Scholar] [CrossRef]
- Wan, Z.; Li, Z.; Zhang, D.; Zheng, H. Design and Research of Slope-Pendulum Wave Energy Conversion Device. J. Mar. Sci. Eng. 2022, 10, 1572. [Google Scholar] [CrossRef]
- Song, T.; Li, Z.; Zheng, H.; Liang, C.; Wan, Z. Optimization on Hydrodynamic Performance for First Level Energy-Capturing Enhancement of a Floating Wave Energy Converter System with Flapping-Panel-Slope. J. Mar. Sci. Eng. 2023, 11, 345. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Functions Snd Ship Motion. Schiffstechnik 1962, 9, 101–109. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Comparing Nonlinear Hydrodynamic Forces in Heaving Point Absorbers and Oscillating Wave Surge Converters. J. Ocean Eng. Mar. Energy 2018, 4, 25–35. [Google Scholar] [CrossRef]
- Wan, Y.; Fan, C.; Zhang, J.; Meng, J.; Dai, Y.; Li, L.; Sun, W.; Zhou, P.; Wang, J.; Zhang, X. Wave Energy Resource Assessment off the Coast of China around the Zhoushan Islands. Energies 2017, 10, 1320. [Google Scholar] [CrossRef]
- NOAA Website. Available online: https://www.ncei.noaa.gov/maps/hourly/ (accessed on 11 May 2025).
- Shi, X.; Li, S.; Liang, B.; Zhao, J.; Liu, Y.; Wang, Z. Numerical Study on the Impact of Wave-Current Interaction on Wave Energy Resource Assessments in Zhoushan Sea Area, China. Renew. Energy 2023, 215, 119017. [Google Scholar] [CrossRef]
- So, R.; Simmons, A.; Brekken, T.; Ruehl, K.; Michelen, C. Development of PTO-Sim: A Power Performance Module for the Open-Source Wave Energy Converter Code WEC-Sim. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 9, p. V009T09A032. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wan, Z.; Li, Z.; Cao, G. Optimization Study of the Line Array Layout of Slope–Pendulum Wave Energy Conversion Device. J. Mar. Sci. Eng. 2025, 13, 1367. https://doi.org/10.3390/jmse13071367
Zhao Y, Wan Z, Li Z, Cao G. Optimization Study of the Line Array Layout of Slope–Pendulum Wave Energy Conversion Device. Journal of Marine Science and Engineering. 2025; 13(7):1367. https://doi.org/10.3390/jmse13071367
Chicago/Turabian StyleZhao, Yue, Zhanhong Wan, Ze Li, and Guiyu Cao. 2025. "Optimization Study of the Line Array Layout of Slope–Pendulum Wave Energy Conversion Device" Journal of Marine Science and Engineering 13, no. 7: 1367. https://doi.org/10.3390/jmse13071367
APA StyleZhao, Y., Wan, Z., Li, Z., & Cao, G. (2025). Optimization Study of the Line Array Layout of Slope–Pendulum Wave Energy Conversion Device. Journal of Marine Science and Engineering, 13(7), 1367. https://doi.org/10.3390/jmse13071367





