Performance Assessment of B-Series Marine Propellers with Cupping and Face Camber Ratio Using Machine Learning Techniques
Abstract
1. Introduction
2. Dataset of Propeller Series
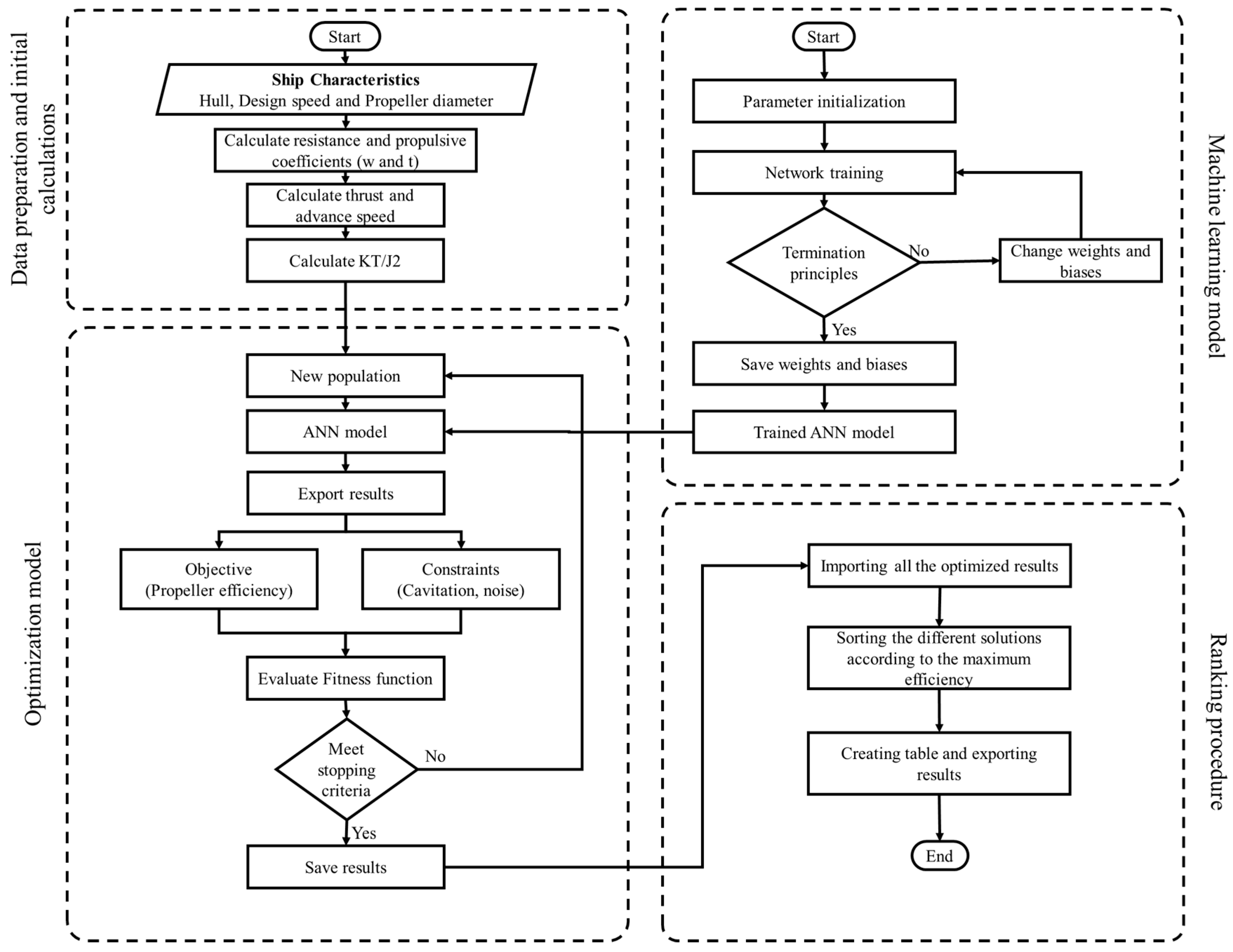
3. ANN Model for Performance Prediction
4. Optimization Model for Propeller Selection
5. Case Study and Computed Results
5.1. Ship Characteristics
5.2. Design Methodology
5.3. Computed Results
6. Conclusions
- Cupping in the range of 1.0% to 1.5% significantly improves propeller performance, increasing ηo by up to 9.3% compared to the reference design, while reducing tip speed and maintaining cavitation safety.
- FCR introduces a minor efficiency penalty (0.1–4.3%) but can still yield acceptable performance when carefully balanced with other parameters, such as EAR, P/D, and blade number.
- High blade count (Z = 5–6), elevated EAR (up to 0.89), and increased P/D (up to 1.40) are common characteristics among the top-performing designs.
- The ANN model, trained on a diverse dataset, demonstrated high prediction accuracy (R2 > 0.9999) and extremely fast execution time (<20 s per design), making it suitable for real-time optimization and early-stage design evaluations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| A | Matrix of linear inequality constraints |
| Aeq | Matrix of linear equality constraints |
| ANN | Artificial neural network |
| b | Vector of linear inequality constraints |
| B | Breadth |
| BEM | Boundary element methods |
| beq | Vector of linear equality constraints |
| Bp-δ | Blade Loading Coefficient vs. Diameter Ratio |
| BSFC | Brake-specific fuel consumption |
| c | Inequality constraints |
| ceq | Equality constraints |
| CFD | Computational fluid dynamics |
| CPP | Controllable pitch propeller |
| D | Propeller diameter |
| EAR | Expanded blade area ratio |
| EARmin | Minimum expanded blade area ratio to avoid cavitation |
| EDA | Exploratory data analysis |
| f(x) | Optimization model objective |
| FCR | Face camber ratio |
| FEM | Finite element method |
| g | Penalty function |
| GA | Genetic algorithm |
| h | Propeller centerline immersion |
| IMO | International Maritime Organization |
| j | Number of constraints |
| J | Advance coefficient |
| k | Constant |
| KCS | KRISO Container Ship |
| KQ | Torque coefficient |
| KT | Thrust coefficient |
| KT/J2 | Thrust loading coefficient |
| lb | Lower bounds |
| LWL | Length water line |
| MARPOL | International Convention for the Prevention of Pollution from Ships |
| ML | Machine learning |
| N | Propeller speed |
| P/D | Pitch to diameter ratio |
| Patm | Atmospheric pressure |
| PSO | Particle swarm optimization |
| Pv | Vapor pressure |
| R | Constant |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
| RT | Total resistance |
| S | Wetted surface area |
| T | Draft |
| t | Thrust deduction factor |
| T | Thrust |
| ub | Upper bounds |
| VA | Advance speed |
| Vs | Ship speed |
| Vtip | Tip speed |
| w | Wake fraction |
| x | Number of variables |
| Z | Number of propeller blades |
| γ | Specific weight |
| Δ | Displacement |
| ηo | Open-water propeller efficiency |
References
- Tadros, M.; Ventura, M.; Guedes Soares, C. Review of current regulations, available technologies, and future trends in the green shipping industry. Ocean Eng. 2023, 280, 114670. [Google Scholar] [CrossRef]
- Nazemian, A.; Ghadimi, P. Multi-objective optimization of ship hull modification based on resistance and wake field improvement: Combination of adjoint solver and CAD-CFD-based approach. J. Braz. Soc. Mech. Sci. 2021, 44, 27. [Google Scholar] [CrossRef]
- Mikkelsen, H.; Walther, J.H. Effect of roughness in full-scale validation of a CFD model of self-propelled ships. Appl. Ocean Res. 2020, 99, 102162. [Google Scholar] [CrossRef]
- Zha, L.; Zhu, R.; Hong, L.; Huang, S. Hull form optimization for reduced calm-water resistance and improved vertical motion performance in irregular head waves. Ocean Eng. 2021, 233, 109208. [Google Scholar] [CrossRef]
- Nazemian, A.; Boulougouris, E.; Aung, M.Z. Utilizing Machine Learning Tools for Calm Water Resistance Prediction and Design Optimization of a Fast Catamaran Ferry. J. Mar. Sci. Eng 2024, 12, 216. [Google Scholar] [CrossRef]
- Altosole, M.; Figari, M. Effective simple methods for numerical modelling of marine engines in ship propulsion control systems design. J. Nav. Archit. Mar. Eng. 2011, 8, 19. [Google Scholar] [CrossRef]
- Zhang, Q.; Pennycott, A.; Brace, C.J. A review of parallel and series turbocharging for the diesel engine. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1723–1733. [Google Scholar] [CrossRef]
- Larsen, U.; Sigthorsson, O.; Haglind, F. A comparison of advanced heat recovery power cycles in a combined cycle for large ships. Energy 2014, 74, 260–268. [Google Scholar] [CrossRef]
- Mancuso, A.; Saporito, A.; Tumino, D. Designing the internal reinforcements of a sailing boat using a topology optimization approach. Appl. Ocean Res. 2022, 129, 103384. [Google Scholar] [CrossRef]
- Vettor, R.; Guedes Soares, C. Development of a ship weather routing system. Ocean Eng. 2016, 123, 1–14. [Google Scholar] [CrossRef]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- Stark, C.; Xu, Y.; Zhang, M.; Yuan, Z.; Tao, L.; Shi, W. Study on Applicability of Energy-Saving Devices to Hydrogen Fuel Cell-Powered Ships. J. Mar. Sci. Eng. 2022, 10, 388. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Review of the IMO Initiatives for Ship Energy Efficiency and Their Implications. J. Mar. Sci. Appl. 2023, 22, 662–680. [Google Scholar] [CrossRef]
- Carlton, J. Marine Propellers and Propulsion, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Ekinci, S. A Practical Approach for Design of Marine Propellers with Systematic Propeller Series. Brodogradnja 2011, 62, 123–129. [Google Scholar]
- Epps, B.P.; Kimball, R.W. OpenProp v3, Open-Source Software for the Design and Analysis of Marine Propellers and Horizontal-Axis Turbines; EPPS Consulting LCC.: Hanover, NH, USA, 2013.
- Lee, K.-J.; Bae, J.-H.; Kim, H.-T.; Hoshino, T. A performance study on the energy recovering turbine behind a marine propeller. Ocean Eng. 2014, 91, 152–158. [Google Scholar] [CrossRef]
- Chreim, J.R.; Pimenta, M.d.M.; Dozzi Dantas, J.L.; Assi, G.R.S.; Katsuno, E.T. Development of a Lifting-Line-Based Method for Preliminary Propeller Design. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. Volume 2: CFD and FSI. [Google Scholar]
- Islam, H.; Guedes Soares, C. Uncertainty analysis in ship resistance prediction using OpenFOAM. Ocean Eng. 2019, 191, 105805. [Google Scholar] [CrossRef]
- Kim, K.; Tillig, F.; Bathfield, N.; Liljenberg, H. Hydrodynamic optimization of twin-skeg LNG ships by CFD and model testing. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 392–405. [Google Scholar] [CrossRef][Green Version]
- Andersson, J.; Shiri, A.A.; Bensow, R.E.; Yixing, J.; Chengsheng, W.; Gengyao, Q.; Deng, G.; Queutey, P.; Xing-Kaeding, Y.; Horn, P.; et al. Ship-scale CFD benchmark study of a pre-swirl duct on KVLCC2. Appl. Ocean Res. 2022, 123, 103134. [Google Scholar] [CrossRef]
- Grlj, C.G.; Degiuli, N.; Farkas, A.; Martić, I. Numerical Study of Scale Effects on Open Water Propeller Performance. J. Mar. Sci. Eng. 2022, 10, 1132. [Google Scholar] [CrossRef]
- Coraddu, A.; Lim, S.; Oneto, L.; Pazouki, K.; Norman, R.; Murphy, A.J. A novelty detection approach to diagnosing hull and propeller fouling. Ocean Eng. 2019, 176, 65–73. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, K.; Abdel-Maksoud, M. noiseNet: A neural network to predict marine propellers’ underwater radiated noise. Ocean Eng. 2021, 236, 109542. [Google Scholar] [CrossRef]
- Vesting, F.; Bensow, R.E. On surrogate methods in propeller optimisation. Ocean Eng. 2014, 88, 214–227. [Google Scholar] [CrossRef]
- Doijode, P.S.; Hickel, S.; van Terwisga, T.; Visser, K. A machine learning approach for propeller design and optimization: Part I. Appl. Ocean Res. 2022, 124, 103178. [Google Scholar] [CrossRef]
- Doijode, P.S.; Hickel, S.; van Terwisga, T.; Visser, K. A machine learning approach for propeller design and optimization: Part II. Appl. Ocean Res. 2022, 124, 103174. [Google Scholar] [CrossRef]
- Gaggero, S.; Coppede, A.; Villa, D.; Vernengo, G.; Bonfiglio, L. A data-driven probabilistic learning approach for the prediction of controllable pitch propellers performance. In MARINE VIII: Proceedings of the VIII International Conference on Computational Methods in Marine Engineering; CIMNE: Göteborg, Sweden, 2019; pp. 544–555. [Google Scholar]
- Li, L.; Chen, Y.; Qiang, Y.; Zhou, B.; Chen, W. Construction and application of numerical diagram for high-skew propeller based on machine learning. Ocean Eng. 2023, 278, 114480. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Hong, S.-Y.; Song, J.-H. Composite propeller design optimization for cavitation minimization using deep learning-based objective parameter prediction model. Ocean Eng. 2023, 287, 115760. [Google Scholar] [CrossRef]
- Hwang, J.-L.; Tsai, J.-F.; Li, C.-Y. Cupped propeller test and analysis. Sh. Technol. Res. 1995, 42, 186–192. [Google Scholar]
- Anevlavi, D.; Zafeiris, S.; Papadakis, G.; Belibassakis, K. Efficiency Enhancement of Marine Propellers via Reformation of Blade Tip-Rake Distribution. J. Mar. Sci. Eng. 2023, 11, 2179. [Google Scholar] [CrossRef]
- Pourmostafa, M.; Ghadimi, P. Applying boundary element method to simulate a high-skew Controllable Pitch Propeller with different hub diameters for preliminary design purposes. Cogent Eng. 2020, 7, 1805857. [Google Scholar] [CrossRef]
- Tadros, M.; Sun, Z.; Shi, W. Effect of Propeller Face Camber Ratio on the Reduction of Fuel Consumption. J. Mar. Sci. Eng. 2024, 12, 2225. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Optimization scheme for the selection of the propeller in ship concept design. In Progress in Maritime Technology and Engineering; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2018; pp. 233–239. [Google Scholar]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. Controllable pitch propeller optimization through meta-heuristic algorithm. Eng. Comput. 2021, 37, 2257–2271. [Google Scholar] [CrossRef]
- Hydrocomp. NavCad: Hydrodynamic and Propulsion System Simulation. HydroComp Inc. Available online: https://www.hydrocompinc.com/solutions/navcad/ (accessed on 15 April 2024).
- Tadros, M.; Shi, W.; Xu, Y.; Song, Y. A unified cross-series marine propeller design method based on machine learning. Ocean Eng. 2024, 314, 119691. [Google Scholar] [CrossRef]
- Gypa, I.; Jansson, M.; Wolff, K.; Bensow, R. Propeller optimization by interactive genetic algorithms and machine learning. Sh. Technol. Res. 2023, 70, 56–71. [Google Scholar] [CrossRef]
- Gypa, I.; Jansson, M.; Bensow, R. Marine propeller optimisation through user interaction and machine learning for advanced blade design scenarios. Sh. Offshore Struct 2023, 19, 1659–1675. [Google Scholar] [CrossRef]
- Mohammad Nouri, N.; Mohammadi, S. Numerical investigation of the effects of camber ratio on the hydrodynamic performance of a marine propeller. Ocean Eng. 2018, 148, 632–636. [Google Scholar] [CrossRef]
- MacPherson, D.M. Small Propeller Cup: A Proposed Geometry Standard and a New Performance Model. In 8th Propeller and Shafting Symposium; SNAME: Virginia Beach, VA, USA, 1997. [Google Scholar]
- Samsul, M.B. Blade Cup Method for Cavitation Reduction in Marine Propellers. Pol. Marit. Res. 2021, 28, 54–62. [Google Scholar] [CrossRef]
- Tadros, M.; Vettor, R.; Ventura, M.; Guedes Soares, C. Effect of propeller cup on the reduction of fuel consumption in realistic weather conditions. J. Mar. Sci. Eng. 2022, 10, 1039. [Google Scholar] [CrossRef]
- Oosterveld, M.; Van Oossanen, P. Further computer-analyzed data of the Wageningen B-screw series. Int. Shipbuild. Prog. 1975, 22, 251–262. [Google Scholar] [CrossRef]
- Blount, D.L.; Hubble, E.N. Sizing Segmental Section Commercially Available Propellers for Small Craft. In SNAME Propeller Symposium; SNAME: Virginia Beach, VA, USA, 1981. [Google Scholar]
- Kaplan, A. Progressive Pitch Distributions: (Part 2) Performance. HydroComp, Inc. Available online: https://www.hydrocompinc.com/wp-content/uploads/2020/02/NMPA-Newsletter-Part-2-HCI.pdf (accessed on 12 May 2024).
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Moreira, L.; Vettor, R.; Guedes Soares, C. Neural Network Approach for Predicting Ship Speed and Fuel Consumption. J. Mar. Sci. Eng. 2021, 9, 119. [Google Scholar] [CrossRef]
- Mittendorf, M.; Nielsen, U.D.; Bingham, H.B. Data-driven prediction of added-wave resistance on ships in oblique waves—A comparison between tree-based ensemble methods and artificial neural networks. Appl. Ocean Res. 2022, 118, 102964. [Google Scholar] [CrossRef]
- Cepowski, T. The use of a set of artificial neural networks to predict added resistance in head waves at the parametric ship design stage. Ocean Eng. 2023, 281, 114744. [Google Scholar] [CrossRef]
- Yu, A.; Li, Y.; Li, S.; Gong, J. Construction High Precision Neural Network Proxy Model for Ship Hull Structure Design Based on Hybrid Datasets of Hydrodynamic Loads. J. Mar. Sci. Appl. 2024, 23, 49–63. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, H.; Yin, L.; Liang, Y.; Wang, B.; Li, Z.; Song, X.; Zhang, Y. A voyage with minimal fuel consumption for cruise ships. J. Clean. Prod. 2019, 215, 144–153. [Google Scholar] [CrossRef]
- Byrd, R.H.; Mary, E.H.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optimiz. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Keller, W.H. Extended Diagrams for Determining the Resistance and Required Power for Single-Screw Ships. Int. Shipbuild. Prog. 1973, 20, 133–142. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. An optimisation procedure for propeller selection for different shaft inclinations. Int. J. Marit. Eng. 2022, 164, 295–315. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Schoenauer, M. Evolutionary algorithms for constrained parameter optimization problems. Evol. Comput. 1996, 4, 1–32. [Google Scholar] [CrossRef]
- The MathWorks Inc. Fmincon. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 2 June 2017).
- SIMMAN. Workshop on Verification and Validation of Ship Maneuvering Simulation Methods. Available online: http://www.simman2008.dk/index.html (accessed on 8 September 2015).
- Holtrop, J. A statistical re-analysis of resistance and propulsion data. Int. Shipbuild. Prog. 1984, 31, 272–276. [Google Scholar]
- Holtrop, J.; Mennen, G.G.J. An approximate power prediction method. Int. Shipbuild. Prog. 1982, 29, 166–170. [Google Scholar] [CrossRef]
- Islam, H.; Ventura, M.; Guedes Soares, C.; Tadros, M.; Abdelwahab, H.S. Comparison between empirical and CFD based methods for ship resistance and power prediction. In Trends in Maritime Technology and Engineering; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2022; pp. 347–357. [Google Scholar]
- Tadros, M.; Xu, Y.; Das, T.; Shi, W. Retrofitting Propeller Procedure for a Hydrogen Fueled Offshore Support Vessel. In Proceedings of the 43rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2024), Singapore, 9–14 June 2024. [Google Scholar]
- Mercury Marine. Prop Bite: How Many Prop Blades Do You Need? Available online: https://www.mercurymarine.com/ca/en/lifestyle/dockline/how-many-prop-blades-do-you-need (accessed on 23 June 2025).
- Ristea, M.; Popa, A.; Neagu, D.I. CFD modeling of a five-bladed propeller by using the RANSE approach. Sci. Bull. “Mircea Cel Batran” Nav. Acad. 2015, 18, 153–158. [Google Scholar]
- Sinaga, N.; Dhande, D.Y.; Yunianto, B. A numerical investigation of the effect of blade number on the performance of an INSEAN E779A marine propeller in a cavitating flow using computational fluid dynamics. Ocean Eng. 2022, 261, 112063. [Google Scholar] [CrossRef]
- Tadros, M.; Vettor, R.; Ventura, M.; Guedes Soares, C. Coupled Engine-Propeller Selection Procedure to Minimize Fuel Consumption at a Specified Speed. J. Mar. Sci. Eng. 2021, 9, 59. [Google Scholar] [CrossRef]
- Karim, M.M.; Naz, N. Numerical Study on Flow Around Modern Ship Hulls with Rudder-Propeller Interactions. J. Mar. Sci. Appl. 2019, 18, 400–416. [Google Scholar] [CrossRef]
- Lungu, A. Numerical simulation of the cavitating KP505 propeller working in open water conditions. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 042035. [Google Scholar] [CrossRef]
- Ge, M.; Sun, C.; Zhang, G.; Coutier-Delgosha, O.; Fan, D. Combined suppression effects on hydrodynamic cavitation performance in Venturi-type reactor for process intensification. Sonochemistry 2022, 86, 106035. [Google Scholar] [CrossRef] [PubMed]




| Parameter[-] | Reference[-] | Number of Blades[-] | Blade Area Ratio[-] | Pitch/Diameter Ratio[-] | Cupping Percentage[%] | FCR Percentage[%] |
|---|---|---|---|---|---|---|
| Wageningen B Series | [37,45,46,47] | 3–7 | 0.35–0.80 for 3 blades 0.40–1.00 for 4 blades 0.45–1.05 for 5 blades 0.50–0.95 for 6 blades 0.55–0.85 for 7 blades | 0.5–1.4 | 0–1.5 | 0–1.5 |
| Propeller Series | B Series | B Series | B Series | |
|---|---|---|---|---|
| Propeller blades | 3 | 4 | 5 | |
| Cupping percentage | 0.0 | 1.0 | 0.0 | |
| FCR | 0.0 | 0.0 | 1.5 | |
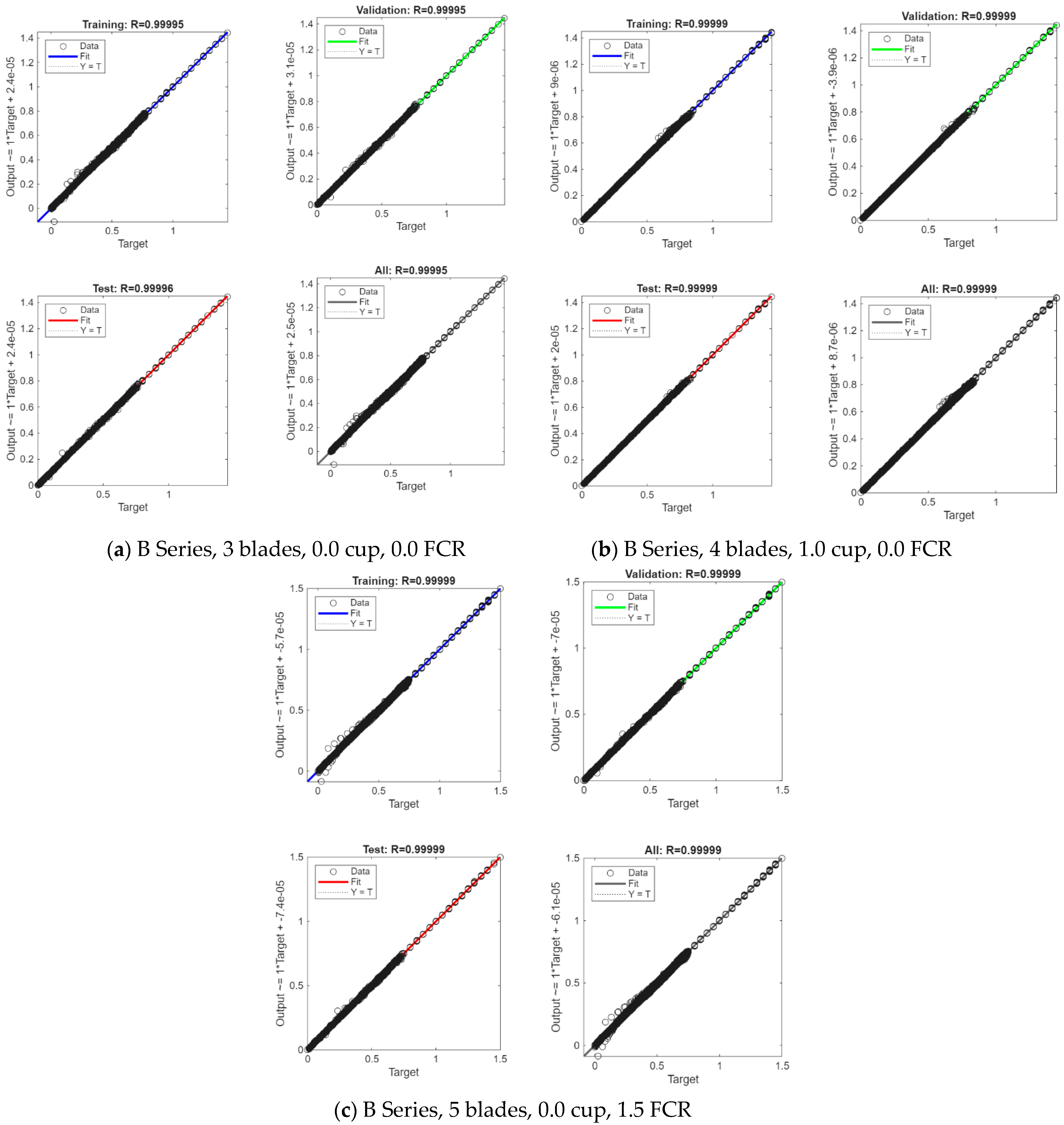
| R2 | Training | 0.99995 | 0.99999 | 0.99999 |
| Validation | 0.99995 | 0.99999 | 0.99999 | |
| Test | 0.99996 | 0.99999 | 0.99999 | |
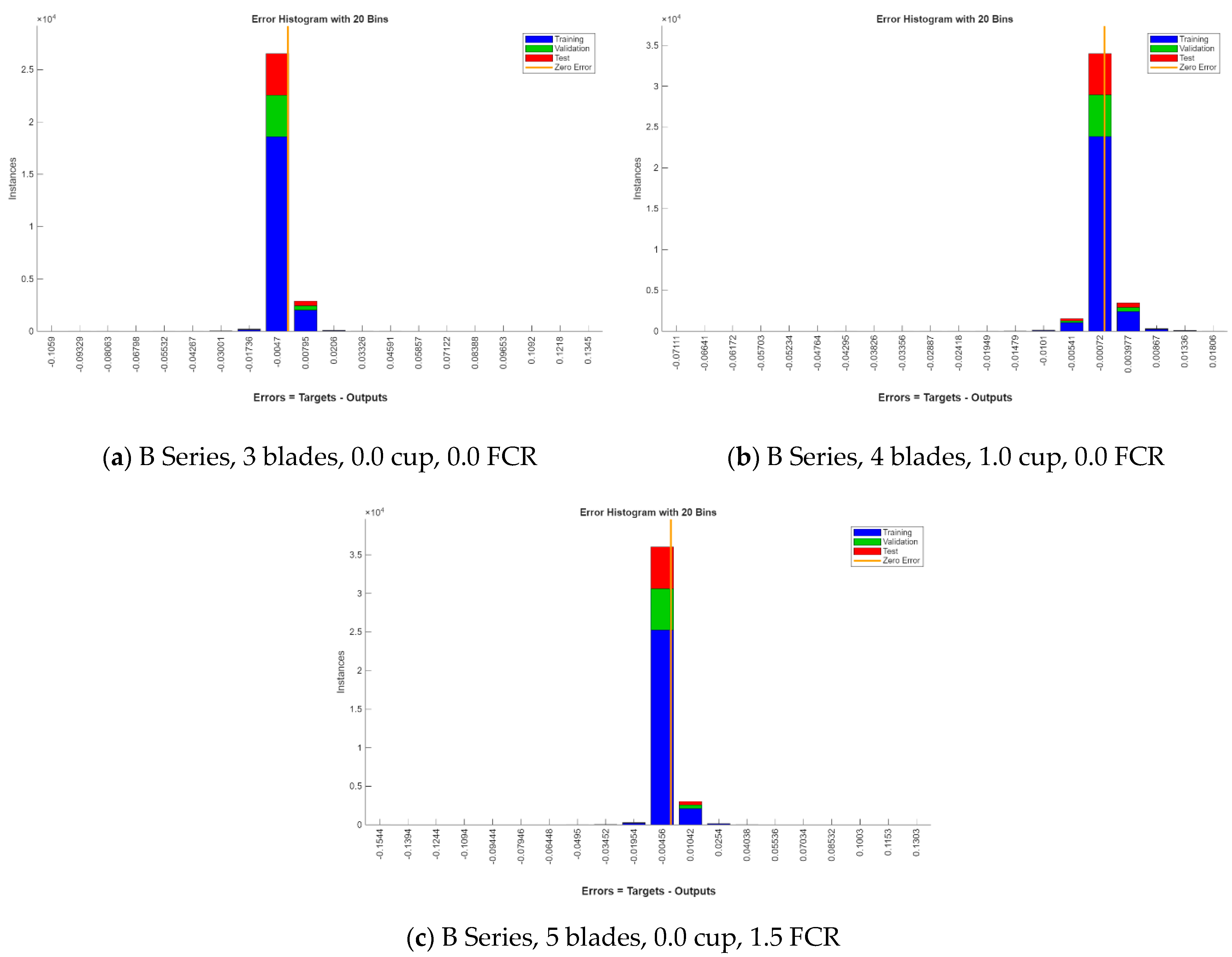
| RMSE | Training | 0.0026 | 0.0020 | 0.0027 |
| Validation | 0.0025 | 0.0018 | 0.0025 | |
| Test | 0.0025 | 0.0020 | 0.0025 |
| Specification | Symbols | Units | KCS Ship |
|---|---|---|---|
| Length water line | LWL | [m] | 232.4 |
| Breadth | B | [m] | 32.2 |
| Draft | T | [m] | 10.8 |
| Wetted surface area | S | [m2] | 9645 |
| Displacement | Δ | [tonne] | 52,030 |
| Ship speed | Vs | [knot] | 24 |
| Propeller Geometry | Propeller Performance | Cavitation and Noise Limits | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rank [-] | Z [-] | EAR [-] | P/D [-] | ηo [%] | J [-] | KT [-] | KQ [-] | Cup [%] | FCR [%] | Vtip [m/s] | EARmin [-] | Vtip-max [m/s] |
| 1 | 6 | 0.89 | 1.40 | 71.7 | 1.017 | 0.443 | 0.101 | 1.5 | 0.0 | 28.5 | 0.89 | 46 |
| 2 | 6 | 0.89 | 1.06 | 68.1 | 0.824 | 0.292 | 0.057 | 1.0 | 0.0 | 35.1 | 0.89 | 46 |
| 3 | 5 | 0.89 | 0.99 | 67.9 | 0.778 | 0.259 | 0.048 | 1.0 | 0.0 | 37.2 | 0.83 | 46 |
| 4 | 3 | 0.80 | 1.40 | 67.1 | 0.953 | 0.392 | 0.090 | 1.5 | 0.0 | 30.4 | 0.69 | 53 |
| 5 | 6 | 0.89 | 1.06 | 67.0 | 0.777 | 0.254 | 0.047 | 0.5 | 0.0 | 37.3 | 0.89 | 46 |
| 6 | 5 | 0.83 | 0.96 | 66.9 | 0.715 | 0.217 | 0.037 | 0.5 | 0.0 | 40.5 | 0.83 | 46 |
| 7 | 5 | 0.83 | 0.97 | 66.6 | 0.818 | 0.285 | 0.056 | 1.5 | 0.0 | 35.4 | 0.83 | 46 |
| 8 | 4 | 0.76 | 0.98 | 66.1 | 0.759 | 0.249 | 0.045 | 1.0 | 0.0 | 38.2 | 0.76 | 53 |
| 9 | 4 | 0.76 | 0.93 | 66.1 | 0.685 | 0.200 | 0.033 | 0.5 | 0.0 | 42.2 | 0.76 | 53 |
| 10 | 4 | 0.76 | 1.01 | 65.4 | 0.818 | 0.287 | 0.057 | 1.5 | 0.0 | 35.4 | 0.76 | 53 |
| 11 | 3 | 0.69 | 0.91 | 65.1 | 0.714 | 0.214 | 0.038 | 1.0 | 0.0 | 40.5 | 0.69 | 53 |
| Ref. | 5 | 0.8 | 0.95 | 65.0 | 0.679 | 0.195 | 0.032 | 0.0 | 0.0 | 42.66 | 0.813 | 46 |
| 12 | 5 | 0.83 | 1.03 | 64.9 | 0.732 | 0.228 | 0.042 | 0.0 | 1.5 | 39.5 | 0.83 | 46 |
| 13 | 5 | 0.83 | 1.04 | 64.7 | 0.726 | 0.224 | 0.041 | 0.0 | 1.0 | 39.9 | 0.83 | 46 |
| 14 | 6 | 0.89 | 1.10 | 64.4 | 0.755 | 0.242 | 0.046 | 0.0 | 0.5 | 38.4 | 0.89 | 46 |
| 15 | 4 | 0.76 | 1.00 | 64.4 | 0.702 | 0.207 | 0.037 | 0.0 | 1.5 | 41.2 | 0.76 | 53 |
| 16 | 3 | 0.69 | 0.85 | 64.4 | 0.640 | 0.169 | 0.026 | 0.5 | 0.0 | 45.3 | 0.69 | 53 |
| 17 | 5 | 0.83 | 1.03 | 64.4 | 0.712 | 0.214 | 0.038 | 0.0 | 0.5 | 40.6 | 0.83 | 46 |
| 18 | 6 | 0.89 | 1.11 | 64.3 | 0.786 | 0.260 | 0.051 | 0.0 | 1.5 | 36.8 | 0.89 | 46 |
| 19 | 6 | 0.89 | 1.08 | 64.2 | 0.758 | 0.243 | 0.046 | 0.0 | 1.0 | 38.2 | 0.89 | 46 |
| 20 | 4 | 0.76 | 1.01 | 64.2 | 0.697 | 0.203 | 0.036 | 0.0 | 1.0 | 41.6 | 0.76 | 53 |
| 21 | 4 | 0.76 | 0.99 | 63.7 | 0.682 | 0.195 | 0.034 | 0.0 | 0.5 | 42.5 | 0.76 | 53 |
| 22 | 3 | 0.69 | 0.94 | 62.9 | 0.656 | 0.179 | 0.030 | 0.0 | 1.5 | 44.1 | 0.69 | 53 |
| 23 | 3 | 0.69 | 1.00 | 62.9 | 0.677 | 0.191 | 0.034 | 0.0 | 1.0 | 42.8 | 0.69 | 53 |
| 24 | 3 | 0.69 | 1.00 | 62.2 | 0.670 | 0.187 | 0.032 | 0.0 | 0.5 | 43.2 | 0.69 | 53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadros, M.; Boulougouris, E. Performance Assessment of B-Series Marine Propellers with Cupping and Face Camber Ratio Using Machine Learning Techniques. J. Mar. Sci. Eng. 2025, 13, 1345. https://doi.org/10.3390/jmse13071345
Tadros M, Boulougouris E. Performance Assessment of B-Series Marine Propellers with Cupping and Face Camber Ratio Using Machine Learning Techniques. Journal of Marine Science and Engineering. 2025; 13(7):1345. https://doi.org/10.3390/jmse13071345
Chicago/Turabian StyleTadros, Mina, and Evangelos Boulougouris. 2025. "Performance Assessment of B-Series Marine Propellers with Cupping and Face Camber Ratio Using Machine Learning Techniques" Journal of Marine Science and Engineering 13, no. 7: 1345. https://doi.org/10.3390/jmse13071345
APA StyleTadros, M., & Boulougouris, E. (2025). Performance Assessment of B-Series Marine Propellers with Cupping and Face Camber Ratio Using Machine Learning Techniques. Journal of Marine Science and Engineering, 13(7), 1345. https://doi.org/10.3390/jmse13071345







