Efficient Prediction of Shallow-Water Acoustic Transmission Loss Using a Hybrid Variational Autoencoder–Flow Framework
Abstract
1. Introduction
2. Method
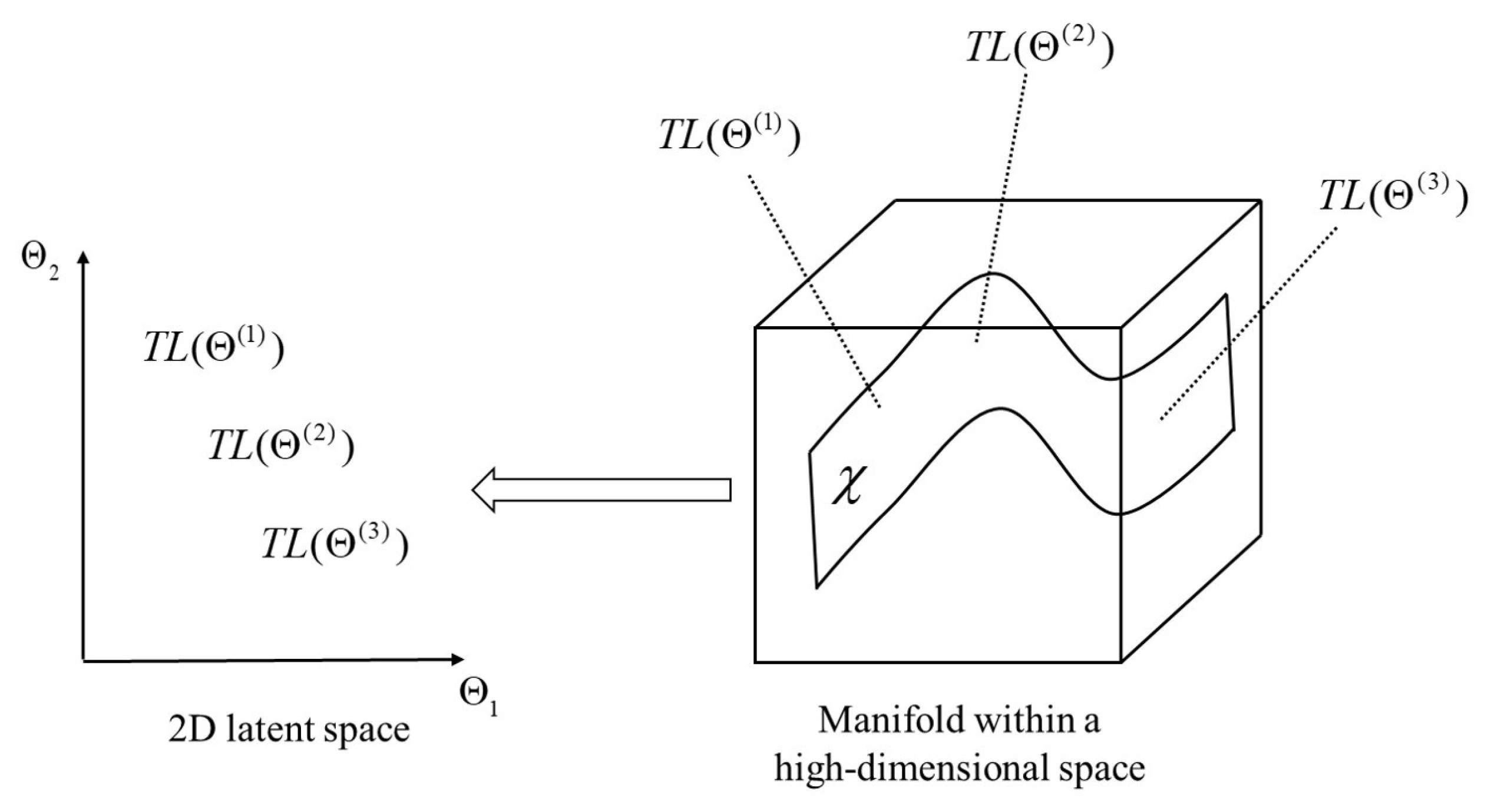
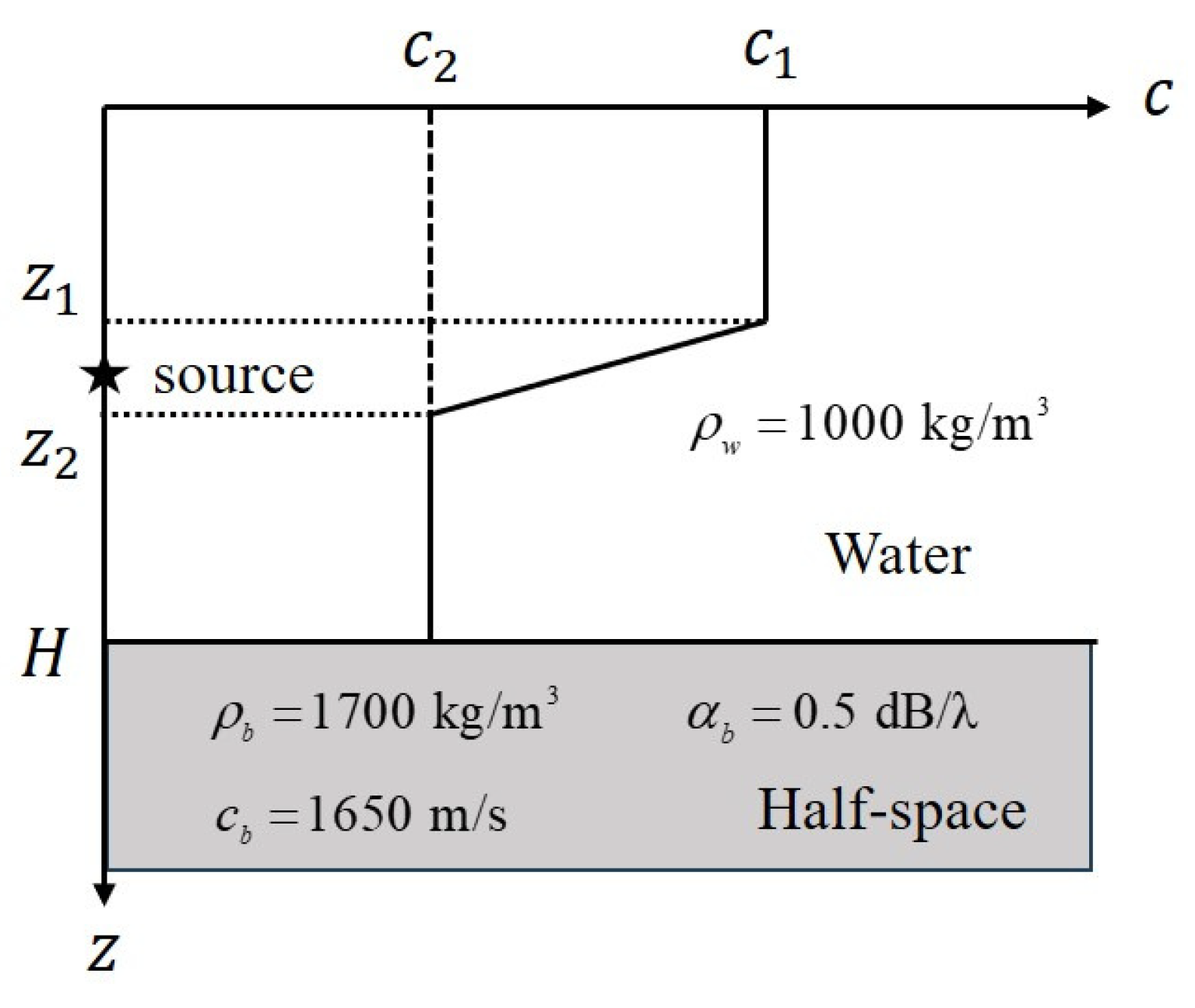
2.1. Problem Description
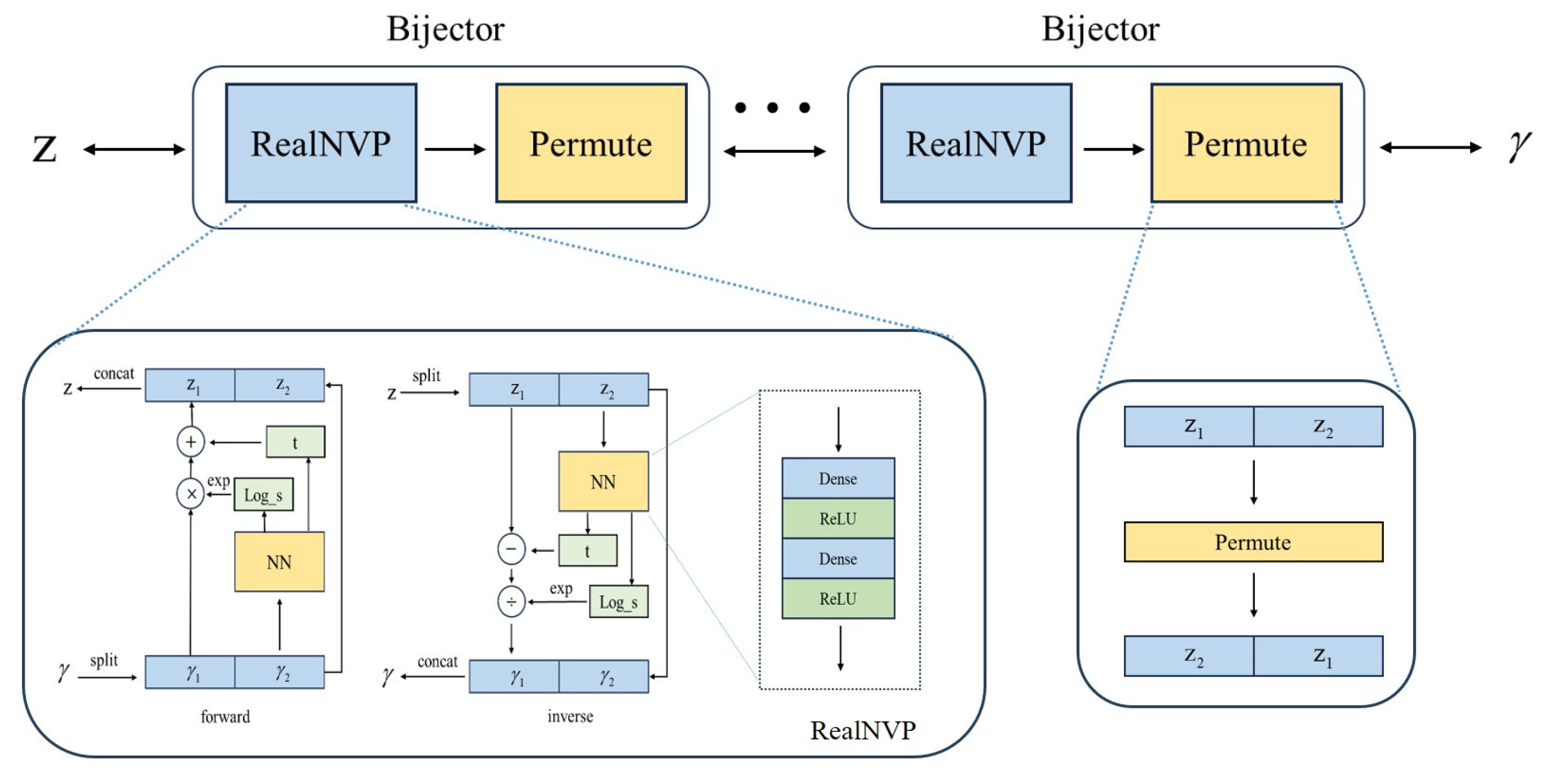
2.2. VAE–Flow Framework
3. Method Implementation
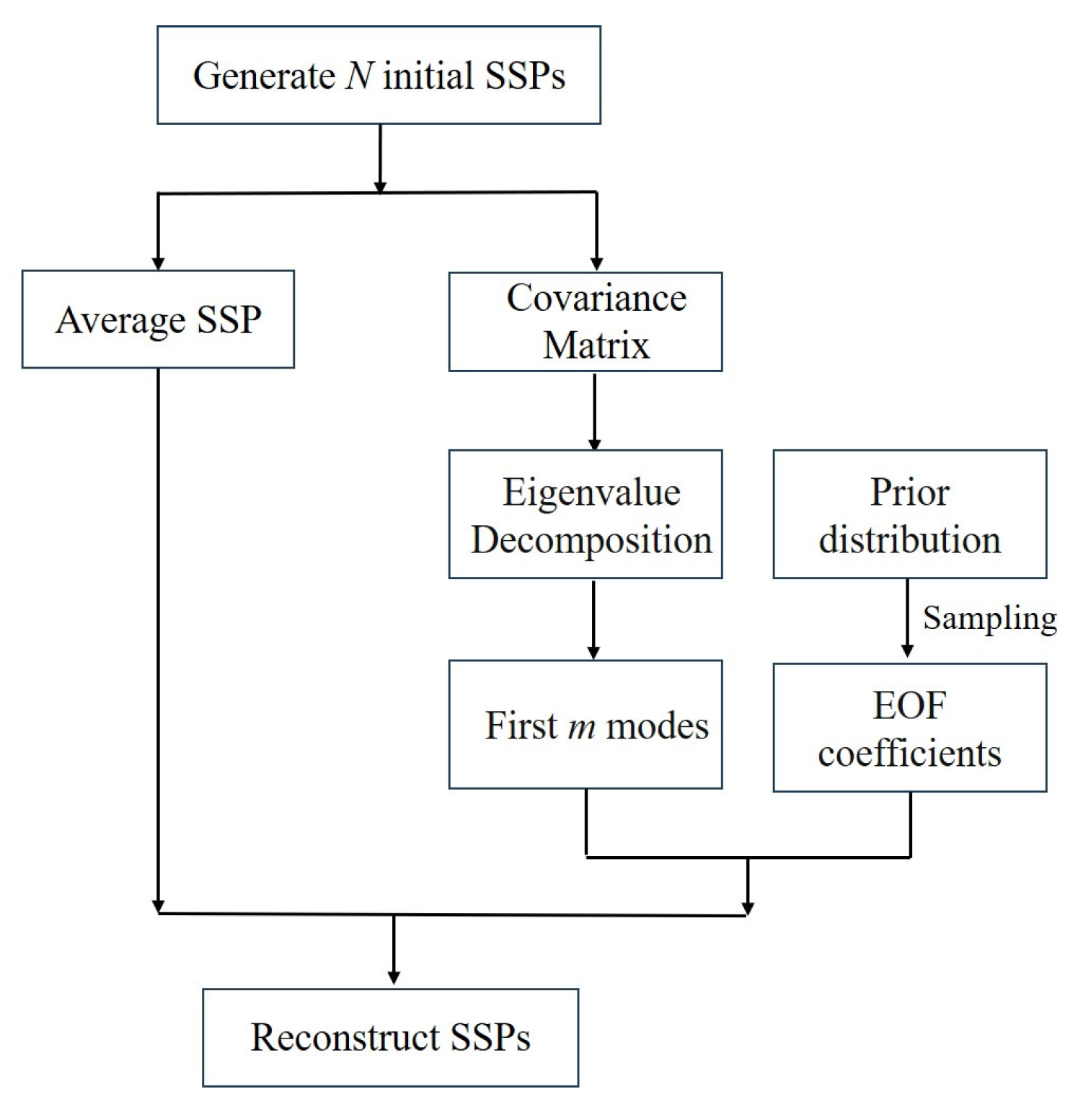
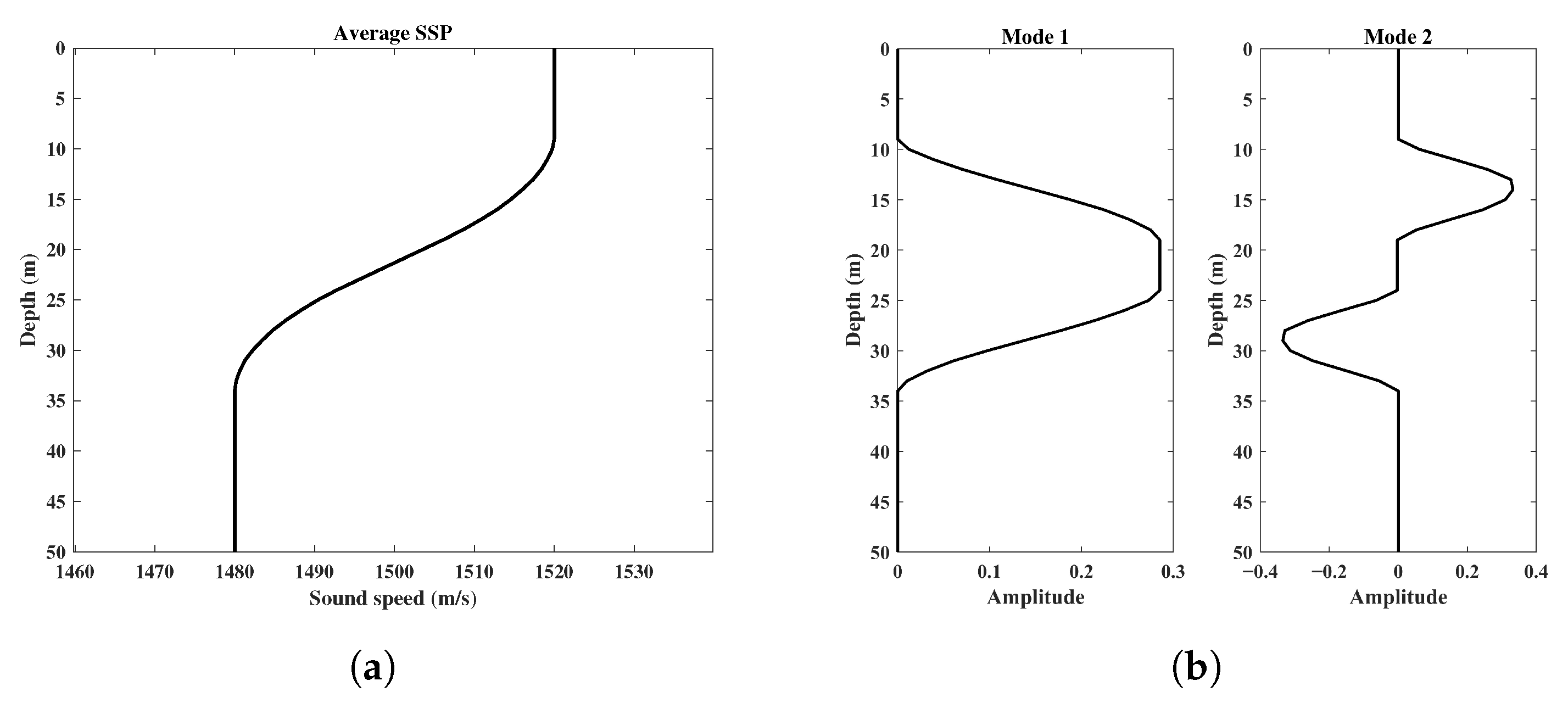
3.1. Dataset Generation Procedures
3.2. VAE–Flow Network Architecture
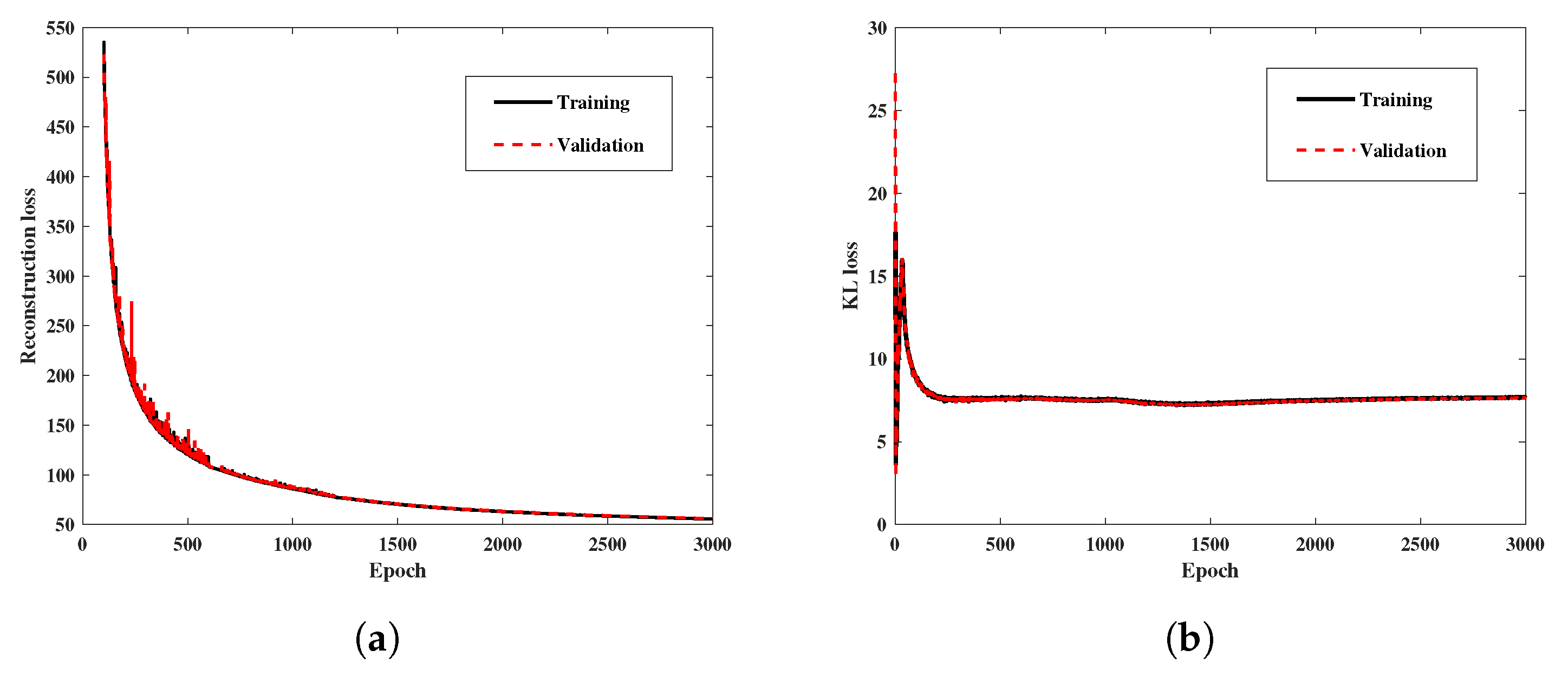
3.3. Training Configurations
3.3.1. Network Training Configuration
3.3.2. Computational Implementation
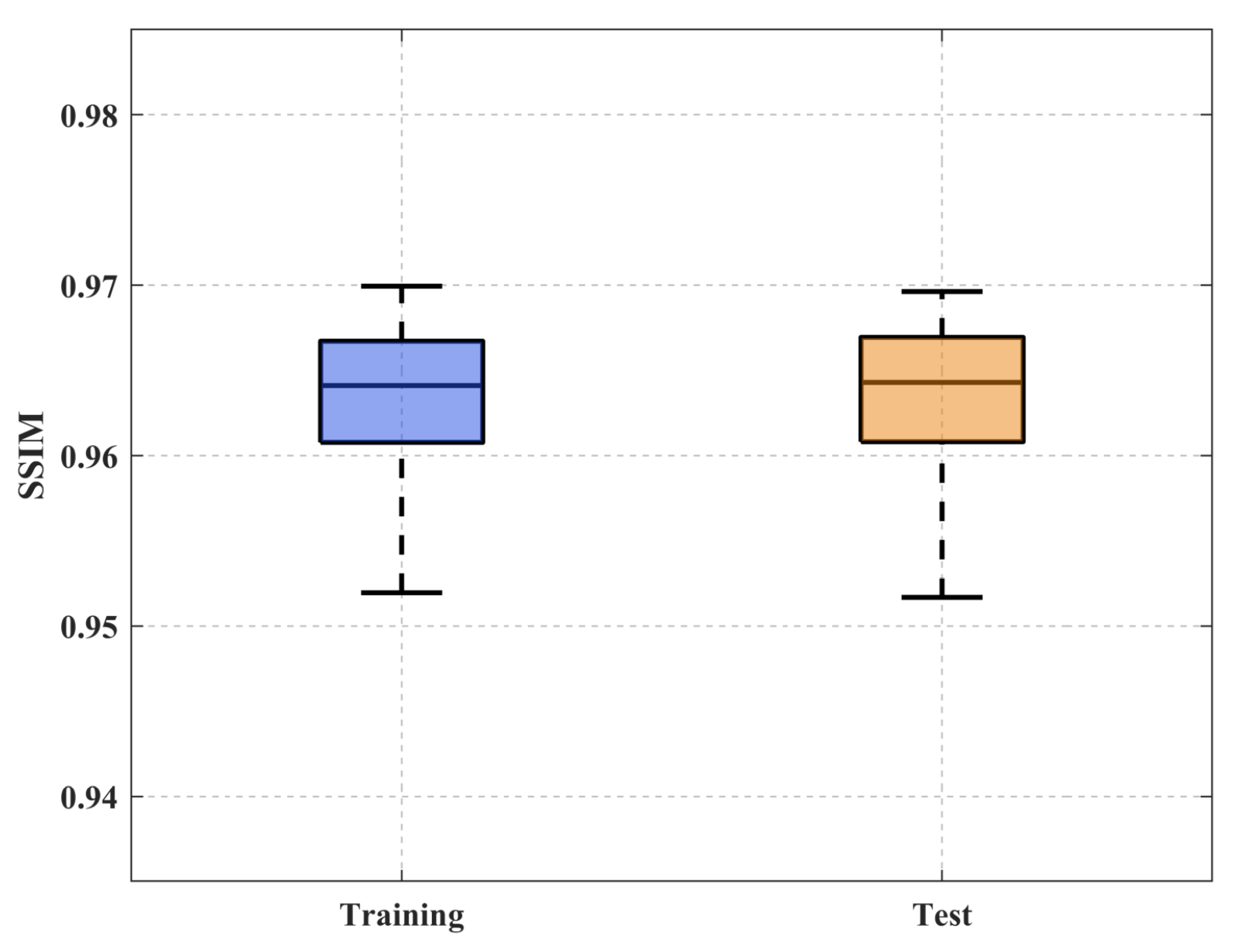
3.4. Evaluation Metrics
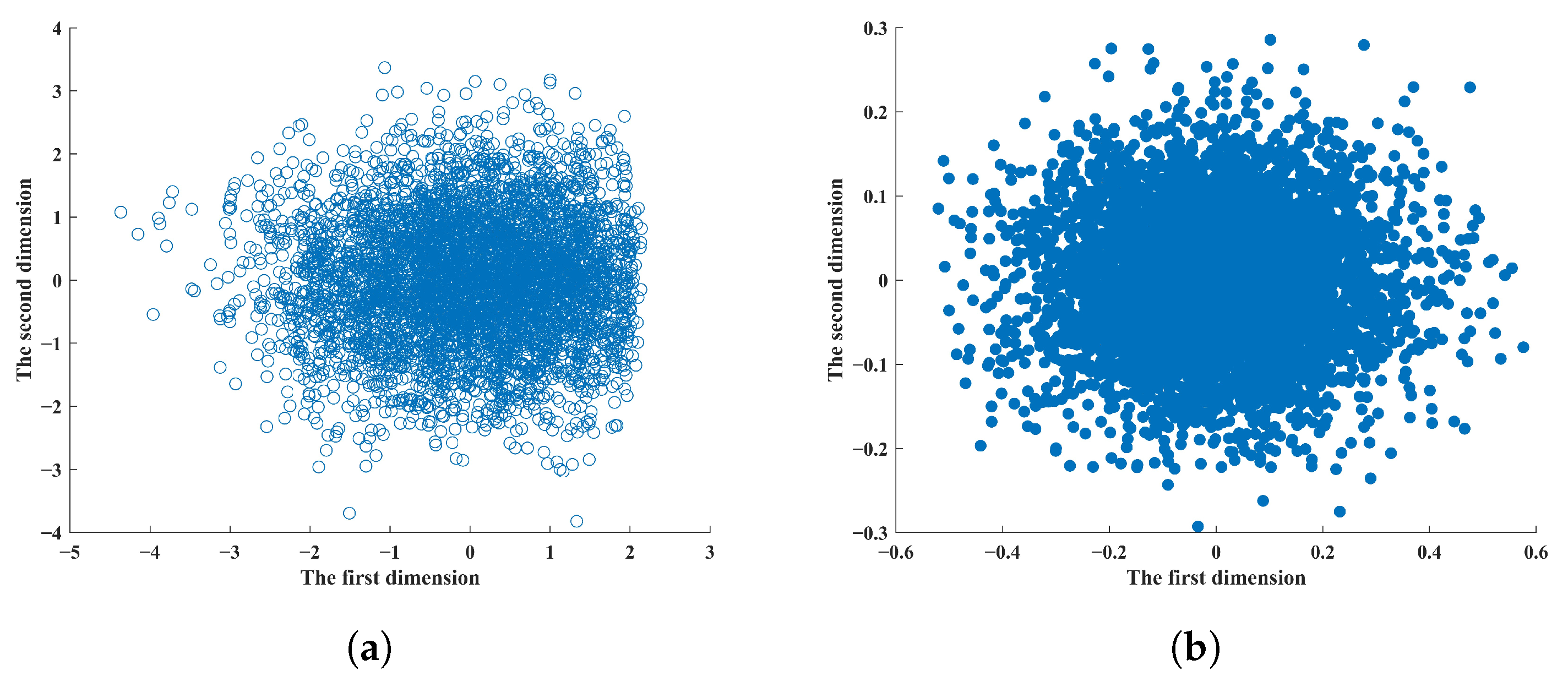
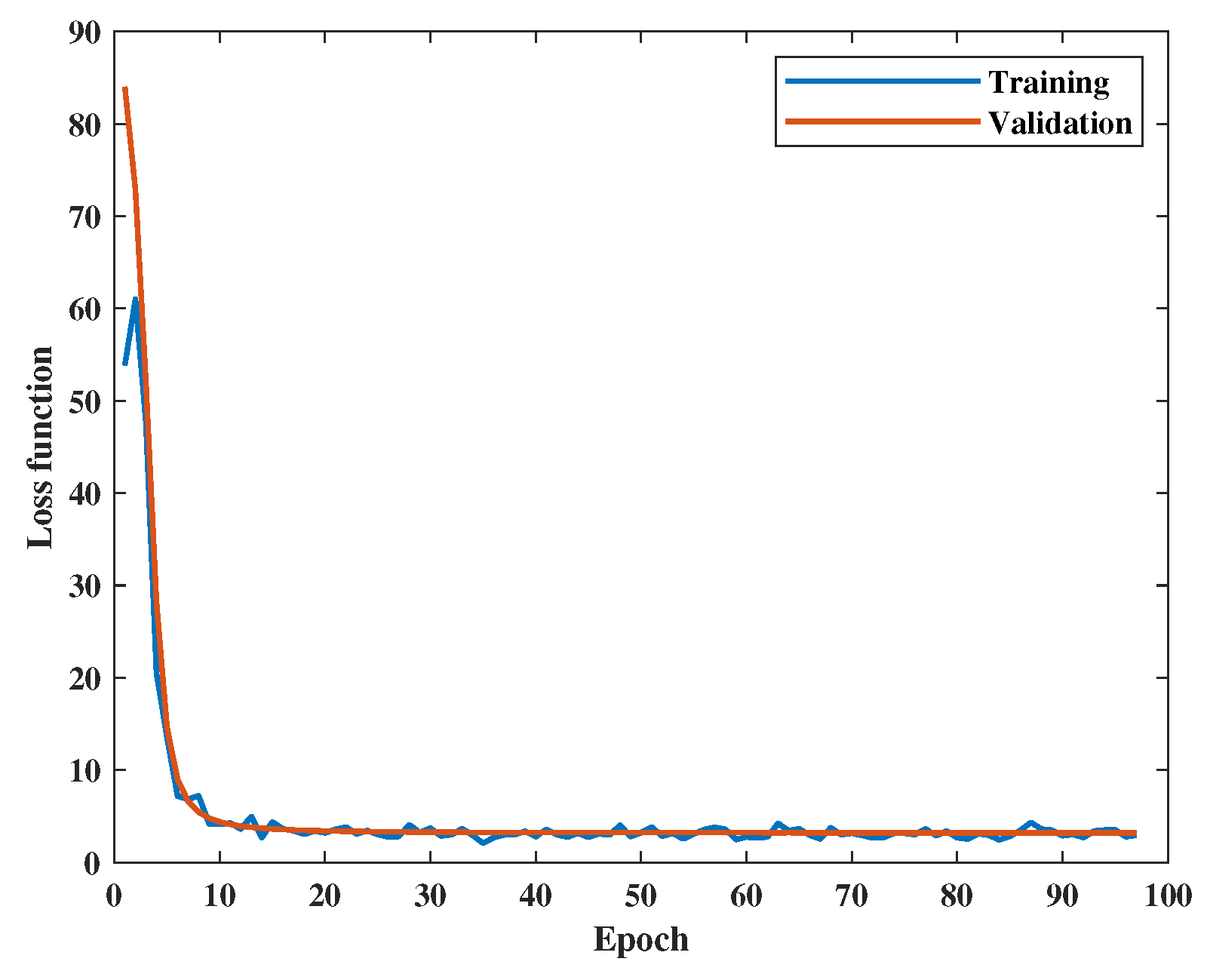
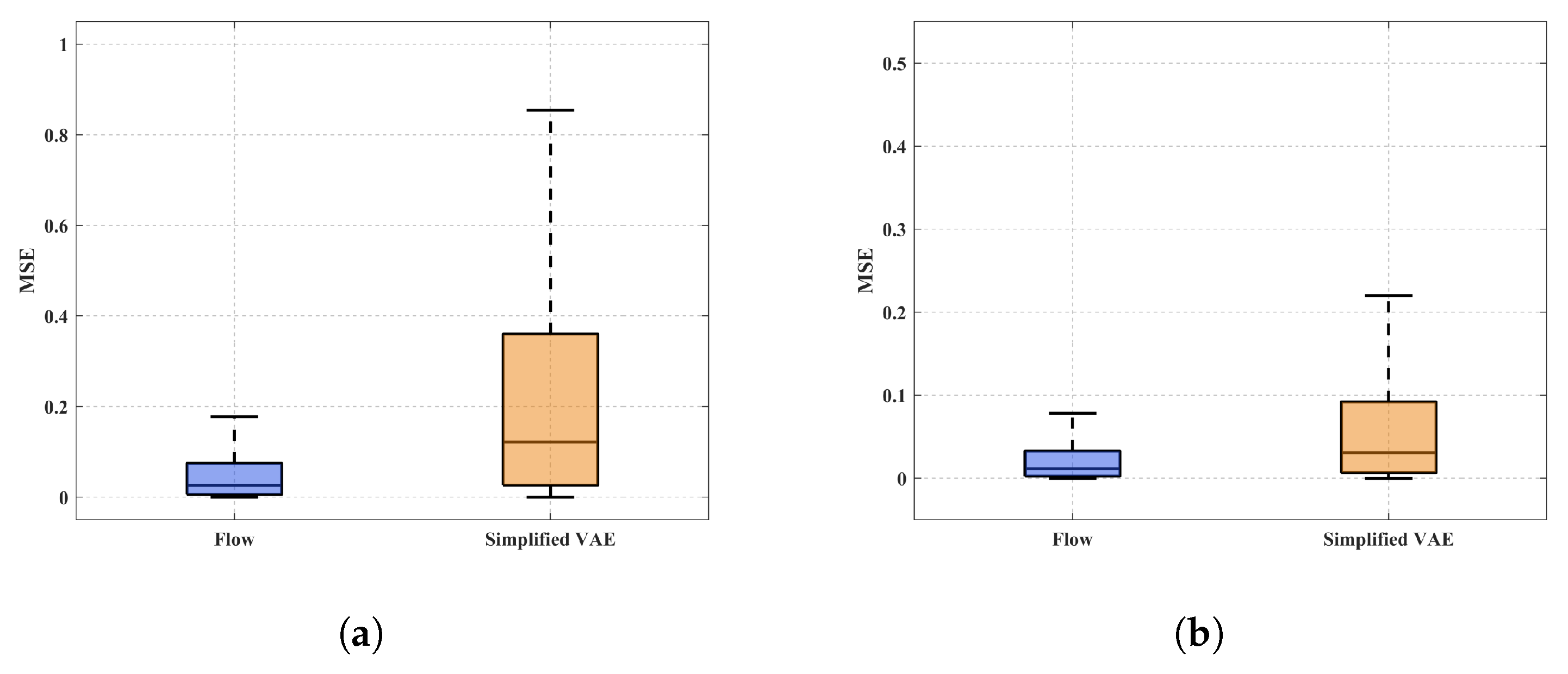
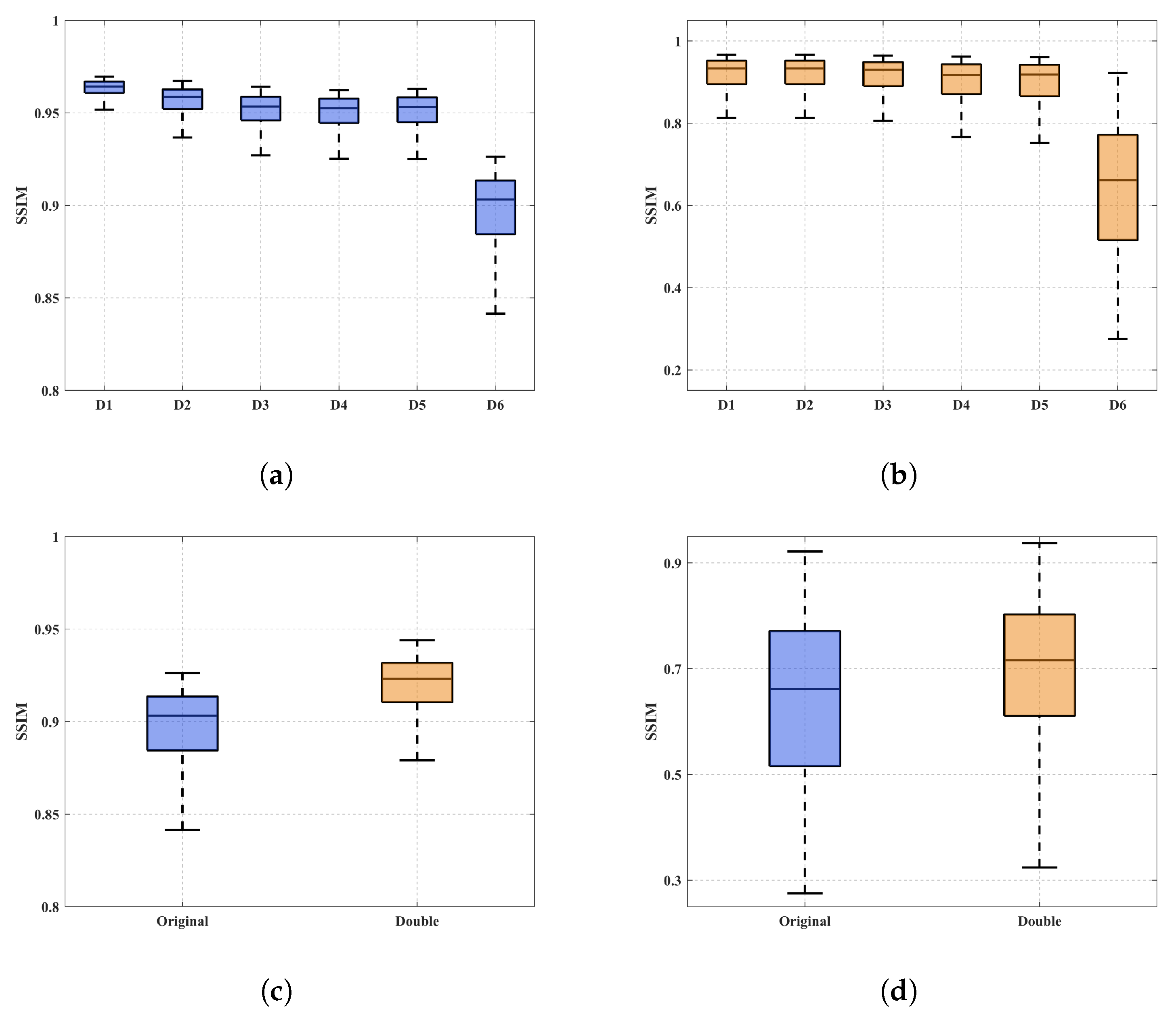
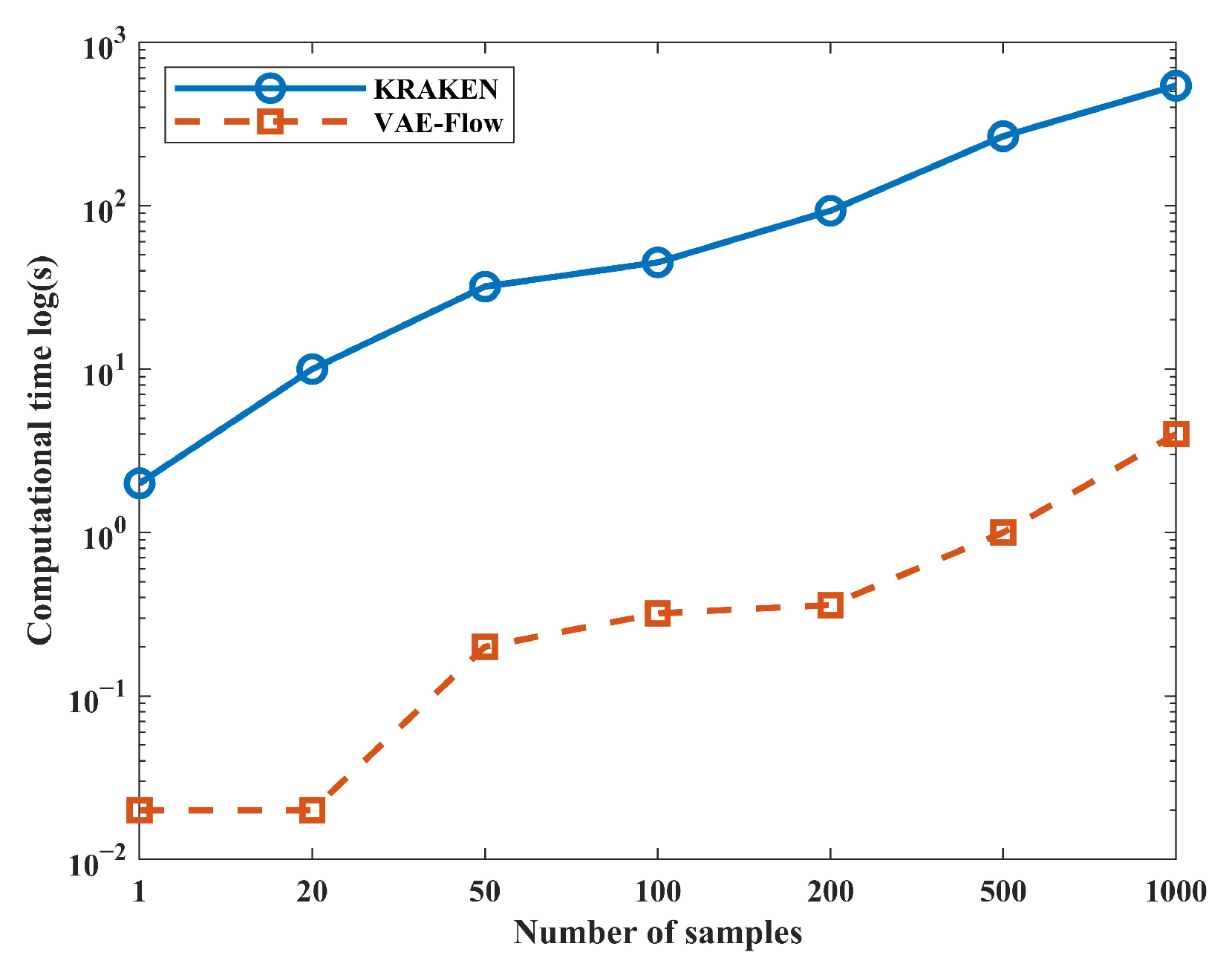
4. Evaluation and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TL | transmission loss |
| VAE | variational autoencoder |
| Flow | normalizing flow |
| SSIM | structural similarity index measure |
| CIRs | channel impulse responses |
| GANs | generative adversarial networks |
| CGAN | conditional generative adversarial network |
| CRAN | convolutional recurrent autoencoder network |
| SSPs | sound speed profiles |
| VAE–Flow | variational autoencoder-normalizing flow |
| MLE | maximum likelihood estimation |
| KL | Kullback–Leibler |
| ELBO | Evidence Lower Bound |
| EOF | empirical orthogonal functions |
| RHS | right-hand side of an equation |
| iff | if and only if |
| TFP | Tensorflow Probability |
| MMD | maximum mean discrepancy |
| RKHS | Reproducing Kernel Hilbert Space |
| MSE | mean squared error |
| MMD | maximum mean discrepancy |
| Variables for Underwater Acoustics | |
| Angular frequency of acoustic source (rad/s) | |
| Source depth (m) | |
| Receiver depth (m) | |
| r | Horizontal distance between source and receiver (m) |
| Medium density (kg/m3) | |
| Wavenumber of m-th normal mode (rad/m) | |
| Depth function of m-th normal mode (dimensionless) | |
| Acoustic pressure field at position (Pa) | |
| Free-space acoustic pressure (Pa) | |
| Transmission loss at receiver location (dB) | |
| Physical parameter vector (sound speed, seabed properties, etc.) | |
| Receiver region in 2D space (m2) | |
| N | Number of spatial points in discretized TL field |
| Variables for Deep Learning | |
| Latent variables (low-dimensional representation) | |
| Low-dimensional manifold of TL data | |
| Probability measure on manifold | |
| Encoder/recognition model | |
| Decoder/generative model | |
| Evidence Lower Bound (ELBO) | |
| Kullback–Leibler divergence | |
| Random noise variable in reparameterization trick | |
| Jacobian matrix of transformations | |
| Decoder output variance hyperparameter | |
References
- Porter, M.B. The Kraken Normal Mode Program; Technical report; Naval Research Laboratory: Washington, DC, USA, 1992. [Google Scholar]
- Porter, M.B. Bellhop: A Beam/Ray Trace Code, Version 2010-1. 2010. Available online: https://oalib-acoustics.org/website_resources/AcousticsToolbox/Bellhop-2010-1.pdf (accessed on 7 March 2025).
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Wei, L.; Wang, Z. A Variational Auto-Encoder Model for Underwater Acoustic Channels. In Proceedings of the 15th International Conference on Underwater Networks & Systems (WUWNet ’21), Shenzhen, China, 21–24 November 2021. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Liu, J.; Zhu, G.; Yin, J. Joint color spectrum and conditional generative adversarial network processing for underwater acoustic source ranging. Appl. Acoust. 2021, 182, 108244. [Google Scholar] [CrossRef]
- C., S.C.; Kamal, S.; Mujeeb, A.; M.H., S. Generative adversarial learning for improved data efficiency in underwater target classification. Eng. Sci. Technol. Int. J. 2022, 30, 101043. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Wang, C.; Deng, J.; Zhang, K.; Yang, Y.; Zhou, J. Data Enhancement of Underwater High-Speed Vehicle Echo Signals Based on Improved Generative Adversarial Networks. Electronics 2022, 11, 2310. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J.; Feng, X.; Sun, H.; Li, J.; Kuai, X. On Generative-Adversarial-Network-Based Underwater Acoustic Noise Modeling. IEEE Trans. Veh. Technol. 2021, 70, 9555–9559. [Google Scholar] [CrossRef]
- Varon, A.; Mars, J.; Bonnel, J. Approximation of modal wavenumbers and group speeds in an oceanic waveguide using a neural network. JASA Express Lett. 2023, 3, 066003. [Google Scholar] [CrossRef] [PubMed]
- Mallik, W.; Jaiman, R.K.; Jelovica, J. Predicting transmission loss in underwater acoustics using convolutional recurrent autoencoder network. J. Acoust. Soc. Am. 2022, 152, 1627–1638. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Y.; Liu, W. End-to-end underwater acoustic transmission loss prediction with adaptive multi-scale dilated network. J. Acoust. Soc. Am. 2025, 157, 382–395. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics, 2nd ed.; Springer Publishing Company, Incorporated: New York, NY, USA, 2011. [Google Scholar]
- Zhang, X.; Wang, P.; Wang, N. Nonlinear dimensionality reduction for the acoustic field measured by a linear sensor array. MATEC Web Conf. 2019, 283, 07009. [Google Scholar] [CrossRef]
- Ray, D.; Pinti, O.; Oberai, A.A. Generative Deep Learning. In Deep Learning and Computational Physics; Springer Nature: Cham, Switzerland, 2024; pp. 121–146. [Google Scholar]
- Dai, B.; Wipf, D.P. Diagnosing and Enhancing VAE Models. In Proceedings of the 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Loaiza-Ganem, G.; Ross, B.L.; Cresswell, J.C.; Caterini, A.L. Diagnosing and Fixing Manifold Overfitting in Deep Generative Models. arXiv 2022, arXiv:2204.07172. [Google Scholar]
- Loaiza-Ganem, G.; Ross, B.L.; Hosseinzadeh, R.; Caterini, A.L.; Cresswell, J.C. Deep Generative Models through the Lens of the Manifold Hypothesis: A Survey and New Connections. arXiv 2024, arXiv:2404.02954. [Google Scholar]
- Rezende, D.J.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the 32nd International Conference on International Conference on Machine Learning (ICML’15), Lille, France, 6–11 July 2015; Volume 37, pp. 1530–1538. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using Real NVP. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. [Google Scholar]
- Su, J.; Wu, G. f-VAEs: Improve VAEs with Conditional Flows. arXiv 2018, arXiv:1809.05861. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. NICE: Non-linear Independent Components Estimation. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Kingma, D.P.; Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. In Proceedings of the Advances in Neural Information Processing Systems 31: Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, QC, Canada, 3–8 December 2018; pp. 10236–10245. [Google Scholar]
- Zhai, S.; Zhang, R.; Nakkiran, P.; Berthelot, D.; Gu, J.; Zheng, H.; Chen, T.; Bautista, M.Á.; Jaitly, N.; Susskind, J.M. Normalizing Flows are Capable Generative Models. arXiv 2024, arXiv:2412.06329. [Google Scholar]





| Dataset | ||
|---|---|---|
| D1 | ||
| D2 | ||
| D3 | ||
| D4 | ||
| D5 | ||
| D6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, B.; Wang, H.; Zhu, X.; Song, P.; Li, X. Efficient Prediction of Shallow-Water Acoustic Transmission Loss Using a Hybrid Variational Autoencoder–Flow Framework. J. Mar. Sci. Eng. 2025, 13, 1325. https://doi.org/10.3390/jmse13071325
Su B, Wang H, Zhu X, Song P, Li X. Efficient Prediction of Shallow-Water Acoustic Transmission Loss Using a Hybrid Variational Autoencoder–Flow Framework. Journal of Marine Science and Engineering. 2025; 13(7):1325. https://doi.org/10.3390/jmse13071325
Chicago/Turabian StyleSu, Bolin, Haozhong Wang, Xingyu Zhu, Penghua Song, and Xiaolei Li. 2025. "Efficient Prediction of Shallow-Water Acoustic Transmission Loss Using a Hybrid Variational Autoencoder–Flow Framework" Journal of Marine Science and Engineering 13, no. 7: 1325. https://doi.org/10.3390/jmse13071325
APA StyleSu, B., Wang, H., Zhu, X., Song, P., & Li, X. (2025). Efficient Prediction of Shallow-Water Acoustic Transmission Loss Using a Hybrid Variational Autoencoder–Flow Framework. Journal of Marine Science and Engineering, 13(7), 1325. https://doi.org/10.3390/jmse13071325






