Vortex-Induced Vibration Analysis of FRP Composite Risers Using Multivariate Nonlinear Regression
Abstract
1. Introduction
2. Design and Methodology
2.1. Riser Design
2.2. Material Properties
2.3. Experimental Matrix and Parameters
2.4. Numerical Simulation
3. Results and Discussion
3.1. Natural Frequencies of Risers for the 18 Different Study Cases
3.2. Deformations of Risers for the 18 Different Study Cases
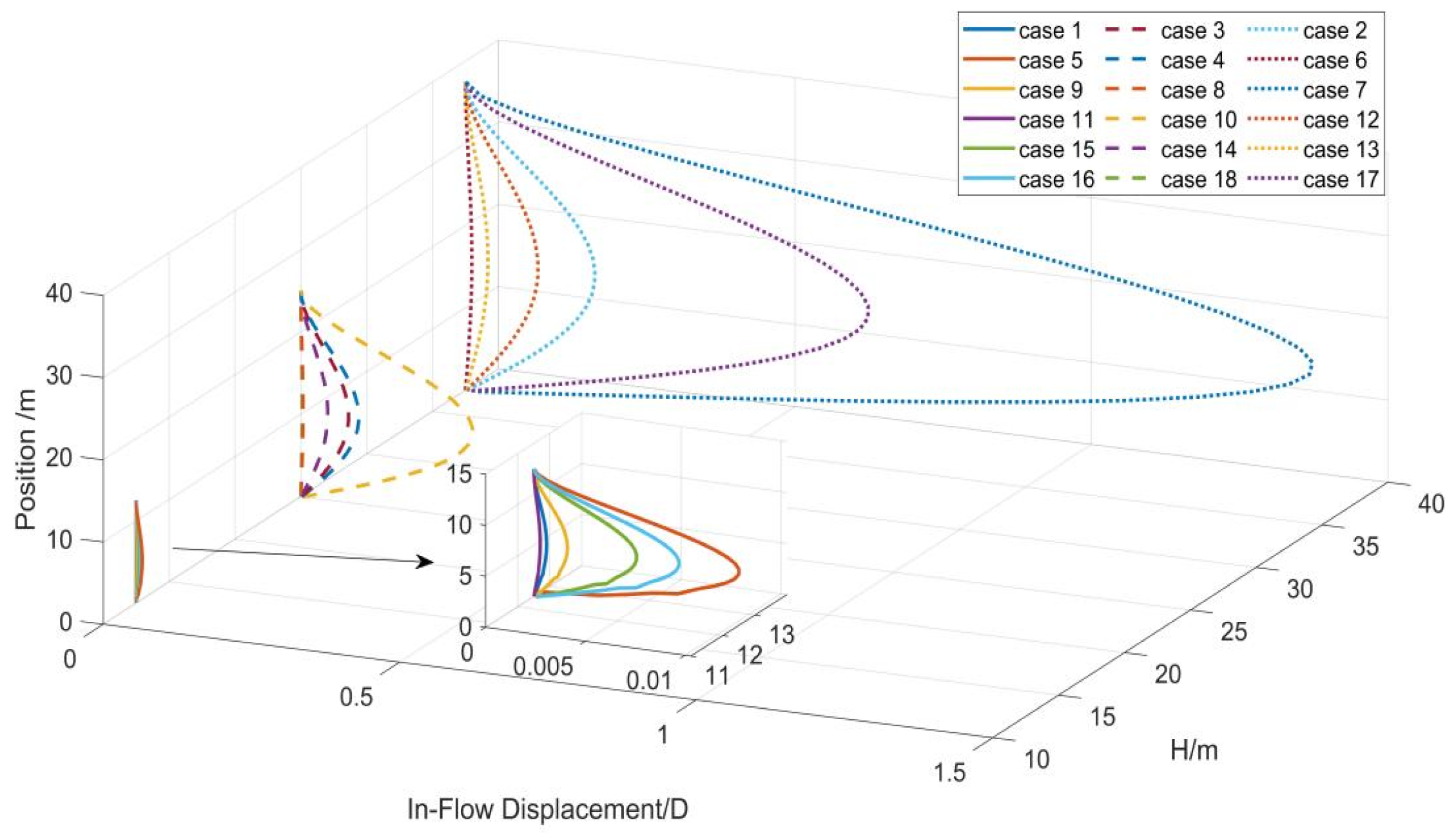
3.2.1. Deformations of Risers in the Downstream Direction
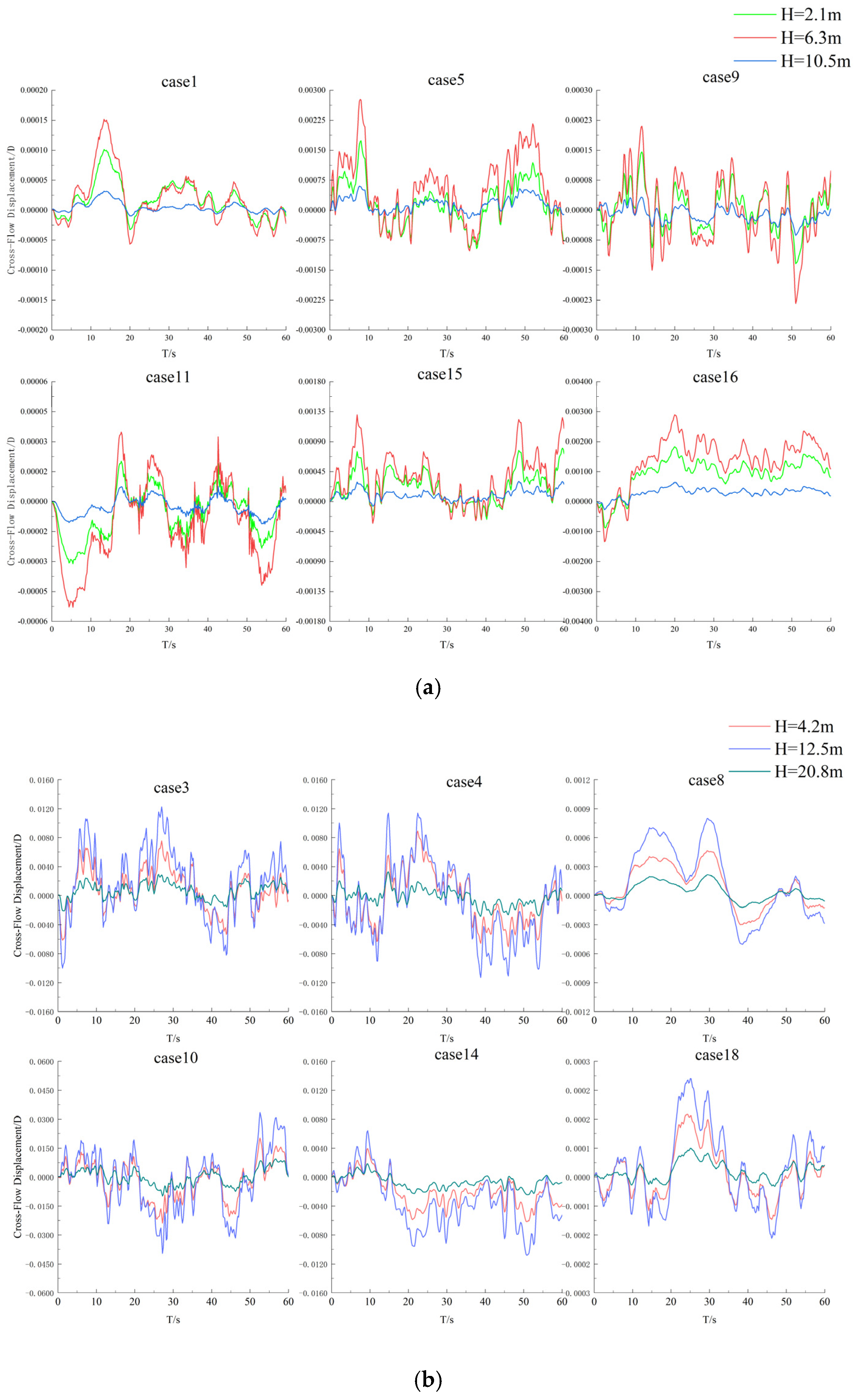
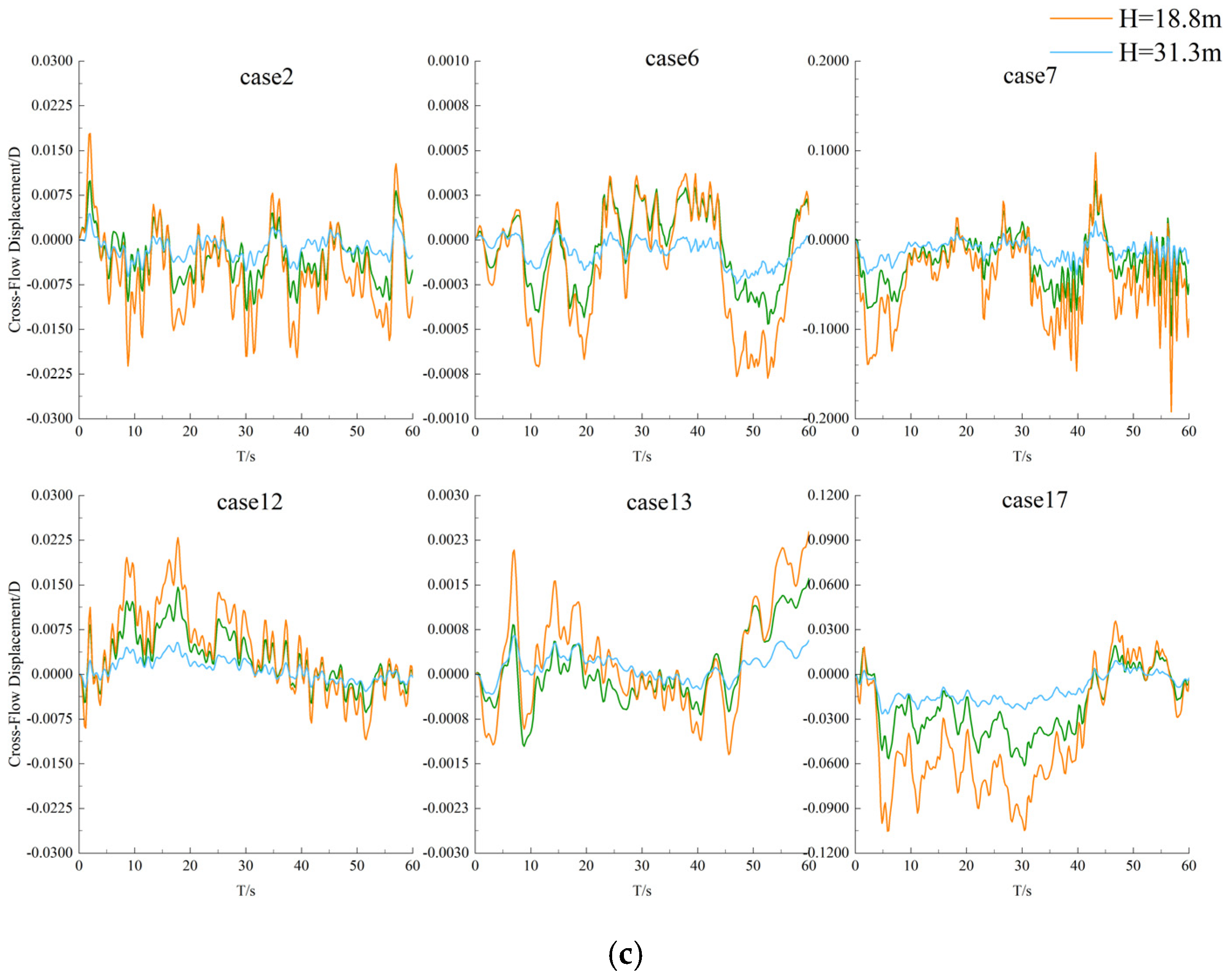
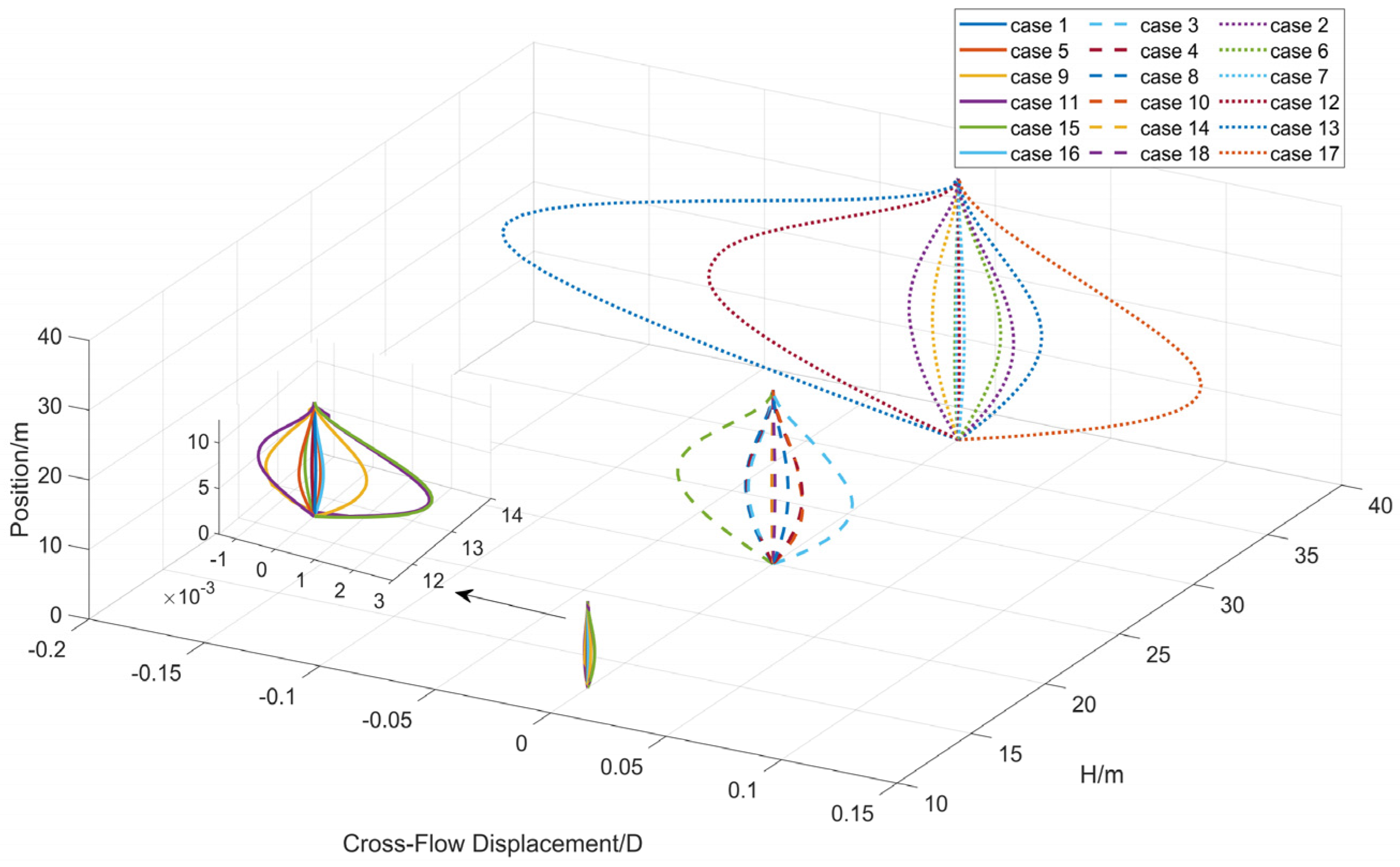
3.2.2. Deformations of Risers in the Crossflow Direction
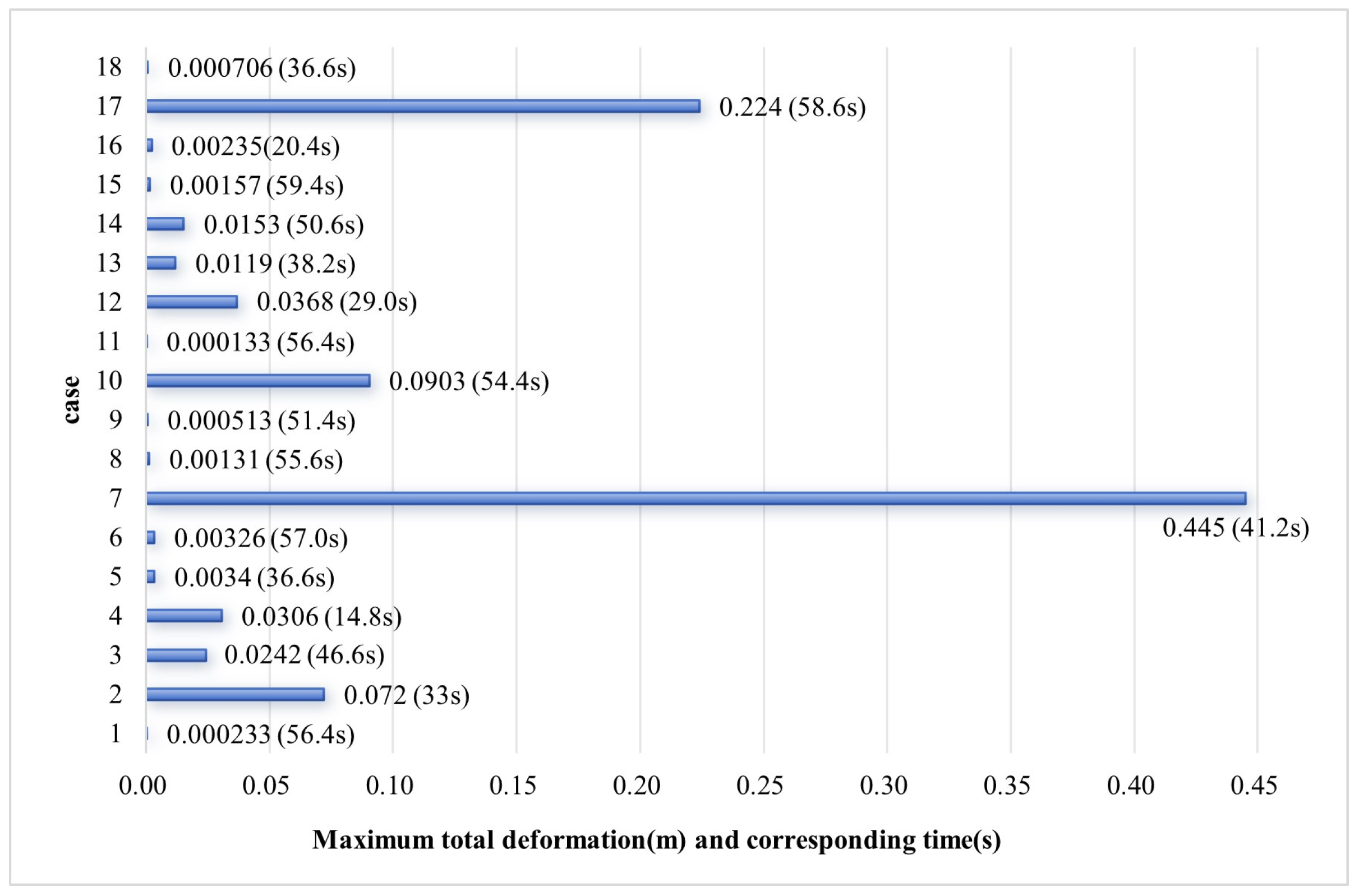
3.2.3. Total Deformations of Risers
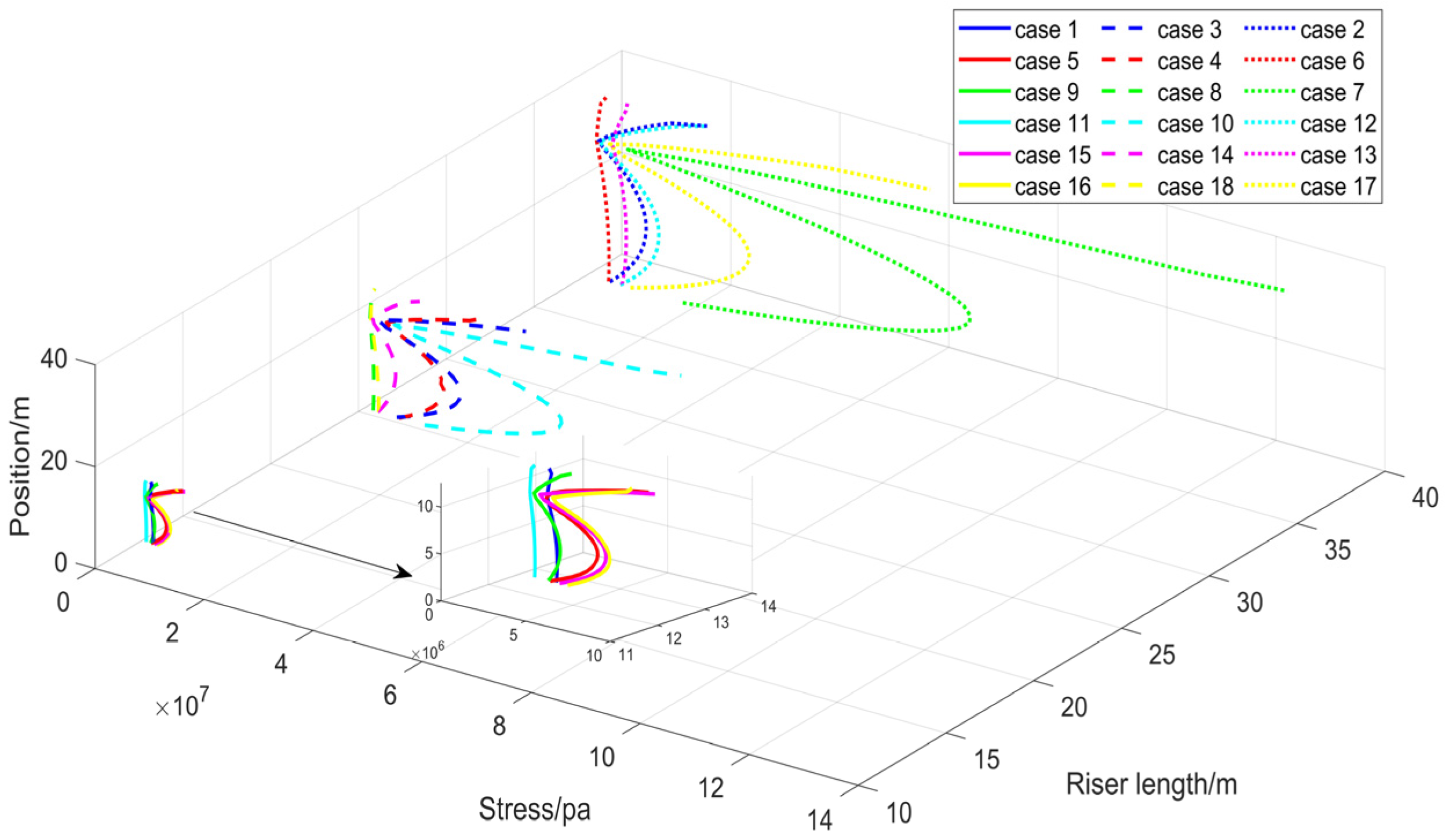
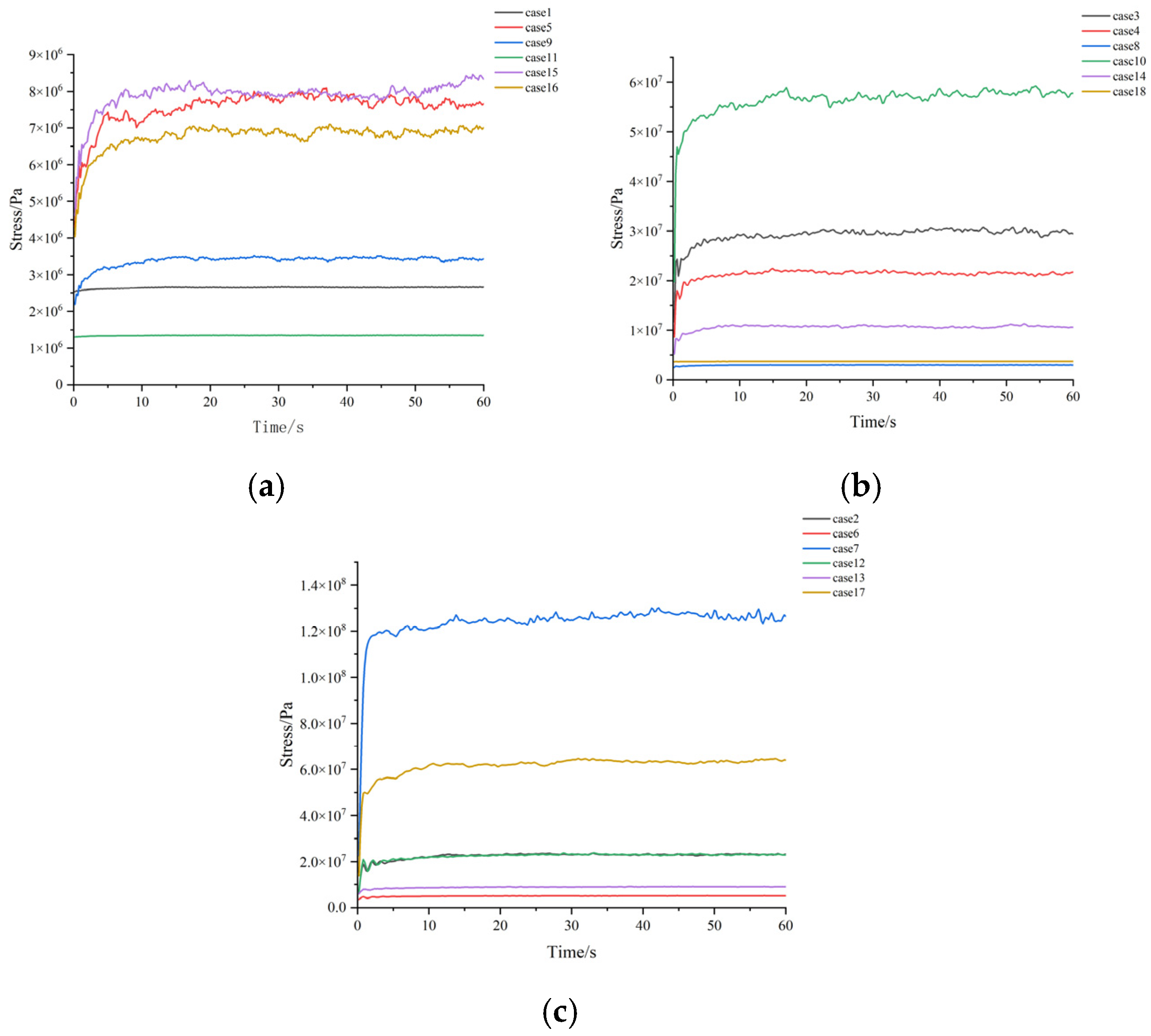
3.3. Stresses of Risers for the 18 Different Study Cases
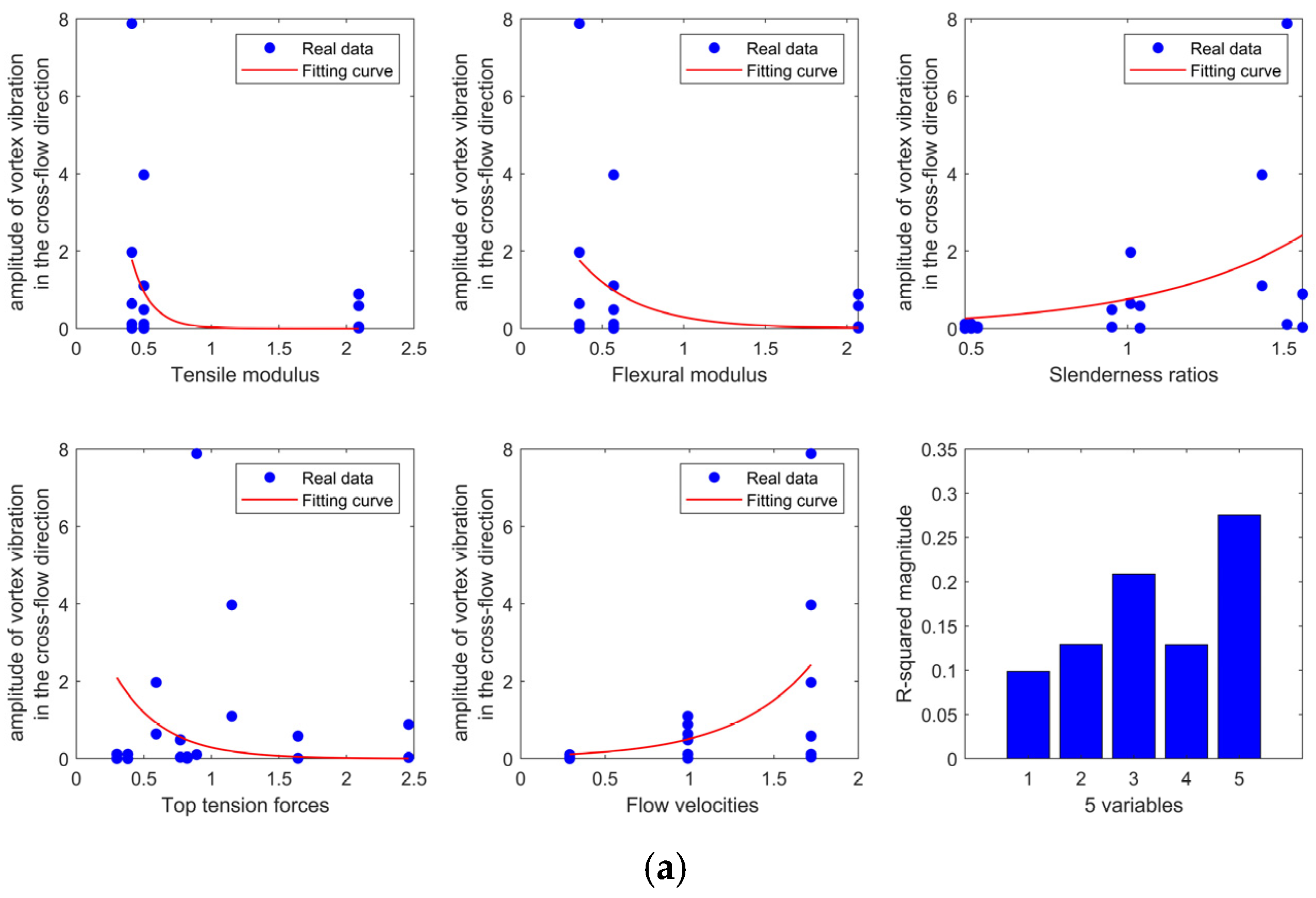
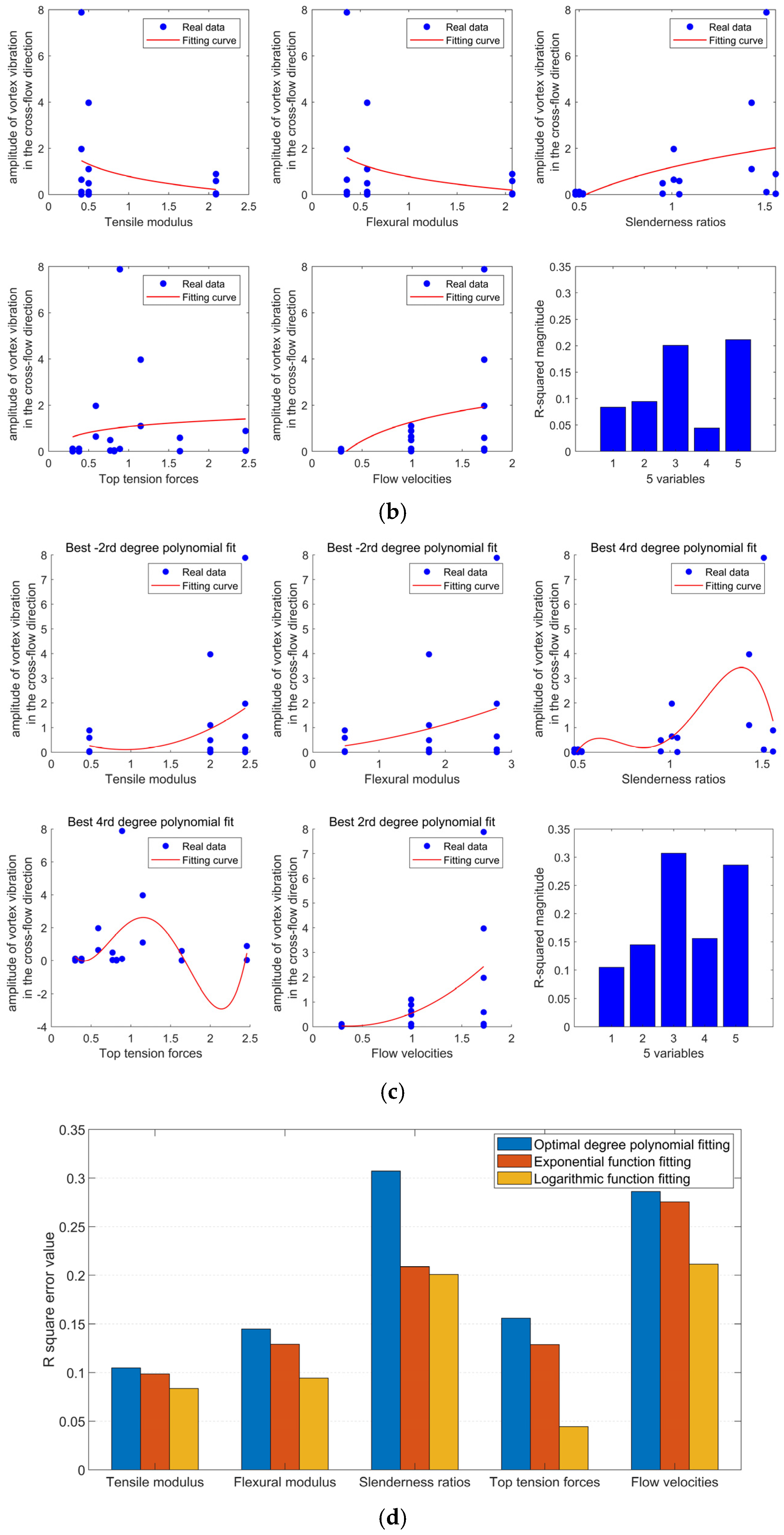
3.4. Fitting Analysis with Multiple Nonlinear Regression Model
3.4.1. Data Handling
3.4.2. Modeling
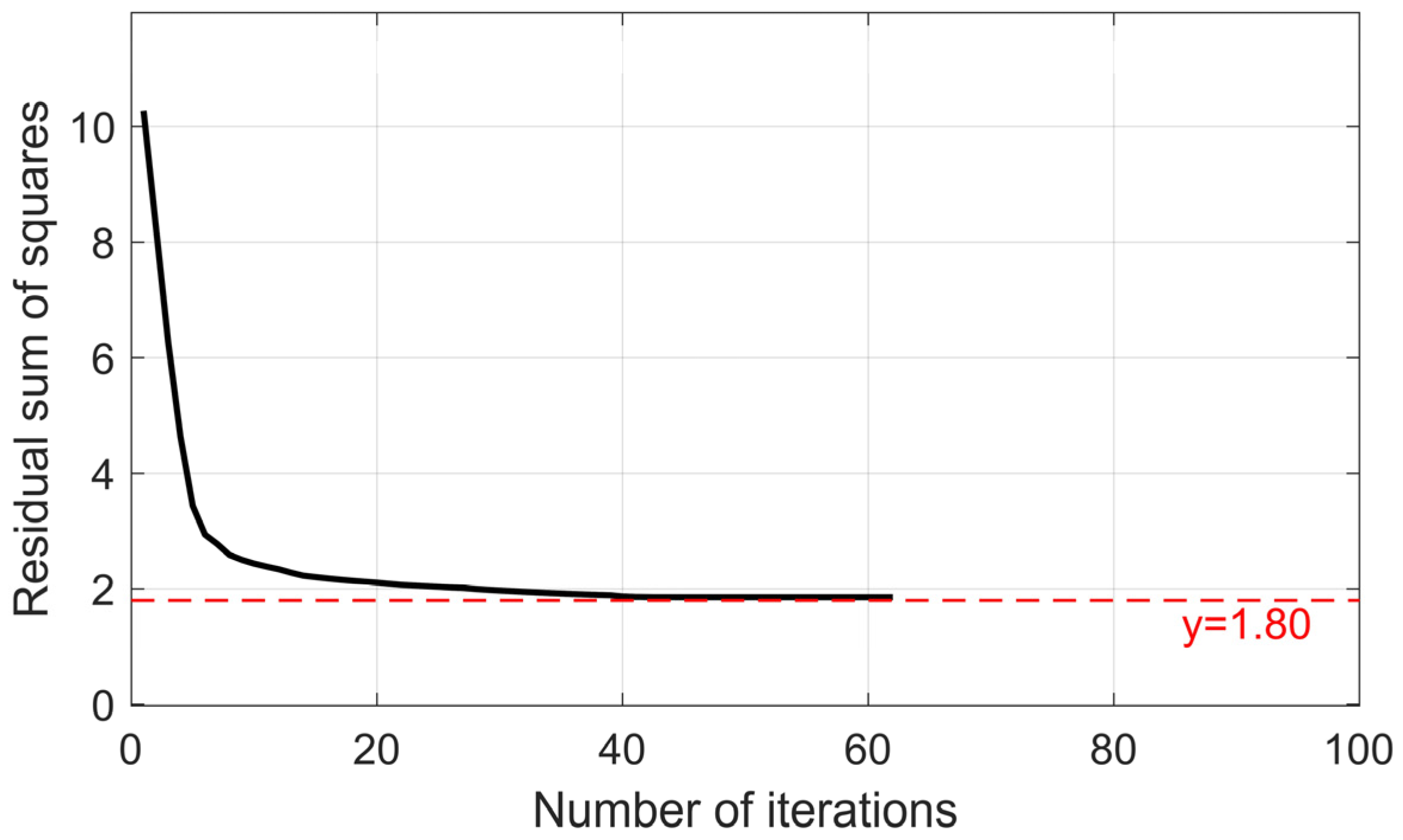
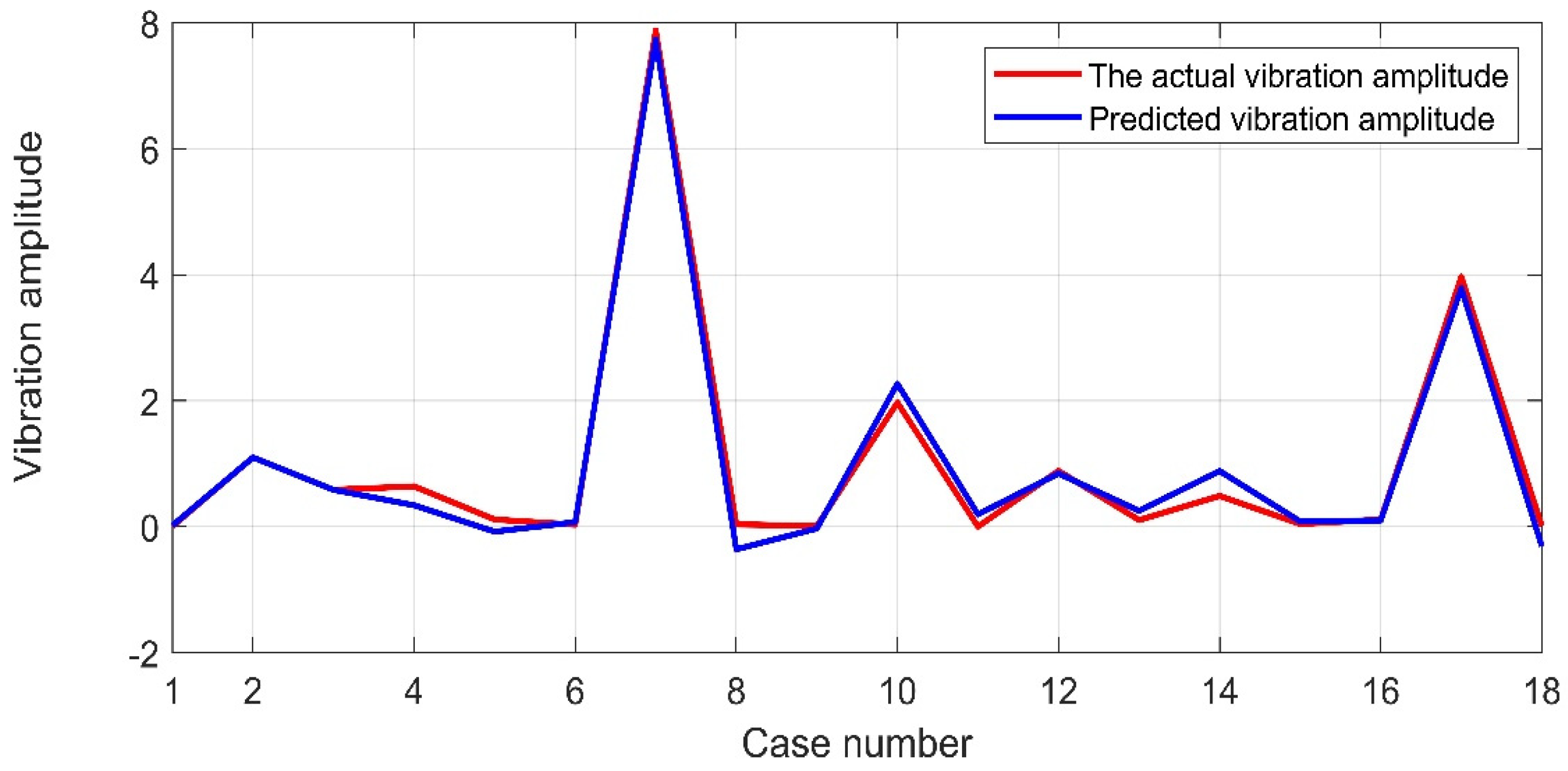
3.4.3. Fitting Method and Process
4. Conclusions
- (1)
- All three types of risers tended to stabilize after the initial growth of displacement in the downstream direction, while the displacement exhibited obvious vibration characteristics in the crossflow direction. With the same condition, the optimized FRP composite riser had the largest displacement, while that of the metal riser was the smallest. Moreover, the increase in the riser’s length and flow velocity, as well as the decrease in the riser’s modulus, led to the increase of downstream displacement and crossflow vibration amplitude.
- (2)
- The overall stresses of both FRP composite risers were less than that of the metal riser, and the optimized FRP composite riser could more effectively use the strength of the reinforced fiber.
- (3)
- When the number of coupled parameters reached two, the accuracy of the established multivariate nonlinear fitting model gained an acceptable level. The most important single factors were b1 (tensile modulus) and b3 (slenderness ratio), and the most significant interacting factors were b11 (flexural modulus + top tension force). Moreover, the crossflow VIV was affected by the interaction of coupled factors, which was generally more remarkable than that of the single factors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, G.; Li, H.; Qiu, Z.; Leng, D.; Li, Z.; Li, W. A mini review of recent progress on vortex-induced vibrations of marine risers. Ocean Eng. 2020, 195, 106704. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Reda, A.; Shahin, M.A.; Sultan, I.A.; Beddu, S.B.; Ja’e, I.A. State-of-the-art review of composite marine risers for floating and fixed platforms in deep seas. Appl. Ocean Res. 2023, 138, 103624. [Google Scholar] [CrossRef]
- Amaechi, C.V. Local tailored design of deep-water composite risers subjected to burst, collapse and tension loads. Ocean Eng. 2022, 250, 110196. [Google Scholar] [CrossRef]
- Ye, J.; Zhou, H.; He, K. A generalized framework of two-way coupled numerical model for fluid-structure-seabed interaction (FSSI): Explicit algorithm. Eng. Geol. 2024, 340, 107679. [Google Scholar] [CrossRef]
- Tan, L.B.; Chen, Y.; Jaiman, R.K.; Sun, X.; Tan, V.B.C.; Tay, T.E. Coupled fluid–structure simulations for evaluating a performance of full-scale deepwater composite riser. Ocean Eng. 2015, 94, 19–35. [Google Scholar] [CrossRef]
- Zheng, R.; Wang, C.; He, W.; Zhang, Z.; Ma, K.; Ren, M. The Experimental Study of Dynamic Response of Marine Riser under Coupling Effect of Multiparameter. J. Mar. Sci. Eng. 2023, 11, 1787. [Google Scholar] [CrossRef]
- Wang, C.; Shankar, K.; Morozov, E.V. Global design and analysis of deep sea FRP composite risers under combined environmental loads. Adv. Compos. Mater. 2017, 26, 79–98. [Google Scholar] [CrossRef]
- Ge, S.; Wang, C.; Sun, M.; Wang, Y. Three-dimensional computational fluid dynamics simulation of vortex-induced vibration of fiber-reinforced composite marine risers considering fluid-structure interaction. Jinan Univ. J. (Nat. Sci. Ed.) 2020, 34, 1–9. [Google Scholar] [CrossRef]
- Wang, C.; Shankar, K.; Ashraf, M.A.; Morozov, E.V.; Ray, T. Surrogate-assisted optimisation design of composite riser. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2016, 230, 18–34. [Google Scholar] [CrossRef]
- Toh, W.; Tan, L.B.; Jaiman, R.K.; Tay, T.E.; Tan, V.B.C. A comprehensive study on composite risers: Material solution, local end fitting design and global response. Mar. Struct. 2018, 61, 155–169. [Google Scholar] [CrossRef]
- Wang, C.; Sun, M.; Shankar, K.; Xing, S.; Zhang, L. CFD Simulation of Vortex Induced Vibration for FRP Composite Riser with Different Modeling Methods. Appl. Sci. 2018, 8, 684. [Google Scholar] [CrossRef]
- Lin, M.Y.; Huang, L.H. Numerical simulation of wave–structure interaction using a Lagrangian vortex method. Ocean. Eng. 2012, 44, 11–22. [Google Scholar] [CrossRef]
- Ragheb, H.A.; Goodridge, M.; Pham, D.C.; Sobey, A.J. Extreme response based reliability analysis of composite risers for applications in deepwater. Mar. Struct. 2021, 78, 103015. [Google Scholar] [CrossRef]
- Nammi, S.K.; Gupta, R.; Pancholi, K. Comparative strength and stability analysis of conventional and lighter composite flexible risers in ultra-deep water subsea environment. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2025, 239, 666–677. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Shen, Y. Numerical Analysis of Mechanical Behaviors of Composite Tensile Armored Flexible Risers in Deep-Sea Oil and Gas. J. Mar. Sci. Eng. 2023, 11, 619. [Google Scholar] [CrossRef]
- Liu, Q.; Xue, H.; Tang, W.; Yuan, Y. Theoretical and numerical methods to predict the behaviour of unbonded flexible riser with composite armour layers subjected to axial tension. Ocean Eng. 2020, 199, 107038. [Google Scholar] [CrossRef]
- Kang, C.; Zhan, J.; Liu, Z.; Jing, X.; Deng, B.; Guo, J.; Weng, H.; Liu, J.; Wang, J. Numerical study of the axial compression strength for nano-reinforced filament-wound riser considering curing residual stress. Appl. Ocean Res. 2024, 142, 103829. [Google Scholar] [CrossRef]
- Edmans, B.D.; Pham, D.C.; Zhang, Z.Q.; Guo, T.F.; Sridhar, N.; Stewart, G. An Effective Multiscale Methodology for the Analysis of Marine Flexible Risers. J. Mar. Sci. Eng. 2019, 7, 340. [Google Scholar] [CrossRef]
- Wang, E.; Xiao, Q. Numerical simulation of vortex-induced vibration of a vertical riser in uniform and linearly sheared currents. Ocean Eng. 2016, 121, 492–515. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, J. A modified multi-objective particle swarm optimization approach and its application to the design of a deepwater composite riser. Acta Mech. Sin. 2018, 34, 275–284. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Gillett, N.; Odijie, A.C.; Hou, X.; Ye, J. Composite risers for deep waters using a numerical modelling approach. Compos. Struct. 2019, 210, 486–499. [Google Scholar] [CrossRef]
- Pham, D.C.; Sridhar, N.; Qian, X.; Sobey, A.J.; Achintha, M.; Shenoi, A. A review on design, manufacture and mechanics of composite risers. Ocean Eng. 2016, 112, 82–96. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, W.; Qian, X.; Su, Z.; Pham, D.-C.; Sridhar, N. Fatigue behaviour and life prediction of filament wound CFRP pipes based on coupon tests. Mar. Struct. 2020, 72, 102756. [Google Scholar] [CrossRef]
- Chang, X.P.; Qu, C.J.; Song, Q.; Li, Y.H.; Liu, J. Coupled cross-flow and in-line vibration characteristics of frequency-locking of marine composite riser subjected to gas-liquid multiphase internal flow. Ocean Eng. 2022, 266, 113019. [Google Scholar] [CrossRef]
- Liu, M. Multi-Fidelity Machine Learning Prediction Method for Vortex-Induced Vibration of Marine Risers. Master’s Thesis, Dalian Maritime University, Dalian, China, 2024. [Google Scholar] [CrossRef]
- Wang, C.; Ge, S.; Jaworski, J.; Liu, L.; Jia, Z. Effects of Different Design Parameters on the Vortex Induced Vibration of FRP Composite Risers Using Grey Relational Analysis. J. Mar. Sci. Eng. 2019, 7, 231. [Google Scholar] [CrossRef]
- Ragheb, H.; Sobey, A. Effects of extensible modelling on composite riser mechanical responses. Ocean Eng. 2021, 220, 108426. [Google Scholar] [CrossRef]
- Khan, R.A.; Ahmad, S. Nonlinear Dynamic and Bilinear Fatigue Performance of Composite Marine Risers in Deep Offshore Fields. In Proceedings of the OMAE2020, Volume 2A: Structures, Safety, and Reliability, Virtual, 3–7 August 2020. [Google Scholar] [CrossRef]
- Wang, C.G.; Ma, Y.H.; Sun, M.Y.; Zhang, L.; Wang, Y.T. Three-dimensional CFD vortex-induced vibration simulation of metal and composite Marine risers. J. Shandong Univ. Technol. (Nat. Sci. Ed.) 2017, 31, 35–41. [Google Scholar] [CrossRef]
- Alexander, C.; Ochoa, O.O. Extending onshore pipeline repair to offshore steel risers with carbon–fiber reinforced composites. Compos. Struct. 2010, 92, 499–507. [Google Scholar] [CrossRef]
- Chen, Y.; Seemann, R.; Krause, D.; Tay, T.-E.; Tan, V.B.C. Prototyping and testing of composite riser joints for deepwater application. J. Reinf. Plast. Compos. 2016, 35, 95–110. [Google Scholar] [CrossRef]
- Lambert, A.; Do, A.T.; Felix-Henry, A.; Grosjean, F. Qualification of Unbonded Dynamic Riser with Carbon Fiber Composite Armours. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; Volume 3: Pipeline and Riser Technology. The American Society of Mechanical Engineers (ASME): New York, NY, USA, 2012; pp. 117–125. [Google Scholar] [CrossRef]
- Jena, R.K.; Yue, C.Y. Development of nanocomposite for rigid riser application. Compos. Sci. Technol. 2016, 124, 27–35. [Google Scholar] [CrossRef]
- Zhai, G.; Ding, Y.; Wang, Y.; Ma, Z. Experimental investigation of the hydrostatic compression of a hollow glass microspheres/epoxy resin under high-pressure conditions at the full ocean depth. Polym. Compos. 2020, 41, 5331–5342. [Google Scholar] [CrossRef]
- Han, Z.; Huang, X.; Yang, Z. Effect of Al–Zn Alloy Coating on Corrosion Fatigue Behavior of X80 Riser Steel. Materials 2019, 12, 1520. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.H.; Zeng, Y.; Baker, D.; Huang, W.; Dunn, G.; Hoyt, D.; Ladeuille, L.; Evin, H. Sulfide Stress Cracking Response of X80 Simulated Heat Affected Zone for Offshore Pipeline and Riser Application. In Proceedings of the 2022 14th International Pipeline Conference, Calgary, AB, Canada, 26–30 September 2022; Volume 3: Operations, Monitoring, and Maintenance, Materials and Joining. The American Society of Mechanical Engineers (ASME): New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Halkyard, J.; Capanoglu, C. Historical Development of Offshore Structures. In Handbook of Offshore Engineering; Chakrabarti, S.K., Ed.; Elsevier: London, UK, 2005; pp. 1–38. [Google Scholar]
- Kim, W. Composite Production Riser Assessment. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2007. [Google Scholar]
- Bose, R.C.; Bush, K.A. Orthogonal Arrays of Strength two and three. Ann. Math. Stat. 1952, 23, 508–524. [Google Scholar] [CrossRef]
- Wang, C. Tailored Design of Composite Risers for Deep Water Applications. Ph.D. Thesis, UNSW Sydney, Sydney, Australia, 2013. [Google Scholar] [CrossRef]
- Ma, K.S.; Wang, C.G.; He, W.T.; Zheng, R.; Zhang, Z.Y.; Zhang, L. The coupling effect of current, wave and platform movement on the dynamic characteristics of marine risers with different elastic modulus and constraint number. Appl. Ocean Res. 2024, submitted.
- Feng, L.H.; Wang, J.J. Modification of a circular cylinder wake with synthetic jet: Vortex shedding modes and mechanism. Eur. J. Mech. B/Fluids 2014, 43, 14–32. [Google Scholar] [CrossRef]
- Chan, P.H.; Tshai, K.Y.; Johnson, M.; Li, S. Finite element analysis (FEA) modelling of fiber-reinforced polymer (FRP) repair in offshore risers. In Rehabilitation of Pipelines Using Fiber-reinforced Polymer (FRP) Composites; Woodhead Publishing: Cambridge, UK, 2015; pp. 177–210. [Google Scholar] [CrossRef]
- Kaw, A.K. Mechanics of Composite Materials, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Bao, Y.; Zhu, H.B.; Huan, P.; Wang, R.; Zhou, D.; Han, Z.L.; Palacios, R.; Graham, M.; Sherwin, S. Numerical Prediction of Vortex-Induced Vibration of Flexible Riser with Thick Strip Method. J. Fluids Struct. 2019, 89, 166–173. [Google Scholar] [CrossRef]
- Xu, W.; He, Z.; Zhai, L.; Wang, E. Vortex-Induced Vibration Prediction of an Inclined Flexible Cylinder Based on Machine Learning Methods. Ocean. Eng. 2023, 282, 114956. [Google Scholar] [CrossRef]
- Deng, D.; Zhao, W.; Wan, D. Vortex-Induced Vibration Prediction of a Flexible Cylinder by Three-Dimensional Strip Model. Ocean. Eng. 2020, 205, 107318. [Google Scholar] [CrossRef]
- Park, H.Y.; Kim, J.; Kuwahara, S. Cyclic behavior of shear-type hysteretic dampers with different cross-sectional shapes. J. Constr. Steel. Res. 2021, 187, 106964. [Google Scholar] [CrossRef]
- Madsen, K. Methods for Non-Linear Least Squares Problems, 2nd ed.; Technical University of Denmark: Kongens Lyngby, Denmark, 2004. [Google Scholar]
- Dai, T.; Li, Z. SLAM graph optimization based on optimized Levenberg-Marquardt method. Harbin Univ. Sci. Technol. J. 2021, 26, 68–74. [Google Scholar] [CrossRef]
- Lamich, M.; Balcells, J.; Corbalán, M.; Griful, E. Nonlinear Loads Model for Harmonics Flow Prediction, Using Multivariate Regression. IEEE Trans. Ind. Electron. 2017, 64, 4820–4827. [Google Scholar] [CrossRef]
- Wang, S.; Hu, X.; Lu, R.; Yan, S.; Li, Y.; Zhang, D. Research on Correlation Analysis and Multivariate Nonlinear Regression Modeling Method for the Tensile Properties of Mugwort Petiole. Sci. Rep. 2024, 14, 31597. [Google Scholar] [CrossRef] [PubMed]
- Sivaprasad, H.; Lekkala, M.R.; Latheef, M.; Seo, J.; Yoo, K.; Jin, C.; Kim, D.K. Fatigue Damage Prediction of Top Tensioned Riser Subjected to Vortex-Induced Vibrations Using Artificial Neural Networks. Ocean. Eng. 2023, 268, 113393. [Google Scholar] [CrossRef]
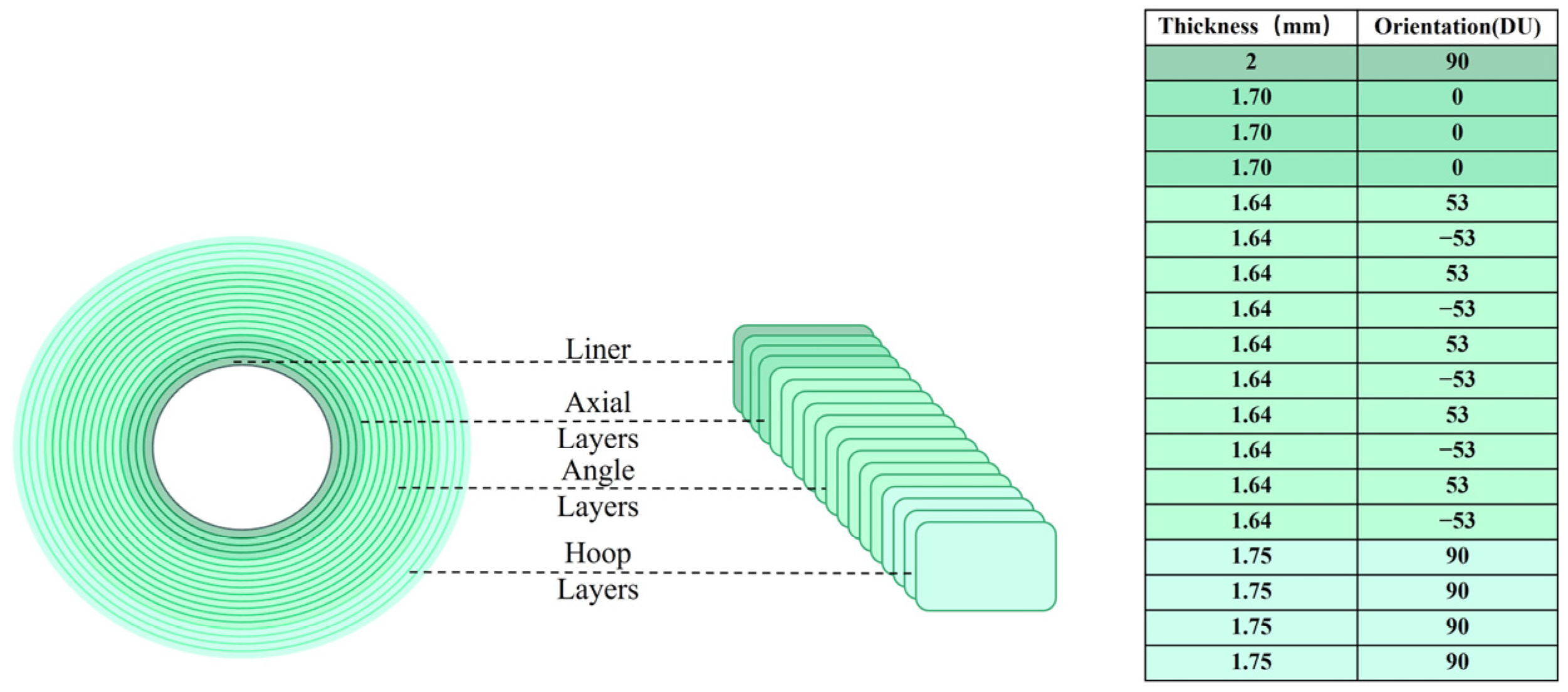
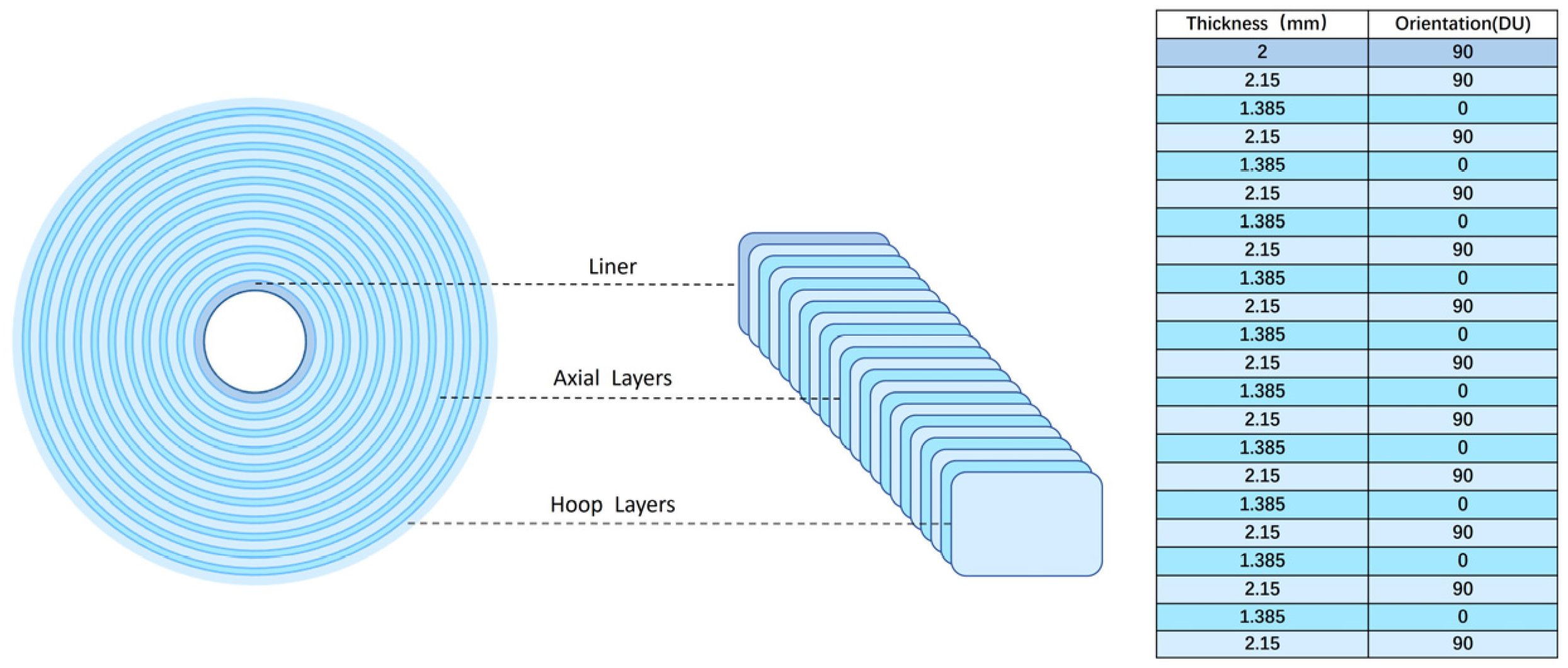
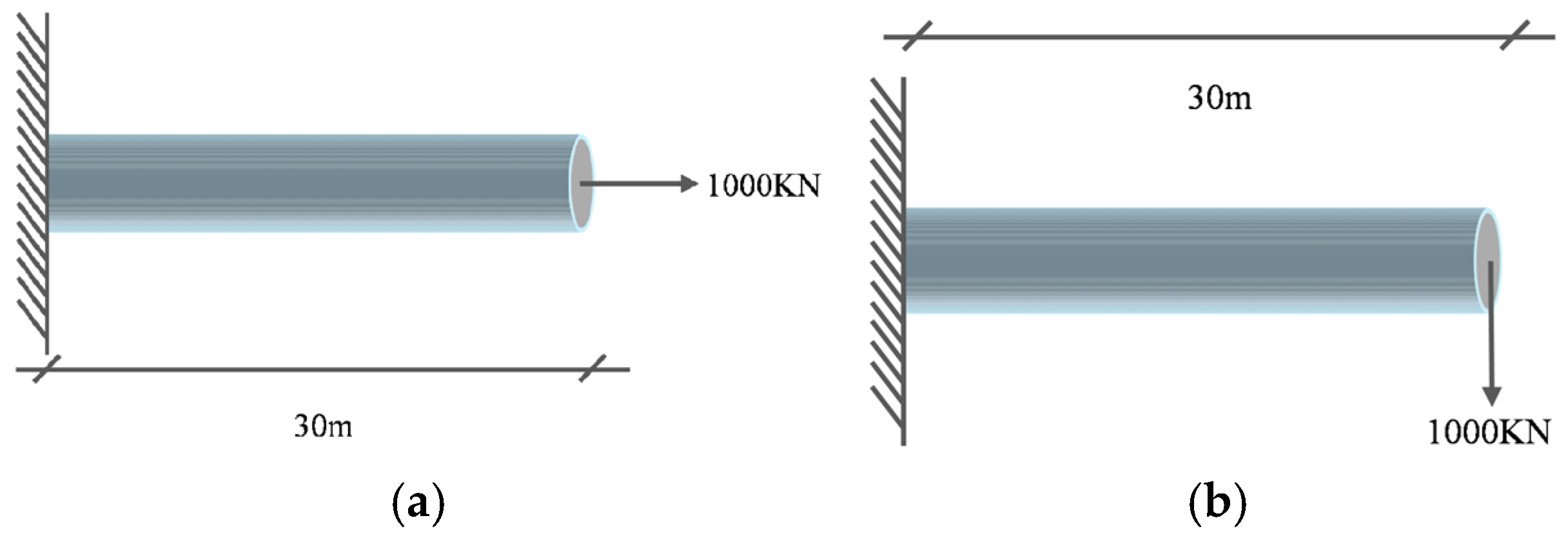


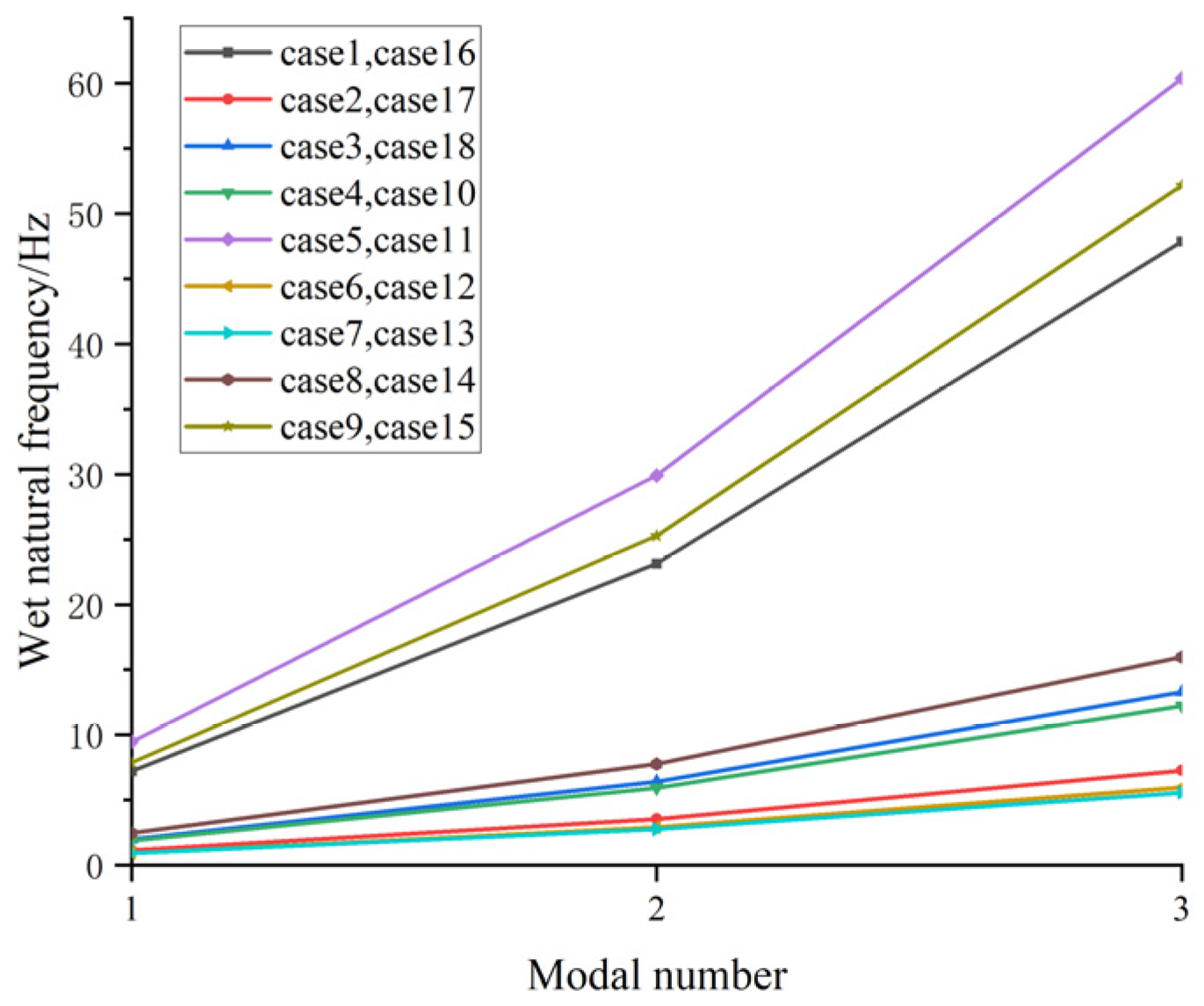




| Type | Number of Layers | Inside Diameter (m) | Outside Diameter (m) | Unit Volume (m3) | Unit Mass (kg/m) |
|---|---|---|---|---|---|
| Optimized FRP composite riser | 18 | 0.25 | 0.311 | 0.0269 | 45.7 |
| Orthogonal FRP composite riser | 22 | 0.25 | 0.329 | 0.0359 | 59.6 |
| X80 riser | 0.25 | 0.3 | 0.0216 | 169 |
| Material | Density (kg/m3) | Modulus of Elasticity (GPa) | Shear Modulus (GPa) | Poisson’s Ratio | Ultimate Strength (MPa) | Yield Strength (MPa) | Elongation at Break (%) |
|---|---|---|---|---|---|---|---|
| AS4 | 1750.00 | E1 = 235.00 | G12 = G13 = 28.00 | υ12 = υ13 = 0.20 | 3590.00 | ||
| E2 = E3 = 14.00 | G23 = 5.60 | υ23 = 0.25 | |||||
| AS4–epoxy composite | 1530.00 | E1 = 135.40 E2 = E3 = 9.37 | G12 = G13 = 4.96 G23 = 3.20 | υ12 = υ13 = 0.32 υ23 = 0.46 | S1 = 1732,S2 = 49.4, S12 = 71.2 | ||
| Epoxy | 1200.00 | 4.50 | 1.60 | 0.40 | 130.00 | ||
| Titanium alloy | 4430.00 | 113.80 | 0.34 | 950.00 | 880.00 | 14.00 | |
| Steel-X80 | 7850.00 | 207.00 | 0.30 | 625.00 | 555.00 | 5.87 | |
| Case | Design of Experiment | Studied Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| Riser Type | Riser Length (m) | Flow Velocity (m/s) | Tensile Modulus (GPa) | Flexural Modulus (GPa) | Slenderness Ratio | Velocity (m/s) | Top Tension (N) | |
| 1 | Optimized FRP riser | 12.5 | 0.36 | 40.5 | 35.7 | 40 | 0.36 | 11,200 |
| 2 | Orthogonal FRP riser | 37.5 | 1.22 | 50.1 | 56.8 | 114 | 1.22 | 43,774 |
| 3 | X80 riser | 25 | 2.13 | 207 | 207 | 83 | 2.13 | 62,309 |
| 4 | Optimized FRP riser | 25 | 1.22 | 40.5 | 35.7 | 80 | 1.22 | 22,400 |
| 5 | Orthogonal FRP riser | 12.5 | 2.13 | 50.1 | 56.8 | 38 | 2.13 | 14,591 |
| 6 | X80 riser | 37.5 | 0.36 | 207 | 207 | 125 | 0.36 | 93,463 |
| 7 | Optimized FRP riser | 37.5 | 2.13 | 40.5 | 35.7 | 121 | 2.13 | 33,600 |
| 8 | Orthogonal FRP riser | 25 | 0.36 | 50.1 | 56.8 | 76 | 0.36 | 29,183 |
| 9 | X80 riser | 12.5 | 1.22 | 207 | 207 | 42 | 1.22 | 31,154 |
| 10 | Optimized FRP riser | 25 | 2.13 | 40.5 | 35.7 | 80 | 2.13 | 22,400 |
| 11 | Orthogonal FRP riser | 12.5 | 0.36 | 50.1 | 56.8 | 38 | 0.36 | 14,591 |
| 12 | X80 riser | 37.5 | 1.22 | 207 | 207 | 125 | 1.22 | 93,463 |
| 13 | Optimized FRP riser | 37.5 | 0.36 | 40.5 | 35.7 | 121 | 0.36 | 33,600 |
| 14 | Orthogonal FRP riser | 25 | 1.22 | 50.1 | 56.8 | 76 | 1.22 | 29,183 |
| 15 | X80 riser | 12.5 | 2.13 | 207 | 207 | 42 | 2.13 | 31,154 |
| 16 | Optimized FRP riser | 12.5 | 1.22 | 40.5 | 35.7 | 40 | 1.22 | 11,200 |
| 17 | Orthogonal FRP riser | 37.5 | 2.13 | 50.1 | 56.8 | 114 | 2.13 | 43,774 |
| 18 | X80 riser | 25 | 0.36 | 207 | 207 | 83 | 0.36 | 62,309 |
| Case | Δ1 (m) | Δ2 (m) | Etensile (GPa) | Eflexural (GPa) | Case | Δ1 (m) | Δ2 (m) | Etensile (GPa) | Eflexural (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0277 | 0.9419 | 40.5 | 35.7 | 10 | 0.0277 | 0.9419 | 40.5 | 35.7 |
| 2 | 0.0141 | 0.4136 | 50.1 | 56.8 | 11 | 0.0141 | 0.4136 | 50.1 | 56.8 |
| 3 | 0.0067 | 0.2112 | 207 | 207 | 12 | 0.0067 | 0.2112 | 207 | 207 |
| 4 | 0.0277 | 0.9419 | 40.5 | 35.7 | 13 | 0.0277 | 0.9419 | 40.5 | 35.7 |
| 5 | 0.0141 | 0.4136 | 50.1 | 56.8 | 14 | 0.0141 | 0.4136 | 50.1 | 56.8 |
| 6 | 0.0067 | 0.2112 | 207 | 207 | 15 | 0.0067 | 0.2112 | 207 | 207 |
| 7 | 0.0277 | 0.9419 | 40.5 | 35.7 | 16 | 0.0277 | 0.9419 | 40.5 | 35.7 |
| 8 | 0.0141 | 0.4136 | 50.1 | 56.8 | 17 | 0.0141 | 0.4136 | 50.1 | 56.8 |
| 9 | 0.0067 | 0.2112 | 207 | 207 | 18 | 0.0067 | 0.2112 | 207 | 207 |
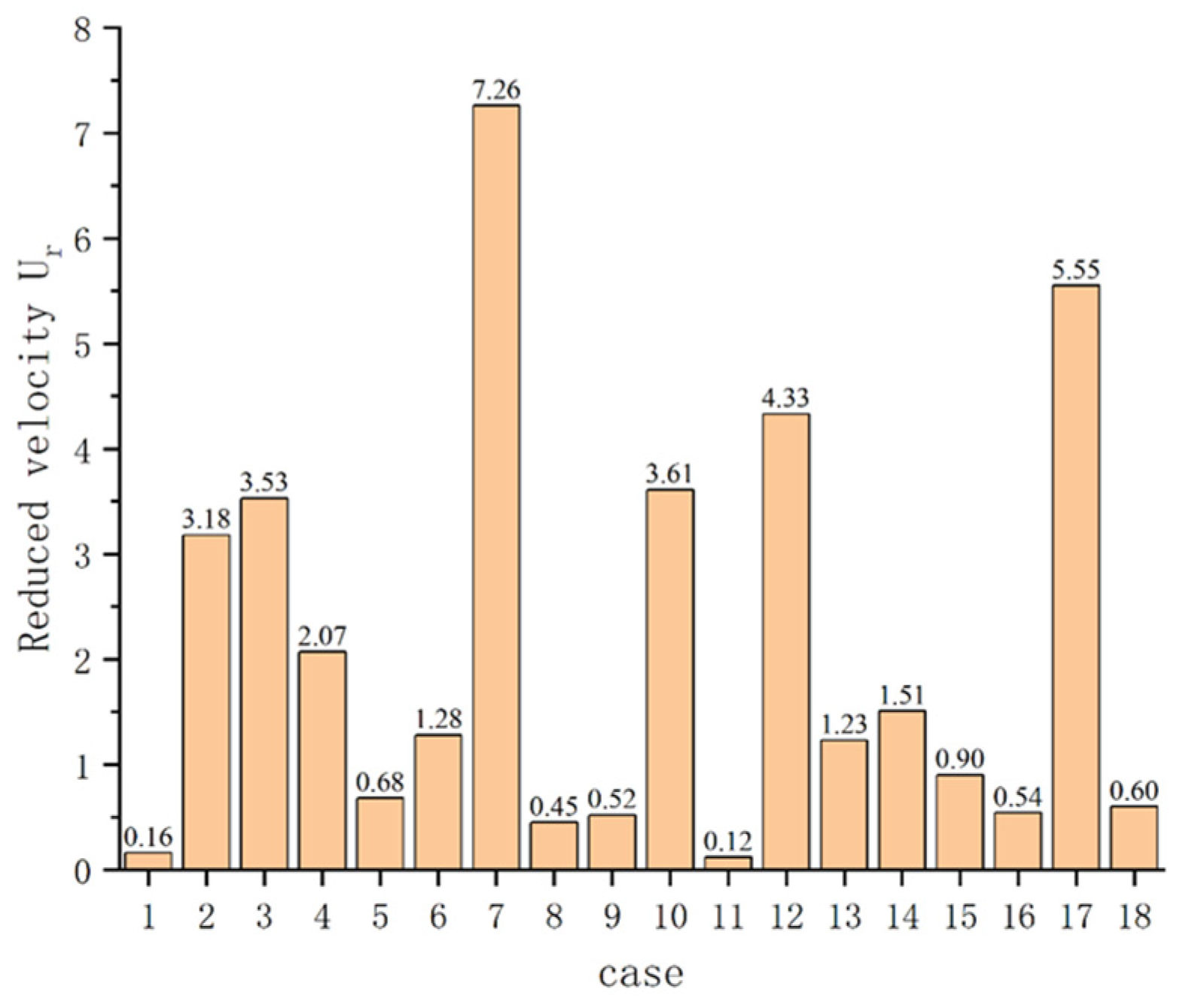
| Case | Flow Density (kg/m3) | v (m2/s) | Re | St | I (%) |
|---|---|---|---|---|---|
| 1 | 1024 | 1.06 × 10−6 | 105,623 | 0.20 | 3.768 |
| 2 | 378,660 | 0.21 | 3.213 | ||
| 3 | 602,830 | 0.22 | 3.031 | ||
| 4 | 357,943 | 0.21 | 3.235 | ||
| 5 | 61,104 | 0.22 | 2.996 | ||
| 6 | 101,887 | 0.20 | 3.785 | ||
| 7 | 624,934 | 0.22 | 3.018 | ||
| 8 | 111,736 | 0.20 | 3.742 | ||
| 9 | 345,283 | 0.21 | 3.250 | ||
| 10 | 624,934 | 0.22 | 3.018 | ||
| 11 | 111,736 | 0.20 | 3.742 | ||
| 12 | 345,283 | 0.21 | 3.250 | ||
| 13 | 105,623 | 0.20 | 3.768 | ||
| 14 | 378,660 | 0.21 | 3.213 | ||
| 15 | 602,830 | 0.22 | 3.031 | ||
| 16 | 357,943 | 0.21 | 3.235 | ||
| 17 | 61,104 | 0.22 | 2.996 | ||
| 18 | 101,887 | 0.20 | 3.785 |
| Exponential Order | ||||||||
|---|---|---|---|---|---|---|---|---|
| −4 | −3 | −2 | −1 | 1 | 2 | 3 | 4 | |
| R2 of tensile modulus (x1) | 0.0001 | 0.0975 | 0.1186 | 0.1143 | 0.0415 | 0.0556 | 0.1170 | 0.0713 |
| R2 of flexural modulus (x2) | 0.0001 | 0.0975 | 0.1386 | 0.1259 | 0.0415 | 0.0556 | 0.1170 | 0.1343 |
| R2 of slenderness ratio (x3) | 0.2183 | 0.2234 | 0.2012 | 0.2789 | 0.1771 | 0.1556 | 0.1547 | 0.3108 |
| R2 of top tension force (x4) | 0.0836 | 0.1032 | 0.1142 | 0.1047 | 0.1033 | 0.1040 | 0.1047 | 0.1683 |
| R2 of flow velocity (x5) | 0.0779 | 0.1047 | 0.1047 | 0.1047 | 0.0915 | 0.2893 | 0.1047 | 0.1047 |
| Coefficient | b0 | b1 | b2 | b3 | b4 | b5 |
|---|---|---|---|---|---|---|
| Fitted values | −0.225 | 1.3089 | −3.091 | 0.622 | 0.826 | 0.686 |
| Coefficient | b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 |
| Fitted values | 1.527 | −7.662 | 3.985 | 6.202 | 3.3473 | 3.669 | −0.893 | 8.559 |
| Coefficient | b8 | b9 | b10 | b11 | b12 | b13 | b14 | b15 |
| Fitted values | 9.322 | −2.110 | 10.375 | 16.487 | −4.230 | −5.069 | 4.382 | −1.655 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, C.; He, W.; Ma, K.; Zheng, R.; Amaechi, C.V.; Zhang, Z. Vortex-Induced Vibration Analysis of FRP Composite Risers Using Multivariate Nonlinear Regression. J. Mar. Sci. Eng. 2025, 13, 1281. https://doi.org/10.3390/jmse13071281
Zhang L, Wang C, He W, Ma K, Zheng R, Amaechi CV, Zhang Z. Vortex-Induced Vibration Analysis of FRP Composite Risers Using Multivariate Nonlinear Regression. Journal of Marine Science and Engineering. 2025; 13(7):1281. https://doi.org/10.3390/jmse13071281
Chicago/Turabian StyleZhang, Lin, Chunguang Wang, Wentao He, Keshun Ma, Run Zheng, Chiemela Victor Amaechi, and Zhenyang Zhang. 2025. "Vortex-Induced Vibration Analysis of FRP Composite Risers Using Multivariate Nonlinear Regression" Journal of Marine Science and Engineering 13, no. 7: 1281. https://doi.org/10.3390/jmse13071281
APA StyleZhang, L., Wang, C., He, W., Ma, K., Zheng, R., Amaechi, C. V., & Zhang, Z. (2025). Vortex-Induced Vibration Analysis of FRP Composite Risers Using Multivariate Nonlinear Regression. Journal of Marine Science and Engineering, 13(7), 1281. https://doi.org/10.3390/jmse13071281








