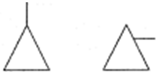A Reliability Assessment of a Vessel’s Main Propulsion Engine

Abstract

Ocean-going vessels rely on marine diesel engines, referred to as the main engine, to carry the vessel’s load and ensure safe travel. These engines play a critical role, as their operation impacts on all aspects of the vessel’s functionality. To meet increasing demands for extended run times while maintaining reliability, it is essential to address the risks of main engine failure. Previous studies have highlighted numerous accidents resulting from such failures. Consequently, the reliability of the main propulsion engine is a crucial component of safe vessel operation. This study addresses the lack of methodologies for predicting engine reliability using failure running hours (FRHs). A data-driven model was developed using FRH data collected from marine engineers during on-board maintenance operations. Additionally, fault tree analysis (FTA) was employed to calculate the reliability of individual subsystems and the overall main propulsion engine. The findings indicate that the lube oil system, freshwater cooling system, scavenge system, and fuel system reach 0% reliability at approximately 2000 h, 14,000 h, 2500 h, and 1400 h of operation, respectively. Additionally, the reliability of the main propulsion engine drops to 0% after around 900 h of operation. By incorporating this prediction model, ship operators can better schedule maintenance, significantly enhancing engine reliability and reducing maritime accidents. This approach contributes to safer and more efficient operations for commercial marine systems. This study represents a vital step toward improving the reliability of ocean-going vessels.

1. Introduction

The reliability of a vessel’s main propulsion engine is a critical aspect of safe maritime operations, especially given that 90% of global cargo is transported via large bulk carriers [1]. These immense ships rely on high-capacity diesel engines, often called main engines, which serve as the heart of the vessel’s propulsion system. Typically, these engines are slow-speed, high-power diesel engines running at up to 120 Revolutions Per Minute (RPM), while smaller vessels utilize high-speed diesels with operating speeds reaching up to 1000 RPM [2]. The main propulsion engine comprises several subsystems, including mechanical components, cooling water systems, fuel oil systems, scavenge air systems, and lubricating oil systems. Ensuring the reliability and extended runtime of these subsystems is vital for safe and efficient maritime travel.

Failures within these systems can have significant consequences for global trade. For instance, the bulk carrier Rava was temporarily disabled while transiting the Bosporus Strait due to a suspected main engine failure [3]. This underscores the crucial role of propulsion system reliability in world trade. Marine engine failures can lead to severe operational, economic, and safety consequences for maritime operations. According to Allianz’s Safety and Shipping Review [4], machinery damage or failure, including main engine faults, was responsible for over 30% of 26,000 marine incidents reported globally over a ten-year period. A case study by [5] demonstrated that critical failures in ship main engines, such as turbocharger or fuel pump malfunctions, can increase repair costs by up to USD 250,000 per incident, excluding downtime and potential cargo delays. In the MV Bright Field incident, a main engine blackout resulted in a collision with the Riverwalk Marketplace in New Orleans, causing over USD 1.8 million in damage and injuring 66 people [6]. Similarly, a recent event involving the container ship Dali in Baltimore (2024) caused catastrophic structural failure of the Francis Scott Key Bridge after an engine blackout, resulting in six fatalities and economic losses estimated at USD 2 billion, including infrastructure damage and port disruption [7]. These incidents underscore the critical need for robust engine maintenance and fault detection strategies to minimize both financial risk and loss of life. A thorough investigation into reliability methodologies for the marine industry has been conducted using academic databases, like Web of Science and Scopus. Recent studies, such as those by the Australian Maritime College, have applied techniques like Bayesian Networks, Weibull Failure Models, and Markov Models. However, methods like fault tree analysis combined with Weibull, Gamma, and normal models remain underutilized in the marine industry. While previous research defined systems using fault tree analysis, such as Laskowski’s investigation, no reliability calculations were performed. Moreover, this application does not implement the methodology in a practical or data-driven manner within the context of ship engine reliability. This study not only references fault tree analysis (FTA) but also extends its foundation by integrating actual failure data (FRH) to develop a reliability model specifically tailored to marine engineering systems. Furthermore, it goes beyond theoretical discourse by applying real-world data to assess system reliability, providing a more practical and empirically grounded contribution.

By contrast, the aviation industry has successfully applied these techniques for reliability assessments, as demonstrated in studies on fuel systems [8]. However, within the marine sector, reliability analyses have often focused on scenarios like grounding probabilities, leaving a gap in studies addressing the failure hours of main systems.

Diesel engines dominate marine propulsion systems due to their operational reliability, thermal efficiency, and ability to burn heavy fuel oils [9]. Typical marine propulsion plants feature slow-speed, turbocharged, two-stroke diesel engines directly coupled to large-diameter, fixed-pitch propellers. These engines eliminate the need for gearboxes or reverse gears, making them ideal for merchant vessels requiring robust and efficient propulsion. The main components of these two-stroke engines include the bedplate and crankcase, crankshaft and flywheel, engine body, cylinder blocks and liners, and pistons with connecting rods [9].

Engine failures can significantly impact maritime operations, as illustrated by the Maersk Emerald incident. This container ship experienced a sudden failure in the Suez Canal, resulting in grounding and disruption [10]. Maintenance logs and schedules provide valuable data for estimating life expectancy and predicting potential failures. By applying failure distribution models, the occurrence of unexpected failures can be minimized.

In a case study on turbocharger failures, which are considered major failures leading to engine immobilization, reliability methods such as Markov analysis and Weibull distribution were used, including cost assessments [11]. Although the turbocharger is an external component of the main engine, this study’s approach demonstrates how dependent failure rates can inform reliability analyses. For example, turbochargers exhibit a constant failure rate under similar conditions, suggesting that reliability assessments must account for time-dependent failure rates.

Table 1. State of oil supply pump.

State	Pump 1	Pump 2
1	Operating	Standby
2	Failed	Operating
3	Failed	Failed

shows the different operating states; hence, there is redundancy. As the main motor does not have any redundancy, if it were to incur a major failure, we can only consider 3 states of operating, standby, and failure. While the primary propulsion systems are generally nonredundant in terms of full duplication, certain redundancy mechanisms, such as auxiliary systems, standby components, or system-level fail-safes, do exist within shipboard machinery configurations. Referring to the DNV GL classifications under the systems and components of a ship in Section 2.1.5, it states that “The reliability and safety of components and complete units may also be documented by means of approved tests or service experience. The latter shall only be considered if a relevant load history can be documented” [12].

This can be better interpreted by saying the comments should be logged and recorded. This can then be assessed to see any abnormalities within the recorded information. According to Charles Ebeling, the Weibull distribution model is one of the most useful probability distributions within reliability. The distribution function can be used for both increasing and decreasing failure rates, which makes it a common theoretical probability method alongside normal Lognormal and Gamma distributions. “These distributions have hazard rate functions that are not constant over time, thus providing a necessary alternative to the exponential failure law” [13]. Normal distribution is an alternative way to model fatigue wear out phenomena due to the relationship between the Lognormal distribution. This method allows for the use of analyzing further Lognormal probabilities, as it provides a common bell-shaped curved. The Gamma model has a similar distribution profile to Weibull, as it has a family that includes the exponential distribution.

According to research by Pinheiro and Bates, the log likelihood of nonlinear mixed-effects models proves highly effective in handling unbalanced repeated-measures data in various fields, such as pharmacokinetics and economics [14]. This methodology is also applicable when using distribution models for reliability assessments. As previously discussed, it can be applied to Weibull, Gamma, and normal probability distributions, and the log likelihood is particularly useful when applied to Probability Density Functions (PDFs).

The mean time to failure (MTTF) is a critical metric in reliability analysis. As defined by Cadence, MTTF “evaluates the reliability of non-repairable items and equals the meantime expected until the first failure of a component, assembly, or system” [15]. In essence, MTTF represents the predicted lifespan of a system or component. It is calculated by dividing the total hours of operation by the total number of units. This metric is widely used to predict when individual system components might fail, facilitating planned maintenance, repairs, or replacements to prevent unexpected breakdowns.

Charles Ebeling describes fault tree analysis as a valuable tool for performing safety assessments on failures. According to Ebeling, “A fault tree analysis is a graphical design technique that provides an alternative to reliability block diagrams” [13]. He outlines six key steps in conducting a fault tree analysis:

• Define the system, its boundaries, and the top event—This includes, for example, the reliability of a vessel’s main propulsion engine.
• Evaluate the system using a data-driven model—Identify and characterize the combination of events leading to failures.
• Construct the fault tree—Graphically represents the total system and its events, typically focusing on failures of individual components.
• Perform a qualitative evaluation—Identify the combinations of events contributing to the top event, such as a failure in the main propulsion engine.
• Conduct a quantitative evaluation—Assign probabilities and reliability values to the events defined in the fault tree.
• Present findings and conclusions—Summarize the results of the analysis with respect to the reliability of the main propulsion engine and its subsystems.

This study seeks to develop a data-driven model and fault tree analysis (FTA) to predict the reliability of the main engine onboard ships. This technique is used for reliability assessments in the aviation industry; however, the model developed in this study is more specific to maritime operations, considering sector-specific parameters, such as environmental conditions, engine load variations, and maintenance schedules, which were incorporated into the model to ensure its relevance and reliability for maritime applications.

The structure of this paper is outlined as follows: Section 2 details the materials and methods used in the research, Section 3 discusses the results and discussion, and Section 4 concludes this study with key findings and implications.

2. Materials and Methods

The methodology for this study is grounded in data collected from on-board marine engineers through a questionnaire survey. The questionnaire was originally presented in a published article by the primary author [8]. This survey aimed to gather valuable insights from experienced marine engineers working in the shipping industry.

A survey was conducted to gather insights from experienced marine engineers in the shipping industry. Respondents were selected based on specific criteria: (i) a minimum of 5–10 years of onboard engine maintenance experience and (ii) prior service as a 3rd engineer, 2nd engineer, or chief engineer in a ship’s engine department. To facilitate data collection, a questionnaire was created using SurveyMonkey. Ethics approval was obtained in accordance with the University of Tasmania’s guidelines, and formal approval was granted by its Human Research Ethics Committee. The survey link was e-mailed to 200 experienced marine engineers across the globe. A total of 101 responses were received, yielding a response rate of 50.5%.

Based on the collected data, a combined approach utilizing three data-driven models was employed to extract and identify the parameters that define the characteristics of the dataset. Fault tree analysis (FTA) served as the reliability method, enabling the evaluation and analysis of the data-driven models to establish relationships between subsystems and derive the overall reliability of the system.

This integrated methodology aims to determine the total reliability of a vessel’s main propulsion engine, considering each subsystem’s contribution. Graphical plots of failure running hours were generated using Probability Density Functions (PDFs) and Cumulative Density Functions (CDFs), providing a visual representation of the data. These distributions help validate the consistency of results and ensure accurate analysis. A graphical representation also highlights the failure of running hour data for each subsystem, offering a clear overview of performance metrics.

The data-driven models applied in this study include Gamma, Weibull, and normal distributions, allowing for the inclusion of a wide range of failure probabilities. By integrating these models into the FTA, reliability functions were defined for each subsystem and used to calculate the total reliability of the vessel’s propulsion engine. This approach combines theoretical modelling with practical insights to achieve a comprehensive reliability assessment.

2.1. Data-Driven Model

Data points significantly deviating from the expected operating range were identified and excluded. Moreover, records with missing critical parameters or incomplete failure time information were excluded from the analysis. Duplicate entries and repetitive log data were identified and removed to prevent skewing the results. Furthermore, the failure running hour data was filtered through MATLAB R2021b, filtering any failure running hours presented as zero or below, as the domain of time must be greater than zero hours. This can be represented by the following domain.

$$Domain\in [t>0]$$

Therefore, using the fit functions, the distributions can be assessed for the Weibull, Gamma, and the normal functions for both the PDF and the CDF. This is represented in the example below, with the left graph in Figure 1 suggesting the PDF and the right representing the CDF.

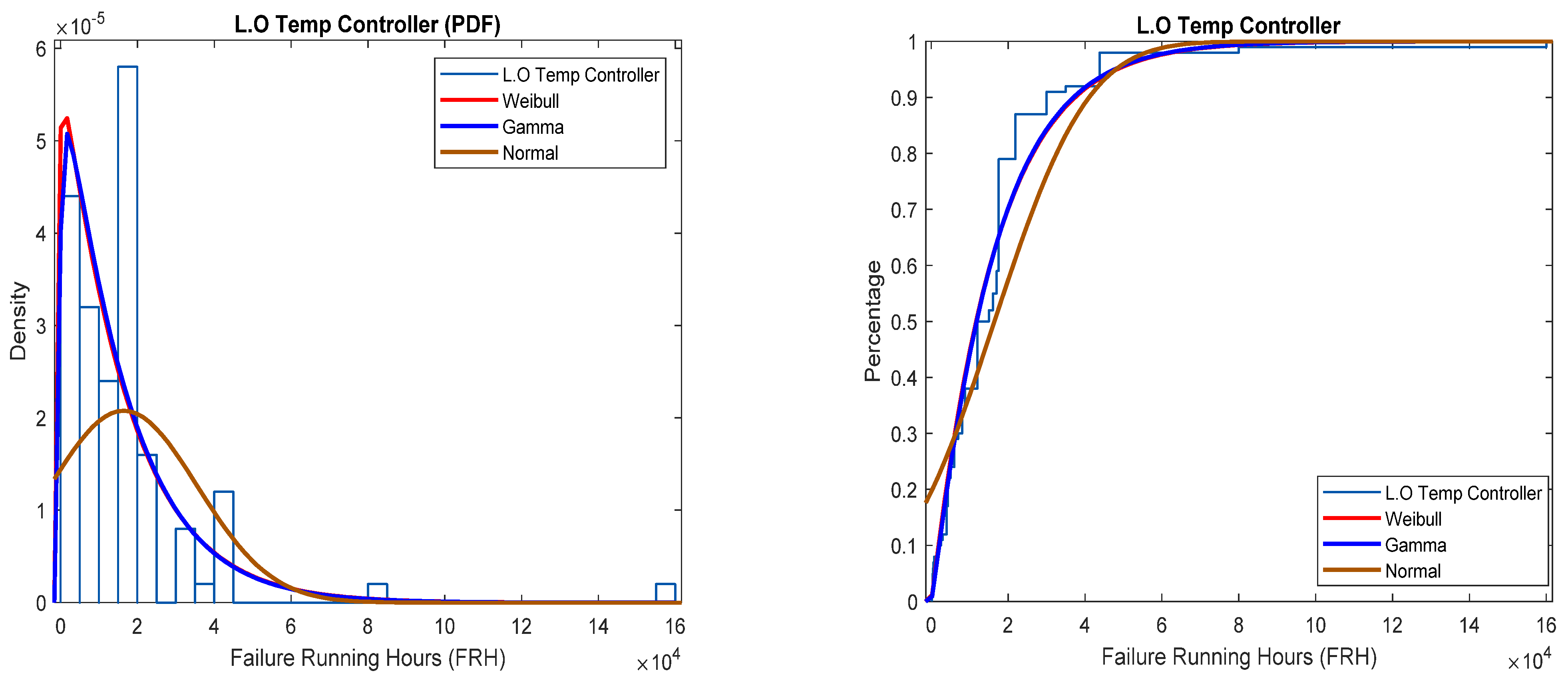
Figure 1 provides a visual representation of the density functions, showing that the Weibull and Gamma probability curves align with the distributions. However, normal distribution does not align, which is supported by the higher log-likelihood value or the curve of best fit. MATLAB R2021b was used to calculate log-likelihood values, determining the best-fitting distribution based on the numerical value closest to 1.

The fitted data will yield corresponding values that establish relationship coefficients. These coefficients will be utilized to generate probabilities and reliability metrics. Key calculations will include metrics such as the mean time to failure (MTTF), median, and standard deviation. The data will incorporate the variables presented in

Table 2. Distribution methods.

Distribution Methods
Weibull	ϴ—Characteristic Life	β—Shape Parameter
Gamma	α—Scale Parameter	γ—Shape Parameter
Normal	µ—Mean	σ—Standard Deviation

to ensure accurate analysis.

Using the distribution coefficients derived from all applied methods, mathematical formulas can be established based on the best-fitting models identified in MATLAB R2021b. These formulas represent the Probability Density Functions (PDFs) for analyzing reliability across the three selected models. The equations incorporate parameters optimized by MATLAB R2021b, ensuring an accurate assessment of reliability. The PDF equations for each reliability model can be expressed as follows:

Weibull Probability Density Function with a domain of $t\in [0,\infty ]$

$$f\left(t\right)={\displaystyle \frac{\beta }{\theta }}{\left({\displaystyle \frac{t}{\theta }}\right)}^{\beta -1}{e}^{{-\left(t/\theta \right)}^{\beta }}$$

(1)

Gamma Probability Density Function with a domain of $t\in [0,\infty ]$

$$f\left(t\right)={\displaystyle \frac{t^{\gamma -1}{e}^{-t/\alpha }}{{\alpha }^{\gamma }\Gamma \left(\gamma \right)}}$$

(2)

Normal Probability Density Function with a domain of $t\in [0,\infty ]$

$$f\left(t\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}{e}^{-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{(t-\mu )}^2}{{\sigma }^2}}}$$

(3)

Equations (1)–(3) represent the best-fit Probability Density Functions (PDFs) for the three selected distribution methods, determined by their respective highest log-likelihood values. These equations enable the calculation of the mean time to failure (MTTF), providing an estimate of the average time to failure for each component based on the available data. The calculated MTTF values for all three methods will be used to evaluate the reliability of the main propulsion engine. Each subsystem’s reliability will contribute to the overall reliability of the main propulsion engine, ensuring that every component’s impact on the system is accounted for in the final analysis.

Weibull MTTF domain of $t>0$

$$MTTF=\theta \Gamma \left(1+{\displaystyle \frac{1}{\beta }}\right)$$

(4)

Gamma MTTF domain of $t>0$

$$MTTF=\gamma \alpha$$

(5)

Normal MTTF domain of $t>0$

$$MTTF=\mu$$

(6)

By utilizing the mean time to failure (MTTF) for each system and component, reliability at a given elapsed time can be calculated and incorporated into the fault tree analysis (FTA). This approach evaluates the overall reliability of the system at the expected failure time for all components.

The reliability equations can then be used to generate a total probability graph, visually representing the reliability of individual subsystems along with the overall reliability of the main engine. The FTA framework enables the construction of system reliability by logically combining the reliability of various subsystems through defined statements. The following equations represent the reliability functions for each selected probability distribution, providing the foundation for these analyses.

Weibull Reliability with respect to time

$$R\left(t\right)=e^{{-(t/\theta )}^{\beta }}$$

(7)

Gamma Reliability with respect to time

$$R\left(t\right)=1-{\displaystyle \frac{{\rm I}(t/\alpha \gamma )}{\Gamma \gamma }}$$

(8)

Normal Reliability with respect to time

$$R\left(t\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}{\int }_t^{\infty }{e}^{-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{t^{\prime }-\mu }{\sigma }}\right)}^2}d{t}^{\prime }$$

(9)

Equations (1)–(9) were sourced from the study ‘An Introduction to Reliability and Maintainability Engineering’ [13].

2.2. Fault Tree Analysis Approach

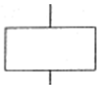
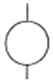
Using fault tree analysis (FTA), the main propulsion engine system is represented using a combination of symbols. This approach follows the four-step process outlined by Charles Ebeling: defining the system, constructing the fault tree, identifying key events, and assigning failure probabilities. The symbols commonly used in fault trees include two primary logical gates: the ‘AND’ and ‘OR’ gates, which describe how events occur within the system. The ‘AND’ gate represents a system primarily arranged in series, lacking redundancy, as all components must function for the system to operate. In contrast, the ‘OR’ gate represents a parallel system, implying a higher level of redundancy, since only one component needs to function for the system to remain operational. These gates are used to relate to various event types, including resultant, basic, and incomplete events, which further extend to conditional and normal events. The relationships and impacts of these events can be effectively summarized in the following diagram.

Shape	Event
	AND gate. A logic gate which outputs only when all inputs have occurred (∩).
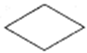
	OR gate. A logic gate which outputs if at least one input event has occurred (∪).
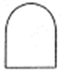
	Resultant event. A fault resulting from the logical combination of other fault events.
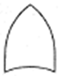
	Basic event. An independent elementary event representing a basic fault or component.
	Incomplete event. An event that has not been fully developed due to lack of knowledge.
	Transfer-in and Transfer-out. Used to link sections that are not contiguous or appear on separate pages.
	Conditional event. A condition or restriction connected to a logical gate.
	Normal event. A normally occurring event that is not a fault.

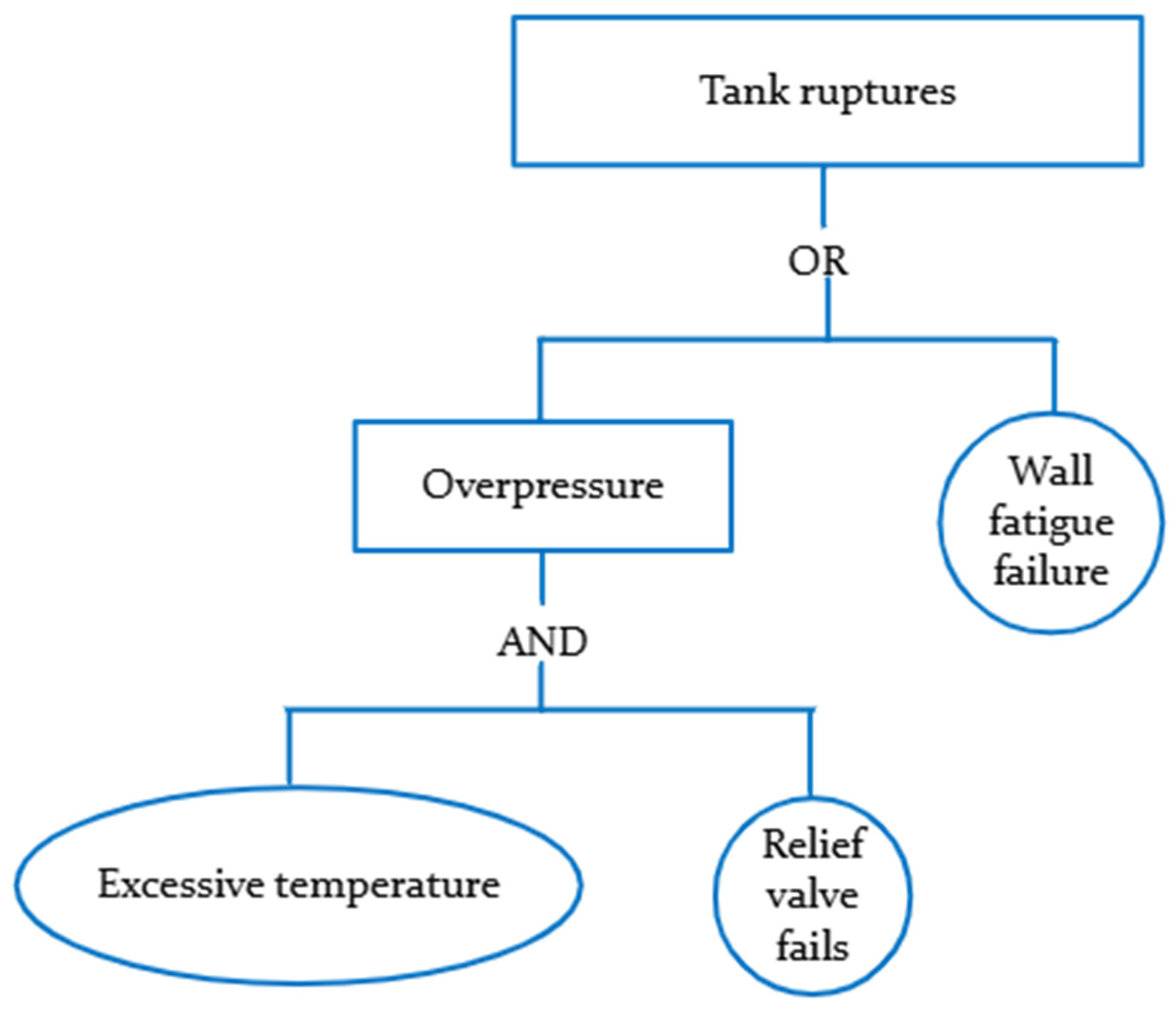
An example of the fault tree analysis is represented by the following figure with both the ‘AND and ‘OR’ gates.

Figure 2 illustrates the application of logical gates in fault tree analysis. It demonstrates that both excessive temperature and relief valve failures must occur for the operation to proceed through the ‘AND’ gate. If either event fails, the resultant condition will be overpressure within the tank, which then leads to an ‘OR’ gate. At this gate, only one failure—either overpressure or wall fatigue—needs to occur for the resulting event, a tank rupture, to take place.

By incorporating Boolean functions alongside the reliability equations for each subsystem, the overall reliability of the vessel’s main propulsion engine can be determined. This analysis enables the calculation of the engine’s reliability over time, considering the interconnections and failure probabilities of its subsystems.

3. Results and Discussion

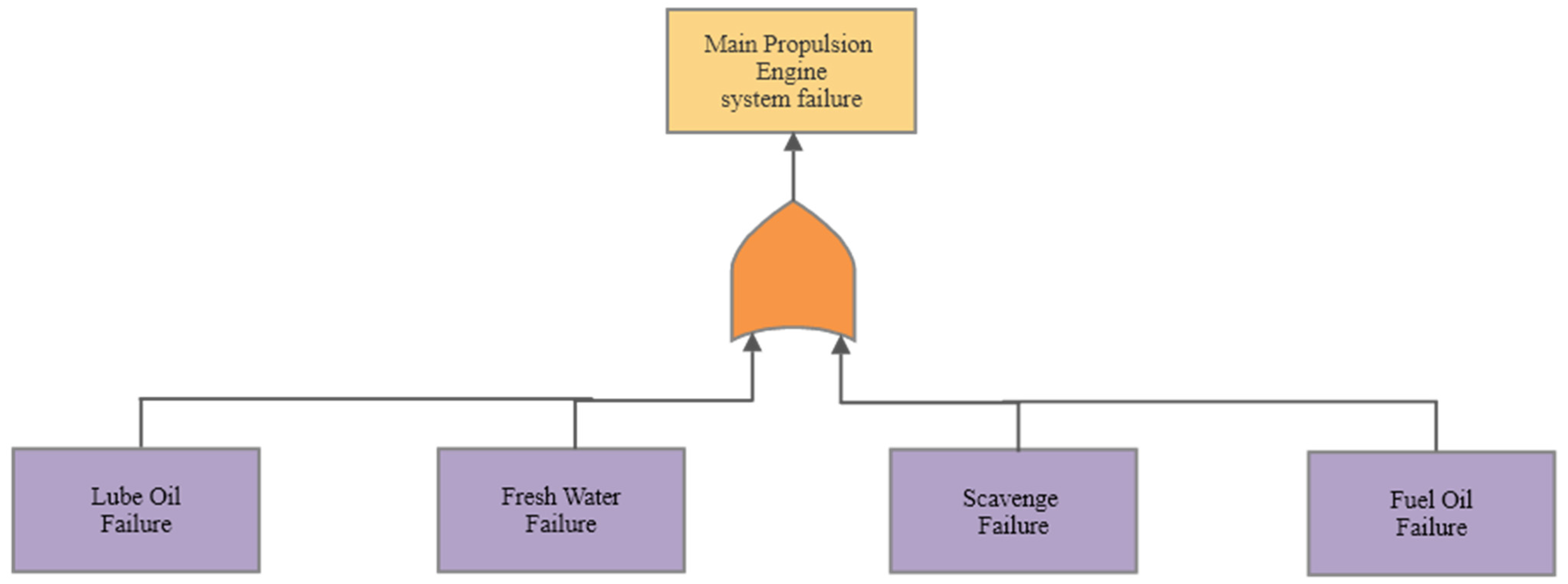
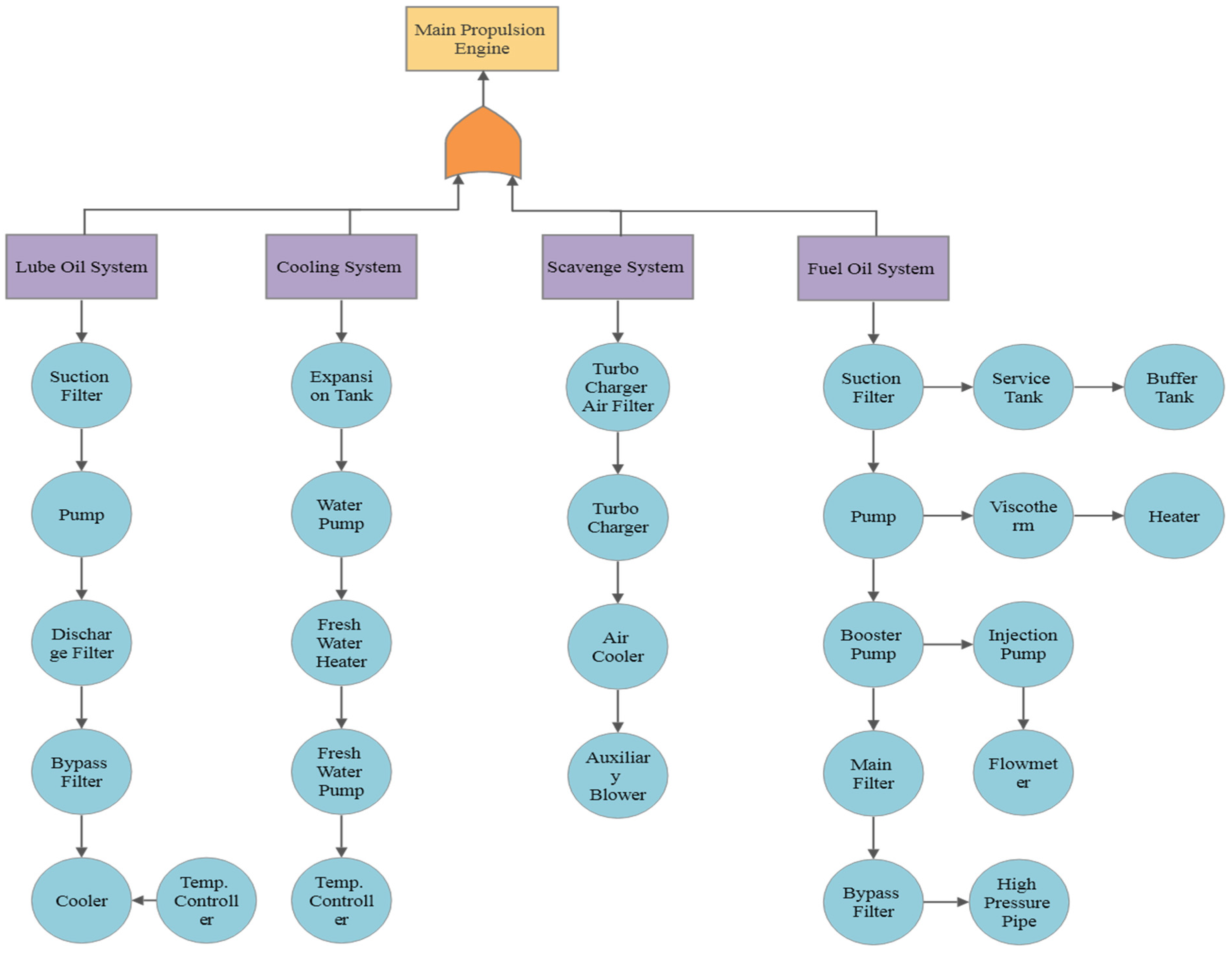
Using the collected data, a previous survey of the FRH was obtained for all 26 systems and 101 different respondents. The data was obtained from a published article which conducted a survey from onboard marine engineers. The systems recorded are shown in the figure below, with the main propulsion engine leading into four subsystems: lube oil, cooling system, scavenge system, and fuel oil.

3.1. Distribution Methods

Figure 3 illustrates all the systems analyzed and incorporated into the fault tree analysis (FTA). The data, filtered and processed through MATLAB R2021b’s distribution filter, enables the creation of Probability Density Functions (PDFs) and Cumulative Density Functions (CDFs). These distributions are visually examined to identify correlations within the results.

Figure 4 provides a comparison of three distributions—Weibull, Gamma, and normal—modelled at a 95% confidence level. The Weibull and Gamma distributions initially appear to align more closely with the dataset trends compared to the normal distribution. This observation is supported by the log-likelihood function, which generates numerical values to determine the best-fit function. Based on the values obtained, Figure 5 suggests that Gamma distribution provides the most accurate fit, further strengthening its reliability in modelling the data.

Table 3. Distribution selection for lube oil temperature controller.

Distribution Type	Log Likelihood
Weibull	−1070.53
Gamma	−1070.36
Normal	−1127.66

shows that the Gamma distribution has a log likelihood that is 0.17 greater than the Weibull function. This suggests the best-fit distribution to be the Gamma function.

The variables derived from the graphs, including shape parameters, scale parameters, and characteristic life, are summarized in

Table A1. Distribution selection table with log likelihood.

System	Components	Weibull			Gamma			Normal			Distribution Mode
		ϴ	β	Log Likelihood	α	γ	Log Likelihood	µ	σ	Log Likelihood
Lube Oil	Pump	1024.37	1.65762	−761.526	287.376	3.15963	−754.085	908	614.141	−783.416	Gamma
	Main Discharge Filter	18,475	1.27116	−1071.32	12,449.3	1.3811	−1072.31	17,193.8	12,839.9	−1087.43	Weibull
	Bypass Filter	3136.4	1.13	−899.016	2266.21	1.31844	−898.048	2987.86	2790.97	−934.808	Gamma
	Cooler	2847.61	1.03096	−893.947	2441.93	1.14998	−893.437	2808.17	2938.38	−939.955	Gamma
	Temp Controller	16,639.9	1.03168	−1070.53	14,986.8	1.09557	−1070.36	16,419.1	19,199.6	−1127.66	Gamma
Fresh Water	Expansion Tank	17,522.8	1.08082	−1073.45	14,255.9	1.19075	−1073.04	16,975.1	16,317.3	−1111.39	Gamma
	Water Pump	14,073.7	1.13597	−1049.02	10,365.2	1.29329	−1048.43	13,405.2	12,505.6	−1084.79	Gamma
	Cooler	11,788.5	0.979777	−1038.48	11,047.9	1.07809	−1038.34	11,910.6	13,785.4	−1094.53	Gamma
	Heater	14,723.2	1.17996	−1051.79	10,447.6	1.32958	−1051.59	13,890.9	12,064.8	−1081.2	Gamma
	Temp Controller	17,290.1	1.22559	−1066.17	11,860.5	1.36463	−1066.46	16,185.2	13,075.7	−1089.25	Weibull
Scavenge	Air Filter	698.556	1.14362	−746.798	372.781	1.76366	−740.679	657.46	870.786	−818.333	Gamma
	Turbo Charger	21,841.5	1.58671	−1071.97	7558.49	2.57168	−1067.9	19,438	13,467.3	−1092.2	Gamma
	Air Cooler	8331.78	0.878744	−1009.03	9784.62	0.922874	−1010.61	9029.97	12,870.1	−1087.66	Weibull
	Aux Blower	18,871.1	1.2482	−1073.54	11,914.4	1.47183	−1073.13	17,535.9	14,368.8	−1098.68	Gamma
Fuel Oil	Suction Filter	748.44	1.52408	−735.546	237.09	2.81378	−727.531	667.12	511.327	−765.095	Gamma
	Booster Pump	11,968.8	1.19566	−1019.31	7392.1	1.51357	−1017.36	11,188.5	10,440.3	−1056.06	Gamma
	Main Filter	1476.02	1.07449	−825.872	1061.84	1.34452	−823.897	1427.67	1697.06	−885.059	Gamma
	By Pass Filter	1515.38	1.0984	−819.305	1116.36	1.30435	−818.064	1456.12	1495	−863.653	Gamma
	Heater	13,586.8	0.941578	−1054.36	14,542.4	0.962729	−1054.64	14,000.4	15,290	−1104.89	Weibull
	ViscoTherm	11,721.2	0.864973	−1042.94	15,210.6	0.834325	−1043.71	12,690.6	14,652.6	−1100.63	Weibull
	Injection Pump	17,927	1.21114	−1069.97	11,872.9	1.41298	−1069.46	16,776.2	14,276.2	−1098.03	Gamma
	H.P Pipe	9601.09	0.885119	−1022.14	11,808.7	0.867747	−1022.78	10,247	11,585.1	−1077.14	Weibull
	Buffer Tank	34,502.7	1.89235	−1112.96	14,258.4	2.16934	−1119.92	30,931.4	16,092.8	−1110.01	Weibull
	Service Tank	31,529.4	1.9197	−1079.89	11,907.3	2.36303	−1085.58	28,137.4	14,814.2	−1079.68	Weibull
	Flowmeter	7943.84	0.854102	−1005.07	10,300.3	0.849249	−1006.72	8747.5	12,111.5	−1081.59	Weibull

, located in Appendix A—Distribution Selection, presents all the distribution values associated with the reliability equations, mean time to failure (MTTF), and density functions. These results are consolidated into the following tables, where the selection of the distribution is based on the highest log-likelihood values.

Table 4. Distribution fits for lube oil systems.

Lube Oil
Pump	Main Discharge Filter	Bypass Filter	Cooler	Temp Controller
Gamma	Weibull	Gamma	Gamma	Gamma

,

Table 5. Distribution fits for freshwater systems.

Fresh Water
Expansion Tank	Water Pump	Cooler	Heater	Temp Controller
Gamma	Gamma	Gamma	Gamma	Weibull

,

Table 6. Distribution fits for scavenge systems.

Scavenge
Air Filter	Turbocharger	Air Cooler	Aux Blower
Gamma	Gamma	Weibull	Gamma

and

Table 7. Distribution fits for fuel oil systems.

Fuel Oil
Suction Filter	Booster Pump	Main Filter	Bypass Filter	Heater	ViscoTherm
Gamma	Gamma	Gamma	Gamma	Weibull	Weibull
Injector Pump	H.P Pipe	Buffer Tank	Service Tank	Flowmeter
Gamma	Weibull	Weibull	Weibull	Weibull

outline the distribution results for all 26 systems, with the Gamma distribution emerging as the most observed. Notably, Table 7 reveals a trend within the Weibull distribution, as 6 out of the 11 subsystems align with it. Using the data presented in Table A1, the reliability of each system can be calculated and incorporated into the fault tree analysis (FTA).

The calculation of variables follows a standardized process, exemplified here using the lube oil Temperature Controller with the Gamma distribution. This approach ensures consistency and accuracy in determining reliability values for each subsystem.

$$R\left(t\right)=1-{\displaystyle \frac{{\rm I}(t/\alpha \gamma )}{\Gamma \gamma }}$$

Using Table A1 with Alpha = 14,986.8 and gamma = 1.096

$$R\left(t\right)=1-{\displaystyle \frac{{\rm I}(t/\mathrm{14,986.8}\times 1.096)}{\Gamma 1.096}}$$

This is calculated using the MATLAB command gamcdf, which is used in the following

$$R\left(t\right)=1-gamcdf(t,\gamma ,\alpha )$$

Similar variables can be calculated using the Weibull reliability equation using the lube oil Main Discharge Filter. This can be shown by the following equations.

$$R\left(t\right)=e^{{-(t/\theta )}^{\beta }}$$

Using Table A1 with Theta = 18,475 and Beta = 1.271

$$R\left(t\right)=e^{{-(t/\mathrm{18,475})}^{1.271}}$$

For both reliability functions, this can be used over a range of time to assess the reliability of each component, which will be used within the fault tree analysis.

3.2. Fault Tree Analysis Results

Fault tree analysis (FTA), as previously discussed, is a reliability method that provides a simplified representation of the entire system using “AND” and “OR” gates to facilitate conditional analysis. The system can be divided into two levels: the primary system, which is the main propulsion engine, and the secondary level, comprising its four primary subsystems. These subsystems—lube oil, cooling system, scavenge system, and fuel oil—are configured to pass through an “OR” gate. This configuration is visually represented in Figure 5.

Figure 5. Main propulsion engine system fault tree analysis.

Figure 5. Main propulsion engine system fault tree analysis.

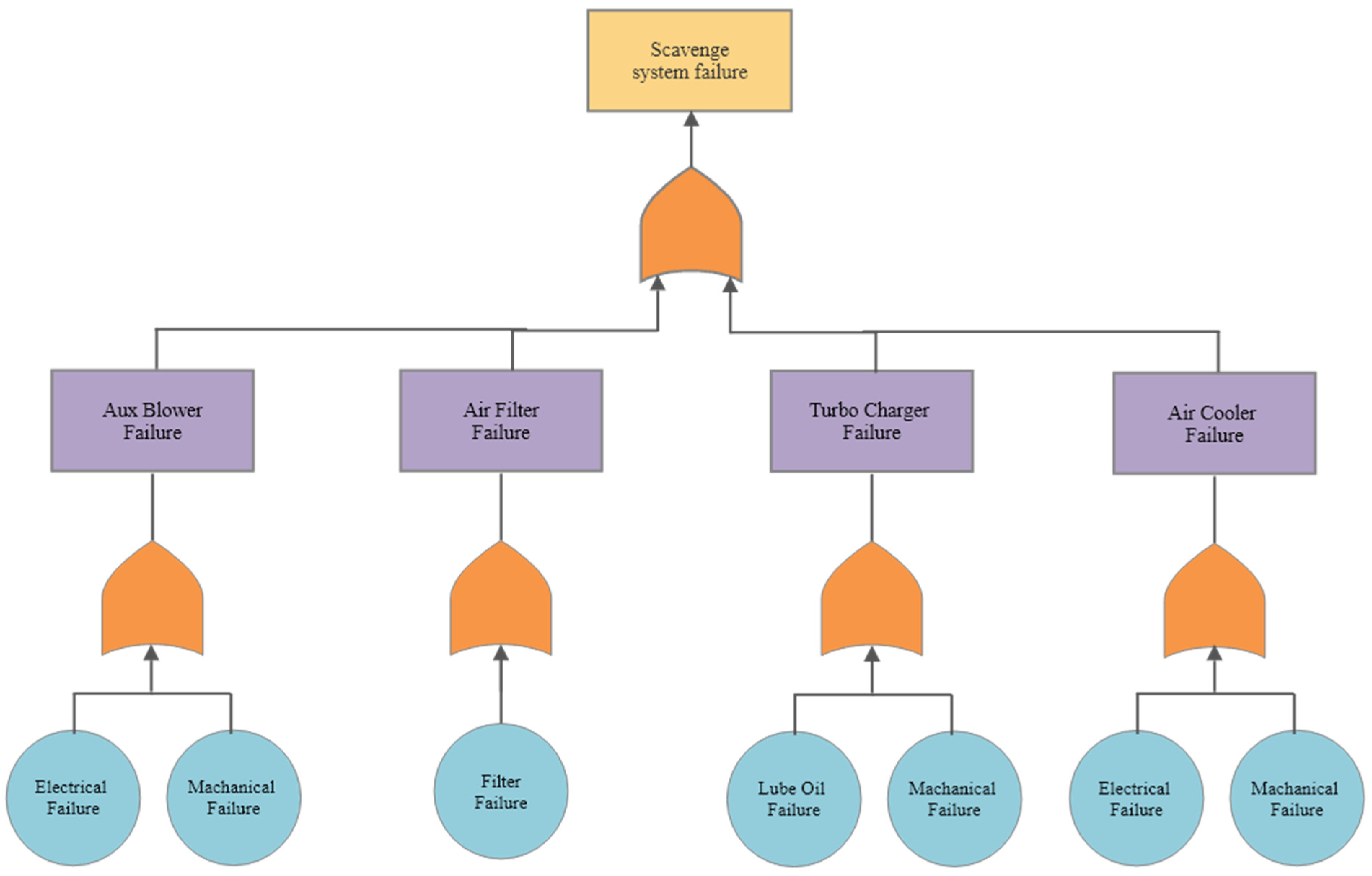
Figure 5 shows the fault tree analysis of the main propulsion engine, which connects using an “or” gate. This suggests no redundancy systems for the calculations. This indicates it is a series system, as all four systems must be operational for the propulsion of a ship to occur. Alternatively, if one system fails, no propulsion will be applied, as the engine is inoperable. 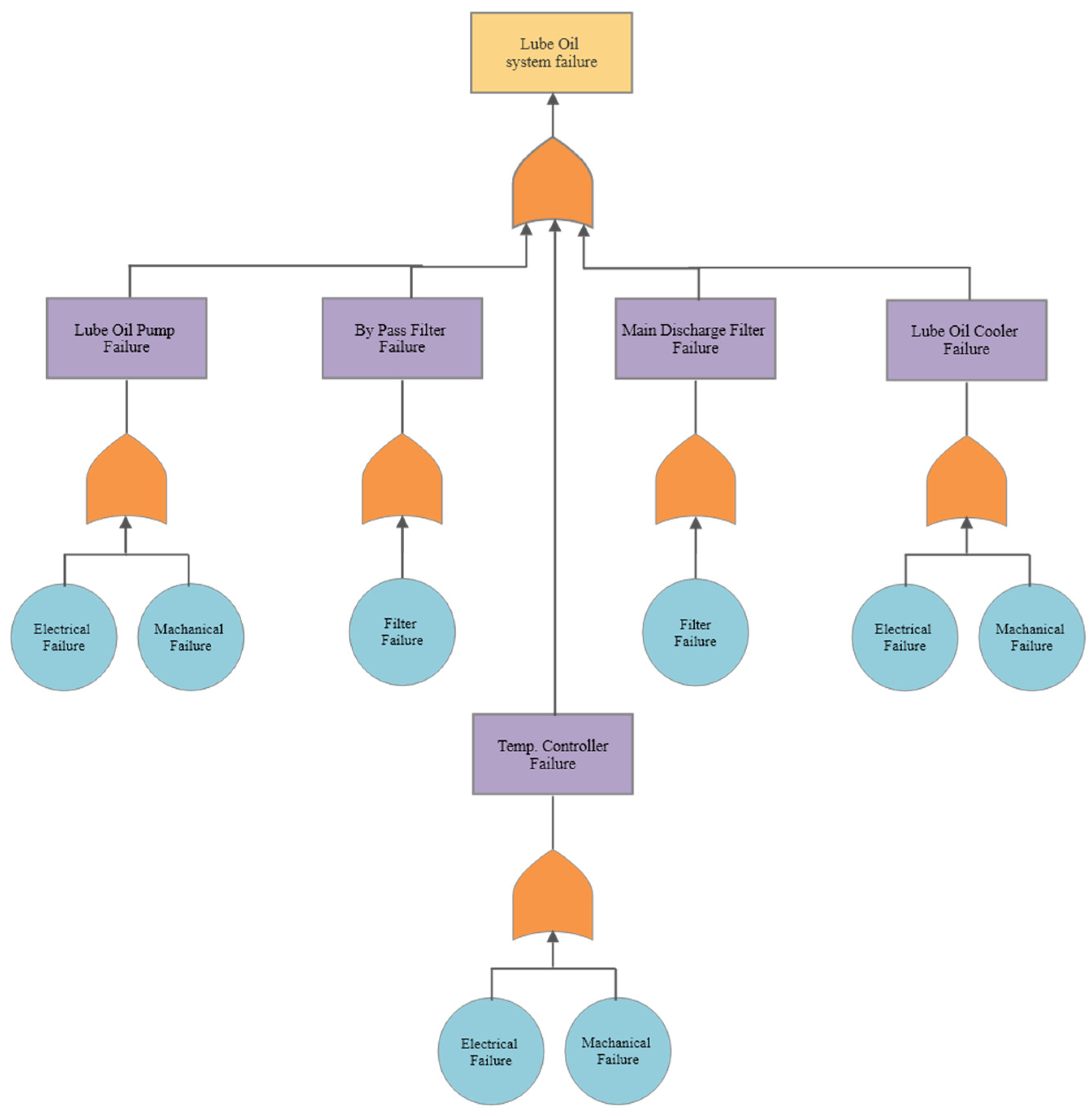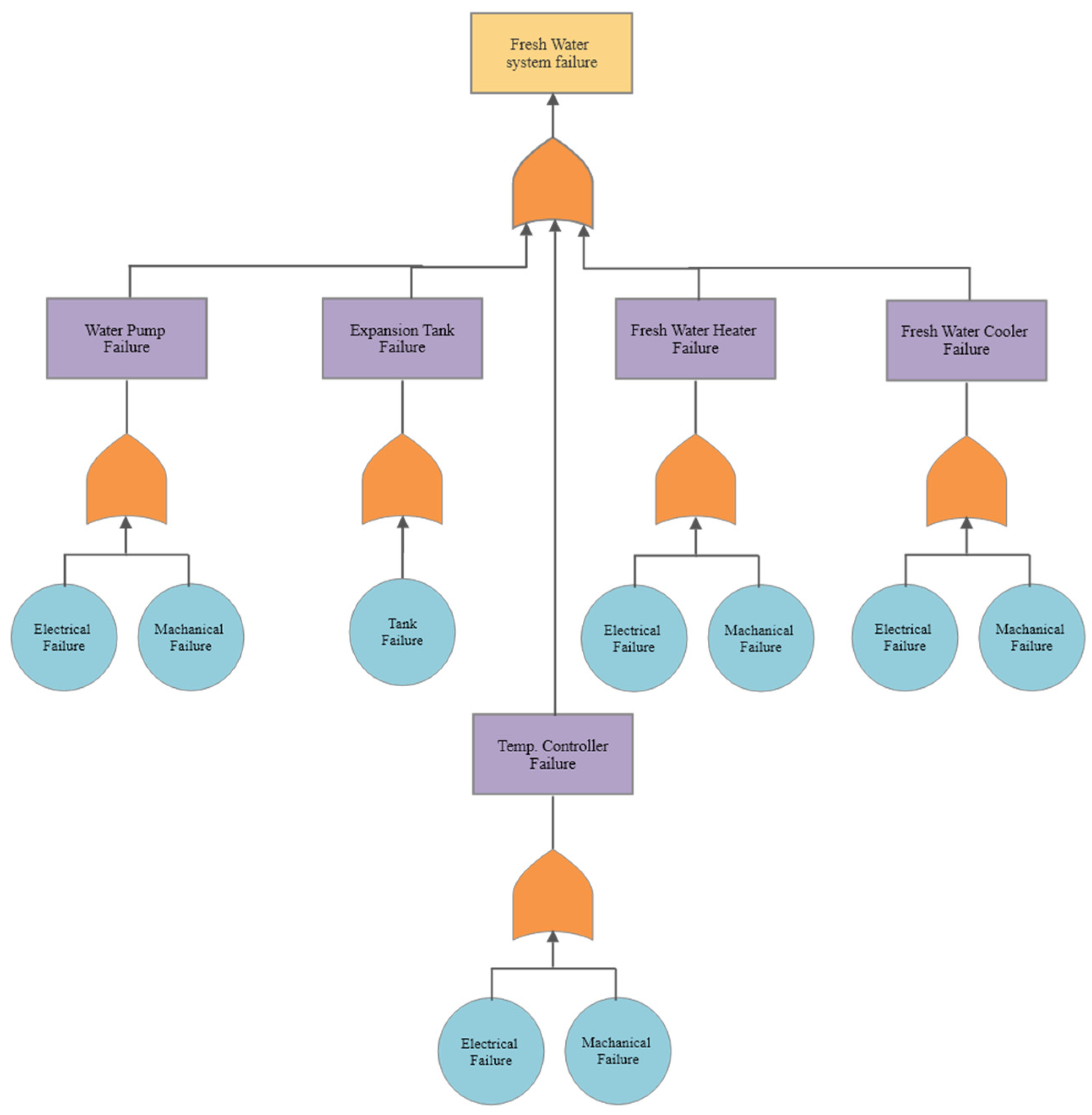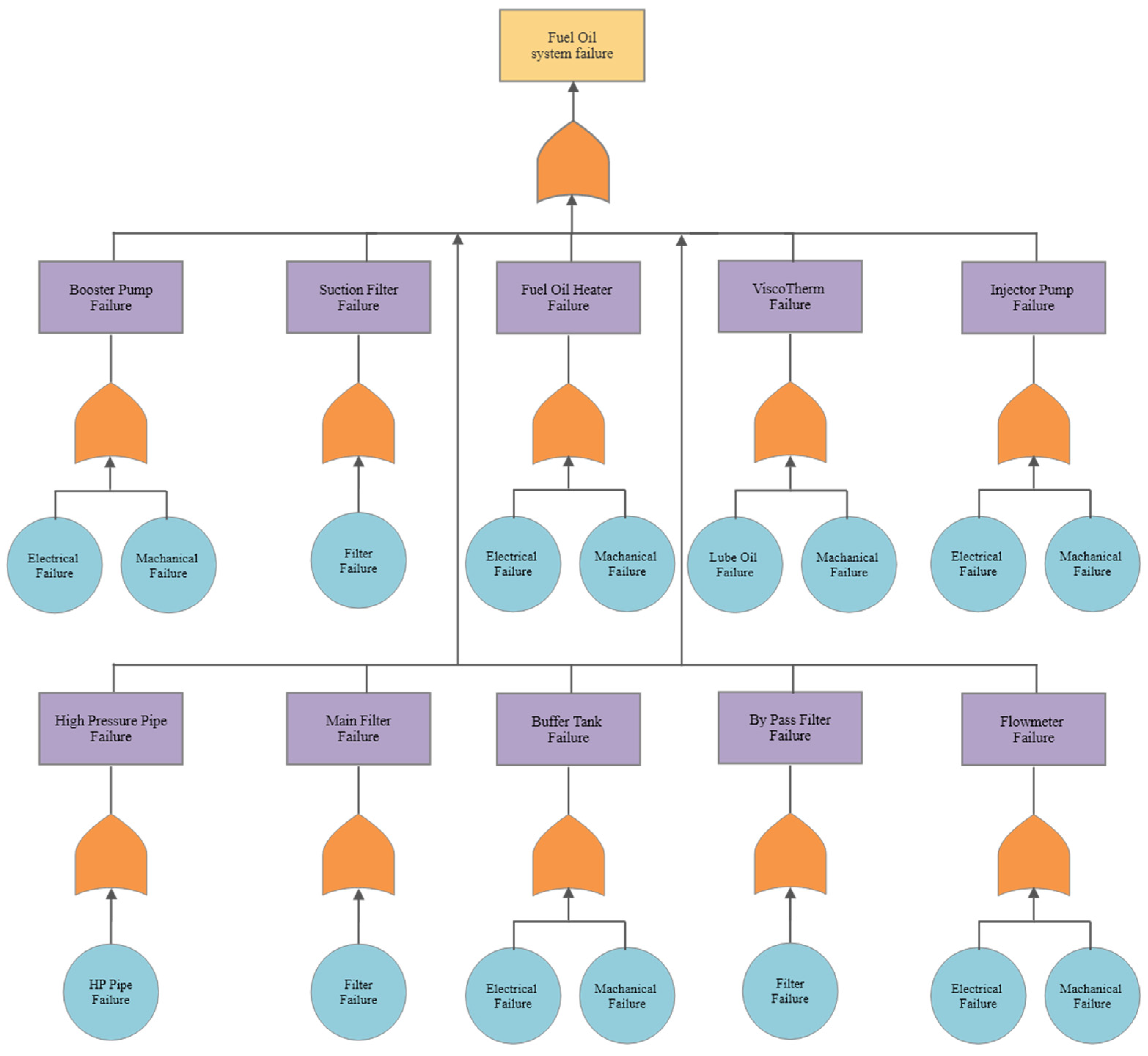This same concept can be applied to each system, which is shown in Figure 6 and Figure A1, Figure A2 and Figure A3 of the Appendix B: Fault Tree Analysis. This shows a similar approach, although the event that fails allows for conditional failures, which surfaces as an electrical/mechanical failure. The scavenge system fault tree shows that all systems will need to be operative for the outcome of the system to function.

The above or gates can be used to define events using Boolean algebra, which is used to express in terms of nonredundant systems. From the figure above, the nonredundant systems are shown in the following equation.

$$T=A\cup B\cup C\cup D$$

(10)

Using the reliability results for the scavenge system, Equation (10) is restructured using the reliability equation. This is shown by the following.

$$R\left(t\right)=1-[1-R(AuxBlower\left)\right][1-R(AirFilter\left)\right][1-R(TurboCharger\left)\right][1-R(AirCooler\left)\right]$$

(11)

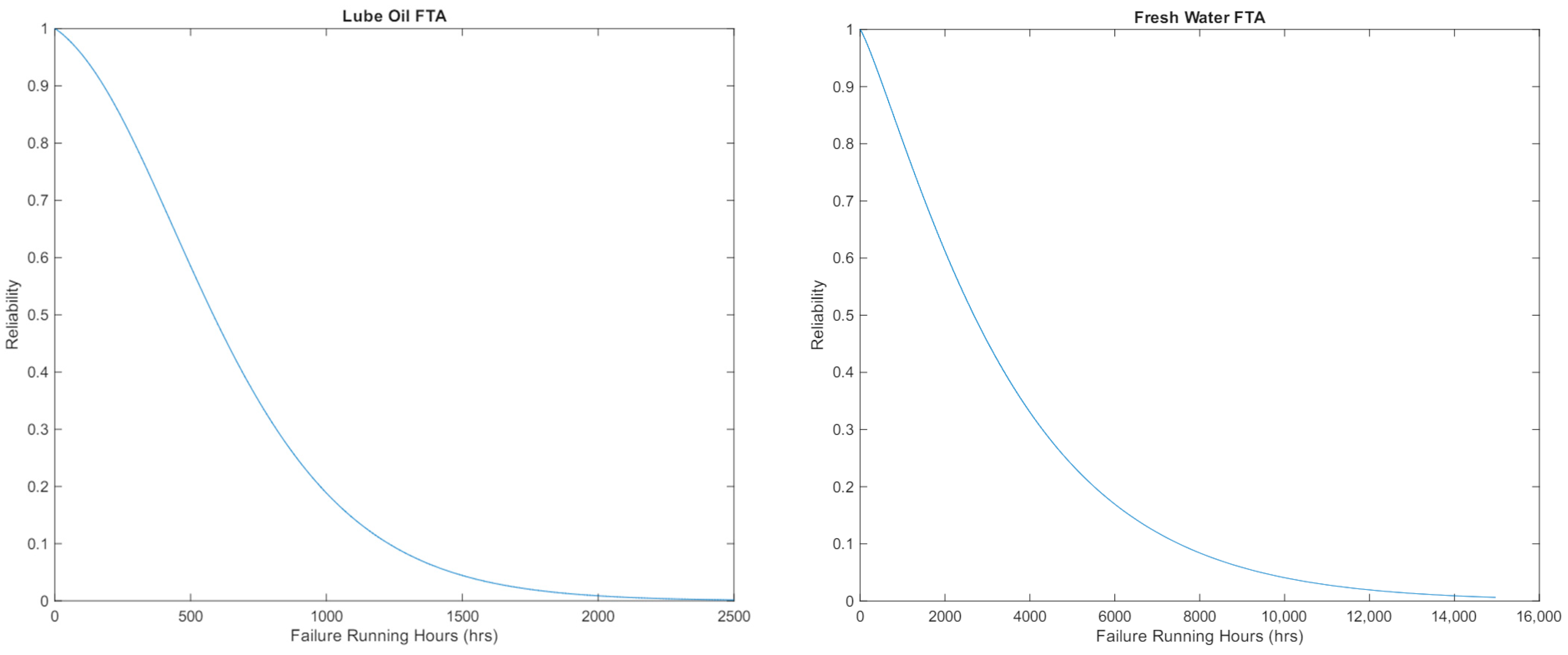
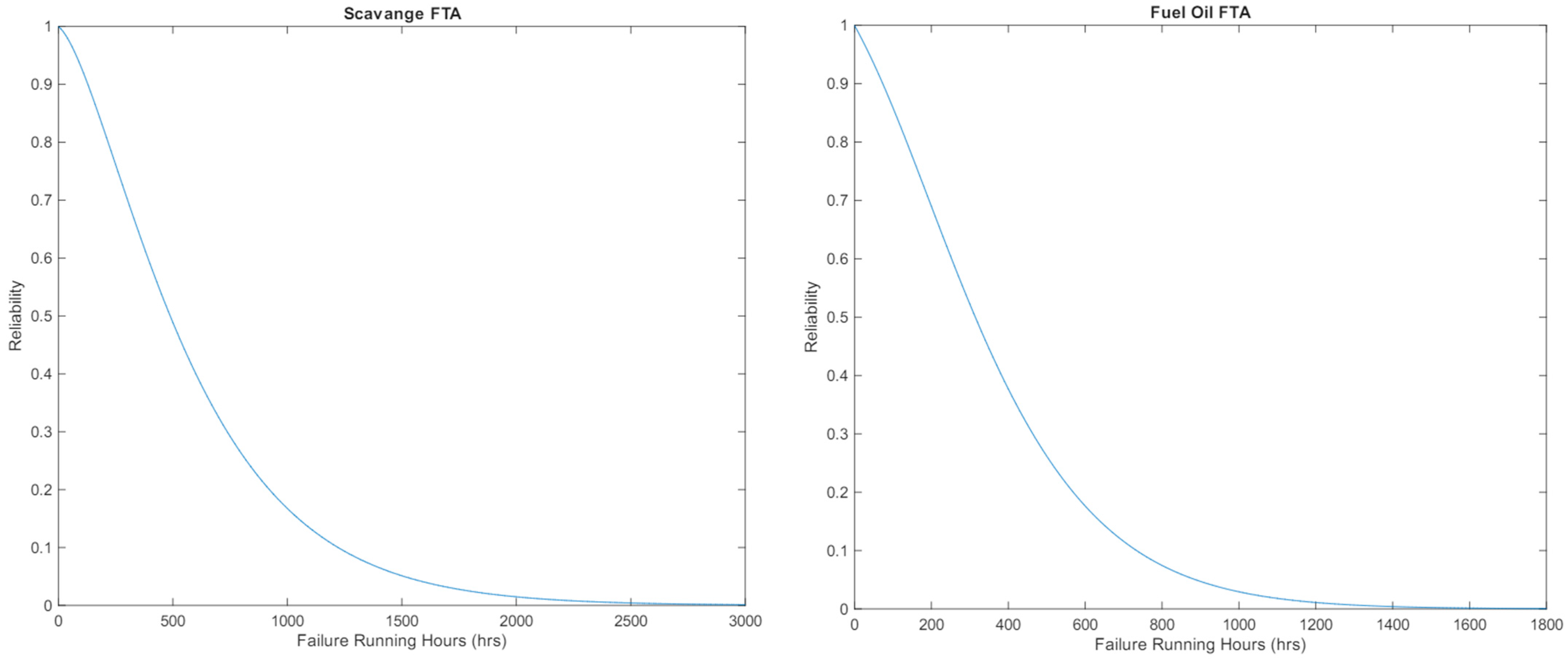
Using the equation above, the reliability distributions can be calculated for time as failure running hours for all four systems. The following figures show the decrease in reliability as time increases.

Figure 7 and Figure 8 show similar correlations with differing failure running characteristics, as Weibull and Gamma typically have similar styles. Using Figure 5, the total reliability of the system can be determined using the same process; however, this is achieved by only using the outcomes of the subsystems in Figure 7 and Figure 8.

Based on our analysis, the fuel system was identified as the engine subsystem with the highest impact on operational downtime. Failures within this system, such as injector malfunctions, fuel pump issues, or contamination, were found to cause significant disruptions due to their direct effect on engine performance and the complexity of repairs required. This finding is highlighted in the revised Results and Discussion Section to emphasize its critical role in overall engine reliability and the importance of targeted maintenance strategies for a fuel system.

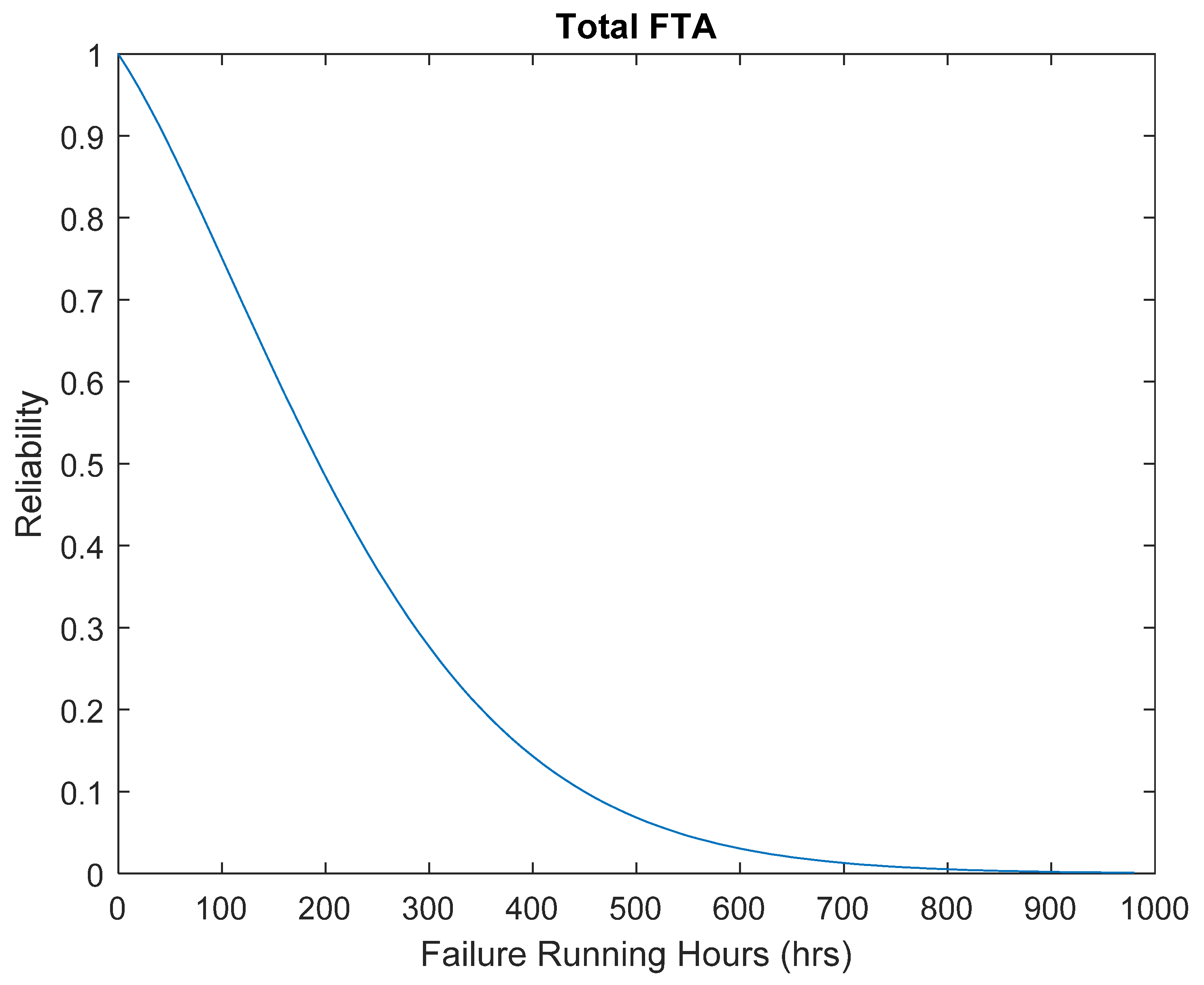
The outcome will represent the total system reliability using both the Weibull and Gamma distributions using the fault tree analysis process.

Figure 9 shows the reliability of the total system, which is the vessel’s main propulsion engine. This shows the reliability of the main propulsion engine between time zero and a reliability of zero at approximately 900 failure running hours. The data for all 26 systems was used to develop the final fault tree analysis, which is based on the Weibull and Gamma models, with the values of theta, alpha, beta, and gamma. This was estimated using MATLAB R2021B at the 95% confidence level, which produced reliability against the running hours. This data can only be taken as an estimation, as no censoring is available within the dataset. “Censored data is any data for which we do not know the exact event time” [16], with the three types of censoring being right censored, left censored, and interval censored. Using censored data, failures can be recorded as accurate or not accurate. The most common for this dataset would be interval-censored data, suggesting items such as filters may fail before the failure running data is recorded.

Sensor calibration errors can introduce inaccuracies in the collected data, leading to deviations within the analyses. These errors may occur due to improper calibration procedures, environmental factors affecting sensor performance, or wear and tear over time.

The fault tree analysis within the vessel’s main propulsion engine shows that all systems are considered important to the engine and are considered equal, as any system failure will result in engine failure. However, each system will have a different repair rate, suggesting that a failure of the filter may have a different impact when compared to a pump failure. Using this assumption, failures within a repair analysis will be considered different.

The results of this study underscore the importance of proactively identifying and addressing critical failure modes to reduce operational disruptions and enhance safety. This study provides valuable insights that can support risk-informed decision-making, prioritization of maintenance efforts, and the development of targeted training and safety protocols. These implications are particularly relevant for improving overall vessel reliability, ensuring compliance with regulatory standards, and minimizing financial and reputational risks.

This study could influence onboard maintenance routines. Specifically, our analysis provides a clearer understanding of critical failure modes and their root causes, which can support the development of more targeted and preventive maintenance schedules. By integrating these insights into daily operations, ship crews can prioritize maintenance tasks more effectively, reduce reactive interventions, and enhance equipment reliability. This practical application not only improves operational efficiency but also contributes to safer and more cost-effective vessel management.

4. Conclusions

This study demonstrates how fault tree analysis (FTA) provides a time-based reliability overview of a vessel’s main propulsion engine, utilizing data collected from surveys. The FTA highlights the relationships and conditions of each subsystem in relation to the main engine, using correlations and distributions across all 26 systems to consolidate them into four key subsystems: lube oil, freshwater, scavenge, and fuel oil. These subsystems were analyzed to calculate reliability metrics over time for each.

The findings indicate the overall reliability of the main propulsion engine, offering critical insights for scheduling maintenance overhauls and identifying key operational thresholds within the marine industry. By subdividing the main propulsion engine into four distinct subsystems, the reliability outcomes provide a clearer understanding of failure probabilities at various elapsed times or failure running hours.

This study contributes to the marine industry by enhancing the reliability analysis of shipping operations, supporting the optimization of maintenance schedules and informing future design improvements. These results pave the way for advancing operational safety and efficiency in maritime transportation systems.