A Design of Leaderless Formation Controller for Multi-ASVs with Sampled Data and Communication Delay
Abstract
1. Introduction
- 1.
- 2.
- 3.
- performance against disturbances: We further design a leaderless formation controller that ensures a specified disturbance attenuation level against marine environmental disturbances using norm analysis.
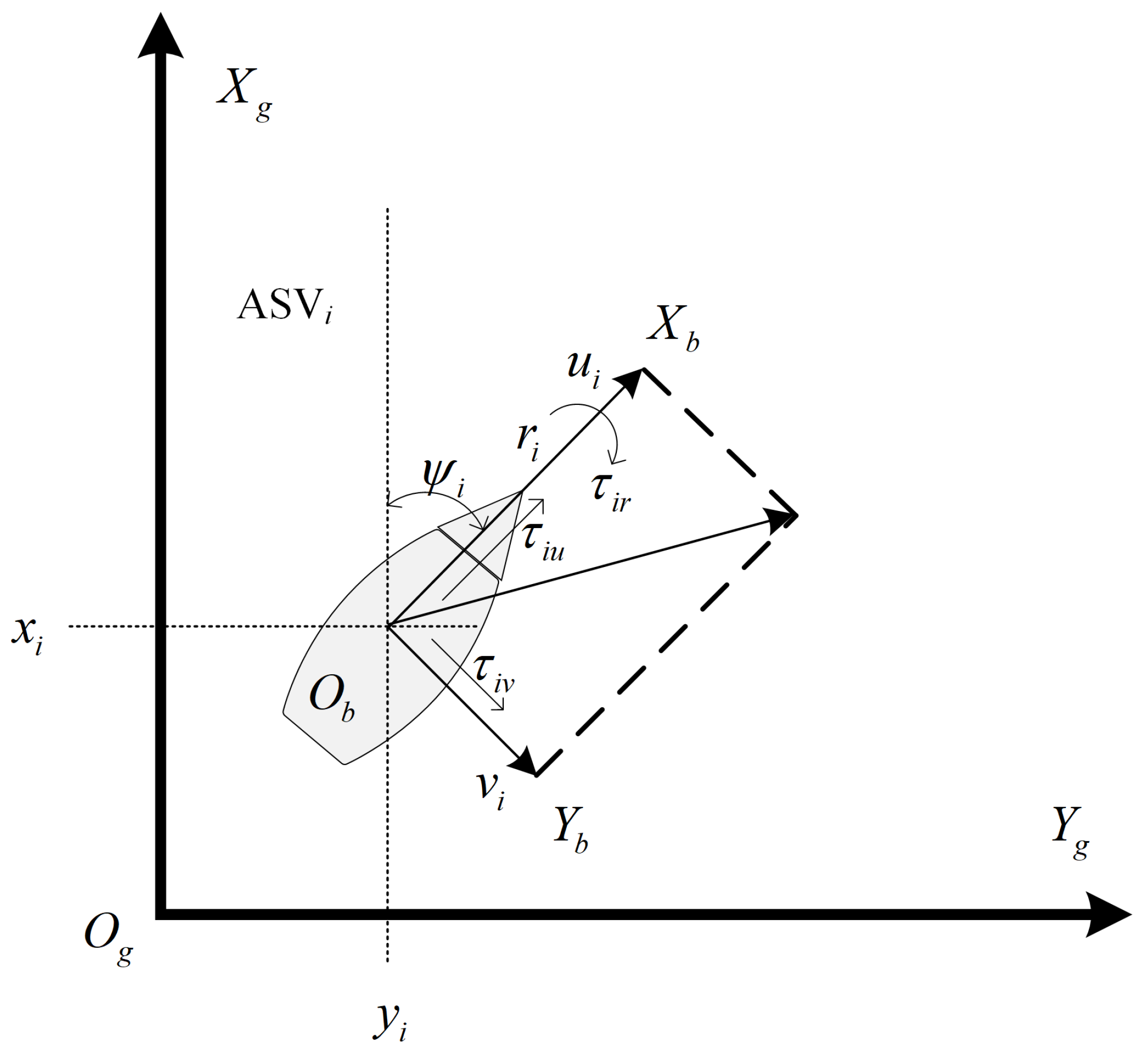
2. System Model and Problem Statement
2.1. System Model
- 1.
- The system state converges to the origin when ;
- 2.
- The following inequality holds for the zero initial statewhere is a designed scalar representing the performance bound.
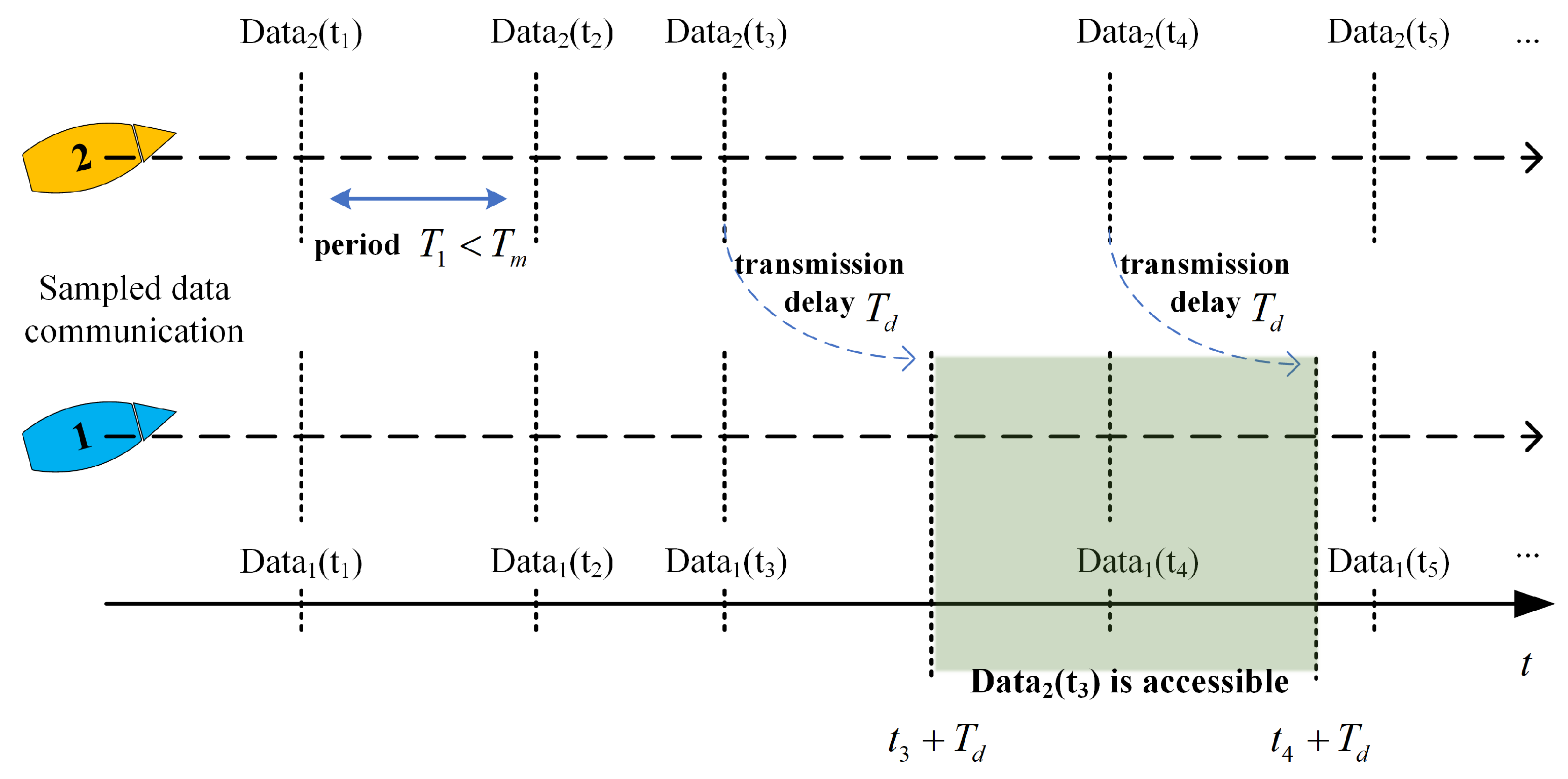
2.2. Problem Statement
3. Controller Design and Stability Analysis
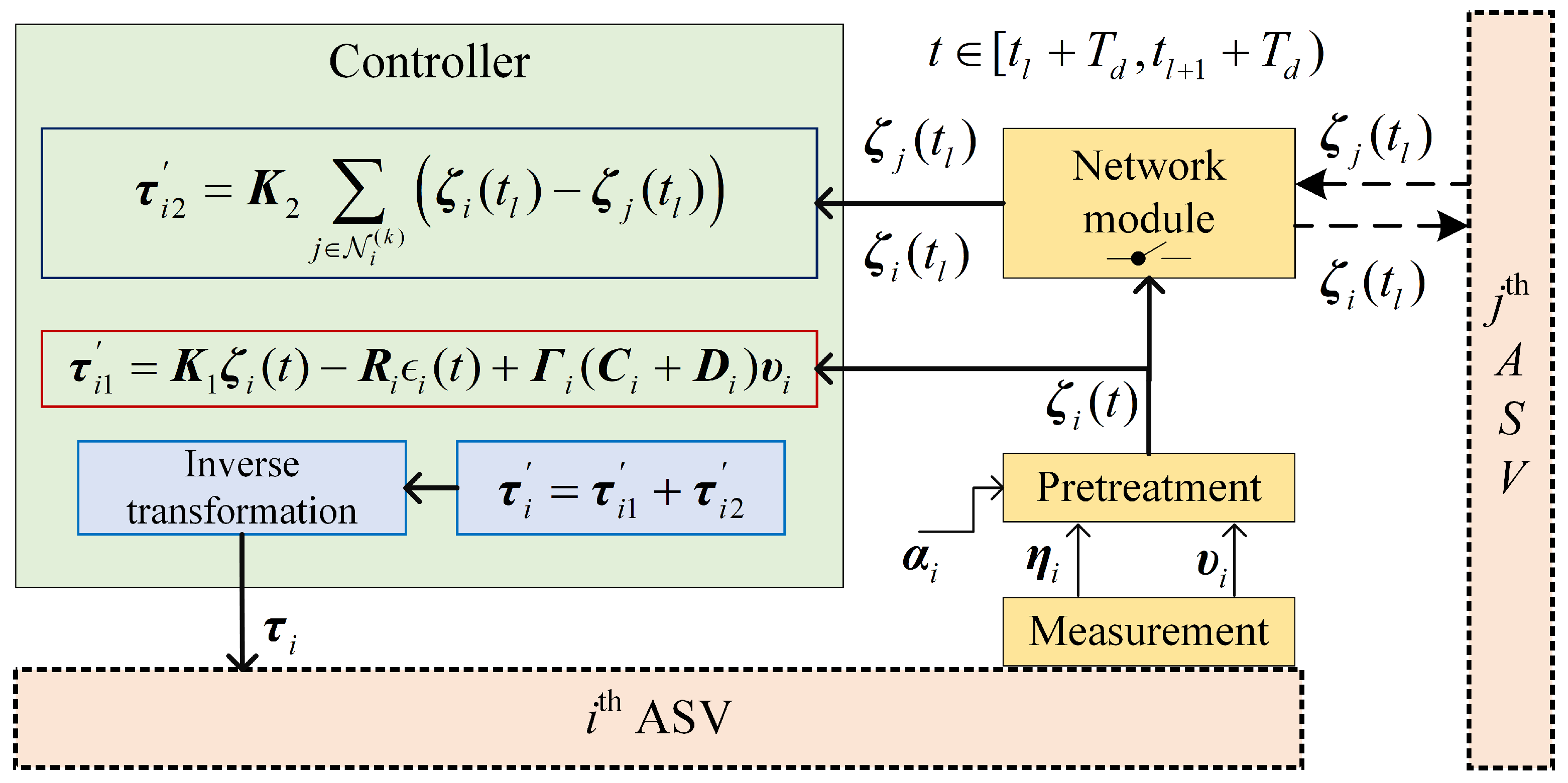
3.1. Controller Design
3.2. Stability Analysis
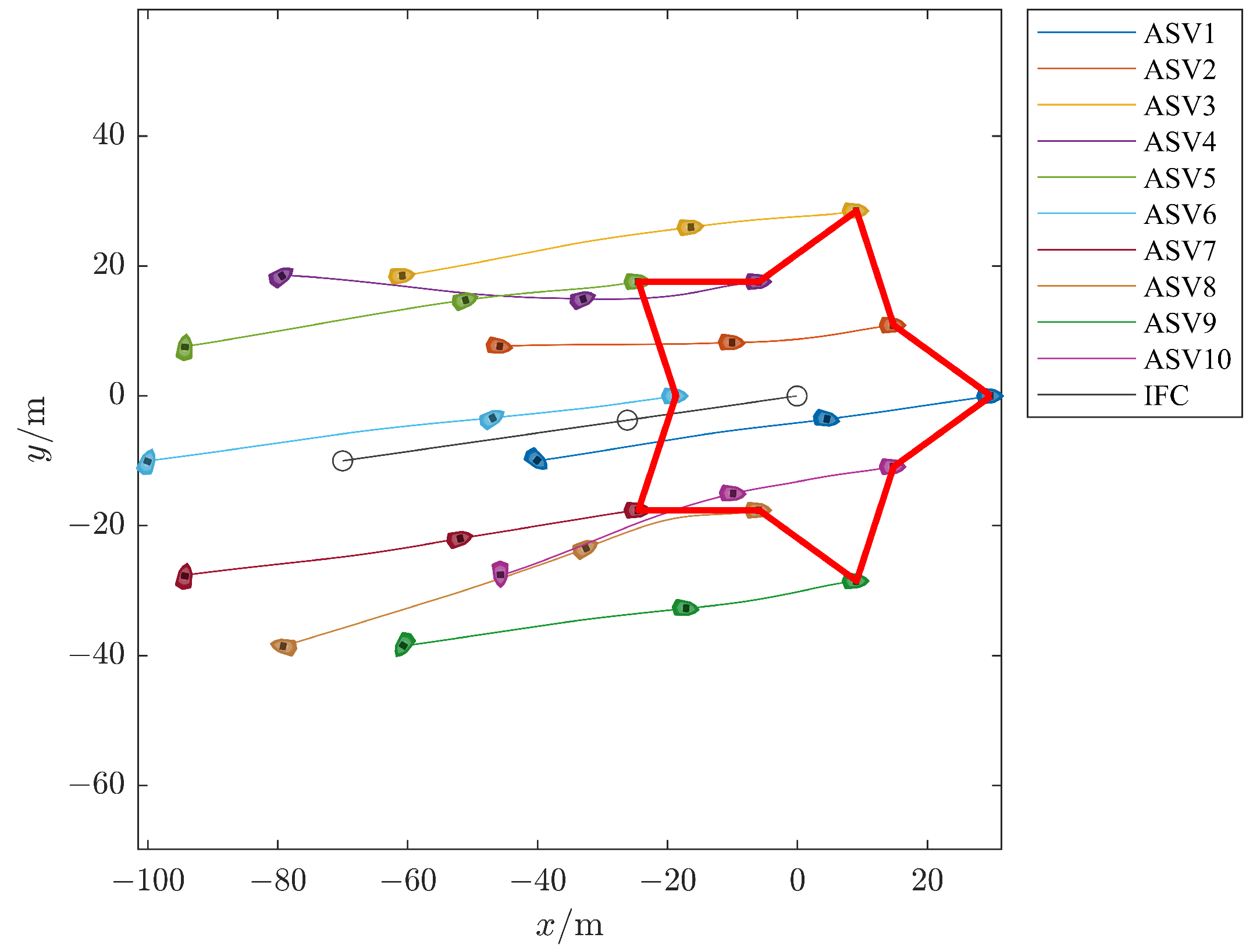
4. Numerical Simulation
| Algorithm 1: Pseudo-code of the leaderless formation control |
|
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lv, Z.; Wang, X.; Wang, G.; Xing, X.; Lv, C.; Yu, F. Unmanned Surface Vessels in Marine Surveillance and Management: Advances in Communication, Navigation, Control, and Data-Driven Research. J. Mar. Sci. Eng. 2025, 13, 969. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Z.; Cai, W.; Yan, Q. Design of Low-cost Unmanned Surface Vessel for Water Surface Cleaning. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 2290–2293. [Google Scholar] [CrossRef]
- Ouelmokhtar, H.; Benmoussa, Y.; Benazzouz, D.; Ait-Chikh, M.A.; Lemarchand, L. Energy-based USV maritime monitoring using multi-objective evolutionary algorithms. Ocean Eng. 2022, 253, 111182. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, Y.; Wang, Z.; Zheng, K. Trajectory Tracking and Docking Control Strategy for Unmanned Surface Vehicles in Water-Based Search and Rescue Missions. J. Mar. Sci. Eng. 2024, 12, 1462. [Google Scholar] [CrossRef]
- Metcalfe, B.; Thomas, B.; Treloar, A.; Rymansaib, Z.; Hunter, A.; Wilson, P. A compact, low-cost unmanned surface vehicle for shallow inshore applications. In Proceedings of the 2017 Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; pp. 961–968. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, Y.; Cui, J.; Li, X.; Pu, H.; Gu, J.; Xie, S.; Luo, J. Development of the USV ‘JingHai-I’ and sea trials in the Southern Yellow Sea. Ocean Eng. 2017, 131, 186–196. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, C.; Han, Q.L.; Song, J. Unmanned Aerial Vehicles: Control Methods and Future Challenges. IEEE/CAA J. Autom. Sinica 2022, 9, 601–614. [Google Scholar] [CrossRef]
- Javaid, S.; Saeed, N.; Qadir, Z.; Fahim, H.; He, B.; Song, H.; Bilal, M. Communication and Control in Collaborative UAVs: Recent Advances and Future Trends. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5719–5739. [Google Scholar] [CrossRef]
- Draganjac, I.; Miklić, D.; Kovačić, Z.; Vasiljević, G.; Bogdan, S. Decentralized Control of Multi-AGV Systems in Autonomous Warehousing Applications. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1433–1447. [Google Scholar] [CrossRef]
- Chen, X.; Xing, Z.; Feng, L.; Zhang, T.; Wu, W.; Hu, R. An ETCEN-Based Motion Coordination Strategy Avoiding Active and Passive Deadlocks for Multi-AGV System. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1364–1377. [Google Scholar] [CrossRef]
- Tan, G.; Zhuang, J.; Zou, J.; Wan, L. Multi-type task allocation for multiple heterogeneous unmanned surface vehicles (USVs) based on the self-organizing map. Appl. Ocean Res. 2022, 126, 103262. [Google Scholar] [CrossRef]
- Chen, C.; Liang, X.; Zhang, Z.; Liu, D.; Li, W. Cooperative strategy based on a two-layer game model for inferior USVs to intercept a superior USV. Ocean Eng. 2024, 293, 116600. [Google Scholar] [CrossRef]
- Wang, J.B.; Zeng, C.; Ding, C.; Zhang, H.; Lin, M.; Wang, J. Unmanned Surface Vessel Assisted Maritime Wireless Communication Toward 6G: Opportunities and Challenges. IEEE Wirel. Commun. 2022, 29, 72–79. [Google Scholar] [CrossRef]
- Li, H.; Li, X. Distributed Consensus of Heterogeneous Linear Time-Varying Systems on UAVs–USVs Coordination. IEEE Trans. Circuits Syst. II 2020, 67, 1264–1268. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wang, D.; Han, Q.L. An Overview of Recent Advances in Coordinated Control of Multiple Autonomous Surface Vehicles. IEEE Trans. Ind. Informat. 2021, 17, 732–745. [Google Scholar] [CrossRef]
- Ghommam, J.; Saad, M.; Mnif, F.; Zhu, Q.M. Guaranteed Performance Design for Formation Tracking and Collision Avoidance of Multiple USVs With Disturbances and Unmodeled Dynamics. IEEE Syst. J. 2021, 15, 4346–4357. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Q.; Xu, L.; Xu, S.; Zhang, Y.; Hu, Y. Dynamic Sliding Mode Formation Control of Unmanned Surface Vehicles Under Actuator Failure. J. Mar. Sci. Eng. 2025, 13, 657. [Google Scholar] [CrossRef]
- Hu, B.B.; Zhang, H.T.; Liu, B.; Meng, H.; Chen, G. Distributed Surrounding Control of Multiple Unmanned Surface Vessels With Varying Interconnection Topologies. IEEE Trans. Control Syst. Technol. 2022, 30, 400–407. [Google Scholar] [CrossRef]
- Dong, Z.; Tan, F.; Yu, M.; Xiong, Y.; Li, Z. A Bio-Inspired Sliding Mode Method for Autonomous Cooperative Formation Control of Underactuated USVs with Ocean Environment Disturbances. J. Mar. Sci. Eng. 2024, 12, 1607. [Google Scholar] [CrossRef]
- Li, J.; Fu, M.; Xu, Y. Disturbance-Observer-Based Adaptive Prescribed Performance Formation Tracking Control for Multiple Underactuated Surface Vehicles. J. Mar. Sci. Eng. 2024, 12, 1136. [Google Scholar] [CrossRef]
- Li, K.; Xie, S.; Zhang, X.; Zhou, G. A multi-USV Formation Control Method Based on BP Neural Network PID Controller. In Proceedings of the 2024 4th International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 19–21 April 2024; pp. 191–195. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, Y.; Ahn, C.K.; Cheng, J.; Chen, C. Adaptive Fuzzy Backstepping-Based Formation Control of Unmanned Surface Vehicles With Unknown Model Nonlinearity and Actuator Saturation. IEEE Trans. Veh. Technol. 2020, 69, 14749–14764. [Google Scholar] [CrossRef]
- Wang, D.; Kong, M.; Zhang, G.; Liang, X. Adaptive Second-Order Fast Terminal Sliding-Mode Formation Control for Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2022, 10, 1782. [Google Scholar] [CrossRef]
- Kheioon, I.A.; Al-Sabur, R.; Sharkawy, A.N. Design and Modeling of an Intelligent Robotic Gripper Using a Cam Mechanism with Position and Force Control Using an Adaptive Neuro-Fuzzy Computing Technique. Automation 2025, 6, 4. [Google Scholar] [CrossRef]
- Kheioon, I.A.; Saleem, K.B.; Sultan, H.S. Analysis of Natural Convection and Radiation from a Solid Rod Under Vacuum Conditions with the Aiding of ANFIS. Exp. Tech. 2023, 47, 139–152. [Google Scholar] [CrossRef]
- Bachi, I.O.; Bahedh, A.S.; Kheioon, I.A. Design of control system for steel strip-rolling mill using NARMA-L2. J. Mech. Sci. Technol. 2021, 35, 1429–1436. [Google Scholar] [CrossRef]
- Ghiaskar, A.; Amiri, A.; Mirjalili, S. Polar fox optimization algorithm: A novel meta-heuristic algorithm. Neural Comput. Appl. 2024, 36, 20983–21022. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, X.; Zhang, J.; Mirjalili, S. Superb Fairy-wren Optimization Algorithm: A novel metaheuristic algorithm for solving feature selection problems. Clust. Comput. 2025, 28, 246. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.L.; Luo, F. Leader–Follower Formation Control of USVs With Prescribed Performance and Collision Avoidance. IEEE Trans. Ind. Informat. 2019, 15, 572–581. [Google Scholar] [CrossRef]
- Lee, J.; Kang, H.; Choi, J.H. A Study on the Improvement of USV’s Leader-Follower Swarm Control Algorithm through Fault Coping Algorithm. In Proceedings of the OCEANS 2023, Limerick, Ireland, 5–8 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wanniarachchi, C.; Wimalaratne, P.; Karunanayaka, K. Formation Control Algorithms for Drone Swarms and The Single Point of Failure Crisis: A Review. In Proceedings of the 2024 IEEE 33rd International Symposium on Industrial Electronics (ISIE), Ulsan, Republic of Korea, 18–21 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, D.; Li, T.; Wu, Z. Leaderless and leader-follower cooperative control of multiple marine surface vehicles with unknown dynamics. Nonlinear Dyn. 2013, 74, 95–106. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, B.; Zhou, B.; Miao, J. An Anti-Congestion Interaction Mechanism Based Leaderless Formation Control for Unmanned Surface Vehicles With Communication Interruptions. IEEE Trans. Veh. Technol. 2024, 73, 16964–16976. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, H.; Baldi, S.; Zhong, R. Leaderless Consensus of Heterogeneous Multiple Euler–Lagrange Systems With Unknown Disturbance. IEEE Trans. Autom. Control 2023, 68, 2399–2406. [Google Scholar] [CrossRef]
- Hu, B.B.; Zhang, H.T. Bearing-Only Motional Target-Surrounding Control for Multiple Unmanned Surface Vessels. IEEE Trans. Ind. Electron. 2022, 69, 3988–3997. [Google Scholar] [CrossRef]
- Yu, K.; Li, Y.; Lv, M.; Tong, S. Adaptive Fuzzy Formation Control for Underactuated Multi-USVs With Dynamic Event-Triggered Communication. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 7783–7793. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Feng, Y.; Li, Y. Fixed-time coordinated guidance for containment maneuvering of unmanned surface vehicles under delayed communications: Theory and experiment. Ocean Eng. 2023, 277, 114249. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P.; Zervos, N. A nonlinear H-infinity control approach for autonomous navigation of underactuated vessels. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Republic of Korea, 16–19 October 2016; pp. 1143–1148. [Google Scholar] [CrossRef]
- Fu, T.; Guan, L.; Gao, Y.; Qin, C. An Anti-Windup Method Based on an LADRC for Miniaturized Inertial Stabilized Platforms on Unmanned Vehicles in Marine Applications. J. Mar. Sci. Eng. 2024, 12, 616. [Google Scholar] [CrossRef]
- Yan, X.; Jiang, D.; Miao, R.; Li, Y. Formation Control and Obstacle Avoidance Algorithm of a Multi-USV System Based on Virtual Structure and Artificial Potential Field. J. Mar. Sci. Eng. 2021, 9, 161. [Google Scholar] [CrossRef]
- Liu, H.; Weng, P.; Tian, X.; Mai, Q. Distributed adaptive fixed-time formation control for UAV-USV heterogeneous multi-agent systems. Ocean Eng. 2023, 267, 113240. [Google Scholar] [CrossRef]
- Yuan, P.; Zhang, Z.; Li, Y.; Cui, J. Leader-follower control and APF for Multi-USV coordination and obstacle avoidance. Ocean Eng. 2024, 313, 119487. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Y.; Hu, S. USV Formation and Path-Following Control via Deep Reinforcement Learning With Random Braking. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5468–5478. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 134–141. [Google Scholar]
- Knorn, S.; Ahlén, A. Deviation bounds in multi agent systems described by undirected graphs. Automatica 2016, 67, 205–210. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, C.; Xie, K.; Lewis, F.L. Online Policy Iteration Algorithms for Linear Continuous-Time H-Infinity Regulation With Completely Unknown Dynamics. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6509–6518. [Google Scholar] [CrossRef]
- Hetel, L.; Fiter, C.; Omran, H.; Seuret, A.; Fridman, E.; Richard, J.P.; Niculescu, S.I. Recent developments on the stability of systems with aperiodic sampling: An overview. Automatica 2017, 76, 309–335. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L.; Zhang, X.M. Achieving Cluster Formation of Multi-Agent Systems Under Aperiodic Sampling and Communication Delays. IEEE Trans. Ind. Electron. 2018, 65, 3417–3426. [Google Scholar] [CrossRef]
- Petersen, I.R. A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- Gu, K. An integral inequality in the stability problem of time-delay systems. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; Volume 3, pp. 2805–2810. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef]
- Park, P.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, G.; Sun, Z.; Zhang, W. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances. Ocean Eng. 2018, 167, 36–44. [Google Scholar] [CrossRef]




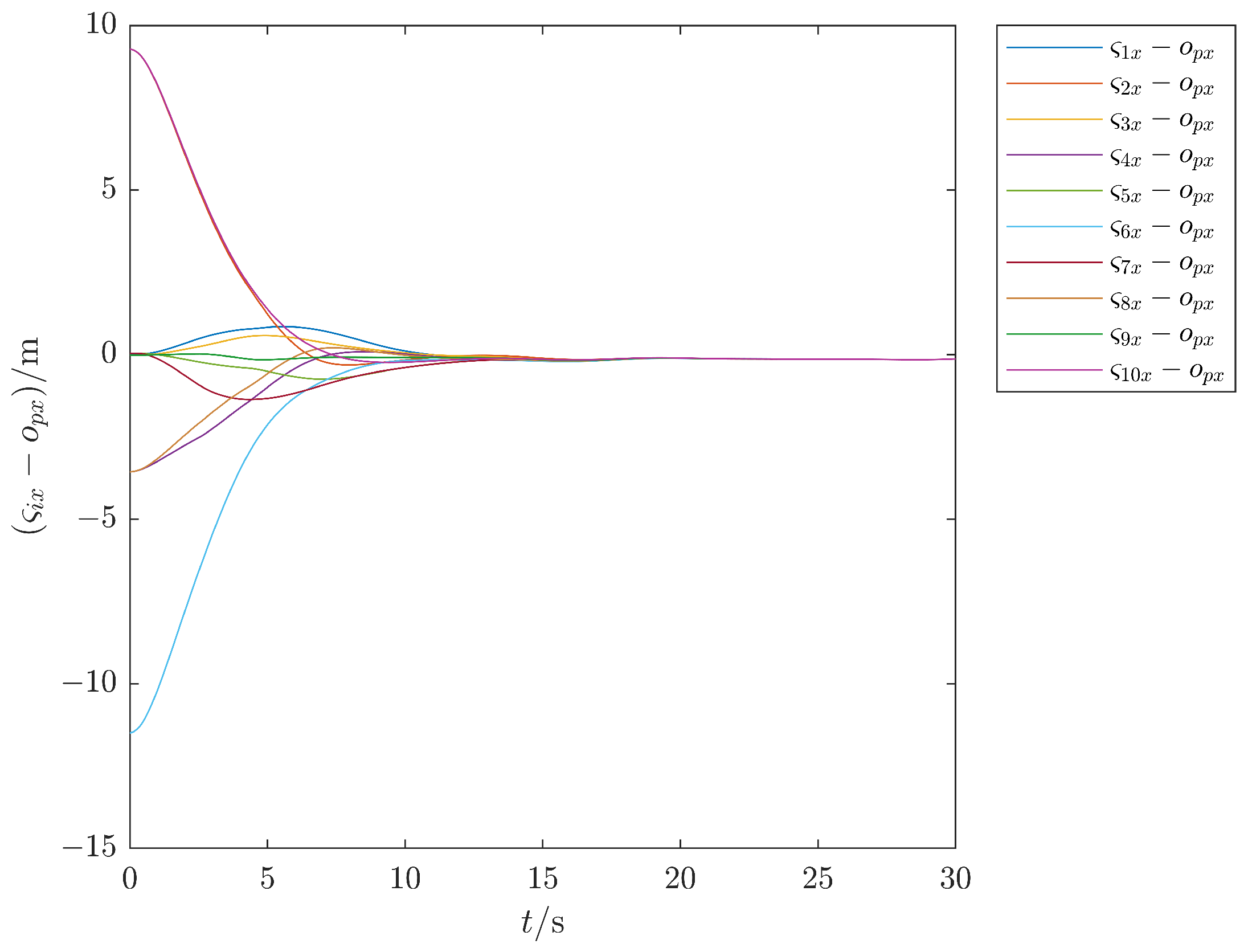
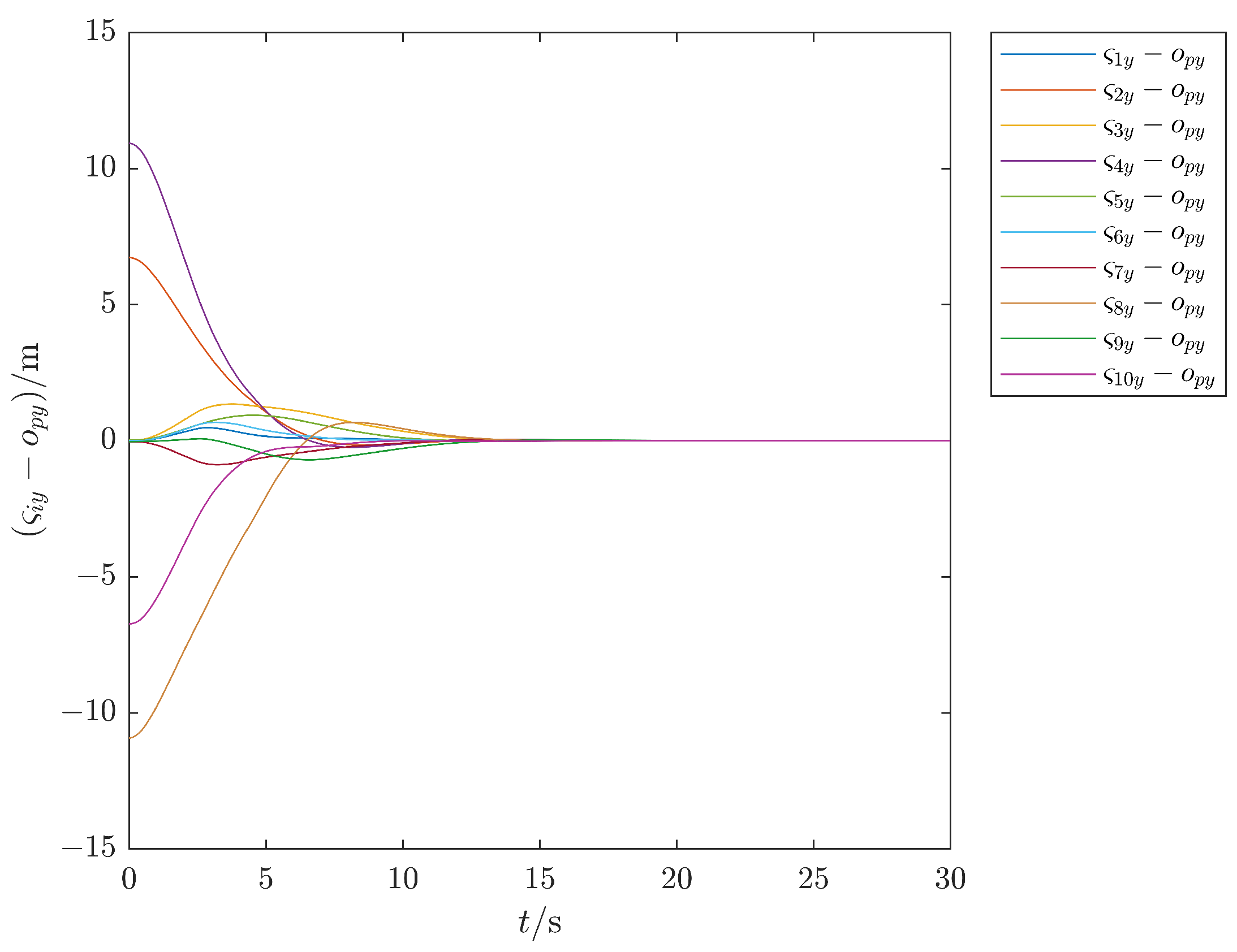
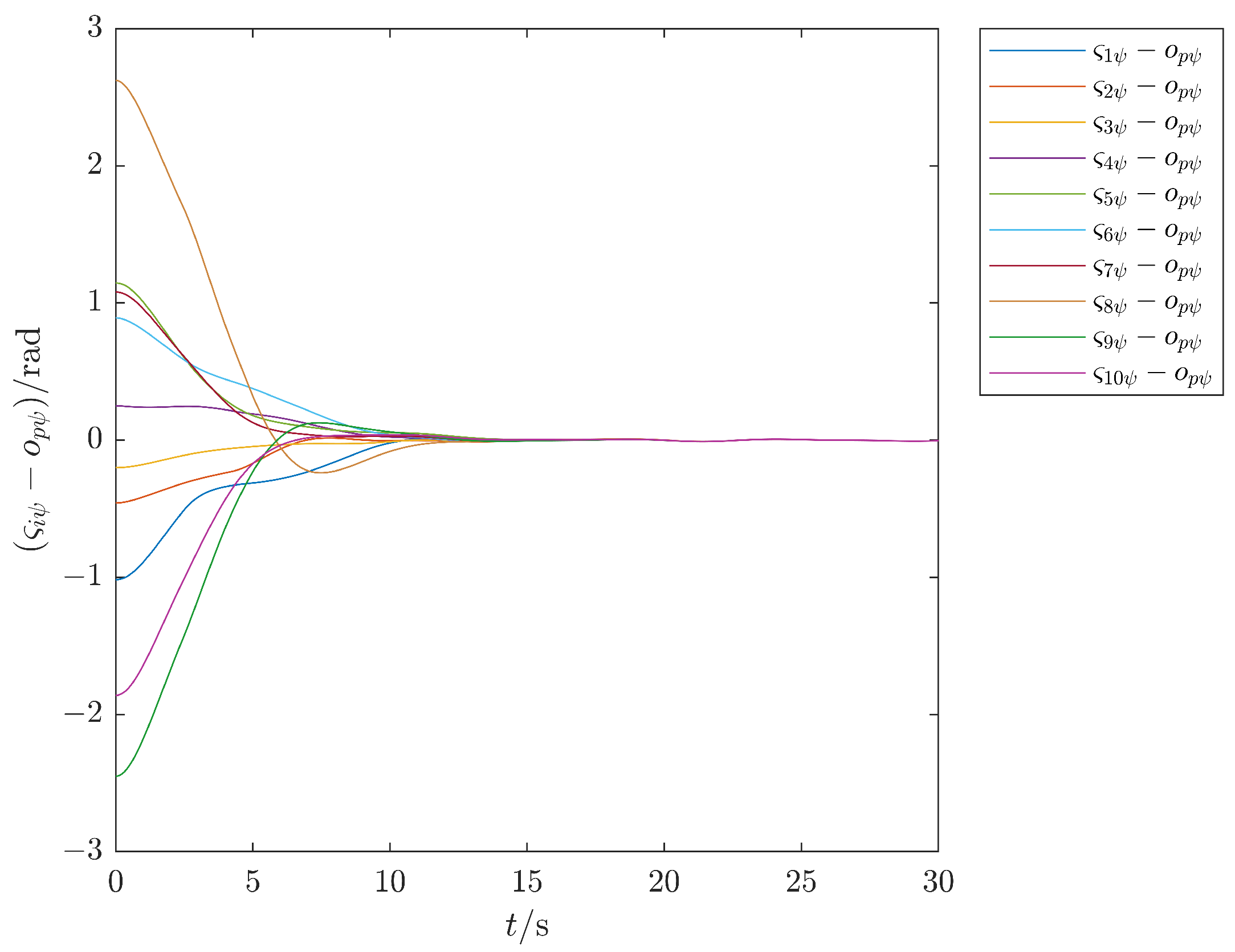
| Works | Formation Framework | Communication Mode | Delay Assumption |
|---|---|---|---|
| Zhang et al. [34] | Leaderless framework | Event-triggered communication | No delay |
| Hu et al. [36] | Leaderless framework | Continuous communication | No delay |
| Yu et al. [37] | Leader–follower framework | Event-triggered communication | No delay |
| Wang et al. [38] | Leader–follower framework | Continuous communication | Time-varying delay |
| Proposed Method | Leaderless framework | Aperiodic sampled communication | Fixed delay |
| Index | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Xia, G.; Jiang, X. A Design of Leaderless Formation Controller for Multi-ASVs with Sampled Data and Communication Delay. J. Mar. Sci. Eng. 2025, 13, 1259. https://doi.org/10.3390/jmse13071259
Zhu W, Xia G, Jiang X. A Design of Leaderless Formation Controller for Multi-ASVs with Sampled Data and Communication Delay. Journal of Marine Science and Engineering. 2025; 13(7):1259. https://doi.org/10.3390/jmse13071259
Chicago/Turabian StyleZhu, Wenxu, Guihua Xia, and Xiangli Jiang. 2025. "A Design of Leaderless Formation Controller for Multi-ASVs with Sampled Data and Communication Delay" Journal of Marine Science and Engineering 13, no. 7: 1259. https://doi.org/10.3390/jmse13071259
APA StyleZhu, W., Xia, G., & Jiang, X. (2025). A Design of Leaderless Formation Controller for Multi-ASVs with Sampled Data and Communication Delay. Journal of Marine Science and Engineering, 13(7), 1259. https://doi.org/10.3390/jmse13071259





