Study on the Dilatancy Behavior of Coral Sand and Its Influence on Shear Strength Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Physical Properties of Coral Sand
2.2. Experimental Design and Procedure
3. Results and Discussion
3.1. Strength and Volumetric Deformation Behavior of Coral Sand
3.2. Influencing Factors and Trends of the Peak Internal Friction Angle
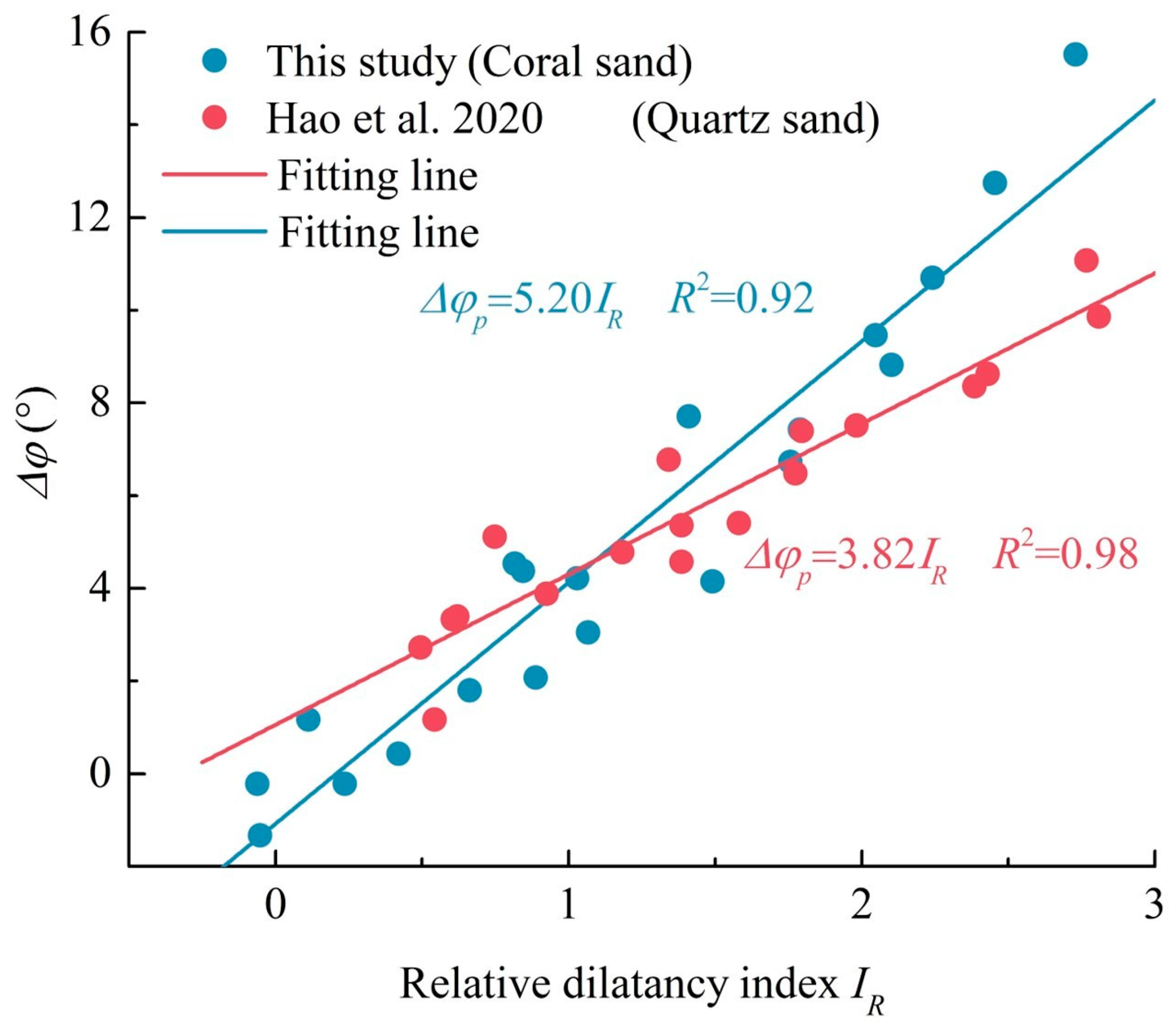
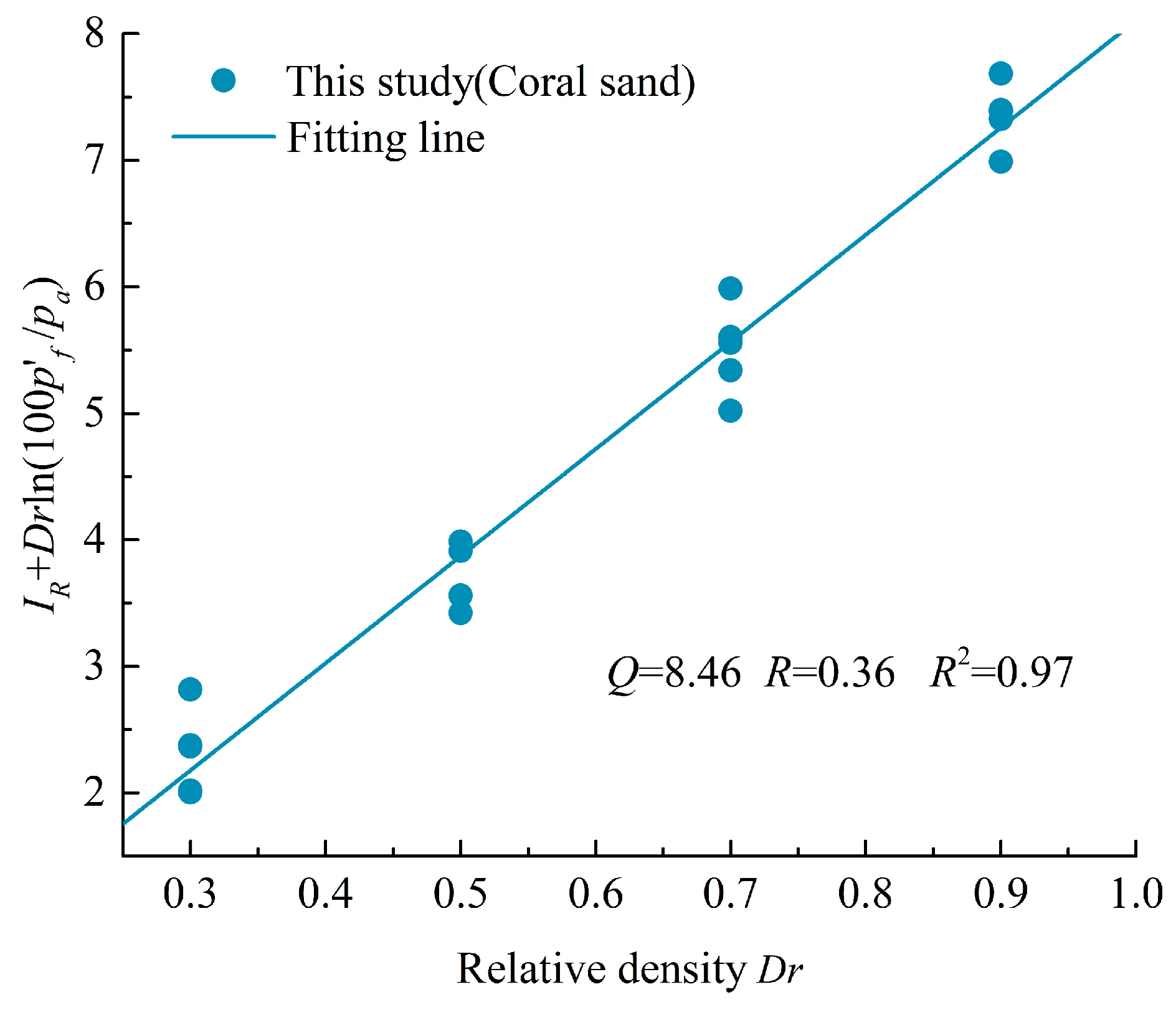
3.3. Stress–Dilatancy Equation for Coral Sand
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Xu, D.; Shen, J.; Wei, H.; Wang, R.; Xiao, X. Effect of Coral Sand Powders and Seawater Salinity on the Impact Mechanical Properties of Cemented Coral Sand. Soils Found. 2022, 62, 101206. [Google Scholar] [CrossRef]
- Chen, B.; Ye, Y.; Wang, D.; Li, Y.; Xiong, J.; Qu, C. Seismic Response Characteristics and Liquefaction Risk of Artificial Island with Saturated Hydraulic Fill Coral Sand. Ocean. Eng. 2024, 317, 120025. [Google Scholar] [CrossRef]
- Wang, X.-Z.; Jiao, Y.-Y.; Wang, R.; Hu, M.-J.; Meng, Q.-S.; Tan, F.-Y. Engineering Characteristics of the Calcareous Sand in Nansha Islands, South China Sea. Eng. Geol. 2011, 120, 40–47. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, Y.; Liu, H.; Li, A.; Ge, H. Macro-Meso Effects of Gradation and Particle Morphology on the Compressibility Characteristics of Calcareous Sand. Bull. Eng. Geol. Environ. 2017, 77, 1047–1055. [Google Scholar] [CrossRef]
- Shahnazari, H.; Jafarian, Y.; Tutunchian, M.A.; Rezvani, R. Probabilistic Assessment of Liquefaction Occurrence in Calcareous Fill Materials of Kawaihae Harbor, Hawaii. Int. J. Geomech. 2016, 16, 05016001. [Google Scholar] [CrossRef]
- Coop, M.R. The Mechanics of Uncemented Carbonate Sands. Géotechnique 1990, 40, 607–626. [Google Scholar] [CrossRef]
- Wang, T.; Ma, L.; Wang, M.; Li, Z.; Zhang, X.; Geng, H. Effects of Particle Shape on Dynamic Mechanical Behaviours of Coral Sand under One-Dimensional Compression. Eng. Geol. 2022, 304, 106624. [Google Scholar] [CrossRef]
- Rowe, P.W. The Stress-Dilatancy Relation for Static Equilibrium of an Assembly of Particles in Contact. Proc. R. Soc. Lond. A Math. Phys. Sci. 1962, 269, 500–527. [Google Scholar] [CrossRef]
- Guo, P.; Su, X. Shear Strength, Interparticle Locking, and Dilatancy of Granular Materials. Can. Geotech. J. 2007, 44, 579–591. [Google Scholar] [CrossRef]
- Koerner, R.M. Effect of Particle Characteristics on Soil Strength. J. Soil Mech. Found. Div. 1970, 96, 1221–1234. [Google Scholar] [CrossRef]
- Mirghasemi, A.A.; Rothenburg, L.; Matyas, E.L. Influence of Particle Shape on Engineering Properties of Assemblies of Two-Dimensional Polygon-Shaped Particles. Géotechnique 2002, 52, 209–217. [Google Scholar] [CrossRef]
- Chen, C.; Gu, J.; Peng, Z.; Dai, X.; Liu, Q.; Zhu, G.-Q. Discrete Element Modeling of Particles Sphericity Effect on Sand Direct Shear Performance. Sci. Rep. 2022, 12, 5490. [Google Scholar] [CrossRef] [PubMed]
- Bolton, M.D. The Strength and Dilatancy of Sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Esposito, M.P.; Andrus, R.D. Peak Shear Strength and Dilatancy of a Pleistocene Age Sand. J. Geotech. Geoenviron. Eng. 2016, 143, 04016079. [Google Scholar] [CrossRef]
- Hao, D.; Yue, C.; Chen, R.; Ren, J.; Chen, F. Shear characteristics and stress-dilation relation of medium sand under normal to high pressures. Chin. J. Geotech. Eng. 2020, 42, 765–772. [Google Scholar] [CrossRef]
- Vaid, Y.P.; Sasitharan, S. The Strength and Dilatancy of Sand. Can. Geotech. J. 1992, 29, 522–526. [Google Scholar] [CrossRef]
- Yin, J.-H.; Wang, Y.-J.; Selvadurai, A.P.S. Influence of Nonassociativity on the Bearing Capacity of a Strip Footing. J. Geotech. Geoenviron. Eng. 2001, 127, 985–989. [Google Scholar] [CrossRef]
- Erickson, H.L.; Drescher, A. Bearing Capacity of Circular Footings. J. Geotech. Geoenviron. Eng. 2002, 128, 38–43. [Google Scholar] [CrossRef]
- De Borst, R.; Vermeer, P.A. Discussion: Possibilities and Limitations of Finite Elements for Limit Analysis. Géotechnique 1985, 35, 90–94. [Google Scholar] [CrossRef]
- Loukidis, D.; Salgado, R. Bearing Capacity of Strip and Circular Footings in Sand Using Finite Elements. Comput. Geotech. 2009, 36, 871–879. [Google Scholar] [CrossRef]
- Griffiths, D.V. Computation of Bearing Capacity Factors Using Finite Elements. Géotechnique 1982, 32, 195–202. [Google Scholar] [CrossRef]
- Lin, H.-D.; Wang, W.-C.; Li, A.-J. Investigation of Dilatancy Angle Effects on Slope Stability Using the 3D Finite Element Method Strength Reduction Technique. Comput. Geotech. 2019, 118, 103295. [Google Scholar] [CrossRef]
- Phuor, T.; Harahap, I.S.H.; Ng, C.Y. Bearing Capacity Factors of Flat Base Footing by Finite Elements. J. Geotech. Geoenviron. Eng. 2022, 148, 04022062. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Lu, Y.; Cui, J.; Wang, X.; Zhu, C. Strength and Dilatancy of Coral Sand in the South China Sea. Bull. Eng. Geol. Environ. 2021, 80, 8279–8299. [Google Scholar] [CrossRef]
- Dong, K.; Ren, H.; Ruan, W.; Huang, K. Dynamic Mechanical Behavior of Different Coral Sand Subjected to Impact Loading. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 235, 1512–1523. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. China Planning Publishing House: Beijing, China, 2019.
- Liu, S.; Matsuoka, H. Microscopic Interpretation on a Stress-Dilatancy Relationship of Granular Materials. Soils Found. 2003, 43, 73–84. [Google Scholar] [CrossRef][Green Version]
- D4767-11 (Reapproved 2020); Standard Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils. ASTM International: West Conshohocken, PA, USA, 2020.
- Lade, P.V.; Yamamuro, J.A. Undrained Sand Behavior in Axisymmetric Tests at High Pressures. J. Geotech. Eng. 1996, 122, 120–129. [Google Scholar] [CrossRef]
- Wu, Y.; Li, N.; Wang, X.; Cui, J.; Chen, Y.; Wu, Y.; Yamamoto, H. Experimental Investigation on Mechanical Behavior and Particle Crushing of Calcareous Sand Retrieved from South China Sea. Eng. Geol. 2020, 280, 105932. [Google Scholar] [CrossRef]
- Gutierrez, M. Modeling of the Steady-State Response of Granular Soils. Soils Found. 2003, 43, 93–105. [Google Scholar] [CrossRef]
- Zhang, J.-M.; Zhang, L.; Jiang, G.-S.; Wang, R. Research on Particle Crushing of Calcareous Sands under Triaxial Shear. Rock Soil Mech. 2008, 29, 2789–2793. [Google Scholar] [CrossRef]
- Lv, C.; Wu, H.; Shi, M.; Zhang, D. Experimental Study on the Mechanical Strength, Deformation Behavior and Infiltration Characteristics of Coral Sand. Sustainability 2024, 16, 3479. [Google Scholar] [CrossRef]
- Vermeer, P.A. Non-Associated Plasticity for Soils, Concrete and Rock. In Physics of Dry Granular Media; Springer: Dordrecht, The Netherlands, 1998; pp. 163–196. [Google Scholar]
- Dickin, E.A. Uplift Behavior of Horizontal Anchor Plates in Sand. J. Geotech. Eng. 1988, 114, 1300–1317. [Google Scholar] [CrossRef]
- Frydman, S.; Shaham, I. Pullout Capacity of Slab Anchors in Sand. Can. Geotech. J. 1989, 26, 385–400. [Google Scholar] [CrossRef]
- Chakraborty, T.; Salgado, R. Dilatancy and Shear Strength of Sand at Low Confining Pressures. J. Geotech. Geoenviron. Eng. 2010, 136, 527–532. [Google Scholar] [CrossRef]
- Hassanlourad, M.; Salehzadeh, H.; Shahnazari, H. Drained Shear Strength of Carbonate Sands Based on Energy Approach. Int. J. Geotech. Eng. 2014, 8, 1–9. [Google Scholar] [CrossRef]
- Salgado, R.; Bandini, P.; Karim, A. Shear Strength and Stiffness of Silty Sand. J. Geotech. Geoenviron. Eng. 2000, 126, 451–462. [Google Scholar] [CrossRef]

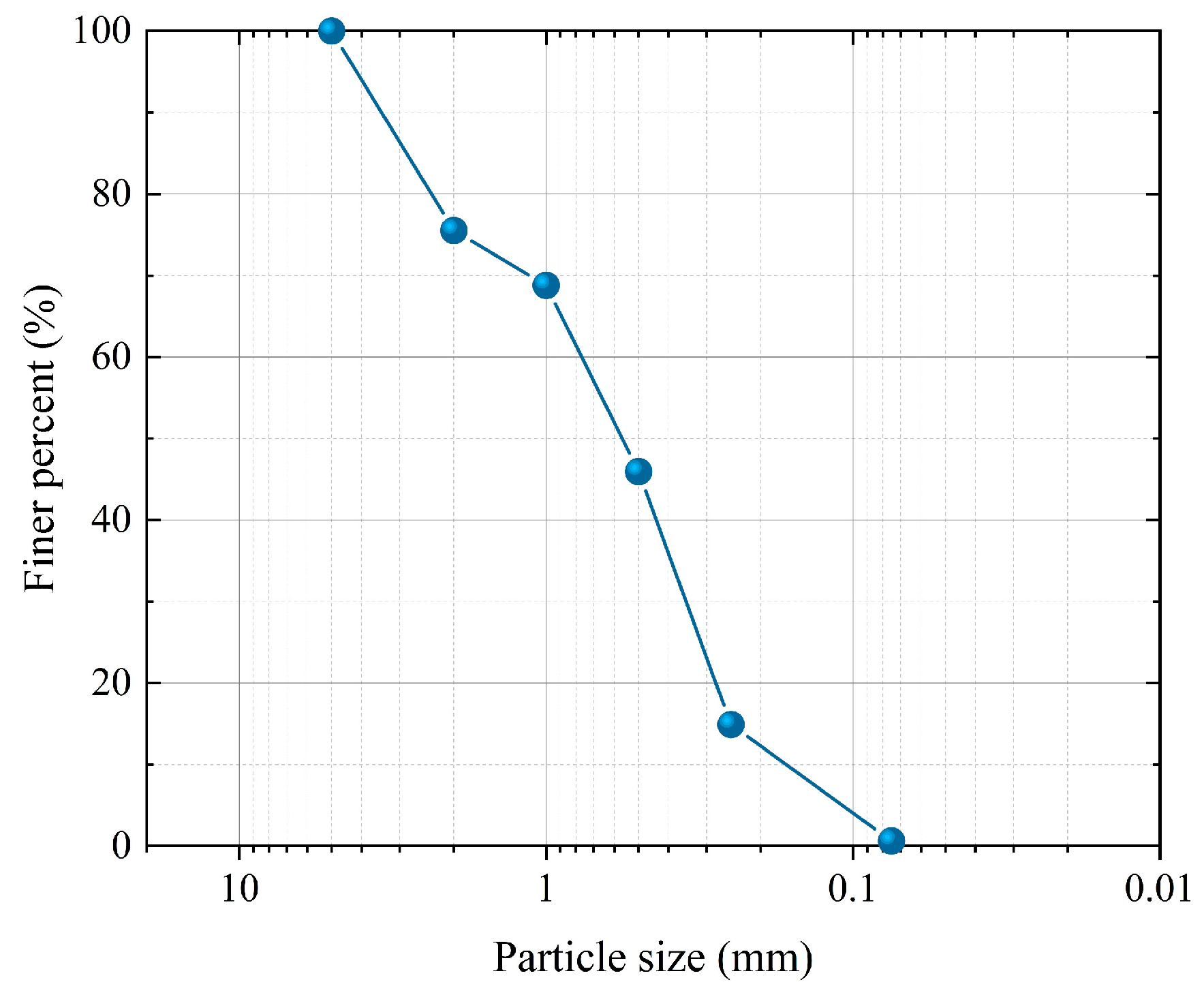


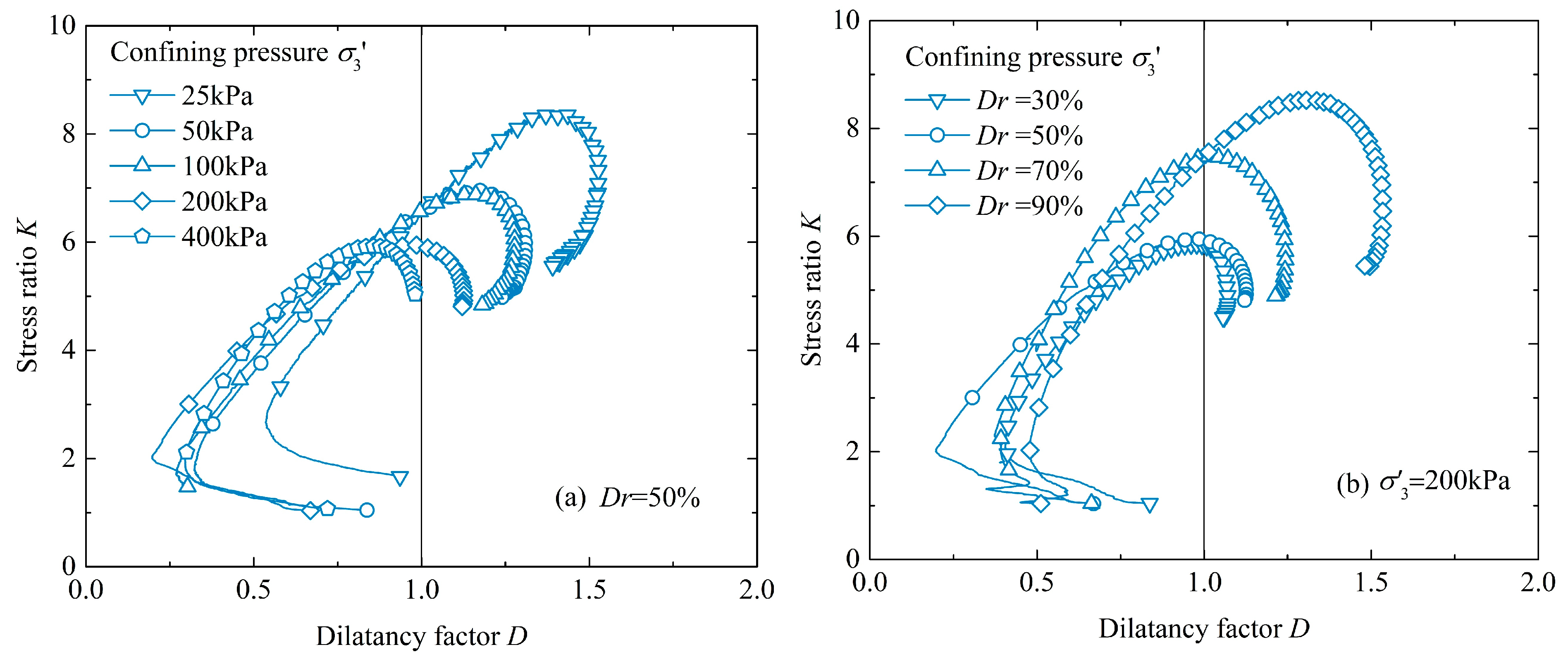
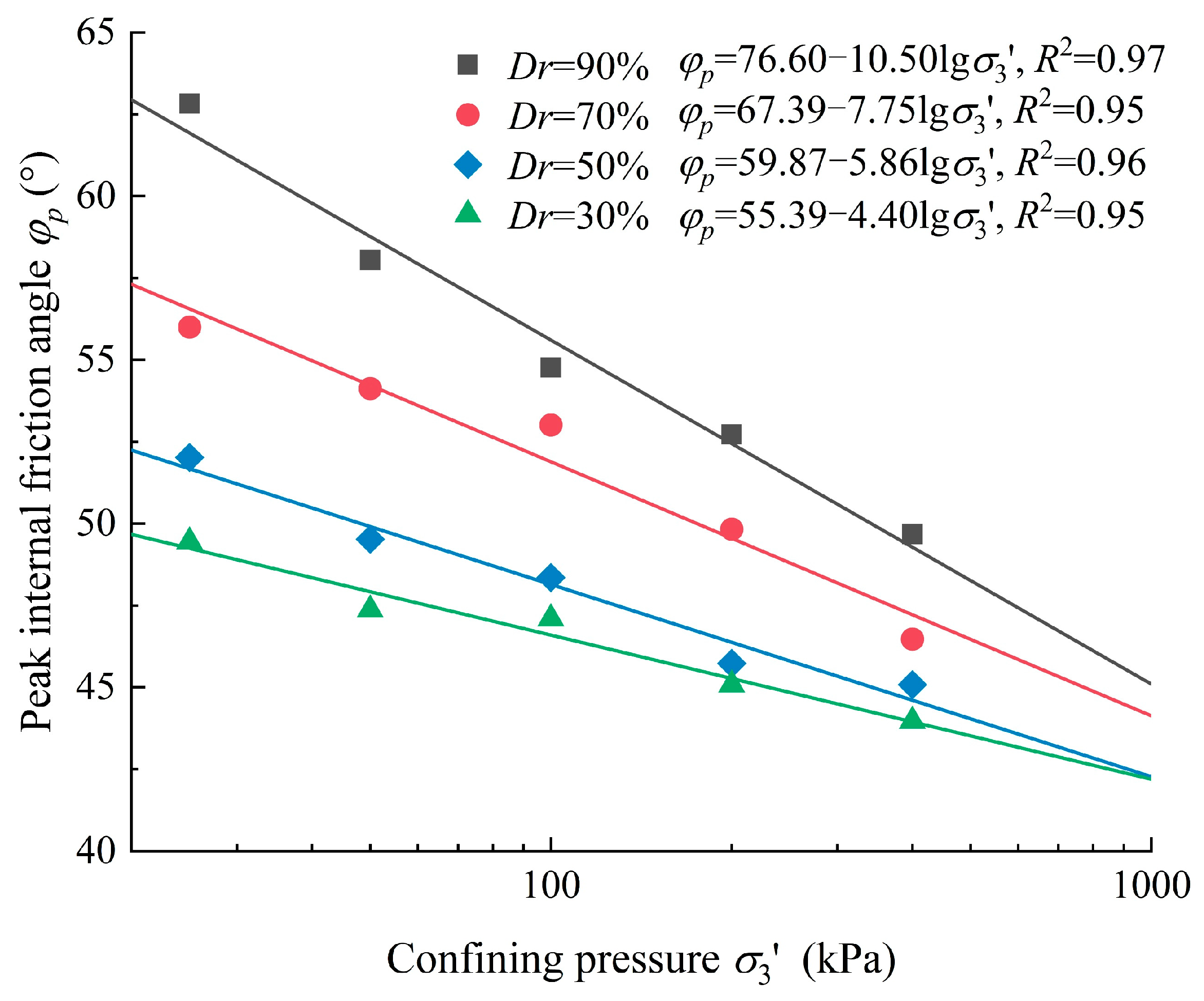

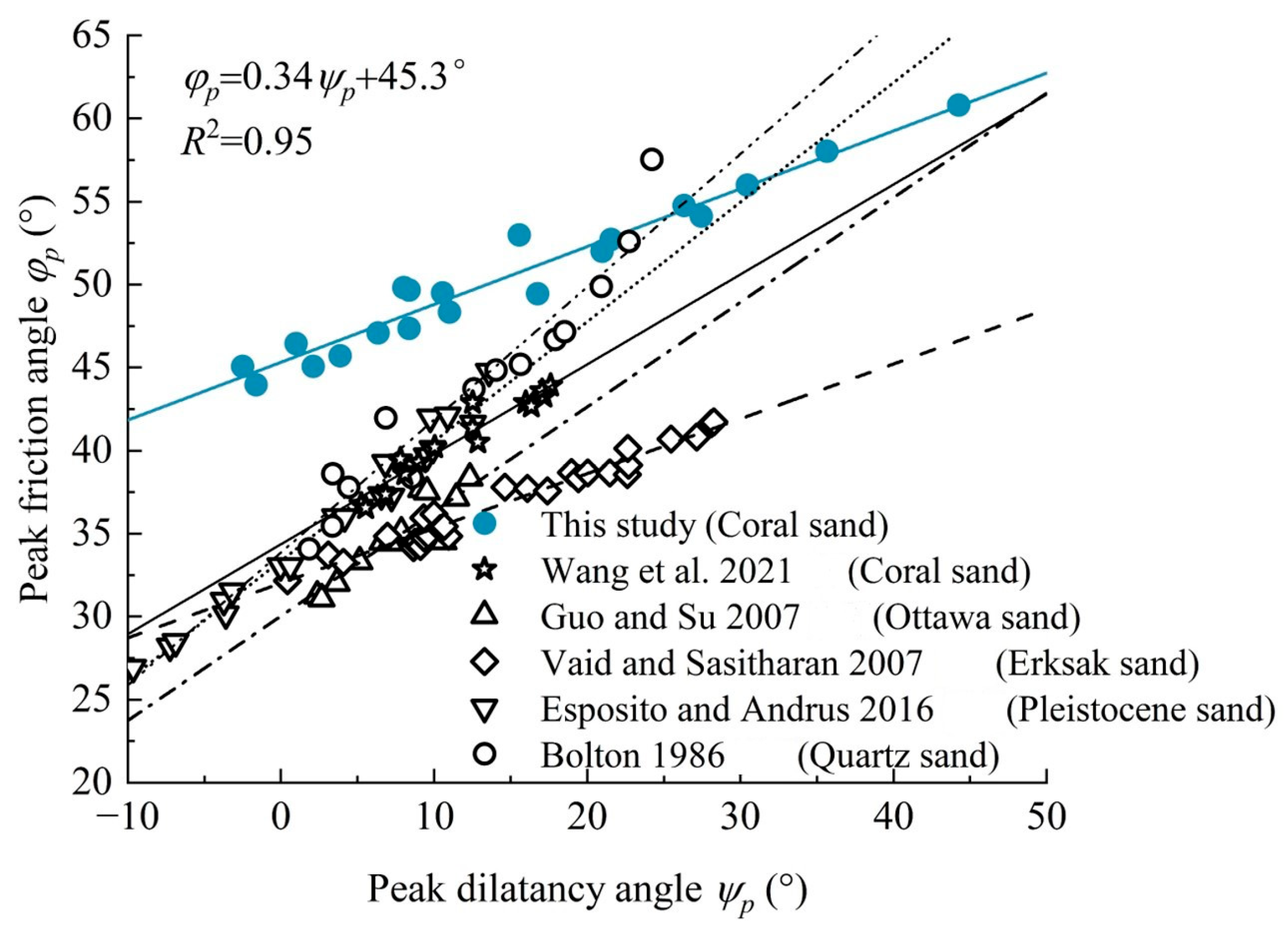
| Parameter | Unit | Value |
|---|---|---|
| CaCO3, Calcium carbonate content | % | 95 |
| Gs, Specific gravity of solids | mm | 2.80 |
| d10, Effective particle size | mm | 0.15 |
| d50, Average particle size | mm | 0.58 |
| Cu, Coefficient of uniformity | - | 5.2 |
| Cc, Coefficient of curvature | - | 1.02 |
| ρmax, Maximum dry density | g/cm3 | 1.78 |
| ρmin, Minimum dry density | g/cm3 | 1.34 |
| Test No. | Dr (%) | σ′3 (kPa) | Test No. | Dr (%) | σ′3 (kPa) |
|---|---|---|---|---|---|
| CD1 | 30 | 25 | CD11 | 70 | 25 |
| CD2 | 30 | 50 | CD12 | 70 | 50 |
| CD3 | 30 | 100 | CD13 | 70 | 100 |
| CD4 | 30 | 200 | CD14 | 70 | 200 |
| CD5 | 30 | 400 | CD15 | 70 | 400 |
| CD6 | 50 | 25 | CD16 | 90 | 25 |
| CD7 | 50 | 50 | CD17 | 90 | 50 |
| CD8 | 50 | 100 | CD18 | 90 | 100 |
| CD9 | 50 | 200 | CD19 | 90 | 200 |
| CD10 | 50 | 400 | CD20 | 90 | 300 |
| σ3′ (kPa) | Peak Internal Friction Angle φp (°) | Peak Dilatancy Angle ψp (°) | ||||||
|---|---|---|---|---|---|---|---|---|
| Dr = 30% | Dr = 50% | Dr = 70% | Dr = 90% | Dr = 30% | Dr = 50% | Dr = 70% | Dr = 90% | |
| 25 | 49.45 | 52.02 | 56.00 | 62.82 | 16.75 | 20.97 | 30.45 | 44.24 |
| 50 | 47.37 | 49.52 | 54.12 | 58.04 | 8.35 | 10.53 | 27.43 | 35.64 |
| 100 | 47.1 | 48.35 | 53.01 | 54.76 | 6.33 | 10.99 | 15.56 | 26.32 |
| 200 | 45.08 | 45.73 | 49.83 | 52.72 | 2.1 | 3.85 | 8.02 | 21.55 |
| 300 | - | - | - | 49.67 | - | - | - | 8.35 |
| 400 | 43.97 | 45.08 | 46.47 | - | −1.63 | −2.51 | 0.98 | - |
| No. | Test Type | Sand Type | Main Composition | σ3′ (kPa) | dmax (mm) | d50 (mm) | φp,max (°) | ψp,max (°) | a | References |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Plane | Quartz sand | Quartz | - | - | - | 57.5 | 24.2 | 0.8 | Bolton [13] |
| 2 | Plane | Toyoura sand | 5~98 | - | 0.16 | 50.4 | 23.3 | 0.62 | Chakraborty and Salgado [37] | |
| 3 | Triaxial | Toyoura sand | 4~197 | - | 0.16 | 44.8 | 19.4 | 0.62 | Chakraborty and Salgado [37] | |
| 4 | Triaxial | Erksak sand | 50~2500 | - | 0.34 | 41.8 | 28.2 | 0.33 | Vaid [16] | |
| 5 | Triaxial | Ottawa sand | 100~500 | 1.2 | 0.37 | 38.4 | 12.3 | 0.63 | Guo and Su [9] | |
| 6 | Triaxial | Pleistocene age sand | 17~138 | 5.0 | 0.18 | 44.8 | 13.6 | 0.72 | Esposito and Andrus [14] | |
| 7 | Triaxial | Chinese standard sand | 200~8000 | 1.0 | 0.35 | 41.8 | 19.1 | 0.59 | Hao et al. [15] | |
| 8 | Triaxial | Limestone sand | Calcium carbonate | 100~500 | 2.0 | 1.64 | 48.1 | 11.7 | 0.91 | Guo and Su [9] |
| 9 | Triaxial | Kish sand | 50~600 | 0.16 | 0.51 | 47.0 | 10.8 | - | Hassanlourad [38] | |
| 10 | Triaxial | Hormuz sand | 50~600 | 0.18 | 0.51 | 53.0 | 12.4 | - | Hassanlourad [38] | |
| 11 | Triaxial | Coral sand | 150~300 | 20 | 0.29 | 44.0 | 17.5 | 0.5 | Wang et al. [24] | |
| 12 | Triaxial | Coral sand | 25~400 | 5.0 | 0.58 | 62.8 | 44.2 | 0.34 | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Cao, Z.; Jing, L.; Zhu, X. Study on the Dilatancy Behavior of Coral Sand and Its Influence on Shear Strength Parameters. J. Mar. Sci. Eng. 2025, 13, 1255. https://doi.org/10.3390/jmse13071255
Shi Y, Cao Z, Jing L, Zhu X. Study on the Dilatancy Behavior of Coral Sand and Its Influence on Shear Strength Parameters. Journal of Marine Science and Engineering. 2025; 13(7):1255. https://doi.org/10.3390/jmse13071255
Chicago/Turabian StyleShi, Yuanqi, Zhenzhong Cao, Liping Jing, and Xiangyu Zhu. 2025. "Study on the Dilatancy Behavior of Coral Sand and Its Influence on Shear Strength Parameters" Journal of Marine Science and Engineering 13, no. 7: 1255. https://doi.org/10.3390/jmse13071255
APA StyleShi, Y., Cao, Z., Jing, L., & Zhu, X. (2025). Study on the Dilatancy Behavior of Coral Sand and Its Influence on Shear Strength Parameters. Journal of Marine Science and Engineering, 13(7), 1255. https://doi.org/10.3390/jmse13071255





