A Review of Vibration Control Studies of Double-Layered Cylindrical Shells Under Transient Excitation in Water
Abstract
1. Introduction
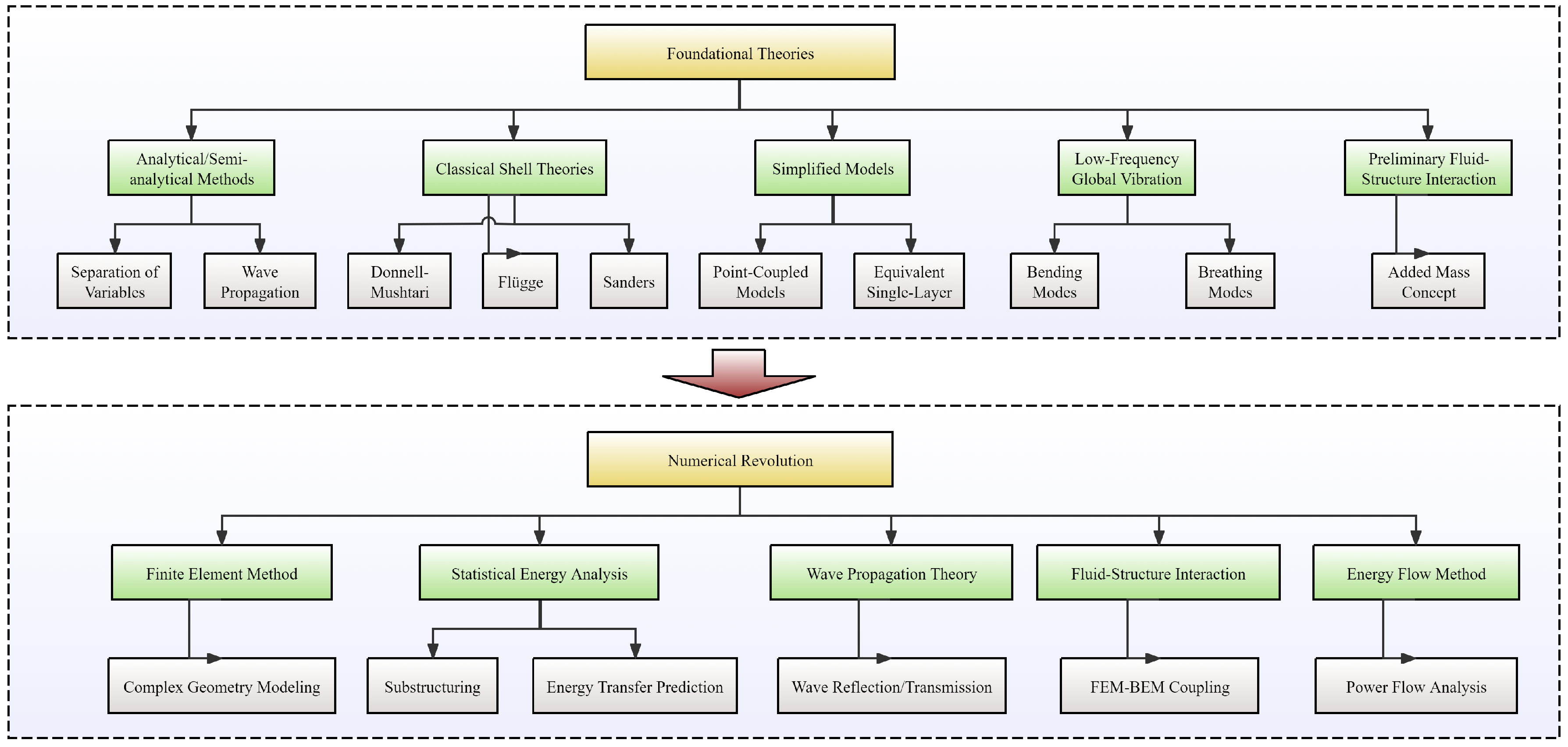
2. Vibration Characterization of Cylindrical Shells
2.1. Coupled Vibration Characteristics of Underwater Single-Layer Cylindrical Shells
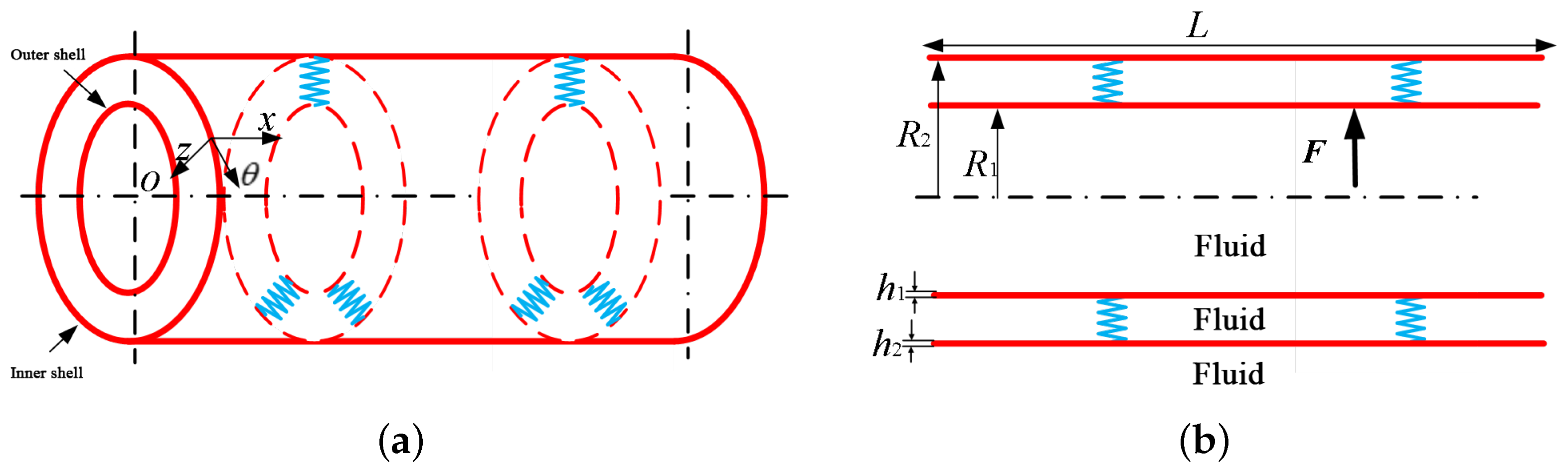
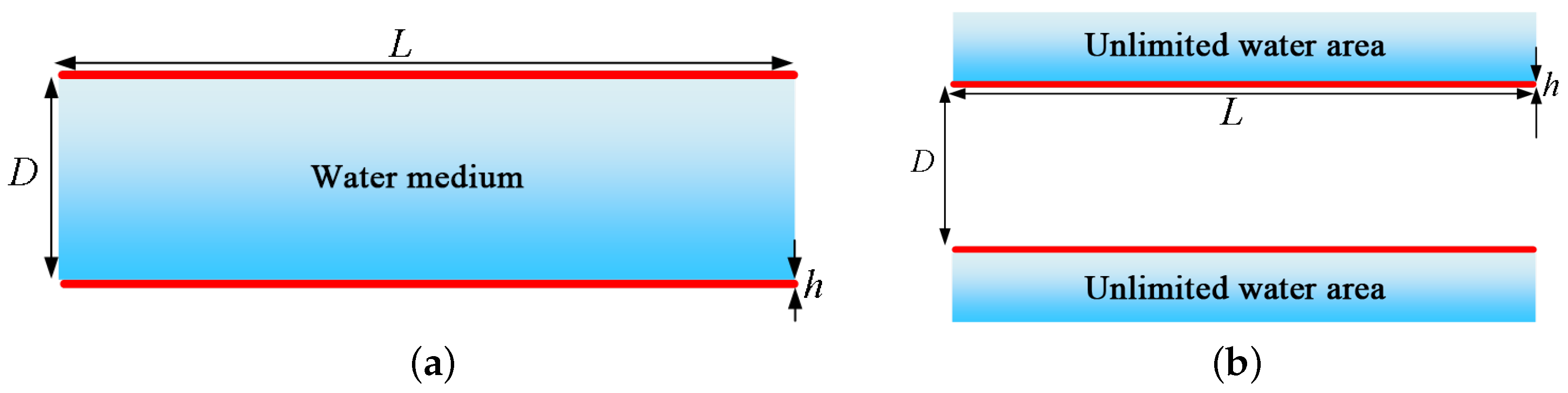
2.2. Coupled Vibration Characterization of Underwater Bilayer Plates and Shells
3. Research on Vibration Control Technology of Cylindrical Shells
3.1. Overview of Passive Control of Cylindrical Shell Vibration Research
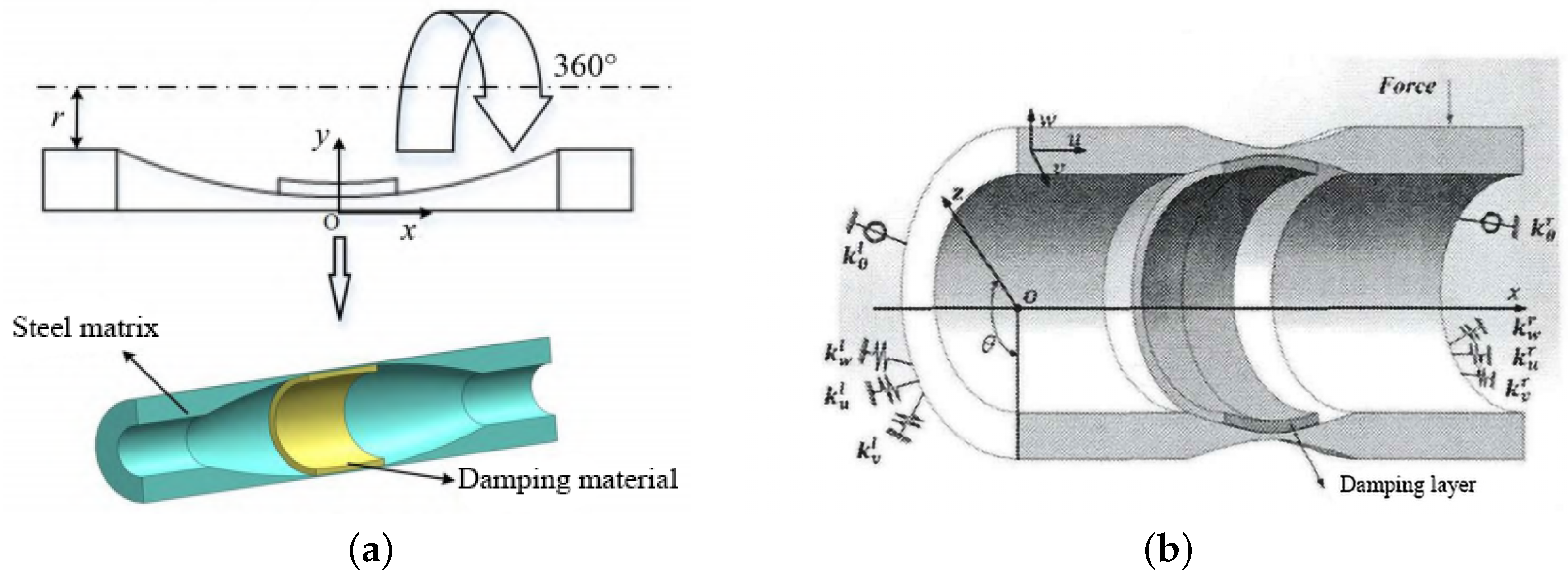
3.1.1. Constrained Damping Layer Passive Vibration Isolation
3.1.2. New Vibration Isolation Materials
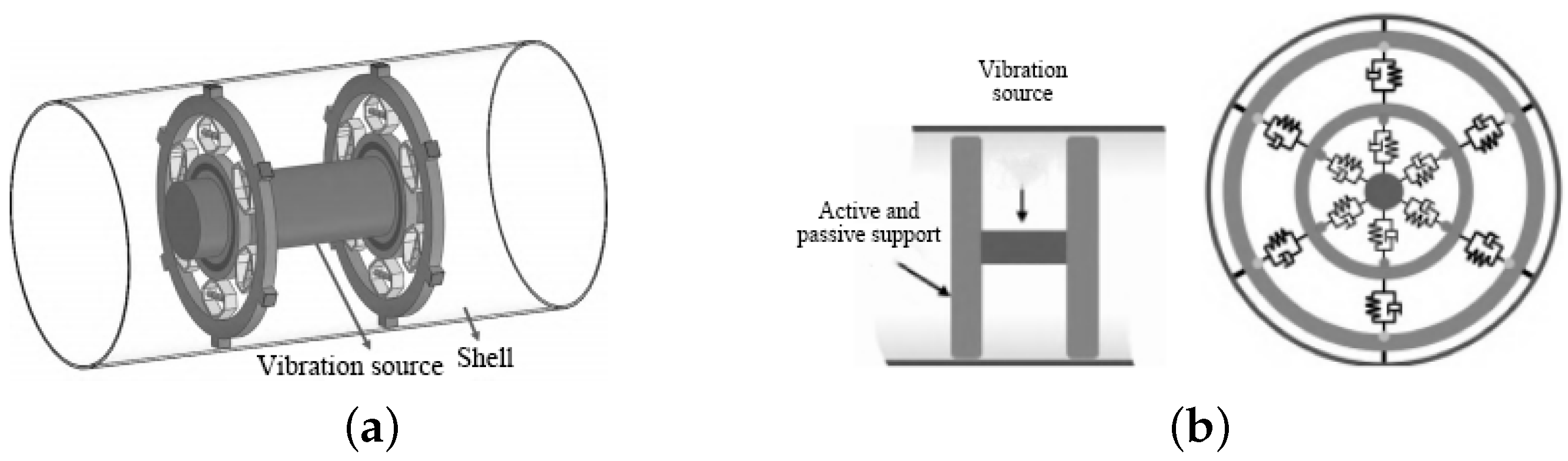
3.1.3. New Vibration Isolation Structures
3.2. Overview of Active Vibration Control Research on Cylindrical Shells
3.2.1. Vibration Isolation Actuator
3.2.2. Active Control Strategy
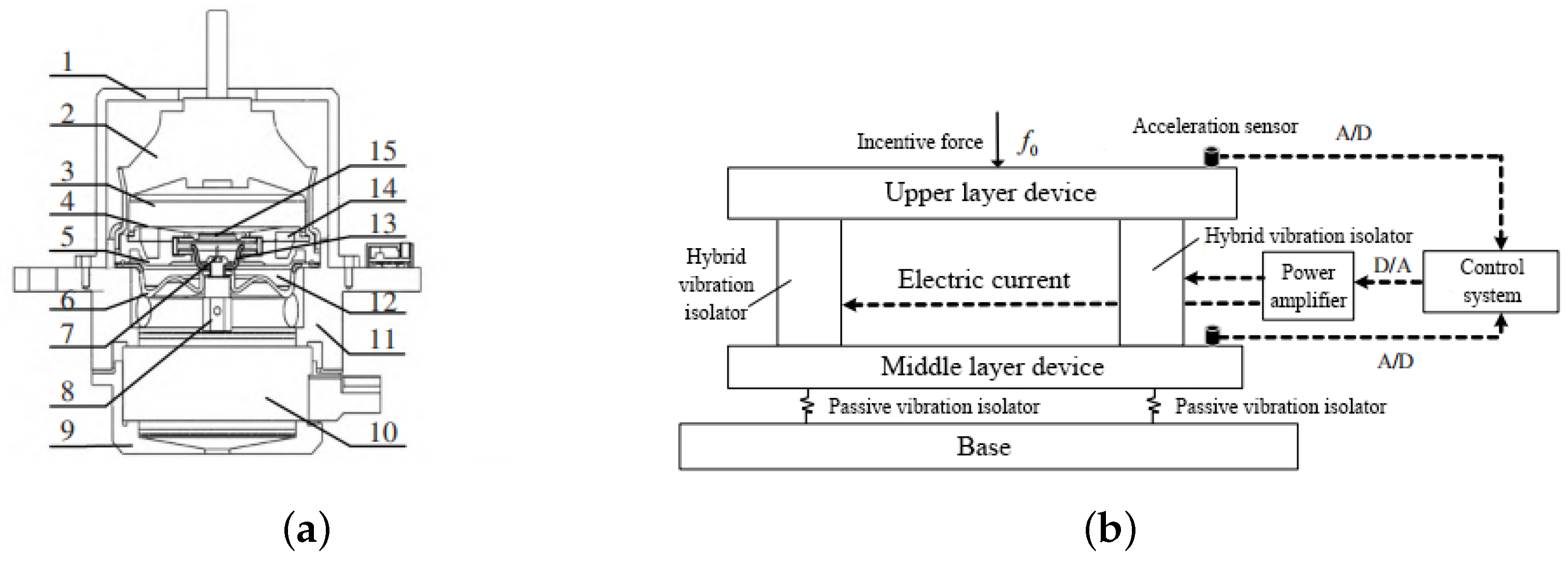
3.3. Overview of Active–Passive Hybrid Control of Vibration in Cylindrical Shells
4. Conclusions
- With the continuous progress of material science, the development of new composite materials, functional gradient materials, and smart materials provides a wide range of possibilities for vibration control technology. Research on emerging vibration control technologies such as quasi-zero stiffness vibration isolators, acoustic black holes, and phononic crystals has significantly improved the performance of passive control in vibration damping and isolation performance. Currently, the main research objectives in passive control are combining the research results of new materials with practical application contexts to reduce frequency range and expand bandwidth.
- With in-depth research into algorithms, especially the development of algorithms based on artificial intelligence, machine learning and neural networks, it is possible to adjust the vibration control strategy in real time to adapt to the complex and changeable underwater environment so as to improve the vibration reduction and isolation effect of active control. Currently, improving the calculation and feedback speed of the active control system while reducing the size of the system has become the focus of research.
- As an important trend in adapting to a wide bandwidth and underwater complex environment, active–passive hybrid control technology combines the advantages of active control and passive control in the low-frequency and high-frequency bands, which can significantly improve the overall vibration damping effect. Vibration control is carried out by utilizing the unique sound-absorbing and damping characteristics or intelligent regulation capability of new materials and combining them with active control technology to effectively suppress low-frequency noise.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, W.; Xu, J.; Yang, Q. Numerical calculation of torpedo launcher wake jet noise. J. Huazhong Univ. Sci. Tech. (Nat. Sci. Ed.) 2016, 44, 1–5. [Google Scholar]
- Zhang, X. Frequency analysis of submerged cylindrical shells with the wave propagation approach. Int. J. Mech. Sci. 2002, 44, 1259–1273. [Google Scholar] [CrossRef]
- Moline, S.A.; Rahaeifard, M.; Ahmadian, M.T. Free vibration analysis of functionally graded cylindrical shells stiffened by uniformly and non-uniformly distributed ring stiffeners. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009; Volume 15, pp. 367–375. [Google Scholar]
- Yang, D. Vibration Characteristics of Fluid-Filled Stiffened Cylindrical Shells. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2003. [Google Scholar]
- Xu, M.; Zhang, X.; Zhang, W. Energy flow input and propagation in forced vibration of fluid-filled cylindrical shells. Acta Acust. 1999, 24, 9. [Google Scholar]
- Pan, L.; Zhu, X.; Li, T. Vibration characteristics of fluid-filled cylindrical shells considering sloshing effect. Chin. J. Ship Res. 2019, 14, 126–134. [Google Scholar]
- Wu, L.; Wang, D.; Zhu, Y. A study on the effects of hydraulic static load on the dynamic characteristics of the partially liquid-filled cylindrical shell. J. Fluids Struct. 2019, 85, 40–54. [Google Scholar] [CrossRef]
- Guo, W.; Feng, Q.; Li, T. A new solution for vibroacoustic analysis of two-dimensional cylindrical shells partially liquid-filled or partially submerged in fluid. Mech. Syst. Signal Process. 2020, 140, 106685. [Google Scholar] [CrossRef]
- Li, X.; Chen, H.; Pan, Z. Study on dynamic characteristics of fluid-filled cylindrical shells. Ship Sci. Technol. 2008, 30, 45–50. [Google Scholar]
- Zhou, X. Vibration and stability of ring-stiffened thin-walled cylindrical shells conveying fluid. Acta Mech. Solida Sin. 2012, 25, 168–176. [Google Scholar] [CrossRef]
- Liang, B.; Liu, X.; Li, R. Wave solution for coupled vibration of fluid-filled ring-stiffened cylindrical shells. Eng. Mech. 2016, 33, 9–14. [Google Scholar]
- Liu, Z. Study on Vibration Power Flow and Acoustic Radiation Characteristics of Cylindrical Shell-Fluid Field Coupling System Under Hydrostatic Pressure. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2009. [Google Scholar]
- Chen, C.; Li, T.; Zhu, X. Non-destructive prediction method for elastic buckling critical load of underwater ring-stiffened cylindrical shells. Ocean Eng. 2014, 32, 89–95. [Google Scholar]
- Cao, L.; Ma, Y.; Huang, Y. Free vibration of ring-stiffened cylindrical shells with variable thickness. J. Huazhong Univ. Sci. Tech. (Urban Sci. Ed.) 2007, 24, 63–66. [Google Scholar]
- Liu, Z.; Li, T.; Zhu, X. Effect of hydrostatic pressure on input flow in submerged ring-stiffened cylindrical shells. J. Ship Mech. 2011, 15, 301–312. [Google Scholar]
- Li, X. Study on free vibration analysis of circular cylindrical shells using wave propagation. J. Sound Vib. 2008, 311, 667–682. [Google Scholar]
- Zhang, X.; Liu, G.; Lam, K.Y. Vibration analysis of thin cylindrical shells using wave propagation approach. J. Sound Vib. 2001, 239, 397–403. [Google Scholar] [CrossRef]
- Li, X. Energy method for free vibration analysis of ring-stiffened cylindrical shells. J. Ship Mech. 2001, 5, 73–81. [Google Scholar]
- Liang, B.; Li, R.; Liu, X. Study on coupled vibration characteristics of ring-stiffened cylindrical shells under hydrostatic pressure based on wave propagation method. J. Vib. Shock 2014, 33, 142–147. [Google Scholar]
- Wang, P.; Li, T.; Zhu, X. Vibration characteristics analysis of finite-length cylindrical shells near water surface. J. Vib. Eng. 2016, 5, 772–778. [Google Scholar]
- Wang, P.; Li, T.; Zhu, X. Analysis of natural vibration characteristics of cylindrical shells in shallow water. Chin. J. Shipbuild. 2016, 57, 72–82. [Google Scholar]
- Wang, P.; Li, T.; Zhu, X. Analysis of natural vibration characteristics of cylindrical shells under finite submergence depth. J. Vib. Shock 2017, 36, 146–151. [Google Scholar]
- Weng, L.; Miao, Y.; Li, T. Vibro-acoustic characteristics of underwater cylindrical shells with complex acoustic boundary constraints. J. Vib. Shock 2019, 38, 186–193+209. [Google Scholar]
- Sun, S.; Cao, D.; Han, Q. Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the Rayleigh-Ritz method. Int. J. Mech. Sci. 2013, 68, 180–189. [Google Scholar] [CrossRef]
- Sun, S.; Chu, S.; Cao, D. Vibration characteristics of thin rotating cylindrical shells with various boundary conditions. J. Sound Vib. 2012, 331, 4170–4186. [Google Scholar] [CrossRef]
- Song, X.; Zhai, J.; Chen, Y. Traveling wave analysis of rotating cross-ply laminated cylindrical shells with arbitrary boundaries conditions via Rayleigh-Ritz method. Compos. Struct. 2015, 133, 1101–1115. [Google Scholar] [CrossRef]
- Jin, G.; Ye, T.; Chen, Y. An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Compos. Struct. 2013, 106, 114–127. [Google Scholar] [CrossRef]
- Chen, J.; Liang, B. Vibration characteristics of functionally graded cylindrical shells under elastic boundary conditions. J. Ship Mech. 2017, 21, 880–887. [Google Scholar]
- Chen, M.; Xie, K.; Jia, W. Free and forced vibration of ring-stiffened conical-cylindrical shells with arbitrary boundary conditions. Ocean Eng. 2015, 108, 241–256. [Google Scholar] [CrossRef]
- Zhang, R. Study on Coupling Characteristics of Internal and External Sound Fields of Underwater Cylindrical Shells. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2019. [Google Scholar]
- Takahashi, D. Sound radiation from periodically connected harmonic double-plate structures. J. Sound Vib. 1983, 90, 541–557. [Google Scholar] [CrossRef]
- Jeong, K.; Yoo, G.; Lee, S. Hydroelastic vibration of two identical rectangular plates. J. Sound Vib. 2004, 272, 539–555. [Google Scholar] [CrossRef]
- Lin, G.-F.; Garrelick, J.M. Sound transmission through two periodically framed parallel plates. J. Acoust. Soc. Am. 1977, 61, 1014–1018. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Y.; Gao, J. Energy transmission in a mechanically-linked double-wall structure coupled to an acoustic enclosure. J. Acoust. Soc. Am. 2005, 117, 2742–2751. [Google Scholar] [CrossRef]
- Li, Z. Study on Vibration Transmission and Control of Double-Beam Structures with Elastic Connections and Interlayer Water. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2010. [Google Scholar]
- Wen, S. Research on Vibration Transmission and Control of Double-Plate Structures with Elastic Connections and Interlayer Fluid. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2023. [Google Scholar]
- Zou, M. Hydrodynamic Analysis and Dynamic Simulation of Magnetorheological Damper. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2007. [Google Scholar]
- Wang, X.Z.; Lin, H.Z.; Jiang, C.B. Study on vibro-acoustic characteristics of underwater double cylindrical shells with arbitrary boundaries. J. Huazhong Univ. Sci. Tech. (Nat. Sci. Ed.) 2025, 1–6. [Google Scholar] [CrossRef]
- Yoshikawa, S.; Willams, E.G.; Washburn, K.B. Vibration of two concentric submerged cylindrical shells coupled by the entrained fluid. J. Acoust. Soc. Am. 1994, 95, 3273–3286. [Google Scholar] [CrossRef]
- Wu, W.; Shen, S. Study on vibration and sound radiation of double-layer ribbed cylindrical shells. J. Ship Mech. 2002, 6, 8. [Google Scholar]
- Zeng, G. Analytical calculation of underwater sound radiation from infinite double-layer ribbed cylindrical shells. J. Vib. Eng. 2004, z2, 4. [Google Scholar]
- Chen, M.; Chen, X.; Shen, R. Analysis of sound radiation performance of complex double-layer shells. Acta Acust. 2004, 29, 7. [Google Scholar]
- Yao, X.; Ji, F.; Qian, D. Influence of inter-shell connection medium on sound radiation performance of double-layer shells. Tech. Acoust. 2009, 3, 6. [Google Scholar]
- Bai, Z. Vibro-Acoustic Coupling Characteristics and Control Technology of Double Cylindrical Shells with Inter-Shell Space. Ph.D. Thesis, China Ship Research and Development Academy, Beijing, China, 2014. [Google Scholar]
- Wang, S.; Yu, M. Vibro-acoustic coupling characteristics and sound radiation control of inter-shell liquid tank model. J. Ship Mech. 2019, 23, 96–109. [Google Scholar]
- Liao, J. Simulation and Experimental Study on Vibro-Acoustic Characteristics of Underwater Cylindrical Shells with Acoustic Boundaries. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Yu, A.; Zhao, Y.; Chen, M. Study on free and forced vibration characteristics of double-sided submerged cylindrical shells. J. Nav. Univ. Eng. 2022, 34, 42–46+98. [Google Scholar]
- Shao, H.; Jin, Y.; Lin, Z. Free vibration analysis of orthotropic cylindrical shells under hydraulic pressure. J. Vib. Shock 2024, 43, 34–40+70. [Google Scholar]
- Han, Y.; Zhu, X.; Li, T. Forced vibration analysis of partially liquid-filled cylindrical shells considering liquid sloshing. J. Vib. Shock 2024, 43, 37–45. [Google Scholar]
- Yang, X. Research on Vibro-Acoustic Coupling Characteristics, Control Methods and Engineering Estimation Formulas of Cylindrical Shells Under Cabin Acoustic Excitation. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Liu, H. Low and Medium Frequency Noise Calculation of Underwater Cylindrical Shells with Finite Submergence Depth. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2022. [Google Scholar]
- Yin, J.; Cai, L.; Fang, X.; Xiao, Y.; Yang, H.B.; Zhang, H.J.; Zhong, J.; Zhao, H.G.; Yu, D.L.; Wen, J.H. Research progress and vibration-damping applications of mechanical metamaterials. Adv. Mech. 2022, 52, 508–586. [Google Scholar]
- Ibrahim, R. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Kerwin, E.M. Damping of flexural waves by a constrained viscoelastic layer. J. Acoust. Soc. Am. 1959, 31, 952–962. [Google Scholar] [CrossRef]
- Mead, D.J.; Markus, S. The forced vibrations of a three-layer damped sandwich beam with arbitrary boundary conditions. J. Sound Vib. 1969, 10, 163–175. [Google Scholar] [CrossRef]
- DiTaranto, R.A. Theory of vibratory bending for elastic and viscoelastic layered finite-length beams. J. Appl. Mech. 1965, 32, 881–886. [Google Scholar] [CrossRef]
- Rao, D.K. Vibration of short sandwich beams. J. Sound Vib. 1977, 52, 253–263. [Google Scholar] [CrossRef]
- Yan, M.J.; Dowell, E.H. Governing equations for vibrating constrained layer damping sandwich plates and beams. J. Appl. Mech. 1972, 94, 1041–1047. [Google Scholar] [CrossRef]
- Pan, H.H. Axisymmetrical vibrations of a circular sandwich shell with a viscoelastic core layer. J. Sound Vib. 1969, 9, 338–348. [Google Scholar] [CrossRef]
- Leissa, A.W.; Iyer, K.M. Modal response of circular cylindrical shells with structural damping. J. Sound Vib. 1981, 77, 1–10. [Google Scholar] [CrossRef]
- Petyt, M. Vibration of curved plates. J. Sound Vib. 1971, 15, 381–395. [Google Scholar] [CrossRef]
- Au, F.T.K.; Cheung, Y.K. Free vibration and stability analysis of shells by the isoparametric spline finite strip method. Thin-Walled Struct. 1996, 24, 53–82. [Google Scholar] [CrossRef]
- Ramesh, T.C.; Ganesan, N. Orthotropic cylindrical shells with a viscoelastic core: A vibration and damping analysis. J. Sound Vib. 1994, 175, 535–555. [Google Scholar] [CrossRef]
- Chen, L.; Huang, S. Vibrations of a cylindrical shell with partially constrained layer damping treatment. Int. J. Mech. Sci. 1999, 41, 1485–1498. [Google Scholar] [CrossRef]
- Chen, L.; Huang, S. Vibration attenuation of a cylindrical shell with constrained layer damping strips treatment. Comput. Struct. 2001, 79, 1355–1362. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, Z.; Hua, H. Free vibration of circular cylindrical shell with constrained layer damping. Appl. Math. Mech. (Engl. Ed.) 2011, 32, 495–506. [Google Scholar] [CrossRef]
- Xiang, Y.; Huang, Y.; Lu, J.; Yuan, L.Y.; Zou, S.Z. New matrix method for analyzing vibration and damping effect of sandwich circular cylindrical shell with viscoelastic core. Appl. Math. Mech. (Engl. Ed.) 2008, 29, 1587–1600. [Google Scholar] [CrossRef]
- Zheng, L.; Qiu, Q.; Wan, H.; Zhang, D. Damping analysis of multilayer passive constrained layer damping on cylindrical shell using transfer function method. J. Vib. Acoust. 2014, 136, 031001. [Google Scholar] [CrossRef]
- Mokhtari, M.; Permoon, M.R.; Haddadpour, H. Dynamic analysis of isotropic sandwich cylindrical shell with fractional viscoelastic core using Rayleigh-Ritz method. Compos. Struct. 2017, 126, 165–174. [Google Scholar] [CrossRef]
- Permoona, M.R.; Shakourib, M.; Haddadpoura, H. Free vibration analysis of sandwich conical shells with fractional viscoelastic core. Compos. Struct. 2019, 214, 62–72. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, F.; Wang, Z. Effects of damping material layout on acoustic radiation performance of double-layered shells. Acta Acust. 2005, 30, 296–302. [Google Scholar]
- Zhang, C. Study on Vibro-Acoustic Coupling Mechanism of Underwater Viscoelastic Composite Cylindrical Shells. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2014. [Google Scholar]
- Wang, H.; Chen, L. Finite element dynamic analysis of orthotropic cylindrical shells with a constrained damping layer. Finite Elem. Anal. Des. 2004, 40, 737–755. [Google Scholar] [CrossRef]
- Ramesh, T.C.; Ganesan, N. Finite element analysis of cylindrical shells with a constrained viscoelastic layer. J. Sound Vib. 1994, 172, 359–370. [Google Scholar] [CrossRef]
- Mohammadi, F.; Sedaghati, R. Linear and nonlinear vibration analysis of sandwich cylindrical shell with constrained viscoelastic core layer. Int. J. Mech. Sci. 2012, 54, 156–171. [Google Scholar] [CrossRef]
- Biswal, D.K.; Mohanty, S.C. Free vibration study of multilayer sandwich spherical shell panels with viscoelastic core and isotropic/laminated face layers. Compos. Part B 2019, 159, 72–85. [Google Scholar] [CrossRef]
- Masti, R.S.; Sainsbury, M.G. Vibration damping of cylindrical shells partially coated with a constrained viscoelastic treatment having a standoff layer. Thin-Walled Struct. 2005, 43, 1355–1379. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, S.P. Experimental study on vibration and damping of curved panel treated with constrained viscoelastic layer. Compos. Struct. 2010, 92, 233–243. [Google Scholar] [CrossRef]
- Balmès, E.; Corus, M.; Stephane, B. Constrained viscoelastic damping, test/analysis correlation on an aircraft engine. Struct. Dyn. 2011, 3, 1177–1185. [Google Scholar]
- Song, X.; Cao, T.; Gao, P.; Han, Q. Vibration and damping analysis of cylindrical shell treated with viscoelastic damping materials under elastic boundary conditions via a unified Rayleigh-Ritz method. Int. J. Mech. Sci. 2019, 165, 105158. [Google Scholar] [CrossRef]
- Song, X. Nonlinear Vibration Characteristics of Laminated Thin-Walled Cylindrical Shell Structures. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2016. [Google Scholar]
- Song, X.; Han, Q. Analysis of inherent characteristics of thin-walled cylindrical shells with fully covered viscoelastic constrained damping layers. In Proceedings of the 14th National Nonlinear Vibration and the 11th National Nonlinear Dynamics and Motion Stability Conference, Nanning, China, 10 May 2013; p. 1. [Google Scholar]
- Han, Y.; Zhang, A.; Hui, C.; Yao, X. Experimental study on vibration transmission and acoustic radiation of double-layer cylindrical shells. Sens. Microsyst. 2007, 7, 41–44. [Google Scholar]
- Qu, Y.; Hua, H.; Meng, G. A domain decomposition approach for vibration analysis of isotropic and composite cylindrical shells with arbitrary boundaries. Compos. Struct. 2013, 95, 307–321. [Google Scholar] [CrossRef]
- Jin, G.; Yang, C.; Liu, Z. A unified method for the vibration and damping analysis of constrained layer damping cylindrical shells with arbitrary boundary conditions. Compos. Struct. 2015, 130, 124–142. [Google Scholar] [CrossRef]
- Jin, G.; Yang, C.; Liu, Z. Vibration and damping analysis of sandwich viscoelastic-core beam using Reddy’s higher-order theory. Compos. Struct. 2016, 140, 390–409. [Google Scholar] [CrossRef]
- Wu, H.; Han, Q. Dynamic characteristics analysis of elastic-supported viscoelastic damping-aeroengine thin-walled casings. J. Aerosp. Power 2020, 35, 1413–1424. [Google Scholar]
- Li, Y.; Wang, W.; Zhang, T.; Liu, Z. Design of composite structure floating raft and its vibration isolation performance. In Proceedings of the 18th Symposium on Underwater Noise of Ships, Kunming, China, 29 September 2021; China Ship Scientific Research Center: Wuxi, China, 2021; p. 10. [Google Scholar]
- Jin, S.; Jin, G.; Ye, T.; Bu, C.; Zhang, B. Self-noise prediction and comprehensive control of bow sonar platform. Chin. J. Ship Res. 2022, 17, 10–18. [Google Scholar]
- Teng, H.D.; Chen, Q. Study on vibration isolation properties of solid and liquid mixture. J. Sound Vib. 2009, 326, 137–149. [Google Scholar] [CrossRef]
- Liu, X.; Huang, X.; Zhang, Z.; Hua, X. Effects of excitation amplitude and load on characteristics of quasi-zero-stiffness vibration isolators. J. Mech. Eng. 2013, 49, 89–94. [Google Scholar] [CrossRef]
- Hao, Z.; Cao, Q. The isolation characteristics of an archetypal dynamical model with stable-quasi-zero-stiffness. J. Sound Vib. 2015, 340, 61–79. [Google Scholar] [CrossRef]
- Li, Y.; Xu, D. Vibration attenuation of high dimensional quasi-zero stiffness floating raft system. Int. J. Mech. Sci. 2017, 126, 1. [Google Scholar] [CrossRef]
- Ren, C. Research on Design Method and Performance of Ship Negative Stiffness Metamaterial and Structure. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2020. [Google Scholar]
- Xia, L.; Yang, D. Analysis of vibration and acoustic performance of double-layer cylindrical shells with negative Poisson’s ratio metamaterial ribbed plates. J. Vib. Shock 2018, 37, 138–144. [Google Scholar]
- Xia, L.; Yang, D. Analysis of vibration and acoustic radiation performance of submarines with negative Poisson’s ratio metamaterial components. J. Vib. Eng. 2019, 32, 956–965. [Google Scholar]
- Luo, J.; Yao, L.; Jiang, G. Study on vibration bandgap and vibration characteristics of cylindrical shell phononic crystals. J. Vib. Shock 2019, 38, 133–138. [Google Scholar]
- Luo, J. Research on the Regulation Mechanism of Broadband Bandgap of Cylindrical Shell Mechanical Metamaterials and the Research of Shaft Tube Vibration Isolators. Ph.D. Thesis, Southwest University, Chongqing, China, 2020. [Google Scholar]
- Huang, H.; Ran, J.; Chen, K. Study on bandgap characteristics of locally resonant cylindrical shell phononic crystals. J. Synth. Cryst. 2020, 49, 1078–1082+1106. [Google Scholar]
- Chen, S.; Yao, D.; Yao, L. Machine learning optimization design of acoustic metamaterial bandgap for cylindrical shells. Noise Vib. Control 2024, 44, 70–76. [Google Scholar]
- Wan, S.; Li, L.; Wang, G. A novel locally resonance metamaterial cylindrical shell with tower-shaped lattice for broadband vibration suppression. Mech. Syst. Signal Process. 2024, 216, 111510. [Google Scholar] [CrossRef]
- An, X.; Yuan, X.; Sun, G. Design of lattice cylindrical shell meta-structures for broadband vibration reduction and high load-bearing capacity. Thin-Walled Struct. 2024, 197, 111647. [Google Scholar] [CrossRef]
- Zuo, Y.; Yang, D.; Zhuang, Y. Broadband transient vibro-acoustic prediction and control for the underwater vehicle power cabin with metamaterial components. Ocean Eng. 2024, 298, 117121. [Google Scholar] [CrossRef]
- Zhang, H.; Qu, Z.; Fu, Z. Influence of main parameters of floating raft isolation system on its isolation performance. J. Vib. Shock 2000, 2, 7–10+6+92. [Google Scholar]
- Jin, Y.; Jia, X.; Wu, Q. Design of cylindrical honeycomb sandwich meta-structures for vibration suppression. Mech. Syst. Signal Process. 2022, 163, 108075. [Google Scholar] [CrossRef]
- Ke, Y.; Yin, J.; He, Y. Locally multi-resonant meta-shells for broadband vibration suppression. Int. J. Mech. Sci. 2024, 278, 109452. [Google Scholar] [CrossRef]
- Tang, Y.; Wei, J.; Qin, Y. Sound insulation characteristics of sandwich thin-plate acoustic metamaterial: Analysis and optimization. Int. J. Comput. Methods 2024, 22, 2450039. [Google Scholar] [CrossRef]
- Machens, K.U.; Dyer, I. Energy partitioning in a truss structure. Acustica 1995, 81, 587–594. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, S.; Yu, M. Review of truss floating raft vibration isolation research. In Proceedings of the 12th Symposium on Underwater Noise of Ships, Changsha, China, 1 October 2009; China Shipbuilding Engineering Society: Beijing, China, 2009; p. 7. [Google Scholar]
- Xu, S. Refined Modeling of Cabin Raft Isolation System and Efficient Raft Frame Design Research. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2016. [Google Scholar]
- Mironov, M.A. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval. Sov. Phys. Acoust. 1988, 34, 318–319. [Google Scholar]
- Pelat, A.; Gautier, F.; Conlon, S.C. The acoustic black hole: A review of theory and applications. J. Sound Vib. 2020, 476, 115316. [Google Scholar] [CrossRef]
- Deng, J.; Gao, N.; Tang, L. Vibroacoustic mitigation for a cylindrical shell coupling with an acoustic black hole plate using Gaussian expansion component mode synthesis. Compos. Struct. 2022, 298, 116002. [Google Scholar] [CrossRef]
- Deng, J.; Guasch, O.; Maxit, L. Vibration of cylindrical shells with embedded annular acoustic black holes using the Rayleigh-Ritz method with Gaussian basis functions. Mech. Syst. Signal Process. 2021, 150, 107225. [Google Scholar] [CrossRef]
- Wang, W.H.; Lin, Y.S.; Liu, H.Y. Simulation analysis of vibration reduction technology for ring-stiffened cylindrical shells based on spiral acoustic black holes [J/OL]. Chin. J. Ship Res. 2025, 1–10. [Google Scholar] [CrossRef]
- Wei, J.; Xiang, Y.; Liao, L. Application and structural optimization of acoustic black holes on cylindrical shells. Noise Vib. Control 2023, 43, 59–65. [Google Scholar]
- Liu, B. Analysis of Vibration Characteristics of Cylindrical Shells Embedded with Acoustic Black Holes and Their Coupled Structures. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2023. [Google Scholar]
- Schenk, M.; Guest, S.D.; Herder, J.L. Zero stiffness tensegrity structures. Int. J. Solids Struct. 2007, 44, 6569–6583. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, D. Study on the piecewise nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator. Appl. Math. Mech. 2014, 35, 50–62. [Google Scholar]
- Cai, C. Design Method and Low-Frequency Vibration Reduction Characteristics of Quasi-zero Stiffness Metamaterials. Ph.D. Thesis, Hunan University, Changsha, China, 2023. [Google Scholar]
- Gardonio, P.; Turco, E.; Kras, A. Semi-active vibration control unit tuned to maximise electric power dissipation. J. Sound Vib. 2021, 499, 116000. [Google Scholar] [CrossRef]
- Wang, Z.; Mak, C.M. Application of a movable active vibration control system on a floating raft. J. Sound Vib. 2018, 414, 233–244. [Google Scholar] [CrossRef]
- Hu, K.; Li, H. Multi-parameter optimization of piezoelectric actuators for multi-mode active vibration control of cylindrical shells. J. Sound Vib. 2018, 426, 166–185. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, W.; Zhang, Y. Active vibration control of functionally graded graphene nanoplatelets reinforced composite plates with piezoelectric layers under multi-order excitation. Eng. Struct. 2025, 322, 119208. [Google Scholar] [CrossRef]
- He, P.; Xie, X.; Zhang, Z. Vibration suppression of a cylindrical shell structure by transmission path control. J. Vib. Control 2024, 2024, 10775463241272996. [Google Scholar] [CrossRef]
- Sun, S.; Zhao, X.; Yang, Y. Active vibration control of rotating carbon nanotube reinforced composite cylindrical shells via piezoelectric patches. J. Vib. Control 2024, 2024, 10775463241260081. [Google Scholar] [CrossRef]
- Niasar, M.J.; Jafari, A.A.; Rahaghi, M.I. Active control of free and forced vibration of a rotating FG cylindrical shell via FG piezoelectric patches. Mech. Based Des. Struct. Mach. 2024, 52, 3900–3924. [Google Scholar] [CrossRef]
- Geng, X.; Yin, S.; Zhou, J. Actuator position optimization method for active vibration control of cylindrical shells. J. Unmanned Undersea Syst. 2020, 28, 650–656. [Google Scholar]
- Soni, T.; Das, A.S.; Dutt, J.K. Active vibration control of ship mounted flexible rotor-shaft-bearing system during seakeeping. J. Sound Vib. 2020, 467, 115046. [Google Scholar] [CrossRef]
- Marinangeli, L.; Alijani, F.; Hosseinnia, S.H. Fractional-order positive position feedback compensator for active vibration control of a smart composite plate. J. Sound Vib. 2018, 412, 1–16. [Google Scholar] [CrossRef]
- Yuan, M.; Qiu, J.; Ji, H. Research on active vibration control based on co-located acceleration negative feedback. J. Vib. Test. Diagn. 2014, 34, 254–260+395. [Google Scholar]
- Yang, C. Active Vibration Control of Ship Floating Raft Isolation System. Master’s Thesis, Dalian Maritime University, Dalian, China, 2012. [Google Scholar]
- Kamaruzaman, N.A.; Robertson, W.S.P.; Ghayesh, M.H. Six degree of freedom quasi-zero stiffness magnetic spring with active control: Theoretical analysis of passive versus active stability for vibration isolation. J. Sound Vib. 2021, 502, 116086. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z. Simulation research on output saturation suppression method in adaptive active vibration isolation. J. Syst. Simul. 2010, 22, 674–677. [Google Scholar]
- Cao, B. Research on Adaptive Noise Cancellation Technology. Ph.D. Thesis, Hunan University, Changsha, China, 2007. [Google Scholar]
- Zhang, M. Simulation and Experimental Study on Active Control of Low-Frequency Line Spectrum of Underwater Noise. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2018. [Google Scholar]
- Zhang, Z.; Zou, H.; Zhu, S. Active control of vibro-acoustic of stiffened cylindrical shells based on spectral element method. J. Vib. Shock 2024, 43, 224–231+300. [Google Scholar]
- He, P.; Wang, S.; Geng, X. Vibration transmission control of internal vibration sources in cylindrical shells based on piezoelectric actuation. J. Vib. Shock 2024, 43, 246–251. [Google Scholar]
- Wu, L. Research on Application of Active-Passive Hybrid Vibration Isolation Technology for Marine Diesel Generator Sets. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2021. [Google Scholar]
- Li, Y.; He, L.; Shuai, C. Improved hybrid isolator with maglev actuator integrated in air spring for active-passive isolation of ship machinery vibration. J. Sound Vib. 2017, 407, 226–239. [Google Scholar] [CrossRef]
- Niu, J.C.; Song, K.J.; Lim, C.W. On active vibration isolation of floating raft system. J. Sound Vib. 2005, 285, 391–406. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q. Adaptive control research of marine active-passive hybrid vibration isolator. J. Ship Mech. 2023, 27, 446–455. [Google Scholar]
- Hasheminejad, S.M.; Kasaeisani, A. Smart hybrid active/semi-active distributed structural acoustic control of thin- and thick-walled piezo-sandwich bimorph spherical shell cloaks. J. Sound Vib. 2023, 552, 117591. [Google Scholar] [CrossRef]
- Wang, X. Modal Characteristics of Thin-Walled Cylindrical Shells and Main Passive Control Strategies of Vibration Isolation Systems. Master’s Thesis, Shandong University, Jinan, China, 2014. [Google Scholar]
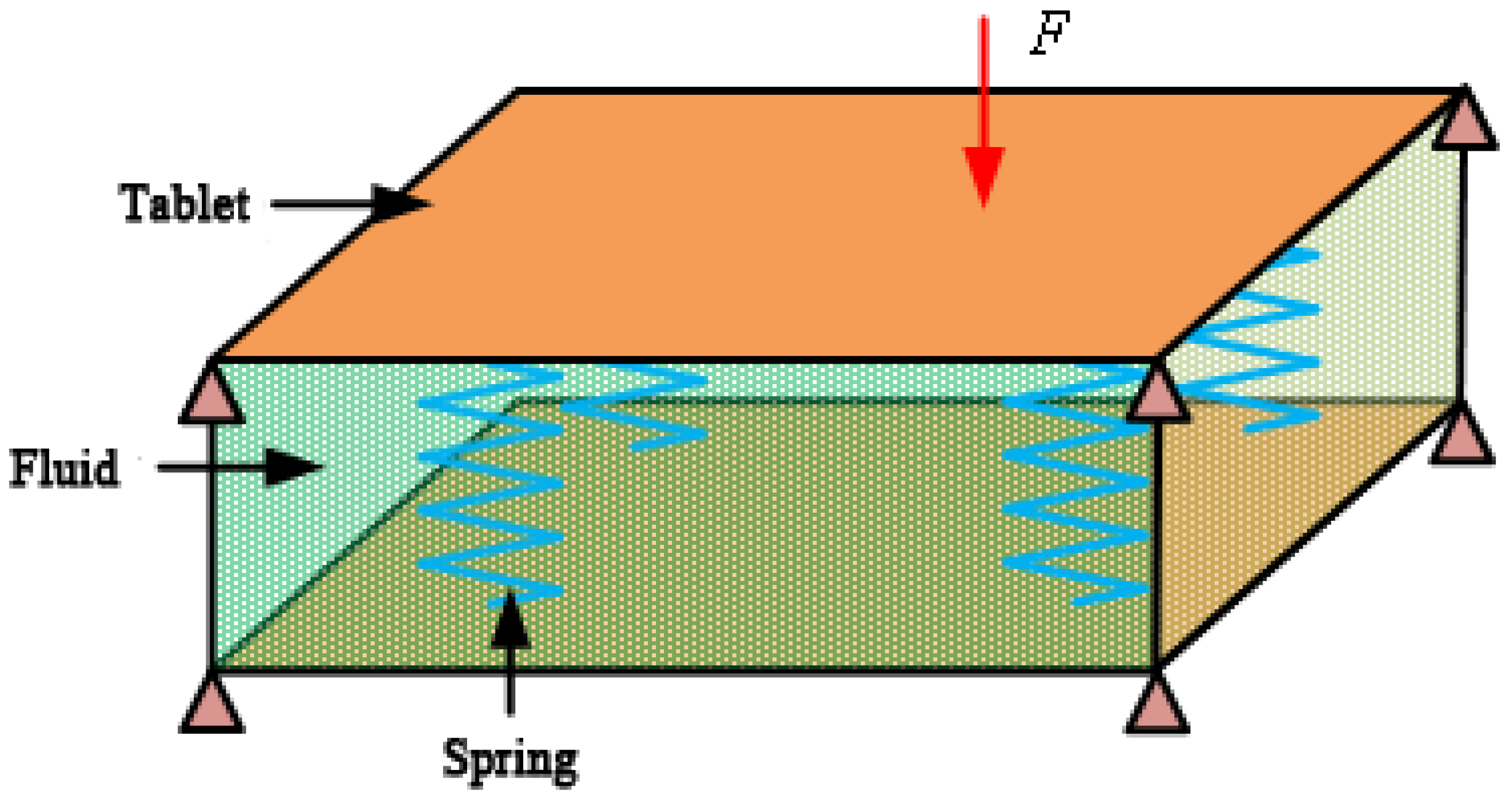
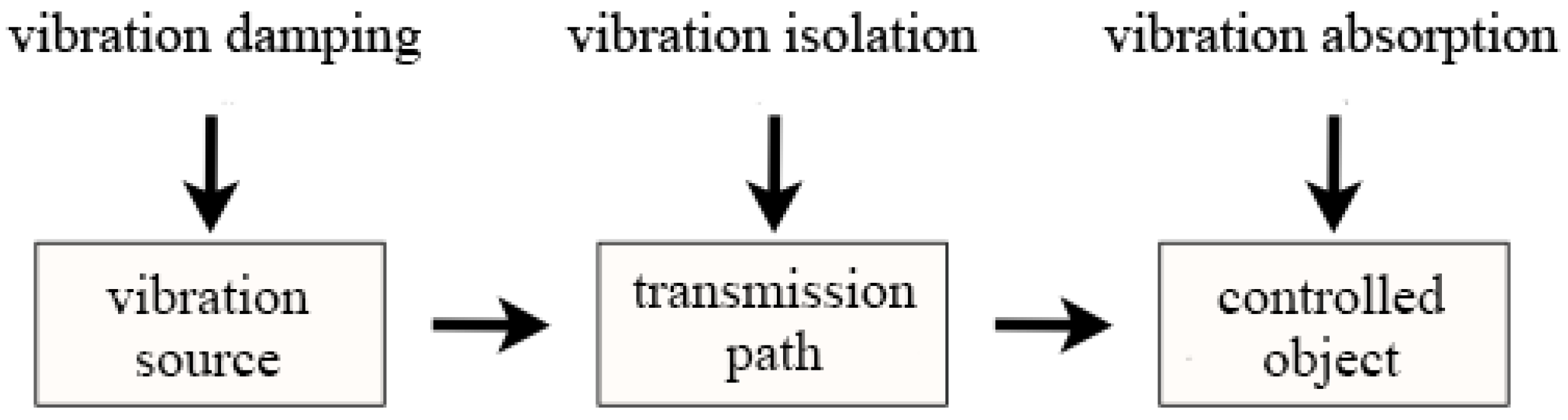
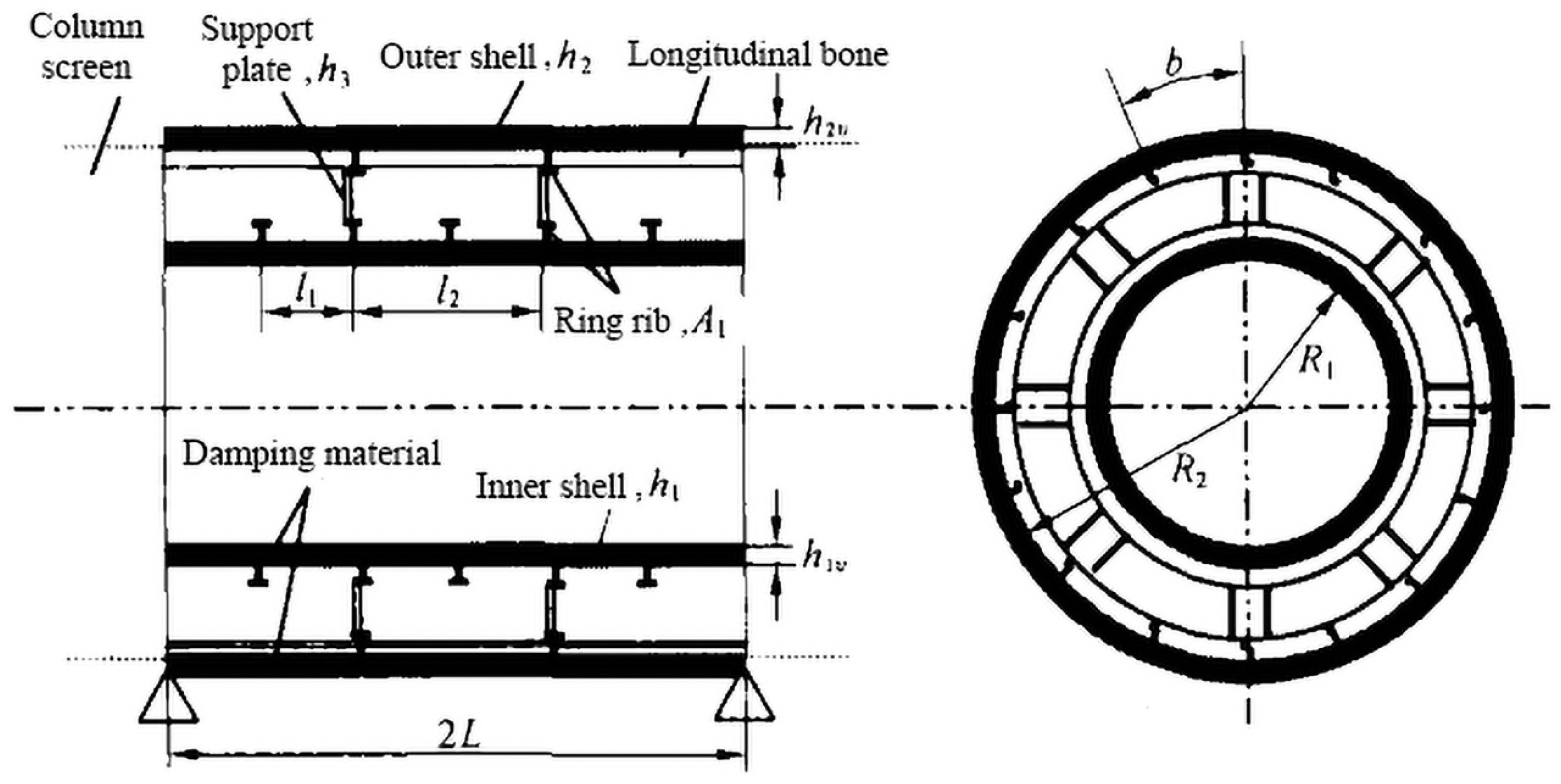
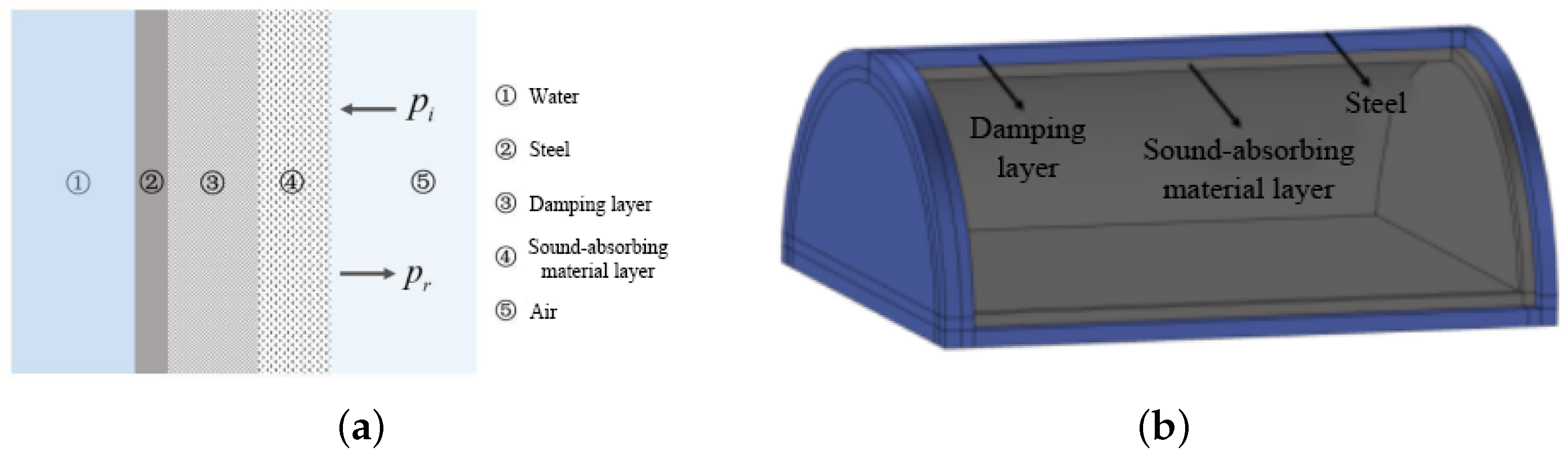
| Theory Name | Mathematical Basis | Applicable Scenarios | Advantages | Limitations |
|---|---|---|---|---|
| Donnell–Mushtari Theory | Thin-shell approximation (neglects shear deformation) | Low-frequency vibration of thin-walled shells |
|
|
| Flügge’s Precision Theory | Simplified 3D elasticity theory | Vibration of medium-thick shells |
|
|
| Point-Coupled Model | Discrete spring-mass system | Rib-connected double shells |
|
|
| Equivalent Single-Layer Theory | Equivalent stiffness method | Overall stiffness assessment in preliminary design |
|
|
| Wave Propagation Theory | Traveling wave solution + boundary matching | Vibration propagation in infinitely long shells |
|
|
| Periodic Structure Theory | Floquet–Bloch theorem | Double shells with equally spaced ribs |
|
|
| Fully Coupled FSI Theory | Potential flow theory + shell dynamics | Vibro-acoustic problems of underwater shells |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, Y.; Chen, F. A Review of Vibration Control Studies of Double-Layered Cylindrical Shells Under Transient Excitation in Water. J. Mar. Sci. Eng. 2025, 13, 1238. https://doi.org/10.3390/jmse13071238
Zhang Z, Zhao Y, Chen F. A Review of Vibration Control Studies of Double-Layered Cylindrical Shells Under Transient Excitation in Water. Journal of Marine Science and Engineering. 2025; 13(7):1238. https://doi.org/10.3390/jmse13071238
Chicago/Turabian StyleZhang, Zhen, Yinglong Zhao, and Feng Chen. 2025. "A Review of Vibration Control Studies of Double-Layered Cylindrical Shells Under Transient Excitation in Water" Journal of Marine Science and Engineering 13, no. 7: 1238. https://doi.org/10.3390/jmse13071238
APA StyleZhang, Z., Zhao, Y., & Chen, F. (2025). A Review of Vibration Control Studies of Double-Layered Cylindrical Shells Under Transient Excitation in Water. Journal of Marine Science and Engineering, 13(7), 1238. https://doi.org/10.3390/jmse13071238






