A Measure–Correlate–Predict Approach for Transferring Wind Speeds from MERRA2 Reanalysis to Wind Turbine Hub Heights
Abstract
1. Introduction
1.1. Literature Review of Reanalysis Wind Speed Transfer Models
1.2. Aim, Novelty, and Key Contributions of This Paper
- Engineering-based and mathematical models, such as the power law and log law.
- Meteorologically derived formulations, including three-parameter log profiles.
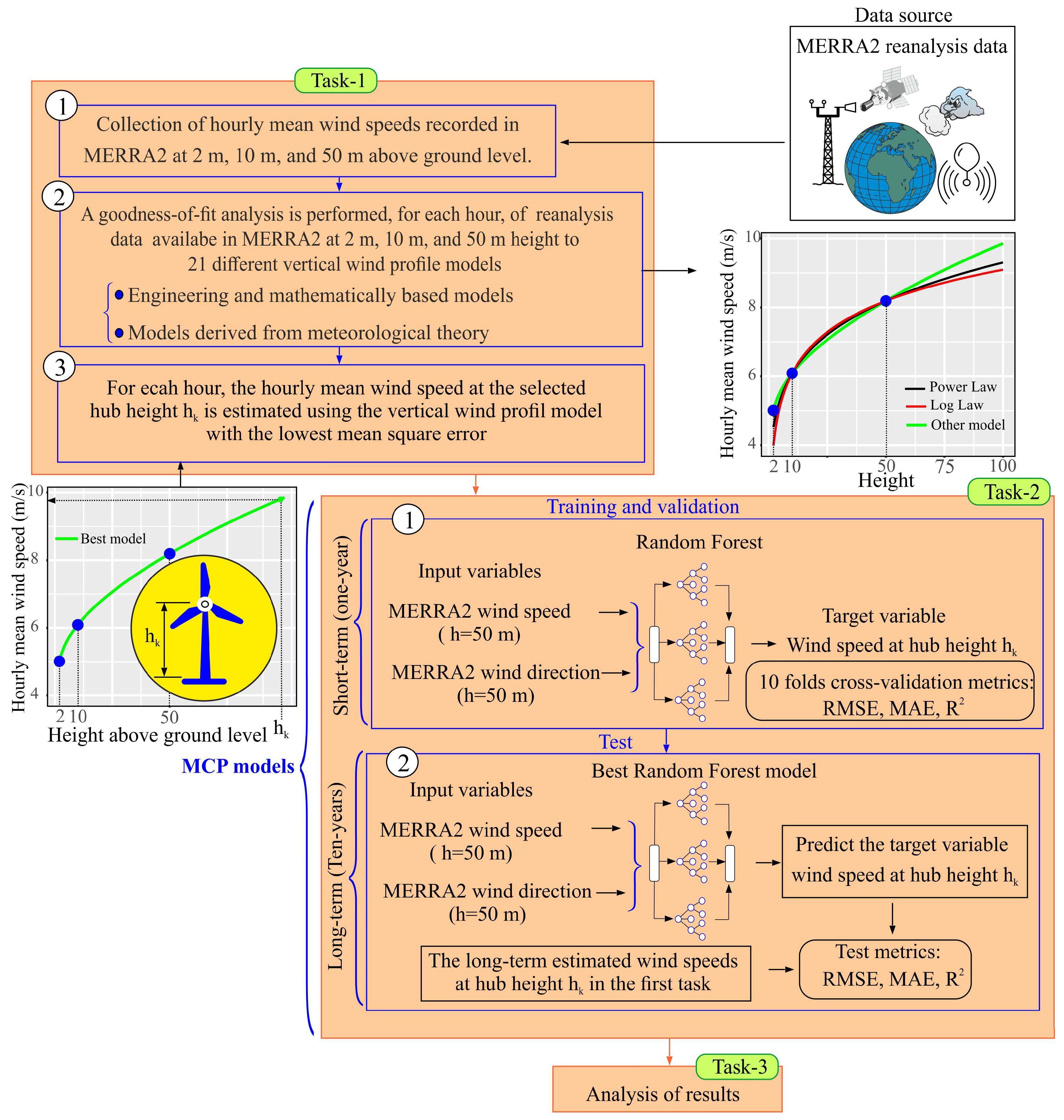
2. Method
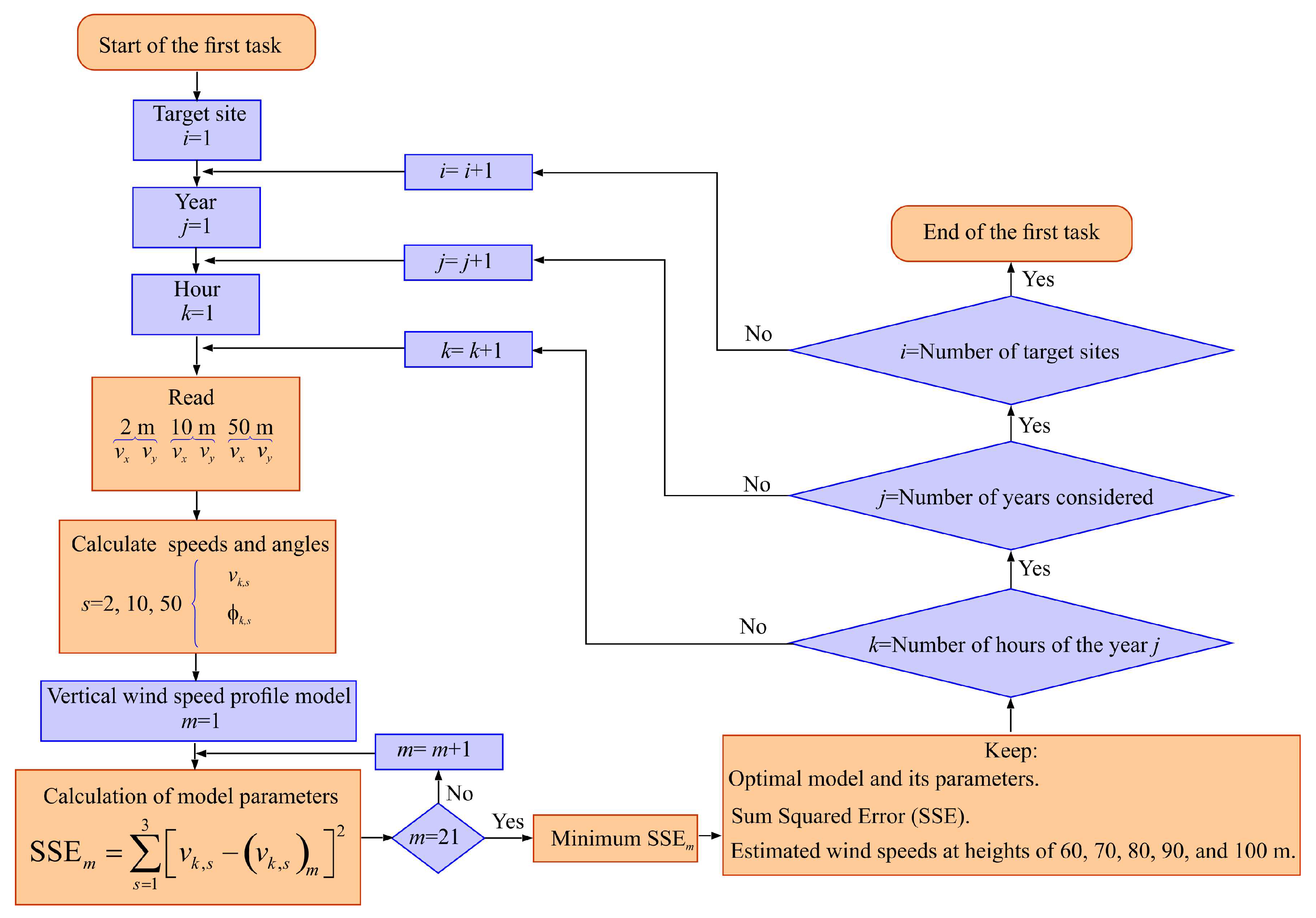
2.1. Task-1: Analysis of the Vertical Wind Speed Models
| Empirical Nonlinear Two-Parameter (a and b) Models | |||
|---|---|---|---|
| Number | Model | Number | Model |
| 1 | 8 | ||
| 2 | 9 | ||
| 3 | 10 | ||
| 4 | 11 | ||
| 5 | 12 | ||
| 6 | 13 | ||
| 7 | 14 | ||
| Logarithm models based on meteorological theory: Surface layer | |||
| Number | Model | Class boundaries | Class name |
| 15 | 200 < L£500 m | Stable | |
| 16 | 0£L < 200 m | Very stable | |
| 17 | > 500 m | Neutral | |
| 18 | −500£L < −200 m | Unstable | |
| 19 | −200£L < 0 m | Very unstable | |
| 20 | > 500 m | Neutral | |
| Number | The power law model, an engineering approximation | ||
| 21 | |||
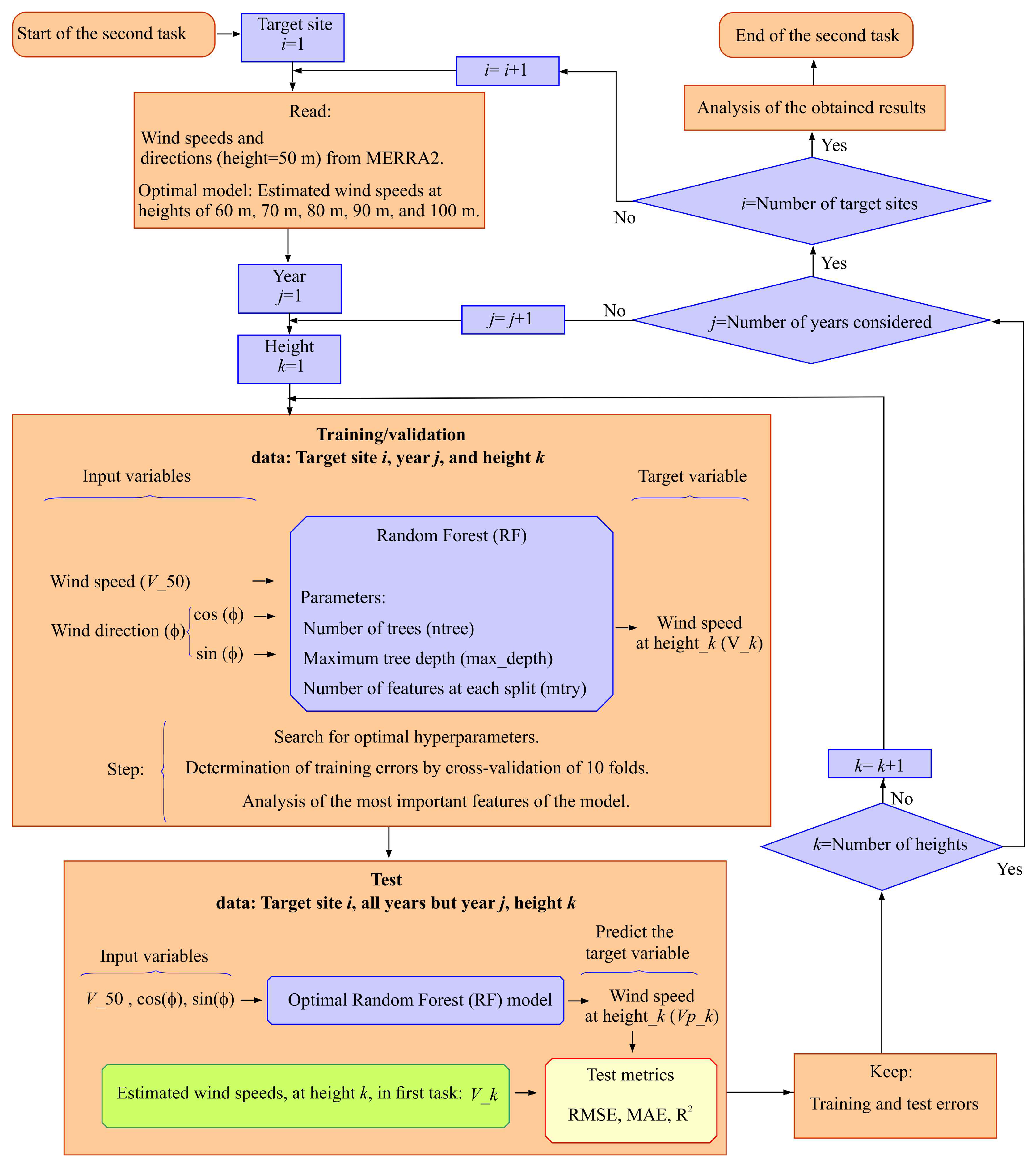
2.2. Second Task: Proposed Machine Learning (ML) Models
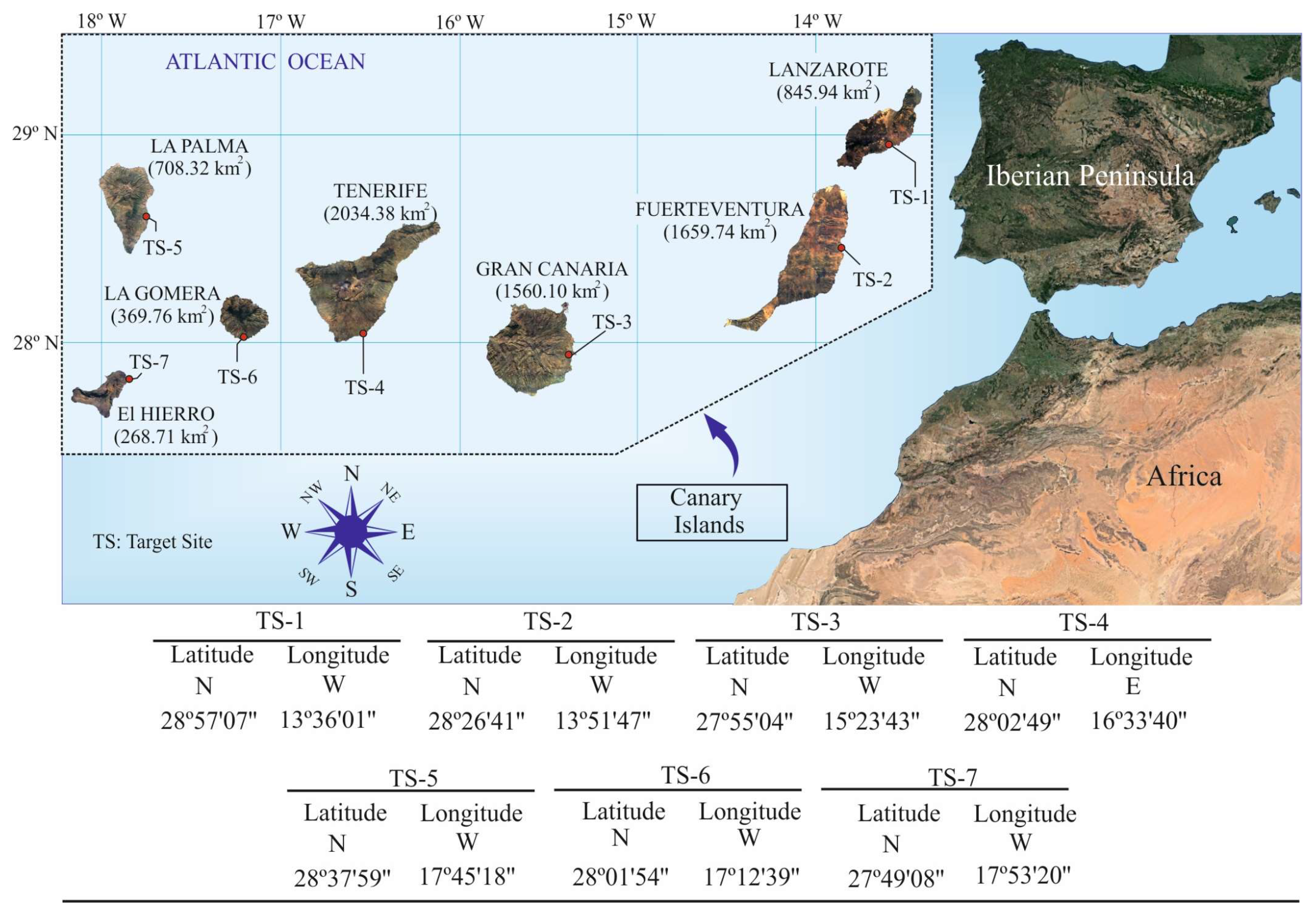
3. Case Study: Canary Islands
4. Results and Discussion
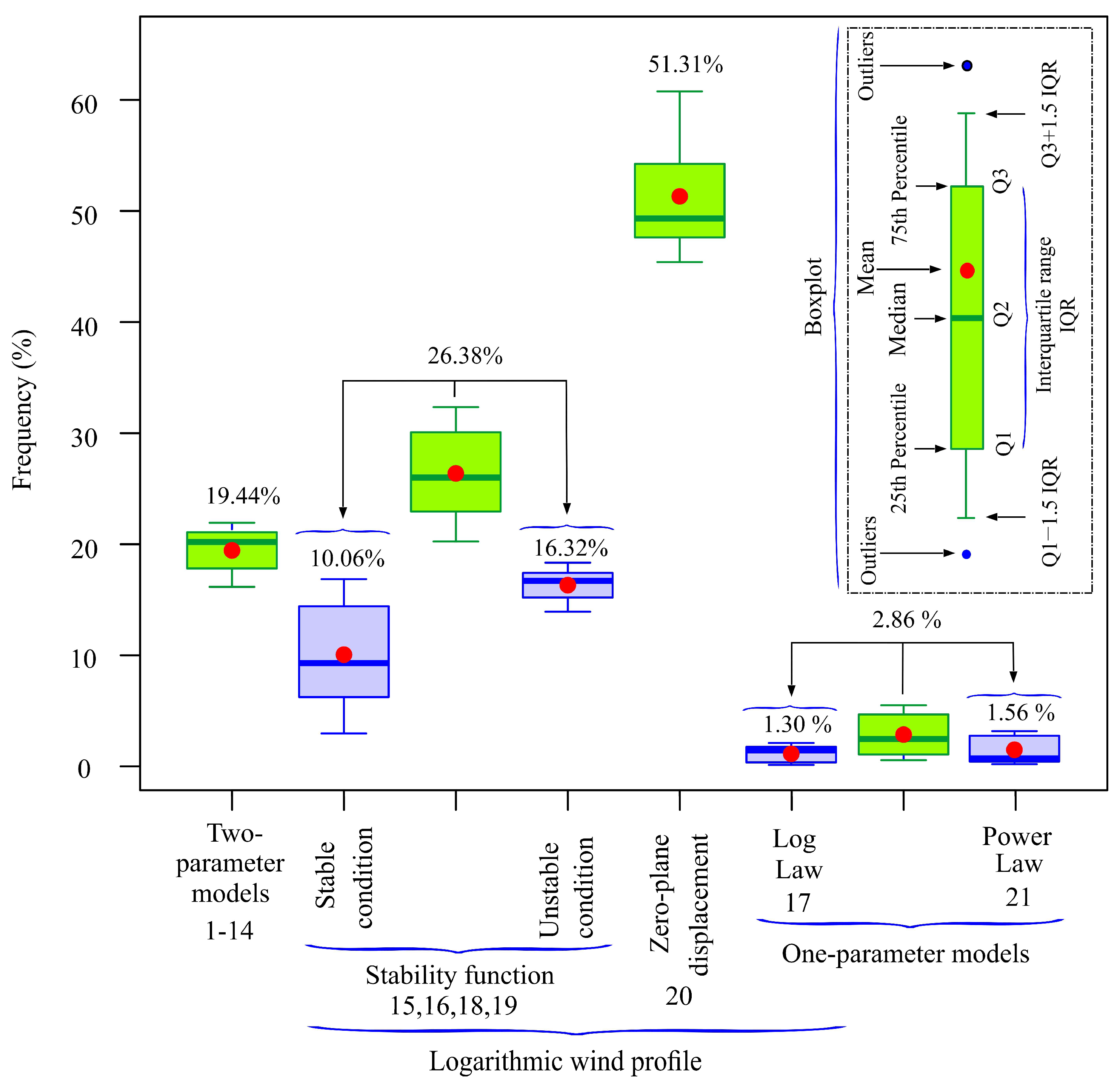
4.1. First Task: Analysis of the Vertical Wind Speed Models
4.2. Second Task: Performance of the Proposed Machine Learning Model
5. Conclusions
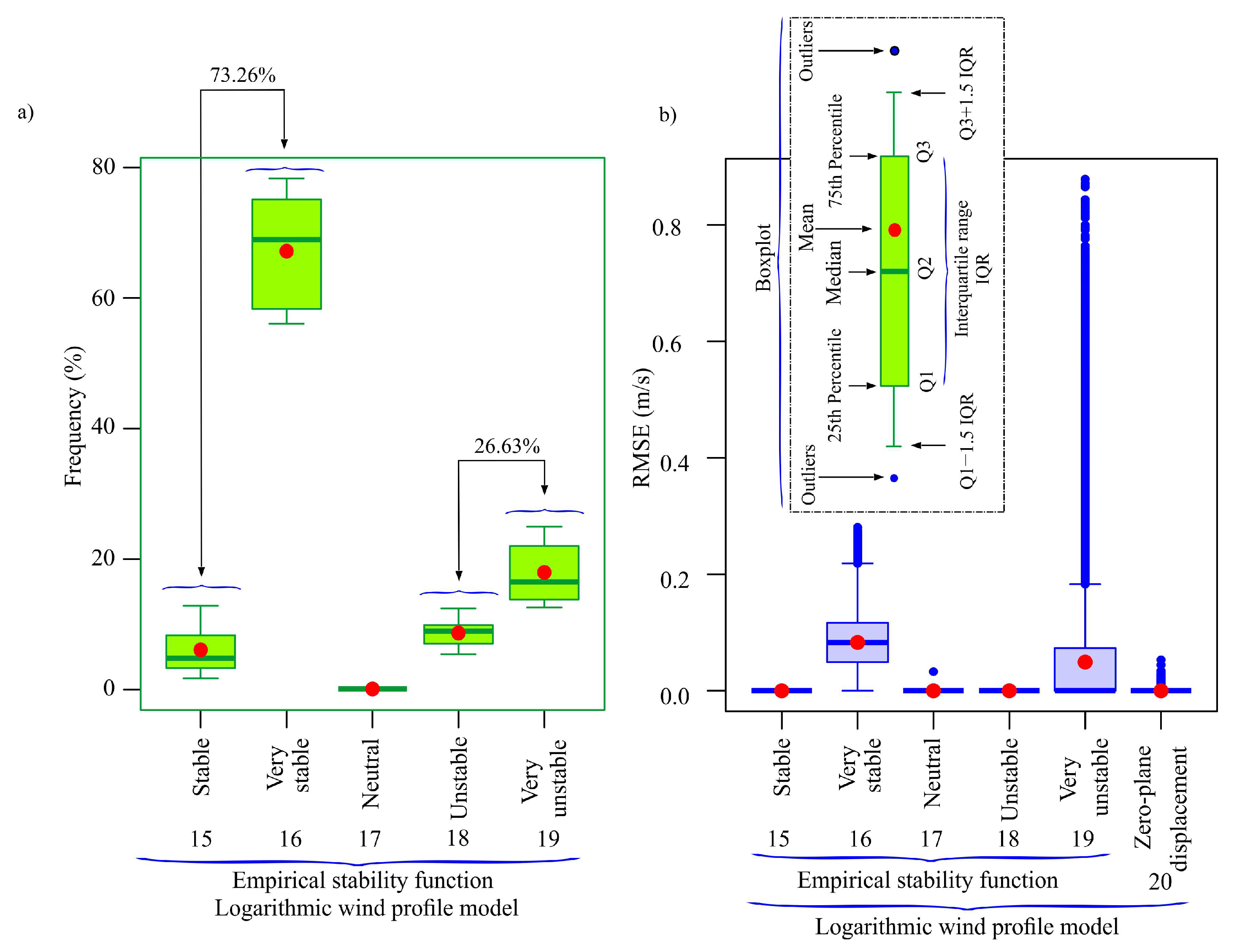
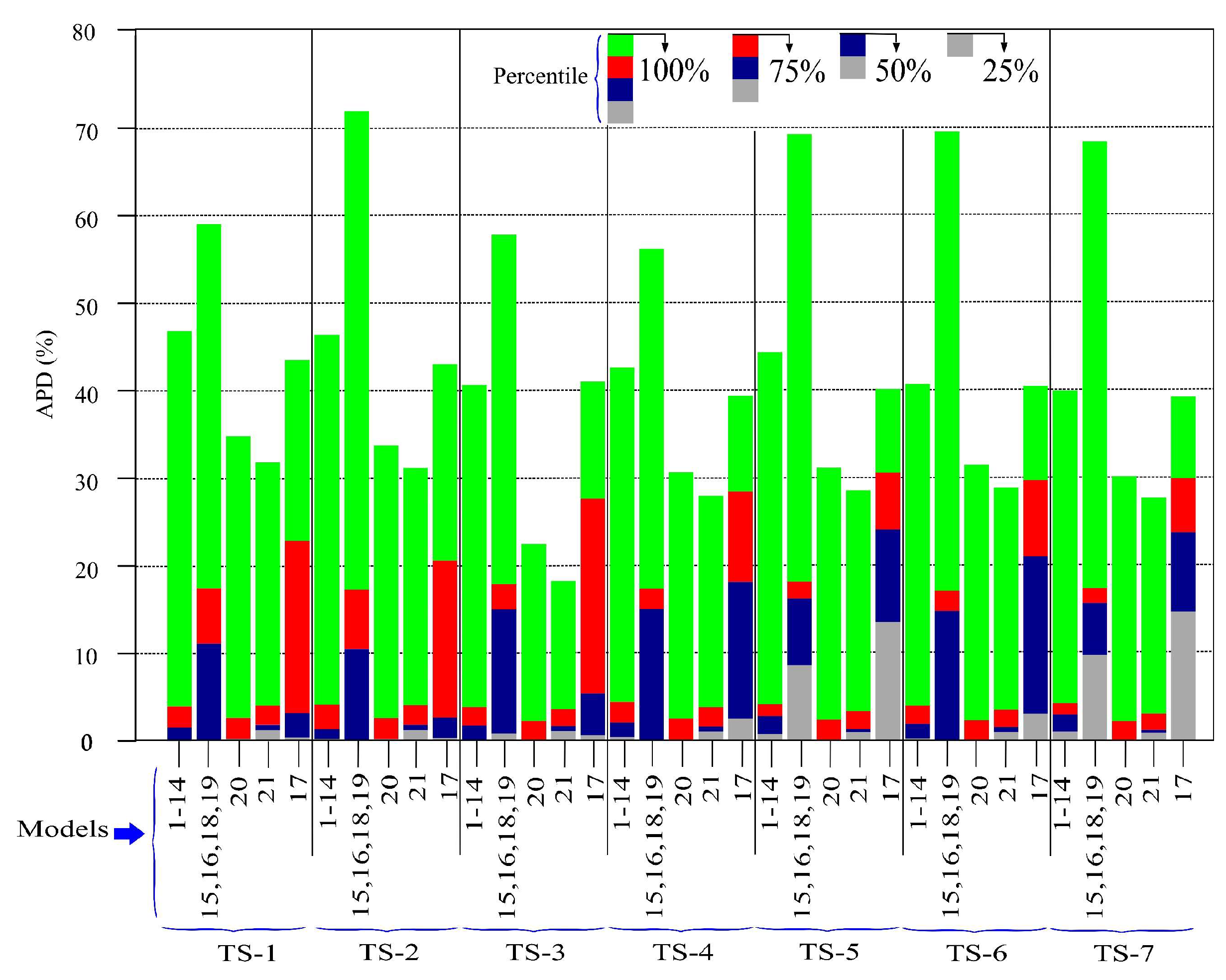
- The three-parameter logarithmic wind profile model, which incorporates zero-plane displacement and assumes a neutrally stratified atmosphere, demonstrated the best fit to the MERRA2 data, with the highest mean frequency (51.31%).
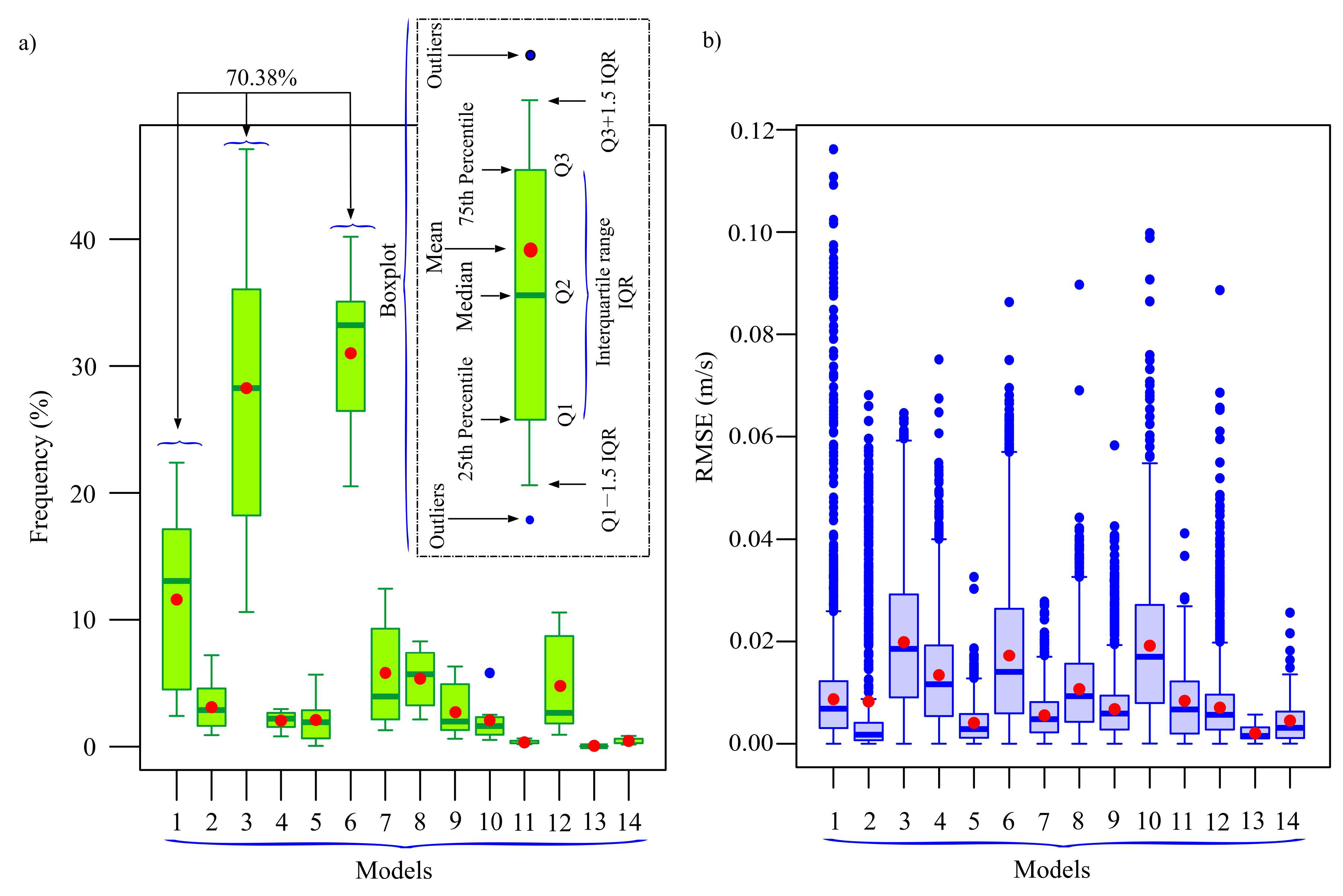
- The fourteen two-parameter vertical wind speed profile models proposed in this study provided the best fit to the MERRA2 data in 19.44% of cases.
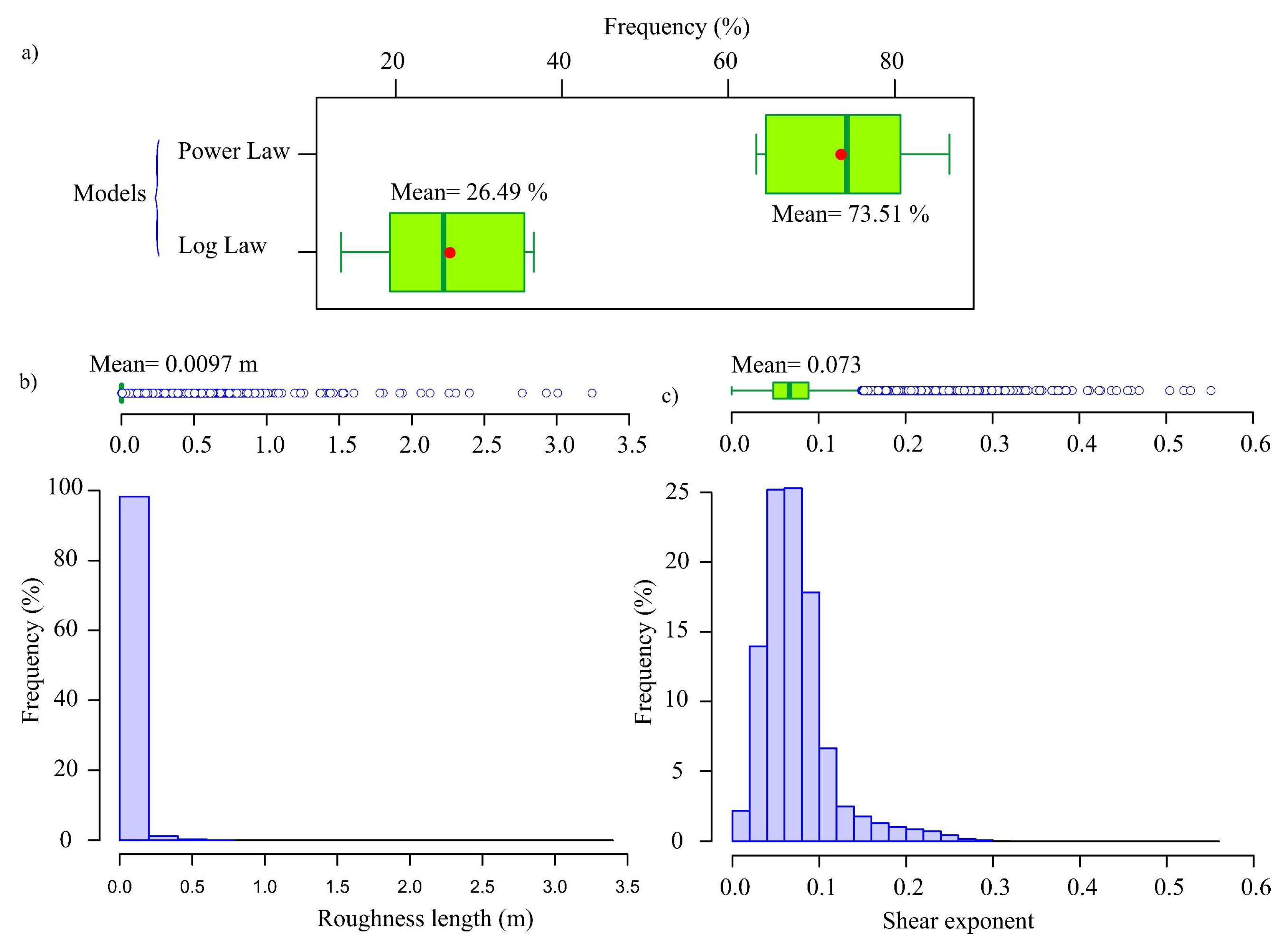
- The single-parameter vertical wind speed profile models (e.g., power law and log law), widely employed in the literature, showed very low best-fit frequencies in the case study. Additionally, non-representative outliers for the surface roughness length and shear exponent factor were identified when these parameters were estimated using MERRA2 wind speeds at 10 m and 50 m heights.
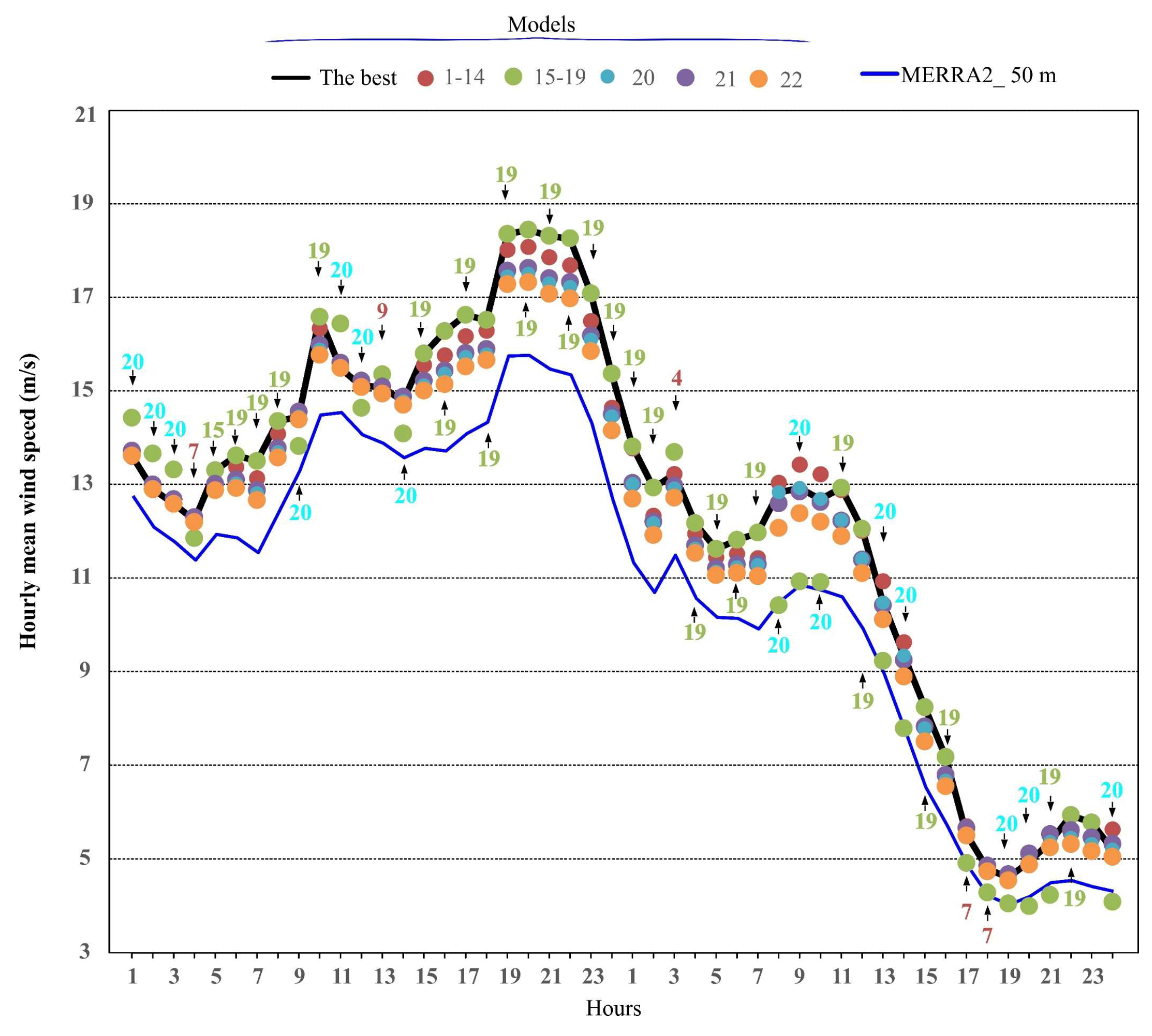
- To minimize significant errors in vertical wind speed estimations, and consequently in wind power density and wind turbine power output estimations, it is recommended to select, at each time step, the vertical wind speed profile model that best fits the available MERRA2 wind speed data at 2 m, 10 m, and 50 m heights.
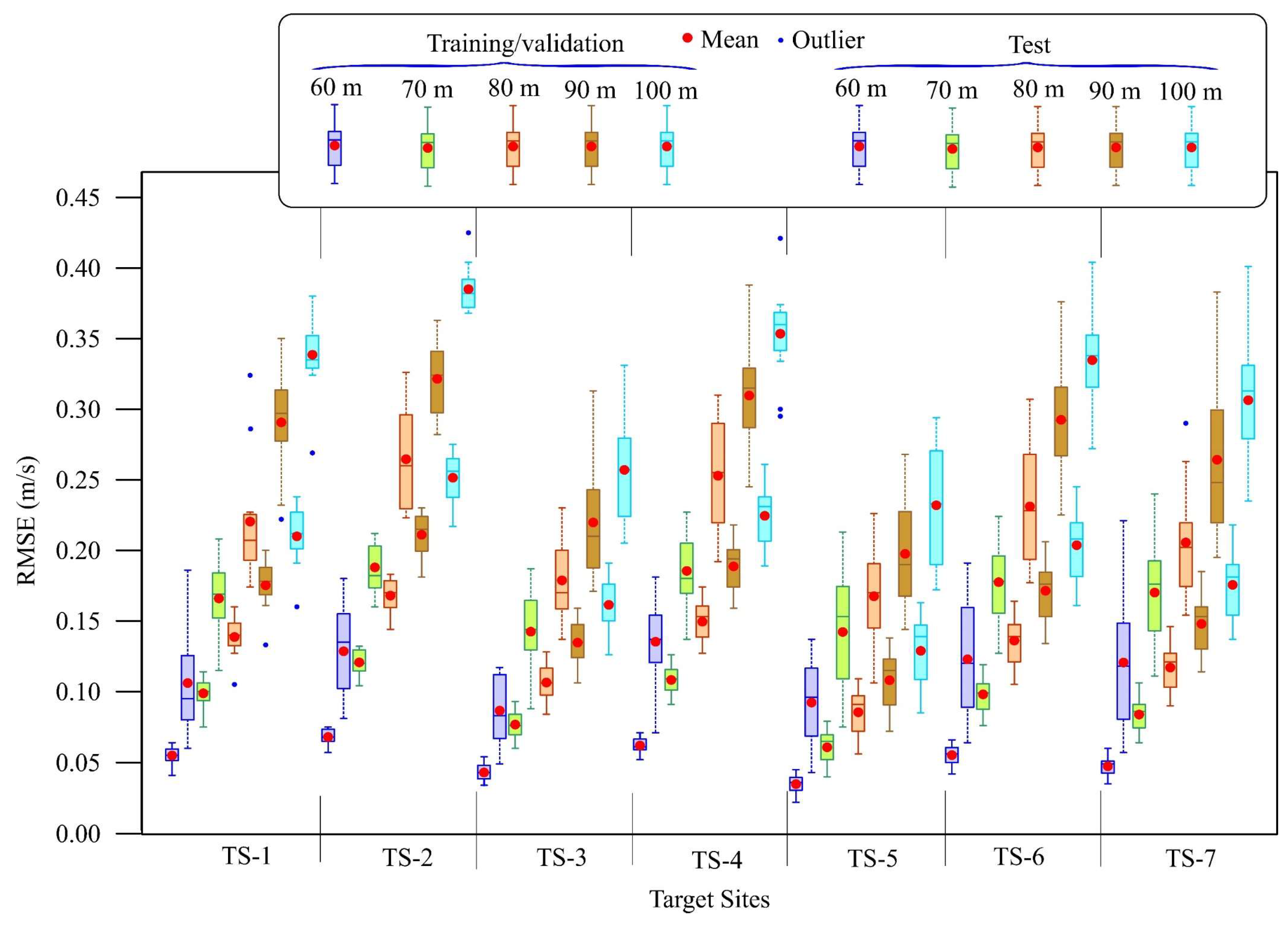
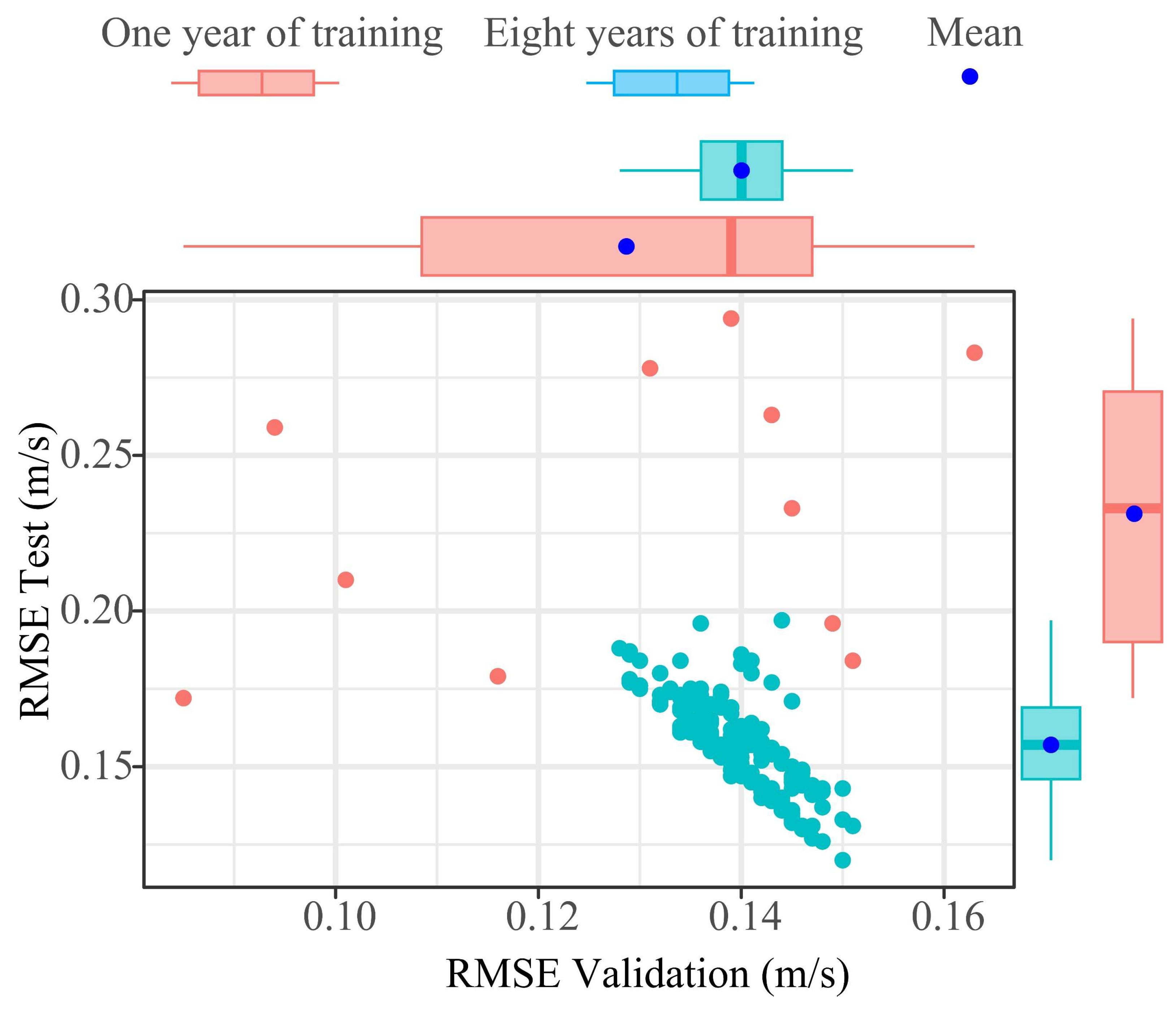
- In applying the RF-based MCP strategy, trained with short-term (one-year) supervised learning, the methodology achieved strong predictive performance. Tested with 10 years of data, RF-based predictions at 100 m hub height yielded a maximum RMSE (outliers) below 0.425 m/s.
- These results underscore the effectiveness of combining MCP techniques with ML in significantly improving the accuracy of wind speed estimations at wind turbine hub heights.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCP | Measure–Correlate–Predict |
| GMAO | NASA’s Global Modelling and Assimilation Office |
| RF | Random Forest |
| MERRA2 | Modern-Era Retrospective Analysis for Research and Applications, Version 2 |
| WT | Wind Turbine |
| WPD | Wind Power Density |
| TS | Target Site |
| ML | Machine Learning |
| MSE | Mean Square Error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| NLOPTR | R Interface to NLopt, a free/open-source library for nonlinear optimization |
| ISRES | Improved Stochastic Ranking Evolution Strategy |
| SSE | Sum of Squared Errors |
| STT | Short-Term Training |
| LTT | Long-Term Training—using multiple years of data for model training |
Appendix A
Appendix A.1. Location of Target Sites (TSs)
Appendix A.2. Results Obtained in the First Task with the 14 Empirical Nonlinear Two-Parameter Models
Appendix A.3. Results Obtained in the First Task with the Logarithmic Models That Include the Empirical Stability Function

Appendix A.4. Results Obtained in the First Task with the Power Law Model and the Log Law Model
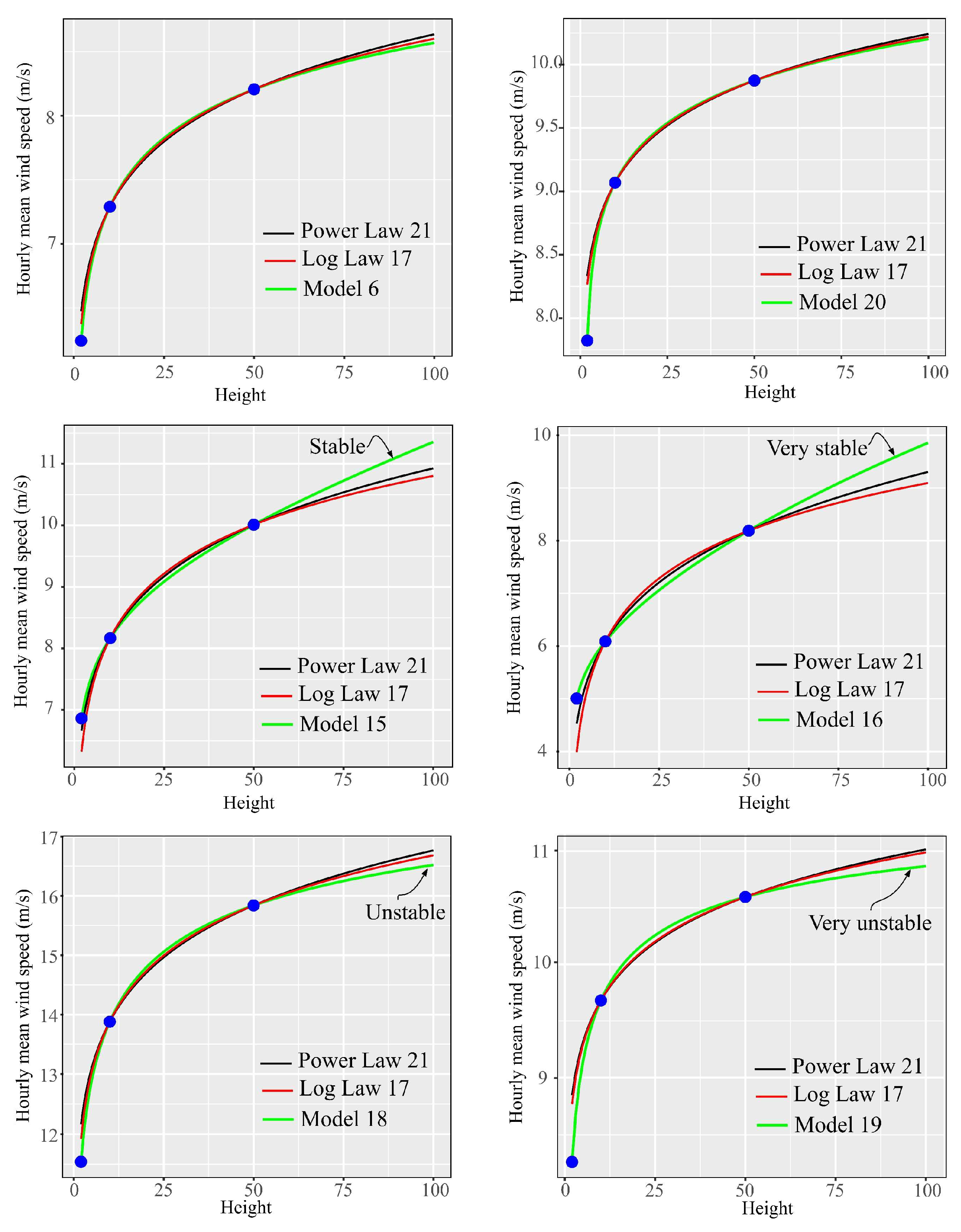
Appendix A.5. Comparative Analysis of the Models
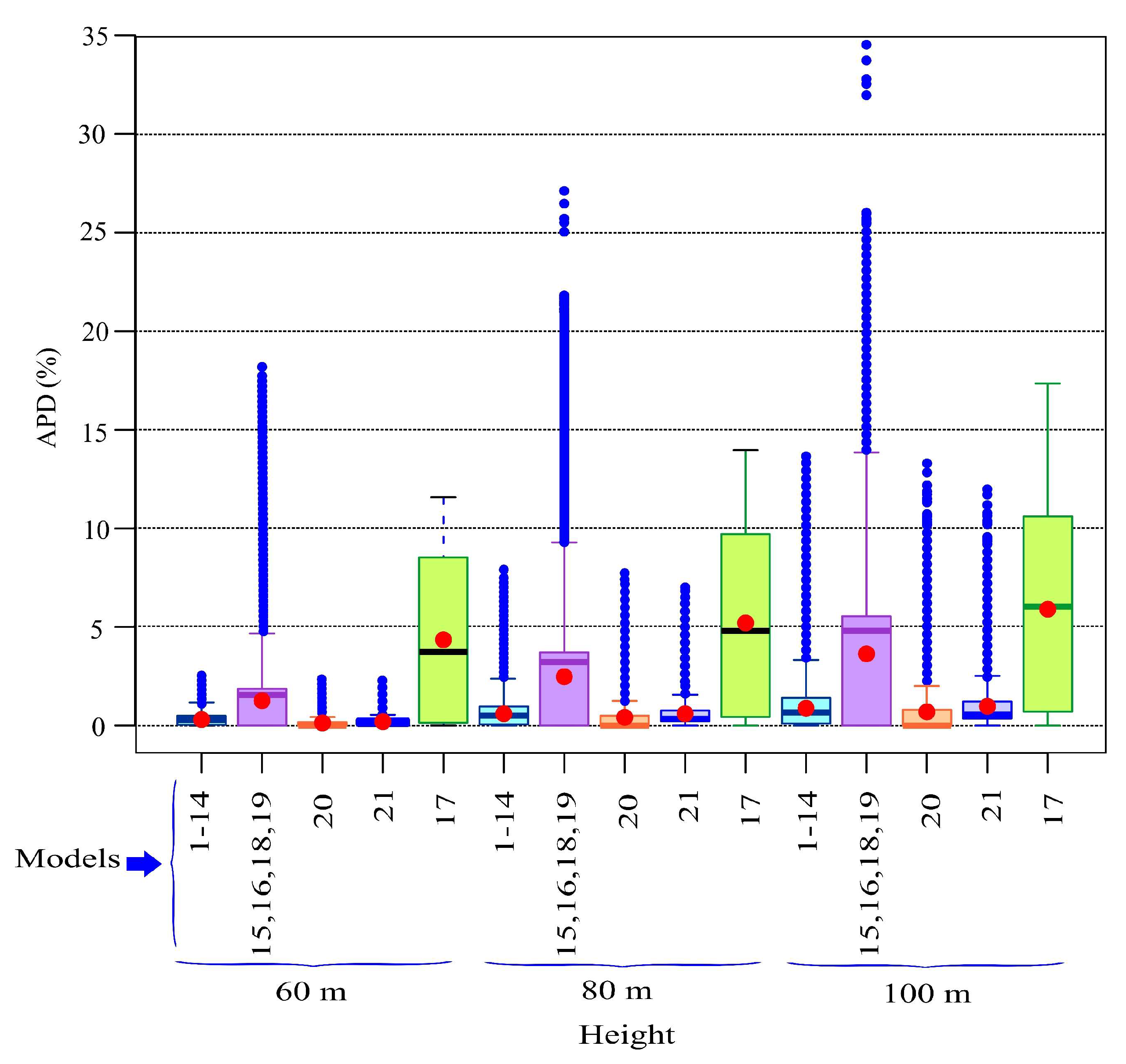
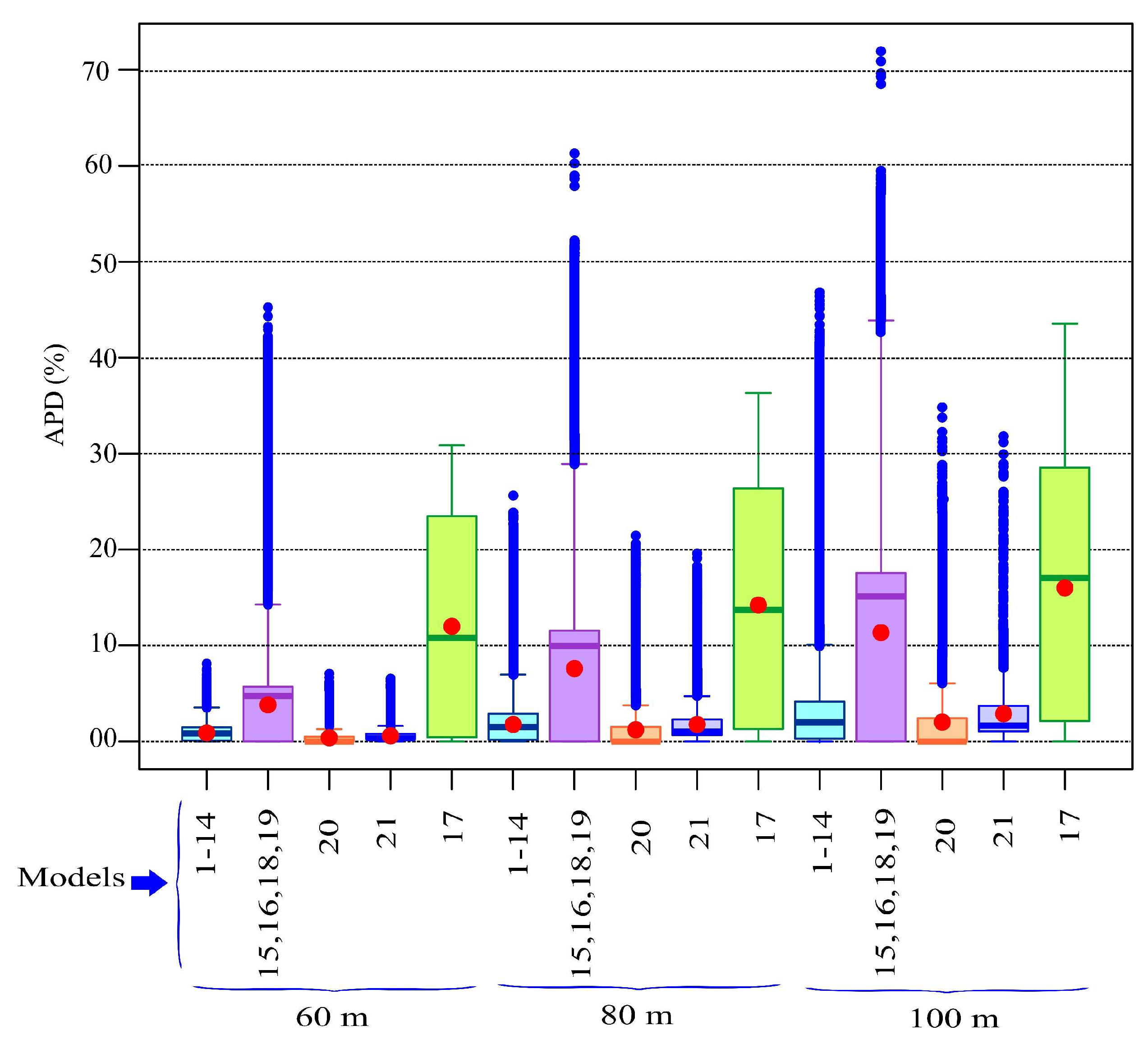
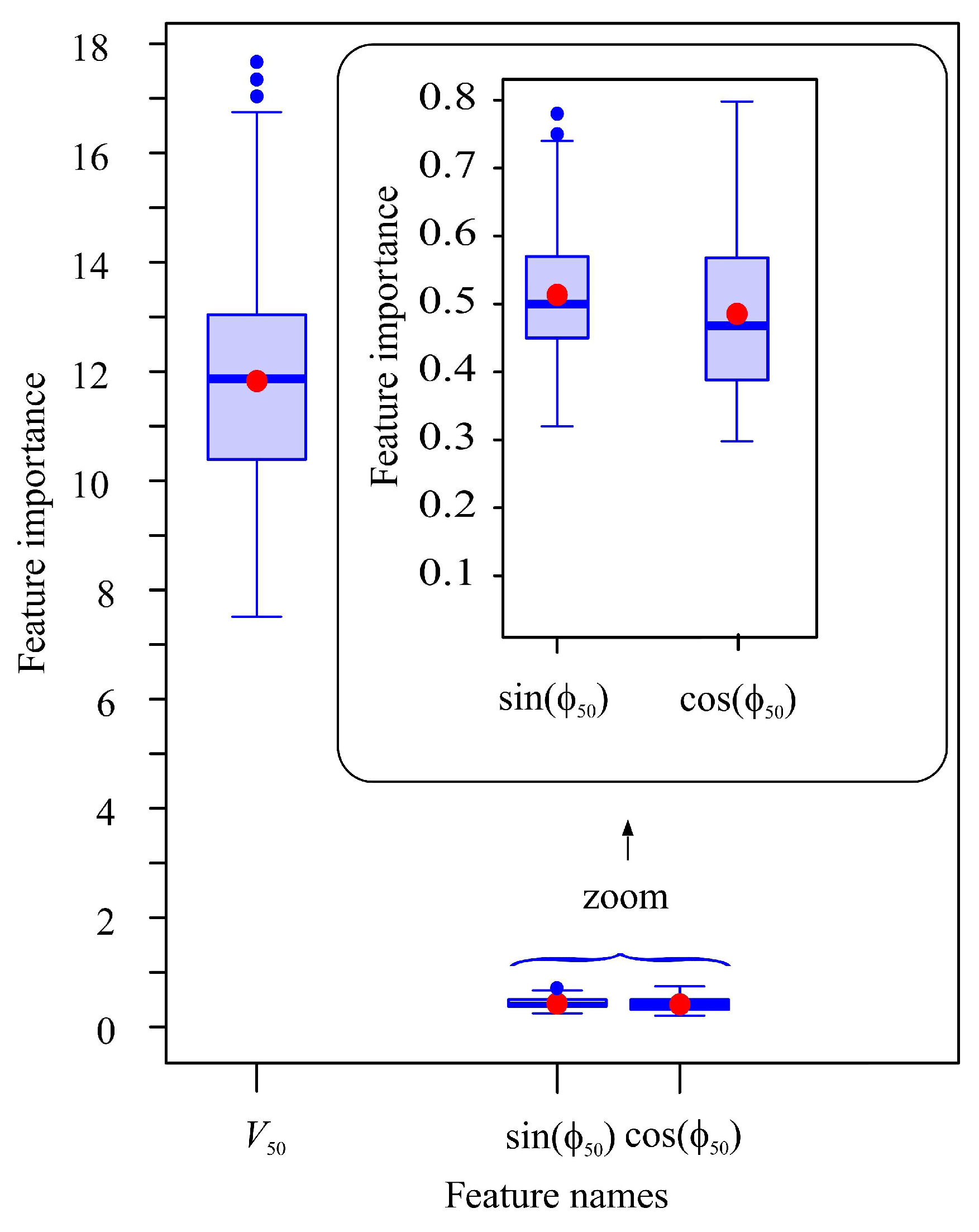
Appendix A.6. Permutation Importance of the Input Features of the RF Models
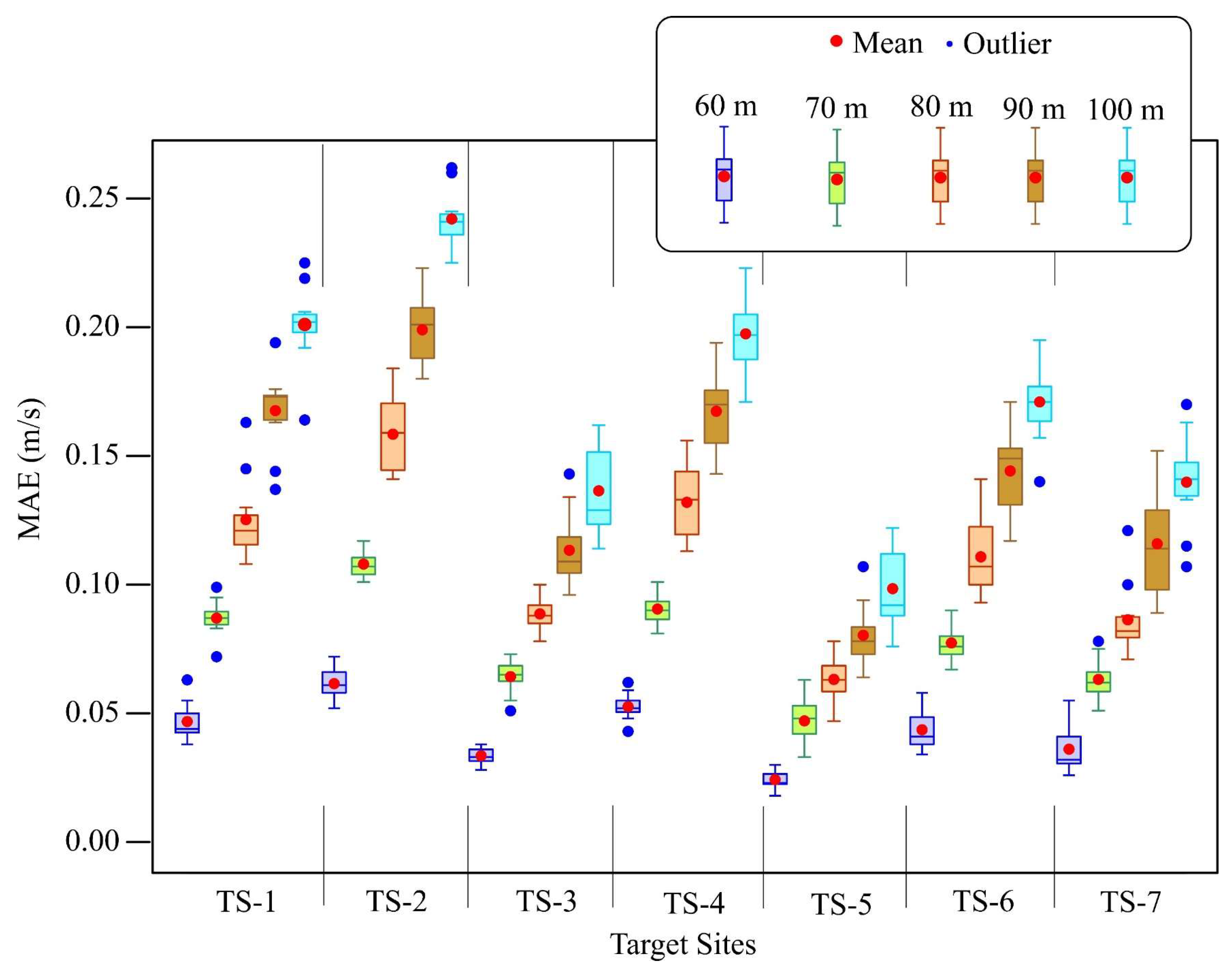
Appendix A.7. Boxplot of the MAEs Obtained in the Tests Undertaken
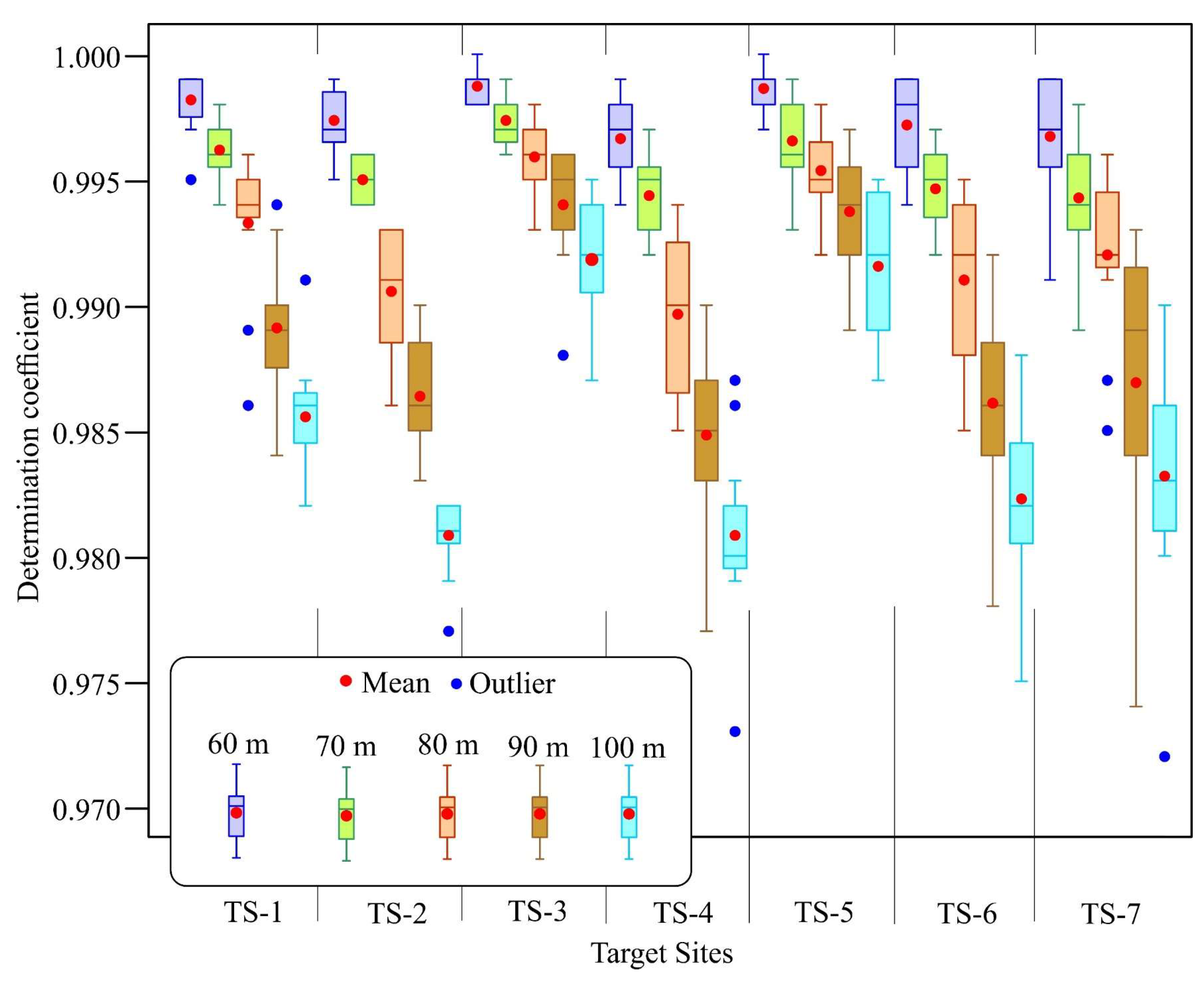
Appendix A.8. Boxplot of the R2 Metrics Obtained in the Tests Undertaken
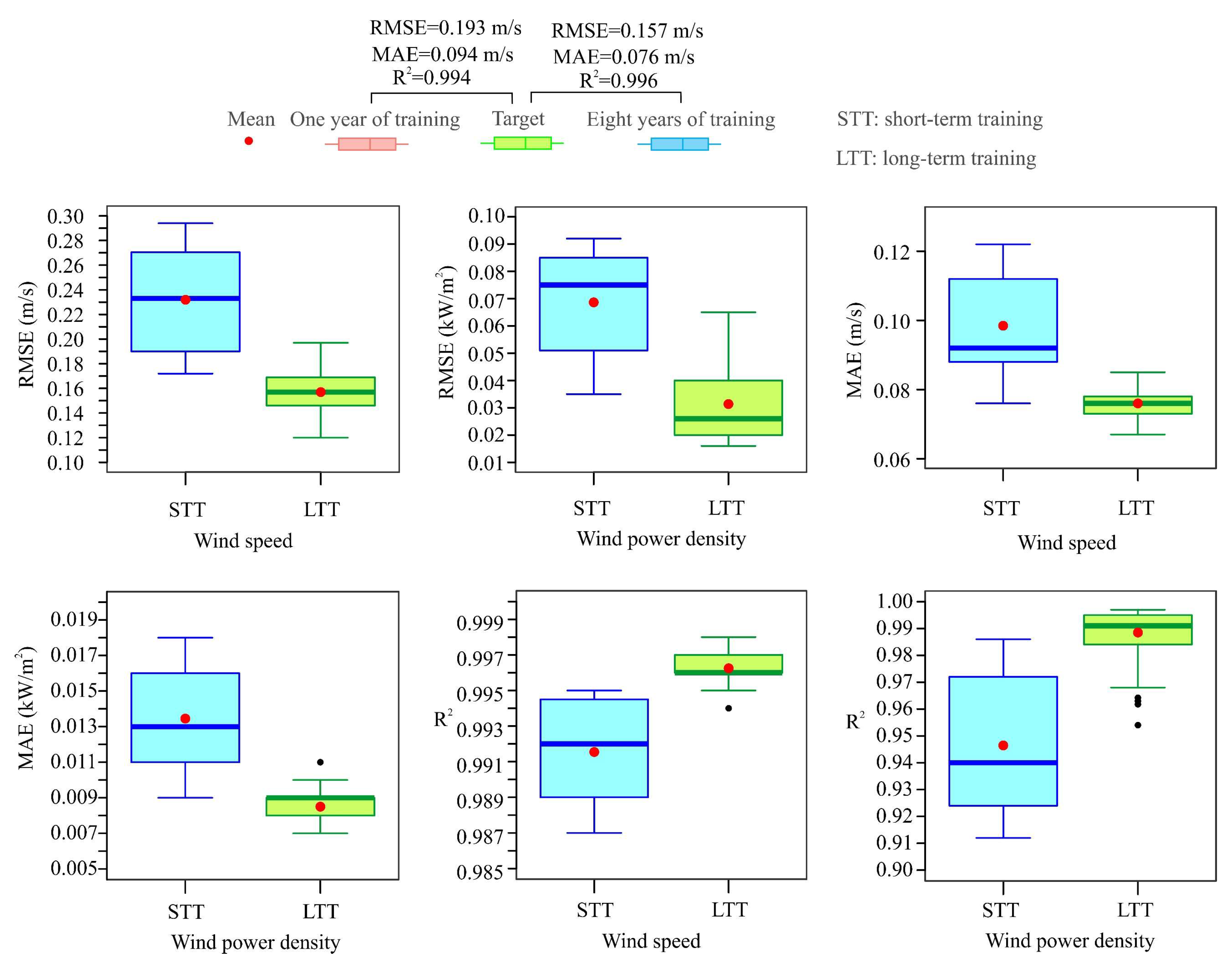
Appendix A.9. Boxplots of the Test Metrics of the RF Models Based on One Year and Eight Years of Training/Validation
References
- Cabrera, P.; Lund, H.; Carta, J.A. Smart renewable energy penetration strategies on islands: The case of Gran Canaria. Energy 2018, 162, 421–443. [Google Scholar] [CrossRef]
- Lund, H.; Thellufsen, J.Z.; Østergaard, P.A.; Sorknæs, P.; Skov, I.R.; Mathiesen, B.V. EnergyPLAN—Advanced analysis of smart energy systems. Smart Energy 2021, 1, 1000007. [Google Scholar] [CrossRef]
- Cabrera, P.; Lund, H.; Thellufsen, J.Z.; Sorknæs, P. The MATLAB Toolbox for EnergyPLAN: A tool to extend energy planning studies. Sci. Comput. Program. 2020, 191, 102405. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L. Uncertainty estimation for wind energy conversion by probabilistic wind turbine power curve modelling. Appl. Energy 2019, 239, 1356–1370. [Google Scholar] [CrossRef]
- Díaz, S.; Carta, J.A.; Matías, J.M. Comparison of several measure-correlate-predict models using support vector regression techniques to estimate wind power densities. A case study. Energy Convers. Manag. 2017, 140, 334–354. [Google Scholar] [CrossRef]
- Díaz, S.; Carta, J.A.; Matías, J.M. Performance assessment of five MCP models proposed for the estimation of long-term wind turbine power outputs at a target site using three machine learning techniques. Appl. Energy 2018, 209, 455–477. [Google Scholar] [CrossRef]
- Ahmad, M.; Zeeshan, M. Validation of weather reanalysis datasets and geospatial and techno-economic viability and potential assessment of concentrated solar power plants. Energy Convers. Manag. 2022, 256, 11536. [Google Scholar] [CrossRef]
- Liang, Y.; Wu, C.; Zhang, M.; Ji, X.; Shen, Y.; He, J.; Zhang, Z. Statistical modelling of the joint probability density function of air density and wind speed for wind resource assessment: A case study from China. Energy Convers. Manag. 2022, 268, 116054. [Google Scholar] [CrossRef]
- Yu, S.; Vautard, R. A transfer method to estimate hub-height wind speed from 10 meters wind speed based on machine learning. Renew. Sustain. Energy Rev. 2022, 169, 112897. [Google Scholar] [CrossRef]
- Crippa, P.; Alifa, M.; Bolster, D.; Genton, M.G.; Castruccio, S. A temporal model for vertical extrapolation of wind speed and wind energy assessment. Appl. Energy 2021, 301, 117378. [Google Scholar] [CrossRef]
- Mohandes, M.; Rehman, S.; Rahman, S. Estimation of wind speed profile using adaptive neuro-fuzzy inference system (ANFIS). Appl. Energy 2011, 88, 4024–4032. [Google Scholar] [CrossRef]
- Carta, J.A.; Velázquez, S.; Cabrera, P. A review of measure-correlate-predict (MCP) methods used to estimate long-term wind characteristics at a target site. Renew. Sustain. Energy Rev. 2013, 27, 362–400. [Google Scholar] [CrossRef]
- de Aquino Ferreira, S.C.; Oliveira, F.L.C.; Maçaira, P.M. Validation of the representativeness of wind speed time series obtained from reanalysis data for Brazilian territory. Energy 2022, 258, 124746. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Pelser, T.; Weinand, J.M.; Kuckertz, P.; McKenna, R.; Linssen, J.; Stolten, D. Reviewing accuracy & reproducibility of large-scale wind resource assessments. Adv. Appl. Energy 2024, 13, 100158. [Google Scholar] [CrossRef]
- Brower, M.C.; Bailey, B.H.; Beaucage, P.; Bernadett, D.W.; Doane, J.; Eberhard, M.J.; Elsholz, K.V.; Filippelli, M.V.; Hale, E.; Markus, M.J.; et al. Wind Resource Assessment: A Practical Guide to Developing a Wind Project; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Landberg, L. Meteorology for Wind Energy: An Introduction; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–204. [Google Scholar] [CrossRef]
- Zhang, M.H. Wind Resource Assessment and Micro-Siting; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 1–293. [Google Scholar] [CrossRef]
- Watson, S. Handbook of Wind Resource Assessment; John Wiley & Sons: Hoboken, NJ, USA, 2023; pp. 1–297. [Google Scholar] [CrossRef]
- de Assis Tavares, L.F.; Shadman, M.; Assad, L.P.d.F.; Estefen, S.F. Influence of the WRF model and atmospheric reanalysis on the offshore wind resource potential and cost estimation: A case study for Rio de Janeiro State. Energy 2022, 240, 122767. [Google Scholar] [CrossRef]
- Gualtieri, G. A comprehensive review on wind resource extrapolation models applied in wind energy. Renew. Sustain. Energy Rev. 2019, 102, 215–233. [Google Scholar] [CrossRef]
- Gruber, K.; Klöckl, C.; Regner, P.; Baumgartner, J.; Schmidt, J. Assessing the Global Wind Atlas and local measurements for bias correction of wind power generation simulated from MERRA-2 in Brazil. Energy 2019, 189, 116212. [Google Scholar] [CrossRef]
- Prasad, A.A.; Taylor, R.A.; Kay, M. Assessment of solar and wind resource synergy in Australia. Appl. Energy 2017, 190, 354–367. [Google Scholar] [CrossRef]
- Yip, C.M.A.; Gunturu, U.B.; Stenchikov, G.L. Wind resource characterization in the Arabian Peninsula. Appl. Energy 2016, 164, 826–836. [Google Scholar] [CrossRef]
- Gunturu, U.B.; Schlosser, C.A. Characterization of wind power resource in the United States. Atmos. Meas. Tech. 2012, 12, 9687–9702. [Google Scholar] [CrossRef]
- Ritter, M.; Deckert, L. Site assessment, turbine selection, and local feed-in tariffs through the wind energy index. Appl. Energy 2017, 185, 1087–1099. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Spatial and temporal assessments of complementarity for renewable energy resources in China. Energy 2019, 177, 262–275. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Characterization of wind resource in China from a new perspective. Energy 2019, 167, 994–1010. [Google Scholar] [CrossRef]
- Gao, Y.; Ma, S.; Wang, T.; Wang, T.; Gong, Y.; Peng, F.; Tsunekawa, A. Assessing the wind energy potential of China in considering its variability/intermittency. Energy Convers. Manag. 2020, 226, 113580. [Google Scholar] [CrossRef]
- Logarithmic Profile for Wind Profile Program. (n.d.). Available online: http://www.met.reading.ac.uk/~marc/it/wind/interp/log_prof/ (accessed on 10 February 2023).
- Valsaraj, P.; Thumba, D.A.; Asokan, K.; Kumar, K.S. Symbolic regression-based improved method for wind speed extrapolation from lower to higher altitudes for wind energy applications. Appl. Energy 2020, 260, 114270. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Rehman, S. Wind Speed Extrapolation Using Machine Learning Methods and LiDAR Measurements. IEEE Access 2018, 6, 77634–77642. [Google Scholar] [CrossRef]
- Nuha, H.; Mohandes, M.; Rehman, S.; A-Shaikhi, A. Vertical wind speed extrapolation using regularized extreme learning machine. FME Trans. 2022, 50, 412–421. [Google Scholar] [CrossRef]
- Islam, S.; Mohandes, M.; Rehman, S. Vertical extrapolation of wind speed using artificial neural network hybrid system. Neural Comput. Appl. 2016, 28, 2351–2361. [Google Scholar] [CrossRef]
- Al-Shaikhi, A.; Nuha, H.; Mohandes, M.; Rehman, S.; Adrian, M. Vertical wind speed extrapolation model using long short-term memory and particle swarm optimization. Energy Sci. Eng. 2022, 10, 4580–4594. [Google Scholar] [CrossRef]
- Al-Shaikhi, A.; Nuha, H.H.; Lawal, A.; Rehman, S.; Mohandes, M. Vertical Wind Profile Estimation Using Hybrid Convolutional Neural Networks and Bidirectional Long Short-Term Memory. Arab. J. Sci. Eng. 2023, 48, 6915–6924. [Google Scholar] [CrossRef]
- Rehman, S.; Nuha, H.H.; Al Shaikhi, A.; Akbar, S.; Mohandes, M. Improving Performance of Recurrent Neural Networks Using Simulated Annealing for Vertical Wind Speed Estimation. Energy Eng. 2023, 120, 775–789. [Google Scholar] [CrossRef]
- R Interface to NLopt, version 2.0.3; R package nloptr; The R Foundation: Vienna, Austria, 2022.
- Holtslag, M.C.; Bierbooms, W.A.A.M.; van Bussel, G.J.W. Estimating atmospheric stability from observations and correcting wind shear models accordingly. J. Phys. Conf. Ser. 2014, 012052. [Google Scholar] [CrossRef]
- Mpholo, M.; Mathaba, T.; Letuma, M. Wind profile assessment at Masitise and Sani in Lesotho for potential off-grid electricity generation. Energy Convers. Manag. 2012, 53, 118–127. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound. Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Beljaars, A.C.M.; Holtslag, A.A.M. American Meteorological Society Flux Parameterization over Land Surfaces for Atmospheric Models. J. Appl. Meteorol. Climatol. 1988, 30, 327–341. [Google Scholar] [CrossRef]
- Paulson, C.A. The Mathematical Representation of Wind Speed and Temperature Profiles in the Unstable Atmospheric Surface Layer. J. Appl. Meteorol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Grachev, A.A.; Fairall, C.W.; Bradley, E.F. Convective Profile Constants Revisited. Bound. Layer Meteorol. 2000, 94, 495–515. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Carta, J.A.; Cabrera, P. Optimal sizing of stand-alone wind-powered seawater reverse osmosis plants without use of massive energy storage. Appl. Energy 2021, 304, 117888. [Google Scholar] [CrossRef]
- Optis, M.; Bodini, N.; Debnath, M.; Doubrawa, P. New methods to improve the vertical extrapolation of near-surface offshore wind speeds. Wind. Energy Sci. 2021, 6, 935–948. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation. Green Energy Technol. 2013, 99, 189–192. [Google Scholar] [CrossRef]
- Carta, J.A.; Cabrera, P.; Matías, J.M.; Castellano, F. Comparison of feature selection methods using ANNs in MCP-wind speed methods. A case study. Appl. Energy 2015, 158, 490–507. [Google Scholar] [CrossRef]
- randomForest: Breiman and Cutler’s Random Forests for Classification and Regression Version 4.6-10 from R-Forge. Available online: https://rdrr.io/rforge/randomForest/ (accessed on 20 February 2023).
- R: The R Project for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 20 February 2023).
- Package “Tune” Title Tidy Tuning Tools, version 1.0.1; The R Foundation: Vienna, Austria, 2022.
- V-Fold Cross-Validation—Vfold_cv—rsample. Available online: https://rsample.tidymodels.org/reference/vfold_cv.html (accessed on 20 February 2023).
- Hatfield, D.; Hasager, C.B.; Karagali, I. Vertical extrapolation of ASCAT ocean surface winds using machine learning techniques. Wind Energy Sci. Discuss. 2022, 8, 1–26. [Google Scholar]
- Carta, J.; Ramírez, P.; Velázquez, S. A review of wind speed probability distributions used in wind energy analysis. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Chavan, D.S.; Gaikwad, S.; Singh, A.; Himanshu; Parashar, D.; Saahil, V.; Sankpal, J.; Karandikar, P.B. Impact of vertical wind shear on wind turbine performance. In Proceedings of the IEEE International Conference on Circuit, Power and Computing Technologies (ICCPCT 2017), Kollam, India, 20–21 April 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Taylor, M.; Mackiewicz, P.; Brower, M.C.; Markus, M. An analysis of wind resource uncertainty in energy production estimates. In Proceedings of the European Wind Energy Conference & Exhibition, London, UK, 22–25 November 2004; pp. 951–952. [Google Scholar]
- Miguel, J.V.P.; Fadigas, E.A.; Sauer, I.L. The Influence of the Wind Measurement Campaign Duration on a Measure-Correlate-Predict (MCP)-Based Wind Resource Assessment. Energies 2019, 12, 3606. [Google Scholar] [CrossRef]
- ENERCON Product Porfolio. Available online: https://portal.ct.gov/-/media/csc/1_dockets-medialibrary/petition_983/dm_plan/2020_0109_dandm_modification/exhibitaenerconturbinesbrochuree138ep3pdf.pdf?rev=b0d2297308b3476fab665df83d8d952c&hash=B1EBFE98A964A8BA9D5A98BB6258828A (accessed on 27 May 2025).
- Tümse, S.; İlhan, A.; Bilgili, M.; Şahin, B. Estimation of wind turbine output power using soft computing models. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 3757–3786. [Google Scholar] [CrossRef]
- Prasad, K.M.; Nagababu, G.; Jani, H.K. Enhancing offshore wind resource assessment with LIDAR-validated reanalysis datasets: A case study in Gujarat, India. Int. J. Thermofluids 2023, 18, 100320. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carta, J.A.; Moreno, D.; Cabrera, P. A Measure–Correlate–Predict Approach for Transferring Wind Speeds from MERRA2 Reanalysis to Wind Turbine Hub Heights. J. Mar. Sci. Eng. 2025, 13, 1213. https://doi.org/10.3390/jmse13071213
Carta JA, Moreno D, Cabrera P. A Measure–Correlate–Predict Approach for Transferring Wind Speeds from MERRA2 Reanalysis to Wind Turbine Hub Heights. Journal of Marine Science and Engineering. 2025; 13(7):1213. https://doi.org/10.3390/jmse13071213
Chicago/Turabian StyleCarta, José A., Diana Moreno, and Pedro Cabrera. 2025. "A Measure–Correlate–Predict Approach for Transferring Wind Speeds from MERRA2 Reanalysis to Wind Turbine Hub Heights" Journal of Marine Science and Engineering 13, no. 7: 1213. https://doi.org/10.3390/jmse13071213
APA StyleCarta, J. A., Moreno, D., & Cabrera, P. (2025). A Measure–Correlate–Predict Approach for Transferring Wind Speeds from MERRA2 Reanalysis to Wind Turbine Hub Heights. Journal of Marine Science and Engineering, 13(7), 1213. https://doi.org/10.3390/jmse13071213






