Application of Large-Scale Rotating Platforms in the Study of Complex Oceanic Dynamic Processes
Abstract
1. Introduction
2. Large-Scale Rotating Platform Experiments for Complex Oceanic Dynamics
2.1. Mesoscale Eddies
2.2. Internal Waves
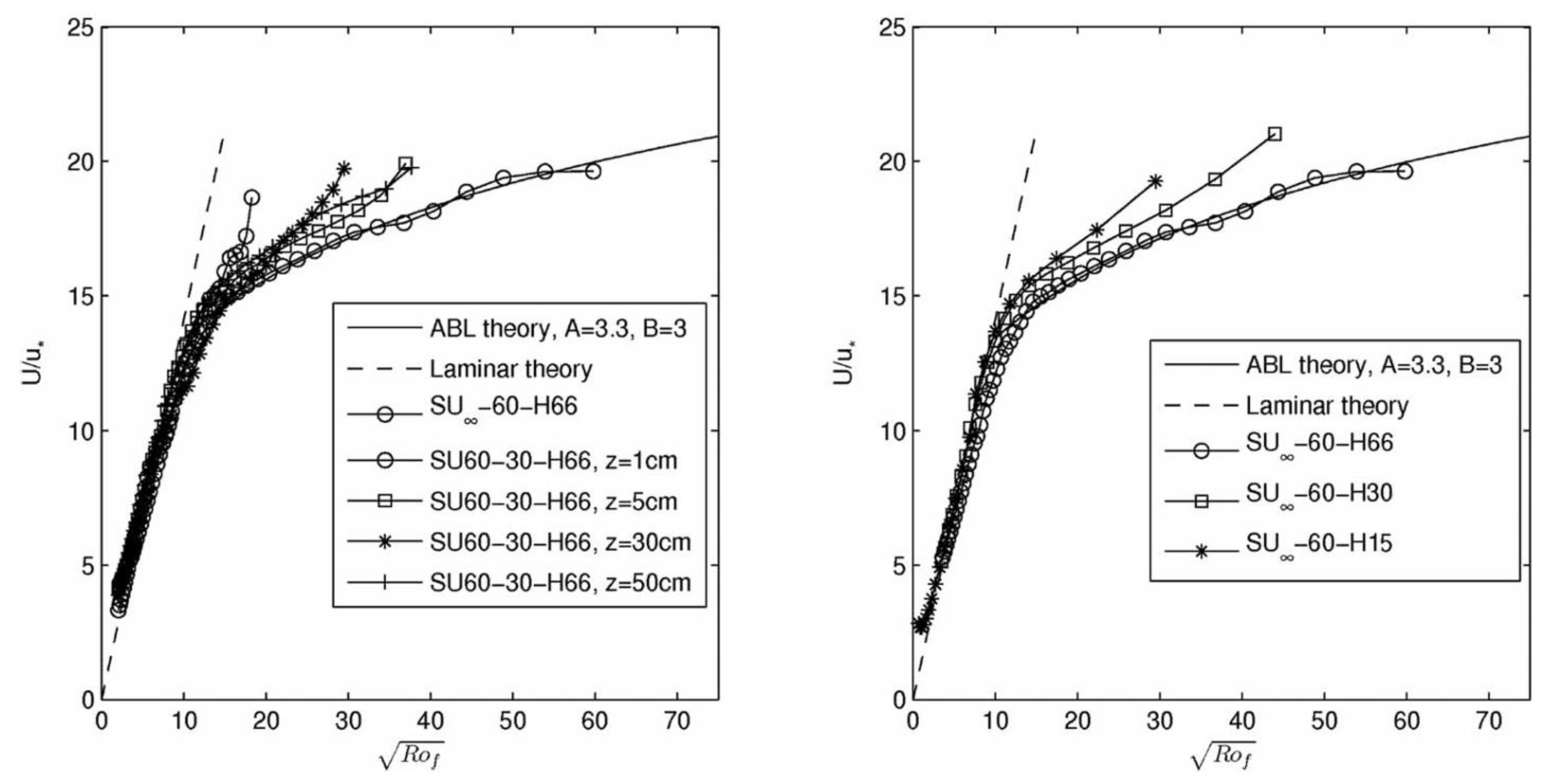
2.3. Ekman Currents
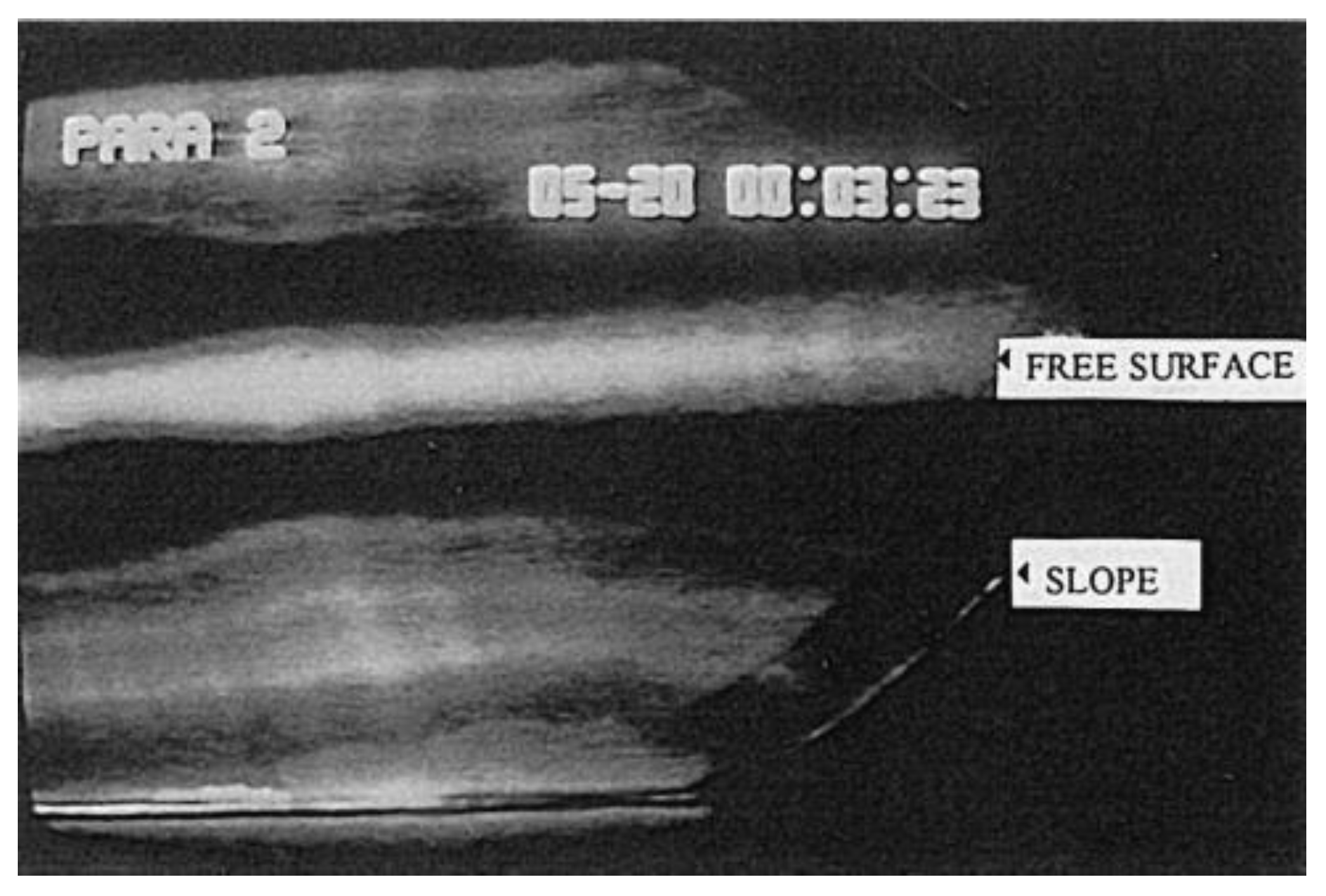
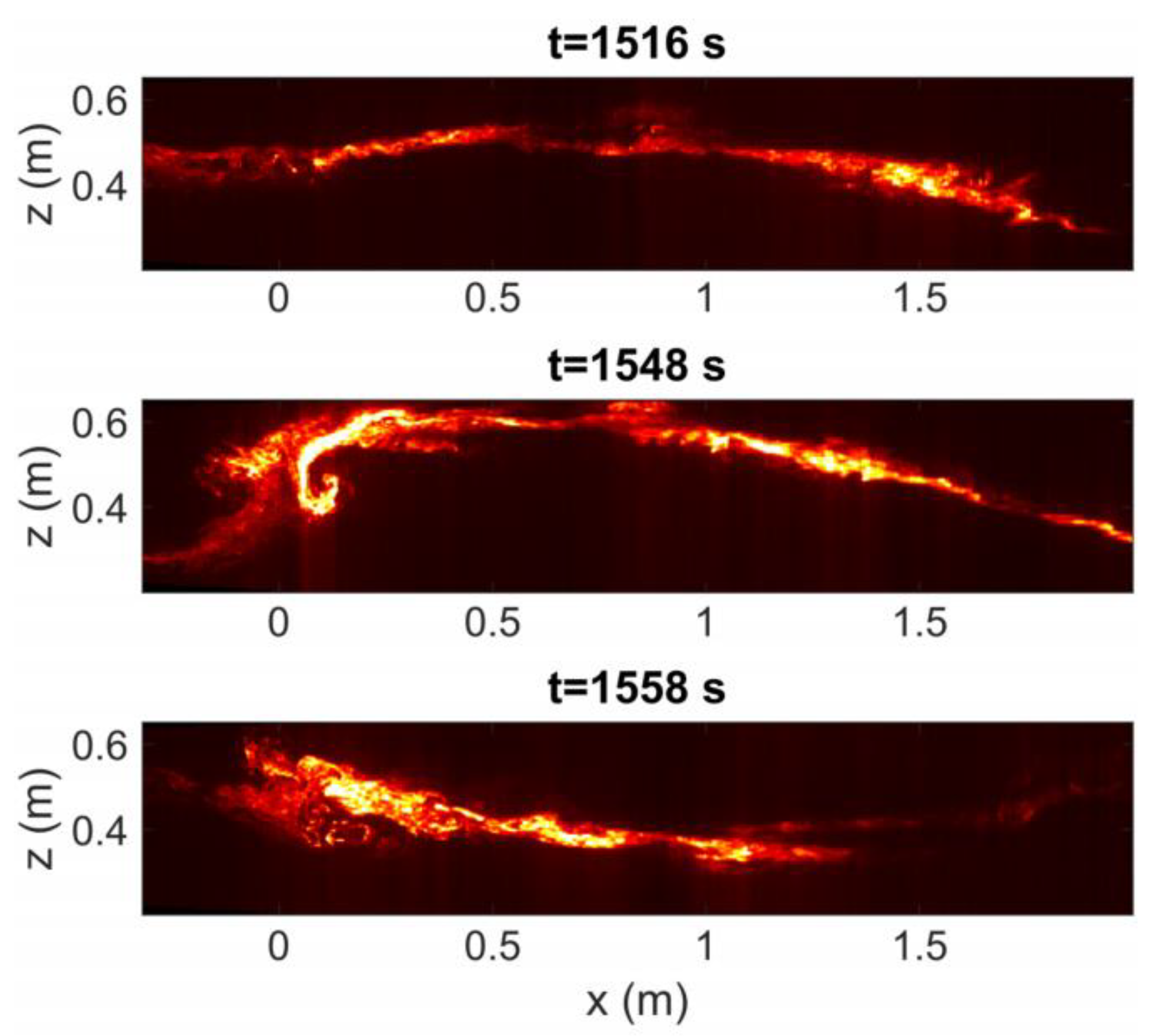
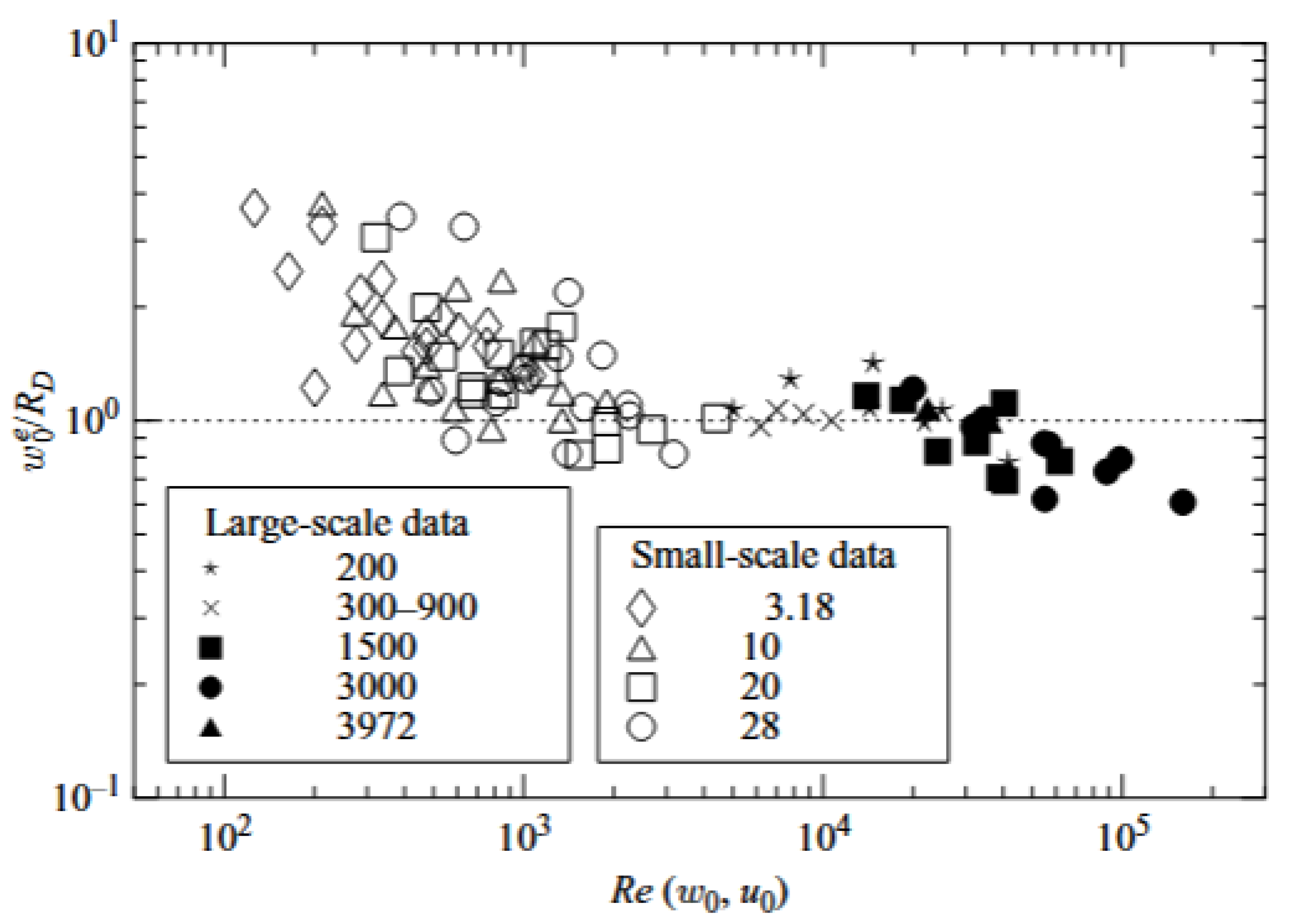
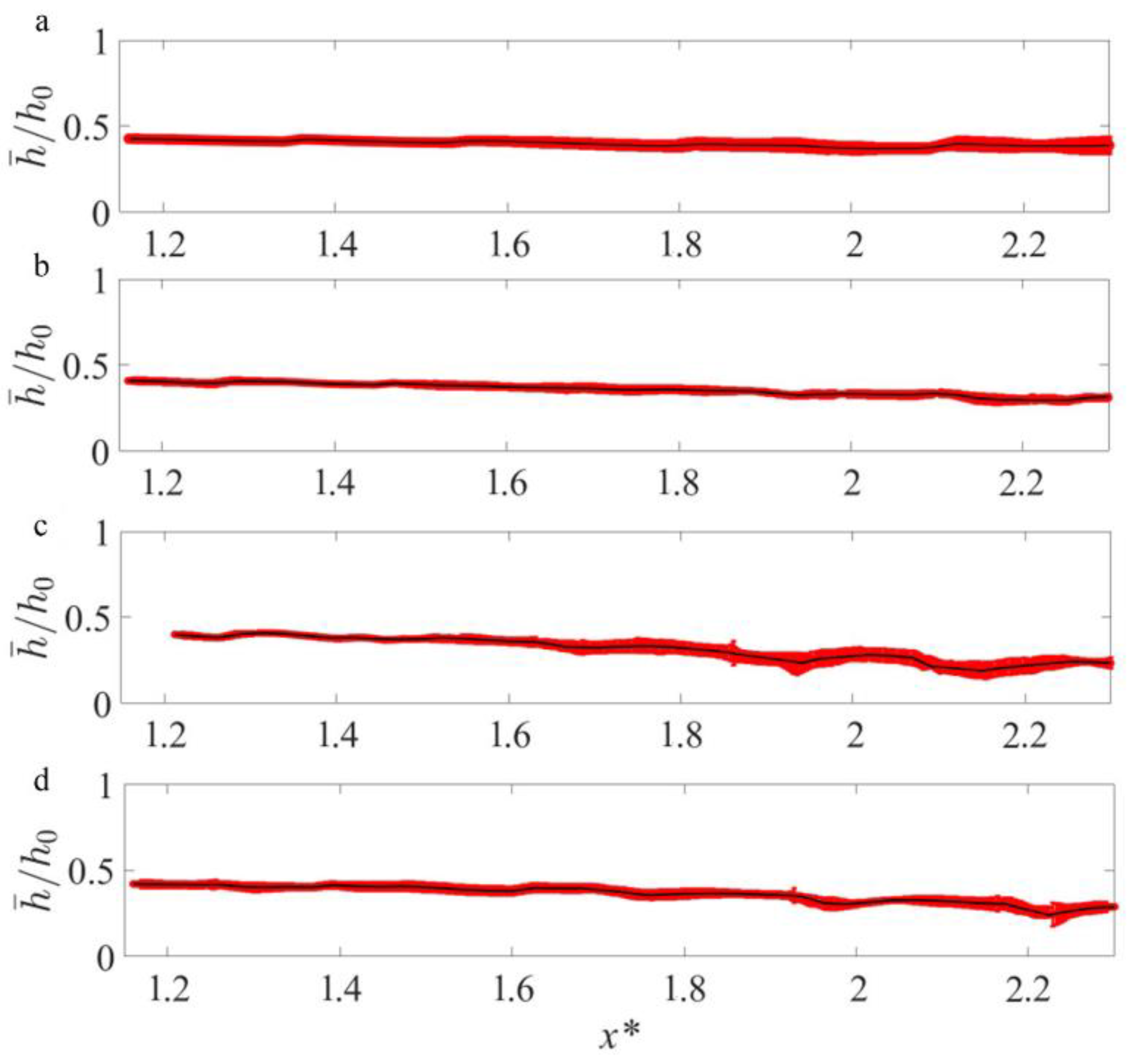
2.4. Gravity Currents
2.5. Rossby Waves

2.6. Bottom Boundary Currents
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cushman-Roisin, B.; Beckers, J.-M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects, 2nd ed.; International Geophysics Series; Academic Press: Waltham, MA, USA, 2011; ISBN 978-0-12-088759-0. [Google Scholar]
- Pedlosky, J. An Inertial Theory of the Equatorial Undercurrent. J. Phys. Oceanogr. 1987, 17, 1978–1985. [Google Scholar] [CrossRef]
- Fritz, M.; Mayer, M.; Haimberger, L.; Winkelbauer, S. Assessment of Indonesian Throughflow Transports from Ocean Reanalyses with Mooring-Based Observations. Ocean Sci. 2023, 19, 1203–1223. [Google Scholar] [CrossRef]
- Wunsch, C.; Stammer, D. Satellite Altimetry, the Marine Geoid, and the Oceanic General Circulation. Annu. Rev. Earth Planet. Sci. 1998, 26, 219–253. [Google Scholar] [CrossRef]
- Robinson, N.M.; Nelson, W.A.; Costello, M.J.; Sutherland, J.E.; Lundquist, C.J. A Systematic Review of Marine-Based Species Distribution Models (SDMs) with Recommendations for Best Practice. Front. Mar. Sci. 2017, 4, 421. [Google Scholar] [CrossRef]
- Dong, C.; Lu, X.; Liu, Y.; Han, G.; Fu, M.; Cao, Q.; Zhang, Y.; Chen, X.; Yuan, Y. Rotating Tank Experiments for the Study of Geophysical Fluid Dynamics. J. Oceanol. Limnol. 2024, 42, 1385–1398. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiu, B.; Klein, P.; Travis, S. The Influence of Geostrophic Strain on Oceanic Ageostrophic Motion and Surface Chlorophyll. Nat. Commun. 2019, 10, 2838. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Dong, C.; Tan, W.; Liu, Y.; He, Y.; Wang, J. Vertical Structure Anomalies of Oceanic Eddies and Eddy-Induced Transports in the South China Sea. Remote Sens. 2018, 10, 795. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global Heat and Salt Transports by Eddy Movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef]
- Gruber, N.; Lachkar, Z.; Frenzel, H.; Marchesiello, P.; Münnich, M.; McWilliams, J.C.; Nagai, T.; Plattner, G.-K. Eddy-Induced Reduction of Biological Production in Eastern Boundary Upwelling Systems. Nat. Geosci. 2011, 4, 787–792. [Google Scholar] [CrossRef]
- Fu, M.; Han, G.; Lu, X.; Sun, W.; Sommeria, J.; Stegner, A.; Caldeira, R.M.A.; Dong, C. Analysis of Vortex Merging from a Rotating Tank Laboratory Experiment. Prog. Oceanogr. 2024, 222, 103227. [Google Scholar] [CrossRef]
- Han, G.; Dong, C.; Yang, J.; Sommeria, J.; Stegner, A.; Caldeira, R.M.A. Strain Evolution and Instability of an Anticyclonic Eddy From a Laboratory Experiment. Front. Mar. Sci. 2021, 8, 645531. [Google Scholar] [CrossRef]
- Lazar, A.; Stegner, A.; Caldeira, R.; Dong, C.; Didelle, H.; Viboud, S. Inertial Instability of Intense Stratified Anticyclones. Part 2. Laboratory Experiments. J. Fluid Mech. 2013, 732, 485–509. [Google Scholar] [CrossRef]
- Longhetto, A.; Briatore, L.; d’Hieres, G.C.; Didelle, H.; Ferrero, E.; Giraud, C. Physical Simulations in Rotating Tank of Lee Cyclogenesis. Exp. Fluids 1997, 22, 387–396. [Google Scholar] [CrossRef]
- Longhetto, A.; D’Hieres, G.C.; Briatore, L.; Didelle, H.; Ferrero, E.; Giraud, C. A Laboratory Experiment on the Development of Cyclogenesis in the Lee of a Mountain. Il Nuovo Cimento C 1996, 19, 561–578. [Google Scholar] [CrossRef]
- Lazar, A.; Stegner, A.; Heifetz, E. Inertial Instability of Intense Stratified Anticyclones. Part 1. Generalized Stability Criterion. J. Fluid Mech. 2013, 732, 457–484. [Google Scholar] [CrossRef]
- Moisy, F.; Morize, C.; Rabaud, M.; Sommeria, J. Decay Laws, Anisotropy and Cyclone–Anticyclone Asymmetry in Decaying Rotating Turbulence. J. Fluid Mech. 2011, 666, 5–35. [Google Scholar] [CrossRef]
- Griffiths, R.W.; Hopfinger, E.J. Coalescing of Geostrophic Vortices. J. Fluid Mech. 1987, 178, 73–97. [Google Scholar] [CrossRef]
- Griffiths, R.W.; Hopfinger, E.J. Experiments with Baroclinic Vortex Pairs in a Rotating Fluid. J. Fluid Mech. 1986, 173, 501–518. [Google Scholar] [CrossRef]
- Meunier, P.; Leweke, T. Three-Dimensional Instability during Vortex Merging. Phys. Fluids 2001, 13, 2747–2750. [Google Scholar] [CrossRef]
- Feng, X.; Wang, L.; Ji, C.; Wang, H.; Zhu, C.; Jia, Y. The Impact of Internal Solitary Waves on Deep-Sea Benthic Organisms on the Continental Slope of the Northern South China Sea. Front. Mar. Sci. 2023, 10, 1184397. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.-F. Numerical and Experimental Study on the Scale Effect of Internal Solitary Wave Loads on Spar Platforms. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 569–577. [Google Scholar] [CrossRef]
- Finette, S.; Orr, M.H.; Turgut, A.; Apel, J.R.; Badiey, M.; Chiu, C.; Headrick, R.H.; Kemp, J.N.; Lynch, J.F.; Newhall, A.E.; et al. Acoustic Field Variability Induced by Time Evolving Internal Wave Fields. J. Acoust. Soc. Am. 2000, 108, 957–972. [Google Scholar] [CrossRef] [PubMed]
- Renouard, D.P.; Baey, J.-M. Two Experimental Studies of Internal Waves Generated by Tide-Topography Interaction. Dyn. Atmos. Ocean. 1993, 19, 205–232. [Google Scholar] [CrossRef]
- Ramirez, C.; Renouard, D. Generation of Internal Waves over a Shelf. Dyn. Atmos. Ocean. 1998, 28, 107–125. [Google Scholar] [CrossRef]
- Mercier, M.J.; Gostiaux, L.; Helfrich, K.; Sommeria, J.; Viboud, S.; Didelle, H.; Ghaemsaidi, S.J.; Dauxois, T.; Peacock, T. Large-scale, Realistic Laboratory Modeling of M2 Internal Tide Generation at the Luzon Strait. Geophys. Res. Lett. 2013, 40, 5704–5709. [Google Scholar] [CrossRef]
- Connan, G.; Griffiths, H.D.; Brennan, P.V.; Renouard, D.; Barthelemy, E.; Garello, R. Experimental Imaging of Internal Waves by a Mm-Wave Radar. In Proceedings of the IEEE Oceanic Engineering Society. OCEANS’98. Conference Proceedings (Cat. No. 98CH36259), Nice, France, 28 September–1 October 1998; Volume 2, pp. 619–623. [Google Scholar]
- Guizien, K.; Ramirez, C.; Barthelemy, E.; Renouard, D. The Passing of Long Internal and External Gravity Wave over a Step. Laboratory and in-Situ Measurements Compared with Analytical Modelling. In Proceedings of the IEEE Oceanic Engineering Society. OCEANS’98. Conference Proceedings (Cat. No. 98CH36259), Nice, France, 28 September–1 October 1998; Volume 2, pp. 866–870. [Google Scholar]
- Pérenne, N.; Renouard, D.P. Internal Waves and Rectification in a Linearly Stratified Fluid. Dyn. Atmospheres Oceans 1999, 29, 65–84. [Google Scholar] [CrossRef]
- Swart, A.; Manders, A.; Harlander, U.; Maas, L.R.M. Experimental Observation of Strong Mixing Due to Internal Wave Focusing over Sloping Terrain. Dyn. Atmos. Ocean. 2010, 50, 16–34. [Google Scholar] [CrossRef]
- Savaro, C.; Campagne, A.; Linares, M.C.; Augier, P.; Sommeria, J.; Valran, T.; Viboud, S.; Mordant, N. Generation of Weakly Nonlinear Turbulence of Internal Gravity Waves in the Coriolis Facility. Phys. Rev. Fluids 2020, 5, 073801. [Google Scholar] [CrossRef]
- Shmakova, N.; Voisin, B.; Sommeria, J.; Flór, J.-B. Internal and Inertia-Gravity Wave Focusing at Large Stokes Numbers. Phys. Rev. Fluids 2021, 6, 114804. [Google Scholar] [CrossRef]
- Rodda, C.; Savaro, C.; Bouillaut, V.; Augier, P.; Sommeria, J.; Valran, T.; Viboud, S.; Mordant, N. From Internal Waves to Turbulence in a Stably Stratified Fluid. Phys. Rev. Lett. 2023, 131, 264101. [Google Scholar] [CrossRef]
- Rodda, C.; Savaro, C.; Davis, G.; Reneuve, J.; Augier, P.; Sommeria, J.; Valran, T.; Viboud, S.; Mordant, N. Experimental Observations of Internal Wave Turbulence Transition in a Stratified Fluid. Phys. Rev. Fluids 2022, 7, 094802. [Google Scholar] [CrossRef]
- Sous, D.; Sommeria, J. A Tsai’s Model Based S-PIV Method for Velocity Measurements in a Turbulent Ekman Layer. Flow Meas. Instrum. 2012, 26, 102–110. [Google Scholar] [CrossRef]
- D’Hieres, G.C.; Didelle, H.; Obaton, D. A Laboratory Study of Surface Boundary Currents: Application to the Algerian Current. J. Geophys. Res. Ocean. 1991, 96, 12539–12548. [Google Scholar] [CrossRef]
- Aelbrecht, D.; D’Hieres, G.; Zhang, X. Generation of a Residual Current by Interaction between the Coastal Boundary-Layer and the Ekman Layer in a Tidal Motion. Oceanol. Acta 1993, 16, 479–487. [Google Scholar]
- Aelbrecht, D.; Chabert D’Hieres, G.; Renouard, D. Experimental Study of the Ekman Layer Instability in Steady or Oscillating Flows. Cont. Shelf Res. 1999, 19, 1851–1867. [Google Scholar] [CrossRef]
- Sous, D.; Sommeria, J.; Boyer, D. Friction Law and Turbulent Properties in a Laboratory Ekman Boundary Layer. Phys. Fluids 2013, 25, 46602. [Google Scholar] [CrossRef]
- Vincze, M.; Fenyvesi, N.; Klein, M.; Sommeria, J.; Viboud, S.; Ashkenazy, Y. Evidence for Wind-Induced Ekman Layer Resonance Based on Rotating Tank Experiments. EPL Europhys. Lett. 2019, 125, 44001. [Google Scholar] [CrossRef]
- Maggi, M.R.; Negretti, M.E.; Martin, A.; Naaim-Bouvet, F.; Hopfinger, E.J. Experimental Study of Gravity Currents Moving over a Sediment Bed: Suspension Criterion and Bed Forms. Environ. Fluid Mech. 2024, 24, 1215–1233. [Google Scholar] [CrossRef]
- Laanaia, N.; Wirth, A.; Molines, J.M.; Barnier, B.; Verron, J. On the Numerical Resolution of the Bottom Layer in Simulations of Oceanic Gravity Currents. Ocean Sci. 2010, 6, 563–572. [Google Scholar] [CrossRef]
- Hallworth, M.A.; Huppert, H.E.; Ungarish, M. Axisymmetric Gravity Currents in a Rotating System: Experimental and Numerical Investigations. J. Fluid Mech. 2001, 447, 1–29. [Google Scholar] [CrossRef]
- Thomas, P.J.; Linden, P.F. Rotating Gravity Currents: Small-Scale and Large-Scale Laboratory Experiments and a Geostrophic Model. J. Fluid Mech. 2007, 578, 35–65. [Google Scholar] [CrossRef]
- Aubourg, Q.; Campagne, A.; Peureux, C.; Ardhuin, F.; Sommeria, J.; Viboud, S.; Mordant, N. Three-Wave and Four-Wave Interactions in Gravity Wave Turbulence. Phys. Rev. Fluids 2017, 2, 114802. [Google Scholar] [CrossRef]
- Maggi, M.R.; Adduce, C.; Negretti, M.E. Lock-Release Gravity Currents Propagating over Roughness Elements. Environ. Fluid Mech. 2022, 22, 383–402. [Google Scholar] [CrossRef]
- Martin, A.; Negretti, M.E.; Ungarish, M.; Zemach, T. Propagation of a Continuously Supplied Gravity Current Head down Bottom Slopes. Phys. Rev. Fluids 2020, 5, 054801. [Google Scholar] [CrossRef]
- De Falco, M.C.; Adduce, C.; Negretti, M.E.; Hopfinger, E.J. On the Dynamics of Quasi-Steady Gravity Currents Flowing up a Slope. Adv. Water Resour. 2021, 147, 103791. [Google Scholar] [CrossRef]
- Sommeria, J.; Meyers, S.D.; Swinney, H.L. Experiments on Vortices and Rossby Waves in Eastward and Westward Jets. Nonlinear Top. Ocean. Phys. 1991, 109, 227–269. [Google Scholar]
- Sommeria, J.; Meyers, S.D.; Swinney, H.L. Laboratory Model of a Planetary Eastward Jet. Nature 1989, 337, 58–61. [Google Scholar] [CrossRef]
- Behringer, R.P.; Meyers, S.D.; Swinney, H.L. Chaos and Mixing in a Geostrophic Flow. Phys. Fluids Fluid Dyn. 1991, 3, 1243–1249. [Google Scholar] [CrossRef]
- Uleysky, M.Y.; Budyansky, M.V.; Prants, S.V. Chaotic Transport across Two-Dimensional Jet Streams. J. Exp. Theor. Phys. 2010, 111, 1039–1049. [Google Scholar] [CrossRef]
- Platzman, G.W.; Curtis, G.A.; Hansen, K.S.; Slater, R.D. Normal Modes of the World Ocean. Part II: Description of Modes in the Period Range 8 to 80 Hours. J. Phys. Oceanogr. 1981, 11, 579–603. [Google Scholar] [CrossRef]
- Miller, A.J.; Lermusiaux, P.F.J.; Poulain, P.-M. A Topographic–Rossby Mode Resonance over the Iceland–Faeroe Ridge. J. Phys. Oceanogr. 1996, 26, 2735–2747. [Google Scholar] [CrossRef]
- Pedlosky, J.; Greenspan, H.P. A Simple Laboratory Model for the Oceanic Circulation. J. Fluid Mech. 1967, 27, 291–304. [Google Scholar] [CrossRef]
- Beardsley, R.C. The ‘Sliced-Cylinder’ Laboratory Model of the Wind-Driven Ocean Circulation. Part 2. Oscillatory Forcing and Rossby Wave Resonance. J. Fluid Mech. 1975, 69, 41–64. [Google Scholar] [CrossRef]
- Pierini, S.; Fincham, A.M.; Renouard, D.; D’Ambrosio, M.R.; Didelle, H. Laboratory Modeling of Topographic Rossby Normal Modes. Dyn. Atmos. Ocean. 2002, 35, 205–225. [Google Scholar] [CrossRef]
- Cohen, Y.; Paldor, N.; Sommeria, J. Laboratory Experiments and a Non-Harmonic Theory for Topographic Rossby Waves over a Linearly Sloping Bottom on the f -Plane. J. Fluid Mech. 2010, 645, 479–496. [Google Scholar] [CrossRef]
- Pirro, A.; Menna, M.; Mauri, E.; Laxenaire, R.; Salon, S.; Bosse, A.; Martellucci, R.; Viboud, S.; Valran, T.; Hayes, D.; et al. Rossby Waves Driven by the Mid Mediterranean Jet Impact the Eastern Mediterranean Mesoscale Dynamics. Sci. Rep. 2024, 14, 29598. [Google Scholar] [CrossRef] [PubMed]
- Pinault, J.-L. Anthropogenic and Natural Radiative Forcing: Positive Feedbacks. J. Mar. Sci. Eng. 2018, 6, 146. [Google Scholar] [CrossRef]
- Pinault, J.-L. A Review of the Role of the Oceanic Rossby Waves in Climate Variability. J. Mar. Sci. Eng. 2022, 10, 493. [Google Scholar] [CrossRef]
- Jacobs, P.; Guo, Y.; Davies, P.A. Boundary Currents over Shelf and Slope Topography. J. Mar. Syst. 1999, 19, 137–158. [Google Scholar] [CrossRef]
- Ferrero, E.; Longhetto, A.; Montabone, L.; Mortarini, L.; Manfrin, M.; Sommeria, J.; Didelle, H.; Giraud, C.; Rizza, U. Physical Simulations of Neutral Boundary Layer in Rotating Tank. Il Nuovo Cimento C 2005, 28, 1–17. [Google Scholar] [CrossRef]
- Davarpanah Jazi, S.; Wells, M.G.; Peakall, J.; Dorrell, R.M.; Thomas, R.E.; Keevil, G.M.; Darby, S.E.; Sommeria, J.; Viboud, S.; Valran, T. Influence of Coriolis Force Upon Bottom Boundary Layers in a Large-Scale Gravity Current Experiment: Implications for Evolution of Sinuous Deep-Water Channel Systems. J. Geophys. Res. Oceans 2020, 125, e2019JC015284. [Google Scholar] [CrossRef]
- Manders, A.M.M.; Maas, L.R.M. Observations of Inertial Waves in a Rectangular Basin with One Sloping Boundary. J. Fluid Mech. 2003, 493, 59–88. [Google Scholar] [CrossRef]
- Shi, H.; Negretti, M.E.; Chauchat, J.; Blanckaert, K.; Lemmin, U.; Barry, D.A. Tracking the Nearfield Evolution of an Initially Shallow, Neutrally Buoyant Plane Jet Over a Sloping Bottom Boundary. Water Resour. Res. 2024, 60, e2023WR034826. [Google Scholar] [CrossRef]



| Case | H/L | h0′/L | U0 cm/s | f0 s−1 | β (ms−1) | b | N s−1 | s | d | λobs m | λth, λMC m | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EXP-H1 | 0.68 | 0.45 | 1.4 | 0.314 | 0.12 | 1.0 | 0.21, 0.13 | - | - | - | 2.0 | 2.1, - |
| EXP-H2 | 0.68 | 0.45 | 0.79 | 0.314 | 0.12 | 1.77 | 0.18, 0.07 | - | - | - | 1.5 | 1.5, - |
| EXP-S1 | 0.68 | 0.45 | 1.4 | 0.314 | 0.12 | 1.04 | 0.2, 0.13 | 1.1 | 0.56 | 0.91 | 2.2 | 1.9, 2.6 |
| EXP-S2 | 0.68 | 0.45 | 0.83 | 0.314 | 0.12 | 1.68 | 0.16, 0.08 | 1.1 | 0.56 | 0.91 | 1.5 | 1.46, 1.3 |
| Ocean | 0.03 | 0.4 | 2–5 | 7.2e−5 | 2e−11 | 1.6–0.65 | e−2 | 3e−3 | 0.96 | 0.9 | (1.8–2.5)e5 | (24, 19–28)e4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Han, G.; Lin, Y.; Cao, Q.; You, Z.; Xue, J.; Zhang, X.; Dong, C. Application of Large-Scale Rotating Platforms in the Study of Complex Oceanic Dynamic Processes. J. Mar. Sci. Eng. 2025, 13, 1187. https://doi.org/10.3390/jmse13061187
Lu X, Han G, Lin Y, Cao Q, You Z, Xue J, Zhang X, Dong C. Application of Large-Scale Rotating Platforms in the Study of Complex Oceanic Dynamic Processes. Journal of Marine Science and Engineering. 2025; 13(6):1187. https://doi.org/10.3390/jmse13061187
Chicago/Turabian StyleLu, Xiaojie, Guoqing Han, Yifan Lin, Qian Cao, Zhiwei You, Jingyuan Xue, Xinyuan Zhang, and Changming Dong. 2025. "Application of Large-Scale Rotating Platforms in the Study of Complex Oceanic Dynamic Processes" Journal of Marine Science and Engineering 13, no. 6: 1187. https://doi.org/10.3390/jmse13061187
APA StyleLu, X., Han, G., Lin, Y., Cao, Q., You, Z., Xue, J., Zhang, X., & Dong, C. (2025). Application of Large-Scale Rotating Platforms in the Study of Complex Oceanic Dynamic Processes. Journal of Marine Science and Engineering, 13(6), 1187. https://doi.org/10.3390/jmse13061187







