Maritime Port Freight Flow Optimization with Underground Container Logistics Systems Under Demand Uncertainty
Abstract
1. Introduction
2. Literature Review
2.1. Research on the Optimization of Maritime Port Freight Flow
2.2. Research on Underground Container Logistics
3. Problem Statement
- (1)
- Multiple cost trade-offs: Decision-makers need to consider transportation costs, environmental costs, and congestion costs simultaneously. These objectives are interrelated and require comprehensive balancing. For example, reducing traffic congestion might increase transportation costs, while choosing low-carbon transportation methods might increase environmental costs.
- (2)
- Demand uncertainty: Port container transportation demand is influenced by various factors and exhibits high uncertainty, requiring the freight flow allocation scheme to be sufficiently robust to adapt to different demand conditions and minimize the impact on the system.
- (3)
- Multiple constraints: These include capacity constraints, time constraints, flow balance constraints, and low-carbon transportation ratio requirements, which add complexity to the problem. Finding the optimal solution while satisfying these various constraints is a significant challenge.
- (4)
- Integration of new transportation modes: The underground container logistics system (UCLS) as a new transportation mode, presents a novel research topic regarding its coordinated optimization with traditional transportation modes. Determining how to effectively integrate the underground logistics system with traditional modes and allocate freight flow between them is an important focus of this study.
4. Model Development
4.1. Objective Function
- (1)
- Transportation cost
- (2)
- Environmental cost
- (3)
- Congestion costs
- (4)
- Carbon Tax and Carbon Subsidy Costs
4.2. Constraint Condition
- (1)
- Capacity constraints
- (2)
- Flow balance constraints
- (3)
- Demand satisfaction probability constraints
- (4)
- Time constraints
- (5)
- Low-carbon-transport-ratio constraints
- (6)
- Carbon-emission-related constraint
- (7)
- Carbon emission calculation constraint
- (8)
- Carbon subsidy constraints
- (9)
- Carbon tax constraints
- (10)
- LPW capacity constraints
- (11)
- Decision variable non-negativity and binary constraints
- (12)
- Demand randomness constraints
5. Methodology
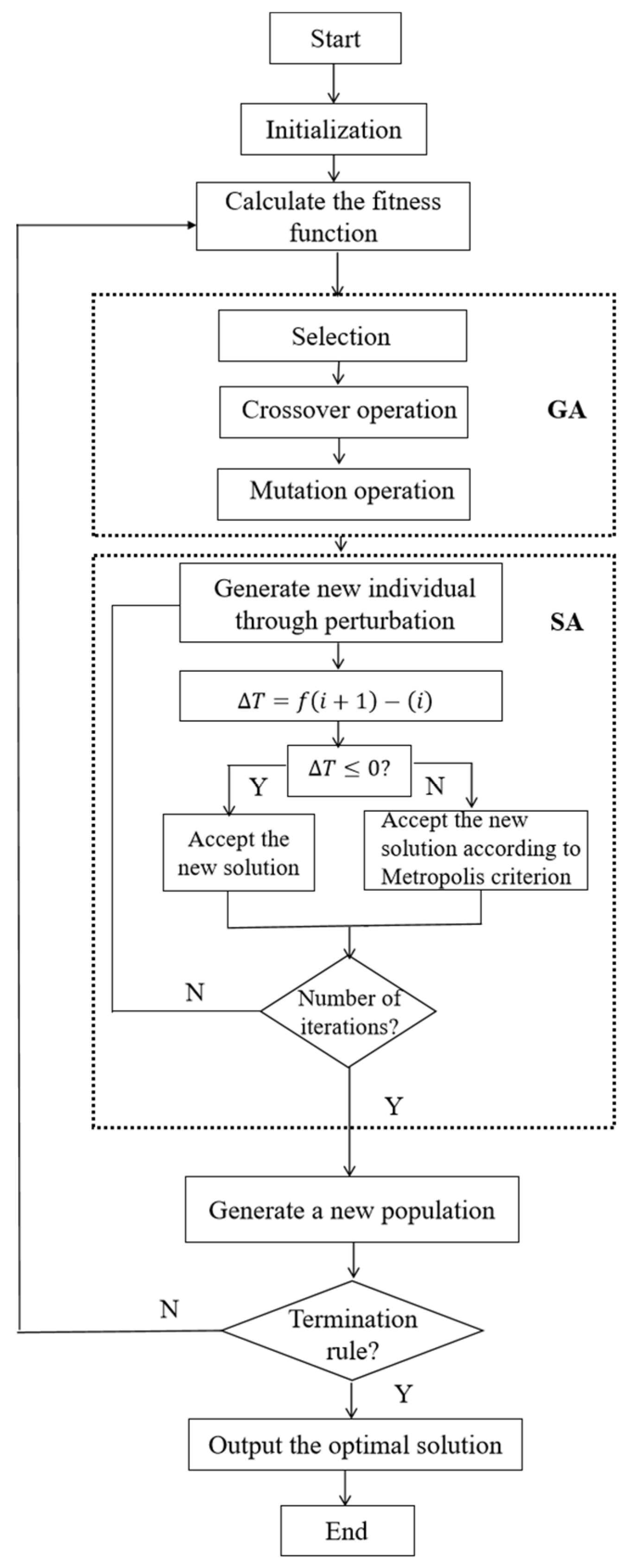
5.1. The Design of GA-SA
5.1.1. Coding and Initialization
5.1.2. Fitness Function
- (1)
- The violation degree of the flow balance constraint is .
- (2)
- The violation degree of the transportation mode selection and freight flow matching constraint is , where A is a sufficiently large positive number.
- (3)
- The violation degree of the chance constraint is .
5.1.3. Crossover Operation
5.1.4. Simulated Annealing
5.1.5. Local Search
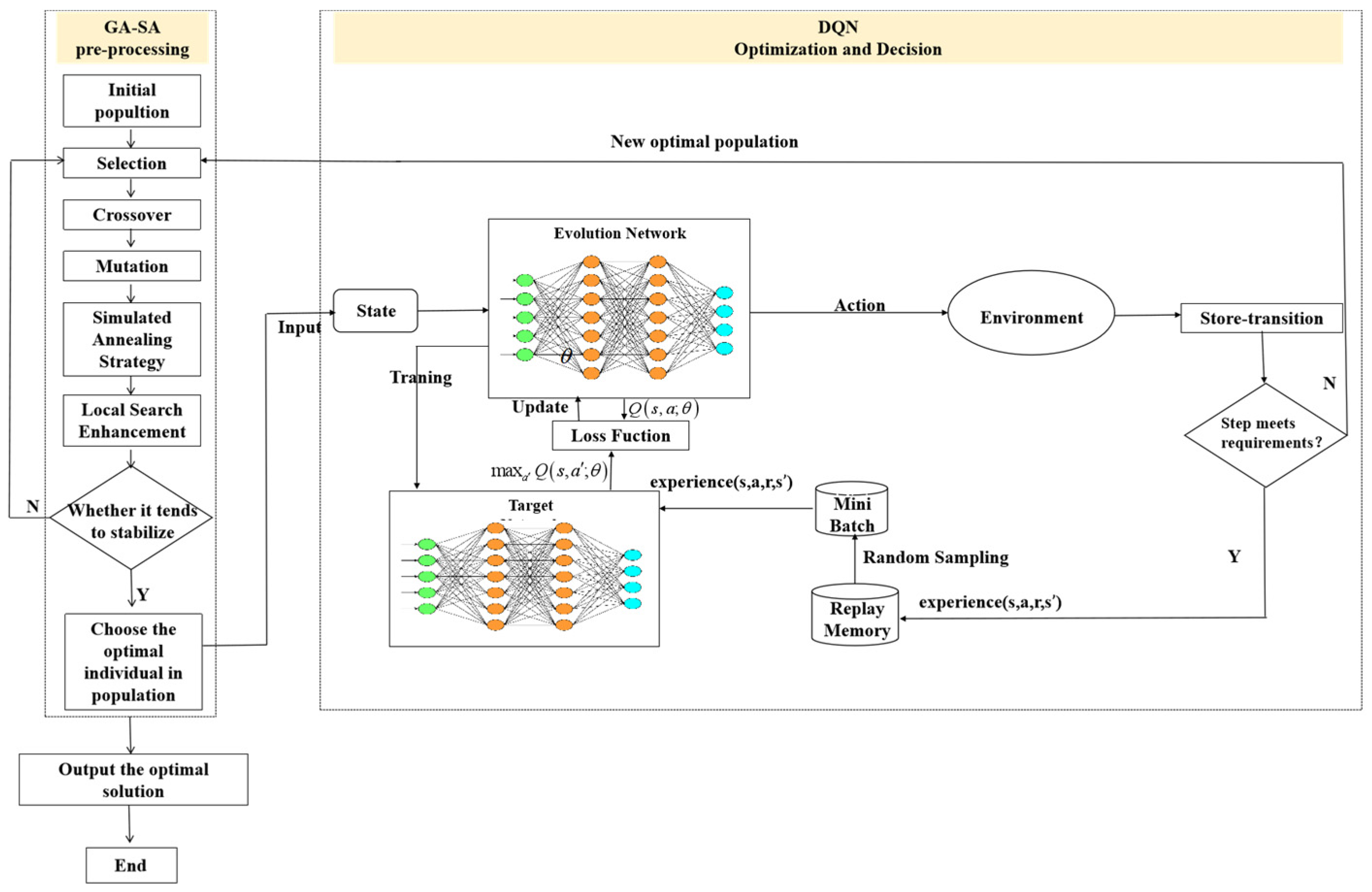
5.2. The Design of DQN
5.2.1. State Space Design
5.2.2. Action Space Design
5.2.3. Reward Function Design
5.2.4. Network Architecture and Training
5.3. The Framework of GA-SA-DQN
6. Numerical Experiments
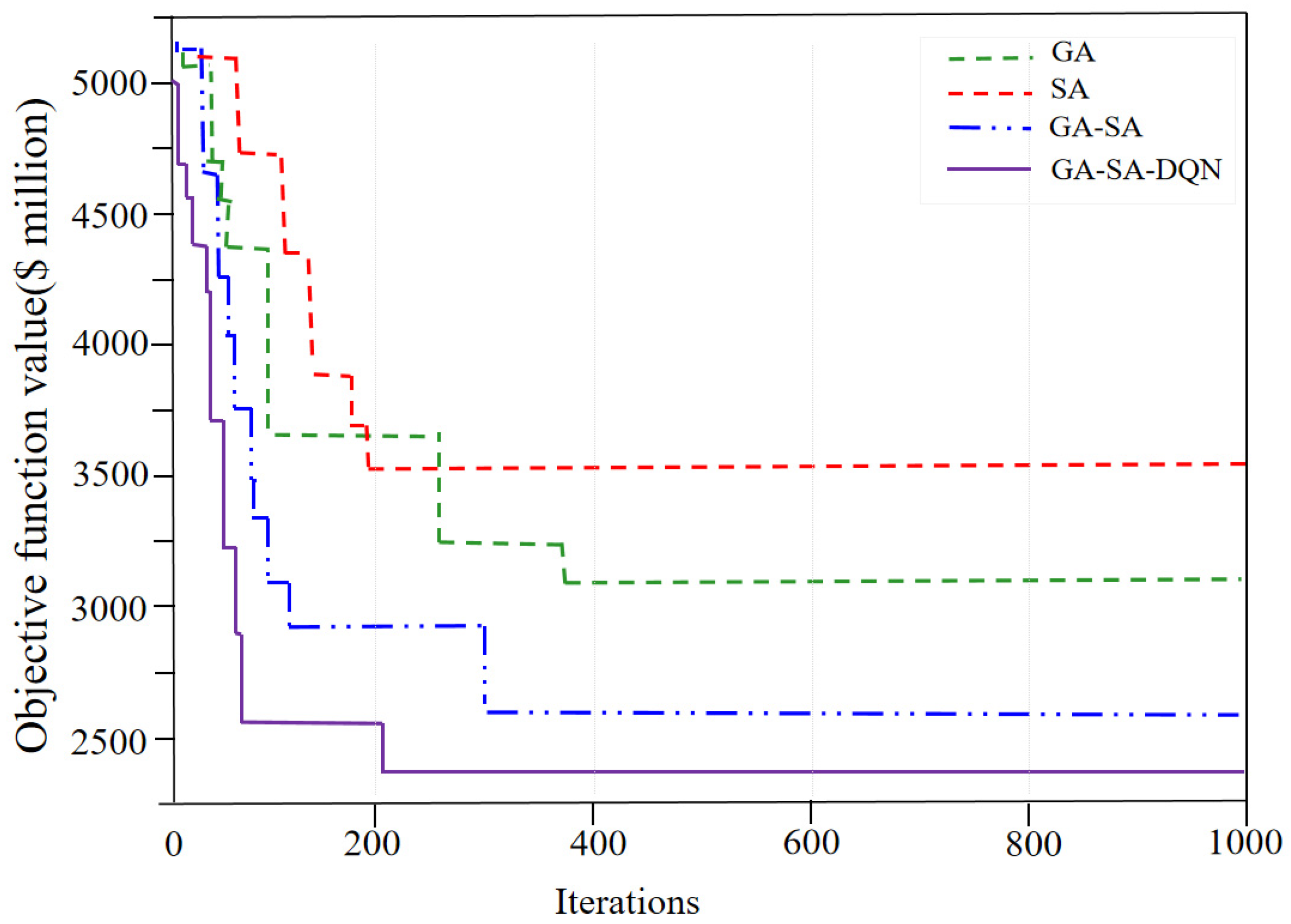
6.1. Algorithm Performance Testing
6.2. Case Study
- (1)
- Transportation demand data: Estimated based on A Port’s daily container throughput of 141,000 TEU in 2024.
- (2)
- Distance data: Measured through electronic maps for the actual transportation distances between LPWs and CPs areas, considering the impact of newly opened highways.
- (3)
- Transportation costs: Referencing the 2024 Shanghai transport price guidelines and the impact of fuel price fluctuations.
- (4)
- Carbon emission factors: Using recommended values from the Transportation Industry Carbon Emission Calculation Methodology.
- (5)
- Underground logistics system parameters: Based on data from the 2023–2024 Shanghai Urban Underground Space Research Institute.
- Scenario A
- (traditional scenario): Only considers road, rail, and water transportation modes, excluding an underground logistics system, and aims to minimize transportation costs.
- Scenario B
- (environmentally prioritized scenario): Incorporates underground logistics system but excludes demand uncertainty, aiming to minimize total costs (including transportation, environmental, carbon tax and subsidy, and congestion costs).
- Scenario C
- (proposed scenario): Includes an underground logistics system and accounts for demand uncertainty, aiming to minimize expected total costs.
6.2.1. Total Cost Analysis
6.2.2. Cargo Flow Distribution Results
6.3. Sensitivity Analysis
6.3.1. Impact of Transportation Cost Changes
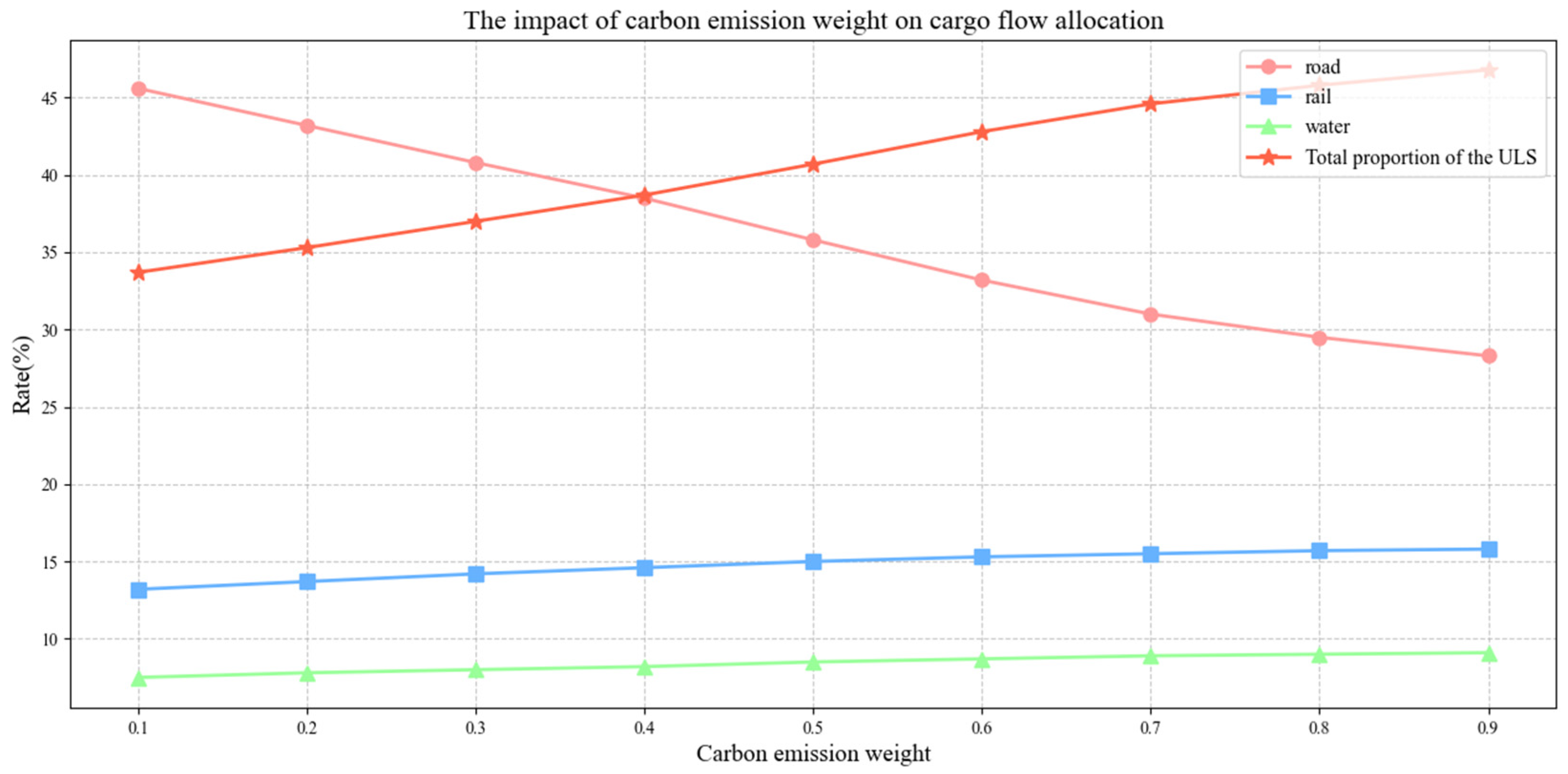
6.3.2. Impact of Carbon Emission Weightings
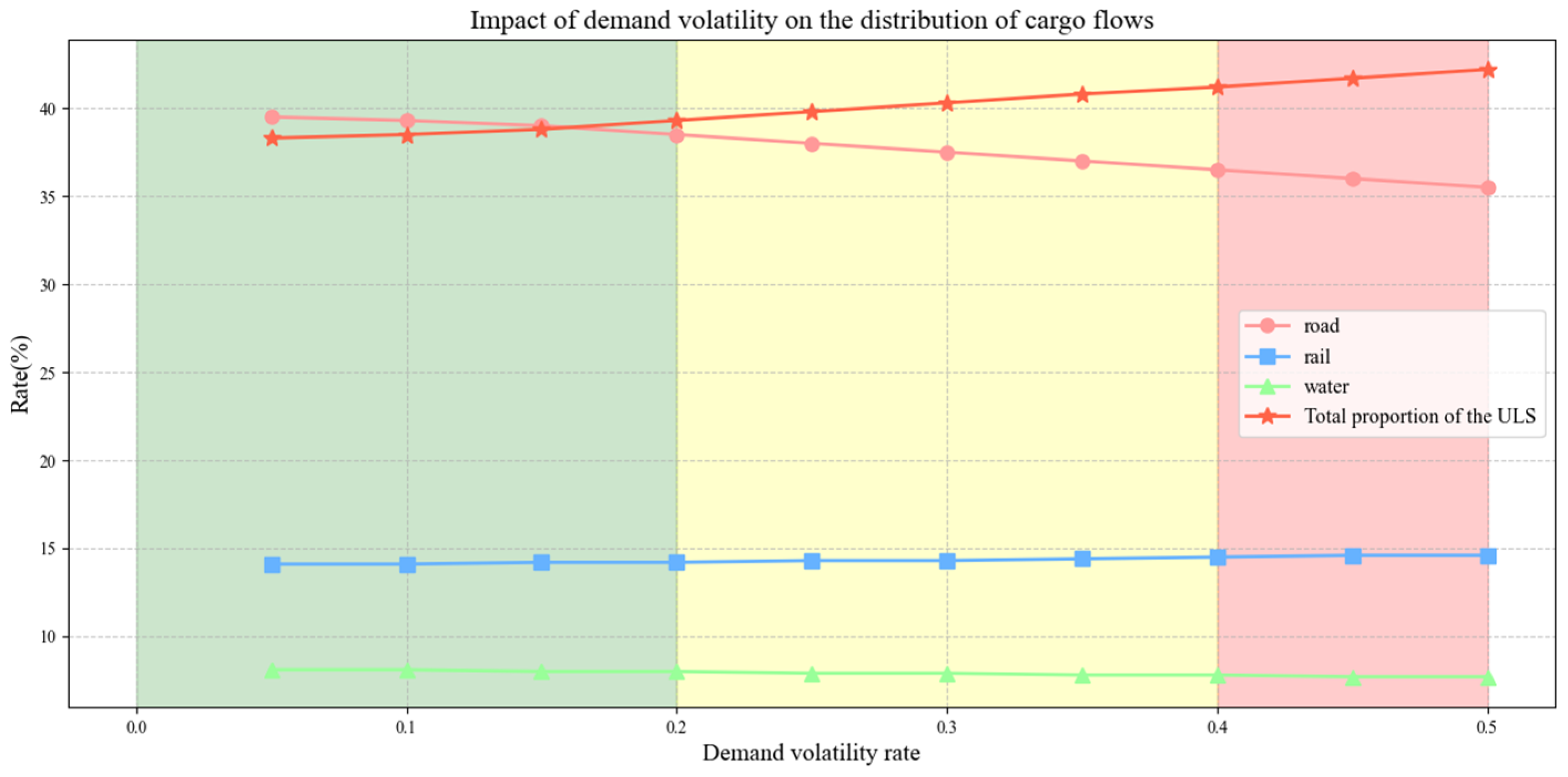
6.3.3. Impact of Demand Uncertainty
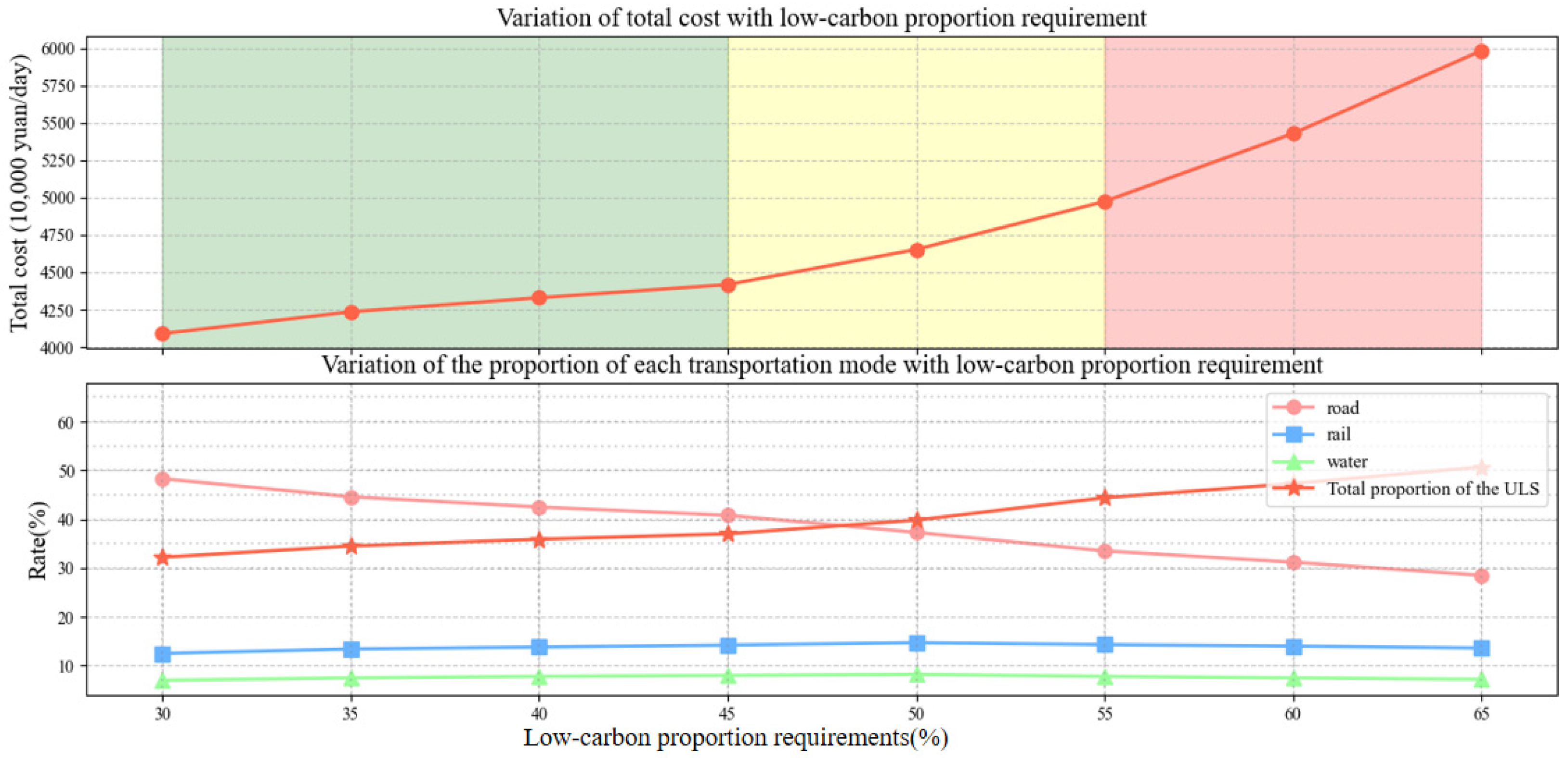
6.3.4. Impact of Low-Carbon-Proportion Requirements
- (1)
- Underground logistics system costs: The cost of an underground logistics system has a significant impact on its adoption. Controlling cost increases to within 25% is crucial for maintaining high usage rates.
- (2)
- Carbon emission weight: increasing the carbon emission cost weight is an effective way to promote the development of underground logistics systems. When the weight exceeds 0.3, the underground logistics system will become the dominant transportation mode.
- (3)
- Demand uncertainty: As demand uncertainty increases, the proportion of road transport rises, and the proportion of the underground logistics system slightly decreases. A shallow underground logistics system shows better adaptability.
- (4)
- Low-carbon-proportion requirements: When the low-carbon-proportion requirement is below 45%, the system can adapt with a relatively small increase in cost. However, when the requirement exceeds 50%, costs rise significantly.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- UNCTAD. Review of Maritime Transport 2024; United Nations: Geneva, Switzerland, 2024; Available online: https://unctad.org/publication/review-maritime-transport-2024 (accessed on 10 May 2025).
- UNCTAD. Global Trade Hits Record $33 Trillion in 2024, Driven by Services and Developing Economies. 2025. Available online: https://unctad.org/news/global-trade-hits-record-33-trillion-2024-driven-services-and-developing-economies (accessed on 10 May 2025).
- Panahi, R.; Ng, A.K.Y.; Afenyo, M.; Lau, Y.Y. Implications of a pandemic outbreak risk: A discussion on China’s emergency logistics in the era of Coronavirus Disease 2019 (COVID-19). J. Int. Logist. Trade 2022, 20, 127–135. [Google Scholar] [CrossRef]
- Zhao, Z.; Shen, M.; Chen, J.; Wang, X.; Wan, Z.; Hu, X.; Liu, W. Design and optimization of the collaborative container logistics system between a dry port and a water port. Comput. Ind. Eng. 2024, 198, 110654. [Google Scholar] [CrossRef]
- Acciaro, M.; Arduino, G.; Borruso, G. Port sustainability in the transition to a low-carbon energy system: A review of digital technologies and decarbonization strategies. Transp. Res. Part D Transp. Environ. 2023, 117, 103615. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Y.; Li, K.X.; Luo, M.; Xie, C. Liner shipping network vulnerability to component disruptions: A China-Europe container flow analysis. Transp. Res. Part D Transp. Environ. 2024, 131, 104232. [Google Scholar] [CrossRef]
- Liang, C.; Sun, W.; Shi, J.; Wang, K.; Zhang, Y.; Lim, G. Decarbonizing Maritime Transport through Green Fuel-Powered Vessel Retrofitting: A Game-Theoretic Approach. J. Mar. Sci. Eng. 2024, 12, 1174. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Chen, K.; Zhou, Q. Port hinterland intermodal container transport efficiency and its influencing factors analysis. Transp. Policy 2022, 124, 143–157. [Google Scholar] [CrossRef]
- Chen, X.; Wei, C.; Xin, Z.; Zhao, J.; Xian, J. Ship Detection under Low-Visibility Weather Interference via an Ensemble Generative Adversarial Network. J. Mar. Sci. Eng. 2023, 11, 2065. [Google Scholar] [CrossRef]
- Hu, X.; Liang, C.; Chang, D.; Zhang, Y. Container storage space assignment problem in two terminals with the consideration of yard sharing. Adv. Eng. Inform. 2021, 47, 101224. [Google Scholar] [CrossRef]
- Martinez-Moya, J.; Vazquez-Paja, B.; Gimenez-Maldonado, J.A. Energy consumption minimization of a container terminal by the optimization of eco-efficient operational strategies. Energy 2021, 222, 119925. [Google Scholar] [CrossRef]
- Karam, A.; Jensen, A.J.K.; Hussein, M. Analysis of the barriers to multimodal freight transport and their mitigation strategies. Eur. Transp. Res. Rev. 2023, 15, 43. [Google Scholar] [CrossRef]
- Intermodal Freight Transportation Market Size Report. 2030. Available online: https://www.grandviewresearch.com/industry-analysis/intermodal-freight-transportation-market-report (accessed on 14 May 2025).
- Mamatok, Y.; Jin, M. A transportation service network design problem with mixed temporal constraints. Transp. Res. Part E Logist. Transp. Rev. 2022, 160, 102689. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing Data Supported Traffic Flow Prediction via Denoising Schemes and ANN: A Comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, W.; Dong, J.; Yang, K.; Ren, R.; Chen, Z. Cost-benefit analysis of road-underground co-modality strategies for sustainable city logistics. Transp. Res. Part D Transp. Environ. 2025, 139, 104585. [Google Scholar] [CrossRef]
- Zhu, L.; Li, W.; Sun, Z.B.; Chen, Y.; Chen, C.; Zhang, L.Y. Evaluating resilience in maritime port and shipping operations under various disruptions: A literature review. Marit. Econ. Logist. 2023, 25, 181–208. [Google Scholar] [CrossRef]
- van Twiller, J.; Adulyasak, Y.; Delage, E.; Grbic, D.; Jensen, R.M. Navigating Demand Uncertainty in Container Shipping: Deep Reinforcement Learning for Enabling Adaptive and Feasible Master Stowage Planning. arXiv 2025, arXiv:2502.12756. [Google Scholar] [CrossRef]
- Toygar, A.; Yildirim, U.; Inegöl, G.M. Investigation of empty container shortage based on SWARA-ARAS methods in the COVID-19 era. Eur. Transp. Res. Rev. 2022, 14, 8. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Dong, C.; Li, S. Container shipping network optimization considering underground container transportation. Marit. Policy Manag. 2022, 49, 389–409. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, B.; Zhu, Y. Underground logistics network design: A review and bibliometric analysis. Transp. Res. Part E Logist. Transp. Rev. 2023, 171, 102978. [Google Scholar]
- Hu, W.; Dong, J.; Ren, R.; Chen, Z. Underground logistics systems: Development overview and new prospects in China. Front. Eng. 2023, 10, 354–359. [Google Scholar] [CrossRef]
- Liang, C.; Hu, X.; Shi, L.; Fu, H.; Xu, D. Joint dispatch of shipment equipment considering underground container logistics. Comput. Ind. Eng. 2022, 165, 16. [Google Scholar] [CrossRef]
- Li, F.; Yuen, K.F. A systematic review on underground logistics system: Designs, impacts, and future directions. Tunn. Undergr. Space Technol. 2025, 159, 106483. [Google Scholar] [CrossRef]
- Hou, L.; Hu, W.; Chen, Y.; Dong, J.; Ren, R.; Chen, Z. Measuring Effectiveness of Metro-Based Underground Logistics System in Sustaining City Logistics Performance During Public Health Emergencies: A Case Study of Shanghai. Transp. Res. Rec. 2024, 2678, 724–748. [Google Scholar] [CrossRef]
- Sun, X.; Hu, W. Multi-objective optimization model for planning metro-based underground logistics system network: Nanjing case study. J. Ind. Manag. Optim. 2023, 19, 2607–2635. [Google Scholar] [CrossRef]
- Xia, N.; Jing, Y.; Wang, W.; Shi, L. Assessment of the carbon emissions and energy efficiency of container terminal: An empirical analysis from China. Sci. Rep. 2021, 11, 1728. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, W.; Xu, Y.; Dong, J.; Yang, K.; Ren, R. Exploring decision-making mechanisms for the metro-based underground logistics system network expansion: An example of Beijing. Tunn. Undergr. Space Technol. 2023, 139, 105240. [Google Scholar] [CrossRef]
- An, N.; Yang, K.; Chen, Y.; Yang, L. Wasserstein distributionally robust optimization for train operation and freight assignment in a metro-based underground logistics system. Comput. Ind. Eng. 2024, 192, 110228. [Google Scholar] [CrossRef]
- Wandel, S.; Anderberg, S.; Larsson, F.E.; Johnsson, A.; Wells, A. Underground capsule pipeline logistic system Feasibility study of an urban application. Transp. Res. Procedia 2023, 72, 3126–3133. [Google Scholar] [CrossRef]
- Hou, L.; Xu, Y.; Ren, R.; Yang, J.; Su, L. Optimization of three-dimensional urban underground logistics system alignment: A deep reinforcement learning approach. Comput. Ind. Eng. 2025, 205, 111185. [Google Scholar] [CrossRef]
- Gong, D.; Tian, J.; Hu, W.; Dong, J.; Chen, Y.; Ren, R.; Chen, Z. Sustainable Design and Operations Management of Metro-Based Underground Logistics Systems: A Thematic Literature Review. Buildings 2023, 13, 1888. [Google Scholar] [CrossRef]
- Vallidevi, K.; Jothi, S.; Karuppiah, S.V. HO-DQLN: Hybrid optimization-based deep Q-learning network for optimizing QoS requirements in service oriented model. Expert Syst. Appl. 2023, 227, 120188. [Google Scholar] [CrossRef]
- Kim, S.; Jang, M.-G.; Kim, J.-K. Process design and optimization of single mixed-refrigerant processes with the application of deep reinforcement learning. Appl. Therm. Eng. 2023, 223, 120038. [Google Scholar] [CrossRef]
- Xu, N.; Shi, Z.; Yin, S.; Xiang, Z. A hyper-heuristic with deep Q-network for the multi-objective unmanned surface vehicles scheduling problem. Neurocomputing 2024, 596, 127943. [Google Scholar] [CrossRef]
- Xue, F.; Hai, Q.; Dong, T.; Cui, Z.; Gong, Y. A deep reinforcement learning based hybrid algorithm for efficient resource scheduling in edge computing environment. Inf. Sci. 2022, 608, 362–374. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, L.; Liu, C.; Zhao, Z.; Mao, Y. Cost-aware scheduling systems for real-time workflows in cloud: An approach based on Genetic Algorithm and Deep Reinforcement Learning. Expert Syst. Appl. 2023, 234, 120972. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, Y.; Zhu, N.; Xu, T.; Jonrinaldi. A selection hyper-heuristic algorithm with Q-learning mechanism. Appl. Soft Comput. 2023, 147, 110815. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. Event-Driven Based Reinforcement Learning Predictive Controller Design for Three-Phase NPC Converters Using Online Approximators. IEEE Trans. Power Electron. 2024, 40, 4914–4926. [Google Scholar] [CrossRef]




| Notations | Description |
|---|---|
| (1) Sets | |
| set of logistics park warehouses (LPWs), indexed by | |
| set of coastal ports (CPs), indexed by | |
| set of transportation modes, indexed by , where represents road transportation, represents rail transportation, represents water transportation, represents the shallow underground container logistics system, represents the deep underground container logistics system | |
| (2) Parameters | |
| (TEU) | represents the container cargo transportation demand of port j, randomly varying |
| (TEU) | average cargo transportation demand at port |
| (TEU) | maximum deviation of cargo demand at port |
| (TEU) | uncertainty level of transportation demand prediction |
| demand satisfaction level, i.e., the minimum confidence level for guaranteeing meeting transportation demand at the port under uncertain conditions | |
| (km) | distance from LPW to port using transportation mode |
| (TEU) | capacity of LPW |
| (TEU/day) | maximum available capacity for transportation from LPW to port using transportation mode |
| (km/h) | speed of transportation mode |
| (h) | maximum allowable time for all containers to reach port |
| (CNY/TEU·km) | unit transportation cost of mode |
| (kg/TEU·km) | carbon emission coefficient of transportation mode |
| carbon emission coefficient of the underground logistics system | |
| base emissions coefficient, typically using road transportation’s emission coefficient as a benchmark | |
| government-set maximum emissions limit | |
| government-set minimum emissions reduction | |
| emission reduction cost for transportation mode | |
| (CNY/kg) | government-specified carbon subsidy rate |
| (CNY/kg) | government-specified carbon tax rate |
| (CNY) | government-set emissions reduction target |
| a very large number | |
| a non-negative number, used for ensuring the continuity of emission reduction compliance | |
| (3) Decision variables | |
| binary variable, if LPW to port chooses transportation mode , then ; otherwise, | |
| freight flow from LPW to port using transportation mode , unit is TEU | |
| binary variable, if cargo from LPW to port is selected for carbon taxation, then ; otherwise, | |
| binary variable, if cargo from LPW to port is selected for carbon subsidy, then ; otherwise, | |
| Instance Number | Number of LPWs | Number of CPs | Number of Transportation Modes |
|---|---|---|---|
| S1 | 2 | 2 | 4 |
| S2 | 3 | 2 | 4 |
| S3 | 3 | 3 | 4 |
| S4 | 4 | 2 | 4 |
| M1 | 4 | 3 | 4 |
| M2 | 5 | 3 | 4 |
| M3 | 5 | 4 | 4 |
| M4 | 6 | 4 | 4 |
| L1 | 8 | 4 | 4 |
| L2 | 10 | 4 | 4 |
| L3 | 10 | 5 | 4 |
| L4 | 12 | 6 | 4 |
| Parameter | Value |
|---|---|
| population size | 100 |
| maximum number of iterations | 1000 |
| crossover probability | 0.85 |
| mutation probability | 0.15 |
| initial temperature | 100 |
| cooling rate | 0.95 |
| local search probability | 0.2 |
| neural network structure | [Input Layer, 256, 128, 64, Output Layer] |
| learning rate | 0.001 |
| discount factor | 0.95 |
| experience replay buffer size | 10,000 |
| target network update frequency | 10 |
| batch size | 64 |
| initial value of ε—greedy exploration | 1.0 |
| minimum value of ε—greedy exploration | 0.01 |
| decay rate of ε—greedy | 0.995 |
| Instance | Algorithm | Objective Function Value (CNY 10,000) | Relative Deviation (%) | Computation Time (Seconds) | Standard Deviation (CNY 10,000) |
|---|---|---|---|---|---|
| S1 | CPLEX | 325.42 | - | 0.58 | 0.00 |
| S1 | GA | 327.85 | 0.75 | 3.24 | 3.15 |
| S1 | SA | 328.67 | 1.00 | 2.87 | 4.23 |
| S1 | GA-SA | 326.18 | 0.23 | 2.35 | 1.84 |
| S1 | GA-SA-DQN | 325.65 | 0.07 | 1.98 | 0.95 |
| S2 | CPLEX | 428.56 | - | 0.92 | 0.00 |
| S2 | GA | 432.13 | 0.11 | 4.56 | 4.26 |
| S2 | SA | 433.74 | 0.73 | 4.12 | 5.34 |
| S2 | GA-SA | 429.87 | 0.07 | 3.75 | 2.13 |
| S2 | GA-SA-DQN | 429.15 | 0.13 | 3.05 | 1.24 |
| S3 | CPLEX | 542.67 | - | 1.25 | 0.00 |
| S3 | GA | 548.81 | 1.13 | 6.53 | 5.37 |
| S3 | SA | 550.42 | 1.43 | 5.78 | 6.85 |
| S3 | GA-SA | 544.32 | 0.30 | 4.67 | 2.45 |
| S3 | GA-SA-DQN | 543.28 | 0.11 | 3.85 | 1.28 |
| S4 | CPLEX | 653.89 | - | 2.34 | 0.00 |
| S4 | GA | 662.57 | 0.41 | 8.46 | 7.24 |
| S4 | SA | 665.21 | 0.65 | 7.65 | 8.56 |
| S4 | GA-SA | 656.35 | 0.08 | 6.23 | 3.65 |
| S4 | GA-SA-DQN | 654.72 | 0.58 | 5.12 | 1.87 |
| M1 | CPLEX | 762.34 | - | 12.56 | 0.00 |
| M1 | GA | 776.52 | 1.27 | 24.78 | 8.45 |
| M1 | SA | 780.15 | 1.05 | 22.35 | 10.27 |
| M1 | GA-SA | 768.53 | 0.04 | 16.42 | 5.32 |
| M1 | GA-SA-DQN | 764.68 | 0.55 | 14.28 | 3.15 |
| M2 | CPLEX | 865.27 | - | 26.34 | 0.00 |
| M2 | GA | 883.75 | 2.14 | 35.67 | 11.28 |
| M2 | SA | 886.92 | 2.50 | 32.45 | 13.56 |
| M2 | GA-SA | 872.43 | 0.25 | 22.37 | 6.75 |
| M2 | GA-SA-DQN | 868.56 | 0.38 | 18.64 | 4.23 |
| M3 | CPLEX | 967.32 | - | 38.76 | 0.00 |
| M3 | GA | 989.85 | 3.03 | 42.34 | 14.56 |
| M3 | SA | 994.27 | 0.66 | 39.65 | 16.32 |
| M3 | GA-SA | 976.24 | 0.66 | 25.48 | 8.83 |
| M3 | GA-SA-DQN | 971.53 | 0.17 | 21.74 | 5.26 |
| M4 | CPLEX | 1124.56 | - | 65.23 | 0.00 |
| M4 | GA | 1153.28 | 1.48 | 68.52 | 18.74 |
| M4 | SA | 1159.75 | 2.05 | 64.37 | 21.45 |
| M4 | GA-SA | 1136.48 | 0.004 | 42.36 | 11.24 |
| L1 | CPLEX | 1856.43 | - | 428.75 | 0.00 |
| L1 | GA | 1932.56 | 3.17 | 165.34 | 32.56 |
| L1 | SA | 1945.23 | 1.97 | 153.27 | 38.42 |
| L1 | GA-SA | 1885.27 | 0.52 | 123.45 | 21.35 |
| L1 | GA-SA-DQN | 1868.34 | 0.37 | 98.76 | 12.45 |
| L2 | CPLEX | 2124.68 | - | 765.42 | 0.00 |
| L2 | GA | 2228.54 | 2.07 | 214.56 | 45.78 |
| L2 | SA | 2246.82 | 1.16 | 198.35 | 52.34 |
| L2 | GA-SA | 2162.37 | 0.41 | 156.43 | 28.53 |
| L2 | GA-SA-DQN | 2138.75 | 0.21 | 124.85 | 15.23 |
| L3 | CPLEX | 2356.85 | - | 1245.67 | 0.00 |
| L3 | GA | 2485.46 | 3.16 | 256.78 | 54.85 |
| L3 | SA | 2508.32 | 1.73 | 238.45 | 63.62 |
| L3 | GA-SA | 2402.56 | 0.32 | 184.32 | 32.34 |
| L3 | GA-SA-DQN | 2372.43 | 0.24 | 145.63 | 18.76 |
| L4 | CPLEX | 2845.32 | - | 2856.45 | 0.00 |
| L4 | GA | 3126.78 | 9.9 | 342.56 | 74.35 |
| L4 | SA | 3658.24 | 28.6 | 318.67 | 85.24 |
| L4 | GA-SA | 2608.67 | 8.3 | 242.85 | 42.56 |
| L4 | GA-SA-DQN | 2467.85 | 13.3 | 187.42 | 24.35 |
| Cost Category | Scenario A | Scenario B | Scenario C |
|---|---|---|---|
| Transportation Cost | 4562.8 | 4285.3 | 4318.6 |
| Environmental Cost | 783.5 | 498.2 | 512.7 |
| Congestion Cost | 625.4 | 267.8 | 293.2 |
| Carbon Tax/Subsidy Cost | 143.2 | 79.5 | 85.3 |
| Total Cost | 6114.9 | 5130.8 | 5209.8 |
| Reduction Compared to Scenario A | - | 16.1% | 14.8% |
| Transportation Mode | Scenario A | Scenario B | Scenario C |
|---|---|---|---|
| Road | 68.5% | 37.2% | 40.4% |
| Railway | 15.8% | 12.5% | 13.2% |
| Waterway | 15.7% | 10.3% | 11.4% |
| Underground Logistics System | 0.0% | 40.0% | 35.0% |
| Total | 100.0% | 100.0% | 100.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Liang, C.; Wang, Y.; Biancardo, S.A. Maritime Port Freight Flow Optimization with Underground Container Logistics Systems Under Demand Uncertainty. J. Mar. Sci. Eng. 2025, 13, 1173. https://doi.org/10.3390/jmse13061173
Sun M, Liang C, Wang Y, Biancardo SA. Maritime Port Freight Flow Optimization with Underground Container Logistics Systems Under Demand Uncertainty. Journal of Marine Science and Engineering. 2025; 13(6):1173. https://doi.org/10.3390/jmse13061173
Chicago/Turabian StyleSun, Miaomiao, Chengji Liang, Yu Wang, and Salvatore Antonio Biancardo. 2025. "Maritime Port Freight Flow Optimization with Underground Container Logistics Systems Under Demand Uncertainty" Journal of Marine Science and Engineering 13, no. 6: 1173. https://doi.org/10.3390/jmse13061173
APA StyleSun, M., Liang, C., Wang, Y., & Biancardo, S. A. (2025). Maritime Port Freight Flow Optimization with Underground Container Logistics Systems Under Demand Uncertainty. Journal of Marine Science and Engineering, 13(6), 1173. https://doi.org/10.3390/jmse13061173







