Monocular Unmanned Boat Ranging System Based on YOLOv11-Pose Critical Point Detection and Camera Geometry
Abstract
1. Introduction
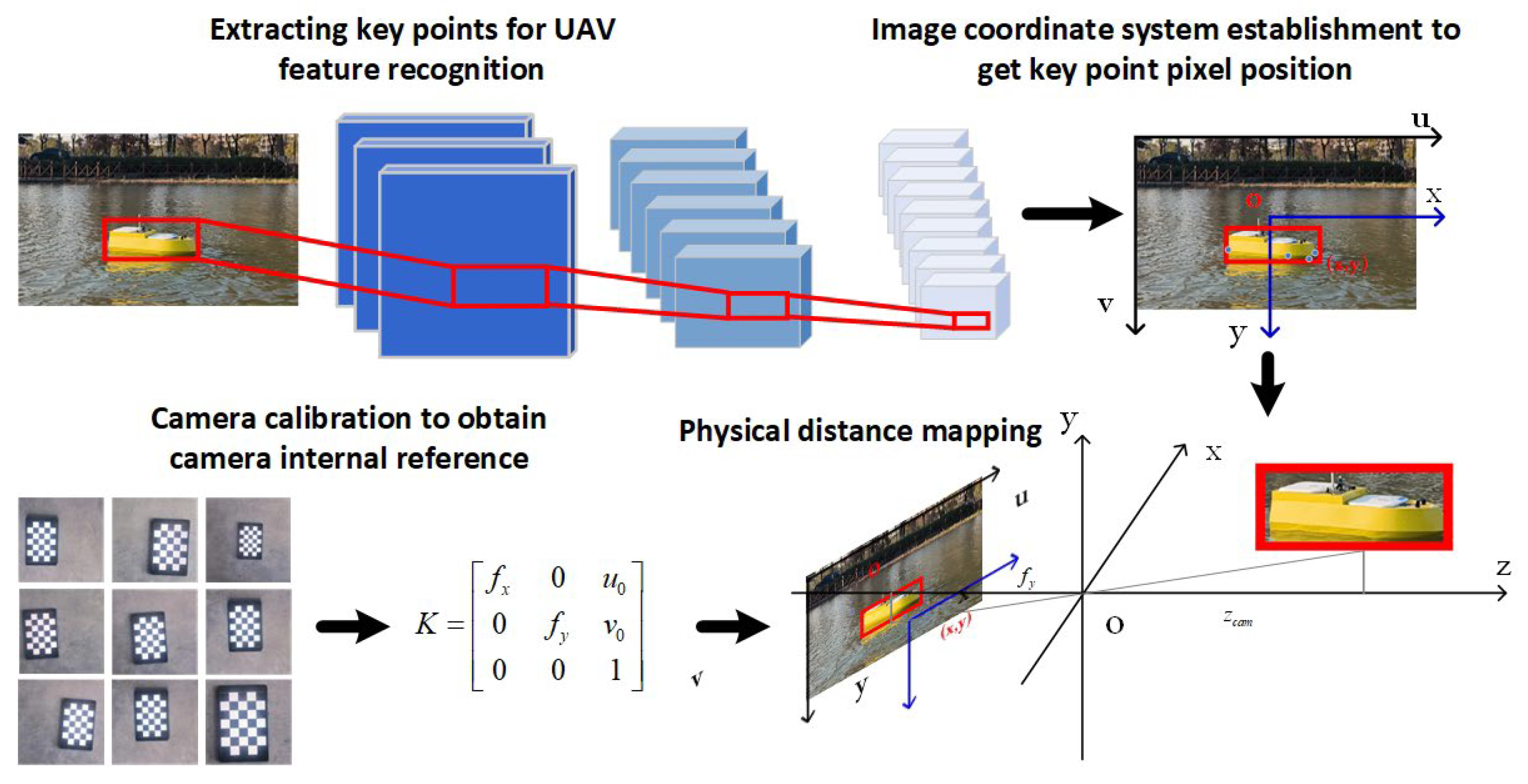
2. Ranging Principle
2.1. Ranging Model Framework
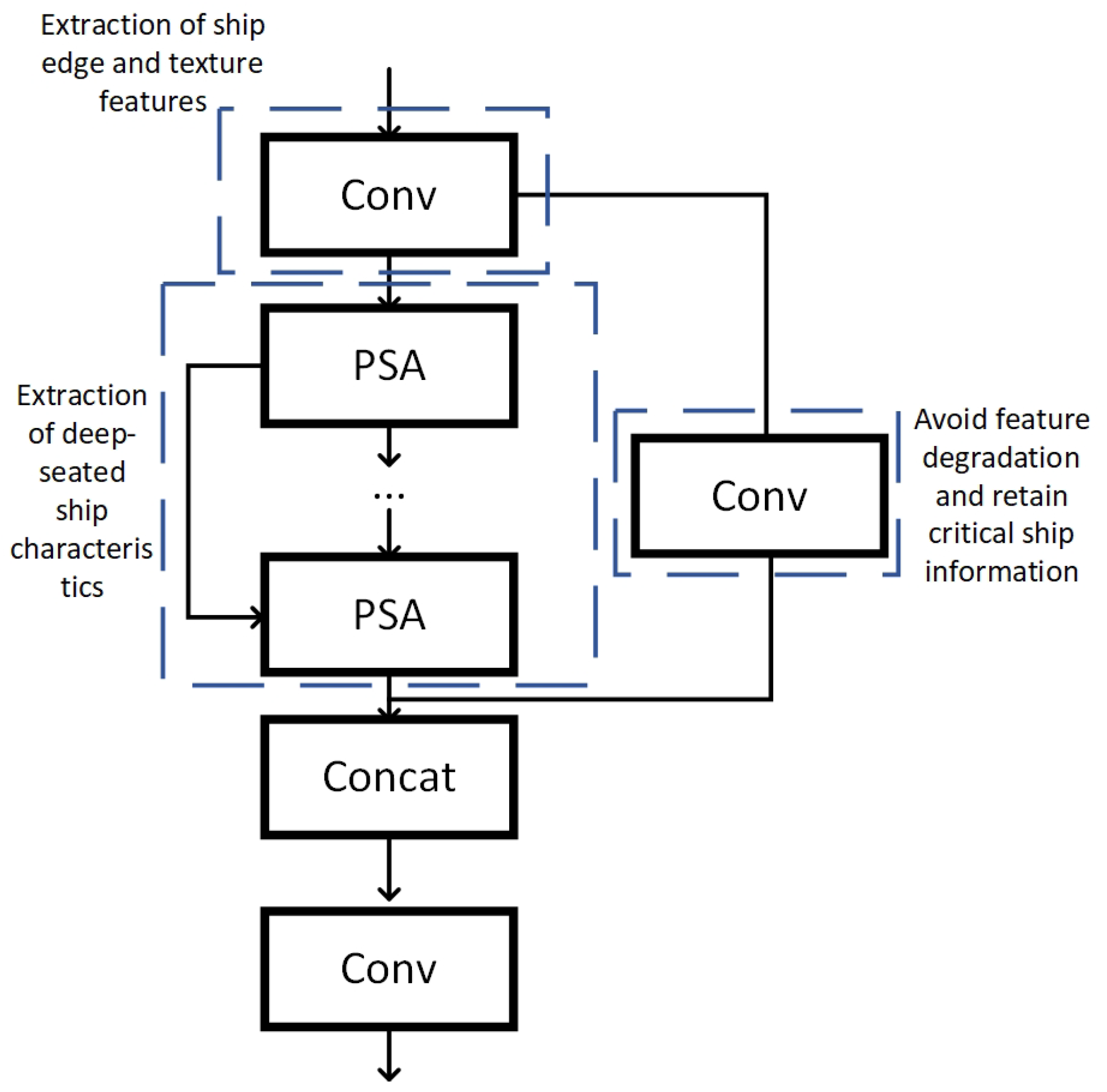
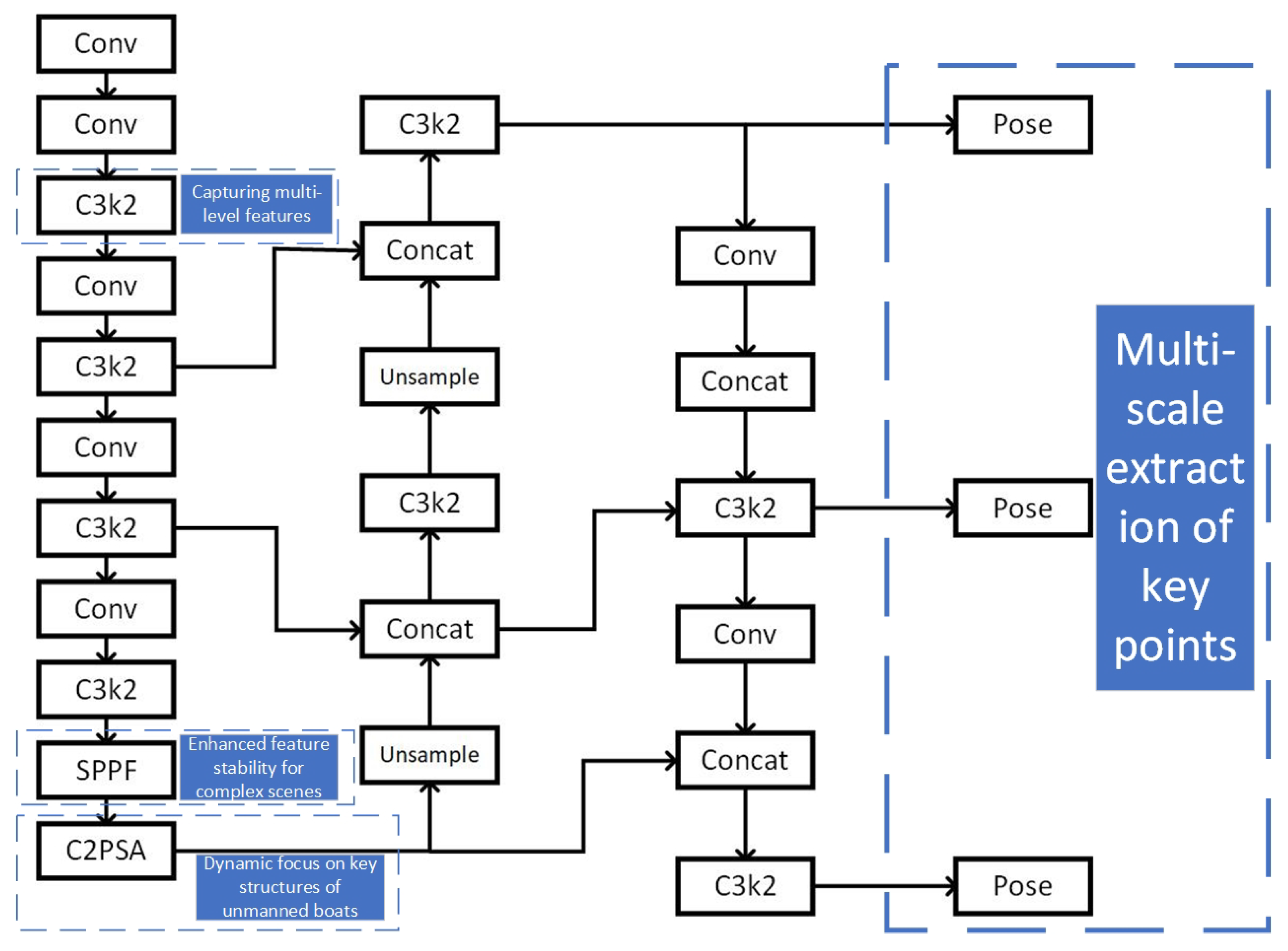
2.2. Critical Point Detection Model
2.3. Key Point Selection
3. Camera Internal Reference Calibration
4. Physical Distance Mapping Principle
5. Experimental Verification
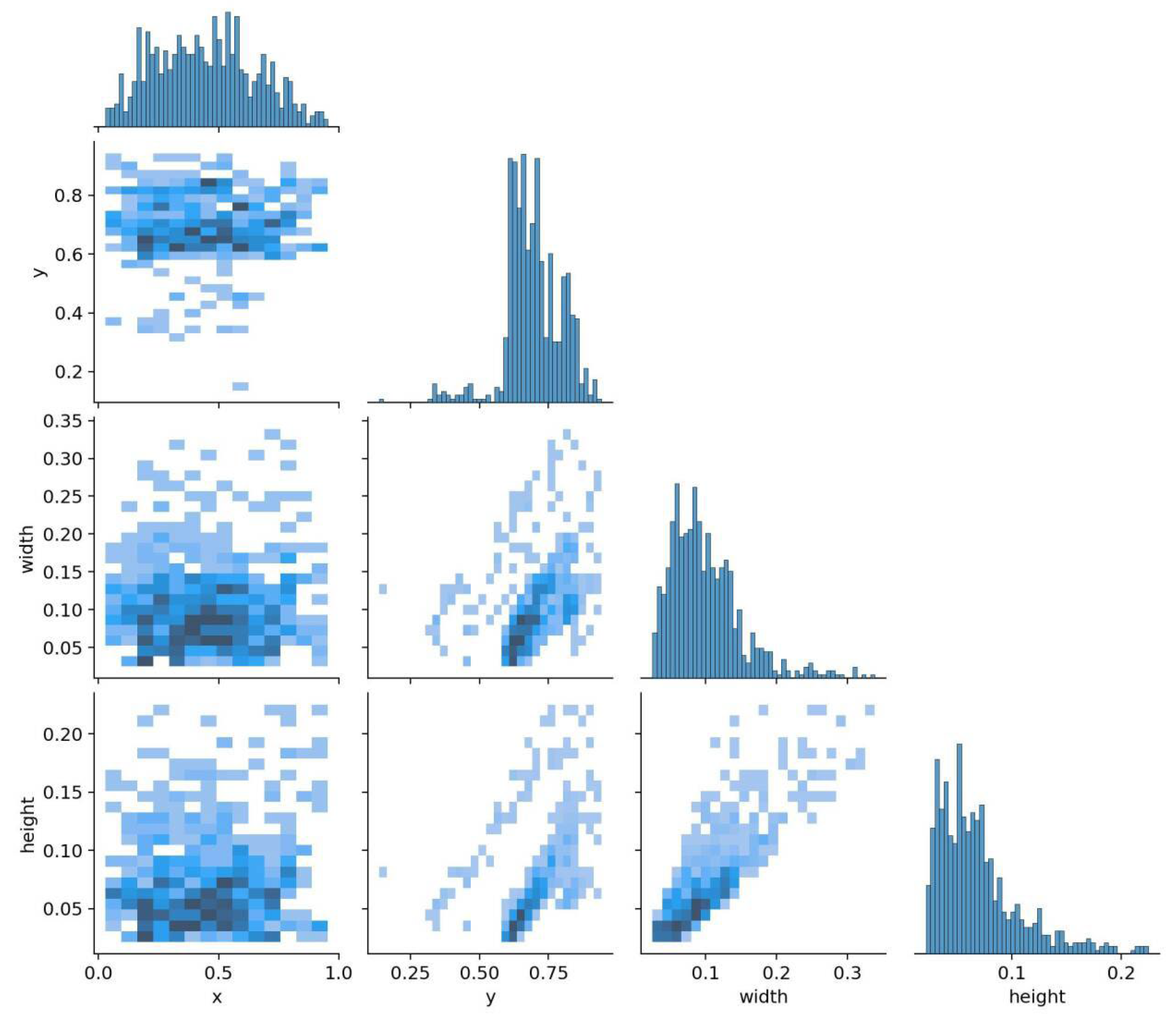
5.1. Introduction to the Dataset
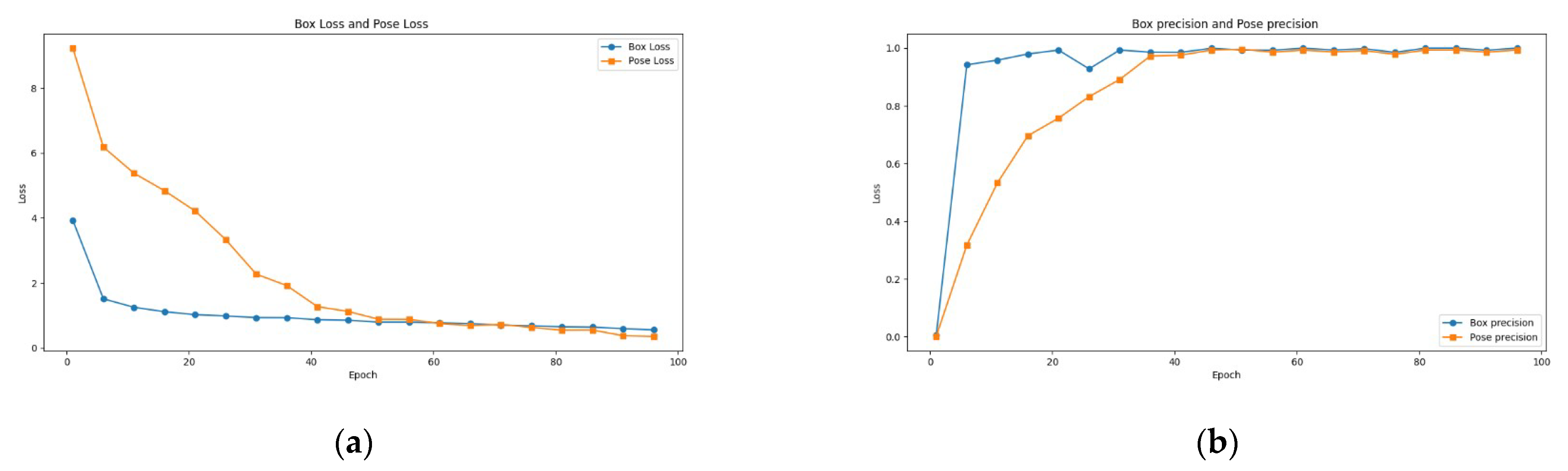
5.2. Model Training
5.3. Comparative Testing of Key Point Detection
5.4. Distance Mapping Comparison Test
5.5. Sensitivity Analysis
5.6. Analysis of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ismail, A.H.; Song, X.; Ouelhadj, D.; Al-Behadili, M.; Fraess-Ehrfeld, A. Unmanned surface vessel routing and unmanned aerial vehicle swarm scheduling for off-shore wind turbine blade inspection. Expert Syst. Appl. 2025, 284, 127534. [Google Scholar] [CrossRef]
- Novák, F.; Báča, T.; Procházka, O.; Saska, M. State estimation of marine vessels affected by waves by unmanned aerial vehicles. Ocean. Eng. 2025, 323, 120606. [Google Scholar] [CrossRef]
- Ng, Y.H.; Hou, Y.; Yuan, Y.; Chang, C.W. Underactuated Unmanned Surface Vessel Coverage Path Planning for Marine Pier Inspection. In Proceedings of the OCEANS 2024-Singapore, Singapore, 15–18 April 2024. [Google Scholar]
- Nguyen, T.-T.; Hamesse, C.; Dutrannois, T.; Halleux, T.; De Cubber, G.; Haelterman, R.; Janssens, B. Visual-based localization methods for unmanned aerial vehicles in landing operation on maritime vessel. Acta IMEKO 2024, 13, 1–13. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, J.; Zhang, X.; Xu, H.; Soares, C.G. Unmanned Surface Vessel–Unmanned Aerial Vehicle Cooperative Path Following Based on a Predictive Line of Sight Guidance Law. J. Mar. Sci. Eng. 2024, 12, 1818. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X. Enhancing offshore parcel delivery efficiency through vessel-unmanned aerial vehicle collaborative routing. Int. J. Prod. Res. 2024, 63, 1–27. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Pei, X.; Wang, T.; Hou, T.; Yang, X. Bioinspiration review of aquatic unmanned aerial vehicle (AquaUAV). Biomim. Intell. Robot. 2024, 4, 100154. [Google Scholar] [CrossRef]
- Collin, A.; James, D.; Lamontagne, N.; Hardy, R.; Monpert, C.; Feunteun, E. Ultra-high-resolution bathymetry estimation using a visible airborne drone, photogrammetry and neural network. In Proceedings of the XVIIIèmes Journées Nationales Génie Côtier—Génie Civil, Anglet, France, 27 June 2024. [Google Scholar]
- Ding, G.; Liu, J.; Li, D.; Fu, X.; Zhou, Y.; Zhang, M.; Li, W.; Wang, Y.; Li, C.; Geng, X. A Cross-Stage Focused Small Object Detection Network for Unmanned Aerial Vehicle Assisted Maritime Applications. J. Mar. Sci. Eng. 2025, 13, 82. [Google Scholar] [CrossRef]
- Li, J.; Liu, Q.; Lai, J.; Li, R. A Novel Marine Ranching Cages Positioning System on Unmanned Surface Vehicles Using LiDAR and Monocular Camera Fusion. In Proceedings of the 2024 14th International Conference on Information Science and Technology (ICIST), Chengdu, China, 6–9 December 2024. [Google Scholar]
- Vergine, V.; Benvenuto, F.L.; de Giuseppe, S.; Spedicato, M.; Largo, A. An Innovative Monitoring System Based on UAV and Auto-Remote Surface Vessel. In Proceedings of the 2024 9th International Conference on Smart and Sustainable Technologies (SpliTech), Bol and Split, Croatia, 25–28 June 2024. [Google Scholar]
- Zhang, G.; Zhang, G.; Yang, H.; Wang, C.; Bao, W.; Chen, W.; Cao, J.; Du, H.; Zhao, Z.; Liu, C. Flexible on-orbit calibration for monocular camera and laser rangefinder integrated pose measurement system. IEEE Trans. Instrum. Meas. 2023, 72, 1–16. [Google Scholar] [CrossRef]
- Liu, M.; Feng, G.; Liu, F.; Wei, Z. Accurate 3D Positioning of Aircraft Based on Laser Rangefinder Combining Monocular Vision Measurement. IEEE Trans. Instrum. Meas. 2024, 73, 5036613. [Google Scholar]
- Tang, Z.; Xu, C.; Yan, S. A laser-assisted depth detection method for underwater monocular vision. Multimed. Tools Appl. 2024, 83, 64683–64716. [Google Scholar] [CrossRef]
- Trinh, H.L.; Kieu, H.T.; Pak, H.Y.; Pang, D.S.C.; Tham, W.W.; Khoo, E.; Law, A.W.-K. A comparative study of multi-rotor unmanned aerial vehicles (UAVs) with spectral sensors for real-time turbidity monitoring in the coastal environment. Drones 2024, 8, 52. [Google Scholar] [CrossRef]
- Kieu, H.T.; Yeong, Y.S.; Trinh, H.L.; Law, A.W.-K. Enhancing turbidity predictions in coastal environments by removing obstructions from unmanned aerial vehicle multispectral imagery using inpainting techniques. Drones 2024, 8, 555. [Google Scholar] [CrossRef]
- Xie, Z.; Yang, C. Binocular Visual Measurement Method Based on Feature Matching. Sensors 2024, 24, 1807. [Google Scholar] [CrossRef]
- Yang, M.; Qiu, Y.; Wang, X.; Gu, J.; Xiao, P. System structural error analysis in binocular vision measurement systems. J. Mar. Sci. Eng. 2024, 12, 1610. [Google Scholar] [CrossRef]
- Nguyen, K.; Dang, T.; Huber, M. Real-time 3d semantic scene perception for egocentric robots with binocular vision. arXiv 2024, arXiv:240211872. [Google Scholar]
- Wei, B.; Liu, J.; Li, A.; Cao, H.; Wang, C.; Shen, C.; Tang, J. Remote distance binocular vision ranging method based on improved YOLOv5. IEEE Sens. J. 2024, 24, 11328–11341. [Google Scholar] [CrossRef]
- Lv, H.; Du, Y.; Ma, Y.; Yuan, Y. Object detection and monocular stable distance estimation for road environments: A fusion architecture using yolo-redeca and abnormal jumping change filter. Electronics 2024, 13, 3058. [Google Scholar] [CrossRef]
- Li, J.; Zheng, H.; Cui, Z.; Huang, Z.; Liang, Y.; Li, P.; Liu, P. D-LDRNet: Monocular vision framework merging prior LiDAR knowledge for all-weather safe monitoring of vehicle in transmission lines. IEEE Trans. Intell. Veh. 2024, 1–13. [Google Scholar] [CrossRef]
- Liu, J.; Xu, D. A vehicle monocular ranging method based on camera attitude estimation and distance estimation networks. World Electr. Veh. J. 2024, 15, 339. [Google Scholar] [CrossRef]
- Li, C.; Yue, C.; Liu, Y.; Bie, M.; Li, G.; Lv, Z.; Li, J. An Improved MonoDepth2 Algorithm for Vehicle Monocular Depth Estimation. Optik 2024, 311, 171936. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Lv, X.; Zhao, R. Intelligent Monocular Visual Dynamic Detection Method for Safe Distance of Hot Work Operation. In Proceedings of the 2025 IEEE 5th International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 17–19 January 2025. [Google Scholar]
- Wang, J.; Guan, Y.; Kang, Z.; Chen, P. A robust monocular and binocular visual ranging fusion method based on an adaptive UKF. Sensors 2024, 24, 4178. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Shi, Z.; Xu, X.; Wu, G.; Li, H.; Wen, S. Target localization and grasping of NAO robot based on YOLOv8 network and monocular ranging. Electronics 2023, 12, 3981. [Google Scholar] [CrossRef]
- Qin, Q.; Qiu, C.; Zhang, Z. A Monocular Ranging Method Based on YOLOv8 for UAV Formation. In Proceedings of the 2024 4th International Conference on Computer, Control and Robotics (ICCCR), Shanghai, China, 19–21 April 2024. [Google Scholar]
- Parikh, D.; Khowaja, H.; Thakur, R.K.; Majji, M. Proximity operations of CubeSats via sensor fusion of ultra-wideband range measurements with rate gyroscopes, accelerometers and monocular vision. arXiv 2024, arXiv:240909665. [Google Scholar]
- Ott, N.; Flegel, T.; Bevly, D. Vehicle to Pedestrian Relative State Estimation via Fusing Ultrawideband Radios and a Monocular Camera; SAE International: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Wang, Z.; Li, X.; Chen, P.; Luo, D.; Zheng, G.; Chen, X. A Monocular Ranging Method for Ship Targets Based on Unmanned Surface Vessels in a Shaking Environment. Remote Sens. 2024, 16, 4220. [Google Scholar] [CrossRef]
- Wang, G.; Huang, J. Unmanned Ship Ranging and Error Correction Method Based on Monocular Vision. In Proceedings of the 2023 International Conference on Intelligent Perception and Computer Vision (CIPCV), Hangzhou, China, 19–21 May 2023. [Google Scholar]
- Zhang, Z. Flexible camera calibration by viewing a plane from unknown orientations. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999; Volume 1, pp. 666–673. [Google Scholar]
- Zou, Y.; Xiao, G.; Li, Q.; Biancardo, S.A. Intelligent Maritime Shipping: A Bibliometric Analysis of Internet Technologies and Automated Port Infrastructure Applications. J. Mar. Sci. Eng. 2025, 13, 979. [Google Scholar] [CrossRef]
- Xiao, G.; Pan, L.; Lai, F. Application, opportunities, and challenges of digital technologies in the decarbonizing shipping industry: A bibliometric analysis. Front. Mar. Sci. 2025, 12, 1523267. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. Event-Driven Based Reinforcement Learning Predictive Controller Design for Three-Phase NPC Converters Using Online Approximators. IEEE Trans. Power Electron. 2024, 40, 4914–4926. [Google Scholar] [CrossRef]
- Chen, X.; Hu, R.; Luo, K.; Wu, H.; Biancardo, S.A.; Zheng, Y.; Xian, J. Intelligent ship route planning via an A∗ search model enhanced double-deep Q-network. Ocean. Eng. 2025, 327, 120956. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, H.; Liang, Z.; Liu, A.; Ni, H.; Wang, Y. A phase search-enhanced Bi-RRT path planning algorithm for mobile robots. Intell. Robot. 2025, 5, 404–418. [Google Scholar] [CrossRef]
- Zeng, T.; Zhu, D.; Gu, C.; Yang, S.X. An effective fault-tolerant control with slime mold algorithm for unmanned underwater vehicle. Intell. Robot. 2025, 5, 276–291. [Google Scholar] [CrossRef]
- Meng, Y.; Liu, C.; Zhao, J.; Huang, J.; Jing, G. Stackelberg game-based anti-disturbance control for unmanned surface vessels via integrative reinforcement learning. Intell. Robot. 2025, 5, 88–104. [Google Scholar] [CrossRef]





| Parameter Type | Parameter Value |
|---|---|
| Epoch | 100 |
| Batch size | 8 |
| Initial learning rate | 0.01 |
| Weight decay | 0.0005 |
| Box loss weights | 7.5 |
| Categorised loss weights | 0.5 |
| Weights for pose | 12 |
| IOU | 0.7 |
| Precision-Pose | Recall-Pose | mAP50-Pose | mAP50-95-Pose | |
|---|---|---|---|---|
| Yolov8-pose | 0.691 | 0.602 | 0.618 | 0.276 |
| Yolov8-pose-P6 | 0.883 | 0.767 | 0.787 | 0.518 |
| Yolov11n-pose | 0.545 | 0.418 | 0.322 | 0.206 |
| Yolov11s-pose | 0.817 | 0.697 | 0.714 | 0.451 |
| Yolov11l-pose | 0.917 | 0.789 | 0.825 | 0.567 |
| Yolov11x-pose | 0.935 | 0.813 | 0.890 | 0.670 |
| Yolov11m-pose | 0.940 | 0.845 | 0.898 | 0.757 |
| Based on Detection Frame | Based on Key Points | |||||
|---|---|---|---|---|---|---|
| MSE | RMSE | MAE | MSE | RMSE | MAE | |
| Scene I | 0.395 | 0.628 | 0.508 | 0.284 | 0.533 | 0.416 |
| Scene II | 2.395 | 1.548 | 1.182 | 1.942 | 1.394 | 1.051 |
| Scene III | 0.918 | 0.958 | 0.720 | 0.917 | 0.957 | 0.716 |
| Scene IV | 2.859 | 1.691 | 1.288 | 2.841 | 1.686 | 1.466 |
| Scene V | 1.096 | 1.047 | 0.869 | 0.343 | 0.586 | 0.470 |
| Scene VI | 3.173 | 1.782 | 1.499 | 2.570 | 1.603 | 1.258 |
| Precision-Pose | Recall-Pose | mAP50-Pose | mAP50-95-Pose | |
|---|---|---|---|---|
| 50epoch | 0.903 | 0.708 | 0.758 | 0.524 |
| 60epoch | 0.912 | 0.749 | 0.812 | 0.654 |
| 70epoch | 0.917 | 0.771 | 0.836 | 0.688 |
| 80epoch | 0.933 | 0.823 | 0.868 | 0.719 |
| 90epoch | 0.936 | 0.827 | 0.872 | 0.762 |
| 100epoch | 0.940 | 0.845 | 0.898 | 0.757 |
| MSE | RMSE | MAE | |
|---|---|---|---|
| original + 150 | 1.817 | 1.348 | 1.174 |
| original + 100 | 1.674 | 1.294 | 1.144 |
| original + 50 | 1.552 | 1.246 | 1.111 |
| original | 1.452 | 1.205 | 1.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Suo, Y.; Chen, X.; Yang, Y.; Zhang, H.; Wang, Z.; Postolache, O. Monocular Unmanned Boat Ranging System Based on YOLOv11-Pose Critical Point Detection and Camera Geometry. J. Mar. Sci. Eng. 2025, 13, 1172. https://doi.org/10.3390/jmse13061172
Wu Y, Suo Y, Chen X, Yang Y, Zhang H, Wang Z, Postolache O. Monocular Unmanned Boat Ranging System Based on YOLOv11-Pose Critical Point Detection and Camera Geometry. Journal of Marine Science and Engineering. 2025; 13(6):1172. https://doi.org/10.3390/jmse13061172
Chicago/Turabian StyleWu, Yuzhen, Yucheng Suo, Xinqiang Chen, Yongsheng Yang, Han Zhang, Zichuang Wang, and Octavian Postolache. 2025. "Monocular Unmanned Boat Ranging System Based on YOLOv11-Pose Critical Point Detection and Camera Geometry" Journal of Marine Science and Engineering 13, no. 6: 1172. https://doi.org/10.3390/jmse13061172
APA StyleWu, Y., Suo, Y., Chen, X., Yang, Y., Zhang, H., Wang, Z., & Postolache, O. (2025). Monocular Unmanned Boat Ranging System Based on YOLOv11-Pose Critical Point Detection and Camera Geometry. Journal of Marine Science and Engineering, 13(6), 1172. https://doi.org/10.3390/jmse13061172









