Next Article in Journal
Research on Power Conversion and Control Technology of Ocean Buoy Tidal Energy Power Supply System
Previous Article in Journal
Stock Assessment of Marine Elasmobranchs (Sharks and Rays) in the Bay of Bengal, Bangladesh
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 13
Issue 6
10.3390/jmse13061127
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Colloidal Silica-Stabilized Subgrade for Self-Sensing Vehicle Stress Affected by Unsaturation and Crack

by
Shuaishuai Ruan
1,2,*,
Weifeng Jin
3,* and
Xiaohui Liao
3
1
College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310023, China
2
Automobile School, Zhejiang Institute of Communications, Hangzhou 311112, China
3
School of Civil Engineering and Architecture, Zhejiang University of Science and Technology, Hangzhou 310023, China
*
Authors to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2025, 13(6), 1127; https://doi.org/10.3390/jmse13061127
Submission received: 23 April 2025 / Revised: 26 May 2025 / Accepted: 29 May 2025 / Published: 5 June 2025
(This article belongs to the Section Ocean Engineering)
Browse Figures
Versions Notes

Abstract

Colloidal silica can seep through calcareous sand in the subgrade, forming colloidal-silica-cemented sand with self-sensing ability—that is, it is sensitive to stress changes caused by vehicle loading. Its self-sensing sensitivity is higher than that of traditional Portland-cement-based self-sensing materials. The self-sensing mechanism is attributed to the ionic conductive network formed by seawater. However, a change in tidal water level causes an unsaturated state, and foundation deformation leads to cracking of the roadbed. The effect of unsaturation and cracking on self-sensing remains unclear, and they have not been studied in the previous literature. The aim of this paper is to study the self-sensing ability of subgrades formed via colloidal-silica-cemented sand under unsaturated and cracked states, as well as to explore the underlying mechanisms. Specimens with different degrees of saturation and different levels of joint roughness in precracks were prepared; then, the self-sensing ability was tested using the four-electrode method for each specimen under cyclic stress loading. NMR (nuclear magnetic resonance) and an unsaturated triaxial apparatus were also used to investigate the underlying mechanisms. This paper discovers that (1) either unsaturation or crack alone can increase self-sensing, but their self-sensing sensitivities are on the same order; (2) under the coupled effect of unsaturation and cracking, the self-sensing sensitivity increases by one order of magnitude, which is higher than when only unsaturation or cracking exists; and (3) the joint roughness of precracks does not affect self-sensing in the saturated state, but it affects self-sensing dramatically in the unsaturated state. The NMR test demonstrated the conductive ionic water within nanopores, which forms the conductive network for self-sensing. Unsaturation causes suction-induced shrinkage based on the unsaturated triaxial apparatus, while unsaturation increases self-sensing sensitivity, indicating that shrinkage is accompanied by self-sensing improvement. This paper provides the effects of unsaturation and cracking on the self-sensing capabilities of colloidal-silica-cemented sand, and the findings can contribute to the knowledge of subgrades formed via colloidal-silica-cemented sand for stress-sensing under traffic loading.

1. Introduction

Colloidal silica can seep through a calcareous sand-based subgrade to form colloidal-silica-cemented sand that has self-sensing abilities. Colloidal silica consists of stably suspended nano-silica particles repelling each other in water. After adding salt, the repulsive forces between the nano-silica particles vanish, and then the nano-silica particles bond together and form a solid silica gel that cements the sand. For engineering applications, attributed to its low viscosity, colloidal silica can seep through sand like water over long distances [1,2,3,4]. This characteristic of colloidal silica can be utilized to seep through the subgrade for a long distance beneath the pavement and subbase, and then colloidal silica transforms into solid silica gel to stabilize the sand without the need to demolish the upper structure of the roadbed, such as the pavement. For example, at Fukuoka International Airport, colloidal silica was used to seep through the sand under the runway, thereby stabilizing the ground [5]. The mechanical characteristics of colloidal-silica–cemented sand have been widely studied, e.g., Gallagher et al. [6] studied the site liquefaction resistance of colloidal-silica–cemented sand, centrifuge tests were performed to study its liquefaction characteristics [7,8], and element-level tests have also been widely performed, such as triaxial tests [9,10,11,12,13,14]. Recently, Jin et al. [15] also discovered that colloidal-silica-cemented sand has self-sensing abilities, and its self-sensing sensitivity is higher than that of Portland-cement-based self-sensing materials. This self-sensing ability is due to the ionic conductive network formed via micropores in the silica gel filled with conductive seawater, and it can be used in marine environments. Due to its self-sensing ability, it is sensitive to stress changes and can perceive vehicle loads. However, the previous literature mainly studied it in a saturated state, while subgrade stabilized with colloidal silica needs to withstand unsaturated and cracking conditions. The difference between the saturated and unsaturated states is that, in the saturated state, only effective stress is needed to describe the mechanical behavior of soil, while in the unsaturated state (also called partially saturated), air pressure is added, and we need two variables to describe the mechanical behavior of the soil, i.e., one variable is net stress σnet, and the other is matrix suction ψ. Here, σnet = σ − ua, and ψ = u − uw, where σ is the total stress, ua is the air pressure, and uw is the pore water pressure. So, here, unsaturation implies the coupled effect of air pressure, pore water pressure, and the skeleton stress of the solid phase [16]. The effects of unsaturation and cracking on the self-sensing ability of colloidal-silica-cemented sand remain unknown, which needs further exploration.
Self-sensing abilities have attracted wide attention [17,18,19,20,21,22,23]. Previous studies have mainly focused on Portland-cement-based materials. Note that Portland-cement-based materials cannot exhibit self-sensing capabilities without conductive fillers. The self-sensing characteristics of Portland-cement-based materials have been applied to traffic stress sensing. For example, Han et al. [19] used the carbon-nanotube-dispersed cement in pavements to sense vehicle loadings, and the results show that the responses to repeated vehicle loadings are sensitive, indicating that such self-sensing materials can be used for traffic monitoring. The effect of carbon nanotubes (CNTs) on self-sensing ability has been widely studied, e.g., Gupta et al. [24] analyzed the effects of CNTs on the self-sensing concrete, Meoni et al. [21] investigated the static and dynamic self-sensing characteristics, Parvaneh et al. [25] studied self-sensing smart concretes, D’Alessandro et al. [26] investigated the effect of scalable fabrication procedures on self-sensing, Siad et al. [27] studied the combined characteristics of self-healing and self-sensing, and Yin et al. [28] increased self-sensing sensitivity by adding Ni nanofibers. Another conductive filler is carbon fiber, e.g., Wen and Chung [29] used carbon fibers to sense damage, Al-Dahawi et al. [30] compared the self-sensing characteristics between different carbon-based materials, and Taheri et al. [31] used multiscale carbon fillers for self-sensing. Graphene has also been used as the conductive filler for self-sensing [32,33]. Steel fiber has also been used as a conductive filler for self-sensing [34]. Unlike the mechanism of Portland-cement-based materials, colloidal-silica-cemented sand does not need the addition of conductive fillers, and its self-sensing mechanism is related to conductive ionic water. When colloidal-silica-cemented sand is in an unsaturated state, air enters the void and causes suction, but it is currently unknown how self-sensing ability changes in this unsaturated state.
A research gap is that the previous literature has not provided the self-sensing characteristics of colloidal-silica-cemented calcareous sand under unsaturation and crack conditions. So, the novelty of this paper is that we investigate how unsaturation and cracking affect the self-sensing ability of colloidal-silica-cemented calcareous sand, thus helping to fill the aforementioned research gap. Our research motivation is that colloidal-silica-cemented sand undergoes unsaturation due to changes in seawater level, but we still do not know the unsaturated characteristics of colloidal-silica-cemented sand, and the effect of cracking on the self-sensing of colloidal-silica-cemented sand also remains unknown. So, the objective of this paper is to clarify the effects of unsaturation and cracking on the self-sensing characteristics of colloidal-silica-cemented sand.

2. Experiment

2.1. Materials

The calcareous sand was obtained from the South China Sea. Calcareous sand is fragile and easy to break under low stress levels. If the gradation is changed, the mechanical behavior is changed accordingly. So, when a gradation is chosen, it is necessary to prevent breakage of sand particles. After sieving, the particle size of 0.25–0.5 mm was used, as shown in Figure 1. Table 1 shows the properties of the calcareous sand, and the Chinese standard JTG3430 (JTG, 2020) [35] was used. We used a direct shear test to obtain the shear strength parameter, such as the internal friction angle of calcareous sand. The hydraulic parameter, such as the permeability coefficient, is also listed in Table 1.
Colloidal silica was produced by Qingdao Marine Chemical Co., Ltd. (Qingdao, China). The silica content in the colloidal silica is 40 wt%, the pH value ranges from 9 to 10.5, and the average particle size of nano-silica particles is 14 nm.

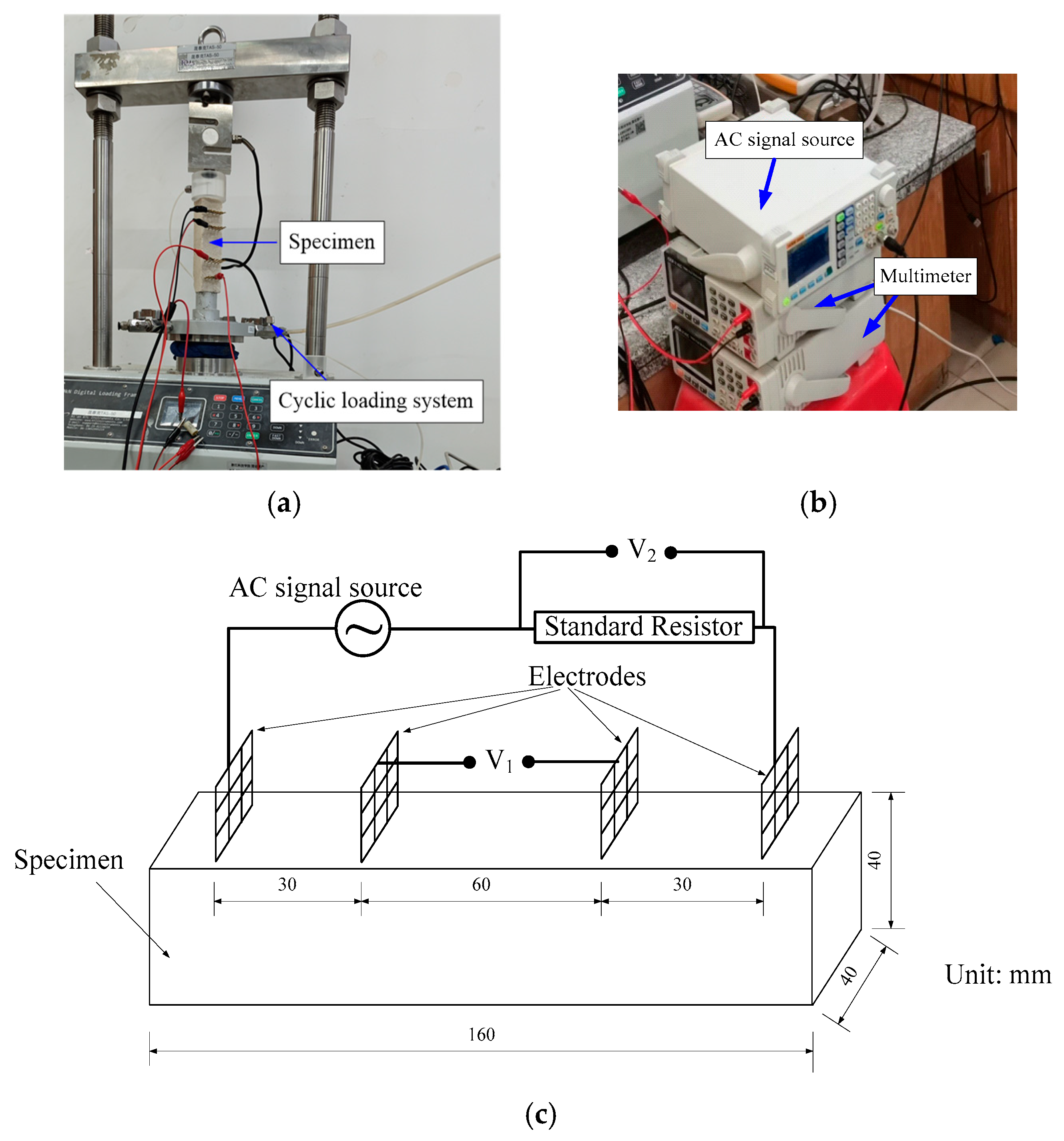
2.2. Specimen Preparation and Testing Plan

2.2.1. Suction Measurement

Suction exists in the unsaturated state. It results from the interaction between water and air in the matrix and causes the matrix to contract [36,37]. Unsaturated specimens for suction measurement were prepared by the following two steps. First, prepare the saturated specimens: put the mixture of 6.25 wt% sodium chloride solution and colloidal silica into the mold (diameter = 61.8 mm and height = 20 mm), with a mass ratio of 0.096:1; using the pluviation method [11,38], sand was poured into the mold; after 24 h, being affected by the coagulant (i.e., sodium chloride), liquid colloidal silica transformed into the silica gel to cement sand particles. Second, saturated specimens were dried in an oven for different hours to obtain the unsaturated specimens with different degrees of saturation, i.e., the drying times are 64 h and 48 h, respectively, with corresponding saturation levels of around 67.5% and 70%, respectively.
Suctions of unsaturated specimens were measured using the filter paper method [39]—that is, the unsaturated specimen and the filter paper were sealed in a container until they reached the state of moisture equilibrium. Then, by measuring the water content of the filter paper, the suction can be obtained by measuring the relationship between water content and the suction. Here, the filter paper, Shuangquan No. 203, was used, and the manufacturer provided the following relationships to calculate the suction:
log ψ = 5 . 493 − 0 . 0767 ω ,   ω ≤ 47 %
log ψ = 2 . 470 − 0 . 0120 ω ,   ω > 47 %
where ψ denotes suction (kPa) and ω denotes the water content (%) within the filter paper. For the filter paper method [39], moisture content is used to describe the filter paper, while the degree of saturation is used to describe the soil. Here, moisture content = water mass/mass of the solid phase of filter paper, and the degree of saturation = water volume/total void volume of the soil. For the filter paper method, the relationship between the moisture content of the filter paper and the suction of soil is utilized; then this suction is combined with the degree of saturation of the soil to plot the soil water retention curve (SWRC) [39].

2.2.2. Self-Sensing Measurement

The rationale of the self-sensing test is that self-sensing materials have piezoresistive properties, i.e., their resistances can change sensitively with stress variation. So the self-sensing sensitivity can be tested by applying cyclic loads while recording the resistance. The size of the self-sensing specimen is 40 mm × 40 mm × 160 mm. For specimen preparation, the process includes placing the mixture of sodium chloride solution and colloidal silica into the mold, as well as pouring sand into the mold by the pluviation method [38], which is the same as in Section 2.2.1. Specimens of colloidal-silica-cemented sand in the molds are shown in Figure 2a. Specimens with and without a precrack were prepared. Four types of precracks were used: plane, JRC9, JRC11, and JRC15, as shown in Figure 2b. The joint roughness coefficient (JRC) was sorted as plane < JRC9 < JRC11 < JRC15. The three roughness curves (i.e., JRC9, JRC11, and JRC15) were obtained from Barton and Coubey’s work [40], which has been widely cited and revisited [41]. Barton’s curves include ten roughness curves, which have been widely used in roughness research. Barton’s curves mean that rock-joint roughness is divided into ten levels, with a roughness variation range of two for each level, resulting in a total of ten joint-roughness curves. For instance, the smoothest one is JRC = 0~2, and the roughest one is JRC = 19~20. Here, JRC9, JRC11, and JRC15 denote Barbon’s curves, JRC = 8~10, JRC = 10~12, and JRC = 14~16, respectively. The reason for choosing these three roughness curves (JRC9, JRC11, and JRC15) is that they are located in the middle of Barton’s ten roughness curves, while it is difficult to keep the shape of the crack surface with a higher roughness coefficient during drying. For the smoothest case, the shape of the precrack is set as a plane. Four types of separators were produced, corresponding to the shapes of four precracks: (1) based on laser cutting, the plane separator was cut from a larger organic glass sheet, and although a 3D printer can also print this plane separator, the price is much higher; and (2) for the other three separators with roughness greater than zero (i.e., with a curved shape), a 3D printer was used, i.e., first import the shape curve data of the separator into the 3D printer, and then this 3D printer automatically printed and solidified resin into the desired curved separator. By inserting the above separators into the molds, precracks can be made (see Figure 2b). Figure 2c shows the specimens with precracks and Figure 2d shows specimens without precracks.
For self-sensing testing, Figure 3a shows the loading system of cyclic stress, Figure 3b shows the AC signal source and multimeters, and Figure 3c shows the circuit diagram for self-sensing. Here the four-probe method was used, i.e., two inner electrodes were used for voltage measurement, while two outer electrodes, a standard resistor, and the AC signal source were connected in series (see Figure 3c). Assuming V1 = voltage on the two inner electrodes in the specimen, V2=voltage on the standard resistor (see Figure 3c), Rs = resistance of the standard resistor, and R = resistance of the specimen, then, according to Ohm’s Law, R can be expressed with Equation (3):
R = V 2 V 1 R s
Let ΔR, A, and L be the increment of R, the cross-section area of the specimen, and the length of the specimen, respectively; then, the resistivity ρ and the increment of resistance Δρ can be expressed with Equations (4) and (5), respectively:
ρ = A L R
Δ ρ = A L Δ R
Fractional change in resistance (FCR) is defined as the ratio of Δρ to ρ. Then FCR can be obtained with Equations (4) and (5), as shown in Equation (6):
FCR = Δ ρ ρ = Δ R R
Self-sensing sensitivity K can be defined as the ratio of FCR to the amplitude of cyclic stress Δσ [22,23], as shown in Equation (7):
K = FCR Δ σ
Table 2 shows the plan for self-sensing testing. For cyclic stress loading, the sinusoidal amplitude is 30 kPa; this stress amplitude is chosen according to Zhao’s (2018) [42] study on the stress response of the subgrade under an airport runway, while the frequency is 0.1 Hz, similar to the stress frequency used for self-sensing pavement in a previous study [23]. For stress sensing, we need to record the resistance change in the specimen, and the four-electrode method was used, and the frequency of the AC signal source was 100 Hz, which was used in the previous literature for self-sensing [16,34]. Specimens with and without precracks were used. Two parallel specimens were tested under the same condition to demonstrate repeatability. For the unsaturated state, specimens were dried in the oven at 40 degrees Celsius for 48 h and 60 h, respectively, with the corresponding degrees of saturation being approximately 70% and 67.5%, respectively. Higher temperature or longer drying time makes the specimen prone to cracking, leading to the difficulty in self-sensing testing. Drying for 60 h causes the bonded sand particles to fall off the surface of the precrack, so only a drying time of 48 h (i.e., the degree of saturation of approximately 70%) is used for the unsaturated state of the specimen with a precrack.

3. Experiment Results and Analysis

Based on suction measurement, Figure 4 shows the soil water retention curve (SWRC), where the degree of saturation decreases with increasing suction. This SWRC describes the unsaturated characteristics of the colloidal-silica-cemented sand.
The test condition for Figure 4 is that the specimen and the dry filter paper were sealed in a container, with the purpose that the filter paper and specimen gradually reach moisture equilibrium. Usually, 14 days is long enough for this moisture equilibrium. So, every 14 days, the moisture content of the filter paper was measured, and it was replaced by a new, dry filter paper. After using several filter papers, the degree of saturation of the specimen gradually decreased (i.e., water in the specimen transferred to the filter paper). At the same time, the variation in the degree of saturation of the specimen was recorded, and the water contents in different filter papers were also recorded. The water content of the filter paper can be used to calculate the suction in the specimen; so, in this way, the soil water retention curve (SWRC), which is expressed as the degree of saturation vs. suction, can be plotted (see Figure 4).
Figure 5, Figure 6 and Figure 7 show FCR (fractional change in resistivity) curves, which are the key and fundamental curves used to assess self-sensing ability. Such FCR curves should be provided after the self-sensing test, according to various self-sensing tests in the previous literature [19,21,22,23,26,29,31,33,34,43,44,45]. The sense of these curves is that, during cyclic stress loading, when the peak absolute value of FCR is larger, the self-sensing ability increases, i.e., the material is more sensitive to stress change.
Figure 5 shows the FCR curves of specimens without precracks. Both parallel specimens show that, as unsaturation increases (i.e., the degree of saturation decreases), FCR increases. So, when without a precrack, self-sensing increases with increasing unsaturation.
Figure 6 shows the effect of cracking on FCR curves in an saturated state. Both parallel sets of specimens show that, as the joint roughness of the precrack varies, the FCR curves are almost the same. So, for the saturated state, the roughness does not affect self-sensing. But comparing Figure 6 with Figure 5, it can be seen that crack improves self-sensing at the saturated state.
Figure 7 shows the coupled effect of unsaturation and cracking on the FCR curves. Both parallel sets of specimens show that, as the joint roughness increases (i.e., the roughness of crack shape increases from plane to JRC15), FCR first increases and then decreases. Therefore, in the unsaturated state, the roughness of the crack can affect self-sensing, which is different from the saturated state. Compared to Figure 5 and Figure 6, Figure 7 shows that, when both unsaturation and a precrack exist, FCR is larger than when only unsaturation or a precrack exists.
Figure 8 shows the effects of unsaturation and precrack on the signal-to-noise ratio (SNR). SNR indicates the smoothness of the curve, i.e., the smoother the FCR curve, the larger the SNR. As unsaturation or roughness increases, SNR does not show obvious regularity. That is, under different degrees of saturation and crack shapes, the range of SNR is between 21 and 27, which is at the same order of magnitude. So, unsaturation and crack shape have no significant effect on SNR. SNR can assess the smoothness of FCR, i.e., higher SNR means a smoother FCR curve. SNR is also provided for self-sensing tests in the previous literature. SNR is related to the smoothness of self-sensing in the topic of this paper.
Figure 9 shows the effects of unsaturation and cracking on self-sensing sensitivity (see the definition in Equation (6)): (1) when no precrack exists, unsaturation improves self-sensing sensitivity, i.e., as the degree of saturation S decreases from 100% to approximately 67.5%, the sensitivity increases from 0.0135%/kPa to 0.0758%/kPa; (2) when a precrack exists, at the saturated state (S = 100%), the crack roughness has no effect on the self-sensing sensitivity, i.e., when the shapes of precracks are plane, JRC9, JRC11, and JRC15, respectively, the corresponding sensitivities are 0.0267%/kPa, 0.028%/kPa, 0.0283%/kPa, and 0.0272%/kPa, respectively, indicating that sensitivity almost does not vary with roughness at the saturated state (sensitivity around 0.027%/kPa); and (3) when both unsaturation and a precrack exist, compared to the case when only unsaturation or a precrack exists, self-sensing sensitivity increases by one order of magnitude, and the self-sensing sensitivity first increases and then decreases with increasing roughness, i.e., when the shapes of the precracks are plane, JRC9, JRC11, and JRC15, respectively, the corresponding self-sensing sensitivities are 0.159%/kPa, 0.185%/kPa, 0.247%/kPa, and 0.233%/kPa, respectively. This sensitivity is used to judge self-sensing ability, i.e., higher sensitivity means higher self-sensing ability. Sensitivity has been provided in the previous literature for assessing self-sensing ability [16,19,29].
Overall, compared to the specimen without a precrack at the saturated state, when only unsaturation or a crack exists, self-sensing sensitivity can increase, but they are still on the same order of magnitude. But when both unsaturation and a precrack exist, self-sensing sensitivity can increase by one order of magnitude.
For traditional Portland cement-based materials with conductive fillers (e.g., CNTs, carbon fibers, steel fibers, and graphene), Table 3 compares the self-sensing sensitivity between this study and previous cement composites. It is shown that, (1) in a saturated state, the self-sensing sensitivity of colloidal-silica-cemented sand is one order higher than cement composites; and (2) when both unsaturation and a precrack exist, self-sensing sensitivity of colloidal-silica-cemented sand is two orders higher than cement composites.

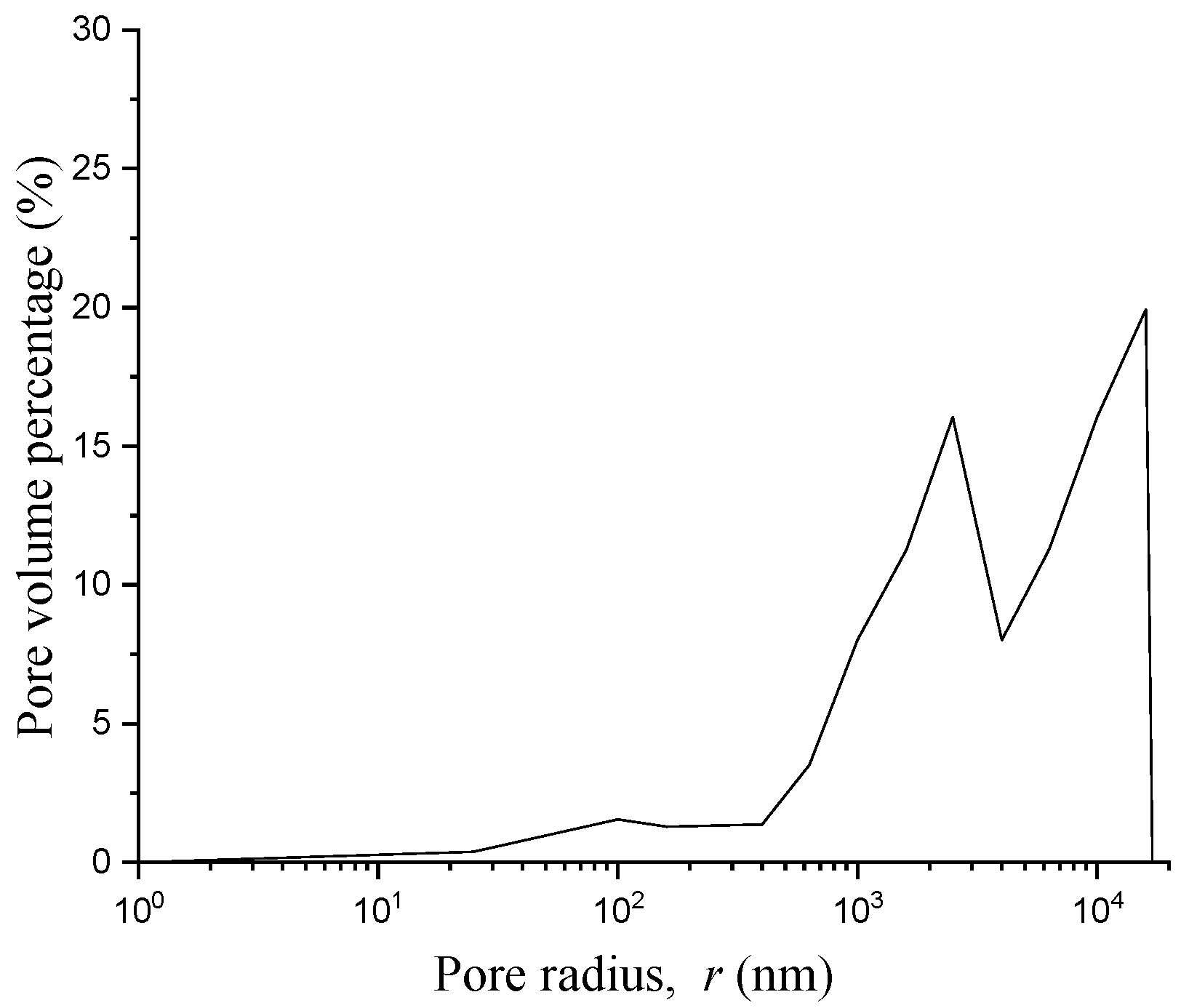
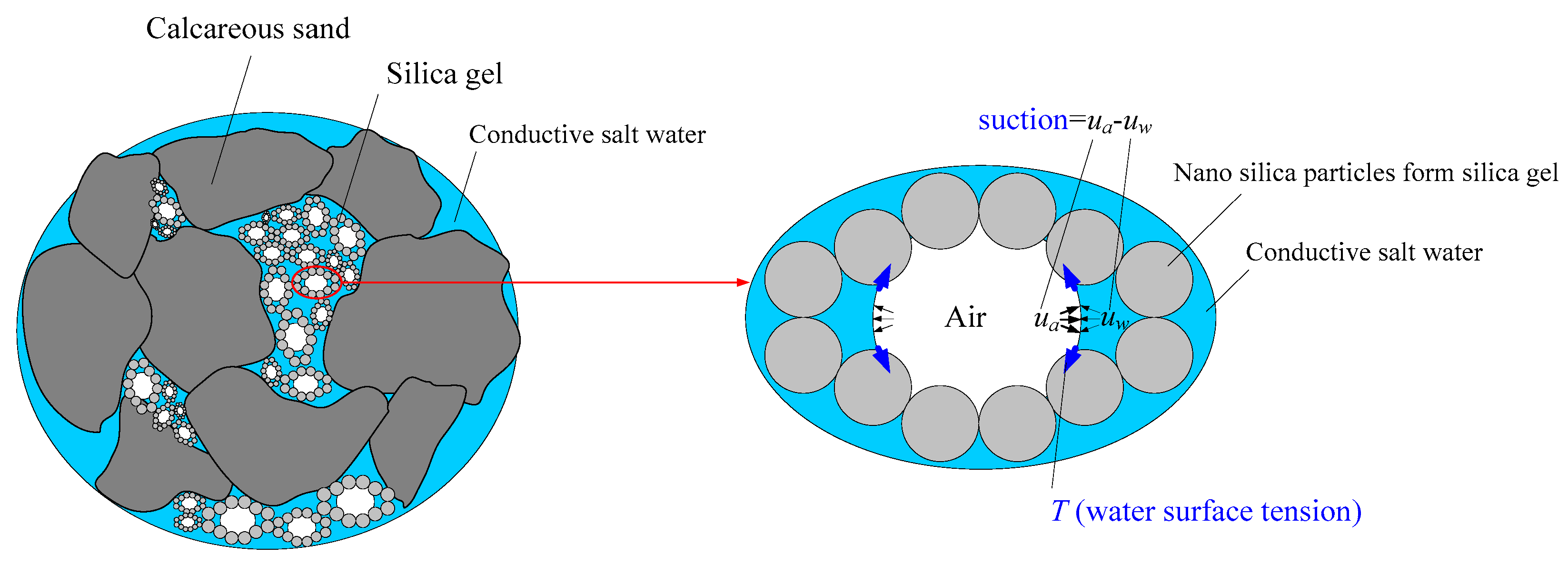
4. Mechanism

Why does colloidal-silica-cemented sand have self-sensing ability (also known as piezoresistivity, where resistance can sensitively respond to stress changes)?
To analyze the mechanism, it is necessary to clarify which materials in the specimen are conductive, since self-sensing is the sensitive resistance of the conductive network that can change with stress. The components of colloidal-silica-cemented sand are silica gel, sand, and saltwater (i.e., conductive ionic water). The saltwater here contains sodium ions, which come from sodium hydroxide (suspension stabilizer for nano-silica particles) and sodium chloride (coagulant accelerator for forming a silica gel); see the specimen preparation in Section 2.2. The conductivity of each material is as follows: (1) the silica gel is not conductive, e.g., after drying the silica gel in the oven, the measured resistance is 52.71 MΩ (see Figure 10), which can be considered as non-conductive; (2) sand is not conductive; and (3) saltwater (i.e., conductive ionic water) is conductive. Therefore, the conductive ability of the specimen arises from saltwater.
NMR (nuclear magnetic resonance) analysis shows that the size of micropores ranges from 25 nm to 25 μm (see Figure 11). So, conductive ionic water in such micro-pores forms the conductive network, which is sensitive to stress change and leads to self-sensing. NMR is used to explore the underlying mechanisms of self-sensing ability. So, NMR is related to the mechanism part of this paper.
Self-sensing ability is improved when the degree of saturation decreases from 100% to 70%, i.e., unsaturation can improve self-sensing, as shown in Section 3. The unsaturation characteristics can be described by the soil water retention curve (SWRC, see Figure 4), which shows that when the degree of saturation decreases from 100% to 70%, the suction increases from 0 kPa to 263 kPa. So, the increase in suction is accompanied by the increase in self-sensing. The previous literature has shown that unsaturation causes suction, which is the difference between air pressure and water pressure [46,47], as shown in Figure 12. Figure 12 is a schematic description not related to a sample.
Figure 13 shows the SEM image of a crack in silica gel. Such cracks can store conductive saltwater to form a conductive network for self-sensing. Since a specimen for SEM must be dried according to SEM operation guidelines, we cannot see the water in the crack for the unsaturated state (i.e., partially saturated).
This suction needs to be balanced by water surface tension, which pulls solid particles tighter (see Figure 12). So, suction causes shrinkage in the skeleton of the colloidal-silica-cemented sand, as demonstrated in Figure 14. By using the GDS unsaturated triaxial apparatus (GDS Instruments, Hook, UK), with the specimen size = diameter 38 mm × height 76 mm, it is shown that, as the suction increases from 0 kPa to 200 kPa, the specimen shrinks, i.e., suction causes a volumetric strain of approximately 1.8% (see Figure 14). So, this shrinkage induced by suction affects the micro-pores partially filled with conductive saltwater, i.e., suction is related to the variation in self-sensing. When the degree of saturation decreases, Figure 14 shows the typical volumetric strain change.

5. Conclusions

Colloidal silica can seep through the sand in the subgrade beneath the upper structures of roadbeds (e.g., the pavement and subbase), attributed to its low viscosity, which is similar to water; then, colloidal silica forms silica gel to stabilize the sand. The benefit of using colloidal silica to seep and stabilize sand is that there is no need to demolish pavement while stabilizing the subgrade. For engineering applications, attributed to the change in sea level, colloidal-silica-cemented sand suffers unsaturation during the drying process, and it is also affected by cracks. But the above two points were not studied in the previous literature. So, this paper aims to obtain the effects of unsaturation and cracking on the self-sensing ability of colloidal-silica-cemented sand. The key points are as follows:
  • For the effect of unsaturation, when without a crack, unsaturation increases self-sensing sensitivity, i.e., as saturation (S) decreases from 100% to 67.5%, sensitivity increases from 0.0135%/kPa to 0.0758%/kPa.
  • For the effect of cracks, when a crack exists, in the saturation state (S = 100%), the crack increases self-sensing sensitivity to around 0.027%/kPa.
  • For the coupled effect of unsaturation and crack, with both unsaturation (S = 70%) and a crack, self-sensing sensitivity increases by one order of magnitude (e.g., 0.247%/kPa), which is greater than when only unsaturation or a crack exists.
  • For the effect from the roughness of a crack, self-sensing sensitivity almost does not change with the roughness of a crack in the saturation state, while self-sensing sensitivity first increases and then decreases with increasing crack roughness in the unsaturated state.
  • For the smoothness of the self-sensing curve, the SNR (signal-to-noise ratio) of the FCR (fractional change in resistivity) curve is almost not affected by unsaturation and cracking.
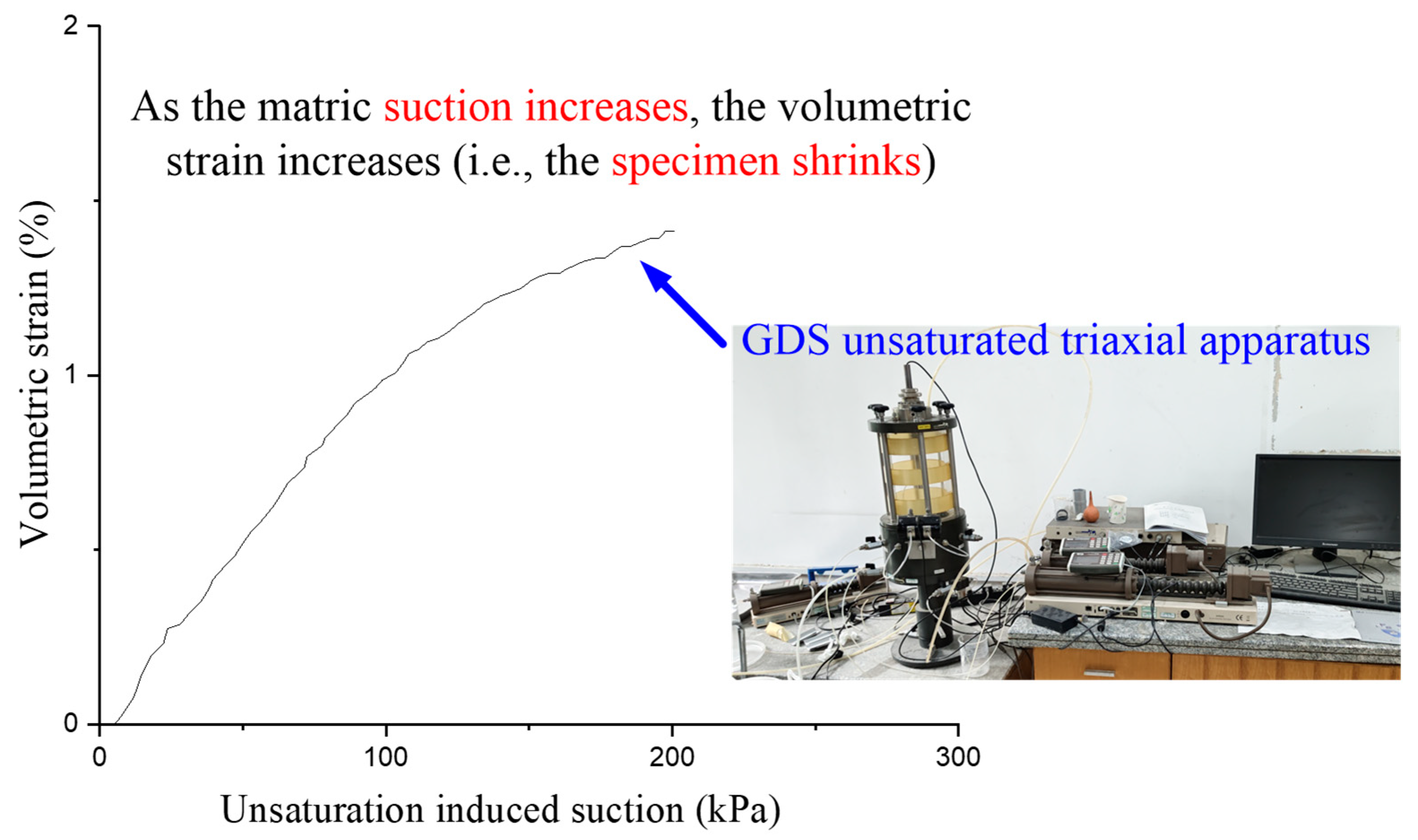
  • For the self-sensing mechanism, the mechanism of the unsaturation-improved self-sensing may be related to suction. Based on the unsaturated triaxial apparatus, it is demonstrated that suction induces shrinkage of the specimen. However, during the increase in suction (i.e., unsaturation increases), self-sensing increases. So, the increase in self-sensing is accompanied by the suction-induced shrinkage.
This study’s impact is that it is the first to provide the effects of unsaturation and cracks on the self-sensing of colloidal-silica-cemented sand, which can be contribute to our knowledge of intelligent subgrades. The sustainability of this study is that it extends the application of colloidal silica for stabilizing subgrades. Overall, colloidal-silica-cemented sand can serve as the intelligent subgrade, but attention should be paid to the effects of unsaturation and cracking on self-sensing.

Author Contributions

S.R., Conceptualization, Formal analysis, Funding acquisition, Methodology, Writing—original draft; W.J., Conceptualization, Formal analysis, Funding acquisition, Methodology, Supervision, Writing—original draft, Writing—review and editing; X.L., Methodology, Data curation, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by National Natural Science Foundation of China under Grant No. 51408547, Zhejiang Provincial Department of Education Project under Grant No. FG2023007, and Science and Technology Foundation of Zhejiang Institute of Communications under Grant No. 2025KJ06.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gallagher, P.M.; Lin, Y. Colloidal silica transport through liquefiable porous media. J. Geotech. Geoenviron. Eng. 2009, 135, 1702–1712. [Google Scholar] [CrossRef]
  2. Hamderi, M.; Gallagher, P.M. An optimization study on the delivery distance of colloidal silica. Sci. Res. Essays 2013, 8, 1314–1323. [Google Scholar] [CrossRef]
  3. Liu, G.; Zhao, M.; Wang, T.; Connolly, D.P.; Cai, Y. Permeation grouting of low-permeability silty sands with colloidal silica. Case Stud. Constr. Mater. 2023, 19, e02327. [Google Scholar] [CrossRef]
  4. Spagnoli, G.; Collico, S. Multivariate analysis of a grouted sand with colloidal silica at different dilution stages. Transp. Geotech. 2023, 40, 100987. [Google Scholar] [CrossRef]
  5. Rasouli, R.; Hayashi, K.; Zen, K. Controlled permeation grouting method for mitigation of liquefaction. J. Geotech. Geoenviron. Eng. 2016, 142, 04016052. [Google Scholar] [CrossRef]
  6. Gallagher, P.M.; Conlee, C.T.; Rollins, K.M. Full-Scale Field Testing of Colloidal Silica Grouting for Mitigation of Liquefaction Risk. J. Geotech. Geoenviron. Eng. 2007, 133, 186–196. [Google Scholar] [CrossRef]
  7. Conlee, C.T.; Gallagher, P.M.; Boulanger, R.W.; Kamai, R. Centrifuge modeling for liquefaction mitigation using colloidal silica stabilizer. J. Geotech. Geoenvironmental Eng. 2012, 138, 1334–1345. [Google Scholar] [CrossRef]
  8. Pamuk, A.; Gallagher, P.M.; Zimmie, T. Remediation of pile foundations against lateral spreading by passive site stabilization technique. Soil Dyn. Earthq. Eng. 2007, 27, 864–874. [Google Scholar] [CrossRef]
  9. Ciardi, G.; Madiai, C. Effects of initial static shear stress on cyclic behaviour of sand stabilised with colloidal silica. Acta Geotech. 2023, 18, 2389–2409. [Google Scholar] [CrossRef]
  10. Gallagher, P.M.; Mitchellb, J.K. Influence of colloidal silica grout on liquefaction potential and cyclic undrained behavior of loose sand. Soil Dyn. Earthq. Eng. 2002, 22, 1017–1026. [Google Scholar] [CrossRef]
  11. Jin, W.F.; Tao, Y.; Chen, R.Z. Capturing the turning hook of stress-dilatancy curve of crushable calcareous sand. J. Mar. Sci. Eng. 2022, 10, 1269. [Google Scholar] [CrossRef]
  12. Jin, W.; Li, Y. Cementation state of sand judged by the stress−dilatancy relationship from a single drained triaxial test. J. Geotech. Geoenviron. Eng. 2025, 151, 04025027. [Google Scholar] [CrossRef]
  13. Pavlopoulou, E.E.; Georgiannou, V.N. Effect of colloidal silica aqueous gel on the monotonic and cyclic response of sands. J. Geotech. Geoenviron. Eng. 2021, 147, 04021122. [Google Scholar] [CrossRef]
  14. Vranna, A.; Tika, T.; Papadimitriou, A. Laboratory investigation into the monotonic and cyclic behaviour of a clean sand stabilised with colloidal silica. Géotechnique 2022, 72, 377–390. [Google Scholar] [CrossRef]
  15. Jin, W.; Liao, X.; Tao, Y. Self–sensing, anti–liquefaction, and long–term settlement characteristics of calcareous sand seeped by high-concentration colloidal silica. Constr. Build. Mater. 2024, 422, 135864. [Google Scholar] [CrossRef]
  16. Fredlund, D.G. Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
  17. Carísio, P.D.A.; Mendonça, Y.G.D.S.; Soares, C.F.T.; Reales, O.A.M.; Fairbairn, E.D.M.R.; Filho, R.D.T. Dispersion of carbon nanotubes with different types of superplasticizer as a dispersing agent for self-sensing cementitious materials. Appl. Sci. 2021, 11, 8452. [Google Scholar] [CrossRef]
  18. Deng, S.J.; Fan, J.; Li, G.Y.; Zhang, M.; Li, M. Influence of styrene-acrylic emulsion additions on the electrical and self-sensing properties of CNT cementitious composites. Constr. Build. Mater. 2023, 403, 133172. [Google Scholar] [CrossRef]
  19. Han, B.; Yu, X.; Kwon, E. A self-sensing carbon nanotube/cement composite for traffic monitoring. Nanotechnology 2009, 20, 445501. [Google Scholar] [CrossRef]
  20. Li, Q.; Hong, C.; Xie, H.; Lai, H.; Shen, Y.; Xu, S.; Kong, P. Piezoresistive behavior in cement-based sensors: Nonlinear modeling and preliminary application. Compos. A Appl. Sci. 2023, 175, 107786. [Google Scholar] [CrossRef]
  21. Meoni, A.; D’Alessandro, A.; Downey, A.; García-Macías, E.; Rallini, M.; Materazzi, A.L.; Torre, L.; Laflamme, S.; Castro-Triguero, R.; Ubertini, F. An Experimental Study on Static and Dynamic Strain Sensitivity of Embeddable Smart Concrete Sensors Doped with Carbon Nanotubes for SHM of Large Structures. Sensors 2018, 18, 831. [Google Scholar] [CrossRef]
  22. Yang, Q.; Liu, P.; Ge, Z.; Wang, D. Self-sensing carbon nanotube-cement composite material for structural health monitoring of pavements. J. Test. Eval. 2020, 48, 1990–2002. [Google Scholar] [CrossRef]
  23. Yuan, J.; Lu, D.; Wu, H.M.; Meng, J.; Song, H.X.; Zhong, J.; Xie, N. Carbon nanotubes-coated cement particles for cement-based sensors with excellent piezoresistivity. Smart Mater. Struct. 2023, 32, 065019. [Google Scholar] [CrossRef]
  24. Gupta, S.; Gonzalez, J.G.; Loh, K.J. Self-sensing concrete enabled by nano-engineered cement-aggregate interfaces. Struct. Health Monit. 2016, 16, 309–323. [Google Scholar] [CrossRef]
  25. Parvaneh, V.; Khiabani, S.H. Mechanical and piezoresistive properties of self-sensing smart concretes reinforced by carbon nanotubes. Mech. Adv. Mater. Struct. 2018, 26, 993–1000. [Google Scholar] [CrossRef]
  26. D’Alessandro, A.; Rallini, M.; Ubertini, F.; Materazzi, A.L.; Kenny, J.M. Investigations on scalable fabrication procedures for self-sensing carbon nanotube cement-matrix composites for SHM applications. Cem. Concr. Compos. 2016, 65, 200–213. [Google Scholar] [CrossRef]
  27. Siad, H.; Lachemi, M.; Sahmaran, M.; Mesbah, H.A.; Hossain, K.A. Advanced engineered cementitious composites with combined self-sensing and self-healing functionalities. Constr. Build. Mater. 2018, 176, 313–322. [Google Scholar] [CrossRef]
  28. Yin, T.J.; Xu, J.X.; Wang, Y.; Liu, L.Y. Increasing self-sensing capability of carbon nanotubes cement-based materials by simultaneous addition of Ni nanofibers with low content. Constr. Build. Mater. 2020, 254, 119306. [Google Scholar] [CrossRef]
  29. Wen, S.; Chung, D.D.L. Electrical-resistance-based damage self-sensing in carbon fiber reinforced cement. Carbon 2007, 45, 710–713. [Google Scholar] [CrossRef]
  30. Al-Dahawi, A.; Öztürk, O.; Emami, F.; Yıldırım, G.; Şahmaran, M. Effect of mixing methods on the electrical properties of cementitious composites incorporating different carbon-based materials. Constr. Build. Mater. 2016, 104, 160–168. [Google Scholar] [CrossRef]
  31. Taheri, S.; Georgaklis, J.; Ams, M.; Patabendigedara, S.; Belford, A.; Wu, S. Smart self-sensing concrete: The use of multiscale carbon fillers. J. Mater. Sci. 2022, 57, 2667–2682. [Google Scholar] [CrossRef]
  32. Roshan, M.J.; Abedi, M.; Correla, A.G.; Fangueiro, R. Application of self-sensing cement-stabilized sand for damage detection. Constr. Build. Mater. 2023, 403, 133080. [Google Scholar] [CrossRef]
  33. Yoo, D.-Y.; You, I.; Zi, G.; Lee, S.-J. Effects of carbon nanomaterial type and amount on self-sensing capacity of cement paste. Measurement 2018, 134, 750–761. [Google Scholar] [CrossRef]
  34. Hou, Y.; Sun, M.; Chen, J. Electrical resistance and capacitance responses of smart ultra-high performance concrete with compressive strain by DC and AC measurements. Constr. Build. Mater. 2022, 327, 127007. [Google Scholar] [CrossRef]
  35. JTG 3430-2020; Test Methods of Soils for Highway Engineering. JTG: Beijing, China, 2020.
  36. Gao, Y.; Sun, D.A.; Zhu, Z.C.; Xu, Y.F. Hydromechanical behavior of unsaturated soil with different initial densities over a wide suction range. Acta Geotech. 2019, 14, 417–428. [Google Scholar] [CrossRef]
  37. Ng, C.W.W.; Sadeghi, H.; Jafarzadeh, F. Compression and shear strength characteristics of compacted loess at high suctions. Can. Geotech. J. 2017, 54, 690–699. [Google Scholar] [CrossRef]
  38. Vaid, Y.P.; Sivathayalan, S.; Stedman, D. Influence of specimen reconstituting method on the undrained response of sand. Geotech. Test. J. 1999, 22, 187–195. [Google Scholar] [CrossRef]
  39. Leong, E.C.; He, L.; Rahardjo, H. Factors affecting the filter paper method for total and matric suction measurements. Geotech. Test. J. 2002, 25, 322–333. [Google Scholar] [CrossRef]
  40. Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. 1977, 10, 1–54. [Google Scholar] [CrossRef]
  41. Asadollahi, P.; Tonon, F. Constitutive model for rock fractures: Revisiting Barton’s empirical model. Eng. Geol. 2010, 113, 11–32. [Google Scholar] [CrossRef]
  42. Zhao, Y. Dynamic Responses and Accumulative Settlement of Subgrade Under Aircraft Load in High-Filled Airport. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2018. [Google Scholar]
  43. Falara, M.G.; Thomoglou, A.K.; Gkountakou, F.I.; Elenas, A.; Chalioris, C.E. Hybrid smart cementitious materials incorporating ladder scale carbon fiber reinforcement: An experimental investigation. Case Stud. Constr. Mater. 2023, 18, e02035. [Google Scholar] [CrossRef]
  44. Sevim, O.; Jiang, Z.F.; Ozbulut, O. EEffects of graphene nanoplatelets type on self-sensing properties of cement mortar composites. Constr. Build. Mater. 2022, 359, 129488. [Google Scholar] [CrossRef]
  45. Suo, Y.X.; Xia, H.T.; Guo, R.X.; Yang, Y. Study on self-sensing capabilities of smart cements filled with graphene oxide under dynamic cyclic loading. J. Build. Eng. 2022, 58, 104775. [Google Scholar] [CrossRef]
  46. Aqtash, U.A.; Bandini, P. Prediction of unsaturated shear strength of an adobe soil from the soil–water characteristic curve. Constr. Build. Mater. 2015, 98, 892–899. [Google Scholar] [CrossRef]
  47. Fredlund, D.G.; Morgenstern, N.R.; Widger, R.A. The shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
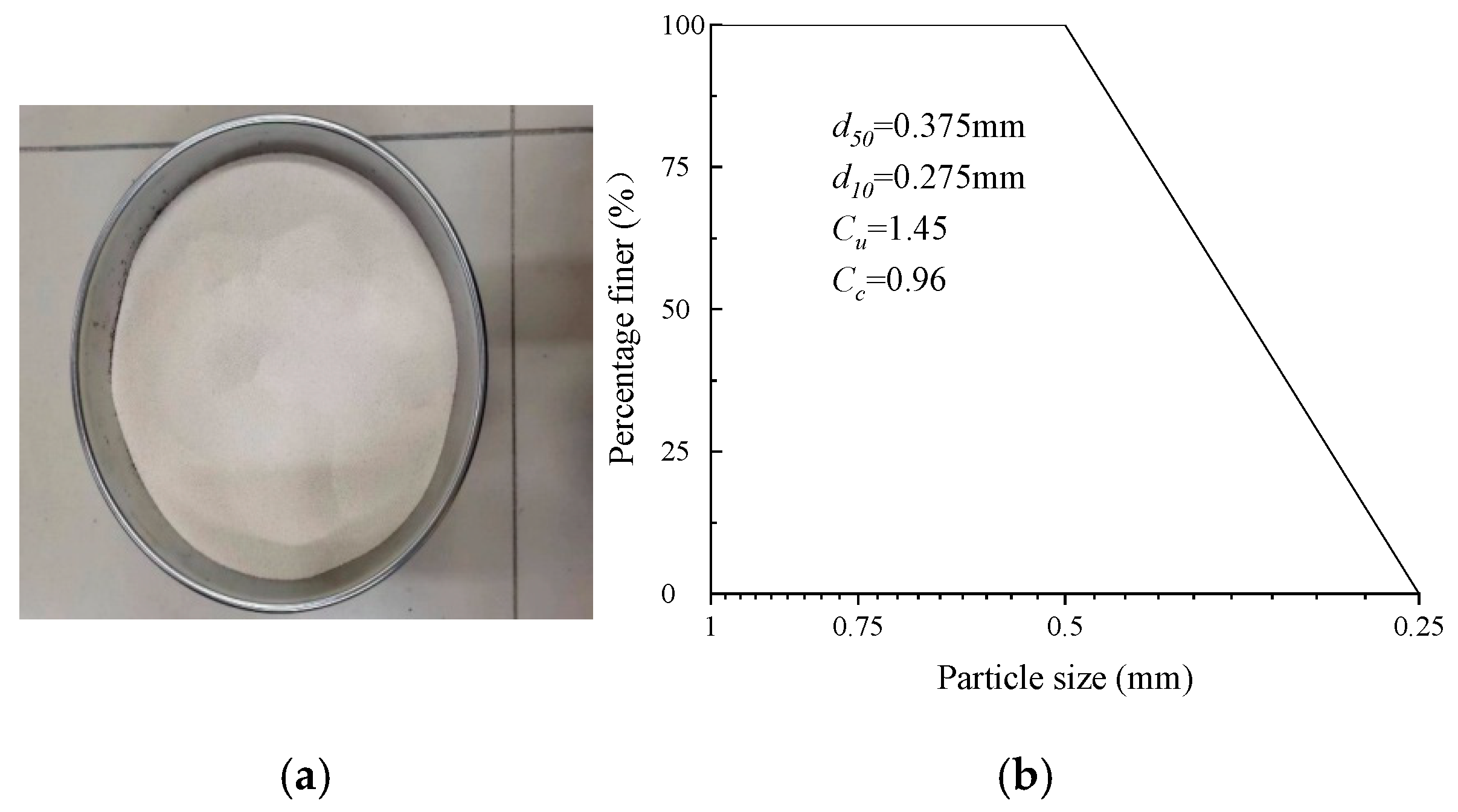
Jmse 13 01127 g001
Figure 1. Calcareous sand: (a) photo of the sand; (b) particle size distribution.
Figure 1. Calcareous sand: (a) photo of the sand; (b) particle size distribution.
Jmse 13 01127 g001
Jmse 13 01127 g002
Figure 2. Specimen preparation: (a) specimens in the mold; (b) four types of crack with different roughness; (c) specimens with precracks; (d) specimens without precracks.
Figure 2. Specimen preparation: (a) specimens in the mold; (b) four types of crack with different roughness; (c) specimens with precracks; (d) specimens without precracks.
Jmse 13 01127 g002
Jmse 13 01127 g003
Figure 3. Self-sensing test: (a) specimen on the cyclic loading system; (b) AC signal source and multimeters; (c) circuit diagram for self-sensing test using the four-probe method.
Figure 3. Self-sensing test: (a) specimen on the cyclic loading system; (b) AC signal source and multimeters; (c) circuit diagram for self-sensing test using the four-probe method.
Jmse 13 01127 g003
Jmse 13 01127 g004
Figure 4. Soil water retention curve (SWRC).
Figure 4. Soil water retention curve (SWRC).
Jmse 13 01127 g004
Jmse 13 01127 g005
Figure 5. FCR under different degrees of saturation S without a precrack: (a) parallel 1; (b) parallel 2.
Figure 5. FCR under different degrees of saturation S without a precrack: (a) parallel 1; (b) parallel 2.
Jmse 13 01127 g005
Jmse 13 01127 g006
Figure 6. FCR in a saturated state with four types of precracks: (a) parallel 1; (b) parallel 2.
Figure 6. FCR in a saturated state with four types of precracks: (a) parallel 1; (b) parallel 2.
Jmse 13 01127 g006
Jmse 13 01127 g007
Figure 7. FCR in an unsaturated state with four types of precracks: (a) parallel 1; (b) parallel 2.
Figure 7. FCR in an unsaturated state with four types of precracks: (a) parallel 1; (b) parallel 2.
Jmse 13 01127 g007
Jmse 13 01127 g008
Figure 8. Signal-to-noise ratio (SNR).
Figure 8. Signal-to-noise ratio (SNR).
Jmse 13 01127 g008
Jmse 13 01127 g009
Figure 9. Sensitivity of self-sensing increases with unsaturation and crack (key points are highlighted in blue and red colors).
Figure 9. Sensitivity of self-sensing increases with unsaturation and crack (key points are highlighted in blue and red colors).
Jmse 13 01127 g009
Jmse 13 01127 g010
Figure 10. Silica gel after desiccation is not conductive (e.g., 52.71 MΩ for the above silica gel after desiccation).
Figure 10. Silica gel after desiccation is not conductive (e.g., 52.71 MΩ for the above silica gel after desiccation).
Jmse 13 01127 g010
Jmse 13 01127 g011
Figure 11. Nuclear magnetic resonance (NMR)-based analysis of pore radius in the specimen.
Figure 11. Nuclear magnetic resonance (NMR)-based analysis of pore radius in the specimen.
Jmse 13 01127 g011
Jmse 13 01127 g012
Figure 12. Unsaturation induces suction, which affects the silica gel between sand particles (suction = ua-uw, ua = air pressure, uw = water pressure. Red arrow indicates local magnification. Key points are highlighted in blue).
Figure 12. Unsaturation induces suction, which affects the silica gel between sand particles (suction = ua-uw, ua = air pressure, uw = water pressure. Red arrow indicates local magnification. Key points are highlighted in blue).
Jmse 13 01127 g012
Jmse 13 01127 g013
Figure 13. SEM photograph of crack in the silica gel.
Figure 13. SEM photograph of crack in the silica gel.
Jmse 13 01127 g013
Jmse 13 01127 g014
Figure 14. Suction induces the shrinkage of the specimen (key points are highlighted in blue and red colors).
Figure 14. Suction induces the shrinkage of the specimen (key points are highlighted in blue and red colors).
Jmse 13 01127 g014
Table 1. Properties of calcareous sand.
Table 1. Properties of calcareous sand.
Max. Void Ratio emaxMin. Void Ratio eminMax. Dry Density ρdmax (g/cm3)Min. Dry Density ρdmin (g/cm3)Particle Size d (mm)Specific Gravity GsRelative Density Dr (%)Internal Friction Angle (Degrees)Permeability Coefficient
(cm/s)
1.110.791.501.2760.25–0.52.697050.11.79 × 10−4 cm/s
Table 2. Experimental plan of self sensing.
Table 2. Experimental plan of self sensing.
Specimen DescriptionFrequency of the AC Signal Source (Hz)Amplitude of the Cyclic Stress
Δσ (kPa)		Frequency of the Cyclic Stress
(Hz)		Type of Pre–CrackDegree of the Saturation
S (%)
Without a precrack100300.1-100, 70, 67.5
With a precrack100300.1plane100, 70
100300.1JRC9100, 70
100300.1JRC11100, 70
100300.1JRC15100, 70
Table 3. Comparison of self-sensing sensitivity.
Table 3. Comparison of self-sensing sensitivity.
Ref.Cement MaterialConductive FillerStress Sensitivity, π = Δρ/ρ/Δσ1 (See Equation (5))
(%/kPa)
This study
(S = 67.5% with a precrack)		Colloidal silica-0.247
This study
(S = 100% with a precrack)		Colloidal silica-0.0283
This study
(S = 67.5% without a precrack)		Colloidal silica-0.0758
This study
(S = 100% without a precrack)		Colloidal silica-0.0135
[26]Portland–cementCNTs (1 wt%)0.0013
[29]Portland–cementCNTs (1.7 vol%) + NiNF (0.1 vol%)0.0025
[23]Portland–cementCNTs (0.1 wt%)0.0015
[22]Portland–cementCNTs (0.5 wt%)0.00025
[21]Portland–cementCNTs (1 wt%)0.001
[19]Portland–cementCNTs (0.01 wt%)0.002
[31]Portland–cementCarbon Fiber (1.5 wt%)0.0004
[43]Portland–cementCarbon Fiber (1.5 wt%)0.0025
[33]Portland–cementGraphene (1 wt%)0.0004
[44]Portland–cementGraphene (7.5 wt%)0.0016
[45]Portland–cementGraphene (0.05 wt%)0.0032
[34]Portland–cementSteel fiber (21 wt%)0.0024
Note: NTs = Carbon nanotubtes, NiNF = Ni nanofibers, wt% means the mass ratio of conductive filler to colloidal silica or cement.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ruan, S.; Jin, W.; Liao, X. Colloidal Silica-Stabilized Subgrade for Self-Sensing Vehicle Stress Affected by Unsaturation and Crack. J. Mar. Sci. Eng. 2025, 13, 1127. https://doi.org/10.3390/jmse13061127

AMA Style

Ruan S, Jin W, Liao X. Colloidal Silica-Stabilized Subgrade for Self-Sensing Vehicle Stress Affected by Unsaturation and Crack. Journal of Marine Science and Engineering. 2025; 13(6):1127. https://doi.org/10.3390/jmse13061127

Chicago/Turabian Style

Ruan, Shuaishuai, Weifeng Jin, and Xiaohui Liao. 2025. "Colloidal Silica-Stabilized Subgrade for Self-Sensing Vehicle Stress Affected by Unsaturation and Crack" Journal of Marine Science and Engineering 13, no. 6: 1127. https://doi.org/10.3390/jmse13061127

APA Style

Ruan, S., Jin, W., & Liao, X. (2025). Colloidal Silica-Stabilized Subgrade for Self-Sensing Vehicle Stress Affected by Unsaturation and Crack. Journal of Marine Science and Engineering, 13(6), 1127. https://doi.org/10.3390/jmse13061127

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop