Generation and Evolution of Cnoidal Waves in a Two-Dimensional Numerical Viscous Wave Flume
Abstract
1. Introduction
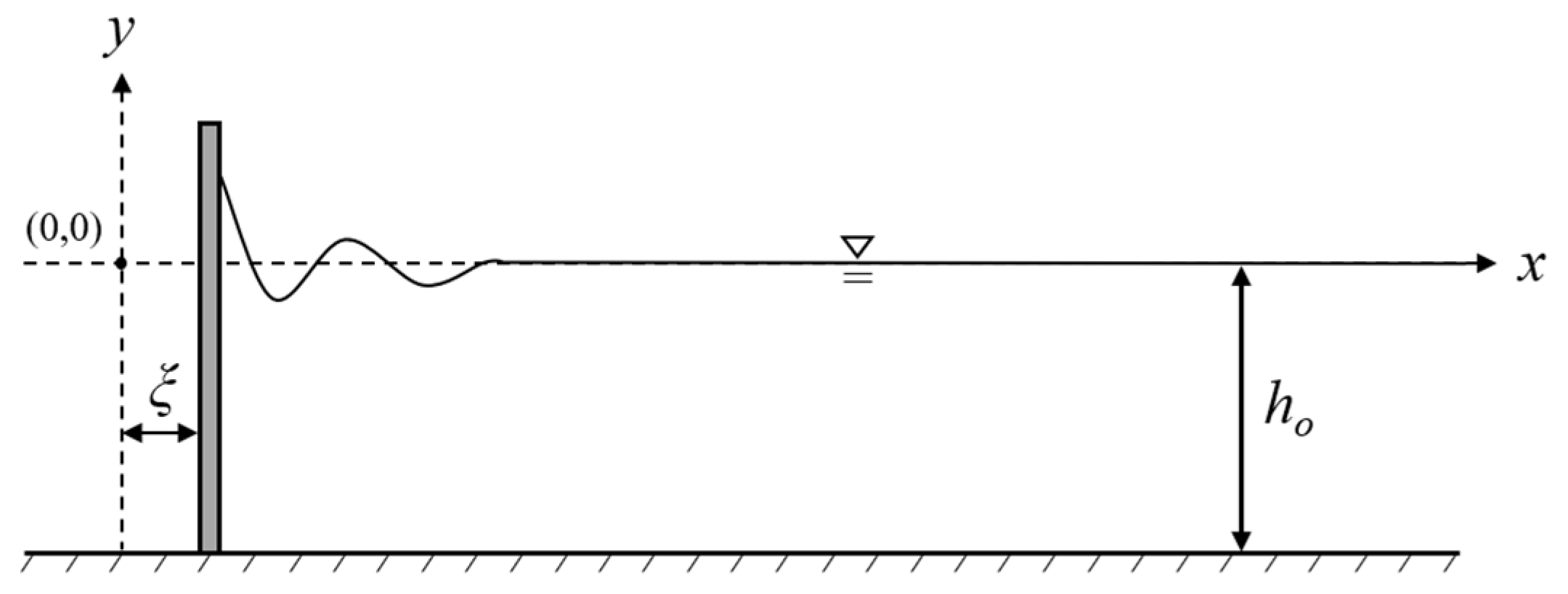
2. Numerical Methods
3. Wavemaker Theories
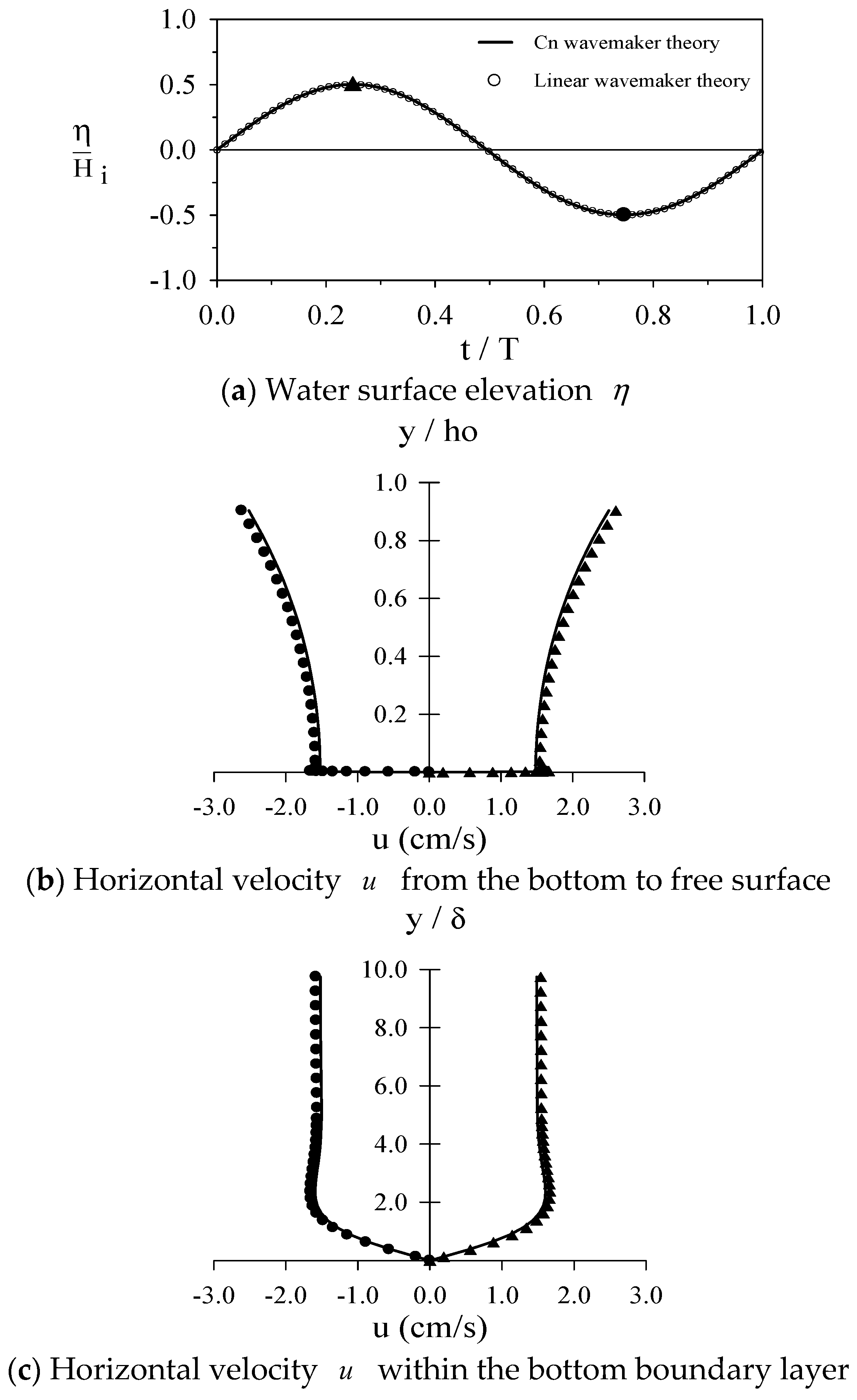
3.1. Linear and Madsen’s Theories
3.2. Goring and Raichlen’s Theory
4. Results and Discussion
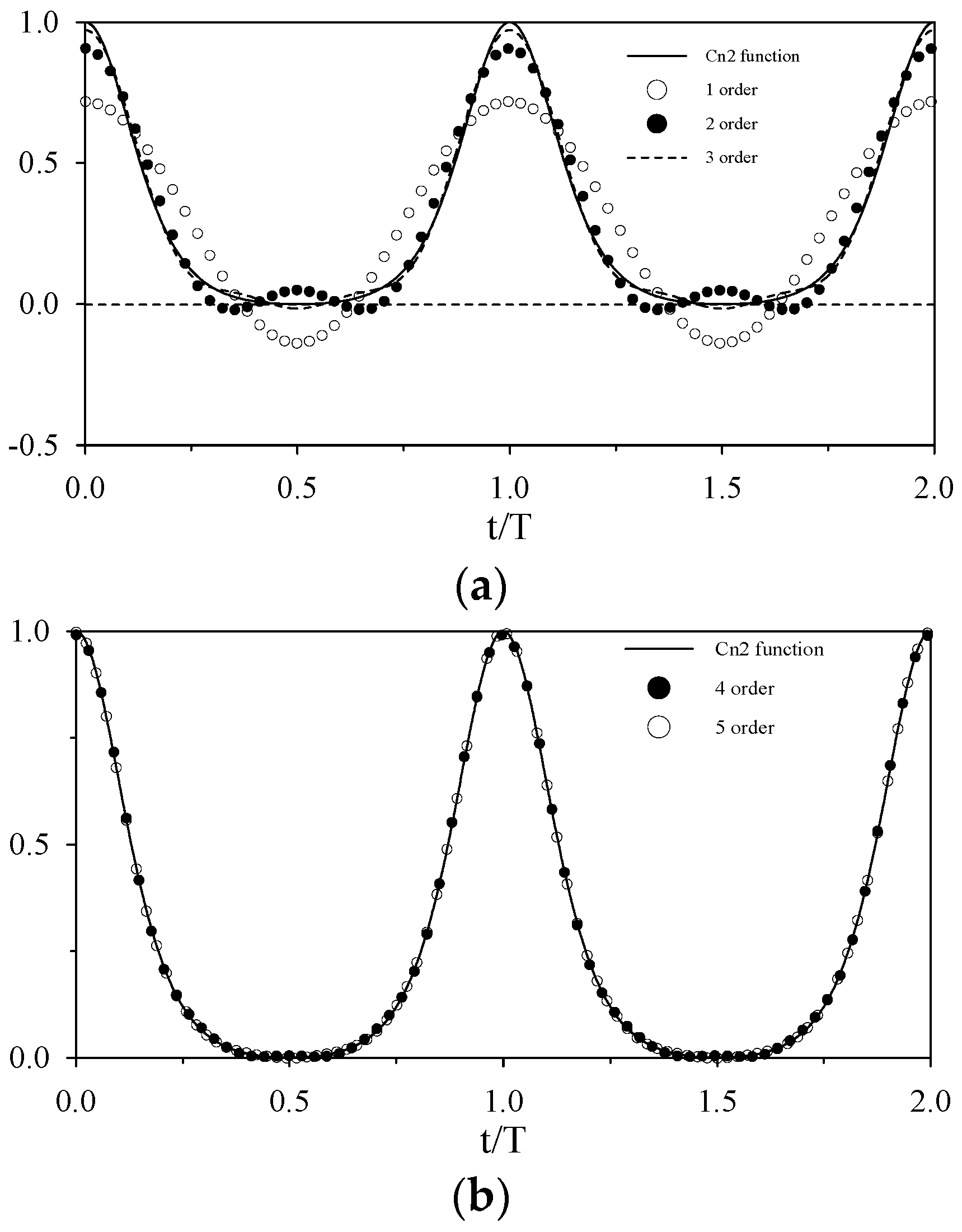
4.1. Cnoidal Waves
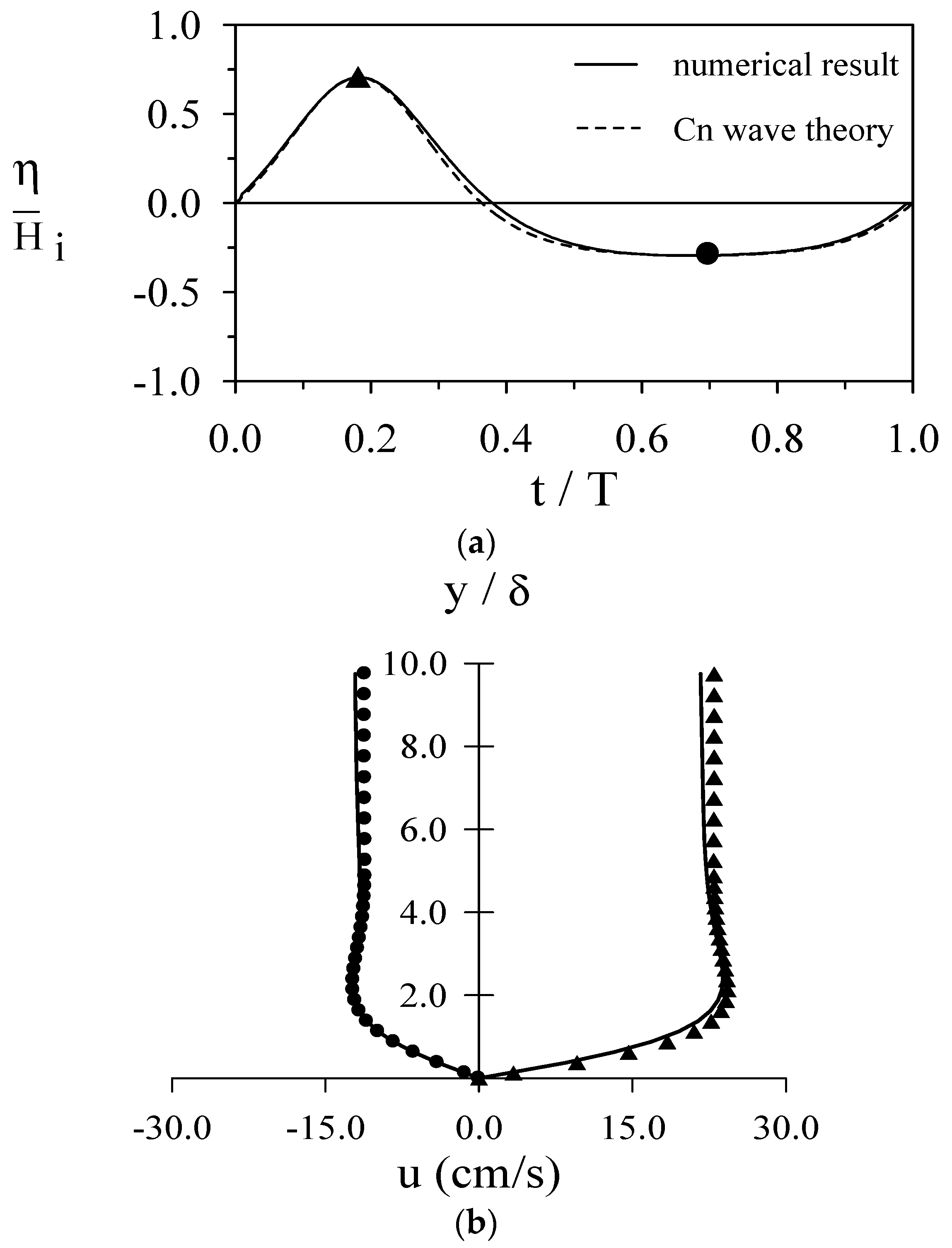
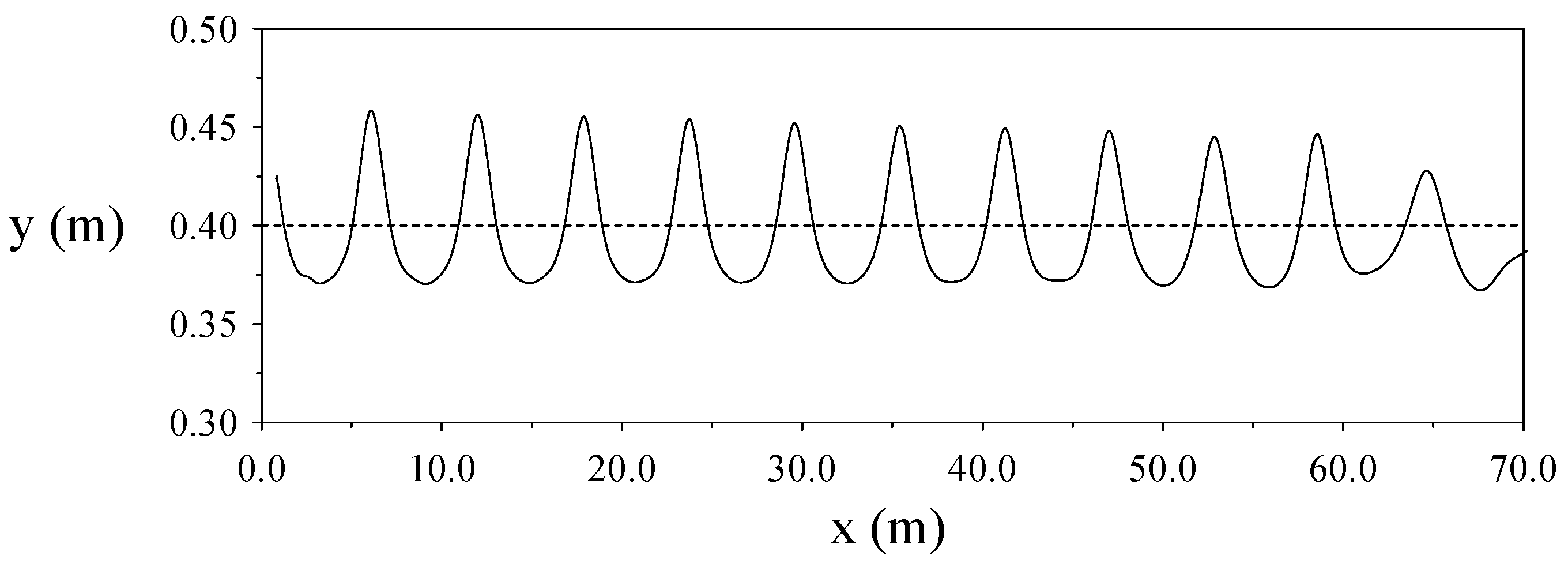
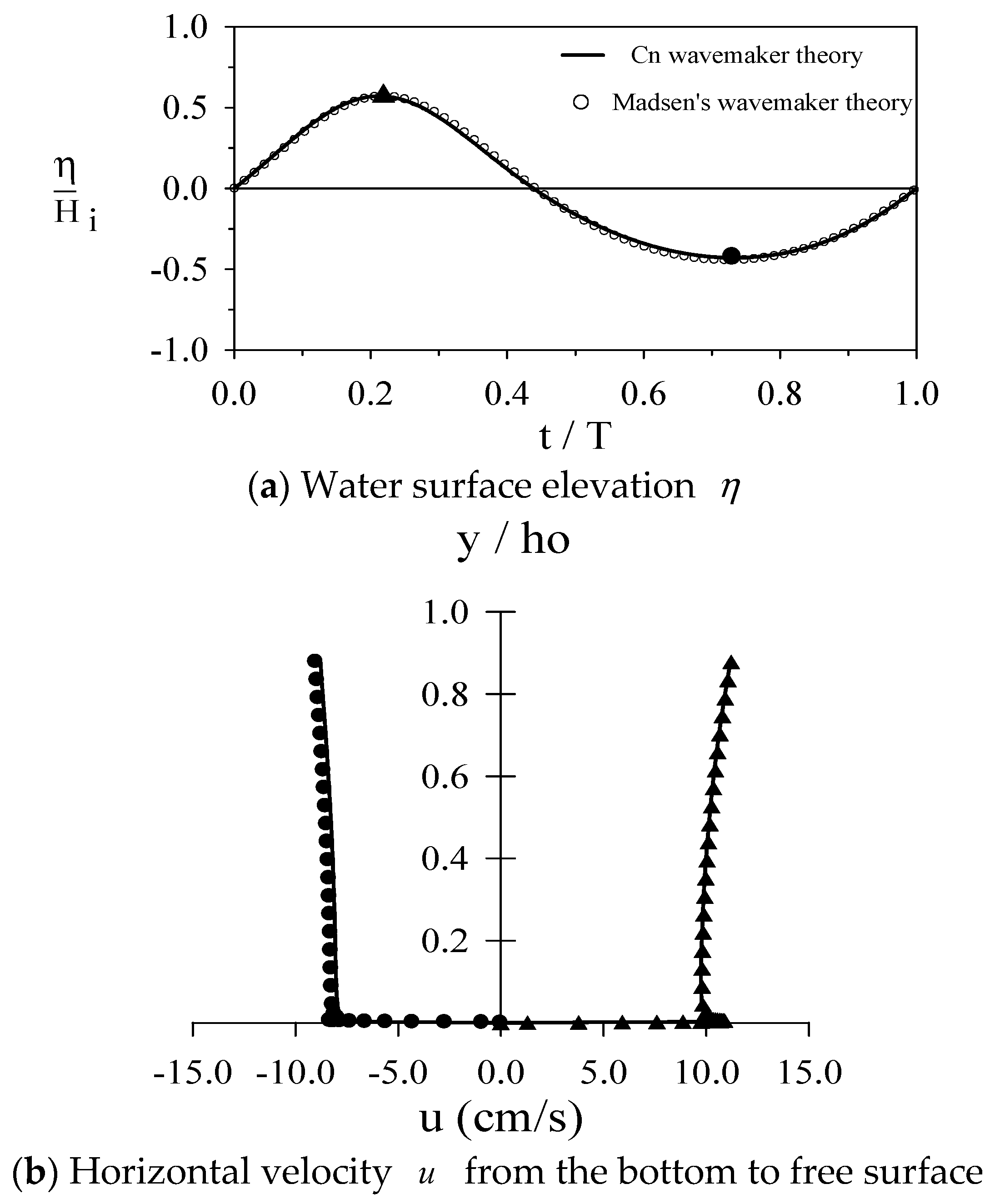
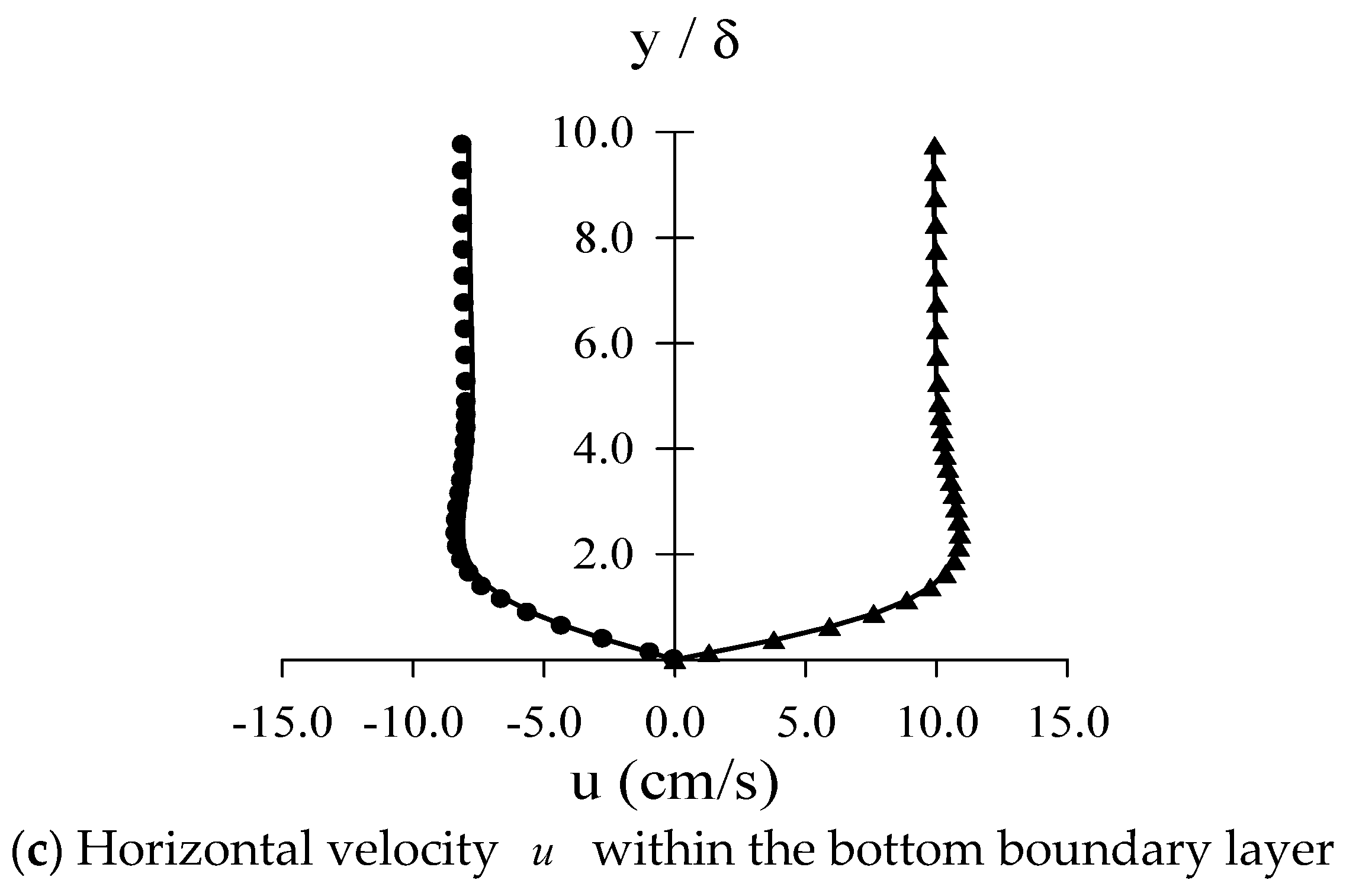
4.2. Verification of the Generated Cnoidal Waveforms and Flow Fields
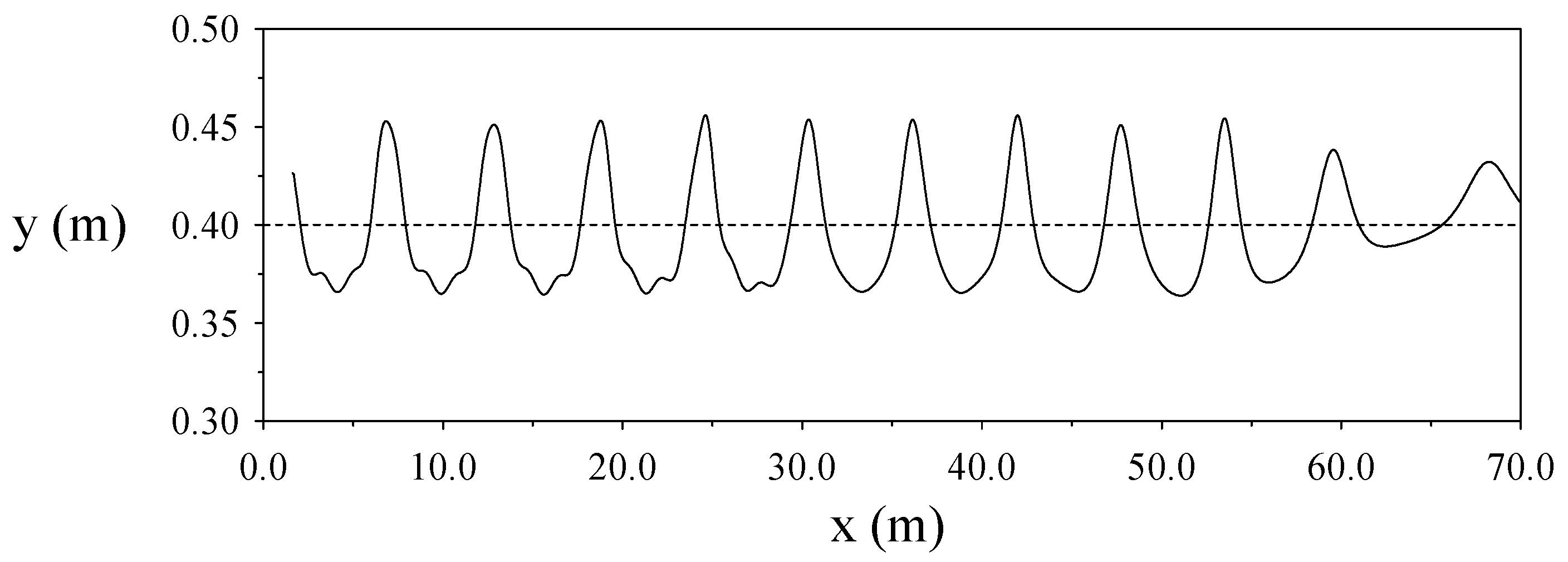
4.3. Examination of Permanent Waveform
4.4. Comparison of Waves with Generated Using Various Methods
4.5. Generation of Solitary Wave
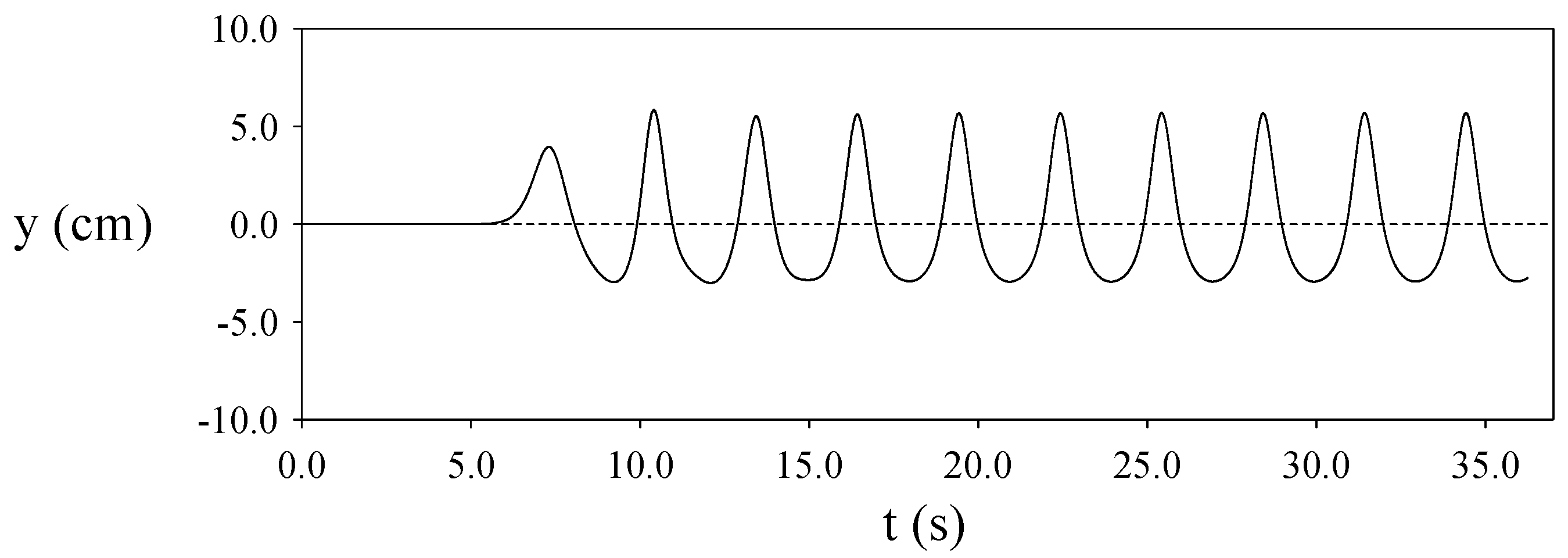
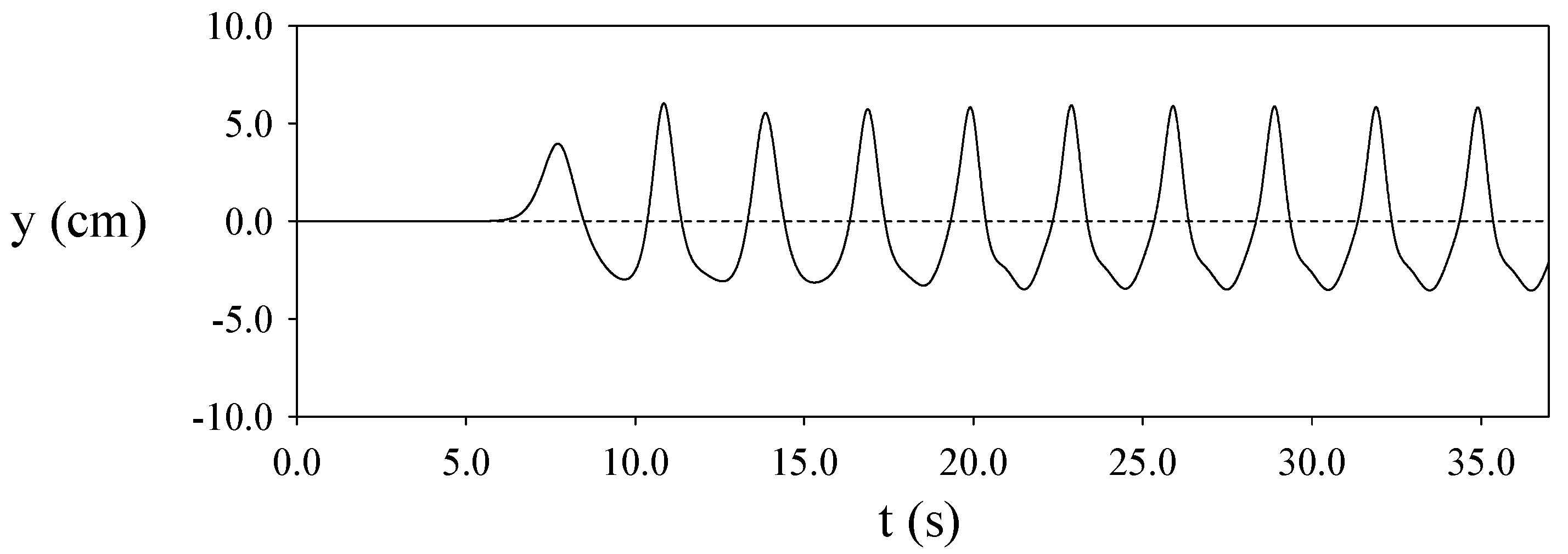
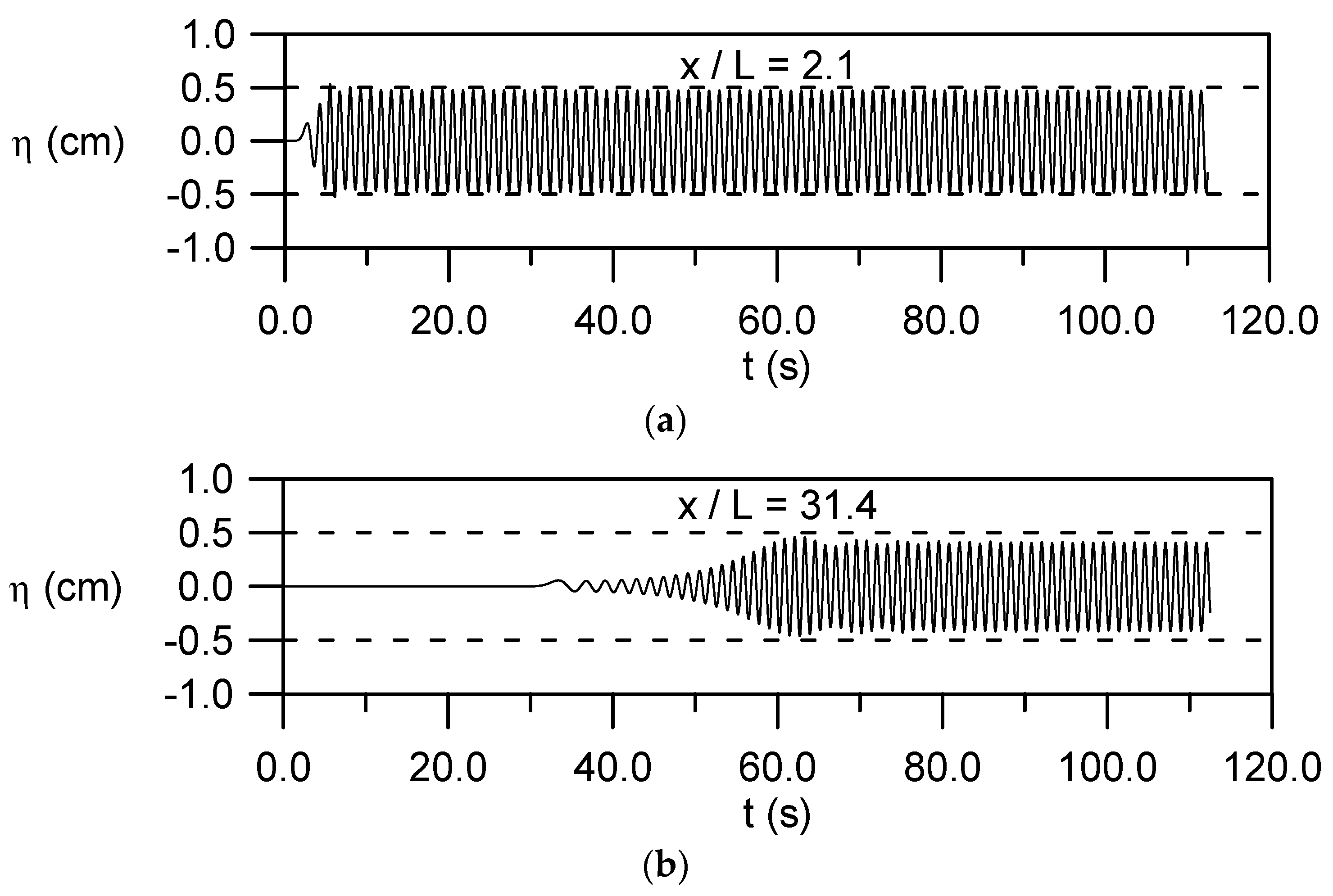
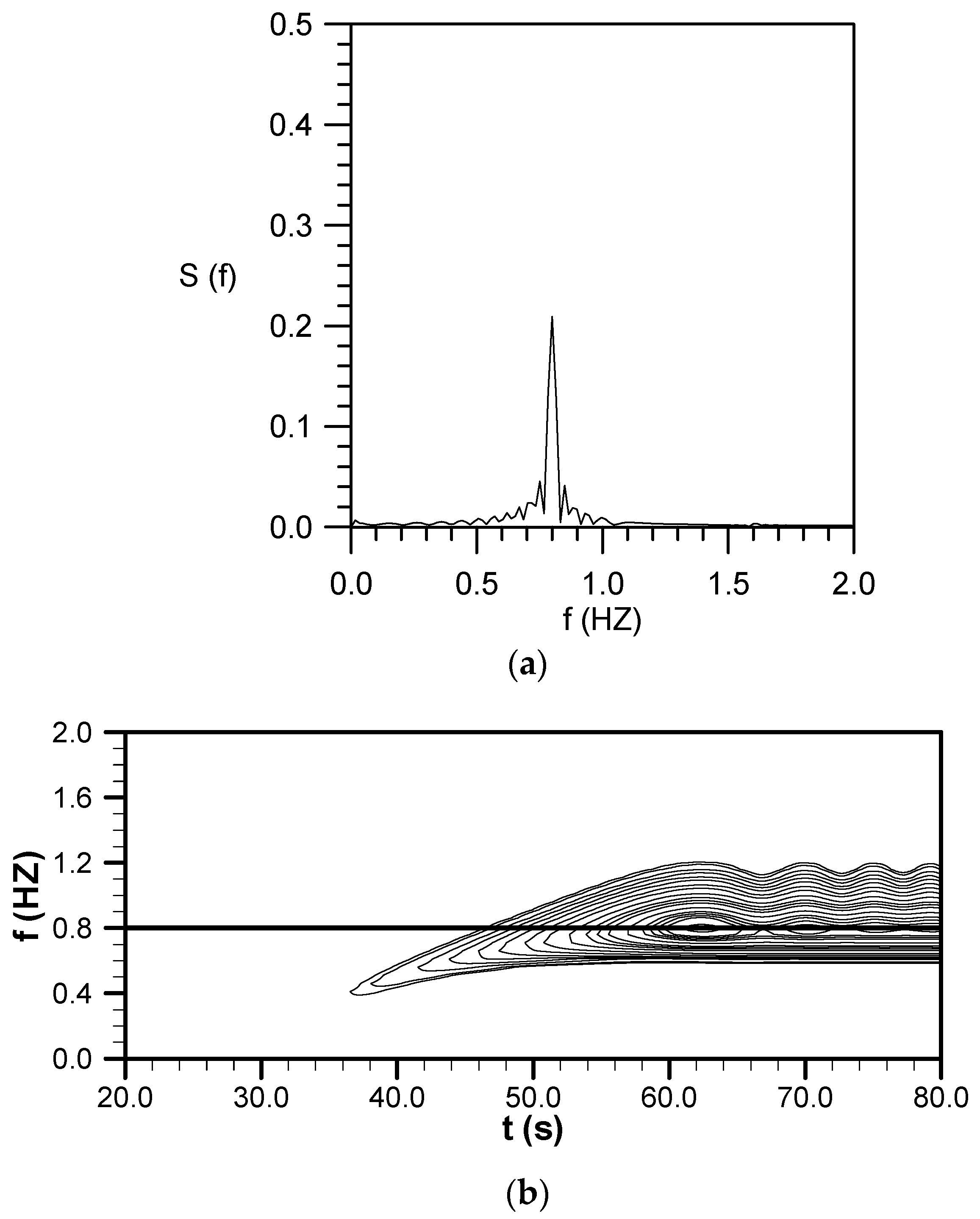
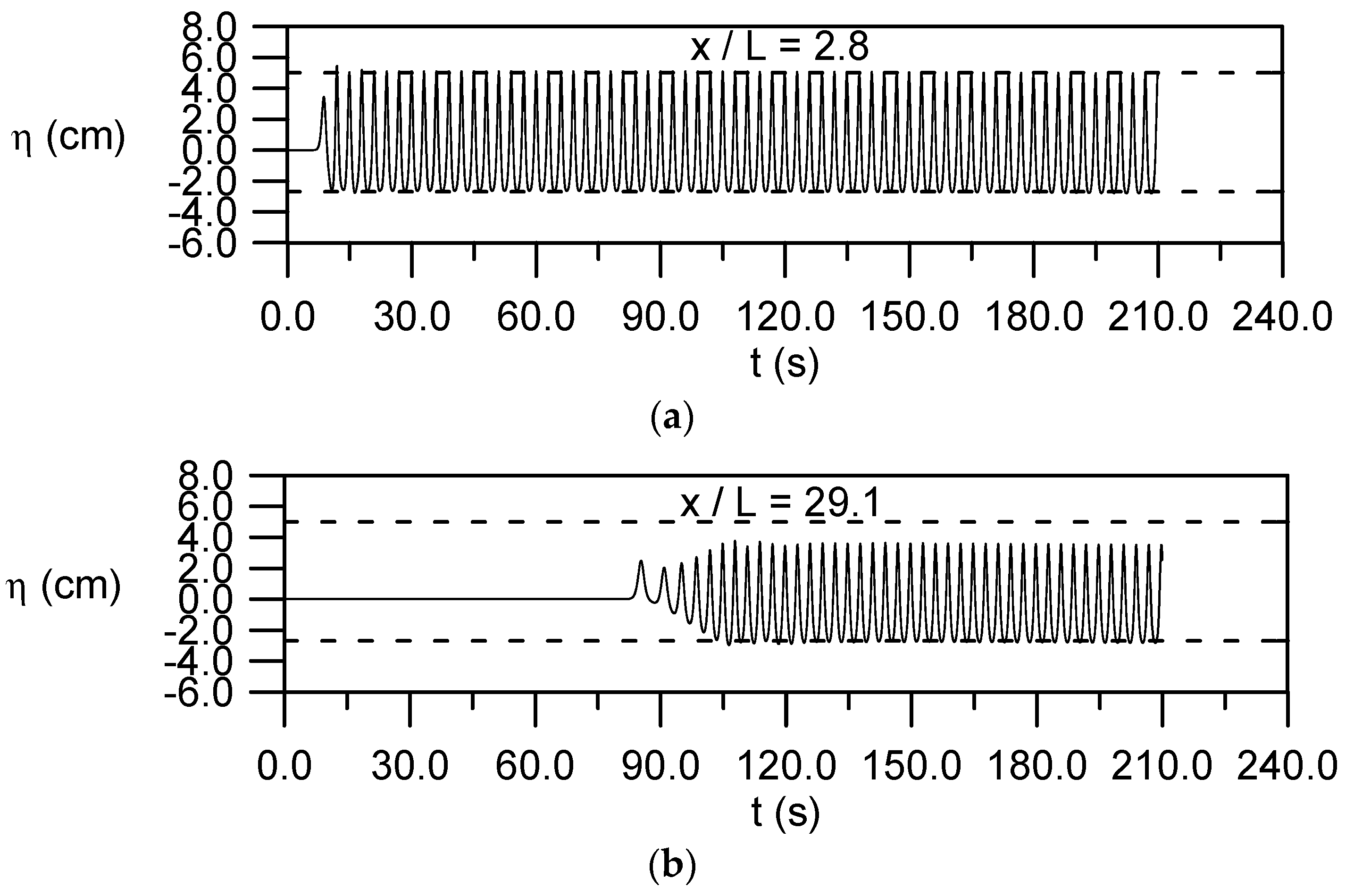
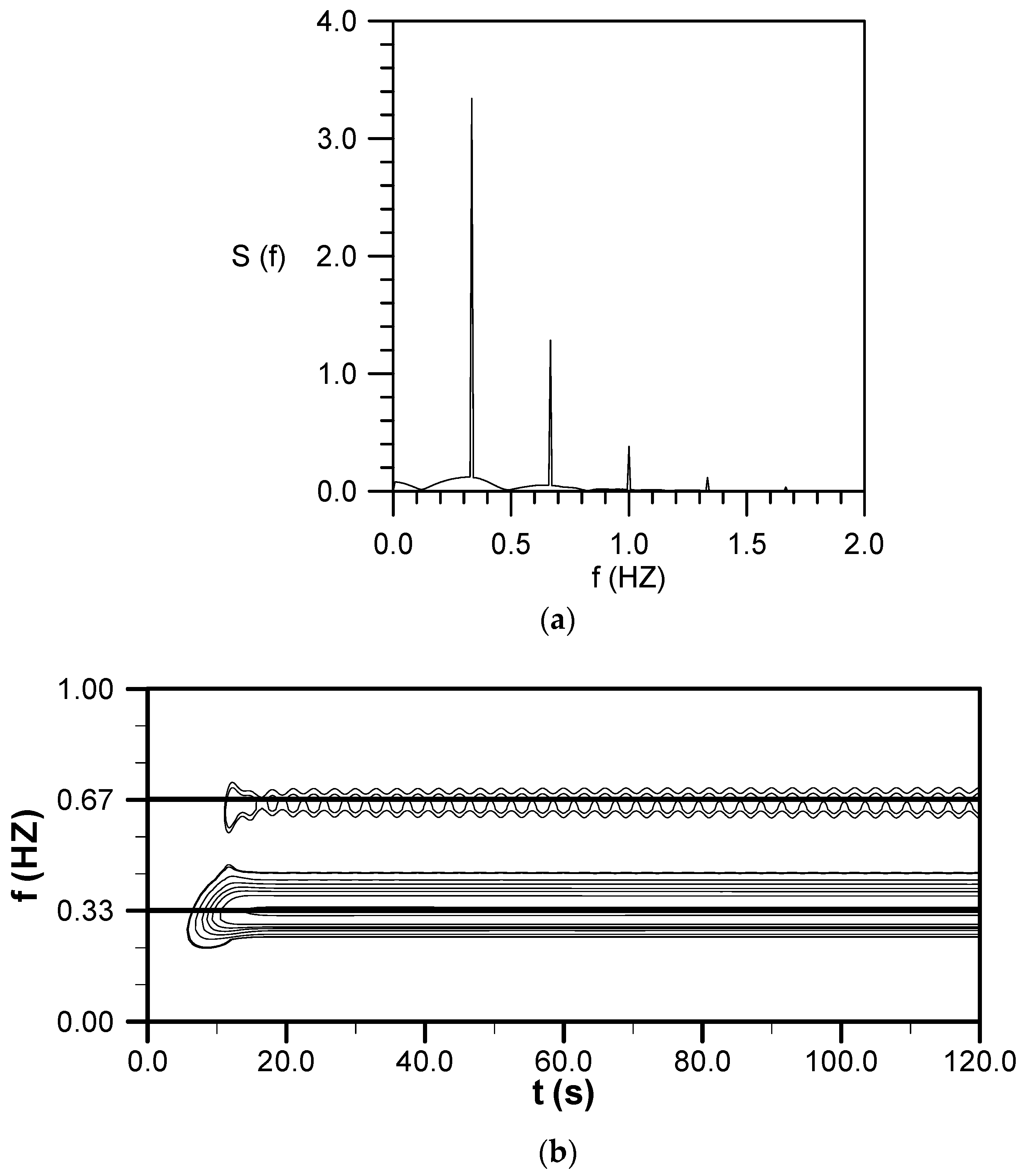
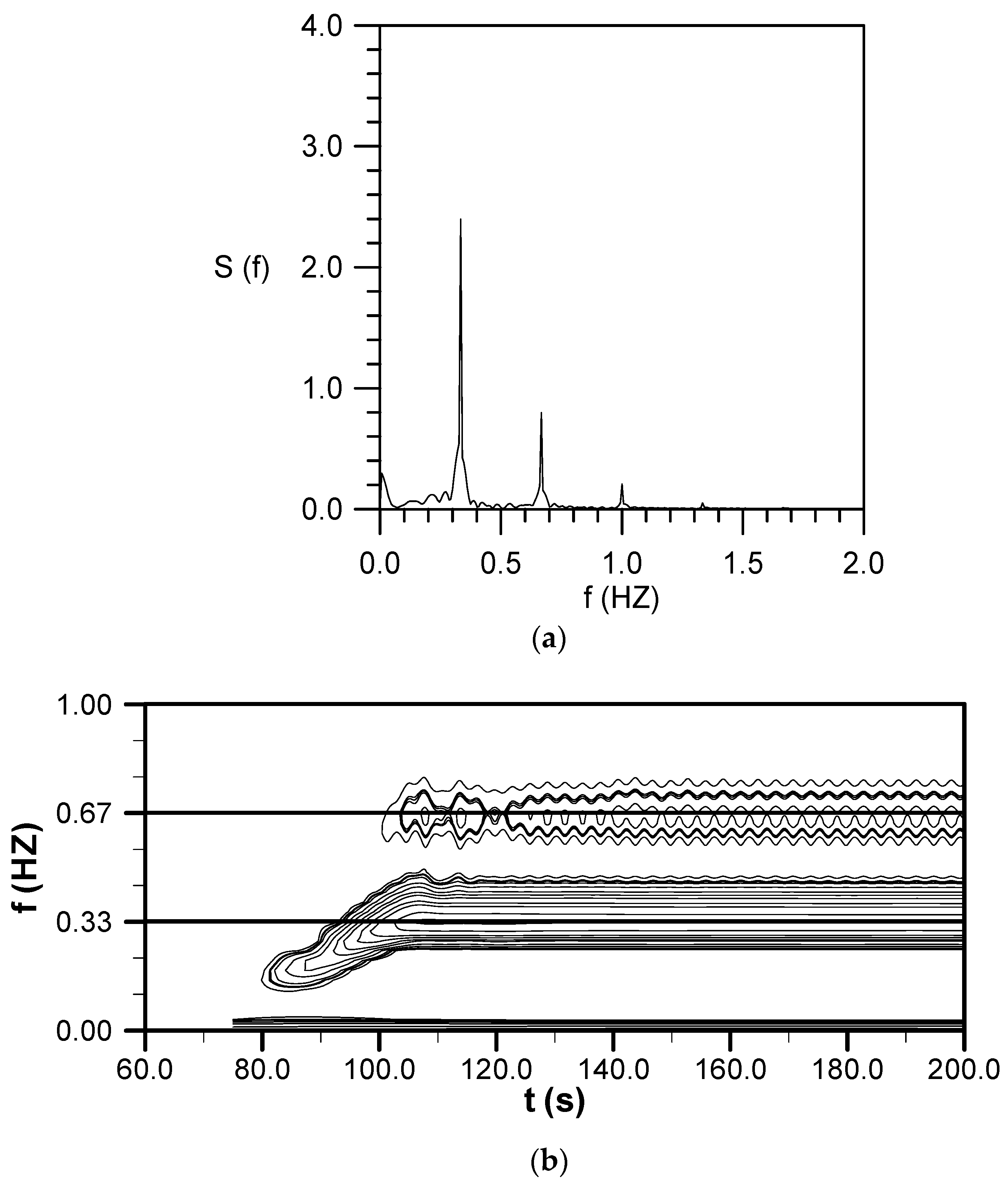
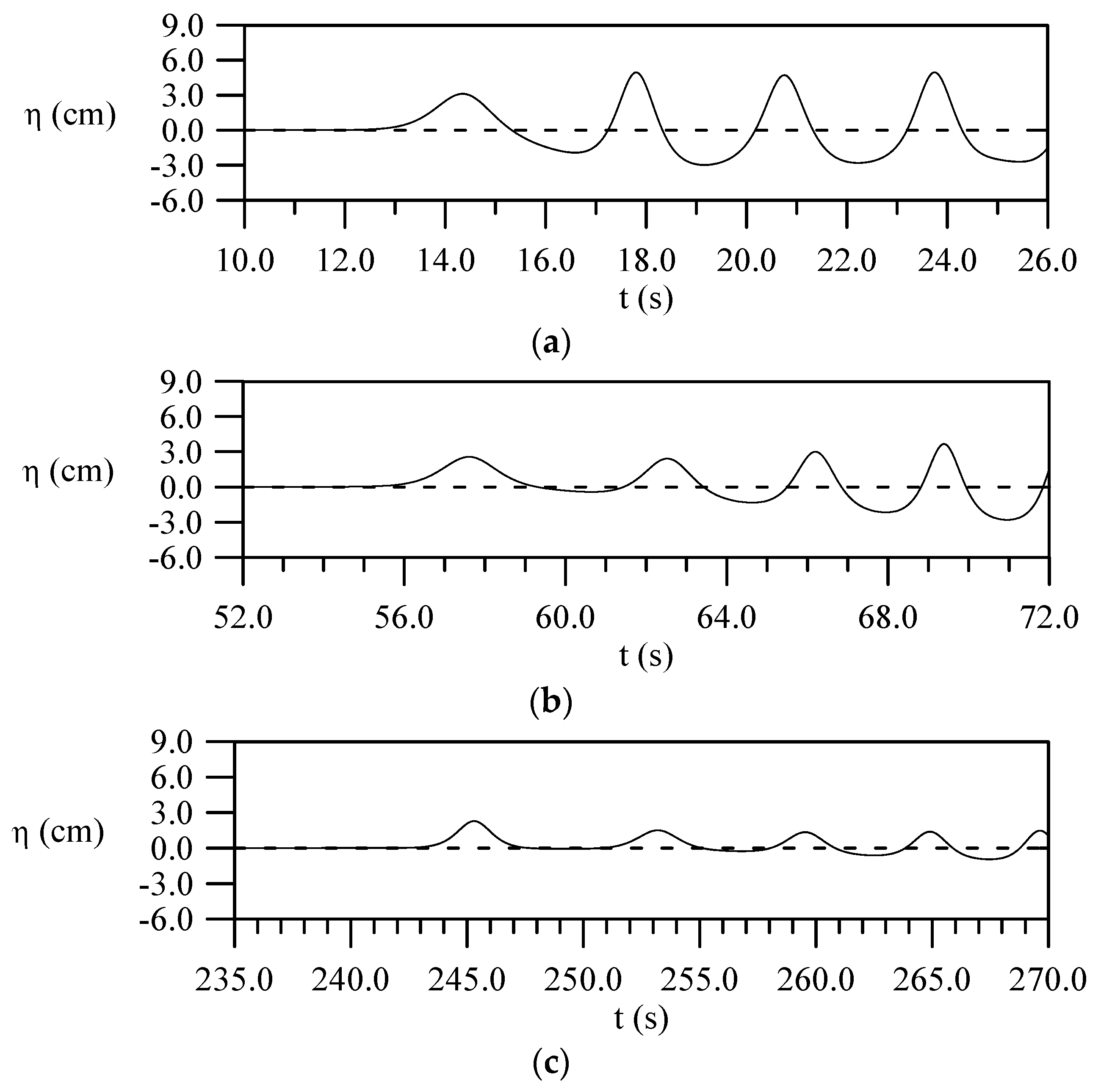
4.6. Evolution of a Small-Amplitude Wave Train with
4.7. Evolution of a Cnoidal Wave Train with
4.8. Effect of Viscosity on Water Wave Motion and Advantage of a Viscous Wave Flume
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientist; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Havelock, T.H. Forced surface wave on water. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1929, 7, 569–576. [Google Scholar] [CrossRef]
- Ursell, F.; Dean, R.G.; Yu, Y.S. Forced small-amplitude water waves: A comparison of theory and experiment. J. Fluid Mech. 1960, 7, 32–53. [Google Scholar] [CrossRef]
- Hudspeth, R.T.; Leonard, J.W.; Chen, M.C. Design curves for hinged wave makers: Experiments. J. Hydraul. Div. Am. Soc. Civ. Eng. 1981, 107, 533–574. [Google Scholar]
- Goda, Y. Traveling Secondary Wave Crests in Wave Channels; Rep. No. 13; Port & Harbor Research Institute: Yokosuka, Japan, 1967; pp. 32–38. [Google Scholar]
- Madsen, O.S. On the generation of long waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Buhr Hansen, J.; Svendsen, I.A. Regular Waves in Shoaling Water—Experimental Data; Series Paper 21; ISVA, Technical University of Denmark: Kongens Lyngby, Denmark, 1974. [Google Scholar]
- Goring, D.; Raichlen, F. The generation of long waves in the laboratory. In Proceedings of the 17th Coastal Engineering Conference, Sydney, Australia, 23–28 March 1980; pp. 763–783. [Google Scholar]
- Ohyama, T.; Nadaoka, K. Development of a numerical wave tank for analysis of nonlinear and irregular wave field. Fluid Dyn. Res. 1991, 8, 231–251. [Google Scholar] [CrossRef]
- Grilli, S.T.; Horillo, J. Numerical generation and absorption of fully nonlinear periodic waves. J. Eng. Mech. 1997, 123, 1060–1069. [Google Scholar] [CrossRef]
- Guyenne, P.; Nicholls, D.P. A high-order spectral method for nonlinear water waves over moving bottom topography. SIAM J. Sci. Comput. 2007, 30, 81–101. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Dover Publications: New York, NY, USA, 1945; pp. 623–625. [Google Scholar]
- Huang, C.J.; Dong, C.M. Wave deformation and vortex generation in water waves propagating over a submerged dike. Coast. Eng. 1999, 37, 123–148. [Google Scholar] [CrossRef]
- Huang, C.J.; Dong, C.M. On the interaction of a solitary wave and a submerged dike. Coast. Eng. 2001, 43, 265–286. [Google Scholar] [CrossRef]
- Huang, C.J.; Zhang, E.C.; Lee, J.F. Numerical simulation of nonlinear viscous wavefields generated by a piston-type wavemaker. J. Eng. Mech. 1998, 124, 1110–1120. [Google Scholar] [CrossRef]
- Dong, C.M.; Huang, C.J. Generation and propagation of water waves in a two-dimensional numerical viscous wave flume. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 143–153. [Google Scholar] [CrossRef]
- Madsen, P.A.; Fuhrman, D.R.; Schäffer, H.A. On the solitary wave paradigm for tsunamis. J. Geophys. Res. 2008, 113, C12012. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. Internal wave-maker for Navier-Stokes equations models. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 207–215. [Google Scholar] [CrossRef]
- Liu, J.; Hayatdavoodi, M.; Ertekin, R.C. A comparative study on generation and propagation of nonlinear waves in shallow waters. J. Mar. Sci. Eng. 2023, 11, 917. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. A derivation of equations for wave propagation in water of variable depth. J. Fluid Mech. 1976, 78, 237–246. [Google Scholar] [CrossRef]
- Keulegan, G.H.; Patterson, J.A. Mathematical theory of irrotational translation waves. J. Res. Natl. Bur. Stand. 1940, 24, 47–101. [Google Scholar] [CrossRef]
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Dingemans, M.W. Water wave propagation over uneven bottoms: Linear wave propagation. Adv. Ser. Ocean. Eng. 1997, 13, 708–715. [Google Scholar]
- Greenshields, C.J. OpenFOAM User Guide, Version 6; OpenFOAM Found. Ltd.: London, UK, 2018.
- Svendsen, I.A.; Brink-Kjær, O. Shoaling of cnoidal waves. In Proceedings of the 13th Coastal Engineering Conference, Vancouver, BC, Canada, 10–14 July 1972; pp. 365–384. [Google Scholar]
- Synolakis, C.E.; Deb, M.K. On the maximum runup of cnoidal waves. In Proceedings of the 21th Coastal Engineering Conference, Malaga, Costa del Sol, Spain, 20–25 June 1988; pp. 553–565. [Google Scholar]
- Lee, T.C.; Tang, C.J. Numerical study on generation of cnoidal waves and induced viscous flow over a wavy bed. In Proceedings of the 19th International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 June 2009; pp. 846–853. [Google Scholar]
- Benjamin, T.B.; Feir, J.E. The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Su, M.Y.; Bergin, M.; Marler, P.; Myrick, R. Experiments on nonlinear instabilities and evolution of steep gravity wave trains. J. Fluid Mech. 1982, 124, 45–72. [Google Scholar] [CrossRef]
- Benjamin, T.B. Instability of periodic wavetrains in nonlinear dispersive systems. Proc. R. Soc. Lond. A 1967, 299, 59–76. [Google Scholar]
- Whitham, G.B. Non-linear dispersion of water waves. J. Fluid Mech. 1967, 27, 399–412. [Google Scholar] [CrossRef]
- Benjamin, T.B. The stability of solitary waves. Proc. R. Soc. Lond. A 1972, 328, 153–183. [Google Scholar]
- Pego, R.L.; Weinstein, M.I. Asymptotic stability of solitary waves. Commun. Math. Phys. 1994, 164, 305–349. [Google Scholar] [CrossRef]
- Angulo Pava, J.; Bona, J.L.; Scialom, M. Stability of cnoidal waves. Adv. Differ. Eq. 2006, 11, 1321–1374. [Google Scholar] [CrossRef]
- Bottman, N.; Deconinck, B. KdV cnoidal waves are spectrally stable. Discret. Cont. Dyn. Syst. 2009, 25, 1163–1180. [Google Scholar] [CrossRef]
- Deconinck, B.; Kapitula, T. The orbital stability of the cnoidal waves of the Korteweg-de Vries equation. Phys. Lett. A 2010, 374, 4018–4022. [Google Scholar] [CrossRef]
- Chen, C.J.; Chen, H.C. The Finite-Analytic Method; IIHR Rep. No. 232-IV; IIHR—Hydroscience & Engineering, The University of Iowa: Iowa City, IA, USA, 1982. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; McGraw-Hill Inc.: New York, NY, USA, 1980. [Google Scholar]
- Chan, R.K.; Street, R.L. A computer study of finite-amplitude water waves. J. Comput. Phys. 1970, 6, 95–104. [Google Scholar] [CrossRef]
- Mizuguchi, M. Second-order solution of laminar boundary layer flow under waves. Coast. Eng. Jpn. 1987, 30, 9–18. [Google Scholar] [CrossRef]
- Mei, C.C.; Stiassine, M.; Yue, D.K.-P. Theory and Applications of Ocean Surface Waves. Part 2: Nonlinear Aspects; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2005; Chapter 12. [Google Scholar]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed.; Springer: New York, NY, USA, 1971. [Google Scholar]
- Isobe, M. Calculation and application of first-order cnoidal wave theory. Coast. Eng. 1985, 9, 309–325. [Google Scholar] [CrossRef]
- Kiper, A. Fourier series coefficients for powers of the Jacobian elliptic functions. Math. Comput. 1984, 43, 247–259. [Google Scholar] [CrossRef]
- Tanaka, H.; Sumer, B.M.; Lodahl, C. Theoretical and experimental investigation on laminar boundary layers under cnoidal wave motion. Coast. Eng. Jpn. 1998, 40, 81–98. [Google Scholar] [CrossRef]
- Keulegan, G.H. Gradual damping of solitary waves. J. Res. Natl. Bur. Stand. 1948, 40, 487–498. [Google Scholar] [CrossRef]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Russel, J.S. Report of the Committee on waves. In Report of the 7th Meeting of British Association for the Advancement of Science; John Murray: London, UK, 1838; pp. 417–496. [Google Scholar]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Young, R.K. Wavelet Theory and Its Applications; Kluwer Academic Publishers: Boston, MA, USA, 1993. [Google Scholar]
- Hammack, J.L.; Segur, H. The Korteweg–de Vries equation and water waves. Part 2: Comparison with experiments. J. Fluid Mech. 1974, 65, 289–314. [Google Scholar] [CrossRef]
- Goring, D.G. Tsunamis—The Propagation of Long Waves onto a Shelf; Rep. Kh-R-38; W. M. Keck Laboratory of Hydraulics and Water Resources, California Institute of Technology: Pasadena, CA, USA, 1978. [Google Scholar]
- Boyd, J.P. Cnoidal waves as exact sums of repeated solitary waves: New series for elliptic functions. SIAM Appl. Math. 1984, 44, 952–955. [Google Scholar] [CrossRef]

| Variable | |||||||
|---|---|---|---|---|---|---|---|
| Case 1 | 1.25 | 1.0 | 0.4 | 2.05 | 0.195 | 1.225 | 0.67 |
| Case 2 | 2.0 | 2.0 | 0.4 | 3.69 | 0.108 | 0.679 | 4.31 |
| Case 3 | 2.5 | 4.0 | 0.4 | 4.72 | 0.085 | 0.534 | 13.98 |
| Case 4 | 3.0 | 5.0 | 0.4 | 5.77 | 0.069 | 0.433 | 25.91 |
| Case 5 | 3.0 | 8.0 | 0.4 | 5.92 | 0.068 | 0.427 | 43.81 |
| Case 6 | - | 12.0 | 0.4 | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, C.-M.; Huang, C.-J.; Huang, H.-C. Generation and Evolution of Cnoidal Waves in a Two-Dimensional Numerical Viscous Wave Flume. J. Mar. Sci. Eng. 2025, 13, 1102. https://doi.org/10.3390/jmse13061102
Dong C-M, Huang C-J, Huang H-C. Generation and Evolution of Cnoidal Waves in a Two-Dimensional Numerical Viscous Wave Flume. Journal of Marine Science and Engineering. 2025; 13(6):1102. https://doi.org/10.3390/jmse13061102
Chicago/Turabian StyleDong, Chih-Ming, Ching-Jer Huang, and Hui-Ching Huang. 2025. "Generation and Evolution of Cnoidal Waves in a Two-Dimensional Numerical Viscous Wave Flume" Journal of Marine Science and Engineering 13, no. 6: 1102. https://doi.org/10.3390/jmse13061102
APA StyleDong, C.-M., Huang, C.-J., & Huang, H.-C. (2025). Generation and Evolution of Cnoidal Waves in a Two-Dimensional Numerical Viscous Wave Flume. Journal of Marine Science and Engineering, 13(6), 1102. https://doi.org/10.3390/jmse13061102






