Multi-Objective Optimization Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization for Pipeline Selection of Replenishment Oiler
Abstract
1. Introduction
2. Methodology
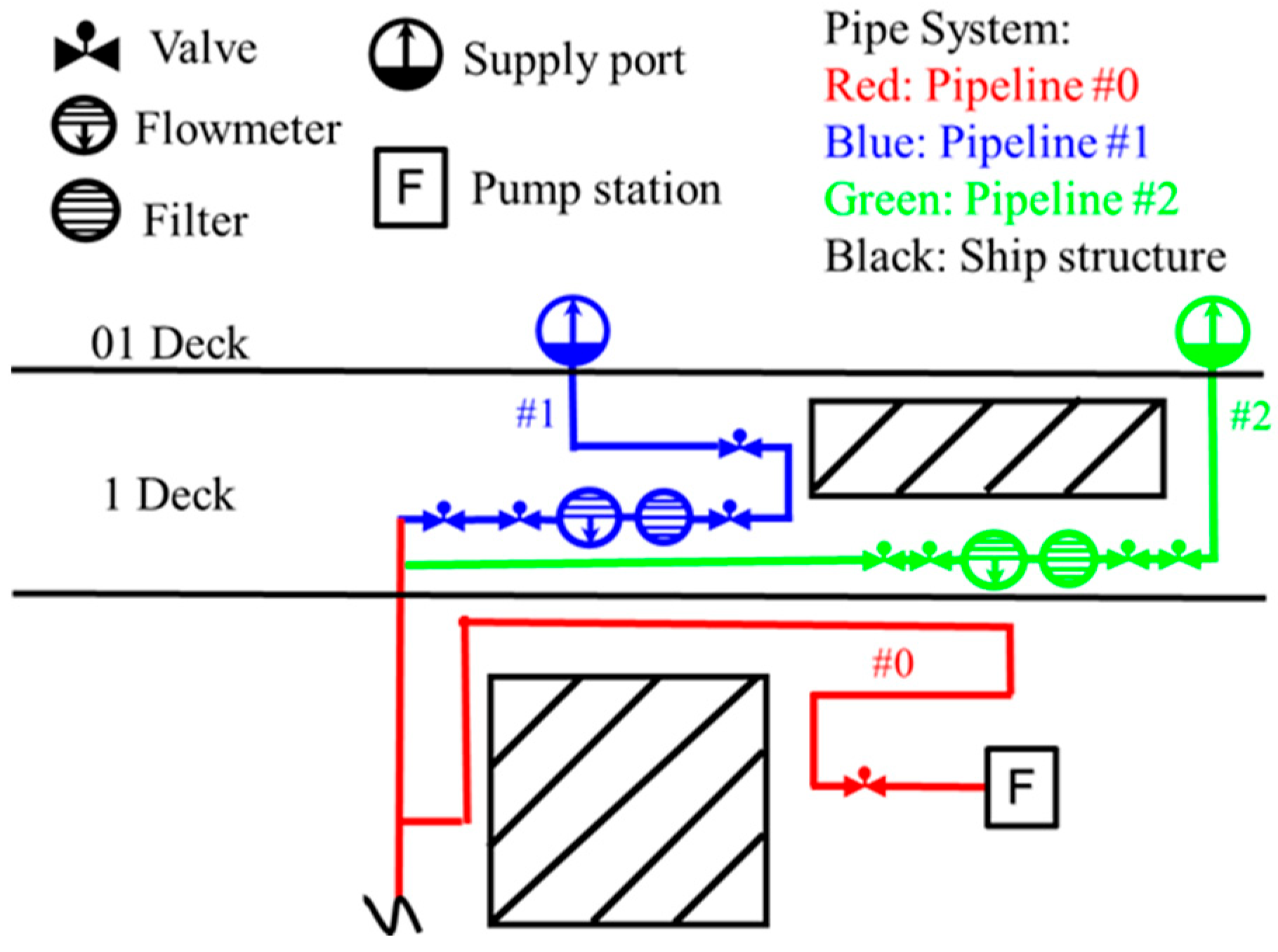
2.1. Problem Description
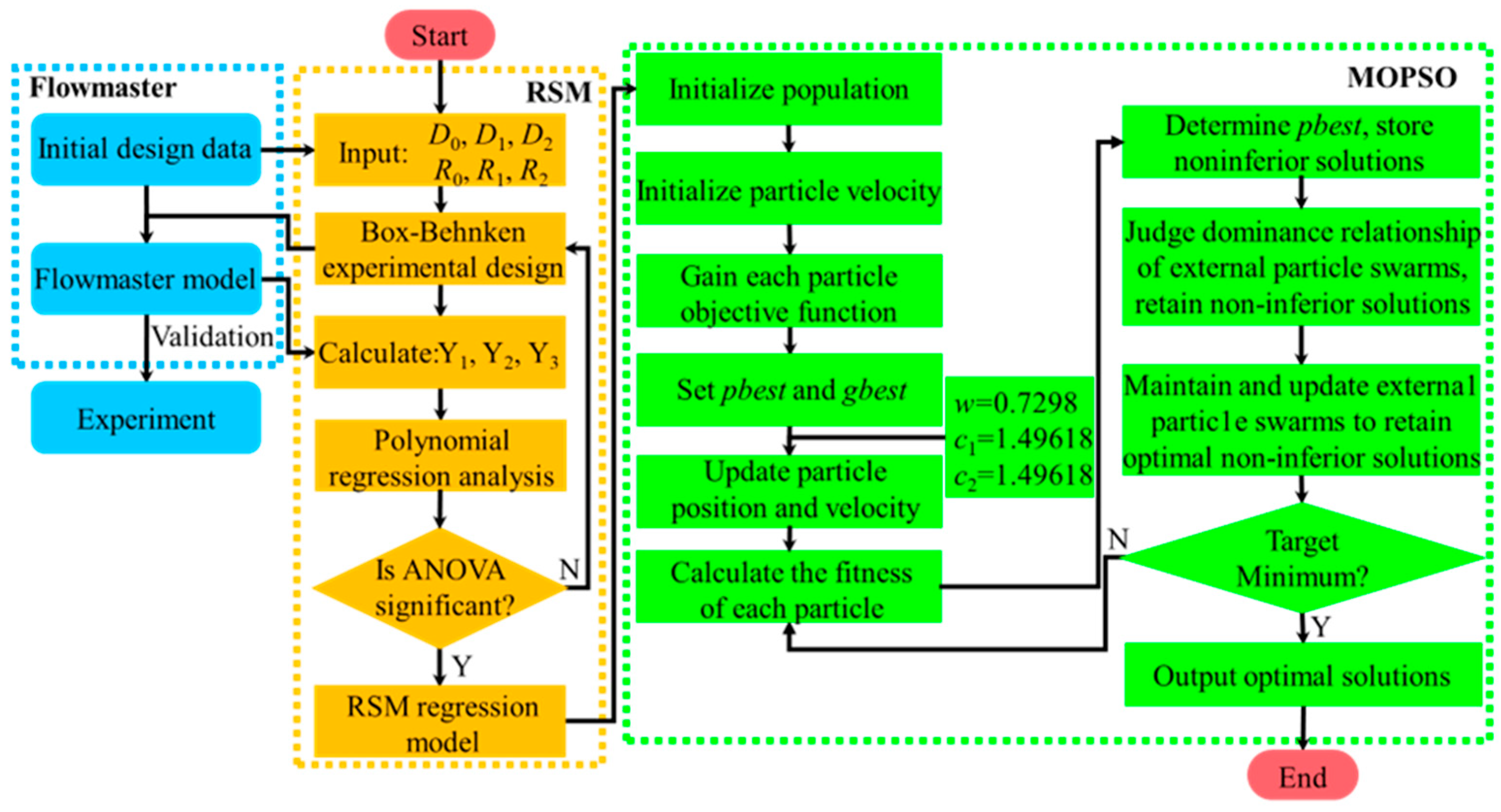
2.2. Response Surface Methodology
2.3. MOPSO Algorithm
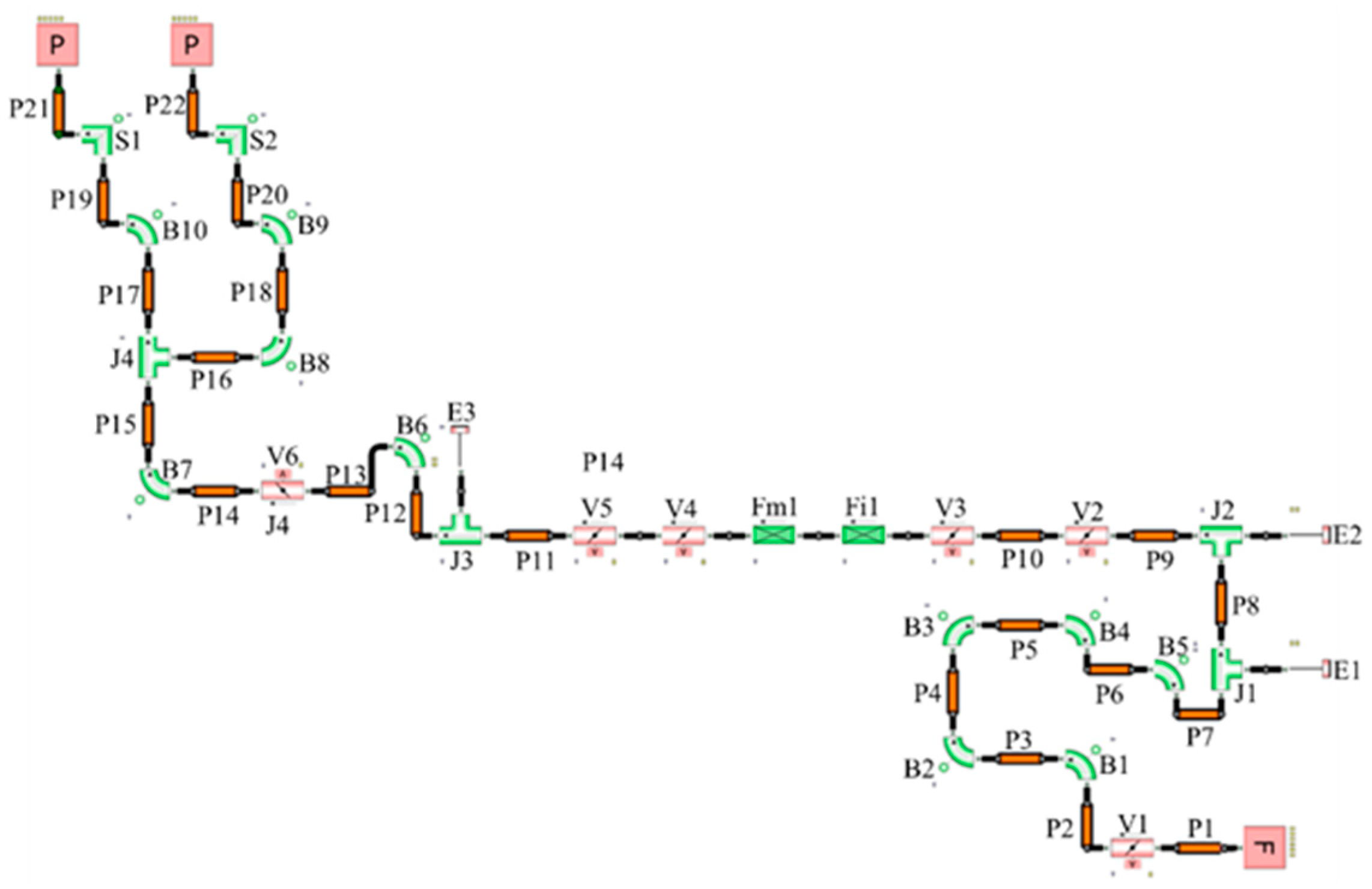
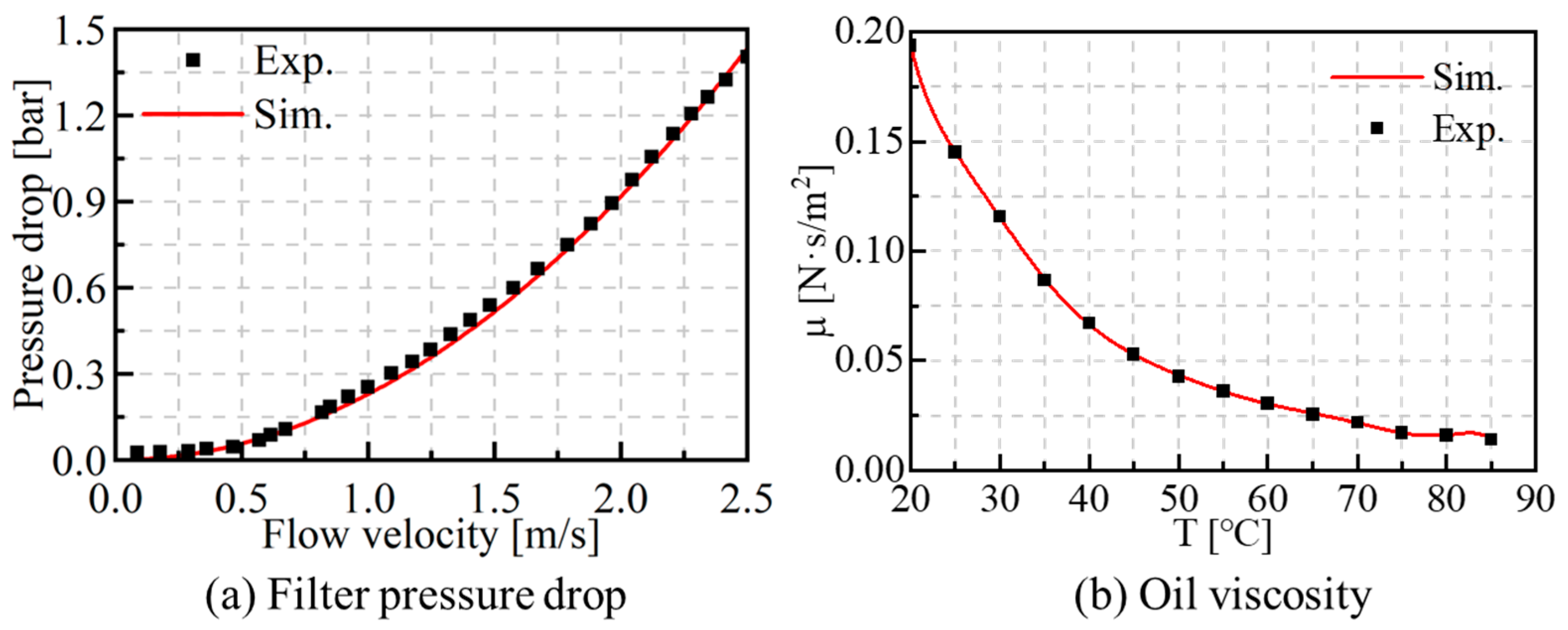
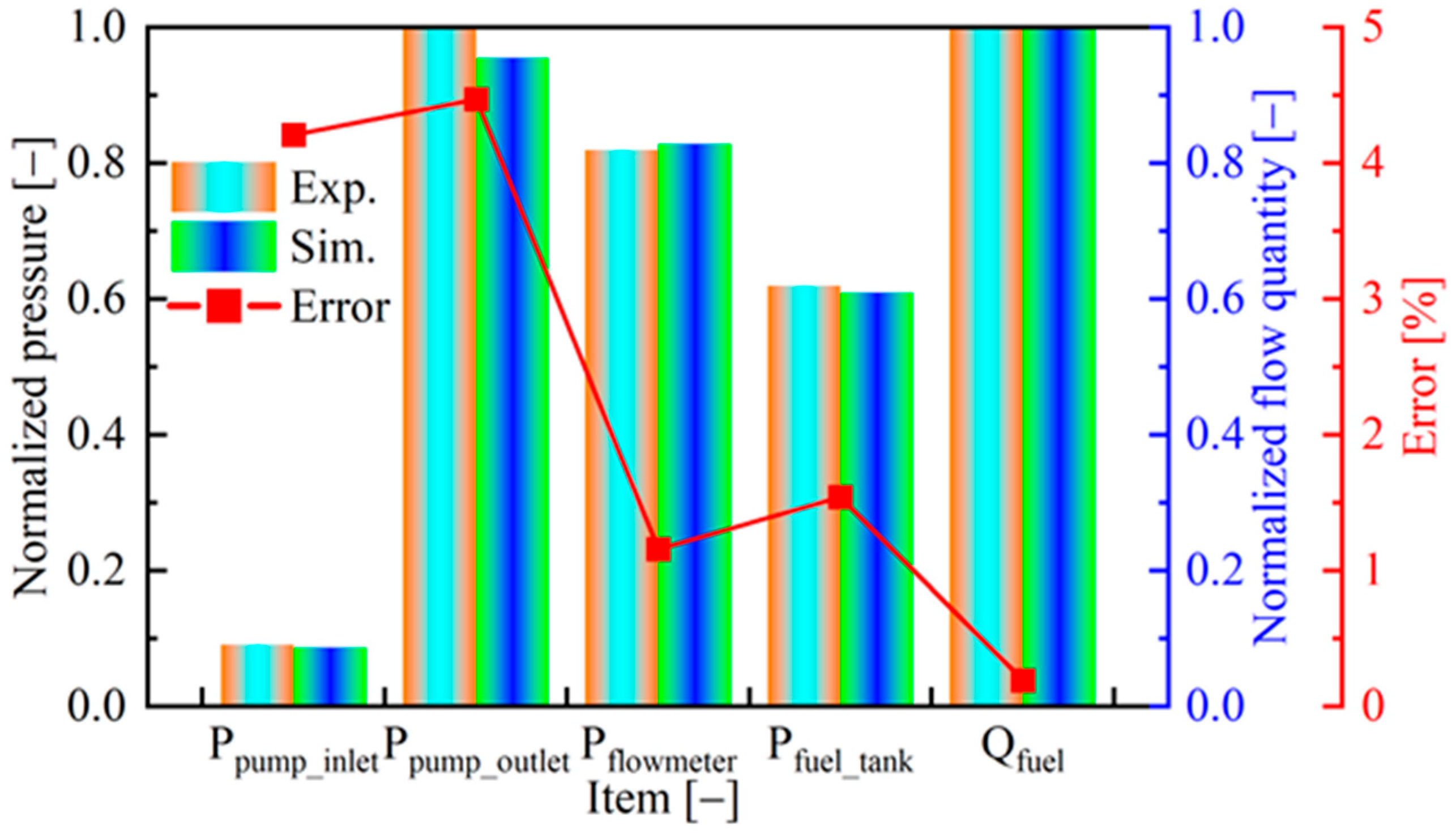
2.4. Establishment and Calibration of Simulation Model
3. RSM Prediction Model
3.1. Model Parameters
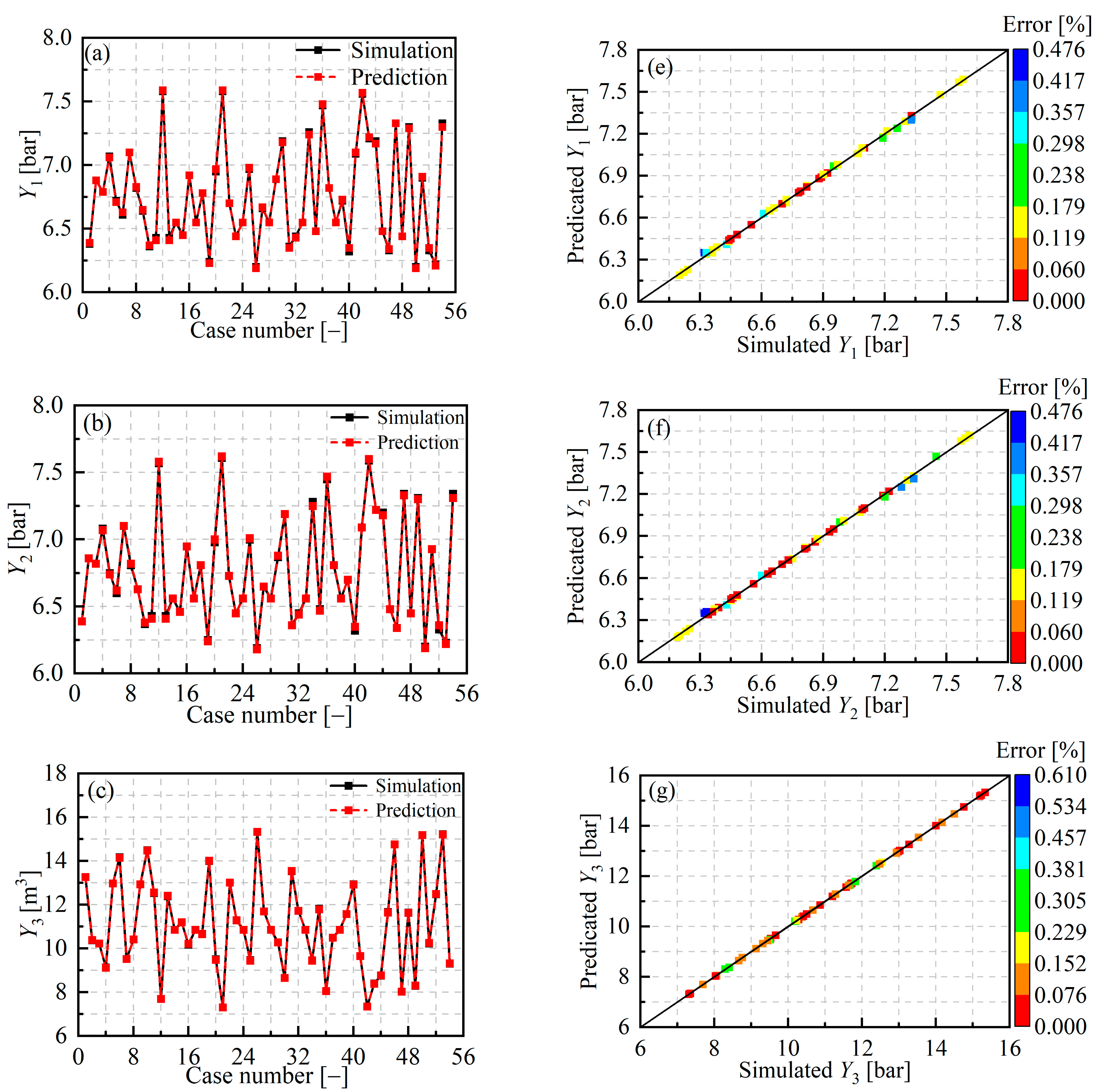
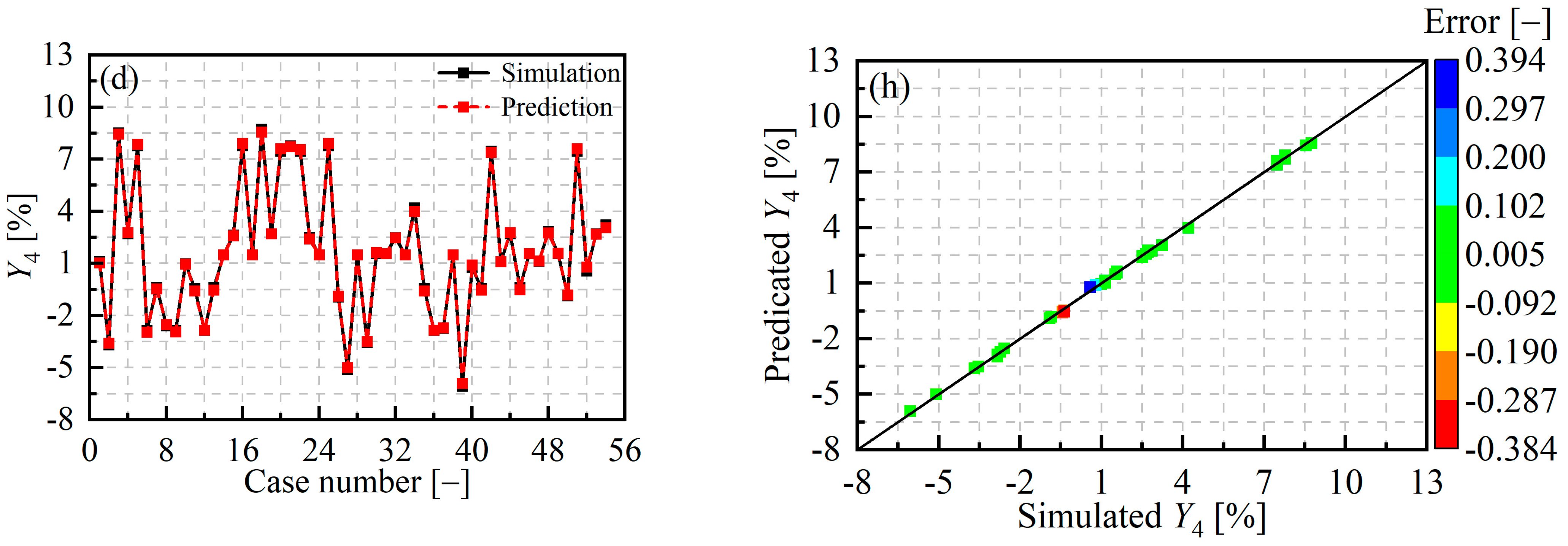
3.2. Predictive Performance
4. Results and Discussion
4.1. Response Surface Parameter Analysis
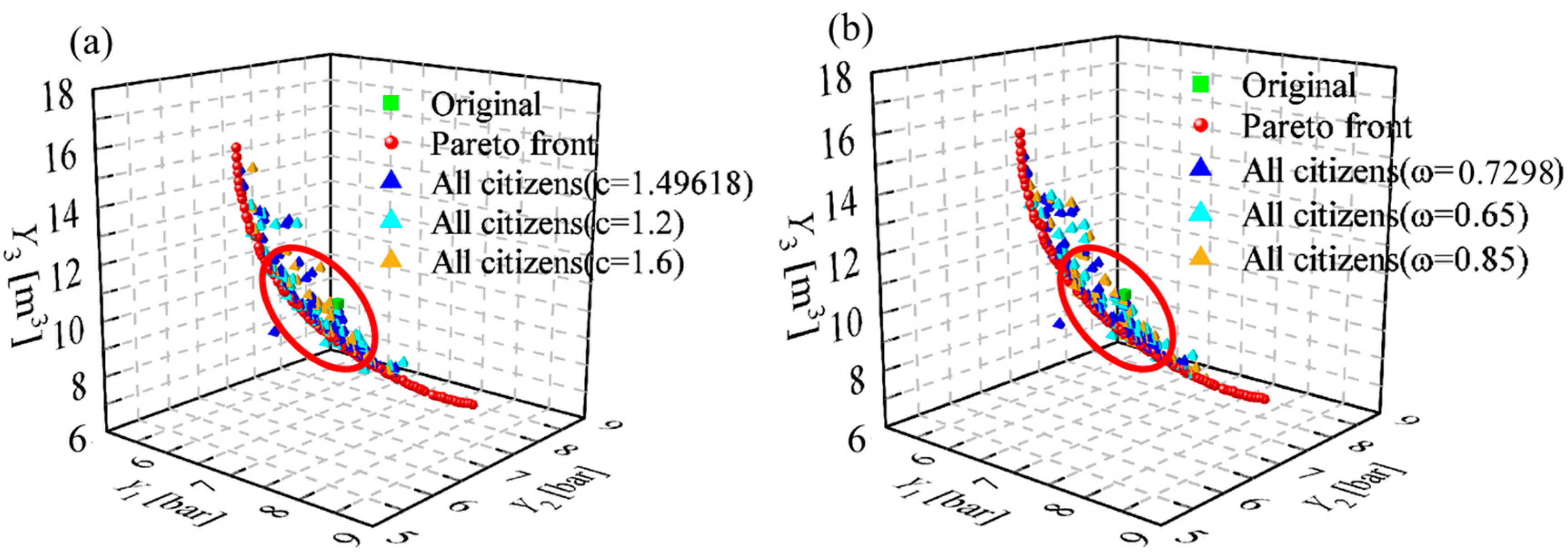
4.2. Multi-Objective Parameter Optimization with MOPSO
5. Conclusions
- (1)
- A 1D Flowmaster simulation model was developed based on the replenishment oiler pipeline system and was validated by completed ship data. Good agreement was obtained, confirming the accuracy of the simulation model, and the maximum error of the model was 4.44%, which is below the allowable error in engineering of 5%.
- (2)
- The RSM method was employed to establish regression prediction models for the resistance of the deck refueling pipelines #1 (Y1) and #2 (Y2), the pipeline system volume (Y3), and the flow imbalance between the two supply ports (Y4). The analysis of variance (ANOVA) result was greater than 0.98, proving the strong predictability of the regression models.
- (3)
- The regression equation established by RSM was combined with the intelligent optimization algorithm MOPSO to optimize the pipeline selection.
- (4)
- Due to the optimization results only considering mathematical relationships, they did not satisfy the national standards and needed to be standardized according to the “Practical Handbook of Ship Design-Engine Section”. The processed results show that the resistance of the deck refueling pipeline #1 (Y1) and #2 (Y2) were reduced by 3.57% and 3.51%, respectively. The pipeline system volume (Y3) was reduced by 5.72%. The simulation results indicate that optimized pipeline selection in replenishment oilers can achieve the dual objectives of resistance reduction and spatial efficiency improvement, thus significantly enhancing in-service refueling performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPD | Ship pipeline design |
| RSM | Response surface methodology |
| ANOVA | Analysis of variance |
| MOPSO | Multi-objective particle swarm optimization |
| R/D | Bend–diameter ratio |
| PSO | Particle swarm optimization |
Appendix A

References
- Fagerholt, K.; Hvattum, L.M.; Johnsen, T.A.V.; Korsvik, J.E. Routing and scheduling in project shipping. Ann. Oper. Res. 2013, 207, 67–81. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Christiansen, M.; Fagerholt, K.; Nygreen, B.; Ronen, D. Ship routing and scheduling in the new millennium. Eur. J. Oper. Res. 2013, 228, 467–483. [Google Scholar] [CrossRef]
- Yan, W.; Yang, M.; Lin, Y. A hybrid algorithm based on the proposed square strategy and NSGA-II for ship pipe route design. Ocean Eng. 2024, 305, 117961. [Google Scholar] [CrossRef]
- Guarracino, F.; Fraldi, M.; Giordano, A. Analysis of testing methods of pipelines for limit state design. Appl. Ocean Res. 2008, 30, 297–304. [Google Scholar] [CrossRef]
- Kyrkjebø, E.; Pettersen, K.Y.; Wondergem, M.; Nijmeijer, H. Output synchronization control of ship replenishment operations: Theory and experiments. Control Eng. Pr. 2007, 15, 741–755. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W. Ship pipe route design based on NSGA-III and multi-population parallel evolution. Ocean Eng. 2024, 293, 116666. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, Z.; Qian, H.; Ye, Y.; Leng, J.; Wei, Y. Design and analysis of a novel ship pipeline welding auxiliary device. Ocean Eng. 2016, 123, 55–64. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Wang, W.; Liu, Z.; Yu, X.; Li, H.; Wang, W.; Hu, X. A review of optimal design for large-scale micro-irrigation pipe network systems. Agronomy 2023, 13, 2966. [Google Scholar] [CrossRef]
- Yeo, I.; Roh, M.; Chun, D.; Jang, S.H.; Heo, J.W. Optimal arrangement design of pipeline support by considering safety and production cost. Int. J. Nav. Archit. Ocean. Eng. 2023, 15, 100531. [Google Scholar] [CrossRef]
- Blokland, M.; Van der Mei, R.D.; Pruyn, J.F.J.; Berkhout, J. Literature survey on automatic pipe routing. Oper. Res. Forum 2023, 4, 35. [Google Scholar] [CrossRef]
- Park, J.; Storch, R.L. Pipe-routing algorithm development: Case study of a ship engine room design. Expert Syst. Applications 2002, 23, 299–309. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, Y.; Zhang, Q.; Yang, Y.; Liu, H.; Lin, Y. A bidirectional collaborative method based on an improved artificial fish swarm algorithm for ship pipe and equipment layout design. Ocean Eng. 2024, 296, 117045. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, Q. A multi-objective cooperative particle swarm optimization based on hybrid dimensions for ship pipe route design. Ocean Eng. 2023, 280, 114772. [Google Scholar] [CrossRef]
- Ha, J.; Roh, M.; Kim, K.; Kim, J. Method for pipe routing using the expert system and the heuristic pathfinding algorithm in shipbuilding. Int. J. Nav. Arch. Ocean 2023, 15, 100533. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Li, K.; Zhao, X.; Guan, G. A human-computer cooperation improved ant colony optimization for ship pipe route design. Ocean Eng. 2018, 150, 12–20. [Google Scholar] [CrossRef]
- Min, J.; Ruy, W.; Park, C.S. Faster pipe auto-routing using improved jump point search. Int. J. Nav. Arch. Ocean 2020, 12, 596–604. [Google Scholar] [CrossRef]
- Huang, H. Practical Handbook of Ship Design-Engine Section, 3rd ed.; National Defense Industry Press: Beijing, China, 2013. [Google Scholar]
- Rai, P.K.; Kant, V.; Sharma, R.K.; Gupta, A. Process optimization for textile industry-based wastewater treatment via ultrasonic-assisted electrochemical processing. Eng. Appl. Artif. Intell. 2023, 122, 106162. [Google Scholar] [CrossRef]
- Li, J.; Jasim, D.J.; Kadir, D.H.; Maleki, H.; Esfahani, N.N.; Shamsborhan, M.; Toghraie, D. Multi-objective optimization of a laterally perforated-finned heat sink with computational fluid dynamics method and statistical modeling using response surface methodology. Eng. Appl. Artif. Intell. 2024, 130, 107674. [Google Scholar] [CrossRef]
- Coppedè, A.; Gaggero, S.; Vernengo, G.; Villa, D. Hydrodynamic shape optimization by high fidelity CFD solver and Gaussian process based response surface method. Appl. Ocean Res. 2019, 90, 101841. [Google Scholar] [CrossRef]
- Cao, Y.; Khan, A.; Abdi, A.; Ghadiri, M. Combination of RSM and NSGA-II algorithm for optimization and prediction of thermal conductivity and viscosity of bioglycol/water mixture containing SiO2 nanoparticles. Arab. J. Chem. 2021, 14, 103204. [Google Scholar] [CrossRef]
- Zhang, Z.; Dong, R.; Tan, D.; Zhang, B. Multi-objective optimization of performance characteristic of diesel particulate filter for a diesel engine by RSM-MOPSO during soot loading. Process Saf. Environ. Prot. 2023, 177, 530–545. [Google Scholar] [CrossRef]
- Li, R.; Gao, Y.; Jiang, B.; Lv, M.; Li, H. Intelligent parameter optimization of sealed airbag vessels with preventing water hammer in cascaded pressurized water transmission system: Based on MOPSO algorithm. J. Water Process Eng. 2025, 70, 106915. [Google Scholar] [CrossRef]
- Wang, Y.; Iris, Ç. Transition to near-zero emission shipping fleet powered by alternative fuels under uncertainty. Transp. Res. Part. D. Transp. Environ. 2025, 142, 104689. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, Y.; Iris, Ç. Integrated Green Technology adoption, ship speed optimization and slot management for shipping alliance under emission limits and uncertain fuel prices. J. Clean. Prod. 2025, 494, 144939. [Google Scholar] [CrossRef]
- Bouchaala, A.; Merroun, O.; Sakim, A. A MOPSO algorithm based on pareto dominance concept for comprehensive analysis of a conventional adsorption desiccant cooling system. J. Build. Eng. 2022, 60, 105189. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, H.; Wang, J.; Zhang, N. Optimization of the injection parameters of a diesel/natural gas dual fuel engine with multi-objective evolutionary algorithms. Appl. Therm. Eng. 2019, 150, 70–79. [Google Scholar] [CrossRef]
- Yin, L.; Ding, W. Multi-objective high-dimensional multi-fractional-order optimization algorithm for multi-objective high-dimensional multi-fractional-order optimization controller parameters of doubly-fed induction generator-based wind turbines. Eng. Appl. Artif. Intell. 2023, 126, 106929. [Google Scholar] [CrossRef]
- Shuai, W.; Xiaohui, L.; Xiaomin, H. Multi-objective optimization of reservoir flood dispatch based on MOPSO algorithm. In Proceedings of the 8th International Conference on Natural Computation, IEEE, Chongqing, China, 29–31 May 2012. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Coello Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. Publ. Information. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Pang, L.; Ng, S.; Aguirre, H. Improved efficiency of MOPSO with adaptive inertia weight and dynamic search space. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018. [Google Scholar]
- Zhang, X.; Liu, H.; Tu, L. A modified particle swarm optimization for multimodal multi-objective optimization. Eng. Appl. Artif. Intell. 2020, 95, 103905. [Google Scholar] [CrossRef]
- Ali, T.; Peng, Y.; Jin, Z.H.; Kun, L.; Renchuan, Y. Crashworthiness optimization method for sandwich plate structure under impact loading. Ocean Eng. 2022, 250, 110870. [Google Scholar] [CrossRef]
- Tuppadung, Y.; Kurutach, W. Comparing nonlinear inertia weights and constriction factors in particle swarm optimization. Int. J. Knowl.-Based Dev. 2011, 15, 65–70. [Google Scholar] [CrossRef]
- Vandenbergh, F.; Engelbrecht, A. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000. [Google Scholar]
- Cong, Y.; Gan, H.; Wang, H.; Hu, G.; Liu, Y. Multi-objective optimization of the performance and emissions of a large low-speed dual-fuel marine engine based on MNLR-MOPSO. J. Mar. Sci. Eng. 2021, 9, 1170. [Google Scholar] [CrossRef]
- Huang, Y.; Ma, F. Intelligent regression algorithm study based on performance and NOx emission experimental data of a hydrogen enriched natural gas engine. Int. J. Hydrogen Energy. 2016, 41, 11308–11320. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Shi, C.; Ge, Y.; Wang, S.; Yang, J. Development of cyclic variation prediction model of the gasoline and n-butanol rotary engines with hydrogen enrichment. Fuel 2021, 299, 120891. [Google Scholar] [CrossRef]
- Kakati, D.; Roy, S.; Banerjee, R. Development of an artificial neural network based virtual sensing platform for the simultaneous prediction of emission-performance-stability parameters of a diesel engine operating in dual fuel mode with port injected methanol. Energy Convers. Management 2019, 184, 488–509. [Google Scholar] [CrossRef]


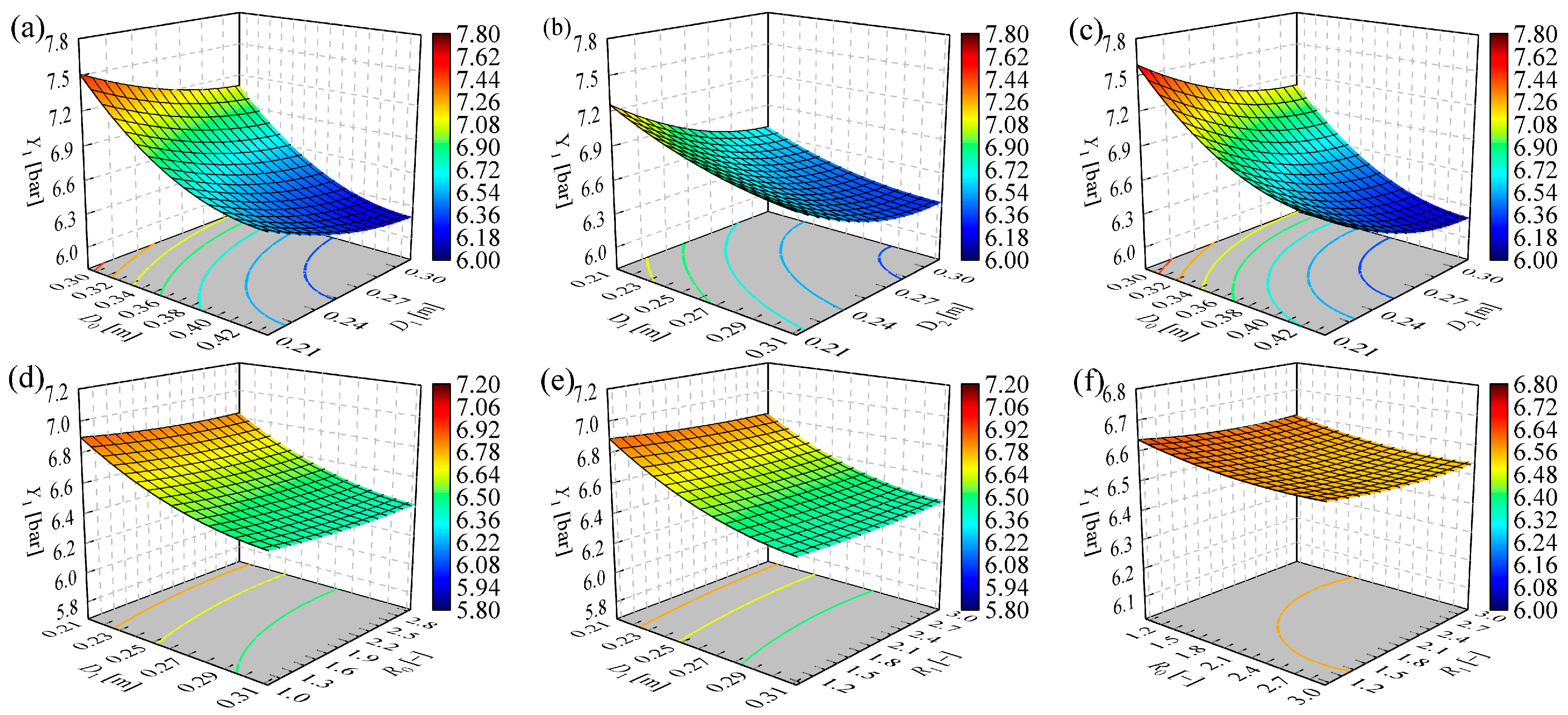
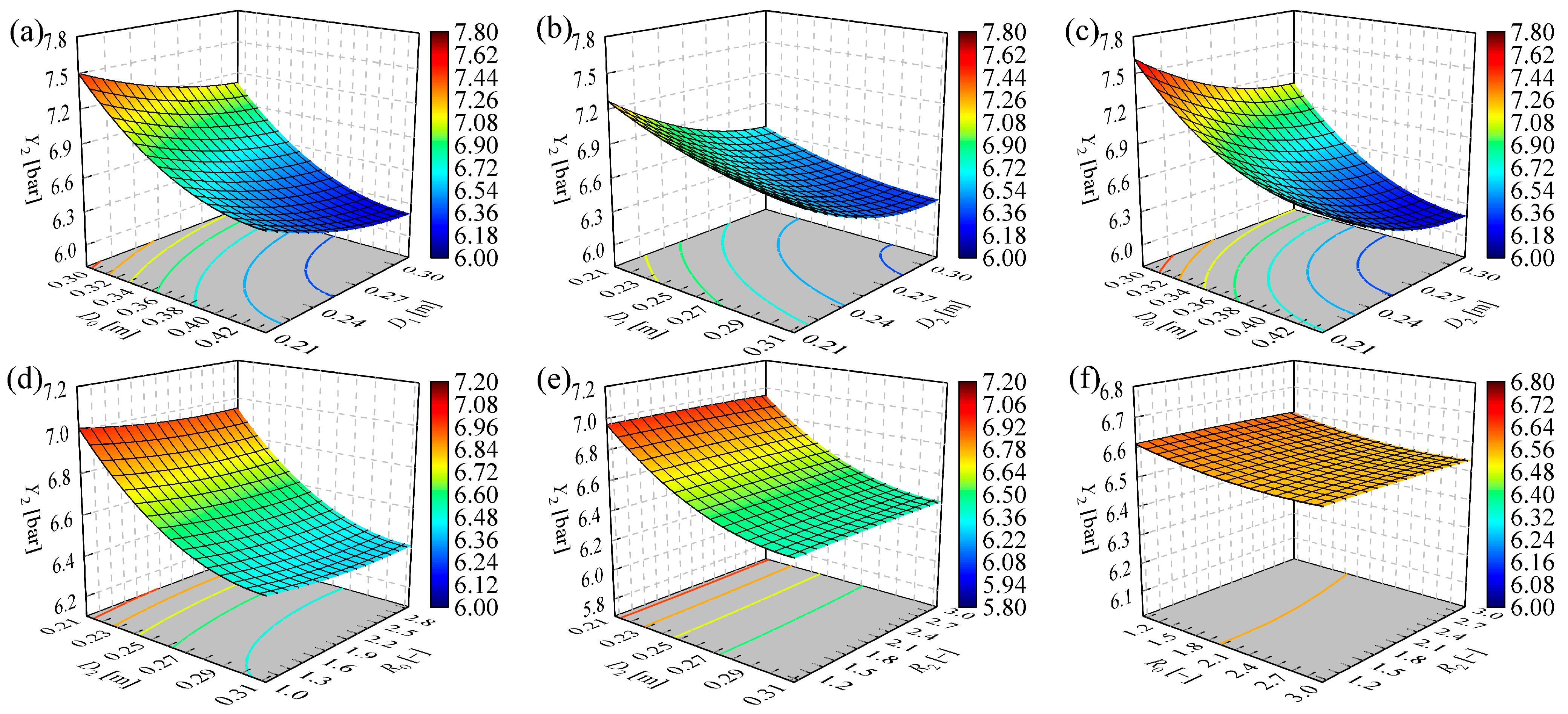
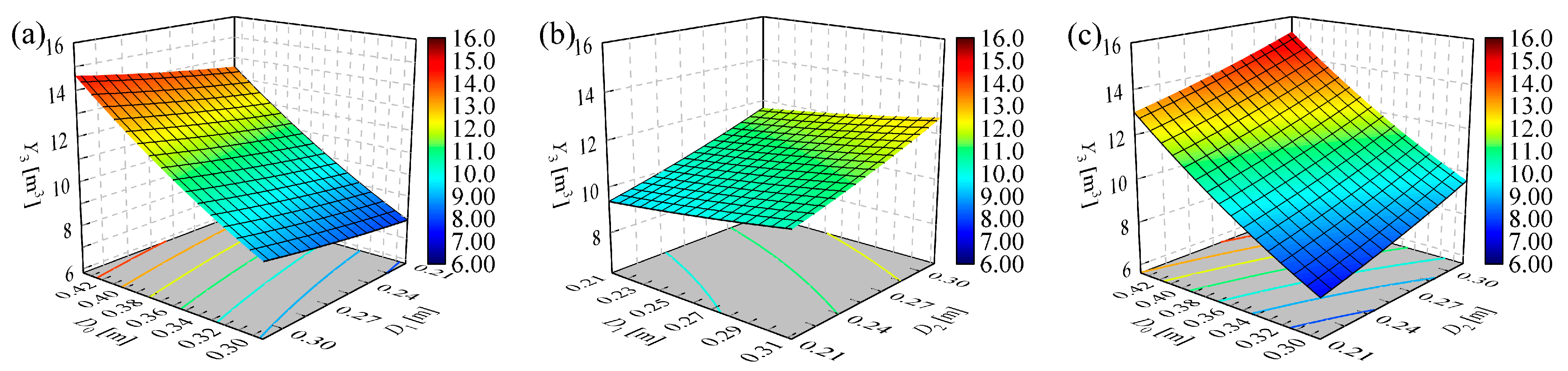
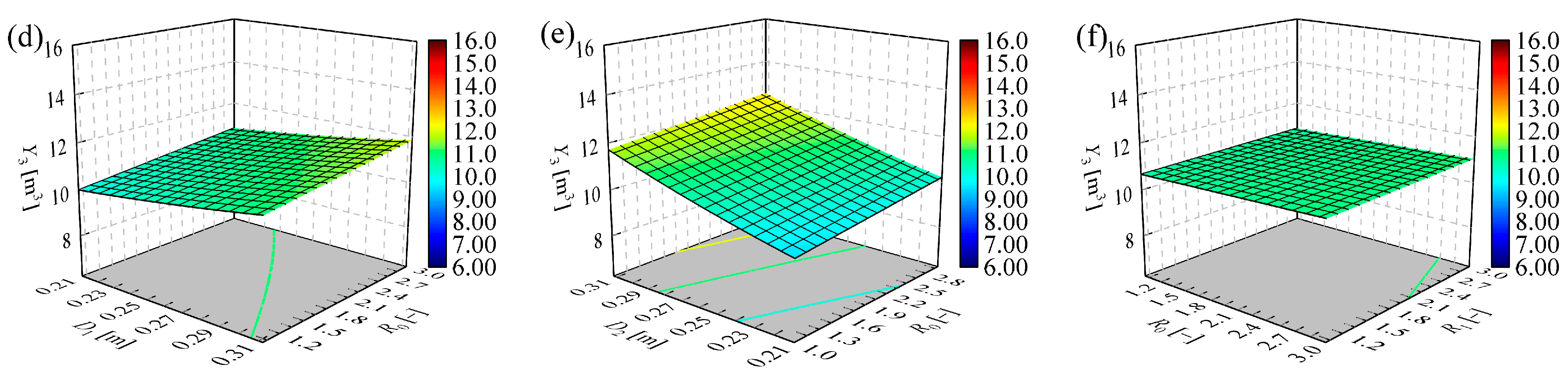
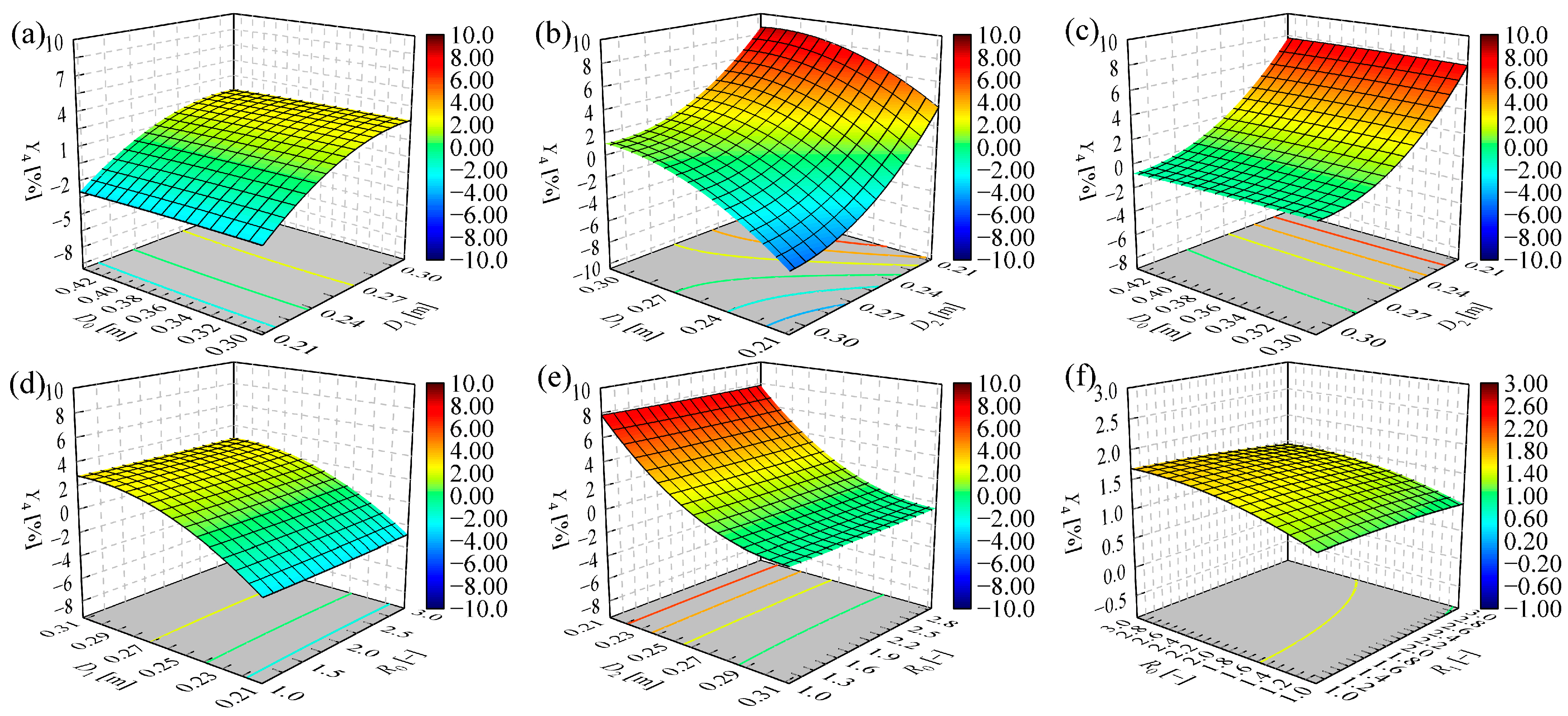
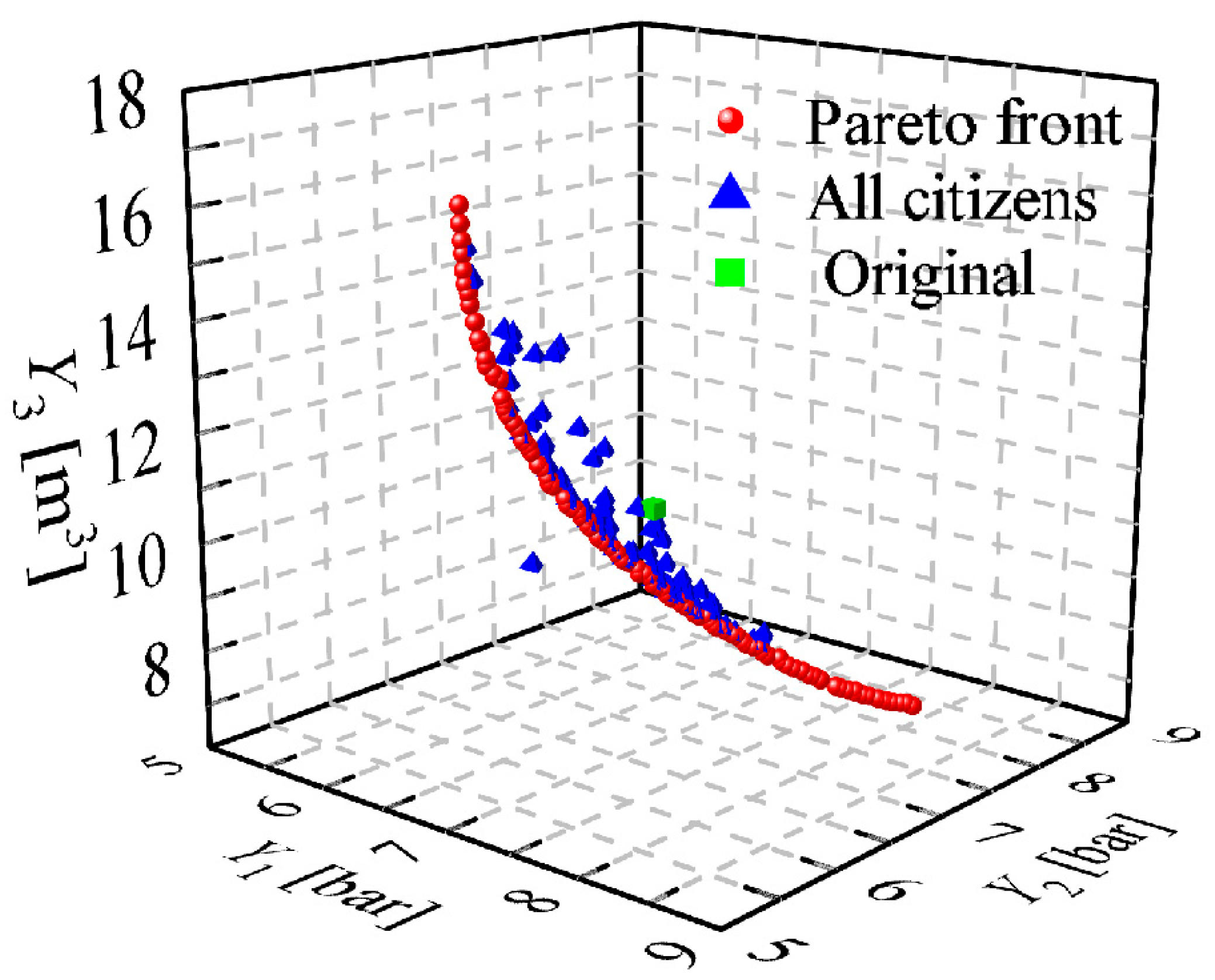
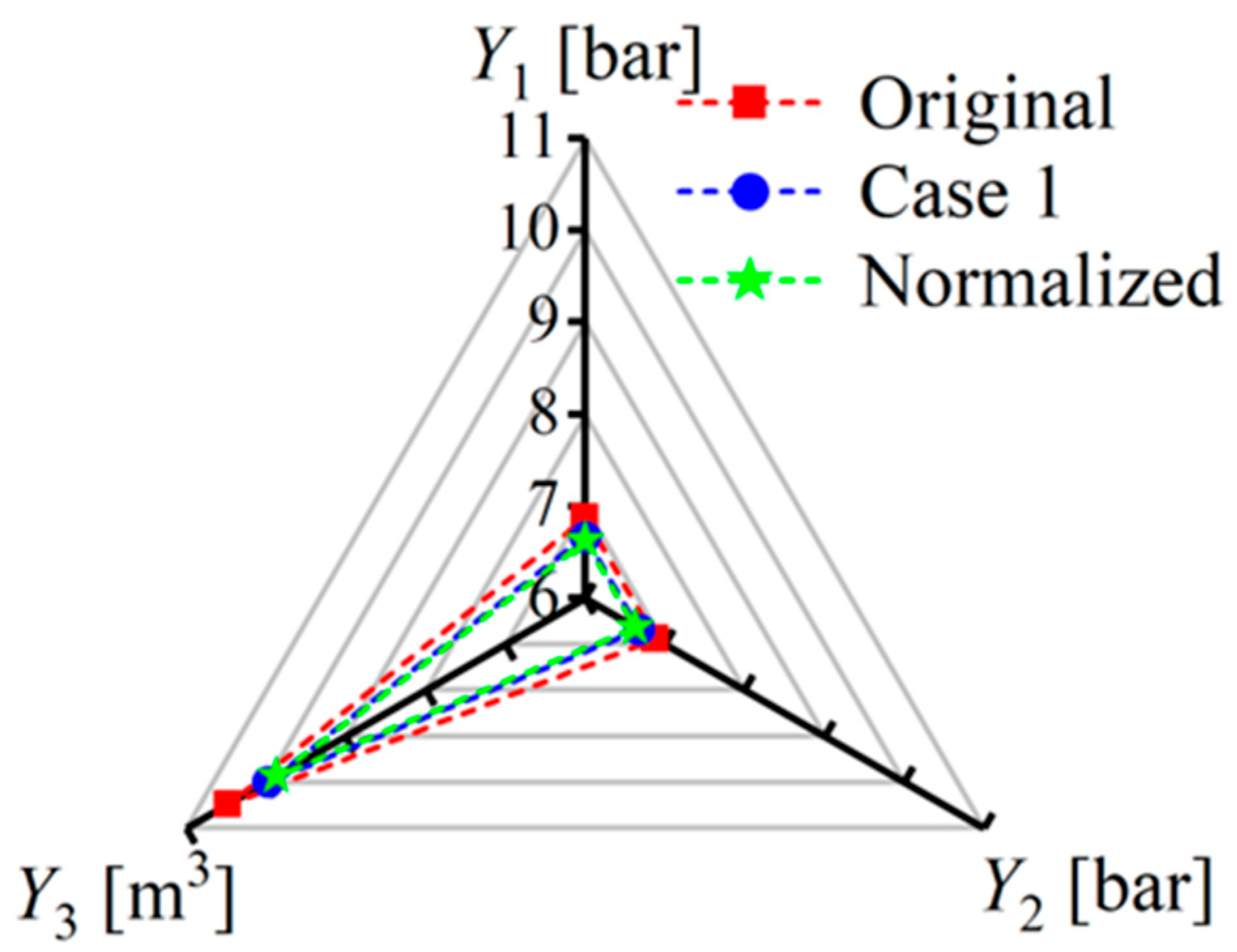
| Item | Y1 | Y2 | Y3 | Y4 | ||||
|---|---|---|---|---|---|---|---|---|
| F Value | p Value | F Value | p Value | F Value | p Value | F Value | p Value | |
| Model | 1156.07 | <0.0001 | 1136.88 | <0.0001 | 21,195.29 | <0.0001 | 1356.51 | <0.0001 |
| D1 | 18,551.16 | <0.0001 | 18,022.45 | <0.0001 | 4.67 × 105 | <0.0001 | 2.6 | 0.1188 |
| D2 | 4016.35 | <0.0001 | 3511.88 | <0.0001 | 16,607.33 | <0.0001 | 9679.11 | <0.0001 |
| D3 | 5828.64 | <0.0001 | 6387.27 | <0.0001 | 73,930.77 | <0.0001 | 21,070.05 | <0.0001 |
| R1 | 92.95 | <0.0001 | 90.24 | <0.0001 | 8737.17 | <0.0001 | 0.0428 | 0.8377 |
| R2 | 25.37 | <0.0001 | 21.83 | <0.0001 | 1114.75 | <0.0001 | 84.6 | <0.0001 |
| R3 | 1.94 | 0.175 | 2.19 | 0.1511 | 123.84 | <0.0001 | 10.64 | 0.0031 |
| D1D2 | 0.0002 | 0.9903 | 0.0001 | 0.9904 | 3.66 × 10−6 | 0.9985 | 0 | 1 |
| D1D3 | 1.8 | 0.1917 | 1.96 | 0.1735 | 1.94 × 10−6 | 0.9989 | 5.93 | 0.022 |
| D1R1 | 34.79 | <0.0001 | 33.78 | <0.0001 | 1801.85 | <0.0001 | 0.0642 | 0.802 |
| D1R2 | 1.21 × 10−6 | 0.9991 | 1.18 × 10−6 | 0.9991 | 1.21 × 10−7 | 0.9997 | 0.1284 | 0.723 |
| D1R3 | 3.10 × 10−6 | 0.9986 | 3.81 × 10−6 | 0.9985 | 1.21 × 10−7 | 0.9997 | 0 | 0.9974 |
| D2D3 | 37.46 | <0.0001 | 39.06 | <0.0001 | 3.03 × 10−8 | 0.9999 | 45.74 | <0.0001 |
| D2R1 | 0 | 1 | 0 | 1 | 3.03 × 10−8 | 0.9999 | 0 | 1 |
| D2R2 | 10.71 | 0.003 | 9.23 | 0.0054 | 229.21 | <0.0001 | 33.1 | <0.0001 |
| D2R3 | 0.0995 | 0.755 | 0.0862 | 0.7714 | 3.02 × 10−6 | 0.9986 | 0.2731 | 0.6057 |
| D3R1 | 4.85 × 10−8 | 0.9998 | 4.70 × 10−8 | 0.9998 | 2.45 × 10−6 | 0.9988 | 0 | 1 |
| D3R2 | 0.0424 | 0.8384 | 0.0408 | 0.8416 | 1.48 × 10−6 | 0.999 | 0.0019 | 0.9656 |
| D3R3 | 0.804 | 0.3781 | 0.8786 | 0.3572 | 25.46 | <0.0001 | 2.84 | 0.1041 |
| R1R2 | 4.85 × 10−8 | 0.9998 | 4.70 × 10−8 | 0.9998 | 0 | 1 | 0.1284 | 0.723 |
| R1R3 | 4.85 × 10−8 | 0.9998 | 4.70 × 10−8 | 0.9998 | 3.03 × 10−8 | 0.9999 | 0 | 1 |
| R2R3 | 0.0818 | 0.7772 | 0.0702 | 0.7931 | 3.02 × 10−6 | 0.9986 | 0.2661 | 0.6103 |
| D12 | 1945.43 | <0.0001 | 1884.7 | <0.0001 | 2565.48 | <0.0001 | 2.27 | 0.144 |
| D22 | 275.06 | <0.0001 | 230.42 | <0.0001 | 113.08 | <0.0001 | 1277.35 | <0.0001 |
| D32 | 629.78 | <0.0001 | 690.12 | <0.0001 | 334.91 | <0.0001 | 2281.39 | <0.0001 |
| R12 | 19.33 | 0.0002 | 19.15 | 0.0002 | 6.93 × 10−7 | 0.9993 | 1.57 | 0.2207 |
| R22 | 9.53 | 0.0048 | 8.59 | 0.007 | 4.61 × 10−7 | 0.9995 | 13.31 | 0.0012 |
| R32 | 0.4971 | 0.487 | 0.5212 | 0.4768 | 2.42 × 10−6 | 0.9988 | 0.6342 | 0.433 |
| 0.9992 | 0.9992 | 1 | 0.9993 | |||||
| 0.9983 | 0.9983 | 0.9999 | 0.9986 | |||||
| 0.9957 | 0.9956 | 0.9998 | 0.9963 | |||||
| Case | D0 [m] | D1 [m] | D2 [m] | R0 [−] | R1 [−] | R2 [−] | Y1 [bar] | Y2 [bar] | Y3 [bar] | Y4 [%] |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.342 | 0.284 | 0.256 | 1.606 | 1.434 | 1.164 | 6.668 | 6.678 | 9.982 | 2.728 |
| 2 | 0.345 | 0.287 | 0.254 | 1.095 | 1.610 | 1.017 | 6.684 | 6.696 | 9.897 | 3.009 |
| 3 | 0.342 | 0.286 | 0.246 | 1.388 | 1.304 | 1.103 | 6.739 | 6.753 | 9.671 | 3.568 |
| 4 | 0.346 | 0.284 | 0.243924 | 1.000 | 1.107 | 1.699 | 6.766 | 6.779 | 9.585 | 3.750 |
| 5 | 0.345 | 0.272 | 0.245 | 1.246 | 1.273 | 1.338 | 6.785 | 6.797 | 9.534 | 3.239 |
| 6 | 0.344 | 0.274 | 0.244 | 1.181 | 1.372 | 1.000 | 6.791 | 6.804 | 9.488 | 3.479 |
| 7 | 0.339 | 0.276 | 0.246 | 1.289 | 1.193 | 1.015 | 6.808 | 6.820 | 9.403 | 3.231 |
| 8 | 0.326 | 0.284 | 0.255 | 1.669 | 1.084 | 1.057 | 6.835 | 6.845 | 9.316 | 2.614 |
| 9 | 0.342 | 0.276 | 0.239 | 1.078 | 1.000 | 1.000 | 6.855 | 6.870 | 9.252 | 3.987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, Y.; Meng, C.; Yang, M.; Liu, Y.; Yi, P.; Li, T.; Huang, S. Multi-Objective Optimization Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization for Pipeline Selection of Replenishment Oiler. J. Mar. Sci. Eng. 2025, 13, 1037. https://doi.org/10.3390/jmse13061037
Cong Y, Meng C, Yang M, Liu Y, Yi P, Li T, Huang S. Multi-Objective Optimization Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization for Pipeline Selection of Replenishment Oiler. Journal of Marine Science and Engineering. 2025; 13(6):1037. https://doi.org/10.3390/jmse13061037
Chicago/Turabian StyleCong, Yujin, Cheng Meng, Ming Yang, Yong Liu, Ping Yi, Tie Li, and Shuai Huang. 2025. "Multi-Objective Optimization Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization for Pipeline Selection of Replenishment Oiler" Journal of Marine Science and Engineering 13, no. 6: 1037. https://doi.org/10.3390/jmse13061037
APA StyleCong, Y., Meng, C., Yang, M., Liu, Y., Yi, P., Li, T., & Huang, S. (2025). Multi-Objective Optimization Based on Response Surface Methodology and Multi-Objective Particle Swarm Optimization for Pipeline Selection of Replenishment Oiler. Journal of Marine Science and Engineering, 13(6), 1037. https://doi.org/10.3390/jmse13061037







