3.1. Scour Hole Morphology
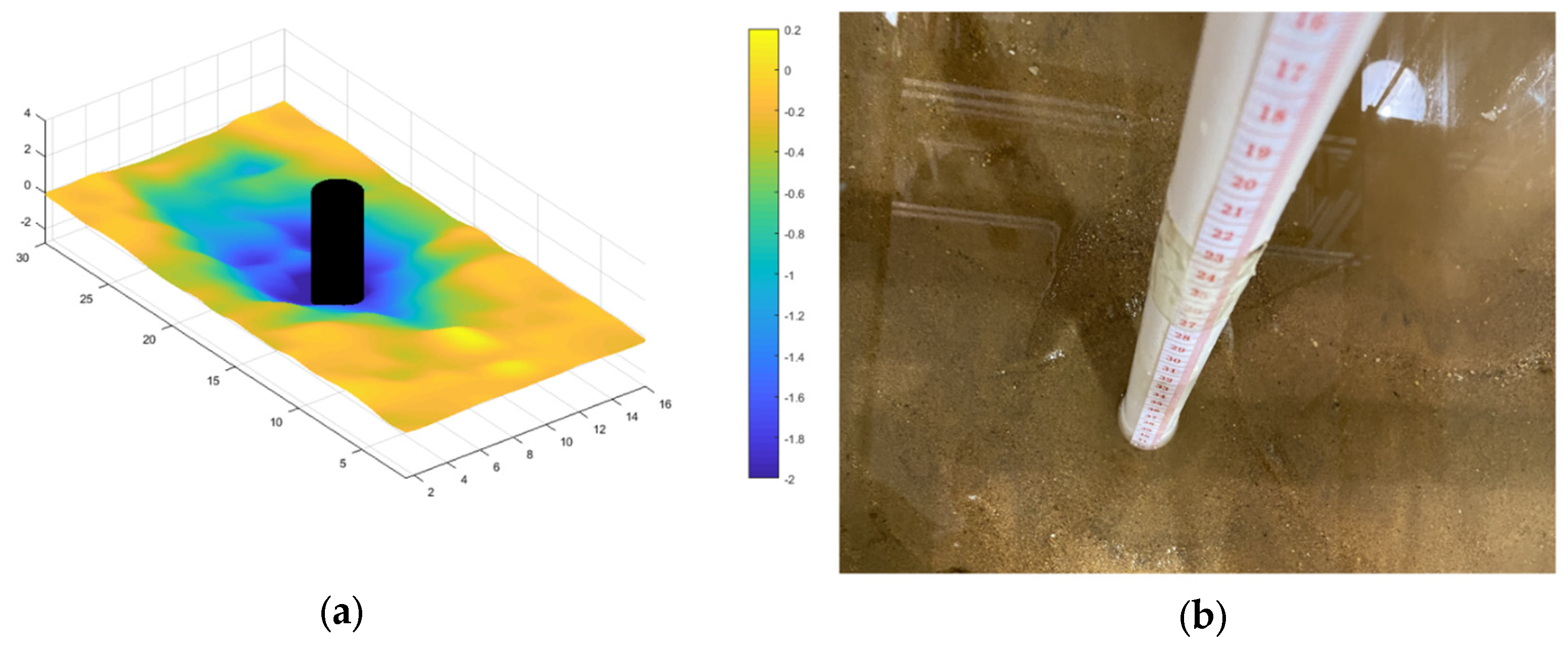
Based on the elevation obtained, a three-dimensional topographic map of the scour hole around the bridge pier was drawn, as shown in
Figure 5,
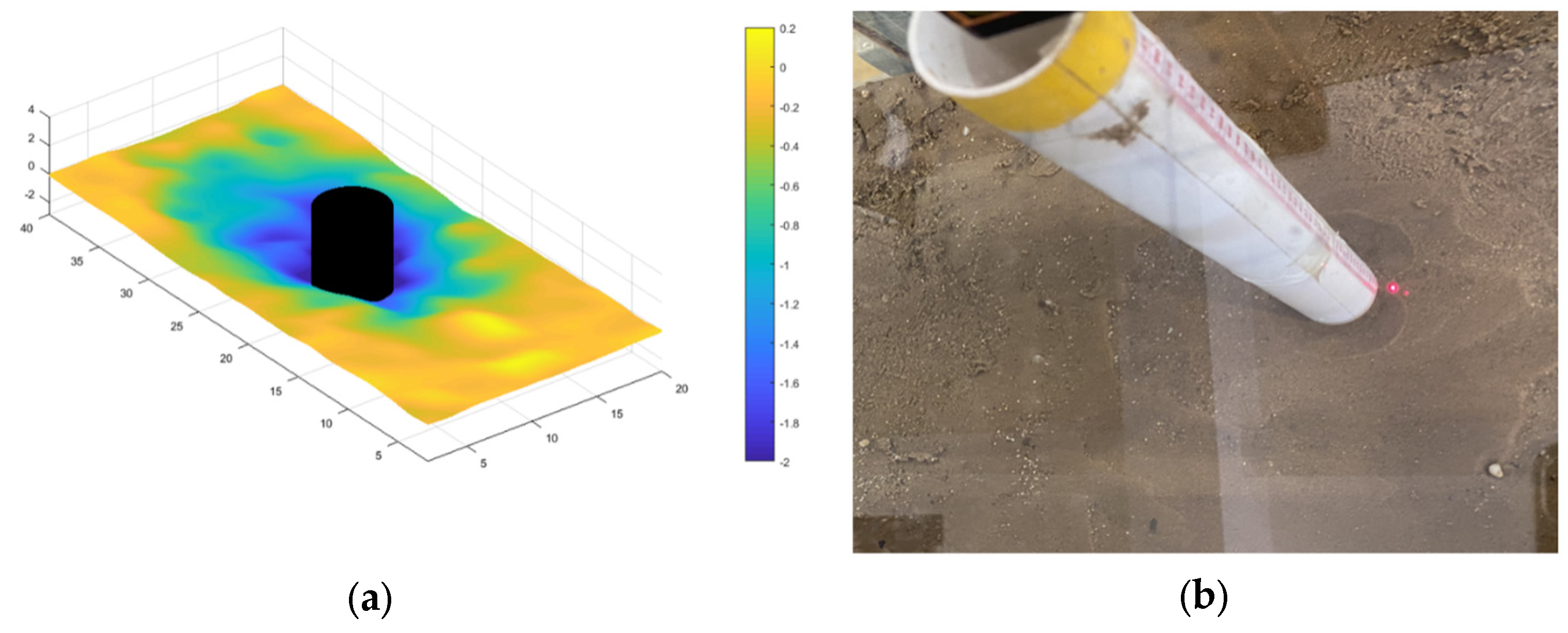
Figure 6,
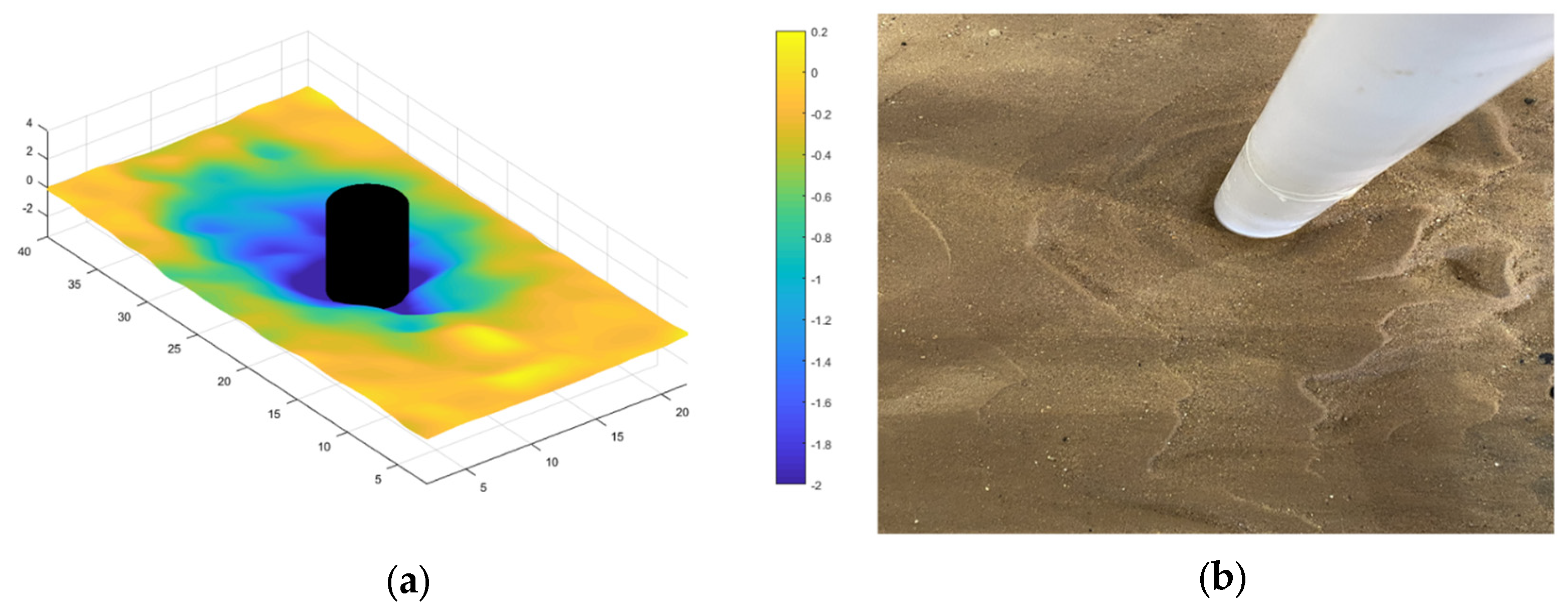
Figure 7 and
Figure 8.
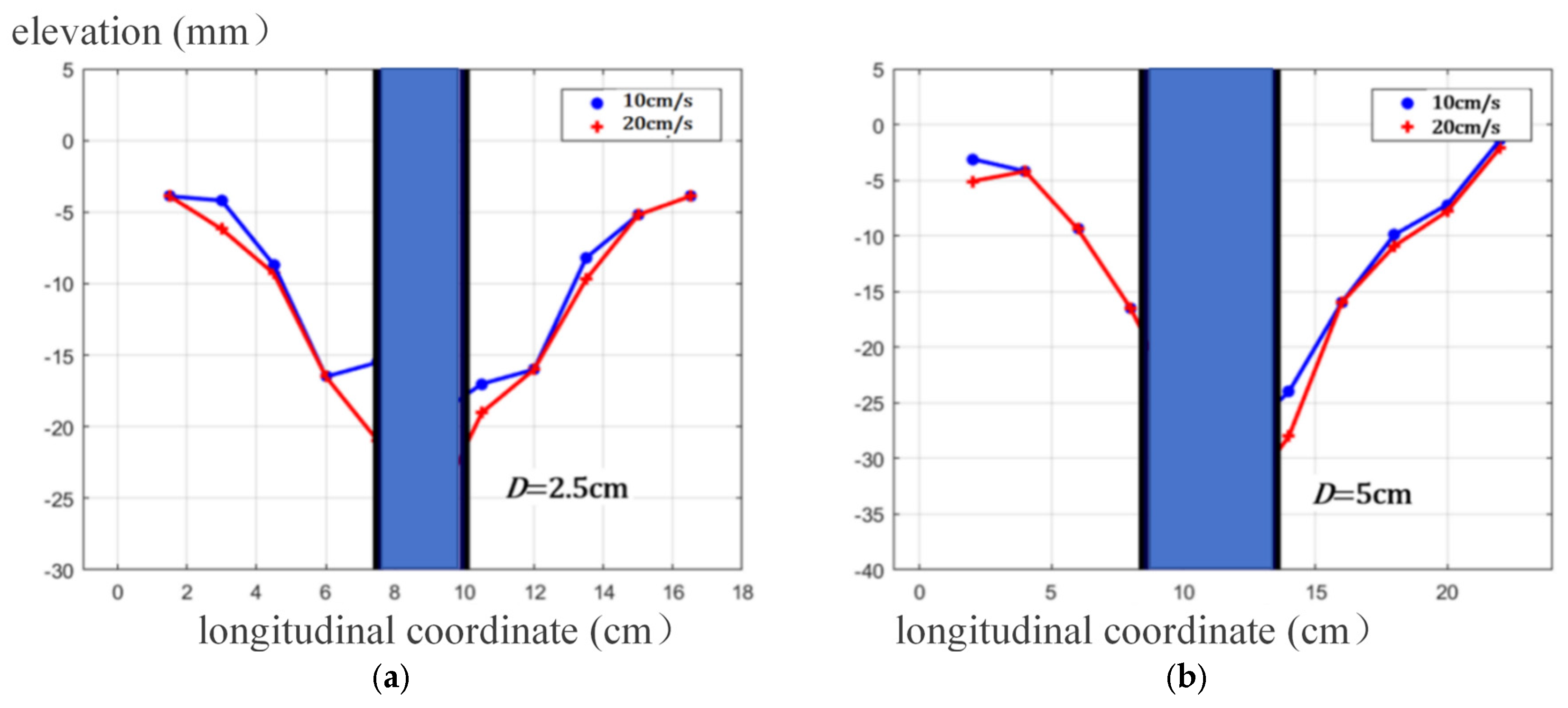
The cross-sectional and longitudinal profiles of the scour hole were drawn, as shown in
Figure 9 and
Figure 10, where the blue column is a simulated bridge pier.
From the scour topography, the left and right slopes on the cross section are basically the same. The slope of the upstream face is short and steep, while that of the stream face is long and gentle, with the maximum depth located at the front edge of the pier. Under given flow and sediment conditions, the profile slope is approximately constant. The cross-sectional slope varies from 0.31 to 0.48, corresponding to a slope angle of between 17.2° and 25.7°. The slope angle of the upstream face varies from 23° to 28.1°, with a slope of between 0.42 and 0.53. The slope angle of the stream face varies from 14.3° to 17.1°, with a slope of between 0.25 and 0.31.
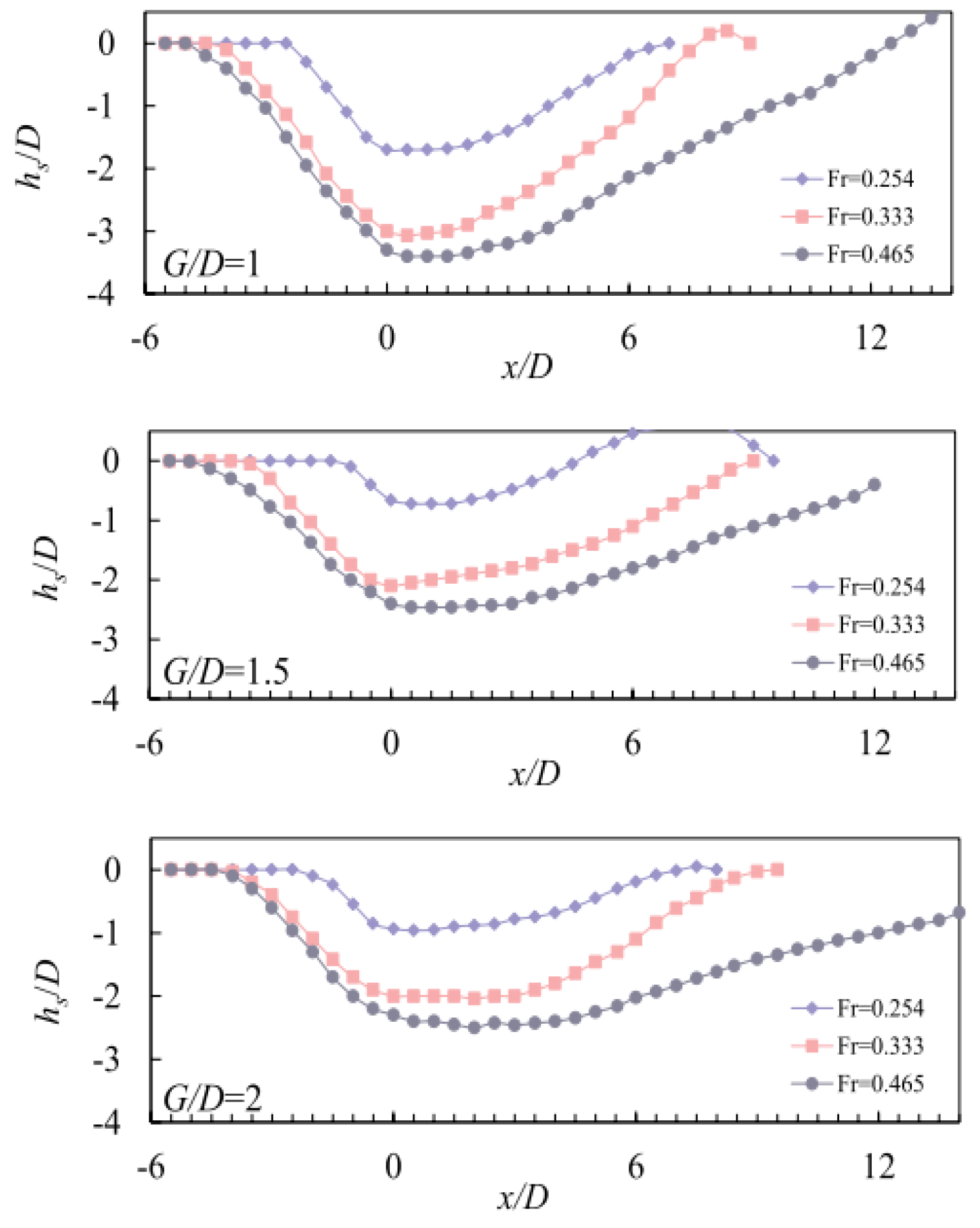
Yilin Yang [
9] observed a phenomenon similar to that in this study during his experiment, and the longitudinal profile of the local scour pit on the pier obtained in his experiment is shown in
Figure 11.
As shown in
Figure 11, the slope of upstream face ranges from 0.46 to 0.9, with a slope angle of 24.7° to 42.0°. The slope of the back surface is approximately 0.2 to 0.29, with a slope angle ranging from 11.3° to 16.4°. With the increase in Fr, the slope of the upstream face changes little, while the slope of the stream face changes greatly.
According to
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11, combined with the observation results from other researchers [
17,
18,
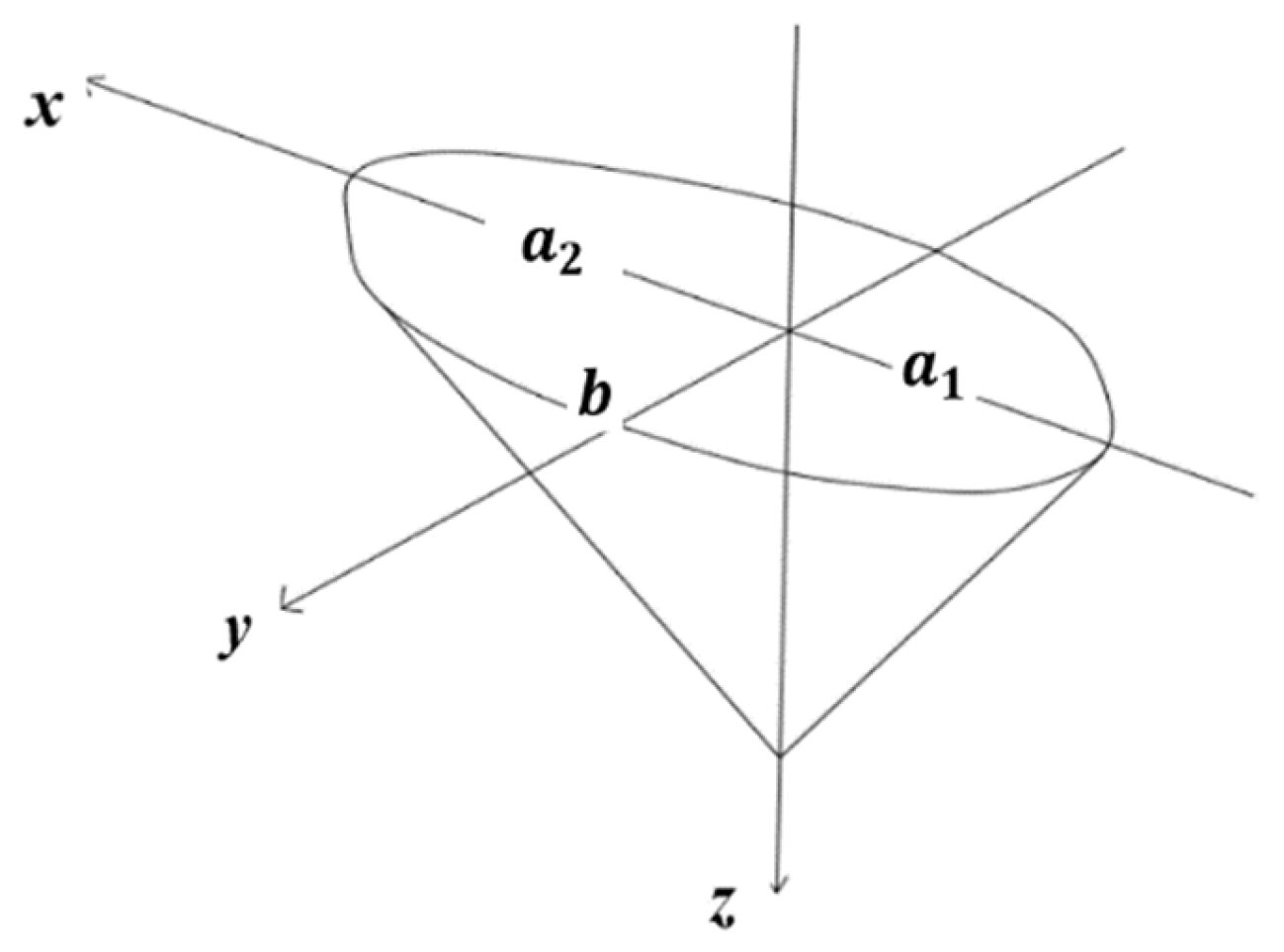
19], it can be summarized that the local scour hole around the pier is composed of two semi-elliptical cones, as shown in
Figure 12. The semi-major axes of the two semi-elliptical cones are
, and the height is
. The length
, and width
= 2
b.
The cone equation for an ellipse is as follows:
where
a is the length of the semi-major axis, and
b is the length of the semi-minor axis. The volume of an elliptical cone can be calculated via integration according to the following formula:
Hence, the volume of the scour hole composed of two semi-elliptical cones is as follows:
The projected area of the scour hole is as follows:
Based on the observation results, the volume of the scour hole can be calculated with Equation (3) using the length
L, width 2
b, and depth
. The measured volume
and calculated
of the local scour hole are listed in
Table 1. It can be seen that the difference between the theoretical calculation of the scour hole volume and the measured value is not significant, indicating that this assumption is reasonable.
Based on the data presented in
Table 2, it is evident that the volume of the local scour pit derived from theoretical calculations
does not significantly differ from the measured volume
, thereby validating this assumption.
Das [
18] measured the length, width, and depth of the scour hole based on local scour experiments and calculated the scour volume
. Based on the double semi-ellipsoidal cone assumption above, the local scour hole volume is also calculated using Das’s experimental data. The calculated volume
is compared with measured ones in
Table 2. The results show that the difference is very small, indicating that this assumption is consistent with reality.
For cylindrical piers, the volume of the scour hole calculated by Equation (3) in this research is in good agreement with the value measured by Das [
18], with a relative error of less than 1%. This means that the double semi-elliptical cone assumption is consistent with the actual condition of cylindrical piers. The relative errors of the three forms of square columns, triangular columns, and flat plates are between 6.84% and 13.65%, which are within a reasonable range. The differences between the scour pit volumes of triangular columns and cylindrical columns and theoretical calculations are the largest.
To summarize, the scour hole around the bridge pier exhibits the following characteristics: local scour hole can be approximated as a combination of two semi-elliptical cones, with a steep slope on the upstream face and a relatively gentle slope on the back face. Under given flow and sediment conditions, the slope of the scour hole profile is approximately constant. The cross-sectional slope angle is between 17.2° and 25.7°, the upstream slope angle is between 23° and 42.0°, and the stream slope angle is between 11.3° and 17.1°.
3.2. Flow Scour Experiments
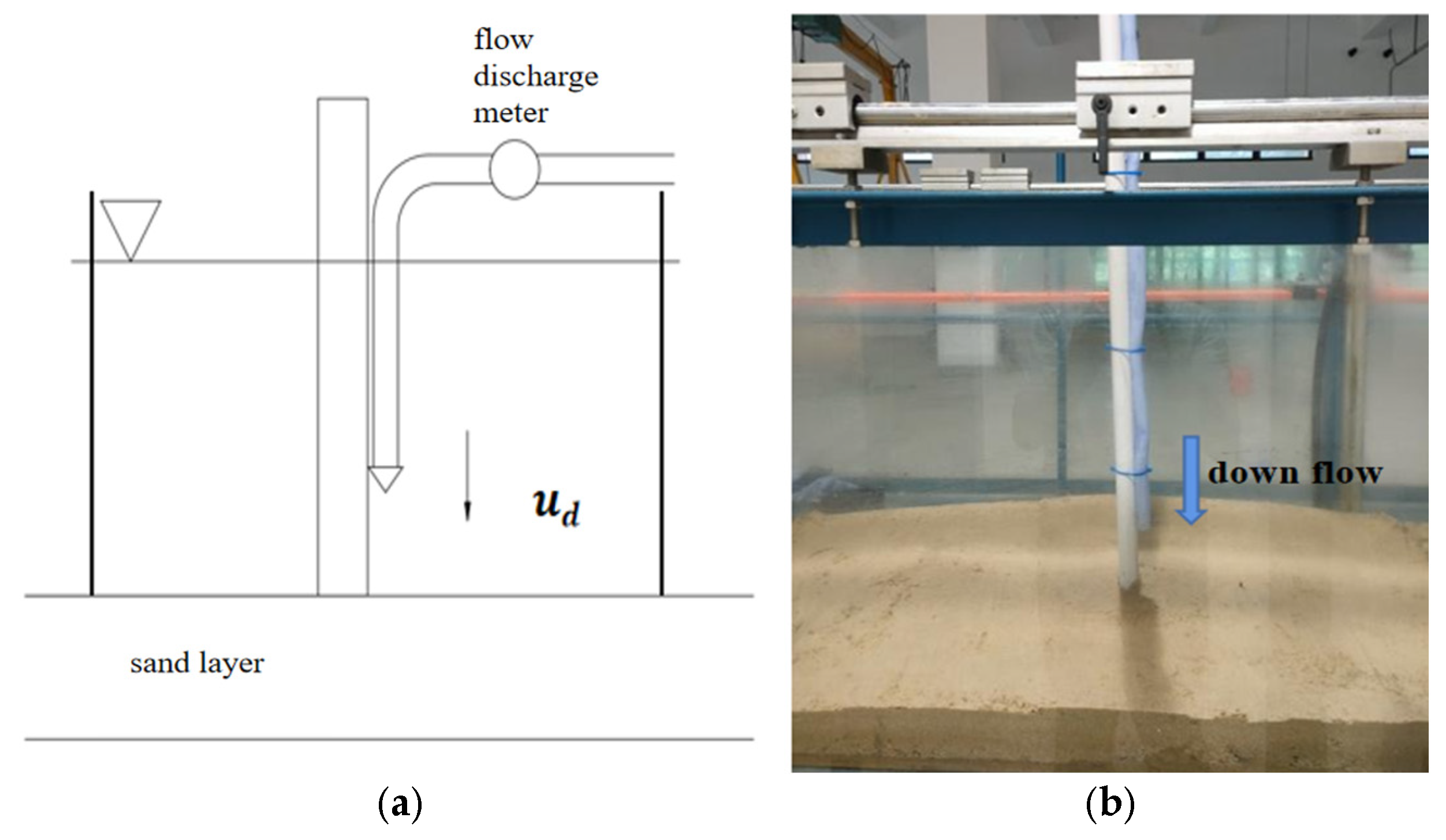
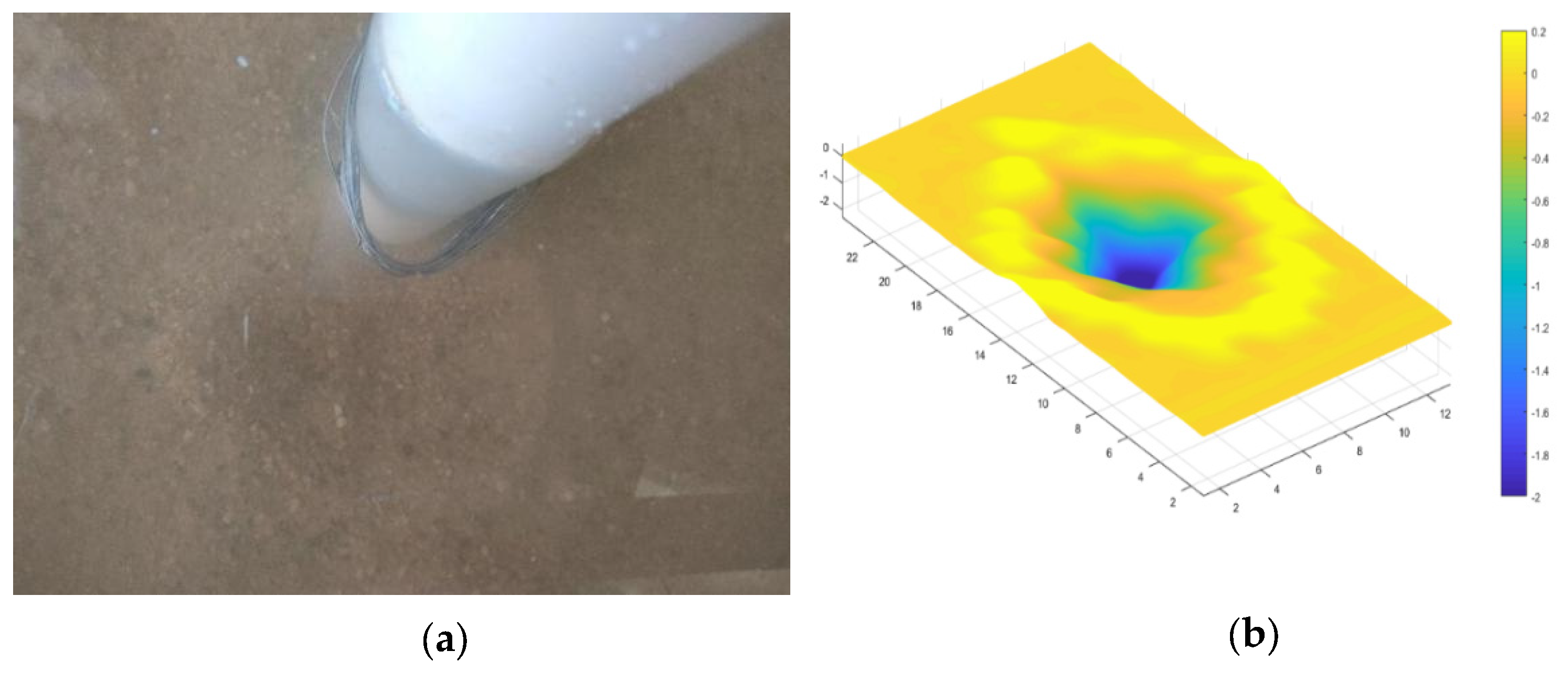
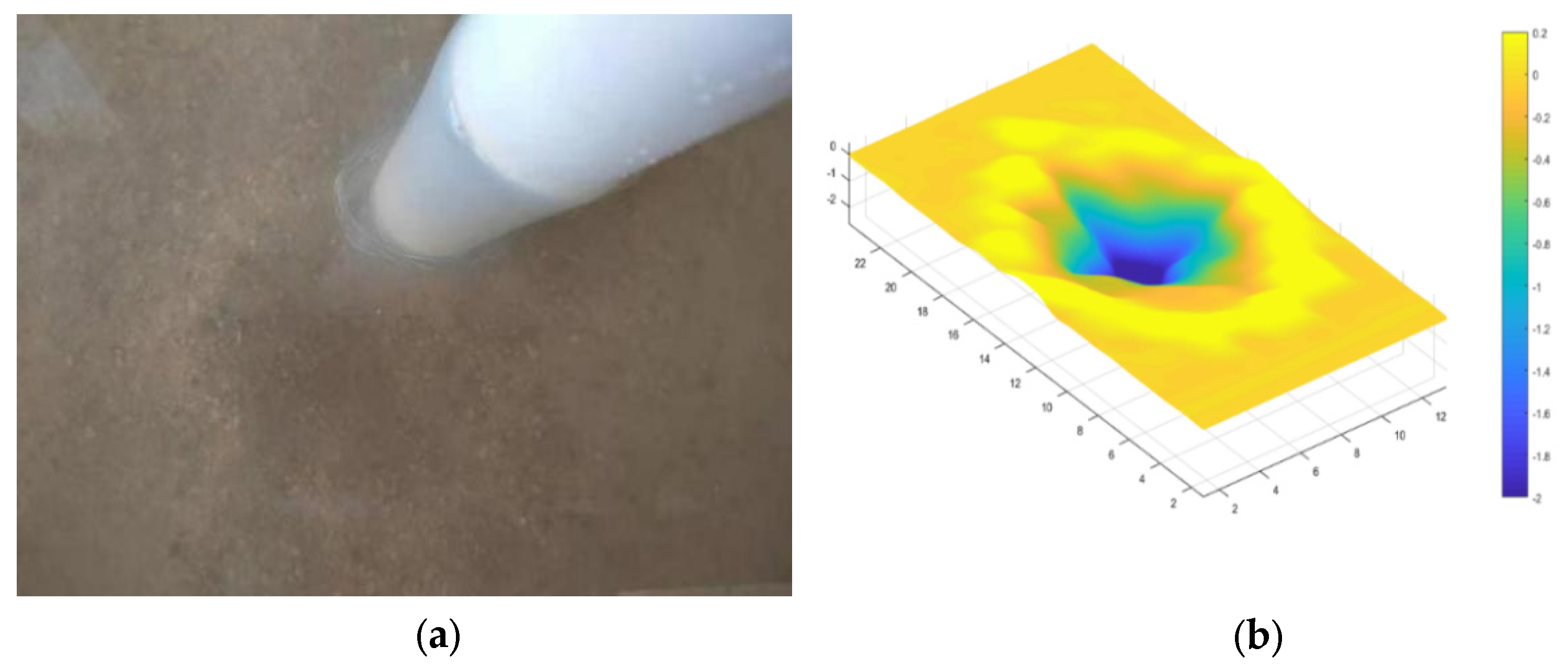
To analyze the contribution of flow to local scour, flow scouring experiments were conducted at Zhejiang University. A cylindrical bridge pier was fixed in a sandy area with a nozzle on the pier side to simulate the flow, which can avoid the scouring effect of longitudinal flow and horseshoe vortex. The range of the flow is equal to the width of the bridge pier, so the inner diameter of the water pipe ought to be the same as the pier diameter. According to the experimental observations and numerical simulation results, the maximum flow velocity in front of the pier is slightly higher than 1/4 of the approaching flow velocity. Therefore, the average pipe flow velocity is taken as 1/4 of the experimental approaching flow velocity. A 2 m long and 10 cm thick sediment was placed at the bottom of the water tank. At both ends of the sand laying section, glass plates with a height of 30 cm are used to maintain a constant water depth of 20 cm. The layout is shown in
Figure 13, where
Figure 13a represents the experimental design, and
Figure 13b represents the actual experiment.
After the water storage is completed, we adjust the flow discharge to ensure that the flow velocity in the pipeline is 2.5 cm s
−1 and 5.0 cm s
−1 in order to simulate the scour conditions in the above experiments, where the inflow velocity is 10 cm/s and 20 cm/s. According to the experiment and simulation results, the maximum velocity of the flow is approximately 1/4 times the approaching velocity and occurs at a depth of 1/3H. The pipe orifice is placed at a distance of 6.7 cm from the bottom. After the experiment, a topographic map was drawn based on the measured data, as shown in
Figure 14,
Figure 15,
Figure 16 and
Figure 17.
From
Figure 14,
Figure 15,
Figure 16 and
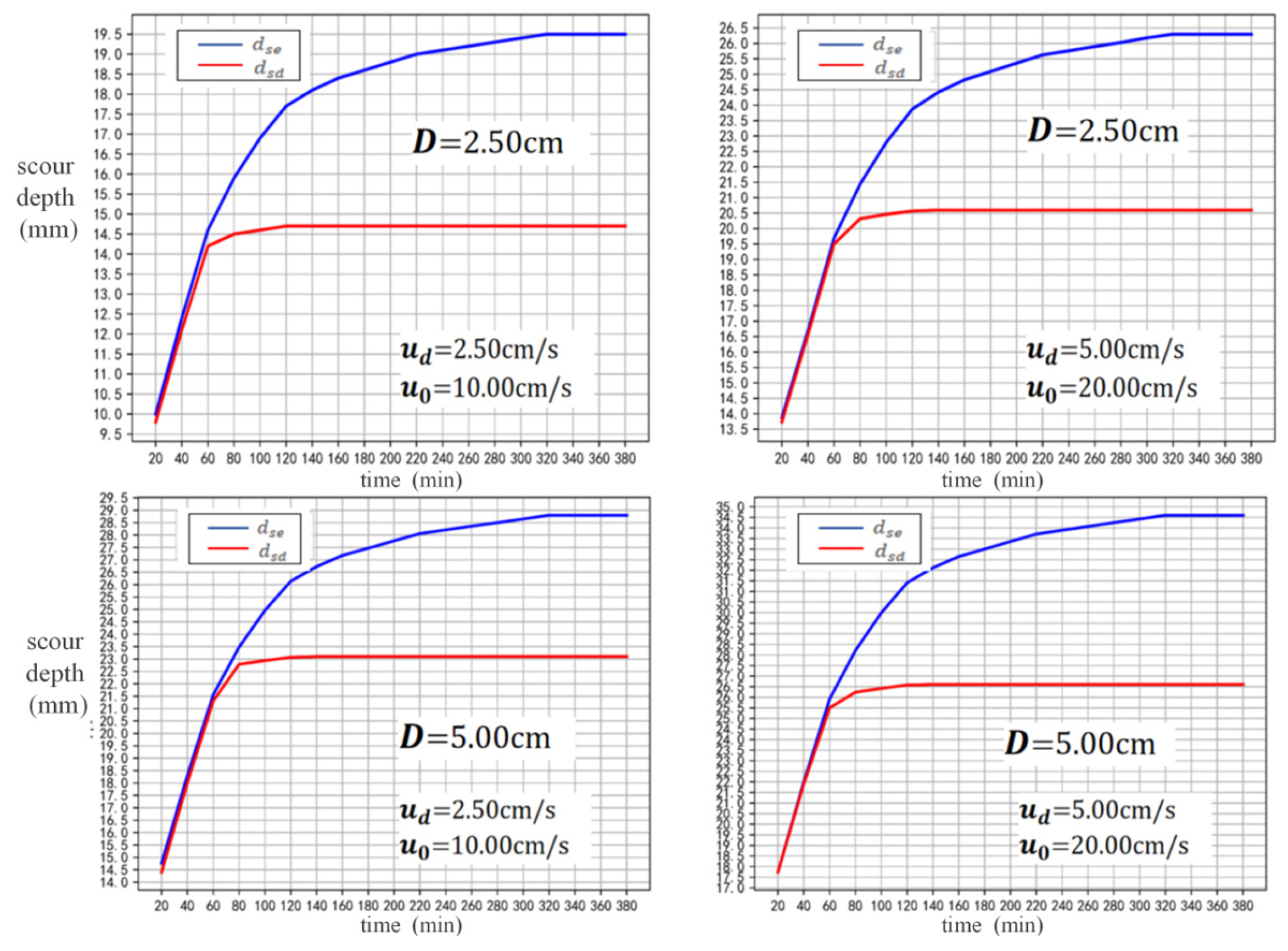
Figure 17, it can be seen that the scour caused by the flow is an inverted conical shape, and most of the sediment that is moved out of scour hole accumulates around it. Longitudinal water flow and the horseshoe vortex will wash away the sediment carried up by the flow, so the scour hole behind the pier will elongate, leading the conical pit to become an elliptical cone. The time-varying curve showing the scour depth under three factors with the flow at different times is drawn in
Figure 18.
From
Figure 18, it can be seen that in the early stage of scouring, the local scouring depth caused by the flow increases rapidly, reaching equilibrium at about 80 min. During this period, the scouring depth change of the flow is basically consistent with the total scouring depth. The area and depth of the erosion pit after the equilibrium of the flow are smaller than the combined effect of multiple factors. The increase in local scour depth and area after 80 min is mainly caused by longitudinal water flow and the horseshoe vortex. The scour depth caused by down-flow
and the total scour depth
are listed in
Table 3.
From
Table 3, it can be inferred that the lower limit of the scour depth dominated by the flow
is basically fixed, accounting for 75–80% of
. Considering that for the local scour depths obtained from the experiments, it was difficult to achieve strict equilibrium, the lower limit of scour dominated by flow is roughly determined to be 3/4 below the original bed surface.
3.3. Longitudinal Flow Scour Depth
The scour depth caused by the redistribution of flow velocity across the cross-section is theoretically analyzed.
Based on field observations and experimental results, when
, both the general and local scouring around the bridge pier will occur. According to studies [
20,
21,
22], when
, local scour around the bridge pier did not occur or was very weak; local scour only occurred after the bridge pier caused a redistribution of flow velocity when
.
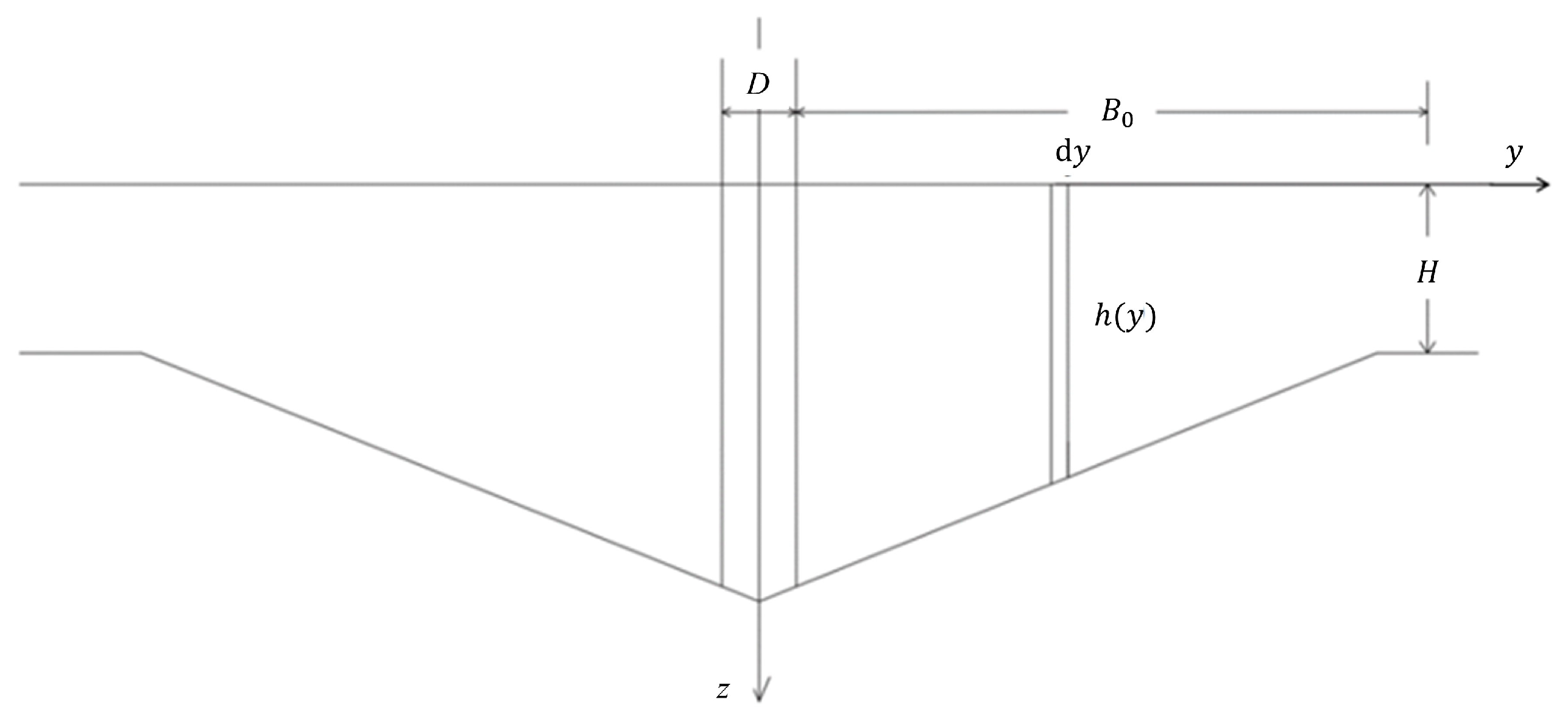
Perpendicular to flow direction, the longitudinal flow velocity gradually decreases from the pier edge. When the flow velocity decreases to the critical velocity, local scour would not occur on the bed surface. Therefore, the flow velocity at the lateral edge of the scour hole satisfies the sediment critical condition; that is, . At the start of scouring, the lateral distribution of dimensionless velocity across the bridge pier section satisfies the following equation.
Assuming the width of the scour pit is
, the following equation is satisfied:
Substitute the initial scour condition
into Equation (5), we obtain the following:
We solve Equation (6) to obtain the following:
Equation (7) indicates that the relative width of the scour hole is a function of the ratio of the critical velocity to the approaching velocity .
According to Equation (7), when = 1, the approaching velocity is equal to the critical velocity. The velocity within the flow width affected by the bridge pier is greater than the critical velocity, and the width of the scour hole is equal to the lateral range affected by the bridge pier, so . When , the maximum velocity in the cross-section is lower than the critical velocity. The local scour caused by the increase in longitudinal velocity is zero, and at this time, .
When
, the sediment on the bed surface is already in a critical motion state. At this time, the longitudinal velocity within the flow width affected by the bridge pier is higher than the critical velocity, causing scour. The width of the scour hole is equal to this flow width. The cross-section where the center of the bridge pier is located after equilibrium is shown in
Figure 19. The flow direction is perpendicular to the paper surface. After the scour reaches equilibrium, the sediment on the bed surface is also in a critical motion state.
Let
H be the initial water depth and
h be the water depth at each point after the scour reaches equilibrium. Based on the constant flow rate before and after the scour, we obtain the following:
In the above formula,
is the critical velocity at a water depth of h:
Substitute Equation (9) into Equation (8) to obtain the following:
According to the research on the morphology inside the scour hole in the above text, it is understood that on the cross-section where the center of the bridge pier is located, the slope is a fixed-value k; that is, the water depth and the lateral coordinate are in a linear relationship:
Substitute Equation (11) into Equation (10) to obtain the following:
Solve Equation (12) to obtain the lower limit of the local scour depth,, considering only the sediment critical motion condition.
We compare the maximum scour depth caused by the increase in longitudinal velocity with the measured total scour depth of the bridge piers in Hangzhou Bay (as well as Jiashao Bridge and Jintang Bridge), as shown in
Figure 20. The abscissa in the figure is the measured value of the local scour depth, and the ordinate is the “proportion”, which represents the ratio of the calculated value of the scour depth caused by the increase in longitudinal velocity to the measured total scour depth.
It can be seen from
Figure 20 that for about 80% of the data points, the ratio of the scour depth of longitudinal velocity to the total scour depth is between 0.15 and 0.30. Therefore, it can be seen that the lower limit position of the local scour depth caused solely by the redistribution of longitudinal velocity is within 0.3
below the original bed surface.
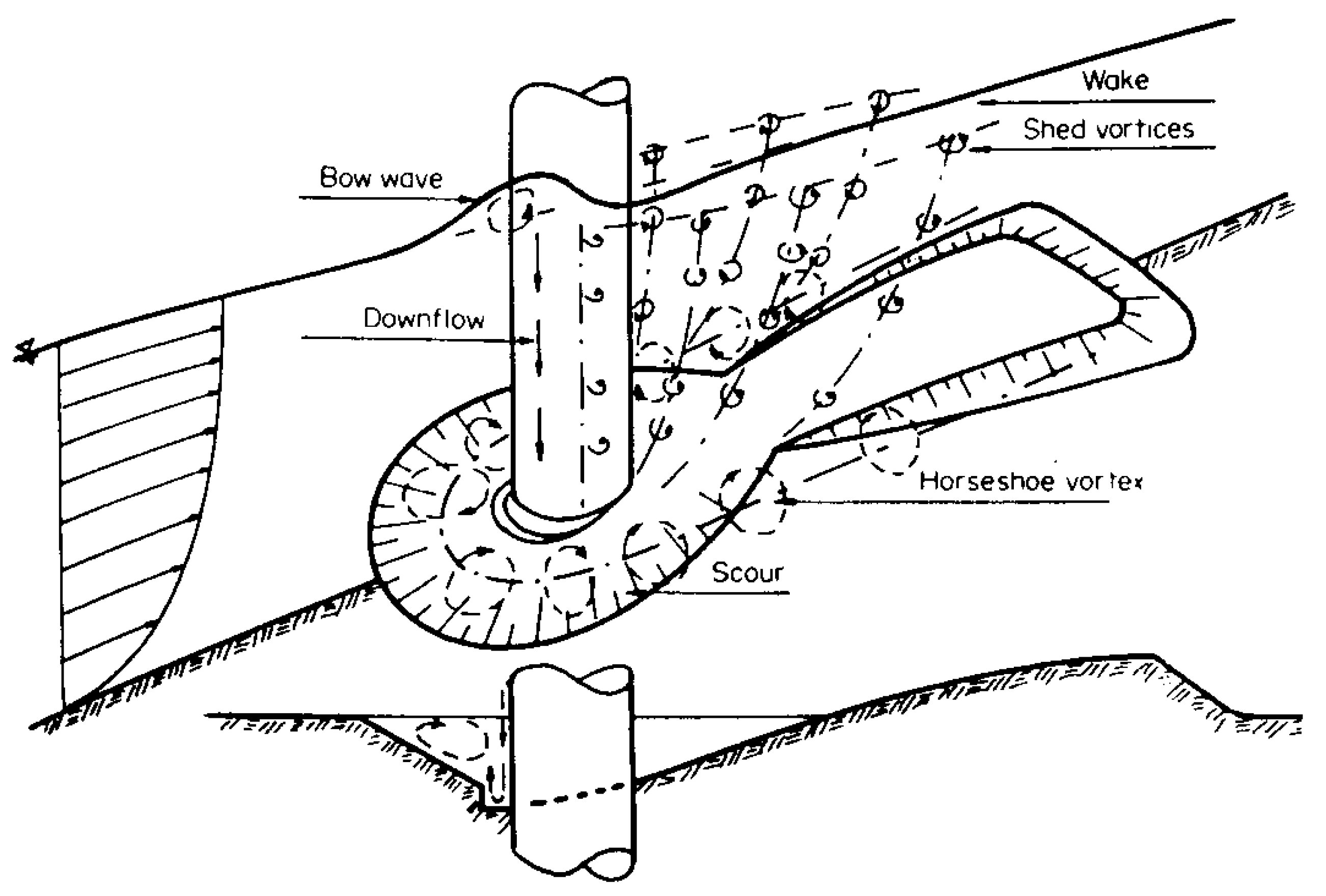
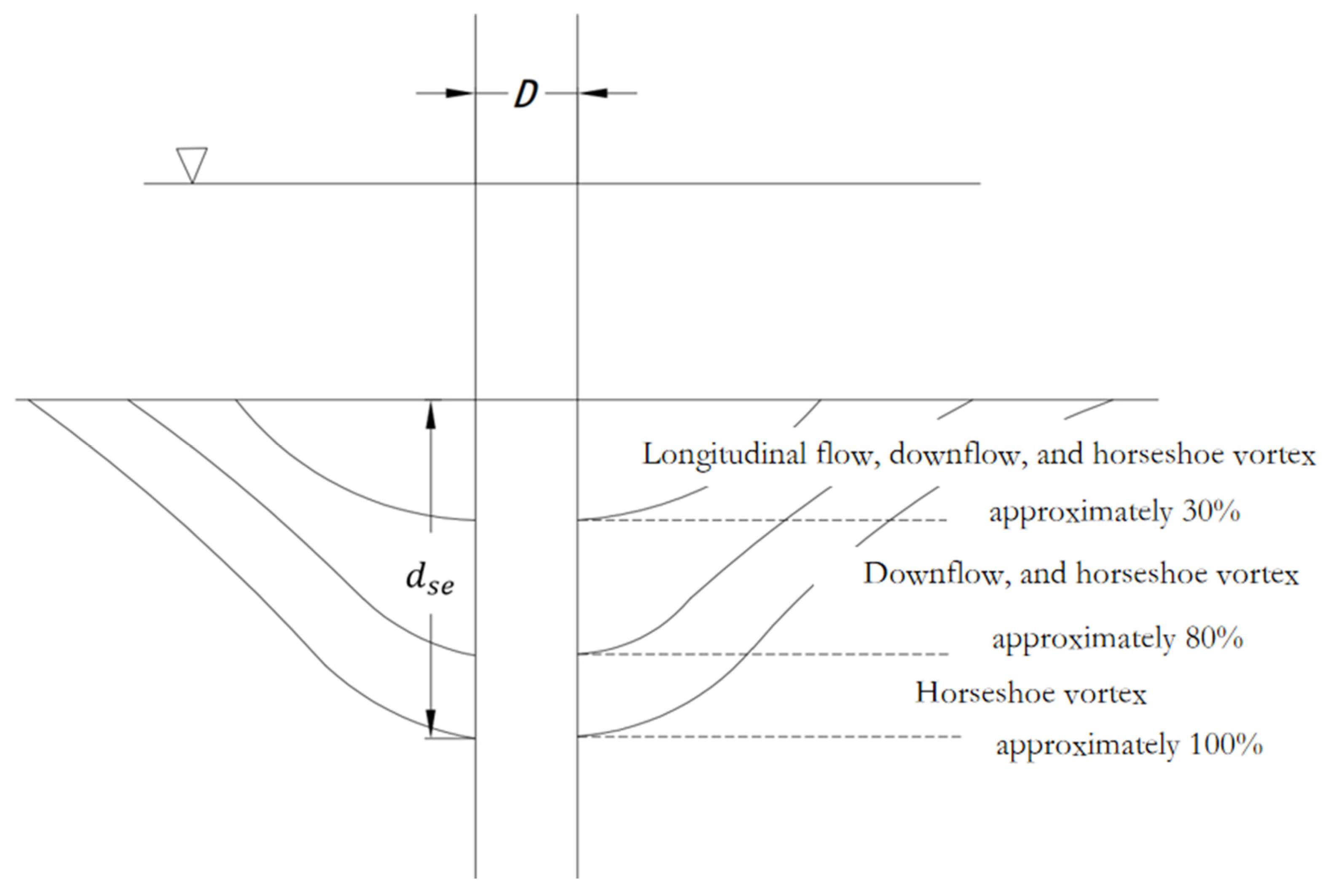
3.4. Local Scour Mechanism Analysis
From the comparative experiments results of the ward flow in front of the pier and the local erosion of longitudinal water flow, it can be seen that the upstream area of the pier is mainly eroded by the direct impact of the ward flow in front of the pier, and the scouring effect is strong. Generally speaking, the deepest scouring position appears here. The main influencing factor on both sides of the pier column is longitudinal water flow, which determines the width of the scour hole. The longitudinal flow velocity at the edge of this area is equal to the starting flow velocity. The main event behind the pier is the horseshoe vortex sucking up and transporting the washed-out sediment stream. The strength of the horseshoe vortex gradually weakens along the direction of the water flow. When its strength is insufficient to maintain sediment suspension or movement, sediment may accumulate on the riverbed, forming a sedimentation area behind the scour hole. In this way, the local scour hole can be divided into three areas, marked as Zone I, Zone II, and Zone III, respectively, as shown in
Figure 21.
Zone I is mainly affected by flow, Zone II is mainly affected by longitudinal water flow, and Zone III is mainly affected by horseshoe vortex. The increase in vertical water flow determines the width of the scour hole, while the decrease in flow intensity affects the scour depth, and the horseshoe vortex is closely related to the length of the scour hole.
According to the previous experimental results, the lower limit of erosion caused by the dominant ward flow is approximately below the original bed surface (0.75~0.8); while according to the starting flow velocity formula, the lower limit of erosion caused by the increase in longitudinal flow velocity is approximately 0.3 below the original bed surface, which is included in the previous flushing depth. According to the different dominant factors, the local erosion process of the bridge pier can be divided into three stages, as shown in
Figure 22.
The first stage is the initial stage, during which the longitudinal flow increases, and the flow in front of the pier and the horseshoe vortex around the pier work together. The flow velocity increases and exceeds the starting flow velocity, causing the sediment around the pier to start. At the same time, the flow in front of the pier has a strong scouring effect on the bed surface, and the horseshoe vortex around the pier can also cause scouring. As the depth of the scour hole increases, the water depth around the bridge pier increases, and the longitudinal flow velocity gradually decreases while the starting flow velocity increases until they are equal. After that, the longitudinal water flow no longer has an effect on local scour, and the scour depth is the lower-limit depth of the longitudinal water flow effect, generally within 0.3.
The second stage is the erosion development stage, during which the sediment initiation caused by longitudinal water flow tends to be weak, and local erosion is mainly caused by flow and horseshoe vortex. Among them, the flow plays a dominant role in the continuous strong scouring of the bed surface, causing sediment to be lifted up from the bed surface and transported stream by the water flow. According to the experimental results, the lower limit of the local scour depth caused by the dominant role of flow is approximately below the original bed surface, indicating that flow plays a major role in the three important factors causing local scour. As the depth of erosion increases, the intensity of flow decreases, making it more difficult for sediment to be washed away. When the scouring pit develops below the original bed surface, a balance is reached between the flow scouring effect and the anti-scouring ability of the sediment.
In the third stage, after the scouring of the flow reaches equilibrium, the scouring effect of the longitudinal water flow and the flow is already very weak, and at this time, the scouring effect is mainly caused by the horseshoe vortex. The horseshoe vortex continuously rolls up the sediment in the scouring pit and transports its stream, deepening the scouring pit and expanding the scouring range. This stage has a weaker erosion intensity than the second stage, which is dominated by the flow, but the duration is longer, often lasting several days in experiments and several years or even longer in actual environments.